上海2021年九年级数学·一模考试(金山)

合集下载

2021年上海市初三数学一模25题汇编

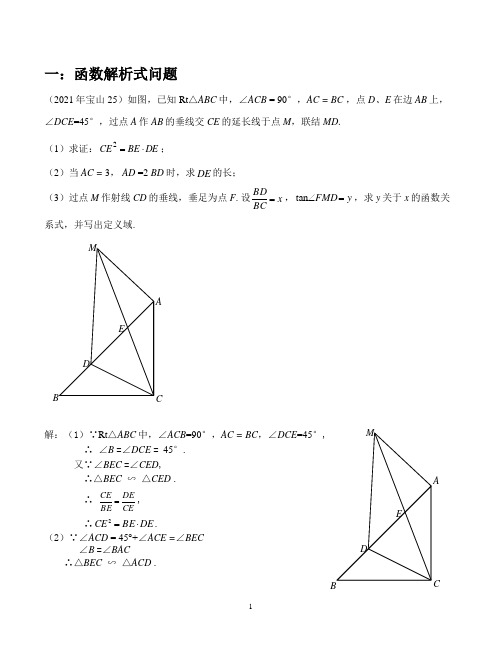
一：函数解析式问题（2021年宝山25）如图，已知Rt △ABC 中，∠ACB = 90°，AC = BC ，点D 、E 在边AB 上，∠DCE =45°，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD. （1）求证：DE BE CE ⋅=2；（2）当AC = 3， AD =2 BD 时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F . 设x BCBD=，y FMD =∠tan ，求y 关于x 的函数关系式，并写出定义域.解：（1）∵Rt △ABC 中，∠ACB =90°，AC = BC ，∠DCE =45∴ ∠B =∠DCE = 45°. 又∵∠BEC =∠CED ,∴△BEC ∽ △CED . ∴ CEDE BECE =,∴DE BE CE ⋅=2.（2）∵∠ACD = 45°+∠ACE =∠BEC ∠B =∠BAC∴△BEC ∽ △ACD .∴ACBE ADBC =.又AC = BC =3 ，∠ACB =90°， ∴23=AB . ∵ AD =2 BD ，∴2=BD ,22=AD . 可得429=BE ，∴425=DE（3）延长BC 交MA 延长线于点G.∵MA ⊥AB ，∠B = 45°，可得∠G =∠B= ∠DCE.又∵∠MCB =∠B +∠BCD ，∠MCB =∠G +∠GMC ， ∴∠GMC =∠BCD.∴△BCD ∽△GMC .∴CMCDCG BD =，∴CM CG CD BD =. ∵∠B =∠DCM = 45°，∴△BCD ∽△CMD .∵ MF ⊥FC ，∴CF CM 2=. ∴x CFCD CM CD BC BD ===2， ∴x CFCD2=. ∴tan ∠FMD =x CFFD21-=，）（22021<<-=x x y .（2021年静安25）已知∠MAN 是锐角，点B 、C 在边AM 上，点D 在边AN 上，∠EBD =∠MAN ，且CE //BD ，sin ∠MAN=35，AB =5，AC =9．（1）如图1，当CE 与边AN 相交于点F 时，求证：DF ·CE=BC ·BE ；（2）当点E 在边AN 上时，求AD 的长；（3）当点E 在∠MAN 外部时，设AD =x ，△BCE 的面积为y ，求y 与x 之间的函数解析式，并写出定义域．解：（1）∵ CE //BD ，∴ ∠CEB =∠DBE ，∠DBA =∠BCE ．∵∠A=∠DBE ，∴ ∠A =∠BEC ．∴ △ABD ∽△ECB ． ∴AD EBAB EC ＝． ∵AD DFAB BC=， ∴EB DFEC BC =，∴ DF ·CE=BC ·BE ．（2）过点B 作BH ⊥AN ，垂足为H ． ∵ CE//BD ，∴∠CEB ＝∠EB D ＝∠A ，又∵∠BCE ＝∠ECA ，∴△CEB ∽△CAE . ∴CE CACB CE =，∴2CE =CB CA ⋅，∵AB =5，AC =9，∴BC =4，∴24936CE ==⨯，∴CE =6. ∵BD ABCE AC=，∴561093AB CE BD ==AC ⋅⨯=. （第25题图）（备用图）BC （图1）FABDC E NM在Rt △ABH 中，3sin 535BH AB A =⋅=⨯=，∴ AH4=． DH=．AD=43±. （3）过点B 作BH ⊥AN ，垂足为H ．BH =4，AH =3，DH =4x -．2222224)3825BD =DH +BH x x x =-+=-+（．∵△ECB ∽△ABD ，∴22EBC ADB S BC S BD△△＝． ∵322ABD S AD BH x =⋅△１＝，∴21638252y x x x =-+， ∴224825x y x x =-+．定义域为44x <<．二：相似三角形问题（2021年闵行25）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF ⊥DE ，交BC 的延长线于点F ，联结EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：△ADE ∽△CDF ，并求EFD ∠的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结BG ．当△BGE 与△DEH 相似时，求x 的值．解：（1）在矩形ABCD 中，∠BAD =∠ADC =∠BCD = 90°，AB = CD ．又∵∠BCD +∠DCF = 180°，∴∠DCF = 90°，∴∠DCF =∠BAD ． ∵DF ⊥DE ，∴∠EDF = 90°，（第25题（备用图）∴∠EDF =∠ADC = 90°，∴EDF EDH ADC EDH ∠-∠=∠-∠． ∴∠ADE =∠CDF ．∴△ADE ∽△CDF ．∴AD DECD DF=．又∵AD = 1，CD = AB = 2，∴12DE DF =．在Rt △DEF 中，∠EDF = 90°，∴1tan 2DE EFD DF ∠==．（2）∵△ADE ∽△CDF ，∴12AE AD CF CD ==． ∵AE = x ，∴2CF x =．在矩形ABCD 中，AB // CD ，AD = BC ．由AB // CD ，得CH CFBE BF=．又∵21BF x =+，2CH y =-，2BE x =-，∴22221y xx x -=-+． ∴ y 关于x 的函数解析式为22221x y x +=+．其定义域为02x <<．（3）延长BG ，交射线CD 于点P ．由AB // CD ，得∠BEG =∠DHE ．∴当△EDH ∽△BEG 时，可以有以下两种情况：① 当∠DEH =∠BGE 时，ED // BG ，又∵AB // CD ，∴四边形BEDP 是平行四边形．∴2EB DP x ==-，∴PC x =．∵DH y =，∴2222(2)222121x x x HC y x x +-=-=-=++． ∵AB // CD ，∴HC HG AE GE =，HG PG GE GB =，PG PC GB AB =．∴HC PC AE AB=．即2(2)212x x x x x -+= 02x <<（），解得x =∴x =． ② 当∠DEH =∠GBE 时，∵EB // DH ，∴∠DEH =∠GBE =∠BPC ．∴tan 2BCBPC PC∠==． ∴14HC PC AE AB ==．即2(2)1214x x x x -+= 02x <<（），解得32x =．∴32x =．综上所述，x =或32x =．（2021年杨浦25）如图，已知在Rt △ABC 中，∠ACB =90°，AC =BC =4，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，∠EDB =∠ADC ，过点E 作EF ⊥AD ，垂足为点G ，交射线AC 于点F .（1）如果点D 为边BC 的中点，求∠DAB 的正切值；（2）当点F 在边AC 上时，设CD =x ，CF =y ，求y 关于x 的函数解析式及定义域；（3）联结DF ，如果△CDF 与△AGE 相似，求线段CD 的长.解：（1）过D 作DH AB ⊥，垂足为点H.在Rt △ABC 中，∵∠ACB =90°，AC =BC =4，∴AB ==在Rt △BDH 中，∵BD =2，∴BH DH =在Rt △ADH中，AH =1tan 3DH DAB AH ∠==. （2）过A 作AH //DE 交BC 的延长线于H ，垂足为点M.∵EF ⊥AD ，∴∠AFG+∠CAD =90°. ∵∠ACB =90°，∴∠ADC +∠CAD=90°. ∴∠AFG=∠ADC . 又∵∠EDB =∠ADC ，∴∠AFG=∠EDB. ∵AC =BC =4，∴∠BAC=∠B=45°.∴△AEF ∽△BED .备用图AC第25题图 ABCEDG F∴AE AFBE BD=. ∵AH //DE ，∴AE DHBE BD=. ∴AF =DH .∵AH //DE ，∴∠H =∠EDB. 又∵∠EDB =∠ADC ，∴∠H=∠ADC . ∴AD =AH .∵AC ⊥DH ，∴HC =CD . ∵CD=x ，∴HC =x . ∴AF =DH =2x .42y x =-（02x <≤）.（3）i ）当点F 在边AC 上时，∵∠FCD =∠AGE =90°，∴当△CDF 与△AGE 相似时，∠DFC =∠GAE 或∠FDC =∠GAE . 过D 作DH AB ⊥，垂足为点H.在Rt △ADH中，)4tan 4x DH x GAE AH x --∠===+. ①当∠DFC =∠GAE 时，∴tan tan DFC GAE ∠=∠.∴44x xy x-=+.∴8x =-（1分） ②当∠FDC =∠GAE 时，∴tan tan FDC GAE ∠=∠.∴44y xx x-=+.∴4x = . ii ）当点F 在边AC的延长线上时，同理可得CD . 综上所述：如果△CDF 与△AGE 相似，线段CD的长为84-、（2021年松江25）如图，已知在等腰△ABC 中，AB =AC=，tan ∠ABC =2，BF ⊥AC ，垂足为F ，点D 是边AB 上一点（不与A ，B 重合）. （1）求边BC 的长；（2）如图2，延长DF 交BC 的延长线于点G ，如果CG=4，求线段AD 的长；（3）过点D 作DE ⊥BC ，垂足为E ，DE 交BF 于点Q ，联结DF ，如果△DQF 和△ABC 相似，求线段BD 的长.解：（1）过点A 作AH ⊥B C ，垂足为H ∵AB =AC ，∴BH=HC在Rt △ABH 中，tan ∠ABC ==2AHBH∴cos ∠ABC==5BH AB ，∵AB= ∴BH=5 ∴BC=10（2）过点A 作AM ∥BG 交GD 的延长线于点M ∴AM AF CG FC =，AM ADBG BD=在Rt △BFC 中，cos ∠ACB =cos ∠ACB=，BC=10 ∴FC=∴AF=CG=4，∴AM=6∴614=，∴AD=2D·BAFC（图1）DBA FC（图2）G BAF（备用图）H（图BA DFCM（图GDFCBA（3）∵BF ⊥AC ，DE ⊥BC ，∴∠BFC=∠DEB=90°，∴∠BQE=∠ACB ∵∠BQE=∠DQF ，∴∠DQF=∠ACB ∵△DQF 和△ABC 相似，∴DQ QF AC BC =或DQ FQBC AC=2DEBE = ∵tan ∠BQE=tan ∠ACB = tan ∠ABC =2，∴2BEQE=,设BE=x ，QE=2x ，则DE=4x ∴，BD=，DQ=3x ∵BF=2CF=QF= （ⅰ）当DQ QF AC BC =10=，解得x=85 ∴BD==5（ⅱ）当DQ FQ BC AC =时，则，310x ，解得x=2011 ∴BD==11综上所述，BD=5或BD=11三：等腰三角形问题（2021年崇明25）如图，Rt △ABC 中，90ACB ∠=︒，6AC =，8BC =．点D 为斜边AB 的中点，ED ⊥AB ，交边BC 于点E ．点P 为射线AC 上的动点，点Q 为边BC 上的动点，且运动过程中始终保持PD QD ⊥．（1）求证：△ADP ∽△EDQ ；（2）设AP x =，BQ y =．求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结PQ ，交线段ED 于点F ．当△PDF 为等腰三角形时，求线段AP 的长．解：（1）证明：∵ED ⊥AB ，PD ⊥QD ，∴∠ADP =∠EDQ=90°—∠PDEAD BCPEQ第25题图AD BCP EQ第25题备用图F（图3）BA DFCQ∵∠ACB= 90°，ED ⊥AB ，∴∠A =∠DEQ=90°—∠B∴△ADP ∽△EDQ（2）∵∠ACB= 90°，AC =6，BC =8，∴AB =10，tan B =34∵点D 为AB 的中点，∴AD = DB= 5 ∴DE =154，BE =254∵△ADP ∽△EDQ ，∴EQ DEAP AD =，即2515445x = ∴32544y x =-+定义域：0≤x ≤253（3）∵ED ⊥AB ，PD ⊥QD ，∴∠PDE =∠QDB=90°—∠EDQ ∵tan ∠QPD =34DQ DE PD AD ==，∴∠QPD=∠B ∴△ADP ∽△EDQ①当PD=PF 时，BD=BQ∴5y =，即325544x -+=，∴53x =②当FP=FD 时，QD=QB ，∴12BQ BE = ∴258y =，即32525448x -+=，∴256x = ③当DP=DF 时，DQ=DB=DC ，即点Q 在点C 处，∴点P 不在射线AC 上，舍去.综上所述，AP 的长为53或256（2021年虹口25）如图12，在△ABC 中，∠ABC =90°，AB =3，BC =4，过点A 作射线AM //BC ，点D 、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），联结BD 、BE 分别交边AC 于点F 、G ，∠DBE =∠C ．（1）当AD =1时，求FB 的长；（2）设AD =x ，FG =y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果△DBH 是等腰三角形，请直接写出AD 的长．∴BC FB=．∴．（2）∵∠ABC =90°，AB =3，BC =4，∴AC=5．∵∠BAD =90°，AB =3，AD x =，∴． ∵AD //BC ，∴4FA FD AD x FCFBBC===． ∴可得 204FC x =+，4FB x =+．∵∠DBE =∠C ，∠BFG =∠CFB ， ∴△FBG ∽△FCB ． ∴2FB FG FC =⋅． ∴220(44y x x =⋅++．即2436520x y x +=+（04x <<）．（3）AD 的长为78或32或94．四：圆为背景问题（2021年奉贤25）已知⊙O 的直径AB =4，点P 为弧AB 上一点，联结PA 、PO ，点C 为劣弧AP 上一点（点C 不与点A 、P 重合），联结BC 交PA 、PO 于点D 、E . （1）如图10，当cos ∠CBO =87时，求BC 的长；（2）当点C 为劣弧AP 的中点，且△EDP 与△AOP 相似时，求∠ABC 的度数；（3）当AD =2DP ，且△BEO 为直角三角形时，求四边形AOED 的面积.解（1）过点O 作OF ⊥BC ，垂足为点F ∵OF ⊥BC ，∴BF=CF=21BC 在Rt △BOF 中，cos ∠CBO =OBBF，87=2BF ∴BF=47，BC=27（2）联结OC ，设∠B 的大小为x ∵OB=OC ∴∠B=∠C= x ，∴∠AOC= 2x 又∵点C 为劣弧AP 的中点，CO 为半径，OA=OP ∴OC ⊥AP ，∴∠AOC=∠POC= 2x ∴∠A=∠P=90°-2x ，∠PEC= 3x ∵△EDP ∽△AOP ，∠PDE >∠A∴∠PED =∠A ∴3x=90°-2x ，x=18°，即∠ABC=18° （3）过点O 作OG ∥AP 交BC 于点G备用图备用图BO图10P A B C DE OAB O∵OG ∥AP ∴21==AB OB AD OG , PE OEDP OG =∴ AD =2OG 又∵AD =2DP ∴OG = DP ∴OE = PE =1 ∵△BEO 为直角三角形①当∠BOE=90°时，过点D 作DM ∥AB 交PO 于点M∵DM ∥AB ∴PAPDAO DM =，∠PMD =∠POA=90° ∵AD =2DP ，PO = AO=2 ∴DM=32∴S AOED = S △AOP - S △PDE =DM PE OP AO ××21××21-=312-=35②当∠BEO=90°时，联结OD∵OE =1，OB =2，∴∠B =30°，∠BOP=60°，BE =3 ∴∠P =∠A =30°∴∠A =∠B =30°，∴AD =BD ∴OD ⊥AB ，OD =332=3OB ∴S AOED = S △ABD - S △OBE =BE OE OD AB ××21××21-=23334-=365（2021年金山25）定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中，O A ∠=∠21. 已知：如图2，AC 是⊙O 的一条弦，点D 在⊙O 上（与A 、C 不重合），联结DC 交射线AO于点E ，联结OD ，⊙O 的半径为5，43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时，若DOE ∆与AEC ∆相似，求DCA ∠的正切值. (3)当1=OE 时，.BOBOA解（1）作AC OH ⊥垂足为点H ，OH 过圆心，由垂径定理得：AC CH AH 21==；∵在OAH R ∆t 中43tan ==∠AH OH OAC ，设x AH x OH 4,3==， ∴在OAH R ∆t 中，可得：222OA AH OH =+，由⊙O 的半径为5可得：()()222543=+x x ，解得：1±=x ，（1-=x 舍去）∴4,3==AH OH , ∴82==AH AC . (2)∵AEC DEO ∠=∠，∴当DOE ∆与AEC ∆相似时可得：A DOE ∠=∠或者ACD DOE ∠=∠；由定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.可知：DOE ACD ∠=∠21，∴DOE ACD ∠≠∠∴当DOE ∆与AEC ∆相似时不存在ACD DOE ∠=∠情况. ∴当DOE ∆与AEC ∆相似时，A DOE ∠=∠， ∴AC OD //，∴AEOEAC OD =； ∵8,5===AC OA OD ，得AE AE -=585,∴1340=AE ；作AC EG ⊥垂足为G ，可得： 90=∠=∠AHO AGE ,∴OH GE //，∴AH AGOH EG AO AE ==即4351340AG EG ==, ∴1324=EG ，1332=AG ，137213328=-=CG ,∴在CEG R ∆t 中，3113721324tan ===∠CG EG DCA .（3）当1=OE 时，AD 的长是52或1452918. 五：定值问题（2021年黄浦25）如图10，四边形ABCD 中，AB =AD =4，CB =CD =3，∠ABC =∠ADC =90°，点M 、N 是边AB 、AD 上的动点，且∠MCN =∠BCD ，CM 、CN 与对角线BD 分别交于点P 、Q .（1）求sin ∠MCN 的值；（2）当DN =DC 时，求∠CNM 的度数；（3）试问：在点M 、N 的运动过程中，线段比的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相应的位置.解：（1）联结AC ，由AB =AD ，CB =CD ，AC =AC ，得△ABC ≌△ADC ，即∠ACB =∠ACD =12∠BCD =∠MCN . 12PQMNP NMDBAQ（图10）于是在△ABC 中，∠ABC=90°，5AC ==，则sin ∠ACB 45AB AC ==，即sin ∠MCN 45=. （2）在△CDN 中，∠CDN =90°，DN =DC ，可得∠DNC =∠DCN =45°.作∠BCS =∠NCD 交边AB 的延长线于点S .又CB =CD ，∠CBS =∠CDN =90°，得△CBS ≌△CDN . 得CS =CN ，∠CSB =∠CND .于是∠MCS =∠MCB +∠BCS =∠MCB +∠DCN =12∠BCD =∠MCN ，又CM =CM ，所以△MCS ≌△MCN ，得∠CNM =∠MSC =∠CND =45°. （3）不变.易知∠ADB =∠ACD =∠MCN ，由（2）知∠CNM =∠CND ，得∠CMN =∠DQN =CQP ，又∠MCN =∠PCQ ，得△CNM ∽△CPQ ，则△CSM ∽△CPQ . 设AC 与BD 的交点为H ，易知CH ⊥PQ ，又CB ⊥MS ，所以PQ CHMN CB=. 在△BCH 中，∠BHC =90°，sin ∠HCB 45=，易知cos ∠HCB 35=，即35PQ CH MN CB ==. 六：线段长度问题（2021年黄浦25）在矩形ABCD 中，6AB =，8AD =，点E 在CD 边上，1tan 2DAE ∠=.点F 是线段AE 上一点，联结BF ，CF.（1）如图11，如果3tan 4CBF ∠=，求线段AF 的长；（2）如图12，如果12CF BC =，①求证：∠CFE =∠DAE ；图11DD②求线段EF 的长.解：（1）过点F 作FH ⊥AB ，垂足为H .得FH ∥BC ∥AD ，∠BFH =∠CBF ，∠AFH =∠DAE. ∵1tan 2EAD ∠=，3tan 4CBF ∠=，∴1tan 2AFH ∠=，3tan 4BFH ∠=.在Rt △BFH 中，设BH =3k ，由3tan 4BFH ∠=易得FH =4k .在Rt △AFH 中，由FH =4k ，1tan 2AFH ∠=易得AH =2k，AF = 又∵AB =6，∴2k+3k=6，解得65k =.∴125AH =，AF =（2）如图12-1，延长AE 交BC 的延长线于G .易得AD ∥BG ，DAE G ∠=∠,AD DE CGCE=在Rt ADE △中，∵90D ∠=︒，1tan 2EAD ∠=，8AD =，∴tan 4DE AD EAD =⋅∠=，642CE CD DE =-=-=.备用图H图11D图13-1G图12-∴842CG=.解得4CG =又∵1=42CF BC =，∴CG CF =，∴CFG G ∠=∠.∴∠CFE =∠DAE.（3）如图13-1，联结BD 交AE 于P ，类似（1）可求AP =∵AB CD ∥，∴DP AB BP DE =.将6AB =，4DE =代入，得32DP BP =.又∵10BD =，∴4DP DE ==. ∴DPE DEP ∠=∠.又∵180-180-APD DPE CEF DEP ∠=︒∠∠=︒∠，，∴APD CEF ∠=∠ 又∵∠CFE =∠DAE ，∴△CEF ∽△APD . ∴AP DP EF CE=.将AP ==4DP 、=-=2CE CD DE代入，得EF =（2021年浦东25）四边形ABCD 是菱形，∠B ≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF ⊥AE ，EF 与边CD 交于点F ，且EC =3CF ．（1）如图1，当∠B =90°时，求ABE S △与ECF S △的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值；（3）如图3，联结AF ，当∠AFE =∠B 且CF =2时，求菱形的边长．解：（1）∵四边形ABCD 是菱形，∠B =90°，∴∠C =90°，∠CFE +∠CEF =90°．∵EF ⊥AE ，∴∠AEB +∠CEF =90°．∴∠CFE =∠BEA ． ∴△ABE ∽△ECF ．FDCBA （第25题图3）（第25题图2）FDCBA（第25题图1）FEDCBA∴AB BE EC CF =．∵EC =3CF ．∴3AB ECBE CF==．∴AB =BC =3BE ．∴32AB EC=．∴2239()()24ABE ECFS ABSEC ===，即94ABE ECFS S =．（2）由（1）中结论可知当E 为BC 中点时，∠B 不为90°．分别过点A 、F 作AG ⊥BC 、 FH ⊥BC ，垂足分别为点G 、H ．∴∠AGE =∠EHF =90°． ∵∠AEG =∠EFH ， ∴△AGE ∽△EHF ．∴AG GE EHHF=．设CF =k ，CH =x ．由题意得 CE =BE =3k ，AB =6k ，EH =3k +x ，HF 由△ABG ∽△FCH ，可得66BG AB k CHFCk===．∴BG =6x．∴AG GE =3k -6x3k x+．化简可得 k =5x ．在Rt △ABG 中，cos B =BG AB =6165x x k k ==．即cos B =15．（3）由于∠B =∠AFE ，所以∠B 不为90°．在DC 的延长线上取点P ，使得EP =EC ． ∴∠P =∠ECP =∠D =∠B =∠AFE ．∵∠AFP =∠EFP +∠AFE =∠D +∠FAD ， ∴∠EFP =∠FAD ．∴△EFP ∽△FAD ．∴cos EP PF EF AFE FDDAFA===∠．∵CF =2，EC =3CF ， ∴EC =EP =6．设菱形ABCD 的边长为m ．∴62cos 2PC AFE m m+==∠-．∴4(1)2m PC m +=-．∴cos P =1123(2)PC m EP m +=-． ∵∠AFE =∠P ，∴cos ∠AFE =cos P．∴6123(2)m m m +=--，解得 m =17．经检验m =17是方程的解． ∴菱形ABCD 的边长是17．（2021年普陀25）如图14，矩形ABCD 中，1AB =，，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DFAB BE=；（2）当点G 在△ADF 的内部时，用x 的代数式表示ADG ∠的余切；（3）当∠FGD =∠AFE 时，求线段BE 的长．解：（1）∵矩形ABCD ，∴90BAD B C CDA ∠=∠=∠=∠=︒，3AD BC ==，1CD AB ==．由90BAD ∠=︒，可得90BAE EAD ∠+∠=︒．由AE AF ⊥，可得90DAF EAD ∠+∠=︒． ∴BAE DAF ∠=∠．3BC =F图14CBADE G备用图C BAD由90CDA ∠=︒，可得90ADF ∠=︒． ∴B ADF ∠=∠． ∴△ABE ∽△ADF ． ∴AD DFAB BE=．（2）由AD AB 可得3DF x =．过点G 作GH DF ⊥，H 为垂足．可证GH //EC ，∴GH FH FGEC FC FE==．由:FG GE =在Rt △DGH 中，3cot 61GH xDGH DH x -∠==-． ∵GH //AD ，3cot cot 61xADG DGH x -∠=∠=-．（3）解法一：过点G 作GH DF ⊥，H 为垂足．同第（2 ∵FGD AFE ∠=∠，∴GD //AF ． ∴FAD ADG ∠=∠．又∵AD //GH ．∴DGH ADG ∠=∠．∴DGH FAD ∠=∠． ∴tan tan DGH FAD ∠=∠．得 12331313x x x -=-，解得 x =．即 BE =．AB CD GF HEAB CD GF M E解法二：过点G 作GM //AF ． ∵FGD AFE ∠=∠，∴GD //AF ．证90AEM ∠=︒，可得 BAE CEM ∠=∠．得1631x xx -=-，解得x =．（2021年徐汇25）如图，在ABC Rt ∆中，︒=∠90ACB ，12=AC ，5=BC ，点D 是边AC 上的动点，以CD 为边在ABC ∆外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ．（1）当BE AE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH ∆和ABG ∆相似，求ABE ∠sin 的值；（3）当AE AG =时，求CD 的长．解：（1）∵四边形CDEF 是正方形，∴CF EF DE CD ===，︒=∠90DEF ；∵BE AE ⊥，∴DEF AEB ∠=︒=∠90；∴FEG DEG DEG AED ∠+∠=∠+∠；∴FEG AED ∠=∠；又︒=∠=∠90F ADE ，∴EFB ADE ∆≅∆；∴BF AD =；设x CD =，则x EF CF ==，x AD -=12； ∴x x +=-512；解得27=x ∴4492==CD S CDEF 正方形．（2）当BEH ∆和ABG ∆相似时，又EBH ABG ∠=∠，所以分两种情况考虑：︒1 ∵︒+∠=∠+∠=∠90BAG ADH BAG BHE ； ∴BAG BHE ∠≠∠；（备用图）BAC（第25题G FE D BAC︒2 当BAG BEH ∠=∠时，∵BC DE //，∴CBG BEH ∠=∠；∴BAG CBG ∠=∠；∴ACBCBAG BC CG CBG =∠==∠tan tan ； ∴1255=CG ；得1225=CG ；∴12119=AG ；过点A 作BE AM ⊥，垂足为M ．在AMG Rt ∆中，︒=∠90AMG ；1312sin sin sin =∠=∠==∠ABC BGC AG AM AGM ；可得13119=AM ；在AMB Rt ∆中，︒=∠90AMB ，169119sin ==∠AB AM ABE ；综合︒1、︒2，如果BEH ∆和ABG ∆相似，ABE ∠sin 的值是169119．（3）同（2），过点A 作BE AM ⊥，垂足为M ．设x CD =．∵EF CD //，∴BF BC EF CG =；即x x CG +=55；解得xxCG +=55； ∴x x AG ++=5760，x x DG +=52；∵AE AG =，∴GE GM 21=；由AGM EGD ∠=∠，︒=∠=∠90AMG EDG ，∴EDG ∆∽AMG ∆； ∴AGGMGE GD =；得AG GD GE ⋅=22；即AG GD DE DG ⋅=+222；即x x x x x x x ++⋅+⨯=++576052)5(2224；化简，得095422=--x x ；解得21942±=x （负值舍去） ∴21942+=CD ．（2021年长宁25）已知，在矩形ABCD 中，点M 是边AB 上的一个点（与点A B 、不重合），联结CM ，作90CMF ︒∠=，且MF 分别交边AD 于点E 、交边CD 的延长线于点F ，点G 为线段MF 的中点，联结DG .（1）如图1，如果4AD AM ==，当点E 与点G 重合时，求MFC ∆的面积；（2）如图2，如果2AM =，4BM =，当点G 在矩形ABCD 内部时，设AD x =，2DG y =，求y 关于x 的函数解析式，并写出定义域；（3）如果6AM =，8CD =，F EDG ∠=∠，求线段AD 的长．（直接写出计算结果）解：（1）四边形ABCD 是矩形，90//.A AB CD ∴∠=︒，//.AG MGAB CD GD GF∴=， 4MG FG AD ==，， 2.AG ∴=在Rt AMG ∆中, 24A AG AM ∠︒===90，，， 1tan .2AG AMG AM ∴∠==MG ==2MG FG MF MG =∴==，//AB CD ，F AMG ∴∠=∠， 1tan tan .2F AMG ∴∠=∠= 在Rt CMF ∆中, 90CMF ︒∠=，tan MC MF F ∴==120.2MFC S MC MF ∆∴=⋅⋅=（2）分别过点G 、点M 作GK CF MH CF ⊥⊥，，垂足分别为点K 、点.H 9090GKF MHF MHC ︒∴∠=︒∠=∠=，，四边形ABCD 是矩形，90ADC A MHF ∴∠=∠=∠=︒，∴四边形ADHM 是矩形，2DH AM ∴==， MH AD x ==，同理可得 4.CH BM ==90CMF ∠=︒ 90F MCF ∴∠+∠=︒ 90MHC ∠=︒90MCF CMH ∴∠+∠=︒F CMH ∴∠=∠， FMH CMH ∴∆∆∽，.MH CH FH MH ∴=2.4x FH ∴=GK CF MH CF ⊥⊥，，//GK MH ∴，.FG GK FK FM MH FH∴== ABCDEF(G ) M图1 CDFM 图2第25题图2FM FG =2x GK ∴=，2.8x KH FK ==22.8x DK DH KH ∴=-=-在Rt GKD ∆中,22290GKD GK DK GK ︒∠=∴=+，，2GK y =424644x x y ∴=-+（4x <<）（3）七：取值范围问题（2021年青浦25）在△ABC 中，∠C= 90°，AC =2，BC=D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且BQ=2BP ，联结PQ 、QD 、DP ．（1）求证：PQ ⊥AB ；（2）如果点P 在线段BC 上，当△PQD 是直角三角形时，求BP 的长；（3）将△PQD 沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于△ABC 内，请直接写出BP 的取值范围．解：（1）∵∠C= 90°，AC =2，BC=∴AB4=．∴=BC AB ． ∵BQ=2BP，∴=BQ BP ∴=BQ BC BP AB． DPABCD Q（第25题图）（备用图）又∵∠B =∠B ，∴△BQP ∽△BCA ． ∴∠BQP =∠BCA ．∵∠C= 90°，∴∠BQP =90°．即PQ ⊥AB ．（2）（i ）当∠PQD =90°时，∵∠PQD < ∠PQA =90°， ∴此种情况不存在．（ii ）当∠QPD =90°时， ∵∠PQB =∠QPD =90°，∴AB ∥PD ，∴=CP CDBP DA． ∵CD =DA ， ∴BP =CP ．∵BC =BP = （iii ）当∠QDP =90°时，过点Q 作QH ⊥AC ，垂足为点H ．设BP =2x ，则BQ x ，PC =2x ，QA =4．∴AH =22-x ，QH =32-x，HD =12-x ．∵∠QDC =∠CDP +90°，∠QDC =∠DQH +90°， ∴∠CDP =∠DQH ． ∴tan ∠CDP =tan ∠DQH ． ∴=CP HD DC QH ．2=x ．解得1x ，2x∴BP ．综上所述，当△PQD 是直角三角形时，线段BP 的长为．（3）33<<BP ．。

2021年上海市16区中考数学一模考点分类汇编专题10锐角三角函数(解析版)

2021年上海市16区中考数学一模汇编专题10锐角三角函数一、单选题1．（2021·上海金山区·九年级一模）在Rt ABC ∆中，90C ∠=，那么锐角A 的正弦等于（）A ．A A 锐角的对边锐角的邻边B ．A 锐角的对边斜边C ．A 锐角的邻边斜边D ．A A 锐角的邻边锐角的对边．【答案】B【分析】根据锐角三角函数的定义可直接得出结果．【详解】在Rt ABC ∆中，90C ∠=，那么锐角A 的正弦=A 锐角的对边斜边，故选：B ．【点睛】本题考查锐角三角函数的定义，属于基础题，需要熟练掌握锐角三角函数的定义．2．（2021·上海杨浦区·九年级一模）在ABC 中，如果1sin 2A =，cot 3=B ，那么这个三角形一定是（） A ．等腰三角形 B ．锐角三角形C ．钝角三角形D ．直角三角形【答案】D【分析】根据特殊的三角函数值可知，∠A ＝30°，∠B ＝60°，即可判断三角形的形状．【详解】∠ 1sin 2A =，cot 3=B ，∠∠A ＝30°，∠B ＝60°，∠ ∠A ＋∠B ＝90°， ∠ 这个三角形一定是直角三角形，故选：D ．【点睛】本题考查特殊角的三角函数值，三角形内角和定理，属于基础题型．3．（2021·上海宝山区·九年级一模）在Rt ABC △中，90C ∠=︒，5AB =，3BC =，那么sin A 的值为（）．A ．35B ．34C ．45D ．43【答案】A【分析】根据正弦的定义解答即可．【详解】解：在Rt∠ABC 中，∠C=90°，AB=5，BC=3，则sinA=35BC AB =，故选：A ．【点睛】本题考查了锐角三角函数的定义，掌握锐角A 的对边a 与斜边c 的比叫做∠A 的正弦是解题的关键．4．（2021·上海奉贤区·九年级一模）在 Rt ABC ∆中，90C =∠，如果33,4AC cosA == ，那么 AB 的长为（）A ．94B ．4C ．5D ．254【答案】B【分析】根据cosA 34==AC AB ，即可得出AB 的值【详解】解：在Rt∠ABC 中，∠C=90°，AC=3，又∠,osA 34c ==AC AB ∠AB=4故选：B ．【点睛】本题考查锐角三角函数的定义，解题的关键是熟练掌握基本知识，属于中考常考题型． 5．（2021·上海虹口区·九年级一模）在Rt ABC ∆中，90C ∠=︒，3BC =，4AC =，那么tan A 的值等于（）A ．34B ．43C ．35D ．45【答案】A【分析】在直角三角形中，锐角的正切等于对边比邻边，由此可得tan A . 【详解】解：如图90C ∠=︒，3tan 4BC A AC ∴==.故选：A. 【点睛】本题主要考查了锐角三角函数中的正切，熟练掌握正切的表示是解题的关键.6．（2021·上海徐汇区·九年级一模）已知海面上一艘货轮A 在灯塔B 的北偏东30方向，海监船C 在灯塔B 的正东方向5海里处，此时海监船C 发现货轮A 在它的正北方向，那么海监船C 与货轮A 的距离是（）A ．10海里B ．C ．5海里D 【答案】B【分析】根据题意先建立直角三角形，然后结合三角函数中正切的定义求解即可．【详解】根据题意建立如图所示Rt∠ABC ，其中∠C=90°，∠B=60°，BC=5，∠560AC BC tan B tan ==⨯︒=B ．【点睛】本题考查解直角三角形的实际应用，准确根据题意构建直角三角形并灵活运用三角函数求解是解题关键．7．（2021·上海徐汇区·九年级一模）在Rt ABC 中，90A ∠=︒，6AB =，10BC =，那么下列结论正确的是（）A．4tan3C=B．4cot5C=C．3sin4C=D．4cos5C=【答案】D【分析】先根据勾股定理解出AB，再逐项根据三角函数的定义判断即可．【详解】根据勾股定理可得：8AC==，则3tan4ABCAC==；4cot3ACCAB==；3sin5ABCBC==；4cos5ACCBC==；故选：D．【点睛】本题考查锐角三角函数的定义，熟悉基本定义是解题关键．8．（2021·上海长宁区·九年级一模）已知在∠ABC中，∠C＝90°，∠B＝50°，AB＝10，那么BC的长为（）A．10cos50°B．10sin50°C．10tan50°D．10cot50°【答案】A【分析】根据三角函数的定义即可求解．【详解】解：∠cosB＝BCAB，∠BC＝ABcosB＝10cos50°．故选：A．【点睛】此题主要考查三角函数的定义．余弦：锐角A的邻边b与斜边c的比叫做∠A的余弦，记作cosA．即cosA＝bc．9．（2021·上海杨浦区·九年级一模）如果小丽在楼上点A处看到楼下点B处小明的俯角是35°，那么点B处小明看点A处小丽的仰角是（）A．35°B．45°C．55°D．65°【答案】A【分析】根据两点之间的仰角与俯角构成的两条水平线夹角的内错角相等，即可得出答案．【详解】解：根据两点之间的仰角与俯角构成的两条水平线夹角的内错角相等，可知，点B 处小明看点A 处小丽的仰角是35°，故选：A ．【点睛】本题考查解直角三角形的应用-仰角俯角问题，正确理解是解题的关键． 10．（2021·上海黄浦区·九年级一模）对于锐角α，下列等式中成立的是（） A ．sin cos tan ααα=⋅ B ．cos tan cot ααα=⋅ C ．tan cot sin ααα=⋅ D ．cot sin cos ααα=⋅【答案】A【分析】根据同角的三角函数关系逐一判断即可．【详解】解：A ．sin cos tan ααα=⋅，故本选项正确； B ．tan cot 1cos ααα⋅=≠，故本选项错误； C ．cot sin cos tan αααα⋅=≠ ，故本选项错误； D ．cos cot sin cos sin ααααα=≠⋅ ，故本选项错误．故选A ．【点睛】此题考查的是同角的三角函数关系，掌握同角的三角函数关系是解题关键．11．（2021·上海松江区·九年级一模）如图，一艘船从A 处向北偏东30°的方向行驶10千米到B 处，再从B 处向正西方向行驶20千米到C 处，这时这艘船与A 的距离（）A ．15千米B ．10千米C ．D ．千米【答案】C【分析】根据题意，利用30BAD ∠=︒，根据锐角三角函数求出AD 和BD 的长，从而得到CD 的长，再用勾股定理求出AC 的长．【详解】解：如图，根据题意，10AB km =，30BAD ∠=︒，∠1sin 301052BD AB km =⋅︒=⨯=，cos30102AD AB =⋅︒=⨯=，∠20BC km =，∠15CD km =，∠AC ==．故选：C ．【点睛】本题考查解直角三角形，解题的关键是掌握利用锐角三角函数解直角三角形的方法．12．（2021·上海浦东新区·九年级一模）已知在Rt ABC ∆中，90C ∠=︒，,2A BC α∠==，那么AB 的长等于（）A ．2sin αB ．2sin αC ．2cos αD ．2cos α【答案】A【分析】根据锐角三角函数的定义得出sinA ＝BCAB，代入求出即可．【详解】解：∠在Rt∠ABC 中，∠C ＝90°，∠A ＝α，BC ＝2，∠sinA ＝BCAB， ∠AB ＝sin BC A =2sin α，故选：A ．【点睛】本题考查了锐角三角函数的定义，能熟记锐角三角函数的定义是解此题的关键．13．（2021·上海金山区·九年级一模）若α是锐角，()2sin 152α+=，那么锐角α等于（） A ．15 B ．30 C ．45D ．60【答案】B【分析】由sin45°=2可得()15α+=45°即可确定α．【详解】解：∠sin45°=2，()2sin 152α+=，α是锐角∠()15α+=45°，即α=30°．故选：B ．【点睛】本题主要考查特殊角的三角函数值，根据特殊角的三角函数值确定()15α+=45°成为解答本题的关键．14．（2021·上海九年级一模）在Rt ABC 中，90C ∠=︒，那么cosA 等于（） A ．BCABB ．ACABC ．BCACD ．ACBC【答案】B【分析】作出草图，根据锐角的正弦=邻边斜边列式即可．【详解】解：如图，∠∠C=90°，∠cosA=ACAB．故选：B ．．【点睛】本题考查了锐角三角函数的定义，能熟记锐角三角函数的定义是解题的关键．15．（2021·上海静安区·九年级一模）在Rt∠ABC 中，∠C =90°，CD 是高，如果AB =m ，∠A =α，那么CD 的长为（）A ．sin tan m αα⋅⋅B ．sin cos m αα⋅⋅C ．cos tan m αα⋅⋅D ．cos cot m αα⋅⋅【答案】B【分析】此题根据题意作图根据锐角三角函数表示出AC ，再表示出CD 即可求出结果．【详解】解：根据题意作图如下：由题意知：AB =m ，∠A =α，∠cos AC AB α=⋅，∠sin cos sin CD AC AB ααα=⋅=⋅⋅，即cos sin CD m αα=⋅⋅，故选：B ．【点睛】此题考查锐角三角函数的应用，主要涉及到正弦和余弦，找准对应边是解题关键．16．（2021·上海静安区·九年级一模）如果锐角α ） A ．30α=︒ B ．60α=︒ C ．3045α︒<<︒D ．4560α︒<<︒【答案】C【分析】利用30度角和45度角的正切值与角α的正切值比较，即可得到答案．【详解】∠tan 30tan tan 451α︒==︒=，22213,1134===，而13134<<，∠3045α︒<<︒，故选：C ．【点睛】此题考查各角的正切值，实数的平方运算，实数的大小比较，熟记各角度的三角函数值是解题的关键．17．（2021·上海崇明区·九年级一模）倍，那么这个正多边形的边数是（） A ．3 B ．4C ．5D ．无法确定【答案】B【分析】如图，画出简图，根据切线的性质可得∠OCA=90°，根据∠AOC 的余弦可得∠AOC=45°，即可得出此多边形的中心角为90°，即可求出多边形的边数．【详解】如图，OA 、OC 分别为此多边形的外接圆和内切圆的半径，AB 为边长，∠OC∠AB ，∠∠OCA=90°，∠倍，∠cos∠AOC=OC OA =2， ∠∠AOC=45°，∠∠AOB=90°，即此多边形的中心角为90°，∠此多边形的边数=360°÷90°=4，故选：B ．【点睛】本题考查正多边形和圆及三角函数的定义，熟练掌握余弦的定义并熟记特殊角的三角函数值是解题关键．18．（2021·上海崇明区·九年级一模）在ABC 中，90C ∠=︒，如果8AC =，6BC =，那么A ∠的正弦值为（）A ．35B ．45C ．34D ．43【答案】A【分析】利用勾股定理可求出AB 的长，根据正弦函数的定义即可得答案．【详解】∠90C ∠=︒，8AC =，6BC =，，∠sinA=BC AB =35，故选：A ．【点睛】本题考查解直角三角形，解题的关键是熟练掌握各三角函数的定义，属于中考常考题型． 19．（2021·上海虹口区·九年级一模）如图，在Rt ABC 中，90ACB ∠=︒，D 是边AB 上一点，过D 作DF AB ⊥交边BC 于点E ，交AC 的延长线于点F ，联结AE ，如果1tan 3EAC ∠=，1CEFS=，那么ABCS的值是（）A ．3B ．6C ．9D ．12【答案】C【分析】证明∠BAC∠∠FEC ，得219EFC BAC S EC S AC ∆∆⎛⎫== ⎪⎝⎭，进一步得出结论．【详解】解：∠90ACB ∠=︒，DF∠AB ，∠∠ACB=∠FCE=∠BDE=90° 又∠FEC=∠BED∠∠F=∠B∠∠ABC∠∠EFC∠()22211tan 39EFC BAC S EC EAC S AC ∆∆⎛⎫⎛⎫==∠== ⎪ ⎪⎝⎭⎝⎭∠1CEFS =∠99BAC FEC S S ∆∆== 故选：C【点睛】此题主要考查了相似三角形的判定与性质以及三角函数的应用，熟练掌握相似三角形的判定与性质是解本题的关键．20．（2021·上海普陀区·九年级一模）如图，在∠ABC 中，∠C ＝90°．若AB ＝3，BC ＝2，则sin A 的值为（）A ．23BCD 【答案】A【分析】根据在直角三角形中，正弦为对边比斜边，可得答案．【详解】解：∠ABC 中，∠C ＝90°，AB ＝3，BC ＝2，得sin A ＝2 3BC AB ＝，故选A ．【点睛】本题考查三角函数，熟记公式是解题关键.21．（2021·上海松江区·九年级一模）已知在Rt∠ABC 中，∠C=90°，如果BC=2，∠A=α，则AC 的长为（） A ．2sinαB ．2cosαC ．2tanαD ．2cotα【答案】D 试题分析：根据锐角三角函数的定义得出cotA=，代入求出即可．∠在Rt∠ABC 中，∠C=90°， ∠cotA=，∠BC=2，∠A=α，∠AC=2cotα，故选D ．考点：锐角三角函数的定义．二、填空题22．（2021·上海九年级一模）在ABC 中，90C ∠=︒，如果cot 2A ∠=，3BC =，那么AC =________________．【答案】6 【分析】直接根据cot AC A BC∠=，将已知条件代入，便可求出AC.【详解】∠cot AC A BC∠==2，3BC =，∠cot 326AC BC A =⋅∠=⨯=，故答案为：6. 【点睛】本题考查余切的定义，正确掌握余切的公式是解题的关键.23．（2021·上海九年级专题练习）已知某斜坡的坡度1:3,当铅垂高度为3米时，水平宽度为_________________米【答案】9【分析】根据斜坡是铅垂高度与水平距离的比值，而这个斜坡的坡度为1:3，铅垂高度为3米，从而求出斜坡的水平宽度．【详解】解：∠斜坡的坡度为1:3，其铅垂高度为3米，∠这个斜坡的水平宽度为：3×3=9米，故答案为：9．【点睛】本题考查解直角三角形的应用中的坡度坡角问题，解题的关键是明确坡度是指斜坡的铅直高度与水平距离的比值．24．（2021·上海松江区·九年级一模）在Rt ABC 中，90C ∠=︒，6AC =，3cos 4A =，那么AB 的长为__．【答案】8【分析】根据余弦函数的定义即可直接求解．【详解】解：∠3cos 4AC A AB ==，∠AB=34AC ＝634＝8，故答案为：8．【点睛】本题考查了余弦函数的定义，是所邻的直角边与斜边的比，理解定义是关键．25．（2021·上海徐汇区·九年级一模）如图，点P 在线段BC 上，AB BC ⊥，DP AP ⊥， CD DP ⊥，如果10BC =，2AB =， 1tan 2C =，那么 DP 的长是 _____ ．【答案】5【分析】由已知条件，根据同角的余角相等得APB C ∠=∠，根据1tan 2C =得1tan 2AB APB BP ==∠，求出4BP =，得出6PC =，利用1tan 2C =和勾股定理即可得DP 的长．【详解】解：∠AB BC ⊥，DP AP ⊥，CD DP ⊥，∠90B APD PDC ∠=∠=∠=︒，90C DPC ∠+∠=︒，90APB DPC ∠+∠︒=，∠APB C ∠=∠， ∠1tan 2C =，∠1tan tan 2AB APB C BP ===∠，∠2AB =，10BC =，∠4BP =，6PC =，设DP 的长是x ，∠1tan 2DP C CD ==，∠22CD DP x ==，∠222PC DP CD =+，即()22262x x =+，解得x =（舍去负值）．【点睛】本题考查三角函数-正切，勾股定理等知识，解题的关键是学会利用数形结合的思想解决问题． 26．（2021·上海杨浦区·九年级一模）如果小明沿着坡度为1:2.4的山坡向上走了130米，那么他的高度上升了______米．【答案】3256【分析】设高度上升了h ，则水平前进了2.4h ，然后根据勾股定理解答即可．【详解】解：设高度上升了h ，则水平前进了2.4h ，130= ，解得h=50．故答案为50．【点睛】本题主要考查了坡度比与勾股定理得应用，根据坡度比和勾股定理列出关于h 的方程成为解答本题的关键．27．（2021·上海黄浦区·九年级一模）如果视线与水平线之间的夹角为36°，那么该视线与铅垂线之间的夹角为________度．【答案】126°或54°【分析】根据仰角或俯角是36°分类讨论，画出图形即可分别求出结论．【详解】解：当仰角是36°时，如下图所示由图可知：该视线与铅垂线之间的夹角为36°＋90°=126°；当俯角是36°时，如下图所示由图可知：该视线与铅垂线之间的夹角为90°－36°=54°；综上：该视线与铅垂线之间的夹角为126°或54°.故答案为：126°或54°．【点睛】此题考查的是仰角和俯角的定义，根据仰角或俯角是36°分类讨论是解题关键．OP ，且OP与x轴负半轴夹角的正切28．（2021·上海黄浦区·九年级一模）已知点P位于第二象限内，5值为2，则点P的坐标是________．【答案】（【分析】根据题意，画出图形，过点P 作PA∠x 轴于A ，根据正切值可知2PA OA=，设OA=x ，则PA=2x ，利用勾股定理列出方程即可求出x ，从而求出OA 和PA ，即可求出结论．【详解】解：如下图所示，过点P 作PA∠x 轴于A由题意可知：tan∠POA=2∠2PA OA=设OA=x ，则PA=2x∠OA 2＋PA 2=OP 2∠x 2＋（2x ）2=52 解得：x=PA=∠点P 在第二象限∠点P的坐标为（（．【点睛】此题考查的是解直角三角形和求点的坐标，掌握利用锐角三角函数和勾股定理解直角三角形是解题关键．29．（2021·上海黄浦区·九年级一模）已知一个锐角的正切值比余切值大，且两者之和是133，则这个锐角的正切值为________．【答案】3【分析】设这个锐角为α，根据题意和三角函数的性质可知：1tan cot 33tan cot 1αααα⎧+=⎪⎨⎪⋅=⎩，解方程即可．【详解】解：设这个锐角为α，∠1tan cot 33tan cot 1αααα⎧+=⎪⎨⎪⋅=⎩①②由①，得10cot tan 3αα=-③将③代入②，得tan tan 0131αα⎛⎫⋅-= ⎪⎝⎭解得：1tan 3α=或tan 3α= 当1tan 3α=时，∠cot α=3＞tan α∠α的正切值比余切值大∠此时不符合题意，舍去；当tan 3α=时，cot α=13＜tan α∠此时符合题意．故答案为：3．【点睛】此题考查的是锐角三角函数值的运算，掌握三角函数的性质是解题关键．30．（2021·上海浦东新区·九年级一模）如果从某一高处甲看低处乙的俯角为36度，那么从低处乙看高处甲的仰角是______度．【答案】36【分析】根据仰角以及俯角的定义，画出图形进而求出即可．【详解】解：如图所示：∠甲处看乙处为俯角∠DBA=36°，//AC BD ，∠乙处看甲处为：仰角∠CAB=∠DBA=36°．故答案为：36．【点睛】此题主要考查了仰角、俯角的定义以及平行线的性质，仰角是向上看的视线与水平线的夹角；俯角是向下看的视线与水平线的夹角．31．（2021·上海嘉定区·九年级一模）已知一个斜坡的坡度i =______．【答案】30【分析】坡度=坡角的正切值，据此直接解答．【详解】解：∠3tan α==，∠坡角=30°．【点睛】此题主要考查学生对坡度及坡角的理解及掌握．32．（2021·上海长宁区·九年级一模）如图，一辆汽车沿着坡度为1:i =50米，则它距离地面的垂直高度下降了米.【答案】25【分析】设出垂直高度，表示出水平距离，利用勾股定理求解即可．【详解】解：设垂直高度下降了x 米．根据勾股定理可得：x 2+）2=502．解得x=25，即它距离地面的垂直高度下降了25米．【点睛】此题考查三角函数的应用.关键是熟悉且会灵活应用公式：tanα（坡度）=垂直高度÷水平宽度，综合利用了勾股定理．33．（2021·上海金山区·九年级一模）在Rt ABC ∆中，90C ∠=，15AB =，4sin 5A =，那么BC =______．【答案】12【分析】直接利用正弦的定义列式求解即可．【详解】解：∠90C ∠=︒，4sin 5A =，∠4sin 5CB A AB == ∠15AB =∠4155CB =，解得：BC=12．故填：12．【点睛】本题主要考查了正弦的定义，正确理解正弦的定义是解答本题的关键．34．（2021·上海金山区·九年级一模）在ABC ∆中，::1:2AB AC BC =tan B =______．【答案】2【分析】先由勾股定理逆定理判断出ABC ∆是直角三角形，再根据正切的定义求解即可.【详解】设2AB x AC x BC ===，，，则()22222225AB AC x x x BC +=+==， ABC ∆∴是直角三角形，且90A ∠=︒，2tan 2AC x B AB x∴===，故答案为：2 【点睛】此题考查了正切的定义.再直角三角形中锐角的正切值等于对边和邻边的比是解答此题的关键. 35．（2021·上海徐汇区·九年级一模）如图，在ABC 中，120ABC ∠=︒，12AB =，点D 在边AC 上，点E 在边BC 上，4sin 5ADE ∠=，5ED =，如果ECD 的面积是6，那么BC 的长是_____．【答案】6【分析】过点F 作EF AC ⊥交AC 于F ，过点A 作BC 的垂线交CB 的延长线于点H ，通过解直角三角形、勾股定理及三角形面积公式求出CF ，再通过解直角三角形求出CH ，即可解得答案．【详解】解；过点F 作EF AC ⊥交AC 于F ，∠4sin =5EF ADE ED∠=，又∠5ED =，∠4EF =，∠3DF ==，又∠114622ECD S CD EF CD =⋅=⋅=，∠3CD =，6CF =，过点A 作BC 的垂线交CB 的延长线于点H ，∠90AHB ∠=︒，又∠120ABC ∠=︒，∠60ABH ∠=︒，∠12AB =，∠1cos602BH AB ︒==，∠6BH =，sin 602AH AB ︒==AH =在CEF △和ACH 中，tan EF AH ACH CF CH ∠== 即46=CH =6BC CH BH =-=【点睛】本题考查了解直角三角形及勾股定理，解题的关键是根据题意做出辅助线．36．（2021·上海徐汇区·九年级一模）如图，已知ABC 是边长为2的等边三角形，正方形DEFG 的顶点,D E 分别在边,AC AB 上，点,F G 在边BC 上，那么AD 的长是_____．【答案】6【分析】根据等边三角形以及正方形的性质，在Rt∠CDG 中运用正弦的定义建立方程求解即可．【详解】根据题可知，∠ADE 为等边三角形，即：AD=DE ，根据正方形的性质可知DE=DG ，DG∠BC ，∠C=60°，设AD=x ，则DG=x ，DC=AC -AD=2-x ，∠在Rt∠CDG 中，DG sinC CD =，即：602DG x sinC sin CD x =︒===-解得：6=x ，经检验6=x 是上述分式方程的解，故答案为：6．【点睛】本题考查正方形和等边三角形的性质，以及利用锐角三角函数解直角三角形，灵活根据题意找准合适的直角三角形是解题关键．37．（2021·上海徐汇区·九年级一模）已知甲、乙两楼相距30米，如果从甲楼底看乙楼顶，测得仰角为45︒，从乙楼顶看甲楼顶，测得俯角为30，那么甲楼高是_____米．【答案】(30-【分析】先依据题意画出图形，再根据等腰直角三角形的判定与性质可得30AB BC ==米，再根据解直角三角形可得CF 的长，然后根据线段的和差即可得．【详解】由题意，画出图形如下，其中AD 长表示甲楼的高度，BC 长表示乙楼的高度，AB 表示地面，且,,AD AB BC AB EC BC ⊥⊥⊥，45,30BAC ECD ∠=︒∠=︒，30AB =米，过点D 作DF BC ⊥于点F ，则四边形ABFD 是矩形，AD BF ∴=，30DF AB ==米，,45BC AB BAC ⊥∠=︒，Rt ABC ∴是等腰三角形，30AB BC ∴==米，30,ECD EC BC ∠=︒⊥，60DCF ∴∠=︒，在Rt CDF 中，30tan tan 60DF CF DCF ===∠︒（米），30BF BC CF ∴=-=-，则甲楼高30AD =-，故答案为：(30-．【点睛】本题考查了等腰直角三角形的判定与性质、解直角三角形等知识点，依据题意，正确画出图形，并通过作辅助线，构造直角三角形是解题关键．38．（2021·上海九年级一模）如图，A 、B 、C 是小正方形的顶点，且每个小正方形的边长相同，那么BAC ∠的正弦值为_________________．【答案】2【分析】连接BC ，根据网格求出AB,BC,AC ，得到∠ABC 是直角三角形，再进行求解.【详解】∠每个小正方形的边长均为1，∠AB =BC =AC =∠AB 2＝BC 2＋AC 2，∠∠ABC 是直角三角形，∠sin∠BAC ＝2BC AB ==，故答案为2．【点睛】此题主要考查正弦的求解，解题的关键熟知勾股定理的运用.39．（2021·上海杨浦区·九年级一模）如图，已知在ABC 中，90ACB ∠=︒，点G 是ABC 的重心，2CG =，4BC =，那么cos GCB ∠=______．【答案】23【分析】根据重心的性质和余弦函数的定义可以得到解答．【详解】解：如图，延长CG 与AB 交于点D ，过D 作DE∠CB 于点E ，∠G是∠ABC 的重心，∠CG=2GD，∠CG=2，∠GD=1，∠CD=2+1=3，∠∠ACB=90°，∠AC∠CB，∠AC∠DE，∠D是AB中点，∠E是CB中点，∠CE=122CB=，∠cos∠GCB=23CECD=，故答案为23．【点睛】本题考查三角形的综合运用，熟练掌握重心的性质和余弦函数的定义是解题关键．40．（2021·上海宝山区·九年级一模）如图，某堤坝的坝高为12米，如果迎水坡的坡度为1:0.75，那么该大坝迎水坡AB的长度为______米．【答案】15【分析】过点B作BC∠AC于C，由迎水坡的坡度为1:0.75，得到tan∠BAC=43=BCAC，求出AC=9米，再利用勾股定理求出答案．【详解】过点B作BC∠AC于C，∠迎水坡的坡度为1:0.75，∠tan∠BAC=43=BCAC，∠BC=12米，∠AC=9米，=15(米)，故答案为：15．．【点睛】此题考查坡度的定义，解直角三角形的实际应用，勾股定理，正确理解迎水坡的坡度为1:0.75得到tan∠BAC=43=BC AC 是解题的关键． 41．（2021·上海宝山区·九年级一模）已知等腰梯形上底为5，高为4，底角的余弦值为35，那么其周长为______．【答案】26 【分析】作DF∠BC 于F ，AE∠BC 于E ，根据等腰梯形的性质就可以得出∠AEB∠∠DFC 就可以求出FC=BE ，然后根据底角的余弦值为35，求得BE ，AB ，从而求出周长．【详解】解：如图示，作DF∠BC 于F ，AE∠BC 于E ，∠四边形ABCD 是等腰梯形，∠∠B=∠C ，AB=CD ，AD∠BC ，∠∠ADF=∠DFC=90°，∠∠AEF=∠DFE=∠ADF=90°，∠四边形AEFD 是矩形，5EF AD ，在∠AEB 和∠DFC 中 ∠∠AEB∠∠DFC （AAS ），∠BE=CF ；∠35cos E AB B B ，设3BE x =，则5AB x =，根据勾股定理，有：2222534AEAB BE x x ，解之得：1x =（取正值）， ∠3BE =，5AB =，∠3FCBE ，5DC AB ==， ∠周长AB BE EF FC CDAD 53535526，故答案是：26．【点睛】本题考查了等腰梯形的性质的运用，三角函数，矩形的判定及性质的运用，等腰三角形的性质的运用，全等三角形的判定及性质的运用，能熟练应用相关性质是解题的关键．42．（2021·上海闵行区·九年级一模）在直角坐标平面内有一点(12,5)A ，点A 与原点O 的连线与x 轴的正半轴的夹角为θ，那么cos θ=_________．【答案】1213【分析】根据锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解即可．【详解】解：∠在直角坐标平面内有一点A （12,5）=13∠cos θ=1213．故答案为：1213．【点睛】本题主要考査了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理等知识点，掌握锐角三角函数的定义成为解答本题的关键．43．（2021·上海松江区·九年级一模）如图，ABC 在边长为1个单位的方格纸中，ABC 的顶点在小正方形顶点位置，那么ABC ∠的正弦值为_____．【分析】利用勾股定理可求出AC 、BC 、AB 的值，利用勾股定理逆定理可得∠ACB=90°，根据正弦的等于即可得答案．【详解】∠ABC 在边长为1个单位的方格纸中，ABC 的顶点在小正方形顶点位置，，BC=，∠（2+）2=2，∠∠ACB=90°，∠sin∠ABC=ACAB 【点睛】本题考查网格的特征、勾股定理及正弦的定义，在直角三角形中，锐角的正弦是角的对边与斜边的比；熟练掌握三角函数的定义是解题关键．44．（2021·上海嘉定区·九年级一模）如图，正方形ABEF 和正方形BCDE 的边长相等，点A 、B 、C 在同一条直线上．连接AD 、BD ，那么cot ADB ∠的值为______．【答案】3【分析】先构造以∠ADB 为内角的直角三角形，根据余切的定义求解即可．【详解】解：如图，作正方形ABEF 关于直线AB 对称的正方形ABGH ，连接AG ，BH ，相交于点O ；∠正方形ABGH ，∠∠AOD=90°，OA=OB=12AG ， ∠正方形ABEF 和正方形BCDE 的边长相等，∠正方形ABGH 和正方形BCDE 的边长相等，∠AG=BD=2OA ，∠OD=OB+BD=3OA ，∠在Rt∠AOD 中，cot ADB ∠=3OD OA OA OA==3．故答案为3．【点睛】本题考查了求角的余切值，掌握相关知识是解题的关键．45．（2021·上海金山区·九年级一模）已知在Rt ABC ∆中，90C ∠=，1BC =，2AC =，以点C 为直角顶点的Rt DCE ∆的顶点D 在BA 的延长线上，DE 交CA 的延长线于点G ，若1tan 2CED ∠=，CE GE =，那么BD 的长等于______．【答案】2【分析】根据题意画图，作AH∠CE 于H ，根据1tan tan 2CED BAC ∠==∠得出E BAC ∠=∠，由等边对等角得CGE ECG ∠=∠，根据三角形的内角和可得出AKC ECG ∠=∠，得出AK=AC ，利用等腰三角形三线合一得KH=CH ，再证出AH 为KCD △的中位线，可得出AK ，AD 的长，利用勾股定理求出AB ，AB+AD 即可得BD 的长．【详解】解：如图，作AH∠CE 于H ，∠1tan tan 2CED BAC ∠==∠，∠E BAC ∠=∠，∠CE GE =，∠CGE ECG ∠=∠， ∠AKC ECG ∠=∠，∠AK=AC=2，∠AH∠CE ，90ECD ∠=，∠KH=CH ，//AH CD ，∠AH 为KCD △的中位线，∠A 为DK 的中点，DK=2AK=4，AD=AK=2，∠90ACB ∠=，1BC =，2AC =，=∠BD=AD+AB=2+．故答案为：2．【点睛】本题考查三角函数-正切，等腰三角形的判定和性质，三角形的中位线，勾股定理等知识，作垂线构造三角形的中位线是解题的关键．。

2021年上海市16区中考数学一模考点分类汇编专题13二次函数综合(解析版)

2021年上海市16区中考数学一模汇编专题13二次函数综合1．（2021·上海黄浦区·九年级一模）将二次函数223y x x =++的图像向右平移3个单位，求所得图像的函数解析式：请结合以上两个函数图像，指出当自变量x 在什么取值范围内时，上述两个函数中恰好其中一个的函数图像是上升的，而另一个的函数图像是下降的．【答案】246y x x =-+，12x -≤≤．【分析】由二次函数的平移规律：左加右减，可得平移后的解析式，再画出两个函数的图像，利用图像可得答案．【详解】解：把二次函数223y x x =++的图像向右平移3个单位可得：()()23233y x x =-+-+，246y x x ∴=-+，又()222312,y x x x =++=++∴函数图像的顶点坐标为：()1,2,-而()224622,y x x x =-+=-+∴函数图像的顶点坐标为：()2,2,函数223y x x =++与246y x x =-+的图像如图示；∴由图像可得：当12x -≤≤时，函数223y x x =++的函数图像是上升的，而函数246y x x =-+的函数图像是下降的．【点睛】本题考查的是二次函数的图像的平移，二次函数的增减性，掌握以上知识是解题的关键．2．（2021·上海浦东新区·九年级一模）已知抛物线223y x x m =++-的顶点在第二象限，求m 的取值范围．【答案】m ＞1【分析】先利用配方法得到抛物线的顶点坐标为(-1，m-1)，再利用第二象限点的坐标特征得到m-1＞0，然后解不等式即可．【详解】解：∵y=x 2+2x+m=(x+1)2+m-1，∴抛物线的顶点坐标为(-1，m-1)，∵抛物线y=x 2+2x+m 顶点在第二象限，∴m-1＞0，∴m ＞1．故答案为m ＞1．【点睛】本题考查了配方法，以及二次函数y =a (x -h )2+k (a ，b ，c 为常数，a ≠0)的性质，熟练掌握二次函数y =a (x -h )2+k 的性质是解答本题的关键．y =a (x -h )2+k 是抛物线的顶点式，a 决定抛物线的形状和开口方向，其顶点是(h ，k )，对称轴是x =h ．3．（2021·上海松江区·九年级一模）用配方法把二次函数2365y x x =-+化为2()y a x m k =++的形式，并指出这个函数图像的开口方向、对称轴和顶点坐标．【答案】化为23(1)2y x =-+，开口方向：向上；对称轴：直线1x =；顶点坐标：()1,2P 【分析】先利用配方法把一般式化成顶点式，再利用二次函数的性质得到图像的开口方向、对称轴和顶点坐标．【详解】解：y =3x 2-6x +5=3（x 2-2x +1）+2=3（x -1）2+2，∴抛物线开口向上，对称轴为直线x =1，顶点P （1，2）．【点睛】本题考查的是二次函数三种形式的转化、二次函数的性质，掌握配方法、二次函数的性质是解题的关键．4．（2021·上海金山区·九年级一模）已知抛物线22y x bx c =-++经过点()01A ,、()1,5B -．（1）求抛物线的表达式；（2）把表达式化成()22y x m k =-++的形式，并写出顶点坐标与对称轴．【答案】（1）2241y x x =--+；（2）()2213y x =-++，顶点坐标为：()1,3-，对称轴为：直线1x =-．【分析】（1）直接将A 、B 的坐标代入22y x bx c =-++求得b 、c 即可；（2）通过配方将（1）求得的解析式化成顶点式，然后直接写出顶点坐标和对称轴即可．【详解】解：（1）由抛物线22y x bx c =-++经过点()01A ,、()1,5B -两点可得：125c b c =⎧⎨-++=-⎩，解得：41b c =-⎧⎨=⎩；∴抛物线的解析式为：2241y x x =--+；（2）2241y x x =--+()2213x =-++；∴()2213y x =-++，∴顶点坐标为：()1,3-，对称轴为：直线1x =-．【点睛】本题主要考查了运用待定系数法求函数解析式以及二次函数的性质，将二次函数的一般式化成顶点式成为解答本题的关键．5．（2021·上海徐汇区·九年级一模）已知抛物线2y x bx c =++与y 轴交于点(0,2)C ，它的顶点为M ，对称轴是直线1x =-．（1）求此抛物线的表达式及点M 的坐标；（2）将上述抛物线向下平移(0)m m >个单位，所得新抛物线经过原点O ，设新抛物线的顶点为N ，请判断MON △的形状，并说明理由．【答案】（1）222=++y x x ，(1,1)-；（2）△MON 是等腰直角三角形．【分析】（1）根据对称轴是直线1x =-，可求b ，再代入点C ，可求抛物线解析式，把1x =-，代入解析式，可求M 点坐标；（2）由原抛物线与y 轴交点可知，抛物线向下平移2个单位，可求新顶点坐标，再求出MO 、ON 、MN 的长，可判断三角形形状．【详解】解：（1）∵抛物线对称轴是直线1x =-，∴121b -=-⨯，解得b=2，把(0,2)C 代入2y x bx c =++得，2c =，∴抛物线解析式为：222=++y x x ；把1x =-代入222=++y x x 得，2(1)2(1)2y =-+⨯-+，1y =，点M 的坐标为：(1,1)-．（2）抛物线222=++y x x 与y 轴交点为(0,2)C ，向下平移(0)m m >个单位后经过原点，∴m=2，新抛物线的顶点N 的坐标为：(1,1)--，∴22112ON =+=，22112OM =+=，MN=2，∴222MN OM ON =+，∴△MON 是等腰直角三角形．【点睛】本题考查了待定系数法求二次函数解析式和函数的平移以及勾股定理逆定理，灵活运用已知条件，准确把握函数图象平移特征，根据三边长判断三角形形状是解题关键．6．（2021·上海长宁区·九年级一模）已知二次函数21722y x x =--+．（1）用配方法把该二次函数的解析式化为()2y a x m k =++的形式；（2）写出该二次函数图象的开口方向、顶点坐标和对称轴，并说明函数值y 随自变量x 的变化而变化的情况．【答案】（1）()21142y x =-++；（2）开口向下，顶点()1,4-，对称轴直线1x =-，x≤-1时，y 随x 增大而增大；x ＞-1时，y 随x 增大而减小．【分析】（1）根据配方法，先提取12-，然后配成完全平方式，整理即可；（2）根据a 是负数以及顶点式解析式分别求解即可．【详解】解:(1)()()22171214222y x x x =-++=-++（2）①二次函数开口方向向下，②顶点坐标()1,4-，对称轴直线1x =-，③x≤-1时，y 随x 增大而增大；x ＞-1时，y 随x 增大而减小．【点睛】本题考查化一般式为顶点式和二次函数的性质．熟练掌握配方法的操作以及根据顶点式形式写出对称轴和顶点坐标的方法是解题的关键．7．（2021·上海杨浦区·九年级一模）已知一个二次函数的图像经过点()1,0A -、()0,3B 、()2,3C ．（1）求这个函数的解析式及对称轴；（2）如果点()11,P x y 、()22,Q x y 在这个二次函数图像上，且120x x <<，那么1y _____2y ．（填“<”或者“>”）【答案】（1）2y x 2x 3=-++，x=1；（2）<【分析】（1）直接用待定系数法代入三点求出函数解析式，运用对称轴公式可求出对称轴；（2）通过判断二次函数增减性可得出结果．【详解】解：（1）设二次函数的表达式为2y ax bx c =++，已知二次函数经过A 、B 、C 三点，将三点坐标代入二次函数表达式中，03423a b c c a b c -+=⎧⎪=⎨⎪++=⎩，可得123a b c =-⎧⎪=⎨⎪=⎩，则这个函数的解析式为2y x 2x 3=-++，其对称轴为直线12b x a=-=；（2）0a < ，∴抛物线开口向下，对称轴为直线x=1，∴x<1时，y 随x 的增大而增大，又本题120x x <<，∴12y y <．故答案为：<．【点睛】本题考查了二次函数的基本性质，包括求解析式，求对称轴以及二次函数增减性，属于基础题，熟练掌握二次函数的性质是解决本题的关键．8．（2021·上海宝山区·九年级一模）已知二次函数()20y ax ax a =-≠的图像经过点()1,2-．（1）求该二次函数的解析式和顶点坐标；（2）能否通过所求得的抛物线的平移得到抛物线2132y x x =++？如果能，请说明怎样平移，如果不能，请说明理由．【答案】（1）2y x x =-，顶点为11,24⎛⎫- ⎪⎝⎭；（2）可以，先向左平移2个单位，再向下平移32个单位【分析】（1）把点()1,2-代入函数解析式，求出a 的值即可得到解析式，再把一般式写成顶点式得到顶点坐标；（2）把所给的函数解析式化为顶点式，根据函数图象的平移法则进行求解．【详解】解：（1）把点()1,2-代入函数解析式，得2a a +=，解得1a =，∴2y x x =-，写成顶点式：21124y x ⎛⎫=-- ⎪⎝⎭，∴顶点坐标是11,24⎛⎫- ⎪⎝⎭；（2）将2132y x x =++也写成顶点式，得23724y x ⎛⎫=+- ⎪⎝⎭，31222⎛⎫--= ⎪⎝⎭，713442-=，∴把原抛物线先向左平移2个单位，再向下平移32个单位．【点睛】本题考查二次函数解析式的求解和图象的平移，解题的关键是掌握解析式的求解方法和函数图象的平移方法．9．（2021·上海虹口区·九年级一模）已知二次函数的解析式为2122y x x =-．（1）用配方法把该二次函数的解析式化为()2y a x m k =++的形式；（2）选取适当的数据填入下表，并在图中所示的平面直角坐标系xOy 内描点，画出该函数的图像．x …………y …………【答案】（1）()21222y x =--；（2）见解析．【分析】（1）直接利用配方法即可把该二次函数的解析式化为顶点式；（2）列表、描点、连线，画出函数的图象即可．【详解】解：（1）2122y x x =-21(4)2x x =-21(444)2x x =-+-()21222x =--∴()21222y x =--；（2）填表如下：x……-20246……y……60-206……图像如下：．【点睛】此题主要考查了二次函数的性质以及二次函数图象，正确掌握配方法以及画二次函数图象的步骤是解题关键．。

2020-2021学年上海市金山区九年级(上)期末数学试卷(一模)

2020-2021学年上海市金山区九年级（上）期末数学试卷（一模）题号一二三总分得分第I卷（选择题）一、选择题（本大题共6小题，共24.0分）1.下列二次函数的图象中，其对称轴是x=1的为()A. y=x2+2xB. y=x2−2xC. y=x2−2D. y=x2−4x2.下列各点中，在二次函数y=−x2的图象上的是()A. (1,−1)B. (2,−2)C. (−2,4)D. (2,4)3.已知Rt△ABC中，∠A=90°，则bc是∠B的()A. 正切B. 余切C. 正弦D. 余弦4.已知α是锐角，且满足2sin(α+20°)=√3，则α的度数为()A. 80°B. 60°C. 40°D. 10°5.如果a⃗=2b⃗ (a⃗,b⃗ 均为非零向量)，那么下列结论错误的是()A. a⃗//b⃗B. a⃗−2b⃗ =0C. b⃗ =12a⃗ D. |a⃗|=2|b⃗ |6.如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，以点A为圆心作圆，如果圆A与线段BC没有公共点，那么圆A的半径r的取值范围是()A. 5≥r≥3B. 3<r<5C. r=3或r=5D. 0<r<3或r>5第II卷（非选择题）二、填空题（本大题共12小题，共48.0分）7.化简：32a⃗−(a⃗−32b⃗ )=______．8.已知函数f(x)=x−22x，那么f(3)=______．9. 如图，二次函数y =ax 2+bx +c 的图象与x 轴交于(3,0)，对称轴是直线x =1，当函数值y >0时，自变量x 的取值范围是____．10. 正五边形的中心角的度数是______ ．11. 已知⊙O 1的半径长为4，⊙O 2的半径长为r ，圆心距O 1O 2=6，当⊙O 1与⊙O 2外切时，r 的长为______．12. 在Rt △ABC 中，∠ACB =90°，BC =6，sinA =35，则AB =______． 13. 如图，在△ABC 中，∠B =45°，tanC =12，AB =√2，则AC =______．14. 如图．△ABC 的中线AD 、BE 相交于点G ，过点G 作GH//AC 交BC 于点H ，如果GH =2，那么AC =______．15. 如图，在△ABC 中，点D 在边AC 上，且CD =2AD.设AB ⃗⃗⃗⃗⃗ =a ⃗ ，AC ⃗⃗⃗⃗⃗ =b ⃗ ，那么BD ⃗⃗⃗⃗⃗⃗ =______.(结果用向量a ⃗ 、b ⃗ 的式子表示)16.如图，B，C，D，E为⊙A上的点，DE=5，∠BAC+∠DAE=180°，则圆心A到弦BC的距离为______．17.如图所示，在▱ABCD中，点E在边DC上，DE：EC=3：1，连接AE交BD于点F，则△DEF的面积与△BAF的面积之比为______．18.如图，点D在△ABC的边BC上，∠C+∠BAD=∠DAC，tan∠BAD=4，AD=√65，CD=13，则7线段AC的长为______．三、解答题（本大题共7小题，共78.0分）19.如图，在Rt△ABC中，∠C=90°，点D是AC边上一点，tan∠DBC=4，且BC=6，3 AD=4.求cos A的值．20.如图，已知AC和BD相交于点O，且AB//DC，OA=OB．求证：OC=OD．21.如图，已知二次函数y=ax2−4x+c的图象经过点A和点B．(1)求该二次函数的表达式；(2)写出该抛物线的对称轴及顶点坐标；(3)若点P(m,m)在该函数图象上，求m的值．22.如图，小山的一个横断面是梯形BCDE，EB//DC，其中斜坡DE的坡长为13米，坡度i=1：2.4，小山上有一座铁塔AB，在山坡的坡顶E处测得铁塔顶端A的仰角为45°，在与山坡的坡底D相距5米的F处测得铁塔顶端A的仰角为31°(点F、D、C在一直线上)，求铁塔AB的高度．(参考数值：sin31°≈0.52，cos31°≈0.86，tan31°≈0.6)23.如图，四边形ABCD是菱形，点E在AB延长线上，连接AC，DE.DE分别交BC，AC于点F，G，且CD·AE=AC·AG．求证：(1)△ABC∽△AGE；(2)AB2=DE·DG．<a<0) 24.如图，点A，B，C都在抛物线y=ax2−2amx+am2+2m−5(其中−14上，AB//x轴，∠ABC=135°，且AB=4．(1)填空：抛物线的顶点坐标为_____(用含m 的代数式表示)； (2)求△ABC 的面积(用含a 的代数式表示)；(3)若△ABC 的面积为2，当2m −5≤x ≤2m −2时，y 的最大值为2，求m 的值．25. 如图①，在Rt △ABC 中，∠ABC =90°，AB 是⊙O 的直径，⊙O 交AC 于点D ，过点D 的直线交BC 于点E ，交AB 的延长线于点P ，∠A =∠PDB ． (1)求证：PD 是⊙O 的切线；(2)若AB =4，DA =DP ，试求弧BD 的长；(3)如图②，点M 是AB ⏜的中点，连结DM ，交AB 于点N.若tanA =12，求DNMN的值．答案和解析1.【答案】B【解析】解：∵y=x2+2x=(x+1)2−1，∴y=x2+2x的对称轴是直线x=−1，故选项A不符合题意；∵y=x2−2x=(x−1)2−1，∴y=x2−2x的对称轴是直线x=1，故选项B符合题意；y=x2−2的对称轴是直线x=0，故选项C不符合题意，∵y=x2−4x=(x−2)2−4，∴y=x2−4x的对称轴是直线x=2，故选项D不符合题意；故选：B．根据各个选项中的函数解析式可以得到相应的对称轴，从而可以解答本题．本题考查二次函数的图象、二次函数的性质，解答本题的关键是明确题意，利用二次函数的性质解答．2.【答案】A【解析】解：当x=1时，y=−x2=−1，当x=−2时，y=−x2=−4，当x=2时，y=−x2=−4，所以点(1,−1)在二次函数y=−x2的图象上．故选：A．分别计算自变量为1和−2、2所对应的函数值，然后根据二次函数图象上点的坐标特征进行判断．本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．3.【答案】A【解析】解：如图，tanB=b．c故选A．根据题意画出直角三角形，根据锐角三角函数的定义便可直接解答．本题考查锐角三角函数的定义及运用：在直角三角形中，锐角的正弦为对边比斜边，余弦为邻边比斜边，正切为对边比邻边．4.【答案】C【解析】解：∵2sin(α+20°)=√3，∴sin(α+20°)=√3，2∴α+20°=60°，∴α=40°．故选C．首先利用特殊角的三角函数值求出α+20°的值，进而求出α即可．此题主要考查了特殊角的三角函数值，得出α+20°的值是解题关键．5.【答案】B【解析】解：A、正确．因为a⃗=2b⃗ (a⃗,b⃗ 均为非零向量)，所以a⃗与b⃗ 是方向相同的向量，即a⃗//b⃗ ；B、错误．应该是a⃗−2b⃗ =0⃗；a⃗；C、正确．由a⃗=2b⃗ 可得b⃗ =12D、正确．因为a⃗=2b⃗ 所以|a⃗|=2|b⃗ |；故选B．根据平行向量以及模的定义的知识求解即可求得答案，注意掌握排除法在选择题中的应用．本题考查了平面向量，注意，平面向量既有大小，又由方向，平行向量，也叫共线向量，是指方向相同或相反的非零向量．零向量和任何向量平行．6.【答案】D【解析】解：∵在Rt△ABC中，∠C=90°，AC=3，BC=4，以点A为圆心作圆，当圆A的半径0<r<3或r>5时，圆A与线段BC没有公共点；故选：D．根据直线与圆的位置关系得出相切时有一交点，再结合图形即可得出答案．此题主要考查了直线与圆的位置关系，结合题意画出符合题意的图形，从而得出答案．7.【答案】12a⃗+32b⃗【解析】解：原式=32a⃗−a⃗+32b⃗ =12a⃗+32b⃗ ．故答案是：12a⃗+32b⃗ ．平面向量的加减计算法则与实数的加减计算法则相同．考查了平面向量，解答此类题目时，直接去括号，然后计算加减法即可．8.【答案】16【解析】解：当x=3时，f(3)=3−22×3=16．故答案为：16．【分析】把x=3代入函数关系式，计算求值即可．本题考查求函数值.题目比较简单，已知函数解析式时，求函数值就是求代数式的值．9.【答案】−1<x<3【解析】解：∵二次函数y=ax2+bx+c的图象与x轴交于(3,0)，对称轴是直线x=1，∴图象与x轴的另一个交点为：(−1,0)，故当函数值y>0时，自变量x的取值范围是：−1<x<3．故答案为：−1<x<3．直接利用二次函数的对称性得出图象与x轴的另一个交点，进而得出答案．此题主要考查了抛物线与x轴的交点以及二次函数的性质，正确利用数形结合分析是解题关键．10.【答案】72°【解析】解：正五边形的中心角为：360°5=72°．故答案为：72°．根据正多边形的圆心角定义可知：正n边形的圆中心角为360°n，则代入求解即可．此题考查了正多边形的中心角的知识．题目比较简单，注意熟记定义．11.【答案】2【解析】解：∵⊙O1的半径长为4，⊙O2的半径长为r，圆心距O1O2=6，当⊙O1与⊙O2外切时，∴r+4=6，解得：r=2，故答案为：2；根据两圆的位置关系和数量之间的联系解答即可．本题考查的是圆与圆的位置关系与数量之间的联系，关键是根据两圆外切⇔d=R+r 解答．12.【答案】10【解析】【分析】本题主要考查锐角三角函数的定义，解题的关键是熟练掌握正弦函数的定义．由sinA=BCAB 知AB=BCsinA，代入计算可得．【解答】解：在Rt△ABC中，∵sinA=BCAB，BC=6，∴AB=BCsinA =635=10，故答案为10．13.【答案】√5【解析】解：过点A作AD⊥BC，垂足是点D，∵AB=√2，∴AD2+BD2=AB2=2，∵∠B=45°，∴∠BAD=∠B=45°，∴AD=BD，∴AD2=BD2=1，∴AD=BD=1，∵tanC=12，∴ADCD =12，∴CD=2，∴AC=√AD2+CD2=√12+22=√5．故答案为：√5．先过点A作AD⊥BC，垂足是点D，得出AD2+BD2=AB2=2，再根据∠B=45°，得出AD=BD=1，然后根据tanC=12，得出ADCD=12，CD=2，最后根据勾股定理即可求出AC．此题考查了解直角三角形，用到的知识点是勾股定理、解直角三角形等，关键是作出辅助线，构造直角三角形．14.【答案】6【解析】解：∵△ABC的中线AD、BE相交于点G，∴AGGD=2，∵GH//AC，∴GHAC =GDAD=13，∵GH=2∴AC=6，故答案为：6根据三角形重心的性质和平行线分线段成比例解答即可．本题考查的是平行线分线段成比例和三角形的重心的概念和性质，掌握三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键．15.【答案】13b⃗ −a⃗【解析】解：∵CD =2AD ，AC ⃗⃗⃗⃗⃗ =b ⃗ ， ∴AD ⃗⃗⃗⃗⃗⃗ =13AC ⃗⃗⃗⃗⃗ =13b ⃗ ，∵BD ⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ ， ∴BD ⃗⃗⃗⃗⃗⃗ =−a ⃗ +13b ⃗ ，故答案为：13b⃗ −a ⃗ ．求出AD ⃗⃗⃗⃗⃗⃗ ，根据BD ⃗⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AD⃗⃗⃗⃗⃗⃗ 求解即可．本题考查平面向量，三角形法则等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．16.【答案】52【解析】【分析】本题考查的是垂径定理、三角形中位线定理、圆心角、弧、弦之间的关系，掌握垂径定理、三角形中位线定理是解题的关键．延长CA 交⊙A 于F ，连接BF ，作AH ⊥BC 于H ，根据圆心角、弧、弦之间的关系定理求出BF ，根据垂径定理得到CH =HB ，根据三角形中位线定理计算即可．【解答】解：延长CA 交⊙A 于F ，连接BF ，作AH ⊥BC 于H ，∵∠BAC +∠DAE =180°，∠BAC +∠BAF =180°， ∴∠BAF =∠DAE ， ∴BF⏜=DE ⏜， ∴BF =DE =5， ∵AH ⊥BC ，∴CH =HB ，又CA =AF ， ∴AH =12BF =52，故答案为：52．17.【答案】9：16【解析】【分析】可证明△DFE∽△BFA，根据相似三角形的面积之比等于相似比的平方即可得出答案．本题考查了平行四边形的性质以及相似三角形的判定和性质，注：相似三角形的面积之比等于相似比的平方．【解答】解：∵四边形ABCD为平行四边形，∴DC//AB，∴△DFE∽△BFA，∵DE：EC=3：1，∴DE：DC=3：4，∴DE：AB=3：4，∴S△DFE：S△BFA=9：16．故答案为：9：16．18.【答案】4√13【解析】解：作∠DAE=∠BAD交BC于E，作DF⊥AE交AE于F，作AG⊥BC交BC于G．∵∠C+∠BAD=∠DAC，∴∠CAE=∠ACB，∴AE=EC，∵tan∠BAD=4，7∴设DF=4x，则AF=7x，在Rt△ADF中，AD2=DF2+AF2，即(√65)2=(4x)2+(7x)2，解得x1=−1(不合题意舍去)，x2=1，∴DF=4，AF=7，设EF=y，则CE=7+y，则DE=6−y，在Rt△DEF中，DE2=DF2+EF2，即(6−y)2=42+y2，，解得y=53∴DE =6−y =133，AE =263，∴设DG =z ，则EG =133−z ，则(√65)2−z 2=(263)2−(133−z)2，解得z =1， ∴CG =12，在Rt △ADG 中，AG =√AD 2−DG 2=8，在Rt △ACG 中，AC =2+CG 2=4√13．故答案为：4√13．作∠DAE =∠BAD 交BC 于E ，作AF ⊥BC 交BC 于F ，作AG ⊥BC 交BC 于G.根据三角函数设DF =4x ，则AF =7x ，在Rt △ADF 中，根据勾股定理得到DF =4，AF =7，设EF =y ，则CE =7+y ，则DE =6−y ，在Rt △DEF 中，根据勾股定理得到DE =133，AE =263，设DG =z ，则EG =133−z ，则(√65)2−z 2=(263)2−(133−z)2，依此可得CG =12，在Rt △ADG 中，据勾股定理得到AG =8，在Rt △ACG 中，据勾股定理得到AC =4√13．考查了勾股定理，等腰三角形的判定与性质，解直角三角形，解题的关键是根据勾股定理得到AG 和CG 的长．19.【答案】解：在Rt △DBC 中，∵∠C =90°，BC =6，∴tan∠DBC =CD BC=43． ∴CD =8．∴AC =AD +CD =12．在Rt △ABC 中，由勾股定理得， AB =√AC 2+BC 2=√122+62=6√5， ∴cosA =ACAB =65=25√5．【解析】先解Rt △DBC ，求出DC 的长，然后根据AC =AD +DC 即可求得AC ，再由勾股定理得到AB ，最后再求cos A 的值即可．本题主要考查了解直角三角形．熟练掌握三角函数的定义是解题的关键．20.【答案】证明：∵AB//DC ，∴∠A =∠C ，∠B =∠D ， ∵OA =OB ， ∴∠A =∠B ，∴∠C =∠D ， ∴OC =OD ．【解析】利用平行线的性质可求得∠A =∠C ，∠B =∠D ，利用OA =OB ，可求得∠A =∠B ，则可求得∠C =∠D ，则可证得OC =OD ．本题主要考查等腰三角形的判定和性质及平行线的性质，利用平行线的性质及等腰三角形的性质证得∠C =∠D 是解题的关键．21.【答案】解：(1)将A(−1,−1)，B(3,−9)代入，得{a +4+c =−19a −12+c =−9， ∴a =1，c =−6， ∴y =x 2−4x −6；(2)由y =x 2−4x −6=(x −2)2−10，对称轴：直线x =2，顶点坐标：(2,−10)；(3)∵点P(m,m)在函数图象上， ∴m 2−4m −6=m ， ∴m =6或−1．【解析】本题主要考查待定系数法求二次函数解析式及二次函数的对称轴、顶点坐标，掌握二次函数的性质及待定系数法是解题的关键．(1)由条件可知点A 和点B 的坐标，代入解析式可得到关于a 和c 的二元一次方程组，解得a 和c ，可写出二次函数的解析式；(2)利用配方法写出把二次函数写成顶点式，即可得其对称轴与顶点坐标； (3)把点的坐标代入可求得m 的值．22.【答案】解：延长AB 交DC 于G ，过E 作EH ⊥CD 于H ，则四边形EHGB 是矩形，∵斜坡DE 的坡长为13米，坡度i =1：2.4， ∴设EH =5x ，则DH =12x ，∵EH2+DH2=DE2，∴(5x)2+(12x)2=132，∴x=1(负值舍去)，∴EH=5，DH=12，∵EB//DC，∴∠ABE=∠AGH=90°，∵∠AEB=45°，∴AB=BE，∴HG=AB，∴FG=5+12+AB，AG=AB+5，∵∠F=31°，∴tanF=tan31°=AGFG =AB+517+AB=0.6，∴AB=13米，答：铁塔AB的高度是13米．【解析】延长AB交DC于G，过E作EH⊥CD于H，则四边形EHGB是矩形，根据勾股定理得到EH=5，DH=12，根据三角函数的定义解直角三角形，然后列方程可得到结论．本题考查了解直角三角形的应用−仰角俯角问题，解直角三角形的应用−坡度坡角问题，矩形的性质，掌握的作出辅助线是解题的关键．23.【答案】证明：(1)∵CD⋅AE=AC⋅AG．∴CDAG =ACAE，∵四边形ABCD是菱形，∴AB=CD，∴ABAG =ACAE，∵∠BAC=∠GAE，∴△ABC∽△AGE；(2)∵△ABC∽△AGE，∴∠ACB=∠E，∵四边形ABCD是菱形，∴AB=AD，BC//AD，∴∠ACB =∠CAD =∠E ， ∵∠ADG =∠ADE ， ∴△ADG∽△EDA ， ∴AD DE=DG AD，∴AD 2=DE ⋅DG ， ∴AB 2=DE ⋅DG ．【解析】本题考查相似三角形的判定与性质、菱形的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．(1)只要证明ABAG =ACAE ，又∠BAC =∠GAE ，即可证明△ABC∽△AGE ； (2)只要证明△ADG∽△EDA ，可得ADDE =DGAD ，推出AD 2=DE ⋅DG 即可证明．24.【答案】(1)(m,2m −5)；(2)S △ABC =−8a+2a；(3)72或10+2√10．【解析】[分析](1)利用配方法将二次函数解析式由一般式变形为顶点式，此题得解；(2)过点C 作直线AB 的垂线，交线段AB 的延长线于点D ，由AB//x 轴且AB =4，可得出点B 的坐标为(m +2,4a +2m −5)，设BD =t ，则点C 的坐标为(m +2+t,4a +2m −5−t)，利用二次函数图象上点的坐标特征可得出关于t 的一元二次方程，解之取其正值即可得出t 值，再利用三角形的面积公式即可得出S △ABC 的值；(3)由(2)的结论结合S △ABC =2可求出a 值，分三种情况考虑：①当m >2m −2，即m <2时，x =2m −2时y 取最大值，利用二次函数图象上点的坐标特征可得出关于m 的一元二次方程，解之可求出m 的值；②当2m −5≤m ≤2m −2，即2≤m ≤5时，x =m 时y 取最大值，利用二次函数图象上点的坐标特征可得出关于m 的一元一次方程，解之可求出m 的值；③当m <2m −5，即m >5时，x =2m −5时y 取最大值，利用二次函数图象上点的坐标特征可得出关于m 的一元一次方程，解之可求出m 的值．综上即可得出结论． [详解]解：(1)∵y =ax 2−2amx +am 2+2m −5=a(x −m)2+2m −5， ∴抛物线的顶点坐标为(m,2m −5)，故答案为：(m,2m −5)；(2)过点C 作直线AB 的垂线，交线段AB 的延长线于点D ，如图所示，∵AB//x轴，且AB=4，∴点B的坐标为(m+2,4a+2m−5)，∵∠ABC=135°，∴设BD=t，则CD=t，∴点C的坐标为(m+2+t,4a+2m−5−t)，∵点C在抛物线y=a(x−m)2+2m−5上，∴4a+2m−5−t=a(2+t)2+2m−5，整理，得：at2+(4a+1)t=0，解得：t1=0(舍去)，t2=−4a+1a，∴S△ABC=12AB⋅CD=−8a+2a；(3)∵△ABC的面积为2，∴−8a+2a=2，解得：a=−15，∴抛物线的解析式为y=−15(x−m)2+2m−5．分三种情况考虑：①当m>2m−2，即m<2时，则当x=2m−2时，y取最大值，有−15(2m−2−m)2+2m−5=2，整理，得：m2−14m+39=0，解得：m1=7−√10(舍去)，m2=7+√10(舍去)；②当2m−5≤m≤2m−2，即2≤m≤5时，则当x=m时，y取最大值，有2m−5=2，解得：m=72；③当m<2m−5，即m>5时，则当x=2m−5时，y取最大值，(2m−5−m)2+2m−5=2，有−15整理，得：m2−20m+60=0，解得：m3=10−2√10(舍去)，m4=10+2√10．或10+2√10．综上所述：m的值为72[点睛]本题考查了二次函数解析式的三种形式、二次函数图象上点的坐标特征、等腰直角三角形、解一元二次方程以及二次函数的最值，解题的关键是：(1)利用配方法将二次函数解析式变形为顶点式；(2)利用等腰直角三角形的性质找出点C的坐标；(3)分m<2、2≤m≤5及m>5三种情况考虑．25.【答案】证明：(1)连结OD，∵AB是⊙O的直径，∴∠ADB=90°，∴∠A+∠ABD=90°，又∵OA=OB=OD，∴∠BDO=∠ABD，又∵∠A=∠PDB，∴∠PDB+∠BDO=90°，即∠PDO=90°，且D在圆上，∴PD是⊙O的切线(2)设∠A=x°，∵DA=DP，∴∠A=∠P=x°，∴∠DBA=∠P+∠BDP=x°+x°=2x°，在△ABD中，∠A+∠ABD=90°，∴x°+2x°=90o，即x=30，∴∠DOB=60°，∴弧BD长=60°×π×2180∘=23π(3)连结OM，过D作DF⊥AB于点F，∴点M是的AB⏜的中点，∴OM⊥AB，∵tanA=12=BDAD，∴设BD=x，则AD=2x，AB=√5x=2OM，∴OM=√5x2，在Rt△BDF中，S△ADB=12×AB×DF=12×AD×DB∴DF=2√55x，∵∠MON=∠DFN=90°，∠DNF=∠MNO ∴△OMN∽△FDN∴DNMN =DFOM=2√55x√52x=45．【解析】(1)由圆周角的定理可得∠ADB=90°，可得∠A+∠ABD=90°，可求∠PDB+∠BDO=90°，可得结论；(2)设∠A=x，由等腰三角形的性质和三角形外角的性质可得∠DBA=∠P+∠BDP= x+x=2x，由三角形内角和可求x的值，由弧长公式可求弧BD的长；(3)连结OM，过D作DF⊥AB于点F，设BD=x，则AD=2x，AB=√5x=2OM，可求OM，DF的长，通过证明△OMN∽△FDN，可求DNMN的值．本题是圆的综合题，考查了圆的知识，弧长公式，相似三角形的判定和性质，勾股定理等知识，添加恰当辅助线构造相似三角形是本题的关键．。

上海市金山初级中学2021-2022学年九年级上学期第一次月考数学试题

解：由题意得：
，
∵AB=4，
∴ ；
故答案为．
本题主要考查黄金分割比，熟练掌握黄金分割比是解题的关键．
11.在△ABC中，中线AD和中线CE相交于G，则AG：AD＝___．
2：3
由三角形重心的概念可知，再根据重心的性质即可求得AG=2GD，AD=3GD，即可求得AG：AD．
解：∵AD、AE分别是三角形的中线，
22.如图，在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO交AD于点F，OE⊥OB交BC边于点E．求证：△ABF∽△COE．
证明见解析
由∠BAD+∠ABC=90°，∠C+∠ABC=90°得∠BAF=∠C；由∠ABO+∠AOB=90°，∠AOB+∠COE=90°得∠ABF=∠COE．由两对角对应相等判定三角形相似．
12
首先证明，，利用等高模型解决问题即可．
解：四边形是平行四边形，
，，，
∴ ，
，
，，
的面积是2，
的面积为4，的面积为8，
的面积为．
故答案为12．
本题考查平行四边形的性质，相似三角形的判定和性质定理，解题的关键是熟练掌握基本知识，属于中考常考题型．
16.如图，已知正方形DEFG的边EF在 ABC的边BC上，顶点D、G分别在边AB、AC上，BC＝15，高AH＝10，则正方形DEFG的边长等于___．
6
设正方形的边长为，则，所以，再证明，则根据相似三角形的对应高之比等于相似比得到，由此计算即可求得答案．
解：设正方形的边长为，则，
又∵高AH＝10，
，
∵四边形DEFG 正方形，
∴ ，

2021上海初三数学一模试题分类整理(几何综合题)

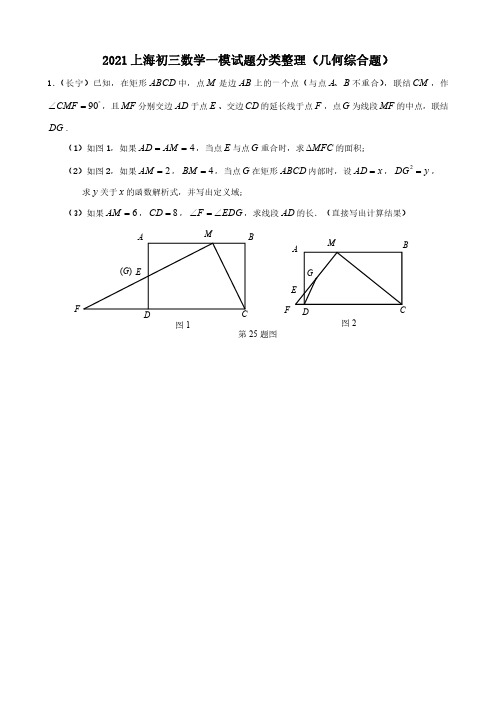
2021上海初三数学一模试题分类整理（几何综合题）1．（长宁）已知，在矩形ABCD 中，点M 是边AB 上的一个点（与点A B 、不重合），联结CM ，作90CMF ︒∠=，且MF 分别交边AD 于点E 、交边CD 的延长线于点F ，点G 为线段MF 的中点，联结DG .（1）如图1，如果4AD AM ==，当点E 与点G 重合时，求MFC ∆的面积；（2）如图2，如果2AM =，4BM =，当点G 在矩形ABCD 内部时，设AD x =，2DG y =，求y 关于x 的函数解析式，并写出定义域；（3）如果6AM =，8CD =，F EDG ∠=∠，求线段AD 的长．（直接写出计算结果）ABCDEF(G )M图1ABCDEFGM图2第25题图2．（杨浦）如图，已知在Rt△ABC 中，∠ACB =90°，AC =BC =4，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，∠EDB =∠ADC ，过点E 作EF ⊥AD ，垂足为点G ，交射线AC 于点F .（1）如果点D 为边BC 的中点，求∠DAB 的正切值；（2）当点F 在边AC 上时，设CD =x ，CF =y ，求y 关于x 的函数解析式及定义域；（3）联结DF ，如果△CDF 与△AGE 相似，求线段CD 的长.备用图ABC第25题图ABCEDG F3．（徐汇）如图，在ABC Rt ∆中，︒=∠90ACB ，12=AC ，5=BC ，点D 是边AC 上的动点，以CD 为边在ABC ∆外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ．（1）当BE AE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH ∆和ABG ∆相似，求ABE ∠sin 的值；（3）当AE AG =时，求CD 的长．（备用图）BAC（第25题图）GFED BAC4．（松江）如图，已知在等腰△ABC中，AB=AC=，tan∠ABC=2，BF⊥AC，垂足为F，点D是边AB上一点（不与A，B重合）.（1）求边BC的长；（2）如图2，延长DF交BC的延长线于点G，如果CG=4，求线段AD的长；（3）过点D作DE⊥BC，垂足为E，DE交BF于点Q，联结DF，如果△DQF和△ABC相似，求线段BD的长.D·B AFC（图1）DBAFC（图2）G BAFC（备用图）5．（普陀）如图，矩形ABCD 中，1AB =，3BC =，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DFAB BE=；（2）当点G 在△ADF 的内部时，用x 的代数式表示ADG ∠的余切；（3）当∠FGD =∠AFE 时，求线段BE 的长．F图14CB A DE G备用图CBAD6．（浦东）四边形ABCD 是菱形，∠B ≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF ⊥AE ，EF 与边CD 交于点F ，且EC =3CF ．（1）如图1，当∠B =90°时，求ABE S △与ECF S △的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值；（3）如图3，联结AF ，当∠AFE =∠B 且CF =2时，求菱形的边长．（第25题图3）（第25题图2）（第25题图1）7．（闵行）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF ⊥DE ，交BC 的延长线于点F ，联结EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：△ADE ∽△CDF ，并求EFD ∠的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结BG ．当△BGE 与△DEH 相似时，求x 的值．（第25题图）B A CF ED GH（备用图）B A CFEDGH8．（静安）已知∠MAN 是锐角，点B 、C 在边AM 上，点D 在边AN 上，∠EBD =∠MAN ，且CE //BD ，sin∠MAN=35，AB =5，AC =9．（1）如图1，当CE 与边AN 相交于点F 时，求证：DF ·CE=BC ·BE ；（2）当点E 在边AN 上时，求AD 的长；（3）当点E 在∠MAN 外部时，设AD =x ，△BCE 的面积为y ，求y 与x 之间的函数解析式，写出定义域．（第25题图）（备用图）（图1）FAB DCE NM9.（嘉定）在矩形ABCD 中，6AB =，8AD =，点E 在CD 边上，1tan 2DAE ∠=.点F 是线段AE 上一点，联结BF ，CF.（1）如图11，如果3tan 4CBF ∠=，求线段AF 的长；（2）如图12，如果12CF BC =，①求证：∠CFE =∠DAE ；②求线段EF 的长.图11图12备用图10．（黄浦）如图10，四边形ABCD 中，AB =AD =4，CB =CD =3，∠ABC =∠ADC =90°，点M 、N 是边AB 、AD 上的动点，且∠MCN =12∠BCD ，CM 、CN 与对角线BD 分别交于点P 、Q .（1）求sin∠MCN 的值；（2）当DN =DC 时，求∠CNM 的度数；（3）试问：在点M 、N 的运动过程中，线段比PQMN的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相应的位置.P NM DC BAQ（图10）11．（虹口）如图12，在△ABC 中，∠ABC =90°，AB =3，BC =4，过点A 作射线AM //BC ，点D、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），联结BD 、BE 分别交边AC 于点F 、G ，∠DBE =∠C ．（1）当AD =1时，求FB 的长；（2）设AD =x ，FG =y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果△DBH 是等腰三角形，请直接写出AD 的长．C FGE D A B 图12C A B 备用图MM12.（奉贤）已知⊙O 的直径AB =4，点P 为弧AB 上一点，联结PA 、PO ，点C 为劣弧AP 上一点（点C 不与点A 、P 重合），联结BC 交PA 、PO 于点D 、E .（1）如图10，当cos∠CBO =87时，求BC 的长；（2）当点C 为劣弧AP 的中点，且△EDP 与△AOP 相似时，求∠ABC 的度数；（3）当AD =2DP ，且△BEO 为直角三角形时，求四边形AOED 的面积.备用图备用图A B图10PA BC D EO A B13．（崇明）如图，Rt△ABC 中，90ACB ∠=︒，6AC =，8BC =．点D 为斜边AB 的中点，ED ⊥AB ，交边BC 于点E ．点P 为射线AC 上的动点，点Q 为边BC 上的动点，且运动过程中始终保持PD QD ⊥．（1）求证：△ADP ∽△EDQ ；（2）设AP x =，BQ y =．求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结PQ ，交线段ED 于点F ．当△PDF 为等腰三角形时，求线段AP 的长．A D BCPEQ 第25题图A D B C P E Q 第25题备用图F14.（宝山）如图3，已知Rt△ABC 中，∠ACB =90°，AC =BC ，点D、E 在边AB 上，∠DCE =45°，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD.（1）求证：DE BE CE ⋅=2；（2）当AC =3，AD =2BD 时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F .设x BCBD =，y FMD =∠tan ，求y 关于x 的函数关系式，并写出定义域.EM DCAB （图3）15．（青浦）在△ABC 中，∠C=90°，AC =2，BC =23，点D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且BQ =32BP ，联结PQ 、QD 、DP ．（1）求证：PQ ⊥AB ；（2）如果点P 在线段BC 上，当△PQD 是直角三角形时，求BP 的长；（3）将△PQD 沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于△ABC 内，请直接写出BP 的取值范围．（第25题图）（备用图）A C O 第25题备用图16.（金山）定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中，O A ∠=∠21.已知：如图2，AC 是⊙O 的一条弦，点D 在⊙O 上（与A 、C 不重合），联结DC 交射线AO 于点E ，联结OD ，⊙O 的半径为5，43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时，若DOE ∆与AEC ∆相似，求DCA ∠的正切值.(3)当1=OE 时，求点A 与点D 之间的距离（直接写出答案）.AB CO第25题图1第25题图2E D C A O。

上海2020-2021学年初三数学一模考1-17题（二次函数汇编）学生版

知识回顾考点①二次函数图像 ②二次函数图像的性质 ③几种二次函数之间的图像变换规律④解析式-通过二次函数过的点的坐标求解析式 ⑤一般式，顶点式，配方法转换 ⑥图像顶点，对称轴，开口方向，最大最小值 ⑦一次函数与二次函数结合的图像问题，求解析式问题一、二次函数概念1．二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数.二次函数2y ax bx c =++的定义域是一切实数.2. 二次函数2y ax bx c =++的结构特征：（1）等号左边是函数，右边是关于自变量x 的二次式，x 的最高次数是2．（2）,,a b c 是常数，a 是二次项系数，b 是一次项系数，c 是常数项．二、二次函数2y ax bx c =++的图像和性质1.二次函数()2y a x m k =++与2y ax bx c =++的比较配方可以得到前者，即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭，其中2b m a =-，244ac b k a -=．2.二次函数2y ax bx c =++图象的画法五点绘图法：抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.三、抛物线与坐标轴的交点（1）与y 轴的交点为()0,c .令0,x y c == （2）与x 轴的交点：二次函数2y ax bx c =++的图像与x 轴的两个交点的横坐标1x 、2x ，是对应一元二次方程20ax bx c ++=的两个实数根.四、二次函数的图像平移平移步骤：⑴将抛物线解析式转化成顶点式()2y a x h k=-+，确定其顶点坐标()h k ，；⑵保持抛物线2y ax =的形状不变，将其顶点平移到()h k ，处，具体平移方法如下：左加右减，上加下减五、二次函数2y ax bx c =++的性质（1）当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．对称轴左侧，y 随x 的增大而减小；对称轴右侧，y 随x 的增大而增大；当2bx a=-时，y 有最小值244ac b a-．（2）当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．对称轴左侧，y 随x 的增大而增大；对称轴右侧，y 随x 的增大而减小；当2bx a=-时，y 有最大值244ac b a-．六、待定系数法求解析式题型一、二次函数的概念（2021虹口一模3）下列函数中，属于二次函数的是（）A ．212y x =-； B ．y C ．22y x =-； D ．22 (2)y x x --=．（2021闵行一模1）下列函数中，是二次函数的是（）（A ）223y x x =--；（B ）22(1)y x x =--+；（C ）21129y x x =+；（D ）2y ax bx c =++．（2021浦东新区一模3）下列y 关于x 的函数中，一定是二次函数的是（）（A ）2(1)3y k x =-+；（B ）211y x=+；（C ）2(1)(2)y x x x =+--；（D ）227y x x =-．（2021普陀一模1）下列函数中，y 关于x 的二次函数是（）（A ）2y ax bx c =++；（B ）211y x =+；（C ）(1)y x x =+；（D ）()222y x x =+-．（2021奉贤一模9）如果二次函数1+2+=2-m x mx y 的图像经过点P （1，2），那么m 的值为．（2021虹口一模9）如果抛物线2y x a =-经过点()2 0，，那么a 的值是．（2021金山一模2）下列各点在抛物线22x y =上的是（）（A ）()2,2；（B ）()42，；（C ）)(8,2；（D ）()16,2. （2021金山一模8）已知()x x x f 32+=，那么()=-2f ．（2021浦东新区一模6）已知点A （1，2）、B （2，3）、C （2，1），那么抛物线21y ax bx =++可以经过的点是（）（A ）点A 、B 、C ；（B ）点A 、B ；（C ）点A 、C ；（D ）点B 、C ．题型二、开口方向（2021静安一模10）二次函数223y x x =-图像的开口方向是．（2021宝山一模13）如果抛物线()m x m y ++=21（m 是常数）的顶点坐标在第二象限，那么它的开口方向 .（2021虹口一模10）如果抛物线2(+1)y k x =有最高点，那么k 的取值范围是_____ （2021嘉定一模13）如果抛物线2(21)y a x =-的开口向下，那么实数a 的取值范围是．（2021杨浦一模13）已知抛物线2(1)1y a x =-+的开口向上，那么a 的取值范围是．（2021浦东新区一模13）如果抛物线()24y m x m =++经过原点，那么该抛物线的开口方向．（填“向上”或“向下”）题型三、对称轴（2021虹口一模11）如果抛物线l 经过点A (2-，0)和B (5，0)，那么该抛物线的对称轴是直线．（2021黄浦一模14）已知二次函数图像经过点（3,4）和（7,4），那么该二次函数图像的对称轴是直线．（2021金山一模1）已知二次函数()122--=x y ，那么该二次函数图像的对称轴是（）（A ）直线2=x ；（B ）直线2-=x ；（C ）直线1=x ；（D ）直线1-=x .（2021嘉定一模16）如果抛物线2(0)y ax bx c a =++≠的对称轴是直线1x =，那么2a b + 0. （从＜，=，＞中选择）（2021静安一模13）在二次函数223y x x =-+图像的上升部分所对应的自变量x 的取值范围是．（2021青浦一模12）二次函数2+2y x x m =+图像上的最低点的横坐标为．（2021徐汇一模3）已知抛物线c x x y ++-=42经过点)3,4(，那么下列各点中，该抛物线必经过的点是（）（A ）)2,0(；（B ）)3,0(；（C ）)4,0(；（D ）)5,0(．题型四、顶点（2021嘉定一模3）抛物线223y x =-的顶点坐标是（）（A ）23-（，）；（B ）23（，）；（C ）03-（，）；（D ）03（，）．（2021静安一模11）抛物线236y x =-的顶点坐标为．（2021普陀一模10）二次函数224y x x =+图像的顶点坐标为．（2021崇明一模5）抛物线2()y a x k k =-+的顶点总在（）(A)第一象限；(B)第二象限；(C)直线y x =上； (D)直线y x =-上．（2021黄浦一模17）如果抛物线()232y x b x c =+++的顶点为（b ，c ），那么该抛物线的顶点坐标是．（2021嘉定一模15）如果抛物线2()2y x m k =++-的顶点在x 轴上，那么常数k 为．（2021青浦一模4）抛物线 ()322---=x y 的顶点坐标是（）（A ）（2，-3）；（B ）（-2，-3）；（C ）（2，3）；（D ）（-2，3）．题型五、与x y 、轴交点（2021崇明一模13）函数2245y x x =+-的图像与y 轴的交点的坐标为．（2021嘉定一模14）二次函数2(+1)3y x =-的图像与y 轴的交点坐标为．题型六、增减性（2021虹口一模12）沿着x 轴正方向看，抛物线22y x =-在y 轴左侧的部分是的（填“上升”或“下降”）．（2021金山一模9）抛物线22x y -=沿着x 轴正方向看，在y 轴的左侧部分是．（填“上升”或“下降”）（2021闵行一模9）抛物线23y x x =--在对称轴的右侧部分是的（填“上升”或“下降”）．（2021青浦一模11）抛物线223y x =-在y 轴左侧的部分是．（填“上升”或“下降”）（2021徐汇一模10）已知二次函数1)23(2-+=x a y 的图像在直线23-=x 的左侧部分是下降的，那么a 的取值范围是_____．（2021普陀一模9）沿着x 轴正方向看，如果抛物线()22y a x =-在对称轴左侧的部分是下降的，那么a 的取值范围是．（2021奉贤一模10）如果二次函数21=）-（x y 的图像上有两点（2，y 1）和（4，y 2），那么y 1 _y 2（填“>”、“=”或“<”）．（2021浦东新区一模14）如果（2，1y ）、（3，2y ）是抛物线()21y x =+上两点，那么1y ___2y ．（填“>”或“<”）（2021松江一模12）已知点()12,A y 、()23,B y 在抛物线22y x x c =-+（c 为常数）上，则1y _____2y ．（填“>”、“=”或“<”）（2021长宁一模13）已知抛物线22y x x c =-+经过点()()212y y -1，，，，试比较1y 和2y 的大小：1y 2y （填“>”，“<”或“=”）．（2021普陀一模8）如果正比例函数y kx =的图像经过第一、三象限，那么y 的值随着x 的值增大而．（填“增大”或“减小”）题型七、函数的平移（2021宝山一模5）将抛物线2x y =先向右平移1个单位长度，再向上平移2个单位长度，两次平移后得到的抛物线的表达式为（）（A ）()212--=x y ；（B ）()212-+=x y ；（B ）()212+-=x y ；（D ）()212++=x y .（2021崇明一模14）如果将抛物线2(1)y x =-先向左平移2个单位，再向上平移1个单位，那么所得的新抛物线的解析式为．（2021奉贤一模1）将抛物线22=x y 向左平移1个单位后得到的抛物线表达式是（）（A ）12=2-x y ；（B ）1+2=2x y ；（C ）21+2=）（x y ；（D ）212=）-（x y .（2021虹口一模4）将抛物线23y x =-向右平移2个单位后得到的新抛物线表达式是（）A ．21y x =-；B ．25y x =-；C ．2+23y x =-（）；D ．223y x =--（）．（2021静安一模3）将抛物线3)1(22-+=x y 平移后与抛物线22x y =重合，那么平移的方法可以是（）（A ）向右平移1个单位，再向上平移3个单位；（B ）向右平移1个单位，再向下平移3个单位；（C ）向左平移1个单位，再向上平移3个单位；（D ）向左平移1个单位，再向下平移3个单位．（2021闵行一模10）将抛物线22y x x =+向下平移1个单位，那么所得抛物线与y 轴的交点的坐标为．（2021青浦一模10）将抛物线2y x =-向上平移2个单位，所得抛物线的表达式是．（2021松江一模3）抛物线22y x =向右平移3个单位后得到的抛物线是（）（A ）223y x =+；（B ）223y x =-；（C ）22(3)y x =+；（D ）22(3)y x =-．（2021徐汇一模1）将抛物线2)1(2+=x y 先向右平移3个单位，再向下平移2个单位后，所得抛物线的表达式是（）（A ）2)2(22--=x y ；（B ）2)2(22+-=x y ；（C ）2)4(22-+=x y ；（D ）2)4(22++=x y ．（2021杨浦一模12）已知抛物线2y x =，把该抛物线向上或向下平移，如果平移后的抛物线经过点A （2，2），那么平移后的抛物线的表达式是．（2021长宁一模11）将抛物线221y x =- 向下平移3个单位后，得到新抛物线的表达式为．题型八、a b c 、、符号的判定（2021宝山一模6）如图所示是二次函数()02≠++=a c bx ax y 图像的一部分，那么下列说法中不正确．．．的是（）（A ）0<ac ；（B ）抛物线的对称轴为直线1=x ；（C ）0=+-c b a ；（D ）点（-2，1y ）和（2，2y ）在抛物线上，则21y y >.（2021闵行一模3）如图，在平面直角坐标系xOy 中，二次函数2y a x b x c =++图像经过点O（0，0），那么根据图像，下列判断中正确的是（）（A ）0a <；（B ）0b >；（C ）0ab >；（D ）0c =．x 3-1 o 1y（第3题图）yx O（2021嘉定一模6）二次函数2()y a x m k =++的图像如图1所示，下列四个选项中，正确的是（）（A ）00m k <<，；（B ）00m k <>，；（C ）00m k ><，；（D ）00m k >>，.（2021长宁一模4）已知二次函数2(0)y ax bx c a =++≠的图像如图所示，那么a c 、满足（）（A ） 0a >，0c >；（B ）0a >，0c < ；（C ） 0a <，0c >；（D ）0a <，0c <．题型九、二次函数的应用（2021奉贤一模11）如图2，用一段篱笆靠墙围成一个大长方形花圃（靠墙处不用篱笆），中间用篱笆隔开分成两个小长方形区域，分别种植两种花草，篱笆总长为17米（恰好用完），围成的大长方形花圃的面积为24平方米．设垂直于墙的一段篱笆长为x 米，可列出方程为．（2021松江一模11）一个边长为2厘米的正方形，如果它的边长增加x （x >0）厘米，则面积随之增加y 平方厘米，那么y 关于x 的函数解析式为_______________________．（2021黄浦一模15）如图2，一个管道的截面图，其内径（即内圆半径）为10分米，管壁厚为x 分米，假设该管道的截面（阴影）面积为y 平方分米，那么y 关于x 的函数解析式是．（不必写定义域）（2021杨浦一模13）如图，已知小李推铅球时，铅球运动过程中离地面的高度y （米）关于水平距离x （米）的函数解析式为21251233y x x =-++，那么铅球运动过程中最高点离地面的距离为米．题型十、图像与性质综合（2021普陀一模11）如图2，已知二次函数2y ax bx c =++的图像经过点()1,0A ，那么()1f - 0．（填“＞”、“＜”或“=”）（2021黄浦一模2）抛物线243y x x =-+-不经过（）（A ）第一象限；（B ）第二象限；（C ）第三象限；（D ）第四象限．（2021静安一模12）如果一次函数(2)1y m x m =-+-的图像经过第一、二、四象限，那么常数m 的取值范围为．（2021宝山一模14）已知一条抛物线具有以下特征：（1）经过原点；（2）在y 轴左侧的部分，图像上升，在y 轴右侧的部分，图像下降．试写出一个符合要求的抛物线的表达式： . （2021黄浦一模5）小明准备画一个二次函数的图像，他首先列表（如下），但在填写函数值），那么这个被蘸上了墨水的函数值是（）（A ）-1；（B ）3；（C ）4；（D ）0．（2021长宁一模15）已知二次函数2()f x ax bx c =++的部分对应值如下表，那么(3)f -的值为．（2021普陀一模4）在下列对抛物线2(1)y x =--的描述中，正确的是（）（A ）开口向上；（B ）顶点在x 轴上；（C ）对称轴是直线1x =-；（D ）与y 轴的交点是（0，1）．（2021杨浦一模1）关于抛物线2y x x =-，下列说法中，正确的是（）（A ）经过坐标原点；（B ）顶点是坐标原点；（C ）有最高点；（D ）对称轴是直线x =1．（2021奉贤一模17）当两条曲线关于某直线l 对称时，我们把这两条曲线叫做关于直线l 的对称曲线．如果抛物线C 1：x x y 2=2-与抛物线C 2是关于直线x =-1的对称曲线，那么抛物线C 2的表达式为．（2021杨浦一模11）已知抛物线243y x x =-+与x 轴交于点A 、B ，与y 轴交于点C ，那么△ABC的面积等于．。

2021年上海市16区中考数学一模考点分类汇编专题05 圆(解析版)

2021年上海市16区中考数学一模汇编专题05 圆一、单选题1．（2021·上海金山区·九年级一模）如图，已知Rt ABC ∆中，90C ∠=，3AC =，4BC =，如果以点C 为圆心的圆与斜边AB 有公共点，那么⊙C 的半径r 的取值范围是（）A ．1205r ≤≤B ．1235r ≤≤C ．1245r ≤≤D ．34r ≤≤【答案】C 【分析】作CD⊙AB 于D ，根据勾股定理计算出AB=13，再利用面积法计算出125CD =然后根据直线与圆的位置关系得到当1254≤≤r 时，以C 为圆心、r 为半径作的圆与斜边AB 有公共点．【详解】解：作CD⊙AB 于D ，如图，⊙⊙C=90°，AC=3，BC=4，⊙22AB 5AC BC =+=1122⋅=⋅CD AB BC AC ⊙CD 125= ⊙以C 为圆心、r 为半径作的圆与斜边AB 有公共点时，r 的取值范围为1254≤≤r故选：C【点睛】本题考查了直线与圆的位置关系：设⊙O 的半径为r ，圆心O 到直线l 的距离为d ：直线l 和⊙O 相交⊙d ＜r ；直线l 和⊙O 相切⊙d=r ；直线l 和⊙O 相离⊙d ＞r ．2．（2021·上海闵行区·九年级一模）已知A 与B 的半径分别是6和8，圆心距2AB =，那么A 与B 的位置关系是（）A ．相交B ．内切C ．外切D ．内含【答案】B【分析】根据圆心距等于两圆半径的差，判断两圆的位置关系即可解题．【详解】A 与B 的半径分别是6和8，圆心距2AB =，又8-6=2AB =∴A 与B 的位置关系是内切，故选:B ．【点睛】本题考查两圆的位置关系，涉及圆心距，是重要考点，难度较易，掌握相关知识是解题关键．3．（2021·上海崇明区·边形的边数是（）A ．3B ．4C ．5D ．无法确定【答案】B【分析】如图，画出简图，根据切线的性质可得⊙OCA=90°，根据⊙AOC 的余弦可得⊙AOC=45°，即可得出此多边形的中心角为90°，即可求出多边形的边数．【详解】如图，OA 、OC 分别为此多边形的外接圆和内切圆的半径，AB 为边长，⊙OC⊙AB ，⊙⊙OCA=90°，⊙倍，⊙cos⊙AOC=OC OA =2， ⊙⊙AOC=45°，⊙⊙AOB=90°，即此多边形的中心角为90°，⊙此多边形的边数=360°÷90°=4，故选：B ．【点睛】本题考查正多边形和圆及三角函数的定义，熟练掌握余弦的定义并熟记特殊角的三角函数值是解题关键．4．（2021·上海奉贤区·九年级一模）如果1O 和2 O 内含，圆心距12 4O O =，1O 的半径长是6，那么2 O 的半径r 的取值范围是（）．A ．02r <<B ．24r <<C ．10r >D ．02r <<或10r >【答案】D 【分析】根据题意得1206OO r ≤<-，结合124O O =，通过求解不等式，即可得到答案．【详解】根据题意得：1206OO r ≤<-，0r >⊙124O O =⊙46r <-⊙64r ->或64r -<-⊙02r <<或10r >⊙2O 的半径r 的取值范围是：02r <<或10r > 故选：D ．【点睛】本题考查圆与圆内含、绝对值、一元一次不等式的知识；解题的关键是熟练掌握圆与圆内含、绝对值、一元一次不等式的性质，从而完成求解．二、填空题5．（2021·上海金山区·九年级一模）正十边形的中心角等于______度．【答案】36【分析】根据正多边形的中心角的定义即可求解．【详解】正十边形的中心角等于360°÷10=36°。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2020学年金山区第一学期期末质量检测
初三数学试卷
（满分150分，考试时间100分钟）（2021．1）
一、选择题：（本大题共6题，每题4分，满分24分）
1.已知二次函数()122
--=x y ，那么该二次函数图像的对称轴是（）（A ）直线2=x ；（B ）直线2-=x ；（C ）直线1=x ；（D ）直线1-=x .
2.下列各点在抛物线2
2x y =上的是（）（A ）()2,2；（B ）()42，
；（C ）)(8,2；（D ）()16,2. 3.在ABC Rt ∆中， 90=∠C ，那么锐角A 的正弦等于（）
（A ）的邻边锐角的对边锐角A A ；（B ）斜边的对边锐角A ；（C ）斜边的邻边锐角A ；（D ）的对边
锐角的邻边锐角A A . 4.若α是锐角，()2215sin =
+ α，那么锐角α等于（）（A ） 15；（B ） 30；（C ） 45；（D ） 60.
5.如图，已知点D 、E 分别在ABC ∆的边AB 、AC 上，BC DE //，2=AD ，3=BD ，=，那么等于（）
（A ）a 32；（B ）a 32-；（C ）52；（D ）a 5
2-. 6.如图，已知ABC Rt ∆中， 90=∠C ，3=AC ，4=BC ，如果以点C 为圆心的圆与斜边AB 有公共点，那么⊙
C 的半径r 的取值范围是（）
（A ）5120≤≤r ；（B ）3512≤≤r ；（C ）45
12≤≤r ；（D ）43≤≤r .
二、填空题：（本大题共12题，每题4分，满分48分）
7.计算：=⎪⎭
⎫ ⎝⎛-+232 ． 8.已知()x x x f 32+=，那么()=-2f ．
第6题图 B C A
第5题图
10.正十边形的中心角等于度．
11.已知⊙1O 和⊙2O 的半径长分别为3和4，若⊙1O 和⊙2O 内切，那么圆心距21O O 的长等于．
12.在ABC Rt ∆中， 90=∠C ，15=AB ，5
4in =A s ，那么=BC ． 13.在ABC ∆中，5:2:1::=BC AC AB ，那么=B tan ．
14.已知：如图，ABC ∆的中线AE 与BD 交于点G ，AE DF //交BC 于F ，那么=AG
DF ． 15.如图，在梯形ABCD 中，BC AD //，AD BC 2=，设=，=，那么向量用向量、表示为． 16.如图，已知⊙O 中， 120=∠AOB ，弦18=AB ，那么⊙O 的半径长等于．
17.如图，在□ABCD 中，点E 在边BC 上，DE 交对角线AC 于F ，若BE CE 2=，ABC ∆的面积等于15，那么FEC ∆的面积等于．
18.已知在ABC Rt ∆中， 90=∠C ，1=BC ，2=AC ，以点C 为直角顶点的DCE Rt ∆的顶点D 在BA 的延长线上，DE 交CA 的延长线于点G ，若21tan =
∠CED ，GE CE =，那么BD 的长等于．
三、解答题（本大题共7题，满分78分）
19.（本题满分10分）
如图，已知在ABC Rt ∆中， 90=∠C ，3=AC ，4=BC .求：
30tan 4tan cos 1sin tan 2A B A B +-+⋅的值.
C
第19题图 B A
第17题图 B A C D E F 第16题图
A B O A
G D C B E 第14题图第15题图
A C
B 第18题图
已知：如图，⊙1O 与⊙2O 外切于点T ，经过点T 的直线与⊙1O 、⊙2O 分别相交于点A 和点B .
（1）求证：B O A O 21//；
（2）若21=A O ，32=B O ,7=AB ，求AT 的长.
21. （本题满分10分，每小题满分5分）
已知抛物线c bx x y ++-=2
2经过点()1,0A 、()5,1-B . （1）求抛物线的表达式；
（2）把表达式化成()k m x y ++-=2
2的形式，并写出顶点坐标与对称轴.
T
第20题图
B
A O 1
O 2
如图，在距某输电铁塔GH （GH 垂直地面）的底部点H 左侧水平距离60米的点B 处有一个山坡，山坡AB 的坡度3:1=i ，山坡坡底点B 到坡顶A 的距离AB 等于40米，在坡顶A 处测得铁塔顶点G 的仰角为 30（铁塔GH
与山坡AB 在同一平面内）.
（1）求山坡的高度；
（2）求铁塔的高度GH .（结果保留根号）
23. （本题满分12分，每小题满分6分）
已知：如图，四边形ABCD 是菱形，点M 、N 分别在边BC 、CD 上，联结AM 、AN 交对角线BD 于E 、F 两点，且ABD MAN ∠=∠.
（1）求证：DE BF AB ⋅=2
；（2）若DC
DN DE BE =，求证：MN EF //.
A
B F E
C
第23题图
D M
N G
第22题图 A
B
H
第25题备用图在平面直角坐标系xoy 中，直线243+-
=x y 与直线321-=x y 相交于点A ，抛物线)0(12≠-+=a bx ax y 经过点A .
（1）求点A 的坐标；
（2）若抛物线12-+=bx ax y 向上平移两个单位后，经过点()2,1-，求抛物线12
-+=bx ax y 的表达式；（3）若抛物线c x b x a y +'+'=2()0<'a 与12
-+=bx ax y 关于x 轴对称，且这两条抛物线的顶点分别是点P '与点P ，当3='∆P OP S 时，求抛物线12
-+=bx ax y 的表达式.
25. （本题满分14分，第(1)分4分，第(2)分6分，第(3)分4分）
定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中，O A ∠=
∠2
1. 已知：如图2，AC 是⊙O 的一条弦，点D 在⊙O 上（与A 、C 不重合），联结DC 交射线AO 于点E ，联结OD ，
⊙O 的半径为5，4
3tan =∠OAC . (1)求弦AC 的长.
(2)当点E 在线段OA 上时，若DOE ∆与AEC ∆相似，求DCA ∠的正切值.
(3)当1=OE 时，求点A 与点D 之间的距离（直接写出答案）.
第24题图 A B C O
第25题图1 第25题图2。