勾股定理与网格问题
八年级《勾股定理》知识点归纳和题型归类

勾股定理知识点归纳和题型归类 一.知识归纳1.勾股定理:直角三角形两直角边的平方和等于斜边的平方; 表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法,用拼图的方法验证勾股定理的思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EF G H S S S∆+=正方形正方形ABCD,2214()2ab b a c ⨯+-=,化简可证. 方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++,所以222a b c +=方法三:1()()2S a b a b=+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证 3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c ,cbaHG F EDCB Abacbac cabcab a bcc baE D CBAb,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a,b,c满足222a b c+=,那么这个三角形是直角三角形,其中c为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b+与较长边的平方2c作比较,若它们相等时,以a,b,c为三边的三角形是直角三角形;若222a b c+<,时,以a,b,c为三边的三角形是钝角三角形;若222a b c+>,时,以a,b,c为三边的三角形是锐角三角形;②定理中a,b,c及222a b c+=只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足222a c b+=,那么以a,b,c为三边的三角形是直角三角形,但是b为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c+=中,a,b,c为正整数时,称a,b,c为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n组勾股数:丢番图发现的:式子nmnmmnnm>+-(,2,2222的正整数)毕达哥拉斯发现的:122,22,1222++++nnnnn(1>n的整数)柏拉图发现的:1,1,222+-n n n (1>n 的整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解. 8..勾股定理逆定理的应用 勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒. ⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长题型二:应用勾股定理建立方程 例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为例3.如图ABC ∆中,90C ∠=︒,12∠=∠,1.5CD =,2.5BD =,求AC 的长例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积题型三:实际问题中应用勾股定理 例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 m 。
网格中的三角函数

1网格中的锐角三角函数网格是同学们从小就熟悉的图形,在网格中隐含的条件有:1.直角;2.单位长度。
所以在网格中可以求一个锐角的三角函数,是近几年中考的热点,下面举例说明。
一、在网格中与勾股定理现结合求一个锐角的三角函数。
【例1】 三角形在正方形网格纸中的位如图1,则sin α的值是( ).[解析] 本题在网格中考查锐角的正弦的意义,首先要用勾股定理计算直角三角形斜边的长.一般情况下,为了减小计算量,把小正方形的边长设为1.选C .练习1(广州市2014)如图2,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( ).(A ) (B ) (C ) (D )练习2 (2014年福州)如图3,在边长为1个单位长度的小正方形所组成的网格中,△ABC 的顶点均在格点上,344543B .; C .35;D .A. 35图3图22sinB 的值是 .3.(2011四川)如图4,在4×4的正方形网格中, tanα= .A .1B .2C .12D4.(2011甘肃兰州)如图5,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC’B’,则tanB’的值为 .A .12B .13C .14 D3. (2011江苏连云港)如图6,△ABC 的顶点都在方格纸的格点上,则sin A =_______.在网格中求一个锐角的三角函数时,根据图中角的位置。
充分利用网格中的直角和边,然后根据勾股定理求出相应的边长,最后利用三角函数公式进行计算,达到解决问题的目的。
二、在网格中与辅助线相结合求一个锐角的三角函数。
【例2】 (2014•贺州)如图7-1网格中的每个小正方形的边长都是1,△ABC 每个顶点都在网格的交点处,则sinA= .[解析] 虽然网格中隐含直角,但是∠A 是△ABC中图7-1图7-2图4图6图5的一个锐角,而△ABC不是直角三角形,不能直接运用三角函数公式进行计算,必须先做辅助线构造直角三角形,使∠A在一个直角三角形中,然后求出所对应的斜边和对边,而后解决问题。
勾股定理知识点总结

17.1勾股定理考点一:勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 技巧归纳:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题考点二:勾股定理的证明一般是通过剪拼,借助面积进行证明。
其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不变。
图1是由4个全等三角形拼成的,得到一个以a+b 为边长的大正方形和以直角三角形斜边c 为边长的小正方形。
则大正方形的面积可表示为(a+b)2,又可表示为12ab ·4+c 2,所以(a+b)2=12ab ·4+c 2,整理得a 2+b 2=c 2在图2的另一种拼法中,以c 为边长的正方形的面积可表示成四个全等的直角三角形与边长为(b-a)的正方形的面积的和,所以12ab ·4+(b-a)2=c 2,整理得a 2+b 2=c 2.考点三:勾股定理的应用(1)勾股定理的应用条件勾股定理只适用于直角三角形,所以常作辅助线——高,构造直角三角形。
(2)勾股定理的实际应用勾股定理反映了直角三角形3条边之间的关系,利用勾股定理,可以解决直角三角形的有关计算和证明.例如:已知直角三角形的两条直角边可求斜边;已知直角三角形的斜边和一条直角边,可求另一条直角边。
勾股定理还可以解决生产生活中的一些实际问题。
在解决问题的过程中,往往利用勾股定理列方程(组),将实际问题转化成直角三角形的模型来解决。
(3)利用勾股定理作长为 n (n 为大于1的整数)的线段实数与数轴上的点是一一对应的,有理数在数轴上较易找到与它对应的点,而若要在数轴上直接标出无理数对应的点则较难。
八年级数学下册【勾股定理】4种简单应用

八年级数学下册【勾股定理】4种简单应用一、勾股定理在网格中的应用例1、已知正方形的边长为1,(1)如图a,可以计算出正方形的对角线长为根号2.①分别求出图(b),(c),(d)中对角线的长_.②九个小正方形排成一排,对角线的长度(用含n的式子表示)为_.分析:借助于网格,构造直角三角形,直接利用勾股定理.二、勾般定理在最短距离中的应用例2、如图,已知C是SB的中点,圆锥的母线长为10cm,侧面展开图是一个半圆,A处有一只蜗牛想吃到C处的食物,它只能沿圆锥曲面爬行.请你求出蜗牛爬行的最短路程.分析在求解几何图形两点间最短距离的问题时,将几何体表面展开,求展开图中两点之间的距离,展开过程中必须要弄清楚所要求的是哪两点之间的距离,以及它们在展开图中的相应位置.点评在求立体几何图形的问题时,一般是通过平面展开图,将其转化成平面图形问题,然后求解.三、勾股定理在生活中的应用例3、如图,学校有一块长方形花园,有较少数同学为了避开拐角走“捷径”,在校园内走出了一条“路”.请同学们算一算,其实这些同学仅仅少走多少步路,却踩伤了花草.(假设1步为0.5m)点评:走“捷径”问题为出发点是常遇到情况,在考查勾股定理的同时,融入了环保教育:少走几步路,就可以留下一片期待的绿色.四、勾股定理在实际生活中的应用例4 小华想知道自家门前小河的宽度,于是按以下办法测出了如下数据:小华在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°,小华沿河岸向前走30m 选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小华计算小河的宽度.点评:此题考查直角三角形的应用,解答本题的关键在于画出示意图,将问题转化为解直角三角形的问题.。
10 专题 勾股定理(逆定理)与网格画图
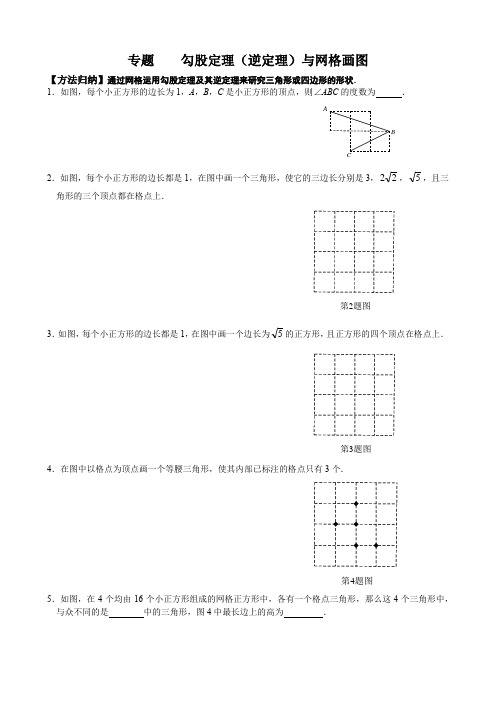
专题 勾股定理(逆定理)与网格画图
【方法归纳】通过网格运用勾股定理及其逆定理来研究三角形或四边形的形状.
1.如图,每个小正方形的边长为1,A ,B ,C 是小正方形的顶点,则∠ABC 的度数为 .
2.如图,每个小正方形的边长都是1,在图中画一个三角形,使它的三边长分别是3,22,5,且三角形的三个顶点都在格点上.
3.如图,每个小正方形的边长都是1,在图中画一个边长为5的正方形,且正方形的四个顶点在格点上.
4.在图中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个.
5.如图,在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个三角形中,与众不同的是 中的三角形,图4中最长边上的高为 . A
C
B
第2
题图第3题图
第4
题图
6.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
7.如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB 的端点在格点上.
(1)图1中,以AB 为腰的等腰三角形有 个,画出其中的一个,并直接写出其
边长.
(2)图2中,以AB 为底边的等腰三角形有 个,画出其中一个,并直接写出其底边上的高.
图4图3图2图
1图2
图1图2图1
A
B A B。
勾股定理的作图及典型计算(课件)八年级数学下册(人教版)

B. 5
C. 7
D. 9
2.如图,在2×2的正方形网格中,每个小正方形的边长为1,点A、B、C均
为格点,以点A为圆心,AB长为半径画弧,交网格线于点D,则CD的长为
( D)
1
A.
2
1
B.
3
C. 3
D.2- 3
3.如图,在平面直角坐标系中,点P的坐标为(-4,3),以点B(-1,0)为圆心,
三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+ 3; 将位置
②的三角形绕点P2顺时针旋转到位置③,可得到点P3, 此时AP3=3+ 3;
.......按此规律继续旋转,直至得到点P2050为止,则AP2050等于( C )
A.2049+683 3
B.2050+683 3
C.2051+683 3
AD=4, AB=8,则DE的长为_______.
5
7.如图,在5×5的正方形网格中,每个小正方形的边长均为1,画出一个三
角形的长分别为 2, 3, 17.
解:如图所示,△ABC为所求.
8.在数轴上作出表示 5, 10的点.
解:如图所示,点C表示 5,点D表示 10.
9.如图,将长方形纸片沿直线折叠,使点C落在边的中点 ′ 处,
是斜边长.
1.如图,点A表示的实数是( D )
A. 3
B. 5
C.- 3
D.- 5
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对
角线AC的长为半径作弧交数轴于点M,则点M表示的数为( C )
A.2
B. 5 − 1
C. 10 − 1
勾股定理的应用(六)在网格图形中的应用

祖π数学
新人教 八年级下册
之高分速成 1
【题型6】网格中的勾股定理
1.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC 中,边长为无理数的边数是( )
A.0
B.1
C.2
D.3
2.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
3.如图,小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )
A.25
B.12.5
C.9
D.8.5
(第1题) (第2题) (第3题)
4.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形:
①使三角形的三边长分别为3;
②使三角形为钝角三角形且面积为4(在图乙中画一个即可).
甲
乙
B C
A B C。
勾股定理的各类题型

勾股定理各种题型:一:勾股定理面积相等法:方法1:方法2:方法3:二:方程思想和勾股定理结合的题目1.2016春宜春期末一旗杆在其的B处折断;量得AC=5米;则旗杆原来的高度为A.米B.2米C.10米D.米考点勾股定理的应用.分析可设AB=x;则BC=2x;进而在△ABC中;利用勾股定理求解x的值即可.解答解:由题意可得;AC2=BC2﹣AB2;即2x2﹣x2=52;解得x=;所以旗杆原来的高度为3x=5;故选D.点评能够利用勾股定理求解一些简单的直角三角形.2.2016春防城区期中如图;在△ABC中;∠B=40°;EF∥AB;∠1=50°;CE=3;EF比CF大1;则EF的长为A.5 B.6 C.3 D.4考点勾股定理;平行线的性质.分析由平行线的性质得出∠A=∠1=50°;得出∠C=90°;设CF=x;则EF=x+1;根据勾股定理得出方程;解方程求出x;即可得出EF的长.解答解:∵EF∥AB;∴∠A=∠1=50°;∴∠A+∠B=50°+40°=90°;∴∠C=90°;设CF=x;则EF=x+1;根据勾股定理得:CE2+CF2=EF2;即32+x2=x+12;解得:x=4;∴EF=4+1=5;故选:A.点评本题考查了平行线的性质、直角三角形的判定、勾股定理;熟练掌握平行线的性质;并能进行推理论证与计算是解决问题的关键.3.2015春蚌埠期中已知;如图长方形ABCD中;AB=3cm;AD=9cm;将此长方形折叠;使点B 与D重合;折痕为EF;则BE的长为A.3cm B.4cm C.5cm D.6cm考点翻折变换折叠问题.分析根据折叠的性质可得BE=ED;设AE=x;表示出BE=9﹣x;然后在Rt△ABE中;利用勾股定理列式计算即可得解.解答解:∵长方形折叠点B与点D重合;∴BE=ED;设AE=x;则ED=9﹣x;BE=9﹣x;在Rt△ABE中;AB2+AE2=BE2;即32+x2=9﹣x2;解得x=4;∴AE的长是4;∴BE=9﹣4=5;故选C.点评本题考查了翻折变换的性质;勾股定理的应用;根据勾股定理列出关于AE的长的方程是解题的关键.4.2008秋奎文区校级期末在我国古代数学着作九章算术中记载了一个有趣的问题;这个问题的意思是:有一个水池;水面是一个边长为10尺的正方形;在水池正中央有一根新生的芦苇;它高出水面1尺;如图所示;如果把这根芦苇垂直拉向岸边;它的顶端恰好到达岸边的水面.那么水深多少芦苇长为多少考点勾股定理的应用.分析找到题中的直角三角形;设水深为x尺;根据勾股定理解答.解答解;设水深为x尺;则芦苇长为x+1尺;根据勾股定理得:;解得:x=12尺;芦苇的长度=x+1=12+1=13尺;答:水池深12尺;芦苇长13尺.点评此题是一道古代问题;体现了我们的祖先对勾股定理的理解;也体现了我国古代数学的辉煌成就.三:勾股定理应用:求最短距离问题1.2014秋环翠区期中如图;长方体的底面边长为1cm和3cm;高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达B;那么所用细线最短需要A.12cm B.11cm C.10cm D.9cm考点平面展开-最短路径问题.分析要求所用细线的最短距离;需将长方体的侧面展开;进而根据“两点之间线段最短”得出结果.解答解:将长方体展开;连接A、B′;则AA′=1+3+1+3=8cm;A′B′=6cm;根据两点之间线段最短;AB′==10cm.故选C.点评本题考查了平面展开﹣最短路径问题;本题就是把长方体的侧面展开“化立体为平面”;用勾股定理解决.2.2016春繁昌县期末如图;是一长、宽都是3cm;高BC=9cm的长方体纸箱;BC上有一点P;PC=BC;一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是A.6cm B.3cm C.10cm D.12cm考点平面展开-最短路径问题.分析将图形展开;可得到安排AP较短的展法两种;通过计算;得到较短的即可.解答解:1如图1;AD=3cm;DP=3+6=9cm;在Rt△ADP中;AP==3cm;2如图2;AC=6cm;CP=3+3=6cm;Rt△ADP中;AP==6cm.综上;蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是6cm.故选A.点评本题考查了平面展开﹣﹣最短路径问题;熟悉平面展开图是解题的关键.3.2016 大悟县二模如图;小红想用一条彩带缠绕易拉罐;正好从A点绕到正上方B点共四圈;已知易拉罐底面周长是12cm;高是20cm;那么所需彩带最短的是A.13cm B.4cm C.4cm D.52cm考点平面展开-最短路径问题.分析要求彩带的长;需将圆柱的侧面展开;进而根据“两点之间线段最短”得出结果;在求线段长时;借助于勾股定理.解答解:由图可知;彩带从易拉罐底端的A处绕易拉罐4圈后到达顶端的B处;将易拉罐表面切开展开呈长方形;则螺旋线长为四个长方形并排后的长方形的对角线长;∵易拉罐底面周长是12cm;高是20cm;∴x2=12×42+202;所以彩带最短是52cm.故选D点评本题考查了平面展开﹣最短路径问题;圆柱的侧面展开图是一个矩形;此矩形的长等于圆柱底面周长;高等于圆柱的高;本题就是把圆柱的侧面展开成矩形;“化曲面为平面”;用勾股定理解决.4.2016 游仙区模拟长方体敞口玻璃罐;长、宽、高分别为16cm、6cm和6cm;在罐内点E处有一小块饼干碎末;此时一只蚂蚁正好在罐外壁;在长方形ABCD中心的正上方2cm处;则蚂蚁到达饼干的最短距离是多少cm.A.7 B.C.24 D.考点平面展开-最短路径问题.分析做此题要把这个长方体中蚂蚁所走的路线放到一个平面内;在平面内线段最短;根据勾股定理即可计算.解答解:①若蚂蚁从平面ABCD和平面CDFE经过;蚂蚁到达饼干的最短距离如图1:H ′E===7;②若蚂蚁从平面ABCD 和平面BCEH 经过;则蚂蚁到达饼干的最短距离如图2:H ′E==故选B .点评考查了平面展开﹣最短路径问题;此题的关键是明确两点之间线段最短这一知识点;然后把立体的长方体放到一个平面内;求出最短的线段.5.2015秋 宜兴市校级期中如图;一圆柱高8cm;底面半径为cm;一只蚂蚁从点A 爬到点B 处吃食;要爬行的最短路程是 10 cm .考点平面展开-最短路径问题.分析此题最直接的解法;就是将圆柱展开;然后利用两点之间线段最短解答.解答解:底面圆周长为2πr;底面半圆弧长为πr;即半圆弧长为:×2π×=6cm;展开得:∵BC=8cm;AC=6cm;根据勾股定理得:AB==10cm . 故答案为:10.点评此题主要考查了立体图形的展开和两点之间线段最短;解题的关键是根据题意画出展开图;表示出各线段的长度.四:网格问题简单1、在边长为1的小正方形组成的网格中;△ABC 的三个顶点均在格点上;则△ABC 中BC 边上的高为答案:设△ABC 中BC 边上的高为h .∵AB^ 2 =5;AC^ 2 =20;BC^ 2 =25;∴BC^ 2 =AB^ 2 +AC ^2 ;∴∠A=90°;S △ABC =21 AB ⨯AC= 21BC ⨯h;即525⨯ =5h .解得;h=2.故答案是:2.2. 如图;方格纸中每个小方格都是边长为1的正方形;我们把以格点连线为边的多边形称为“格点多边形”.如图一中四边形ABCD 就是一个“格点四边形”.1求图一中四边形ABCD 的面积;2在图二方格纸中画一个格点三角形EFG;使△EFG 的面积等于四边形ABCD 的面积且为轴对称图形.图一 图二答案:解:1方法一:S=12×6×4=12方法二:S=4×6-12×2×1-12×4×1-12×3×4-12×2×3=122只要画出一种即可3、如图;在由边长为1的小正方形组成的网格中;△ABC的三个顶点均在格点上.请按要求完成下列各题:1画AD∥BCD为格点;连接CD;2试判断△ABC的形状请说明理由;答案:1图象如图所示;2由图象可知AB2=12+22=5;AC2=22+42=20;BC2=32+42=25;∴BC2=AB2+AC2;△ABC是直角三角形..4、如图;是一块由边长为20cm的正方形地砖铺设的广场;一只鸽子落在点A处;•它想先后吃到小朋友撒在B、C处的鸟食;则鸽子至少需要走多远的路程答案:AB=5cm;BC=13cm.•所以其最短路程为18cm难题5、如图中的虚线网格我们称之为正三角形网格;它的每一个小三角形都是边长为1的正三角形;这样的三角形称为单位正三角形..1直接写出单位正三角形的高与面积..2图中的平行四边形ABCD含有多少个单位正三角形平行四边形ABCD的面积是多少3求出图中线段AC的长可作辅助线..答案1单位正三角形的高为;面积是..2如图可直接得出平行四边形ABCD含有24个单位正三角形;因此其面积..3过A作AK⊥BC于点K如图所示;则在Rt△ACK中;;;故五:方位角问题1、如图所示;在一次夏令营活动中;小明从营地A点出发;沿北偏东60°方向走了3500m到达B点;然后再沿北偏西30°方向走了500m到达目的地C点.1求A、C两点之间的距离;2确定目的地C在营地A的什么方向2、甲、乙两位探险者到沙漠进行探险;没有了水;需要寻找水源.为了不致于走散;他们用两部对话机联系;已知对话机的有效距离为15千米.早晨8:00甲先出发;他以6千米/时的速度向东行走;1小时后乙出发;他以5千米/时的速度向北行进;上午10:00;甲、乙二人相距多远还能保持联系吗答案:如图;甲从上午8:00到上午10:00一共走了2小时;走了12千米;即OA=12.乙从上午9:00到上午10:00一共走了1小时;走了5千米;即OB=5.在Rt△OAB中;AB2=122十52=169;∴AB=13;因此;上午10:00时;甲、乙两人相距13千米.∵15>13;∴甲、乙两人还能保持联系.答:上午10:00甲、乙两人相距13千米;两人还能保持联系.3、如图;甲乙两船从港口A同时出发;甲船以16海里/时速度向北偏东40°航行;乙船向南偏东50°航行;3小时后;甲船到达C岛;乙船到达B岛.若C、B两岛相距60海里;问乙船的航速是多少答案:从两船航行的方向看;北偏东40度和南偏东50度的夹角为90AC⊥AB甲船速度每小时16海里;所以AC=16×3=48海里AB2=BC2-AC2=3600-2304=1296AB=36所以乙船速度为每小时:36÷3=12海里4、如图;北海海面上;一艘解放军军舰正在基地A的正东方向且距A地40海里的B处训练;突然接基地命令;要该舰前往C岛;接送一病危渔民到基地医院救治;已知C岛在A的北偏东600方向;且在B北偏西450方向;军舰从B处出发;平均每小时走20海里;需要多少时间才能把患病渔民送到基地医院精确到0.1小时;参考数据:73.13≈;41.12≈解:作CD⊥AB于D;根据题意;得∠CAB=30°;∠CBD=45°不妨设CD=x海里;则BD=x海里;AD=2x海里;AC=x海里; BC=2x海里;∴3x+x=40∴x=203 -20海里∴AC+BC=)()(203202203202-+-=206+403 -202 -40=)(2-2-22620+≈49.98海里 49.98÷20=2.499≈2.5小时答:需要大约2.5小时才能把患病渔民送到基地医院..。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
c2 c
a a2
例1 如图是由边长为1m的正方形地 砖铺设的地面示意图,小明沿图中 所示的折线从A→B→C所走的路程 为__2_5__m(结果保留根号).
A
B C
例2 如图,在由单位正方形组成的
网格图中标有AB、CD、EF、GH
四条线段,其中能构成一个直角三
角形三边的线段是( C )
求△ABC的面积.
m
A
n
C B
S△ABC=8mn
1.如图,在正方形网格中,每个小正 方形的边长为1,则网格上的△ABC的 边长为无理数的边数是( C ) A.0 B.1 C.2 D.3
A
C
B
2.在5×5的正方形网格中,每个小正 方形的边长都为1,请在给定网格中按 下列要求画出图形.
(1)从点A出发画一条线段AB,使它的 另一端点B在格点上,且长度为 5 ; (2)画出所有的以(1)中的AB为边的等
5
22
3
5、2 2、3
29 10
37
10、 29、 37
例5 如图,在4×4的正方形网格中, 小正方形的边长为1,A、B、C三点 都是小正方形的格点.请你过点C做 出线段AB的垂线CD,使得点D也是 正方形的格点,并说明理由.
A
C
B
D
例6 如图,在4×4的正方形网格中画出 格点△DEF,使△DEF∽△ABC,且 相似比为 2 .
A.CD、EF、GH C E B
B.AB、CD、GH
H
C.AB、EF、GH D.AB、CD、EF
F
A
D
G
例3 如图,小正方形的边长为1, 则△ABC的AC 边上的高是( D)
A.3
2 2
C.4 5 5
B.3105
A
B
D.3
5 5
C
例4 如图,每一个小正方形的边 长都是1.请以图中的格点为顶点 画出相应的三角形.
D
F
E
C
AB
例7 如图,在5×5的网格中画出格点 △DEF,使△DEF∽△ABC,且面积 最大,并求出相似比.
F
D
E C
D A4的正方形网格中, 每个小正方形的边长都是1.请判断格 点△ABC和△DEF是否相似,并证明 你的结论. A B
C D
FE
问题1 在△ABC中, AB= 5,BC= 10,AC= 13, 求△ABC的面积.
腰三角形,使另一个顶点在格点上, 且每边的长度都是无理数.
C1
C2
C5
C6
A
B
C4
C3
C8
C7
你能通过建立正方形网格,再在网 格中画出格点△ABC,利用割补法 求出△ABC的面积吗?
A
1
B C
S△ABC=3.5
问题2 在△ABC中, AB= 5a ,BC=2 2a,AC= 17a, 求△ABC的面积.
A
a
B
C S△ABC=3a2
问题3
在△ABC中,
AB= m2 16n2 , BC= 9m2 4n , AC= 2 m2 n2 , 其中m>0,n>0且m≠n,
