勾股定理与网格问题
八年级《勾股定理》知识点归纳和题型归类

勾股定理知识点归纳和题型归类 一.知识归纳1.勾股定理:直角三角形两直角边的平方和等于斜边的平方; 表示方法:如果直角三角形的两直角边分别为a ,b ,斜边为c ,那么222a b c +=2.勾股定理的证明勾股定理的证明方法很多,常见的是拼图的方法,用拼图的方法验证勾股定理的思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积不会改变②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理常见方法如下:方法一:4EF G H S S S∆+=正方形正方形ABCD,2214()2ab b a c ⨯+-=,化简可证. 方法二:四个直角三角形的面积与小正方形面积的和等于大正方形的面积. 四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++,所以222a b c +=方法三:1()()2S a b a b=+⋅+梯形,2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形,化简得证 3.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系,它只适用于直角三角形,对于锐角三角形和钝角三角形的三边就不具有这一特征,因而在应用勾股定理时,必须明了所考察的对象是直角三角形4.勾股定理的应用①已知直角三角形的任意两边长,求第三边在ABC ∆中,90C ∠=︒,则c ,cbaHG F EDCB Abacbac cabcab a bcc baE D CBAb,a②知道直角三角形一边,可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题5.勾股定理的逆定理如果三角形三边长a,b,c满足222a b c+=,那么这个三角形是直角三角形,其中c为斜边①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法,它通过“数转化为形”来确定三角形的可能形状,在运用这一定理时,可用两小边的平方和22a b+与较长边的平方2c作比较,若它们相等时,以a,b,c为三边的三角形是直角三角形;若222a b c+<,时,以a,b,c为三边的三角形是钝角三角形;若222a b c+>,时,以a,b,c为三边的三角形是锐角三角形;②定理中a,b,c及222a b c+=只是一种表现形式,不可认为是唯一的,如若三角形三边长a,b,c满足222a c b+=,那么以a,b,c为三边的三角形是直角三角形,但是b为斜边③勾股定理的逆定理在用问题描述时,不能说成:当斜边的平方等于两条直角边的平方和时,这个三角形是直角三角形6.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数,即222a b c+=中,a,b,c为正整数时,称a,b,c为一组勾股数②记住常见的勾股数可以提高解题速度,如3,4,5;6,8,10;5,12,13;7,24,25等③用含字母的代数式表示n组勾股数:丢番图发现的:式子nmnmmnnm>+-(,2,2222的正整数)毕达哥拉斯发现的:122,22,1222++++nnnnn(1>n的整数)柏拉图发现的:1,1,222+-n n n (1>n 的整数)7.勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题.在使用勾股定理时,必须把握直角三角形的前提条件,了解直角三角形中,斜边和直角边各是什么,以便运用勾股定理进行计算,应设法添加辅助线(通常作垂线),构造直角三角形,以便正确使用勾股定理进行求解. 8..勾股定理逆定理的应用 勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形,在具体推算过程中,应用两短边的平方和与最长边的平方进行比较,切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论. 9.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中,是密不可分的一个整体.通常既要通过逆定理判定一个三角形是直角三角形,又要用勾股定理求出边的长度,二者相辅相成,完成对问题的解决. 题型一:直接考查勾股定理 例1.在ABC ∆中,90C ∠=︒. ⑴已知6AC =,8BC =.求AB 的长 ⑵已知17AB =,15AC =,求BC 的长题型二:应用勾股定理建立方程 例2.⑴在ABC ∆中,90ACB ∠=︒,5AB =cm ,3BC =cm ,CD AB ⊥于D ,CD =⑵已知直角三角形的两直角边长之比为3:4,斜边长为15,则这个三角形的面积为⑶已知直角三角形的周长为30cm ,斜边长为13cm ,则这个三角形的面积为例3.如图ABC ∆中,90C ∠=︒,12∠=∠,1.5CD =,2.5BD =,求AC 的长例4.如图Rt ABC ∆,90C ∠=︒3,4AC BC ==,分别以各边为直径作半圆,求阴影部分面积题型三:实际问题中应用勾股定理 例5.如图有两棵树,一棵高8cm ,另一棵高2cm ,两树相距8cm ,一只小鸟从一棵树的树梢飞到另一棵数的树梢,至少飞了 m 。
网格中的三角函数

1网格中的锐角三角函数网格是同学们从小就熟悉的图形,在网格中隐含的条件有:1.直角;2.单位长度。
所以在网格中可以求一个锐角的三角函数,是近几年中考的热点,下面举例说明。
一、在网格中与勾股定理现结合求一个锐角的三角函数。
【例1】 三角形在正方形网格纸中的位如图1,则sin α的值是( ).[解析] 本题在网格中考查锐角的正弦的意义,首先要用勾股定理计算直角三角形斜边的长.一般情况下,为了减小计算量,把小正方形的边长设为1.选C .练习1(广州市2014)如图2,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( ).(A ) (B ) (C ) (D )练习2 (2014年福州)如图3,在边长为1个单位长度的小正方形所组成的网格中,△ABC 的顶点均在格点上,344543B .; C .35;D .A. 35图3图22sinB 的值是 .3.(2011四川)如图4,在4×4的正方形网格中, tanα= .A .1B .2C .12D4.(2011甘肃兰州)如图5,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC’B’,则tanB’的值为 .A .12B .13C .14 D3. (2011江苏连云港)如图6,△ABC 的顶点都在方格纸的格点上,则sin A =_______.在网格中求一个锐角的三角函数时,根据图中角的位置。
充分利用网格中的直角和边,然后根据勾股定理求出相应的边长,最后利用三角函数公式进行计算,达到解决问题的目的。
二、在网格中与辅助线相结合求一个锐角的三角函数。
【例2】 (2014•贺州)如图7-1网格中的每个小正方形的边长都是1,△ABC 每个顶点都在网格的交点处,则sinA= .[解析] 虽然网格中隐含直角,但是∠A 是△ABC中图7-1图7-2图4图6图5的一个锐角,而△ABC不是直角三角形,不能直接运用三角函数公式进行计算,必须先做辅助线构造直角三角形,使∠A在一个直角三角形中,然后求出所对应的斜边和对边,而后解决问题。
勾股定理知识点总结

17.1勾股定理考点一:勾股定理直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
(即:a 2+b 2=c 2) 技巧归纳:勾股定理反映了直角三角形三边之间的关系,是直角三角形的重要性质之一,其主要应用:(1)已知直角三角形的两边求第三边(在ABC ∆中,90C ∠=︒,则22c a b =+,22b c a =-,22a c b =-)(2)已知直角三角形的一边与另两边的关系,求直角三角形的另两边(3)利用勾股定理可以证明线段平方关系的问题考点二:勾股定理的证明一般是通过剪拼,借助面积进行证明。
其中的依据是图形经过割补拼接后,只要没有重叠,没有空隙,面积不变。
图1是由4个全等三角形拼成的,得到一个以a+b 为边长的大正方形和以直角三角形斜边c 为边长的小正方形。
则大正方形的面积可表示为(a+b)2,又可表示为12ab ·4+c 2,所以(a+b)2=12ab ·4+c 2,整理得a 2+b 2=c 2在图2的另一种拼法中,以c 为边长的正方形的面积可表示成四个全等的直角三角形与边长为(b-a)的正方形的面积的和,所以12ab ·4+(b-a)2=c 2,整理得a 2+b 2=c 2.考点三:勾股定理的应用(1)勾股定理的应用条件勾股定理只适用于直角三角形,所以常作辅助线——高,构造直角三角形。
(2)勾股定理的实际应用勾股定理反映了直角三角形3条边之间的关系,利用勾股定理,可以解决直角三角形的有关计算和证明.例如:已知直角三角形的两条直角边可求斜边;已知直角三角形的斜边和一条直角边,可求另一条直角边。
勾股定理还可以解决生产生活中的一些实际问题。
在解决问题的过程中,往往利用勾股定理列方程(组),将实际问题转化成直角三角形的模型来解决。
(3)利用勾股定理作长为 n (n 为大于1的整数)的线段实数与数轴上的点是一一对应的,有理数在数轴上较易找到与它对应的点,而若要在数轴上直接标出无理数对应的点则较难。
勾股定理与网格问题

勾股定理与网格问题
1、在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则△ABC中BC边上的高为
2、如图,在4×4的正方形网格中,每个小正方形的边长都是1,△ABC三个顶点分别在正方形网格的格点上,试判断△ABC是否是直角三角形.
3、如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则△ABC的周
长是
4、如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则BC边上的高为.
5、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: (1)用签字笔画AD∥BC(D为格点),连接C
D;
(2)通过计算说明三角形ABC是直角三角形;
(3)线段CD的长为
(4)四边形ABCD的面积是
ﻫ
6、如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:ﻫ(1)画AD∥BC(D为格点),连
接CD;
(2)通过计算说明△ABC是直角三角形;
7、如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.ﻫ请按要求完成下列各题:ﻫ(1)画AD∥BC(D为格点),连接CD;ﻫ(2)试判断△ABC的形状?请说明理由;
(3)若E为BC中点,F为AD中点.四边形AECF是什么特殊的四边形?
请说明理由.
7、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点
上,请按要求完成下列各题:ﻫ(1)画线段AD∥BC且使AD=BC,连接C
D;
(2)线段AC的长为;
(3)△ACD的形状为;
(4)若E为BC的中点,则AE的长为.。
八年级数学下册【勾股定理】4种简单应用

八年级数学下册【勾股定理】4种简单应用一、勾股定理在网格中的应用例1、已知正方形的边长为1,(1)如图a,可以计算出正方形的对角线长为根号2.①分别求出图(b),(c),(d)中对角线的长_.②九个小正方形排成一排,对角线的长度(用含n的式子表示)为_.分析:借助于网格,构造直角三角形,直接利用勾股定理.二、勾般定理在最短距离中的应用例2、如图,已知C是SB的中点,圆锥的母线长为10cm,侧面展开图是一个半圆,A处有一只蜗牛想吃到C处的食物,它只能沿圆锥曲面爬行.请你求出蜗牛爬行的最短路程.分析在求解几何图形两点间最短距离的问题时,将几何体表面展开,求展开图中两点之间的距离,展开过程中必须要弄清楚所要求的是哪两点之间的距离,以及它们在展开图中的相应位置.点评在求立体几何图形的问题时,一般是通过平面展开图,将其转化成平面图形问题,然后求解.三、勾股定理在生活中的应用例3、如图,学校有一块长方形花园,有较少数同学为了避开拐角走“捷径”,在校园内走出了一条“路”.请同学们算一算,其实这些同学仅仅少走多少步路,却踩伤了花草.(假设1步为0.5m)点评:走“捷径”问题为出发点是常遇到情况,在考查勾股定理的同时,融入了环保教育:少走几步路,就可以留下一片期待的绿色.四、勾股定理在实际生活中的应用例4 小华想知道自家门前小河的宽度,于是按以下办法测出了如下数据:小华在河岸边选取点A,在点A的对岸选取一个参照点C,测得∠CAD=30°,小华沿河岸向前走30m 选取点B,并测得∠CBD=60°.请根据以上数据,用你所学的数学知识,帮小华计算小河的宽度.点评:此题考查直角三角形的应用,解答本题的关键在于画出示意图,将问题转化为解直角三角形的问题.。
10 专题 勾股定理(逆定理)与网格画图
专题 勾股定理(逆定理)与网格画图
【方法归纳】通过网格运用勾股定理及其逆定理来研究三角形或四边形的形状.
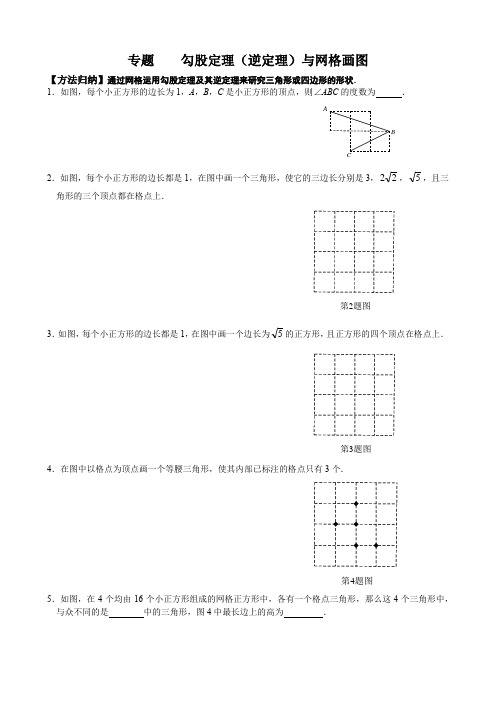
1.如图,每个小正方形的边长为1,A ,B ,C 是小正方形的顶点,则∠ABC 的度数为 .
2.如图,每个小正方形的边长都是1,在图中画一个三角形,使它的三边长分别是3,22,5,且三角形的三个顶点都在格点上.
3.如图,每个小正方形的边长都是1,在图中画一个边长为5的正方形,且正方形的四个顶点在格点上.
4.在图中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个.
5.如图,在4个均由16个小正方形组成的网格正方形中,各有一个格点三角形,那么这4个三角形中,与众不同的是 中的三角形,图4中最长边上的高为 . A
C
B
第2
题图第3题图
第4
题图
6.如图,正方形网格中的每个小正方形边长都为1,每个小正方形的顶点叫格点,以格点为顶点分别按下列要求画图:
7.如图,在5×5的正方形网格中,每个小正方形的边长均为1,线段AB 的端点在格点上.
(1)图1中,以AB 为腰的等腰三角形有 个,画出其中的一个,并直接写出其
边长.
(2)图2中,以AB 为底边的等腰三角形有 个,画出其中一个,并直接写出其底边上的高.
图4图3图2图
1图2
图1图2图1
A
B A B。
勾股定理的作图及典型计算(课件)八年级数学下册(人教版)

B. 5
C. 7
D. 9
2.如图,在2×2的正方形网格中,每个小正方形的边长为1,点A、B、C均
为格点,以点A为圆心,AB长为半径画弧,交网格线于点D,则CD的长为
( D)
1
A.
2
1
B.
3
C. 3
D.2- 3
3.如图,在平面直角坐标系中,点P的坐标为(-4,3),以点B(-1,0)为圆心,
三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=2+ 3; 将位置
②的三角形绕点P2顺时针旋转到位置③,可得到点P3, 此时AP3=3+ 3;
.......按此规律继续旋转,直至得到点P2050为止,则AP2050等于( C )
A.2049+683 3
B.2050+683 3
C.2051+683 3
AD=4, AB=8,则DE的长为_______.
5
7.如图,在5×5的正方形网格中,每个小正方形的边长均为1,画出一个三
角形的长分别为 2, 3, 17.
解:如图所示,△ABC为所求.
8.在数轴上作出表示 5, 10的点.
解:如图所示,点C表示 5,点D表示 10.
9.如图,将长方形纸片沿直线折叠,使点C落在边的中点 ′ 处,
是斜边长.
1.如图,点A表示的实数是( D )
A. 3
B. 5
C.- 3
D.- 5
2.如图,在矩形ABCD中,AB=3,AD=1,AB在数轴上,若以点A为圆心,对
角线AC的长为半径作弧交数轴于点M,则点M表示的数为( C )
A.2
B. 5 − 1
C. 10 − 1
勾股定理的应用(六)在网格图形中的应用

祖π数学
新人教 八年级下册
之高分速成 1
【题型6】网格中的勾股定理
1.如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC 中,边长为无理数的边数是( )
A.0
B.1
C.2
D.3
2.如图,正方形网格中的△ABC ,若小方格边长为1,则△ABC 是( )
A.直角三角形
B.锐角三角形
C.钝角三角形
D.以上答案都不对
3.如图,小方格都是边长为1的正方形,则四边形ABCD 的面积是 ( )
A.25
B.12.5
C.9
D.8.5
(第1题) (第2题) (第3题)
4.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫格点,以格点为顶点分别按下列要求画三角形:
①使三角形的三边长分别为3;
②使三角形为钝角三角形且面积为4(在图乙中画一个即可).
甲
乙
B C
A B C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理与网格问题
1、在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,则△ABC中BC边上的高为
2、如图,在4×4的正方形网格中,每个小正方形的边长都是1,△ABC三个顶点分别在正方形网格的格点上,试判断△ABC是否是直角三角形.
3、如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则△ABC的周
长是
4、如图,在正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在格点上,则BC边上的高为.
5、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:(1)用签字笔画AD∥BC(D为格点),连接
CD;
(2)通过计算说明三角形ABC是直角三角形;
(3)线段CD的长为
(4)四边形ABCD的面积是
6、如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)通过计算说明△ABC是直角三角形;
7、如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上.
请按要求完成下列各题:
(1)画AD∥BC(D为格点),连接CD;
(2)试判断△ABC的形状?请说明理由;
(3)若E为BC中点,F为AD中点.四边形AECF是什么特殊的四边
形?请说明理由.
7、如图,在边长为1的小正方形组成的网格中,△ABC的三个顶点均在格
点上,请按要求完成下列各题:
(1)画线段AD∥BC且使AD=BC,连接CD;
(2)线段AC的长为;
(3)△ACD的形状为;
(4)若E为BC的中点,则AE的长为.。
