沪教版(上海)数学八年级第二学期-22.4 梯形 课件
沪教版(上海)数学八年级第二学期-22.4 四 边 形 复 习(二)—梯形 课件(共26张ppt)

A B
DG E
FC
方法三:考虑把FC平移到与AD相接的位置;
可通过延长FE交AD的延长线于G来实现 这样就只要证明DG=FC即可.
18.如图,梯形ABCD 中,AD∥BC, ∠B=90°,AD=2,BC=5,E是AB上一点,将△ BCE
沿着直线CE翻折,点B恰好与D点重合,则BE=
.(16松江)
谈谈这节课你有什么收 获、体会或想法?
判定方法
图形
符号语言
1、定义:两腰相等的 梯形是等腰梯形
A
2、在同一底上的两内 角相等的梯形是等腰
B
梯形
3、对角线相等的梯 形是等腰梯形
D ∵梯形ABCD,AB=CD ∴梯形ABCD是等腰梯形
∵梯形ABCD,∠BAD=∠CDA(或 C ∠ABC=∠DCB)
∴梯形ABCD是等腰梯形
∵梯形ABCD,AC=BD ∴梯形ABCD是等腰梯形
1、概念辨析 1)四边形可以分为平行四边形和梯形两类 ( X ) 2)等腰梯形和直角梯形是两种特殊的梯形 ( √ )
3)梯形的对角线相等
(X )
2、等腰梯形性质:
四边形 对边
角
等腰 两底平行 同一底上两 梯形 两腰相等 个内角相等
对角线
两条对角 线相等
对称性
轴对称 图形
A
D
O
B
C
3、等腰梯形的常用判定方法
∴ AE BF
EG FG
∴BF=FG,即BF= 1BG=
1 ( AD BC)
2
2
∵ BG=BC+CG,
例题分析
例4.(学科基本要求P109 例3)已知:如图,在梯形
ABCD中,AD//BC,点E是边CD的中点,点F在边BC上 ,
沪教版(上海)数学八年级第二学期第22章小结梯形常用辅助线复习课课件

6
10 10
d
6E 7 13
例题1 已知梯形ABCD中,AD//BC,上 底AD=1厘米,下底BC=4厘米, 对角线AC、BD交于O点, 且BD=3厘米,AC=4厘米, 求梯形ABCD的面积?
3
4
H4 1 E 5
变式1:在梯形ABCD中,AD//BC, 对角线AC与BD垂直相交于O , MN是中位线,∠DBC=30。 求证AC=MN
是正方形
1、直角梯形两底差为6厘米,高为6 厘米,则梯形中最小的内角为 _____4_5___度
E
2、梯形ABCD中,AD//BC,AD=8,BC=17, ∠C=70度,∠B=55度,则DC的长度为__9
8
55 9
55
55 70
8E9
3、以线段a=6, b=13为梯形的两底,以 c=10为一腰,则另一腰d的范围是 ___3_<_d_<_1_7____
90 90
30 下底
上底 E
例2 已知:如图,梯形ABCD中AD//BC, ∠ABC=90度, E为CD的中点 求证:EA=EB
F F
两平行线夹板+中点=三角形全等
变式2、等腰梯形ABCD中,AB//CD, △COD为等边三角形,
E、F、G分别为OD、OA、BC的中点 求证:(1)△AOB为等边三角形 (2)△EFG为等边三角形
梯形常用辅助线复习课
梯形的定义:_____
等腰梯形 性质1: 性质2:
判定1: 判定2:
概念定理辨析: 1、下列四边形中,
对角线一定相等的是( B)
A菱形和矩形 B 矩形和等腰梯形 C 平行四边形和等腰梯形 D 菱形和直角梯形
2、下列说法中,正确的有哪些( B、F )
沪教版(上海)数学八年级第二学期-22.4 因动点产生的梯形 教案

年级八年级学科数学教师时间课题因动点产生的梯形课型新授课时 1教学目标1、通过阅读、画图,提高分析问题,解决问题的能力.2、经历动手实践探究的过程,体会数形结合与分类讨论的思想.3、培养勇于探究的精神和归纳总结的能力.教材分析教学重点探究一次函数背景下的梯形存在性问题.教学难点根据梯形,等腰梯形,直角梯形的定义和性质,准确画出所有符合条件的点.教学设计教学内容(含二次备课)设计意图教学过程一:复习提问梯形定义:等腰梯形定义:等腰梯形性质:直角梯形定义:二:例题讲解:(小组合作,交流展示)例1:已知A(-1,m)与B(2,m+)是反比例函数图像上的两点.(1)求k值.(2)若点C(-1,0),在反比例函数图像上求点D,使得以ABCD为顶点的四边形是梯形.(3)在(2)的条件下,反比例函数图像上是否存在异于(2)中的点D,使得以A、B、C、D为顶点的四边形是梯形?若存在,请在图中画出D的位置.已知平面内三个点,求梯形的第四个点,注意有无顿号的区别,引导学生分类讨论。
例2:在平面直角坐标系中,直线经过O,A(1,2)两点,将直线向下平移6个单位得到,交x轴于点C,B是直线上一点,且四边形ABCO是平行四边形.(1)求直线的表达式及点B的坐标;(2)若D是平面直角坐标系内的一点,且以OACD四个点为顶点的四边形是等腰梯形,求点D的坐标.(3)平面内是否存在异于(2)中的点D,且以O、A、C、D四个点为顶点的四边形是等腰梯形? 若存在,请在图中画出D的位置.例3:一次函数的图像与x轴交于点A(,0),与y轴交于点B.(1)求B坐标及∠ABO的度数;(2)如果点C的坐标为(0,3),D是平面直角坐标系内的一点,四边形ABCD是直角梯形,求点D的坐标.(3) 在(2)的条件下,平面内是否存在异于(2)中的点D,且以A、B、C、D四个点为顶点的四边形是等腰梯形? 若存在,请在图中画出D的位置三:练习在平面直角坐标系中,函数y=2x+12的图像分别交x轴,y轴于点A、B两点,过点A 的直线交y轴正半轴于点M,且M为线段OB的中点.(1)求直线AM的表达式;(2)若H为坐标平面内任意一点,是否存在点H,使得以A、B、M、H为顶点的四边形是等腰梯形?若存在,请写出H点的坐标;若不存在,请说明理由. 继上题梯形之后已知三个点,求等腰梯形的第四个点。
沪教版(上海)数学八年级第二学期-22.4 梯形 教案

22.4 梯形教学目标:通过操作实践、复习回顾、自学交流、小组讨论、总结归纳等学习过程,理解梯形的相关概念及与三角形之间的关系;并学会将梯形问题转化为平行四边形、三角形等基本图形来解决梯形中有关角度、线段、梯形的周长和面积等的计算问题;在活动中培养学生乐于探索、合作学习的习惯,培养学生“用数学”的意识和能力。
教学重点:梯形有关概念、与基本图形的相互转化及相关计算。
教学难点:添加辅助线解决梯形相关问题。
教学过程:教学过程设计意图一、创设情境,复习引入1.操作实践利用“七巧板”,拼出四边形。
要求:①小组讨论,合作拼图。
②教师参与,并选择个别学生展示。
2.回顾交流复习四边形相关定义及分类。
3.揭示课题22.4 梯形爱因斯坦说过:“兴趣是最好的老师。
”通过“七巧板”操作拼图,不仅让学生感受到数学学习的乐趣,引起了学生的好奇,也为后面的探究活动作好了情感准备。
二、自学交流,探索新知1.阅读课本第91页(课题起,图22-46止),完成以下问题:1)什么是梯形?什么是直角梯形?什么是等腰梯形?2)在图中标注上底、下底,腰,并画出高。
要求:①学生阅读课本,圈划关键词。
②同桌讨论,师生交流。
小结:上底和下底是习惯性的说法,注意对它们的区分是依据长度而不是依据位置。
2.小试牛刀以问题为出发点,培养学生的直觉思维及数学悟性,以自学的形式,强调学生的主体性,培养学生自主学习,培养数学阅读中的分析能力。
师生交流过程中,强调梯形的定义及相关元素。
A B DCABC(1)填空①如图,四边形ABCD 中,当____________,且AB 不平行于CD 时,四边形ABCD 是梯形。
②如图,梯形ABCD 中,AD ∥BC ,则上底是______,下底是______,腰是_______ 。
③如图,梯形ABCD 中,AD ∥BC ,当______ =_______时,梯形ABCD 是等腰梯形。
(2)辨析下列四边形一定是梯形吗?若不是,请说明理由。
沪教版(上海)数学八年级第二学期-22.4 梯形 教案

22.4 梯形教学目标:1、在梯形定义的形成过程中,感受从一般到特殊的研究问题的方法.2、在梯形及其有关概念形成过程中,培养数学语言归纳及规范表达的能力.3、会添加适当的辅助线,将梯形问题转化成三角形、平行四边形的问题来解决.4、在学习过程中,领悟数形结合、由一般到特殊、转化及分类讨论的数学思想. 教学重点:梯形概念的形成及应用.教学难点:添加适当的辅助线.教师活动设计意图一、复习引入1、思考:对于一个一般的四边形,它的两组对边有怎样特殊的位置关系?引出课题:22.4梯形通过对四边形两组对边位置关系的分类讨论,使学生感受从一般到特殊的研究问题的方法,从而引出今天的研究对象:梯形。
二、探索新知1、梯形的定义梯形的定义:一组对边平行而另一组对边不平行的四边形叫做梯形..符号语言:∵AD∥BC,且AB不平行CD∴四边形ABCD是梯形(梯形的定义)2、认识梯形的各元素3、两种特殊梯形的研究操作:(1)任意画一个△EBC(2)再画一条直线,使它与边BC平行,且与边BE,CE分别相交于点A和D(与点E不重合).观察并思考:这样得到的四边形是什么图形?归纳:直角梯形:有一个角是直角的梯形.表示方法:梯形ABCD,AD∥BC,∠A=90°等腰梯形:两腰相等的梯形.表示方法:梯形ABCD,AD∥BC,AB=CD 让学生自己归纳梯形的定义,培养学生数学语言的归纳能力。
对于证明一个四边形为梯形,学生往往会遗漏另一组对边不平行的条件,说出符号语言能起到强化2个条件的作用。
让学生正确认识梯形的各元素,并且知道通常由梯形上底两端点作下底的垂线段作为梯形的高。
通过改变三角形的形状研究,引出两种特殊的梯形:直角梯形和等腰梯形。
4、探索三角形与梯形的关系观察并思考:(1)如何由一个三角形得到梯形?(2)如何由一个梯形得到三角形?归纳:(1)作三角形一边的平行线可得梯形(2)延长梯形的两腰可得三角形引导学生认识梯形与三角形之间的联系,知道梯形可由三角形的一边的平行线截得;同时,让学生感受延长两腰能得到三角形,是梯形常用的添加辅助线的方法。
沪教版八年级数学下册2梯形课件

(2)试探究四边形ABCD四条边之间存在 的等量关系,并说明理由;
A
D
B 图8E
C
图9
(3)现有图8中的等腰梯形四个, 利用它们你能拼出一个新的等腰梯形 吗?若能,四人小组合作拼图,并贴 到答题卡背面。
A
D
B
C
图8
图
10
假如你是一位设计师,请选择安 阳具有代表性的一处地方(如:火车 站,殷墟博物苑,人民公园,市政广 场…)进行设计。你准备怎样用这些 等腰梯形图案来装扮节日的安阳?
ABCD四个内角的度数; ∠A=∠D=120°,∠B=∠C=60°
(2)试探究四边形ABCD四条边之间存在
的等量关系,并说明理由; BC=2AB=2AD=2CD
A
D
B
C
图8
图9
如图8,四边形ABCD是等腰梯形, AD//BC.由四个这样的等腰梯形可以拼出如 图9所示的平行四边形。
(1)求四边形ABCD四个内角的度数;
A
D
E
B
图5
C
B
C
图5
林州市红旗渠某一段的横截面可近似地
看作等腰梯形,如图:测得上口宽为7米,
渠底为3米,渠深为3米。求斜坡AB的长。
AB=√13
AE
米
F DA
E FD
B
C
图6
B
C
图7
如图8,四边形ABCD是等腰梯形,
AD//边形。 (1)求四边形
一组对边平行,另一组对边
不平行的四边形叫做梯形。
AE
D
B 图1 C
F
如图2,有一个角是直角的梯形叫做 直 角梯形。
如图3,两腰相等的梯形叫等腰梯形。
沪教版(上海)数学八年级第二学期-22.4 梯形复习 课件

典型习题
例1 判断下列说法是否正确:
1.一组对边相等,另一组对边平行的四边形
是等腰梯形.
(×)
2.有两个角相等的梯形是等腰梯形. (×)
3.一组对边平行但不相等的四边形是梯形.
(√)
4.两组对角分别互补的四边形一定是等腰梯
形.
(×)
知识梳理 梯形常用辅助线
A
D
A
D
A
D
B
CB
CB
C
A
D
A
D
A
D
B
CB
小结
梯形问题
转化 添加辅助线
三角形或平行四边形
小结
梯形中常作的辅助线
.
.
小结 梯形常用辅助线
1.延长两腰交于一点 作用:使梯形问题转化为三角形问题,
E
A
D
若是等腰梯形则得到等腰三角形.
B
C
2.平移一腰
A
D
作用:使梯形问题转化为平行四边形
及三角形问题.
B
E
C
CE等于上、下底的差
小结 梯形常用辅助线
A、24 B、12 C、6 D、16
AD M
BF
CE
61.在这世界上没有什么美好的东西,也许时间就是我们拥有的唯一美好的东西,我们不能荒废它!谁能知道明天会发生什么事呢。时间就是永恒,人们荒废时间就是荒废永恒。 79.不拼不搏人生白活,不苦不累人生无味。 73.忍耐力较诸脑力,尤胜一筹。 50.人生是一条没有回程的单行线,上帝不会给你一张返程的票。 54.在比夜更深的地方,一定有比夜更黑的眼睛。 67.人是可以快乐地生活的,只是我们自己选择了复杂,选择了叹息! 90.先知三日,富贵十年。 96.不要让未来的你,讨厌现在的自己,困惑谁都有,但成功只配得上勇敢的行动派。 63.总会有一个人是第一,我为什么不能是那一个人呢。 20.当你握着两手沙子时,一定就拿不到地上那颗珍珠了。 68.如果周围有人嫉妒你,那么你可以把他从你的竞争者之列排除了,嫉妒人之人,难以成大事。 77.我们不行,往往不是因为我们不行,而是因为别人说了我们不行。 24.第二名意味着你是头号输家。 20.耐得住寂寞,守得住繁华! 2.在真实的生命里,每桩伟业都由信心开始,并由信心跨出第一步。 84.毁灭人只要一句话,培植一个人却要千句话,请你多口下留情。
上海数学八级下“梯形”第一课时课件
B
C
四边形DECB是直角梯形? A 一组对边平行且不相等;
如图:有一块四边形土地ABCD,测得AD=26m,CD=10m,BC=5m,顶点D、C到AB的距离分别是10m,4m;求这块地的面积。 梯形ABCD,AD∥ BC
如图:有一块四边形土地ABCD,测得AD=26m,CD=10m,BC=5m,顶点D、C到AB的距离分别是10m,4m;求这块地的面积。
在直角梯形ABCD中,AD//BC,∠A=90°, AD=10cm, DC=13cm,BC=15cm,求AB的长。
边AB、AC于D,E 一组对边平行而另一组对边不平行的四边形叫做梯形.
(A)3∶4∶5 ∶ 6 (B)3∶5∶4∶6 平行的两边叫做梯形的底
B
C A
得△ADE与四边形DECB 在直角梯形ABCD中,AD//BC,∠A=90°, AD=10cm, DC=13cm,BC=15cm,求AB的长。
那么:四边形DECB是梯形吗?
满足什么条件时,四边形DECB 在直角梯形ABCD中,AD//BC,∠A=90°, AD=10cm, DC=13cm,BC=15cm,求AB的长。
两底之间的距离叫做梯形的高
D
E
是等腰梯形? 如图:有一块四边形土地ABCD,测得AD=26m,CD=10m,BC=5m,顶点D、C到AB的距离分别是10m,4m;求这块地的面积。
(A)3∶4∶5 ∶ 6 (B)3∶5∶4∶6
(C)6∶3∶4∶5 (D)4∶6∶5∶3
A 上底 D 梯形ABCD,AD∥ BC
E
腰
平行的两边叫做梯形的底
腰
高
不平行的两边叫做梯形的腰
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
的边AB、AC于D,E, 得
B
C
A
△ADE与四边形DECB
那么:四边形DECB是梯形吗?
D
E
2、满足什么条件时,四边形DECB B 是直角梯形?
3、满足什么条件时,四边形DECB D 是等腰梯形?
B
C
A
E
C
例题1:
如图:已知梯形ABCD中,AB//CD,DE//BC, 点E在AB上且BE=4,△AED的周长是18,求梯 形ABCD的周长
D
C
A
E
B
例题2:
如图:已知梯形ABCD是一座大坝的横截面, 其中AD//BC,∠B=30°,∠C=45°;AD=6m, CD=20m,求坝底BC的长以及横截面的面积。
A
D
B
C
梯形中常用的辅助线:
小试牛刀1:
在直角梯形ABCD中,AD//BC,∠A=90°, AD=10cm, DC=13cm,BC=15cm,求AB的长。
上底
腰 练高习册:腰 P4直7角/习梯形题22.4等腰梯形?
下底
梯形概念: 梯形中的各部分名称: 特殊的梯形:
作业:
1.练习册22.4 2.拓展:四边形AOBC是直角梯形, OC=5,OB=5AC,OC所在的直线解析式 为y=2x,平行于OC的直线l为:y=2x+t,l由 A点平移到C点的过程中,l与AC、AO两 边所围成的三角形的面积记为S. (1)求点C的坐标 (2)求t的取值范围 (3)求出S与t之间的函数关系式
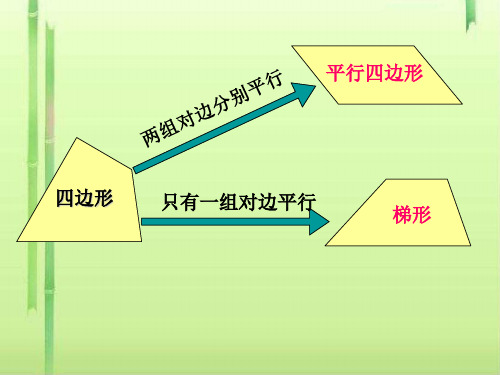
22.4
平行四边形
四边形
只有一组对边平行
梯形
定义:一组对边平行而另一组对 边不平行的四边形叫做梯形.
想一想
一、下列四边形一定是梯形吗?
1. 一组对边平行;
A
D
2. 一组对边平行且不相等;
3. 4.
一组对边平行另组对边不平行; 一组对边平行另组对边不相等. B
C
二、梯形ABCD中,AD∥BC,
∠A∶∠B∶∠C∶∠D有可能是( C )
A
D
B
C
小试牛刀2:
如图:有一块四边形土地ABCD,测得 AD=26m,CD=10m,BC=5m,顶点D、C到AB的 距离分别是10m,4m;求这块地的面积。
D
C
A
E
B F
小试牛刀3:
如图:梯形ABCD中,对角线AC,BD 相交于点O,那么△AOB和△COD的面积 相等吗?为什么?
A
D
O
B
C
课堂布小置结作业
(A)3∶4∶5 ∶ 6 (B)3∶5∶4∶6
(C)6∶3∶4∶5 (D)4∶6∶5∶3
A 上底 D 梯形ABCD,AD∥ BC
E
腰
平行的两边叫做梯形的底
腰
高
不平行的两边叫做梯形的腰
F
B
下底
C 两底之间的距离叫做梯形的高
A
D
等腰梯形
B
C
梯形
A
D
直角梯形
B
C
思考:
A
D
E
1、如图:DE//BC分别交△ABC
