诱导公式的化简与求值20题教学内容
诱导公式 课件

[活学活用] 化简:(1)csionsπα--απ·sinα-π2cosπ2+α;
(2)sin(-α-5π)cosα-π2-sin32π+αcos(α-2π). 解:(1)原式=cos[-sinπα-α]·sin-π2-α(-sin α) =cossiπn-α α·-sinπ2-α(-sin α) =-sicnosαα·(-cos α)(-sin α) =-cos2α.
[活学活用] 已知cos(75°+α)=13,求cos(105°-α)-sin(15°-α)的值.
解:cos(105°-α)-sin(15°-α) =cos[180°-(75°+α)]-sin[90°-(75°+α)] =-cos(75°+α)-cos(75°+α) =-23.
利用诱导公式求值
[典例]
已
知
cosπ-θ cos θsin32π-θ-1
=
5 8,Βιβλιοθήκη 求cosπ+θscinosπ22+π-θ-θsin32π+θ的值.
[解]
∵ cos
θcsoins3π2π--θθ -1=cos
-cos θ θ-cos θ-1
=1+c1os θ=58,
∴cos θ=35.
∴cosπ+θscinosπ22+π-θ-θsin32π+θ
[证明] 左边=-2sin32π1--θ2s·in-2θsin θ-1
=2sinπ+1-π2-2siθn2θsin θ-1=-2sin1-π2-2sθins2iθn θ-1
=co-s2θ2+cossinθ2sθin-θ2-sin12θ=ssiinn2θθ+-ccooss2θθ2=ssiinn
θ+cos θ-cos
θ θ.
右边=ttaann
θθ+ -11=ssiinn
高中数学 诱导公式
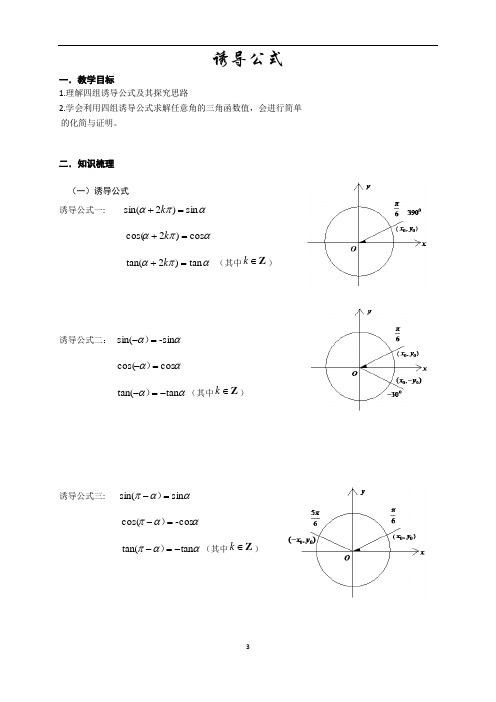
诱导公式一.教学目标1.理解四组诱导公式及其探究思路2.学会利用四组诱导公式求解任意角的三角函数值,会进行简单 的化简与证明。
二.知识梳理(一)诱导公式诱导公式一: απαsin )2sin(=+k απαcos )2cos(=+kαπαtan )2tan(=+k (其中Z ∈k )诱导公式二: αα-sin sin(=-)ααcos cos(=-)ααtan tan(-=-)(其中Z ∈k )诱导公式三: ααπsin sin(=-)ααπ-cos cos(=-) ααπtan tan(-=-)(其中Z ∈k )诱导公式四:ααπ-sin sin(=+) ααπ-cos cos(=+)ααπtan tan(=+)(其中Z ∈k )作用:实现正弦(切)函数和余弦(切)函数的互化。
口决:奇变偶不变,符号看象限.)(2由象限决定数的符号符号指的是前面三角函的奇偶性;中奇偶指的是k kπ三.例题讲解类型一:利用诱导公式求值例1 (直接应用) 求下列各三角函数值(1)16sin()3π-; (2)o cos(945)-. 解:(1)原式16443sinsin(4)sin sin()sin 33333πππππππ=-=-+=-=-+==. (2)原式oooooocos945cos(2360225)cos225cos(18045)==⨯+==+=ocos45-22=-.点评:对于负角的三角函数求值,可先用诱导公式化为正角的三角函数.若转化得到的正角大于o 360,则再利用诱导公式化为o o (0,360)范围内的角的三角函数;若这时的角是o o (90,360)范围内的角,再利用有关的诱导公式化为o o(0,90)范围内的角的三角函数.口诀:负化正,大化小,化到锐角再求值.练习:求oooosin10sin(260)cos100cos(170)---的值. (答案:1sin cos αα)例2 (变式应用) 求o o o o osin(1200)cos1290cos(1020)sin(1050)tan 945-+--+的值思路:负角三角函数→正角三角函数→o 0~o360角三角函数→锐角三角函数→求值. 解:原式点评:解决这类问题要注意观察角的特点,然后把角化为o360k α⋅+,o180α±,o360α-等形式,最后再利用诱导公式求解.练习:求35463755tan()sin()cos tan6366ππππ---. (答案:0) 提示:按口诀:“负化正,大化小,化到锐角再求值”进行求值即可.例3 (综合应用) 已知o1cos(75)3α-=-,且α为第四象限角,求osin(105)α+的值.导思:(1)角o 75α-与角o105α+有什么关系? (2)osin(105)α+与osin(75)α-有什么关系?(3)已知ocos(75)α-如何求osin(75)α-?应注意什么问题?解:由题意知o75α-为第三象限角,故osin(75)α-==3=-,故o o o osin(105)sin[180(75)]sin(75)3ααα+=+-=--=. 点评:本题主要考查诱导公式的灵活运用和同角三角函数的基本关系.本题的易错点是开平方运算中的符号问题,即o75α-的范围的确定,应注意到已知条件o1cos(75)3α-=-中的隐含信息.练习:若o1cos(75)3α+=,且α为第三象限角,求o ocos(15)sin(15)αα-+-的值. (答案:13--类型二:利用诱导公式化简三角函数式例3(直接应用) 化简cos()2sin()cos(2)5sin()2παπαπαπα-⋅-⋅-+. 解:原式2cos()sin 2sin cos sin cos sin cos sin()2παααααααπαα-=⋅⋅=⋅⋅=+.练习:化简:sin(6)cos(10)tan()cos()sin(8)tan(5)παπααπαππαπα-+---+-; (答案:1)例4 (变式应用) 求值24sin(2)cos()(Z)33n n n ππππ+⋅+∈. 解:当n 为奇数时,原式24sin (cos )sin()[(cos()]sin cos 333333ππππππππ=-=--+=1224=⋅=. 当n 为偶数时,原式24sincos sin()cos()sin (cos )333333ππππππππ==-+=-1()224=⋅-=- 点评:因为诱导公式对于α加π的奇数倍和偶数倍是不同的,故用诱导公式求值时,若遇到π的整数倍,必须对整数分奇数和偶数进行讨论.例5 (综合应用) 已知α为第三象限角,且sin()cos(2)tan()()sin()tan()f παπααπαπααπ----=--+.(1)化简()f α; (2)若31cos()25πα-=,求()f α的值; (3)若o1860α=-,求()f α的值.导思:(1)负角的三角函数如何化简?(2)与π、2π有关的三角函数名称变不变?符号又该如何确定?解:(1)由题意sin()cos(2)tan()sin cos (tan )()cos sin()tan()(sin )tan f παπααπαααααπααπαα-----===---+--.(2)用诱导公式化简3cos()2πα-,得3cos()sin 2παα-=-,故由题意得1sin 5α=-,故cos α=()f α=. (3)因o o o1860219030-=-⨯+,故ooo(1860)cos(1860)cos(2190f -=--=--⨯o30)+o1sin 302=-=-. 四.课堂练习一、选择题1.已知sin(α-π3)=13,则cos ⎝⎛⎭⎫π6+α的值为( )A .13B .-13C .233D .-233[答案] B[解析] ∵sin ⎝⎛⎭⎫α-π3=13 ∴cos ⎝⎛⎭⎫π6+α=cos ⎣⎡⎦⎤π2+⎝⎛⎭⎫α-π3 =-sin ⎝⎛⎭⎫α-π3=-13, 故选B.2.已知sin110°=a ,则cos20°的值为( ) A .a B .-a C .1-a 2 D .-1-a 2[答案] A[解析] sin110°=sin(90°+20°)=cos20°=a .3.已知点P (sin(π+θ),sin(3π2-θ))在第三象限,则角θ所在的象限是( )A .第一象限B .第二象限C .第三象限D .第四象限 [答案] A[解析] sin(π+θ)=-sin θ, sin(3π2-θ)=sin[π+(π2-θ)]=-sin(π2-θ)=-cos θ,∵点P 在第三象限,∴-sin θ<0,-cos θ<0,∴sin θ>0,cos θ>0, ∴θ是第一象限角.4.已知tan θ=2,则sin ⎝⎛⎭⎫π2+θ-cos (π-θ)sin ⎝⎛⎭⎫π2-θ-sin (π-θ)=( )A .2B .-2C .0D .23[答案] B[解析] 原式=cos θ+cos θcos θ-sin θ=21-tan θ∵tan θ=2,∴原式=21-2=-2,故选B.5.化简sin (θ-5π)tan (3π-θ)·cot ⎝⎛⎭⎫π2-θtan ⎝⎛⎭⎫θ-32π·cos (8π-θ)sin (-θ-4π)+sin(-θ)的结果为( )A .0B .1C .2D .32[答案] A[解析] 原式=-sin θ-tan θ·tan θ-cot θ·cos θ-sin θ-sin θ=cos θ·(-tan 2θ)(-cot θ)-sin θ=sin θ-sin θ=0. 6.计算sin 4π3·cos 25π6·tan 5π4的值是( )A .-34B .34C .-34D .34 [答案] A[解析] sin 4π3·cos 25π6·tan 5π4=sin(π+π3)·cos(4π+π6)·tan(π+π4)=-sin π3·cos π6·tan π4=-32×32×1=-34. 二、填空题7.化简tan1°·tan2°·tan3°·…·tan89°=________. [答案] 1[解析] ∵tan k °·tan(90°-k °)=tan k °·cot k °=1,∴tan1°·tan2°…tan89°=(tan1°·tan89°)(tan2°·tan88°)…(tan44°·tan46°)·tan45°=1. 8.设φ(x )=sin 2⎝⎛⎭⎫π2-x +cos 2⎝⎛⎭⎫x -π2+cot(19π-x ),则φ⎝⎛⎭⎫π3=________. [答案] 1-33[解析] ∵φ(x )=cos 2x +sin 2x +cot(-x )=1-cot x , ∴φ⎝⎛⎭⎫π3=1-cot π3=1-33. 三、解答题9.已知角α终边上一点P (-4,3), 求cos (π2+α)sin (-π-α)cos (11π2-α)sin (9π2+α)的值.[解析] cos (π2+α)sin (-π-α)cos (11π2-α)sin (9π2+α)=cos (π2+α)sin[-(π+α)]cos[5π+(π2-α)]sin[4π+(π2+α)]=-cos (π2+α)sin (π+α)-cos (π2-α)sin (π2+α)=-(-sin α)(-sin α)-sin αcos α=tan α,由题意得tan α=-34.∴cos (π2+α)sin (-π-α)cos (11π2-α)sin (9π2+α)=-34.五.课后作业基础巩固一、选择题1.(2014·浙江临海市杜桥中学高一月考)sin600°=( ) A .-12B .12C .-32D .32[答案] C[解析] sin600°=sin(360°+240°)=sin240° =sin(180°+60°)=-sin60°=-32. 2.已知角θ的终边过点(4,-3),则cos(π-θ)=( ) A .45B .-45C .35D .-35[答案] B[解析] 由题意,知cos θ=x r =45,∴cos(π-θ)=-cos θ=-45.3.设A 、B 、C 是一个三角形的三个内角,则在①sin(A +B )-sin C ;②cos(A +B )+cos C ;③tan(A +B )+tan C ;④cot(A +B )-cot C (C ≠π2),这四个式子中值为常数的有( )A .1个B .2个C .3个D .4个[答案] C[解析] ∵A +B +C =π,∴A +B =π-C . ∴sin(A +B )=sin(π-C )=sin C , cos(A +B )=cos(π-C )=-cos C , tan(A +B )=tan(π-C )=-tan C , cot(A +B )=cot(π-C )=-cot C ,故选C. 原题四个式子中①②③式为常数. 4.下列各三角函数值: ①sin1 125°; ②tan 37π12·sin 37π12;③sin3tan3; ④sin1-cos1.其中为负值的个数是( ) A .1个 B .2个 C .3个 D .4个[答案] B[解析] 1 125°=1 080°+45°,则1 125°是第一象限的角,所以sin1 125°>0;因37π12=2π+1312π,则3712π是第三象限角,所以tan 3712π>0,sin 3712π<0,故tan 3712π·sin 3712π<0;因3弧度的角在第二象限,则sin3>0.tan3<0,故sin3tan3<0;因π4<1<π2,则sin1-cos1>0.∴②③为负数.因此选B. 5.化简1+2sin (π-3)cos (π+3)的结果是( ) A .sin3-cos3 B .cos3-sin3 C .±(sin3-cos3)D .以上都不对[答案] A [解析]1+2sin (π-3)cos (π+3)=1+2sin3(-cos3)=(cos3-sin3)2=|cos3-sin3|. ∵π2<3<π,∴sin3>0>cos3. ∴原式=sin3-cos3.6.记cos(-80°)=k ,那么tan100°=( ) A .1-k 2kB .-1-k 2kC .k1-k2D .-k1-k2[答案] B[解析] 解法一:∵cos(-80°)=k ,∴cos80°=k ,∴sin80°=1-k 2, ∴tan80°=1-k 2k ,∴tan100°=-tan80°=-1-k 2k .解法二:由cos(-80°)=k ,得cos80°=k >0,∴0<k <1. 又sin 280°+cos 280°=1,∴tan 280°+1=1cos 280°.∴tan 280°=1k 2-1=1-k 2k 2.∴tan80°=1-k 2k. ∴tan100°=-tan80°=-1-k 2k .二、填空题7.已知cos(π+α)=-12,则tan(α-9π)=________.[答案] ±3[解析] cos(π+α)=-cos α=-12,cos α=12,∴tan α=±3,tan(α-9π)=-tan(9π-α) =-tan(π-α)=tan α=±3.8.已知角α的终边上一点P (3a,4a ),a <0,则cos(540°-α)=________. [答案] 35[解析] cos α=3a 9a 2+16a 2=3a 5|a |=-35,cos(540°-α)=cos(180°-α)=-cos α=35.三、解答题9.求下列三角函数式的值:(1)sin(-840°)cos1 470°-cos(-420°)sin(-930°); (2)sin(-60°)+cos225°+tan135°.[解析] (1)sin(-840°)·cos1470°-cos(-420°)sin(-930°) =-sin840°cos1 470°+cos420°sin930°=-sin(2×360°+120°)cos(4×360°+30°)+cos(360°+60°)sin(2×360°+210°) =-sin120°cos30°+cos60°sin210°=-sin(180°-60°)cos30°+cos60°sin(180°+30°)=-sin60°cos30°-cos60°sin30° =-32×32-12×12=-1. (2)原式=-sin60°+cos(180°+45°)+tan(180°-45°) =-32-cos45°-tan45° =-32-22-1 =-2+3+22. 能力提升一、选择题1.已知sin(α-360°)-cos(180°-α)=m ,则sin(180°+α)·cos(180°-α)等于( ) A .m 2-12B .m 2+12C .1-m 22D .-m 2+12[答案] A[解析] sin(α-360°)-cos(180°-α)=m , ∴sin α+cos α=m , 而sin(180°+α)·cos(180°-α) =(-sin α)·(-cos α)=sin αcos α =(sin α+cos α)2-12=m 2-12.2.若tan(7π+α)=a ,则sin (α-3π)+cos (π-α)sin (-α)-cos (π+α)的值为( )A .a -1a +1B .a +1a -1C .-1D .1[答案] B[解析] tan(7π+α)=tan α=a , 原式=-sin α-cos α-sin α+cos α=sin α+cos αsin α-cos α=tan α+1tan α-1=a +1a -1. 3.化简sin[α+(2n +1)π]+sin[α-(2n +1)π]sin (α+2n π)cos (α-2n π)(n ∈Z )得到的结果是( )A .0B .-2sec αC .2csc αD .2sec α[答案] B[解析] 原式=-sin α-sin αsin α·cos α=-2sec α.4.已知sin(π-α)=log 814,且α∈⎝⎛⎭⎫-π2,0,则tan(2π-α)的值为( ) A .-255B .255C .±255D .52 [答案] B[解析] ∵log 814=log 232-2=-23,∴sin α=-23,又∵α∈⎝⎛⎭⎫-π2,0,∴cos α=1-⎝⎛⎭⎫-232=53. ∴tan α=-255,∴tan(2π-α)=-tan α=255.二、填空题5.sin ⎝⎛⎭⎫-π3+2sin 4π3+3sin 2π3等于________. [答案] 0[解析] 原式=-sin π3+2sin ⎝⎛⎭⎫π+π3+3sin ⎝⎛⎭⎫π-π3 =-sin π3-2sin π3+3sin π3=0.6.求值:tan (-150°)cos (-570°)cos (-1 140°)cot (-240°)sin (-690°)=________.[答案]32[解析] 原式=-tan150°·cos570°·cos1 140°cot240°·sin690°=-tan (180°-30°)·cos (360°+180°+30°)·cos (3×360°+60°)cot (180°+60°)·sin (720°-30°)=tan30°·(-cos30°)·cos60°cot60°·(-sin30°)=33×⎝⎛⎭⎫-32×1233×⎝⎛⎭⎫-12=32.三、解答题7.已知tan(π+α)=-12,求下列各式的值.(1)2cos (π-α)-3sin (π+α)4cos (α-2π)+sin (4π-α); (2)sin(α-7π)·cos(α+5π).[解析] tan(π+α)=-12⇒tan α=-12,(1)原式=-2cos α+3sin α4cos α-sin α=-2+3tan α4-tan α=-2+3×⎝⎛⎭⎫-124-⎝⎛⎭⎫-12=-79.(2)原式=-sin α·(-cos α) =sin α·cos α=sin α·cos αsin 2α+cos 2α=tan αtan 2α+1=-12⎝⎛⎭⎫-122+1=-25.8.化简:cot α·cos (π+α)·sin 2(3π+α)tan α·cos 3(-π-α).[解析] 原式=cot α·(-cos α)·sin 2(π+α)tan α·cos 3(π+α)=cot α·(-cos α)·(-sin α)2tan α·(-cos α)3=cot α·(-cos α)·sin 2αtan α·(-cos 3α)=cos 2αsin 2α·sin 2αcos 2α=1.9.已知cos(75°+α)=13,其中α为第三象限角,求cos(105°-α)+sin(α-105°)的值.[解析] ∵cos(105°-α)=cos[180°-(75°+α)] =-cos(75°+α)=-13,sin(α-105°)=-sin[180°-(75°+α)] =-sin(75°+α), ∵cos(75°+α)=13>0,又∵α为第三象限角,∴α+75°为第四象限角, ∴sin(75°+α)=-1-cos 2(75°+α) =-1-⎝⎛⎭⎫132=-223, ∴cos(105°-α)+sin(α-105°) =-13+223=22-13. 备选题目:(2015年1月·密云期末·2)sin 240=A .B .12-C .12D 答案:A(2015年1月·顺义期末·2)sin120的值等于A .12 B .12- C D .-答案:C(2015年1月·海淀期末·11).已知(,)αππ∈-,且sin cos7πα=-,则α=A. 514π-或914π-B. 914π-或914πC. 514π或514π-D. 514π或914π答案:A(2015年1月·海淀期末·2) 7sin6π=A. B. C. 12D. 12-答案:D(2015年1月·丰台期末·4)已知135sin =α,α是第一象限角,则cos(π)α-的值为( ) A .513-B .513C .1213- D . 1213答案:C(2015年1月·房山期末·13)已知3cos5=-α,且α为第二象限的角,则sin()α-= .答案:4 5 -(15年1月·东城期末·12)已知1tan(3)2απ-=-,则πcos()cos()2sin(π+)2cos(π)αααα++---的值是.答案:1 3。
诱导公式的化简与求值

诱导公式的化简与求值1.已知角α终边上一点P(﹣,1)(1)求的值(2)写出角α的集合S.考点:任意角的三角函数的定义;运用诱导公式化简求值.专题:计算题.分析:先求出点P(﹣,1)到原点的距离,再由定义求出角α的三角函数值,(1)先用诱导公式化简,再代入角α的三角函数值求值;(2)写出角α的集合S,由于本题中的角是一个特殊角,故可以用终边相同的角将它表示出来.解答:解:点P(﹣,1)到原点的距离是2,由定义sinα=,cosα=﹣(1)==﹣==﹣(2)由sinα=,cosα=﹣知角α的终边与角的终边相同,故α=2kπ+,k∈z故S={α|α=2kπ+,k∈z}2.已知角α的终边经过点P(,﹣).(1)求sinα的值.(2)求式﹣的值考点:任意角的三角函数的定义;运用诱导公式化简求值.专题:计算题.分析:(1)求出|OP|,利用三角函数的定义,直接求出sinα的值.(2)利用诱导公式化简表达式,根据角的终边所在象限,求出cosα=,可得结果.解答:解:(1)∵|OP|=,∴点P在单位圆上.(2分)由正弦函数的定义得sinα=﹣(5分)(2)原式=(9分)=..(10分)由余弦的定义可知,cosα=(11分)即所求式的值为(12分)3.已知角α终边上一点A的坐标为,(1)求角α的集合(6分)(2)化简下列式子并求其值:(6分)考点:三角函数的化简求值;终边相同的角;同角三角函数间的基本关系;诱导公式的作用.专题:计算题.分析:(1)根据角的终边过一个定点,根据三角函数的定义做出角的正弦值,根据角的终边在第四象限,写出与角终边相同的所有的角的集合.(2)首先用诱导公式进行整理,再把正割与余割变化成正弦与余弦的形式,约分整理出最简形式,得到结果.解答:解:(1)点P到原点的距离为r=根据三角函数的定义,得….(2分)∵点P在第四象限,也就是角α在第四象限….(4分)∴α的集合是…(6分)(2)原式=….(8分)==﹣sinα=4.(1)已知tanα=2,求的值(2)已知cos(75°+α)=,其中﹣180°<α<﹣90°,求sin(105°﹣α)+cos(375°﹣α)的值.考点:同角三角函数基本关系的运用;运用诱导公式化简求值.专题:计算题.分析:(1)利用诱导公式化简表达式,应用tanα=2求出,代入化简后的表达式即可求出原式的值.(2)利用诱导公式化简sin(105°﹣α)+cos(375°﹣α),为2sin(75°+α),利用求出2sin(75°+α)即可.。
诱导公式的应用教学课件

在积分运算中的应用
积分运算
诱导公式在积分运 算中有着广泛的应 用,通过诱导公式 可以将复杂的积分 问题化简为简单的 计算。
三角函数积 分
利用诱导公式,可 以快速求解三角函 数的积分,提高解 题效率。
拓展应用
诱导公式不仅在积 分运算中有应用, 还可以拓展到其他 数学领域,如求解 微分方程等。
04
诱导公式的应用 实例
诱导公式的应用教 学课件
目录
01 诱导公式的基本概念 02 诱导公式的基本应用 03 诱导公式的拓展应用 04 诱导公式的应用实例 05 诱导公式的注意事项
01
诱导公式的基本 概念
诱导公式定义
基本概念
诱导公式是三角函数中一些具有 特殊性质的恒等式。
应用领域
诱导公式在三角函数的化简、求 值、证明等方面有广泛应用。
导公式来解决一些复杂的数学问题。
解决实际问题
三角函数的图像变换
诱导公式可以应用于三角函数的图像变换中, 例如平移、伸缩和对称变换等,以帮助我们更
好地理解和分析函数的性质。
03
诱导公式的拓展 应用
在解三角形中的应用
解决角度问题
诱导公式可以用于解决解三角形 中的角度问题,通过将角度转换 到已知的坐标系中,简化计算过 程。
角度的化简
利用诱导公式,将角度化简到0到 360度之间,便于后续的三角函数 计算。
特殊角的三角函数值
利用诱导公式,求出特殊角的三 角函数值,为解决实际问题提供 基础数据。
三角函数的求值
在解决三角函数的求值问题时,需 要将角度与弧度制进行转换,利用 诱导公式简化计算。
利用诱导公式,可以快速求出特殊 角的三角函数值,如30°、45°、 60°等。
诱导公式一、二、三、四 Word版含解析

第7课时 诱导公式一、二、三、四1.2诱导公式:公式一:sin(2k π+α)=sin α,cos(2k π+α)=cos α,tan(2k π+α)=tan α;公式二:sin(π+α)=-sin α,cos(π+α)=-cos α,tan(π+α)=tan α;公式三:sin(-α)=-sin α,cos(-α)=cos α,tan(-α)=-tan α;公式四:sin(π-α)=sin α,cos(π-α)=-cos α,tan(π-α)=-tan α;一、选择题1.sin2 015°=( )A .sin35°B .-sin35°C .sin58°D .-sin58°答案:B解析:sin2 015°=sin(5×360°+215°)=sin215°=sin(180°+35°)=-sin35°.故选B.2.化简sin 2(π+α)-cos(π+α)·cos(-α)+1的值为( )A .1B .2sin 2αC .0D .2答案:D解析:原式=(-sin α)2-(-cos α)·cos α+1=sin 2α+cos 2α+1=2.3.计算:cos1°+cos2°+cos3°+…+cos179°+cos180°=( )A .0B .1C .-1D .以上均不对答案:C解析:cos1°+cos179°=0,cos2°+cos178°=0,…,cos89°+cos91°=0,原式=cos90°+cos180°=-1.4.在△ABC 中,cos(A +B )的值等于( )A .cos CB .-cos CC .sin CD .-sin C答案:B解析:cos(A +B )=cos(π-C )=-cos C5.tan(π+α)=-2,则sin (-α)-cos (π+α)sin (π-α)+cos (-α)的值为( ) A .3 B .-3C .2D .-2答案:B解析:sin (-α)-cos (π+α)sin (π-α)+cos (-α)=-sin α+cos αsin α+cos α=-tan α+1tan α+1又tan(π+α)=-2,tan α=-2,∴原式=3-1=-3. 6.已知f (cos x )=cos2x ,则f (sin15°)的值为( )A.12 B .-12C.32 D .-32答案:D解析:f (sin15°)=f (cos75°)=cos150°=-32.二、填空题7.cos 2600°=________.答案:12解析:cos 2600°=|cos120°|=|-cos60°|=⎪⎪⎪⎪⎪⎪-12=12. 8.化简函数式sin 2500°+sin 2770°-cos 2(1620°-x )的结果是________________.(其中x ∈(π,2π)).答案:-sin x解析: 原式=sin 2140°+sin 250°-cos 2(1620°-x )=sin 240°+cos 240°-cos 2x =1-cos 2x =sin 2x=-sin x .9.已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z ),则A 的值构成的集合是________.答案:{-2,2}解析:当k 为偶数时,由诱导公式得A =sin (k π+α)sin α+cos (k π+α)cos α=sin αsin α+cos αcos α=2当k 为奇数时,则有A =sin (k π+α)sin α+cos (k π+α)cos α=-sin αsin α+-cos αcos α=-2.三、解答题10.求下列三角函数值:(1)sin(-1320°);(2)cos ⎝ ⎛⎭⎪⎫-263π; (3)tan 176π.解:(1)sin(-1320°)=sin(-1440°+120°)=sin120°=32.(2)cos ⎝ ⎛⎭⎪⎫-263π=cos ⎝ ⎛⎭⎪⎫-8π-23π=cos 23π=-cos π3=-12. (3)tan 176π=tan ⎝ ⎛⎭⎪⎫2π+56π=tan 56π=-tan π6=-33. 11.化简下列各式:(1)sin (2π-α)·cos (π+α)cos (π-α)·sin (3π-α)·sin (-π-α); (2)cos (α-π)sin (π-α)·sin(α-2π)·cos(2π-α); (3)cos 2(-α)-tan (360°+α)sin (-α). 解:(1)原式=(-sin α)·(-cos α)(-cos α)·sin α·sin α=-1sin α; (2)原式=-cos αsin α·(sin α)·cos α=-cos 2α;(3)原式=cos 2α+tan αsin α=cos 2α+1cos α.12.若k ∈Z ,则sin (k π-α)cos (k π+α)sin[(k +1)π+α]cos[(k +1)π-α]=________ 答案:-1 解析:若k 为偶数,则左边=sin (-α)cos αsin (π+α)cos (π-α)=-sin αcos α(-sin α)(-cos α)=-1;若k 为奇数,则 左边=sin (π-α)cos (π+α)sin αcos (-α)=sin α(-cos α)sin αcos α=-1. 13.已知1+tan α1-tan α=3+22,求cos 2(π-α)+sin(π+α)cos(π-α)+2sin 2(α-π)的值. 解:∵1+tan α1-tan α=3+2 2,∴tan α=2+2 24+2 2=22.∴cos 2(π-α)+sin(π+α)cos(π-α)+2sin 2(α-π)=cos 2α+sin αcos α+2sin 2α=cos 2α(1+tan α+2tan 2α)=cos 2αcos 2α+sin 2α(1+tan α+2tan 2α)=1+tan α+2tan 2α1+tan 2α=1+22+11+12=4+23.。
(2024年)三角函数的诱导公式说课完整版PPT课件

三角函数的诱导公式说课完整版PPT课件•课程介绍与目标•三角函数基本概念回顾•诱导公式推导与理解目录•典型例题分析与解答•学生自主练习与互动环节•课程总结与拓展延伸课程介绍与目标说课内容01020304知识与技能过程与方法情感态度与价值观030201教学目标教学方法与手段教学方法教学手段三角函数基本概念回顾三角函数定义及性质三角函数值的范围三角函数的定义正弦、余弦函数值在正切函数值在全体实数范围内。
三角函数的周期性三角函数在各象限的符号规律正弦、余弦、正切函数均为正值。
正弦函数为正值,余弦、正切函数为负值。
正弦、余弦函数为负值,正切函数为正值。
余弦函数为正值,正弦、正切函数为负值。
第一象限第二象限第三象限第四象限三角函数线及其应用三角函数线的定义三角函数线的性质三角函数线的应用诱导公式推导与理解角度制与弧度制转换关系角度制与弧度制的定义及关系角度与弧度的互化方法特殊角的弧度表示诱导公式推导过程口诀记忆法通过编口诀或顺口溜等方式帮助记忆规律记忆法根据公式间的内在联系和规律进行记忆图像记忆法结合三角函数图像进行记忆和理解诱导公式记忆方法典型例题分析与解答例题1例题2分析解答解答分析利用诱导公式求三角函数值例题3例题4分析解答解答分析判断三角函数符号问题学生自主练习与互动环节学生自主完成练习题练习题一01练习题二02练习题三03小组内成员相互激励和讨论,共同探究解题方法和思路。
通过交流和比较,发现自身在解题过程中的不足和错误,并及时进行纠正和改进。
小组代表向全班汇报讨论结果和解题思路,促进全班同学的共同进步。
小组讨论与交流解题思路教师点评与总结教师针对学生在自主练习和小组讨论中的表现进行点评,肯定学生的优点和进步,指出需要改进的地方。
教师总结本节课的重点和难点,强调诱导公式在三角函数求解中的重要性和应用广泛性。
教师引导学生对本节课所学内容进行回顾和反思,帮助学生加深对知识点的理解和记忆。
课程总结与拓展延伸本节课重点内容回顾三角函数的定义及基本性质三角函数的诱导公式推导与记忆方法诱导公式在三角函数计算中的应用举例三角函数在其他领域的应用举例物理学中的应用振动、波动等物理现象中,三角函数可描述周期性变化。
专题5.3 诱导公式(解析版)
专题5.3诱导公式一、单选题1.函数3()3x f x a -=+(0a >,且1a ≠)的图象恒过定点A ,点A 在角θ终边上,则3cos π2θ⎛⎫-= ⎪⎝⎭()A .35-B .35C .45-D .45【答案】C【解析】3()3x f x a -=+(0a >,且1a ≠)恒过点()3,4A ,因为点A 在角θ终边上,所以4sin 5θ=,则34cos πsin 25θθ⎛⎫-=-=- ⎪⎝⎭故选:C2.若4π5cos 513α⎛⎫+=- ⎪⎝⎭,则7πsin 10α⎛⎫-=⎪⎝⎭()A .513-B .1213-C .513D .1213【答案】C【解析】7π7π4π3π4π5sin sin sin cos 101052513αααα⎛⎫⎛⎫⎛⎫⎛⎫-=--=-+-=-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.故选:C3.若1sin ,63a π⎛⎫+= ⎪⎝⎭则2cos 3a π⎛⎫+= ⎪⎝⎭()A .13B .13-C .79D .79-【答案】B【解析】:因为1sin 63a π⎛⎫+= ⎪⎝⎭,所以21cos cos sin 32663ππππααα⎡⎤⎛⎫⎛⎫⎛⎫+=++=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,故选:B.4.已知角,02πα⎛⎫∈- ⎪⎝⎭,且22tan 3tan sin 4sin 0αααα--=,则()sin 2021απ+=()A B .14C .34-D .【答案】A【解析】解:因为22tan 3tan sin 4sin 0αααα--=,所以()()tan 4sin tan sin 0αααα-+=,因为,02πα⎛⎫∈- ⎪⎝⎭,所以tan 0α<且sin 0α<,所以tan 4sin 0αα-=,即sin 4sin cos ααα=,所以1cos 4α=,所以sin 4α==-,所以()()()sin 2021sin 10102sin sin 4απαππαπα+=++⨯=+=-=;故选:A5.已知3cos 34πα⎛⎫+=- ⎪⎝⎭,则sin 6πα⎛⎫-= ⎪⎝⎭()A .35B .35-C .34D .34-【答案】C【解析】因为362πππαα⎛⎫⎛⎫+--= ⎪ ⎪⎝⎭⎝⎭,所以632πππαα⎛⎫⎛⎫-=+- ⎪ ⎝⎭⎝⎭,所以3sin sincos 63234ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=+-=-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故答案为:C 6.已知()cos ,1,1,,2k k πααπ⎛⎫=∈-∈ ⎪⎝⎭,则()sin πα+=()A.BC.D .1k-【答案】A【解析】解:因为()cos ,1,1,,2k k πααπ⎛⎫=∈-∈ ⎪⎝⎭,所以sin α==所以()sin sin παα+=-=A7.已知()()()sin cos 5sin sin 22αππαπαπα++-=⎛⎫-+- ⎪⎝⎭,则tan α=()A .34B .43C .32-D .32【答案】D【解析】()()()sin cos sin cos 5cos sin sin sin 22αππαααπαααπα++---==-⎛⎫-+- ⎪⎝⎭,可得()sin cos 5cos sin αααα--=-,即4sin 6cos αα=,故3tan 2α=.故选:D.8.已知71sin 123πα⎛⎫+=- ⎪⎝⎭,5sin 12πα⎛⎫-= ⎪⎝⎭()A .13-B.3-C .13D.3【答案】C【解析】由题意,5571sin sin sin 1212123πππαπαα⎡⎤⎛⎫⎛⎫⎛⎫-=-+-=-+= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故选:C.9.已知角α终边上一点P 的坐标为4sin ,cos55ππ⎛⎫⎪⎝⎭,则角α的一个可能值为()A .5πB .310π-C .5π-D .45π【答案】B 【解析】πsin 05>,4πcos 05<,因此α是第四象限角,2222π4πππsin cos sin cos 15555+=+=,因此πππ3π3πcos sin cos()cos cos()5251010α==-==-,所以3π2π,10k k Z α=±∈,只有B 符合.故选:B .10)A .sin 4cos4-B .sin 4cos4--C .cos 4sin 4-D .sin 4cos4+【答案】C【解析】=,cos 4sin 4=-,故选:C11.若33sin 25πα⎛⎫+= ⎪⎝⎭,且α是第三象限角,则2021cos 2πα⎛⎫+= ⎪⎝⎭()A .35B .35-C .45D .45-【答案】C【解析】33sin cos 25παα⎛⎫+=-= ⎪⎝⎭,3cos 5α∴=-,又α是第三象限角,4sin 5α∴==-,20214cos sin 25παα⎛⎫∴+=-= ⎪⎝⎭.故选:C.12.若()sin cos 12232sin sin 2ππααππαα⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭=⎛⎫-+- ⎪⎝⎭,则22sin sin cos 3cos αααα--=()A .110B .310C .910D .32【答案】C【解析】解:()sin cos cos sin 1tan 1223sin cos tan 12sin sin 2ππαααααπαααπαα⎛⎫⎛⎫++- ⎪ ⎪++⎝⎭⎝⎭===--⎛⎫-+- ⎪⎝⎭,解得tan 3α=-,则222222sin sin cos 3cos sin sin cos 3cos sin cos αααααααααα----=+22tan tan 39339tan 19110ααα--+-===++.故选:C.13.已知角α终边上点A 的坐标为34,55⎛⎫- ⎪⎝⎭,则()3cos cos 2ππαα⎛⎫-+-+= ⎪⎝⎭()A .75B .75-C .65-D .15-【答案】D【解析】∵角α终边上点A 的坐标为34,55⎛⎫- ⎪⎝⎭,35x ∴=-,45y =,1r OA ==.4sin 5α∴==y r ,cos 53x r α==-,()3341cos cos cos sin 2555ππαααα⎛⎫⎛⎫∴-+-+=--=---=- ⎪ ⎪⎝⎭⎝⎭.故选:D14.已知角,02πα⎛⎫∈- ⎪⎝⎭,且22tan 3tan sin 4sin 0αααα--=,则()cos 2021απ+=()A .14-B.4-C .14D.4【答案】A【解析】因为22tan 3tan sin 4sin 0αααα--=,所以()()tan 4sin tan sin 0αααα-+=,因为,02πα⎛⎫∈- ⎪⎝⎭,所以tan 0<α且sin 0α<,所以tan 4sin 0αα-=,即sin 4sin cos ααα=,所以1cos 4α=,所以()()()1cos 2021cos 10102cos cos 4+=++⨯=+=-=-απαππαπα;故选:A15.若()tan π3α-=,则sin 2cos sin cos αααα-=+()A .52B .52-C .14-D .14【答案】D 【解析】由()tan π3α-=可得,tan 3α=,故sin 2cos tan 2321sin cos tan 1314αααααα---===+++,故选:D二、填空题16.已知1sin 62πα⎛⎫-= ⎪⎝⎭,那么2cos 3πα⎛⎫-=⎪⎝⎭______.【答案】12-或0.5-【解析】:因为2362πππαα⎛⎫⎛⎫---= ⎪ ⎪⎝⎭⎝⎭,所以2326πππαα⎛⎫⎛⎫-=+- ⎪ ⎪⎝⎭⎝⎭所以21cos cos sin 32662ππππααα⎡⎤⎛⎫⎛⎫⎛⎫-=+-=--=-⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故答案为:12-17__________.【答案】1【解析】原式=sin 20cos 201cos 20sin160sin 20cos 20+==++.故答案为:1.18.若sin θcos(π)cos(2π)3ππ3πcos [sin()1]cos(π)sin()sin()222θθθθθθθ--+--++-+的值_______【答案】6【解析】原式=cos cos (cos 1)θθθ---+cos cos cos cos θθθθ-⋅+11cos 11cos θθ=++-1cos 1cos (1cos )(1cos )θθθθ-++=+-221cos θ=-22sin θ=,因为sin θ=,所以22261sin 3θ==.所以cos(π)cos(2π)63ππ3πcos [sin()1]cos(π)sin()sin()222θθθθθθθ--+=--++-+.故答案为:6.19.若角α的终边落在直线y x =上,则co 3si 22n s παπα⎛⎫⎛⎫++= ⎪ ⎪⎝⎭⎝⎭-_____.或【解析】因为角α的终边落在直线y x =上,所以角α为第一或第三象限角,3sin cos cos sin 22ππαααα⎛⎫⎛⎫⎪ ⎪-++=--⎝⎭⎝⎭,当角α为第一象限角时,cos sin 2αα==,cos sin 22αα--=--=当角α为第三象限角时,cos sin 2αα==,cos sin 22αα--=+=20.已知π3cos 64α⎛⎫+=- ⎪⎝⎭,则5ππcos sin 63αα⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭______.【答案】32或1.5【解析】因为π3cos 64α⎛⎫+=- ⎪⎝⎭,所以5ππcos sin 63αα⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭5ππcos sin 63αα⎛⎫⎛⎫=--- ⎪ ⎪⎝⎭⎝⎭cos sin 626ππππαα⎡⎤⎡⎤⎛⎫⎛⎫=-+--+ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦cos cos 66ππαα⎛⎫⎛⎫=-+-+ ⎪ ⎪⎝⎭⎝⎭332cos 2642πα⎛⎫⎛⎫=-+=-⨯= ⎪ ⎪⎝⎭⎝⎭,故答案为:32三、解答题21.已知()()()()sin cos 2sin cos 2f πθπθθπθπθ--=⎛⎫-+ ⎪⎝⎭.(1)化简()f θ,并求83f π⎛⎫⎪⎝⎭的值;(2)若()3f θ=,求22sin 3sin cos θθθ-的值.【答案】(1)()tan f θθ=,83f π⎛⎫=⎪⎝⎭(2)910【解析】(1)()()()()sin cos 2sin()cos 2f πθπθθπθπθ--=-+sin cos()sin (cos )2θθπθθ-=⎛⎫--- ⎪⎝⎭sin cos cos (cos )θθθθ=--tan θ=则83f π⎛⎫⎪⎝⎭8tan 3π⎛⎫= ⎪⎝⎭2tan 3π⎛⎫= ⎪⎝⎭tan 3π⎛⎫=- ⎪⎝⎭=(2)由(1)知,tan 3θ=.则22sin 3sin cos θθθ-2222sin 3sin cos sin cos θθθθθ-=+222222sin 3sin cos cos sin cos cos θθθθθθθ-=+222tan 3tan tan 1θθθ-=+22233331⨯-⨯=+9.10=22.(1)若α是第二象限角,且π1cos 23α⎛⎫+=- ⎪⎝⎭,求tan α的值;(2)已知()()()()()3πsin 3πcos 2πsin 2cos πsin πf αααααα⎛⎫--- ⎪⎝⎭=---,化简()f α,在(1)的条件下,求()f α的值.【答案】(1)4-(2)3-【解析】(1)π1cos sin 23αα⎛⎫+=-=- ⎪⎝⎭,1sin 3α=,α是第二象限角,cos 3α∴==-,则sin 2tan cos 4ααα==-.(2)()()()()()()()3πsin 3πcos 2πsin sin cos cos 2cos cos πsin πcos sin f αααααααααααα⎛⎫--- ⎪-⎝⎭===----,由(1)知:cos 3α=-,则()cos 3f αα==-.23.已知函数()()3sin sin 2cos 3tan x x f x x x ππ⎛⎫⋅- ⎪⎝⎭=--⋅.(1)求353f π⎛⎫- ⎪⎝⎭;(2)若()1332f f πθθ⎛⎫=-- ⎪⎝⎭,求2cos 2sin 10sin 2cos sin θθθθθ++-的值.【答案】(1)12-(2)2【解析】(1)()()3sin sin sin cos 2cos cos 3tan cos tan x x x x f x x x x x x ππ⎛⎫⋅- ⎪⋅⎝⎭===---⋅-⋅,35351cos cos 3332f πππ⎛⎫⎛⎫⎛⎫-=--=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(2)由()1332f f πθθ⎛⎫=-- ⎪⎝⎭得1cos sin 3θθ=,tan 3θ=,所以222cos 2sin 12tan 10tan 10sin 7922cos sin 2tan 1tan θθθθθθθθθ+++=+=-+=--+.24.已知cos sin 22333sin()sin 2ππααππαα⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭=⎛⎫-++ ⎪⎝⎭.(1)求tan()πα+的值;(2)求2sin cos cos ααα+的值.【答案】(1)12(2)65【解析】(1)由cos sin 22333sin()sin 2ππααππαα⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭=⎛⎫-++ ⎪⎝⎭,可得sin cos 33sin cos αααα+=-,所以8sin 4cos αα=,解得1tan 2α=,所以1tan()tan 2παα+==.(2)由(1)知1tan 2α=,所以22222sin cos cos tan 16sin cos cos sin cos tan 15αααααααααα+++===++.。
《诱导公式(二)》教案

1.2.4诱导公式(二)一、学习目标1.通过本节内容的教学,使学生掌握α+π1)k +2(,α2π+角的正弦、余弦和正切的诱导公式及其探求思路,并能正确地运用这些公式进行任意角的正弦、余弦和正切值的求解、简单三角函数式的化简与三角恒等式的证明;2.通过公式的应用,培养学生的化归思想,以及信息加工能力、运算推理能力、分析问题和解决问题的能力;二、教学重点、难点重点:四组诱导公式及这四组诱导公式的综合运用.难点:公式(四)的推导和对称变换思想在学生学习过程中的渗透. 三、教学方法先由学生自己看书,在此基础上,可以通过讲授再现概念,通过练习理解概念,完成教学.+-=-=x x9017)cos(9017)sin17 480︒)+cos(-330︒)5.3.2同角三角比的关系(2)诱导公式【教学目标】1.通过本节课的教学,使学生掌握五组诱导公式的推导方法和记忆方法.2.在理解、记忆五组诱导公式的基础上,会运用这些公式求解任意角的三角函数的值,并会进行一般的三角关系式的化简和证明.3.加深理解化归思想,培养学生观察问题、解决问题、抽象概括问题的能力,并注意完善学生的基本数学思想和数学意识.【教学重点】五组诱导公式的记忆、理解、运用。
【教学难点】五组诱导公式的推导教学过程:【情景引入】与6π终边相同角α的集合如何表示?αsin 与6sin π具有怎样的数量关系?与β终边相同角α的集合如何表示?αsin 与βsin 具有怎样的数量关系?βα,其它的五个三角比数量关系又如何呢?【问题探究】诱导公式一:文字叙述:终边相同的角的同一个三角函数的值相等.sin(k·360°+α)=sinα,cos(k·360°+α)=cosα, tan(k·360°+α)=tanα,cot(k·360°+α)=cotα.(k ∈Z )试求出sin 2016°的值.由公式一:sin 2016°=sin(5×360°×216°)=sin 216° 问题二:如何求出进一步sin 216°的值诱导公式二:①同名函数关系;②符号规律:右边符号与180°+α角所在象限(第三象限)角的原三角函数值的符号相同. sin(180°+α)=-sinα, cos(180°+α)=-cosα,tan(180°+α)=tanα, cot(180°+α)=cot α.诱导公式三:①同名函数关系;②符号规律是:右边符号与-α所在的第四象限角的原三角函数值的符号相同.sin(-α)=-sinα,cos(-α)=cosα, tan(-α)=tanα, cot(-α)=-cotα.诱导公式四:sin(180)sin αα-=;cos(180)cos αα-=-. t sin(180)sin αα-=;cos(180)cos αα-=-(1)请学生自行仿上节课的推导方法得出它们的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
诱导公式的化简与求值20题诱导公式的化简与求值20题诱导公式的化简与求值20题一.解答题(共20小题)1.已知角α终边上一点P(﹣,1)(1)求的值(2)写出角α的集合S.2.已知角α的终边经过点P(,﹣).(1)求sinα的值.(2)求式﹣的值3.已知角α终边上一点A的坐标为,(1)求角α的集合(6分)(2)化简下列式子并求其值:(6分)4.(1)已知tanα=2,求的值(2)已知cos(75°+α)=,其中﹣180°<α<﹣90°,求sin(105°﹣α)+cos(375°﹣α)的值.5.已知α是第三象限角,且(1)化简f(α);(2)若,求f(α)的值.6.已知角α的终边上一点P(x,4),且cosα=﹣.(1)求x的值;(2)求sin(α+π)的值;(3)将角α的终边沿顺时针旋转π弧度得到角β,求sinβ的值.7.已知(1)化简f(α)(2)若α是第三象限角,且,求f(α)的值.8.求值:①sin870°+cos660°+tan1215°﹣tan(﹣300°)+cot(﹣330°)②.9.已知sin(3π+θ)=,求+的值.10.已知.(1)求sinx﹣cosx的值;(2)求的值.11.已知α是第四象限角,且.(1)求tanα的值;(2)求的值.12.已知.①化简f(α).②若sinα是方程10x2+x﹣3=0的根,且α在第三象限,求f(α)的值.③若a=,求f(α)的值.13.(1)已知,求sinα﹣cosα的值.(2)已知且,求cosα﹣sinα的值.14.已知f(α)=(1)化简f(α);(2)若α是第三象限角,且cos()=,求f(α+π)的值;(3)若,求f(α)的值.15.已知f(a)=.(1)化简f(a);(2)若角a的终边经过点P(﹣2,3),求f(a)的值.16.已知.(1)若α是第三象限角,,求f(α)的值;(2)若,求f(α)的值.17.已知0<α<π,tanα=﹣2.(1)求sin(α+)的值;(2)求的值;(3)2sin2α﹣sinαcosα+cos2α18.已知α是第三象限角,且f(α)=.(1)化简f(α);(2)若tan(π﹣α)=﹣2,求f(α)的值;(3)若α=﹣420°,求f(α)的值.19.已知.(Ⅰ)化简f(α);(Ⅱ)若α是第三象限角,且,求f(α)的值.20.(1)已知,计算:(2)已知α为第二象限角,化简.诱导公式的化简与求值20题参考答案与试题解析一.解答题(共20小题)1.已知角α终边上一点P(﹣,1)(1)求的值(2)写出角α的集合S.考点:任意角的三角函数的定义;运用诱导公式化简求值.专题:计算题.分析:先求出点P(﹣,1)到原点的距离,再由定义求出角α的三角函数值,(1)先用诱导公式化简,再代入角α的三角函数值求值;(2)写出角α的集合S,由于本题中的角是一个特殊角,故可以用终边相同的角将它表示出来.解答:解:点P(﹣,1)到原点的距离是2,由定义sinα=,cosα=﹣(1)==﹣==﹣(2)由sinα=,cosα=﹣知角α的终边与角的终边相同,故α=2kπ+,k∈z故S={α|α=2kπ+,k∈z}点评:本题考查任意角三角函数的定义以及终边相同角的表示,利用诱导公式化简求值,求解本题的关键是熟练掌握定义与诱导公式,基础概念只有在掌握熟练得基础上才能正确运用它做题,不出错误.2.已知角α的终边经过点P(,﹣).(1)求sinα的值.(2)求式﹣的值考点:任意角的三角函数的定义;运用诱导公式化简求值.专题:计算题.分析:(1)求出|OP|,利用三角函数的定义,直接求出sinα的值.(2)利用诱导公式化简表达式,根据角的终边所在象限,求出cosα=,可得结果.解答:解:(1)∵|OP|=,∴点P在单位圆上.(2分)由正弦函数的定义得sinα=﹣(5分)(2)原式=(9分)=..(10分)由余弦的定义可知,cosα=(11分)即所求式的值为(12分)点评:本题考查任意角的三角函数的定义,运用诱导公式化简求值,考查计算能力,推理能力,是基础题.3.已知角α终边上一点A的坐标为,(1)求角α的集合(6分)(2)化简下列式子并求其值:(6分)考点:三角函数的化简求值;终边相同的角;同角三角函数间的基本关系;诱导公式的作用.专题:计算题.分析:(1)根据角的终边过一个定点,根据三角函数的定义做出角的正弦值,根据角的终边在第四象限,写出与角终边相同的所有的角的集合.(2)首先用诱导公式进行整理,再把正割与余割变化成正弦与余弦的形式,约分整理出最简形式,得到结果.解答:解:(1)点P到原点的距离为r=根据三角函数的定义,得….(2分)∵点P在第四象限,也就是角α在第四象限….(4分)∴α的集合是…(6分)(2)原式=….(8分)==﹣sinα=点评:本题考查三角函数的恒等变化求值即终边相同的角,本题解题的关键是先用诱导公式进行整理,再把正割与余割变化成正弦与余弦.本题是一个中档题目.4.(1)已知tanα=2,求的值(2)已知cos(75°+α)=,其中﹣180°<α<﹣90°,求sin(105°﹣α)+cos(375°﹣α)的值.考点:同角三角函数基本关系的运用;运用诱导公式化简求值.专题:计算题.分析:(1)利用诱导公式化简表达式,应用tanα=2求出,代入化简后的表达式即可求出原式的值.(2)利用诱导公式化简sin(105°﹣α)+cos(375°﹣α),为2sin(75°+α),利用求出2sin(75°+α)即可.解答:解:(1)原式=(2分)=(3分)∵,∴(6分),∴原式=(7分)(2)原式=sin(75°+α)+cos(15°﹣α)=2sin(75°+α)(9分)∵,且﹣105°<75°+α<﹣15°,∴sin(75°+α)<0∴(12分)故原式=(14分)点评:本题考查诱导公式的应用,同角三角函数的基本关系式,考查计算能力,是基础题.5.已知α是第三象限角,且(1)化简f(α);(2)若,求f(α)的值.考点:运用诱导公式化简求值;同角三角函数间的基本关系.专题:计算题.分析:(1)直接利用诱导公式化简f(α),应用正切化为正弦、余弦函数,推出结果;(2)求出的最简形式,弦长f(α)的表达式,通过同角三角函数的基本关系式求出它的值.解答:解:(1)f(α)=====﹣cosα(2)∵cos()=﹣sinα=,∴sinα=﹣,∵α是第三象限角,∴cosα=﹣=﹣,∴f(α)=﹣cosα=点评:本题是基础题,考查诱导公式的应用,同角三角函数的基本关系式的应用,考查计算能力,常考题型.6.已知角α的终边上一点P(x,4),且cosα=﹣.(1)求x的值;(2)求sin(α+π)的值;(3)将角α的终边沿顺时针旋转π弧度得到角β,求sinβ的值.考点:任意角的三角函数的定义;运用诱导公式化简求值.专题:计算题.分析:(1)利用三角函数的定义,求出x的值;(2)直接利用诱导公式化简sin(α+π),然后求出它的值;(3)将角α的终边沿顺时针旋转π弧度得到角β,然后直接利用诱导公式,求sinβ的值.解答:解:(1)因为cosα=﹣,所以,所以,x=﹣3;(2)因为cosα=﹣,所以sin(α+π)=cosα=﹣;(3)将角α的终边沿顺时针旋转π弧度得到角β,,sinβ=sin()=cosα=﹣.点评:本题是基础题,考查三角函数的定义,诱导公式的应用,考查计算能力.7.已知(1)化简f(α)(2)若α是第三象限角,且,求f(α)的值.考点:运用诱导公式化简求值.专题:计算题.分析:(1)利用诱导公式化简f(α)的结果为cosα.(2)利用诱导公式求出sinα,再由同角三角函数的基本关系求出cosα,从而得到f(α)的值.解答:解:(1)==cosα.(2)∵,∴,又∵α为第三象限角,∴,∴.点评:本题考查同角三角函数的基本关系,诱导公式的应用,以及三角函数在各个象限中的符号,化简f(α)是解题的突破口.8.求值:①sin870°+cos660°+tan1215°﹣tan(﹣300°)+cot(﹣330°)②.考点:运用诱导公式化简求值.专题:计算题.分析:①先利用诱导公式:终边相同的角的三角函数值相等,将题中的角化到[0°,360°)上,再利用诱导公式将其转化为锐角三角函数值即可②先利用诱导公式化简所求三角式,再利用同角三角函数基本关系式化简即可解答:解:①sin870°+cos660°+tan1215°﹣tan(﹣300°)+cot(﹣330°)=sin(720°+150°)+cos(720°﹣60°)+tan(﹣360°+60°)+cot(﹣360°+30°)=sin150°+cos(﹣60°)+tan60°+cot30°=sin30°+cos60°+tan60°+cot30°=+++=1+2②=====﹣1点评:本题考查了诱导公式的运用和同角三角函数基本关系式的运用,细心和运用恰当的公式是解决本题的关键9.已知sin(3π+θ)=,求+的值.考点:运用诱导公式化简求值.专题:计算题.分析:先根据诱导公式化简已知得到sinθ的值,然后把原式也利用诱导公式及同角三角函数的基本关系化简后,把sinθ代入求值即可.解答:解:∵sin(3π+θ)=﹣sinθ=,∴sinθ=﹣,原式=+=+=+====18.点评:此题要求学生灵活运用诱导公式及同角三角函数间的基本公式化简求值,做题的思路是把所有余弦都要化成正弦.10.已知.(1)求sinx﹣cosx的值;(2)求的值.考点:运用诱导公式化简求值;同角三角函数间的基本关系.专题:三角函数的求值.分析:(1)利用同角三角函数基本关系式直接求出sinx和cosx的值,进而求出结果.(2)先利用诱导公式化简所求的式子,将原式分子分母同除以cos2x,转化成tanx的表达式去解.解答:解:∵sinx=﹣2cosx,又sin2x+cos2x=1,∴5cos2x=1,∴(1)(2)原式==…(12分)点评:本题考查同角三角函数基本关系式的应用和三角函数的诱导公式,计算要准确,属于中档题.11.已知α是第四象限角,且.(1)求tanα的值;(2)求的值.考点:同角三角函数间的基本关系;诱导公式的作用.专题:计算题.分析:(1)由题意知求出,再求tanα的值.(2)利用诱导公式,等价转化为.解答:解:(1)由题意知,,∴;(2)=.点评:本题考查诱导公式的合理运用,解题时要认真审题,注意三角函数恒等变换的灵活运用.12.已知.①化简f(α).②若sinα是方程10x2+x﹣3=0的根,且α在第三象限,求f(α)的值.③若a=,求f(α)的值.考点:三角函数的化简求值;诱导公式的作用.专题:计算题.分析:①把f(α)的分子最后一项的角﹣α变为6π﹣(+α),分母第一项的角3π+α变形为2π+(π+α),第二项中的角变形为﹣(π+α),最后一项变形为4π+(+α),然后各项利用诱导公式及正弦、余弦函数的奇偶性进行化简,约分后即可得到最简结果;②把已知的方程分解因式后,求出方程的两个解,由sinα是方程10x2+x﹣3=0的根,且α在第三象限,可得出sinα的值,代入第一问化简后的式子中,即可求出f(α)的值;③把α的值变形为﹣6π﹣,代入第一问化简后的式子中,利用诱导公式及正弦函数的奇偶性化简,再利用特殊角的三角函数值即可求出f(α)的值.解答:解:①===﹣sinα;…(4分)②由方程10x2+x﹣3=0,解得:,又α在第三象限,∴,则;…(8分)(3)当a=时,.…(12分)点评:此题考查了三角函数的恒等变形,涉及的知识有:正弦、余弦函数的奇偶性,诱导公式,函数的值,以及特殊角的三角函数值,灵活变换角度,熟练掌握诱导公式是解本题的关键.13.(1)已知,求sinα﹣cosα的值.(2)已知且,求cosα﹣sinα的值.考点:运用诱导公式化简求值.专题:计算题.分析:(1)由题意得 sinα+cosα=,平方可得 2sinαcosα=﹣,代入sinα﹣cosα=﹣=﹣进行运算.(2)由题意得cosα﹣sinα=﹣=﹣,把已知条件代入运算.解答:解:(1)已知,∴sinα+cosα=,1+2sinαcosα=,2sinαcosα=﹣,∴sinα﹣cosα=﹣=﹣=﹣.(2)已知,且,cosα﹣sinα=﹣=﹣=.点评:本题考查同角三角函数的基本关系的应用,诱导公式的应用,判断所求式子的符号是解题的关键.14.已知f(α)=(1)化简f(α);(2)若α是第三象限角,且cos()=,求f(α+π)的值;(3)若,求f(α)的值.考点:诱导公式的作用.专题:三角函数的求值.分析:(1)利用诱导公式化简 f(α)=,整理可得结果.(2)利用诱导公式求得 sinα=﹣,再利用同角三角函数的基本关系求得 cosα=﹣,再由f(α+π)=﹣cos(π+α)=cosα求得结果.(3)利用诱导公式可得f(α)=﹣cos(670π+)=﹣cos,计算求得它的值.解答:解:(1)f(α)===﹣cosα.(2)若α是第三象限角,且cos()=,故﹣sinα=,sinα=﹣,∴cosα=﹣=﹣.∴f(α+π)=﹣cos(π+α)=cosα=﹣.(3)若,则f(α)=﹣cos=﹣cos(670π+)=﹣cos=﹣.点评:本题主要考查应用诱导公式化简三角函数式,同角三角函数的基本关系的应用,要特别注意符号的选取,这是解题的易错点,属于基础题.15.已知f(a)=.(1)化简f(a);(2)若角a的终边经过点P(﹣2,3),求f(a)的值.考点:诱导公式的作用;任意角的三角函数的定义.专题:计算题.分析:(1)利用三角函数的诱导公式即可求得f(a);(2)角a的终边经过点P(﹣2,3),利用任意角的三角函数的定义,可求得f(a)的值.解答:解:(1)∵sin(a﹣)=﹣cosa,cos(﹣a)=﹣sina,tan(7π﹣a)=﹣tana,tan(﹣a﹣5π)=﹣tan (5π+a)=﹣tana,sin(a﹣3π)=﹣sina,∴f(a)==﹣cosa;(2)∵a的终边经过点P(﹣2,3),∴cosa=﹣=﹣,∴f(a)=.点评:本题考查三角函数的诱导公式与任意角的三角函数的定义,掌握诱导公式是基础,属于基础题.16.已知.(1)若α是第三象限角,,求f(α)的值;(2)若,求f(α)的值.考点:诱导公式的作用;同角三角函数间的基本关系.专题:三角函数的求值.分析:利用诱导公式化简f(α)得到最简结果,(1)由α为第三象限,sinα的值小于0,得到cosα的值小于0,由sinα的值,利用同角三角函数间的基本关系求出cosα的值,即可确定出f(α)的值;(2)将α的度数代入f(α)中,利用诱导公式化简即可得到结果.解答:解:f(α)==﹣cosα,(1)∵α是第三象限角,sinα=﹣<0,∴cosα<0,∴cosα=﹣=﹣,则f(α)=﹣cosα=;(2)将α=﹣代入得:f(﹣)=﹣cos(﹣)=﹣cos(11π+)=﹣cos(π+)=cos=.点评:此题考查了诱导公式的作用,以及同角三角函数间的基本关系,熟练掌握诱导公式是解本题的关键.17.已知0<α<π,tanα=﹣2.(1)求sin(α+)的值;(2)求的值;(3)2sin2α﹣sinαcosα+cos2α考点:同角三角函数间的基本关系;诱导公式的作用.专题:计算题.分析:(1)由已知中0<α<π,tanα=﹣2,根据同角三角函数关系,我们可以求出sinα,cosα的值,代入两角和的正弦公式,即可求出sin(α+)的值;(2)利用诱导公式,我们可以将原式化为用α的三角函数表示的形式,弦化切后,tanα=﹣2,即可得到答案.(3)根据sin2α+cos2α=1,我们可以将2sin2α﹣sinαcosα+cos2α化为齐次分式,弦化切后,代入tanα=﹣2,即可得到答案.解答:解:因为0<α<π,tanα=﹣2,所以sinα=,cosα=(1)sin(α+)=sinαcos+cosαsin=+()×=(2)原式===﹣1(3)原式===点评:本题考查的知识点是同角三角函数间的基本关系,诱导公式,两角和的正弦公式,其中(2)(3)中齐次分式弦化切是三角函数给值求值中最常用的方法.18.已知α是第三象限角,且f(α)=.(1)化简f(α);(2)若tan(π﹣α)=﹣2,求f(α)的值;(3)若α=﹣420°,求f(α)的值.考点:诱导公式的作用.专题:三角函数的求值.分析:(1)直接利用诱导公式化简函数 f(α)为﹣cosα.(2)由tan(π﹣α)=﹣2,求得tanα=2,再利用同角三角函数的基本关系求出cosα的值即可求得f(α)=﹣cosα的值.(3)先利用诱导公式求得 cosα=cos(﹣420°)=,即可求得f(α)=﹣cosα的值.解答:解:(1)f(α)===﹣cosα.﹣﹣﹣﹣﹣﹣﹣﹣﹣(4分)(2)∵tan(π﹣α)=﹣2,∴tanα=2.﹣﹣﹣﹣﹣﹣﹣﹣﹣(5分).﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(6分)∵α是第三象限角,∴,∴f(α)=.﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣(8分)(3)∵,∴f(α)=﹣cosα=.﹣﹣﹣﹣﹣﹣(12分)点评:本题主要考查同角三角函数的基本关系,诱导公式的应用,属于基础题.19.已知.(Ⅰ)化简f(α);(Ⅱ)若α是第三象限角,且,求f(α)的值.考点:诱导公式的作用;同角三角函数基本关系的运用.专题:计算题.分析:(Ⅰ)利用诱导公式对函数的解析式化简整理求得函数的解析式.(Ⅱ)利用诱导公式整理求得sinα的值,进而利用同角三角函数的基本关系求得cosα的值,代入函数的解析式求得答案.解答:解:(Ⅰ)==tanα(Ⅱ)=﹣sinα=,∴sinα=﹣∵α是第三象限角∴cosα=﹣=﹣∴f(α)=tanα==2点评:本题主要考查了诱导公式的化简求值,同角三角函数的基本关系的应用.解题的关键是熟练掌握“奇边偶不变,正负看象限”的原则.20.(1)已知,计算:(2)已知α为第二象限角,化简.考点:诱导公式的作用;同角三角函数间的基本关系.专题:计算题.分析:(1)将所求式子的分母1用sin2α+cos2α代替,然后分子分母同除以cos2α,(2)利用诱导公式及三角函数关系式即可将化简,并求得其值.解答:(1)解:∵,cosα≠0,∴====;(2)∵α为第二象限角,∴===﹣1.点评:本题考查三角函数的诱导公式及三角函数间的基本关系,关键是熟练掌握三角函数的诱导公式及三角函数间的基本关系并灵活应用,属于中档题.。
