算法设计第六章答案
算法设计与分析C语言描述(陈慧南版)课后答案

算法设计与分析C语⾔描述(陈慧南版)课后答案第⼀章15P1-3. 最⼤公约数为1。
快1414倍。
主要考虑循环次数,程序1-2的while 循环体做了10次,程序1-3的while 循环体做了14141次(14142-2循环)若考虑其他语句,则没有这么多,可能就601倍。
第⼆章32P2-8.(1)画线语句的执⾏次数为log n 。
(log )n O 。
划线语句的执⾏次数应该理解为⼀格整体。
(2)画线语句的执⾏次数为111(1)(2)16jnii j k n n n ===++=∑∑∑。
3()n O 。
(3)画线语句的执⾏次数为。
O 。
(4)当n 为奇数时画线语句的执⾏次数为(1)(3)4n n ++,当n 为偶数时画线语句的执⾏次数为 2(2)4n +。
2()n O 。
2-10.(1)当 1n ≥ 时,225825n n n -+≤,所以,可选 5c =,01n =。
对于0n n ≥,22()5825f n n n n =-+≤,所以,22582()n n n -+=O 。
(2)当 8n ≥ 时,2222582524n n n n n -+≥-+≥,所以,可选 4c =,08n =。
对于0n n ≥,22()5824f n n n n =-+≥,所以,22582()n n n -+=Ω。
(3)由(1)、(2)可知,取14c =,25c =,08n =,当0n n ≥时,有22212582c n n n c n ≤-+≤,所以22582()n n n -+=Θ。
2-11. (1) 当3n ≥时,3log log n n n <<,所以()20log 21f n n n n =+<,3()log 2g n n n n =+>。
可选 212c =,03n =。
对于0n n ≥,()()f n cg n ≤,即()(())f n g n =O 。
注意:是f (n )和g (n )的关系。
国开作业程序设计基础-第六章 自测题78参考(含答案)

题目:下列叙述中正确的是_________________。
选项A:以上三种说法都不对
选项B:设计算法时只需要考虑结果的可靠性
选项C:算法就是程序
选项D:设计算法时只需要考虑数据结构的设计
答案:以上三种说法都不对
题目:当一个算法输入不合法的数据时,应当能够作适当处理,不致于引起严重后果,这属于算法的( ) 。
选项A:可读性
选项B:高效性
选项C:正确性
选项D:健壮性
答案:健壮性
题目:下列叙述中正确的是_________________。
选项A:以上三种说法都不对
选项B:一个算法的时间复杂度大,则其空间复杂度必定小
选项C:一个算法的空间复杂度大,则其时间复杂度也必定大
选项D:一个算法的空间复杂度大,则其时间复杂度必定小
答案:以上三种说法都不对
题目:一个算法应该具有“确定性”等5个特性,下面对另外4个特性的描述中错误的是()。
选项A:可行性
选项B:有穷性
选项C:有零个或多个输入
选项D:有零个或多个输出
答案:有零个或多个输出
题目:下面叙述正确的是()。
选项A:数据的逻辑结构与存储结构是一一对应的
选项B:算法的效率只与问题的规模有关,而与数据的存储结构无关
选项C:算法的时间复杂度与空间复杂度一定相关
选项D:算法的时间复杂度是指执行算法所需要的计算工作量
答案:算法的时间复杂度是指执行算法所需要的计算工作量
题目:根据问题条件估计答案的范围,在此范围内对所有可能情况逐一验证,直到全部情况均通过验证为止。
这种算法是()。
选项A:递归法
选项B:回溯法
选项C:穷举法
选项D:分治法。
C语言程序设计(第三版)谭浩强著 各章习题答疑

以八、 /* 以八、十六进制输出 */
} ???? 是对应的带符号短整数。 输出结果是八进制整数 十六进制整数
2
3.9 计算某个表达式的值。 通用程序清单如下: stdio.h” #include ”stdio.h stdio.h void main() { ?????? x; 计算表达式值存入x x=( 表达式 );/* 计算表达式值存入x */ printf(”% printf( %?\n”,x); ,x); } ?????? 表达式对应的数据类型符(需事先判断) ? 表达式为整型,则为d 表达式为实型,则为f 3
第七章习题答疑(二)
折半查找法在排序数组中查找某个数。 上课时已有提示。 7.13 字符串连接(b[]中字符串连接到a[]中字符串后) 设:a[10]=”12 ,b[]=”abc 12”, abc” 12 abc (1)找到a串的’\0’的下标(i=2) ’ (2)j=0; 当型循环(b[j]!=’\0’) ’\ ’ a[i]=b[j],i++,j++ (3)a[i]=’\0’ \ 7.15 字符串复制(b[]中字符串复制到a[]中) 设:a[10]=”12”,b[]=”abc” (1)i=0; 当型循环(b[i]!=’\0’) a[i]=b[i],i++ (2)a[i]=’\0’ 7.9
18
第十章习题答疑(一)
输入3个整数,按照由小到大顺序输出。 int x,y,z,*px=&x,*py=&y,*pz=&x; 用以前的程序,其中的x、y、z换成*px、*py、*pz 10.3 输入10个整数存入一维数组a[10],将其中最小数与第1 个数交换,最大数与最后一个数交换。 要求编3个函数: 10 10 输入10个整数、交换、输出交换后的10个整数。 输入函数: void in(int *p,int n) 输出函数: void out(int *p,int n) 交换函数: void change(int *p,int n) 其中寻找最大最小数的方法: int *q,*max,*min; for (max=min=p,q=p+1;q<p+n;q++) { if(*max<*q) max=q; if(*min>*q) min=q; } 19 交换的方法:*p和*min,*(p+n-1)和*max 10.1
(陈慧南 第3版)算法设计与分析——第6章课后习题答案

⑥ 选择作业 1,则 X 6, 2,3,5,1 。将其按照期限 di 非减次序排列可
得:
ID
di
5
1
6
2
3
3
1
3
2
4
作业5
作业3 作业2
-1
0
1
2
3
4
作业6 作业1(冲突)
该集合无可行排序,因此 X 6, 2,3,5,1 不可行, X 6, 2,3,5 ;
3
⑦ 选择作业 0,则 X 6, 2,3,5, 0 。将其按照期限 di 非减次序排列
可得:
ID
di
5
1
0
1
6
2
3
3
2
4
作业5
作业3 作业2
-1
0
1
2
3
4
作业0(冲突)作业6
该集合无可行排序,因此 X 6, 2,3,5, 0 不可行,X 6, 2,3,5 ;
⑧ 选择作业 4,则 X 6, 2,3,5, 4 。将其按照期限 di 非减次序排列
可得:
ID
Hale Waihona Puke di516
12,5,8,32, 7,5,18, 26, 4,3,11,10, 6 。请给出最优存储方案。
解析:首先将这 13 个程序按照程序长度非降序排列,得:
程序 ID
9 8 1 5 12 4 2 11 10 0 6 7 3
程序长度 ai 3 4 5 5 6 7 8 10 11 12 18 26 32
根据定理可知,按照程序编号存放方案如下:
解析:已知 Prim 算法时间复杂度为 O n2 ,受顶点 n 影响;
Kruskal 算法时间复杂度为 O m logm ,受边数 m 影响;
[高等教育]《算法设计与分析》第06章
![[高等教育]《算法设计与分析》第06章](https://img.taocdn.com/s3/m/684fc218941ea76e59fa0493.png)
if (w[i]>u) break; x[i]=1.0; u=u-w[i]; } if (i<=n) x[i]=u/w[i]; }
6.2.3 算法正确性
定理6-1 如果p0/w0p1/w1pn-1/wn-1,则程序6-2求 得的背包问题的解是最优解。
活动安排问题
活动安排问题就是要在所给的活动集合中 选出最大的相容活动子集合,是可以用贪心算 法有效求解的很好例子。该问题要求高效地安 排一系列争用某一公共资源的活动。贪心算法 提供了一个简单、漂亮的方法使得尽可能多的 活动能兼容地使用公共资源。
设有n个活动的集合E={1,2,…,n},其中每个活动 都要求使用同一资源,如演讲会场等,而在同一时间 内只有一个活动能使用这一资源。每个活动i都有一个 要求使用该资源的起始时间si和一个结束时间fi,且si <fi 。如果选择了活动i,则它在半开时间区间[si, fi) 内占用资源。若区间[si, fi)与区间[sj, fj)不相交,则 称活动i与活动j是相容的。也就是说,当si≥fj或sj≥fi 时,活动i与活动j相容。
void GreedyKnapsack(float* x); …… private:
float m,*w; T *p; int n; };
template<class T> void Knapsack<T>::GreedyKnapsack(float* x) { //前置条件:w[i]已按p[i]/w[i]的非增次序排列
贪心法是通过分步决策(stepwise decision)的方 法来求解问题的。
算法设计技巧与分析 第6章 分治法

Realization of MERGE
已分类序列A 数组A A(0) A(1) A(2) …
比较大小 小 值 比较大小 小 值
已分类序列B
A((n1)/2)
A((n1)/2+1)
…
A(n-1)
……
剩余已分类元素
辅助 A(0) 数组B
A((n-1)/2+1)
考虑函数需要的参数 原数组a[ ] 目标数组b[ ] a前段的起始位置l a前段的终止位置m,则后段起始位置为m+1 a后段的终止位置r
Analysis
由上可得 O(1) T (n)= kT(n/m)+f(n) 解上式得到
n=1
n>1
T (n) nlogm k
logm n 1 j 0
k j f (n / m j )
Content
分治法原理 算法实例
求最大/最小值 二分搜索 合并排序 寻找中项和第k小元素 快速排序 矩阵乘法 最近点对问题
恰好是在观察结论1.5中对算法BOTTOMUP
SORT下的结论。
Analysis
若n是任意的正整数,则:
C(n)=
0 C( n / 2 )+C( n / 2 )+bn
若 n=1 若 n≥2
C(n)=Θ(n log n)
算法MERGESORT对一个n个元素的数 组排序所需的时间是Θ(n log n),空间 是Θ(n)。
输出: (x, y),A中的最大元素和最小元素。 过程
minmax (low,high)
if A[low]<A[high]
then return (A[low], A[high]) else return (A[high], A[low]) end if
算法设计与分析智慧树知到课后章节答案2023年下山东交通学院

算法设计与分析智慧树知到课后章节答案2023年下山东交通学院山东交通学院第一章测试1.解决一个问题通常有多种方法。
若说一个算法“有效”是指( )A:这个算法能在一定的时间和空间资源限制内将问题解决B:这个算法能在人的反应时间内将问题解决C:这个算法比其他已知算法都更快地将问题解决D:(这个算法能在一定的时间和空间资源限制内将问题解决)和(这个算法比其他已知算法都更快地将问题解决)答案:(这个算法能在一定的时间和空间资源限制内将问题解决)和(这个算法比其他已知算法都更快地将问题解决)2.农夫带着狼、羊、白菜从河的左岸到河的右岸,农夫每次只能带一样东西过河,而且,没有农夫看管,狼会吃羊,羊会吃白菜。
请问农夫能不能过去?()A:不一定B:不能过去 C:能过去答案:能过去3.下述()不是是算法的描述方式。
A:自然语言 B:E-R图 C:程序设计语言 D:伪代码答案:E-R图4.有一个国家只有6元和7元两种纸币,如果你是央行行长,你会设置()为自动取款机的取款最低限额。
A:40 B:29 C:30 D:42答案:305.算法是一系列解决问题的明确指令。
()A:对 B:错答案:对6.程序=数据结构+算法()A:对 B:错答案:对7.同一个问题可以用不同的算法解决,同一个算法也可以解决不同的问题。
()A:错 B:对答案:对8.算法中的每一条指令不需有确切的含义,对于相同的输入不一定得到相同的输出。
( )A:错 B:对答案:错9.可以用同样的方法证明算法的正确性与错误性 ( )A:错 B:对答案:错10.求解2个数的最大公约数至少有3种方法。
( )A:对 B:错答案:错11.没有好的算法,就编不出好的程序。
()A:对 B:错答案:对12.算法与程序没有关系。
( )A:错 B:对答案:错13.我将来不进行软件开发,所以学习算法没什么用。
( )A:错 B:对答案:错14.gcd(m,n)=gcd(n,m m od n)并不是对每一对正整数(m,n)都成立。
数据结构与算法第六章课后答案第六章 树和二叉树
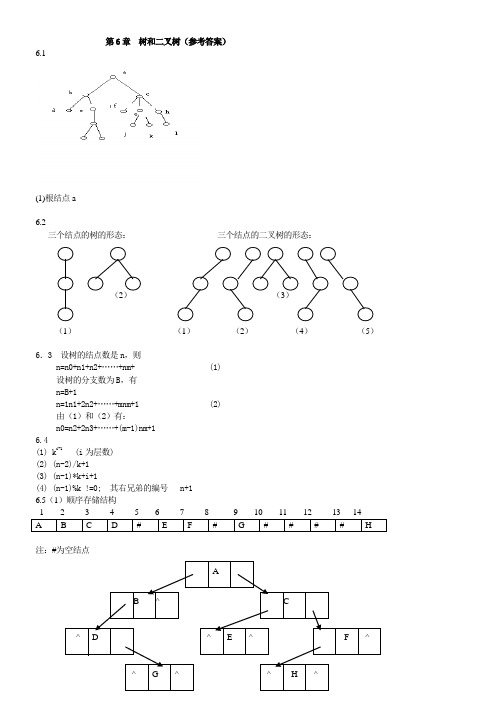
第6章 树和二叉树(参考答案)6.1(1)根结点a6.2三个结点的树的形态: 三个结点的二叉树的形态:(1) (1) (2) (4) (5)6.3 设树的结点数是n ,则n=n0+n1+n2+……+nm+ (1)设树的分支数为B ,有n=B+1n=1n1+2n2+……+mnm+1 (2)由(1)和(2)有:n0=n2+2n3+……+(m-1)nm+16.4(1) k i-1 (i 为层数)(2) (n-2)/k+1(3) (n-1)*k+i+1(4) (n-1)%k !=0; 其右兄弟的编号 n+16.5(1)顺序存储结构注:#为空结点6.6(1) 前序 ABDGCEFH(2) 中序 DGBAECHF(3) 后序 GDBEHFCA6.7(1) 空二叉树或任何结点均无左子树的非空二叉树(2) 空二叉树或任何结点均无右子树的非空二叉树(3) 空二叉树或只有根结点的二叉树6.8int height(bitree bt)// bt是以二叉链表为存储结构的二叉树,本算法求二叉树bt的高度{ int bl,br; // 局部变量,分别表示二叉树左、右子树的高度if (bt==null) return(0);else { bl=height(bt->lchild);br=height(bt->rchild);return(bl>br? bl+1: br+1); // 左右子树高度的大者加1(根) }}// 算法结束6.9void preorder(cbt[],int n,int i);// cbt是以完全二叉树形式存储的n个结点的二叉树,i是数// 组下标,初始调用时为1。
本算法以非递归形式前序遍历该二叉树{ int i=1,s[],top=0; // s是栈,栈中元素是二叉树结点在cbt中的序号 // top是栈顶指针,栈空时top=0if (n<=0) { printf(“输入错误”);exit(0);}while (i<=n ||top>0){ while(i<=n){visit(cbt[i]); // 访问根结点if (2*i+1<=n) s[++top]=2*i+1; //若右子树非空,其编号进栈i=2*i;// 先序访问左子树}if (top>0) i=s[top--]; // 退栈,先序访问右子树} // END OF while (i<=n ||top>0)}// 算法结束//以下是非完全二叉树顺序存储时的递归遍历算法,“虚结点”用‘*’表示void preorder(bt[],int n,int i);// bt是以完全二叉树形式存储的一维数组,n是数组元素个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解空间:深度为 n 完全 m 叉树 两个部件,三个供应商
A
1
2
3
B 1 23
C 1 23
EF G
HI J
D 1 23
KL M
根据条件可知:剪枝函数,约束函数是总价格不超过 d,界限函数是当前扩展结 点的总质量最小值大于当前最优总重量; 优先队列式分支限界法:优先级定义为结点已知部分的总重量;因而,每一次选 择新的扩展结点都是选择已知部分总重量最小的结点,因而界限函数可以省略; 算法流程: 主函数是一个 while 循环,结束条件是当前扩展结点的深度是 n,因为是优先队 列式分支限界(每一次都选择当前最小重量的结点作为扩展结点),因而第一个 找到的叶结点肯定是最优解; 每一次循环所需要完成的工作包括:1)将扩展结点的所有儿子结点加至活结点 列表中;其中,需要利用约束函数进行剪枝;2)按照“先进先出”原则,选择 下一个扩展结点。
活结点列表
是
为空?
否
是
当前扩展结点 在排列树中的深度
是n-1?
否
将当前扩展结点的儿子结点 分别加至活结点列表
输出最优解 结束
是
所有儿子结点
都已经得到判断?
否
选择下一个儿子结点,并且计 算各连接块的最大长度
各连接块的 当前最大长度小于当前
否
最优长度?
是
将当前儿子结点加至 活结点列表
将儿子结点加至活 结点列表
开始 根结点加入活结点列表,
并作为当前扩展结点
活结点列表
是
为空?
否
将当前扩展结点的儿子结点 分别加至活结点列表
左儿子结点
否
满足容量约束?
是
将左儿子结点加至 活结点列表
右儿子结点的 最大价值大于当前
否
最优价值?
是
将右儿子结点加至 活结点列表
按照“后进先出”,选择下 一个扩展结点
输出最优解 结束
将儿子结点加至活 结点列表
if(ok(r,c,board[r][i])) { Swap(board[r][c],board[r][i]); if(c==n) { if(r==m) count+=1.0; else Backtrace(r+1,2); } else Backtrace(r,c+1); Swap(board[r][c],board[r][i]); } }
解空间:对于每一行而言,是一个深度为 n 的排列树;因而,整个空间是 m 个 深度为 n 的排列树。 剪枝函数:每一列上的 m 个元素存在重复。 因而,这个问题存在两个有关深度的变量 r(行)和 c(列),即 Backtrace(r,c)
void Backtrace(int r,int c) { for(int i=c;i<=n;i++)
按照“先进先出”原则,选 择下一个扩展结点
开始
根结点加入活结点列表, 并作为当前扩展结点
当前扩展结点在解 是 空间数的深度是n?
否 将当前扩展结点的儿子结点
分别加至活结点列表
是
所有儿子结点
都已经得到判断?
否
选择下一个儿子结点,并且计算 当前儿子结点的总重量和总价格
当前儿子结点的
否
当前总价格小于d?
算法流程: 主函数是一个 while 循环,结束条件是活结点列表为空,表示所有叶结点都已经 遍历完成;此时,应该输出整个问题的最优解。 每一次循环需要完成的工作包括:1)如果当前扩展结点的深度是 n-1计算每一个连接块的长度,并且计算所有连接块的 最大长度;2)如果当前深度小于 n-1,则需要将扩展结点的儿子结点加至活结点 列表;其中,需要利用界限函数进行剪枝(界限函数就是各连接块的当前最大长 度小于当前最优长度);3)按照“先进先出”原则,选择下一个扩展结点。
设计一个解 01 背包问题的栈式分支限界法,并说明栈式分支限界法与回溯法的 区别。
解空间:子集树
A
1
0
B
1
0
C
1
0
D
E
F
G
1)队列式分支界限法和栈式分支界限法对比: 队列式分支限界法活结点列表变化过程:(先进先出)
1{A} 2{B,C} 3{C,D,E} 4{D,E,F,G} 5{E,F,G} 6{F,G} 7{G} 8{}
1
B
2
3
E
F
3
2
K
L
A 2
C
1
3
3
D
1
2
G
H
I
J
3
1
2
1
M
NO
P
注意:与课本例题最小密度电路板排列问题不同,在每一次将当前扩展结点的儿 子结点加至活结点列表时(当深度加 1 时),应该更新和计算儿子结点的当前最 小长度; 对于每一个结点而言,需要维护两个数组,low[1:m]和 high[1:m],分别记录着每 一个连接块的当前已知的起点插槽序号和终点插槽序号,当深度增加 1 时,首先 判断连接块 Nj 是否需要跨越 x[i+1]所对应的电路板; 假设 x[1:i]已知,x[i+1]是当前儿子结点所对应的第 i+1 层元素取值,则数组 low 和 high 更新方法是: 1) 如果连接块 Nj 跨越 x[i+1]电路板,而且当前 low[j]大于 i+1,则将 low[j]更新
算法实现题 6-4: 最小重量机器设计问题 问题描述:设某一个机器由 n 个部件组成,每一种部件都可以从 m 个不同的供 应商处购得。设 wij 是从供应商 j 处购得的部件 i 的重量,cij 是相应的价格。 设计一个优先队列式分支限界法,给出总价格不超过 d 的最小重量机器设计。 编程任务: 对于给定的机器部件重量和机器部件价格,设计一个优先队列式分支限界法,计 算总价格不超过 d 的最小机器设计。
是
将当前儿子结点加至 活结点列表
输出最优解 结束
将儿子结点加至活 结点列表
为 i+1; 2) 如果连接块 Nj 跨越 x[i+1]电路板,而且当前 high[j]小于 i+1,则将 high[j]更
新为 i+1; 3) 其余情况,则不需要更新 low[j]和 high[j]。
开始
根结点加入活结点列表, 并作为当前扩展结点
按照“先进先出”,选择下 一个扩展结点
计算各连接块的最小长度, 并且更新当前最优长度
2)程序流程 整个流程与队列式分支限界法的 01 背包问题一样,只是插入活结点的操作:由 insert()改为 push(),重新选择下一个扩展结点的操作:由 delete()改为 pop()。 算法主函数是: 一个 while(1)循环,循环结束条件是活结点列表为空,即当前扩展结点为空,表 示所有可行的结点都已经得到遍历;并且输出最优解。 每一次循环作用是:在当前的扩展结点下,将以当前扩展结点作为父结点的下一 层子结点都加入到活结点列表里,并且选择一个新的扩展结点,进入下一层循环; 其中,剪枝函数包括左结点的容量约束(约束函数)和右结点的最大价值判断(界 限函数);
算法实现题 6-1:最小长度电路板排列问题 问题描述:最小长度电路板排列问题是大规模电子系统设计中提出的实际问题。 该问题的提法是,将 n 块电路板以最佳排列方案插入带有 n 个插槽的机箱中。n 块电路板的不同排列方式对应与不同的电路板插入方式。 设 B={1,2,···,n}是 n 块电路板的集合。集合 L={N1,N2,···,Nm}是 n 块电 路板的 m 个连接块。其中,每个连接块 Ni 是 B 的一个子集,且 Ni 中的电路板 用同一根导线连接在一起。 在最小长度电路板排列问题中,连接块的长度是指该连接块中第一块电路板到最 后一块电路板之间的距离; 试设计一个队列式分支界限法找出所给 n 个电路板的最佳排列,使得 m 个连接 块中最大长度达到最小。 解空间:排列树
算法实现题 5-9:拉丁矩阵问题 问题描述:现有 n 种不同形状的宝石,每种宝石有足够多颗。欲将这些宝石排列 成 m 行 n 列的一个矩阵,m<=n,使矩阵中每一行和每一列的宝石都没有相同形 状。试设计一个算法,计算出对于给定的 m 和 n,有多少中不同的宝石排列方案。 即,给定一个 m*n 大小的矩阵,每一行 n 个元素是 1~n 的一种排列, 拉丁矩阵要求每一列上的 m 个元素不能够有重复。
栈式分支限界法活结点列表变化过程:(后进先出)
1{A} 2{B,C} 3{B,F,G} 4{B,F} 5{B} 6{D,E} 7{D} 8{} 从各结点的扩展次序来讲,队列式分支限界法是标准的宽度优先,栈式分支限界 则类似于深度优先。 回溯法: 各结点的遍历次序是:
A->B->D->B->E->A->C->F->C->G 回溯法是深度优先,而且结点 A,B,C 都两次成为扩展结点; 但是,栈式分支限界法各结点只有一次机会成为扩展结点。
其中,第一个 for 循环:同一深度上的各子结点扩展;ok 函数是剪枝函数; 如果不考虑“行 r”,并且去掉红色方框中的代码,则整个回溯函数跟排列树形式 的代码框架一样;其中,红色部分主要是针对“行 r”进行递归(深度加 1)。
习题 6.1:01 背包问题的栈式分支限界法 栈式分支限界法将活结点表以后进先出(LIFO)的方式存储于一个栈中。试
