高等土力学(李广信)3.6-土的强度理论
奇谈怪论土力学李广信

奇谈怪论土力学 李广信 在教学中关于概念和原理恰当的议论、比喻和穿插小故事将会加深学生的理解和记忆、活跃课堂气氛。
但亦不能用滥,以致喧宾夺主。
这里举一些例子供参考。
1 土“普天之下,莫非王土;率土之宾,莫非王臣”,“弃之如粪土”,“粪土当年万户侯”……土,是尊贵还是轻贱?土力学值得一学吗?卡特在“表土与人类文明”一书中断言:土,生长了人类文明。
只要量测人类古文明发源的尼罗河、两河(幼发拉底河与底格里斯河)、印度河与黄河、长江流域土层深度就应当承认这一断言是正确的。
2 土的级配土中颗粒尺寸大小基本一致称为级配均匀;大、中、小各种尺寸颗粒比例合适称为级配良好。
在工程中是否级配良好就一定“好”,这要看具体情况。
比如作一般填料,希望级配良好;而用于反滤料,则希望每层土料级配均匀。
正如在军队中,要求战士们年龄级配均匀,以便于训练与战斗,而不同级别军官年龄则应级配良好,可发挥不同年龄段人的经验,阅历和威望。
同样,希望学生级配均匀,教师级配良好。
但是听说,已经允许接近70岁的大学生入学,则是新问题。
3 塑性指数与液性指数粘性土的塑性指数I P=w L-w P,即由液限含水量减去塑限含水量,它是由土性决定的,所以常用于土的分类。
液性指数I L=(w-w P)/I P,它主要由土目前的含水量w决定,是表明粘性土软硬的一种状态。
对于粘性土,前者是不变的,后者是可变化的。
塑性指数如同你的姓,将你划归了哪一家就不变了。
液性指数如同你的年龄,是“状态”的描述。
4 关于不均匀系数等不均匀系数C u越大,土就越不均匀;液性指数I L越大,土性就越接近于液态;相对密度D r越大,砂土就越密实;渗透系数K不叫“阻力系数”,它们都是由其定义决定的。
记住了这一点,就不会将它们的定义公式记反。
5 土的强度土的强度不是由组成土颗粒的矿物强度决定的,主要由颗粒间的结合和相互作用决定的。
所以砂土常被称为“一般散沙”;而粘性土的粘聚力与岩石晶粒之间的键连结相比很微弱,所以我们用石块打人会打破头,而用土块打人顶多起个包。
2023年高等土力学试题考博专用

参考书目《高等土力学》李广信第1章土工实验及测试一、简述土工实验的目的和意义。
1)揭示土的一般或特有的物理力学性质。
2)针对具体土样的实验,揭示区域性土、特殊土、人工复合土的物理力学性质。
3)拟定理论计算和工程设计的参数。
4)验证理论计算的对的性及实用性。
5)原位测试、原型监测直接为土木工程服务,也是分析和实现信息化施工的手段。
第2章土的本构关系★二、广义讲,什么是土的本构关系?与其他金属材料比,它有什么变形特性(应力应变特性)?(2.3节)P51土的本构关系广义上讲是指反映土的力学性状的数学表达式,表达形似一般为应力-应变-强度-时间的关系。
与金属材料相比,土的变形特性包含:①土应力应变的非线性。
由于土由碎散的固体颗粒组成,土的宏观变形重要不是由土颗粒自身变形,而是由于颗粒间位置的变化。
这样在不同的应力水平下由相同应力增量引起的应变增量就不会相同,即表现出非线性。
②土的剪胀性。
由于土石由碎散颗粒组成的,在各向等压或等比压缩时,孔隙总是减少的,从而可发生较大的体积压缩,这种体积压缩大部分死不可恢复的,剪应力会引起土塑性体积变形,这叫剪胀性,另一方面,球应力又会产生剪应变,这种交叉的,或者耦合的效应,在其他材料中很少见。
③土体变形的弹塑性。
在加载后再卸载到本来的应力状态时,土一般不会完全恢复到本来的应变状态,其中有一部分变形是可以恢复的,部分应变式不可恢复的塑性应变,并且后者往往占很大的比例。
④土应力应变的各向异性和土的结构性。
不仅存在原生的由于土结的各向构异性带来的变形各向异性,并且对于各向受力不同时,也会产生心的变形和各向异性。
⑤土的流变性。
土的变形有时会表现出随时间变化的特性,即流变性。
与土的流变特性有关的现象只要是土的蠕变和应力松弛。
影响土的应力应变关系的应力条件重要有应力水平,应力途径和应力历史。
★三、何为土的剪胀性,产生剪胀的因素?P52(2.3.2)土体由于剪应力引起的体积变化称为剪胀性,广义的剪胀性指剪切引起的体积变化,既涉及体胀,也涉及体缩,但后者常被称为“剪缩”。
高等土力学主要知识点整理(李广信版)

第二章 土的本构关系(一)概述材料的本构关系是反映其力学性能的数学表达式,一般为应力-应变时间-强度的关系,也称本构定律、本构方程。
土的强度是土受力变形的一个阶段,即微小应力增量小,发生无限大(或不可控制)应变增量,实际是本构关系一个组成部分,是土受力变形的最后阶段。
第一应力不变量kk z y x I σσσσ=++=1第二应力不变量kk yz xz xy z y z x y x I στττσσσσσσ=---++=2222第三应力不变量22232xyz xz y yz x yz xz xy z y x I τστστστττσσσ---+= 坐标系选择使剪应力为零 3211σσσ++=I ,3231212σσσσσσ++=I 3213σσσ=I 球应力张量)(31)(3131321332211σσσσσσσσ++=++==kk m 偏应力张量ii kk ij ij s δσσ31-=,其中⎩⎨⎧=≠=j i j i ii 10δ,克罗内克解第一偏应力不变量01≡=kk s J 第二偏应力不变量()()()[]23123222126121σσσσσσ-+-+-==ji ij s s J 第二偏应力不变量()()()213312321322227131σσσσσσσσσ------==ki jk ij s s s J 1.土的应力应变特性:非线性(应变/加工硬化、应变/加工软化)、剪胀性、弹塑性、各向异性、结构性、流变性(蠕变、应力松弛)。
加工硬化:应力随应变增加而增加,但增加速率越来越慢,最后趋于稳定(正常固结黏土、松砂)加工软化:应力一开始随应变增加而增加,超过一个峰值后,应力随应变增加而减小,最后趋于稳定(超固结黏土、松砂)剪胀性:剪应力引起的体积变化,含剪胀和剪缩土的结构性:由土颗粒空间排列集合、土中各相和颗粒间作用力造成,可明显提高土的强度和刚度。
灵敏度:原状黏性土与重塑土的无侧限抗压强度之比土的蠕变:应力状态不变条件下,应变随时间逐渐增长的现象,随土的塑性、活动性、含水量增加而加剧土的应力松弛:维持应变不变,材料内应力随时间逐渐减小的现象压硬性:土的变形模量(指无侧限,压缩模指完全侧限)随围压而提高的现象。
高等土力学第三章强度

第十页,编辑于星期六:一点 五十九分。
三、关于土强度的讨论
如用弹性—完全塑性模型分 析,则内壁土单元a路径很快
达到强度线,且继续沿强度线
移动,等待外径土单元b路径 也达到强度线,试样发生整 体破坏;
若用应变硬化的弹塑性模型 分析,则内壁应力路径逐渐 靠近破坏线,最后内外径一 起达到破坏线而发生整体破 坏。
第九页,编辑于星期六:一点 五十九分。
三、关于土强度的讨论
用完全塑性理论分析,当 地基中塑性区发展到一定 深度时, 当:Zmax=1/3b or,1/4b 对应的荷载是设计容许的 ,整体还远未失稳。--这 主要就是由于达到强度( 屈服)的部分土体被尚未 达到强度的土体所包围。 而变形主要由尚未屈服的 土体所形成的边界条件所 决定
高等土力学教材 第三章 土的强度
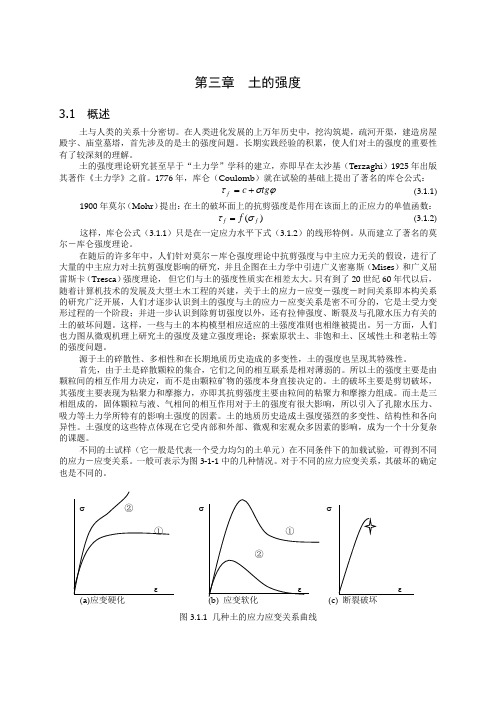
第三章 土的强度3.1 概述土与人类的关系十分密切。
在人类进化发展的上万年历史中,挖沟筑堤,疏河开渠,建造房屋殿宇、庙堂墓塔,首先涉及的是土的强度问题。
长期实践经验的积累,使人们对土的强度的重要性有了较深刻的理解。
土的强度理论研究甚至早于“土力学”学科的建立,亦即早在太沙基(Terzaghi )1925年出版其著作《土力学》之前。
1776年,库仑(Coulomb )就在试验的基础上提出了著名的库仑公式:ϕστtg c f += (3.1.1)1900年莫尔(Mohr )提出:在土的破坏面上的抗剪强度是作用在该面上的正应力的单值函数:)(f f f στ= (3.1.2)这样,库仑公式(3.1.1)只是在一定应力水平下式(3.1.2)的线形特例。
从而建立了著名的莫尔-库仑强度理论。
在随后的许多年中,人们针对莫尔-库仑强度理论中抗剪强度与中主应力无关的假设,进行了大量的中主应力对土抗剪强度影响的研究,并且企图在土力学中引进广义密塞斯(Mises )和广义屈雷斯卡(Tresca )强度理论, 但它们与土的强度性质实在相差太大。
只有到了20世纪60年代以后,随着计算机技术的发展及大型土木工程的兴建,关于土的应力-应变-强度-时间关系即本构关系的研究广泛开展,人们才逐步认识到土的强度与土的应力-应变关系是密不可分的,它是土受力变形过程的一个阶段;并进一步认识到除剪切强度以外,还有拉伸强度、断裂及与孔隙水压力有关的土的破坏问题。
这样,一些与土的本构模型相应适应的土强度准则也相继被提出。
另一方面,人们也力图从微观机理上研究土的强度及建立强度理论;探索原状土、非饱和土、区域性土和老粘土等的强度问题。
源于土的碎散性、多相性和在长期地质历史造成的多变性,土的强度也呈现其特殊性。
首先,由于土是碎散颗粒的集合,它们之间的相互联系是相对薄弱的。
所以土的强度主要是由颗粒间的相互作用力决定,而不是由颗粒矿物的强度本身直接决定的。
高等土力学-习题解答-李广信

第3章习题摩尔-库仑公式推导:ϕ+ϕσ+σ=σ-σcos c sin 223131 即: 231231]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ,同理有;232232]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ; 221221]cos c 2sin )[()(ϕ+ϕσ+σ=σ-σ破坏面条件:{}{}{}0]cos c 2sin )[()(]cos c 2sin )[()(]cos c 2sin )[()(221221232232231231=ϕ+ϕσ+σ=σ-σ⨯ϕ+ϕσ+σ=σ-σ⨯ϕ+ϕσ+σ=σ-σ⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧+⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧π-θ-θπ+θ=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧σσσ1112321I 31I 31I 31)6cos()sin()6cos(J 32 将该式代入上式得:0cos C J )3sin sin (cos sin I 3121=ϕ+ϕθ+θ-ϕ π平面上各轴的投影:在1σ轴上的投影:2S 2321321=σ-σ-σ在2σ轴上的投影:2S 2322312=σ-σ-σ在3σ轴上的投影:2S 2323213=σ-σ-σ如: 1σ=400kPa, 2σ=3σ=100kPa. 则在三个轴上的投影分别为: 141kPa, -71kPa, -71kPa.1、临界状态:是指土在常应力和常孔隙比下不断变形的状态。
临界孔隙比:表示土在这种密度状态下,受剪作用只产生剪应变而不产生体应变。
水力劈裂:由于孔隙水压力的升高,引起土体产生拉伸裂缝发生和发展的现象。
饱和松砂的流滑:饱和松砂在受静力剪切后,因体积收缩导致超孔压骤然升高,从而失去强度和流动的现象。
真强度理论:为了反映孔隙比对粘土抗剪强度及其指标的影响,将抗剪强度分为受孔隙比影响的粘聚分量与不受孔隙比影响的摩擦分量。
通过不同的固结历史,形成等孔隙比的试样,在不同的法向压力下剪切,试样破坏时的孔隙比相同,强度包线即为孔隙比相同的试样的强度包线,该强度称为在此孔隙比时的真强度。
高等土力学土的强度理论资料.

2k
1
3
J2
sin
π 2
k
0
1=3, 2=2, 3=1, k=(1- 3)/2=1
=0
广义形式
J2
1 2
sij sij
1 6
(1 2)2 ( 2 3)2 (3 1)2
1
K=1
1
3
2k
I 1
J2
sin
π 2
k
1 2
I1
0
图3-79 特雷斯卡与米泽斯准则
六棱柱的表面:
J2
sin
π 2
3. 6 土的强度理论
3.6.1 概述 3.6.2 土的古典强度理论 3.6.3 近代的强度理论 3.6.4 关于强度理论的讨论
3.6.1概述
(1)材料的强度是指材料破坏时的(应 力)状态。
(2)定义破坏的方法(数学表达式) 是破坏准则。破坏准则常常是应力 状态的组合。
(3)强度理论是揭示土破坏的机理的 理论,它也以一定的应力状态的组 合来表示。因而强度理论与破坏准 则的表达式是一致的。
-
图3-85 平面
36.90 对于广义米泽斯及特雷斯卡准则, 将有一个主应力为拉应力(<0)
3.6.3 近代的强度理论
1. 莱特-邓肯(Lade-Duncan)破坏准则 2. 松冈元-中井照夫 (Matsuoka- Nakai)强度理论 3. 双剪应力强度理论 4. 隐式的破坏准则
本构关系-应力应变与强度关系
某土单元上的两个占主导地位的主剪应力及相 应的主正应力的函数达到某一极限值时,土单 元发生破坏。
b、c和为三个试验常数。
图3-93 强度极限面
F 13 b12 13 b12 c 0
高等土力学土的强度

缺点:不能反映球应力张量对材料屈服的影响
Drucker-Prager准则(广义Von Mises ):
I1
式中:
3 sin 3 sin
2
J2 k f
kf 3C c o s 3 s in
2
3、Mohr-Coulomb强度准则:
f
C n tg
1、瞬时加载下土的动强度
2、土的蠕变强度
3、土的时效性 —— 拟似超固结土
3.5 土的排水与不排水强度
3.5.1 有效应力原理及孔压系数
1、有效应力原理
P P A Ac u
P A
P A
A Ac A
u
1 c u Βιβλιοθήκη Ac A uf
1、内部因素
土的组成(C) 土的状态(e) 土的结构(S) 2、外部因素
应力水平
应力历史 加载速率和排水条件
3.3.2 影响土强度的一般物理性质
1、颗粒矿物成分的影响 粘土矿物
滑动摩擦角:高岭石>伊利石>蒙脱石 总内摩擦角:高岭石>伊利石>蒙脱石
粗粒土
2、粗粒土颗粒的几何性质
u1
1 3
B 1 3
u1 A B 1 3
3.5.2 砂土的排水强度和不排水强度
砂土的排水试验:
砂土的不排水试验:
3.5.3 粘土的排水和不排水强度
1、饱和粘土的排水试验
2、饱和粘土的三轴固结不排水试验(CU)
3、饱和粘土的不固结不排水试验(UU)
边坡稳定问题; 土压力问题; 地基承载力问题。
