专题8.7 高考解答题热点题型-立体几何(解析版)
高考数学立体几何多选题知识点及练习题附解析

高考数学立体几何多选题知识点及练习题附解析一、立体几何多选题1.一副三角板由一块有一个内角为60°的直角三角形和一块等腰直角三角形组成,如图所示,090B F ∠=∠=,060,45,A D BC DE ∠=∠==,现将两块三角形板拼接在一起,得三棱锥F CAB -,取BC 中点O 与AC 中点M ,则下列判断中正确的是( )A .BC FM ⊥B .AC 与平面MOF 所成的角的余弦值为32C .平面MOF 与平面AFB 所成的二面角的平面角为45°D .设平面ABF 平面MOF l =,则有//l AB【答案】AD 【分析】证明BC ⊥面FOM 可判断A ;根据AC 与平面MOF 所成的角为060CMO ∠=判断B ;利用特殊位置判断C ;先证明//AB 面MOF ,由线面平行的性质定理可判断D ; 【详解】由三角形中位线定理以及等腰三角形的性质可得,,BC OF BC OM OM OF O ⊥⊥=,所以BC ⊥面FOM BC FM ⇒⊥,故A 正确;因为BC ⊥面FOM ,所以AC 与平面MOF 所成的角为060CMO ∠=,所以余弦值为12,故B 错误; 对于C 选项可以考虑特殊位置法,由BC ⊥面FOM 得面ABC ⊥面FOM ,所以点F 在平面ABC 内的射影在直线OM 上,不妨设点F 平面ABC 内的射影为M ,过点M 作//BC MN ,连结NF .易证AB ⊥面MNF ,则l ⊥面MNF ,所以MFN ∠为平面MOF与平面AFB 所成的二面角的平面角,不妨设2AB =,因为060A,所以23BC =,则13,12OF BC OM ===,显然MFN ∠不等于45°,故C 错误. 设面MOF 与平面ABF 的交线为l ,又因为//,AB OM AB ⊄面MOF ,OM ⊂面MOF ,所以//AB 面MOF ,由线面平行的性质定理可得://l AB ,故D 正确; 故选:AD.【点睛】方法点睛:求直线与平面所成的角有两种方法:一是传统法,证明线面垂直找到直线与平面所成的角,利用平面几何知识解答;二是利用空间向量,求出直线的方向向量以及平面的方向向量,利用空间向量夹角余弦公式求解即可.2.如图,正方体1111ABCD A B C D -的棱长为3,点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动,且满足直线//BM 平面1D EF ,则( )A .过1D ,E ,F 的平面截正方体所得截面为等腰梯形B .三棱锥1D EFM -的体积为定值C .动点M 10D .过B ,E ,M 的平面截正方体所得截面面积的最小值为10【答案】BCD 【分析】由题做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,进而计算即可排除A 选项;根据//BM平面1D EF ,由等体积转化法得1111D EFM M D EF B D EF D BEFV V V V ----===即可得B 选项正确;取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知M 的轨迹为线段HI 10,故C 选项正确;过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,易知过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而得当H 位于点I 时,截面面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=. 【详解】解:对于A 选项,如图,取BF 中点G ,连接1A G ,由点E ,F 分别在1CC ,1BB 上,12C E EC →→=,12BF FB →→=,故四边形11A D EG 为平行四边形,故11//AGD E ,由于在11A B G △,F 为1B G 中点,当N 为11A B 中点时,有11////NF A G D E ,故过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,此时22133532D N ⎛⎫=+= ⎪⎝⎭,223110EF =+=,故梯形1D EFN 不是等腰梯形,故A 选项错误;对于B 选项,三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积,由于//BM平面1D EF ,故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积,三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积,而三棱锥1D BEF -的体积为定值,故B 选项正确; 对于C 选项,取1AA 靠近1A 点的三等分点H , 1DD 靠近D 点的三等分点I ,易知1////HB AG NF ,1//BI D F ,由于1,HI BI I NFD F F ==,故平面//BHI 平面1D EF ,故M 的轨迹为线段HI ,其长度为10,故C 选项正确;对于D 选项,过M 点做BE 的平行线交1AA 于P ,交1DD 于O ,连接,BP OE ,则过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,易知当H 位于点I 时,平行四边形BPOE 边BP 最小,且为AB ,此时截面平行四边形BPOE 的面积最小,为四边形ABEI 的面积,且面积为310S AB BE =⋅=,故D 选项正确; 故选:BCD【点睛】本题解题的关键在于根据题意,依次做出过1D ,E ,F 的平面截正方体所得截面为梯形1D EFN ,过B ,E ,M 的平面截正方体所得截面即为平行四边形BPOE ,进而讨论AD选项,通过//BM平面1D EF ,并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确,通过构造面面平行得M 的轨迹为线段HI ,进而讨论C 选项,考查回归转化思想和空间思维能力,是中档题.3.如图,正方体1111ABCD A B C D -的棱长为3,线段11B D 上有两个动点,E F ,且1EF =,以下结论正确的有( )A .AC BE ⊥B .异面直线,AE BF 所成的角为定值C .点A 到平面BEF 的距离为定值D .三棱锥A BEF -的体积是定值 【答案】ACD 【详解】由AC BD ⊥,1AC DD ⊥可证AC ⊥平面11D DBB ,从而AC BE ⊥,故A 正确; 取特例,当E 与1D 重合时,F 是F ',AE 即1AD ,1AD 平行1BC ,异面直线,AE BF '所成的角是1C BF '∠,当F 与1B 重合时,E 是E ',BF 即1BB ,异面直线,AE BF '所成的角是1A AE '∠,可知1C BF '∠与1A AE '∠不相等,故异面直线,AE BF 所成的角不是定值,故B 错误;连结BD 交AC 于O ,又AC ⊥平面11D DBB ,点A 到平面11BDD B 的距离是2=2AO ,也即点A 到平面BEF 的距离是22,故C 正确; 2=2AO 为三棱锥A BEF -的高,又1111224BEF S =⨯⨯=△,故三棱锥A BEF -的体积为112234224⨯⨯=为定值,D 正确. 故选:ACD 【点睛】求空间中点到平面的距离常见方法为: (1)定义法:直接作平面的垂线,求垂线;(2)等体积法:不作垂线,通过等体积法间接求点到面的距离; (3)向量法:计算斜线在平面的法向量上的投影即可.4.如图,点E 为正方形ABCD 边CD 上异于点C ,D 的动点,将ADE 沿AE 翻折成SAE △,在翻折过程中,下列说法正确的是( )A .存在点E 和某一翻折位置,使得SB SE ⊥ B .存在点E 和某一翻折位置,使得//AE 平面SBCC .存在点E 和某一翻折位置,使得直线SB 与平面ABC 所成的角为45°D .存在点E 和某一翻折位置,使得二面角S AB C --的大小为60° 【答案】ACD 【分析】依次判断每个选项:当SE CE ⊥时,⊥SE SB ,A 正确,//AE 平面SBC ,则//AE CB ,这与已知矛盾,故B 错误,取二面角D AE B --的平面角为α,取4=AD ,计算得到2cos 3α=,C 正确,取二面角D AE B --的平面角为60︒,计算得到5tan 5θ=,故D 正确,得到答案. 【详解】当SE CE ⊥时,SE AB ⊥,SE SA ⊥,故SE ⊥平面SAB ,故⊥SE SB ,A 正确;若//AE 平面SBC ,因AE ⊂平面ABC ,平面ABC 平面SBC BC =,则//AE CB ,这与已知矛盾,故B 错误;如图所示:DF AE ⊥交BC 于F ,交AE 于G ,S 在平面ABCE 的投影O 在GF 上, 连接BO ,故SBO ∠为直线SB 与平面ABC 所成的角,取二面角D AE B --的平面角为α,取4=AD ,3DE =,故5AE DF ==,1CE BF ==,125DG =,12cos 5OG α=,故只需满足12sin 5SO OB α==, 在OFB △中,根据余弦定理:2221213121312sin 1cos 2cos cos 55555OFB ααα⎛⎫⎛⎫⎛⎫=+---∠ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,解得2cos 3α=,故C 正确; 过O 作OMAB ⊥交AB 于M ,则SMO ∠为二面角S AB C --的平面角,取二面角D AE B --的平面角为60︒,故只需满足22DG GO OM ==,设OAG OAM θ∠=∠=,84ππθ<<,则22DAG πθ∠=-,tan tan 22DG OGAG πθθ==⎛⎫- ⎪⎝⎭,化简得到2tan tan 21θθ=,解得5tan 5θ=,验证满足,故D 正确; 故选:ACD .【点睛】本题考查了线线垂直,线面平行,线面夹角,二面角,意在考查学生的计算能力,推断能力和空间想象能力.5.如图四棱锥P ABCD -,平面PAD ⊥平面ABCD ,侧面PAD 是边长为26的正三角形,底面ABCD 为矩形,23CD =,点Q 是PD 的中点,则下列结论正确的是( )A .CQ ⊥平面PADB .PC 与平面AQC所成角的余弦值为3C .三棱锥B ACQ -的体积为D .四棱锥Q ABCD -外接球的内接正四面体的表面积为【答案】BD 【分析】取AD 的中点O ,BC 的中点E ,连接,OE OP ,则由已知可得OP ⊥平面 ABCD ,而底面ABCD 为矩形,所以以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,利用空间向量依次求解即可. 【详解】解:取AD 的中点O ,BC 的中点E ,连接,OE OP , 因为三角形PAD 为等边三角形,所以OP AD ⊥, 因为平面PAD ⊥平面ABCD ,所以OP ⊥平面 ABCD , 因为AD OE ⊥,所以,,OD OE OP 两两垂直,所以,如下图,以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,则(0,0,0),(O D A ,(P C B ,因为点Q 是PD的中点,所以)2Q , 平面PAD 的一个法向量为(0,1,0)m =,6(QC =,显然 m 与QC 不共线, 所以CQ 与平面PAD 不垂直,所以A 不正确;3632(6,23,32),(,0,),(26,PC AQ AC =-==, 设平面AQC 的法向量为(,,)n x y z =,则36022260n AQ xz n AC ⎧⋅=+=⎪⎨⎪⋅=+=⎩, 令=1x ,则y z ==, 所以(1,2,n =-, 设PC 与平面AQC 所成角为θ, 则21sin 36n PC n PCθ⋅===,所以22cos θ=,所以B 正确; 三棱锥B ACQ -的体积为1132B ACQ Q ABC ABCV V SOP --==⋅ 1112326326322=⨯⨯⨯⨯⨯=, 所以C 不正确;设四棱锥Q ABCD -外接球的球心为(0,3,)M a ,则MQ MD =,所以()()()2222226323632a a ⎛⎫⎛⎫++-=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,解得0a =,即(0,3,0)M 为矩形ABCD 对角线的交点, 所以四棱锥Q ABCD -外接球的半径为3,设四棱锥Q ABCD -外接球的内接正四面体的棱长为x , 将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,故正方体的棱长为2x ,所以222362x ⎛⎫= ⎪ ⎪⎝⎭,得224x =, 所以正四面体的表面积为234243x ⨯=,所以D 正确. 故选:BD【点睛】此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.6.在长方体1111ABCD A B C D -中,23AB =12AD AA ==,,,P Q R 分别是11,,AB BB AC 上的动点,下列结论正确的是( )A .对于任意给定的点P ,存在点Q 使得1D P CQ ⊥B .对于任意给定的点Q ,存在点R 使得1D R CQ ⊥C .当1AR A C ⊥时,1ARD R ⊥D .当113AC A R =时,1//D R 平面1BDC 【答案】ABD 【分析】如图所示建立空间直角坐标系,计算142D P CQ b ⋅=-,()12222D R CQ b λλ⋅=--,134AR D R ⋅=-,10D R n ⋅=,得到答案.【详解】如图所示,建立空间直角坐标系,设()2,,0P a,a ⎡∈⎣,()Q b ,[]0,2b ∈,设11A R AC λ=,得到()22,22R λλ--,[]0,1λ∈. ()12,,2P a D -=,()2,0,CQ b =,142D P CQ b ⋅=-,当2b =时,1D P CQ ⊥,A 正确;()122,2D R λλ=--,()12222D R CQ b λλ⋅=--,取22bλ=+时,1D R CQ ⊥,B 正确; 1AR A C ⊥,则()()12,222212440AR AC λλλλλ⋅=--⋅--=-+-+=, 14λ=,此时113313,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,C 错误; 113AC A R =,则4433R ⎛⎫ ⎪ ⎪⎝⎭,14233D R ⎛⎫=- ⎪ ⎪⎝⎭,设平面1BDC 的法向量为(),,n x y z =,则10n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩,解得(3,n =-,故10D R n ⋅=,故1//D R 平面1BDC ,D 正确. 故选:ABD .【点睛】本题考查了空间中的线线垂直,线面平行,意在考查学生的计算能力和空间想象能力,推断能力.7.已知棱长为1的正方体1111ABCD A B C D -,过对角线1BD 作平面α交棱1AA 于点E ,交棱1CC 于点F ,以下结论正确的是( ) A .四边形1BFD E 不一定是平行四边形 B .平面α分正方体所得两部分的体积相等 C .平面α与平面1DBB 不可能垂直 D .四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E 、F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】 如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误;对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥,又1BD BB B ⋂=,所以AC ⊥平面1BB D ,当E 、F 分别为棱11,AA CC 的中点时,有//AC EF ,则EF ⊥平面1BB D ,又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD ,当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=⋅=,故D 正确;故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.8.如图,正四棱锥S -BCDE 底面边长与侧棱长均为a ,正三棱锥A -SBE 底面边长与侧棱长均为a ,则下列说法正确的是( )A .AS ⊥CDB .正四棱锥S -BCDE 的外接球半径为22C .正四棱锥S -BCDE 的内切球半径为212a ⎛- ⎝⎭ D .由正四棱锥S -BCDE 与正三棱锥A -SBE 拼成的多面体是一个三棱柱【答案】ABD【分析】取BE 中点H ,证明BE ⊥平面SAH 即可证AS CD ⊥;设底面中心为1O ,有112O B O S a ==,可求得球半径为2a ;用等体积法求内切球半径即可判断;由////SA DE BC 且==SA DE BC 可知多面体是一个三棱柱.【详解】如图所示:A 选项:取BE 中点H 连接,AH SH ,正三棱锥A SBE -中,,AH BE SH BE ⊥⊥又AH SH H =,所以BE ⊥平面SAH ,则BE AS ⊥,又//BE CD 所以AS CD ⊥ ,故A 正确;B 选项:设底面中心为1O ,球心为O 半径为R ,因为正四棱锥S -BCDE 外接球球心在1O S 上,所以OS OB R ==,因为,正四棱锥S -BCDE 底面边长与侧棱长均为a 所以112O B O S ==,由()22211OB O B O S OS =+- 得2222222R a R ⎛⎫⎛⎫=+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭解得22R =,故B 正确; C 选项:设内切球半径为r ,易求得侧面面积为2213sin 234S a a π=⋅=, 由等体积法得222121134333a a r r =⋅+⋅⋅ 解得624a r = ,故C 错;D 选项:取SE 中点F ,连结AF ,DF ,BF ,则BFD ∠和BFA ∠分别是D SE B --和A SE B --的二面角的平面角,由)22222221cos2322BF DF BDBFDBF DFa⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===-⋅⎛⎫⎪⎝⎭22222221cos2322aAF BF BAAFDAF BFa⎫⎫+-⎪⎪+-⎝⎭⎝⎭∠===⋅⎛⎫⎪⎝⎭,故BFD∠与BFA∠互补,所以ASDE共面,又因为AS AE ED SD===,则ASDE为平行四边形,故////AS ED BC故正四棱锥S-BCDE与正三棱锥A-SBE拼成的多面体是一个三棱柱,所以D正确故选:ABD【点睛】求外接球半径的常用方法:(1)补形法:侧面为直角三角形或正四面体或对棱二面角均相等的模型,可以还原到正方体或长方体中去求解;(2)利用球的性质:几何体在不同面均对直角的棱必然是球的直径;(3)定义法:到各个顶点距离均相等的点为球心,借助有特殊性底面的外接圆圆心,找其垂线,则球心一定在垂线上,再根据带其他顶点距离也是半径,列关系求解即可.。
2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)

2023年高考数学----立体几何解答题常考全归类真题练习题(含答案解析)1.(2022·天津·统考高考真题)直三棱柱111ABC A B C -中,112,,AA AB AC AA AB AC AB ===⊥⊥,D 为11A B 的中点,E 为1AA 的中点,F 为CD 的中点.(1)求证://EF 平面ABC ;(2)求直线BE 与平面1CC D 所成角的正弦值; (3)求平面1ACD 与平面1CC D 所成二面角的余弦值. 【解析】(1)证明:在直三棱柱111ABC A B C -中,1AA ⊥平面111A B C ,且AC AB ⊥,则1111AC A B ⊥以点1A 为坐标原点,1A A 、11A B 、11AC 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则()2,0,0A 、()2,2,0B 、()2,0,2C 、()10,0,0A 、()10,0,2B 、()10,0,2C 、()0,1,0D 、()1,0,0E 、11,,12F ⎛⎫⎪⎝⎭,则10,,12EF ⎛⎫= ⎪⎝⎭, 易知平面ABC 的一个法向量为()1,0,0m =,则0EF m ⋅=,故EF m ⊥,EF ⊄平面ABC ,故//EF 平面ABC .(2)()12,0,0C C =,()10,1,2C D =−,()1,2,0EB =,设平面1CC D 的法向量为()111,,u x y z =,则111112020u C C x u C D y z ⎧⋅==⎪⎨⋅=−=⎪⎩,取12y =,可得()0,2,1u =,4cos ,5EB u EB u EB u⋅<>==⋅. 因此,直线BE 与平面1CC D 夹角的正弦值为45.(3)()12,0,2AC =,()10,1,0A D =, 设平面1ACD 的法向量为()222,,v x y z =,则122122200v AC x z v A D y ⎧⋅=+=⎪⎨⋅==⎪⎩,取21x =,可得()1,0,1v =−,则1cos ,5u v u v u v⋅<>==−=⨯⋅因此,平面1ACD 与平面1CC D 2.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求CF 与平面ABD 所成的角的正弦值.【解析】(1)因为AD CD =,E 为AC 的中点,所以AC DE ⊥; 在ABD △和CBD △中,因为,,B A C D CD ADB DB DB D ∠=∠==,所以ABD CBD ≌△△,所以AB CB =,又因为E 为AC的中点,所以AC BE ⊥; 又因为,DE BE ⊂平面BED ,DE BE E ⋂=,所以AC ⊥平面BED ,因为AC ⊂平面ACD ,所以平面BED ⊥平面ACD .(2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED , 所以AC EF ⊥,所以1=2AFC S AC EF ⋅△, 当EF BD ⊥时,EF 最小,即AFC △的面积最小. 因为ABD CBD ≌△△,所以2CB AB ==, 又因为60ACB ∠=︒,所以ABC 是等边三角形, 因为E 为AC 的中点,所以1AE EC ==,BE 因为AD CD ⊥,所以112DE AC ==, 在DEB 中,222DE BE BD +=,所以BE DE ⊥.以E 为坐标原点建立如图所示的空间直角坐标系E xyz −,则()()()1,0,0,,0,0,1A B D ,所以()()1,0,1,AD AB =−=−, 设平面ABD 的一个法向量为(),,n x y z =,则00n AD x z n AB x ⎧⋅=−+=⎪⎨⋅=−+=⎪⎩,取y =()3,3,3n =, 又因为()31,0,0,4C F ⎛⎫− ⎪ ⎪⎝⎭,所以31,4CF ⎛⎫= ⎪ ⎪⎝⎭,所以cos ,21n CF n CF n CF⋅===设CF 与平面ABD 所成的角的正弦值为02πθθ⎛⎫≤≤ ⎪⎝⎭,所以4sin cos ,7nCF θ==所以CF 与平面ABD3.(2022·浙江·统考高考真题)如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE ∠=∠=︒,二面角F DC B −−的平面角为60︒.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ⊥;(2)求直线BM 与平面ADE 所成角的正弦值.【解析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H . ∵四边形ABCD 和EFCD 都是直角梯形,//,//,5,3,1AB DC CD EF AB DC EF ===,60BAD CDE ∠=∠=︒,由平面几何知识易知,2,90DG AH EFC DCF DCB ABC ==∠=∠=∠=∠=︒,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt EGD 和Rt DHA ,EG DH == ∵,DC CF DC CB ⊥⊥,且CF CB C ⋂=,∴DC ⊥平面,BCF BCF ∠是二面角F DC B −−的平面角,则60BCF ∠=, ∴BCF △是正三角形,由DC ⊂平面ABCD ,得平面ABCD ⊥平面BCF ,∵N 是BC 的中点,∴FN BC ⊥,又DC ⊥平面BCF ,FN ⊂平面BCF ,可得FN CD ⊥,而BC CD C ⋂=,∴FN ⊥平面ABCD ,而AD ⊂平面ABCD FN AD ∴⊥.(2)因为FN ⊥平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点, NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz −,设(3,(1,0,3)A B D E,则32M ⎛⎫ ⎪ ⎪⎝⎭,333,,,(2,23,0),(2,22BM AD DE ⎛⎫∴=−=−−=− ⎪ ⎪⎝⎭ 设平面ADE 的法向量为(,,)nx y z =由00n AD n DE ⎧⋅=⎨⋅=⎩,得20230x x z ⎧−−=⎪⎨−+=⎪⎩,取(3,n =−,设直线BM 与平面ADE 所成角为θ,∴3||sin cos ,|||3n BM n BM n BMθ⋅=〈〉====⋅4.(2022·全国·统考高考真题)如图,PO 是三棱锥−P ABC 的高,PA PB =,AB AC ⊥,E 是PB 的中点.(1)证明://OE 平面PAC ;(2)若30ABO CBO ∠=∠=︒,3PO =,5PA =,求二面角C AE B −−的正弦值. 【解析】(1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥−P ABC 的高,所以PO ⊥平面ABC ,,AO BO ⊂平面ABC , 所以PO AO ⊥、PO BO ⊥,又PA PB =,所以POA POB ≅△△,即OA OB =,所以OAB OBA ∠=∠,又AB AC ⊥,即90BAC ∠=︒,所以90OAB OAD ∠+∠=︒,90OBA ODA ∠+∠=︒, 所以ODA OAD ∠=∠所以AO DO =,即AO DO OB ==,所以O 为BD 的中点,又E 为PB 的中点,所以//OE PD , 又OE ⊄平面PAC ,PD ⊂平面PAC , 所以//OE 平面PAC(2)过点A 作//Az OP ,如图建立平面直角坐标系, 因为3PO =,5AP =,所以4OA =,又30OBA OBC ∠=∠=︒,所以28BD OA ==,则4=AD,AB = 所以12AC =,所以()O,()B,()P ,()0,12,0C ,所以32E ⎛⎫ ⎪⎝⎭,则332AE ⎛⎫= ⎪⎝⎭,()43,0,0AB =,()0,12,0AC =,设平面AEB 的法向量为(),,n x y z =,则33302430n AE y z n AB ⎧⋅=++=⎪⎨⎪⋅==⎩,令2z =,则=3y −,0x =,所以()0,3,2n =−;设平面AEC 的法向量为(),,m a b c =,则33302120m AE a bc m AC b ⎧⋅=++=⎪⎨⎪⋅==⎩,令a =6c =−,0b =,所以()3,0,6m =−;所以cos ,13n m n m n m⋅−===设二面角C AE B −−的大小为θ,则43cos cos ,=13n m θ=, 所以11sin 13θ=,即二面角C AE B −−的正弦值为1113.5.(2022·全国·统考高考真题)如图,四面体ABCD 中,,,AD CD AD CD ADB BDC ⊥=∠=∠,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设2,60AB BD ACB ==∠=︒,点F 在BD 上,当AFC △的面积最小时,求三棱锥F ABC −的体积.【解析】(1)由于AD CD =,E 是AC 的中点,所以AC DE ⊥.由于AD CDBD BD ADB CDB =⎧⎪=⎨⎪∠=∠⎩,所以ADB CDB ≅△△,所以AB CB =,故AC BD ⊥,由于DE BD D ⋂=,,DE BD Ì平面BED , 所以AC ⊥平面BED ,由于AC ⊂平面ACD ,所以平面BED ⊥平面ACD . (2)[方法一]:判别几何关系依题意2AB BD BC ===,60ACB ∠=︒,三角形ABC 是等边三角形,所以2,1,AC AE CE BE ===由于,AD CD AD CD =⊥,所以三角形ACD 是等腰直角三角形,所以1DE =. 222DE BE BD +=,所以DE BE ⊥,由于AC BE E ⋂=,,AC BE ⊂平面ABC ,所以DE ⊥平面ABC . 由于ADB CDB ≅△△,所以FBA FBC ∠=∠,由于BF BF FBA FBC AB CB =⎧⎪∠=∠⎨⎪=⎩,所以FBA FBC ≅,所以AF CF =,所以EF AC ⊥, 由于12AFCSAC EF =⋅⋅,所以当EF 最短时,三角形AFC 的面积最小 过E 作EF BD ⊥,垂足为F ,在Rt BED △中,1122BE DE BD EF ⋅⋅=⋅⋅,解得EF =所以13,222DF BF DF ===−=, 所以34BF BD =过F 作FH BE ⊥,垂足为H ,则//FH DE ,所以FH ⊥平面ABC ,且34FH BF DE BD ==, 所以34FH =,所以111323324F ABC ABCV SFH −=⋅⋅=⨯⨯=[方法二]:等体积转换AB BC =,60ACB ∠=︒,2AB =ABC ∴∆是边长为2的等边三角形,BE ∴=连接EFADB CDB AF CF EF ACBED EF BD ∆≅∆∴=∴⊥∴∆⊥∆在中,当时,AFC 面积最小222,,2,,BED EF AD CD AD CD AC E AC DE BE BD BE EDBE DE EF BD BD ⊥==∴+=∴⊥⋅⊥∆==为中点DE=1若在中,32113222BEFBF S BF EF ∆∴=⋅=⋅11233F ABC A BEF C BEF BEF V V V S AC −−−∆∴=+=⋅=6.(2022·全国·统考高考真题)在四棱锥P ABCD −中,PD ⊥底面,,1,2,ABCD CD AB AD DC CB AB DP ====∥(1)证明:BD PA ⊥;(2)求PD 与平面PAB 所成的角的正弦值.【解析】(1)证明:在四边形ABCD 中,作DE AB ⊥于E ,CF AB ⊥于F , 因为//,1,2CD AB AD CD CB AB ====, 所以四边形ABCD 为等腰梯形, 所以12AE BF ==,故DE =BD = 所以222AD BD AB +=, 所以AD BD ⊥,因为PD ⊥平面ABCD ,BD ⊂平面ABCD , 所以PD BD ⊥, 又=PD AD D ⋂, 所以BD ⊥平面PAD , 又因为PA ⊂平面PAD , 所以BD PA ⊥;(2)如图,以点D 为原点建立空间直角坐标系,BD =则()()(1,0,0,,A B P ,则()()(1,0,3,0,3,3,AP BP DP =−=−=,设平面PAB 的法向量(),,n x y z =,则有0{30n AP x n BP ⋅=−=⋅=−=,可取()3,1,1n =, 则5cos ,5n DPn DP n DP ⋅==所以PD 与平面PAB7.(2022·北京·统考高考真题)如图,在三棱柱111ABC A B C -中,侧面11BCC B 为正方形,平面11BCC B ⊥平面11ABB A ,2AB BC ==,M ,N 分别为11A B ,AC 的中点.(1)求证:MN ∥平面11BCC B ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB 与平面BMN 所成角的正弦值.条件①:AB MN ⊥;条件②:BM MN =.注:如果选择条件①和条件②分别解答,按第一个解答计分.【解析】(1)取AB 的中点为K ,连接,MK NK ,由三棱柱111ABC A B C -可得四边形11ABB A 为平行四边形,而11,B M MA BK KA ==,则1//MK BB ,而MK ⊄平面11BCC B ,1BB ⊂平面11BCC B ,故//MK 平面11BCC B ,而,CN NA BK KA ==,则//NK BC ,同理可得//NK 平面11BCC B ,而,,NK MK K NK MK =⊂平面MKN ,故平面//MKN 平面11BCC B ,而MN ⊂平面MKN ,故//MN 平面11BCC B ,(2)因为侧面11BCC B 为正方形,故1CB BB ⊥,而CB ⊂平面11BCC B ,平面11CBB C ⊥平面11ABB A ,平面11CBB C ⋂平面111ABB A BB =,故CB ⊥平面11ABB A ,因为//NK BC ,故NK ⊥平面11ABB A ,因为AB ⊂平面11ABB A ,故NK AB ⊥,若选①,则AB MN ⊥,而NK AB ⊥,NK MN N =,故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB MK ⊥,所以1AB BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯. 若选②,因为//NK BC ,故NK ⊥平面11ABB A ,而KM ⊂平面MKN , 故NK KM ⊥,而11,1B M BK NK ===,故1B M NK =,而12B B MK ==,MB MN =,故1BB M MKN ≅,所以190BB M MKN ∠=∠=︒,故111A B BB ⊥,而1CB BB ⊥,CB AB B ⋂=,故1BB ⊥平面ABC ,故可建立如所示的空间直角坐标系,则()()()()0,0,0,0,2,0,1,1,0,0,1,2B A N M , 故()()()0,2,0,1,1,0,0,1,2BA BN BM ===,设平面BNM 的法向量为(),,n x y z =,则00n BN n BM ⎧⋅=⎨⋅=⎩,从而020x y y z +=⎧⎨+=⎩,取1z =−,则()2,2,1n =−−, 设直线AB 与平面BNM 所成的角为θ,则42sin cos ,233n AB θ===⨯.8.(2022·全国·统考高考真题)如图,直三棱柱111ABC A B C -的体积为4,1A BC 的面积为(1)求A 到平面1A BC 的距离;(2)设D 为1AC 的中点,1AA AB =,平面1A BC ⊥平面11ABB A ,求二面角A BD C −−的正弦值. 【解析】(1)在直三棱柱111ABC A B C -中,设点A 到平面1A BC 的距离为h , 则111111112211433333A A BC A A ABC A ABC AB BC C C B V S h h V S A A V −−−=⋅===⋅==,解得h =所以点A 到平面1A BC (2)取1A B 的中点E ,连接AE ,如图,因为1AA AB =,所以1AE A B ⊥, 又平面1A BC ⊥平面11ABB A ,平面1A BC ⋂平面111ABB A A B =, 且AE ⊂平面11ABB A ,所以⊥AE 平面1A BC , 在直三棱柱111ABC A B C -中,1BB ⊥平面ABC , 由BC ⊂平面1A BC ,BC ⊂平面ABC 可得AE BC ⊥,1BB BC ⊥,又1,AE BB ⊂平面11ABB A 且相交,所以BC ⊥平面11ABB A , 所以1,,BC BA BB 两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE 12AA AB ==,1A B =2BC =, 则()()()()10,2,0,0,2,2,0,0,0,2,0,0A A B C ,所以1AC 的中点()1,1,1D , 则()1,1,1BD =,()()0,2,0,2,0,0BA BC ==,设平面ABD 的一个法向量(),,m x y z =,则020m BD x y z m BA y ⎧⋅=++=⎨⋅==⎩, 可取()1,0,1m =−,设平面BDC 的一个法向量(),,n a b c =,则020n BD a b c n BC a ⎧⋅=++=⎨⋅==⎩, 可取()0,1,1n =−r , 则11cos ,22m nm n m n ⋅===⨯⋅,所以二面角A BD C −−=本课结束。
高考数学立体几何多选题知识点总结附解析

高考数学立体几何多选题知识点总结附解析一、立体几何多选题1.在棱长为1的正方体1111ABCD A B C D -中,P 为底面ABCD 内(含边界)一点.( ) A .若13A P =,则满足条件的P 点有且只有一个 B .若12A P =,则点P 的轨迹是一段圆弧 C .若1//A P 平面11B DC ,则1A P 长的最小值为2D .若12A P =且1//A P 平面11B DC ,则平面11A PC 截正方体外接球所得截面的面积为23π 【答案】ABD【分析】选项A ,B 可利用球的截面小圆的半径来判断;由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD 上,1A P 长的最大值为2;结合以上条件点P 与B 或D 重合,利用12sin 60A P r =︒,求出63r =,进而求出面积. 【详解】对A 选项,如下图:由13A P =,知点P 在以1A 为球心,半径为3的球上,又因为P 在底面ABCD 内(含边界),底面截球可得一个小圆,由1A A ⊥底面ABCD ,知点P 的轨迹是在底面上以A 为圆心的小圆圆弧,半径为22112r A P A A =-=,则只有唯一一点C满足,故A 正确;对B 选项,同理可得点P 在以A 为圆心,半径为22111r A P A A =-=的小圆圆弧上,在底面ABCD 内(含边界)中,可得点P 轨迹为四分之一圆弧BD .故B 正确;对C 选项,移动点P 可得两相交的动直线与平面11B D C 平行,则点P 必在过1A 且与平面11B D C 平行的平面内,由平面1//A BD 平面11B D C ,知满足1//A P 平面11B D C 的点P 在BD上,则1A P 长的最大值为12A B =,则C 不正确; 对选项D ,由以上推理可知,点P 既在以A 为圆心,半径为1的小圆圆弧上,又在线段BD 上,即与B 或D 重合,不妨取点B ,则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆,利用2126622,,sin 60333A B r r S r ππ==∴=∴==︒.故D 正确.故选:ABD【点睛】(1)平面截球所得截面为圆面,且满足222=R r d +(其中R 为球半径,r 为小圆半径,d 为球心到小圆距离);(2)过定点A 的动直线平行一平面α,则这些动直线都在过A 且与α平行的平面内.2.如图,一个结晶体的形状为平行六面体1111ABCD A B C D -,其中,以顶点A 为端点的三条棱长都等于1,且它们彼此的夹角都是60,下列说法中正确的是( )A .()()2212AA AB AD AC ++= B .1A 在底面ABCD 上的射影是线段BD 的中点C .1AA 与平面ABCD 所成角大于45D .1BD 与AC所成角的余弦值为3 【答案】AC【分析】对A ,分别计算()21++AA AB AD 和2AC ,进行判断;对B ,设BD 中点为O ,连接1A O ,假设1A 在底面ABCD 上的射影是线段BD 的中点,应得10⋅=O AB A ,计算10⋅≠O AB A ,即可判断1A 在底面ABCD 上的射影不是线段BD 的中点;对C ,计算11,,A A AC AC ,根据勾股定理逆定理判断得11⊥A A AC ,1AA 与平面ABCD 所成角为1A AC ∠,再计算1tan ∠A AC ;对D ,计算1,AC BD 以及1BD AC ⋅,再利用向量的夹角公式代入计算夹角的余弦值.【详解】对A ,由题意,11111cos602⋅=⋅=⋅=⨯⨯=AA AB AA AD AD AB ,所以()2222111112221113262++=+++⋅+⋅+⋅=+++⨯⨯=AA AB AD AA AB AD AA AB AB AD AA AD ,AC AB AD =+,所以()222221113=+=+⋅+=++=AC AB AD AB AB AD AD , 所以()()22126++==AA AB AD AC ,故A 正确;对B ,设BD 中点为O ,连接1A O ,1111111222=+=+=++AO A A AO A A AC A A AD AB ,若1A 在底面ABCD 上的射影是线段BD 的中点,则1A O ⊥平面ABCD ,则应10⋅=O AB A ,又因为21111111111110222222224⎛⎫⋅=++⋅=-⋅+⋅+=-+⨯+=≠ ⎪⎝⎭O AB A A AD AB AB AA AB AD AB AB A ,故B 错误;对D ,11,BD AD AA AB AC AB AD =+-=+, 所以()()2211=2,=3=+-=+AD A B A AB AC AB AD D ()()2211111⋅=+-⋅+=⋅++⋅+⋅--⋅=AC AD AA AB AB AD AD AB AD AA AB AA AD AB AB AD BD,111cos ,2⋅<>===B ACD BD BD AC AC D 不正确;对C,112==AC BD ,在1A AC 中,111,===A A AC AC 22211+=A A AC AC ,所以11⊥A A AC ,所以1AA 与平面ABCD 所成角为1A AC ∠,又1tan 1∠=>A AC ,即145∠>A AC ,故C 正确;故选:AC【点睛】方法点睛:用向量方法解决立体几何问题,需要树立“基底”意识,利用基向量进行线性运算,要理解空间向量概念、性质、运算,注意和平面向量类比;同时对于立体几何中角的计算问题,往往可以利用空间向量法,利用向量的夹角公式求解.3.在正方体1111ABCD A B C D -中,M 、N 分别是棱AB 、1CC 的中点,1MB P 的顶点P 在棱1CC 与棱11C D 上运动,有以下四个命题正确命题的序号是( )A .平面1MB P 1ND ⊥B .平面1MB P ⊥平面11ND AC .1MB P 在底面ABCD 上的射影图形的面积为定值D .1MB P 在侧面11D C CD 上射影图形是三角形【答案】BC【分析】取N 与P 重合,结合勾股定理可判断A 选项的正误;利用面面垂直的判定定理可判断B 选项的正误;分点P 在棱1CC 、11C D 上运动两种情况讨论,利用三角形的面积公式可判断C 选项的正误;取点P 与点1C 重合,判断1MB P 在侧面11D C CD 上射影图形形状,可判断D 选项的正误.【详解】对于A 选项,设正方体1111ABCD A B C D -的棱长为2,如下图所示:当点P 与点N 重合时,若1ND ⊥平面1MB P ,1B N ⊂平面1MB P ,则11ND B N ⊥, 由勾股定理可得2211115D N C N C D =+=,同理可得15B N =,1122B D =, 2221111B N D N B D ∴+≠,则1ND 与1B N 不垂直,假设不成立,A 选项错误; 对于B 选项,取1BB 的中点E ,连接1A E 、EN ,在正方体1111ABCD A B C D -中,11//BB CC ,且E 、N 分别为1BB 、1CC 的中点, 则11//B E C N 且11B E C N =,所以,四边形11B ENC 为平行四边形,则11//EN B C 且11EN B C =,1111//A D B C 且1111A D B C =,所以,11//A D EN 且11A D EN =,所以,四边形11A END 为平行四边形,所以,11//A E D N ,111A B BB =,1B E BM =,11190A B E B BM ∠=∠=,所以,111Rt A B E Rt B BM ≅△△,所以,111B A E BB M ∠=∠,所以,111111190A EB BB M A EB B A E ∠+∠=∠+∠=, 190B FE ∴∠=,所以,11B M A E ⊥,11A D ⊥平面11AA B B ,1B M ⊂平面11AA B B ,111B M A D ∴⊥,1111A D A E A =,11A D 、1A E ⊂平面11ND A ,1MB ∴⊥平面11ND A ,1MB ⊂平面1MB P ,所以,平面1MB P ⊥平面11ND A ,B 选项正确;对于C 选项,设正方体1111ABCD A B C D -的棱长为a .若点P 在棱1CC 上运动时,1MB P 在底面ABCD 上的射影为MBC △, 此时,射影图形的面积为21224MBC a a S a =⋅=△; 若点P 在棱11C D 上运动时,设点P 在底面ABCD 上的射影点为G ,则G CD ∈, 且点G 到AB 的距离为a ,1MB 在底面ABCD 内的射影为MB ,则1MB P 在底面ABCD 内的射影为MBG △, 且21224MBG a a S a =⋅⋅=△.综上所述,1MB P 在底面ABCD 内的射影图形的面积为定值,C 选项正确; 对于D 选项,当点P 与1C 重合时,P 、1B 两点在平面11D C CD 上的射影重合, 此时,1MB P 在侧面11D C CD 上的射影不构成三角形,D 选项错误.故选:BC.【点睛】方法点睛:证明面面垂直常用的方法:(1)面面垂直的定义;(2)面面垂直的判定定理.在证明面面垂直时,一般假设面面垂直成立,然后利用面面垂直转化为线面垂直,即为所证的线面垂直,组织论据证明即可.4.已知正方体1111ABCD A B C D -的棱长为2,点O 为11A D 的中点,若以O 为球心,6为半径的球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,则下列结论正确的是( )A .11//A D 平面EFGHB .1AC ⊥平面EFGHC .11A B 与平面EFGH 所成的角的大小为45°D .平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7【答案】ACD【分析】如图,计算可得,,,E F G H 分别为所在棱的中点,利用空间中点线面的位置关系的判断方法可判断A 、B 的正确与否,计算出直线AB 与平面EFGH 所成的角为45︒后可得C 正确,而几何体BHE CGF -为三棱柱,利用公式可求其体积,从而可判断D 正确与否.【详解】如图,连接OA ,则2115OA AA =+=,故棱1111,,,A A A D D D AD 与球面没有交点. 同理,棱111111,,A B B C C D 与球面没有交点.因为棱11A D 与棱BC 之间的距离为26>BC 与球面没有交点. 因为正方体的棱长为2,而26<球面与正方体1111ABCD A B C D -的棱有四个交点E ,F ,G ,H ,所以棱11,,,AB CD C C B B 与球面各有一个交点, 如图各记为,,,E F G H .因为OAE △为直角三角形,故22651AE OE OA -=-=,故E 为棱AB 的中点. 同理,,F G H 分别为棱11,,CD C C B B 的中点.由正方形ABCD 、,E F 为所在棱的中点可得//EF BC ,同理//GH BC ,故//EF GH ,故,,,E F G H 共面.由正方体1111ABCD A B C D -可得11//A D BC ,故11//A D EF因为11A D ⊄平面EFGH ,EF ⊂平面EFGH ,故11//A D 平面EFGH ,故A 正确.因为在直角三角1BA C 中,122A B =,2BC = ,190A BC ∠=︒, 1A C 与BC 不垂直,故1A C 与GH 不垂直,故1A C ⊥平面EFGH 不成立,故B 错误. 由正方体1111ABCD A B C D -可得BC ⊥平面11AA B B ,而1A B ⊂平面11AA B B , 所以1BC A B ⊥,所以1EF A B ⊥在正方形11AA B B 中,因为,E H 分别为1,AB BB 的中点,故1EH A B ⊥,因为EF EH E =,故1A B ⊥平面EFGH ,所以BEH ∠为直线AB 与平面EFGH 所成的角,而45BEH ∠=︒,故直线AB 与平面EFGH 所成的角为45︒,因为11//AB A B ,故11A B 与平面EFGH 所成的角的大小为45°.故C 正确.因为,,,E F G H 分别为所在棱的中点,故几何体BHE CGF -为三棱柱,其体积为111212⨯⨯⨯=,而正方体的体积为8, 故平面EFGH 将正方体1111ABCD A B C D -分成两部分的体积的比为1:7,故D 正确. 故选:ACD.【点睛】本题考查空间中线面位置的判断、空间角的计算和体积的计算,注意根据球的半径确定哪些棱与球面有交点,本题属于中档题.5.如图四棱锥P ABCD -,平面PAD ⊥平面ABCD ,侧面PAD 是边长为26的正三角形,底面ABCD 为矩形,23CD =,点Q 是PD 的中点,则下列结论正确的是( )A .CQ ⊥平面PADB .PC 与平面AQC 所成角的余弦值为223C .三棱锥B ACQ -的体积为62D .四棱锥Q ABCD -外接球的内接正四面体的表面积为3【答案】BD【分析】取AD 的中点O ,BC 的中点E ,连接,OE OP ,则由已知可得OP ⊥平面 ABCD ,而底面ABCD 为矩形,所以以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,利用空间向量依次求解即可.【详解】解:取AD 的中点O ,BC 的中点E ,连接,OE OP ,因为三角形PAD 为等边三角形,所以OP AD ⊥,因为平面PAD ⊥平面ABCD ,所以OP ⊥平面 ABCD ,因为AD OE ⊥,所以,,OD OE OP 两两垂直,所以,如下图,以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,则(0,0,0),(O D A ,(P C B ,因为点Q 是PD的中点,所以)2Q , 平面PAD 的一个法向量为(0,1,0)m =,6(QC =,显然 m 与QC 不共线, 所以CQ 与平面PAD 不垂直,所以A 不正确;3632(6,23,32),(,0,),(26,22PC AQ AC =-==, 设平面AQC 的法向量为(,,)n x y z =,则 3602260n AQ x zn AC ⎧⋅=+=⎪⎨⎪⋅=+=⎩,令=1x ,则y z ==, 所以(1,2,n =-,设PC 与平面AQC 所成角为θ,则21sin 36n PCn PC θ⋅===, 所以cos 3θ=,所以B 正确; 三棱锥B ACQ -的体积为1132BACQ Q ABC ABC V V S OP --==⋅ 1116322=⨯⨯⨯=,所以C 不正确;设四棱锥Q ABCD -外接球的球心为(0,3,)M a ,则MQ MD =, 所以()()()2222226323632a a ⎛⎫⎛⎫++-=++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,解得0a =,即(0,3,0)M 为矩形ABCD 对角线的交点,所以四棱锥Q ABCD -外接球的半径为3,设四棱锥Q ABCD -外接球的内接正四面体的棱长为x ,将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,故正方体的棱长为22x ,所以22236x ⎛⎫= ⎪ ⎪⎝⎭,得224x =, 所以正四面体的表面积为2342434x ⨯=,所以D 正确. 故选:BD【点睛】此题考查线面垂直,线面角,棱锥的体积,棱锥的外接球等知识,综合性强,考查了计算能力,属于较难题.6.如图,点O 是正四面体P ABC -底面ABC 的中心,过点O 的直线交AC ,BC 于点M ,N ,S 是棱PC 上的点,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,则( )A .若//MN 平面PAB ,则//AB RQ B .存在点S 与直线MN ,使PC ⊥平面SRQC .存在点S 与直线MN ,使()0PS PQ PR ⋅+= D .111PQPRPS++是常数【答案】ABD 【分析】对于选项A ,根据线面平行的性质定理,进行推理判断即可;对于选项B ,当直线MN 平行于直线AB , 13SC PC =时,通过线面垂直的判定定理,证明此时PC ⊥平面SRQ ,即可证明,存在点S 与直线MN ,使PC ⊥平面SRQ ;对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=,利用线面垂直的判定定理可证得PC ⊥平面PAB ,此时通过反证法说明矛盾性,即可判断; 对于选项D ,利用S PQR O PSR O PSQ O PQR V V V V ----=++,即可求得111PQPRPS++是常数.【详解】 对于选项A , 若//MN 平面PAB ,平面SMN 与棱PA 的延长线相交于点Q ,与棱PB 的延长线相交于点R ,∴平面SMN 平面PAB =RQ ,又MN ⊂平面SMN ,//MN 平面PAB ,∴//MN RQ ,点O 在面ABC 上,过点O 的直线交AC ,BC 于点M ,N ,∴MN ⊂平面ABC ,又//MN 平面PAB ,平面ABC平面PAB AB =,∴//MN AB , ∴//AB RQ ,故A 正确; 对于选项B ,当直线MN 平行于直线AB ,S 为线段PC 上靠近C 的三等分点,即13SC PC =,此时PC ⊥平面SRQ ,以下给出证明: 在正四面体P ABC -中,设各棱长为a ,∴ABC ,PBC ,PAC △,PAB △均为正三角形,点O 为ABC 的中心,//MN AB ,∴由正三角形中的性质,易得23CN CM a ==, 在CNS 中,23CN a =,13SC a =,3SCN π∠=,∴由余弦定理得,3SN a ==, ∴222249SC SN a CN +==,则SN PC ⊥, 同理,SM PC ⊥,又SM SN S =,SM ⊂平面SRQ ,SN ⊂平面SRQ ,∴PC ⊥平面SRQ ,∴存在点S 与直线MN ,使PC ⊥平面SRQ ,故B 正确; 对于选项C ,假设存在点S 与直线MN ,使()0PS PQ PR ⋅+=, 设QR 中点为K ,则2PQ PR PK +=,∴PS PK ⊥,即PC PK ⊥,()cos cos 0PC AB PC PB PA PC PB CPB PC PA CPA ⋅=⋅-=⋅∠-⋅∠=,∴PC AB ⊥,又易知AB 与PK 为相交直线,AB 与PK 均在平面PQR 上,∴PC ⊥平面PQR ,即PC ⊥平面PAB ,与正四面体P ABC -相矛盾,所以假设不成立, 故C 错误; 对于选项D ,易知点O 到面PBC ,面PAC ,面PAB 的距离相等,记为d , 记PC 与平面PAB 所处角的平面角为α,α为常数,则sin α也为常数, 则点S 到PQR 的距离为sin PS α, 又13sin 234PQRSPQ PR PQ PR π=⋅=⋅ ∴()()1133sin sin sin 33412S PQR PQRV PS S PS PQ PR PQ PR PS ααα-=⋅=⋅⋅=⋅⋅, 又13sin 234PSRSPS PR PS PR π=⋅=⋅, 13sin 234PSQS PS PQ PS PQ π=⋅=⋅, 13sin 234PQRSPQ PR PQ PR π=⋅=⋅, ()3S PQR O PSR O PSQ O PQR V V V V d PS PR PS PQ PQ PR ----=++=⋅+⋅+⋅, ∴()33sin 1212PQ PR PS d PS PR PS PQ PQ PR α⋅⋅=⋅+⋅+⋅, ∴111sin d PQPRPSα++=为常数,故D 正确. 故选:ABD. 【点睛】本题考查了线面平行的性质定理、线面垂直的判定定理,考查了三棱锥体积的计算,考查了向量的运算,考查了转化能力与探究能力,属于较难题.7.如图所示,在长方体1111ABCD A B C D -中,11,2,AB BC AA P ===是1A B 上的一动点,则下列选项正确的是( )A .DP 35B .DP 5C .1AP PC +6D .1AP PC +的最小值为1705【答案】AD 【分析】DP 的最小值,即求1DA B △底边1A B 上的高即可;旋转11A BC 所在平面到平面11ABB A ,1AP PC +的最小值转化为求AC '即可.【详解】求DP 的最小值,即求1DA B △底边1A B 上的高,易知115,2A B A D BD ===,所以1A B 边上的高为355h =,连接111,AC BC ,得11A BC ,以1A B 所在直线为轴,将11A BC 所在平面旋转到平面11ABB A ,设点1C 的新位置为C ',连接AC ',则AC '即为所求的最小值,易知11122,2,cos AA AC AAC ''==∠=-, 所以217042222()105AC '=+-⨯⨯⨯-=. 故选:AD. 【点睛】本题考查利用旋转求解线段最小值问题.求解翻折、旋转问题的关键是弄清原有的性质变化与否, (1)点的变化,点与点的重合及点的位置变化;(2)线的变化,翻折、旋转前后应注意其位置关系的变化;(3)长度、角度等几何度量的变化.8.如图,1111ABCD A B C D -为正方体,下列结论中正确的是( )A .11A C ⊥平面11BB D D B .1BD ⊥平面1ACBC .1BD 与底面11BCC B 2 D .过点1A 与异面直线AD 与1CB 成60角的直线有2条 【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ;求解1BD 与底面11BCC B 所成角的正切值判断C ;利用空间向量法可判断D . 【详解】对于A 选项,如图,在正方体1111ABCD A B C D -中,1BB ⊥平面1111D C B A ,11A C ⊂平面1111D C B A ,则111BB A C ⊥, 由于四边形1111D C B A 为正方形,则1111AC B D ⊥, 1111BB B D B =,因此,11A C ⊥平面11BB D D ,故A 正确;对于B 选项,在正方体1111ABCD A B C D -中,1DD ⊥平面ABCD ,AC ⊂平面ABCD ,1AC DD ∴⊥,因为四边形ABCD 为正方形,所以,AC BD ⊥,1D DD BD =,AC ∴⊥平面11BB D D , 1BD ⊂平面11BB D D ,1AC BD ∴⊥,同理可得11BD B C ⊥,1ACB C C =,1BD ∴⊥平面1ACB ,故B 正确;对于C 选项,由11C D ⊥平面11BCC B ,得11C BD ∠为1BD 与平面11BCC B 所成角, 且111112tan C D C BD BC ∠==,故C 错误; 对于D 选项,以点D 为坐标原点,DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设正方体的棱长为1,则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ,()1,0,0DA =,()11,0,1CB =,设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =, 则221cos ,21DA m DA m DA my z ⋅<>===⋅++, 1122111cos ,221CB m zCB m CB my z ⋅+<>===⋅⋅++, 整理可得2222341y z y z z ⎧+=⎨=++⎩,消去y 并整理得2210z z +-=,解得12z =-12z =-由已知可得3z ≤,所以,12z =-+22y =± 因此,过点1A 与异面直线AD 与1CB 成60角的直线有2条,D 选项正确. 故选:ABD. 【点睛】方法点睛:证明线面垂直的方法:一是线面垂直的判定定理;二是利用面面垂直的性质定理;三是平行线法(若两条平行线中一条垂直于这个平面,则另一条也垂直于这个平面),解题时,注意线线、线面与面面关系的相互转化;另外,在证明线线垂直时,要注意题中隐含的垂直关系,如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形(或给出线段长度,经计算满足勾股定理)、直角梯形等等.。
高中数学立体几何(解析版)

立体几何立体几何一直在高中数学中占有很大的分值,未来的高考中立体几何也会持续成为高考的一个热点,文科高考中立体几何主要考查三视图的相关性质利用,简单几何体的体积,表面积以及外接圆问题.另外选择部分主要考查在点线面位置关系,简单几何体三视图.选择题主要还是以几何体的基本性质为主,解答题部分主要考查平行,垂直关系以及简单几何体的变面积以及体积.本专题针对高考高频知识点以及题型进行总结,希望通过本专题的学习,能够掌握高考数学中的立体几何的题型,将高考有关的立体几何所有分数拿到.【满分技巧】基础知识点考查:一般来说遵循三短一长选最长.要学会抽象问题具体会,将题目中的直线转化成显示中的具体事务,例如立体坐标系可以看做是一个教室的墙角有关外接圆问题:一般图形可以采用补形法,将几何体补成正方体或者是长方体,再利用不在同一个平面的四点确定一个立体平面原理,从而去求.内切圆问题:转化成正方体的内切圆去求.求点到平面的距离问题:采用等体积法.求几何体的表面积体积问题:应注意巧妙选取底面积与高.【考查题型】选择,填空,解答题【限时检测】(建议用时:90分钟)一、单选题AA是1.(2018·上海高考真题)《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马,设1AA为底面矩形的一边,则这样的阳正六棱柱的一条侧棱,如图,若阳马以该正六棱柱的顶点为顶点、以1马的个数是()A.4 B.8 C.12 D.16【答案】D【分析】根据新定义和正六边形的性质可得答案.【详解】根据正六边形的性质,则D1﹣A1ABB1,D1﹣A1AFF1满足题意,而C1,E1,C,D,E,和D1一样,有2×4=8,当A1ACC1为底面矩形,有4个满足题意,当A1AEE1为底面矩形,有4个满足题意,故有8+4+4=16故选D.【点睛】本题考查了新定义,以及排除组合的问题,考查了棱柱的特征,属于中档题.2.(2020·上海虹口区·高三一模)在空间,已知直线l及不在l上两个不重合的点A、B,过直线l做平面α,使得点A、B到平面α的距离相等,则这样的平面α的个数不可能是()A.1个B.2个C.3个D.无数个【答案】C【分析】分情况讨论可得出.【详解】(1)如图,当直线AB与l异面时,则只有一种情况;(2)当直线AB与l平行时,则有无数种情况,平面α可以绕着l转动;(3)如图,当l过线段AB的中垂面时,有两种情况.故选:C.3.(2020·上海高三一模)如图,在正四棱柱1111ABCD A B C D -中,底面边长2AB =,高14A A =,E 为棱1A A 的中点.设BAD ∠=α、BED θ∠=、1B ED γ∠=,则α、β、γ之间的关系正确的是( ).A .αγθ=>B .γαθ>>C .θγα>>D .αθγ>>【答案】B 【分析】求出α、β、γ的大小即可求解. 【详解】由题意可得2BAD πα∠==,连接BD ,则BDE 为等边三角形,所以3BED πθ∠==, 连接1B D ,则222122426B D =++=22222BE DE ==+=取1B D 的中点O ,连接EO ,则16BO 862EO =-=所以16tan 32B EO ∠==, 所以13B EO π∠=,即123B ED πγ∠==,所以γαθ>>.故选:B4.已知长方体1111ABCD A B C D -,下列向量的数量积一定不为0的是( )A .1AD AB ⋅B .11AD BC ⋅ C .1BD BC ⋅ D .1BD AC ⋅【答案】C【分析】利用正方体几何性质计算出数量积为零的选项,根据长方体的性质证明数量积一定不为零的选项.【详解】当长方体1111ABCD A B C D -为正方体时,根据正方体的性质可知: 1111,,AB AD AD B C BD AC ⊥⊥⊥,所以10AB AD ⋅=、110AD B C ⋅=、10BD AC ⋅=.根据长方体的性质可知:1BC CD ⊥,所以1BD 与BC 不垂直,即1BD BC ⋅一定不为0.故选:C5.(2020·上海高三一模)已知正方体1111ABCD A B C D -,点P 是棱1CC 的中点,设直线AB 为a ,直线11A D 为b .对于下列两个命题:①过点P 有且只有一条直线l 与a 、b 都相交;②过点P 有且只有一条直线l 与a 、b 都成45︒角.以下判断正确的是( )A .①为真命题,②为真命题B .①为真命题,②为假命题C .①为假命题,②为真命题D .①为假命题,②为假命题【答案】B 【分析】作出过P 与两直线相交的直线l 判断①;通过平移直线a ,b ,结合异面直线所成角的概念判断②.【详解】解:直线AB 与A 1D 1 是两条互相垂直的异面直线,点P 不在这两异面直线中的任何一条上,如图所示:取BB 1的中点Q ,则PQ ∥A 1D 1,且 PQ =A 1D 1,设A 1Q 与AB 交于E ,则点A 1、D 1、Q 、E 、P 共面, 直线EP 必与A 1D 1 相交于某点F ,则过P 点有且只有一条直线EF 与a 、b 都相交,故①为真命题; 分别平移a ,b ,使a 与b 均经过P ,则有两条互相垂直的直线与a ,b 都成45°角,故②为假命题. ∴①为真命题,②为假命题.故选:B .【点睛】本题考查立体几何图形中直线和平面的相交、平行、垂直的性质,体现了数形结合的数学思想,是中档题.二、填空题6.(2020·上海青浦区·高三一模)圆锥底面半径为1cm ,母线长为2cm ,则其侧面展开图扇形的圆心角θ=___________.【答案】π;【分析】根据圆的周长公式易得圆锥底面周长,也就是圆锥侧面展开图的弧长,利用弧长公式可得圆锥侧面展开图扇形的圆心角的大小.【详解】因为圆锥底面半径为1cm ,所以圆锥的底面周长为2cm π, 则其侧面展开图扇形的圆心角22πθπ==, 故答案为:π.【点睛】思路点睛:该题考查的是有关圆锥侧面展开图的问题,解题思路如下:(1)首先根据底面半径求得底面圆的周长;(2)根据圆锥侧面展开图扇形的弧长就是底面圆的周长,结合母线长,利用弧长公式求得圆心角的大小. 7.(2020·上海闵行区·高三一模)如图,已知正四棱柱1111ABCD A B C D -的底面边长为2,高为3,则异面直线1AA 与1BD 所成角的大小是_______.【答案】22;【分析】根据11//AA DD ,得到1DD B ∠异面直线1AA 与1BD 所成的角,然后在1Rt DD B △,利用正切函数求解.【详解】因为11//AA DD ,所以1DD B ∠异面直线1AA 与1BD 所成的角,在正四棱柱1111ABCD A B C D -的底面边长为2,高为3, 所以1122tan 3BD DD B DD ∠==, 因为1(0,)2DD B π∠∈, 所以122arctan3DD B ∠=, 故答案为:22arctan 38.(2019·上海市建平中学高三月考)某几何体由一个半圆锥和一个三棱锥组合而成,其三视图如图所示(单位:厘米),则该几何体的体积(单位:立方厘米)是________.【答案】12π+2,高为3;半圆锥的底面是半径为1的半圆,高为3;据此计算出该几何体的体积.【详解】由三视图可知,三棱锥的体积:1223132V ⎛=⨯⨯= ⎝⎭;半圆锥体积:()11113232V ππ=⨯⨯⨯⨯⨯=,所以总体积为:12π+. 故答案为12π+.【点睛】本题考查空间几何体的体积计算,难度较易.计算组合体的体积时,可将几何体拆分为几个容易求解的常见几何体,然后根据体积公式完成求解.9.(2020·上海高三其他模拟)如图直三棱柱ABB 1-DCC 1中, BB 1⊥AB ,AB=4,BC=2,CC 1=1,DC 上有一动点P ,则△APC 1周长的最小值是 .【答案】521+试题分析:要求周长的最小值,因边为定值,只要求另两边之和的最小值,因两点直线线段最短,所以的最小值为因此△APC 1周长的最小值是521考点:棱柱的相关知识.10.(2020·上海高三一模)已知母线长为6cm 的圆锥的侧面积是底面积的3倍,则该圆锥的底面半径为________cm .【答案】2【分析】设底面半径为r ,由两个面积的关系可得底面半径的值.【详解】解:设底面半径为r ,则由题意,可得213262r r ππ=⨯⨯,解得2r , 故答案为:2.【点睛】本题考查圆锥的侧面积及圆的面积公式,属于基础题.11.(2020·上海高三其他模拟)已知圆锥的母线长为l ,过圆锥顶点的最大截面三角形的面积为212l ,则此圆锥底面半径r 与母线长l 的比r l的取值范围是____________. 【答案】22【分析】先判断两条母线的夹角=90θ时最大截面三角形的面积为212l 22l r ≤和r l <,最后求出r l 的取值范围即可. 【详解】解:过圆锥顶点的截面三角形的面积:1sin 2S l l θ=⋅⋅(θ为两母线的夹角), 因为过圆锥顶点的最大截面三角形的面积为212l ,即两条母线的夹角=90θ时的截面面积,此时底面弦长为2l ,所以22l r ≤,又r l <,所以212r l≤<, 故答案为:2[,1)2【点睛】本题考查空间几何体,是基础题.12.(2020·上海青浦区·高三二模)用一平面去截球所得截面的面积为23cm π,已知球心到该截面的距离为1cm ,则该球的表面积是___________2cm .【答案】16π【分析】由已知求出小圆的半径,然后利用勾股定理求出球的半径,即可求出球的表面积【详解】解:因为用一平面去截球所得截面的面积为23cm π,所以小圆的半径为3cm ,因为球心到该截面的距离为1cm ,所以球的半径为221(3)2+=cm ,所以球的表面积为24216S ππ=⨯=2cm ,故答案为:16π【点睛】此题考查球的截面的半径、球心到截面的距离与球的半径间的关系,属于基础题13.(2020·上海普陀区·高三月考)已知一个半圆柱的高为4,其俯视图如图所示,其左视图的面积为8,则该半圆柱的表面积为______.【答案】1612+π【分析】由圆柱的主视图和左视图知该圆柱的底面直径为4,高为3,由此能求出该几何体的表面积,得到答案.【详解】由题意,其左视图为矩形,其左视图的面积为8,半圆柱的高h 为4,可得半圆的半径r 为2,由于半圆柱的表面积为两个底面半圆面积加侧面展开图形的面积, 即2211222224224161222S r rh rh πππππ=⨯⨯++=⨯⨯⨯+⨯⨯+⨯⨯=+.故答案为:1612+π.【点睛】本题主要考查了空间几何体的三视图的应用,以及圆柱的表面积的计算问题,同时考查了圆柱的结构特征的应用,属于基础题.三、解答题14.(2020·上海虹口区·高三一模)如图在三棱锥P ABC -中,棱AB 、AC 、AP 两两垂直,3AB AC AP ===,点M 在AP 上,且1AM =.(1)求异面直线BM 和PC 所成的角的大小;(2)求三棱锥P BMC -的体积.【答案】(1)5(2)3. 【分析】(1)以点A 为坐标原点,AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -,利用空间向量法可求得异面直线BM 和PC 所成的角的大小;(2)计算出PMC △的面积,并推导出AB ⊥平面PMC ,利用锥体的体积公式可求得三棱锥P BMC -的体积.【详解】(1)由于AB 、AC 、AP 两两垂直,以点A 为坐标原点,AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立空间直角坐标系A xyz -,如下图所示:则()3,0,0B 、()0,0,0A 、()0,3,0C 、()0,0,3P 、()0,0,1M ,()3,0,1BM =-,()0,3,3PC =-,5cos ,101032BM PC BM PC BM PC⋅<>===-⨯⋅,因此,异面直线BM 和PC 所成的角的大小为5arccos 10; (2)AB AC ⊥,AB AP ⊥,AC AP A =,AB ∴⊥平面APC ,AC AP ⊥,1AM =,2PM AP AM ∴=-=,132PMC S PM AC ∴=⋅=△, 1133333B PMC PMC V S AB -=⋅=⨯⨯=△.【点睛】方法点睛:求空间角的常用方法:(1)定义法:由异面直线所成角、线面角、二面角的定义,结合图形,作出所求空间角,再结合题中条件,解对应的三角形,即可求出结果;(2)向量法:建立适当的空间直角坐标系,通过计算向量的夹角(两直线的方向向量、直线的方向向量与平面的法向量、两平面的法向量)的余弦值,即可求得结果.15.(2020·上海青浦区·高三一模)如图,在长方体1111ABCD A B C D -中,1AB AD ==,12AA =,点P 为棱1DD 的中点.(1)证明:1//BD 平面P AC ;(2)求异面直线1BD 与AP 所成角的大小. 【答案】(1)证明见解析;(2)30.【分析】(1)AC 和BD 交于点O ,则O 为BD 的中点.推导出1//PO BD .由此能证明直线1//BD 平面PAC ;(2)由1//PO BD ,得APO ∠即为异面直线1BD 与AP 所成的角或其补角.由此能求出异面直线1BD 与AP 所成角的大小.【详解】(1)证明:设AC 和BD 交于点O ,则O 为BD 的中点. 连结PO ,又因为P 是1DD 的中点,所以1//PO BD . 又因为PO ⊂平面P AC ,1BD ⊄平面P AC 所以直线1//BD 平面P AC.(2)解:由(1)知,1//PO BD ,所以APO ∠即为异面直线1BD 与AP 所成的角或其补角.因为2PA PC ==,2122AO AC ==且PO AO ⊥, 所以212sin 22AO APO AP ∠===. 又(0,90APO ︒︒⎤∠∈⎦,所以30APO ∠=︒ 故异面直线1BD 与AP 所成角的大小为30. 【点睛】方法点睛:异面直线所成的角的求法方法一:(几何法)找→作(平移法、补形法)→证(定义)→指→求(解三角形) 方法二:(向量法)cos m n m nα=,其中α是异面直线,m n 所成的角,,m n 分别是直线,m n 的方向向量.16.(2020·上海长宁区·高三一模)如图,已知圆锥的顶点为P ,底面圆心为O ,高为23,底面半径为2.(1)求该圆锥的侧面积;(2)设OA 、OB 为该圆锥的底面半径,且90AOB ∠=︒,M 为线段AB 的中点,求直线PM 与直线OB 所成的角的正切值.【答案】(1)8π;(213【分析】(1)利用圆锥侧面积公式即可;(2)通过中点作辅助线即可. 【详解】解:(1)OP ⊥底面OAB 由题意高3h =2r ,所以母线4l圆锥的侧面积S =12lr 12242π=⨯⨯⨯8π= (2)取OA 的中点为N ,因为M 为AB 的中点所以//MN OB ,PMN ∠就是直线PM 与直线OB 所成的角. 因为OB OA ⊥,OB OP ⊥,所以OB ⊥平面POA ,MN ⊥平面POA ,MN PN ⊥ 在Rt △PNM 中,22()132rPN h =+=,112MN OB ==.所以PMN ∠的正切值为13.即直线PM 与直线OB 所成的角正切值为13.17.(2020·上海徐汇区·高三一模)如图:在直三棱柱111ABC A B C -中,2AC BC ==,14CC =,90ACB ∠=,E 、F 分别为棱1AA 、AB 的中点.(1)求异面直线1A C 与EF 所成的角的大小(结果用反三角函数值表示); (2)求五棱锥11C EFBB A -的体积11C EFBB A V -. 【答案】(1)5arctan (2)143.【分析】(1)连接1A B ,利用中位线的性质可得出1//A B EF ,由此可得出1BA C ∠(或其补角)就是异面直线1A C 与EF 所成的角,利用解三角形的知识求出1BA C ∠的正切值,即可得解;(2)计算出五边形1EFBB A 的面积,并推导出CF ⊥平面11AA B B ,再利用锥体的体积公式可计算出五棱锥11C EFBB A -的体积11C EFBB A V -. 【详解】 (1)连接1A B ,E 、F 分别为1AA 、AB 的中点,所以,1//A B EF ,于是1BA C ∠(或其补角)就是异面直线1A C 与EF 所成的角, 在1A BC 中,2BC =,221125AC AA AC =+=,221126A B AA AB =+=,22211A C BC A B ∴+=,所以1BC A C ⊥,所以,1125tan 525BC BAC AC ∠===. 所以,异面直线1A C 与EF 所成角的大小为5arctan5;(2)由于111111822722AEFEFBB A ABB A S S S AB AA AE AF =-=⋅-⋅==五边形矩形 连接CF ,2AC BC ==,F 为AB 的中点,90ACB ∠=,CF AB ∴⊥,且122CF AB == 1AA ⊥平面ABC ,CF ⊂平面ABC ,1CF AA ∴⊥,1AB AA A ⋂=,CF ∴⊥平面11AA B B ,所以11111114722333C EFBB A EFBB A V S CF -=⋅=⨯⨯=五边形. 【点睛】思路点睛:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形; (4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.18.(2020·上海大学附属中学高三三模)如图,正四棱锥P ABCD -中.(1)求证:BD ⊥平面PAC ; (2)若2AB =,423P ABCD V -=,求二面角A PB C --的余弦值. 【答案】(1)证明见解析;(2)1arccos 3⎛⎫- ⎪⎝⎭【分析】(1)先证明PO BD ⊥,结合,BD AC ⊥利用线面垂直的判定定理可得结论;(2)由423P ABCD V -=求出棱锥的高,可求得侧棱长,判定侧面的形状后可得二面角的平面角,利用余弦定理可得答案. 【详解】(1)因为P ABCD -是正棱锥,P ∴在面ABCD 内射影是AC 与BD 的交点O ,即PO ⊥面ABCD ,PO BD ∴⊥,又,BD AC PO ⊥与AC 在面PAC 内相交,BD ∴⊥面PAC ;(2)2142233P ABCD V PO -=⨯⨯=, 2PO ∴=,222PB =+=,则PAB △与PBC 为边长是2的正三角形,取PB 的中点E ,连,AE CE , 则AE PB ⊥,CE PB ⊥,AEC ∠是二面角的平面角,3381cos 3233AEC +-∠==-⨯⨯,1cos 3AEC arc ⎛⎫∠=- ⎪⎝⎭【点睛】本题主要考查线面垂直的证明以及二面角的求解,考查了正四棱锥的性质,属于中档题.19.(2019·上海市建平中学高三月考)如图:四面体ABCD 的底面ABC 是直角三角形,AC BC ⊥,3AC =,4BC =,DA ⊥平面ABC ,5DA =,E 是BD 上的动点(不包括端点).(1)求证:AE 与BC 不垂直;(2)当AE DC ⊥时,求DEEB的值. 【答案】(1)证明见解析;(2)259.【分析】(1)利用反证法,先假设AE 与BC 垂直,然后根据条件推出与题设矛盾的结论,即可证明出AE与BC 不垂直;(2)先作辅助线//EF BC ,利用AE DC ⊥以及BC ⊥平面DAC 得到DC ⊥平面AEF ,由此得到AF DC ⊥,从而确定出F 点位置,再由DE DFEB FC=得到结果. 【详解】(1)假设AE BC ⊥,因为DA ⊥平面ABC ,所以DA BC ⊥,且DA AE A =,所以BC ⊥平面DAE ,又因为AB平面DAE ,所以BC AB ⊥,又因为由条件可知BC AC ⊥,所以BC AB ⊥不成立, 故假设不成立,所以AE 与BC 不垂直;(2)过E 作//EF BC ,交DC 于F ,连接AF ,因为AC BC ⊥,DA BC ⊥且DA AC A =,所以BC ⊥平面DAC ,因为//EF BC ,所以EF ⊥平面DAC ,所以EF DC ⊥, 又因为AE DC ⊥,EF DC ⊥,EF AE E =,所以DC ⊥平面AEF ,所以DC AF ⊥,又cos 25934AD ADC DC ∠===+,所以cos cos 34DF ADF ADC AD ∠=∠==, 所以34DF =,所以34FC =,所以259DF FC =,所以由相似可知259DE DF EB FC ==. 【点睛】本题考查空间中的垂直关系的判断与证明,难度一般.空间中的不平行、不垂直关系的证明,如果正面证明比较麻烦,可采用反证法去证明.20.(2020·上海市七宝中学高三其他模拟)如图,四边形11ABB A 是圆柱1OO 的轴载面,4AB =,12OO =,以圆柱上底面为底面作高为2的圆锥1PO ,C 、1C 分别在AB 、11A B 上,2AOC π∠=,1113AO C π∠=.(1)求这个几何体的表面积和体积; (2)求二面角111O AC C --的余弦值. 【答案】(1)表面积为(1242π+,体积为323π;(23823-. 【分析】(1)计算出圆锥的母线长,利用圆锥的侧面积公式和圆柱的侧面积、底面积公式可计算出几何体的表面积,结合柱体和锥体的体积公式可求得几何体的体积;(2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立空间直角坐标系O xyz -,利用空间向量法可求得二面角111O AC C --的余弦值. 【详解】(1)由题意可知,圆柱的底面半径为22ABr ==, 因为1PO 为圆锥的高,且12PO =,所以,圆锥的母线长为221122PA PO r =+=,又12OO =,因此,该几何体的表面积为(22+2222221242S ππππ=⨯⨯⨯+⨯=+.该几何体的体积为22132222233V πππ=⨯⨯+⨯⨯⨯=; (2)以点O 为坐标原点,OA 、OC 、OP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系O xyz -,则点()10,0,2O ,()12,0,2A ,()13,2C ,()0,2,0C ,设平面11A CC 的一个法向量为(),,m x y z =,()113,0AC =-,()12,2,2AC =--, 由11100m AC m AC ⎧⋅=⎪⎨⋅=⎪⎩,得302220x x y z ⎧-=⎪⎨-+-=⎪⎩,令3x =1y =,13z =所以,平面11A CC 的一个法向量为(3,1,13m =,易知平面111O AC 的一个法向量为()0,0,1n =,()()22233cos ,82331131m n m n m n⋅<>===⋅-++-⨯,由图象可知,二面角111O AC C --31823--【点睛】本题考查组合体的表面积与体积的计算,同时也考查了利用空间向量法计算二面角的余弦值,考查计算能力,属于中等题.21.(2020·上海高三其他模拟)如图,已知⊙O 的直径AB=3,点C 为⊙O 上异于A ,B 的一点,VC ⊥平面ABC ,且VC=2,点M 为线段VB 的中点.(1)求证:BC ⊥平面VAC ;(2)若直线AM 与平面V AC 所成角为4π.求三棱锥B-ACM 的体积. 【答案】(1))祥见解析;(2)试题分析:(1)由线面垂直得VC ⊥BC ,由直径性质得AC ⊥BC ,由此能证明BC ⊥平面V AC .(2)首先由(1)作出直线AM 与平面V AC 所成的角:取VC 的中点N ,连接MN ,AN ,则MN ∥BC ,由(I )得BC ⊥平面VAC ,所以MN ⊥平面V AC ,则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π,所以MN=AN ;这样就可求出AC 的长,且而求得体积.试题解析:(1)证明:因为VC ⊥平面ABC ,BC ABC ⊂平面,所以VC ⊥BC ,又因为点C 为圆O 上一点,且AB 为直径,所以AC ⊥BC ,又因为VC ,AC ⊂平面V AC ,VC∩AC=C ,所以BC ⊥平面V AC.(2)如图,取VC 的中点N ,连接MN ,AN ,则MN ∥BC ,由(I )得BC ⊥平面V AC ,所以MN ⊥平面V AC ,则∠MAN 为直线AM 与平面V AC 所成的角.即∠MAN=4π,所以MN=AN ;令AC=a,则29-a ,MN=292a -;因为VC=2,M 为VC 中点,所以21a + 所以,292a -=21a +,解得a=1 因为MN ∥BC,所以考点:1.直线与平面垂直的判定;2. 棱柱、棱锥、棱台的体积;3. 直线与平面所成的角.22.(2020·上海高三其他模拟)已知正方体1111ABCD A B C D -,12AA =,E 为棱1CC 的中点.(1)求异面直线AE 与1DD 所成角的大小(结果用反三角表示);(2)求C 点到平面ABE 的距离,并求出三锥C ADE -的体积.【答案】(1)1arccos 3;(2)C 点到平面ABE 25,三锥C ADE -的体积为23. 【分析】(1)由已知得AEC ∠(或补角)是异面直线AE 与1DD 所成角,求解AEC 可得答案;(2)利用等体积E ABC C ABE V V --=,可求得设C 点到平面ABE 的距离,利用C ADE A CDE V V --=,可求得三锥C ADE -的体积.【详解】解:(1)连接AC ,因为11//CC DD ,所以AEC ∠(或补角)是异面直线AE 与1DD 所成角, 在AEC 中,()22221cos 3221EC AEC AE AC EC ∠====++, 所以异面直线AE 与1DD 所成角是1arccos 3;(2)设C 点到平面ABE 的距离为h ,因为E ABC C ABE V V --=,即1133ABC ABE S EC S h ⋅=⋅△△, 又正方体1111ABCD A B C D -中,AB ⊥面11BB C C ,所以ABE △是Rt ABE △,又2222215BE BC EC =+=+=, 所以1111221253232h ⨯⨯⨯⨯=⨯⨯⨯⋅,解得255h =, 所以C ADE A CDE V V --=111212332DCE S AD ⎛⎫=⋅=⨯⨯⨯⨯ ⎪⎝⎭△23=.【点睛】本题考查空间中异面直线所成的角,运用等体积法求点到面的距离以及三棱锥的体积,属于中档题.。
高考立体几何知识点与题型精讲

高考立体几何知识点与题型精讲在高考数学中,立体几何是一个重要的板块,它不仅考查学生的空间想象能力,还对逻辑推理和数学运算能力有较高要求。
接下来,咱们就一起深入探讨一下高考立体几何的知识点和常见题型。
一、知识点梳理1、空间几何体的结构特征(1)棱柱:有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行。
(2)棱锥:有一个面是多边形,其余各面是有一个公共顶点的三角形。
(3)棱台:用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分。
2、空间几何体的表面积和体积(1)圆柱的表面积:S =2πr² +2πrl (r 为底面半径,l 为母线长)。
体积:V =πr²h (h 为高)。
(2)圆锥的表面积:S =πr² +πrl 。
体积:V =1/3πr²h 。
(3)球的表面积:S =4πR² 。
体积:V =4/3πR³ 。
3、空间点、直线、平面之间的位置关系(1)公理 1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。
(2)公理 2:过不在一条直线上的三点,有且只有一个平面。
(3)公理 3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
4、直线与平面平行的判定与性质(1)判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
(2)性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行。
5、平面与平面平行的判定与性质(1)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
(2)性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行。
6、直线与平面垂直的判定与性质(1)判定定理:一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
(2)性质定理:垂直于同一个平面的两条直线平行。
7、平面与平面垂直的判定与性质(1)判定定理:一个平面过另一个平面的垂线,则这两个平面垂直。
立体几何(7大题型)(解析版)2024年高考数学立体几何大题突破

立体几何立体几何是高考数学的必考内容,在大题中一般分两问,第一问考查空间直线与平面的位置关系证明;第二问考查空间角、空间距离等的求解。
考题难度中等,常结合空间向量知识进行考查。
2024年高考有很大可能延续往年的出题方式。
题型一:空间异面直线夹角的求解1(2023·上海长宁·统考一模)如图,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.(1)求证:AO⊥CD;(2)若BD⊥DC,BD=DC,AO=BO,求异面直线BC与AD所成的角的大小.【思路分析】(1)利用面面垂直的性质、线面垂直的性质推理即得.(2)分别取AB,AC的中点M,N,利用几何法求出异面直线BC与AD所成的角.【规范解答】(1)在三棱锥A-BCD中,由AB=AD,O为BD的中点,得AO⊥BD,而平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,AO⊂平面ABD,因此AO⊥平面BCD,又CD⊂平面BCD,所以AO⊥CD.(2)分别取AB,AC的中点M,N,连接OM,ON,MN,于是MN⎳BC,OM⎳AD,则∠OMN是异面直线BC与AD所成的角或其补角,由(1)知,AO ⊥BD ,又AO =BO ,AB =AD ,则∠ADB =∠ABD =π4,于是∠BAD =π2,令AB =AD =2,则DC =BD =22,又BD ⊥DC ,则有BC =BD 2+DC 2=4,OC =DC 2+OD 2=10,又AO ⊥平面BCD ,OC ⊂平面BCD ,则AO ⊥OC ,AO =2,AC =AO 2+OC 2=23,由M ,N 分别为AB ,AC 的中点,得MN =12BC =2,OM =12AD =1,ON =12AC =3,显然MN 2=4=OM 2+ON 2,即有∠MON =π2,cos ∠OMN =OM MN =12,则∠OMN =π3,所以异面直线BC 与AD 所成的角的大小π3.1、求异面直线所成角一般步骤:(1)平移:选择适当的点,线段的中点或端点,平移异面直线中的一条或两条成为相交直线.(2)证明:证明所作的角是异面直线所成的角.(3)寻找:在立体图形中,寻找或作出含有此角的三角形,并解之.(4)取舍:因为异面直线所成角θ的取值范围是0,π2,所以所作的角为钝角时,应取它的补角作为异面直线所成的角.2、可通过多种方法平移产生,主要有三种方法:(1)直接平移法(可利用图中已有的平行线);(2)中位线平移法;(3)补形平移法(在已知图形中,补作一个相同的几何体,以便找到平行线).3、异面直线所成角:若n 1 ,n 2分别为直线l 1,l 2的方向向量,θ为直线l 1,l 2的夹角,则cos θ=cos <n 1 ,n 2 > =n 1 ⋅n 2n 1 n 2.1(2023·江西萍乡·高三统考期中)如图,在正四棱台ABCD -A 1B 1C 1D 1中,E ,F 分别是BB 1,CD 的中点.(1)证明:EF ⎳平面AB1C 1D ;(2)若AB =2A 1B 1,且正四棱台的侧面积为9,其内切球半径为22,O 为ABCD 的中心,求异面直线OB 1与CC 1所成角的余弦值.【答案】(1)证明见解析;(2)45【分析】(1)根据中位线定理,结合线面平行判定定理以及面面平行判定定理,利用面面平行的性质,可得答案;(2)根据题意,结合正四棱台的几何性质,求得各棱长,利用线线角的定义,可得答案.【解析】(1)取CC 1中点G ,连接GE ,GF ,如下图:在梯形BB 1C 1C 中,E ,G 分别为BB 1,CC 1的中点,则EG ⎳B 1C 1,同理可得FG ⎳C 1D ,因为EG ⊄平面AB 1C 1D ,B 1C 1⊂平面AB 1C 1D ,所以EG ⎳平面AB 1C 1D ,同理可得GF ⎳平面AB 1C 1D ,因为EG ∩FG =G ,EG ,FG ⊆平面EFG ,所以平面EFG ⎳平面AB 1C 1D ,又因为EF ⊆平面EFG ,所以EF ⎳平面AB 1C 1D ;(2)连接AC ,BD ,则AC ∩BD =O ,连接A 1O ,A 1C 1,B 1O ,在平面BB 1C 1C 中,作B 1N ⊥BC 交BC 于N ,在平面BB 1D 1D 中,作B 1M ⊥BD 交BD 于M ,连接MN ,如下图:因为AB =2A 1B 1,则OC =A 1C 1,且OC ⎳A 1C 1,所以A 1C 1CO 为平行四边形,则A 1O ⎳CC 1,且A 1O =CC 1,所以∠A 1OB 1为异面直线OB 1与CC 1所成角或其补角,同理可得:B 1D 1DO 为平行四边形,则B 1O =D 1D ,在正四棱台ABCD -A 1B 1C 1D 1中,易知对角面BB 1D 1D ⊥底面ABCD ,因为平面ABCD ∩平面BB 1D 1D =BD ,且B 1M ⊥BD ,B 1M ⊂平面BB 1D 1D ,所以B 1M ⊥平面ABCD ,由内切球的半径为22,则B 1M =2,在等腰梯形BB 1C 1C 中,BC =2B 1C 1且B 1N ⊥BC ,易知BN =14BC ,同理可得BM =14BD ,在△BCD 中,BN BC=BM BD =14,则MN =14CD ,设正方形ABCD 的边长为4x x >0 ,则正方形A 1B 1C 1D 1的边长为2x ,MN =x ,由正四棱台的侧面积为9,则等腰梯形BB 1C 1C 的面积S =94,因为B 1M ⊥平面ABCD ,MN ⊂平面ABCD ,所以B 1M ⊥MN ,在Rt △B 1MN ,B 1N =B 1M 2+MN 2=2+x 2,可得S =12⋅B 1N ⋅B 1C 1+BC ,则94=12×2+x 2×4x +2x ,解得x =12,所以BC =2,B 1C 1=1,BN =14BC =12,B 1N =32,则A 1B 1=1,在Rt △BB 1N 中,BB 1=B 1N 2+BN 2=102,则CC 1=DD 1=102,所以在△A 1OB 1中,则cos ∠A 1OB 1=A 1O 2+B 1O 2-A 1B 212⋅A 1O ⋅B 1O=1022+102 2-12×102×102=45,所以异面直线OB 1与CC 1所成角的余弦值为45.2(2023·辽宁丹东·统考二模)如图,平行六面体ABCD -A 1B 1C 1D 1的所有棱长都相等,平面CDD 1C 1⊥平面ABCD ,AD ⊥DC ,二面角D 1-AD -C 的大小为120°,E 为棱C 1D 1的中点.(1)证明:CD ⊥AE ;(2)点F 在棱CC 1上,AE ⎳平面BDF ,求直线AE 与DF 所成角的余弦值.【答案】(1)证明见解析;(2)37【分析】(1)根据面面垂直可得线面垂直进而得线线垂直,由二面角定义可得∠D 1DC =120°,进而根据中点得线线垂直即可求;(2)由线面平行的性质可得线线平行,由线线角的几何法可利用三角形的边角关系求解,或者建立空间直角坐标系,利用向量的夹角即可求解.【解析】(1)因为平面CDD 1C 1⊥平面ABCD ,且两平面交线为DC ,AD ⊥DC ,AD ⊂平面ABCD , 所以AD ⊥平面CDD 1C 1,所以AD ⊥D 1D ,AD ⊥DC ,∠D 1DC 是二面角D 1-AD -C 的平面角,故∠D 1DC =120°.连接DE ,E 为棱C 1D 1的中点,则DE ⊥C 1D 1,C 1D 1⎳CD ,从而DE ⊥CD .又AD ⊥CD ,DE ∩AD =D ,DE ,AD ⊂平面AED ,所以CD ⊥平面AED ,ED ⊂平面AED ,因此CD ⊥AE .(2)解法1:设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.连AC 交BD 于点O ,连接CE 交DF 于点G ,连OG .因为AE ⎳平面BDF ,AE ⊂平面AEC ,平面AEC ∩平面BDF =OG ,所以AE ∥OG ,因为O 为AC 中点,所以G 为CE 中点,故OG =12AE =72.且直线OG 与DF 所成角等于直线AE 与DF 所成角.在Rt △EDC 中,DG =12CE =72,因为OD =2,所以cos ∠OGD =722+72 2-(2)22×72×72=37.因此直线AE 与DF 所成角的余弦值为37.解法2;设AB =2,则DE =D 1D 2-12D 1C 1 2=3,所以CE =AE =AD 2+DE 2=7.取DC 中点为G ,连接EG 交DF 于点H ,则EG =DD 1=2.连接AG 交BD 于点I ,连HI ,因为AE ⎳平面BDF ,AE ⊂平面AGE ,平面AGE ∩平面BDF =IH ,所以AE ∥IH .HI 与DH 所成角等于直线AE 与DF 所成角.正方形ABCD 中,GI =13AG ,DI =13DB =223,所以GH =13EG ,故HI =13AE =73.在△DHG 中,GH =13EG =23,GD =1,∠EGD =60°,由余弦定理DH =1+49-1×23=73.在△DHI 中,cos ∠DHI =732+73 2-223 22×73×73=37.因此直线AE 与DF 所成角的余弦值为37.解法3:由(1)知DE ⊥平面ABCD ,以D 为坐标原点,DA为x 轴正方向,DA为2个单位长,建立如图所示的空间直角坐标系D -xyz .由(1)知DE =3,得A 2,0,0 ,B 2,2,0 ,C 0,2,0 ,E (0,0,3),C 1(0,1,3).则CC 1=(0,-1,3),DC =(0,2,0),AE =(-2,0,3),DB =(2,2,0).由CF =tCC 1 0≤t ≤1 ,得DF =DC +CF =(0,2-t ,3t ).因为AE ⎳平面BDF ,所以存在唯一的λ,μ∈R ,使得AE =λDB +μDF=λ2,2,0 +μ(0,2-t ,3t )=2λ,2λ+2μ-tμ,3μt ,故2λ=-2,2λ+2μ-tμ=0,3μt =3,解得t =23,从而DF =0,43,233 .所以直线AE 与DF 所成角的余弦值为cos AE ,DF =AE ⋅DF|AE ||DF |=37.题型二:空间直线与平面夹角的求解2(2024·安徽合肥·统考一模)如图,三棱柱ABC -A 1B 1C 1中,四边形ACC 1A 1,BCC 1B 1均为正方形,D ,E 分别是棱AB ,A 1B 1的中点,N 为C 1E 上一点.(1)证明:BN ⎳平面A 1DC ;(2)若AB =AC ,C 1E =3C 1N,求直线DN 与平面A 1DC 所成角的正弦值.【思路分析】(1)连接BE ,BC 1,DE ,则有平面BEC 1⎳平面A 1DC ,可得BN ⎳平面A 1DC ;(2)建立空间直角坐标系,利用空间向量进行计算即可.【规范解答】(1)连接BE ,BC 1,DE .因为AB ⎳A 1B 1,且AB =A 1B 1,又D ,E 分别是棱AB ,A 1B 1的中点,所以BD ⎳A 1E ,且BD =A 1E ,所以四边形BDA 1E 为平行四边形,所以A 1D ⎳EB ,又A 1D ⊂平面A 1DC ,EB ⊄平面A 1DC ,所以EB ⎳平面A 1DC ,因为DE ⎳BB 1⎳CC 1,且DE =BB 1=CC 1,所以四边形DCC 1E 为平行四边形,所以C 1E ⎳CD ,又CD ⊂平面A 1DC ,C 1E ⊄平面A 1DC ,所以C 1E ⎳平面A 1DC ,因为C 1E ∩EB =E ,C 1E ,EB ⊂平面BEC 1,所以平面BEC 1⎳平面A 1DC ,因为BN ⊂平面BEC 1,所以BN ⎳平面A 1DC .(2)四边形ACC 1A 1,BCC 1B 1均为正方形,所以CC 1⊥AC ,CC 1⊥BC ,所以CC 1⊥平面ABC .因为DE ⎳CC 1,所以DE ⊥平面ABC ,从而DE ⊥DB ,DE ⊥DC .又AB =AC ,所以△ABC 为等边三角形.因为D 是棱AB 的中点,所以CD ⊥DB ,即DB ,DC ,DE 两两垂直.以D 为原点,DB ,DC ,DE 所在直线为x ,y ,z 轴,建立如图所示的空间直角坐标系D -xyz .设AB =23,则D 0,0,0 ,E 0,0,23 ,C 0,3,0 ,C 10,3,23 ,A 1-3,0,23 ,所以DC =0,3,0 ,DA 1=-3,0,23 .设n=x ,y ,z 为平面A 1DC 的法向量,则n ⋅DC=0n ⋅DA 1 =0,即3y =0-3x +23z =0 ,可取n=2,0,1 .因为C 1E =3C 1N ,所以N 0,2,23 ,DN =0,2,23 .设直线DN 与平面A 1DC 所成角为θ,则sin θ=|cos ‹n ,DN ›|=|n ⋅DN ||n |⋅|DN |=235×4=1510,即直线DN 与平面A 1DC 所成角正弦值为1510.1、垂线法求线面角(也称直接法):(1)先确定斜线与平面,找到线面的交点B 为斜足;找线在面外的一点A ,过点A 向平面α做垂线,确定垂足O ;(2)连结斜足与垂足为斜线AB 在面α上的投影;投影BO 与斜线AB 之间的夹角为线面角;(3)把投影BO 与斜线AB 归到一个三角形中进行求解(可能利用余弦定理或者直角三角形)。
高三精选立体几何大题30题(含详细解答)
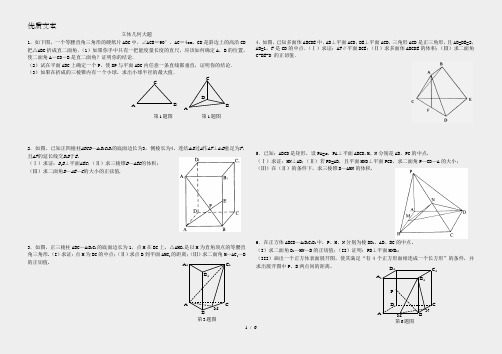
A BC第1题图ABCD第1题图立体几何大题1.如下图,一个等腰直角三角形的硬纸片ABC中,∠ACB=90°,AC=4cm,CD是斜边上的高沿CD 把△ABC折成直二面角.(1)如果你手中只有一把能度量长度的直尺,应该如何确定A,B的位置,使二面角A-CD-B是直二面角?证明你的结论.(2)试在平面ABC上确定一个P,使DP与平面ABC内任意一条直线都垂直,证明你的结论.(3)如果在折成的三棱锥内有一个小球,求出小球半径的最大值.2.如图,已知正四棱柱ABCD—A1B1C1D1的底面边长为3,侧棱长为4,连结A1B过A作AF⊥A1B垂足为F,且AF的延长线交B1B于E。
(Ⅰ)求证:D1B⊥平面AEC;(Ⅱ)求三棱锥B—AEC的体积;(Ⅲ)求二面角B—AE—C的大小的正弦值.3.如图,正三棱柱ABC—A1B1C1的底面边长为1,点M在BC上,△AMC1是以M为直角顶点的等腰直角三角形.(I)求证:点M为BC的中点;(Ⅱ)求点B到平面AMC1的距离;(Ⅲ)求二面角M—AC1—B 的正切值. 4.如图,已知多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,三角形ACD是正三角形,且AD=DE=2,AB=1,F是CD的中点.(Ⅰ)求证:AF∥平面BCE;(Ⅱ)求多面体ABCDE的体积;(Ⅲ)求二面角C-BE-D 的正切值.5.已知:ABCD是矩形,设PA=a,PA⊥平面ABCD.M、N分别是AB、PC的中点.(Ⅰ)求证:MN⊥AB;(Ⅱ)若PD=AB,且平面MND⊥平面PCD,求二面角P—CD—A的大小;(Ⅲ)在(Ⅱ)的条件下,求三棱锥D—AMN的体积.6.在正方体ABCD—A1B1C1D1中,P、M、N分别为棱DD1、AB、BC的中点。
(I)求二面角B1—MN—B的正切值;(II)证明:PB⊥平面MNB1;(III)画出一个正方体表面展开图,使其满足“有4个正方形面相连成一个长方形”的条件,并求出展开图中P、B两点间的距离。
立体几何高考题及解析,高中数学立体几何题型及解题方法(理科)

- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考理科数学一轮复习:题型全归纳与高效训练突破专题8.7高考解答题热点题型---立体几何目录一、题型综述 (1)二题型全归纳 (1)题型一空间点、线、面的位置关系及空. (1)题型二平面图形的折叠问题 (7)题型三立体几何中的探索性问题 (10)三、高效训练突破 (15)一、题型综述立体几何是每年高考的重要内容,基本上都是一道客观题和一道解答题,客观题主要考查考生的空间想象能力及简单的计算能力.解答题主要采用证明与计算相结合的模式,即首先利用定义、定理、公理等证明空间线线、线面、面面的平行或垂直关系,再利用空间向量进行空间角的计算求解.重在考查考生的逻辑推理及计算能力,试题难度一般不大,属中档题,且主要有以下几种常见的热点题型.二题型全归纳题型一空间点、线、面的位置关系及空.1证明点共面或线共面的常用方法(1)直接法:证明直线平行或相交,从而证明线共面.(2)纳入平面法:先确定一个平面,再证明有关点、线在此平面内..(3)辅助平面法:先证明有关的点、线确定平面α,再证明其余元素确定平面β,最后证明平面α,β重合.2.证明空间点共线问题的方法(1)公理法:一般转化为证明这些点是某两个平面的公共点,再根据公理3证明这些点都在这两个平面的交线上(2)纳入直线法:选择其中两点确定一条直线,然后证明其余点也在该直线上.3.证明线共点问题的常用方法先证其中两条直线交于一点,再证其他直线经过该点.4.求异面直线所成角的方法(1)几何法①作:利用定义转化为平面角,对于异面直线所成的角,可固定一条,平移一条,或两条同时平移到某个特殊的位置,顶点选在特殊的位置上.①证:证明作出的角为所求角.①求:把这个平面角置于一个三角形中,通过解三角形求空间角.(2)向量法建立空间直角坐标系,利用公式|cos θ|=|m ·n ||m ||n |求出异面直线的方向向量的夹角.若向量夹角是锐角或直角,则该角即为异面直线所成角;若向量夹角是钝角,则异面直线所成的角为该角的补角.【例1】如图,AE ①平面ABCD ,CF ①AE ,AD ①BC ,AD ①AB ,AB =AD =1,AE =BC =2.(1)求证:BF ①平面ADE ;(2)求直线CE 与平面BDE 所成角的正弦值;(3)若二面角E -BD -F 的余弦值为13,求线段CF 的长. 【解题思路】由条件知AB ,AD ,AE 两两垂直,可以A 为坐标原点建立空间直角坐标系,用空间向量解决.(1)寻找平面ADE 的法向量,证明BF →与此法向量垂直,即得线面平行.(2)CE →与平面BDE 的法向量所成角的余弦值的绝对值,即为直线CE 和平面BDE 所成角的正弦值;(3)设CF =h ,用h 表示二面角E -BD -F 的余弦值,通过解方程得到线段长.【规范解答】 (1)证明:以A 为坐标原点,AB 所在的直线为x 轴,AD 所在的直线为y 轴,AE 所在的直线为z 轴,建立如图所示的空间直角坐标系.则A (0,0,0),B (1,0,0),设F (1,2,h ).依题意,AB →=(1,0,0)是平面ADE 的一个法向量,又BF →=(0,2,h ),可得BF →·AB →=0,又直线BF ①平面ADE ,所以BF ①平面ADE .(2)依题意,D (0,1,0),E (0,0,2),C (1,2,0),则BD →=(-1,1,0),BE →=(-1,0,2),CE →=(-1,-2,2).设n =(x ,y ,z )为平面BDE 的法向量,则⎩⎪⎨⎪⎧ n ·BD →=0,n ·BE →=0,即⎩⎪⎨⎪⎧-x +y =0,-x +2z =0,不妨令z =1,可得n =(2,2,1). 因此有cos 〈CE →,n 〉=CE →·n |CE →||n |=-49. 所以直线CE 与平面BDE 所成角的正弦值为49. (3)设m =(x 1,y 1,z 1)为平面BDF 的法向量,则⎩⎪⎨⎪⎧ m ·BD →=0,m ·BF →=0,即⎩⎪⎨⎪⎧-x 1+y 1=0,2y 1+hz 1=0, 不妨令y 1=1,可得m =⎝⎛⎭⎫1,1,-2h . 由题意,有|cos 〈m ,n 〉|=|m ·n ||m ||n |=⎪⎪⎪⎪4-2h 3 2+4h2=13, 解得h =87.经检验,符合题意. 所以线段CF 的长为87. 【例2】.如图,在三棱锥P ABC 中,P A ①底面ABC ,①BAC =90°.点D ,E ,N 分别为棱P A ,PC ,BC 的中点,M 是线段AD 的中点,P A =AC =4,AB =2.(1)求证:MN ①平面BDE ;(2)已知点H 在棱P A 上,且直线NH 与直线BE 所成角的余弦值为721,求线段AH 的长. 【解析】:如图,以A 为原点,分别以AB →,AC →,AP →的方向为x 轴,y 轴,z 轴的正方向建立空间直角坐标系.依题意可得A (0,0,0),B (2,0,0),C (0,4,0),P (0,0,4),D (0,0,2),E (0,2,2),M (0,0,1),N (1,2,0).(1)证明:DE →=(0,2,0),DB →=(2,0,-2).设n =(x ,y ,z )为平面BDE 的法向量,则⎩⎪⎨⎪⎧n ·DE →=0,n ·DB →=0,即⎩⎪⎨⎪⎧2y =0,2x -2z =0. 不妨设z =1,可取n =(1,0,1).又MN →=(1,2,-1),可得MN →·n =0.因为MN ①平面BDE ,所以MN ①平面BDE .(2)依题意,设AH =h (0≤h ≤4),则H (0,0,h ),进而可得NH →=(-1,-2,h ),BE →=(-2,2,2).由已知,得|cos 〈NH →,BE →〉|=|NH →·BE →||NH →||BE →|=|2h -2|h 2+5×23=721, 整理得10h 2-21h +8=0,解得h =85或h =12. 所以,线段AH 的长为85或12. 【例3】如图,在几何体ACD -A 1B 1C 1D 1中,四边形ADD 1A 1与四边形CDD 1C 1均为矩形,平面ADD 1A 1①平面CDD 1C 1,B 1A 1①平面ADD 1A 1,AD =CD =1,AA 1=A 1B 1=2,E 为棱AA 1的中点.(1)证明:B 1C 1①平面CC 1E ;(2)求直线B 1C 1与平面B 1CE 所成角的正弦值.【解析】(1)证明:因为B 1A 1①平面ADD 1A 1,所以B 1A 1①DD 1,又DD 1①D 1A 1,B 1A 1∩D 1A 1=A 1,所以DD 1①平面A 1B 1C 1D 1,又DD 1①CC 1,所以CC 1①平面A 1B 1C 1D 1.因为B 1C 1①平面A 1B 1C 1D 1,所以CC 1①B 1C 1.因为平面ADD 1A 1①平面CDD 1C 1,平面ADD 1A 1∩平面CDD 1C 1=DD 1,C 1D 1①DD 1,所以C 1D 1①平面ADD 1A 1.经计算可得B 1E =5,B 1C 1=2,EC 1=3,从而B 1E 2=B 1C 21+EC 21,所以在①B 1EC 1中,B 1C 1①C 1E .又CC 1,C 1E ①平面CC 1E ,CC 1∩C 1E =C 1,所以B 1C 1①平面CC 1E .(2)如图,以点A 为坐标原点,建立空间直角坐标系,依题意得A (0,0,0),C (1,0,1),B 1(0,2,2),C 1(1,2,1),E (0,1,0),则CE →=(-1,1,-1),B 1C →=(1,-2,-1).设平面B 1CE 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·B 1C →=0,m ·CE →=0,即⎩⎪⎨⎪⎧x -2y -z =0,-x +y -z =0,消去x 得y +2z =0, 不妨设z =1,可得m =(-3,-2,1)为平面B 1CE 的一个法向量,易得B 1C 1→=(1,0,-1),设直线B 1C 1与平面B 1CE 所成角为θ,则sin θ=|cos 〈m ,B 1C 1→〉|=⎪⎪⎪⎪⎪⎪m ·B 1C 1→|m |·|B 1C 1→|=⎪⎪⎪⎪⎪⎪-414×2=277,故直线B 1C 1与平面B 1CE 所成角的正弦值为277. 题型二 平面图形的折叠问题【解法】解决平面图形翻折问题的关键是抓住“折痕”,准确把握平面图形翻折前后的两个“不变”.(1)与折痕垂直的线段,翻折前后垂直关系不改变;(2)与折痕平行的线段,翻折前后平行关系不改变.【例1】如图,四边形ABCD 为正方形,E ,F 分别为AD ,BC 的中点,以DF 为折痕把①DFC 折起,使点C 到达点P 的位置,且PF ①BF .(1)证明:平面PEF ①平面ABFD ;(2)求DP 与平面ABFD 所成角的正弦值.【解题思路】(1)①翻折前后的不变关系,四边形ABFE 是矩形.①证明BF ①平面PEF .①证明平面PEF ①平面ABFD .(2)解法一:①建系:借助第(1)问,过P 作平面ABFD 的垂线为z 轴,垂足为原点,EF 所在直线为y 轴,建系.①求直线DP 的方向向量和平面ABFD 的法向量.①由公式计算所求角的正弦值.解法二:①作:过P 作PH ①EF 交EF 于点H ,连接DH .①证:证明PH ①平面ABFD ,得①PDH 为直线DP 与平面ABFD 所成角.①算:在Rt①PDH 中,PD 的长度是正方形ABCD 的边长,①PHD =90°,易知要求sin①PDH ,关键是求PH ;由此想到判断①PEF 的形状,进一步想到证明PF ①平面PED .【规范解答】(1)证明:由已知可得,BF ①PF ,BF ①EF ,又PF ∩EF =F ,所以BF ①平面PEF .又BF ①平面ABFD ,所以平面PEF ①平面ABFD .(2)解法一:作PH ①EF ,垂足为H .由(1)得,PH ①平面ABFD .以H 为坐标原点,HF →的方向为y 轴正方向,建立如图所示的空间直角坐标系Hxyz ,设正方形ABCD 的边长为2.由(1)可得,DE ①PE .又DP =2,DE =1,所以PE = 3.又PF =1,EF =2,故PE ①PF .所以PH =32,EH =32,则H (0,0,0),P ⎝⎛⎭⎫0,0,32, D ⎝⎛⎭⎫-1,-32,0,DP →=⎝⎛⎭⎫1,32,32,HP →=⎝⎛⎭⎫0,0,32为平面ABFD 的一个法向量. 设DP 与平面ABFD 所成角为θ,则sin θ=|HP →·DP →||HP →||DP →|=343=34. 所以DP 与平面ABFD 所成角的正弦值为34. 解法二:因为PF ①BF ,BF ①ED ,所以PF ①ED ,又PF ①PD ,ED ∩PD =D ,所以PF ①平面PED ,所以PF ①PE ,设AB =4,则EF =4,PF =2,所以PE =23,过P 作PH ①EF 交EF 于点H ,因为平面PEF ①平面ABFD ,所以PH ①平面ABFD ,连接DH ,则①PDH 即为直线DP 与平面ABFD 所成的角,因为PE ·PF =EF ·PH ,所以PH =23×24=3, 因为PD =4,所以sin①PDH =PH PD =34, 所以DP 与平面ABFD 所成角的正弦值为34. 题型三 立体几何中的探索性问题【技巧要点】对命题条件的探索的三种途径途径一:先猜后证,即先观察与尝试给出条件再证明.途径二:先通过命题成立的必要条件探索出命题成立的条件,再证明充分性.途径三:将几何问题转化为代数问题【例1】(2020·湖北“四地七校”联考)在四棱锥P -ABCD 中,底面ABCD 是边长为22的正方形,平面P AC ①底面ABCD ,P A =PC =2 2.(1)求证:PB =PD ;(2)若点M ,N 分别是棱P A ,PC 的中点,平面DMN 与棱PB 的交点为点Q ,则在线段BC 上是否存在一点H ,使得DQ ①PH ?若存在,求BH 的长;若不存在,请说明理由.【解题思路】 (1)要证PB =PD ,想到在①PBD 中,证明BD 边上的中线垂直于BD ,联系题目条件想到用面面垂直的性质证明线面垂直.(2)借助第(1)问的垂直关系建立空间直角坐标系,求平面DMN 的法向量n ,分别依据P ,B ,Q 共线和B ,C ,H 共线,设PQ →=λPB →和BH →=tBC →,利用垂直关系列方程先求λ再求t ,确定点H 的位置.【规范解答】 (1)证明:记AC ∩BD =O ,连接PO ,①底面ABCD 为正方形,①OA =OC =OB =OD =2.①P A =PC ,①PO ①AC ,①平面P AC ①底面ABCD ,且平面P AC ∩底面ABCD =AC ,PO ①平面P AC ,①PO ①底面ABCD .①BD ①底面ABCD ,①PO ①BD .①PB =PD .(2)存在.以O 为坐标原点,射线OB ,OC ,OP 的方向分别为x 轴、y 轴、z 轴的正方向建立空间直角坐标系如图所示,由(1)可知OP =2.可得P (0,0,2),A (0,-2,0),B (2,0,0),C (0,2,0),D (-2,0,0),可得M (0,-1,1),N (0,1,1),DM →=(2,-1,1),MN →=(0,2,0).设平面DMN 的法向量n =(x ,y ,z ),①DM →·n =0,MN →·n =0,①⎩⎪⎨⎪⎧2x -y +z =0,2y =0. 令x =1,可得n =(1,0,-2).记PQ →=λPB →=(2λ,0,-2λ),可得Q (2λ,0,2-2λ),DQ →=(2λ+2,0,2-2λ),DQ →·n =0,可得2λ+2-4+4λ=0,解得λ=13. 可得DQ →=⎝⎛⎭⎫83,0,43. 记BH →=tBC →=(-2t,2t,0),可得H (2-2t,2t,0),PH →=(2-2t,2t ,-2),若DQ ①PH ,则DQ →·PH →=0,83(2-2t )+43×(-2)=0,解得t =12. 故BH = 2.故在线段BC 上存在一点H ,使得DQ ①PH ,此时BH= 2.【例2】如图,在四棱锥PABCD中,P A①平面ABCD,底面ABCD为菱形,E为CD的中点.(1)求证:BD①平面P AC;(2)若①ABC=60°,求证:平面P AB①平面P AE;(3)棱PB上是否存在点F,使得CF①平面P AE?说明理由.【解】(1)证明:因为P A①平面ABCD,所以P A①BD.因为底面ABCD为菱形,所以BD①A C.又P A∩AC=A,所以BD①平面P A C.(2)证明:因为P A①平面ABCD,AE①平面ABCD,所以P A①AE.因为底面ABCD为菱形,①ABC=60°,且E为CD的中点,所以AE①CD,所以AB①AE.又AB∩P A=A,所以AE ①平面P AB .因为AE ①平面P AE ,所以平面P AB ①平面P AE .(3)棱PB 上存在点F ,使得CF ①平面P AE .取F 为PB 的中点,取G 为P A 的中点,连接CF ,FG ,EG .则FG ①AB ,且FG =12AB . 因为底面ABCD 为菱形,且E 为CD 的中点,所以CE ①AB ,且CE =12AB . 所以FG ①CE ,且FG =CE .所以四边形CEGF 为平行四边形.所以CF ①EG .因为CF ①平面P AE ,EG ①平面P AE ,所以CF ①平面P AE .【例3】图1是由矩形ADEB ,Rt①ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,①FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图2.(1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ①平面BCGE ;(2)求图2中的二面角B -CG -A 的大小.【解析】:(1)证明:由已知得AD ①BE ,CG ①BE ,所以AD ①CG ,故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ①BE ,AB ①BC ,故AB ①平面BCGE .又因为AB ①平面ABC , 所以平面ABC ①平面BCGE .(2)作EH ①BC ,垂足为H .因为EH ①平面BCGE ,平面BCGE ①平面ABC ,所以EH ①平面ABC .由已知,菱形BCGE 的边长为2,①EBC =60°,可求得BH =1,EH = 3.以H 为坐标原点,HC →的方向为x 轴的正方向,建立如图所示的空间直角坐标系H xyz ,则A (-1,1,0),C (1,0,0),G (2,0,3),CG →=(1,0,3),AC →=(2,-1,0).设平面ACGD 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧CG →·n =0AC →·n =0,即⎩⎨⎧x +3z =0,2x -y =0. 所以可取n =(3,6,-3).又平面BCGE 的法向量可取为m =(0,1,0),所以cos n ,m =n ·m |n ||m |=32. 因此二面角B CG A 的大小为30°.三、高效训练突破1.(2020·深圳模拟)已知四棱锥PABCD,底面ABCD为菱形,PD=PB,H为PC上的点,过AH的平面分别交PB,PD于点M,N,且BD①平面AMHN.(1)证明:MN①PC;(2)当H为PC的中点,P A=PC=3AB,P A与平面ABCD所成的角为60°,求AD与平面AMHN所成角的正弦值.【解析】(1)证明:连接AC、BD且AC∩BD=O,连接PO.因为ABCD为菱形,所以BD①AC,因为PD=PB,所以PO①BD,因为AC∩PO=O且AC、PO①平面P AC,所以BD①平面P AC,因为PC①平面P AC,所以BD①PC,因为BD①平面AMHN,且平面AMHN∩平面PBD=MN,所以BD①MN,MN①平面P AC,所以MN①P C.(2)由(1)知BD ①AC 且PO ①BD ,因为P A =PC ,且O 为AC 的中点,所以PO ①AC ,所以PO ①平面ABCD ,所以P A 与平面ABCD 所成的角为①P AO ,所以①P AO =60°,所以AO =12P A ,PO =32P A , 因为P A =3AB ,所以BO =36P A . 以OA →,OD →,OP →分别为x ,y ,z 轴,建立空间直角坐标系,如图所示.设P A =2,所以O (0,0,0),A (1,0,0),B (0,-33,0),C (-1,0,0),D (0,33,0),P (0,0,3),H (-12,0,32), 所以BD →=(0,233,0),AH →=(-32,0,32),AD →=(-1,33,0). 设平面AMHN 的法向量为n =(x ,y ,z ),所以⎩⎪⎨⎪⎧n ·BD →=0,n ·AH →=0,即⎩⎨⎧233y =0,-32x +32z =0, 令x =2,则y =0,z =23,所以n =(2,0,23),设AD 与平面AMHN 所成角为θ,所以sin θ=|cos 〈n ,AD →〉|=|n ·AD →|n ||AD →||=34. 所以AD 与平面AMHN 所成角的正弦值为34. 2.(2020·河南联考)如图所示,在四棱锥P -ABCD 中,底面ABCD 为平行四边形,平面P AD ①平面ABCD ,①P AD 是边长为4的等边三角形,BC ①PB ,E 是AD 的中点.(1)求证:BE ①PD ;(2)若直线AB 与平面P AD 所成角的正弦值为154,求平面P AD 与平面PBC 所成的锐二面角的余弦值. 【解析】:(1)证明:因为①P AD 是等边三角形,E 是AD 的中点,所以PE ①AD .又平面P AD ①平面ABCD ,平面P AD ∩平面ABCD =AD ,PE ①平面P AD ,所以PE ①平面ABCD ,所以PE ①BC ,PE ①BE .又BC ①PB ,PB ∩PE =P ,所以BC ①平面PBE ,所以BC ①BE .又BC ①AD ,所以AD ①BE .又AD ∩PE =E 且AD ,PE ①平面P AD ,所以BE ①平面P AD ,所以BE ①PD .(2)由(1)得BE ①平面P AD ,所以①BAE 就是直线AB 与平面P AD 所成的角.因为直线AB 与平面P AD 所成角的正弦值为154, 即sin①BAE =154 ,所以cos①BAE =14. 所以cos①BAE =AE AB =2AB =14,解得AB =8,则BE =AB 2-AE 2=215.由(1)得EA ,EB ,EP 两两垂直,所以以E 为坐标原点,EA ,EB ,EP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则点P (0,0,23),A (2,0,0),D (-2,0,0),B (0,215,0),C (-4,215,0),所以PB →=(0,215,-23),PC →=(-4,215,-23).设平面PBC 的法向量为m =(x ,y ,z ),由⎩⎪⎨⎪⎧PB →·m =0,PC →·m =0,得⎩⎨⎧215y -23z =0,-4x +215y -23z =0, 解得⎩⎨⎧x =0,z =5y . 令y =1,可得平面PBC 的一个法向量为m =(0,1,5).易知平面P AD 的一个法向量为n =(0,1,0),设平面P AD 与平面PBC 所成的锐二面角的大小为θ,则cos θ=⎪⎪⎪⎪m ·n |m ||n |=⎪⎪⎪⎪⎪⎪(0,1,5)·(0,1,0)6×1=66. 所以平面P AD 与平面PBC 所成的锐二面角的余弦值为66. 3.(2020·云南师范大学附属中学3月月考)如图,在直三棱柱ABC A 1B 1C 1中,①ABC 是边长为2的正三角形,AA 1=26,D 是CC 1的中点,E 是A 1B 1的中点.(1)证明:DE ①平面A 1BC;(2)求点A 到平面A 1BC 的距离.【解析】 (1)证明:如图取A 1B 的中点F ,连接FC ,FE .因为E ,F 分别是A 1B 1,A 1B 的中点,所以EF ①BB 1,且EF =12BB 1. 又在平行四边形BB 1C 1C 中,D 是CC 1的中点,所以CD ①BB 1,且CD =12BB 1,所以CD ①EF ,且CD =EF . 所以四边形CFED 是平行四边形,所以DE ①CF .因为DE ①/平面A 1BC ,CF ①平面A 1BC ,所以DE ①平面A 1BC .(2)法一:(等体积法)因为BC =AC =AB =2,AA 1=26,三棱柱ABC A 1B 1C 1为直三棱柱,所以V 三棱锥A 1-ABC =13S ①ABC ×AA 1=13×34×22×26=2 2. 又在①A 1BC 中,A 1B =A 1C =27,BC =2,BC 边上的高h = A 1B 2-⎝⎛⎭⎫12BC 2=33, 所以S ①A 1BC =12BC ·h =3 3. 设点A 到平面A 1BC 的距离为d ,则V 三棱锥A -A 1BC =13S ①A 1BC ×d =13×33×d =3d . 因为V 三棱锥A 1-ABC =V 三棱锥A -A 1BC ,所以22=3d ,解得d =263, 所以点A 到平面A 1BC 的距离为263. 法二:(向量法)由题意知,三棱柱ABC A 1B 1C 1是正三棱柱.取AB 的中点O ,连接OC ,OE .因为AC =BC ,所以CO ①AB .又平面ABC ①平面ABB 1A 1,平面ABC ∩平面ABB 1A 1=AB ,所以CO ①平面ABB 1A 1.因为O 为AB 的中点,E 为A 1B 1的中点,所以OE ①AB ,所以OC ,OA ,OE 两两垂直.如图,以O 为坐标原点,以OA ,OE ,OC 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,则C (0,0,3),A (1,0,0),A 1(1,26,0),B (-1,0,0).则BA 1→=(2,26,0),BC →=(1,0,3).设平面A 1BC 的法向量为n =(x ,y ,z ),则由⎩⎪⎨⎪⎧n ①BA 1→,n ①BC →,可得⎩⎪⎨⎪⎧n ·BA 1→=2x +26y =0,n ·BC →=x +3z =0,整理得⎩⎨⎧x +6y =0,x +3z =0,令x =6,则y =-1,z =- 2. 所以n =(6,-1,-2)为平面A 1BC 的一个法向量.而BA →=(2,0,0),所以点A 到平面A 1BC 的距离d =|BA →·n ||n |=6×26+1+2=263. 4.(2020·湖北十堰4月调研)如图,在三棱锥P -ABC 中,M 为AC 的中点,P A ①PC ,AB ①BC ,AB =BC ,PB =2,AC =2,①P AC =30°.(1)证明:BM ①平面P AC ;(2)求二面角B -P A -C 的余弦值.【答案】:见解析(1)证明:因为P A ①PC ,AB ①BC ,所以MP =MB =12AC =1,又MP 2+MB 2=BP 2,所以MP ①MB .因为AB =BC ,M 为AC 的中点,所以BM ①AC , 又AC ∩MP =M ,所以BM ①平面P AC .(2)法一:取MC 的中点O ,连接PO ,取BC 的中点E ,连接EO ,则OE ①BM ,从而OE ①AC . 因为P A ①PC ,①P AC =30°,所以MP =MC =PC =1. 又O 为MC 的中点,所以PO ①AC .由(1)知BM ①平面P AC ,OP ①平面P AC ,所以BM ①PO . 又BM ∩AC =M ,所以PO ①平面ABC .以O 为坐标原点,OA ,OE ,OP 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系,如图所示, 由题意知A ⎝⎛⎭⎫32,0,0,B ⎝⎛⎭⎫12,1,0,P ⎝⎛⎭⎫0,0,32,BP →=⎝⎛⎭⎫-12,-1,32,BA →=(1,-1,0), 设平面APB 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧n ·BP→=-12x -y +32z =0,n ·BA →=x -y =0,令x =1,得n =(1,1,3)为平面APB 的一个法向量,易得平面P AC 的一个法向量为π=(0,1,0),cos 〈n ,π〉=55, 由图知二面角B -P A -C 为锐角,所以二面角B -P A -C 的余弦值为55. 法二:取P A 的中点H ,连接HM ,HB ,因为M 为AC 的中点,所以HM ①PC ,又P A ①PC ,所以HM ①P A .由(1)知BM ①平面P AC ,则BH ①P A , 所以①BHM 为二面角B -P A -C 的平面角.因为AC =2,P A ①PC ,①P AC =30°,所以HM =12PC =12.又BM =1,则BH =BM 2+HM 2=52, 所以cos①BHM =HM BH =55,即二面角B -P A -C 的余弦值为55.5.(2020·合肥模拟)如图,在多面体ABCDEF 中,四边形ABCD 是正方形,BF ①平面ABCD ,DE ①平面ABCD ,BF =DE ,M 为棱AE 的中点.(1)求证:平面BDM ①平面EFC ;(2)若DE =2AB ,求直线AE 与平面BDM 所成角的正弦值. 【答案】:见解析(1)证明:连接AC ,交BD 于点N ,连接MN , 则N 为AC 的中点,又M 为AE 的中点,所以MN ①EC . 因为MN ①平面EFC ,EC ①平面EFC , 所以MN ①平面EFC .因为BF ,DE 都垂直底面ABCD ,所以BF ①DE . 因为BF =DE ,所以四边形BDEF 为平行四边形,所以BD ①EF .因为BD ①平面EFC ,EF ①平面EFC , 所以BD ①平面EFC .又MN ∩BD =N ,所以平面BDM ①平面EFC . (2)因为DE ①平面ABCD ,四边形ABCD 是正方形,所以DA ,DC ,DE 两两垂直,如图,建立空间直角坐标系D xyz .设AB =2,则DE =4,从而D (0,0,0),B (2,2,0),M (1,0,2),A (2,0,0),E (0,0,4), 所以DB →=(2,2,0),DM →=(1,0,2), 设平面BDM 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧n ·DB →=0,n ·DM →=0,得⎩⎪⎨⎪⎧2x +2y =0,x +2z =0.令x =2,则y =-2,z =-1,从而n =(2,-2,-1)为平面BDM 的一个法向量. 因为AE →=(-2,0,4),设直线AE 与平面BDM 所成的角为θ,则 sin θ=|cos 〈n ·AE →〉|=⎪⎪⎪⎪⎪⎪n ·AE →|n |·|AE →|=4515, 所以直线AE 与平面BDM 所成角的正弦值为4515.6.(2020·河南郑州三测)如图①,①ABC 中,AB =BC =2,①ABC =90°,E ,F 分别为边AB ,AC 的中点,以EF 为折痕把①AEF 折起,使点A 到达点P 的位置(如图①),且PB =BE .(1)证明:EF ①平面PBE ;(2)设N 为线段PF 上的动点(包含端点),求直线BN 与平面PCF 所成角的正弦值的最大值. 【解析】:(1)证明:因为E ,F 分别为边AB ,AC 的中点,所以EF ①BC . 因为①ABC =90°,所以EF ①BE ,EF ①PE ,又BE ∩PE =E ,所以EF ①平面PBE . (2)取BE 的中点O ,连接PO ,因为PB =BE =PE ,所以PO ①BE .由(1)知EF ①平面PBE ,EF ①平面BCFE ,所以平面PBE ①平面BCFE . 又PO ①平面PBE ,平面PBE ∩平面BCFE =BE ,所以PO ①平面BCFE .过点O 作OM ①BC 交CF 于点M ,分别以OB ,OM ,OP 所在的直线为x 轴,y 轴,z 轴建立空间直角坐标系,如图所示,则B ⎝⎛⎭⎫12,0,0,P ⎝⎛⎭⎫0,0,32,C ⎝⎛⎭⎫12,2,0, F ⎝⎛⎭⎫-12,1,0,PC →=⎝⎛⎭⎫12,2,-32, PF →=⎝⎛⎭⎫-12,1,-32,由N 为线段PF 上一动点,得PN →=λPF →(0≤λ≤1),则可得N ⎝⎛⎭⎫-λ2,λ,32(1-λ),BN →=⎝⎛⎭⎫-λ+12,λ,32(1-λ).设平面PCF 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧PC →·m =0,PF →·m =0,即⎩⎨⎧12x +2y -32z =0,-12x +y -32z =0,取y =1,则x =-1,z =3,所以m =(-1,1,3)为平面PCF 的一个法向量.设直线BN 与平面PCF 所成的角为θ, 则sin θ=|cos 〈BN →,m 〉|=|BN →·m ||BN →|·|m |=25·2λ2-λ+1=25·2⎝⎛⎭⎫λ-142+78≤25·78=47035(当且仅当λ=14时取等号),所以直线BN 与平面PCF 所成角的正弦值的最大值为47035.7.(2020·山东淄博三模)如图①,已知正方形ABCD 的边长为4,E ,F 分别为AD ,BC 的中点,将正方形ABCD 沿EF 折成如图①所示的二面角,且二面角的大小为60°,点M 在线段AB 上(包含端点),连接AD .(1)若M 为AB 的中点,直线MF 与平面ADE 的交点为O ,试确定点O 的位置,并证明直线OD ①平面EMC ; (2)是否存在点M ,使得直线DE 与平面EMC 所成的角为60°?若存在,求此时二面角M EC F 的余弦值;若不存在,说明理由. 【答案】见解析【解析】:(1)因为直线MF ①平面ABFE ,故点O 在平面ABFE 内,也在平面ADE 内, 所以点O 在平面ABFE 与平面ADE的交线(即直线AE )上(如图所示).因为AO ①BF ,M 为AB 的中点,所以①OAM ①①FBM ,所以OM =MF ,AO =BF ,所以AO =2. 故点O 在EA 的延长线上且与点A 间的距离为2. 连接DF ,交EC 于点N ,因为四边形CDEF 为矩形, 所以N 是EC 的中点.连接MN ,则MN 为①DOF 的中位线,所以MN ①OD ,又MN ①平面EMC ,OD ①/ 平面EMC ,所以直线OD ①平面EMC . (2)由已知可得EF ①AE ,EF ①DE ,又AE ∩DE =E ,所以EF ①平面ADE .所以平面ABFE ①平面ADE ,易知①ADE 为等边三角形,取AE 的中点H ,则易得DH ①平面ABFE ,以H 为坐标原点,建立如图所示的空间直角坐标系,则E (-1,0,0),D (0,0,3),C (0,4,3),F (-1,4,0),所以ED →=(1,0,3),EC →=(1,4,3). 设M (1,t ,0)(0≤t ≤4),则EM →=(2,t ,0),设平面EMC 的法向量为m =(x ,y ,z ),则⎩⎪⎨⎪⎧m ·EM →=0,m ·EC →=0①⎩⎨⎧2x +ty =0,x +4y +3z =0,取y =-2,则x =t ,z =8-t 3,所以m =⎝ ⎛⎭⎪⎫t ,-2,8-t 3为平面EMC 的一个法向量.要使直线DE 与平面EMC 所成的角为60°,则82t 2+4+(8-t )23=32,所以23t 2-4t +19=32,整理得t 2-4t +3=0, 解得t=1或t =3,所以存在点M ,使得直线DE 与平面EMC 所成的角为60°,取ED 的中点Q ,连接QA ,则QA →为平面CEF 的法向量, 易得Q ⎝⎛⎭⎫-12,0,32,A (1,0,0),所以QA →=⎝⎛⎭⎫32,0,-32.设二面角M -EC -F 的大小为θ, 则|cos θ|=|QA →·m ||QA →|·|m |=|2t -4|3t 2+4+(8-t )23=|t -2|t2-4t +19. 因为当t =2时,cos θ=0,平面EMC ①平面CDEF ,所以当t =1时,cos θ=-14,θ为钝角;当t =3时,cos θ=14,θ为锐角.综上,二面角M -EC -F 的余弦值为±14.。
