高考立体几何大题20题汇总
高考立体几何大题及答案(理)

资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载高考立体几何大题及答案(理)地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容1.如图,四棱锥中,底面为矩形,底面,,,点在侧棱上,。
(I)证明:是侧棱的中点;求二面角的大小。
2.如图,直三棱柱ABC-A1B1C1中,AB⊥AC,D、E分别为AA1、B1C的中点,DE⊥平面BCC1(Ⅰ)证明:AB=AC (Ⅱ)设二面角A-BACBA1B1C1DED-C为60°,求B1C与平面BCD所成的角的大小3.如图,平面,,,,分别为的中点.(I)证明:平面;(II)求与平面所成角的正弦值.4.如图,四棱锥的底面是正方形,,点E在棱PB上.(Ⅰ)求证:平面;(Ⅱ)当且E为PB的中点时,求AE与平面PDB所成的角的大小.5.如图,在四棱锥中,底面是矩形,平面,,.以的中点为球心、为直径的球面交于点.(1)求证:平面⊥平面;(2)求直线与平面所成的角;(3)求点到平面的距离.6.如图,正方形所在平面与平面四边形所在平面互相垂直,△是等腰直角三角形,(I)求证:;(II)设线段、的中点分别为、,求证:∥(III)求二面角的大小。
7.如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD =AD=a,点E是SD上的点,且DE=a(0<≦1). (Ⅰ)求证:对任意的(0、1),都有AC⊥BE:(Ⅱ)若二面角C-AE-D的大小为600C,求的值。
8.如图3,在正三棱柱中,AB=4, ,点D是BC的中点,点E 在AC上,且DEE.(Ⅰ)证明:平面平面; (Ⅱ)求直线AD 和平面所成角的正弦值。
9.如图,正方形所在平面与平面四边形所在平面互相垂直,△是等腰直角三角形,(I)求证:;(II)设线段、的中点分别为、,求证:∥(III)求二面角的大小。
浙江省历年高考立体几何大题总汇(题目及答案)

1.(本题满分15分)如图,平面⊥平面,是以为斜边的等腰直角PAC ABC ABC ∆AC 三角形。
分别为的中点,。
,,E F O ,,PA PB PC 16,10AC PA PC ===(I ) 设是的中点,证明:平面;C OC //PC BOE (II )证明:在内存在一点,使⊥平面,并求点到,的距ABO ∆M FM BOE M OA OB 离。
2.如图,在棱长为1的正方体ABCD -A 1B 1C 1D 1中,P 是侧棱CC 1上的一点,CP=m ,(Ⅰ)试确定m ,使得直线AP 与平面BDB 1D 1所成角的正切值为(Ⅱ)在线段A 1C 1上是否存在一个定点Q ,使得对任意的m ,D 1Q 在平面APD 1上的射影垂直于AP ,并证明你的结论。
3. 如图甲,△ABC 是边长为6的等边三角形,E ,D 分别为AB 、AC 靠近B 、C 的三等分点,点G 为BC 边的中点.线段AG 交线段ED 于F 点,将△AED 沿ED 翻折,使平面AED ⊥平面BCDE ,连接AB 、AC 、AG 形成如图乙所示的几何体。
(I )求证BC ⊥平面AFG ;(II )求二面角B -AE -D的余弦值..4在如图所示的几何体中,平面ABC ,平面ABC ,,EA ⊥DB ⊥AC BC ⊥,M 是AB 的中点.2AC BC BD AE ===(1)求证:;CM EM ⊥(2)求CM 与平面CDE 所成的角5.如图,矩形和梯形所在平面互相垂直,,ABCD BEFC BE CF ∥,,.90BCF CEF ∠=∠=o AD =2EF =(Ⅰ)求证:平面;AE ∥DCF (Ⅱ)当的长为何值时,二面角的大小为?AB A EF C --60o6. 如图,在矩形ABCD 中,点E ,F 分别在线段AB ,AD 上,AE=EB=AF=沿.432=FD 直线EF 将翻折成使平面平面BEF.AEF ∆,'EF A ∆⊥EF A ' (I )求二面角的余弦值;C FD A --' (II )点M ,N 分别在线段FD ,BC 上,若沿直线MN 将四边形MNCD 向上翻折,使C与重合,求线段FM 的长.'A EMACBD DABEFC(第18题)7. 如图,在三棱锥P-ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2(Ⅰ)证明:AP⊥BC;(Ⅱ)在线段AP上是否存在点M,使得二面角A-MC-B为直二面角?若存在,求出AM的长;若不存在,请说明理由。
专题20 立体几何解答题
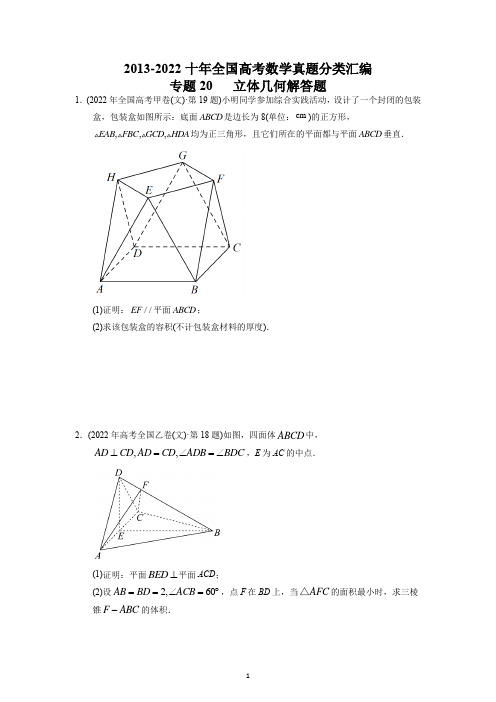
11.(2020年高考数学课标Ⅰ卷文科·第19题)如图, 为圆锥的顶点, 是圆锥底面的圆心, 是底面的内接正三角形, 为 上一点,∠APC=90°.
(1)证明:平面PAB⊥平面PAC;
(2)设DO= ,圆锥 侧面积为 ,求三棱锥P−ABC的体积.
12.(2020年高考数学课标Ⅱ卷文科·第20题)如图,已知三棱柱ABC–A1B1C1 底面是正三角形,侧面BB1C1C是矩形,M,N分别为BC,B1C1的中点,P为AM上一点.过B1C1和P的平面交AB于E,交AC于F.
(Ⅱ)求平面 把该长方体分成的两部分体积的比值.
27.(2015年高考数学课标Ⅰ卷文科·第18题)(本小题满分12分)如图四边形ABCD 为菱形, 为 与 交点, ,
( )证明:平面 平面 ;
( )若 , 三棱锥 的体积为 ,求该三棱锥的侧面积.
28.(2014年高考数学课标Ⅱ卷文科·第18题)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
( )证明G是AB的中点;
( )在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
26.(2015年高考数学课标Ⅱ卷文科·第19题)(本小题满分12分)如图,长方体 中 ,点 分别在 上, 过点 的平面 与此长方体的面相交,交线围成一个正方形.
(Ⅰ)在图中画出这个正方形(不必说明画法与理由);
(1)证明: 平面 ;
(2)求点 到平面 的距离.
17.(2018年高考数学课标Ⅲ卷文科·第19题)(12分)如图,矩形 所在平面与半圆弧 所在平面垂直, 是 上异于 , 的点.
(1)证明:平面 平面 ;
(2)在线段 上是否存在点 ,使得 平面 ?说明理由.
高考立体几何题大全

高考立体几何题大全一、一个正方体的棱长为2,若在其一个顶点处削去一个棱长为1的小正方体,则剩余部分的体积为多少?A. 6B. 7C. 8-√3D. 8-1/3(答案)B。
解析:原正方体的体积为2的三次方等于8,削去的小正方体的体积为1的三次方等于1,但由于是在顶点处削去,会同时影响到三个相邻的小正方体,因此实际减少的体积只有一个小正方体的三分之一,即1/3。
所以剩余部分的体积为8-1/3=7+2/3,取整数部分为7。
二、一个圆柱的底面半径为r,高为h,若将其侧面展开,得到的矩形的长与宽分别是什么?A. 2πr, hB. πr, 2hC. r, 2πhD. 2r, πh(答案)A。
解析:圆柱的侧面展开后是一个矩形,其长等于圆柱底面的周长,即2πr,宽等于圆柱的高,即h。
三、一个圆锥的底面半径为3,高为4,则它的侧面积为多少?A. 12πB. 15πC. 20πD. 24π(答案)B。
解析:圆锥的母线长可以通过勾股定理求得,为根号下(3的平方+4的平方)=5。
圆锥的侧面积公式为π乘以底面半径乘以母线长,即π35=15π。
四、一个球体的半径为R,若在其内部挖去一个半径为R/2的小球,则剩余部分的体积与小球体积的比值为多少?A. 7B. 8-1C. 8D. 9(答案)A。
解析:大球的体积为(4/3)πR的三次方,小球的体积为(4/3)π(R/2)的三次方,即(1/8)(4/3)πR的三次方。
剩余部分的体积为大球体积减去小球体积,即(7/8)(4/3)πR 的三次方。
所以剩余部分的体积与小球体积的比值为((7/8)(4/3)πR的三次方)除以((1/8)(4/3)πR的三次方)=7。
五、一个长方体的长、宽、高分别为a、b、c,若将其切割成若干个小正方体,每个小正方体的棱长为1,则最多可以切割成多少个小正方体?A. abcB. a+b+cC. abcD. (a+b+c)/3(答案)C。
解析:长方体的体积为长乘以宽乘以高,即abc。
2024届新高考数学大题精选30题--立体几何含答案
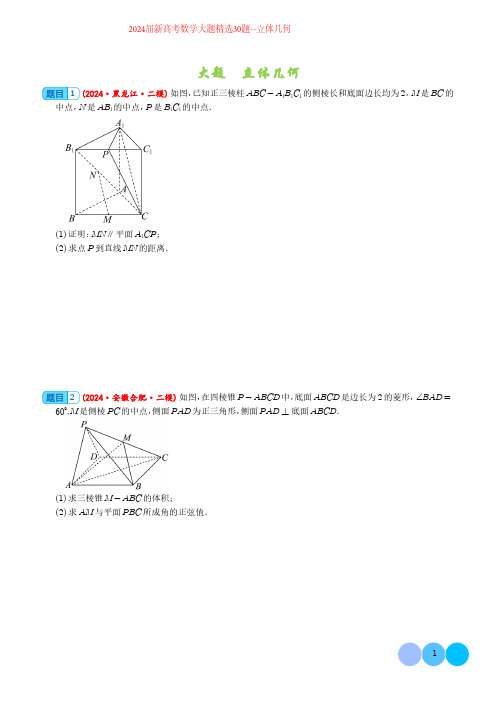
大题立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,M是BC的中点,N是AB1的中点,P是B1C1的中点.(1)证明:MN⎳平面A1CP;(2)求点P到直线MN 的距离.2(2024·安徽合肥·二模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,∠BAD=60°,M是侧棱PC的中点,侧面PAD为正三角形,侧面PAD⊥底面ABCD.(1)求三棱锥M-ABC的体积;(2)求AM与平面PBC所成角的正弦值.2024届新高考数学大题精选30题--立体几何3(2023·福建福州·模拟预测)如图,在三棱柱ABC-A1B1C1中,平面AA1C1C⊥平面ABC,AB= AC=BC=AA1=2,A1B=6.(1)设D为AC中点,证明:AC⊥平面A1DB;(2)求平面A1AB1与平面ACC1A1夹角的余弦值.4(2024·山西晋中·三模)如图,在六面体ABCDE中,BC=BD=6,EC⊥ED,且EC=ED= 2,AB平行于平面CDE,AE平行于平面BCD,AE⊥CD.(1)证明:平面ABE⊥平面CDE;(2)若点A到直线CD的距离为22,F为棱AE的中点,求平面BDF与平面BCD夹角的余弦值.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC-A1B1C1中,A1在平面ABC内的射影O在棱AC的中点处,P为棱A1B1(包含端点)上的动点.(1)求点P到平面ABC1的距离;(2)若AP⊥平面α,求直线BC1与平面α所成角的正弦值的取值范围.6(2024·重庆·模拟预测)在如图所示的四棱锥P-ABCD中,已知AB∥CD,∠BAD=90°,CD= 2AB,△PAB是正三角形,点M在侧棱PB上且使得PD⎳平面AMC.(1)证明:PM=2BM;(2)若侧面PAB⊥底面ABCD,CM与底面ABCD所成角的正切值为311,求二面角P-AC-B的余弦值.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.8(2024·重庆·模拟预测)如图,ACDE为菱形,AC=BC=2,∠ACB=120°,平面ACDE⊥平面ABC,点F在AB上,且AF=2FB,M,N分别在直线CD,AB上.(1)求证:CF⊥平面ACDE;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC=60°,MN为直线CD,AB的公垂线,求ANAF的值;(3)记直线BE与平面ABC所成角为α,若tanα>217,求平面BCD与平面CFD所成角余弦值的范围.9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF 上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1 ,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.13(2024·广东广州·一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,△DCP是等边三角形,∠DCB=∠PCB=π4,点M,N分别为DP和AB的中点.(1)求证:MN⎳平面PBC;(2)求证:平面PBC⊥平面ABCD;(3)求CM与平面PAD所成角的正弦值.14(2024·广东梅州·二模)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD 为直角梯形,△PAD为等边三角形,AD⎳BC,AD⊥AB,AD=AB=2BC=2.(1)求证:AD⊥PC;(2)点N在棱PC上运动,求△ADN面积的最小值;(3)点M为PB的中点,在棱PC上找一点Q,使得AM⎳平面BDQ,求PQQC的值.15(2024·广东广州·模拟预测)如图所示,圆台O1O2的轴截面A1ACC1为等腰梯形,AC=2AA1= 2A1C1=4,B为底面圆周上异于A,C的点,且AB=BC,P是线段BC的中点.(1)求证:C1P⎳平面A1AB.(2)求平面A1AB与平面C1CB夹角的余弦值.16(2024·广东深圳·二模)如图,三棱柱ABC-A1B1C1中,侧面BB1C1C⊥底面ABC,且AB= AC,A1B=A1C.(1)证明:AA1⊥平面ABC;(2)若AA1=BC=2,∠BAC=90°,求平面A1BC与平面A1BC1夹角的余弦值.17(2024·河北保定·二模)如图,在四棱锥P -ABCD 中,平面PCD 内存在一条直线EF 与AB 平行,PA ⊥平面ABCD ,直线PC 与平面ABCD 所成的角的正切值为32,PA =BC =23,CD =2AB =4.(1)证明:四边形ABCD 是直角梯形.(2)若点E 满足PE =2ED ,求二面角P -EF -B 的正弦值.18(2024·湖南衡阳·模拟预测)如图,在圆锥PO 中,P 是圆锥的顶点,O 是圆锥底面圆的圆心,AC 是圆锥底面圆的直径,等边三角形ABD 是圆锥底面圆O 的内接三角形,E 是圆锥母线PC 的中点,PO =6,AC =4.(1)求证:平面BED ⊥平面ABD ;(2)设点M 在线段PO 上,且OM =2,求直线DM 与平面ABE 所成角的正弦值.19(2024·湖南岳阳·三模)已知四棱锥P -ABCD 的底面ABCD 是边长为4的菱形,∠DAB =60°,PA =PC ,PB =PD =210,M 是线段PC 上的点,且PC =4MC .(1)证明:PC ⊥平面BDM ;(2)点E 在直线DM 上,求BE 与平面ABCD 所成角的最大值.20(2024·湖南·二模)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是边长为2的菱形,∠ABC =60°,BD 1⊥平面A 1C 1D .(1)求四棱柱ABCD -A 1B 1C 1D 1的体积;(2)设点D 1关于平面A 1C 1D 的对称点为E ,点E 和点C 1关于平面α对称(E 和α未在图中标出),求平面A 1C 1D 与平面α所成锐二面角的大小.21(2024·山东济南·二模)如图,在四棱锥P-ABCD中,四边形ABCD为直角梯形,AB∥CD,∠DAB=∠PCB=60°,CD=1,AB=3,PC=23,平面PCB⊥平面ABCD,F为线段BC的中点,E为线段PF上一点.(1)证明:PF⊥AD;(2)当EF为何值时,直线BE与平面PAD夹角的正弦值为74.22(2024·山东潍坊·二模)如图1,在平行四边形ABCD中,AB=2BC=4,∠ABC=60°,E为CD 的中点,将△ADE沿AE折起,连结BD,CD,且BD=4,如图2.(1)求证:图2中的平面ADE⊥平面ABCE;(2)在图2中,若点F在棱BD上,直线AF与平面ABCE所成的角的正弦值为3010,求点F到平面DEC 的距离.23(2024·福建·模拟预测)如图,在三棱锥P-ABC中,PA⊥PB,AB⊥BC,AB=3,BC=6,已知二面角P-AB-C的大小为θ,∠PAB=θ.(1)求点P到平面ABC的距离;(2)当三棱锥P-ABC的体积取得最大值时,求:(Ⅰ)二面角P-AB-C的余弦值;(Ⅱ)直线PC与平面PAB所成角.24(2024·浙江杭州·二模)如图,在多面体ABCDPQ中,底面ABCD是平行四边形,∠DAB=60°, BC=2PQ=4AB=4,M为BC的中点,PQ∥BC,PD⊥DC,QB⊥MD.(1)证明:∠ABQ=90°;(2)若多面体ABCDPQ的体积为152,求平面PCD与平面QAB夹角的余弦值.25(2024·浙江嘉兴·二模)在如图所示的几何体中,四边形ABCD为平行四边形,PA⊥平面ABCD,PA∥QD,BC=2AB=2PA=2,∠ABC=60°.(1)证明:平面PCD⊥平面PAC;(2)若PQ=22,求平面PCQ与平面DCQ夹角的余弦值.26(2024·浙江绍兴·二模)如图,在三棱锥P-ABC中,AB=4,AC=2,∠CAB=60°,BC⊥AP.(1)证明:平面ACP⊥平面ABC;(2)若PA=2,PB=4,求二面角P-AB-C的平面角的正切值.27(2024·河北沧州·一模)如图,在正三棱锥A -BCD 中,BC =CD =BD =4,点P 满足AP=λAC ,λ∈(0,1),过点P 作平面α分别与棱AB ,BD ,CD 交于Q ,S ,T 三点,且AD ⎳α,BC ⎳α.(1)证明:∀λ∈(0,1),四边形PQST 总是矩形;(2)若AC =4,求四棱锥C -PQST 体积的最大值.28(2024·湖北·二模)如图1.在菱形ABCD 中,∠ABC =120°,AB =4,AE =λAD ,AF =λAB(0<λ<1),沿EF 将△AEF 向上折起得到棱锥P -BCDEP .如图2所示,设二面角P -EF -B 的平面角为θ.(1)当λ为何值时,三棱锥P -BCD 和四棱锥P -BDEF 的体积之比为95(2)当θ为何值时,∀λ∈0,1 ,平面PEF 与平面PFB 的夹角φ的余弦值为5529(2024·湖北·模拟预测)空间中有一个平面α和两条直线m ,n ,其中m ,n 与α的交点分别为A ,B ,AB =1,设直线m 与n 之间的夹角为π3,(1)如图1,若直线m ,n 交于点C ,求点C 到平面α距离的最大值;(2)如图2,若直线m ,n 互为异面直线,直线m 上一点P 和直线n 上一点Q 满足PQ ⎳α,PQ ⊥n 且PQ ⊥m ,(i )求直线m ,n 与平面α的夹角之和;(ii )设PQ =d 0<d <1 ,求点P 到平面α距离的最大值关于d 的函数f d .30(2024·浙江绍兴·模拟预测)如图所示,四棱台ABCD -A 1B 1C 1D 1,底面ABCD 为一个菱形,且∠BAD =120°. 底面与顶面的对角线交点分别为O ,O 1. AB =2A 1B 1=2,BB 1=DD 1=392,AA 1与底面夹角余弦值为3737.(1)证明:OO 1⊥平面ABCD ;(2)现将顶面绕OO 1旋转θ角,旋转方向为自上而下看的逆时针方向. 此时使得底面与DC 1的夹角正弦值为64343,此时求θ的值(θ<90°);(3)求旋转后AA 1与BB 1的夹角余弦值.大题 立体几何1(2024·黑龙江·二模)如图,已知正三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2,M 是BC 的中点,N 是AB 1的中点,P 是B 1C 1的中点.(1)证明:MN ⎳平面A 1CP ;(2)求点P 到直线MN 的距离.【答案】(1)证明见解析(2)3【分析】(1)建立如图空间直角坐标系A -xyz ,设平面A 1CP 的一个法向量为n=(x ,y ,z ),利用空间向量法证明MN ⋅n=0即可;(2)利用空间向量法即可求解点线距.【详解】(1)由题意知,AA 1⊥平面ABC ,∠BAC =60°,而AB ⊂平面ABC ,所以AA 1⊥AB ,在平面ABC 内过点A 作y 轴,使得AB ⊥y 轴,建立如图空间直角坐标系A -xyz ,则A (0,0,0),B (2,0,0),C (1,3,0),A 1(0,0,2),B 1(2,0,2),得M 32,32,0,N (1,0,1),P 32,32,2,所以A 1C =(1,3,-2),A 1P =32,32,0 ,MN =-12,-32,1 ,设平面A1CP 的一个法向量为n=(x ,y ,z ),则n ⋅A 1C=x +3y -2z =0n ⋅A 1P =32x +32y =0,令x =1,得y =-3,z =-1,所以n=(1,-3,-1),所以MN ⋅n =-12×1+-32×(-3)+1×(-1)=0,又MN 不在平面A 1CP 内即MN ⎳平面A 1CP ;(2)如图,连接PM ,由(1)得PM =(0,0,-2),则MN ⋅PM =-2,MN =2,PM =2,所以点P 到直线MN 的距离为d =PM 2-MN ⋅PMPM2= 3.2(2024·安徽合肥·二模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,∠BAD =60°,M 是侧棱PC 的中点,侧面PAD 为正三角形,侧面PAD ⊥底面ABCD .(1)求三棱锥M -ABC 的体积;(2)求AM 与平面PBC 所成角的正弦值.【答案】(1)12(2)3311.【分析】(1)作出辅助线,得到线线垂直,进而得到线面垂直,由中位线得到M 到平面ABCD 的距离为32,进而由锥体体积公式求出答案;(2)证明出BO ⊥AD ,建立空间直角坐标系,求出平面的法向量,进而由法向量的夹角余弦值的绝对值求出线面角的正弦值.【详解】(1)如图所示,取AD 的中点O ,连接PO .因为△PAD 是正三角形,所以PO ⊥AD .又因为平面PAD ⊥底面ABCD ,PO ⊂平面PAD ,平面PAD ∩平面ABCD =AD ,所以PO ⊥平面ABCD ,且PO =3.又因为M 是PC 的中点,M 到平面ABCD 的距离为32,S △ABC =12×2×2×sin 2π3=3,所以三棱锥M -ABC 的体积为13×3×32=12.(2)连接BO ,BD ,因为∠BAD =π3,所以△ABD 为等边三角形,所以BO ⊥AD ,以O 为原点,OA ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系,则P 0,0,3 ,A 1,0,0 ,B 0,3,0 ,C -2,3,0 ,所以M -1,32,32 ,AM =-2,32,32,PB =0,3,-3 ,BC =-2,0,0 .设平面PBC 的法向量为n=x ,y ,z ,则PB ⋅n =0BC ⋅n =0,即3y -3z =0-2x =0 ,解得x =0,取z =1,则y =1,所以n=0,1,1 .设AM 与平面PBC 所成角为θ,则sin θ=cos AM ,n =AM ⋅nAM ⋅n=-2,32,32 ⋅0,1,14+34+34×1+1=3311.即AM 与平面PBC 所成角的正弦值为3311.3(2023·福建福州·模拟预测)如图,在三棱柱ABC -A 1B 1C 1中,平面AA 1C 1C ⊥平面ABC ,AB =AC =BC =AA 1=2,A 1B =6.(1)设D 为AC 中点,证明:AC ⊥平面A 1DB ;(2)求平面A 1AB 1与平面ACC 1A 1夹角的余弦值.【答案】(1)证明见解析;(2)55【分析】(1)根据等边三角形的性质得出BD ⊥AC ,根据平面ACC 1A 1⊥平面ABC 得出BD ⊥平面ACC 1A 1,BD ⊥A 1D ,利用勾股定理得出AC ⊥A 1D ,从而证明AC ⊥平面A 1DB ;(2)建立空间直角坐标系,利用坐标表示向量,求出平面A 1AB 1的法向量和平面ACC 1A 1的一个法向量,利用向量求平面A 1AB 1与平面ACC 1A 1的夹角余弦值.【详解】(1)证明:因为D 为AC 中点,且AB =AC =BC =2,所以在△ABC 中,有BD ⊥AC ,且BD =3,又平面ACC 1A 1⊥平面ABC ,且平面ACC 1A 1∩平面ABC =AC ,BD ⊂平面ABC ,所以BD ⊥平面ACC 1A 1,又A 1D ⊂平面ACC 1A 1,则BD ⊥A 1D ,由A 1B =6,BD =3,得A 1D =3,因为AD =1,AA 1=2,A 1D =3,所以由勾股定理,得AC ⊥A 1D ,又AC ⊥BD ,A 1D ∩BD =D ,A 1D ,BD ⊂平面A 1DB ,所以AC ⊥平面A 1DB ;(2)如图所示,以D 为原点,建立空间直角坐标系D -xyz ,可得A (1,0,0),A 1(0,0,3),B (0,3,0),则AA 1 =-1,0,3 ,AB=-1,3,0 ,设平面A 1AB 1的法向量为n=(x ,y ,z ),由n ⋅AA 1=-x +3z =0n ⋅AB=-x +3y =0,令x =3,得y =1,z =1,所以n=3,1,1 ,由(1)知,BD ⊥平面ACC 1A 1,所以平面ACC 1A 1的一个法向量为BD=(0,-3,0),记平面A 1AB 1与平面ACC 1A 1的夹角为α,则cos α=|n ⋅BD ||n ||BD |=35×3=55,所以平面A 1AB 1与平面ACC 1A 1夹角的余弦值为55.4(2024·山西晋中·三模)如图,在六面体ABCDE 中,BC =BD =6,EC ⊥ED ,且EC =ED =2,AB 平行于平面CDE ,AE 平行于平面BCD ,AE ⊥CD .(1)证明:平面ABE ⊥平面CDE ;(2)若点A 到直线CD 的距离为22,F 为棱AE 的中点,求平面BDF 与平面BCD 夹角的余弦值.【答案】(1)证明见解析(2)10535【分析】(1)设平面ABE 与直线CD 交于点M ,使用线面平行的性质,然后用面面垂直的判定定理即可;(2)证明BE ⊥平面CDE ,然后构造空间直角坐标系,直接用空间向量方法即可得出结果.【详解】(1)设平面ABE 与直线CD 交于点M ,连接ME ,MB ,则平面ABE 与平面CDE 的交线为ME ,平面ABE 与平面BCD 的交线为MB ,因为AB 平行于平面CDE ,AB ⊂平面ABE ,平面ABE 和平面CDE 的交线为ME ,所以AB ∥ME .同理AE ∥MB ,所以四边形ABME 是平行四边形,故AE ∥MB ,AB ∥ME .因为CD ⊥AE ,AE ∥MB ,所以CD ⊥MB ,又BC =BD =6,所以M 为棱CD 的中点在△CDE 中,EC =ED ,MC =MD ,所以CD ⊥ME ,由于AB ∥ME ,故CD ⊥AB .而CD ⊥AE ,AB ∩AE =A ,AB ,AE ⊂平面ABE ,所以CD ⊥平面ABE ,又CD ⊂平面CDE ,所以平面ABE ⊥平面CDE .(2)由(1)可知,CD ⊥平面ABME ,又AM ⊂平面ABME ,所以CD ⊥AM .而点A 到直线CD 的距离为22,故AM =2 2.在等腰直角三角形CDE 中,由EC =ED =2,得CD =2,MC =MD =ME =1.在等腰三角形BCD 中,由MC =MD =1,BC =BD =6,得BM = 5.在平行四边形ABME 中,AE =BM =5,AB =EM =1,AM =22,由余弦定理得cos ∠MEA =EM 2+AE 2-AM 22EM ·AE=-55,所以cos ∠BME =55,所以BE =BM 2+EM 2-2BM ·EM cos ∠BME =2.因为BE 2+ME 2=22+12=5 2=BM 2,所以BE ⊥ME .因为平面ABME ⊥平面CDE ,平面ABME 和平面CDE 的交线为ME ,BE 在平面ABME 内.所以BE ⊥平面CDE .如图,以E 为坐标原点,EC ,ED ,EB 分别为x ,y ,z 轴正方向,建立空间直角坐标系.则E 0,0,0 ,C 2,0,0 ,D 0,2,0 ,B 0,0,2 ,A -22,-22,2 ,F -24,-24,1.所以CD =-2,2,0 ,DB =0,-2,2 ,FB =24,24,1 .设平面BCD 的法向量为m=x 1,y 1,z 1 ,则m ⋅CD=0m ⋅DB =0,即-2x 1+2y 1=0-2y 1+2z 1=0 .则可取x 1=2,得m=2,2,2 .设平面BDF 的法向量为n =x 2,y 2,z 2 ,则n ⋅FB =0n ⋅DB=0,即24x 2+24y 2+z 2=0-2y 2+2z 2=0.取z 2=1,则n=-32,2,1 .设平面BDF 与平面BCD 的夹角为θ,则cos θ=m ⋅n m ⋅n =-3210×21=10535.所以平面BDF 与平面BCD 夹角的余弦值为10535.5(2024·辽宁·二模)棱长均为2的斜三棱柱ABC -A 1B 1C 1中,A 1在平面ABC 内的射影O 在棱AC 的中点处,P 为棱A 1B 1(包含端点)上的动点.(1)求点P 到平面ABC 1的距离;(2)若AP ⊥平面α,求直线BC 1与平面α所成角的正弦值的取值范围.【答案】(1)23913;(2)25,104.【分析】(1)以O 为原点建立空间直角坐标系,求出平面ABC 1的法向量,再利用点到平面距离的向量求法求解即得.(2)由向量共线求出向量AP的坐标,再利用线面角的向量求法列出函数关系,并求出函数的值域即可.【详解】(1)依题意,A 1O ⊥平面ABC ,OB ⊥AC (底面为正三角形),且A 1O =OB =3,以O 为原点,OB ,OC ,OA 1的方向分别为x ,y ,z 轴的正方向,建立空间直角坐标系,如图,则O (0,0,0),A (0,-1,0),B (3,0,0),C (0,1,0),A 1(0,0,3),C 1(0,2,3),AC 1 =(0,3,3),BC 1 =(-3,2,3),AA 1 =(0,1,3),由A 1B 1⎳AB ,A 1B 1⊄平面ABC 1,AB ⊂平面ABC 1,则A 1B 1⎳平面ABC 1,即点P 到平面ABC 1的距离等于点A 1到平面ABC 1的距离,设n =(x ,y ,z )为平面ABC 1的一个法向量,由n ⋅AC 1=3y +3z =0n ⋅BC 1=-3x +2y +3z =0,取z =3,得n=(1,-3,3),因此点A 1到平面ABC 1的距离d =|AA 1 ⋅n||n |=2313=23913,所以点P 到平面ABC 1的距离为23913.(2)设A 1P =λA 1B 1 ,λ∈[0,1],则AP =AA 1 +A 1P =AA 1 +λAB=(0,1,3)+λ(3,1,0)=(3λ,1+λ,3),由AP ⊥α,得AP为平面α的一个法向量,设直线BC 1与平面α所成角为θ,则sin θ=|cos ‹BC 1 ,AP ›|=|BC 1 ⋅AP||BC 1 ||AP |=|5-λ|10⋅3λ2+(1+λ)2+3=5-λ25⋅2λ2+λ+2,令t =5-λ,则λ=5-t ,t ∈[4,5],则sin θ=t 25⋅2(5-t )2+(5-t )+2=t25⋅2t 2-21t +57=125⋅2-21t+57t 2=125571t-7382+576,由t ∈[4,5],得1t ∈15,14 ,于是571t -738 2+576∈225,516,25⋅571t -738 2+576∈2105,52 ,则sin θ∈25,104,所以直线BC 1与平面α所成角的正弦值的取值范围是25,104.6(2024·重庆·模拟预测)在如图所示的四棱锥P -ABCD 中,已知AB ∥CD ,∠BAD =90°,CD =2AB ,△PAB 是正三角形,点M 在侧棱PB 上且使得PD ⎳平面AMC .(1)证明:PM =2BM ;(2)若侧面PAB ⊥底面ABCD ,CM 与底面ABCD 所成角的正切值为311,求二面角P -AC -B 的余弦值.【答案】(1)证明见解析;(2)1010.【分析】(1)连接BD 与AC 交于点E ,连接EM ,由已知得AB CD=EBED ,由线面平行的性质得PD ∥EM ,根据三角形相似可得EB ED =BM PM=12,即PM =2BM(2)设AB 的中点O ,首先由已知得PO ⊥底面ABCD ,在△PAB 中过点M 作MF ∥PO 交AB 于点F ,得MF ⊥底面ABCD ,则∠MCF 为CM 与底面ABCD 所成角,在底面ABCD 上过点O 作OG ⊥AC 于点G ,则∠PGO 是二面角P -AC -B 的平面角,根据条件求解即可【详解】(1)证明:连接BD 与AC 交于点E ,连接EM ,在△EAB 与△ECD 中,∵AB ∥CD ,∴AB CD=EBED ,由CD =2AB ,得ED =2EB ,又∵PD ⎳平面AMC ,而平面PBD ∩平面AMC =ME ,PD ⊂平面PBD ,∴PD ∥EM ,∴在△PBD 中,EB ED =BM PM=12,∴PM =2BM ;(2)设AB 的中点O ,在正△PAB 中,PO ⊥AB ,而侧面PAB ⊥底面ABCD ,侧面PAB ∩底面ABCD =AB ,且PO ⊂平面PAB ,∴PO ⊥底面ABCD ,在△PAB 中过点M 作MF ⎳PO 交AB 于点F ,∴MF ⊥底面ABCD ,∴∠MCF 为CM 与底面ABCD 所成角,∴MF CF=311,设AB =6a ,则MF=3a,∴CF=11a,BF=MF3=a,则在直角梯形ABCD中,AF=5a,而CD=12a,则AD=11a2-12a-5a2=62a,在底面ABCD上过点O作OG⊥AC于点G,则∠PGO是二面角P-AC-B的平面角,易得OA=3a,AC=66a,在梯形ABCD中,由OAOG=ACAD⇒3aOG=66a62a,得OG=3a,在Rt△POG中,PG=30a,∴cos∠PGO=OGPG=1010.7(2024·安徽·模拟预测)2023年12月19日至20日,中央农村工作会议在北京召开,习近平主席对“三农”工作作出指示.某地区为响应习近平主席的号召,积极发展特色农业,建设蔬菜大棚.如图所示的七面体ABG-CDEHF是一个放置在地面上的蔬菜大棚钢架,四边形ABCD是矩形,AB=8m,AD=4m,ED=CF=1m,且ED,CF都垂直于平面ABCD,GA=GB=5m,HE=HF,平面ABG⊥平面ABCD.(1)求点H到平面ABCD的距离;(2)求平面BFHG与平面AGHE所成锐二面角的余弦值.【答案】(1)4(2)413【分析】(1)取AB,CD的中点M,N,证得平面ADE⎳平面MNHG,得到AE⎳GH,再由平面ABG⎳平面CDEHG,证得AG⎳EH,得到平行四边形AGHE,得到GH=AE,求得HN=4,结合HN⊥平面ABCD,即可求解;(2)以点N为原点,建立空间直角坐标系,分别求得平面BFHG和平面AGHE的法向量n =(1,3,4)和m =(1,-3,4),结合向量的夹角公式,即可求解.【详解】(1)如图所示,取AB,CD的中点M,N,连接GM,MN,HN,因为GA=GB,可得GM⊥AB,又因为平面ABG⊥平面ABCD,且平面ABG∩平面ABCD=AB,GM⊂平面ABG,所以GM⊥平面ABCD,同理可得:HN⊥平面ABCD,因为ED⊥平面ABCD,所以ED⎳HN,又因为ED⊄平面MNHG,HN⊂平面MNHG,所以ED⎳平面MNHG,因为MN⎳AD,且AD⊄平面MNHG,MN⊂平面MNHG,所以AD⎳平面MNHG,又因为AD∩DE=D,且AD,DE⊂平面ADE,所以平面ADE⎳平面MNHG,因为平面AEHG与平面ADE和平面MNHG于AE,GH,可得AE⎳GH,又由GM⎳HN,AB⎳CD,且AB∩GM=M和CD∩HN=N,所以平面ABG⎳平面CDEHG,因为平面AEHG与平面ABG和平面CDEHF于AG,EH,所以AG⎳EH,可得四边形AGHE 为平行四边形,所以GH =AE ,因为AE =AD 2+DE 2=42+12=17,所以GH =17,在直角△AMG ,可得GM =GB 2-AB 22=52-42=3,在直角梯形GMNH 中,可得HN =3+17-42=4,因为HN ⊥平面ABCD ,所以点H 到平面ABCD 的距离为4.(2)解:以点N 为原点,以NM ,NC ,NH 所在的直线分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,则E (0,-4,1),F (0,4,1),G (4,0,3),H (0,0,4),可得HE =(0,-4,-3),HF =(0,4,-3),HG=(4,0,-1),设平面BFHG 的法向量为n=(x ,y ,z ),则n ⋅HG=4x -z =0n ⋅HF=4y -3z =0,取z =4,可得x =1,y =3,所以n=(1,3,4),设平面AGHE 的法向量为m=(a ,b ,c ),则m ⋅HG=4a -c =0m ⋅HE=-4b -3c =0,取c =4,可得a =1,b =-3,所以m=(1,-3,4),则cos m ,n =m ⋅n m n=1-9+161+9+16⋅1+9+16=413,即平面BFHG 与平面AGHE 所成锐二面角的余弦值413.8(2024·重庆·模拟预测)如图,ACDE 为菱形,AC =BC =2,∠ACB =120°,平面ACDE ⊥平面ABC ,点F 在AB 上,且AF =2FB ,M ,N 分别在直线CD ,AB 上.(1)求证:CF ⊥平面ACDE ;(2)把与两条异面直线都垂直且相交的直线叫做这两条异面直线的公垂线,若∠EAC =60°,MN 为直线CD ,AB 的公垂线,求ANAF的值;(3)记直线BE 与平面ABC 所成角为α,若tan α>217,求平面BCD 与平面CFD 所成角余弦值的范围.【答案】(1)证明见解析(2)AN AF=913(3)528,255 【分析】(1)先通过余弦定理及勾股定理得到CF ⊥AC ,再根据面面垂直的性质证明;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,利用向量的坐标运算根据MN ⋅CD =0MN ⋅AF =0,列方程求解即可;(3)利用向量法求面面角,然后根据tan α>217列不等式求解.【详解】(1)AB 2=AC 2+BC 2-2AC ⋅BC ⋅cos ∠ACB =12,AB =23,AF =2FB ,所以AF =433,CF=13CA +23CB ,CF 2=19CA 2+49CB 2+49CA ⋅CB =43,AC 2+CF 2=4+43=163=AF 2,则CF ⊥AC ,又因为平面ACDE ⊥平面ABC ,平面ACDE ∩平面ABC =AC ,CF ⊂面ABC ,故CF ⊥平面ACDE ;(2)以C 为原点,CA 的方向为x 轴正方向,建立如图所示空间直角坐标系C -xyz ,由∠EAC =60°,可得∠DCA =120°,DC =2,所以C 0,0,0 ,D -1,0,3 ,A 2,0,0 ,F 0,233,0 所以AF =-2,233,0 ,CD =-1,0,3 ,设AN =λAF =-2λ,233λ,0 ,则N 2-2λ,233λ,0 ,设CM =μCD ,则M -μ,0,3μ ,MN =2-2λ+μ,233λ,-3μ ,由题知,MN ⋅CD=0MN ⋅AF =0 ⇒2λ-2-μ-3μ=04λ-4-2μ+43λ=0 ,解得λ=913,μ=-213,故AN AF=913;(3)B -1,3,0 ,设∠EAC =θ,则E 2-2cos θ,0,2sin θ ,BE=3-2cos θ,-3,2sin θ ,可取平面ABC 的法向量n=0,0,1 ,则sin α=cos n ,BE=n ⋅BEn ⋅BE =2sin θ 3-2cos θ 2+3+4sin 2θ=sin θ4-3cos θ,cos α=4-3cos θ-sin 2θ4-3cos θ,则tan α=sin θ4-3cos θ-sin 2θ>217,整理得10cos 2θ-9cos θ+2<0,故cos θ∈25,12,CF =0,23,0,CD =-2cos θ,0,2sin θ ,CB =-1,3,0 ,记平面CDF 的法向量为n 1 =x ,y ,z ,则有n 1 ⋅CD =0n 1 ⋅CF =0 ⇒-2x cos θ+2z sin θ=023y =0,可得n 1=sin θ,0,cos θ ,记平面CBD 的法向量为n 2 =a ,b ,c ,则有n 2 ⋅CD=0n 2 ⋅CB =0 ⇒-2a cos θ+2c sin θ=0-a +3b =0,可得n 2=3sin θ,sin θ,3cos θ ,记平面BCD 与平面CFD 所成角为γ,则cos γ=cos n 1 ,n 2 =33+sin 2θ,cos θ∈25,12 ,所以sin 2θ∈34,2125 ,3+sin 2θ∈152,465 ,故cos γ=33+sin 2θ∈528,255 .9(2024·安徽·二模)将正方形ABCD 绕直线AB 逆时针旋转90°,使得CD 到EF 的位置,得到如图所示的几何体.(1)求证:平面ACF ⊥平面BDE ;(2)点M 为DF上一点,若二面角C -AM -E 的余弦值为13,求∠MAD .【答案】(1)证明见解析(2)∠MAD =45°【分析】(1)根据面面与线面垂直的性质可得BD ⊥AF ,结合线面、面面垂直的判定定理即可证明;(2)建立如图空间直角坐标系,设∠MAD =α,AB =1,利用空间向量法求出二面角C -AM -E 的余弦值,建立方程1-sin αcos α1+sin 2α1+cos 2α=13,结合三角恒等变换求出α即可.【详解】(1)由已知得平面ABCD ⊥平面ABEF ,AF ⊥AB ,平面ABCD ∩平面ABEF =AB ,AF ⊂平面ABEF ,所以AF ⊥平面ABCD ,又BD ⊂平面ABCD ,故BD ⊥AF ,因为ABCD 是正方形,所以BD ⊥AC ,AC ,AF ⊂平面ACF ,AC ∩AF =A ,所以BD ⊥平面ACF ,又BD ⊂平面BDE ,所以平面ACF ⊥平面BDE .(2)由(1)知AD ,AF ,AB 两两垂直,以AD ,AF ,AB 所在直线分别为x ,y ,z 轴,建立空间直角坐标系,如图.设∠MAD =α,AB =1,则A 0,0,0 ,M cos α,sin α,0 ,C 1,0,1 ,E 0,1,1 ,故AM =cos α,sin α,0 ,AC =1,0,1 ,AE =0,1,1设平面AMC 的法向量为m =x 1,y 1,z 1 ,则m ⋅AC =0,m ⋅AM=0故x 1+z 1=0x 1cos α+y 1sin α=0,取x 1=sin α,则y 1=-cos α,z 1=-sin α所以m=sin α,-cos α,-sin α设平面AME 的法向量为n =x 2,y 2,z 2 ,n ⋅AE =0,n ⋅AM=0故y 2+z 2=0x 2cos α+y 2sin α=0,取x 2=sin α,则y 2=-cos α,z 2=cos α所以n=sin α,-cos α,cos α ,所以cos m ,n =1-sin αcos α1+sin 2α1+cos 2α,由已知得1-sin αcos α1+sin 2α1+cos 2α=13,化简得:2sin 22α-9sin2α+7=0,解得sin2α=1或sin2α=72(舍去)故α=45°,即∠MAD =45°.10(2024·安徽黄山·二模)如图,已知AB 为圆台下底面圆O 1的直径,C 是圆O 1上异于A ,B 的点,D 是圆台上底面圆O 2上的点,且平面DAC ⊥平面ABC ,DA =DC =AC =2,BC =4,E 是CD 的中点,BF =2FD .(1)证明:DO 2⎳BC ;(2)求直线DB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析(2)68585【分析】(1)取AC 的中点O ,根据面面垂直的性质定理,可得DO ⊥平面ABC ,即可求证DO 2⎳OO 1,进而可证矩形,即可根据线线平行以及平行的传递性求解.(2)建系,利用向量法,求解法向量n =1,-12,3 与方向向量DB =(-1,4,-3)的夹角,即可求解.【详解】(1)证明:取AC 的中点为O ,连接DO ,OO 1,O 1O 2,∵DA =DC ,O 为AC 中点,∴DO ⊥AC ,又平面DAC ⊥平面ABC ,且平面DAC ∩平面ABC =AC ,DO ⊂平面DAC ,∴DO ⊥平面ABC ,∴DO ⎳O 1O 2,DO =O 1O 2,故四边形DOO 1O 2为矩形,∴DO 2⎳OO 1,又O ,O 1分别是AC ,AB 的中点,∴OO 1⎳BC ,∴DO 2⎳BC ;(2)∵C 是圆O 1上异于A ,B 的点,且AB 为圆O 1的直径,∴BC ⊥AC ,∴OO 1⊥AC ,∴如图以O 为原点建立空间直角坐标系,由条件知DO =3,∴A (1,0,0),B (-1,4,0),C (-1,0,0),D (0,0,3),∴E -12,0,32 ,设F (x ,y ,z ),∴BF =(x +1,y -4,z ),FD=(-x ,-y ,3-z ),由BF =2FD ,得F -13,43,233 ,∴AF =-43,43,233 ,∴DB =(-1,4,-3),AE =-32,0,32 ,设平面AEF 法向量为n=(x 1,y 1,z 1),则n ⋅AE=-32x 1+32z 1=0n ⋅AF =-43x 1+43y 1+233z 1=0,取n =1,-12,3 ,设直线BD 与平面AEF 所成角为θ,则sin θ=|cos <n ,DB>|=625⋅172=68585∴直线BD 与平面AEF 所成角的正弦值为68585.11(2024·黑龙江哈尔滨·一模)正四棱台ABCD -A 1B 1C 1D 1的下底面边长为22,A 1B 1=12AB ,M 为BC 中点,已知点P 满足AP =1-λ AB +12λ⋅AD +λAA 1,其中λ∈0,1 .(1)求证D 1P ⊥AC ;(2)已知平面AMC 1与平面ABCD 所成角的余弦值为37,当λ=23时,求直线DP 与平面AMC 1所成角的正弦值.【答案】(1)证明见解析(2)241391【分析】(1)方法一运用空间向量的线性运算,进行空间位置关系的向量证明即可.方法二:建立空间直角坐标系,进行空间位置关系的向量证明即可.(2)建立空间直角坐标系,利用线面角的向量求法求解即可.【详解】(1)方法一:∵A 1B 1=12AB ,∴AA 1 ⋅AB =AA 1 ⋅AD =22×22=2.∵D 1A =-12AD-AA 1∴D 1P =D 1A +AP =1-λ AB +12λ-12AD+λ-1 AA 1∴D 1P ⋅AC =1-λ AB +12λ-12AD +λ-1 AA 1 ⋅AB +AD =1-λ AB 2+12λ-12 AD2+λ-1 AB ⋅AA 1 +λ-1 AD ⋅AA 1=81-λ +812λ-12+4λ-1 =0.∴D 1P ⊥AC ,即D 1P ⊥AC .方法二:以底面ABCD 的中心O 为原点,以OM 方向为y 轴,过O 点平行于AD 向前方向为x 轴,以过点O 垂直平面ABCD 向上方向为z 轴,建立如图所示空间直角坐标系,设正四棱台的高度为h ,则有 A 2,-2,0 ,B 2,2,0 ,C -2,2,0 ,D -2,-2,0 ,A 122,-22,h ,C 1-22,22,h ,D 1-22,-22,h ,M 0,2,0 ,AC =-22,22,0AP =1-λ 0,22,0 +12λ-22,0,0 +λ-22,22,0 =-322λ,22-322λ,λhD 1A =322,-22,-h ,D 1P =D 1A +AP =-322λ+322,-322λ+322,λh -h .故AC ⋅D 1P=0,所以D 1P ⊥AC .(2)设平面ABCD 的法向量为n=0,0,1 ,设平面AMC 1的法向量为m =x ,y ,z ,AM =-2,22,0 ,AC 1 =-322,322,h ,则有AM ⋅m=0AC 1 ⋅m=0 ,即-2x +22y =0-322x +322y +hz =0,令x =22h ,则m=22h ,2h ,3 .又题意可得cos m ,n =38h 2+2h 2+9=37,可得h =2.因为λ=23,经过计算可得P 0,0,43 ,D 1-22,-22,2 ,D 1P =2,2,43.将h =2代入,可得平面AMC 1的法向量m=42,22,3 .设直线DP 与平面AMC 1所成角的为θsin θ=cos DP ,m =8+4+42+2+16932+8+9=241391.12(2024·辽宁·三模)如图,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1⊥底面ABC ,AC =AA 1=2,AB =1,BC =3,点E 为线段AC 的中点.(1)求证:AB 1∥平面BEC 1;(2)若∠A 1AC =π3,求二面角A -BE -C 1的余弦值.【答案】(1)证明见详解(2)-22【分析】(1)连接BC 1,交B 1C 于点N ,连接NE ,利用线面平行的判定定理证明;(2)由已知可知,△AA 1C 为等边三角形,故A 1E ⊥AC ,利用面面垂直的性质定理可证得A 1E ⊥底面ABC ,进而建立空间直角坐标系,利用向量法即可求二面角余弦值.【详解】(1)连接BC 1,交B 1C 于点N ,连接NE ,因为侧面BCC 1B 1是平行四边形,所以N 为B 1C 的中点,又因为点E 为线段AC 的中点,所以NE ⎳AB 1,因为AB 1⊄面BEC 1,NE ⊂面BEC 1,所以AB 1⎳面BEC 1.(2)连接A 1C ,A 1E ,因为∠A 1AC =π3,AC =AA 1=2,所以△AA 1C 为等边三角形,A 1C =2,因为点E 为线段AC 的中点,所以A 1E ⊥AC ,因为侧面ACC 1A 1⊥底面ABC ,平面ACC 1A 1∩平面ABC =AC ,A 1E ⊂平面ACC 1A 1,所以A 1E ⊥底面ABC ,过点E 在底面ABC 内作EF ⊥AC ,如图以E 为坐标原点,分布以EF ,EC ,EA 1 的方向为x ,y ,z 轴正方向建立空间直角坐标系,则E 0,0,0 ,B 32,-12,0 ,C 10,2,3 ,所以EB =32,-12,0 ,EC 1 =0,2,3 ,设平面BEC 1的法向量为m=x ,y ,z ,则m ⋅EB =32x -12y =0m ⋅EC 1=2y +3z =0,令x =1,则y =3,z =-2,所以平面BEC 1的法向量为m=1,3,-2 ,又因为平面ABE 的法向量为n=0,0,1 ,则cos m ,n =-21+3+4=-22,经观察,二面角A -BE -C 1的平面角为钝角,所以二面角A -BE -C 1的余弦值为-22.13(2024·广东广州·一模)如图,在四棱锥P -ABCD 中,底面ABCD 是边长为2的菱形,△DCP 是等边三角形,∠DCB =∠PCB =π4,点M ,N 分别为DP 和AB 的中点.(1)求证:MN ⎳平面PBC ;(2)求证:平面PBC ⊥平面ABCD ;(3)求CM 与平面PAD 所成角的正弦值.【答案】(1)证明见解析;(2)证明见解析;(3)33.【分析】(1)取PC 中点E ,由已知条件,结合线面平行的判断推理即得.(2)过P 作PQ ⊥BC 于点Q ,借助三角形全等,及线面垂直的判定、面面垂直的判定推理即得.(3)建立空间直角坐标系,利用线面角的向量求法求解即得.【详解】(1)取PC 中点E ,连接ME ,BE ,由M 为DP 中点,N 为AB 中点,得ME ⎳DC ,ME =12DC ,又BN ⎳CD ,BN =12CD ,则ME ⎳BN ,ME =BN ,因此四边形BEMN 为平行四边形,于是MN ⎳BE ,而MN ⊄平面PBC ,BE ⊂平面PBC ,所以MN ⎳平面PBC .(2)过P 作PQ ⊥BC 于点Q ,连接DQ ,由∠DCB =∠PCB =π4,CD =PC ,QC =QC ,得△QCD ≌△QCP ,则∠DQC =∠PQC =π2,即DQ ⊥BC ,而PQ =DQ =2,PQ 2+DQ 2=4=PD 2,因此PQ ⊥DQ ,又DQ ∩BC =Q ,DQ ,BC ⊂平面ABCD ,则PQ ⊥平面ABCD ,PQ ⊂平面PBC ,所以平面PBC ⊥平面ABCD .(3)由(2)知,直线QC ,QD ,QP 两两垂直,以点Q 为原点,直线QC ,QD ,QP 分别为x ,y ,z 轴建立空间直角坐标系,则C (2,0,0),P (0,0,2),D (0,2,0),M 0,22,22,A (-2,2,0),CM =-2,22,22,AD =(2,0,0),DP =(0,-2,2),设平面PAD 的一个法向量n =(x ,y ,z ),则n ⋅AD=2x =0n ⋅DP=-2y +2z =0,令y =1,得n=(0,1,1),设CM 与平面PAD 所成角为θ,sin θ=|cos ‹CM ,n ›|=|CM ⋅n||CM ||n |=23⋅2=33,所以CM 与平面PAD 所成角的正弦值是33.14(2024·广东梅州·二模)如图,在四棱锥P -ABCD 中,平面PAD ⊥平面ABCD ,底面ABCD 为直角梯形,△PAD 为等边三角形,AD ⎳BC ,AD ⊥AB ,AD =AB =2BC =2.(1)求证:AD ⊥PC ;(2)点N 在棱PC 上运动,求△ADN 面积的最小值;(3)点M 为PB 的中点,在棱PC 上找一点Q ,使得AM ⎳平面BDQ ,求PQQC的值.【答案】(1)证明见解析(2)2217(3)4【分析】(1)取AD 的中点H ,连接PH ,CH ,依题意可得四边形ABCH 为矩形,即可证明CH ⊥AD ,再由PH ⊥AD ,即可证明AD ⊥平面PHC ,从而得证;(2)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,即可得到CG AG=12,再根据线面平行的性质得到CF FM =12,在△PBC 中,过点M 作MK ⎳PC ,即可得到MKCQ=2,最后由PQ =2MK 即可得解.【详解】(1)取AD 的中点H ,连接PH ,CH ,则AH ⎳BC 且AH =BC ,又AD ⊥AB ,所以四边形ABCH 为矩形,所以CH ⊥AD ,又△PAD 为等边三角形,所以PH ⊥AD ,PH ∩CH =H ,PH ,CH ⊂平面PHC ,所以AD ⊥平面PHC ,又PC ⊂平面PHC ,所以AD ⊥PC .(2)连接HN ,由AD ⊥平面PHC ,又HN ⊂平面PHC ,所以AD ⊥HN ,所以S △ADH =12AD ⋅HN =HN ,要使△ADN 的面积最小,即要使HN 最小,当且仅当HN ⊥PC 时HN 取最小值,因为平面PAD ⊥平面ABCD ,平面PAD ∩平面ABCD =AD ,PH ⊂平面PAD ,所以PH ⊥平面ABCD ,又HC ⊂平面ABCD ,所以PH ⊥HC ,在Rt △HPC 中,CH =2,PH =3,所以PC =CH 2+PH 2=7,当HN ⊥PC 时HN =PH ⋅CH PC =237=2217,所以△ADN 面积的最小值为2217.(3)连接AC 交BD 于点G ,连接MC 交BQ 于点F ,连接FG ,因为AD ⎳BC 且AD =2BC =2,所以△CGB ∽△AGD ,所以CG AG =BC AD=12,因为AM ⎳平面BDQ ,又AM ⊂平面ACM ,平面BDQ ∩平面ACM =GF ,所以GF ⎳AM ,所以CF FM =CG AG=12,在△PBC 中,过点M 作MK ⎳PC ,则有MK CQ =MF CF=2,所以PQ =2MK ,所以PQ =2MK =4CQ ,即PQQC=415(2024·广东广州·模拟预测)如图所示,圆台O 1O 2的轴截面A 1ACC 1为等腰梯形,AC =2AA 1=2A 1C 1=4,B 为底面圆周上异于A ,C 的点,且AB =BC ,P 是线段BC 的中点.(1)求证:C 1P ⎳平面A 1AB .(2)求平面A 1AB 与平面C 1CB 夹角的余弦值.【答案】(1)证明见解析(2)17【分析】(1)取AB 的中点H ,连接A 1H ,PH ,证明四边形A 1C 1PH 为平行四边形,进而得C 1P ⎳A 1H ,即可证明;(2)建立空间直角坐标系,求两平面的法向量,利用平面夹角公式求解.【详解】(1)取AB 的中点H ,连接A1H ,PH ,如图所示,因为P 为BC 的中点,所以PH ⎳AC ,PH =12AC .在等腰梯形A 1ACC 1中,A 1C 1⎳AC ,A 1C 1=12AC ,所以HP ⎳A 1C 1,HP =A 1C 1,所以四边形A 1C 1PH 为平行四边形,所以C 1P ⎳A 1H ,又A 1H ⊂平面A 1AB ,C 1P ⊄平面A 1AB ,所以C 1P ⎳平面A 1AB .(2)因为AB =BC ,故O 2B ⊥AC ,以直线O 2A ,O 2B ,O 2O 1分别为x ,y ,z 轴,建立空间直角坐标系,如图所示,在等腰梯形A 1ACC 1中,AC =2AA 1=2A 1C 1=4,此梯形的高为h =AA 21-AC -A 1C 122= 3.因为A 1C 1=12AC ,A 1C 1⎳AC ,。
高考数学-立体几何(含22年真题讲解)

高考数学-立体几何(含22年真题讲解)1.【2022年全国甲卷】如图,网格纸上绘制的是一个多面体的三视图,网格小正方形的边长为1,则该多面体的体积为()A.8B.12C.16D.20【答案】B【解析】【分析】由三视图还原几何体,再由棱柱的体积公式即可得解.【详解】由三视图还原几何体,如图,×2×2=12.则该直四棱柱的体积V=2+42故选:B.2.【2022年全国甲卷】在长方体ABCD−A1B1C1D1中,已知B1D与平面ABCD和平面AA1B1B 所成的角均为30°,则()A.AB=2AD B.AB与平面AB1C1D所成的角为30°C.AC=CB1D.B1D与平面BB1C1C所成的角为45°【解析】 【分析】根据线面角的定义以及长方体的结构特征即可求出. 【详解】 如图所示:不妨设AB =a,AD =b,AA 1=c ,依题以及长方体的结构特征可知,B 1D 与平面ABCD 所成角为∠B 1DB ,B 1D 与平面AA 1B 1B 所成角为∠DB 1A ,所以sin30∘=cB 1D=bB 1D ,即b =c ,B 1D =2c =√a 2+b 2+c 2,解得a =√2c .对于A ,AB =a ,AD =b ,AB =√2AD ,A 错误;对于B ,过B 作BE ⊥AB 1于E ,易知BE ⊥平面AB 1C 1D ,所以AB 与平面AB 1C 1D 所成角为∠BAE ,因为tan∠BAE =c a=√22,所以∠BAE ≠30∘,B 错误;对于C ,AC =√a 2+b 2=√3c ,CB 1=√b 2+c 2=√2c ,AC ≠CB 1,C 错误; 对于D ,B 1D 与平面BB 1C 1C 所成角为∠DB 1C ,sin∠DB 1C =CDB 1D=a2c =√22,而0<∠DB 1C <90∘,所以∠DB 1C =45∘.D 正确. 故选:D .3.【2022年全国甲卷】甲、乙两个圆锥的母线长相等,侧面展开图的圆心角之和为2π,侧面积分别为S 甲和S 乙,体积分别为V 甲和V 乙.若S 甲S 乙=2,则V 甲V 乙=( )A .√5B .2√2C .√10D .5√104【答案】C 【解析】设母线长为l ,甲圆锥底面半径为r 1,乙圆锥底面圆半径为r 2,根据圆锥的侧面积公式可得r 1=2r 2,再结合圆心角之和可将r 1,r 2分别用l 表示,再利用勾股定理分别求出两圆锥的高,再根据圆锥的体积公式即可得解. 【详解】解:设母线长为l ,甲圆锥底面半径为r 1,乙圆锥底面圆半径为r 2,则S 甲S 乙=πr 1l πr 2l =r1r 2=2, 所以r 1=2r 2, 又2πr 1l+2πr 2l=2π,则r 1+r 2l=1,所以r 1=23l,r 2=13l ,所以甲圆锥的高ℎ1=√l 2−49l 2=√53l ,乙圆锥的高ℎ2=√l 2−19l 2=2√23l , 所以V 甲V 乙=13πr 12ℎ113πr 22ℎ2=49l 2×√53l 19l ×2√23l =√10.故选:C.4.【2022年全国乙卷】在正方体ABCD −A 1B 1C 1D 1中,E ,F 分别为AB,BC 的中点,则( ) A .平面B 1EF ⊥平面BDD 1 B .平面B 1EF ⊥平面A 1BD C .平面B 1EF//平面A 1AC D .平面B 1EF//平面A 1C 1D【答案】A 【解析】 【分析】证明EF ⊥平面BDD 1,即可判断A ;如图,以点D 为原点,建立空间直角坐标系,设AB =2,分别求出平面B 1EF ,A 1BD ,A 1C 1D 的法向量,根据法向量的位置关系,即可判断BCD . 【详解】解:在正方体ABCD −A 1B 1C 1D 1中, AC ⊥BD 且DD 1⊥平面ABCD , 又EF ⊂平面ABCD ,所以EF ⊥DD 1,因为E,F 分别为AB,BC 的中点, 所以EF ∥AC ,所以EF ⊥BD , 又BD ∩DD 1=D , 所以EF ⊥平面BDD 1, 又EF ⊂平面B 1EF ,所以平面B 1EF ⊥平面BDD 1,故A 正确;如图,以点D 为原点,建立空间直角坐标系,设AB =2,则B 1(2,2,2),E (2,1,0),F (1,2,0),B (2,2,0),A 1(2,0,2),A (2,0,0),C (0,2,0), C 1(0,2,2),则EF ⃑⃑⃑⃑⃑ =(−1,1,0),EB 1⃑⃑⃑⃑⃑⃑⃑ =(0,1,2),DB ⃑⃑⃑⃑⃑⃑ =(2,2,0),DA 1⃑⃑⃑⃑⃑⃑⃑⃑ =(2,0,2),AA 1⃑⃑⃑⃑⃑⃑⃑ =(0,0,2),AC ⃑⃑⃑⃑⃑ =(−2,2,0),A 1C 1⃑⃑⃑⃑⃑⃑⃑⃑⃑ =(−2,2,0),设平面B 1EF 的法向量为m ⃑⃑ =(x 1,y 1,z 1), 则有{m ⃑⃑ ⋅EF ⃑⃑⃑⃑⃑ =−x 1+y 1=0m ⃑⃑ ⋅EB 1⃑⃑⃑⃑⃑⃑⃑ =y 1+2z 1=0 ,可取m ⃑⃑ =(2,2,−1),同理可得平面A 1BD 的法向量为n 1⃑⃑⃑⃑ =(1,−1,−1), 平面A 1AC 的法向量为n 2⃑⃑⃑⃑ =(1,1,0), 平面A 1C 1D 的法向量为n 3⃑⃑⃑⃑ =(1,1,−1), 则m ⃑⃑ ⋅n 1⃑⃑⃑⃑ =2−2+1=1≠0,所以平面B 1EF 与平面A 1BD 不垂直,故B 错误; 因为m ⃑⃑ 与n 2⃑⃑⃑⃑ 不平行,所以平面B 1EF 与平面A 1AC 不平行,故C 错误; 因为m ⃑⃑ 与n 3⃑⃑⃑⃑ 不平行,所以平面B 1EF 与平面A 1C 1D 不平行,故D 错误, 故选:A.5.【2022年全国乙卷】已知球O的半径为1,四棱锥的顶点为O,底面的四个顶点均在球O 的球面上,则当该四棱锥的体积最大时,其高为()A.13B.12C.√33D.√22【答案】C【解析】【分析】先证明当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为2r2,进而得到四棱锥体积表达式,再利用均值定理去求四棱锥体积的最大值,从而得到当该四棱锥的体积最大时其高的值.【详解】设该四棱锥底面为四边形ABCD,四边形ABCD所在小圆半径为r,设四边形ABCD对角线夹角为α,则S ABCD=12⋅AC⋅BD⋅sinα≤12⋅AC⋅BD≤12⋅2r⋅2r=2r2(当且仅当四边形ABCD为正方形时等号成立)即当四棱锥的顶点O到底面ABCD所在小圆距离一定时,底面ABCD面积最大值为2r2又r2+ℎ2=1则VO−ABCD =13⋅2r2⋅ℎ=√23√r2⋅r2⋅2ℎ2≤√23√(r2+r2+2ℎ23)3=4√327当且仅当r2=2ℎ2即ℎ=√33时等号成立,故选:C6.【2022年新高考1卷】南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5m 时,相应水面的面积为140.0km 2;水位为海拔157.5m 时,相应水面的面积为180.0km 2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m 上升到157.5m 时,增加的水量约为(√7≈2.65)( ) A .1.0×109m 3 B .1.2×109m 3 C .1.4×109m 3 D .1.6×109m 3【答案】C 【解析】 【分析】根据题意只要求出棱台的高,即可利用棱台的体积公式求出. 【详解】依题意可知棱台的高为MN =157.5−148.5=9(m),所以增加的水量即为棱台的体积V . 棱台上底面积S =140.0km 2=140×106m 2,下底面积S ′=180.0km 2=180×106m 2, ∴V =13ℎ(S +S ′+√SS ′)=13×9×(140×106+180×106+√140×180×1012) =3×(320+60√7)×106≈(96+18×2.65)×107=1.437×109≈1.4×109(m 3).故选:C .7.【2022年新高考1卷】已知正四棱锥的侧棱长为l ,其各顶点都在同一球面上.若该球的体积为36π,且3≤l ≤3√3,则该正四棱锥体积的取值范围是( ) A .[18,814]B .[274,814]C .[274,643]D .[18,27]【答案】C 【解析】 【分析】设正四棱锥的高为ℎ,由球的截面性质列方程求出正四棱锥的底面边长与高的关系,由此确定正四棱锥体积的取值范围. 【详解】∵ 球的体积为36π,所以球的半径R =3, 设正四棱锥的底面边长为2a ,高为ℎ, 则l 2=2a 2+ℎ2,32=2a 2+(3−ℎ)2, 所以6ℎ=l 2,2a 2=l 2−ℎ2所以正四棱锥的体积V =13Sℎ=13×4a 2×ℎ=23×(l 2−l 436)×l 26=19(l 4−l 636), 所以V ′=19(4l 3−l 56)=19l 3(24−l 26),当3≤l ≤2√6时,V ′>0,当2√6<l ≤3√3时,V ′<0, 所以当l =2√6时,正四棱锥的体积V 取最大值,最大值为643, 又l =3时,V =274,l =3√3时,V =814,所以正四棱锥的体积V 的最小值为274, 所以该正四棱锥体积的取值范围是[274,643]. 故选:C.8.【2022年新高考2卷】已知正三棱台的高为1,上、下底面边长分别为3√3和4√3,其顶点都在同一球面上,则该球的表面积为( ) A .100π B .128π C .144π D .192π【答案】A 【解析】 【分析】根据题意可求出正三棱台上下底面所在圆面的半径r 1,r 2,再根据球心距,圆面半径,以及球的半径之间的关系,即可解出球的半径,从而得出球的表面积. 【详解】设正三棱台上下底面所在圆面的半径r 1,r 2,所以2r 1=3√3sin60∘,2r 2=4√3sin60∘,即r 1=3,r 2=4,设球心到上下底面的距离分别为d 1,d 2,球的半径为R ,所以d 1=√R 2−9,d 2=√R 2−16,故|d 1−d 2|=1或d 1+d 2=1,即|√R 2−9−√R 2−16|=1或√R 2−9+√R 2−16=1,解得R2=25符合题意,所以球的表面积为S=4πR2=100π.故选:A.9.【2022年北京】已知正三棱锥P−ABC的六条棱长均为6,S是△ABC及其内部的点构成的集合.设集合T={Q∈S|PQ≤5},则T表示的区域的面积为()A.3π4B.πC.2πD.3π【答案】B【解析】【分析】求出以P为球心,5为半径的球与底面ABC的截面圆的半径后可求区域的面积.【详解】设顶点P在底面上的投影为O,连接BO,则O为三角形ABC的中心,且BO=23×6×√32=2√3,故PO=√36−12=2√6.因为PQ=5,故OQ=1,故S的轨迹为以O为圆心,1为半径的圆,而三角形ABC内切圆的圆心为O,半径为2×√34×363×6=√3>1,故S的轨迹圆在三角形ABC内部,故其面积为π故选:B10.【2022年浙江】某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是()A.22πB.8πC.223πD.163π【答案】C【解析】【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可根据球,圆柱,圆台的体积公式求出.【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的底面半径,圆台的上底面半径都为1cm,圆台的下底面半径为2cm,所以该几何体的体积V=12×43π×13+π×12×2+13×2×(π×22+π×12+√π×22×π×12)=22π3cm3.故选:C.11.【2022年浙江】如图,已知正三棱柱ABC−A1B1C1,AC=AA1,E,F分别是棱BC,A1C1上的点.记EF与AA1所成的角为α,EF与平面ABC所成的角为β,二面角F−BC−A的平面角为γ,则()A.α≤β≤γB.β≤α≤γC.β≤γ≤αD.α≤γ≤β【答案】A【解析】【分析】先用几何法表示出α,β,γ,再根据边长关系即可比较大小.【详解】如图所示,过点F作FP⊥AC于P,过P作PM⊥BC于M,连接PE,则α=∠EFP,β=∠FEP,γ=FMP,tanα=PEFP =PEAB≤1,tanβ=FPPE=ABPE≥1,tanγ=FPPM≥FPPE=tanβ,所以α≤β≤γ,故选:A.12.【2022年新高考1卷】(多选)已知正方体ABCD−A1B1C1D1,则()A.直线BC1与DA1所成的角为90°B.直线BC1与CA1所成的角为90°C.直线BC1与平面BB1D1D所成的角为45°D.直线BC1与平面ABCD所成的角为45°【答案】ABD【解析】【分析】数形结合,依次对所给选项进行判断即可. 【详解】如图,连接B 1C 、BC 1,因为DA 1//B 1C ,所以直线BC 1与B 1C 所成的角即为直线BC 1与DA 1所成的角,因为四边形BB 1C 1C 为正方形,则B 1C ⊥ BC 1,故直线BC 1与DA 1所成的角为90°,A 正确;连接A 1C ,因为A 1B 1⊥平面BB 1C 1C ,BC 1⊂平面BB 1C 1C ,则A 1B 1⊥BC 1, 因为B 1C ⊥ BC 1,A 1B 1∩B 1C =B 1,所以BC 1⊥平面A 1B 1C , 又A 1C ⊂平面A 1B 1C ,所以BC 1⊥CA 1,故B 正确; 连接A 1C 1,设A 1C 1∩B 1D 1=O ,连接BO ,因为BB 1⊥平面A 1B 1C 1D 1,C 1O ⊂平面A 1B 1C 1D 1,则C 1O ⊥B 1B , 因为C 1O ⊥B 1D 1,B 1D 1∩B 1B =B 1,所以C 1O ⊥平面BB 1D 1D , 所以∠C 1BO 为直线BC 1与平面BB 1D 1D 所成的角,设正方体棱长为1,则C 1O =√22,BC 1=√2,sin∠C 1BO =C 1O BC 1=12,所以,直线BC 1与平面BB 1D 1D 所成的角为30∘,故C 错误;因为C 1C ⊥平面ABCD ,所以∠C 1BC 为直线BC 1与平面ABCD 所成的角,易得∠C 1BC =45∘,故D 正确. 故选:ABD13.【2022年新高考2卷】(多选)如图,四边形ABCD 为正方形,ED ⊥平面ABCD ,FB ∥ED,AB =ED =2FB ,记三棱锥E −ACD ,F −ABC ,F −ACE 的体积分别为V 1,V 2,V 3,则( )A.V3=2V2B.V3=V1C.V3=V1+V2D.2V3=3V1【答案】CD【解析】【分析】直接由体积公式计算V1,V2,连接BD交AC于点M,连接EM,FM,由V3=V A−EFM+V C−EFM计算出V3,依次判断选项即可.【详解】设AB=ED=2FB=2a,因为ED⊥平面ABCD,FB∥ED,则V1=13⋅ED⋅S△ACD=13⋅2a⋅12⋅(2a)2=43a3,V2=13⋅FB⋅S△ABC=13⋅a⋅12⋅(2a)2=23a3,连接BD交AC于点M,连接EM,FM,易得BD⊥AC,又ED⊥平面ABCD,AC⊂平面ABCD,则ED⊥AC,又ED∩BD=D,ED,BD⊂平面BDEF,则AC⊥平面BDEF,又BM=DM=12BD=√2a,过F作FG⊥DE于G,易得四边形BDGF为矩形,则FG=BD=2√2a,EG=a,则EM=√(2a)2+(√2a)2=√6a,FM=√a2+(√2a)2=√3a,EF=√a2+(2√2a)2=3a,EM2+FM2=EF2,则EM⊥FM,S△EFM=12EM⋅FM=3√22a2,AC=2√2a,则V3=V A−EFM+V C−EFM=13AC⋅S△EFM=2a3,则2V3=3V1,V3=3V2,V3=V1+V2,故A、B错误;C、D正确.故选:CD.14.【2022年全国甲卷】小明同学参加综合实践活动,设计了一个封闭的包装盒,包装盒如图所示:底面ABCD是边长为8(单位:cm)的正方形,△EAB,△FBC,△GCD,△HDA均为正三角形,且它们所在的平面都与平面ABCD垂直.(1)证明:EF//平面ABCD;(2)求该包装盒的容积(不计包装盒材料的厚度).【答案】(1)证明见解析;(2)6403√3.【解析】【分析】(1)分别取AB,BC的中点M,N,连接MN,由平面知识可知EM⊥AB,FN⊥BC,EM=FN,依题从而可证EM⊥平面ABCD,FN⊥平面ABCD,根据线面垂直的性质定理可知EM//FN,即可知四边形EMNF为平行四边形,于是EF//MN,最后根据线面平行的判定定理即可证出;(2)再分别取AD,DC中点K,L,由(1)知,该几何体的体积等于长方体KMNL−EFGH的体积加上四棱锥B−MNFE体积的4倍,即可解出.(1)如图所示:,分别取AB,BC 的中点M,N ,连接MN ,因为△EAB,△FBC 为全等的正三角形,所以EM ⊥AB,FN ⊥BC ,EM =FN ,又平面EAB ⊥平面ABCD ,平面EAB ∩平面ABCD =AB ,EM ⊂平面EAB ,所以EM ⊥平面ABCD ,同理可得FN ⊥平面ABCD ,根据线面垂直的性质定理可知EM//FN ,而EM =FN ,所以四边形EMNF 为平行四边形,所以EF//MN ,又EF ⊄平面ABCD ,MN ⊂平面ABCD ,所以EF//平面ABCD . (2)如图所示:,分别取AD,DC 中点K,L ,由(1)知,EF//MN 且EF =MN ,同理有,HE//KM,HE =KM ,HG//KL,HG =KL ,GF//LN,GF =LN ,由平面知识可知,BD ⊥MN ,MN ⊥MK ,KM =MN =NL =LK ,所以该几何体的体积等于长方体KMNL −EFGH 的体积加上四棱锥B −MNFE 体积的4倍.因为MN =NL =LK =KM =4√2,EM =8sin60∘=4√3,点B 到平面MNFE 的距离即为点B 到直线MN 的距离d ,d =2√2,所以该几何体的体积V =(4√2)2×4√3+4×13×4√2×4√3×2√2=128√3+2563√3=6403√3.15.【2022年全国甲卷】在四棱锥P−ABCD中,PD⊥底面ABCD,CD∥AB,AD=DC=CB=1 ,AB=2,DP=√3.(1)证明:BD⊥PA;(2)求PD与平面PAB所成的角的正弦值.【答案】(1)证明见解析;(2)√55.【解析】【分析】(1)作DE⊥AB于E,CF⊥AB于F,利用勾股定理证明AD⊥BD,根据线面垂直的性质可得PD⊥BD,从而可得BD⊥平面PAD,再根据线面垂直的性质即可得证;(2)以点D为原点建立空间直角坐标系,利用向量法即可得出答案.(1)证明:在四边形ABCD中,作DE⊥AB于E,CF⊥AB于F,因为CD//AB,AD=CD=CB=1,AB=2,所以四边形ABCD为等腰梯形,所以AE=BF=12,故DE=√32,BD=√DE2+BE2=√3,所以AD2+BD2=AB2,所以AD⊥BD,因为PD⊥平面ABCD,BD⊂平面ABCD,所以PD⊥BD,又PD∩AD=D,所以BD ⊥平面PAD , 又因PA ⊂平面PAD , 所以BD ⊥PA ;(2)解:如图,以点D 为原点建立空间直角坐标系, BD =√3,则A(1,0,0),B(0,√3,0),P(0,0,√3),则AP⃑⃑⃑⃑⃑ =(−1,0,√3),BP ⃑⃑⃑⃑⃑ =(0,−√3,√3),DP ⃑⃑⃑⃑⃑ =(0,0,√3), 设平面PAB 的法向量n⃑ =(x,y,z), 则有{n →⋅AP →=−x +√3z =0n →⋅BP →=−√3y +√3z =0,可取n ⃑ =(√3,1,1), 则cos〈n ⃑ ,DP ⃑⃑⃑⃑⃑ 〉=n ⃑ ⋅DP ⃑⃑⃑⃑⃑⃑|n ⃑ ||DP ⃑⃑⃑⃑⃑⃑ |=√55, 所以PD 与平面PAB 所成角的正弦值为√55.16.【2022年全国乙卷】如图,四面体ABCD 中,AD ⊥CD,AD =CD,∠ADB =∠BDC ,E 为AC 的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求三棱锥F−ABC 的体积.【答案】(1)证明详见解析(2)√34【解析】【分析】(1)通过证明AC⊥平面BED来证得平面BED⊥平面ACD.(2)首先判断出三角形AFC的面积最小时F点的位置,然后求得F到平面ABC的距离,从而求得三棱锥F−ABC的体积.(1)由于AD=CD,E是AC的中点,所以AC⊥DE.由于{AD=CDBD=BD∠ADB=∠CDB,所以△ADB≅△CDB,所以AB=CB,故AC⊥BD,由于DE∩BD=D,DE,BD⊂平面BED,所以AC⊥平面BED,由于AC⊂平面ACD,所以平面BED⊥平面ACD.(2)依题意AB=BD=BC=2,∠ACB=60°,三角形ABC是等边三角形,所以AC=2,AE=CE=1,BE=√3,由于AD=CD,AD⊥CD,所以三角形ACD是等腰直角三角形,所以DE=1. DE2+BE2=BD2,所以DE⊥BE,由于AC∩BE=E,AC,BE⊂平面ABC,所以DE⊥平面ABC.由于△ADB ≅△CDB ,所以∠FBA =∠FBC , 由于{BF =BF∠FBA =∠FBC AB =CB ,所以△FBA ≅△FBC ,所以AF =CF ,所以EF ⊥AC ,由于S △AFC =12⋅AC ⋅EF ,所以当EF 最短时,三角形AFC 的面积最小值. 过E 作EF ⊥BD ,垂足为F ,在Rt △BED 中,12⋅BE ⋅DE =12⋅BD ⋅EF ,解得EF =√32,所以DF =√12−(√32)2=12,BF =2−DF =32,所以BF BD =34.过F 作FH ⊥BE ,垂足为H ,则FH //DE ,所以FH ⊥平面ABC ,且FHDE =BFBD =34, 所以FH =34,所以V F−ABC =13⋅S △ABC ⋅FH =13×12×2×√3×34=√34.17.【2022年全国乙卷】如图,四面体ABCD 中,AD ⊥CD,AD =CD,∠ADB =∠BDC ,E 为AC 的中点.(1)证明:平面BED ⊥平面ACD ;(2)设AB =BD =2,∠ACB =60°,点F 在BD 上,当△AFC 的面积最小时,求CF 与平面ABD 所成的角的正弦值.【答案】(1)证明过程见解析(2)CF 与平面ABD 所成的角的正弦值为4√37【解析】 【分析】(1)根据已知关系证明△ABD ≌△CBD ,得到AB =CB ,结合等腰三角形三线合一得到垂直关系,结合面面垂直的判定定理即可证明;(2)根据勾股定理逆用得到BE ⊥DE ,从而建立空间直角坐标系,结合线面角的运算法则进行计算即可. (1)因为AD =CD ,E 为AC 的中点,所以AC ⊥DE ;在△ABD 和△CBD 中,因为AD =CD,∠ADB =∠CDB,DB =DB ,所以△ABD ≌△CBD ,所以AB =CB ,又因为E 为AC 的中点,所以AC ⊥BE ; 又因为DE,BE ⊂平面BED ,DE ∩BE =E ,所以AC ⊥平面BED , 因为AC ⊂平面ACD ,所以平面BED ⊥平面ACD . (2)连接EF ,由(1)知,AC ⊥平面BED ,因为EF ⊂平面BED , 所以AC ⊥EF ,所以S △AFC =12AC ⋅EF , 当EF ⊥BD 时,EF 最小,即△AFC 的面积最小. 因为△ABD ≌△CBD ,所以CB =AB =2, 又因为∠ACB =60°,所以△ABC 是等边三角形, 因为E 为AC 的中点,所以AE =EC =1,BE =√3, 因为AD ⊥CD ,所以DE =12AC =1,在△DEB 中,DE 2+BE 2=BD 2,所以BE ⊥DE .以E 为坐标原点建立如图所示的空间直角坐标系E −xyz ,则A (1,0,0),B(0,√3,0),D (0,0,1),所以AD ⃑⃑⃑⃑⃑ =(−1,0,1),AB ⃑⃑⃑⃑⃑ =(−1,√3,0), 设平面ABD 的一个法向量为n⃑ =(x,y,z ), 则{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =−x +z =0n ⃑ ⋅AB⃑⃑⃑⃑⃑ =−x +√3y =0,取y =√3,则n ⃑ =(3,√3,3),又因为C (−1,0,0),F (0,√34,34),所以CF⃑⃑⃑⃑⃑ =(1,√34,34), 所以cos⟨n ⃑ ,CF ⃑⃑⃑⃑⃑ ⟩=n ⃑ ⋅CF⃑⃑⃑⃑⃑|n ⃑ ||CF⃑⃑⃑⃑⃑ |=√21×√74=4√37,设CF 与平面ABD 所成的角的正弦值为θ(0≤θ≤π2), 所以sinθ=|cos⟨n ⃑ ,CF⃑⃑⃑⃑⃑ ⟩|=4√37, 所以CF 与平面ABD 所成的角的正弦值为4√37.18.【2022年新高考1卷】如图,直三棱柱ABC −A 1B 1C 1的体积为4,△A 1BC 的面积为2√2.(1)求A 到平面A 1BC 的距离;(2)设D 为A 1C 的中点,AA 1=AB ,平面A 1BC ⊥平面ABB 1A 1,求二面角A −BD −C 的正弦值. 【答案】(1)√2 (2)√32【解析】 【分析】(1)由等体积法运算即可得解;(2)由面面垂直的性质及判定可得BC ⊥平面ABB 1A 1,建立空间直角坐标系,利用空间向量法即可得解. (1)在直三棱柱ABC −A 1B 1C 1中,设点A 到平面A 1BC 的距离为h , 则V A−A 1BC =13S △A 1BC ⋅ℎ=2√23ℎ=V A 1−ABC =13S △ABC ⋅A 1A =13V ABC−A 1B 1C 1=43,解得ℎ=√2,所以点A 到平面A 1BC 的距离为√2; (2)取A 1B 的中点E ,连接AE ,如图,因为AA 1=AB ,所以AE ⊥A 1B , 又平面A 1BC ⊥平面ABB 1A 1,平面A 1BC ∩平面ABB 1A 1=A 1B , 且AE ⊂平面ABB 1A 1,所以AE ⊥平面A 1BC , 在直三棱柱ABC −A 1B 1C 1中,BB 1⊥平面ABC ,由BC ⊂平面A 1BC ,BC ⊂平面ABC 可得AE ⊥BC ,BB 1⊥BC , 又AE,BB 1⊂平面ABB 1A 1且相交,所以BC ⊥平面ABB 1A 1,所以BC,BA,BB 1两两垂直,以B 为原点,建立空间直角坐标系,如图,由(1)得AE =√2,所以AA 1=AB =2,A 1B =2√2,所以BC =2, 则A(0,2,0),A 1(0,2,2),B(0,0,0),C(2,0,0),所以A 1C 的中点D(1,1,1), 则BD⃑⃑⃑⃑⃑⃑ =(1,1,1),BA ⃑⃑⃑⃑⃑ =(0,2,0),BC ⃑⃑⃑⃑⃑ =(2,0,0), 设平面ABD 的一个法向量m ⃑⃑ =(x,y,z),则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =x +y +z =0m ⃑⃑ ⋅BA ⃑⃑⃑⃑⃑ =2y =0,可取m⃑⃑ =(1,0,−1),设平面BDC 的一个法向量n ⃑ =(a,b,c),则{m ⃑⃑ ⋅BD ⃑⃑⃑⃑⃑⃑ =a +b +c =0m ⃑⃑ ⋅BC ⃑⃑⃑⃑⃑ =2a =0, 可取n⃑ =(0,1,−1), 则cos〈m ⃑⃑ ,n ⃑ 〉=m⃑⃑⃑ ⋅n ⃑ |m ⃑⃑⃑ |⋅|n ⃑ |=√2×√2=12, 所以二面角A −BD −C 的正弦值为√1−(12)2=√32.19.【2022年新高考2卷】如图,PO 是三棱锥P −ABC 的高,PA =PB ,AB ⊥AC ,E 是PB 的中点.(1)证明:OE//平面PAC ;(2)若∠ABO =∠CBO =30°,PO =3,PA =5,求二面角C −AE −B 的正弦值. 【答案】(1)证明见解析 (2)1113 【解析】 【分析】(1)连接BO 并延长交AC 于点D ,连接OA 、PD ,根据三角形全等得到OA =OB ,再根据直角三角形的性质得到AO =DO ,即可得到O 为BD 的中点从而得到OE //PD ,即可得证; (2)过点A 作Az //OP ,如图建立平面直角坐标系,利用空间向量法求出二面角的余弦值,再根据同角三角函数的基本关系计算可得; (1)证明:连接BO 并延长交AC 于点D ,连接OA 、PD ,因为PO 是三棱锥P −ABC 的高,所以PO ⊥平面ABC ,AO,BO ⊂平面ABC , 所以PO ⊥AO 、PO ⊥BO ,又PA =PB ,所以△POA ≅△POB ,即OA =OB ,所以∠OAB =∠OBA ,又AB ⊥AC ,即∠BAC =90°,所以∠OAB +∠OAD =90°,∠OBA +∠ODA =90°, 所以∠ODA =∠OAD所以AO =DO ,即AO =DO =OB ,所以O 为BD 的中点,又E 为PB 的中点,所以OE //PD ,又OE ⊄平面PAC ,PD ⊂平面PAC , 所以OE //平面PAC(2)解:过点A 作Az //OP ,如图建立平面直角坐标系, 因为PO =3,AP =5,所以OA =√AP 2−PO 2=4,又∠OBA =∠OBC =30°,所以BD =2OA =8,则AD =4,AB =4√3,所以AC =12,所以O(2√3,2,0),B(4√3,0,0),P(2√3,2,3),C (0,12,0),所以E (3√3,1,32), 则AE ⃑⃑⃑⃑⃑ =(3√3,1,32),AB ⃑⃑⃑⃑⃑ =(4√3,0,0),AC ⃑⃑⃑⃑⃑ =(0,12,0), 设平面AEB 的法向量为n ⃑ =(x,y,z ),则{n ⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3x +y +32z =0n ⃑ ⋅AB ⃑⃑⃑⃑⃑ =4√3x =0 ,令z =2,则y =−3,x =0,所以n ⃑ =(0,−3,2);设平面AEC 的法向量为m⃑⃑ =(a,b,c ),则{m ⃑⃑ ⋅AE ⃑⃑⃑⃑⃑ =3√3a +b +32c =0m ⃑⃑ ⋅AC ⃑⃑⃑⃑⃑ =12b =0 ,令a =√3,则c =−6,b =0,所以m ⃑⃑ =(√3,0,−6);所以cos⟨n⃑ ,m⃑⃑ ⟩=n⃑ ⋅m⃑⃑⃑|n⃑ ||m⃑⃑⃑ |=√13×√39=−4√313设二面角C−AE−B为θ,由图可知二面角C−AE−B为钝二面角,所以cosθ=−4√313,所以sinθ=√1−cos2θ=1113故二面角C−AE−B的正弦值为1113;20.【2022年北京】如图,在三棱柱ABC−A1B1C1中,侧面BCC1B1为正方形,平面BCC1B1⊥平面ABB1A1,AB=BC=2,M,N分别为A1B1,AC的中点.(1)求证:MN∥平面BCC1B1;(2)再从条件①、条件②这两个条件中选择一个作为已知,求直线AB与平面BMN所成角的正弦值.条件①:AB⊥MN;条件②:BM=MN.注:如果选择条件①和条件②分别解答,按第一个解答计分.【答案】(1)见解析(2)见解析【解析】【分析】(1)取AB的中点为K,连接MK,NK,可证平面MKN//平面CBB1C1,从而可证MN//平面CB B1C1.(2)选①②均可证明BB1⊥平面ABC,从而可建立如图所示的空间直角坐标系,利用空间向量可求线面角的正弦值.(1)取AB的中点为K,连接MK,NK,由三棱柱ABC −A 1B 1C 1可得四边形ABB 1A 1为平行四边形, 而B 1M =MA 1,BK =KA ,则MK //BB 1,而MK ⊄平面CBB 1C 1,BB 1⊂平面CBB 1C 1,故MK //平面CBB 1C 1, 而CN =NA,BK =KA ,则NK //BC ,同理可得NK //平面CBB 1C 1, 而NK ∩MK =K,NK,MK ⊂平面MKN ,故平面MKN //平面CBB 1C 1,而MN ⊂平面MKN ,故MN //平面CBB 1C 1, (2)因为侧面CBB 1C 1为正方形,故CB ⊥BB 1, 而CB ⊂平面CBB 1C 1,平面CBB 1C 1⊥平面ABB 1A 1, 平面CBB 1C 1∩平面ABB 1A 1=BB 1,故CB ⊥平面ABB 1A 1, 因为NK //BC ,故NK ⊥平面ABB 1A 1, 因为AB ⊂平面ABB 1A 1,故NK ⊥AB ,若选①,则AB ⊥MN ,而NK ⊥AB ,NK ∩MN =N , 故AB ⊥平面MNK ,而MK ⊂平面MNK ,故AB ⊥MK ,所以AB ⊥BB 1,而CB ⊥BB 1,CB ∩AB =B ,故BB 1⊥平面ABC ,故可建立如所示的空间直角坐标系,则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2), 故BA ⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2), 设平面BNM 的法向量为n⃑ =(x,y,z), 则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0,从而{x +y =0y +2z =0,取z =−1,则n⃑ =(−2,2,−1), 设直线AB 与平面BNM 所成的角为θ,则 sinθ=|cos〈n ⃑ ,AB ⃑⃑⃑⃑⃑ 〉|=42×3=23. 若选②,因为NK //BC ,故NK ⊥平面ABB 1A 1,而KM ⊂平面MKN , 故NK ⊥KM ,而B 1M =BK =1,NK =1,故B 1M =NK , 而B 1B =MK =2,MB =MN ,故△BB 1M ≅△MKN , 所以∠BB 1M =∠MKN =90°,故A 1B 1⊥BB 1, 而CB ⊥BB 1,CB ∩AB =B ,故BB 1⊥平面ABC ,故可建立如所示的空间直角坐标系,则B(0,0,0),A(0,2,0),N(1,1,0),M(0,1,2), 故BA⃑⃑⃑⃑⃑ =(0,2,0),BN ⃑⃑⃑⃑⃑⃑ =(1,1,0),BM ⃑⃑⃑⃑⃑⃑ =(0,1,2), 设平面BNM 的法向量为n⃑ =(x,y,z),则{n ⃑ ⋅BN ⃑⃑⃑⃑⃑⃑ =0n ⃑ ⋅BM ⃑⃑⃑⃑⃑⃑ =0,从而{x +y =0y +2z =0,取z =−1,则n ⃑ =(−2,2,−1), 设直线AB 与平面BNM 所成的角为θ,则 sinθ=|cos〈n ⃑ ,AB⃑⃑⃑⃑⃑ 〉|=42×3=23.21.【2022年浙江】如图,已知ABCD 和CDEF 都是直角梯形,AB//DC ,DC//EF ,AB =5,DC =3,EF =1,∠BAD =∠CDE =60°,二面角F −DC −B 的平面角为60°.设M ,N 分别为AE,BC 的中点.(1)证明:FN ⊥AD ;(2)求直线BM 与平面ADE 所成角的正弦值. 【答案】(1)证明见解析; (2)5√714.【解析】 【分析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ,由平面知识易得FC =BC ,再根据二面角的定义可知,∠BCF =60∘,由此可知,FN ⊥BC ,FN ⊥CD ,从而可证得FN ⊥平面ABCD ,即得FN ⊥AD ;(2)由(1)可知FN ⊥平面ABCD ,过点N 做AB 平行线NK ,所以可以以点N 为原点,NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ,求出平面ADE 的一个法向量,以及BM ⃑⃑⃑⃑⃑⃑ ,即可利用线面角的向量公式解出. (1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H .∵四边形ABCD 和EFCD 都是直角梯形,AB//DC,CD//EF,AB =5,DC =3,EF =1,∠BAD =∠CDE =60°,由平面几何知识易知,DG =AH =2,∠EFC =∠DCF =∠DCB =∠ABC =90°,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt △EGD 和Rt △DHA ,EG =DH =2√3, ∵DC ⊥CF,DC ⊥CB ,且CF ∩CB =C ,∴DC ⊥平面BCF,∠BCF 是二面角F −DC −B 的平面角,则∠BCF =60∘, ∴△BCF 是正三角形,由DC ⊂平面ABCD ,得平面ABCD ⊥平面BCF ,∵N 是BC 的中点,∴ FN ⊥BC ,又DC ⊥平面BCF ,FN ⊂平面BCF ,可得FN ⊥CD ,而BC ∩CD =C ,∴FN ⊥平面ABCD ,而AD ⊂平面ABCD ∴FN ⊥AD . (2)因为FN ⊥平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点, NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N −xyz ,设A(5,√3,0),B(0,√3,0),D(3,−√3,0),E(1,0,3),则M (3,√32,32),∴BM ⃑⃑⃑⃑⃑⃑ =(3,−√32,32),AD ⃑⃑⃑⃑⃑ =(−2,−2√3,0),DE⃑⃑⃑⃑⃑ =(−2,√3,3) 设平面ADE 的法向量为n⃑ =(x,y,z) 由{n ⃑ ⋅AD ⃑⃑⃑⃑⃑ =0n ⃑ ⋅DE ⃑⃑⃑⃑⃑ =0 ,得{−2x −2√3y =0−2x +√3y +3z =0 ,取n ⃑ =(√3,−1,√3),设直线BM 与平面ADE 所成角为θ, ∴sinθ=|cos〈n⃑ ,BM ⃑⃑⃑⃑⃑⃑ 〉|=|n⃑ ⋅BM ⃑⃑⃑⃑⃑⃑⃑ ||n⃑ |⋅BM ⃑⃑⃑⃑⃑⃑⃑ |=|3√3+√32+3√32|√3+1+3⋅√9+34+94=√3√7⋅2√3=5√714.1.(2022·全国·模拟预测)已知正方体中1111ABCD A B C D -,E ,G 分别为11A D ,11C D 的中点,则直线1A G ,CE 所成角的余弦值为( )A B C D 【答案】C 【解析】 【分析】根据异面直线所成角的定义,取AB 的中点F ,则∠ECF (或其补角)为直线1A G 与CE 所成角,再解三角形即可得解. 【详解】如图所示:,取AB 的中点F ,连接EF ,CF ,易知1A G CF ∥,则∠ECF (或其补角)为直线1A G 与CE 所成角.不妨设2AB =,则CF =EF =3EC =,由余弦定理得cosECF ∠==,即直线1A G 与CE 故选:C .2.(2022·全国·模拟预测(理))如图,在三棱台111ABC A B C -中,1AA ⊥平面ABC ,90ABC ∠=︒,111111AA A B B C ===,2AB =,则AC 与平面11BCC B 所成的角为( )A .30B .45︒C .60︒D .90︒【答案】A 【解析】 【分析】将棱台补全为棱锥,利用等体积法求A 到面11BCC B 的距离,结合线面角的定义求AC 与平面11BCC B 所成角的大小. 【详解】将棱台补全为如下棱锥D ABC -,由90ABC ∠=︒,111111AA A B B C ===,2AB =,易知:2DA BC ==,AC = 由1AA ⊥平面ABC ,,AB AC ⊥平面ABC ,则1AA AB ⊥,1AA AC ⊥,所以BD =CD =222BC BD CD +=,所以122BCD S =⨯⨯=△A 到面11BCC B 的距离为h ,又D ABC A BCD V V --=,则111222323h ⨯⨯⨯⨯=⨯h = 综上,AC 与平面11BCC B 所成角[0,]2πθ∈,则1sin 2h AC θ==,即6πθ=. 故选:A3.(2022·浙江湖州·模拟预测)如图,已知四边形ABCD ,BCD △是以BD 为斜边的等腰直角三角形,ABD △为等边三角形,2BD =,将ABD △沿对角线BD 翻折到PBD △在翻折的过程中,下列结论中不正确...的是( )A .BD PC ⊥B .DP 与BC 可能垂直C .直线DP 与平面BCD 所成角的最大值是45︒ D .四面体PBCD 【答案】C 【解析】 【分析】对于A ,取BD 的中点M ,即可得到BD ⊥面PMC ,A 选项可判断对于B ,采用反证法,假设DP BC ⊥,则BC ⊥面PCD ,再根据题目所给的长度即可判断;对于C ,当面PBD ⊥面BCD 时,此时直线DP 与平面BCD 所成角有最大值,判断即可;对于D ,当面PBD ⊥面BCD 时,此时四面体PBCD 的体积有最大值,计算最大体积判断即可 【详解】如图所示,取BD 的中点M ,连接,PM CMBCD △是以BD 为斜边的等腰直角三角形,BD CM ∴⊥ABD △为等边三角形,BD PM ∴⊥BD ∴⊥面PMC ,BD PC ∴⊥ ,故A 正确 对于B ,假设DP BC ⊥,又BC CD ⊥BC ∴⊥面PCD ,BC PC ∴⊥,又2,PB BC ==1PC ⎤⎦,故DP 与BC 可能垂直,故B 正确当面PBD ⊥面BCD 时,此时PM ⊥面BCD ,PDB ∠即为直线DP 与平面BCD 所成角 此时60PDB ︒∠=,故C 错误当面PBD ⊥面BCD 时,此时四面体PBCD 的体积最大,此时的体积为:111(332BCDV S PM ==⨯=,故D 正确 故选:C4.(2022·河南安阳·模拟预测(理))已知球O 的体积为125π6,高为1的圆锥内接于球O ,经过圆锥顶点的平面α截球O 和圆锥所得的截面面积分别为12,S S ,若125π8S =,则2S =( )A .2BCD .【答案】C 【解析】 【分析】根据给定条件,求出球O 半径,平面α截球O 所得截面小圆半径,圆锥底面圆半径,再求出平面α截圆锥所得的截面等腰三角形底边长及高即可计算作答. 【详解】球O 半径为R ,由34π125π36R =得52R =,平面α截球O 所得截面小圆半径1r ,由21128π5πS r ==得1r =因此,球心O 到平面α的距离1d r ===,而球心O 在圆锥的轴上,则圆锥的轴与平面α所成的角为45,因圆锥的高为1,则球心O 到圆锥底面圆的距离为132d =,于是得圆锥底面圆半径2r =,令平面α截圆锥所得截面为等腰PAB △,线段AB 为圆锥底面圆1O 的弦,点C 为弦AB 中点,依题意,145CPO ∠=,111CO PO ==,PC =AB ==所以212AB S PC =⋅=. 故选:C 【点睛】关键点睛:解决与球有关的内切或外接问题时,关键是确定球心的位置,再利用球的截面小圆性质求解.5.(2022·浙江·模拟预测)如图,矩形BDEF 所在平面与正方形ABCD 所在平面互相垂直,2,1BD DE ==,点P 在线段EF 上,给出下列命题:①存在点P ,使得直线//DP 平面ACF ②存在点P ,使得直线DP ⊥平面ACF③直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦④三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π 其中所有真命题的序号是( ) A .①③ B .①④C .②④D .①③④ 【答案】D 【解析】 【分析】取EF 中点推理判断①;假定DP ⊥平面ACF ,分析判断②;确定直线DP 与平面ABCD 所成角,求出临界值判断③;求出ACF 外接圆面积判断④作答.令AC BD O =,连接,FO DF ,令EF 中点为G ,连DG ,如图,依题意,O 是,BD AC 的中点,对于①,在矩形BDEF 中,//DO FG ,DO FG =,四边形DOFG 是平行四边形,直线//DG OF ,OF ⊂平面ACF ,DG ⊄平面ACF ,则//DG 平面ACF ,当P 是线段EF 中点G 时,直线//DP 平面ACF ,①正确;对于②,假定直线DP ⊥平面ACF ,由①知,DP OF ⊥,DP DG ⊥,当点P 在线段EF 上任意位置(除点G 外),PDG ∠均为锐角,即DP 不垂直于DG ,也不垂直于OF ,因此,不存在点P ,使得直线DP ⊥平面ACF ,②不正确;对于③,平面BDEF ⊥平面ABCD ,DP 在平面ABCD 内射影在直线BD 上,直线DP 与平面ABCD 所成角为PDB ∠,当点P 由点E 运动到点F 的过程中,PDB ∠逐渐减小,当P 与E 重合时,PDB ∠最大,为90EDB ∠=,max (sin )1PDB ∠=,当P 与F 重合时,PDB ∠最小,为FDB ∠,min (sin )BF PDB DF ∠==所以直线DP 与平面ABCD 所成角的正弦值的取值范围是⎤⎥⎣⎦,③正确;对于④,在ACF 中,2AC =,|AF CF ==FO sin OF FAC AF ∠==由正弦定理得ACF 外接圆直径2sin FC r FAC ==∠半径r =圆面积为298S r ππ==,三棱锥A CDE -的外接球被平面ACF 所截取的截面是ACF 外接圆, 因此三棱锥A CDE -的外接球被平面ACF 所截取的截面面积是98π,④正确, 所以所有真命题的序号是①③④. 故选:D6.(2022·四川省泸县第二中学模拟预测(文))已知1O 是正方体1111ABCD A B C D -的中心O 关于平面1111D C B A 的对称点,则下列说法中正确的是( )A .11O C 与1A C 是异面直线B .11OC ∥平面11A BCD C .11O C AD ⊥ D .11O C ⊥平面11BDD B【答案】B 【解析】 【分析】根据正方体的性质、空间直线与平面的位置关系,即可对选项做出判断. 【详解】连接1A C 、1AC ,交于点O ,连接11A C 、11B D ,交于点P . 连接AC 、BD 、1A B 、1D C 、1O O .由题可知,1O 在平面11A C CA 上,所以11O C 与1A C 共面,故A 错误;在四边形11OO C C 中,11//O O C C 且11O O C C =,所以四边形11OO C C 为平行四边形. 11//O C OC ∴.OC ⊂平面11A BCD ,11O C ⊄平面11A BCD ,11O C ∴∥平面11A BCD ,故B 正确;由正方体的性质可得1111AC B D ⊥,因为1111O B O D =,所以111O P B D ⊥,又111O P AC P =,11B D ∴⊥平面111O AC , 1111B D O C ∴⊥,又11//B D BD , 11BD O C ∴⊥,而AD 与BD 所成角为45︒,所以显然11O C 与AD 不垂直,故C 错误;显然11O C 与11O B 不垂直,而11O B ⊂平面11BDD B ,所以11O C 与平面11BDD B 不垂直,故D 错误. 故选:B.7.(2022·北京·北大附中三模)已知平面,,αβγ,直线m 和n ,则下列命题中正确的是( ) A .若,m m αβ⊥⊥,则αβ∥ B .若,αγβγ⊥⊥,则αβ∥ C .若,m n m α⊥⊥,则n α∥ D .若,m n αα∥∥,则m n ∥ 【答案】A 【解析】 【分析】对于A 选项,垂直于同一条直线的两个平面互相平行;对于B 选项,垂直于同一个平面的两个平面有可能相交,也有可能互相平行; 对于C 选项,由线面垂直的性质即可判断;对于D 选项,平行于同一个平面的两条直线有可能相交、平行或异面. 【详解】选项A 正确,因为垂直于同一直线的两个平面互相平行; 选项B 错误,平面α和β也可以相交; 选项C 错误,直线n 可能在平面α内; 选项D 错误,直线m 和n 还可能相交或者异面. 故选:A.8.(2022·云南师大附中模拟预测(理))已知正方形ABCD 的边长为ABC 沿对角线AC 折起,使得二面角B AC D --的大小为90°.若三棱锥B ACD -的四个顶点都在球O 的球面上,G 为AC 边的中点,E ,F 分别为线段BG ,DC 上的动点(不包括端点),且BE ,当三棱锥E ACF -的体积最大时,过点F 作球O 的截面,则截面面积的最小值为( )A .B .2πC .32πD .89π【答案】D 【解析】 【分析】根据面面垂直的判定定理得BG ⊥平面ACD ,继而表示出三棱锥E ACF -的体积,求出x =V 取得最大值,在∠GCF 中,由余弦定理,得GF =当GF 垂直于截面时,截面圆的面积最小,继而得解. 【详解】因为正方形ABCD 的边长为4AC =.如图,由于平面ABC ⊥平面ACD ,平面ABC 平面ACD AC =,又G 为AC 边的中点,则有BG AC ⊥,所以BG ⊥平面ACD .设CF x =(0x <<,则BE =,所以三棱锥E ACF -的体积13ACF V S EG ==△2111122sin 4(22))323223AC CF ACF EG x x x ⨯∠=⨯⨯-=-,当x =时,V 取得最大值.由于GA GB GC GD ===,则球O 的球心即为G ,且球O 的半径2R =.又在△GCF中,由余弦定理,得cos GF GC CF ACF =∠=。
千题百炼- 立体几何综合大题必刷100题(原卷版)
专题20 立体几何综合大题必刷100题任务一:善良模式(基础)1-30题1.在棱长为1的正方体1111ABCD A B C D -中,E 为线段11A B 的中点,F 为线段AB 的中点.(1)求点B 到直线1AC 的距离;(2)求直线FC 到平面1AEC 的距离.2.如图,正方形11ABB A 的边长为2,11,AB A B 的中点分别为C ,1C ,正方形11ABB A 沿着1CC 折起形成三棱柱111ABC A B C -,三棱柱111ABC A B C -中,1,AC BC AD AA λ⊥=.(1)证明:当12λ=时,求证:1DC ⊥平面BCD ;(2)当14λ=时,求二面角1D BC C --的余弦值.3.如图,直三棱柱111ABC A B C -的底面为直角三角形,两直角边AB 和AC 的长分别为4和2,侧棱1AA 的长为5.(1)求三棱柱111ABC A B C -的体积;(2)设M 是BC 中点,求直线1A M 与平面ABC 所成角的正切值.4.如图,在三棱锥P ABC -中,PA ⊥底面ABC ,90.BAC ∠=︒点D ,E ,N 分别为棱P A ,PC ,BC 的中点,M 是线段AD 的中点,4PA AC ==,2AB =.(1)求证://MN 平面BDE ;(2)求二面角C EM N --的正弦值;(3)已知点H 在棱P A 上,且直线NH 与直线BE ,求线段AH 的长.5.已知圆锥的顶点为P ,底面圆心为O ,半径为2.(1)设圆锥的母线长为4,求圆锥的体积;(2)设4PO =,OA 、OB 是底面半径,且90AOB ∠=︒,M 为线段AB 的中点,如图.求异面直线PM 与OB 所成的角的余弦值.6.如图所示,已知四棱锥P ABCD -中,四边形ABCD 为正方形,三角形PAB 为正三角形,侧面PAB ⊥底面ABCD ,M 是棱AD 的中点.(1)求证:PC BM ⊥;(2)求二面角B PM C --的正弦值.7.已知点E ,F 分别是正方形ABCD 的边AD ,BC 的中点.现将四边形EFCD 沿EF 折起,使二面角C EF B --为直二面角,如图所示.(1)若点G ,H 分别是AC ,BF 的中点,求证://GH 平面EFCD ;(2)求直线AC 与平面ABFE 所成角的正弦值.8.已知如图1所示,等腰ABC 中,4AB AC ==,BC =D 为BC 中点,现将ABD 沿折痕AD 翻折至如图2所示位置,使得3BDC π∠=,E 、F 分别为AB 、AC 的中点.(1)证明://BC 平面DEF ;(2)求四面体BCDE 的体积.9.在三棱柱ABC -A 1B 1C 1中,AB =2,BC =BB 1=4,1AC AB ==BCC 1=60°.(1)求证:平面ABC 1⊥平面BCC 1B 1:(2)设二面角C -AC 1-B 的大小为θ,求sinθ的值.10.如图,四棱锥P ABCD -中,底面ABCD 是直角梯形,//AD BC ,∠BAD =90°,已知PA PC ==,2,3AD AB BC ===.(1)证明:AC PD ⊥;(2)若二面角P AC B --的余弦值为13,求四棱锥P ABCD -的体积.11.如图,四棱柱ABCD —A 1B 1C 1D 1中,底面ABCD 和侧面BCC 1B 1都是矩形,E 是CD 的中点,D 1E ⊥CD ,AB =2BC =2.(1)求证:平面CC 1D 1D ⊥底面ABCD ;(2)若平面BCC 1B 1与平面BED 1所成的锐二面角的大小为3π,求线段ED 1的长度.12.如图,四棱锥P ABCD -的底面ABCD 是边长为2的正方形,平面PAD ⊥平面ABCD ,PAD △是斜边PA 的长为E ,F 分别是棱PA ,PC 的中点,M 是棱BC 上一点.(1)求证:平面DEM ⊥平面PAB ;(2)若直线MF 与平面ABCD E DM F --的余弦值.13.如图所示,四棱锥E ABCD -的底面ABCD 是边长为2的正方形,侧面EAB ⊥底面ABCD ,EA EB =,F 在侧棱CE 上,且BF ⊥平面ACE .(1)求证:AE ⊥平面BCE ;(2)求点D 到平面ACE 的距离.14.在三棱锥B -ACD 中,平面ABD ⊥平面ACD ,若棱长AC =CD =AD =AB =1,且∠BAD =30°,求点D 到平面ABC 的距离.15.如图,在长方体1111ABCD A B C D -中,1AB BC ==,12BB =,E 为棱1AA 的中点.(1)证明:BE ⊥平面11EB C ;(2)求二面角1B EC C --的大小.16.如下图,在四棱锥S ABCD -中,底面ABCD 是正方形,平面SAD ⊥平面ABCD ,2SA SD ==,3AB =.(1)求SA 与BC 所成角的余弦值;(2)求证:AB SD ⊥.17.如图,四棱锥P ABCD -的底面是矩形,PD ⊥底面ABCD ,M 为BC 的中点,且PB AM ⊥.(1)证明:平面PAM ⊥平面PBD ;(2)若1PD DC ==,求四棱锥P ABCD -的体积.18.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,120,1,4,ABC AB BC PA ∠=︒===M ,N 分别为,BC PC 的中点,,PD DC PM MD ⊥⊥.(1)证明:AB PM ⊥;(2)求直线AN 与平面PDM 所成角的正弦值.19.如图,.AB O PA O C O 是圆的直径,垂直圆所在的平面,是圆上的点(I )求证BC PAC ⊥平面;(II )设//.Q PA G AOC QG PBC ∆为的中点,为的重心,求证:平面20.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD ⊥,点E 在线段AD 上,且CE AB ∥.(Ⅰ)求证:CE ⊥平面PAD ;(Ⅰ)若1==PA AB ,3AD =,CD =,45CDA ∠=︒,求四棱锥P ABCD -的体积.21.如图,直三棱柱ABC A B C '''-,90BAC ∠=,,AB AC AA λ'==点M ,N 分别为A B '和B C ''的中点. (∠)证明:MN ∠平面A ACC '';(∠)若二面角A MN C '--为直二面角,求λ的值.22.如图,在三棱锥S ABC -中, 侧面SAB 与侧面SAC 均为等边三角形,90,BAC ∠=︒O 为BC 中点. (∠)证明:SO ⊥平面;ABC(∠)求二面角A SC B --的余弦值.23.如图,在四棱锥P—ABCD 中,底面是边长为ⅠBAD =120°,且PAⅠ平面ABCD ,PA =M ,N 分别为PB ,PD 的中点.(1)证明:MNⅠ平面ABCD ;(2) 过点A 作AQⅠPC ,垂足为点Q ,求二面角A—MN—Q 的平面角的余弦值.24.如图,在三棱锥P ABC -中,AB BC ==4PA PB PC AC ====∠O 为AC 的中点. ∠1)证明:PO ⊥平面ABC ∠∠2)若点M在棱BC上,且2,求点C到平面POM的距离.MC MB25.如图,在三棱锥P∠ABC中,P A∠AB∠P A∠BC∠AB∠BC∠P A∠AB∠BC∠2∠D为线段AC的中点,E为线段PC上一点.(1)求证:P A∠BD∠(2)求证:平面BDE∠平面P AC∠(3)当P A∠平面BDE时,求三棱锥E∠BCD的体积.26.如图,在四棱锥P-ABCD中,PAⅠCD,ADⅠBC,ⅠADC=ⅠPAB=90°,BC=CD=1AD.2(Ⅰ)在平面PAD 内找一点M ,使得直线CMⅠ平面PAB ,并说明理由;(Ⅰ)证明:平面PABⅠ平面PBD .27.如图,在三棱台ABC–DEF 中,平面BCFEⅠ平面ABC ,ⅠACB=90°,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BFⅠ平面ACFD ;(Ⅰ)求直线BD 与平面ACFD 所成角的余弦值.28.如图,在直三棱柱ABC-A 1B 1C 1中,D ,E 分别为AB ,BC 的中点,点F 在侧棱B 1B 上,且11B D A F ⊥ ,1111AC A B ⊥.求证:(1)直线DE 平面A 1C 1F ;(2)平面B 1DEⅠ平面A 1C 1F.29.如图,在三棱锥111ABC A B C -中,11BAC 90AB AC 2,4,A AA ∠====,在底面ABC 的射影为BC 的中点,D 为11B C 的中点.∠1)证明:11D A BC A ⊥平面∠∠2)求直线1A B 和平面11B C B C 所成的角的正弦值.30.如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,,,60,AB AD AC CD ABC PA AB BC ⊥⊥∠===,E 是PC 的中点.(∠)证明CD AE ⊥;(∠)证明PD ⊥平面ABE ;--的大小.(∠)求二面角A PD C任务二:中立模式(中档)30-70题31.如图,在四棱锥P-ABCD中,底面ABCD为菱形,△P AD为正三角形,平面P AD⊥平面ABCD,E,F 分别是AD,CD的中点.(1)证明:BD⊥PF;(2)若AD=DB=2,求点C到平面PBD的距离;32.如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠P AD为正三角形,平面P AD⊥平面ABCD,E,F 分别是AD,CD的中点.(1)证明:BD⊥PF;(2)若∠BAD=60°,求直线PC与平面PBD所成角的正弦值;33.如图,在四棱锥E -ABCD 中,AB ⊥CE ,AE ⊥CD ,BC AD ∥,AB =3,CD =4,AD =2BC =10.(1)证明:∠AED 是锐角;(2)若AE =10,求二面角A -BE -C 的余弦值.34.如图,在直四棱柱1111ABCD A B C D -中,12A E EA =(1)若F 为1BB 的中点,试在11A B 上找一点P ,使//PF 平面1CD E ;(2)若四边形ABCD 是正方形,且1BB 与平面1CD E ,求二面角1E D C D --的余弦值.35.如图1,已知ADE 为等边三角形,四边形ABCD 为平行四边形,1,2,BC BD BA ===ADE 沿AD 向上折起,使点E 到达点P 位置,如图2所示;且平面PAD ⊥平面PBD .(1)证明:PA BD ⊥;(2)在(1)的条件下求二面角A PB C --的余弦值.36.如图所示,在四棱锥P ABCD -中,PA ⊥平面ABCD ,2PA =,四边形ABCD 为梯形,//AB CD ,3AB =,1CD =,AD =60ABC ∠=,30BAD ∠=,点E 在AB 上,满足AD DE ⊥.(1)求证:平面PAD ⊥平面PBC ;(2)若点F 为PA 的中点,求平面PCD 与平面DEF 所成角的余弦值.37.在四棱锥P ABCD -中,PA ⊥平面ABCD ,22PA AB ==,90ABC ACD ∠=∠=,60BAC CAD ∠=∠=,E 为PD 的中点,在平面PCD 内作EF PC ⊥于点F .(1)求证:平面AEF ⊥平面PAC ;(2)求二面角P AC E --的余弦值.38.在正方体1111ABCD A B C D -中,点E 、F 分别在AB 、BC 上,且13AE AB =,13BF BC =.(1)求证:11A F C E ⊥;(2)求直线1A F 与平面1B EF 所成角的正弦值.39.如图,在多面体1111ABCD A B C D -中,1111,,,AA BB CC DD 均垂直于平面ABCD ,//AD BC ,11=2AB BC CD AA CC ====,1=1BB ,14AD DD ==.(1)证明:11A C ⊥平面11CDD C ;(2)求1BC 与平面11AA B B 所成角的余弦值.40.某商品的包装纸如图1,其中菱形ABCD 的边长为3,且60ABC ∠=︒,AE AF ==BE DF ==E ,F ,M ,N 汇聚为一点P ,恰好形成如图2的四棱锥形的包裹.(1)证明PA ⊥底面ABCD ;(2)设点T 为BC 上的点,且二面角B PA T --,试求PC 与平面P AT 所成角的正弦值.41.如图,在四棱锥P ABCD -中,底面ABCD 是菱形,侧面PAB ⊥底面ABCD ,且P A =AB ,90PAB ∠=.(1)证明:PC BD ⊥;(2)若60ABC ∠=,求直线PC 与平面PBD 所成角的正弦值.42.1.如图,正方形ABCD 所在平面与等边ABE △所在平面成的锐二面角为60,设平面ABE 与平面CDE 相交于直线l .(1)求证://l CD ;(2)求直线DE 与平面BCE 所成角的正弦值.43.如图,在四棱锥P ABCD -中,//AD BC ,AB AD ⊥,平面APD ⊥平面ABCD ,点E 在AD 上,且AB BC AE ED ===,PA PD ==.(1)求证:CE PD ⊥.(2)设平面PAB ⋂平面PCD l =,求二面角E l A --的余弦值.44.如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,120ADC =∠︒,4BC =,M ,N 分别为BC ,PC 的中点,1,,CD PD DC PM MD =⊥⊥.(1)证明:BC PM ⊥;(2)若PA =BN 与平面PDC 所成角的正弦值.45.如图,已知点P 在圆柱1OO 的底面圆O 上,120AOP ∠=,圆O 的直径4AB =,圆柱的高13OO =.(1)求点A到平面1A PO的距离;--的余弦值大小.(2)求二面角1A PB O46.如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=2,点P为棱B1C1的中点,点Q为线段A1B上的一动点.(1)求证:当点Q为线段A1B的中点时,PQ⊥平面A1BC;BA,试问:是否存在实数λ,使得平面A1PQ与平面B1PQ(2)设BQ=λ1在,求出这个实数λ;若不存在,请说明理由.47.如图,在三棱锥P ABC -中,PA ⊥底面ABC ,90ABC ∠=︒,2PA =,AC =(1)求证:平面PBC ⊥平面PAB ;(2)若二面角P BC A --的大小为45︒,过点A 作AN PC ⊥于N ,求直线AN 与平面PBC 所成角的大小.48.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是菱形,2PA AB ==,60BAD ∠=︒.(1)求证:直线BD ⊥平面PAC ;(2)设点M 在线段PC 上,且二面角C MB A --的余弦值为57,求点M 到底面ABCD 的距离.49.如图,在三棱锥P ABC -中,底面ABC 是边长2的等边三角形,PA PC ==F 在线段BC 上,且3FC BF =,D 为AC 的中点,E 为的PD 中点.(Ⅰ)求证:EF //平面PAB ;(Ⅱ)若二面角P AC B --的平面角的大小为2π3,求直线DF 与平面PAC 所成角的正弦值.50.如图,直四棱柱1111ABCD A B C D -的底面是菱形,侧面是正方形,60DAB ∠=︒,经过对角线1AC 的平面和侧棱1BB 相交于点F ,且12B F BF =.(1)求证:平面1AC F ⊥平面11BCC B ;(2)求二面角1F AC C --的余弦值.51.直角梯形11AA B B 绕直角边1AA 旋转一周的旋转的上底面面积为9π,下底面面积为36π,侧面积为,且二面角111B AA C --为90,P ,Q 分别在线段1CC ,BC 上.(∠)若P ,Q 分别为1CC ,BC 中点,求1AB 与PQ 所成角的余弦值;(∠)若P 为1CC 上的动点、Q 为BC 的中点,求PQ 与平面11AAC C 所成最大角的正切值,并求此时二面角Q AP C --的余弦值.52.正多面体也称柏拉图立体,被喻为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体QPTR 和一个正八面体AEFBHC 的棱长都是a (如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.(1)求新多面体的体积;(2)求二面角A BF C --的余弦值;(3)求新多面体为几面体?并证明.53.中国是风筝的故乡,南方称“鹞”,北方称“鸢”,如图,某种风筝的骨架模型是四棱锥P ABCD -,其中AC BD ⊥于O ,4OA OB OD ===,8OC =,PO ⊥平面ABCD .(1)求证:PD AC ⊥;(2)试验表明,当12PO OA =时,风筝表现最好,求此时直线PD 与平面PBC 所成角的正弦值.54.在陕西汉中勉县的汉江河与定军山武侯坪一带,经常出土有铜、铁扎马钉等兵器文物.扎马钉(如题21图(1))是三国时蜀汉的著名政治家、军事家诸葛亮所发明的一种对付骑兵的武器,状若荆刺,故学名蒺藜,有铜、铁两种.扎马钉有四个锋利的尖爪,随手一掷,三尖撑地,一尖直立向上,推倒上尖,下尖又起,始终如此,使触者不能避其锋而被刺伤.即总有一个尖垂直向上,三尖对称支承于地.简化扎马钉的结构,如图(2),记组成该“钉”的四条等长的线段公共点为O ,钉尖为i A (1,2,3,4i =).(Ⅰ)判断四面体1234A A A A -的形状特征; (Ⅱ)若某个出土的扎马钉因年代久远,有一尖爪受损,其长度仅剩其他尖爪长度的23(即4123OA OA '=),如图(3),将2A ,3A ,4A '置于地面,求1OA 与面234A A A '所成角θ的正弦值.55.正多面体也称柏拉图立体,被誉为最有规律的立体结构,其所有面都只由一种正多边形构成的多面体(各面都是全等的正多边形,且每一个顶点所接的面数都一样,各相邻面所成二面角都相等).数学家已经证明世界上只存在五种柏拉图立体,即正四面体、正六面体、正八面体、正十二面体、正二十面体.已知一个正四面体QPTR 和一个正八面体AEFBHC 的棱长都是a (如图),把它们拼接起来,使它们一个表面重合,得到一个新多面体.(1)求新多面体的体积;(2)求正八面体AEFBH 中二面角A BF C --的余弦值;(3)判断新多面体为几面体?(只需给出答案,无需证明)56.如图,已知在四棱锥P ABCD -中,底面ABCD 为等腰梯形,//BC AD ,AB CD =,E 为棱PB 上一点,AC 与BD 交于点O ,且AC BD ⊥,1AD =,3BC PC PB ===,PO =(1)证明:AC DE ⊥;(2)是否存在点E ,使二面角B DC E --E 点位置,若不存在,请说明理由.57.如图,在三棱柱111ABC A B C ﹣中点,E 在棱1BB 上,点F 在棱CC 1上,且点,E F 均不是棱的端点,1,AB AC BB ⊥=平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.(1)求证:四边形BEFC 是矩形;(2)若2,AE EF BE ==ABC 与平面AEF 所成角的正弦值.58.如图,在三棱台111ABC A B C -中,11190,4,2,BAC AB AC A A A B ∠=︒====侧棱1A A ⊥平面,ABC 点D 在棱1CC 上,且1CD CC λ=(1)证明:1BB ⊥平面1AB C ;(2)当二面角C BD A --的余弦值为,求λ的值.59.在直四棱柱1111ABCD A B C D -中,底面ABCD 为平行四边形,1,45AB BC ABC ∠===,点M 在棱1CC 上,点N 是BC 的中点,且满足1AM B N ⊥.(1)证明:AM ⊥平面11A B N ;(2)若M 是1CC 的中点,求二面角111A B N C --的正弦值.60.在四棱锥P ABCD -中,四边形ABCD 是边长为4的菱形,PB BD PD ===PA =(1)证明:PC ⊥平面ABCD ;(2)如图,取BC 的中点为E ,在线段DE 上取一点F 使得23DF FE =,求二面角F PA C --的大小.61.如图,在底面是菱形的四棱柱1111ABCD A B C D -中,60ABC ∠=,1112,AA AC A B A D ====E 在1A D 上.(1)求证:1AA ⊥平面ABCD ;(2)当E 为线段1A D 的中点时,求点1A 到平面EAC 的距离.62.已知四棱锥P ABCD -的底面是菱形,对角线AC 、BD 交于点O ,4OP OA ==,3OB =,OP ⊥底面ABCD ,设点M 满足()01PM MC λλ=<<.(1)若三棱锥P MBD -体积是169,求λ的值;(2)若直线PA 与平面MBD λ的值.63.光学器件在制作的过程中往往需要进行切割,现生产一种光学器件,有一道工序为将原材料切割为两个部分,然后在截面上涂抹一种光触媒化学试剂,加入纳米纤维导管后粘合.在如图所示的原材料器件直三棱柱ABC﹣A'B'C'中,AB⊥AC,AB=AC=AA'=a,现经过AB作与底面ABC所成角为θ的截面,且截面与B'C',A'C'分别交于不同的两点E,F.(1)试求截面面积S随θ变化的函数关系式S(θ);(2)当E和F分别为B C''和A C''的中点时,需要在线段AF上寻找一个点Q,用纳米纤维导管连接EQ,使得EQ与AB'所在直线的夹角最小,试求出纤维导管EQ的长.64.如图,四棱锥P﹣ABCD的底面ABCD为菱形,∠ABC=60°,P A⊥平面ABCD,且E,M分别为BC,PD的中点,点F为棱PC上一动点.(1)证明:平面AEF ⊥平面P AD .(2)若AB =P A ,在线段PC 上是否存在一点F ,使得二面角F ﹣AE ﹣M 定F 的位置;若不存在,说明理由.65.如图,三棱柱111ABC A B C -中,111AA B C =,11120BB C ∠=︒,1190AB C ∠=︒.(1)求证:ABC 为等腰三角形;(2)若11111AB C B AC ∠=∠,11B AB B BA ∠=∠,点M 在线段11B C 上,设111102B M B C λλ⎛⎫=<< ⎪⎝⎭,若二面角11A CM C --λ的值.66.如图,四棱锥P ABCD -中,底面ABCD 为菱形,2AB AD ==,60ABC ∠=︒,PA ⊥平面ABCD ,PA =(1)点E 在线段PC 上,37PE PC =,点F 在线段PD 上,35PF PD =,求证:PC ⊥平面AEF ; (2)设M 是直线AC 上一点,求CM 的长,使得MP 与平面PCD 所成角为45︒.67.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,侧棱PA ⊥底面ABCD ,1AB =,2PA =,E 为PB 的中点,点F 在棱PC 上,且PF PC λ=.(1)求直线CE 与直线PD 所成角的余弦值;(2)当直线BF 与平面CDE 所成的角最大时,求此时λ的值.68.如图,在四棱锥P ABCD ﹣中,四边形ABCD 为直角梯形,//AD BC ,90BAD ∠=︒,且1AB BC ==,2AD =,PA PD =,M 为AD 的中点,平面PAD ⊥平面ABCD ,直线PB 与平面ABCD 所成角的正切值为(1)求四棱锥PABCD ﹣的体积;(2)在棱CD 上(不含端点)是否存在一点Q ,使得二面角C AP Q --?若存在,请确定点Q 的位置;若不存在,请说明理由.69.已知四棱锥P ABCD -P 中,底面ABCD 是平行四边形,PA AB =,PAD BAD ∠=∠,,E F 分别是,AB DC 的中点,2,3,AD PF PE ===(1)求证:AD ⊥平面PAB ;(2)若PB =B PC A --的余弦值.70.如图,矩形ABCD 中,AB ADλ=()1λ>,将其沿AC 翻折,使点D 到达点E 的位置,且二面角C AB E --为直二面角.(1)求证:平面ACE ⊥平面BCE ;(2)设F 是BE 的中点,二面角E AC F --的平面角的大小为θ,当[]2,3λ∈时,求cos θ的取值范围.任务三:邪恶模式(困难)70-100题71.如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,E ,F 分别为,PA BD 中点,2PA PD AD ===.(1)求证://EF 平面PBC ;(2)求二面角E DF A --的余弦值;(3)在棱PC 上是否存在一点G ,使GF ⊥平面EDF ?若存在,指出点G 的位置;若不存在,说明理由.72.请从下面三个条件中任选一个,补充在下面的横线上,并作答.∠()0BA PA PD ⋅+=;∠PC ∠点P 在平面ABCD 的射影在直线AD 上.如图,平面五边形PABCD 中,PAD △是边长为2的等边三角形,//AD BC ,22AB BC ==,AB BC ⊥,将PAD △沿AD 翻折成四棱锥P ABCD -,E 是棱PD 上的动点(端点除外),F M 、分别是AB CE 、的中点,且___________.(1)求证:AB FM ⊥;(2)当EF 与平面PAD 所成角最大时,求平面ACE 与平面PAD 所成的锐二面角的余弦值.注:如果选择多个条件分别解答,按第一个解答计分.73.蜂房是自然界最神奇的“建筑”之一,如图1所示.蜂房结构是由正六棱柱截去三个相等的三棱锥H ABC -,J CDE -,K EFA -,再分别以AC ,CE ,EA 为轴将ACH ∆,CEJ ∆,EAK ∆分别向上翻转180︒,使H ,J ,K 三点重合为点S 所围成的曲顶多面体(下底面开口),如图2所示.蜂房曲顶空间的弯曲度可用曲率来刻画,定义其度量值等于蜂房顶端三个菱形的各个顶点的曲率之和,而每一顶点的曲率规定等于2π减去蜂房多面体在该点的各个面角之和(多面体的面角是多面体的面的内角,用弧度制表示).(1)求蜂房曲顶空间的弯曲度;(2)若正六棱柱的侧面积一定,当蜂房表面积最小时,求其顶点S 的曲率的余弦值.74.2022年北京冬奥会标志性场馆——国家速滑馆的设计理念来源于一个冰和速度结合的创意,沿着外墙面由低到高盘旋而成的“冰丝带”,就像速度滑冰运动员高速滑动时留下的一圈圈风驰电掣的轨迹,冰上划痕成丝带,22条“冰丝带”又象征北京2022年冬奥会.其中“冰丝带”呈现出圆形平面、椭圆形平面、马鞍形双曲面三种造型,这种造型富有动感,体现了冰上运动的速度和激情这三种造型取自于球、椭球、椭圆柱等空间几何体,其设计参数包括曲率、挠率、面积体积等对几何图形的面积、体积计算方法的研究在中国数学史上有过辉煌的成就,如《九章算术》中记录了数学家刘徽提出利用牟合方盖的体积来推导球的体积公式,但由于不能计算牟合方盖的体积并没有得出球的体积计算公式直到200年以后数学家祖冲之、祖眶父子在《缀术》提出祖暅原理:“幂势既同,则积不容异”,才利用牟合方盖的体积推导出球的体积公式原理的意思是:两个等高的几何体若在所有等高处的水平截面的面积相等,则这两个几何体的体积相等.(Ⅰ)利用祖暅原理推导半径为R 的球的体积公式时,可以构造如图②所示的几何体M ,几何体M 的底面半径和高都为R ,其底面和半球体的底面同在平面α内.设与平面α平行且距离为d 的平面β截两个几何体得到两个截面,请在图②中用阴影画出与图①中阴影截面面积相等的图形并给出证明;(Ⅱ)现将椭圆()222210x y a b a b+=>>所围成的椭圆面分别绕其长轴、短轴旋转一周后得两个不同的椭球A ,B (如图),类比(Ⅰ)中的方法,探究椭球A 的体积公式,并写出椭球A ,B 的体积之比.75.如图,已知边长为2的正方形材料ABCD ,截去如图所示的阴影部分后,可焊接成一个正四棱锥的封闭容器.设FCB θ∠=.(1)用θ表示此容器的体积;(2)当此容器的体积最大时,求tan θ的值.76.如图,在四面体ABCD 中,AB AC ⊥,平面ACD 与平面BCD 垂直且CD =(1)若2AB AC ==,证明:45BCD ∠<︒;(2)若33AB AC ==,当ACD △与BCD 面积之和最大时,求二面角C AB D --的余弦值.77.某人设计了一个工作台,如图所示,工作台的下半部分是个正四棱柱ABCD ﹣A 1B 1C 1D 1,其底面边长为4,高为1(1)当圆弧E 2F 2(包括端点)上的点P 与B 1的最短距离为DB 1Ⅰ平面D 2EF .(2)若D 1D 2=3.当点P 在圆弧E 2E 2(包括端点)上移动时,求二面角P ﹣A 1C 1﹣B 1的正切值的取值范围.78.平面凸六边形11MBB NC C 的边长相等,其中11BB C C 为矩形,1190BMC B NC ∠=∠=︒.将BCM ,11B C N △分别沿BC ,11B C 折至ABC ,111A B C ,且均在同侧与平面11BB C C 垂直,连接1AA ,如图所示,E ,G 分别是BC ,1CC 的中点.(1)求证:多面体111ABC A B C -为直三棱柱;(2)求二面角1A EG A --平面角的余弦值.79.如图,AB 是圆O 的直径,点C 是圆O 上异于,A B 的点,直线PC ⊥平面ABC ,,E F 分别是,PA PC 的中点.(1)记平面BEF 与平面ABC 的交线为l ,试判断直线l 与平面PAC 的位置关系,并加以证明;(2)设(1)中的直线l 与圆O 的另一个交点为D ,且点Q 满足12DQ CP =.记直线PQ 与平面ABC 所成的角为θ,异面直线PQ 与EF 所成的角为α,二面角E l C --的大小为β,求证:sin sin sin θαβ=.80.已知,图中直棱柱1111ABCD A B C D -的底面是菱形,其中124AA AC BD ===.又点,,,E F P Q 分别在棱1111,,,AA BB CC DD 上运动,且满足:BF DQ =,1CP BF DQ AE -=-=.(1)求证:,,,E F P Q 四点共面,并证明EF Ⅰ平面PQB .(2)是否存在点P 使得二面角B PQ E --?如果存在,求出CP 的长;如果不存在,请说明理由.81.如图1,ADC ∆与ABC ∆是处在同-个平面内的两个全等的直角三角形,30ACB ACD ︒∠=∠=90ABC ADC ︒∠=∠=,2AB =,连接是,BD E 边BC 上一点,过E 作// EF BD ,交CD 于点F ,沿EF 将CEF ∆向上翻折,得到如图2所示的六面体,P ABEFD -(1)求证:;BD AP ⊥(2)设),(BE EC R λλ=∈若平面PEF ⊥底面ABEFD ,若平面PAB 与平面PDF λ的值;(3)若平面PEF ⊥底面ABEFD ,求六面体P ABEFD -的体积的最大值.82.设三棱锥P ABC -的每个顶点都在球O 的球面上,PAB ∆是面积为AC BC ⊥,AC BC =,且平面PAB ⊥平面ABC .(1)确定O 的位置(需要说明理由),并证明:平面POC ⊥平面ABC .(2)与侧面PAB 平行的平面α与棱AC ,BC ,PC 分别交于D ,E ,F ,求四面体ODEF 的体积的最大值.83.如图,在三棱柱111ABC A B C -中,1AA ⊥平面ABC ,D 是AB 的中点,BC AC =,2AB DC ==,14AA =.(Ⅰ)求证:1//BC 平面1A CD ;(Ⅰ)求平面11BCC B 与平面1A CD 所成锐二面角的平面角的余弦值.84.如图,P 为圆锥的顶点,O 是圆锥底面的圆心,AC 为底面直径,ABD △为底面圆O 的内接正三角E 在母线PC 上,且1,AE CE EC BD ==⊥.(1)求证:平面BED ⊥平面ABD ;(2)设线段PO 上动点为M ,求直线DM 与平面ABE 所成角的正弦值的最大值.85.如图,三棱柱111ABC A B C -的底面是边长为4的正三角形,侧面11ACC A ⊥底面ABC ,且侧面11ACC A 为菱形,160A AC ∠=.(1)求二面角1A AB C 所成角θ的正弦值.(2),M N 分别是棱11A C ,11B C 的中点,又2AP BP =.求经过,,M N P 三点的平面截三棱柱111ABC A B C -的截面的周长.86.如图,在三棱台111ABC A B C -中,底面ABC 是边长为2的正三角形,侧面11ACC A 为等腰梯形,且1111AC AA ==,D 为11A C 的中点.(1)证明:AC BD ⊥;(2)记二面角1A AC B --的大小为θ,2,33ππθ⎡⎤∈⎢⎥⎣⎦时,求直线1AA 与平面11BB C C 所成角的正弦值的取值范围.87.如图,在四棱锥P ABCD -中,M ,N 分别是AB ,AP 的中点,AB BC ⊥,MD PC ⊥,//MD BC ,1BC =,2AB =,3PB =,CD =PD =(Ⅰ)证明://PC 平面MND ;(Ⅱ)求直线PA 与平面PBC 所成角的正弦值.88.设P 为多面体M 的一个顶点,定义多面体M 在点P 处的离散曲率为12231111()2k k k Q PQ Q PQ Q PQ Q PQ π--∠+∠++∠+∠,其中Q i (i =1,2,…,k ,k ≥3)为多面体M 的所有与点P 相邻的顶点,且平面Q 1PQ 2,平面Q 2PQ 3,…,平面Q k ﹣1PQ k 和平面Q k PQ 1遍历多面体M 的所有以P 为公共点的面.(1)如图1,已知长方体A 1B 1C 1D 1﹣ABCD ,AB =BC =1,1AA =P 为底面A 1B 1C 1D 1内的一个动点,则求四棱锥P ﹣ABCD 在点P 处的离散曲率的最小值;(2)图2为对某个女孩面部识别过程中的三角剖分结果,所谓三角剖分,就是先在面部取若干采样点,然后用短小的直线段连接相邻三个采样点形成三角形网格.区域α和区域β中点的离散曲率的平均值更大的是哪个区域?(确定“区域α”还是“区域β”)89.如图,四棱锥P ABCD -的底面ABCD 是边长为2的正方形,3PA PB ==.(1)证明:PAD PBC ∠=∠;(2)当直线PA 与平面PCD 所成角的正弦值最大时,求此时二面角P AB C 的大小.90.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和.例如:正四面体在每个顶点有3个面角,每个面角是3π,所以正四面体在各顶点的曲率为233πππ-⨯=,故其总曲率为4π.(1)求四棱锥的总曲率;(2)若多面体满足:顶点数-棱数+面数2=,证明:这类多面体的总曲率是常数.91.已知四棱锥T ABCD -的底面是平行四边形,平面α与直线AD ,TA ,TC 分别交于点P ,Q ,R 且AP TQ CRx AD TA CT===,点M 在直线TB 上,N 为CD 的中点,且直线//MN 平面α.(1)设TA a =,TB b =,TC c =,试用基底{},,a b c 表示向量TD ;(2)证明,四面体T ABC -中至少存在一个顶点从其出发的三条棱能够组成一个三角形;(3)证明,对所有满足条件的平面α,点M 的线段上.92.如图,在四棱台ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,ⅠABC =3π,ⅠB 1BD =6π,11,B BA B BC ∠=∠11122,3AB A B B B ===。
高考立体几何大题20题汇总
(2012江西省)(本小题满分12分)如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42,DE=4.现将△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG. (1) 求证:平面DEG ⊥平面CFG ; (2)求多面体C DEFG 的体积。
2012,山东(19) (本小题满分12分)如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,,CB CD EC BD =⊥.(Ⅰ)求证:BE DE =;(Ⅱ)若∠120BCD =︒,M 为线段AE 的中点,求证:DM ∥平面BEC .2012浙江20.(本题满分15分)如图,在侧棱锥垂直底面的四棱锥1111ABCD A B C D -中,,AD BC //AD11,2,2,4,2,AB AB AD BC AA E DD ⊥====是的中点,F 是平面11B C E 与直线1AA 的交点。
(Ⅰ)证明:(i) 11;EF A D //ii ()111;BA B C EF ⊥平面 (Ⅱ)求1BC 与平面11B C EF 所成的角的正弦值。
(2010四川)18、(本小题满分12分)已知正方体''''ABCD A B C D -中,点M 是棱'AA 的中点,点O 是对角线'BD 的中点,(Ⅰ)求证:OM 为异面直线'AA 与'BD 的公垂线; (Ⅱ)求二面角''M BC B --的大小; 2010辽宁文(19)(本小题满分12分)如图,棱柱111ABC A B C -的侧面11BCC B 是菱形,11B C A B ⊥(第20题图)F EC 1B 1D 1A 1ADBC(Ⅰ)证明:平面11A B C ⊥平面11A BC ;(Ⅱ)设D 是11A C 上的点,且1//AB 平面1B CD ,求11:A D DC 的值。
专题05 立体几何专项高考真题总汇(带答案与解析)
专题05立体几何(选择题、填空题)1.【2021·浙江高考真题】某几何体的三视图如图所示,则该几何体的体积是()A .32B .3C.2D.【答案】A【分析】根据三视图可得如图所示的几何体,根据棱柱的体积公式可求其体积.【解析】几何体为如图所示的四棱柱1111ABCD A B C D -,其高为1,底面为等腰梯形ABCD ,,下底为12=,故1111131222ABCD A B C D V -=⨯+⨯⨯=,故选:A.2.【2021·北京高考真题】某四面体的三视图如图所示,该四面体的表面积为()A .332+B .4C .33D .2【答案】A【分析】根据三视图可得如图所示的几何体(三棱锥),根据三视图中的数据可计算该几何体的表面积.【解析】根据三视图可得如图所示的几何体-正三棱锥O ABC -,其侧面为等腰直角三角形,底面等边三角形,由三视图可得该正三棱锥的侧棱长为1,故其表面积为213333112242+⨯⨯⨯+⨯=,故选:A.3.【2021·浙江高考真题】如图已知正方体1111ABCD A B C D -,M ,N 分别是1A D ,1D B 的中点,则()A .直线1A D 与直线1DB 垂直,直线//MN 平面ABCD B .直线1A D 与直线1D B 平行,直线MN ⊥平面11BDD BC .直线1AD 与直线1D B 相交,直线//MN 平面ABCD D .直线1A D 与直线1D B 异面,直线MN ⊥平面11BDD B 【答案】A【分析】由正方体间的垂直、平行关系,可证1//,MN AB A D ⊥平面1ABD ,即可得出结论.【解析】连1AD ,在正方体1111ABCD A B C D -中,M 是1A D 的中点,所以M 为1AD 中点,又N 是1D B 的中点,所以//MN AB ,MN ⊄平面,ABCD AB ⊂平面ABCD ,所以//MN 平面ABCD .因为AB 不垂直BD ,所以MN 不垂直BD 则MN 不垂直平面11BDD B ,所以选项B,D 不正确;在正方体1111ABCD A B C D -中,11AD A D ⊥,AB ⊥平面11AA D D ,所以1AB A D ⊥,1AD AB A ⋂=,所以1A D ⊥平面1ABD ,1D B ⊂平面1ABD ,所以11A D D B ⊥,且直线11,A D D B 是异面直线,所以选项B 错误,选项A 正确.故选:A.【点睛】关键点点睛:熟练掌握正方体中的垂直、平行关系是解题的关键,如两条棱平行或垂直,同一个面对角线互相垂直,正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.4.【2021·全国高考真题(理)】已如A ,B ,C 是半径为1的球O 的球面上的三个点,且,1AC BC AC BC ⊥==,则三棱锥O ABC -的体积为()A .212B .312C .24D .34【答案】A【分析】由题可得ABC 为等腰直角三角形,得出ABC 外接圆的半径,则可求得O 到平面ABC 的距离,进而求得体积.【解析】,1AC BC AC BC ⊥== ,ABC ∴ 为等腰直角三角形,AB ∴=,则ABC 外接圆的半径为22,又球的半径为1,设O 到平面ABC 的距离为d ,则2d ==,所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选:A.【点睛】关键点睛:本题考查球内几何体问题,解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.5.【2021·全国高考真题(理)】在正方体1111ABCD A B C D -中,P 为11B D 的中点,则直线PB 与1AD 所成的角为()A .π2B .π3C .π4D .π6【答案】D【分析】平移直线1AD 至1BC ,将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角,解三角形即可.【解析】如图,连接11,,BC PC PB ,因为1AD ∥1BC ,所以1PBC ∠或其补角为直线PB 与1AD 所成的角,因为1BB ⊥平面1111D C B A ,所以11BB PC ⊥,又111PC B D ⊥,1111BB B D B ⋂=,所以1PC ⊥平面1P B B ,所以1PC PB ⊥,设正方体棱长为2,则111112BC PC D B ===1111sin 2PC PBC BC ∠==,所以16PBC π∠=.故选:D6.【2021·全国高考真题】已知圆锥的底面半径为,其侧面展开图为一个半圆,则该圆锥的母线长为()A .2B.C .4D.【答案】B【分析】设圆锥的母线长为l ,根据圆锥底面圆的周长等于扇形的弧长可求得l 的值,即为所求.【解析】设圆锥的母线长为l,由于圆锥底面圆的周长等于扇形的弧长,则2l ππ=解得l =.故选:B.7.【2021·北京高考真题】定义:24小时内降水在平地上积水厚度(mm )来判断降雨程度.其中小雨(10mm <),中雨(10mm 25mm -),大雨(25mm 50mm -),暴雨(50mm 100mm -),小明用一个圆锥形容器接了24小时的雨水,如图,则这天降雨属于哪个等级()A .小雨B .中雨C .大雨D .暴雨【答案】B【分析】计算出圆锥体积,除以圆面的面积即可得降雨量,即可得解.【解析】由题意,一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=,高为()150mm 的圆锥,所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯,属于中雨.故选:B.8.【2021·全国高考真题】在正三棱柱111ABC A B C -中,11AB AA ==,点P 满足1BP BC BB λμ=+,其中[]0,1λ∈,[]0,1μ∈,则()A .当1λ=时,1AB P △的周长为定值B .当1μ=时,三棱锥1P A BC -的体积为定值C .当12λ=时,有且仅有一个点P ,使得1A P BP ⊥D .当12μ=时,有且仅有一个点P ,使得1A B ⊥平面1AB P 【答案】BD【分析】对于A ,由于等价向量关系,联系到一个三角形内,进而确定点的坐标;对于B ,将P 点的运动轨迹考虑到一个三角形内,确定路线,进而考虑体积是否为定值;对于C ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数;对于D ,考虑借助向量的平移将P 点轨迹确定,进而考虑建立合适的直角坐标系来求解P 点的个数.【解析】易知,点P 在矩形11BCC B 内部(含边界).对于A ,当1λ=时,11=BP BC BB BC CC μμ=++,即此时P ∈线段1CC ,1AB P △周长不是定值,故A 错误;对于B ,当1μ=时,1111=BP BC BB BB B C λλ=++,故此时P 点轨迹为线段11B C ,而11//B C BC ,11//B C 平面1A BC ,则有P 到平面1A BC 的距离为定值,所以其体积为定值,故B 正确.对于C ,当12λ=时,112BP BC BB μ=+,取BC ,11B C 中点分别为Q ,H ,则BP BQ QH μ=+,所以P 点轨迹为线段QH ,不妨建系解决,建立空间直角坐标系如图,13,0,12A ⎛⎫ ⎪ ⎪⎝⎭,()0,0P μ,,10,,02B ⎛⎫⎪⎝⎭,则13,0,12A P μ⎛⎫=-- ⎪ ⎪⎝⎭,10,,2BP μ⎛⎫=- ⎪⎝⎭ ,()110A P BP μμ⋅=-=,所以0μ=或1μ=.故,H Q 均满足,故C 错误;对于D ,当12μ=时,112BP BC BB λ=+ ,取1BB ,1CC 中点为,M N .BP BM MN λ=+ ,所以P 点轨迹为线段MN .设010,,2P y ⎛⎫ ⎪⎝⎭,因为0,02A ⎛⎫ ⎪ ⎪⎝⎭,所以01,22AP y ⎛⎫= ⎪ ⎪⎝⎭,11,,122A B ⎛⎫=-- ⎪ ⎪⎝⎭,所以00311104222y y +-=⇒=-,此时P 与N 重合,故D 正确.故选:BD .【点睛】本题主要考查向量的等价替换,关键之处在于所求点的坐标放在三角形内.9.【2021·全国高考真题(理)】以图①为正视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某三棱锥的三视图,则所选侧视图和俯视图的编号依次为_________(写出符合要求的一组答案即可).【答案】③④(答案不唯一)【分析】由题意结合所给的图形确定一组三视图的组合即可.【解析】选择侧视图为③,俯视图为④,如图所示,长方体1111ABCD A B C D -中,12,1AB BC BB ===,,E F 分别为棱11,BC BC 的中点,则正视图①,侧视图③,俯视图④对应的几何体为三棱锥E ADF -.故答案为:③④.【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.10.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为A .514-B .512-C .514D .512+【答案】C【解析】如图,设,CD a PE b ==,则22224a PO PE OEb =-=-由题意得212PO ab =,即22142a b ab-=,化简得24()210b b a a -⋅-=,解得14b a +=(负值舍去).故选C .【点晴】本题主要考查正四棱锥的概念及其有关计算,考查学生的数学计算能力,是一道容易题.11.【2020年高考全国Ⅱ卷理数】如图是一个多面体的三视图,这个多面体某条棱的一个端点在正视图中对应的点为M ,在俯视图中对应的点为N ,则该端点在侧视图中对应的点为A .EB .FC .GD .H【答案】A【解析】根据三视图,画出多面体立体图形,14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选A.【点睛】本题主要考查了根据三视图判断点的位置,解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法,考查了分析能力和空间想象,属于基础题.12.【2020年高考全国II 卷理数】已知△ABC 是面积为934O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为A 3B .32C .1D .32【答案】C【解析】设球O 的半径为R ,则2416R π=π,解得:2R =.设ABC △外接圆半径为r ,边长为a ,ABC △是面积为934的等边三角形,21393224a ∴⨯=,解得:3a =,22229933434a r a ∴=-=⨯-,∴球心O 到平面ABC 的距离22431d R r =-=-=.故选:C .【点睛】本题考查球的相关问题的求解,涉及到球的表面积公式和三角形面积公式的应用;解题关键是明确球的性质,即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.13.【2020年高考全国Ⅲ卷理数】如图为某几何体的三视图,则该几何体的表面积是A .2B .4+42C .3D .4+23【答案】C 【解析】根据三视图特征,在正方体中截取出符合题意的立体图形根据立体图形可得:12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得:22AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得:2113sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是:632=⨯++.故选:C .【点睛】本题主要考查了根据三视图求立体图形的表面积问题,解题关键是掌握根据三视图画出立体图形,考查了分析能力和空间想象能力,属于基础题.14.【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点,⊙1O 为ABC △的外接圆,若⊙1O 的面积为4π,1AB BC AC OO ===,则球O 的表面积为A .64πB .48πC .36πD .32π【答案】A【解析】设圆1O 半径为r ,球的半径为R ,依题意,得24,2r r π=π=∴, ABC 为等边三角形,由正弦定理可得2sin 60AB r =︒=,1OO AB ∴==,根据球的截面性质1OO ⊥平面ABC ,11,4OO O A R OA ∴⊥====,∴球O 的表面积2464S R ππ==.故选:A.【点睛】本题考查球的表面积,应用球的截面性质是解题的关键,考查计算求解能力,属于基础题.15.【2020年高考天津】若棱长为为A .12πB .24πC .36πD .144π【答案】C【解析】这个球是正方体的外接球,其半径等于正方体的体对角线的一半,即3R ==,所以,这个球的表面积为2244336S R πππ==⨯=.故选:C .【点睛】本题考查正方体的外接球的表面积的求法,求出外接球的半径是本题的解题关键,属于基础题.求多面体的外接球的面积和体积问题,常用方法有:(1)三条棱两两互相垂直时,可恢复为长方体,利用长方体的体对角线为外接球的直径,求出球的半径;(2)直棱柱的外接球可利用棱柱的上下底面平行,借助球的对称性,球心为上下底面外接圆的圆心连线的中点,再根据勾股定理求球的半径;(3)如果设计几何体有两个面相交,可过两个面的外心分别作两个面的垂线,垂线的交点为几何体的球心.16.【2020年高考北京】某三棱柱的底面为正三角形,其三视图如图所示,该三棱柱的表面积为A .6+B .6+C .12+D .12+【答案】D 【解析】由题意可得,三棱柱的上下底面为边长为2的等边三角形,侧面为三个边长为2的正方形,则其表面积为:()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭故选:D .【点睛】(1)以三视图为载体考查几何体的表面积,关键是能够对给出的三视图进行恰当的分析,从三视图中发现几何体中各元素间的位置关系及数量关系.(2)多面体的表面积是各个面的面积之和;组合体的表面积应注意重合部分的处理.(3)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展为平面图形计算,而表面积是侧面积与底面圆的面积之和.17.【2020年高考浙江】某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是A .73B .143C .3D .6【答案】A 【解析】由三视图可知,该几何体是上半部分是三棱锥,下半部分是三棱柱,且三棱锥的一个侧面垂直于底面,且棱锥的高为1,棱柱的底面为等腰直角三角形,棱柱的高为2,所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+=⎪ ⎪⎝⎭⎝⎭.故选:A【点睛】本小题主要考查根据三视图计算几何体的体积,属于基础题.18.【2020年高考浙江】已知空间中不过同一点的三条直线l ,m ,n .“l ,m ,n 共面”是“l ,m ,n 两两相交”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线,当,,m n l 在同一平面时,可能////m n l ,故不能得出,,m n l 两两相交.当,,m n l 两两相交时,设,,m n A m l B n l C ⋂=⋂=⋂=,根据公理2可知,m n 确定一个平面α,而,B m C n αα∈⊂∈⊂,根据公理1可知,直线BC 即l α⊂,所以,,m n l 在同一平面.综上所述,“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件.故选:B【点睛】本小题主要考查充分、必要条件的判断,考查公理1和公理2的运用,属于中档题.19.【2020年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器,利用与晷面垂直的晷针投射到晷面的影子来测定时间.把地球看成一个球(球心记为O ),地球上一点A 的纬度是指OA 与地球赤道所在平面所成角,点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷,若晷面与赤道所在平面平行,点A 处的纬度为北纬40°,则晷针与点A 处的水平面所成角为A .20°B .40°C .50°D .90°【答案】B 【解析】画出截面图如下图所示,其中CD 是赤道所在平面的截线;l 是点A 处的水平面的截线,依题意可知OA l ⊥;AB 是晷针所在直线.m 是晷面的截线,依题意依题意,晷面和赤道平面平行,晷针与晷面垂直,根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒,所以40OAG AOC ∠=∠=︒,由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒,所以40BAE OAG ∠=∠=︒,也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选:B.【点睛】本小题主要考查中国古代数学文化,考查球体有关计算,涉及平面平行,线面垂直的性质,属于中档题.20.【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上,PA =PB =PC ,△ABC 是边长为2的正三角形,E ,F 分别是PA ,AB 的中点,∠CEF =90°,则球O 的体积为A .B .C .D 【答案】D【解析】解法一:,PA PB PC ABC == △为边长为2的等边三角形,P ABC ∴-为正三棱锥,PB AC ∴⊥,又E ,F 分别为PA ,AB 的中点,EF PB ∴∥,EF AC ∴⊥,又EF CE ⊥,,CE AC C EF =∴⊥ 平面PAC ,∴PB ⊥平面PAC ,APB PA PB PC ∴∠=90︒,∴===,P ABC ∴-为正方体的一部分,2R ==364466,π2338R V R =∴=π=⨯=,故选D .解法二:设2PA PB PC x ===,,E F 分别为,PA AB 的中点,EF PB ∴∥,且12EF PB x ==,ABC △为边长为2的等边三角形,CF ∴=又90CEF ∠=︒,12CE AE PA x ∴===,AEC △中,由余弦定理可得()2243cos 22x x EAC x +--∠=⨯⨯,作PD AC ⊥于D ,PA PC = ,D \为AC 的中点,1cos 2AD EAC PA x ∠==,2243142x x x x+-+∴=,221221222x x x ∴+=∴==,,,PA PB PC ∴===,又===2AB BC AC ,,,PA PB PC ∴两两垂直,2R ∴==,62R ∴=,34466338V R ∴=π=π⨯=,故选D.【名师点睛】本题主要考查学生的空间想象能力,补体法解决外接球问题.可通过线面垂直定理,得到三棱两两互相垂直关系,快速得到侧棱长,进而补体成正方体解决.21.【2019年高考全国Ⅱ卷理数】设α,β为两个平面,则α∥β的充要条件是A .α内有无数条直线与β平行B .α内有两条相交直线与β平行C .α,β平行于同一条直线D .α,β垂直于同一平面【答案】B【解析】由面面平行的判定定理知:α内两条相交直线都与β平行是αβ∥的充分条件,由面面平行性质定理知,若αβ∥,则α内任意一条直线都与β平行,所以α内两条相交直线都与β平行是αβ∥的必要条件,故选B .【名师点睛】本题考查了空间两个平面的判定与性质及充要条件,渗透直观想象、逻辑推理素养,利用面面平行的判定定理与性质定理即可作出判断.面面平行的判定问题要紧扣面面平行判定定理,最容易犯的错误为定理记不住,凭主观臆断,如:“若,,a b a b αβ⊂⊂∥,则αβ∥”此类的错误.22.【2019年高考全国Ⅲ卷理数】如图,点N 为正方形ABCD 的中心,△ECD 为正三角形,平面ECD ⊥平面ABCD ,M 是线段ED 的中点,则A .BM =EN ,且直线BM ,EN 是相交直线B .BM ≠EN ,且直线BM ,EN 是相交直线C .BM =EN ,且直线BM ,EN 是异面直线D .BM ≠EN ,且直线BM ,EN 是异面直线【答案】B【解析】如图所示,作EO CD ⊥于O ,连接ON ,BD ,易得直线BM ,EN 是三角形EBD 的中线,是相交直线.过M 作MF OD ⊥于F ,连接BF ,平面CDE ⊥平面ABCD ,,EO CD EO ⊥⊂平面CDE ,EO ∴⊥平面ABCD ,MF ⊥平面ABCD ,MFB ∴△与EON △均为直角三角形.设正方形边长为2,易知12EO ON EN ===,,5,,22MF BF BM ==∴=BM EN ∴≠,故选B .【名师点睛】本题考查空间想象能力和计算能力,解答本题的关键是构造直角三角形.解答本题时,先利用垂直关系,再结合勾股定理进而解决问题.23.【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家,他提出的“幂势既同,则积不容异”称为祖暅原理,利用该原理可以得到柱体的体积公式V柱体=Sh,其中S是柱体的底面积,h是柱体的高.若某柱体的三视图如图所示(单位:cm),则该柱体的体积(单位:cm3)是A.158B.162C.182D.324【答案】B【解析】由三视图得该棱柱的高为6,底面可以看作是由两个直角梯形组合而成的,其中一个上底为4,下底为6,高为3,另一个的上底为2,下底为6,高为3,则该棱柱的体积为2646336162 22++⎛⎫⨯+⨯⨯=⎪⎝⎭.故选B.【名师点睛】本题首先根据三视图,还原得到几何体——棱柱,根据题目给定的数据,计算几何体的体积,常规题目.难度不大,注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二,一是不能正确还原几何体;二是计算体积有误.为避免出错,应注重多观察、细心算.24.【2019年高考浙江卷】设三棱锥V–ABC的底面是正三角形,侧棱长均相等,P是棱VA 上的点(不含端点).记直线PB与直线AC所成的角为α,直线PB与平面ABC所成的角为β,二面角P–AC–B的平面角为γ,则A.β<γ,α<γB.β<α,β<γC.β<α,γ<αD.α<β,γ<β【答案】B【解析】如图,G 为AC 中点,连接VG ,V 在底面ABC 的投影为O ,则P 在底面的投影D 在线段AO 上,过D 作DE 垂直于AC 于E ,连接PE ,BD ,易得PE VG ∥,过P 作PF AC ∥交VG 于F ,连接BF ,过D 作DH AC ∥,交BG 于H ,则,,BPF PBD PED αβγ=∠=∠=∠,结合△PFB ,△BDH ,△PDB 均为直角三角形,可得cos cos PF EG DH BD PB PB PB PB αβ===<=,即αβ>;在Rt △PED 中,tan tan PD PD ED BD γβ=>=,即γβ>,综上所述,答案为B.【名师点睛】本题以三棱锥为载体,综合考查异面直线所成的角、直线与平面所成的角、二面角的概念,以及各种角的计算.解答的基本方法是通过明确各种角,应用三角函数知识求解,而后比较大小.而充分利用图形特征,则可事倍功半.常规解法下易出现的错误有,不能正确作图得出各种角,未能想到利用“特殊位置法”,寻求简便解法.25.【2020年高考全国Ⅱ卷理数】设有下列四个命题:p 1:两两相交且不过同一点的三条直线必在同一平面内.p 2:过空间中任意三点有且仅有一个平面.p 3:若空间两条直线不相交,则这两条直线平行.p 4:若直线l ⊂平面α,直线m ⊥平面α,则m ⊥l .则下述命题中所有真命题的序号是__________.①14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝【答案】①③④【解析】对于命题1p ,可设1l 与2l 相交,这两条直线确定的平面为α;若3l 与1l 相交,则交点A 在平面α内,同理,3l 与2l 的交点B 也在平面α内,所以,AB α⊂,即3l α⊂,命题1p 为真命题;对于命题2p ,若三点共线,则过这三个点的平面有无数个,命题2p 为假命题;对于命题3p ,空间中两条直线相交、平行或异面,命题3p 为假命题;对于命题4p ,若直线m ⊥平面α,则m 垂直于平面α内所有直线,直线l ⊂平面α,∴直线m ⊥直线l ,命题4p 为真命题.综上可知,,为真命题,,为假命题,14p p ∧为真命题,12p p ∧为假命题,23p p ⌝∨为真命题,34p p ⌝∨⌝为真命题.故答案为:①③④.【点睛】本题考查复合命题的真假,同时也考查了空间中线面关系有关命题真假的判断,考查推理能力,属于中等题.26.【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1,母线长为3,则该圆锥内半径最大的球的体积为_________.【答案】23【解析】易知半径最大球为圆锥的内切球,球与圆锥内切时的轴截面如图所示,其中2,3BC AB AC ===,且点M 为BC 边上的中点,设内切圆的圆心为O ,由于223122AM =-=,故1222222S =⨯⨯=△ABC 设内切圆半径为r ,则:ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()1332222r =⨯++⨯=解得:22r =,其体积:34233V r =π=π.故答案为:23π.【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.27.【2020年高考浙江】已知圆锥的侧面积(单位:cm 2)为2π,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.【答案】1【解析】设圆锥底面半径为r ,母线长为l ,则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩,解得1,2r l ==.故答案为:1【点睛】本小题主要考查圆锥侧面展开图有关计算,属于基础题.28.【2020年高考江苏】如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2cm ,高为2cm ,内孔半轻为0.5cm ,则此六角螺帽毛坯的体积是▲cm.【答案】2π【解析】正六棱柱体积为2624⨯⨯⨯,圆柱体积为21()222ππ⋅=,所求几何体体积为2π.故答案为:2π-【点睛】本题考查正六棱柱体积、圆柱体积,考查基本分析求解能力,属基础题.29.【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2,∠BAD =60°.以1D 为球心,为半径的球面与侧面BCC 1B 1的交线长为________.【答案】22π.【解析】如图:取11B C 的中点为E ,1BB 的中点为F ,1CC 的中点为G ,因为BAD ∠=60°,直四棱柱1111ABCD A B C D -的棱长均为2,所以△111D B C 为等边三角形,所以1D E =111D E B C ⊥,又四棱柱1111ABCD A B C D -为直四棱柱,所以1BB ⊥平面1111D C B A ,所以111BB B C ⊥,因为1111BB B C B = ,所以1D E ⊥侧面11B C CB ,设P 为侧面11B C CB 与球面的交线上的点,则1D E EP ⊥,,1D E =,所以||EP ===,所以侧面11B C CB 与球面的交线上的点到E ,因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧 FG ,因为114B EF C EG π∠=∠=,所以2FEG π∠=,所以根据弧长公式可得 22FGπ==.故答案为:22π.【点睛】本题考查了直棱柱的结构特征,考查了直线与平面垂直的判定,考查了立体几何中的轨迹问题,考查了扇形中的弧长公式,属于中档题.30.【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践,利用3D 打印技术制作模型.如图,该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体,其中O 为长方体的中心,E ,F ,G ,H 分别为所在棱的中点,16cm 4cm AB =BC =, AA =,3D 打印所用原料密度为0.9g/cm 3,不考虑打印损耗,制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得,214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形,∵四棱锥O −EFGH 的高为3cm ,∴3112312cm 3O EFGH V -=⨯⨯=.又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=,所以该模型体积为3214412132cm O EFGH V V V -=-=-=,其质量为0.9132118.8g ⨯=.【名师点睛】本题考查几何体的体积问题,理解题中信息联系几何体的体积和质量关系,从而利用公式求解.根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积,再求出模型的质量即可.31.【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得,其三视图如图所示.如果网格纸上小正方形的边长为1,那么该几何体的体积为__________.【答案】40【解析】如图所示,在棱长为4的正方体中,三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体,则几何体的体积()3142424402V =-⨯+⨯⨯=.【名师点睛】本题首先根据三视图,还原得到几何体,再根据题目给定的数据,计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.32.【2019年高考北京卷理数】已知l ,m 是平面α外的两条不同直线.给出下列三个论断:①l ⊥m ;②m ∥α;③l ⊥α.以其中的两个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:__________.【答案】如果l ⊥α,m ∥α,则l ⊥m .【解析】将所给论断,分别作为条件、结论,得到如下三个命题:(1)如果l ⊥α,m ∥α,则l ⊥m ,正确;(2)如果l ⊥α,l ⊥m ,则m ∥α,不正确,有可能m 在平面α内;(3)如果l ⊥m ,m ∥α,则l ⊥α,不正确,有可能l 与α斜交、l ∥α.故答案为:如果l ⊥α,m ∥α,则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断,分别作为条件、结论加以分析即可.33.【2019年高考天津卷理数】2的正方形,5若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.【答案】π4【解析】由题意,的正方形,借助勾股定理,2=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,一个底面的圆心为四棱锥底面的中心,故圆柱的高为1,圆柱的底面半径为12,故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭.【名师点睛】根据棱锥的结构特点,确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.34.【2019年高考江苏卷】如图,长方体1111ABCD A B C D -的体积是120,E 为1CC 的中点,则三棱锥E −BCD 的体积是▲.【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120,所以1120AB BC CC ⋅⋅=,因为E 为1CC 的中点,所以112CE CC =,由长方体的性质知1CC ⊥底面ABCD ,所以CE 是三棱锥E BCD -的底面BCD 上的高,所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中,往往需要注意理清整体和局部的关系,灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.35.【2019年高考全国Ⅱ卷理数】中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有________个面,其棱长为_________.(本题第一空2分,第二空3分.)【答案】261【解析】由图可知第一层(包括上底面)与第三层(包括下底面)各有9个面,计18个面,第二层共有8个面,所以该半正多面体共有18826+=个面.如图,设该半正多面体的棱长为x ,则AB BE x ==,延长CB 与FE 的延长线交于点G ,延长BC 交正方体的棱于H ,由半正多面体对称性可知,BGE △为等腰直角三角形,22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=,1x ∴=1.。
立体几何大题20道
立体几何大题20道1、(17年浙江)如图,已知四棱锥P-ABCD ,△PAD 是以AD 为斜边的等腰直角三角形,BC ∥AD ,CD ⊥AD ,PC=AD=2DC=2CB,E 为PD 的中点.(I )证明:CE ∥平面PAB ;(II )求直线CE 与平面PBC 所成角的正弦值2、(17新课标3)如图,四面体ABCD 中,△ABC 是正三角形,AD =CD .(1)证明:AC ⊥BD ;(2)已知△ACD 是直角三角形,AB =BD .若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.3、(17新课标2)如图,四棱锥P ABCD -中,侧面PAD 为等边三角形且垂直于底ABCD ,1,2AB BC AD BAD ==∠90.ABC =∠=︒(1)证明:直线BC ∥平面PAD ;(2)若△PCD 的面积为,求四棱锥P ABCD -的体积.4、(17新课标1)如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠=,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积.5、(17年山东)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD , (Ⅰ)证明:1A O ∥平面B 1CD 1;(Ⅱ)设M 是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1.6、(17年北京)如图,在三棱锥P –ABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,D 为线段AC 的中点,E 为线段PC 上一点.(Ⅰ)求证:PA ⊥BD ;(Ⅱ)求证:平面BDE ⊥平面PAC ; (Ⅲ)当PA ∥平面BD E 时,求三棱锥E –BCD 的体积.7、(16年北京)如图,在四棱锥P-ABCD 中,PC ⊥平面ABCD ,,AB DC DC AC ⊥∥(I )求证:DC PAC ⊥平面;(II )求证:PAB PAC ⊥平面平面;(III)设点E 为AB 的中点,在棱PB 上是否存在点F ,使得PA CEF ∥平面?说明理由.8、(16年山东)在如图所示的几何体中,D 是AC 的中点,EF ∥DB. (I )已知AB=BC ,AE=EC.求证:AC ⊥FB ;(II )已知G,H 分别是EC 和FB 的中点.求证:GH ∥平面ABC.9、(16年上海)将边长为1的正方形AA 1O 1O (及其内部)绕OO 1旋转一周形成圆柱,如图,AC 长为56π,11A B 长为3π,其中B 1与C 在平面AA 1O 1O 的同侧. (1)求圆柱的体积与侧面积;(2)求异面直线O 1B 1与OC 所成的角的大小.10、如图,在四棱锥P-ABCD 中,PA ⊥CD ,AD ∥BC ,∠ADC=∠PAB=90°,12BC CD AD ==。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2012省)(本小题满分12分)
如图,在梯形ABCD 中,AB ∥CD ,E ,F 是线段AB 上的两点,且DE ⊥AB ,CF ⊥AB ,AB=12,AD=5,BC=42,DE=4.现将△ADE ,△CFB 分别沿DE ,CF 折起,使A ,B 两点重合与点G ,得到多面体CDEFG.
(1) 求证:平面DEG ⊥平面CFG ; (2)求多面体CDEFG 的体积。
2012,(19) (本小题满分12分)
如图,几何体E ABCD -是四棱锥,△ABD 为正三角形,
,CB CD EC BD =⊥. (Ⅰ)求证:BE DE =;
(Ⅱ)若∠120BCD =︒,M 为线段AE 的中点,求证:DM ∥平面BEC .
201220.(本题满分15分)如图,在侧棱锥垂直底面
的四棱锥1111ABCD A B C D -中,,AD BC //AD
11,2,2,4,2,AB AB AD BC AA E DD ⊥====是的中点,F
是平面11B C E 与直线1AA 的交点。
(Ⅰ)证明:(i) 11;EF A D //ii ()111;BA B C EF ⊥平面 (Ⅱ)求1BC 与平面11B C EF 所成的角的正弦值。
(2010)18、(本小题满分12分)已知正方体''''ABCD A B C D -中,点M 是棱'AA 的中点,点O 是对角线'BD 的中点,
(Ⅰ)求证:OM 为异面直线'AA 与'BD 的公垂线; (Ⅱ)求二面角''M BC B --的大小;
(第20题图)
F E
C 1
B 1
D 1A 1
A D
B
C
2010文(19)(本小题满分12分)
如图,棱柱111ABC A B C -的侧面11BCC B 是菱形,11B C A B ⊥
(Ⅰ)证明:平面11A B C ⊥平面11A BC ;
(Ⅱ)设D 是11A C 上的点,且1//AB 平面1B CD ,求11:A D DC 的值。
2012(18)(本小题满分12分)
如图,直三棱柱/
/
/
ABC A B C -,90BAC ∠=,
2,AB AC ==AA ′=1,点M ,N 分别为/A B 和//B C 的
中点。
(Ⅰ)证明:MN ∥平面/
/
A ACC ;
(Ⅱ)求三棱锥/
A MNC -的体积。
(椎体体积公式V=
1
3
Sh,其中S 为地面面积,h 为高)
2012,(16)(本小题共14分)
如图1,在Rt ABC ∆中,90C ∠=︒,D ,E 分别为
AC ,AB 的中点,点F 为线段CD 上的一点,将ADE ∆
沿DE 折起到1A DE ∆的位置,使1A F CD ⊥,如图2.
D F
D
E
B
C
A 1
F E
C
B
A
(Ⅰ)求证:DE //平面1A CB ; (Ⅱ)求证:1A F BE ⊥;
(Ⅲ)线段1A B 上是否存在点Q ,使1
AC ⊥⊥平面DEQ ? 说明理由.
201217.(本小题满分13分)
如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,AD ⊥PD ,BC=1,PC=23,PD=CD=2.
(I )求异面直线PA 与BC 所成角的正切值; (II )证明平面PDC ⊥平面ABCD ; (III )求直线PB 与平面ABCD 所成角的正弦值。
18.(本题满分12分)
如图,已知直三棱柱ABC —A 1B 1C 1,
90ACB ︒∠=,
2AC BC ==, 14AA =,E 、F 分别是棱CC 1、AB 中点.
(1)判断直线CF 和平面AEB 1的位置关系,
并加以证明;
(2)求四棱锥A —ECBB 1的体积.
(本小题满分12分) 如图,三棱锥A —BPC 中,AP ⊥PC ,AC ⊥BC ,M 为AB 中点,D 为PB 中点,且△PMB 为正三角形. (Ⅰ)求证:DM //平面APC ;
(Ⅱ)求 证:平面ABC ⊥平面APC ;
(Ⅲ)若BC =4,AB =20,求三棱锥D —BCM 的体积.
【2012高考全国文19】(本小题满分12分)(注意:在试题卷上.....作答无效....
) 如图,四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥底面ABCD ,22AC =,2PA =,E 是PC 上的一点,2PE EC =。
(Ⅰ)证明:PC ⊥平面BED ;
E
D
A
P
(Ⅱ)设二面角A PB C --为90,求PD 与平面PBC 所成角的大小。
27.【2012高考文19】(本小题满分 12分)
如图,长方体1111D C B A ABCD -中,底面1111D C B A 是正方形,O 是BD 的中点,E 是棱1AA 上任意一点。
(Ⅰ)证明:BD 1EC ⊥ ;
(Ⅱ)如果AB =2,AE =2,1EC OE ⊥,,求1AA 的长。
【2012高考文19】(本小题满分12分)
如图,在三棱锥P ABC -中,90APB ∠=,60PAB ∠=,AB BC CA ==,点P 在平面ABC 的射影O 在AB 上。
(Ⅰ)求直线PC 与平面ABC 所成的角的大小; (Ⅱ)求二面角B AP C --的大小。
【2012高考文科17】(本小题满分13分)
如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,AD ⊥PD ,BC=1,PC=23,PD=CD=2.
(I )求异面直线PA 与BC 所成角的正切值;
(II )证明平面PDC ⊥平面ABCD ;
(III )求直线PB 与平面ABCD 所成角的正弦值。
【2012高考新课标文19】(本小题满分12分)
如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=1
2
AA 1,D 是棱AA 1的中点
(I)证明:平面BDC 1⊥平面BDC
(Ⅱ)平面BDC 1分此棱柱为两部分,求这两部分体积的比.
【2102高考文16】(本小题共14分)如图1,在Rt △ABC 中,∠C=90°,D ,E 分别为AC ,AB 的中点,点F 为线段CD 上的一点,将△ADE 沿DE 折起到△A1DE 的
C
B
A D
C 1
A 1
位置,使A1F ⊥CD ,如图2。
(I)求证:DE ∥平面A1CB ; (II)求证:A1F ⊥BE ;
(III)线段A1B 上是否存在点Q ,使A1C ⊥平面DEQ ?说明理由。
【2012高考文18】(本小题满分12分) 直三棱柱ABC- A 1B 1C 1中,AB=A A 1 ,CAB ∠=2
π
(Ⅰ)证明11B A C B ⊥;
(Ⅱ)已知AB=2,BC=5,求三棱锥11C A AB - 的体积
【2012高考文18】(本小题满分12分)
如图,直三棱柱///
ABC A B C -,90BAC ∠=,2,AB AC ==
AA ′=1,点M ,N 分
别为/A B 和//
B C 的中点。
(Ⅰ)证明:MN ∥平面/
/
A ACC ;
(Ⅱ)求三棱锥/
A MNC -的体积。
(椎体体积公式V=1
3
Sh,其中S 为地面面积,h 为高)
【2012高考16】(14分)如图,在直三棱柱111ABC A B C -中,1111A B AC =,D E ,分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 求证:(1)平面ADE ⊥平面11BCC B ; (2)直线1//A F 平面ADE .
【2102高考文19】(本小题满分12分)
如图,在长方体ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,M 为棱DD 1上的一点。
(1) 求三棱锥A-MCC 1的体积;
(2) 当A 1M+MC 取得最小值时,求证:B 1M ⊥平面MAC 。
