【全国百强校】安徽师范大学附属中学2016-2017学年高二下学期期中考查化学试题

合集下载

安徽师大附中2016-2017学年高二(下)期中数学试卷(理科)(解析版)

安徽师大附中2016-2017学年高二（下）期中数学试卷（理科）（解析版）一、选择题：1、下列语句不是命题的是（） A 、﹣3＞4 B 、0.3是整数 C 、a ＞3 D 、4是3的约数2、“直线x ﹣y ﹣k=0与圆（x ﹣1）2+y 2=2有两个不同的交点”的一个充分不必要条件可以是（） A 、﹣1＜k ＜3 B 、﹣1≤k≤3 C 、0＜k ＜3 D 、k ＜﹣1或k ＞3 3、已知向量=（1，0，﹣1），则下列向量中与成60°夹角的是（）A 、（﹣1，1，0）B 、（1，﹣1，0）C 、（0，﹣1，1）D 、（﹣1，0，1）4、已知：，，类比上述等式，则：a+t=（） A 、70 B 、68 C 、69 D 、715、已知命题“∀x ∈R ，x 2﹣2ax+3≥0”是假命题，则实数a 的取值范围为（） A 、B 、或C 、D 、6、在正方体ABCD ﹣A 1B 1C 1D 1中，已知 =，=，=，O 为底面ABCD 中心，G 为△D 1C 1O 重心，则=（）（用表示）A、B、C、D、7、设函数，则曲线f（x）在点（1，f（1））处切线方程为（）A、B、C、D、8、设，都是非零向量，命题P：，命题Q：的夹角为钝角．则P是Q的（）A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件9、过点A（2，1）做曲线f（x）=x3﹣3x的切线，最多有（）A、3条B、2条C、1条D、0条10、若f（x）=x2+2 f（x）dx，则f（x）dx=（）A、﹣1B、﹣C、D、111、已知；，则f（n+1）﹣f（n）=（）A、B、C、D、12、若点P（a，b）在函数y=﹣x2+3lnx的图象上，点Q（c，d）在函数y=x+2的图象上，则（a﹣c）2+（b ﹣d）2的最小值为（）A、B、2C、2D、8二、填空题：13、观察下列算式：13=1，23=3+5，33=7+9+11，43=13+15+17+19，…若某数n3按上述规律展开后，发现右边含有“2017”这个数，则：n=________．14、命题：等腰三角形两底角相等的逆命题是：________．15、设，对任意x∈R，不等式a（cos2x﹣m）+πcosx≥0恒成立，则实数m的取值范围为________．16、设函数f（x）=（x﹣3）3+（x﹣1），数列{a n}是公差不为零的等差数列，f（a1）+f（a2）+…+f（a7）=14，则a1+a2+…+a7=________．三、解答题：17、设p：|4x﹣3|≤1，q：（x﹣a）（x﹣a﹣1）≤0，若：非q是非p的充分不必要条件，求实数a取值范围．18、已知函数f（x）=x3+bx2+cx的导函数图象关于直线x=2对称(1)求b值；(2)若f（x）在x=t处取得极小值，记此极小值为g（t），求g（t）的定义域．19、已知数列{a n}满足：(1)求a2，a3；(2)猜想{a n}通项公式并加以证明．20、如图，在直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE=EB，点F在CE上，且BF⊥平面ACE；(1)求证：AE⊥平面BCE；(2)求二面角B﹣AC﹣E的正弦值；(3)求点D到平面ACE的距离．21、已知函数f（x）=x﹣﹣2lnx，a∈R．(1)讨论函数f（x）的单调性；(2)若函数f（x）有两个极值点x1，x2，且x1＜x2，①求a的取值范围；②证明：f（x2）＜x2﹣1．答案解析部分一、选择题：1、【答案】C【考点】四种命题【解析】【解答】解：A，B，D都是表示判断一件事情，C无法判断，故选：C【分析】命题是表示判断一件事情的语句，根据定义分别判断即可．2、【答案】C【考点】必要条件、充分条件与充要条件的判断【解析】【解答】解：联立直线与圆的方程得：，消去y得：2x2+（﹣2k﹣2）x+k2﹣1=0，由题意得：△=（﹣2k﹣2）2﹣8（k2﹣1）＞0，变形得：（k﹣3）（k+1）＜0，解得：﹣1＜k＜3，∵0＜k＜3是﹣1＜k＜3的一个真子集，∴直线与圆有两个不同交点的一个充分不必要条件是0＜k＜3．故选C．【分析】把直线与圆的方程联立，消去y得到一个关于x的一元二次方程，根据直线与圆有两个不同的交点得到此方程有两个不等的实根，即△＞0，列出关于k的不等式，求出不等式的解集得到k的范围，在四个选项中找出解集的一个真子集即为满足题意的充分不必要条件．3、【答案】B【考点】数量积表示两个向量的夹角【解析】【解答】解：不妨设向量为=（x，y，z），A．若=（﹣1，1，0），则cosθ= =，不满足条件．B．若=（1，﹣1，0），则cosθ= = = ，满足条件．C．若=（0，﹣1，1），则cosθ= = ，不满足条件．D．若=（﹣1，0，1），则cosθ= = ，不满足条件．故选：B【分析】根据空间向量数量积的坐标公式，即可得到结论．4、【答案】D【考点】类比推理【解析】【解答】解：观察下列等式：，照此规律，第7个等式中：a=8，t=82﹣1=63a+t=71．故选D．【分析】观察所给的等式，第n个式子应该是=（n+1）•，即可写出结果．5、【答案】B【考点】命题的真假判断与应用【解析】【解答】解：∵命题“∀x∈R，x2﹣2ax+3≥0”是假命题，∴命题“∃x∈R，x2﹣2ax+3＜0”是真命题，故△=4a2﹣12＞0，解得：或，故选：B【分析】若命题“∀x∈R，x2﹣2ax+3≥0”是假命题，则命题“∃x∈R，x2﹣2ax+3＜0”是真命题，即△=4a2﹣12＞0，解得答案．6、【答案】C【考点】空间向量的基本定理及其意义【解析】【解答】解：取D1C1的中点E，∵G为△D1C1O重心，∴= = × （+ ）= （+ + + ）= （+ + ）=﹣，∵= = （+ ）= + ，∴= + = + + ﹣=﹣+ + ，故选：C【分析】根据向量的三角形法则和平行四边形法则化简计算即可．7、【答案】B【考点】利用导数研究曲线上某点切线方程【解析】【解答】解：函数，导数为f′（x）= •e x﹣f（0）+x，令x=1可得f′（1）=f′（1）﹣f（0）+1，解得f（0）=1，可令x=0，则f（0）= •e0=1，可得f′（1）=e，即有f′（x）=e x﹣1+x，可得曲线f（x）在点（1，f（1））处切线斜率为e，切点为（1，e﹣），即有切线的方程为y﹣e+ =e（x﹣1），即为y=ex﹣．故选：B．【分析】求出f（x）的导数，可令x=0，x=1，可得f（0）=1，f′（1）=e，求得切点，再由点斜式方程即可得到所求切线的方程．8、【答案】B【考点】必要条件、充分条件与充要条件的判断，数量积表示两个向量的夹角【解析】【解答】解：设，都是非零向量，由命题P：成立，可得的夹角为钝角或平角，故不能推出Q成立，故充分性不成立．由命题命题Q：的夹角为钝角成立，可得命题P：成立，故必要性成立．综上可得，P是Q的必要不充分条件，故选B．【分析】由命题P成立不能推出Q成立，但由命题Q成立能推出命题P成立，由此可得结论．9、【答案】A【考点】利用导数研究曲线上某点切线方程【解析】【解答】解：设切点为P（x0，x03﹣3x0），f′（x0）=3x02﹣3，则切线方程y﹣x03+3x0=（3x02﹣3）（x﹣x0），代入A（2，1）得，2x03﹣6x02+7=0．令y=2x03﹣6x02+7=0，则由y′=0，得x0=0或x0=2，且当x0=0时，y=7＞0，x0=2时，y=﹣1＜0．所以方程2x03﹣6x02+7=0有3个解，则过点A（2，1）作曲线f（x）=x3﹣3x的切线的条数是3条．故选：A．【分析】设出切点，求出切点处的导数，写出切线方程把A的坐标代入后得到关于切点横坐标的方程，再利用其导函数判断极值点，根据极值得到切点横坐标的个数，从而答案可求．10、【答案】B【考点】定积分【解析】【解答】解：令f（x）dx=t，对f（x）=x2+2 f（x）dx，两边积分可得：t= +2 tdx= +2t，解得t= f（x）dx=﹣，故选：B．【分析】把定积分项看成常数对两侧积分，化简求解即可．11、【答案】D【考点】归纳推理【解析】【解答】解：∵，∴f（n+1）﹣f（n）= ，故选：D．【分析】利用，计算f（n+1）﹣f（n）即可．12、【答案】D【考点】两点间距离公式的应用【解析】【解答】解：设直线y=x+m与曲线y=﹣x2+3lnx相切于P（x0，y0），由函数y=﹣x2+3lnx，∴，令，又x0＞0，解得x0=1．∴y0=﹣1+3ln1=﹣1，可得切点P（1，﹣1）．代入﹣1=1+m，解得m=﹣2．可得与直线y=x+2平行且与曲线y=﹣x2+3lnx相切的直线y=x﹣2．而两条平行线y=x+2与y=x﹣2的距离d= =2 ．∴（a﹣c）2+（b﹣d）2的最小值= =8．故选：D．【分析】先求出与直线y=x+2平行且与曲线y=﹣x2+3lnx相切的直线y=x+m．再求出此两条平行线之间的距离（的平方）即可得出．二、填空题：13、【答案】45【考点】归纳推理【解析】【解答】解：由题意可得第n个式子的左边是n3，右边是n个连续奇数的和，设第n个式子的第一个数为a n，则有a2﹣a1=3﹣1=2，a3﹣a2=7﹣3=4，…a n﹣a n﹣1=2（n﹣1），以上（n﹣1）个式子相加可得a n﹣a1= ，故a n=n2﹣n+1，可得a45=1981，a46=2071，故可知2017在第45个式子，故答案为：45【分析】可得规律：第n个式子的左边是n3，右边是n个连续奇数的和，设第n个式子的第一个数为a n，累加可得a n，计算可得a45=1981，a46=2071，可知2015在第45 个式子14、【答案】若一个三角形有两个角相等，则这个三角形为等腰三角形【考点】四种命题间的逆否关系【解析】【解答】解：等腰三角形两底角相等，即为若一个三角形为等腰三角形，则这个三角形的两个底角相等，那么它的逆命题为：若一个三角形有两个角相等，则这个三角形为等腰三角形，故答案为：若一个三角形有两个角相等，则这个三角形为等腰三角形【分析】根据四种命题的关系即可求出．15、【答案】（﹣∞，﹣3]【考点】定积分，函数最值的应用【解析】【解答】解：∵，表示y= 在[0，1]上的积分，也得圆面积的四分之一，∴a= ×π，∴对任意x∈R，不等式（cos2x﹣m）+πcosx≥0恒成立，可得m≤cos2x+4cosx在x∈R上恒成立，cosx∈[﹣1，1]，求出cos2x+4cosx的最小值即可，cos2x+4cosx=（cosx+2）2﹣4，∵函数开口向上，cosx∈[﹣1，1]，函数f（cosx）=cos2x+4cosx在[﹣1，1]上增函数，当cosx=﹣1时取得最小值，可得（﹣1）2+4×（﹣1）=﹣3，∴cos2x+4cosx的最小值为﹣3，∴m≤﹣3，故答案为（﹣∞，﹣3]；【分析】根据定积分几何意义求出a值，根据任意x∈R，不等式a（cos2x﹣m）+πcosx≥0恒成立，利用常数分离法进行求解；16、【答案】21【考点】数列与函数的综合【解析】【解答】解：由题意可得，[（a1﹣3）3+a1﹣1]+[（a2﹣3）3+a2﹣1]+…+[（a7﹣3）3+a7﹣1]=14，∴[（a1﹣3）3+a1﹣3]+[（a2﹣3）3+a2﹣3]+…+[（a7﹣3）3+a7﹣3]=0，根据等差数列的性质可得（a4﹣3﹣3d）3 +（a4﹣3﹣2d）3 +…+（a4﹣3﹣d）3+7（a4﹣3）=0，（a4﹣3）3 +7（a4﹣3）=0，（a4﹣3）[7（a4﹣3）3 +84d2+7]=0，∴a4﹣3=0，即a4=3．∴a1+a2+…+a7=7a4=21，故答案为：21【分析】由题意可得[（a1﹣3）3+a1﹣3]+[（a2﹣3）3+a2﹣3]+…+[（a7﹣3）3+a7﹣3]=0，再利用等差数列的性质求得a4=3，从而求得a1+a2+…+a7 的值．三、解答题：17、【答案】解：p：|4x﹣3|≤1，解得≤x≤1，q：（x﹣a）（x﹣a﹣1）≤0，解得a≤x≤a+1，∵非q是非p的充分不必要条件，∴p是q的充分不必要条件，∴解得0≤a≤ ，故实数a取值范围为[0，]【考点】必要条件、充分条件与充要条件的判断【解析】【分析】求出命题p，q的等价条件，结合充分条件和必要条件的定义建立条件关系即可．18、【答案】（1）解：f′（x）=3x2+2bx+c 因为函数f′（x）的图象关于直线x=2对称，所以﹣=2，于是b=﹣6（2）解：由（1）知，f（x）=x3﹣6x2+cx，f′（x）=3x2﹣12x+c=3（x﹣2）2+c﹣12，（ⅰ）当c≥12时，f′（x）≥0，此时f（x）无极值．（ii）当c＜12时，f′（x）=0有两个互异实根x1，x2．不妨设x1＜x2，则x1＜2＜x2．当x＜x1时，f′（x）＞0，f（x）在区间（﹣∞，x1）内为增函数；当x1＜x＜x2时，f′（x）＜0，f（x）在区间（x1，x2）内为减函数；当x＞x2时，f′（x）＞0，f（x）在区间（x2，+∞）内为增函数．所以f（x）在x=x1处取极大值，在x=x2处取极小值．因此，当且仅当c＜12时，函数f（x）在x=x2处存在唯一极小值，所以t=x2＞2．于是g（t）的定义域为（2，+∞）【考点】利用导数研究函数的极值【解析】【分析】（1）函数f（x）=x3+bx2+cx的导函数的图象关于直线x=2对称，则求出f′（x）得到一个二次函数，利用x=﹣=2求出b即可；（2）求出f′（x），由（1）得函数的对称轴为x=2，讨论c的取值范围求出g（t）的定义域和值域即可．19、【答案】（1）解：数列{a n}满足：，∴n=2时，=22a2，可得a2= ，∴n=3时，+a3=9a3，解得a3=（2）解：猜想a n= ．证明：∵，∴n≥2时，a 1+a 2+…+a n ﹣1=（n ﹣1）2a n ﹣1 ．∴n 2a n ﹣（n ﹣1）2a n ﹣1=a n ．化为：．∴a n = • •… •a 1= • • •…× × ×=【考点】数列递推式【解析】【分析】（1）数列{a n }满足：，n=2时， =22a 2 ，可得a 2= ，n=3时， +a 3=9a 3 ，解得a 3 ．（2）猜想a n = ．利用递推关系化为：．再利用a n = • •… •a 1即可得出．20、【答案】（1）证明：∵BF ⊥平面ACE ，∴BF ⊥AE ， ∵二面角D ﹣AB ﹣E 为直二面角，∴平面ABCD ⊥平面ABE ，又BC ⊥AB ，∴BC ⊥平面ABE ，则BC ⊥AE ，又BF ⊂平面BCE ，BF∩BC=B ，∴AE ⊥平面BCE（2）法一、解：连接AC 、BD 交于G ，连接FG ，∵ABCD 为正方形，∴BD ⊥AC ，∵BF ⊥平面ACE ，BG ⊥AC ，∴AC ⊥平面BFG ，∴FG ⊥AC ，即∠FGB 为二面角B ﹣AC ﹣E 的平面角，由（1）可知，AE ⊥平面BCE ，∴AE ⊥EB ，又AE=EB ，AB=2，AE=BE= ，在直角三角形BCE 中，CE= = ，BF= = ，在正方形中，BG= ，在直角三角形BFG中，sin∠FGB= ；法二、以线段AB的中点为原点O，OE所在直线为x轴，AB所在直线为y轴，过O点平行于AD的直线为z轴，建立空间直角坐标系O﹣xyz，如图．∵AE⊥面BCE，BE⊂面BCE，∴AE⊥BE，在Rt△AEB中，AB=2，O为AB的中点，∴OE=1．∴A（0，﹣1，0），E（1，0，0），C（0，1，2），=（1，1，0），=（0，2，2）．设平面AEC的一个法向量为=（x，y，z），则，令x=1，得=（1，﹣1，1）是平面AEC的一个法向量．又平面BAC的一个法向量为=（1，0，0），∴cos＜＞= = ．∴二面角B﹣AC﹣E的正弦值为（3）法一、由（2）可知，在正方形ABCD中，BG=DG，D到平面ACE的距离等于B到平面ACE的距离，BF ⊥平面ACE，线段BF的长度就是点B到平面ACE的距离，即为D到平面ACE的距离所以D到平面的距离为．法二、解：∵AD∥z轴，AD=2，∴=（0，0，2），∴点D到平面ACE的距离d=| |•|cos＜＞= = ．【考点】点、线、面间的距离计算，二面角的平面角及求法【解析】【分析】（1）要证AE⊥平面BCE，只需证明AE垂直平面BCE内的两条相交直线BF、BC即可；（2）连接AC、BD交于G，连接FG，说明∠FGB为二面角B﹣AC﹣E的平面角，然后求二面角B﹣AC﹣E 的大小；（3）利用V D﹣ACE=V E﹣ACD，求点D到平面ACE的距离，也可以利用空间直角坐标系，向量的数量积，证明垂直，求出向量的模．21、【答案】（1）解：函数的定义域为（0，+∞），，令f′（x）=0，得x2﹣2x+a=0，其判别式△=4﹣4a，①当△≤0，即a≥1时，x2﹣2x+a≥0，f′（x）≥0，此时，f（x）在（0，+∞）上单调递增；②当△＞0，即a＜1时，方程x2﹣2x+a=0的两根为，，若a≤0，则x1≤0，则x∈（0，x2）时，f′（x）＜0，x∈（x2，+∞）时，f′（x）＞0，此时，f（x）在（0，x2）上单调递减，在（x2，+∞）上单调递增；若a＞0，则x1＞0，则x∈（0，x1）时，f′（x）＞0，x∈（x1，x2）时，f′（x）＜0，x∈（x2，+∞）时，f′（x）＞0，此时，f（x）在（0，x1）上单调递增，在（x1，x2）上单调递减，在（x2，+∞）上单调递增．综上所述，当a≤0时，函数f（x）在（0，1+ ）上单调递减，在（1+ ，+∞）上单调递增；当0＜a＜1时，函数f（x）在（0，1﹣）上单调递增，在（1﹣，1+ ）上单调递减，在（1+ ，+∞）上单调递增；当a≥1时，函数f（x）在（0，+∞）上单调递增（2）①解：由（1）可知，函数f（x）有两个极值点x1，x2，等价于方程x2﹣2x+a=0在（0，+∞）有两不等实根，故0＜a＜1．②证明：由上述过程得0＜a＜1，，且1＜x2＜2，．，令g（t）=t﹣2lnt﹣1，1＜t＜2，则，由于1＜t＜2，则g′（t）＜0，故g（t）在（1，2）上单调递减．故g（t）＜g（1）=1﹣2ln1﹣1=0．∴f（x2）﹣x2+1=g（x2）＜0．∴f（x2）＜x2﹣1．【考点】利用导数研究函数的单调性，利用导数研究函数的极值【解析】【分析】（1）求出函数的定义域为（0，+∞），函数的导数，令f′（x）=0，①当△≤0，②当△＞0进行分类讨论．（2）①求出函数f（x）有两个极值点x1，x2，等价于方程x2﹣2x+a=0在（0，+∞），直接推出结果．②通过（1），（2），推出0＜a＜1，构造新函数g（t）=t﹣2lnt﹣1，1＜t＜2，利用新函数的单调性证明求解即可．。

精品：【全国百强校】安徽省安徽师范大学附属中学2015-2016学年高二下学期期中考试物理试题(解析版)

一、单选题（本题共7小题，每小题4分，共28分，每小题的四个选项中只有一个符合题意）1.下列不属于反冲运动的是（）A. 喷气式飞机的运动B.直升机的运动C.火箭的运动D.反击式水轮机的运动【答案】B考点：反冲运动【名师点睛】本题考查反冲运动的应用；明确反冲运动是相互作用的物体之间的作用力与反作用力产生的效果，并且要知道反冲在实际生活中的运用。

2. 如图为手机无线充电的原理图，下列哪种装置的工作原理与其相同（）A. 电磁炉B.电动机C.回旋加速器D.速度选择器【答案】A【解析】试题分析：手机无线充电及电磁炉均应用了电磁感应原理；而电动机是导线在磁场中受力；回放旋加速度利用电场的加速及磁场中的偏转；速度选择器采用的是复合场中的运动；故选A。

考点：电磁感应【名师点睛】电磁感应在生产生活有很多的应用，要注意明确它们的工作原理。

3. 下列实验现象，属于电磁感应现象的是（）A.导线通电后，其下方的小磁场偏转B.通电导线AB 在磁场中运动C.金属杆切割磁感线时，电流表指针偏转D.通电线圈在磁场中转动【答案】C考点：电磁感应现象【名师点睛】知道电磁感应现象的概念、导体棒切割磁感线产生感应感应电流的现象或者穿过线圈的磁通量发生变化时产生感应电流的现象是电磁感应现象;分析清楚图示实验情景即可正确解题。

4、一只电阻分别通过四种不同形式的电流，电流随时间变化的情况如图所示，在相同时间内电阻产生的热量最大的是（）A ．B ．C ．D ．【答案】D【解析】试题分析：对A 、对于正弦式电流，有效值：1m I I ==．根据焦耳定律得：22112Q I RT RT RT ===；对B 、对于正弦式电流，有效值：2m I I ==．根据焦耳定律得：22222Q I RT RT RT ===；对C 、根据焦耳定律得：Q 3＝I 2RT ＝2.25RT对D 、对于方波，根据焦耳定律得：2244422422T T Q I R I R RT RT RT =⋅+'⋅=+=；故选D 。

安徽师范大学附属中学高二下学期期中考查化学试题含答案

说明：1、考试时间：100 分钟；本卷满分： 100 分2、请将答案填写在答案卷上，考试结束后只交答案卷。

可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Cl35.5 Fe 56 Cu 64 Ne 20 Na 23 Mg 24 K 39 Al 27 Ca 40第Ⅰ卷(选择题共51分)一、选择题(本题包括17小题，每小题3分，共51分，每小题只有一个选项符合题意) 1．“优化结构、提高效益和降低消耗、保护环境”，这是我国国民经济和社会发展的基础性要求。

你认为下列行为不符合这个要求的是A．将煤转化成气体燃料可以有效地减少“温室效应”的气体产生B．加快太阳能、风能、生物质能、海洋能等清洁能源的开发利用C．研制开发以水代替有机溶剂的化工涂料D．大力发展农村沼气，将废弃的秸秆转化为清洁高效的能源2．甲醇质子交换膜燃料电池中将甲醉蒸气转化为氢气的两种反应原理是①CH3OH(g)+H2O(g)→CO2(g)+3H2(g)△H=+49.0kJ②CH3OH(g)+O2(g)→CO2(g)+2H2(g) △H=-192.9kJ下列说法正确的是( )A．CH3OH的燃烧热为192.9kJ/molB．CH3OH转变成H2的过程一定要吸收能量C．可推知2H2(g)+O2(g)═2H2O(g) △H=-483.8 kJ/molD．根据②推知反应：CH3OH(l)+O2(g)→CO2(g)+2H2(g)，△H＜-192.9kJ3．N A表示阿伏加罗常数的值，则关于热化学方程式：C2H2(g)+2.5O2(g)=2CO2(g)+H2O(l) △H= -1300kJ•mol-1的说法中，正确的是A．当5N A个电子转移时，该反应放出650kJ的能量B．当1N A个水分子生成且为气体时，放出多于1300kJ的能量C．当2N A个碳氧双键生成时，放出1300kJ的能量D．当4N A个碳氧共用电子对生成时，放出1300kJ的能量4．下列变化不能用勒夏特列原理解释的是A．红棕色的NO2气体加压后颜色先变深再变浅B．实验室中常用饱和食盐水除去Cl2中混有的HClC．二氧化硫转化为三氧化硫时增加空气的量以提高二氧化硫的转化率D．H2、I2、HI混合气体加压后颜色变深晶体硅在氧气中燃烧的热化学方程式为Si(s)+O2(g)═SiO2(s)△H=-989.2kJ•mol-1，则X 的值为(已知1mol Si中含有2mol Si-Si键，1mol SiO2中含有4mol Si-O键)A．34.6 B．460 C．832 D．9206．一定温度下，将一定质量的冰醋酸加水稀释，溶液的导电能力变化如图所示，下列说法中，正确的是A．a，b，c三点溶液的n(H+)：c＜a＜bB．a，b，c三点醋酸的电离程度：a＜b＜cC．用湿润的pH试纸测量a处溶液的pH，测量结果偏大D．a，b，c三点溶液用1 mol•L-1的氢氧化钠溶液中和，消耗氢氧化钠溶液的体积：c＜a ＜b7．下列说法可表示方法正确的是A．将0.5molN2和1.5molH2充入一密闭容器中充分反应，放出热量19.6kJ则该热化学方程式为N2(g)+3H2(g)2NH3(g) △H=-39.2kJ•mol-1B．由C(石墨)=C(金刚石)；△H=+1.9kJ•mol-1，可知金刚石比石墨稳定C．在稀溶液中：H++OH-═H2O△H=-57.3kJ/mol，若将含40.0gNaOH的稀溶液与稀醋酸完全中和，放出的热量小于57.3kJD．在101kPa时，2gH2完全燃烧生成液态水，放出285.8kJ热量，氢气燃烧的热化学方程式表示为：2H2(g)+O2(g)═2H2O(l) △H= -285.8kJ/mol8．反应A(g)十2B(g)===C(g)的反应过程中能最变化如下图所示。

安徽2016-2017学年高二下学期期中考试英语试卷含答案

安徽师范大学附属中学2016—2017学年第二学期期中考查高二英语试题命题：王建华审题：徐琼本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分100分，考试时间120分钟.第I卷（选择题，共60分)第一部分:听力（共两节，满分10分）第一节（共5小题;每小题0.5分，满分2.5分）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题.每段对话仅读一遍.1。

What time is it now?A. 7：15. B。

6：40。

C. 7:45。

2. What does the man mean？A. The woman should go away.B. He will get close to the woman。

C。

He can hear the woman very well.3. Where does the conversation possibly take place？A。

At home。

B。

At a school. C. In a restaurant.4。

What are the two speakers doing？A. Listening to music.B. Playing a musical instrument.C. Listening to a classical concert.5。

Why did so many people die last month?A. Because they were too old.B. Because of serious illness。

C. Because of the bad weather.第二节（共15小题；每小题0。

5分，满分7。

5分）听下面5段对话或独白。

每段对话或独白后有几个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置.听每段对话或独白前，你将有时间阅读各个小题，每小题5秒钟；听完后，各小题将给出5秒钟的作答时间。

2016-2017年安徽师大附中高二(下)期中数学试卷(理科)和答案

2016-2017学年安徽师大附中高二（下）期中数学试卷（理科）一、选择题：本大题共12个小题，每小题3分，共36分．每小题给出的四个选项中，只有一项符合题目要求的．1．（3分）下列语句不是命题的是（）A．﹣3＞4B．0.3是整数C．a＞3D．4是3的约数2．（3分）“直线x﹣y﹣k＝0与圆（x﹣1）2+y2＝2有两个不同的交点”的一个充分不必要条件可以是（）A．﹣1＜k＜3B．﹣1≤k≤3C．0＜k＜3D．k＜﹣1或k＞3 3．（3分）已知向量＝（1，0，﹣1），则下列向量中与成60°夹角的是（）A．（﹣1，1，0）B．（1，﹣1，0）C．（0，﹣1，1）D．（﹣1，0，1）4．（3分）已知：，，类比上述等式，则：a+t＝（）A．70B．68C．69D．715．（3分）已知命题“∀x∈R，x2﹣2ax+3≥0”是假命题，则实数a的取值范围为（）A．B．或C．D．6．（3分）在正方体ABCD﹣A1B1C1D1中，已知＝，＝，＝，O为底面ABCD中心，G为△D 1C1O重心，则＝（）（用表示）A．B．C．D．7．（3分）设函数，则曲线f（x）在点（1，f（1））处切线方程为（）A．B．C．D．8．（3分）设，都是非零向量，命题P：，命题Q：的夹角为钝角．则P是Q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件9．（3分）过点A（2，1）做曲线f（x）＝x3﹣3x的切线，最多有（）A．3条B．2条C．1条D．0条10．（3分）若f（x）＝x2+2f（x）dx，则f（x）dx＝（）A．﹣1B．﹣C．D．111．（3分）已知；，则f（n+1）﹣f（n）＝（）A．B．C．D．12．（3分）若点P（a，b）在函数y＝x2+3lnx的图象上，点Q（c，d）在函数y ＝x+2的图象上，则（a﹣c）2+（b﹣d）2的最小值为（）A．B．8C．2D．2二、填空题：本大题共4小题，每题4分，共16分．13．（4分）观察下列算式：13＝1，23＝3+5，33＝7+9+11，43＝13+15+17+19，…若某数n3按上述规律展开后，发现右边含有“2017”这个数，则：n＝．14．（4分）命题：等腰三角形两底角相等的逆命题是：．15．（4分）设，对任意x∈R，不等式a（cos2x﹣m）+πcos x≥0恒成立，则实数m的取值范围为．16．（4分）设函数f（x）＝（x﹣3）3+（x﹣1），数列{a n}是公差不为零的等差数列，f（a1）+f（a2）+…+f（a7）＝14，则a1+a2+…+a7＝．三、解答题：本大题共5小题，共48分，解答应写出文字说明，证明过程或演算步骤．17．（8分）设p：|4x﹣3|≤1，q：（x﹣a）（x﹣a﹣1）≤0，若：非q是非p的充分不必要条件，求实数a取值范围．18．（8分）已知函数f（x）＝x3+bx2+cx的导函数图象关于直线x＝2对称（1）求b值；（2）若f（x）在x＝t处取得极小值，记此极小值为g（t），求g（t）的定义域．19．（8分）已知数列{a n}满足：（1）求a2，a3；（2）猜想{a n}通项公式并加以证明．20．（12分）如图，在直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE＝EB，点F在CE上，且BF⊥平面ACE；（1）求证：AE⊥平面BCE；（2）求二面角B﹣AC﹣E的正弦值；（3）求点D到平面ACE的距离．21．（12分）已知函数f（x）＝x﹣﹣2lnx，a∈R．（1）讨论函数f（x）的单调性；（2）若函数f（x）有两个极值点x1，x2，且x1＜x2，①求a的取值范围；②证明：f（x2）＜x2﹣1．2016-2017学年安徽师大附中高二（下）期中数学试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题3分，共36分．每小题给出的四个选项中，只有一项符合题目要求的．1．（3分）下列语句不是命题的是（）A．﹣3＞4B．0.3是整数C．a＞3D．4是3的约数【解答】解：A，B，D都是表示判断一件事情，C无法判断，故选：C．2．（3分）“直线x﹣y﹣k＝0与圆（x﹣1）2+y2＝2有两个不同的交点”的一个充分不必要条件可以是（）A．﹣1＜k＜3B．﹣1≤k≤3C．0＜k＜3D．k＜﹣1或k＞3【解答】解：联立直线与圆的方程得：，消去y得：2x2+（﹣2k﹣2）x+k2﹣1＝0，由题意得：△＝（﹣2k﹣2）2﹣8（k2﹣1）＞0，变形得：（k﹣3）（k+1）＜0，解得：﹣1＜k＜3，∵0＜k＜3是﹣1＜k＜3的一个真子集，∴直线与圆有两个不同交点的一个充分不必要条件是0＜k＜3．故选：C．3．（3分）已知向量＝（1，0，﹣1），则下列向量中与成60°夹角的是（）A．（﹣1，1，0）B．（1，﹣1，0）C．（0，﹣1，1）D．（﹣1，0，1）【解答】解：不妨设向量为＝（x，y，z），A．若＝（﹣1，1，0），则cosθ＝＝，不满足条件．B．若＝（1，﹣1，0），则cosθ＝＝＝，满足条件．C．若＝（0，﹣1，1），则cosθ＝＝，不满足条件．D．若＝（﹣1，0，1），则cosθ＝＝，不满足条件．故选：B．4．（3分）已知：，，类比上述等式，则：a+t＝（）A．70B．68C．69D．71【解答】解：观察下列等式：，照此规律，第7个等式中：a＝8，t＝82﹣1＝63a+t＝71．故选：D．5．（3分）已知命题“∀x∈R，x2﹣2ax+3≥0”是假命题，则实数a的取值范围为（）A．B．或C．D．【解答】解：∵命题“∀x∈R，x2﹣2ax+3≥0”是假命题，∴命题“∃x∈R，x2﹣2ax+3＜0”是真命题，故△＝4a2﹣12＞0，解得：或，故选：B．6．（3分）在正方体ABCD﹣A1B1C1D1中，已知＝，＝，＝，O为底面ABCD中心，G为△D 1C1O重心，则＝（）（用表示）A．B．C．D．【解答】解：取D1C1的中点E，∵G为△D1C1O重心，∴＝＝×（+）＝（+++）＝（++）＝﹣，∵＝＝（+）＝+，∴＝+＝++﹣＝﹣++，故选：C．7．（3分）设函数，则曲线f（x）在点（1，f（1））处切线方程为（）A．B．C．D．【解答】解：函数，导数为f′（x）＝•e x﹣f（0）+x，令x＝1可得f′（1）＝f′（1）﹣f（0）+1，解得f（0）＝1，可令x＝0，则f（0）＝•e0＝1，可得f′（1）＝e，即有f′（x）＝e x﹣1+x，可得曲线f（x）在点（1，f（1））处切线斜率为e，切点为（1，e﹣），即有切线的方程为y﹣e+＝e（x﹣1），即为y＝ex﹣．故选：B．8．（3分）设，都是非零向量，命题P：，命题Q：的夹角为钝角．则P是Q的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【解答】解：设，都是非零向量，由命题P：成立，可得的夹角为钝角或平角，故不能推出Q成立，故充分性不成立．由命题命题Q：的夹角为钝角成立，可得命题P：成立，故必要性成立．综上可得，P是Q的必要不充分条件，故选：B．9．（3分）过点A（2，1）做曲线f（x）＝x3﹣3x的切线，最多有（）A．3条B．2条C．1条D．0条【解答】解：设切点为P（x0，x03﹣3x0），f′（x0）＝3x02﹣3，则切线方程y﹣x03+3x0＝（3x02﹣3）（x﹣x0），代入A（2，1）得，2x03﹣6x02+7＝0．令y＝2x03﹣6x02+7＝0，则由y′＝0，得x0＝0或x0＝2，且当x0＝0时，y＝7＞0，x0＝2时，y＝﹣1＜0．所以方程2x03﹣6x02+7＝0有3个解，则过点A（2，1）作曲线f（x）＝x3﹣3x的切线的条数是3条．故选：A．10．（3分）若f（x）＝x2+2f（x）dx，则f（x）dx＝（）A．﹣1B．﹣C．D．1【解答】解：令f（x）dx＝t，对f（x）＝x2+2f（x）dx，两边积分可得：t＝+2tdx＝+2t，解得t＝f（x）dx＝﹣，故选：B．11．（3分）已知；，则f（n+1）﹣f（n）＝（）A．B．C．D．【解答】解：∵，∴f（n+1）﹣f（n）＝，故选：D．12．（3分）若点P（a，b）在函数y＝x2+3lnx的图象上，点Q（c，d）在函数y ＝x+2的图象上，则（a﹣c）2+（b﹣d）2的最小值为（）A．B．8C．2D．2【解答】解：设直线y＝x+m与曲线y＝﹣x2+3lnx相切于P（x0，y0），由函数y＝﹣x2+3lnx，∴y′＝﹣2x+，令﹣2x0+＝1，又x0＞0，解得x0＝1．∴y0＝﹣1+3ln1＝﹣1，可得切点P（1，﹣1）．代入﹣1＝1+m，解得m＝﹣2．可得与直线y＝x+2平行且与曲线y＝﹣x2+3lnx相切的直线y＝x﹣2．而两条平行线y＝x+2与y＝x﹣2的距离d＝＝2．∴（a﹣c）2+（b﹣d）2的最小值＝（2）2＝8．故选：B．二、填空题：本大题共4小题，每题4分，共16分．13．（4分）观察下列算式：13＝1，23＝3+5，33＝7+9+11，43＝13+15+17+19，…若某数n3按上述规律展开后，发现右边含有“2017”这个数，则：n＝45．【解答】解：由题意可得第n个式子的左边是n3，右边是n个连续奇数的和，设第n个式子的第一个数为a n，则有a2﹣a1＝3﹣1＝2，a3﹣a2＝7﹣3＝4，…a n﹣a n﹣1＝2（n﹣1），以上（n﹣1）个式子相加可得a n﹣a1＝，故a n＝n2﹣n+1，可得a45＝1981，a46＝2071，故可知2017在第45个式子，故答案为：4514．（4分）命题：等腰三角形两底角相等的逆命题是：若一个三角形有两个角相等，则这个三角形为等腰三角形．【解答】解：等腰三角形两底角相等，即为若一个三角形为等腰三角形，则这个三角形的两个底角相等，那么它的逆命题为：若一个三角形有两个角相等，则这个三角形为等腰三角形，故答案为：若一个三角形有两个角相等，则这个三角形为等腰三角形15．（4分）设，对任意x∈R，不等式a（cos2x﹣m）+πcos x≥0恒成立，则实数m的取值范围为（﹣∞，﹣3]．【解答】解：∵，表示y＝在[0，1]上的积分，也得圆面积的四分之一，∴a＝×π，∴对任意x∈R，不等式（cos2x﹣m）+πcos x≥0恒成立，可得m≤cos2x+4cos x在x∈R上恒成立，cos x∈[﹣1，1]，求出cos2x+4cos x的最小值即可，cos2x+4cos x＝（cos x+2）2﹣4，∵函数开口向上，cos x∈[﹣1，1]，函数f（cos x）＝cos2x+4cos x在[﹣1，1]上增函数，当cos x＝﹣1时取得最小值，可得（﹣1）2+4×（﹣1）＝﹣3，∴cos2x+4cos x的最小值为﹣3，∴m≤﹣3，故答案为（﹣∞，﹣3]；16．（4分）设函数f（x）＝（x﹣3）3+（x﹣1），数列{a n}是公差不为零的等差数列，f（a1）+f（a2）+…+f（a7）＝14，则a1+a2+…+a7＝21．【解答】解：由题意可得，[（a1﹣3）3+a1﹣1]+[（a2﹣3）3+a2﹣1]+…+[（a7﹣3）3+a﹣1]＝14，7∴[（a1﹣3）3+a1﹣3]+[（a2﹣3）3+a2﹣3]+…+[（a7﹣3）3+a7﹣3]＝0，根据等差数列的性质可得（a4﹣3﹣3d）3 +（a4﹣3﹣2d）3 +…+（a4﹣3﹣d）3+7（a4﹣3）＝0，（a4﹣3）3 +7（a4﹣3）＝0，（a4﹣3）[7（a4﹣3）3 +84d2+7]＝0，∴a4﹣3＝0，即a4＝3．∴a1+a2+…+a7＝7a4＝21，故答案为：21三、解答题：本大题共5小题，共48分，解答应写出文字说明，证明过程或演算步骤．17．（8分）设p：|4x﹣3|≤1，q：（x﹣a）（x﹣a﹣1）≤0，若：非q是非p的充分不必要条件，求实数a取值范围．【解答】解：p：|4x﹣3|≤1，解得≤x≤1，q：（x﹣a）（x﹣a﹣1）≤0，解得a≤x≤a+1，∵非q是非p的充分不必要条件，∴p是q的充分不必要条件，∴解得0≤a≤，故实数a取值范围为[0，]18．（8分）已知函数f（x）＝x3+bx2+cx的导函数图象关于直线x＝2对称（1）求b值；（2）若f（x）在x＝t处取得极小值，记此极小值为g（t），求g（t）的定义域．【解答】解：（1）f′（x）＝3x2+2bx+c因为函数f′（x）的图象关于直线x＝2对称，所以﹣＝2，于是b＝﹣6；（2）由（1）知，f（x）＝x3﹣6x2+cx，f′（x）＝3x2﹣12x+c＝3（x﹣2）2+c﹣12，（ⅰ）当c≥12时，f′（x）≥0，此时f（x）无极值．（ii）当c＜12时，f′（x）＝0有两个互异实根x1，x2．不妨设x1＜x2，则x1＜2＜x2．当x＜x1时，f′（x）＞0，f（x）在区间（﹣∞，x1）内为增函数；当x1＜x＜x2时，f′（x）＜0，f（x）在区间（x1，x2）内为减函数；当x＞x2时，f′（x）＞0，f（x）在区间（x2，+∞）内为增函数．所以f（x）在x＝x1处取极大值，在x＝x2处取极小值．因此，当且仅当c＜12时，函数f（x）在x＝x2处存在唯一极小值，所以t＝x2＞2．于是g（t）的定义域为（2，+∞）．19．（8分）已知数列{a n}满足：（1）求a2，a3；（2）猜想{a n}通项公式并加以证明．【解答】解：（1）数列{a n}满足：，∴n＝2时，＝22a2，可得a2＝，∴n＝3时，+a3＝9a3，解得a3＝．（2）猜想a n＝．证明：∵，∴n≥2时，a1+a2+…+a n﹣1＝（n﹣1）2a n﹣1．∴n2a n﹣（n﹣1）2a n﹣1＝a n．化为：．∴a n＝••…•a1＝•••…×××＝．20．（12分）如图，在直二面角D﹣AB﹣E中，四边形ABCD是边长为2的正方形，AE＝EB，点F在CE上，且BF⊥平面ACE；（1）求证：AE⊥平面BCE；（2）求二面角B﹣AC﹣E的正弦值；（3）求点D到平面ACE的距离．【解答】法一、（1）证明：∵BF⊥平面ACE，∴BF⊥AE，∵二面角D﹣AB﹣E为直二面角，∴平面ABCD⊥平面ABE，又BC⊥AB，∴BC⊥平面ABE，则BC⊥AE，又BF⊂平面BCE，BF∩BC＝B，∴AE⊥平面BCE；（2）解：连接AC、BD交于G，连接FG，∵ABCD为正方形，∴BD⊥AC，∵BF⊥平面ACE，BG⊥AC，∴AC⊥平面BFG，∴FG⊥AC，即∠FGB为二面角B﹣AC﹣E的平面角，由（1）可知，AE⊥平面BCE，∴AE⊥EB，又AE＝EB，AB＝2，AE＝BE＝，在直角三角形BCE中，CE＝＝，BF＝＝，在正方形中，BG＝，在直角三角形BFG中，sin∠FGB＝；（3）由（2）可知，在正方形ABCD中，BG＝DG，D到平面ACE的距离等于B 到平面ACE的距离，BF⊥平面ACE，线段BF的长度就是点B到平面ACE的距离，即为D到平面ACE的距离所以D到平面的距离为．法二、（1）证明：同法一；（2）解：以线段AB的中点为原点O，OE所在直线为x轴，AB所在直线为y 轴，过O点平行于AD的直线为z轴，建立空间直角坐标系O﹣xyz，如图．∵AE⊥面BCE，BE⊂面BCE，∴AE⊥BE，在Rt△AEB中，AB＝2，O为AB的中点，∴OE＝1．∴A（0，﹣1，0），E（1，0，0），C（0，1，2），＝（1，1，0），＝（0，2，2）．设平面AEC的一个法向量为＝（x，y，z），则，令x＝1，得＝（1，﹣1，1）是平面AEC的一个法向量．又平面BAC的一个法向量为＝（1，0，0），∴cos＜＞＝＝．∴二面角B﹣AC﹣E的正弦值为；（3）解：∵AD∥z轴，AD＝2，∴＝（0，0，2），∴点D到平面ACE的距离d＝||•|cos＜＞＝＝．21．（12分）已知函数f（x）＝x﹣﹣2lnx，a∈R．（1）讨论函数f（x）的单调性；（2）若函数f（x）有两个极值点x1，x2，且x1＜x2，①求a的取值范围；②证明：f（x2）＜x2﹣1．【解答】（1）解：函数的定义域为（0，+∞），，令f′（x）＝0，得x2﹣2x+a＝0，其判别式△＝4﹣4a，①当△≤0，即a≥1时，x2﹣2x+a≥0，f′（x）≥0，此时，f（x）在（0，+∞）上单调递增；②当△＞0，即a＜1时，方程x2﹣2x+a＝0的两根为，，若a≤0，则x1≤0，则x∈（0，x2）时，f′（x）＜0，x∈（x2，+∞）时，f′（x）＞0，此时，f（x）在（0，x2）上单调递减，在（x2，+∞）上单调递增；若a＞0，则x1＞0，则x∈（0，x1）时，f′（x）＞0，x∈（x1，x2）时，f′（x）＜0，x∈（x2，+∞）时，f′（x）＞0，此时，f（x）在（0，x1）上单调递增，在（x1，x2）上单调递减，在（x2，+∞）上单调递增．综上所述，当a≤0时，函数f（x）在（0，1+）上单调递减，在（1+，+∞）上单调递增；当0＜a＜1时，函数f（x）在（0，1﹣）上单调递增，在（1﹣，1+）上单调递减，在（1+，+∞）上单调递增；当a≥1时，函数f（x）在（0，+∞）上单调递增．（2）①解：由（1）可知，函数f（x）有两个极值点x1，x2，等价于方程x2﹣2x+a ＝0在（0，+∞）有两不等实根，故0＜a＜1．②证明：由上述过程得0＜a＜1，，且1＜x＜2，．，令g（t）＝t﹣2lnt﹣1，1＜t＜2，则，由于1＜t＜2，则g′（t）＜0，故g（t）在（1，2）上单调递减．故g（t）＜g（1）＝1﹣2ln1﹣1＝0．∴f（x2）﹣x2+1＝g（x2）＜0．∴f（x2）＜x2﹣1．。

安徽师范大学附属中学高二数学下学期期中考查试题(含解析)

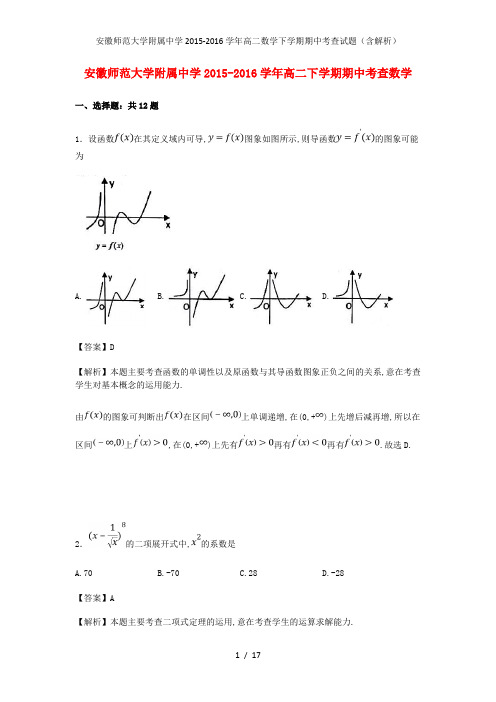
安徽师范大学附属中学2015-2016学年高二下学期期中考查数学一、选择题：共12题1．设函数在其定义域内可导,图象如图所示,则导函数的图象可能为A. B. C. D.【答案】D【解析】本题主要考查函数的单调性以及原函数与其导函数图象正负之间的关系,意在考查学生对基本概念的运用能力.由的图象可判断出在区间上单调递增,在(0,+)上先增后减再增,所以在区间上,在(0,+)上先有再有再有.故选D.2．的二项展开式中,的系数是A.70B.-70C.28D.-28【答案】A【解析】本题主要考查二项式定理的运用,意在考查学生的运算求解能力.根据二项式定理,可得的通项公式为,令=2,则,此时,即的系数是70.故选A.3．设是一个离散型随机变量,其分布列如下表,则的等于A.1B.C.D.【答案】C【解析】本题主要考查离散型随机变量的性质,意在考查学生对基本概念的理解运用.根据离散型随机变量的性质可得:,即,解得,而时,舍去,故.故选C.4．房间有8个人坐成一排,现要调换其中3个人中每一个人的位置,其余5个人的位置不变,则不同的调换方式有A. B. C. D.【答案】B【解析】本题主要考查的是排列组合的应用,意在考查学生的逻辑思维能力.分步进行考虑,先从8人中选出3人有种方法,3人位置全调,由于不能是自己原来的位置,因此有种排法,故有种调换方式,故选B.5．已知函数,则A. B. C.1 D.0【答案】C【解析】本题主要考查的是函数导数的求法,意在考查学生的运算求解能力.由可得,故,解得,所以故选C.6．已知,猜想的表达式A. B. C. D.【答案】B【解析】本题主要考查的是等差数列的性质和函数解析式的求法,意在考查学生分析问题和解决问题的能力.由可得所以是为公差的等差数列,所以,又所以即.故选B.7．某射手射击一次命中的概率是0.7,连续两次均射中的概率是0.4,已知某次射中,则随后一次射中的概率是A. B. C. D.【答案】C【解析】本题主要考查的是相互独立事件的概率乘法公式,意在考查学生的计算能力.设“某次射中”为事件,“随后一次的射中”为事件则,所以,故选C.8．某微信群中甲、乙、丙、丁、戊五名成员同时抢4个红包,每人最多抢一个,且红包被全部抢光,4个红包中有两个2元,两个3元(红包中金额相同视为相同的红包),则甲乙两人都抢到红包的情况有A.35种B.24种C.18种D.9种【答案】C【解析】本题主要考查的是分类计数原理的运用,意在考查学生的逻辑思维能力.若甲乙抢的是一个2元和一个3元,剩下的2个红包,被剩下的3人中2个人抢走,有种情况;若甲乙抢的是两个2元或两个3元,剩下的2个红包,被剩下的3人中2个人抢走,有种情况;根据分类计数原理可得:12+6=18种情况.故选C.9．同时抛掷5枚均匀的硬币80次,设5枚硬币正好出现2枚正面向上,3枚反面向上的次数为,则的数学期望是A.20B.25C.30D.40【答案】B【解析】本题主要考查是二项分布的应用,意在考查学生的计算能力.因为抛掷一次,正好出现2枚正面向上,3枚反面向上的概率为,因为5枚硬币正好出现2枚正面向上,3枚反面向上的概率是相同的,且各次试验中的事件是相互独立的,所以服从二项分布.故选B.10．点在曲线上移动时,过点的切线的倾斜角的取值范围是A. B. C. D.【答案】D【解析】本题主要考查的是导数的几何意义,意在考查学生的运算求解能力.因为点在曲线上移动,所以过点的切线的倾率,所以k的取值范围是,所以倾斜角的取值范围是,故选D.11．由直线,曲线以及轴所围成的图形面积为A. B.13 C. D.15【答案】A【解析】本题主要考查的是定积分的几何意义,意在考查学生的数形结合能力和运算能力. 由直线,曲线以及轴所围成的图形如图所示:故所围成的图形OAB的面积为:=.故选A.12．已知函数对定义域内的任意都有,且当时其导函数满足,若,则A. B.C. D.【答案】B【解析】本题主要考查的是导数的应用,用导数的正负来判断函数的单调性,意在考查学生的分析问题、解决问题的能力.函数对定义域内的任意都有,即函数图象的对称轴是x=2,又导函数满足,即,所以当时,当时,,即在上递减,在上递增,因为,所以1<,所以.故选B.二、填空题：共4题13．已知与之间的一组数据如表,则与的线性回归方程必过定点________．【答案】(1.5,4)【解析】本题主要考查的是线性回归方程,意在考查学生的运算求解能力.根据表中数据可得:,又线性回归直线必过样本中心点,故答案为(1.5,4).14．小明、小红等4位同学各自申请甲、乙两所大学的自主招生考试资格,则每所大学恰有两位同学申请,且小明、小红没有申请同一所大学的可能性有_______种．【答案】4【解析】本题主要考查简单的排列组合,意在考查学生的整体思想.设小明、小红等4位同学分别为小明、小红没有申请同一所大学,则组合为,,,,故共有4种方法.故答案为4.15．设随机变量服从正态分布,则函数不存在零点的概率为________．【答案】【解析】本题主要考查的是函数的零点以及正态分布曲线的对称性,意在考查学生分析问题、解决问题的能力.因为函数不存在零点,所以∆,因为随机变量服从正态分布,所以曲线关于直线对称,所以.故答案为.16．如图,将自然数按如下规则“放置”在平面直角坐标系中,使其满足条件:(1)每个自然数“放置”在一个“整点”(横纵坐标均为整数的点)上;(2)0在原点,1在点,2在点,3在点,4在点,5在点,,即所有自然数按顺时针“缠绕”在以“0”为中心的“桩”上,则放置数字的整点坐标是_________．【答案】【解析】本题主要考查的知识点是归纳推理,意在考查学生的逻辑推理能力. 观察已知点(0,1)处标1,即;点(-1,2)处标9,即;点(-2,3)处标25,即;由此推断,点处标,故放置数字的整点坐标是三、解答题：共5题17．已知函数．(1)求的单调区间和极值;(2)求曲线在点处的切线方程．【答案】(1),令解得;令解得,故函数的单调增区间为和,单调递减区间为.令,得x=-1或当x在R上变化时,与的变化情况如下:故在R上有极大值,极小值为(2)因为,所以曲线在点处的切线方程为:即【解析】本题主要考查的是函数的极值和单调区间的求法,意在考查学生分析问题、解决问题的能力.(1)先对函数求导,通过判断导数的正负确定函数的单调区间;列表讨论,确定函数的极值;(2)根据导数的几何意义确定直线的斜率,再根据点斜式写出直线的方程.18．甲乙两人各自独立地进行射击比赛,甲、乙两人向射击一次,击中目标的概率分别是和,假设每次射击是否击中目标相互之间没有影响．(1)求甲射击3次,至少有1次未击中目标的概率;(2)求两人各射击3次,甲恰好击中目标2次且乙恰好击中目标1次的概率．【答案】(1)记“甲连续射击3次至少有1次未击中目标”为事件,由题意,射击3次,相当于3次独立重复试验,由. (2)记“甲射击3 次,恰有2次击中目标”,为事件,“乙射击3次,恰有1次击中目标”为事件,则．由于甲、乙射击相互独立,故．【解析】本题主要考查的是次独立重复试验中恰好发生次的概率,意在考查学生的计算能力.(1)由次独立重复试验中恰好发生次的概率公式计算即可得到答案;(2)分别计算甲恰好击中目标2次,乙恰好击中目标1次的概率,然后用独立事件的计算公式即可得到.19．在各项均为正数的数列中,数列的前项和满足．(1)求;(2)由(1)猜想数列的通项公式,并用数字归纳法证明．【答案】(1)令,有,解得; 令,有,解得或(舍去); 令,有,解得或(舍去);故,(2)猜想,证明:①当时,,命题成立②假设时,成立,则时,,所以,,解得,即时,命题成立．由①②知,时,【解析】本题主要考查的是数列的递推公式以及用数学归纳法证明等式的成立,意在考查学生的计算能力.(1)由题意,将分别代入计算即可求得;(2)检验时等式成立,假设时命题成立,证明当时等式也成立.20．某学校研究性学习小组对该校高二学生视力情况进行调查,在高二的全体1000名学生中随机抽取了100名学生的体检表.学习小组成员发现,学习成绩突出的学生,近视的比较多,为了研究学生的视力与学习成绩是否有关系,对年级名次在名和名的学生进行了调查,得到如下数据:(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?附:．(2)在(1)中调查的100名学生中,按照分层抽样的不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在的学生人数为,求的分布列和数学期望．【答案】(1),因此能够在犯错误的概率不超过0.05的前提下认为视力与学习成绩有关系.(2)依题意抽取的9人中年级名次在名和名的分别有3人和6人,可能的取值为0,1,2,3,,,,的分布列为:的数学期望.【解析】本题主要考查的是独立性检验的应用问题以及计算离散型随机变量的分布列与期望的问题,意在考查学生的数据处理能力.(1)根据表中的数据,计算观测值,对照数表,得出结论;(2)列出的可能取值,计算对应的概率,求出的分布列与数学期望值.21．已知函数．(1)若函数在区间上为增函数,求的取值范围;(2)当且时,不等式在上恒成立,求的最大值．【答案】(1)因为,,又函数在区间上为增函数,所以当时,恒成立,所以,即的取值范围为. (2)当时,,故不等式,即对任意恒成立,令则．令,则在上单调递增,因为,所以存在使,即当时,,即,当时,,即,所以在上单调递减,在上单调递增．令,即,所以,因为且.所以的最大值为3.【解析】本题主要考查的是利用导数研究函数的单调性及利用导数求闭区间上函数的最值,意在考查学生的化归能力和计算能力.(1)由题意可得当时,恒成立,即,从而求得的取值范围;(2)把不等式在上恒成立转化为对任意恒成立,进而求解.。

《首发》安徽省师大附中2016-2017学年高二下学期期中考试历史试卷Word版含答案

安徽师范大学附属中学2016-2017学年第二学期期中考查高二历史试题命题：唐淑云审题：何永保一、选择题（本大题共25小题，每小题2分，共50分。

在每小题列出的四个选项中，只有一项符合题意）1.《吕氏春秋》载：“纣之同母三人，其长曰微子启，其次曰仲衍，其次曰受德。

受德乃纣也，甚少矣。

纣母生微子启与仲衍，尚为妾，已而为妻而生纣。

纣之母欲置微子启以为太子。

太史据法而争之曰：‘有妻之子，而不可置妾之子。

故纣为后。

’”上述材料最能说明A．商纣为王不符合当时的制度规定B．商纣因得到大臣的支持得以继位C．商王对于王位继承的发言权很少 D．商朝末期嫡长子继承制已经显现2.《小雅·鹿鸣》本是西周贵族宣扬宴飨之仪的乐歌，后扩散到民间，在乡人宴会上也可传唱。

这表明西周时期A．周人生活较为富足 B．礼乐文明得到广泛认同C．乡人社会地位提高 D．贵族奢靡之风波及民间3.北宋时，欧阳修等主持重建了《新唐书》和《新五代史》，司马光则主持编纂了《资治通鉴》。

这反映出当时北宋A．统治者注重吸取历史教训 B．统治者推行重文轻武政策C．政治体制未形成完整体系 D．君主专制制度进一步完善4.北宋初年，“置诸路转运使”，掌一路财赋，后其权力有膨胀之势，俨然为路级行政长官。

宋廷在各路又置提点刑狱司等三司分转运使之权。

宋代路级地方行政制度最终形成。

这表明A．分权是宋代集权的必然选择B．控制地方财权是宋代集权的核心思想C．宋代形成路、州、郡、县四级地方行政体制D．宋代地方官制的创新围绕中央权力的加强5.明太祖废丞相后，曾下令：“内臣（宦官）不得干预政事，预者斩”。

但不久后又制定半印勘合制度：六部所行一切都须经内府勘合，方可施用。

出现这种变化的原因是A．牵制日益权重的内阁 B．减轻皇帝的行政负担C．协调政府各部门关系 D．加强君主专制的需要汉唐明三代都出现了比较严重的宦官专权现象，而魏晋南北朝时期基本没有出现这种现象。

这是因为魏晋南北朝时A．宦官势力衰落 B．政治比较清明C．长期处于分裂 D．皇权相对削弱6.明成祖时，“特简（选拔）解缙、胡广、杨荣等直文渊阁，参预机务。

安徽师范大学附属中学高二下学期期中考试查英语试题解析版

安徽师范大学附属中学高二第二学期期中考查英语试题（考试时间：120分钟试卷满分：100分）第Ⅰ卷（选择题，共60分）第一部分听力（满分10分）（共20小题:每小题0.5分, 满分10分）第一节（共5小题）听下面5段对话。

每段对话后有一个小题，从题中所给的A、B、C三个选项中选出最佳选项，并标在试卷的相应位置。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1. What does the woman think of the cleaner’s job?A. Boring.B. Exciting.C. Dangerous.2. What are the speakers talking about?A. Rain-forests.B. Animals.C. Weather.3. Where does Sandra sit in the classroom now?A. By the window.B. In the back row.C. By the door.4. Why didn’t Peter go for a trip last weekend?A. He missed the train.B. He didn’t buy the ticket.C. He didn’t get to the station.5. What’s the man’s idea about the skirt?A Change it. B. Buy it. C. Reject it.第二节（共15小题）听下面5段对话或独白。

每段对话或独白后有几个小题, 从题中所给的A、B、C三个选项中选出最佳选项, 并标在试卷的相应位置。

听每段对话或独白前, 你将有时间阅读各个小题, 每小题5秒钟；听完后, 各小题将给出5秒钟的作答时间。

每段对话或独白读两遍。

听第6段材料，回答第6和第7题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

安徽师范大学附属中学2016-2017学年第二学期期中考查高二化学试题命题：审题：可能用到的相对原子质量：C 12 H 1 O 16第Ⅰ卷(选择题，共38分)选择题(包括19个小题，每小题2分，共38分，每小题有1个正确选项。

)1．下列说法中正确的是()A．烷烃中除甲烷外，很多烷烃都能被酸性KMnO4溶液氧化B．烯烃、炔烃、芳香烃都能使溴的四氯化碳溶液褪色C．乙烯、乙炔、苯、甲苯的分子中所有原子都在同一平面上D．烃类都能在空气中燃烧生成CO2和H2O2．下列关于的分子结构说法正确的是()A．分子中12个碳原子一定在同一平面内B．分子中12个碳原子可能在同一直线上C．分子中最多有6个碳原子在同一直线上D．分子中最多有8个碳原子在同一直线上3．以下物质：①甲烷、②2-丁炔、③顺-2-丁烯、④环己烯、⑤环己烷、⑥苯、⑦聚苯乙烯、⑧邻二甲苯，既能使高锰酸钾酸性溶液褪色，又能使溴的四氯化碳溶液因反应而褪色的是()A．①③⑤B．②③④C．②③④⑦D．④⑦⑧4. 下列4种有机物：其中一氯取代物的同分异构体数目相同的是()A. ①和②B. ②和③C. ①和③D. ②和④5．下列关于烃性质的说法中正确的是()A．乙烯可以与酸性高锰酸钾溶液反应，因此可以用酸性高锰酸钾溶液除去乙烷中混有的乙烯B．溴乙烷可以通过乙烯与溴化氢加成得到，也可以通过乙烷与溴发生取代反应制备C．区分甲苯和苯可以使用酸性高锰酸钾溶液，也可以用溴的四氯化碳溶液D．鉴别己烯中是否混有少量甲苯，正确的实验方法是可以加足量溴的四氯化碳溶液，然后再加入酸性高锰酸钾溶液6．将等质量的铜片在酒精灯上加热后，分别插入下列溶液中，铜片质量增加的是（）A．硝酸B．稀盐酸C．Ca(OH)2溶液D．乙醇7．下列有关叙述正确的是（）A．煤经过分馏可得到焦炭、煤焦油和焦炉气B．石油裂化是为了获得更多的汽油C．医用酒精的浓度通常为95%D．甲烷、汽油、酒精都是可燃性烃，都可作燃料8．要检验溴乙烷中的溴元素，正确的实验方法是()A．加入氯水振荡，观察水层是否有棕红色出现B．滴入AgNO3溶液，再加入稀盐酸呈酸性，观察有无浅黄色沉淀生成C．加入NaOH溶液共热，冷却后加入稀硝酸使溶液呈酸性，再滴入AgNO3溶液，观察有无浅黄色沉淀出现D．加入NaOH溶液共热，冷却后加入AgNO3溶液，观察有无浅黄色沉淀生成9．有机物的结构可用“键线式”简化表示，如CH3﹣CH=CH﹣CH3可简写为．有机物X的键线式为，下列说法中不正确．．．的是（）A．X的化学式为C8H8B．有机物Y是X的同分异构体，且属于芳香烃，则Y中所有原子可能共平面C．X可使酸性高锰酸钾和溴水褪色，但原理不同D．X与足量的H2在一定条件下反应可生成环状的饱和烃Z，Z的一氯代物有4种10．分子式为C 3H 6Cl 2的氯代烷分子中的一个氢原子被氯原子取代后，可得到两种同分异构体，则C 3H 6Cl 2的名称是 ( ) A ．1,3-二氯丙烷 B ．1,1-二氯丙烷 C ．1,2-二氯丙烷 D ．2,2-二氯丙烷11.（）A.装置①可用于除去乙醇中的溴苯B.用图②所示装置检验溴乙烷与NaOH 醇溶液共热产生的C 2H 4C.装置③可证明非金属性Cl>C>Si D 装置④可用于收集O 212．分子式为C 5H 10的烯烃共有(要考虑顺反异构体) ( )A ．5种B ．6种C ．7种D ．8种13．运动员的腿部肌肉不小心挫伤，队医马上对准该运动员的受伤部位喷射一种名叫氯乙烷的药剂（沸点约为12℃）进行冷冻麻醉处理．关于氯乙烷的说法不正确的是（）A. 在一定条件下能发生水解反应 B ．在一定条件下可以制备乙烯 C ．该物质易溶于水D ．该物质的官能团名称为氯原子14．下列反应中，生成的有机物只有一种的是 ( )C ．甲苯在一定条件下发生硝化反应生成一硝基甲苯的反应① ② ③ ④D．新戊烷和氯气发生取代反应生成一氯取代物的反应15．下列说法正确的是（N A表示阿伏加德罗常数的值）（）A . 1mol苯乙烯（）中含有的C=C数为4N AB. 在标准状况下，11.2 L己烷含有分子数为0.5N AC. 2.8 g乙烯和丙烯的混合气体中所含碳原子数为0.2N AD. 1mol甲基含10N A个电子16. 某有机物其结构简式为Cl，关于该有机物下列叙述不正确的是（）A．能使溴水褪色B．一定条件下，能和NaOH醇溶液反应C．在加热和催化剂作用下，最多能和4 mol H2发生加成反应D．能使酸性KMnO4溶液褪色17．在实验室中，下列除去杂质的方法正确的是（）A. 硝基苯中混有的少量硫酸和硝酸，将其倒入盛有NaOH溶液的分液漏斗中，振荡，静置，分液B. 乙烷中混有乙烯，通入氢气在一定条件下反应，使乙烯转化为乙烷C. 溴苯中混有溴，加入KI溶液，振荡，用汽油萃取出碘D. 乙烯中混有SO2和CO2，将其通入溴水中洗气18．25℃和101kPa时，乙烷、乙炔和丙烯组成的混合烃4L与过量氧气混合并完全燃烧，除去水蒸气，恢复到原来的温度和压强，气体总体积缩小了9L，原混合烃中乙烷、乙炔和丙烯的体积比不可能为（）A．1:1:1 B．2:1:1 C．3:2:3 D．5:3:419．常温下，1 mol某烷烃在光照条件下与氯气发生取代反应，若在适当的条件下，完全取代需要消耗6 mol Cl2，则下列判断正确的是( )A、该烷烃的分子式为C5H12B、反应所生成的有机产物能直接使AgNO3溶液产生白色沉淀C、该烷烃的四氯代物有2种D、反应容器中，一氯代物所占的物质的量分数最大第Ⅱ卷(非选择题，共62分)20．（12分）（1）已知某有机物X在标况下的密度为1.34g/L，取X与氧气反应，得到等物质的量的CO2和H2O，则该有机物的分子式为．为测定X的结构，作核磁共振氢谱，发现只有一种吸收峰，则A可能的结构式为．（2）已知C7H16有多种同分异构体，其中主链含有五个碳原子，有两个甲基作支链，符合条件的烷烃有种，其中有一种同分异构体的一氯代物有4种同分异构体，请写出其结构简式，该烷烃分子的名称，C7H16另一种同分异构体分子是由烯烃和氢气加成得到，而且该烯烃分子中的碳碳双键只有一种位置，试写出这种烯烃分子的名称.21．（10分）有机物M可从酸牛奶中提取。

已知纯净的M为无色黏稠液体，易溶于水。

为研究M的组成与结构，进行了如下实验：(5)综上所述，M的结构简式为22．（14分）实验室制备溴代烃的反应如下：NaBr+H2SO4==HBr+NaHSO4①R-OH+HBr R-Br+H2O ②可能存在的副反应有：醇在浓硫酸的存在下脱水生成烯和醚，Br-被浓硫酸氧化为Br2等。

有关数据列表如下；请回答下列问题：（1）在溴乙烷和1-溴丁烷的制备实验中，下列仪器最不可能．．．．用到的是。

a．圆底烧瓶b量筒c．锥形瓶d．容量瓶（2）溴代烃的水溶性（填“大于”、“等于”或“小于”）相应的醇；其原因是。

（3）将1-溴丁烷粗产品置于分液漏斗中加水，振荡后静置，水层在（填“上层”、“下层”或“不分层”）。

（4）制备操作中，加入的浓硫酸必须进行稀释，其目的不正确．．．的是。

a．水是反应的催化剂b．减少Br2的生成c．减少HBr的挥发d．减少副产物烯和醚的生成（5）在制备溴乙烷时，采用边反应边蒸出产物的方法，其原因是；但在制备1-溴丁烷时却不能边反应边蒸出产物，其原因是。

23．(12分)化学式为C8H10O的化合物A具有如下性质：①A和Na 能慢慢产生气泡②A和RCOOH在浓硫酸和加热条件下能生成有香味的产物③A能被酸性高锰酸钾溶液氧化成苯甲酸④经催化氧化得到(R、R′为烃基)结构的分子⑤脱水反应的产物，经聚合反应可制得一种塑料品(它是目前造成“白色污染”的主要污染源之一)试回答：(1)根据上述信息，对该化合物的结构可做出的判断是________；(填编号)A．苯环上直接连有羟基B．苯环侧链末端有甲基C．肯定有醇羟基D．肯定是芳香烃(2)化合物A的结构简式________________；(3)A和金属钠反应的化学方程式_____；(4)A发生④的化学方程式_____。

(5)A发生⑤脱水反应的化学方程式_____。

脱水后的产物，发生聚合反应的化学方程式。

24．(14分)A～E都是有机化合物，A为一取代芳香烃，B中含有一个甲基。

它们的转化关系如下：请回答下列问题：(1) A的名称为(2)由B生成C的化学方程式为_______________________________(3)由B生成D、由C生成D的反应条件分别是________、________。

(4)由A生成B、由D生成E的反应类型分别是________、________。

(5)在E的同分异构体中，苯环上一硝化的产物只有一种的共有___种，其中核磁共振氢谱有两组峰，且峰面积比为1∶1的是_____(填结构简式)。

CH 3C CH 3CH 2CH 2CH 3CH 3高二化学参考答案20. （每空2分，共12分）（1）CH 2O （2）42，2—二甲基戊烷 3，3—二甲基—1—戊烯21. （每空2分，共10分）(1)90g/mol (2)C 3H 6O 3 (3)(4)4 (5)22（每空2分，共14分）（1）d （2）< 醇可与水分子之间形成氢键，溴代烃不能与水分子之间形成氢键（3）上层（4）a （5）平衡向生成溴乙烷的方向移动（或反应②向右移动） 1-溴丁烷与正丁醇的沸点差较小，若边反应边蒸馏，会有较多的正丁醇被蒸出 23（每空2分12分）24.，（共14分） (1)乙苯（2分）(2)（2分）(3)NaOH 醇溶液、加热浓硫酸、加热（3、4两小题每空1分） (4)取代反应加成反应 (5)。