静电场作业答案共22页
静电场习题(有答案)
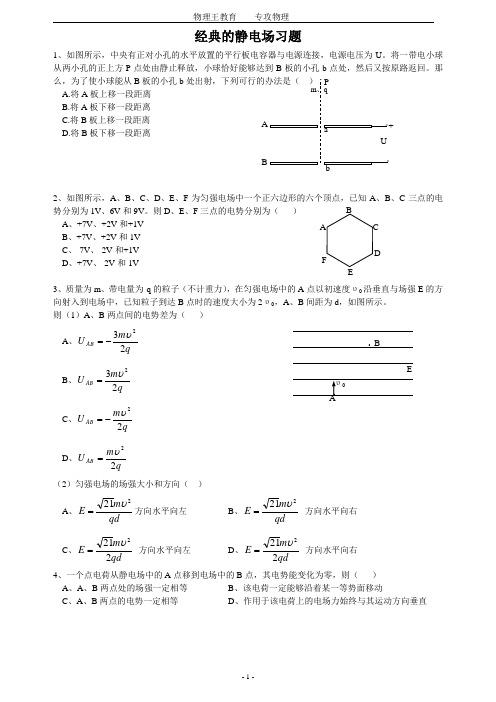
经典的静电场习题1、如图所示,中央有正对小孔的水平放置的平行板电容器与电源连接,电源电压为U 。
将一带电小球从两小孔的正上方P 点处由静止释放,小球恰好能够达到B 板的小孔b 点处,然后又按原路返回。
那么,为了使小球能从B 板的小孔b 处出射,下列可行的办法是( ) A.将A 板上移一段距离 B.将A 板下移一段距离 C.将B 板上移一段距离 D.将B 板下移一段距离2、如图所示,A 、B 、C 、D 、E 、F 为匀强电场中一个正六边形的六个顶点,已知A 、B 、C 三点的电势分别为1V 、6V 和9V 。
则D 、E 、F 三点的电势分别为( )A 、+7V 、+2V 和+1VB 、+7V 、+2V 和1VC 、-7V 、-2V 和+1VD 、+7V 、-2V 和1V3、质量为m 、带电量为-q 的粒子(不计重力),在匀强电场中的A 点以初速度υ0沿垂直与场强E 的方向射入到电场中,已知粒子到达B 点时的速度大小为2υ0,A 、B 间距为d ,如图所示。
则(1)A 、B 两点间的电势差为( ) A 、q m U AB232υ-= B 、q m U AB232υ= C 、q m U AB22υ-= D 、qm U AB22υ= (2)匀强电场的场强大小和方向( ) A 、qdm E 221υ=方向水平向左 B 、qdm E 221υ=方向水平向右 C 、qdm E 2212υ= 方向水平向左D 、qdm E 2212υ=方向水平向右4、一个点电荷从静电场中的A 点移到电场中的B 点,其电势能变化为零,则( ) A 、A 、B 两点处的场强一定相等 B 、该电荷一定能够沿着某一等势面移动 C 、A 、B 两点的电势一定相等 D 、作用于该电荷上的电场力始终与其运动方向垂直 A B a bP· m 、q。
。
U+ -A B C DEF E· Aυ0 B·5、在静电场中( )A.电场强度处处为零的区域内,电势也一定处处为零B.电场强度处处相等的区域内,电势也一定处处相等C.电场强度的方向总是跟等势面垂直D.沿着电场线的方向电势是不断降低的6、一个初动能为E K 的带电粒子,沿着与电场线垂直的方向射入两平行金属板间的匀强电场中,飞出时该粒子的动能为2E K ,如果粒子射入时的初速度变为原来的2倍,那么当它飞出电场时动能为( ) A 、4E K B 、4.25E K C 、5E K D 、8E K7、如图所示,实线为一簇电场线,虚线是间距相等的等势面,一带电粒子沿着电场线方向运动,当它位于等势面φ1上时,其动能为20eV ,当它运动到等势面φ3上时,动能恰好等于零,设φ2=0,则,当粒子的动能为8eV 时,其电势能为( ) A 、12eV B 、2eV C 、10eV D 、08、如图10—7所示,在两电荷+Q 1和-Q 2连线的延长线上有a 、b 、c 三点,测得b 点的场强为零。
静电场练习题及答案解析

静电场练习题及答案解析练习1一、选择题1. 一带电体可作为点电荷处理的条件是( )A. 电荷必须呈球形分布;B. 带电体的线度与其它有关长度相比可忽略不计;C. 电量很小;D. 带电体的线度很小。
2. 试验点和q0在电场中受力为F⃗,其电场强度的大小为F,以下说法正确的( )q0A. 电场强度的大小E是由产生电场的电荷所决定的,不以试验电荷q0及其受力的大小决定;B. 电场强度的大小E正比于F且反比与q0;C. 电场强度的大小E反比与q0;D. 电场强度的大小E正比于F。
3. 如果通过闭合面S的电通量Φe为零,则可以肯定( )A. 面S内没有电荷;B. 面S内没有净电荷;C. 面S上每一点的场强都等于零;D. 面S上每一点的场强都不等于零。
4. 如图所示为一具有球对称性分布的静电场的E~r关系曲线,产生该静电场的带电体是( ) A 半径为R的均匀带电球面;B半径为R的均匀带电球体;C半径为R的、电荷体密度为ρ=Ar(A为常数)的非均匀带电球体;D半径为R的、电荷体密度为ρ=A r⁄(A为常数)的非均匀带电球体。
5. 在匀强电场中,将一负电荷从A移动B,如图所示,则( )A. 电场力做负功,负电荷的电荷能增加;B. 电场力做负功,负电荷的电势能减少;C. 电场力做正功,负电荷的电势能增加;D. 电场力做正功,负电荷的电势能减少。
二、填空题1. 点电荷q1、q2、q3和q4在真空中的分布如图所示,图中S为闭合曲面,则通过该闭合曲面的电通量∮E⃗⃗∙dS⃗=,式中E⃗⃗是点电荷在闭合曲面上任一点产生的场强的矢量和。
2. 真空环境中正电荷q均匀地分布在半径为R的细圆环上.在环环心O处电场强度为,环心的电势为。
=0,这表3. 在静电场中,场强沿任意闭合路径的线积分等于零,即∮E⃗⃗∙dl⃗L明静电场中的电场线。
4. 一半径为R的均匀带电球面,其电荷面密度为σ,该球面内、外的场强分布为(r⃗表示从球心引出的矢径):E⃗⃗r=(r<R);E⃗⃗r=(r>R)。
静电场作业答案

电荷体密度为,求板内sD 、d外s 场2强s的D分d 布 s内 s。q
2D ssd
d
o
s
x
D外2d, Dds2
E外20
Dd s
qi
s
s
s内
(侧视图)
2D ss2x
D内x,E内x
5. 图示一球形电容器,在外球壳的内半径b和内外 导体间的电压U维持恒定的条件下,内球半径a为 多大时,才能使内球面上的电场强度最小?这个
从电势为U的a点,移动到电势为零的bபைடு நூலகம்,若已
知小球在b点的速率为Vb,则小球在a点的速率
Va=
Vb2
2qU m
。
11. 两根互相平行的长直导线,相距为a,其上均
匀带电,电荷线密度分别为λ1和λ2,则导线单
位长度所受电场力的大小为F0= 12/20a 。
1.三图、中计所算示题为一沿 x 轴放置的长度为l的不均匀
S Q
去ΔS后球心处电场强度大小E= 4 0R2 4R2 , 其方向为 指向S 。
R
O
S
3. 在相对介电常数为εr的各向同性的电介质中,
电位移矢量与场强之间D 的关0系r是E
。
4. 两块“无限大”的带电平行电板,其电荷面密
度分别为(>0)及-2 ,如图所示,试写出各
区域的电场强度E
І区 E大小
/ 20
2. 带电细棒,其电荷线密度为 = 0(x-a), 0为 一
3. 常量。取无穷远处为电势零点,求坐标原点o
处
的解电:势U。 dU q
a
O
l
x dx
x
al dx
a 4 0 x
40l0 40a0lnaal
高中物理静电场(精选100题答案)

3 2kQ 强为三个场强的竖直分量之和,即 4L2 ,选项 D 正确。
7. 解析:选 A 设在 O 点的球壳为完整的带电荷量为 2q 的带电球壳,则在 M、N 两点产生的场强大
k·2q kq 小为 E0=2R2=2R2。题图中左半球壳在 M 点产生的场强为 E,则右半球壳在 M 点产生的场强为 E′=
4Q·2Q
Q2
FAC=k 12L2 =32kL2
B、C 之间为引力,大小为 Q·2Q Q2
FBC=k12L2=8k L2
Q2 F 合=FAC+FBC=40kL2 。
(2)根据三个点电荷的平衡规律,D 为正电荷,且 D 应放在 AB 连线的延长线上靠近 B 的一侧,设 D 到 B 的距离为 x,电荷量为 q,
静电场典型题目 70 题参考答案
1. 解析:选 A 库仑力作用符合牛顿第三定律,即两小球所带电荷量不相等时,相互作用的库仑力
大小相等,因此 α>β 不是电荷量不相等造成的。根据受力平衡条件及 α>β,可得 m1<m2,故 A 正确。
2. 解析:选 D 由于小球 c 所受库仑力的合力的方向平行于 a、b 的连线,根据受
库仑力与 b 对 c 的库仑力关于 Oc 对称,即 qa=qb,B 正确;对 a、b 整体受力分析可得:因为 a、b 连线
水平,则 ma=mb,但与 c 的质量关系不能确定,A 错误;因 c 对 a、b 的库仑力关于 Oc 对称,由受力分
析知,细线 Oa、Ob 所受拉力大小相等,C 正确;c 所带电荷量与 a、b 所带电荷量不一定相等,所以 a、
kq
kq
大学物理静电场习题答案

第12章 静电场P35.12.3 如图所示,在直角三角形ABCD 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强.[解答]根据点电荷的场强大小的公式22014q qE k r r ==πε, 其中1/(4πε0) = k = 9.0×109N·m 2·C -2.点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯, 方向向下.点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯,方向向右.C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.12.4 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电线密度分别为+λ和-λ,求圆心处的场强.[解答]在带正电的圆弧上取一弧元 d s = R d θ,电荷元为d q = λd s ,在O 点产生的场强大小为220001d 1d d d 444q s E R R R λλθπεπεπε===, 场强的分量为d E x = d E cos θ,d E y = d E sin θ.对于带负电的圆弧,同样可得在O 点的场强的两个分量.由于弧形是对称的,x 方向的合场强为零,总场强沿着y 轴正方向,大小为2d sin y LE E E ==⎰θ/6/60000sin d (cos )22R R==-⎰ππλλθθθπεπε0(1)22R=-λπε.12.5 均匀带电细棒,棒长a = 20cm ,电荷线密度为λ = 3×10-8C·m -1,求:(1)棒的延长线上与棒的近端d 1 = 8cm 处的场强;(2)棒的垂直平分线上与棒的中点相距d 2 = 8cm 处的场强.[解答](1)建立坐标系,其中L = a /2 = 0.1(m),x = L+d 1 = 0.18(m).在细棒上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的场强公式,电荷元在P 1点产图13.1生的场强的大小为1220d d d 4()q lE k r x l ==-λπε场强的方向沿x 轴正向.因此P 1点的总场强大小通过积分得120d 4()L L l E x l λπε-=-⎰014LLx lλπε-=-011()4x L x Lλπε=--+ 220124L x L λπε=-. ①将数值代入公式得P 1点的场强为8912220.13109100.180.1E -⨯⨯⨯=⨯⨯- = 2.41×103(N·C -1),方向沿着x 轴正向.(2)建立坐标系,y = d 2. 在细棒上取一线元d l ,所带的电量为 d q = λd l ,在棒的垂直平分线上的P 2点产生的场强的大小为2220d d d 4q lE kr r λπε==, 由于棒是对称的,x 方向的合场强为零,y 分量为 d E y = d E 2sin θ.由图可知:r = d 2/sin θ,l = d 2cot θ, 所以 d l = -d 2d θ/sin 2θ, 因此 02d sin d 4y E d λθθπε-=,总场强大小为02sin d 4Ly l LE d λθθπε=--=⎰02cos 4Ll Ld λθπε=-=LL=-==. ②将数值代入公式得P 2点的场强为89221/220.13109100.08(0.080.1)y E -⨯⨯⨯=⨯⨯+= 5.27×103(N·C -1). 方向沿着y 轴正向.[讨论](1)由于L = a /2,x = L+d 1,代入①式,化简得1011011144/1a E d d a d d a λλπεπε==++,保持d 1不变,当a →∞时,可得1014E d λπε→, ③这就是半无限长带电直线在相距为d 1的延长线上产生的场强大小.(2)由②式得y E ==,当a →∞时,得 022y E d λπε→, ④这就是无限长带电直线在线外产生的场强公式.如果d 1=d 2,则有大小关系E y = 2E 1.12.6 一均匀带电无限长细棒被弯成如图所示的对称形状,试问θ为何值时,圆心O 点处的场强为零.[解答]设电荷线密度为λ,先计算圆弧的电荷在圆心产生的场强.在圆弧上取一弧元 d s =R d φ, 所带的电量为d q = λd s ,在圆心处产生的场强的大小为2200d d d d 44q s E kr R Rλλϕπεπε===, 由于弧是对称的,场强只剩x 分量,取x 轴方向为正,场强为d E x = -d E cos φ. 总场强为2/20/2cos d 4x E R πθθλϕϕπε--=⎰2/20/2sin 4Rπθθλϕπε--=0sin 22R λθπε=,方向沿着x 轴正向.再计算两根半无限长带电直线在圆心产生的场强.根据上一题的公式③可得半无限长带电直线在延长上O 点产生的场强大小为`04E Rλπε=,由于两根半无限长带电直线对称放置,它们在O 点产生的合场强为``02coscos 222x E E R θλθπε==,方向沿着x 轴负向.当O 点合场强为零时,必有`x x E E =,可得 tan θ/2 = 1, 因此 θ/2 = π/4, 所以 θ = π/2.12.7 一宽为b 的无限长均匀带电平面薄板,其电荷密度为σ,如图所示.试求:(1)平板所在平面内,距薄板边缘为a处的场强.(2)通过薄板几何中心的垂直线上与薄板距离为d 处的场强.[解答](1)建立坐标系.在平面薄板上取一宽度为d x 的带电直线,电荷的线密度为d λ = σd x , 根据直线带电线的场强公式02E rλπε=, 得带电直线在P 点产生的场强为00d d d 22(/2)xE rb a x λσπεπε==+-,其方向沿x 轴正向.由于每条无限长直线在P 点的产生的场强方向相同,所以总场强为/20/21d 2/2b b E x b a x σπε-=+-⎰ /20/2ln(/2)2b b b a x σπε--=+-0ln(1)2baσπε=+. ①图13.4图13.5.场强方向沿x 轴正向.(2)为了便于观察,将薄板旋转建立坐标系.仍然在平面薄板上取一宽度为d x 的带电直线,电荷的线密度仍然为d λ = σd x ,带电直线在Q 点产生的场强为221/200d d d 22()xE rb x λσπεπε==+,沿z 轴方向的分量为221/20cos d d d cos 2()z xE E b x σθθπε==+,设x = d tan θ,则d x = d d θ/cos 2θ,因此d d cos d 2z E E σθθπε==积分得arctan(/2)0arctan(/2)d 2b d z b d E σθπε-=⎰ 0arctan()2bdσπε=. ② 场强方向沿z 轴正向.[讨论](1)薄板单位长度上电荷为λ = σb ,①式的场强可化为0ln(1/)2/b a E a b aλπε+=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02E aλπε→, ③ 这正是带电直线的场强公式.(2)②也可以化为0arctan(/2)2/2z b d E d b dλπε=,当b →0时,薄板就变成一根直线,应用罗必塔法则或泰勒展开式,场强公式变为02z E dλπε→,这也是带电直线的场强公式.当b →∞时,可得2z E σε→, ④ 这是无限大带电平面所产生的场强公式.12.8 (1)点电荷q 位于一个边长为a 的立方体中心,试求在该点电荷电场中穿过立方体一面的电通量是多少?(2)如果将该场源点电荷移到立方体的的一个角上,这时通过立方体各面的电通量是多少?[解答]点电荷产生的电通量为Φe = q/ε0.(1)当点电荷放在中心时,电通量要穿过6个面,通过每一面的电通量为Φ1 = Φe /6 = q /6ε0.(2)当点电荷放在一个顶角时,电通量要穿过8个卦限,立方体的3个面在一个卦限中,通过每个面的电通量为Φ1 = Φe /24 = q /24ε0;立方体的另外3个面的法向与电力线垂直,通过每个面的电通量为零.12.9 面电荷密度为σ的均匀无限大带电平板,以平板上的一点O 为中心,R 为半径作一半球面,如图所示.求通过此半球面的电通量.[解答]设想在平板下面补一个半球面,与上面的半球面合成一个球面.球面内包含的电荷为q = πR 2σ, 通过球面的电通量为图13.7Φe = q /ε0, 通过半球面的电通量为Φ`e = Φe /2 = πR 2σ/2ε0.12.10 两无限长同轴圆柱面,半径分别为R 1和R 2(R 1 > R 2),带有等量异号电荷,单位长度的电量为λ和-λ,求(1)r < R 1;(2) R 1 < r < R 2;(3)r > R 2处各点的场强.[解答]由于电荷分布具有轴对称性,所以电场分布也具有轴对称性.(1)在内圆柱面内做一同轴圆柱形高斯面,由于高斯内没有电荷,所以E = 0,(r < R 1).(2)在两个圆柱之间做一长度为l ,半径为r 的同轴圆柱形高斯面,高斯面内包含的电荷为 q = λl , 穿过高斯面的电通量为d d 2e SSE S E rl Φπ=⋅==⎰⎰E S Ñ,根据高斯定理Φe = q /ε0,所以02E rλπε=, (R 1 < r < R 2). (3)在外圆柱面之外做一同轴圆柱形高斯面,由于高斯内电荷的代数和为零,所以E = 0,(r > R 2).12.11 一厚度为d 的均匀带电无限大平板,电荷体密度为ρ,求板内外各点的场强.[解答]方法一:高斯定理法.(1)由于平板具有面对称性,因此产生的场强的方向与平板垂直且对称于中心面:E = E`.在板内取一底面积为S ,高为2r 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E S2d d d S S S =⋅+⋅+⋅⎰⎰⎰E S E S E S 1`02ES E S ES =++=,高斯面内的体积为 V = 2rS , 包含的电量为 q =ρV = 2ρrS , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρr/ε0,(0≦r ≦d /2).①(2)穿过平板作一底面积为S ,高为2r 的圆柱形高斯面,通过高斯面的电通量仍为 Φe = 2ES , 高斯面在板内的体积为V = Sd , 包含的电量为 q =ρV = ρSd , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρd /2ε0,(r ≧d /2). ②方法二:场强叠加法. (1)由于平板的可视很多薄板叠而成的,以r 为界,下面平板产生的场强方向向上,上面平板产生的场强方向向下.在下面板中取一薄层d y ,面电荷密度为d σ = ρd y ,产生的场强为 d E 1 = d σ/2ε0, 积分得100/2d ()222rd y dE r ρρεε-==+⎰,③ 同理,上面板产生的场强为/2200d ()222d ry d E r ρρεε==-⎰,④ r 处的总场强为E = E 1-E 2 = ρr/ε0.(2)在公式③和④中,令r = d /2,得E 2 = 0、E = E 1 = ρd /2ε0,E 就是平板表面的场强.平板外的场强是无数个无限薄的带电平板产生的电场叠加的结果,是均强电场,方向与平板垂直,大小等于平板表面的场强,也能得出②式.12.1212.13 一半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为R`<R的小球体,如图所示,试求两球心O 与O`处的电场强度,并证明小球空腔内的电场为均强电场.[解答]挖去一块小球体,相当于在该处填充一块电荷体密度为-ρ的小球体,因此,空间任何一点的场强是两个球体产生的场强的叠加.对于一个半径为R ,电荷体密度为ρ的球体来说,当场点P 在球内时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r r ππρε=P 点场强大小为3E r ρε=.当场点P 在球外时,过P 点作一半径为r 的同心球形高斯面,根据高斯定理可得方程2301443E r R ππρε=P 点场强大小为3203R E rρε=. O 点在大球体中心、小球体之外.大球体在O 点产生的场强为零,小球在O 点产生的场强大小为320`3O R E aρε=, 方向由O 指向O `.O`点在小球体中心、大球体之内.小球体在O`点产生的场强为零,大球在O 点产生的场强大小为`03O E a ρε=, 方向也由O 指向O `.[证明]在小球内任一点P ,大球和小球产生的场强大小分别为 03r E r ρε=, `0`3r E r ρε=,方向如图所示.设两场强之间的夹角为θ,合场强的平方为222``2cos r r r r E E E E E θ=++2220()(`2`cos )3r r rr ρθε=++, 根据余弦定理得222`2`c o s ()a r rr r πθ=+--, 所以 03E a ρε=, 可见:空腔内任意点的电场是一个常量.还可以证明:场强的方向沿着O 到O `的方向.因此空腔内的电场为匀强电场.12.14 如图所示,在A 、B 两点处放有电量分别为+q 和-q 的点电荷,AB 间距离为2R ,现将另一正试验电荷q 0从O 点经过半圆弧路径移到C点,求移动过程中电场力所做的功.[解答]正负电荷在O 点的电势的和为零:U O = 0;图13.10图13.11在C 点产生的电势为0004346C q q q U RRRπεπεπε--=+=,电场力将正电荷q 0从O 移到C 所做的功为W = q 0U OD = q 0(U O -U D ) = q 0q /6πε0R .12.15 真空中有两块相互平行的无限大均匀带电平面A 和B .A 平面的电荷面密度为2σ,B 平面的电荷面密度为σ,两面间的距离为d .当点电荷q 从A 面移到B 面时,电场力做的功为多少?[解答]两平面产生的电场强度大小分别为E A = 2σ/2ε0 = σ/ε0,E B = σ/2ε0,两平面在它们之间产生的场强方向相反,因此,总场强大小为E = E A - E B = σ/2ε0, 方向由A 平面指向B 平面.两平面间的电势差为U = Ed = σd /2ε0,当点电荷q 从A 面移到B 面时,电场力做的功为W = qU = qσd /2ε0.12.16 一半径为R 的均匀带电球面,带电量为Q .若规定该球面上电势值为零,则无限远处的电势为多少?[解答]带电球面在外部产生的场强为204Q E rπε=,由于d d R RRU U E r ∞∞∞-=⋅=⎰⎰E l200d 44RR QQr r r πεπε∞∞-==⎰04Q Rπε=,当U R = 0时,04Q U Rπε∞=-.12.17 电荷Q 均匀地分布在半径为R 的球体内,试证明离球心r (r <R )处的电势为2230(3)8Q R r U Rπε-=. [证明]球的体积为343V R π=, 电荷的体密度为 334Q QV R ρπ==. 利用13.10题的方法可求球内外的电场强度大小为30034QE r r R ρεπε==,(r ≦R ); 204Q E rπε=,(r ≧R ).取无穷远处的电势为零,则r 处的电势为d d d RrrRU E r E r ∞∞=⋅=+⎰⎰⎰E l3200d d 44RrRQ Qr r r R r πεπε∞=+⎰⎰230084R rRQQ rRrπεπε∞-=+22300()84Q Q R r RRπεπε=-+2230(3)8Q R r Rπε-=. 12.18 在y = -b 和y = b 两个“无限大”平面间均匀充满电荷,电荷体密度为ρ,其他地方无电荷.(1)求此带电系统的电场分布,画E-y 图;(2)以y = 0作为零电势面,求电势分布,画E-y 图.[解答]平板电荷产生的场强的方向与平板垂直且对称于中心面:E = E`,但方向相反.(1)在板内取一底面积为S ,高为2y 的圆柱面作为高斯面,场强与上下两表面的法线方向平等而与侧面垂直,通过高斯面的电通量为d e SΦ=⋅⎰E Sd d d 2S S S ES =⋅+⋅+⋅=⎰⎰⎰E S E S E S 12.高斯面内的体积为 V = 2yS ,包含的电量为 q = ρV = 2ρSy , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρy/ε0, (-b ≦y ≦b ).穿过平板作一底面积为S ,高为2y 的圆柱形高斯面,通过高斯面的电通量仍为地Φe = 2ES ,高斯面在板内的体积为 V = S 2b , 包含的电量为 q = ρV = ρS 2b , 根据高斯定理 Φe = q/ε0,可得场强为 E = ρb/ε0, (b ≦y );E = -ρb/ε0, (y ≦-b ).E-y 图如左图所示.(2)对于平面之间的点,电势为d d yU y ρε=-⋅=-⎰⎰E l 202y C ρε=-+,在y = 0处U = 0,所以C = 0,因此电势为22y U ρε=-,(-b ≦y ≦b ). 这是一条开口向下的抛物线.当y ≧b 时,电势为d d nqbnqbU y y C εε=-⋅=-=-+⎰⎰E l ,在y = b 处U = -ρb 2/2ε0,所以C = ρb 2/2ε0,因此电势为2002b b U y ρρεε=-+,(b ≦y ). 当y ≦-b 时,电势为00d d b bU y y C ρρεε=-⋅==+⎰⎰E l ,在y = -b 处U = -ρb 2/2ε0,所以C = ρd 2/2ε0,因此电势为2002b b U y ρρεε=+, 两个公式综合得200||2b b U y ρρεε=-+,(|y |≧d ). 这是两条直线.U-y 图如右图所示.U-y 图的斜率就形成E-y 图,在y = ±b 点,电场强度是连续的,因此,在U-y 图中两条直线与抛物线在y = ±b 点相切.[注意]根据电场求电势时,如果无法确定零势点,可不加积分的上下限,但是要在积分之后加一个积分常量.根据其他关系确定常量,就能求出电势,不过,线积分前面要加一个负号,即d U =-⋅⎰E l这是因为积分的起点位置是积分下限.12.19 两块“无限大”平行带电板如图所示,A 板带正电,B 板带负电并接地(地的电势为零),设A 和B 两板相隔5.0cm ,板上各带电荷σ=3.3×10-6C·m -2,求: (1)在两板之间离A板1.0cm 处P 点的电势;(2)A 板的电势.[解答]两板之间的电场强度为E=σ/ε0,方向从A 指向B .以B 板为原点建立坐标系,则r B = 0,r P = -0.04m ,r A = -0.05m . (1)P 点和B 板间的电势差为d d BBPPr r P B r r U U E r -=⋅=⎰⎰E l()B P r r σε=-, 由于U B = 0,所以P 点的电势为6123.3100.048.8410P U --⨯=⨯⨯=1.493×104(V). (2)同理可得A 板的电势为()A B A U r r σε=-=1.866×104(V).12.20 电量q 均匀分布在长为2L 的细直线上,试求:(1)带电直线延长线上离中点为r 处的电势;(2)带电直线中垂线上离中点为r 处的电势;(3)由电势梯度算出上述两点的场强. [解答]电荷的线密度为λ = q/2L . (1)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,根据点电荷的电势公式,它在P 1点产生的电势为101d d 4lU r lλπε=-总电势为10d 4L L l U r lλπε-=-⎰ 0ln()4Ll Lr l λπε=--=-0ln8q r LLr Lπε+=-. (2)建立坐标系,在细线上取一线元d l ,所带的电量为d q = λd l ,在线的垂直平分线上的P 2点产生的电势为2221/20d d 4()lU r l λπε=+, 积分得2221/201d 4()LLU l r l λπε-=+⎰)4Ll Ll λπε=-=0ln8q Lπε=0ln4q LLrπε=.(3)P 1点的场强大小为11U E r∂=-∂ 011()8qL r L r L πε=--+22014qr L πε=-, ①方向沿着x 轴正向.P 2点的场强为22U E r∂=-∂01[4qL r πε==, ②方向沿着y 轴正向.[讨论]习题13.3的解答已经计算了带电线的延长线上的场强为1220124L E x L λπε=-, 由于2L λ = q ,取x = r ,就得公式①.(2)习题13.3的解答还计算了中垂线上的场强为y E =取d 2 = r ,可得公式②. 由此可见,电场强度可用场强叠加原理计算,也可以用电势的关系计算.12.21 如图所示,一个均匀带电,内、外半径分别为R 1和R 2的均匀带电球壳,所带电荷体密度为ρ,试计算:(1)A ,B 两点的电势;(2)利用电势梯度求A ,B 两点的场强.[解答](1)A 点在球壳的空腔内,空腔内的电势处处相等,因此A 点的电势就等于球心O 点的电势.在半径为r 的球壳处取一厚度为d r 的薄壳,其体积为d V = 4πr 2d r ,包含的电量为 d q = ρd V = 4πρr 2d r ,在球心处产生的电势为00d d d 4O q U r r rρπεε==, 球心处的总电势为2122210d ()2R O R U r r R R ρρεε==-⎰, 这就是A 点的电势U A .过B 点作一球面,B 的点电势是球面外的电荷和球面内的电荷共同产生的.球面外的电荷在B 点产生的电势就等于这些电荷在球心处产生的电势,根据上面的推导可得22120()2B U R r ρε=-. 球面内的电荷在B 点产生的电势等于这些电荷集中在球心处在B 点产生的电势.球壳在球面内的体积为3314()3B V r R π=-, 包含的电量为 Q = ρV ,这些电荷集中在球心时在B 点产生的电势为332100()43B BBQ U r R r r ρπεε==-. B 点的电势为U B = U 1 + U 2322120(32)6B BR R r r ρε=--. (2)A 点的场强为0AA AU E r ∂=-=∂. B 点的场强为3120()3B B B B BU R E r r r ρε∂=-=-∂.图13.18[讨论] 过空腔中A 点作一半径为r 的同心球形高斯面,由于面内没有电荷,根据高斯定理,可得空腔中A 点场强为E = 0, (r ≦R 1).过球壳中B 点作一半径为r 的同心球形高斯面,面内球壳的体积为3314()3V r R π=-,包含的电量为 q = ρV ,根据高斯定理得方程 4πr 2E = q/ε0, 可得B 点的场强为3120()3R E r rρε=-, (R 1≦r ≦R 2).这两个结果与上面计算的结果相同.在球壳外面作一半径为r 的同心球形高斯面,面内球壳的体积为33214()3V R R π=-,包含的电量为 q = ρV ,根据高斯定理得可得球壳外的场强为33212200()43R R qE r rρπεε-==,(R 2≦r ). A 点的电势为d d AAA r r U E r ∞∞=⋅=⎰⎰E l12131200d ()d 3AR R r RR r r r r ρε=+-⎰⎰2332120()d 3RR R r r ρε∞-+⎰ 22210()2R R ρε=-. B 点的电势为d d BBB r r U E r ∞∞=⋅=⎰⎰E l23120()d 3BR rR r r r ρε=-⎰2332120()d 3R R R r r ρε∞-+⎰ 322120(32)6B BR R r r ρε=--.A 和B 点的电势与前面计算的结果相同.12.21 (1)设地球表面附近的场强约为200V·m -1,方向指向地球中心,试求地球所带有的总电量.(2)在离地面1400m 高处,场强降为20V·m -1,方向仍指向地球中心,试计算在1400m 下大气层里的平均电荷密度.[解答]地球的平均半径为R =6.371×106m .(1)将地球当作导体,电荷分布在地球表面,由于场强方向指向地面,所以地球带负量.根据公式 E = -σ/ε0, 电荷面密度为 σ = -ε0E ; 地球表面积为 S = 4πR 2, 地球所带有的总电量为Q = σS = -4πε0R 2E = -R 2E /k ,k 是静电力常量,因此电量为629(6.37110)200910Q ⨯⨯=-⨯=-9.02×105(C). (2)在离地面高为h = 1400m 的球面内的电量为2()``R h E Q k+=-=-0.9×105(C),大气层中的电荷为q = Q - Q` = 8.12×105(C).由于大气层的厚度远小于地球的半径,其体积约为V = 4πR 2h = 0.714×1018(m 3), 平均电荷密度为ρ = q /V = 1.137×10-12(C·m -3).。
静电场(参考资料答案解析)

E
dE
x dx
a dx
k
(2x2 a2)
0 2 0
x 2 0
4 0
(3)场强最小为 Emin 0
即, k (2x2 a2 ) 0 4 0
则x 2a 2
7. 一球体内均匀分布着电荷体密度为 的正电荷,若保持电 荷分布不变,在该球体中挖去半径为 r 的一个小球体,球心为 O , 两球心间距离 OO d ,如图所示. 求:
解题分析 根据欧姆定律,由地球表面的电荷面密度 e (R) 及电场强度 E(R) ,可知地球表面的电流密度 j(R) 及电流强度 I ;由 E(R) ,运用高斯定理可 得 e ;由于电流强度 I 恒定,电流密度 j(r) 的分布可求出,从而电场强度 E(r) 的 分布可求出,再用高斯定理可求 e (r) ;对电场强度作积分可得电位差V .
6
r 从地球中心算起.已知地球表面的电场强度为 E(R) 100V m1 ,负号表示场 强指向地球中心.设地球作为导体,其内部无电荷,并设大气中的体电荷密度 e (r) 及 地球表面的面电荷密度 e 均不随时间变化(稳态近似),即大气中的径 向电流是稳恒的.试求: (1)地球表面的总电流强度 I ; (2)地球表面的面电荷密度 e ; (3)地球大气中体电荷密度的分布 e (r) ; 参考解答
由圆心 O 指向 S
2. 如图所示, 真空中有两个点电荷, 带电量分别 为 Q 和Q, 相距 2R.若以负电荷所在处 O 点为中心, 以 R 为半径作高斯球面 S, 则通过该球面的电场强度通量
S R
Q aO
=
;若以 r0 表示高斯面外法线方向的单
位矢量,则高斯面上 a、b 两点的电场强度分别为
、
答案:Q/0, 2Qr0/(90R2), Qr0/(20R2).
静电场练习测试题及参考答案

静电场练习题一、电荷守恒定律、库仑定律练习题4.把两个完全相同的金属球A和B接触一下,再分开一段距离,发现两球之间相互排斥,则A、B两球原来的带电情况可能是 [ ]A.带有等量异种电荷 B.带有等量同种电荷C.带有不等量异种电荷 D.一个带电,另一个不带电8.真空中有两个固定的带正电的点电荷,其电量Q1>Q2,点电荷q置于Q1、Q2连线上某点时,正好处于平衡,则 [ ]A.q一定是正电荷 B.q一定是负电荷C.q离Q2比离Q1远D.q离Q2比离Q1近14.如图3所示,把质量为0.2克的带电小球A用丝线吊起,若将带电量为4×10-8库的小球B靠近它,当两小球在同一高度相距3cm时,丝线与竖直夹角为45°,此时小球B受到的库仑力F=______,小球A带的电量q A=______.二、电场电场强度电场线练习题6.关于电场线的说法,正确的是 [ ]A.电场线的方向,就是电荷受力的方向B.正电荷只在电场力作用下一定沿电场线运动C.电场线越密的地方,同一电荷所受电场力越大D.静电场的电场线不可能是闭合的7.如图1所示,带箭头的直线是某一电场中的一条电场线,在这条线上有A、B两点,用E A、E B表示A、B两处的场强,则 [ ]A.A、B两处的场强方向相同B.因为A、B在一条电场上,且电场线是直线,所以E A=E BC.电场线从A指向B,所以E A>E BD.不知A、B附近电场线的分布情况,E A、E B的大小不能确定8.真空中两个等量异种点电荷电量的值均为q,相距r,两点电荷连线中点处的场强为 [ ]A.0 B.2kq/r2 C.4kq/r2 D.8kq/r29.四种电场的电场线如图2所示.一正电荷q仅在电场力作用下由M点向N点作加速运动,且加速度越来越大.则该电荷所在的电场是图中的 [ ] 11.如图4,真空中三个点电荷A、B、C,可以自由移动,依次排列在同一直线上,都处于平衡状态,若三个电荷的带电量、电性及相互距离都未知,但AB>BC,则根据平衡条件可断定 [ ]A.A、B、C分别带什么性质的电B.A、B、C中哪几个带同种电荷,哪几个带异种电荷C.A、B、C中哪个电量最大D.A、B、C中哪个电量最小二、填空题12.图5所示为某区域的电场线,把一个带负电的点电荷q放在点A或B时,在________点受的电场力大,方向为______.16.在x轴上有两个点电荷,一个带正电荷Q1,另一个带负电荷Q2,且Q1=2Q2,用E1、E2表示这两个点电荷所产生的场强的大小,则在x轴上,E1=E2的点共有____处,其中_______处的合场强为零,______处的合场强为2E2。
大学物理静电场作业题参考答案

解得 q 2l sin 4 0mg tan 7.3.4 长 l =15.0cm的直导线AB上均匀地分布着线密度 =5.0x10-9C·m-1的正电荷.试
求:(1)在导线的延长线上与导线B端相距 a1 =5.0cm处 P 点的场强;(2)在导线的垂直 平分线上与导线中点相距 d2 =5.0cm 处 Q 点的场强.
S
(D) 曲 面 S 的 电 场 强 度 通 量 不 变 , 曲 面 上 各 点 场 强 变
化.
题 7.1(2)图
[答案 D ]
(3)在电场中的导体内部的 [ ] (A)电场和电势均为零; (B)电场不为零,电势均为零; (C)电势和表面电势相等; (D)电势低于表面电势。 [答案:C]
(4)两个同心均匀带电球面,半径分别为 Ra 和 Rb (Ra<Rb), 所带电荷分别为 Qa 和
Uo
4U1
4
8.99
109
1.25 5
108 102
8.99 103V
(2)根据电势差的定义,有UO q0 (U UO )
选取无穷远处为电势零点WO q0 (U UO ) 8.99 106 J
电场力做负功,说明实际需要外力克服电场力做功。
题 7.3.11 图 7.3.11 如题7.3.11图所示,在 A ,B 两点处放有电量分别为+ q ,- q 的点电荷,AB
解:如题 7.3.4 图所示
(1) 在带电直线上取线元 dx ,其上电量 dq 在 P 点产生场强为 dEP
1 4π 0
dx (a x)2
EP
dE P
4π 0
l 2 l 2
dx (a x)2
4π 0
[ a
1
l
1 a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A . Φ 1Φ 2, Φ Sq/0 S 2
q S1 q
B . Φ 1Φ 2, Φ S2 q/0
O a 2a X
C . Φ 1Φ 2, Φ Sq/0
D . Φ 1Φ 2, Φ Sq/0
10.一均匀带电球面,若球内电场强度处处为
零,则球面上的带电量σdS 面元在球面内产生
的电场强度是
A.处处为零
3. 在真空中的静电场中,作一封闭的曲面,则 下列结论中正确的是
A.通过封闭曲面电通量仅是面内电荷提供 B.封闭曲面上各点的场强是面内电荷激发 C.由高斯定理求得的场强仅由面内电荷所激发 D.由高斯定理求得场强是空间所有电荷激发
4. 关于静电场中的电位移线,下列说法中,哪 一种是正确的?
A.起自正电荷,止于负电荷,不形成闭合线,不中断 B.任何两条电位移线互相平行 C.起自正自由电荷,止于负自由电荷,任何两
为一常数,则球体上的总电量Q= A R4 。
9. 把一个均匀带电量+Q的球形肥皂泡由半径 r1吹胀到r2,则半径为R( r1< R < r2)的高斯
球面上任一点场强大小E由 Q/40R2 变为 0 ; 电势U由 Q/4 0R 变为__Q_/_4___0r_2 .
(选无穷远处为电势零点)。
10. 一质量为m、电量为q小球,在电场力作用下
B.二球中至少有一种表面上有正、负两种 电荷分布
C.无论接近到什么程度二球表面都不能 有负电荷分布
D.结果不能判断,要视电荷Q的大小而定
二、填空题
1. 真空中有一半径为R均匀带正电的细圆环,其
电荷线密度为λ,则电荷在圆心处产生的电场强 度 E的大小为 0 。
2. 真空中一半径为R的均匀带电球面,总电量为 Q(Q > 0)。在球面上挖去非常小块的面积ΔS (连 同电荷),且假设不影响原来的电荷分布,则挖
,方向
x轴正向
.
2
Π区 E大小 3 /20 ,方向 x轴正向 .
Ш区E大小 / 20
,方向 x轴负向
.
I
II III
x
5. 半径为R1和R2 两个同轴金属圆筒,其间充满 着相对介电常数为εr 均匀介质,设两筒上单位长 度带电量分别为+λ和-λ, 则介质中电位移矢
量大小D=/2r ,电场强度大小E= /20rr
1 r
1 R
C. 1 q Q
4 0 r R
B. Q 1 1
4 0 R r q
D.
4 0r
9. 两个点电荷电量都是 +q,相距为2a。以左边
点电荷所在处为球心,以a为半径作一球形高斯
面, 在球面上取两块相等的小面积S1和S2, 其位 置如图所示。设通过S1 和 S2的电场强度通量分
别为Φ 1 和 Φ 2 ,通过整个球面电场强度通量为 Φ S
S Q
去ΔS后球心处电场强度大小E= 4 0R2 4R2 , 其方向为 指向S 。
R
O
S
3. 在相对介电常数为εr的各向同性的电介质中,
电位移矢量与场强之间D 的关0系r是E
。
4. 两块“无限大”的带电平行电板,其电荷面密
度分别为(>0)及-2 ,如图所示,试写出各 区域的电场强度E
І区
E大小
/ 20
3.如图示,AB2l ,OCD是以B为中心,l为半经
的半圆,A点有正电荷+q,B点有负电荷-q,求:
(1)把单位正电荷从O点沿OCD移到D点,电场
力对它作的功?
(2)把单位正电荷从D点沿AB的延长线移到无穷
B.不一定为零
C.一定不为零
D.是常数
11. 如图,沿x轴放置“无限长”分段均匀带电
直线,电荷线密度分别为+ λ和- λ,点(0,a)
处的电场强度
A.0
B.
i
2 0a
C.
i
4 0a
D.
(i j)
4 0a
12.有两个完全相同的导体球,带等量的正电 荷Q,现使两球相互接近到一定程度时,则
A.二球表面都将有正、负两种电荷分布
7.静电场中a、b两点的电势差 Ua Ub 取决于
A. 零电势位置选取 B. 检验电荷由a到b路径
C. a、b点场强的值
b
D.a
E
dl (任意路径)
8. 半径为 r 均匀带电球面1,带电量为q;其外有 一同心半径为R的均匀带电球面2,带电量为Q, 则此两球面之间的电势差U1-U2为:
A.
q
4 0
带电细棒,其电荷线密度为 = 0(x-a), 0为一 常量。取无穷远处为电势零点,求坐标原点o处
的电势。
解: U dU q
a
O
l
x dx
x
al dx
a 4 0 x
40l0 40a0lnaal
2.一半径为R的带电球体,其电荷体密度分布为
分布0A和r 电势((rr分RR))布,A。为一常数,试求球体内R外的场强
6. 描述静电场性质两个基本物理量是 E和U ;
参考点
它们定义式是 Ef/q0 和 Up p Edl 。
7. 在场强为E 均匀电场中,A、B两点间距离为 d,A、B连线方向与E方向一致,从A点经任意
路径到B点的场强线积分 AB Edl = Ed .
8.半径为R的不均匀带电球体,电荷体密度分 布为ρ=Ar,式中 r 为离球心的距离,(r≤R)、A
r
解: SD dS S内 qi
D 内 D内 4rA2 42 r;0rE4 内 = rA 42d2rrAr4U 内 = ArR (E R内 3d + r3r)R E A外 d R3 r
D 外 4r20R4r2drAR4
12 40
D外A 4r2R 4;E外4A 0rR 42.
U外rE外dr4A0Rr4
条电位移线在无自由电荷的空间不相交 D.电位移线只出现在有电介质的空间
6.两无限大均匀带电平行平面A和B,电荷面密
度分别为+σ和-σ,在两平面中间插入另一电荷
面密度为+σ平行平面C后,P点场强大小
A.不变
B.原来的 1/2
C.原来的2倍 D.零
5.高斯定理 SDdsVdV
A.适用于任何静电场 B.只适用于真空中的静电场 C.只适用于具有球对称性、轴对称性和平面 D.对称性的静电场 E.D.只适用于虽然不具有(C)中所述的对称 性、但可以找到合适的高斯面的静电场
从电势为U的a点,移动到电势为零的b点,若已
知小球在b点的速率为Vb,则小球在a点的速率
Va=
Vb2
2qU m
。
11. 两根互相平行的长直导线,相距为a,其上均
匀带电,电荷线密度分别为λ1和λ2,则导线单
位长度所受电场力的大小为F0= 12/20a 。
三、计算题
1. 图中所示为一沿 x 轴放置的长度为l的不均匀
