方差分析与回归分析习题答案
茆诗松《概率论与数理统计教程》(第2版)(课后习题 方差分析与回归分析)【圣才出品】
第8章 方差分析与回归分析一、方差分析1．在一个单因子试验中，因子A有三个水平，每个水平下各重复4次，具体数据如下：表8-1试计算误差平方和s e、因子A的平方和S A与总平方和S T，并指出它们各自的自由度．解：此处因子水平数r＝3，每个水平下的重复次数m＝4，总试验次数为n＝mr＝12．首先，算出每个水平下的数据和以及总数据和：T1＝8＋5＋7＋4＝24．T2＝6＋10＋12＋9＝37．T3＝0＋1＋5＋2＝8．T＝T l＋T2＋T3＝24＋37＋8＝69．误差平方和S e由三个平方和组成：于是而2．在一个单因子试验中，因子A有4个水平，每个水平下重复次数分别为5，7，6，8．那么误差平方和、A的平方和及总平方和的自由度各是多少？解：此处因子水平数r＝4，总试验的次数n＝5＋7＋6＋8＝26，因而有误差平方和的自由度因子A的平方和的自由度总平方和的自由度3．在单因子试验中，因子A有4个水平，每个水平下各重复3次试验，现已求得每个水平下试验结果的样本标准差分别为1.5，2.0，1.6，1.2，则其误差平方和为多少？误差的方差σ2的估计值是多少？解：此处因子水平数r＝4，每个水平下的试验次数m＝3，误差平方和S e由四个平方组成，它们分别为于是其自由度为，误差方差σ2的估计值为4．在单因子方差分析中，因子A有三个水平，每个水平各做4次重复试验．请完成下列方差分析表，并在显著性水平α＝0.05下对因子A是否显著作出检验．表8-2 方差分析表解：补充的方差分析表如下所示：表8-3 方差分析表对于给定的显著性水平，查表知，故拒绝域为，由于，因而认为因子A是显著的．此处检验的p值为5．用4种安眠药在兔子身上进行试验，特选24只健康的兔子，随机把它们均分为4组，每组各服一种安眠药，安眠时间如下所示．表8-4 安眠药试验数据在显著性水平下对其进行方差分析，可以得到什么结果？解：这是一个单因子方差分析的问题，根据样本数据计算，列表如下：表8-5于是根据以上结果进行方差分析，并继续计算得到各均方以及F 比，列于下表：表8-6在显著性水平下，查表得，拒绝域为，由于故认为因子A （安眠药）是显著的，即四种安眠药对兔子的安眠作用有明显的差别．此处检验的p 值为6．为研究咖啡因对人体功能的影响，特选30名体质大致相同的健康男大学生进行手指叩击训练，此外咖啡因选三个水平：每个水平下冲泡l0杯水，外观无差别，并加以编号，然后让30位大学生每人从中任选一杯服下，2h后，请每人做手指叩击，统计员记录其每分钟叩击次数，试验结果统计如下表：表8-7请对上述数据进行方差分析，从中可得到什么结论？解：我们知道，对数据作线性变换不会影响方差分析的结果，这里将原始数据同时减去240，并作相应的计算，计算结果列入下表：表8-8于是可计算得到三个平方和把上述诸平方和及其自由度填入方差分析表，并继续计算得到各均方以及F比：表8-9若取查表知，从而拒绝域为，由于．故认为因子A（咖啡因剂量）是显著的，即三种不同剂量对人的作用有明显的差别．此处检验的p值为7．某粮食加工厂试验三种储藏方法对粮食含水率有无显著影响．现取一批粮食分成若干份，分别用三种不同的方法储藏，过一段时间后测得的含水率如下表：表8-10（1）假定各种方法储藏的粮食的含水率服从正态分布，且方差相等，试在下检验这三种方法对含水率有无显著影响；（2）对每种方法的平均含水率给出置信水平为0.95的置信区间．解：（1）这是一个单因子方差分析的问题，由所给数据计算如下表：表8-11三个平方和分别为。
回归分析练习题及参考答案
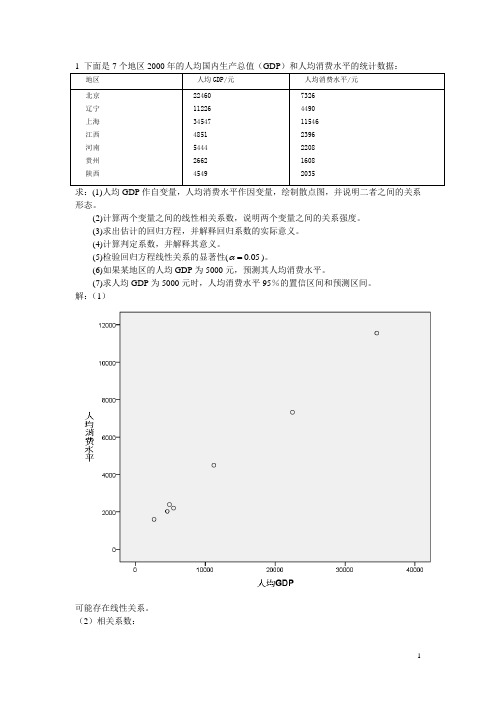
1 下面是7个地区2000年的人均国内生产总值（GDP）和人均消费水平的统计数据：地区人均GDP/元人均消费水平/元北京辽宁上海江西河南贵州陕西 224601122634547485154442662454973264490115462396220816082035求：(1)人均GDP作自变量，人均消费水平作因变量，绘制散点图，并说明二者之间的关系形态。
(2)计算两个变量之间的线性相关系数，说明两个变量之间的关系强度。
(3)求出估计的回归方程，并解释回归系数的实际意义。
(4)计算判定系数，并解释其意义。
(5)检验回归方程线性关系的显著性(0.05α=)。
(6)如果某地区的人均GDP为5000元，预测其人均消费水平。
(7)求人均GDP为5000元时，人均消费水平95％的置信区间和预测区间。
解：（1）可能存在线性关系。
（2）相关系数：（3）回归方程：734.6930.309y x=+回归系数的含义：人均GDP没增加1元，人均消费增加0.309元。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。
系数(a)模型非标准化系数标准化系数t 显著性B 标准误Beta1 （常量）734.693 139.540 5.265 0.003人均GDP（元）0.309 0.008 0.998 36.492 0.000 a. 因变量: 人均消费水平（元）%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%（4）模型汇总模型R R 方调整 R 方标准估计的误差1 .998a.996 .996 247.303a. 预测变量: (常量), 人均GDP。
人均GDP对人均消费的影响达到99.6%。
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%注意：图标不要原封不动的完全复制软件中的图标，要按规范排版。
数理统计期末练习题0汇总
统 计 分 析（方差分析和回归分析）三、典型题解例1：某水产研究所为了比较四种不同配合饲料对鱼的饲喂效果，选取了条件基本相同的鱼20尾，随机分成四组，投喂不同饲料，经一个月试验以后，各组鱼的增重结果列于下表.饲喂不同饲料的鱼的增重 （单位：10g ）饲料鱼的增重（x ij ）合计.i x 平均.i x A 1 31.9 27.9 31.8 28.4 35.9 155.9 31.18 A 2 24.8 25.7 26.8 27.9 26.2 131.4 26.28 A 3 22.1 23.6 27.3 24.9 25.8 123.7 24.74 A 427.0 30.829.024.528.5139.827.96合计..x =550.8解：这是一个单因素等重复试验，因素数4s =，重复数05n =.各项平方和及自由度计算如下：220/550.8/(45)15169.03C T n s ==⨯=总平方和 222231.927.928.5T ij S x T C =∑∑-=+++-67.19903.151697.15368=-=组间平方和22222011(155.9131.4123.7139.8)515283.315169.03114.27A jS x C C n =-=+++-=-=∑ 组内平方和 199.67114.2785.40E T A S S S =-=-= 总自由度 0154119T f n s =-=⨯-= 处理间自由度 1413A f s =-=-= 处理内自由度 19316E T A f f f =-=-=用A S 、E S 分别除以A f 和E f 便得到处理间均方A MS 及处理内均方E MS ./114.27/338.09/85.40/16 5.34A A A E E E MS S f MS S f ======因为/38.09/5.347.13A E F MS MS ===；根据13A f f ==，216E f f ==，查表得F ＞F 0.01(3，16) =5.29,，表明四种不同饲料对鱼的增重效果差异极显著，用不同的饲料饲喂，增重是不同的.例2：抽测5个不同品种的若干头母猪的窝产仔数，结果见下表，试检验不同品种母猪平均窝产仔数的差异是否显著.五个不同品种母猪的窝产仔数品种号 观 察 值x ij (头/窝) x i..i x1 8 13 12 9 9 51 10.2 2 7 8 10 9 7 41 8.23 13 14 10 11 12 60 12 4 13 9 8 8 10 48 9.65 121115 14136513 合计T =265解：这是一个单因素试验，因素数5s =，重复数05n =.现对此试验结果进行方差分析如下：计算各项平方和与自由度220/265/(55)2809.00C T sn ==⨯=22222222222.0(8131413)2809.002945.002809.00136.0011(5141604865)2809.0052882.202809.0073.20T ij A jS x C S x C n =-=++++-=-==-=++++-=-=∑∑∑ 136.0073.2062.80E T A S S S =-=-=0155124,1514,24420T A E T A f sn f s f f f =-=⨯-==-=-==-=-= 列出方差分析表，进行F 检验不同品种母猪的窝产仔数的方差分析表变异来源 平方和 自由度 均方 F 值品种间 73.20 4 18.30 5.83 误差 62.80 20 3.14 总变异136.0024根据14A f f ==，220E f f ==查临界F 值得：F 0.05(4,20) =2.87,F 0.05(4,20) =4.43，因为F ＞F 0.01(4,20)，表明品种间产仔数的差异达到1%显著水平.例3：以A 、B 、C 、D 4种药剂处理水稻种子，其中A 为对照，每处理各得4个苗高观察值(cm)，其结果如下表，试分解其自由度和平方和.水稻不同药剂处理的苗高(cm )药 剂苗高观察值总和i T平均i yA 18 21 20 13 72 18B 20 24 26 22 92 23C 10 15 17 14 56 14D 28 27 29 3211629T =336=y 21解：计算各项平方和与自由度20T C n s ===⨯23367056442T ij S y C C =-=+++-=∑∑222182132602201()()kT i i S n y y T n C C =-=-=+++-=∑∑2222729256116/4504或 A S =⨯-+-+-+-=22224[(1821)(2321)(1421)(2921)]5042221111()k n nk kE ij i iji T A S y y y T n S S =-=-=-=-=∑∑∑∑60250498进而可得均方：T MS ==602/1540.13 A MS ==504/3168.00 E MS ==98/128.17总方差自由度44115T f =⨯-=，药剂间自由度413A f =-=，药剂内自由度15312E f =-=例4：为研究雌激素对子宫发育的影响，现有4窝不同品系未成年的大白鼠，每窝3只，随机分别注射不同剂量的雌激素，然后在相同条件下试验，并称得它们的子宫重量，见下表，试作方差分析.各品系大白鼠不同剂量雌激素的子宫重量(g)品系(A )雌激素注射剂量(mg/100g)(B )合计x i. 平均.i x B 1(0.2)B 2(0.4)B 3(0.8)A 1 106 116 145 367 122.3 A 2 42 68 115 225 75.0 A 3 70 111 133 314 104.7 A 442 63 87 192 64.0 合计x .j 260 358 480 1098 平均j x .65.089.5120.0解：这是一个双因素单独观测值试验结果.A 因素(品系)有4个水平，即a =4；B 因素(雌激素注射剂量)有3个水平，即b =3，共有a ×b =3×4=12个观测值.方差分析如下：计算各项平方和与自由度22/1098/(43)100467.0000C T ab ==⨯=22222222222222.(1061166387)100467.0000113542100467.000013075.000011(367225314192)100467.00003106924.6667100467.00006457.666711(260358480)100467.00004T ij A jB jS x C S x C b S x C a =-=++++-=-==-=+++-=-==-=++-∑∑∑∑106541.0000100467.00006074.0000=-=13075.00006457.66676070000543.3333143111,14131312,11326e T A B T A B e T A B S S S S f ab f a f b f f f f =--=--==-=⨯-==-=-==-=-==--=--=列出方差分析表，进行F 检验方差分析表变异来源平方和 自由度 均方 F 值A 因素(品系) 6457.6667 3 2152.5556 23.77B 因素(剂量)6074.0000 2 3037.0000 33.54误差 543.3333 6 90.5556总变异13075.000011根据13A f f ==，26E f f ==查临界F 值，F 0.01(3,6)=9.78；根据12B f f ==，26E f f ==查临界F 值，F 0.01(2,6)=10.92.因为A 因素的F 值23.77＞F 0.01(3,6)，差异极显著；B 因素的F 值33.54＞F 0.01(2,6)，差异极显著.说明不同品系和不同雌激素剂量对大白鼠子宫的发育均有极显著影响.例7：在某个地区抽取了9家生产同类产品的企业，其月产量和单位产品成本的资料如表8-1，建立月产量x 和单位产品成本y 之间的直线方程.并估计当月产量x=10（千件）时，单位产品成本的数值.22293332.953.7613ˆ 6.46()9370.6553.7n xy x y bn x x -⋅⨯-⨯===--⨯-∑∑∑∑∑ 5.97x =，68.11y =，ˆ68.11( 6.46) 5.97106.68ay bx =-=--⨯= 所以回归方程为：ˆ106.68 6.46y x =-当10x =（千件），ˆ106.68 6.4642.08yx =-=（元）.例8：为研究某一化学反应过程中，温度()x C ο对产品得率(%)Y 的影响，测得数据如下：（1） 求变量Y 关于x 的线性回归方程. （2） 2σ的无偏估计.（3） 检验回归方程的回归效果是否显著（取0.05α=）. 解： （1）10n =，经计算得101101010102211111450, 673, 218500, 47225, 101570ii i iii i i i i i xy x y x y ==========∑∑∑∑∑21218500145082501011015701450673398510xx xy S S =-⨯==-⨯⨯=故得ˆ0.48303xx xyS bS ==，11ˆ67314500.48303 2.739351010a=⨯-⨯⨯=- 于是得到回归直线方程ˆ 2.739350.48303yx =-+ 或写成ˆ67.30.48303(145)yx =+- （2）由以上计算计算结果得2221111()472256731932.110nn yy i i i i S y y n ===-=-⨯=∑∑ 又已知3985xyS =，ˆ0.48303b=，故 2ˆ7.23ˆ0.9082yy xy S bSn σ-===-（3）待检验假设0: 0H b =，1: 0H b ≠由（1）和（2）知2ˆˆ0.48303, 8250, 0.9xx bS σ===.查表得0.0520.025(2)(8) 2.3060t n t -==假设0: 0H b =的拒绝域为|| 2.3060t =现在||46.25 2.3060t ==> 故拒绝0: 0H b =，认为回归效果是显著的.例9：某商品的需求量（单位：件）y 与价格x （单位：元）的统计资料如下所示求需求函数的回归方程.解：画散点图，根据散点图选择曲线类型b y ax -=来描绘需求量y 与价格x 的关系经变换，得''ln ln ln y y a b x x αβ==-=+ 利用最小二乘法的α和β的估计值ˆ9.1206α=， ˆ0.6902β=- 所以ˆˆ9141.685ae α==，ˆˆ0.6902b β=-=. 故需求回归方程为：0.6902ˆ9141.658yx -=，将y 与ˆy的值加以对比如下：可见y 与ˆy数据相近，效果较好. 四、练习题1.把下面的方差分析表填写完整，方差来源平方和自由度修正（方差）组间 131.37 （1） （3） 组内 （2） 15 （4） 总和332.4819临界值参考答案：（1）4（2）201.11（3）32.84（4）13.412.一批由相同材料织成的布料，使用染整工艺1B ，2B ，3B ，分别处理后进行强度试验，实测数据（单位：2/kg m ）为：工艺1B ：0.94 0.86 0.90 1.26 1.04 工艺2B ：1.28 1.72 1.60 1.60工艺3B ：1.02 0.86 1.00 1.22 1.33 1.10试分析不同染整工艺下布料强度的差异显著性？(0.1α=) 参考答案：0.10.7615(2,11) 2.86F F =<=，不显著.3.为考察苗猪品种对增重的影响，今选择1A ，2A ，3A 等3个品种各5头发育良好体重相等的苗猪作实验，在同等条件下喂养一段时间后重新过磅，其实际增重（单位：kg ）为：工艺1A ：129 122 140 140 129 工艺2A ：123 135 124 104 114 工艺3A ：147 131 138 150 124试问猪的品种对增重的影响是否显著？(05.0=α) 参考答案：0.14.0064(2,12) 2.81F F =>=，显著.4.设四名工人操作机器321,,A A A 各一天, 其日产量如表8.7所示, 问不同机器或不同工人对日产量是否有显著影响(0.1α=)?参考答案：0.19.3183(3,6) 3.29A F F =>=，显著；0.11.8992(2,6) 3.46B F F =<=，不显著8．某地高校教育经费（x ）与高校学生人数（y ）连续6年的统计资料如下：要求：（1）建立议程回归直线方程，估计教育经费为500万元的在校学生数； （2）计算估计标准误差.参考答案：（1）Y=-17.92+0.096X ， 29.84338（2）2ˆ0.8649σ= 9. 以下是子代和父代受教育年限的抽样调查求：（1）子代受教育年限（Y ）关于父代受教育年限（X ）的回归直线. （2）2σ的无偏估计.（3）判断该结论是否具有推论意义（0.05α=）.参考答案：（1）Y=3+0.6X ，（2）2ˆ0.93σ=（3）0025|| 3.928(3) 3.1824t t =>=，显著. 10. 设对某产品的价格P 与供给量S 的一组观察数据如下表：据此求：（1）该产品的价格P 关于供给量S 的回归直线.（2）2σ的无偏估计.（3）是否具有推论意义？（0.05α=）.参考答案：（1）Y=-0.1754+6.2281X ，（2）2ˆ11.84σ=（3）0025||0.3722(6) 2.4469t t =<=，不显著.11.以下是生活期望值与个人成就的抽样调查求：（1）回归直线 （2）2σ的无偏估计.（3）是否具有推论意义（0.05α=）.参考答案：（1）Y=0.2668+0.8748X ，（2）2ˆ 5.089σ=（3）0025||0.2703(6) 2.4469t t =<=，不显著.。
方差分析与回归分析
以及浓度和温度的交互作用对产量无显著性影响，也就是说为
了提高产量必须控制好浓度。
2 、双因素无重复试验的方差分析 在双因素试验中,对每一对水平组合只做一次试验,即不 重复实验,得到
上一页 下一页 返回
上一页 下一页 返回
总平方和 误差平方和
例9.3 某化工企业为了提高产量，选了三种不同浓度、四种不同 温度做试验。在同一浓度与温度组合下各做两次试验，其数据如
下表所示，在显著性水平α=0.05下不同浓度和不同温度以及它们
间的交叉作用对产量有无显著性影响？
B A
A1 A2 A3
B1
14,10 9,7 5,11
B2
11,11 10,8 13,14
检验温度对该化工产品的得率是否有显著影响。
解: 计算各个水平下的样本均值，得
上一页 下一页 返回
计算 ST=106.4, SA=68.4, SE =38.0
单因素试验的方差分析表：
方差来源 平方和 自由度 F值 临界值
显著性
因素A 误差
总计
68.4 4 38.0 10
106.4 14
4.5 F0.05(4,10)=3.48 ※ 4.5 F0.01(4,10)=5.99
变量Y服从正态分布
，即Y的概率密度为
其中
，而 是不依赖于x的常数。
上一页 下一页 返回
在n次独立试验中得到观测值（x1,y1）,（x2,y2）,… （xn,yn），利用极大似然估计法估计未知参数a1, a2，… ak,时，
有似然函数
似然函数L取得极大值，上式指数中的平方和
取最小值。
即为了使观测值（xi , yi）(i=1,2,…,n)出现的可能性最大，应当选 择参数a1,a2,…,ak，使得观测值yi与相应的函数值
茆诗松《概率论与数理统计教程》第3版笔记和课后习题含考研真题详解(方差分析与回归分析)【圣才出品】
（4）各平方和的计算
Ti
=
mi j =1
yij，yi =
Ti mi
r
， T=
i =1
mi j =1
yij
=
r i =1
Ti，y
=
T n
r mi
则 ST
i1 j1
yij－y
2
r i 1
mi j 1
yij2－
T2 n
，fT＝n－1；
r
SA mi
i 1
yi－y
2
r
Ti
2
－
T
2
8 / 48
圣才电子书 十万种考研考证电子书、题库视频学习平台
n＝mr＝12。每个水平下的数据和以及总数据和为：
圣才电子书 十万种考研考证电子书、题库视频学习平台
茆诗松《概率论与数理统计教程》第 3 版笔记和课后习题含考研真题详解 第 8 章 方差分析与回归分析
8.1 复习笔记
一、方差分析
1．单因子方差分析的统计模型
yij
=
+ai
+
ij
,i
=1,2,,r
r
ai =0,
i =1
之，无明显差别，这一方法称为 T 法。
3．重复数不等场合的 S 法
cij
r－1 F1- (r－1,
fe
)
1 mi
1 mj
ˆ 2
三、方差齐性检验（见表 8-1-2）
表 8-1-2 方差齐性检验
5 / 48
圣才电子书 十万种考研考证电子书、题库视频学习平台
四、一元线性回归
0 t1/2 n 2ˆ
1 x0 x 2
回归分析课后习题
第一章习题1.1变量间统计关系和函数关系的区别是什么？1.2回归分析与相关分析的区别和联系是什么？1.3回归模型中随机误差项的意义是什么？1.4线性回归模型中的基本假设是什么？1.5回归变量设置的理论依据是什么？在设置回归变量时应注意哪些问题？1.6收集、整理数据包括哪些基本内容？1.7构造回归理论模型的基本依据是什么？1.8为什么要对回归模型进行检验？1.9回归模型有哪几个方面的应用？1.10为什么强调运用回归分析研究经济问题要定性分析和定量分析相结合？第二章 习题2.1一元线性回归模型有哪些基本假定？ 2.2 考虑过原点的线性回归模型1,1,,i i i y x i n βε=+=误差1,,n εε仍满足基本假定。
求1β的最小二乘估计。
2.3证明（2.27）式，10nii e==∑，10ni i i x e ==∑。
2.4回归方程01Ey x ββ=+的参数01,ββ的最小二乘估计与极大似然估计在什么条件下等价？给出证明。
2.5 证明0ˆβ是0β的无偏估计。
2.6 证明(2.42)式 ()()222021,i x Var n x x βσ⎡⎤=+⎢⎥-⎢⎥⎣⎦∑成立 2.7 证明平方和分解式SST SSR SSE =+2.8 验证三种检验的关系，即验证：（1）t ==（2）2212ˆ1ˆ2xx L SSR F t SSE n βσ===-2.9 验证（2..63）式：()()221var 1i i xx x x e n L σ⎡⎤-=--⎢⎥⎢⎥⎣⎦2.10 用第9题证明()2211ˆˆ2n i ii y y n σ==--∑是2σ的无偏估计。
2.11* 验证决定系数2r 与F 值之间的关系式 22Fr F n =+-以上表达式说明2r 与F 值是等价的，那么我们为什么要分别引入这两个统计量，而不是只使用其中的一个。
2.12* 如果把自变量观测值都乘以2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？如果把自变量观测值都加上2，回归参数的最小二乘估计0ˆβ和1ˆβ会发生什么变化？ 2.13 如果回归方程01ˆˆˆy x ββ=+相应的相关系数r 很大，则用它预测时，预测误差一定较小。
实验设计方法课后习题答案46章
▪ 习题不能用正交表78(2)L ，因为会产生混杂。
需选用正交表1516(2)L 。
表头设计如下：▪ 说明：也可有其他不同的表头设计（试验方案）。
▪ 习题 由于1AB C D A B A C B C f f f f f f f ⨯⨯⨯=======, 7f =总，故可选用正交表78(2)L ，且不会产生混杂。
表头设计如下：根据直观分析结果，因素的主次顺序为：AXB AXC C B BXC A D A 与B 的二元表,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,A 与C 的二元表,▪根据A与B的二元表，A1 B2的效果最好；▪根据A与C的二元表，A1 C2的效果最好；▪从直观分析结果可以得到，D1效果最好；▪故最优生产条件为：A1 B2 C2 D1▪（3）方差分析由于没有误差列，故不能对各因素进行显著性检验。
但是，我们选择离差平方和最小的因素D所在的列作为误差列，对各因素进行显著性检验，得到结果如下：因素的主次顺序与直观分析的一样，从显著性来看，只有AXB显著，其他的因素或交互作用都不显著。
▪习题其中A ×B 的离差平方和349.85222.29632.148A B SS SS SS ⨯=+=+=A ×B 的自由度,,,,,,344A B f f f ⨯=+=32.14841.973 5.14024.446A B F ⨯==<故A ×B 不显著。
B ×C 的离差平方和81134.7417.6342.371B C SS SS SS ⨯=+=+=B ×C 的自由度,,,,,,8114B C f f f ⨯=+=42.3714 2.601 5.14024.446B CF ⨯==<故B ×C 不显著。
▪ 因素的主次顺序（根据极差大小或F 值大小） A D F BXC AXB B E C ▪ 最优工艺条件的确定:可以根据直观分析结果选择每个因素的最优水平，得到最优工艺条件为：,,,,,,,,,,,,,,,A1,D1,F1,E0,B0,C0,,.,,,,,,,,,,也可以计算各因素的水平效应 根据水平效应来确定，具体如下: 对于因素A ，,,,115221319ˆ9.148927927A K T a=-=-= 224251319ˆ 1.630927927A K T a =-=-=-333721319ˆ7.519927927A K T a =-=-=-故A 的第1水平的效应最大。
方差分析与回归分析习题答案精修订
方差分析与回归分析习题答案SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第九章 方差分析与回归分析习题参考答案1. 为研究不同品种对某种果树产量的影响，进行试验，得试验结果（产量）如下表，试分析果树品种对产量是否有显着影响.（0.05(2,9) 4.26F =，0.01(2,9)8.02F =）解：r=3,12444n n 321=++=++=n n ,T=120 ,12001212022===n T C 计算统计值?7228.53,38A A A e e SS f F SS f ==≈……方差分析表结论:由于0.018.53(2,9)8.02,A F F ≈>=故果树品种对产量有特别显着影响.2.2700=10.523.56=≈结论: 由以上方差分析知，进器对火箭的射程有特别显着影响；燃料对火箭的射程有显着影响. 3．为了研究某商品的需求量Y 与价格x 之间的关系，收集到下列10对数据：2231,58,147,112,410.5,i i i i i i x y x y x y =====∑∑∑∑∑（1）求需求量Y 与价格x 之间的线性回归方程； （2）计算样本相关系数；（3）用F 检验法作线性回归关系显着性检验. 解：引入记号10, 3.1,5.8n x y ===∴需求量Y 与价格x 之间的线性回归方程为（2）样本相关系数32.80.955634.3248l r-==≈≈- 在0H 成立的条件下，取统计量(2)~(1,2)Ren S FF n S -=-计算统计值22(32.8)15.967.66,74.167.66 6.44R xy xx e yy R S l l S l S ==-≈=-≈-=故需求量Y 与价格x 之间的线性回归关系特别显着.4. 随机调查10个城市居民的家庭平均收入(x)与电器用电支出(y)情况得数据（单位：千元）如下:(1) 求电器用电支出y 与家庭平均收入x 之间的线性回归方程； (2) 计算样本相关系数； (3) 作线性回归关系显着性检验;(4) 若线性回归关系显着,求x =25时, y 的置信度为的预测区间. 解：引入记号10,27,1.9n x y ===∴电器用电支出y 与家庭平均收入x 之间的线性回归方程为（2）样本相关系数 0.9845l r==≈在0H 成立的条件下，取统计量(2)~(1,2)Rn S FF n S -=-e计算统计值2243.6354 5.37,5.54 5.370.17xy xx yy s l l s l s ==≈=-≈-=R e R故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显着. 相关系数检验法 01:0;:0H R H R =≠故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显着. (4) 因为0xx =处,0y 的置信度为1α-的预测区间为其中00.025垐 1.42640.123225 1.6536,(8) 2.31,0.1458y t σ=-+⨯====代入计算得当x =25时, y 的置信度为的预测区间为。
概率论与数理统计教程-魏宗舒-课后习题解答答案-7-8章
概率论与数理统计教程-魏宗舒-课后习题解答答案-7-8章概率论与数理统计教程-魏宗舒-课后习题解答答案-7-8章第七章假设检验7.1 设总体2(,)N ξµσ~，其中参数µ，2σ为未知，试指出下⾯统计假设中哪些是简单假设，哪些是复合假设：（1）0:0,1H µσ==；（2）0:0,1H µσ=>；（3）0:3,1H µσ<=；（4）0:03H µ<<；（5）0:0H µ=.解：（1）是简单假设，其余位复合假设 7.2 设1225,,,ξξξ取⾃正态总体(,9)N µ，其中参数µ未知，x 是⼦样均值，如对检验问题0010:,:H H µµµµ=≠取检验的拒绝域：12250{(,,,):||}c x x x x c µ=-≥，试决定常数c ，使检验的显著性⽔平为0.05解：因为(,9)N ξµ~，故9(,)25N ξµ~ 在0H 成⽴的条件下，00053(||)(||)53521()0.053cP c P c ξµξµ-≥=-≥??=-Φ=55()0.975,1.9633c cΦ==，所以c =1.176。
7.3 设⼦样1225,,,ξξξ取⾃正态总体2(,)N µσ，20σ已知，对假设检验0010:,:H H µµµµ=>，取临界域12n 0{(,,,):|}c x x x c ξ=>，（1）求此检验犯第⼀类错误概率为α时，犯第⼆类错误的概率β，并讨论它们之间的关系；（2）设0µ=0.05，20σ=0.004，α=0.05，n=9，求µ=0.65时不犯第⼆类错误的概率。
解：（1）在0H 成⽴的条件下，200(,)nN σξµ~，此时00000()P c P ξαξ=≥=10，由此式解出010c αµ-=+在1H 成⽴的条件下，20(,)nN σξµ~，此时101010()(P c P αξβξµ-=<=<=Φ=Φ=Φ由此可知，当α增加时，1αµ-减⼩，从⽽β减⼩；反之当α减少时，则β增加。
实验设计与数据处理第三四五章例题及课后习题答案
1
8.9
4
70
30
3 11.2
5
90
10
1
8.4
6
90
10
3 11.1
7
90
30
1
9.8
8
90
30
3 12.6
SUM
640
160
16 79.9
AVE
80
SUMMARY OUTPUT
回归统计
Multiple
R
0.99645389
R Square 0.992920354
Adjusted
R Square 0.987610619
x3 13 19 25 10 16 22 28 133
y 1.5
3 1 2.5 0.5 2 3.5 14
0.33 0.336 0.294 0.476 0.209 0.451 0.482 2.578
SUMMARY OUTPUT
回归统计
Multiple
R
0.983812569
R Square 0.967887171
SSt SSr Sse
x3 13 19 25 10 16 22 28 133 19
y 1.5 0.33
3 0.336 1 0.294 2.5 0.476 0.5 0.209 2 0.451 3.5 0.482 14 2.578 2 0.368286
方程 1 1E-06 2 1E-06 3 2.32E-09 4 7.24E-11
2.05
7.4
0.125
0
6 11.2 1.866666667 0.130666667
6 35.8 5.966666667 1.298666667
回归分析试题答案
诚信应考 考出水平 考出风格浙江大学城市学院2011 — 2012 学年第一学期期末考试卷《 回归分析 》开课单位： 计算分院 ；考试形式：开卷（A4纸一张）；考试时间：2011年01月6日； 所需时间： 120 分钟一．计算题(10分。
)1，考虑过原点的线性回归模型1,1,2,...,i i i y x i n βε=+=误差1,...,n εε仍满足基本假定。
求1β的最小二乘估计。
并求出1β 的期望和方差，写出1β的分布。
1221111111121,1,2,...,ˆ()()2()0ˆi i i nni i i i i i ni i i i ni ii nii y x i n Q y yy x Qy x x x yxβεββββ======+==-=-∂=--=∂=∑∑∑∑∑解:第1页共 6 页二. 证明题(本大题共2小题，每小题7分，共14分。
)1，证明：（1）22()1var()[1]i i xxx x e n L σ-=--(2)2211ˆˆ()2n i ii y y n σ==--∑是2σ的无偏估计。
011111122ˆˆˆ()()1()()1var()var[()()]()1var()var((()))()12cov[,(())](1(i i i i i nn i i j j jj j xx ni i i j j j xx ni i j j j xx ni i j j j xxe y y y x x x x y y x x y n L x x e y x x y n L x x y x x y n L x x y x x y n L x n ββσσ======-=----=----=-+--=++---+-=++∑∑∑∑∑解(1):222122222221212211)()1())2()()()11(12()]()1[1]1ˆˆ(2)()(())21ˆ[()]2()111var()[1]2212n i i j j xx xxi i xx xxi xx ni i i ni i i n n i i i i xx x x x x x L n L x x x x n L n L x x n L E E y y n E y y n x x e n n n L n σσσσσ=====----+--=++-+-=--=--=---==----=-∑∑∑∑∑22(11)n σσ--=三．填空题.(每空2分，共46分)1.为了研究家庭收入和家庭消费的关系，通过调查得到数据如下：6.22893,29.12349,43008,97.29,5422=====∑∑∑xy yxy x1)用最小二乘估计求出线性回归方程的参数估计值0ˆβ= 。
第八章方差分析与回归分析（1）
第⼋章⽅差分析与回归分析（1）第⼋章⽅差分析与回归分析习题8.1 P3801、在⼀个单因⼦试验中，因⼦A 有三个⽔平，每个⽔平下各重复4次，具体数据如下：试计算误差平⽅和e S 、因⼦A 的平⽅和A 、总平⽅和T ，并指出它们各⾃的⾃由度．2、在⼀个单因⼦试验中，因⼦A 有四个⽔平，每个⽔平下各重复的次数分别为5，7，6，8。
那么误差平⽅和、A 的平⽅和及总平⽅和的⾃由度各是多少？5、⽤4种安眠药在兔⼦⾝上进⾏试验，特选24只健康的兔⼦，随机把它们均分为4组，每组各服⼀种安眠药，安眠时间如下所⽰:在显著⽔平α=习题8.2 P3873、有7种⼈造纤维，每种抽4根测其强度，得每种纤维的平均强度及标准差如下：（1）试问七种纤维强度间有⽆显著性差异（0.05α=）（2）若七种纤维的强度间⽆显著性差异，则给出平均强度的置信⽔平为0.95的置信区间；若各种纤维的强度间有显著差异，请进⼀步在0.05α=下进⾏多重⽐较，并指出那种纤维的平均强度最⼤，同时该种纤维平均强度的置信⽔平为0.95的置信区间。
习题8.3 P3942、在安眠药试验中（见习题8.1.5）中已求得到四个样本⽅差：222212340.02,0.08,0.036,0.1307s s s s ====请⽤Hartley 检验在显著⽔平0.05α=下考察四个总体⽅差是否彼此相等。
习题8.4 P4111、假设回归直线过原点，即⼀元线性回归模型为,1,2,...i i i y x i n βε=+=()()20,,i i E Var εεσ==诸观测值相互独⽴。
（1）写出2,βσ的最⼩⼆乘估计；（2）对给定的0x ，其对应的因变量均值的估计为0y ，求()0Var y 。
3、在回归分析计算中，常对数据进⾏变换1212,,1,...i i i i y c x cy x i n d d --=== 其中()()121122,,0,0c c d d d d >>是适当选取的常数。
概率论与数理统计(茆诗松)第二版课后第八章习题参考答案
第八章 方差分析与回归分析本章前三节研究方差分析，讨论多个正态总体的比较，后两节研究回归分析．讨论两个变量之间的相关关系．§8.1 方差分析8.1.1问题的提出上一章讨论了单个或两个正态总体的假设检验，这里讨论多个正态总体的均值比较问题．通常为了研究某一因素对某项指标的影响情况，将该因素在多种情形下进行抽样检验，作出比较．一般将该因素称为一个因子，所检验的每种情形称为水平．在每个水平下需要考察的指标都分别构成一个总体，比较它们的总体均值是否相等．对每一个总体都分别抽取一个样本，样本容量称为重复数．如果只对一个因子中的多个水平进行比较，称为单因子方差分析，对多个因子的水平进行比较，称为多因子方差分析．本章只进行单因子方差分析．例 在饲料养鸡增肥的研究中，现有三种饲料配方：A 1 , A 2 , A 3 ，为比较三种饲料的效果，特选24只相似的雏鸡随机均分为三组，每组各喂一种饲料，60天后观察它们的重量．实验结果如下表所示： 饲料鸡重/gA 1 1073 1009 1060 1001 1002 1012 1009 1028 A 2 1107 1092 990 1109 1090 1074 1122 1001 A 3 1093 1029 1080 1021 1022 1032 1029 1048 在此例中，就是要考察饲料对鸡增重的影响，需要比较三种饲料对鸡增肥的作用是否相同．这里，饲料就是一个因子，三种饲料配方就是该因子的三个水平，每种饲料喂养的雏鸡60天后的重量分别构成一个总体，这里共有3个总体，每一个总体抽取样本的重复数都是8，比较这3个总体的均值是否相等． 8.1.2单因子方差分析的统计模型设因子A 有r 个水平A 1 , A 2 , …, A r ，在每个水平下需要考察的指标都构成一个总体，即有r 个总体，分别记为Y 1 , Y 2 , …, Y r ，对每一个总体都分别抽取一个样本，首先考虑重复数相等的情形，设重复数都是m ，总体Y i 的样本Y i 1 , Y i 2 , …, Y im ，i = 1, 2, …, r ．作出以下假定：（1）每一个总体都服从正态分布，即r i N Y i i i ,,2,1),,(~2L =σµ；（2）各个总体的方差都相等，即22221r σσσ===L ，都记为σ 2；（3）各个总体及抽取的样本相互独立，即Y ij 相互独立，i = 1, 2, …, r ，j = 1, 2, …, m ． 需要比较它们的总体均值是否相等，即检验的原假设与备择假设为H 0：µ 1 = µ 2 = … = µ r vs H 1：µ 1 , µ 2 , …, µ r 不全相等，如果H 0成立，就可以认为这r 个水平下的总体均值相同，称为因子A 不显著；反之，如果H 0不成立，就称为因子A 显著．在水平A i 下的样品Y ij 与该水平下的总体均值µ i 之差ε ij = Y ij − µ i 为随机误差．由于Y ij ~ N (µ i , σ 2 )，因此随机误差ε ij ~ N (0 , σ 2 )．对所有r 个水平下的总体均值求平均，即∑==+++=ri i r r r 1211)(1µµµµµL称为总均值．每个水平A i 下的总体均值µ i 与总均值µ 之差a i = µ i − µ 称为该水平A i 下主效应．显然所有主效应a i 之和等于0，即01=∑=ri ia，检验所有水平下的总体均值是否相等，也就是检验所有主效应a i 是否全等于0．这样单因子方差分析在重复数相等的情形下，统计模型为⎪⎪⎩⎪⎪⎨⎧===++=∑=).,0(;0;,,2,1,,,2,1,21σεεµN a m j r i a Y ij r i i ij i ij 相互独立，且都服从L L 检验的原假设与备择假设为H 0：a 1 = a 2 = … = a r = 0 vs H 1：a 1 , a 2 , …, a r 不全等于0． 8.1.3平方和分解一．试验数据对于r 个总体下的试验数据Y ij , i = 1, 2, …, r ，j = 1, 2, …, m ，记T i 表示第i 个总体下试验数据总和，⋅i Y 表示第i 个总体下样本均值，n = rm 表示总的样本容量，T 表示总的试验数据总和，Y 表示总的样本均值，即∑==mj ij i Y T 1，∑=⋅==mj ij i i Y m m T Y 11， i = 1, 2, …, r ，∑∑∑=====r i mj ij r i i Y T T 111，∑∑∑=⋅=====ri i r i m j ij Y r Y rm T n Y 111111， 用⋅i Y 作为µ i 的点估计，Y 作为µ 的点估计．又记⋅i ε表示第i 个总体下随机误差平均值，ε表示总的随机误差平均值，即∑=⋅=mj ij i m 11εε， i = 1, 2, …, r ，∑∑∑=⋅====ri i r i m j ij r n 11111εεε．显然有⋅⋅+=i i i Y εµ，εµ+=Y ．在单因子方差分析中通常将试验数据及基本计算结果写成表格形式 因子水平试验数据和 和的平方平方和A 1 Y 11 Y 12 … Y 1m T 1 21T∑21jY A 2 Y 21 Y 22 … Y 2m T 2 22T∑22jY┆ ┆ ┆ ┆ ┆ ┆ ┆┆A rY r 1Y r 2…Y rmT r2r T ∑2rjYΣ T∑=ri i T 12∑∑==ri mj ijY112二．组内偏差与组间偏差数据Y ij 与样本总均值Y 之差Y Y ij −称为样本总偏差，可以分成两部分之和：)()(Y Y Y Y Y Y i i ij ij −+−=−⋅⋅，其中⋅⋅⋅−=+−+=−i ij i i ij i i ij Y Y εεεµεµ)()(是第i 个总体内数据与该总体内样本均值的偏差，称为组内偏差，反映第i 个总体内的随机误差；εεεµεµ−+=+−+=−⋅⋅⋅i i i i i a Y Y )()(是第i 个总体内样本均值与总样本均值的偏差，称为组间偏差，反映第i 个总体的主效应． 三．偏差平方和及其自由度在统计学中，对于k 个独立数据Y 1 , Y 2 , …, Y k ，平均值∑==ki i Y k Y 11，称Y i 与Y 之差为偏差，所有偏差的平方和∑=−=ki i Y Y Q 12)(称为这k 个数据的偏差平方和，反映这k 个数据的分散程度．由于所有偏差之和0)(11=−=−∑∑==Y k Y Y Y ki i k i i ， 即这k 个偏差由k 个独立数据受到一个约束条件形成，可以证明它们与k − 1个独立（随机）变量可以相互线性表示，称之为等价于k − 1个独立（随机）变量．一般地，若k 个独立数据受到r 个不相关的约束条件，则它们等价于k − r 个独立（随机）变量．在统计学中，把形成平方和的变量所等价的独立变量个数，称为该平方和的自由度，通常记为f ．如上述偏差平方和Q 的自由度为k − 1，即f Q = k − 1．由于平方和的大小与变量个数（或自由度）有关，为了对偏差进行比较，通常考虑偏差平方和与其自由度之商，称为均方和，记为MS ，反映一组数据的平均分散程度，如样本方差∑=−−=ni i X X n S 122)(11就是样本数据偏差的均方和． 四．总平方和分解公式总偏差平方和记为S T 或SST ，其自由度记为f T ，有∑∑==−=r i mj ij T Y Y S 112)(，f T = rm − 1 = n − 1；组内偏差平方和记为S e 或SSE ，其自由度记为f e ，有∑∑==⋅−=r i mj i ij e Y Y S 112)(，f e = r (m − 1) = n − r ；组间偏差平方和记为S A 或SSA ，其自由度记为f A ，有∑∑∑=⋅==⋅−=−=ri i r i m j i A Y Y m Y Y S 12112()(，f A = r − 1．组内偏差平方和反映所有总体内的随机误差，组间偏差平方和反映所有总体的主效应．定理 总偏差平方和S T 可以分解为组内偏差平方和S e 与组间偏差平方和S A 之和，其自由度也可作相应的分解，即S T = S e + S A ，f T = f e + f A ，称之为平方和分解公式． 证：∑∑∑∑==⋅⋅==−+−=−=ri mj i i ij ri mj ij T Y Y Y Y Y Y S 112112()[()(∑∑∑∑∑∑==⋅⋅==⋅==⋅−−+−+−=ri mj i i ij ri mj i ri mj i ij Y Y Y Y Y Y Y Y 11112112))((2)()(A e A e ri i A e ri mj i ij i A e S S S S Y Y S S Y Y Y Y S S +=++=×−++=−−++=∑∑∑=⋅==⋅⋅0]0[(2])()[(2111，且显然有f T = n − 1 = (n − r ) + (r − 1) = f e + f A ． 8.1.4检验方法由于组内偏差平方和反映所有总体内的随机误差，组间偏差平方和反映所有总体的主效应，通过比较组内偏差平方和与组间偏差平方和检验因子的显著性．下面将证明在假设所有主效应都等于0成立的条件下，它们的均方和之商服从F 分布．定理 在单因子方差分析模型中，组内偏差平方和S e 与组间偏差平方和S A 满足（1）E(S e ) = (n − r )σ 2，且)(~22r n Se −χσ； （2）∑=+−=ri i A a m r S 122)1()E(σ，且当H 0：a 1 = a 2 = … = a r = 0成立时，)1(~22−r S Aχσ；（3）S e 与S A 相互独立． 证：根据第五章的定理结论知：设X 1 , X 2 , …, X n 相互独立且都服从正态分布N (µ , σ 2)，记∑==ni i X n X 11，∑=−=ni i X X S 120)(，则X 与S 0相互独立，且)1(~22−n S χσ．（1）∑∑==⋅−=ri mj i ij e Y Y S 112)(，Y i 1 , Y i 2 , …, Y im 相互独立且都服从正态分布N(µ i , σ 2)，∑=⋅=mi ij i Y m Y 11，则∑=⋅−mj i ij Y Y 12)(与⋅i Y 相互独立，且)1(~)(12122−−∑=⋅m Y Y mj i ijχσ，因在不同水平下的样本都相互独立，则∑∑==⋅−ri mj i ij Y Y 112)(与⋅⋅⋅r Y Y Y ,,,21L 也相互独立，且根据独立χ 2变量的可加性知)(~)(121122r rm Y Y r i mj i ij−−∑∑==⋅χσ，故)(~)(1211222r n Y Y S r i mj i ije−−=∑∑==⋅χσσ，即得E(S e ) = (n − r )σ 2；（2）∑∑∑∑∑=⋅=⋅==⋅=⋅−+−+=−+=−=ri i i r i i r i ir i i i r i i A a m m a m a m Y Y m S 112121212(2)()()(εεεεεε，因ε ij (i = 1, 2, …, r , j = 1, 2, …, m ) 相互独立且都服从正态分布N (0, σ 2 )，有∑=⋅=m j ij i m 11εε (i = 1, 2, …, r ) 相互独立且都服从正态分布,0(2m N σ，∑=⋅=ri i r 11εε，则0)E()E()E(=−=−⋅⋅εεεεi i 且)1(~)(2212−−∑=⋅r mri i χσεε，即m r r i i 212)1()(E σεε−=⎥⎦⎤⎢⎣⎡−∑=⋅， 故21211212)1()E(2)(E )E(σεεεε−+=−+⎥⎦⎤⎢⎣⎡−+=∑∑∑∑==⋅=⋅=r a m a m m a m S ri i r i i i r i i ri iA ，当H 0：a 1 = a 2 = … = a r = 0成立时，∑∑=⋅=⋅−=−=ri i r i i A m Y Y m S 1212)()(εε，故)1(~)(22122−−=∑=⋅r mS ri i Aχσεεσ；（3）因∑∑==⋅−=ri mj i ij e Y Y S 112)(与⋅⋅⋅r Y Y Y ,,,21L 相互独立，有S e 与∑=⋅=ri i Y r Y 11相互独立，且∑=⋅−=ri i A Y Y m S 12(，故S e 与S A 相互独立．由于)(~22r n S e −χσ，当H 0：a 1 = a 2 = … = a r = 0成立时，)1(~22−r S A χσ，且S e 与S A 相互独立，则根据F 分布的定义可知：当H 0成立时，有),1(~)()1(22r n r F MS MS f S f S r n S r S F eAe e A A eA−−==−−=σσ．由于∑=+−=ri i A a m r S 122)1()E(σ，则F 越大，即S A 越大时，越有可能发生a i ≠ 0，则检验的拒绝域为右侧．步骤：假设H 0：a 1 = a 2 = … = a r = 0 vs H 1：a 1 , a 2 , …, a r 不全等于0，统计量),1(~r n r F MS MS f S f S F eAe e A A −−==， 显著水平α ，右侧拒绝域W = {f ≥ f 1 − α (r − 1, n − r )}，计算f ，并作出判断． 这是F 检验法．通常列成方差分析表： 来源 平方和 自由度 均方和 F 比 因子 S A f A = r − 1 MS A = S A / f A F = MS A / MS e误差 S e f e = n − r MS e = S e / f A总和S Tf T = n − 1为了计算方便，可给出三个偏差平方和的计算公式．对于一组数据X 1 , X 2 , …, X n ，记∑==ni i X n X 11，则有2112212121)(⎟⎟⎠⎞⎜⎜⎝⎛−=−=−∑∑∑∑====n i i ni i n i i n i i X n X X n X X X ， 记∑==m j ij i Y T 1，∑∑∑=====r i mj ij r i i Y T T 111，可得2112211112211211211)(T n Y Y n Y Y n Y Y Y S r i mj ij r i m j ij ri mj ij ri mj ij ri mj ij T −=⎟⎟⎠⎞⎜⎜⎝⎛−=−=−=∑∑∑∑∑∑∑∑∑∑==========， 212211121212121111)(T n T m Y n mr Y m m Y r Y m Y Y m S r i i r i m j ij r i m j ij r i i ri i A −=⎟⎟⎠⎞⎜⎜⎝⎛−⎟⎟⎠⎞⎜⎜⎝⎛=⎥⎦⎤⎢⎣⎡−=−=∑∑∑∑∑∑∑======⋅=⋅， ∑∑∑===−=−=r i i r i mj ijA T e T m Y S S S 121121．例 在饲料养鸡增肥的研究中，现有三种饲料配方：A 1 , A 2 , A 3 ，为比较三种饲料的效果，特选24只相似的雏鸡随机均分为三组，每组各喂一种饲料，60天后观察它们的重量．实验结果如下表所示： 饲料鸡重/gA 1 1073 1009 1060 1001 1002 1012 1009 1028 A 2 1107 1092 990 1109 1090 1074 1122 1001 A 3 1093 1029 1080 1021 1022 1032 1029 1048 在显著水平α = 0.05下检验这三种饲料对雏鸡增重是否有显著差别． 解：假设H 0：a 1 = a 2 = a 3 = 0 vs H 1：a 1 , a 2 , a 3不全等于0，统计量),1(~r n r F MS MS f S f S F eAe e A A −−==，平方和显著水平α = 0.05，n = 24，r = 3，m = 8，右侧拒绝域W = { f ≥ f 0.95 (2, 21)} = { f ≥ 3.47}，试验数据计算表 因子水平试验数据Y ijT i2i T∑=mj ijY 12A 1 1073 1009 1060 1001 10021012100910288194 67141636 8398024 A 2 1107 1092 990 1109 10901074112210018585 73702225 9230355 A 31093 1029 1080 1021 10221032102910488354 69789316 8728984总和 25133 210633177 26357363计算可得0833.96602513324121063317781112212=×−×=−=∑=T n T m S r i i A ，875.282152106331778126357363112112=×−=−=∑∑∑===r i i r i mj ije T m Y S ，方差分析表来源平方和自由度均方和F 比因子 9660.0833 2 4830.0417 3.5948 误差 28215.875 21 1343.6131 总和 37875.958323有F 比f = 3.5948 ∈ W ，故拒绝H 0 ，接受H 1 ，可以认为这三种饲料对雏鸡增重有显著差别， 并且检验的p 值p = P {F ≥ 3.5948} = 1 − 0.9546 = 0.0454 < α = 0.05． 8.1.5参数估计在方差分析问题中，可对总均值µ ，误差的方差σ 2作参数估计．当检验结果为因子不显著时，各水平下指标的总体均值与总体方差都相同，可将所有水平的指标看作一个统一的总体，全部试验数据是来自正态总体Y ~ N (µ , σ 2 ) 的一个容量为n = rm 的样本，因此样本均值nT Y n Y r i m j ij ==∑∑==111，样本方差1)(111122−=−−=∑∑==n S Y Y n S T r i m j ij．这样总均值µ 和误差的方差σ 2的点估计分别为Y =µˆ，22S =∧σ，置信度为1 − α 的置信区间分别是 ])1([2/1nSn t Y −±∈−αµ，])1()1(,)1()1([22/222/122−−−−∈−n S n n S n ααχχσ．当检验结果为因子显著时，还可进一步对主效应a i 作参数估计． 一．点估计由于试验数据Y ij , (i = 1, 2, …, r , j = 1, 2, …, m ) 相互独立且都服从正态分布N (µ + a i , σ 2 )，根据最大似然估计法，得到总均值µ ，误差的方差σ 2及主效应a i 的点估计．似然函数∏∏∏∏====⎪⎭⎪⎫⎪⎩⎪⎨⎧−−−==r i mj i ij r i m j ij r a y y p a a a L 11222112212)(exp π21)(),,,,,(σµσσµL ⎭⎬⎫⎩⎨⎧−−−=∑∑==ri mj iij na y 112222)(21exp )π2(1µσσ， 取对数，得∑∑==−−−−−=r i mj i ija yn n L 11222)(21)ln(2π)2ln(2ln µσσ．令关于µ 的偏导数等于0，有⎟⎟⎠⎞⎜⎜⎝⎛−−=−⋅−−−=∂∂∑∑∑∑∑=====r i i r i mj ijri mj i ij a m n y a y L 11121121)1()(221ln µσµσµ0101112112=⎟⎟⎠⎞⎜⎜⎝⎛−=⎟⎟⎠⎞⎜⎜⎝⎛−−=∑∑∑∑====µσµσn y n y r i m j ij r i mj ij ， 得y y n r i mj ij ==∑∑==111µ，故总均值µ 的最大似然估计为Y =µˆ． 令关于a k 的偏导数等于0，有01)1()(221ln 1212=⎟⎟⎠⎞⎜⎜⎝⎛−−=−⋅−−−=∂∂∑∑==k mj kj mj k kj k ma m y a y a L µσµσ， k = 1, 2, …, r ， 得µµ−=−=⋅=∑k mj kj k y y m a 11，故主效应a i 的最大似然估计为Y Y Y a i i i −=−=⋅⋅µˆˆ， i = 1, 2, …, r ，相应，第i 个水平下的总体均值µ i 的最大似然估计为⋅=+=i i i Y a ˆˆˆµµ． 令关于σ 2的偏导数等于0，有0)(2112)(ln 112422=−−+⋅−=∂∂∑∑==r i mj i ija yn L µσσσ，得∑∑==−−=r i m j i ij a y n 1122)(1µσ，故误差的方差σ 2的最大似然估计为nS Y Y n e r i m j i ij M =−=∑∑==⋅∧1122)(1σ．由于E(S e ) = (n − r )σ 2，可知∧2Mσ不是σ 2的无偏估计，修偏得σ 2的无偏估计e eMS rn S =−=∧2σ． 二．置信区间对总均值µ ，误差的方差σ 2及第i 个水平下的总体均值µ i 给出置信区间．第i 个水平下总体均值µ i 的点估计为∑=⋅==mj ij i i Y m Y 11ˆµ，因试验数据Y ij , (i = 1, 2, …, r , j = 1, 2, …, m )相互独立且都服从正态分布N(µ i , σ 2)，则有),(~2mN Y i i σµ⋅，即)1,0(~N mY ii σµ−⋅，但σ 未知，用r n S e −=σˆ替换．由于)(~22r n S e −χσ且S e 与⋅i Y 相互独立，则根据χ 2分布的定义可得 )(~ˆ)(2r n t mY r n S m Y i i eii −−=−−⋅⋅σµσσµ，故第i 个水平下总体均值µ i 的置信度为1 − α 的置信区间是]ˆ)([2/1mr n t Y i i σµα−±∈−⋅．总均值µ 的点估计为∑∑====r i mj ij Y n Y 111ˆµ，因数据Y ij , (i = 1, 2, …, r , j = 1, 2, …, m ) 相互独立且都服从正态分布N (µ i , σ 2 )，有Y 服从正态分布，且µµµ====∑∑∑∑∑=====r i i r i mj i r i m j ij n m n Y n Y 111111)E(1)E(，n n n n Y nY ri mj r i mj ij 222112211211)Var(1)Var(σσσ=⋅===∑∑∑∑====， 得,(~2nN Y σµ，即)1,0(~N nY σµ−，但σ 未知，用r n S e −=σˆ替换．由于)(~22r n S e −χσ且S e 与Y 相互独立，则根据t 分布的定义可得 )(~ˆ)(2r n t nY r n S n Y e−−=−−σµσσµ， 故总均值µ 的置信度为1 − α 的置信区间是ˆ)([2/1nr n t Y σµα−±∈−．误差的方差σ 2的点估计为r n S e −=∧2σ，且)(~22r n Se −χσ，故误差的方差σ 2的置信度为1 − α 的置信区间是⎥⎦⎤⎢⎢⎢⎣⎡−−−−=⎥⎦⎤⎢⎣⎡−−∈∧−∧−)()(,)()()(,)(22/222/1222/22/12r n r n r n r n r n S r n S e e ααααχσχσχχσ． 例 由前面的鸡饲料对鸡增重问题的数据给出总均值µ ，误差的方差σ 2及三个水平下总体均值µ1 , µ 2 , µ 3的点估计和置信区间（α = 0.05）．解：前面已检验知因子显著，则三个水平下总体均值µ1 , µ 2 , µ 3的点估计为25.102488194ˆ111====⋅m T Y µ， 125.107388585ˆ222====⋅m T Y µ，25.104488354ˆ333====⋅m T Y µ，总均值µ 的点估计为2083.10472425133ˆ====n T Y µ，误差的方差σ 2的点估计为6131.13432==−=∧e eMS rn S σ， 置信度为0.95的置信区间是]2008.1051,2992.997[86131.13430796.225.1024[]ˆ)21([975.011=×±=±∈⋅m t Y σµ，]0758.1100,1742.1046[86131.13430796.2125.1073[]ˆ)21([975.022=×±=±∈⋅m t Y σµ，]2008.1071,2992.1017[]86131.13430796.225.1044[]ˆ)21([975.033=×±=±∈⋅mt Y σµ，]7684.1062,6482.1031[]246131.13430796.22083.1047[]ˆ)21([975.0=×±=±∈nt Y σµ，[]9608.2743,2861.7952829.10875.28215,4789.35875.28215)21(,)21(2025.02975.02=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∈χχσe e S S ． 8.1.6重复数不等的情形如果每个水平下试验次数不全相等，称为重复数不等的情形，其检验方法与在重复数相等的情形下类似，只是在对数据的表述和处理上有几点区别． 一．数据设第i 个水平A i 下的重复数为m i ，所取得的样本为i im i i Y Y Y ,,,21L ，i = 1, 2, …, r ．显然重复数总数为n ，即m 1 + m 2 + … + m r = n ． 二．总均值总均值µ 是各水平下总体均值µ i 的以频率nm i为权数的加权平均，即 ∑==+++=r i i i r r m n n m n m n m 122111µµµµµL ．三．主效应约束条件第i 个水平下主效应a i = µ i − µ ，则满足011=−=∑∑==µµn m a m ri iir i ii ．四．模型单因子方差分析在重复数不等的情形下，统计模型为⎪⎪⎩⎪⎪⎨⎧===++=∑=).,0(;0;,,2,1,,,2,1,21σεεµN a m m j r i a Y ij r i i i i ij i ij 相互独立，且都服从L L 检验H 0：a 1 = a 2 = … = a r = 0 vs H 1：a 1 , a 2 , …, a r 不全等于0．五．平方和的计算记∑==im j ij i Y T 1，∑=⋅==im j ij i i i i Y m m T Y 11，∑∑∑=====ri i ri m j ij T Y T i111，∑∑∑=⋅=====ri i i r i m j ij Y m n Y n n T Y i 11111， 则各平方和的计算公式为n T Y Y n Y Y Y S ri m j ijri m j ijri m j ij T iii21122112112)(−=−=−=∑∑∑∑∑∑======， n T m T Y n Y m Y Y m Y Y S ri ii ri i i ri i i ri m j i A i21221212112)()(−=−=−=−=∑∑∑∑∑==⋅=⋅==⋅， ∑∑∑===−=−=ri ii ri m j ijA T e m T Y S S S i12112． 例 某食品公司对一种食品设计了四种新包装，为了考察哪种包装最受顾客欢迎，选了10个地段繁华程度相似、规模相近的商店做试验，其中两种包装各指定两个商店销售，另两种包装各指定三个商店销售．在试验期内各店货架排放的位置、空间都相同，营业员的促销方法也基本相同，经过一段时间，记录其销售量数据，见下表包装类型销售量数据A 1 12 18 A 2 14 12 13 A 3 19 17 21 A 4 24 30在显著水平α = 0.01下检验这四种包装对销售量是否有显著影响． 解：假设H 0：a 1 = a 2 = a 3 = a 4 = 0 vs H 1：a 1 , a 2 , a 3 , a 4不全等于0，统计量),1(~r n r F MS MS f S f S F eAe e A A −−==，显著水平α = 0.01，n = 10，r = 4，右侧拒绝域W = { f ≥ f 0.99 (3, 6)} = { f ≥ 9.78}，销售量数据计算表计算可得258180101349812212=×−=−=∑=T n m T S ri ii A ，463498354412112=−=−=∑∑∑===ri i i ri mj ije m T Y S ，方差分析表来源平方和自由度均方和F 比因子 258 3 86 11.2174 误差 46 6 7.6667 总和 3049有F 比f = 11.2174 ∈ W ，故拒绝H 0 ，接受H 1 ，可以认为这四种包装对销售量有显著影响， 并且检验的p 值p = P {F ≥ 11.2174} = 1 − 0.9929 = 0.0071 < α = 0.01． 由于因子显著，则四个水平下总体均值µ1 , µ 2 , µ 3 , µ 4的点估计为15230ˆ1111====⋅m T Y µ， 13339ˆ2222====⋅m T Y µ， 19357ˆ3333====⋅m T Y µ， 27254ˆ4444====⋅m T Y µ， 总均值µ 的点估计为1810180ˆ====n T Y µ， 误差的方差σ 2的点估计为6667.72==−=∧e eMS rn S σ， 置信度为0.99的置信区间是]2587.22,7413.7[]26667.77074.315[]ˆ)6([1995.011=×±=±∈⋅m t Y σµ，]9267.18,0733.7[]36667.77074.313[]ˆ)6([2995.022=×±=±∈⋅m t Y σµ，]9267.24,0733.13[]36667.77074.319[]ˆ)6([3995.033=×±=±∈⋅m t Y σµ，]2587.34,7413.19[]26667.77074.327[]ˆ)6([4995.044=×±=±∈⋅m t Y σµ，]2462.21,7538.14[106667.77074.318[]ˆ)6([995.0=×±=±∈nt Y σµ，[]0775.68,4801.26757.046,5476.1846)6(,)6(2005.02995.02=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡∈χχσeeS S ．§8.2 多重比较上一节是将多个总体作为一个整体进行检验．如果检验结果是因子A 显著，则可以认为各水平下的均值µ i 不全相等，但却不能直接说明µ i 中哪些可以认为相等，哪些可以认为不等．这一节是对各个µ i 两两之间进行比较，对µ i − µ j ，也就是效应差a i − a j 作出估计、检验． 8.2.1效应差的置信区间效应差a i − a j = µ i − µ j 的点估计为⋅⋅−j i Y Y ．因Y ik ~ N (µ i , σ 2 ), (i = 1, 2, …, r , k = 1, 2, …, m i )，则),(~121i i m k ik i i m N Y m Y iσµ∑=⋅=，,(~121jj m k jkj j m N Ym Y jσµ∑=⋅=，且当i ≠ j 时，⋅i Y 与⋅j Y 相互独立，可得))11(,(~2σµµji j i j i m m N Y Y +−−⋅⋅， 即)1,0(~11)()(N m m Y Y ji j i j i +−−−⋅⋅σµµ，但σ 未知，用r n S e −=σˆ替换．由于)(~22r n S e −χσ且S e 与⋅⋅j i Y Y ,相互独立，则根据t 分布的定义可得 )(~11ˆ)()()(11)()(2r n t m m Y Y r n S m m Y Y ji j i j i ej i j i j i −+−−−=−+−−−⋅⋅⋅⋅σµµσσµµ，故效应差a i − a j = µ i − µ j 的置信度为1 − α 的置信区间是]11ˆ)([2/1ji j i j i m m r n t Y Y +⋅−±−∈−−⋅⋅σµµα． 例 由前面的鸡饲料对鸡增重问题的数据给出各效应差µ i − µ j 的点估计和置信区间（α = 0.05）． 解：因m 1 = m 2 = m 3 = 8，n = 24，r = 3，有25.102488194111===⋅m T Y ，125.107388585222===⋅m T Y ，25.104488354333===⋅m T Y ， 则各效应差µ i − µ j 的点估计分别为875.48125.107325.10242121−=−=−=−⋅⋅∧Y Y µµ， 2025.104425.10243131−=−=−=−⋅⋅∧Y Y µµ， 875.2825.1044125.10733232=−=−=−⋅⋅∧Y Y µµ；因6553.3621875.28215ˆ==−=r n S e σ，有1142.385.06553.360796.211ˆ)21(975.0=××=+⋅j i m m t σ，则各效应差µ i − µ j 的置信度为0.95的置信区间分别是]7608.10,9892.86[]1142.38875.48[]8181ˆ)21([975.02121−−=±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]1142.18,1142.58[]1142.3820[]8181ˆ)21([975.03131−=±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]9892.66,2392.9[]1142.38875.28[]8181ˆ)21([975.03232−=±=+⋅±−∈−⋅⋅σµµt Y Y ． 例 由前面的食品包装对销售量影响问题的数据给出各效应差µ i − µ j 的点估计和置信区间（α = 0.01）． 解：因m 1 = 2，m 2 = 3，m 3 = 3，m 4 = 2，n = 10，r = 4，有15230111===⋅m T Y ，13339222===⋅m T Y ，19357333===⋅m T Y ，27254444===⋅m T Y ， 则各效应差µ i − µ j 的点估计分别为213152121=−=−=−⋅⋅∧Y Y µµ，419153131−=−=−=−⋅⋅∧Y Y µµ， 1227154141−=−=−=−⋅⋅∧Y Y µµ，619133232−=−=−=−⋅⋅∧Y Y µµ， 1427134242−=−=−=−⋅⋅∧Y Y µµ，827194343−=−=−=−⋅⋅∧Y Y µµ；因7689.2646ˆ==−=r n S e σ，有2653.107689.27074.3ˆ)6(995.0=×=⋅σt ，则各效应差µ i − µ j 的置信度为0.99的置信区间分别是]3709.11,3709.7[]9129.02653.102[]3121ˆ)6([995.02121−=×±=+⋅±−∈−⋅⋅σµµt Y Y ， ]3709.5,3709.13[]9129.02653.104[]3121ˆ)6([995.03131−=×±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]7347.1,2653.22[]12653.1012[]2121ˆ)6([995.04141−−=×±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]3816.2,3816.14[]8165.02653.106[]3131ˆ)6([995.03232−=×±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]6291.4,3709.23[]9129.02653.1014[]2131ˆ)6([995.04242−−=×±−=+⋅±−∈−⋅⋅σµµt Y Y ， ]3709.1,3709.17[]9129.02653.108[]2131ˆ)6([995.04343−=×±−=+⋅±−∈−⋅⋅σµµt Y Y ．8.2.2 多重比较问题对各个µ i 两两之间进行比较，也就是检验任意两个水平A i 与A j 下的总体均值是否相等，即检验假设j i ij H µµ=:0 vs j i ij H µµ≠:1， i , j = 1, 2, …, r ．对于每一个假设ijH 0可以采取上一章两个正态总体的均值比较方法进行检验，但这里需要同时检验2)1(2−=r r C r 个这种假设． 设需要同时检验k 个假设k i H i ,,2,1,0L =，每一个假设的显著水平是α ，即在iH 0成立的条件下，接受i H 0的概率为1 − α ，但在所有k 个假设i H 0都成立的条件下，要同时接受所有假设iH 0的概率就可能远小于1 − α ．事实上，此时对每一个假设i H 0，拒绝i H 0的概率为α ，而对所有k 个假设k i H i ,,2,1,0L =，至少拒绝其中一个i H 0的概率最大时可能达到k α ，即同时接受所有假设i H 0的概率就可能只有1 − k α ．可见，需要同时检验多个假设时，一般不应逐个检验每一个假设，而是采用多重比较方法同时检验多个假设．多重比较方法，就是针对所有假设，构造一个统一的拒绝域，再逐个进行比较．这里，需要检验假设j i ijH µµ=:0 vs j i ij H µµ≠:1， 1≤ i < j ≤ r ， 在ij H 0成立的条件下，⋅i Y 与⋅j Y 不应相差太大．对每一个假设ijH 0，拒绝域可以取为}|{|ij j i ij c Y Y W ≥−=⋅⋅，其中c ij 是常数．对所有的假设ijH 0，统一的拒绝域取为U U rj i ij j i rj i ijc Y YWW ≤<≤⋅⋅≤<≤≥−==11}|{|．分成重复数相等与不等两种场合进行讨论． 8.2.3重复数相等场合的T 法重复数相等时，各水平是平等的，由对称性，可以要求所有的c ij 相等，记为c ，即统一的拒绝域为}min max {}||max {}|{|1111c Y Y c Y Y c Y YW i ri i ri j i rj i rj i j i ≥−=≥−=≥−=⋅≤≤⋅≤≤⋅⋅≤<≤≤<≤⋅⋅U ．因Y ij , (i = 1, 2, …, r , j = 1, 2, …, m ) 相互独立且都服从正态分布N (µ i , σ 2)，有,(~2mN Y i i σµ⋅．当所有的假设ijH 0都成立时，即µ 1 = µ 2 = … = µ r = µ ，有,(~2mN Y i σµ⋅，则)1,0(~N mY i σµ−⋅．但σ 未知，用r n S e−=σˆ替换．由于)(~22r n S e −χσ且S e 与⋅i Y 相互独立，则根据t 分布的定义可得 )()(~ˆ)(2e i ei f t r n t mY r n S m Y =−−=−−⋅⋅σµσσµ．统一的拒绝域W 的形式可改写为⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≥−−−=≥−=⋅≤≤⋅≤≤⋅≤≤⋅≤≤m c m Y m Y c Y Y W i r i i r i i r i i r i σσµσµˆˆmin ˆmax }min max {1111， 其中mY Y mY mY Q i ri i ri i ri i ri σσµσµˆmin max ˆminˆmax1111⋅≤≤⋅≤≤⋅≤≤⋅≤≤−=−−−=是从分布为t ( f e )的总体中抽取容量为r 的样本所得的最大与最小顺序统计量之差（极差），称之为t 化极差统计量，其分布记为q (r , f e )．显然，t 化极差统计量Q 的分布q (r , f e ) 只与水平个数r 以及t 分布的自由度f e 有关，而与参数µ , σ 2及重复数m 无关．分布q (r , f e )的准确形式比较复杂，通常采用随机模拟方法得到其分位数q 1 − α (r , f e )．对于给定的容量r 及自由度f e ，随机模拟方法是（1）随机生成r 个标准正态分布N (0, 1) 随机数x 1 , x 2 , …, x r ，将这r 个随机数按由小到大的顺序排列，得到其最小随机数x (1) 和最大随机数x (r ) ；（2）随机生成1个自由度为f e 的χ 2分布χ 2 ( f e ) 随机数y ； （3）计算er f y x x q )1()(−=；（4）重复（1）至（3）步N 次，得到t 化极差统计量Q 的N 个观测值，只要N 非常大（如10 4或10 5次），就可得q (r , f e )的各种分位数q 1 − α (r , f e )的近似值．当显著水平为α 时，拒绝域{}),(ˆ1ef r q Q m c Q W ασ−≥=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≥=，有m c f r q e σαˆ),(1=−，可得 mf r q c e σαˆ),(1⋅=−，再逐个将||⋅⋅−j i Y Y 与c 比较，得出每一对µ i 与µ j 是否有显著差异的结论．步骤：假设j i ijH µµ=:0 vs j i ij H µµ≠:1， 1≤ i < j ≤ r ， 统计量mY Y mY mY Q i ri i ri i ri i ri σσµσµˆmin max ˆminˆmax1111⋅≤≤⋅≤≤⋅≤≤⋅≤≤−=−−−=，显著水平α ，右侧拒绝域{}),(ˆ1e f r q Q m c Q W ασ−≥=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧≥=，计算mf r q c e σαˆ),(1⋅=−，逐个将||⋅⋅−j i Y Y 与c 比较，得出结论．例 由前面的鸡饲料对鸡增重影响问题的数据对各因子作多重比较（α = 0.05）．解：假设j i ijH µµ=:0 vs j i ij H µµ≠:1， 1≤ i < j ≤ 3， 统计量mY Y mY mY Q i ri i ri i ri i ri σσµσµˆmin max ˆminˆmax1111⋅≤≤⋅≤≤⋅≤≤⋅≤≤−=−−−=，显著水平α = 0.05，r = 3，f e = n − r = 21，右侧拒绝域W = {Q ≥ q 0.95 (3, 21)} = {Q ≥ 3.57}，因m = 8，6553.3621875.28215ˆ==−=r n S e σ，有2658.4686553.3657.3=×=c ， 由于c Y Y >=−=−⋅⋅875.48|125.107325.1024|||21，故µ 1与µ 2有显著差异；c Y Y <=−=−⋅⋅20|25.104425.1024|||31，故µ 1与µ 3没有显著差异； c Y Y <=−=−⋅⋅875.28|25.1044125.1073|||32，故µ 2与µ 3没有显著差异；8.2.4重复数不等场合的S 法重复数不等时，因)1,0(~11)()(N m m Y Y ji j i j i +−−−⋅⋅σµµ，但σ 未知，用r n S e−=σˆ替换．由于)(~22r n S e −χσ且S e 与⋅⋅j i Y Y ,相互独立，则根据t 分布的定义可得 )()(~11ˆ)()(e ji j i j i f t r n t m m Y Y =−+−−−⋅⋅σµµ，当所有的假设ijH 0都成立时，即µ 1 = µ 2 = … = µ r = µ ，有)(~11ˆe ji j i ij f t m m Y Y T +−=⋅⋅σ，得),1(~11ˆ)(222e j i j i ijij f F m m Y Y T F ⎟⎟⎠⎞⎜⎜⎝⎛+−==⋅⋅σ，从而统一的拒绝域可以取为U U r j i ji j i r j i ji j i c m m Y Y m m c Y Y W ≤<≤⋅⋅≤<≤⋅⋅≥+−=+≥−=11}11||{}11|{| }ˆmax {}ˆ11ˆ)(max {}ˆ11ˆ||max {221222211σσσσσc F c m m Y Y cm m Y Y ij r j i j i j i r j i ji j i r j i ≥=≥⎟⎟⎠⎞⎜⎜⎝⎛+−=≥+−=≤<≤⋅⋅≤<≤⋅⋅≤<≤，可以证明，),1(~1max 1e ij rj i f r F r F −−≤<≤&．当显著水平为α 时，拒绝域{}),1(ˆ)1(122e f r f F r c F W −≥=⎭⎬⎫⎩⎨⎧−≥=−ασ，有221ˆ)1(),1(σα−=−−r c f r f e ，可得),1()1(ˆ1e f r f r c −−=−ασ，因此⎟⎟⎠⎞⎜⎜⎝⎛+−−=+=−j i e ji ij m m f r f r m m c c 11),1()1(ˆ111ασ， 再逐个将||⋅⋅−j i Y Y 与ji ij m m cc 11+=比较，得出每一对µ i 与µ j 是否有显著差异的结论． 步骤：假设j i ijH µµ=:0 vs j i ij H µµ≠:1， 1≤ i < j ≤ r ， 统计量),1(~11ˆ)1()(max1max 2211e j i j i rj i ijrj i f r F m m r Y Y r F F −⎟⎟⎠⎞⎜⎜⎝⎛+−−=−=⋅⋅≤<≤≤<≤&σ，显著水平α ，右侧拒绝域{}),1(ˆ)1(122e f r f F r c F W −≥=⎭⎬⎫⎩⎨⎧−≥=−ασ， 计算⎟⎟⎠⎞⎜⎜⎝⎛+−−=+=−j i e ji ij m m f r f r m m cc 11),1()1(ˆ111ασ， 逐个将||⋅⋅−j i Y Y 与c ij 比较，得出结论．例 由前面的食品包装对销售量影响问题的数据对各因子作多重比较（α = 0.01）． 解：假设j i ijH µµ=:0 vs j i ij H µµ≠:1， 1≤ i < j ≤ 4， 统计量),1(~11ˆ)1()(max)1(max 224141e j i j i j i ij j i f r F m m r Y Y r F F −⎟⎟⎠⎞⎜⎜⎝⎛+−−=−=⋅⋅≤<≤≤<≤&σ，显著水平α = 0.01，r = 4，f e = n − r = 6，右侧拒绝域W = {F ≥ f 0.99 (3, 6)} = {F ≥ 9.78}，因m 1 = m 4 = 2，m 2 = m 3 = 3，7689.2646ˆ==−=r n S e σ，有9981.1478.937689.2=××=c ， 则6914.13312134241312=+====cc c c c ，9981.14212114=+=c c ，2459.12313123=+=c c ， 由于12212|1315|||c Y Y <=−=−⋅⋅，故µ 1与µ 2没有显著差异；13314|1915|||c Y Y <=−=−⋅⋅，故µ 1与µ 3没有显著差异； 144112|2715|||c Y Y <=−=−⋅⋅，故µ 1与µ 4没有显著差异； 23326|1913|||c Y Y <=−=−⋅⋅，故µ 2与µ 3没有显著差异； 244214|2713|||c Y Y >=−=−⋅⋅，故µ 2与µ 4有显著差异； 34438|2719|||c Y Y <=−=−⋅⋅，故µ 3与µ 4没有显著差异．§8.3 方差齐性检验在单因子方差分析统计模型中，总是假设各个水平下的总体方差都相等，即222221σσσσ====r L ，称之为方差齐性．但方差齐性不一定自然成立，需要对其进行检验，检验的原假设与备择假设为H 0：22221r σσσ===L vs H 1：22221,,,r σσσL 不全相等，称为方差齐性检验．各水平下的总体方差2i σ分别是以该水平下的样本方差2i S 作为点估计，以由22221,,,r S S S L 构成的函数作为检验的统计量．分成重复数相等与不等两种场合进行讨论． 8.3.1重复数相等场合的Hartley 检验法重复数相等时，样本方差⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−−=−−=∑∑∑=⋅==⋅m T Y m Y m Y m Y Y m S i m j ij i m j ij m j i ij i2122121221111)(11，i = 1, 2, …, r ， 各水平是平等的，以r 个水平下样本方差),,2,1(,2r i S i L =的最大值与最小值之比作为检验的统计量H ，即},,,min{},,,max{2222122221r r S S S S S S H L L =．在方差齐性成立的条件下，统计量H 的分布只与水平个数r 及样本方差2i S 的自由度f = m − 1有关，记为H (r , f )．分布H (r , f )的准确形式比较复杂，通常采用随机模拟方法得到其分位数H 1 − α (r , f )．显然有H ≥ 1，且H 的观测值越接近1，方差齐性越应该成立，因此拒绝域取为W = {H ≥ H 1 − α (r , f )}．步骤：假设H 0：22221r σσσ===L vs H 1：22221,,,r σσσL 不全相等，统计量},,,min{},,,max{2222122221rr S S S S S S H L L =，显著水平α ，右侧拒绝域W = {H ≥ H 1 − α (r , f )}， 计算H ，并作出判断． 这称之为Hartley 检验法．例 由前面的鸡饲料对鸡增重影响问题的数据采用Hartley 检验法进行方差齐性检验（α = 0.05）．解：假设H 0：232221σσσ== vs H 1：232221,,σσσ不全相等，统计量},,min{},,max{232221232221S S S S S S H =， 显著水平α = 0.05，且r = 3，f = m − 1，右侧拒绝域W = {H ≥ H 0.95 (3, 7)} = {H ≥ 6.94}，根据试验数据计算表，可得T 1 = 8194，T 2 = 8585，T 3 = 8354，8398024121=∑=mj j Y ，9230355122=∑=mj jY，8728984123=∑=mj j Y ，则9286.759)881948398024(71221=−=S ，9821.2510885859230355(71222=−=S ，9286.759)883548728984(71223=−=S ，可得W H ∉==3042.39286.7599821.2510，故拒绝H 0 ，接受H 1 ，可以认为三个水平下的总体方差满足方差齐性．8.3.2 重复数不等场合大样本情形的Bartlett 检验法重复数不等时，样本方差⎥⎦⎤⎢⎣⎡−−=⎥⎦⎤⎢⎣⎡−−=−−=∑∑∑=⋅==⋅i i m j ij i i i m j ij i m j i ij i im T Y m Y m Y m Y Y m S i i i 2122121221111)(11，i = 1, 2, …, r ， 记i i m j ijm j i ij i m T Y Y Y Q ii21212)(−=−=∑∑==⋅为第i 个水平下的偏差平方和，f i = m i − 1为其自由度，有i i i f Q S =2，且e r i m j i ijr i i S Y YQ i=−=∑∑∑==⋅=1121)(，e ri ir i i f r n r mf =−=−=∑∑==11，则组内偏差均方和∑∑∑=======ri i ei ri ii e ri ie e e e Sf f S f f Q f f S MS 1212111， 即MS e 等于样本方差22221,,,r S S S L 以各自自由度所占比例为权数的加权算术平均，而相应的加权几何平均记为GMS e ，即∏==ri f f i e eiS GMS 12)(．以MS e 与GMS e 之商的一个函数作为检验统计量．可以证明，大样本情形，在方差齐性成立的条件下，)1(~])ln()ln([1ln 212−−==∑=r S f MS f C GMS MS C f B ri i i e e e e e χ&，其中常数⎟⎟⎠⎞⎜⎜⎝⎛−−+=∑=e r i i f f r C 11)1(3111． 由于算术平均必大于等于几何平均，即MS e ≥ GMS e ，当且仅当所有2i S 都相等时等号成立，即B 的观测值越小，方差齐性越应该成立，因此拒绝域取为)}1({21−≥=−r B W αχ．。
方差分析线性回归
1线性回归要研究最大积雪深度X与灌溉面积y之间的关系，测试得到近10年的数据如下表：使用线性回归的方法可以估计x与y之间的线性关系。
线性回归方程式：对应的估计方程式为线性回归完成的任务是，依据观测数据集仗l,yl）,仗2,y2）,...,仗n,yn）使用线性拟合估计回归方程中的参数a和b。
a,b都为估计结果，原方程中的真实值一般用a 和P表示。
为什么要做这种拟合呢？答案是：为了预测。
比如根据前期的股票数据拟合得到股票的变化趋势C、勺然股票的变化可就不是这么简单的线性关系了）。
线性回归的拟合过程使用最小二乘法，最小二乘法的原理是：选择a,b的值，使得残差的平方和最小。
为什么是平方和最小，不是绝对值的和？答案是，绝对值也可以，但是，绝对值进行代数运算没有平方那样的方便，4次方乂显得太复杂，数学中这种“转化化归”的思路表现得是那么的优美！残差平方和Q ,求最小，方法有很多。
代数方法是求导，还有一些运筹学优化的方法（梯度下降、牛顿法），这里只需要使用求导就0K 了，为表示方便，引入一些符号，最终估计参数a与b的结果是：自此，针对前•面的例子，只要将观测数据带入上面表达式即可汁算得到拟合之后的d和b。
不妨试一试？从线性函数的角度，b表示的拟合直线的斜率，不考虑数学的严谨性，从应用的角度，结果的b可以看成是离散点的斜率，表示变化趋势，b的绝对值越大，表示数据的变化越快。
线性回归的估计方法存在误差，误差的大小通过Q衡量。
1 -2误差分析考虑获取观测数据的实验中存在其它的影响因素，将这些因素全部考虑到e~N(0QA2)中，回归方程重写为y = a + bx + e由此汁算估计量a与b的方差结果为，a与b的方差不仅与6和x的波动大小有关，而且还与观察数据的个数有关。
在设计观测实验时，x的取值越分散，佔汁ab的误差就越小，数据量越大，佔计量b的效果越好。
这也许能为设计实验搜集数据提供某些指导。
1.3拟合优度检验及统计量拟合优度检验模型对样本观测值的拟合程度，其方法是构造一个可以表征拟合程度的指标，称为统汁量，统讣量是样本的函数。
(完整版)数理统计课后习题答案—杨虎
习题一、基本概念1．解： 设12345,,,,X X X X X 为总体的样本1）51151~(1,) (,,)(1)i ix x i X B p f x x p p -==-∏555(1)11(1),5x x i i p p x x -==-=∑2）λλλλλ55155151!!),,( )(~-==-∏∏==e x ex x x f P X i ixi i xi3）5155111~(,) (,,),,1,...,5()i X U a b f x x a xi b i b a b a ===≤≤=--∏所以5151,,1,...,5()(,,)0,a xi b i b a f x x ⎧≤≤=⎪-=⎨⎪⎩其他 4）()⎪⎭⎫ ⎝⎛-==∑∏=-=-5122/55125121exp 221),,( )1,(~2i i i x x e x x f N X i ππμ 2.解： 由题意得：因为0110,(),1,n k k k x x k F x x x x n x x ++<⎧⎪⎪≤<⎨⎪≥⎪⎩，所以40,00.3,010.65,12()0.8,230.9,341,4x x x F x x x x <⎧⎪≤<⎪⎪≤<⎨≤<⎪⎪≤<⎪≥⎩3．解：它近似服从均值为172，方差为5.64的正态分布，即(172,5.64)N 4．解：()55-5 510/2- -⎪⎪⎭⎫ ⎝⎛<<-=⎪⎪⎭⎫ ⎝⎛<=<k X k P k X P k X P μμμ 因k 较大()()()()()()()-555(15)2510.950.95P X k k k k k k k μ<≈Φ-Φ-=Φ--Φ=Φ-=Φ=,5 1.65,0.33k k ==查表1 0.9 0.8 0.7 0.6 0.5 0.4 0.30.2 0.11 2 3 4 xy5．解：()-5250.853.8 1.1429 1.7143(1.7143)( 1.14296.3/6X P X P ⎛⎫<<=-<<=Φ-Φ- ⎪⎝⎭）0.9564(10.8729)0.8293=--=6．解：()()()~(20,0.3),~(20,0.2),~(0,0.5),0.3 0.30.3Y N Z N Y Z Y Z N P Y Z P Y Z P Y Z -->=->+-<-设与相互独立，0.42430.42431(0.4243)(1(0.4243))22(0.4243)P P ⎫⎫=>=+<-⎪⎪⎭⎭=-Φ+-Φ=-Φ220.66280.6744=-⨯= 7.解：101010222111~(0,4),~(0,1),2111 10.05,0.95444444ii i i i i i i X X N N c c c P X P X P X ===⎛⎫⎛⎫⎛⎫>=-≤=≤= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭∑∑∑则查卡方分位数表 c/4=18.31,c=73.24 8．解：由已知条件得：(1,),1()iX Y B p p F μ=-由i X 互相独立，知i Y 也互相独立，所以1(,),1().niX i Y B n p p F μ==-∑9.解: 1))1(,)1(,2p Np DX ES np Np n DX X D Np EX X E -==-==== 2)λλλ======DX ES nn DX X D EX X E 2,, 3)()()12,12,2222a b DX ES n a b n DX X D b a EX X E -==-==+==4)1,1,2======DX ES nn DX X D EX X E μ 10.解：1)()22212)1()1()1()1(σ-=-=-=-=-∑=n DX n ES n S n E X X E ni i2)()222242221(1)(1)(1), ~(1)nii n S n S DXX D n S D n σχσσ=⎛⎫---=-=- ⎪⎝⎭∑ ()2412(1)nii DXX n σ=∴-=-∑ 11.解：ππππππn X E dt e dy ey dy ey X nE Y E nn DY X E EY N X n Y n N X t y y 2)(,2)1(222222||21)(),11,0(),1,0(~),/1,0(~)102222==Γ==========-∞+-∞+-∞+∞-⎰⎰⎰ 令ππππππ211,2)1(222222||21),1,0(~)21102222===Γ====∑∑⎰⎰⎰==-∞+-∞+-∞+∞-n i i n i i t x x X E n X n E dt e dx ex dx ex X E N X12.解：1)()2224X E X E X E n μμ-=-=()244100.1X X D E n n⎡⎤=+=+≤⎢⎥⎣⎦ 40n ∴≥2)2222,2u u X u E u e du u du +∞+∞---∞===⎰⎰222220022002(1)0.1,80010,254.6,255u uutue du ue duue d e dtE X En nμπ+∞+∞--+∞+∞--===Γ=-==≤≥≥=∴≥⎰⎰⎰⎰3) ()()111P X P X Pμμ⎛-≤=-≤-≤=≤≤⎝⎭0.975210.95,2221.96,15.36,162u n n⎛⎛⎫⎛=Φ-Φ-=Φ-≥⎪⎪⎝⎭⎝⎭⎝⎭≥=≥≥13.解：()()()112221111111,n ni ii iY XY X a X na X an b b n bEY EX a S Sb b==⎛⎫=-=-=-⎪⎝⎭=-=∑∑14．解：1）12345~(0,2),~(0,3)X X N X X X N+++~~(0,1)N N1111,, 2.23c d n∴===2）()2345222212~(2),~(1)3X X XX Xχχ+++()()22122234523~(2,1),,2,123XX F c m n X X X +===++15.解： 设1(1,)p F n α-=，即()1(1P F p P p α≤=-⇔≤≤=-((12(2(12P T P T pP T p p P T ⇔≤-≤=-⇔≤=-⇔≤=-122112()()(1,)p p p t n tn F n α---=∴==16．解：()()()()()()()()()121222222221212222212121212212221212~(0,2),~(0,~~(0,1)~~(2)2210.1,2X X N X X N N N X X X X t P t P X X X X X X X X X X t P X X X X c χχ+-+⎛⎫⎛⎫++>=> ⎪ ⎪ ⎪ ⎪++-++-⎝⎭⎝⎭⎧⎫+⎪⎪=-≤=⎨⎬++-⎪⎪⎩⎭=0.9(1,2)8.532tF ==17.证明： 1）2211122211()0,(),(0,)1(1)(1)n n n n n E X X D X X X X N nnn S n t n σσχσ+++++-=-=∴---=-又2）2211111()0,(),(0,)n n n n n E XX D X X X X N nnσσ+++++-=-=∴- 3）2211111()0,(),(0,)n n E X X D X X X X N nnσσ---=-=∴- 18. 解：()()()62,47.61,96.125.0,975.025.0,95.0125.0225.0/25.025.0975.0≥≥=≥≥Φ≥-Φ=⎪⎪⎭⎫ ⎝⎛≤-≤-=≤-n n u n n n n n X n P X P σμσμ 19.解[,]0,1,[,](),(),0,[,]1,X U a b x a x a b x af x F x a x b b a b a x a b x b ≤⎧⎧⎪∈-⎪⎪∴==<≤-⎨⎨-⎪⎪∉⎩>⎪⎩1(1)()(1())()n f x n F x f x -∴=-111()1(),[,]0,[,]1(),[,]()(())()0,[,]n n n n b a n x a b b a b a x a b x a n x a b f x n F x f x b a b ax a b ----⎧∈⎪=--⎨⎪∉⎩-⎧∈⎪==--⎨⎪∉⎩20.解：()()()()()()()55(1)(1)11515555555(5)111011011011101211121(1(1))1(11(1))1(1)0.5785121515 1.5(1.5)0.93320.70772i i i i i i i i i i P X P X P X P X X P X P XP X P =====<=-≥=-≥=--≤⎛-⎫⎛⎫=--≤- ⎪⎪⎝⎭⎝⎭=--Φ-=--+Φ=-Φ=-⎛⎫<==<=<=Φ== ⎪⎝⎭∏∏∏∏∏21. 解：1)因为21~(0,)mii XN m σ=∑，从而~(0,1)miXN ∑2221~()m ni i m Xn χσ+=+∑，所以~()miX t n ξ=2）因为22211~()mii Xm χσ=∑，22211~()m n i i m X n χσ+=+∑所以2121~(,)mi i m ni i m n X F m n m X =+=+∑∑3)因为21~(0,)m i i X N m σ=∑，21~(0,)m n i i m X N n σ+=+∑所以2212()~(1)mi i X m χσ=∑，2212()~(1)m ni i m X n χσ+=+∑故222221111~(2)m m n i i i i m X X m n χσσ+==+⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭∑∑ 22.解：由Th1.4.1 (2)()(),95.047.321),1(~122222=⎪⎪⎭⎫⎝⎛≤---σχσS n P n S n查表:n 121,n 22-==23.解： 由推论1.4.3(2)05.095.0139.2139.2),14,19(~222122212221=-=⎪⎪⎭⎫ ⎝⎛≤-=⎪⎪⎭⎫ ⎝⎛>S S P S S P F S S 24.解： 1)()()94.005.099.057.3785.10)20(~),1,0(~),,0(~2201222220122=-=≤≤=⎪⎭⎫ ⎝⎛-=---∑∑==χχχσμσμσμσμP X XN X N X i i i ii i2)()895.01.0995.058.381965.11),19(~192222222012=-=⎪⎪⎭⎫ ⎝⎛≤≤=-∑=σχσσS P S X Xi i25. 解： 1)()4532.07734.0221)75.0(21431435/2080380=⨯-=+Φ-=⎪⎭⎫ ⎝⎛≤-=⎪⎪⎭⎫ ⎝⎛>-=>-U P X P X P2)()()05.01975.021064.21064.25/2674.780380=+⨯-=≤-=⎪⎪⎭⎫ ⎝⎛>-=>-T P X P X P 26.解： 1)8413.0120472.4472.4=⎪⎪⎭⎫ ⎝⎛<-=⎪⎪⎭⎫ ⎝⎛<-=⎪⎭⎫ ⎝⎛+<σσσa X P a X P a XP 2)2222222222223132222222S P S P S P S P σσσσσσσσ⎛⎫⎛⎫⎛⎫⎛⎫-<=-<-<=<<=<< ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭22199.528.50.950.050.9S P σ⎛⎫=<<=-= ⎪⎝⎭3)3676.3,328.120,1.020,9.02012020/1===⎪⎪⎭⎫ ⎝⎛≤=⎪⎪⎭⎫⎝⎛≤-=⎪⎪⎭⎫⎝⎛>-=⎪⎪⎭⎫⎝⎛>-=⎪⎪⎭⎫ ⎝⎛>-c c c T P c T P c S X P c S X P c X S P μμμ27．解：22cov(,)(,))(1()()1cov(,)()1(,)1j i j j i j i j i j i j i j X X X X r X X X X D X n D X X D X X nX X X X E X X X X X X X X nr X X X X n σσ----=---=-=--=---=-∴--=--28.解：()2221212)1(2)1(,)1(,21),2,2(~σσμ-=-=-=-===+=∑∑==+n ES n ET S n Y Y T X Y n Y N X X Y Y Y ni i ni i in i i 令习题二、参数估计1．解：矩估计()1 3.40.10.20.90.80.70.766X =+++++=()()11111ln ln(1)ln nnni i i i nii L x x L n x αααααα===⎡⎤=+=+⎣⎦=++∏∏∑121ln ln 01ˆ10.2112ln n i i n ii d n L x d n x αααα====+=+=--=∑∑3077.0121ˆ,212)1()1(110121=--==++=++=+=⎰++X XX x dx x EX αααααααα所以12112ˆˆ,11ln n ii X nX X αα=⎛⎫⎪- ⎪==-+-⎪ ⎪⎝⎭∑，12ˆˆ0.3079,0.2112αα≈≈ 2．解： 1）3077.02ˆ,21====X X EX θθ111ln 0nni L nL θθθ====-=∏无解，依定义：21ˆmax ii nX θ≤≤= 2）矩法：211ˆˆ1.2,0.472212EX DX θθ====极大似然估计：22ˆˆ1.1,0.1833212EX DX θθ====3． 1）解：矩法估计：111ˆ,EX X Xλλ===最大似然估计：111,ln ln niii nnx x ni i i L eeL n L x λλλλλ=--==∑===-∑∏2111ˆln 0,ni ni ii d n nL x d Xxλλλ===-===∑∑2)解：~()X P λ矩估计：X X EX ===1ˆ,λλ最大似然估计：1,ln ln ixnxnn i i iiL eeL n nx x x xλλλλλλ--====-+-∑∏∏2ˆln 0,d nx L n X d λλλ=-+==3）解：矩估计：()2,212b a a bEX DX -+==联立方程：()2*221ˆ2ˆa X b X a bX b a M ⎧=-⎪→+⎧=⎪⎪⎨-⎪=⎪⎩⎨=+⎪⎩极大似然估计：依照定义，11ˆˆmin ,max i ii ni na Xb X ≤≤≤≤== 4) 解： 矩估计：00ln EX dx xxθθ+∞+∞==⎰，不存在22111,ln ln 2ln nnni i i i iL L n x x x θθθ=====-∑∏∏ln 0n L αθ∂==∂，无解；故，依照定义，(1)ˆX θ= 5)解： 矩法：()/0()(1)(2)x txEX edx t e dt αβααβαββ+∞+∞---==+=Γ+Γ⎰⎰ Xαβ=+=2222()(1)2(2)(3)t EX t e dt αβααββ+∞-=+=Γ+Γ+Γ⎰ 222222122()i M X nααββαββ=++=++==∑22222*2111ˆˆi M X X X M nX βαβ=-=-==-=∑即11ˆˆX X αβ====极大似然估计：()()/1111exp ,ln ln i nx ni n L enx n L n nx αβαβαβββββ---=⎡⎤==--=--+⎢⎥⎣⎦∏2ln 0,ln ()0n n nL L x ααββββ∂∂===-+-=∂∂ α无解，依定义有：(1)(1)ˆˆ,L L X X X X αβα==-=- 7)解： 矩法：22223222(2)x x tx EX dx dte dt Xθθθ+∞+∞+∞---=====⎰⎰⎰ˆMθ=极大似然估计：22222211iixnxn ni ii iL x eθθ--==∑⎛⎫⎛== ⎪⎝⎝⎭∏222ln ln43ln ln iixL n n n xθθ=---∑∑233ˆln20,iLxnLθθθθ∂=-+==∂∑8)解：矩法：2222222222022222223(1)(1)[(1)](1)(1)(1)1221x x x x x xxxd dEX x xd dd dq Xdq dq qθθθθθθθθθθθθθ∞∞∞-===∞==--=-=---=====-∑∑∑∑2ˆM Xθ=极大似然估计：22221(1)(1)(1)(1)ln2ln(2)ln(1)ln(1)inx n nx ni iiiL x xL n nx n xθθθθθθ--==--=--=+--+-∏∏∑222ˆln0,1Ln nx nLXθθθθ∂-=-==∂-4解：11112112(,,)(1)(1)ln(,,)ln(1)ln(1)n ni ii i i iy yny y nninL p y y y p p p pL p y y y ny p n y p==--=∑∑=-=-=+--∏12(,,)0(1)ny pd L p y y y ndp p p-==-ˆp Y=记001,;0,i i i iy x a y x a=≥=<则(1,)iY B p；5.解：1,ln lninx n nxiL e e L n nxλλλλλλ--====-∏711120000ˆln 0,,2010001000i i i d n L nx X x v d X λλλ==-=====∑ 1ˆ0.05Xλ== 6解：因为其寿命服从正态分布，所以极大似然估计为：2211ˆˆ,()ni i x x n μσμ===-∑ 根据样本数据得到：2ˆˆ997.1,17235.811μσ==。
方差分析习题答案
方差分析习题答案【篇一：方差分析习题】lass=txt>班级_______ 学号_______ 姓名________ 得分_________一、单项选择题1、方差分析所要研究的问题是（） a、各总体的方差是否相等 b、各样本数据之间是否有显著差异 c、分类型自变量对数值型因变量的影响是否显著 d、分类型因变量对数值型自变量是否显著2、组间误差是衡量因素的不同水平（不同总体）下各样本之间的误差，它（）a、只包含随机误差b、只包含系统误差c、既包含随机误差也包含系统误差d、有时包含随机误差，有时包含系统误差3、组内误差（） a、只包含随机误差b、只包含系统误差 c、既包含随机误差也包含系统误差d、有时包含随机误差，有时包含系统误差4、在单因素方差分析中，各次实验观察值应（）a、相互关联b、相互独立c、计量逐步精确d、方法逐步改进5、在单因素方差分析中，若因子的水平个数为k，全部观察值的个数为n，那么（）a、sst的自由度为n b 、ssa的自由度为k c、 sse的自由度为n-k-1 d、sst的自由度等于sse的自由度与ssa的自由度之和。
6、在方差分析中，如果拒绝原假设，则说明（）a、自变量对因变量有显著影响b、所检验的各总体均值之间全部相等c、不能认为自变量对因变量有显著影响d、所检验的各样本均值之间全不相等7、在单因素分析中，用于检验的统计量f的计算公式为（） a、ssa/sseb、ssa/sst c、msa/msed、mse/msa8、在单因素分析中，如果不能拒绝原假设，那么说明组间平方和ssa （） a、等于0 b、等于总平方和c、完全由抽样的随机误差所决定d、显著含有系统误差9、ssa自由度为（）a、r-1b、n-1c、n-rd、r-n二、实验分析题1、某公司采用四种颜色包装产品，为了检验不同包装方式的效果，抽样得到了一些数据并进行单因素方差分析实验。
实验依据四种包装方式将数据分为4组，每组有5个观察值，用excel中的数据分析工具，在0.05的显著水平下得到如下方差分析表：方差分析(1)填表：请计算表中序号标出的七处缺失值，并直接填在表上。
方差分析与回归分析
不同行业被投诉次数的散点图
行业
1. 随机误差
▪ 因素的同一水平(总体)下，样本各观察值之间的差异 ▪ 比如，同一行业下不同企业被投诉次数是不同的 ▪ 这种差异可以看成是随机因素的影响，
2. 系统误差
▪ 因素的不同水平(不同总体)下，各观察值之间的差异 ▪ 比如，不同行业之间的被投诉次数之间的差异
▪ 这种差异可能是由于抽样的随机性所造成的，也可
a.画散点图
较强的线性正相关关系
b. 求r
• 样本容量n＝14，查教材附录540页《相关系数 检验表》，当显著性水平为1％时，r0.01＝0.661。 显然，样本相关系数r> r0.01 ，因此线性回归效果 显著，认为抗拉强度y与含碳量x之间存在高度显 著的正相关关系。
c.求抗拉强度y关于含碳量x 的线性回归方程
无线性相关
完全正相关
-1.0 -0.5 0 +0.5 +1.0
r
负相关程度增加 正相关程度增加
非线性回归
• 在许多实际问题中，变量之间并不一定是 变量的关系，而是某种非线性相关关系， 称为一元非线性回归。许多有价值的非线 性回归方程，可以利用适当的变换，转换 为线性回归方程，例如，倒数变换、半对 数变换、双对数变换、多项式变换等；然 后再利用线性回归分析的最小二乘法进行 估计和检验。
k
ni
k
k
xij x 2 ni xi x 2
ni
xij x 2
i1 j1
i1
i1 j1
SST = SSA + SSE
▪ 前例的计算结果：
4164.608696=1456.608696+2708
关系强度的测量
1. 拒绝原假设表明因素(自变量)与观测值之间有
整理回归分析练习题与参考答案
20 年 月 日
A4打印 / 可编辑
2019
年招收攻读硕士学位研究生入学
考试试题
2019年招收攻读硕士学位研究生入学考试试题
********************************************************************************************招生专业与代码：流行病与卫生统计学100401、劳动卫生与环境卫生学100402、营养与食品卫生学100403、儿少卫生与妇幼保健学100404、卫生毒理学100405、公共卫生（专业学位）105300考试科目名称及代码：卫生综合353
整理丨尼克
本文档信息来自于网络，如您发现内容不准确或不完善，欢迎您联系我修正；如您发现内容涉嫌侵权，请与我们联系，我们将按照相关法律规定及时处理。
数理统计期末练习题0.
统 计 分 析（方差分析和回归分析）三、典型题解例1：某水产研究所为了比较四种不同配合饲料对鱼的饲喂效果，选取了条件基本相同的鱼20尾，随机分成四组，投喂不同饲料，经一个月试验以后，各组鱼的增重结果列于下表.饲喂不同饲料的鱼的增重 （单位：10g ）饲料鱼的增重（x ij ）合计.i x 平均.i x A 1 31.9 27.9 31.8 28.4 35.9 155.9 31.18 A 2 24.8 25.7 26.8 27.9 26.2 131.4 26.28 A 3 22.1 23.6 27.3 24.9 25.8 123.7 24.74 A 427.0 30.829.024.528.5139.827.96合计..x =550.8解：这是一个单因素等重复试验，因素数4s =，重复数05n =.各项平方和及自由度计算如下：220/550.8/(45)15169.03C T n s ==⨯=总平方和 222231.927.928.5T ij S x T C =∑∑-=+++-67.19903.151697.15368=-=组间平方和22222011(155.9131.4123.7139.8)515283.315169.03114.27A jS x C C n =-=+++-=-=∑ 组内平方和 199.67114.2785.40E T A S S S =-=-= 总自由度 0154119T f n s =-=⨯-= 处理间自由度 1413A f s =-=-= 处理内自由度 19316E T A f f f =-=-=用A S 、E S 分别除以A f 和E f 便得到处理间均方A MS 及处理内均方E MS ./114.27/338.09/85.40/16 5.34A A A E E E MS S f MS S f ======因为/38.09/5.347.13A E F MS MS ===；根据13A f f ==，216E f f ==，查表得F ＞F 0.01(3，16) =5.29,，表明四种不同饲料对鱼的增重效果差异极显著，用不同的饲料饲喂，增重是不同的.例2：抽测5个不同品种的若干头母猪的窝产仔数，结果见下表，试检验不同品种母猪平均窝产仔数的差异是否显著.五个不同品种母猪的窝产仔数品种号 观 察 值x ij (头/窝) x i..i x1 8 13 12 9 9 51 10.2 2 7 8 10 9 7 41 8.23 13 14 10 11 12 60 12 4 13 9 8 8 10 48 9.65 121115 14136513 合计T =265解：这是一个单因素试验，因素数5s =，重复数05n =.现对此试验结果进行方差分析如下：计算各项平方和与自由度220/265/(55)2809.00C T sn ==⨯=22222222222.0(8131413)2809.002945.002809.00136.0011(5141604865)2809.0052882.202809.0073.20T ij A jS x C S x C n =-=++++-=-==-=++++-=-=∑∑∑ 136.0073.2062.80E T A S S S =-=-=0155124,1514,24420T A E T A f sn f s f f f =-=⨯-==-=-==-=-=列出方差分析表，进行F 检验不同品种母猪的窝产仔数的方差分析表变异来源 平方和 自由度 均方 F 值品种间 73.20 4 18.30 5.83 误差 62.80 20 3.14 总变异136.0024根据14A f f ==，220E f f ==查临界F 值得：F 0.05(4,20) =2.87,F 0.05(4,20) =4.43，因为F ＞F 0.01(4,20)，表明品种间产仔数的差异达到1%显著水平.例3：以A 、B 、C 、D 4种药剂处理水稻种子，其中A 为对照，每处理各得4个苗高观察值(cm)，其结果如下表，试分解其自由度和平方和.水稻不同药剂处理的苗高(cm )药 剂苗高观察值总和i T平均i yA 18 21 20 13 72 18B 20 24 26 22 92 23C 10 15 17 14 56 14D 28 27 29 3211629T =336 =y 21解：计算各项平方和与自由度20T C n s ===⨯23367056442T ijS y C C =-=+++-=∑∑222182132602201()()kT i i S n y y T n C C =-=-=+++-=∑∑2222729256116/4504或 A S =⨯-+-+-+-=22224[(1821)(2321)(1421)(2921)]504 2221111()knnkkE ij i iji T A S y y y T n S S =-=-=-=-=∑∑∑∑60250498进而可得均方：T MS ==602/1540.13 A MS ==504/3168.00 E MS ==98/128.17总方差自由度44115T f =⨯-=，药剂间自由度413A f =-=，药剂内自由度15312E f =-=例4：为研究雌激素对子宫发育的影响，现有4窝不同品系未成年的大白鼠，每窝3只，随机分别注射不同剂量的雌激素，然后在相同条件下试验，并称得它们的子宫重量，见下表，试作方差分析.各品系大白鼠不同剂量雌激素的子宫重量(g)品系(A )雌激素注射剂量(mg/100g)(B )合计x i. 平均.i x B 1(0.2)B 2(0.4)B 3(0.8)A 1 106 116 145 367 122.3 A 2 42 68 115 225 75.0 A 3 70 111 133 314 104.7 A 442 63 87 192 64.0 合计x .j 260 358 480 1098 平均j x .65.089.5120.0解：这是一个双因素单独观测值试验结果.A 因素(品系)有4个水平，即a =4；B 因素(雌激素注射剂量)有3个水平，即b =3，共有a ×b =3×4=12个观测值.方差分析如下：计算各项平方和与自由度22/1098/(43)100467.0000C T ab ==⨯=22222222222222.(1061166387)100467.0000113542100467.000013075.000011(367225314192)100467.00003106924.6667100467.00006457.666711(260358480)100467.00004T ij A j B j S x C S x C b S x C a =-=++++-=-==-=+++-=-==-=++-∑∑∑∑106541.0000100467.00006074.0000=-=13075.00006457.66676070000543.3333143111,14131312,11326e T A B T A B e T A B S S S S f ab f a f b f f f f =--=--==-=⨯-==-=-==-=-==--=--=列出方差分析表，进行F 检验方差分析表变异来源平方和 自由度 均方 F 值A 因素(品系) 6457.6667 3 2152.5556 23.77B 因素(剂量)6074.0000 2 3037.0000 33.54误差 543.3333 6 90.5556总变异13075.000011根据13A f f ==，26E f f ==查临界F 值，F 0.01(3,6)=9.78；根据12B f f ==，26E f f ==查临界F 值，F 0.01(2,6)=10.92.因为A 因素的F 值23.77＞F 0.01(3,6)，差异极显著；B 因素的F 值33.54＞F 0.01(2,6)，差异极显著.说明不同品系和不同雌激素剂量对大白鼠子宫的发育均有极显著影响.例7：在某个地区抽取了9家生产同类产品的企业，其月产量和单位产品成本的资料如表8-1，建立月产量x 和单位产品成本y 之间的直线方程.并估计当月产量x=10（千件）时，单位产品成本的数值.22293332.953.7613ˆ 6.46()9370.6553.7n xy x y bn x x -⋅⨯-⨯===--⨯-∑∑∑∑∑ 5.97x =，68.11y =，ˆ68.11( 6.46) 5.97106.68ay bx =-=--⨯= 所以回归方程为：ˆ106.68 6.46yx =- 当10x =（千件），ˆ106.68 6.4642.08yx =-=（元）.例8：为研究某一化学反应过程中，温度()x C ο对产品得率(%)Y 的影响，测得数据如下：（1） 求变量Y 关于x 的线性回归方程. （2） 2σ的无偏估计.（3） 检验回归方程的回归效果是否显著（取0.05α=）. 解： （1）10n =，经计算得101101010102211111450, 673, 218500, 47225, 101570ii i iii i i i i i xy x y x y ==========∑∑∑∑∑21218500145082501011015701450673398510xx xy S S =-⨯==-⨯⨯=故得ˆ0.48303xx xyS bS ==，11ˆ67314500.48303 2.739351010a=⨯-⨯⨯=- 于是得到回归直线方程ˆ 2.739350.48303yx =-+ 或写成ˆ67.30.48303(145)yx =+- （2）由以上计算计算结果得2221111()472256731932.110nn yy i i i i S y y n ===-=-⨯=∑∑ 又已知3985xyS =，ˆ0.48303b=，故 2ˆ7.23ˆ0.9082yy xy S bSn σ-===-（3）待检验假设0: 0H b =，1: 0H b ≠由（1）和（2）知2ˆˆ0.48303, 8250, 0.9xx bS σ===.查表得0.0520.025(2)(8) 2.3060t n t -==假设0: 0H b =的拒绝域为|| 2.3060ˆˆ||xx t S bσ=≥现在0.48303||825046.25 2.30600.90t =⨯=> 故拒绝0: 0H b =，认为回归效果是显著的.例9：某商品的需求量（单位：件）y 与价格x （单位：元）的统计资料如下所示y543 580 618 695 724 812 887 991 1186 1904 x45515461667074788589求需求函数的回归方程.解：画散点图，根据散点图选择曲线类型by ax-=来描绘需求量y 与价格x 的关系经变换，得''ln ln ln y y a b x x αβ==-=+ 利用最小二乘法的α和β的估计值ˆ9.1206α=， ˆ0.6902β=- 所以ˆˆ9141.685ae α==，ˆˆ0.6902b β=-=. 故需求回归方程为：0.6902ˆ9141.658yx -=，将y 与ˆy的值加以对比如下： y543 580 618 695 724 812 887 991 1186 1904ˆy5365836146827427719171050 1198 1886可见y 与ˆy数据相近，效果较好. 四、练习题1.把下面的方差分析表填写完整，方差来源平方和自由度修正（方差）组间 131.37 （1） （3） 组内 （2） 15 （4） 总和332.4819临界值参考答案：（1）4（2）201.11（3）32.84（4）13.412.一批由相同材料织成的布料，使用染整工艺1B ，2B ，3B ，分别处理后进行强度试验，实测数据（单位：2/kg m ）为：工艺1B ：0.94 0.86 0.90 1.26 1.04 工艺2B ：1.28 1.72 1.60 1.60工艺3B ：1.02 0.86 1.00 1.22 1.33 1.10试分析不同染整工艺下布料强度的差异显著性？(0.1α=) 参考答案：0.10.7615(2,11)2.86FF ，不显著.3.为考察苗猪品种对增重的影响，今选择1A ，2A ，3A 等3个品种各5头发育良好体重相等的苗猪作实验，在同等条件下喂养一段时间后重新过磅，其实际增重（单位：kg ）为：工艺1A ：129 122 140 140 129 工艺2A ：123 135 124 104 114 工艺3A ：147 131 138 150 124试问猪的品种对增重的影响是否显著？(05.0=α) 参考答案：0.14.0064(2,12)2.81FF ，显著.4.设四名工人操作机器321,,A A A 各一天, 其日产量如表8.7所示, 问不同机器或不同工人对日产量是否有显著影响(0.1α=)?参考答案：0.19.3183(3,6) 3.29AF F ，显著； 0.11.8992(2,6)3.46BF F ，不显著8．某地高校教育经费（x ）与高校学生人数（y ）连续6年的统计资料如下：要求：（1）建立议程回归直线方程，估计教育经费为500万元的在校学生数； （2）计算估计标准误差.参考答案：（1）Y=-17.92+0.096X ， 29.84338（2）2ˆ0.8649σ= 9. 以下是子代和父代受教育年限的抽样调查求：（1）子代受教育年限（Y ）关于父代受教育年限（X ）的回归直线. （2）2σ的无偏估计.（3）判断该结论是否具有推论意义（0.05α=）.参考答案：（1）Y=3+0.6X ，（2）2ˆ0.93σ=（3）0025|| 3.928(3) 3.1824t t =>=，显著. 10. 设对某产品的价格P 与供给量S 的一组观察数据如下表：据此求：（1）该产品的价格P 关于供给量S 的回归直线.（2）2σ的无偏估计.（3）是否具有推论意义？（0.05α=）.参考答案：（1）Y=-0.1754+6.2281X ，（2）2ˆ11.84σ=（3）0025||0.3722(6) 2.4469t t =<=，不显著.11.以下是生活期望值与个人成就的抽样调查求：（1）回归直线 （2）2σ的无偏估计.（3）是否具有推论意义（0.05α=）.参考答案：（1）Y=0.2668+0.8748X ，（2）2ˆ 5.089σ=（3）0025||0.2703(6) 2.4469t t =<=，不显著.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第九章 方差分析与回归分析习题参考答案
1. 为研究不同品种对某种果树产量的影响，进行试验，得试验结果（产量）如下表，试分析果树品种对产量是否有显著影响.
（0.05(2,9) 4.26F =，0.01(2,9)
8.02F =）
解
：
r=3,
12
444n n 321=++=++=n n ,
T=120 ,120012
1202
2===n T C 计
算
统
计
值
722
8.53,
389
A A A e e SS f F SS f =
=≈……
方差分析表
方差来源 平方和 自由度 均方 F 值 临界值 显著性
品种A 72 2 36
8.53
误差 38 9 4.22
总 计
110
11
结论:由于0.018.53(2,9)8.02,
A F F ≈>=故果树品种对产量有特别显著影响.
2.
解
：
22..4,3,12,180122700
l m n lm C x n ======= 计算
统
计
值
90310.52
51.43,3.56 3.56
A A
B B A B e e e e S f S f F F S f S f =
=≈==≈
方差来源
平方和
自由度
F 值
临界值
显著性
品种 试验结果 行和⋅⋅=i x T i 行均值.i x
A 1 10 7 13 10 40 10 A 2 12 13 15 12 52 13 A 3
8
4
7
9
28
7
试验 结果
燃料B
B 1 B 2 B 3
推进器 A
A 1 14 13 12 39 13 A 2 18 16 14 48 16 A 3 13 12 11 36 12 A 4
20 18 19 57 19
65
59
56
180
16.25 14.75 14
15
结论: 由以上方差分析知，进器对火箭的射程有特别显著影响；燃料对火箭的射程有显著影响. 3．为了研究某商品的需求量Y 与价格x 之间的关系，收集到下列10对数据：
31,58,147,112,410.5,i i i i i i x y x y x y =====（1）求
需求量Y 与价格x 之间的线性回归方程； （2）计算样本相关系数；
（3）用F 检验法作线性回归关系显著性检验. 解：引入记号
10, 3.1,
5.8n x y ===
∴需求量Y 与价格x 之间的线性回归方程为
（2）样本相关系数 32.8
0.955634.3248l r
-==
≈≈- 在0H 成立的条件下，取统计量(2)~(1,2)R
e
n S F
F n S -=
-
计算统计值
2
2(32.8)15.967.66,
74.167.66 6.44
R xy xx e yy R S l l S l S ==-≈=-≈-=
故需求量Y 与价格x 之间的线性回归关系特别显著.
4. 随机调查10个城市居民的家庭平均收入(x)与电器用电支出(y)情况得数据（单位：千元）如下:
(1) 求电器用电支出y 与家庭平均收入x 之间的线性回归方程； (2) 计算样本相关系数； (3) 作线性回归关系显著性检验;
(4) 若线性回归关系显著,求x =25时, y 的置信度为0.95的预测区间. 解：引入记号
10,27,
1.9n x y ===
∴电器用电支出y 与家庭平均收入x 之间的线性回归方程为
（2）样本相关系数 0.9845l r
==
≈
在0H 成立的条件下，取统计量(2)~(1,2)R
n S F
F n S -=
-e
计算统计值
2
243.6354 5.37,
5.54 5.370.17
xy xx yy s l l s l s ==≈=-≈-=R e R
故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显著. 相关系数检验法 0
1:0;:0H R H R =≠
故家庭电器用电支出y 与家庭平均收入x 之间的线性回归关系特别显著. (4) 因为0x
x =处,0y 的置信度为1α-的预测区间为
其中
00.025垐 1.42640.123225 1.6536,
(8) 2.31,0.1458y t σ=-+⨯====
代入计算得当x =25时, y 的置信度为0.95的预测区间为。