高数实验报告56649
《高等数学实验》实验报告
精品文档高等数学实验报告实验四：微分方程实验五：空间解析几何实验六：多元函数微积分班级：姓名：学号：指导教师：李老师实验成绩：完成日期： 2010 年 4 月 27 日实验四微分方程一、实验目的1．理解常微分方程解的概念；2．掌握求微分方程及方程组解的常用命令和方法。
二、实验类型验证型。
三、必做实验四、选做实验实验五空间解析几何一、实验目的1．掌握绘制空间曲面和曲线的方法；2．熟悉常用空间曲线和空间曲面的图形特征，提高空间想像能力； 3．深入理解二次曲面方程及其图形。
二、实验类型验证型。
三、必做实验>> > t=0:pi/50:10*pi;>> plot3(cos(t),sin(t),t)>> xlabel('x');ylabel('y');zlabel('z');grid onxyz> t=0:0.05:100;>> x=t;y=sin(t);z=sin(2*t); >> plot3(x,y,z)>> xlabel('x');ylabel('y');zlabel('z')xyzezsurf('f')>> ezsurf('-cos(2*x)*sin(3*y)',[-3,3])-1-0.50.51x-cos(2 x) sin(3 y)yezsurf('sin(pi*(x^2+y^2)^(1/2))')-1-0.50.51xsin( (x 2+y 2)1/2)yezsurf('(x*y)/(x^2+y^2)',[-2,2])x(x y)/(x 2+y 2)y> ezsurf('(3+cos(u))*cos(v)','(3+cos(u))*sin(v)','sin(u)',[0,2*pi])-1-0.500.51xx = (3+cos(u)) cos(v), y = (3+cos(u)) sin(v), z = sin(u)yzezsurf('u*cos(v)','u*sin(v)','v/3',[-1,1],[0,8])0.511.522.53xx = u cos(v), y = u sin(v), z = v/3yz>> ezsurf('cos(u)','sin(u)','v') >> hold on>> ezsurf('cos(u)','v','sin(u)')-1-0.500.51z实验六 多元函数微积分一、实验目的1．掌握计算多元函数偏导数和全微分的方法； 2．掌握计算二重积分与三重积分的方法；3．提高应用重积分和曲线、曲面积分解决各种问题的能力。
高数实验报告 (2)
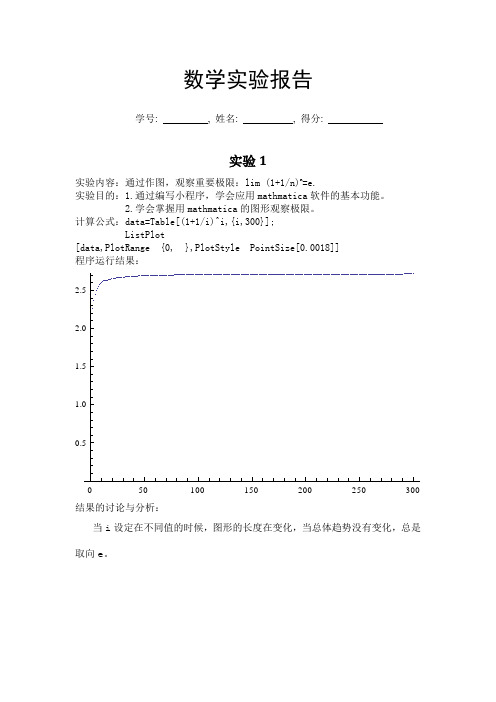
数学实验报告学号: , 姓名: , 得分:实验1实验内容：通过作图，观察重要极限：lim (1+1/n)n=e.实验目的：1.通过编写小程序，学会应用mathmatica软件的基本功能。
2.学会掌握用mathmatica的图形观察极限。
计算公式：data=Table[(1+1/i)^i,{i,300}];ListPlot[data,PlotRange {0, },PlotStyle PointSize[0.0018]]程序运行结果：结果的讨论与分析：当i设定在不同值的时候，图形的长度在变化，当总体趋势没有变化，总是取向e。
实验2实验内容：设数列｛Xn｝由下列递推关系式给出：x1=1/2,xn+1=xn2+xn(n=1,2………)观察数列1/(x1+1)+ 1/(x2+1) +…….+1/(xn+1)的极限。
实验目的和意义：1:掌握mathmatica数学实验的基本用法。
2：学会利用mathmatica 编程求数列极限。
3：了解函数与数列的关系。
计算公式：f[x_]:=x^2+x;xn=0.5;g[x_,y_]:=y+1/(1+x);y n=0;For[n=1,n 15,n++,xN=xn;yN=yn;xn=N[f[x N]];yn=N[g[xN,yN]]];Print[" y30=",yn]程序运行结果：y30= 2.结果与讨论：这个实验，当yn中n趋向无穷大的时候，能够更加接近极限，当取30以上时候，2就是极限值。
实验3实验内容：已知函数：f（x）=1/(x2+2x+c)(-5<=x<=4),作出并比较当c 取不同的值的时候（-1，0，1，2，3），并从图上观察出极值点，驻点，单调区间，凹凸区间和渐进线。
实验目的：1.通过实验掌握如何用mathmatica作图。
2.学会观察图像来求函数的相关数据。
计算公式：f[x_]=1/(x2+2 x+(-1))Plot[f[x],{x,-5,4},GridLines Automatic,Frame True,PlotStyle RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(0))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(2))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]f[x_]=1/(x2+2 x+(3))Plot[f[x],{x,-5,4},GridLines→Automatic,Frame→True,PlotStyle→RGBColor[1,0,0]]程序运行结果：结果的讨论与分析：不同的c，函数的形态有较大的不同，也就是原方程=0什么情况下有解的问题，根据图像很容易的得到驻点，拐点，等相关信息。
高数 实验报告
高数实验报告高数实验报告引言：高等数学是大学数学的一门基础课程，它在培养学生的逻辑思维能力、分析问题的能力以及推理能力方面发挥着重要作用。
在高数课程中，实验是一种重要的教学手段，通过实验可以帮助学生更好地理解和应用数学知识。
本篇实验报告将介绍我参与的一次高数实验，并分享其中的心得体会。
实验目的：本次实验的目的是通过实际操作，加深对数列和级数的理解，并掌握相应的计算方法。
同时，通过实验过程中的观察和分析，培养学生的数学建模能力和解决实际问题的能力。
实验过程：实验开始前，我们小组成员首先进行了讨论，确定了实验的具体内容和步骤。
我们选择了两个具体的数列和级数问题进行研究。
第一个问题是求解一个递推数列的通项公式。
我们首先观察数列的前几项，发现数列中的每一项与前一项之间存在着一定的关系。
通过分析这种关系，我们猜测数列的通项公式，并通过数学归纳法进行验证。
最终，我们成功地找到了数列的通项公式，并通过计算验证了其正确性。
第二个问题是求解一个级数的和。
我们选择了一个著名的几何级数进行研究。
通过观察级数的前几项，我们发现级数中的每一项与前一项之间存在着一定的比例关系。
根据这种关系，我们得出级数的和的公式，并通过计算验证了其正确性。
实验结果：通过实验，我们成功地求解了两个数列和级数的问题，并得到了相应的结果。
这些结果不仅帮助我们更好地理解了数列和级数的概念，还提高了我们的计算能力和问题解决能力。
心得体会：通过参与这次高数实验，我深刻体会到了实践对于学习的重要性。
在实验过程中，我们不仅仅是被动地接受知识，更是主动地去探索和发现。
通过观察、分析和计算，我们能够更加深入地理解数学知识，并将其应用到实际问题中去。
此外，实验还培养了我们的团队合作能力和沟通能力。
在小组讨论中，我们需要相互协作，共同解决问题。
通过合作，我们不仅能够更好地理解和应用数学知识，还能够互相学习和促进成长。
总结：通过这次高数实验，我不仅加深了对数列和级数的理解，还提高了自己的数学建模能力和问题解决能力。
数学实验报告高中
一、实验目的1. 深入理解数学概念和原理，提高数学思维能力和实践能力。
2. 掌握数学实验的基本方法和步骤，培养科学实验精神。
3. 通过实验验证数学理论，提高数学应用能力。
二、实验内容本次实验以《高中数学实验指导》中的“一元二次方程的解法探究”为例，进行以下实验：1. 实验一：验证一元二次方程的求根公式2. 实验二：探究一元二次方程的根与系数的关系3. 实验三：利用一元二次方程解决实际问题三、实验方法1. 实验一：利用计算机软件（如MATLAB、Mathematica等）或手工计算验证一元二次方程的求根公式。
2. 实验二：通过编程或手工计算，观察一元二次方程的根与系数之间的关系。
3. 实验三：结合实际情境，运用一元二次方程解决实际问题。
四、实验步骤1. 实验一：（1）选择一组一元二次方程，如ax^2 + bx + c = 0（a≠0）；（2）利用计算机软件或手工计算，分别求出该方程的两个根；（3）将求得的根代入求根公式，验证其正确性。
2. 实验二：（1）选择一组一元二次方程，如ax^2 + bx + c = 0（a≠0）；（2）观察方程的根与系数a、b、c之间的关系；（3）通过编程或手工计算，验证根与系数的关系。
3. 实验三：（1）选择一个实际问题，如：某商品的原价为x元，降价10%后，售价为0.9x元，求原价x；（2）根据实际问题，列出相应的一元二次方程；（3）求解方程，得到原价x；（4）验证求解结果是否满足实际问题。
五、实验结果与分析1. 实验一：通过实验验证，一元二次方程的求根公式在计算机软件或手工计算中均能得出正确结果。
2. 实验二：通过观察和验证，一元二次方程的根与系数之间存在以下关系：（1）当b^2 - 4ac > 0时，方程有两个不相等的实数根；（2）当b^2 - 4ac = 0时，方程有两个相等的实数根；（3）当b^2 - 4ac < 0时，方程无实数根。
3. 实验三：以实际问题为例，设原价为x元，根据题意列出方程0.9x = 100，解得x =100/0.9 ≈ 111.11。
高数实验报告doc(两篇)
高数实验报告引言：高等数学是大学理工科专业中必修的一门基础课程，通过实验可以帮助学生更好地理解和应用数学知识。
本实验报告旨在介绍高等数学实验的目的、原理和实验结果，以及对实验过程的详细阐述。
通过实验，学生可以深入了解高等数学的概念和方法，并提高其数学建模和问题解决的能力。
概述：一、数列与数学归纳法：1.数列的概念和性质2.等差数列和等比数列的求和公式3.斐波那契数列4.数学归纳法的原理和应用5.数学归纳法在证明数学命题中的应用二、函数与导数：1.函数的概念和分类2.复合函数的求导法则3.高阶导数与泰勒展开4.特殊函数的导数求解5.函数与导数在实际问题中的应用三、不定积分与定积分：1.不定积分的定义和性质2.基本初等函数的不定积分3.分部积分和换元积分法4.定积分的概念和性质5.定积分在几何、物理等领域中的应用四、微分方程：1.微分方程的基本概念和分类2.一阶常微分方程的解法3.二阶常微分方程的解法4.高阶常微分方程与常系数线性齐次微分方程5.微分方程在科学和工程领域的应用五、级数与幂级数：1.级数的概念和性质2.级数的收敛与发散3.幂级数的收敛域4.幂级数的求和与展开5.幂级数在数学分析中的应用总结：通过本次高等数学实验，我们对数列与数学归纳法、函数与导数、不定积分与定积分、微分方程以及级数与幂级数等知识进行了深入了解和实践。
实验过程中，我们运用数学原理和方法解决了一系列数学问题，并将理论知识应用到实际问题解决中。
通过实验，我们不仅加深了对高等数学的理解和掌握，也提高了自己的数学建模和问题解决能力。
这次实验为我们的数学学习和应用提供了宝贵的经验和机会。
引言概述本文是一篇关于高数实验的报告，主要探讨了高数实验的意义、目的、实验方法以及实验结果和分析等内容。
高数实验是大学高数课程的重要组成部分，通过实验能够帮助学生更好地理解和应用数学知识，提高解决实际问题的能力。
本文将从实验目的、实验方法和实验结果三个方面进行详细阐述，并对实验进行总结与分析。
高等数学实验报告
综合实验报告空间曲线与曲面的绘制一、实验目的：1、利用数学软件Mathematica绘制三维图形来观察空间曲线和空间曲面图形的特点，以加强几何的直观性。
2、学会用Mathematica绘制空间立体图形。
二、实验环境：mathematica 4.0三、实验原理：空间曲面的绘制作参数方程],[],,[,),(),(),(maxminmaxminvvvuuvuzzvuyyvuxx∈∈⎪⎩⎪⎨⎧===所确定的曲面图形的Mathematica命令为：ParametricPlot3D[{x[u,v],y[u,v],z[u,v]},{u,umin,umax}, {v,vmin,vmax},选项]四、实验内容及步骤：x y x y x z =+--=2222,1及xOy 平面围成的图形xxyz及.0=y1+,=-z围成的图像=五、结果分析：1、通过参数方程的方法做出的图形，可以比较完整的显示出空间中的曲面和立体图形。
2、可以通过mathematica 软件作出多重积分的积分区域，使积分能够较直观的被观察。
3、从(1)中的实验结果可以看出，所围成的立体图形是球面和圆柱面所围成的立体空间。
4、从(2)中的实验结果可以看出围成的立体图形的上面曲面的方程是xy z =，下底面的方程是z=0，右边的平面是01=-+y x 。
无穷级数与函数逼近一、 实验目的：(1) 用Mathematica 显示级数部分和的变化趋势；(2) 展示Fourier 级数对周期函数的逼近情况;(3) 学会如何利用幂级数的部分和对函数进行逼近以及函数值的近似计算。
二、实验环境：mathematica 4.0三、实验原理：设()x f 是以2T 为周期的周期函数，在任一周期内，)(x f 除在有限个第一类间断点外都连续，并且只有有限个极值点，则)(x f 可以展开为Fourier 级数：∑∞=++10)sin cos (2n n n T x n b T x n a a ππ，其中⎪⎩⎪⎨⎧====⎰⎰--T T n T T n n dx T x n x f T b n dx T x n x f T a ,3,2,1 ,sin )(1,2,1,0 ,cos )(1ππ，且Fourier 级数在任一x 0处收敛于2)0()0(00++-x f x f 。
高数大一下实验报告
高数大一下实验报告高等数学数学实验报告实验人员：院（系）__电子科学与工程学院__学号__ 姓名____实验地点：计算机中心机房实验一一、实验题目：作出各种标准二次曲面的图形二、实验目的和意义利用数学软件Mathematic绘制三维图形来观察空间曲线和空间曲面图形的特点，以加强几何的直观性。
三、程序设计Plot3D[x2+y2,{x,−1,1},{y,−1,1}]Plot3D[√x2+y2,{x,−1,1},{y,−1,1}]Plot3D[x2/2−y2/2,{x,−1,1},{y,−1,1}]四、程序运行结果PlotPoints→50,DisplayFunction→Iden tity];Show[s1,DisplayFunction→$DisplayFu nction]3．Z=√1−x2−y2,x2+y2=x及xOy面在同一坐标系下显示s1=ParametricPlot3D[{Cos[u]*Sin[v], Sin[u]*Sin[v],Cos[v]},{u,0,2π},{v,0 ,π/2},PlotPoints→50,DisplayFunction→Iden tity];s2=ParametricPlot3D[{1/2+1/2*Cos[u],Sin[u]*1/2,v},{u,0,2π},{v,0,1},PlotPoints→50,DisplayFunction→Iden tity];s3=ParametricPlot3D[{u,v,0},{u,-1,1 },{v,-1,1},AxesLabel→{"x","y","z"},DisplayFun ction→Identity];Show[s1,s2,s3,DisplayFunction→$Dis playFunction]4．Z=√1−x2−y2,x2+y2=x及xOy面围成的立体图形f[x_,y_]:=If[x2+y2<=x, √1−x2−y2,0] s1=Plot3D[f[x,y],{x,-1,1},{y,-1,1},PlotPoints→50,DisplayFunction→Iden tity];s2=ParametricPlot3D[{1/2+1/2*Cos[u] ,Sin[u]*1/2,v},{u,0,2π},{v,0,f[1/2+ 1/2*Cos[u],1/2*Sin[u]]},PlotPoints→50,DisplayFunction→Iden tity];s3=ParametricPlot3D[{u,v,0},{u,-1,1 },{v,-1,1},AxesLabel→{"x","y","z"},DisplayFun ction→Identity];Show[s1,s2,s3,DisplayFunction→$Dis playFunction]四、结果的讨论和分析在绘图过程中，我们依次画出两个曲面，使其在一个坐标系下显示，再求出所围立体图形。
高数实验报告
高等数学实验报告实验人员：院系：学号：姓名：实验地点：计算机中心机房实验一：1、实验题目：观察二次曲面族的图形，特别注意确定k的这样一些量，当k经过这些值时，曲面从一种类型变成了另一种类型。
2、实验的目的和意义：熟练运用数学软件Mathematica绘制三维图形来观察空间曲线和曲面的图形特点，以加强集合的直观性。
3、程序设计：For[k = -3, k <= 3，k++, Plot3D[x^2 + y^2 + k*x*y, {x, -20, 20}, {y, -20, 20},AxesLabel -> {"X", "Y", "Z"}, PlotPoints -> 30]]4、程序运行结果：K=-3 k=-2k=-1 k=0k=1 k=2k=35、结果的讨论及分析：K有变化，图形就会改变，当k=0，改变曲面类型。
实验二：1、实验题目：观察函数，展成的Fourier级数的部分和和逼近f(x)的情况。
2、 实验的目的和意义：用Mathematica 显示级数部分和的变化趋势；学会如何利用幂级数的部分和对函数进行部分逼近以及函数值得近似计算；展示Fourier 级数对周期函数的逼近情况。
3、 程序设计：设()x f 是以2T 为周期的周期函数，在任一周期内，)(x f 除在有限个第一类间断点外都连续，并且只有有限个极值点，则)(x f 可以展开为Fourier 级数：∑∞=++10)sin cos (2n n n T x n b T x n a a ππ，其中⎪⎩⎪⎨⎧====⎰⎰--T T n T Tn n dx T xn x f T b n dx T x n x f T a,3,2,1 ,sin )(1,2,1,0 ,cos )(1ππ，且Fourier 级数在任一x 0处收敛于2)0()0(00++-x f x f 。
高数实验报告
引言概述：本文是关于高数实验的报告，主要通过引言概述、正文内容、总结等部分对高数实验进行详细阐述。
高数实验是通过实际操作和观察，探索和应用数学中的基本原理和概念。
它有助于加深对高数理论的理解、提高数学思维和解决问题的能力。
正文内容：一、实验目的本次高数实验的目的是通过实际操作，加深对数学概念和原理的理解，并掌握基本数学实验的方法和技巧，提高数学思维和解决问题的能力。
二、实验材料和仪器本次实验所需材料和仪器包括实验记录表、计算器、尺子、直角尺、量角器等。
三、实验一：极限的探究1.设立实验任务：研究函数f(x)在某点a的极限。
2.实验步骤：a.确定函数f(x)和点a的取值范围，并在实验记录表中记录下来。
b.设定x的取值逐渐接近a的过程，并依次计算f(x)的值。
c.绘制出随着x的接近程度增加，f(x)的变化趋势图，并通过图像分析来研究f(x)在点a的极限。
3.实验结果和讨论：a.根据实验数据绘制的图像分析可以看出，当x接近a的时候，f(x)的值逐渐趋近于某一数值，这个数值就是f(x)在点a的极限。
b.实验结果和数学概念相符，证明了极限的定义和性质。
四、实验二：导数的计算1.设立实验任务：求函数f(x)在某点的导数。
2.实验步骤：a.确定函数f(x)和点a的取值范围，并在实验记录表中记录下来。
b.通过逐渐缩小x的取值范围，计算f(x)在点a的导数值。
c.通过实验数据绘制出f(x)在点a处导数的变化趋势图，并通过图像分析来研究f(x)在点a的导数。
3.实验结果和讨论：a.根据实验结果和图像分析可以得出结论，f(x)在点a的导数值表示了函数在该点的斜率。
b.实验结果和导数的定义和性质相符，进一步验证了导数的计算方法和应用。
五、实验三：定积分的求解1.设立实验任务：求函数f(x)在某区间的定积分。
2.实验步骤：a.确定函数f(x)和求解区间的取值范围，并在实验记录表中记录下来。
b.将求解区间分成若干个小区间，计算出每个小区间的面积。
高等数学实验报告
高等数学实验报告实验目的：本次实验旨在通过实际操作，加深学生对高等数学中一些重要概念和定理的理解，并培养学生分析和解决实际问题的能力。
实验原理：本实验主要涵盖了高等数学中的微积分部分内容，包括极限、导数、积分等。
实验仪器和材料：1. 笔记本电脑2. 数学软件3. 实验数据表格实验步骤：1. 在计算机上下载并安装数学软件。
2. 打开软件，并按照实验要求选择相应的数学题目。
3. 根据题目要求，运用软件进行计算，并将结果记录在实验数据表格中。
4. 对于给定的函数，求其极限、导数和积分。
5. 分析并解释计算结果，得出结论。
实验结果与讨论：通过本次实验，我们掌握了一些重要的数学概念和计算方法。
以下是实验结果的总结：1. 极限：通过计算不同函数的极限，我们发现当自变量趋于某个特定值时，函数的取值趋于一个确定的值或趋于无穷大。
这一概念在解决实际问题中具有重要意义，可以用于分析函数的增减性、收敛性等。
2. 导数：对于给定的函数，我们求得了其导数，并分析了导数的意义。
导数表示了函数在特定点的变化率，可以用于求解最值、判断函数图像的凹凸性等问题。
3. 积分：通过计算不同函数的积分，我们掌握了积分的计算方法和应用。
积分可以用于求解曲线下的面积、求解有限空间内的体积等问题。
根据实验结果，我们可以得出以下结论：1. 数学是一门既抽象又实际的学科，高等数学为我们提供了一种更深入、更精确的问题描述和解决方法。
2. 实际问题中的数学模型可以通过符号计算软件进行数值计算和模拟，从而得到更准确的结果和结论。
3. 数学实验可以锻炼我们的计算和分析能力，培养我们解决实际问题的思维方式。
结论：通过本次实验，我们深入学习了高等数学中的一些重要概念和计算方法，并应用这些知识解决了实际问题。
实验结果表明，数学实验具有重要的教学和科研价值，并能够提高学生的数学素养和解决实际问题的能力。
参考文献：[1] 高等数学课程教学大纲（试行）. (2017).[2] Stewart, J. (2015). Calculus: Early Transcendentals. Cengage Learning.。
高等数学实验报告
高等数学实验报告（2007年下学期）实验一 函数、极限和连续一、实验目的：通过画图语句Plot [f[x], {x, xmin, xmax}]作出函数的图形，利用图形研究函数的性态；加深了解函数趋向 的速度、 的阶和 等概念；学会“ ”的思考方法。
二、实验内容：1. 通过画图语句 作出函数的图形，利用图形研究函数的性态.2. Mathematica 中函数的近景图意味着较小的作图范围，远景图意味着较大的作图范围。
函数x e y =的近景图和远景图分别表示了该函数在 和 函数的性态。
3. 函数2x 、5182++x x 和 100502+-x x 的 是无穷远处函数的性态。
4. 我们称2x 是函数5182++x x 和 100502+-x x 当x →∞时的 。
通常，我们也称这三个函数趋向无穷大的速度是一样的。
三、实验过程记录1. 观察函数 4x , 571512738234+--+x x x x 和 8649587312234-+--x x x x 的近景图和远景图。
你的观察结果如何? 解释你所看到的现象。
2. 函数161452)(2324+++++=x x x x x x f 的远景图为一直线，为什么？写出该直线表示的函数)(x g 的表达式，比较)()(x g x f 和的远景图和近景图。
3.通过前面的实验，你能立即求出以下极限吗？ 13502lim 2626+++∞→x x x x x 分别用图形和Mathematica 中的 Limit 命令验证你的结论。
你能推广到一般情形吗？4 研究函数7)(x x f =和x ex g 3.0)(=在同一坐标轴上的近景图和远景图。
你能得出什么结论？5．给定正数a ，b ，k 和r ，你能否猜测出极限 rxkx ae bx +∞→lim . 的值。
分别用图形和Limit 命令验证你的结论。
6．求以下极限,sin 86cos 5lim 7.036x e x x x x x +--∞→,cos 3lim 224x e e e e x x x x x ----+∞→+-xe e e e x x xx x 224cos 3lim -----∞→+- 用图形和求极限命令分别验证你的结论。
高等数学数学实验报告(完成版)参考模板
高等数学数学实验报告实验人员：院（系）____土木工程学院工程力学系________ 学号____05313132___________姓名___姜煜___________实验地点：计算机中心机房实验一一、实验题目根据上面的实验步骤，通过作图，观察重要极限：ennn=+∞→)11(lim。
二、实验目的和意义利用数形结合的方法观察数列的极限，可以从点图上看出数列的收敛性，以及近似地观察出数列的收敛值，通过此实验对数列极限概念的理解形象化、具体化。
三、计算公式无四、程序设计五、程序运行结果六、结果的讨论和分析若将{i，1000}改为{i，10}，则得到如上图像，可以看出，在[0，10]区间上，函数已有趋向于e的倾向，但不明显。
当范围扩大到[0，1000]时，便已经能大致看出其渐近线x=e。
当范围进一步扩大，效果将更加明显。
实验二一、实验题目作出函数)44()sinln(cos2ππ≤≤-+=xxxy的函数图形和泰勒展开式（选取不同的0x和n值）图形，并将图形进行比较。
二、实验目的和意义目的：使用数学软件Mathematic计算函数f（x）的各阶泰勒多项式，绘制曲线图形，观察泰勒展开后结果与函数的关系。
意义：（1）通过本次实验，增强对泰勒公式的理解，以求能够熟练的掌握并使用泰勒公式求取近似值。
（2）比较泰勒公式展开后结果与函数逼近值的大小，以认识泰勒公式对于函数逼近的意义，以及泰勒公式的实际应用范围。
三、计算公式四、程序设计固定x=0，改变n的值固定n=8，改变x的值五、程序运行结果固定x=0，改变的n的值固定n=8，改变x的值六、结果的讨论和分析当选取不同的x0与n的值时，输出的结果会改变。
如果固定x的值，这随n的增加，函数的函数图形和泰勒展开式的图形会趋于吻合；如果固定n的值，图像只在展开点附近的一个局部范围内才有叫近似精确度。
实验三一、实验题目分别用梯形法、抛物线法计算定积分22sin dx xπ⎰的近似值（精确到0.0001）。
高数实验报告
高等数学数学实验报告实验一一、实验题目观察数列极限二、实验目的和意义通过作图观察数列极限：n趋向于无穷时，（1+1/n）^n三、计算公式四、程序设计data = Table[(1 + 1/i)^i, {i, 30}];ListPlot[data, PlotRange -> {2, 3}, PlotStyle -> PointSize[0.018]]五、程序运行结果六、结果的讨论和分析通过图像观察出数列趋向于重要极限e实验二一、实验题目一元函数图形及其性态二、实验目的和意义制作函数y=sincx的图形动画，并观察参数c对函数图形的影响三、计算公式请写出在程序中所需要的计算公式。
比如定积分的数值计算中，如用梯形法计算的，请描述梯形法的公式。
四、程序设计Animate[Plot[Sin[c x], {x, 0, 10}, PlotRange -> {-1, 1}], {c, -1, 4, 1/3}]五、程序运行结果0.51.00.51.01.00.5六、结果的讨论和分析通过图像观察出常数c 影响y=sincx 的周期和频率，函数周期为2Pi/c,频率为c/2Pi.实验三 一、实验题目泰勒公式与函数逼近 二、实验目的和意义对y=cosx 分别在[-Pi,Pi],[-2Pi,2Pi]上进行n 阶泰勒展开 三、计算公式请写出在程序中所需要的计算公式。
比如定积分的数值计算中，如用梯形法计算的，请描述梯形法的公式。
四、程序设计（1）t = Table[Normal[Series[Cos[x], {x, 0, i}]], {i, 0, 12, 2}]; PrependTo[t, Cos[x]];Plot[Evaluate[t], {x, -Pi, Pi}]（2）For[i = 0, i <= 10, a = Normal[Series[Cos[x], {x, 0, i}]]; Plot[{a, Cos[x]}, {x, -Pi, Pi},PlotStyle -> {RGBColor[0, 0, 1], RGBColor[1, 0, 0]}]; i = i + 2] (3)For[ =6, ≤16, =Normal[Series[Cos[ ],{ ,0, ,Cos[ ]},{ ,−2Pi,2Pi}, PlotStyle→{RGBC olor[0,0,1],RGBColor[1,0,0]}]; = +2](4)tt[x0_]:=Normal[Series[Cos[ ],{ ,x0,6}]];gs0=tt[0];gs3=tt[3];gs6=tt[6];Plot[{Cos [ ],gs0,gs3,gs6},{ ,−3Pi,3Pi},PlotRange→{−2,2},PlotStyle→{RGBColor[0,0,1],RGB Color[1,0,1],RGBColor[1,0,0],RGBColor[0,1,0]}] (5) f[x_]:=Sin[x 2];a=0;b=0.5Pi;m2=N[f''[0.0000635627]];dalta=10^(-4);n0=90;t[n_]:=(b-a)/n×((f[a]+f[b])/2+Sum[f[a+i×(b-a)/n],{i,1,n-1}]);Do[Print[n," ",N[t[n]]];If[(b-a)^3/(12n^2)×m2<dalta,Break[],If[n n0,Print["fail"]]],{n,n0}](6) f[x_]:=Sin[x 2];a=0;b=0.5Pi;m4=N[f''''[x→1.68676]];dalta=10^(-4);k0=100; p[k_]:=(b-a)/(6k)×(f[a]+f[b]+2Sum[f[a+i×(b-a)/(2k)],{i,2,2k-2,2}]+ 4Sum[f[a+i×(b-a)/(2k)],{i,1,2k-1,2}]);Do[Print[k," ",N[p[k]]];If[(b-a)^5/(180×(2k)^4)×m4<dalta,Break[],If[k n0,Print["fail"]五、程序运行结果(1)六、结果的讨论和分析步骤（1）（2）中为观察函数y=cosx在x=0处的泰勒展开，可以看出cos x 在x=0展开的10阶泰勒公式与cos x 逼近程度很高.步骤（3）过大显示区间范围，观察偏离x=0时泰勒公式对函数的逼近情况.，可以看出阶数越高，吻合程度越好，如cos x 的18阶泰勒展开式.步骤（4）固定阶数n=6，观察对函数的逼近情况.，可知可知，对于一确定的阶数，只在展开点附近的一个局部范围内才能较好地吻合.实验四定积分的近似计算一、实验题目观察数列极限二、实验目的和意义分别用梯形法、抛物线法计算定积分的近似值（精确到0.0001）三、计算公式四、程序设计<1>梯形法输入如下命令：f[x_]:=Sin[x^2];a=0;b=Pi/2;m2=N[f''[0]];dalta=0.0001;n0=100;t[n_]:=(b-a)/n*((f[a]-f[b])/2+Sum[f[a+i*(b-a)/n],{i,1,n-1}]);Do[Print[n,"",N[t[n]]];If[(b-a)^3/(12n^2)*m2<dalta,五、程序运行结果运行输出结果为：1__-0.490297 2__0.20918 3__0.444154 4__0.551059 5__0.611654 6__0.650588 7__0.67769 8__0.697632 9__0.712916 10__0.725 11__0.734794 12__0.742891 13__0.749696 14__0.75549615__0.760498 16__0.764856 17__0.768687 18__0.7720819__0.775107 20__0.777824 21__0.780277 22__0.78250123__0.784527 24__0.786382 25__0.788085 26__0.78965427__0.791106 28__0.792451 29__0.793703 30__0.79486931__0.795959 32__0.79698 33__0.797938 34__0.79883935__0.799687 36__0.800488 37__0.801245 38__0.80196239__0.802641 40__0.803286 41__0.803899 42__0.80448343__0.805039 44__0.805569 45__0.806076 46__0.80656147__0.807024 48__0.807468 49__0.807894 50__0.80830351__0.808695 52__0.809072 53__0.809435 54__0.80978455__0.810121 56__0.810445 57__0.810758 58__0.8110659__0.811351 60__0.811633 61__0.811905 62__0.81216963__0.812424 64__0.812671 65__0.812911 66__0.81314367__0.813368 68__0.813587 69__0.813799 70__0.81400571__0.814205 72__0.8144 73__0.814589 74__0.81477375__0.814952 76__0.815126 77__0.815296 78__0.81546279__0.815623 80__0.81578 81__0.815933三、计算公式四、程序设计<2>抛物线法输入如下命令：f[x_]:=Sin[x^2];p[k_]:=(b-a)/(6k)*(f[a]+f[b]+2Sum[f[a+i*(b-a)/(2k)],{i,2,2k-2,2}]+4Sum[f[a+i*(b-a)/(2k)],{i,2,2k-1,2}]);Do[Print[k,"",N[p[k]]];If[(b-a)^5/(180*(2k)^4)*m4<delta,五、程序运行结果运行输出结果为：1_ _0.163432 2_ _0.536045 3_ _0.662064 4_ _0.7144925_ _0.7424 6_ _0.759543 7_ _0.77108 8_ _0.7793489_ _0.785552 10_ _0.790373 11_ _0.794224 12_ _0.79736813_ _0.799983 14_ _0.802191 15_ _0.80408 16_ _0.805714 17_ _0.807142 18_ _0.808399 19_ _0.809514 20_ _0.810511 21_ _0.811406 22_ _0.812216 23_ _0.81295 24_ _0.813621 25_ _0.814234 26_ _0.814798 27_ _0.815318 28_ _0.815799 29_ _0.816245 30_ _0.81666 31_ _0.817047 32_ _0.817409 33_ _0.817748 34_ _0.818066 35_ _0.818365 36_ _0.818647 37_ _0.818913 38_ _0.819165 39_ _0.819403 40_ _0.819629 41_ _0.819844 42_ _0.820048 43_ _0.820242 44_ _0.820427 45_ _0.820603 46_ _0.820772 47_ _0.820933 48_ _0.821088 49_ _0.821235 50_ _0.821377 51_ _0.821513 52_ _0.821644 53_ _0.821769 54_ _0.82189 55_ _0.822006 56_ _0.822119 57_ _0.822227 58_ _0.822331 59_ _0.822431 60_ _0.822528 61_ _0.822622 62_ _0.822713 63_ _0.822801 64_ _0.822886 65_ _0.822968 66_ _0.823048 67_ _0.823125 68_ _0.8232 69_ _0.823273 70_ _0.823344 71_ _0.823412 72_ _0.823479 73_ _0.823544 74_ _0.823607 75_ _0.823668 76_ _0.823728 77_ _0.823786 78_ _0.823843 79_ _0.823898 80_ _0.823952 81_ _0.824004 82_ _0.824055 83_ _0.824105 84_ _0.824154 85_ _0.824201 86_ _0.824247 87_ _0.824293 88_ _0.824337 89_ _0.82438 90_ _0.824422 91_ _0.824463 92_ _0.824504 93_ _0.824543 94_ _0.824582 95_ _0.82462 96_ _0.824657 97_ _0.824693 98_ _0.824728 99_ _0.824763 100_ _0.824797实验结论：六、结果的讨论和分析梯形法：从运行结果看，循环81次后时因达到精度要求结束循环，并得到积分的近似值为：0.815933。
高数实验报告(上)
高等数学 数学实验报告实验人员：院（系） ：电子科学与工程学院 学号： 姓名：成绩_________ 实验时间：2015.11实验一:观察数列的极限一、 实验题目通过作图，观察重要极限 e nn n =+∞→)11(lim二、实验目的和意义利用数形结合的方法观察数列的重要极限，可以从点图上看出数列的收敛性，以及近似地观察出数列的收敛值；通过点图可以得出极限值为e 。
此实验得出了数列的一个重要极限。
三、计算公式(1+1/i)i i取50个点观察收敛值四、程序设计data=Table[(1+1/i)i ,{i,50}];ListPlot[data,PlotRange →{1,3},PlotStyle →PointSize[0.018]]五、程序运行结果六、结果的讨论和分析通过实验结果，更加了解重要极限的值的产生，初步体验程序的编写过程，实现求极限值。
在试验中，出现了因取点过少而无法观察极限的问题，在修正取点数后得到解决。
实验二：一元函数图形及其性态一、实验题目制作函数y=sincx的图形动画，并观察参数c对函数图形的影响。
二、实验目的和意义通过绘制图像，简单直观地展现函数图像，观察出参数c对函数图形的影响。
通过编程可以改变参数c的值，以此来发现参数改变对正弦函数周期的影响。
此实验使对正弦函数理解更为直观、明了。
三、计算公式y=sincx四、程序设计Do[Plot[Sin[c*x],{x,-3,3},PlotRange {-1,1}],{c,1,3,1/ 2}]五、程序运行结果六、结果的讨论和分析参数c 从1到3以1/2为步长，改变参数值c 使得正弦函数的周期发生变化，C 值越大，周期越小。
通过程序展示参数改变过程中图形变化情况，要使之更加生动，可以对这些图形进行动画演示。
实验三：泰勒公式与函数逼近一、 实验题目（根据图形观察泰勒展开的误差）观察sx x f co )(=的各阶泰勒展开的图形。
二、 实验目的和意义利用Mathematica 计算函数)(x f 的各阶泰勒多项式，并通过绘制曲线图形，来进一步掌握泰勒展开与函数逼近的思想。
高等数学实验报告分析
高等数学实验报告分析高等数学实验本学期安排8个学时，主要包括空间解析几何、多元函数微分学、积分学、级数、微分方程等内容，根据平时指导情况和学生的实验报告，情况如下：一、基本情况1. 多数学生能够按照实验指导书完成有关实验，通过实验学生学会了运用数学软件处理数学问题，体会到数学软件的强大威力，提高了解决实际问题的能力，为今后了解和学习数学建模知识奠定了基础。
2. 实验室管理规范，学生能够按照实验室要求和制度进行实验，实验秩序基本正常。
个别学生控制不住自己，乘实验指导教师不注意干其它事情，经老师批评教育，改正了错误。
二、实验存在问题1. 高等数学实验使用数学软件为MATLAB，MATLAB是一种强有力的数学软件，但高等数学实验指导书不可能包含MATLAB的很多命令，学生在处理一些灵活性较强、超出实验指导书的问题时会遇到困难，需要教师针对学生的问题予以耐心解答。
部分同学主动借阅或购买了数学软件方面的书籍，学到了较多知识。
2. 有些同学计算机基础较差，一些基本操作不熟练，也需要指导教师予以帮助，基本上可以在教师指导下完成有关实验任务。
三、实验报告批改中发现的问题1，由于本人承担的3院学生有精工实习，实验安排与课程进度不太协调，因此没有要求学生及时提交实验报告，多数同学在提交实验报告时将几次实验打印在一起，但基本符合有关实验报告的要求。
批阅中只要命令、结果正确即为A, 排版不规范的为B, 未完成规定要求的为C，结果不正确的为D.2. 个别学生WORD不熟练，排版不够规范。
3. 多数同学的实验报告缺乏进一步的分析，对实验中遇到的问题、老师如何提示、自己如何解决、如何利用所学知识处理类似数学问题没有进行深入分析，这是今后需要注意的问题。
4. 因本学期时间紧张，属于选作的提高性、综合性实验做的同学不多，做的同学也基本上没有提交实验报告。
四、今后需要改进的地方1. 引导学生自觉学习有关数学软件知识，根据实验中发现的问题修订实验指导书，尽可能将学生进行实验时遇到的问题在实验指导书中体现出来。
高数(上)实验报告
一、实验题目
泰勒公式与函数逼近
二、实验目的和意义
可以看出泰勒公式与原函数的比较
三、计算公式
L计
For[i=1,i11,a=Normal[Series[Log[Cos[x^2]+Sin[x]],{x,0,i}]];Plot[{a,Log[Cos[x^2]+Sin[x]]},{x,-Pi/4,Pi/4},PlotStyle{RGBColor[0,0,1],RGBColor[1,0,0]}];i=i+2]
三、计算公式
，n=1，2，3……
四、程序设计
五、程序运行结果
六、结果的讨论和分析
通过绘图，发现f（n）= 在n→+∞时，函数值无限靠近2.7左右的某一数值（e≈2.7），可判断数列 在n→+∞时，必收敛.
实验二
一、实验题目
制作函数y=sin cx图形动画并观察参数c对函数图形的影响。
二、实验目的和意义
高等数学数学实验报告
实验人员：院（系）机械工程学院学号_02A10314_姓名褚东宇
实验地点：计算机中心机房
实验一
一、实验题目
通过作图，观察重要极限： .
二、实验目的和意义
利用数形结合的方法观察数列极限，可从点图上看出数列的收敛性及近似得出数列的收敛值；通过编程可以输出数列的任意多项值，以此来得到数列的收敛性。
五、程序运行结果
六、结果的讨论和分析
随n值增大，泰勒公式的函数越来越趋向于原函数
掌握图形动画的应用，通过图形的变化找出参数对函数的影响。
三、计算公式
Sin cx
四、程序设计
Do[Plot[Sin[c*x],{x,-Pi,Pi},PlotRange{-1,1}],{c,1,3,1/2}]
高等数学数学实验报告(两篇)2024
引言概述:高等数学数学实验报告（二）旨在对高等数学的相关实验进行探究与研究。
本次实验报告共分为五个大点，每个大点讨论了不同的实验内容。
在每个大点下，我们进一步细分了五到九个小点，对实验过程、数据收集、数据分析等进行了详细描述。
通过本次实验，我们可以更好地理解高等数学的概念和应用。
正文内容:一、微分方程实验1.利用欧拉法求解微分方程a.介绍欧拉法的原理和步骤b.详细阐述欧拉法在实际问题中的应用c.给出具体的实例，展示欧拉法的计算步骤2.应用微分方程建立模型求解实际问题a.介绍微分方程模型的建立方法b.给出一个具体的实际问题，使用微分方程建立模型c.详细阐述模型求解步骤和结果分析3.使用MATLAB求解微分方程a.MATLAB求解微分方程的基本语法和函数b.给出一个具体的微分方程问题，在MATLAB中进行求解c.分析结果的准确性和稳定性二、级数实验1.了解级数的概念和性质a.简要介绍级数的定义和基本概念b.阐述级数收敛和发散的判别法c.讨论级数的性质和重要定理2.使用级数展开函数a.介绍级数展开函数的原理和步骤b.给出一个函数，使用级数展开进行近似计算c.分析级数近似计算的精确度和效果3.级数的收敛性与运算a.讨论级数收敛性的判别法b.介绍级数的运算性质和求和法则c.给出具体的例题，进行级数的运算和求和三、多元函数极值与最值实验1.多元函数的极值点求解a.介绍多元函数的极值点的定义和求解方法b.给出一个多元函数的实例，详细阐述求解过程c.分析极值点对应的函数值和意义2.多元函数的条件极值与最值a.讨论多元函数的条件极值的判定法b.给出一个具体的多元函数，求解其条件极值和最值c.分析条件极值和最值对应的函数值和意义3.利用MATLAB进行多元函数极值与最值的计算a.MATLAB求解多元函数极值与最值的基本语法和函数b.给出一个多元函数的具体问题，在MATLAB中进行求解c.分析结果的准确性和可行性四、曲线积分与曲面积分实验1.曲线积分的计算方法与应用a.介绍曲线积分的定义和计算方法b.给出一个具体的曲线积分问题，详细阐述计算过程c.分析曲线积分结果的几何意义2.曲线积分的应用举例a.讨论曲线积分在实际问题中的应用b.给出一个实际问题，使用曲线积分进行求解c.分析曲线积分结果的实际意义和应用价值3.曲面积分的计算方法与应用a.介绍曲面积分的定义和计算方法b.给出一个具体的曲面积分问题，详细阐述计算过程c.分析曲面积分结果的几何意义五、空间解析几何实验1.空间曲线的参数方程表示与性质a.介绍空间曲线的参数方程表示和性质b.给出一个具体的空间曲线，转化为参数方程表示c.分析参数方程对应的几何意义和性质2.平面与空间直线的位置关系a.讨论平面与空间直线的位置关系的判定方法b.给出一个具体的平面与空间直线的问题，判定其位置关系c.分析位置关系对应的几何意义和应用实例3.空间直线与平面的夹角和距离计算a.介绍空间直线与平面的夹角和距离的计算方法b.给出一个具体的空间直线和平面，计算其夹角和距离c.分析夹角和距离计算结果的几何意义总结:通过本次高等数学数学实验报告（二），我们深入了解了微分方程、级数、多元函数极值与最值、曲线积分、曲面积分以及空间解析几何的相关概念和应用。
高等数学实验报告 (2)
高等数学实验报告引言高等数学作为大学数学的一门基础课程，其实验内容十分重要。
本文将针对高等数学实验进行详细报告，通过实验分析和计算，进一步加深对高等数学理论的理解和掌握。
实验目的本次实验的目的是让学生掌握应用高等数学的知识和技巧，通过实验求解数学问题，巩固理论知识。
实验内容本次实验分为以下几个部分：1. 极限与连续通过实验验证极限和连续的相关性质，探究函数极限的计算方法，并通过实验加深对函数连续性的理解。
2. 导数与微分通过实验分析函数的导数和微分，验证微分中的等式，探究函数的单调性和极值，并通过实验加深对导数的理解。
3. 积分与不定积分通过实验求解函数的积分和不定积分，验证积分规则，分析函数的定积分，加深对积分的理解和应用。
4. 二元函数与偏导数通过实验分析二元函数的性质和偏导数的计算方法，探究偏导数在多元函数中的应用，并通过实验加深对多元函数的理解。
实验步骤与数据分析在每个实验部分，我们按照以下步骤进行实验，并对结果进行数据分析。
1. 实验步骤•阅读实验指导书，了解实验要求和内容；•在实验室中，根据实验内容准备实验所需的工具和材料；•按照实验步骤进行实验，进行数据记录和计算；•将实验结果整理并进行分析。
2. 数据分析通过实验得到的数据，我们进行以下分析和计算： - 对于极限和连续的实验，我们可以通过计算和绘制函数图像验证实验结果； - 对于导数和微分的实验，我们可以通过计算导数和微分系数来验证实验结果； - 对于积分和不定积分的实验，我们可以通过计算定积分和不定积分来验证实验结果； - 对于二元函数和偏导数的实验，我们可以通过计算偏导数和绘制二元函数图像来验证实验结果。
实验结果与讨论根据实验步骤和数据分析，我们得出以下实验结果和结论： - 在极限和连续的实验中，通过实验验证了函数极限的性质和函数连续的条件； - 在导数和微分的实验中，通过实验验证了函数导数的计算方法和微分的等式； - 在积分和不定积分的实验中，通过实验验证了积分规则和定积分的计算方法； - 在二元函数和偏导数的实验中，通过实验验证了多元函数的性质和偏导数的计算方法。
高等数学实验报告
高等数学实验报告
实验题目：求解非齐次线性方程组
实验目的：通过实验掌握求解非齐次线性方程组的基本原理和方法，掌握矩阵变换的基本概念和方法。
实验原理：对于非齐次线性方程组Ax=b，A为系数矩阵，b为常数列向量，如果Ax0=0，其中x0为齐次线性方程组Ax=0的通解，则非齐次线性方程组的通解为x=x0+xp，其中xp为Ax=b的一组特解。
实验内容：以3x3线性方程组为例，进行求解非齐次线性方程组的操作。
步骤1：对系数矩阵A进行初等变换，将矩阵化为上三角矩阵U。
此时方程组变为Ux=y，其中y为常数向量b经过初等变换得到的向量。
步骤2：利用回带法（也称为消元法的“回退”版），求出Ux=y 的解。
将求解过程记录在表格中（见表1）。
表1 回带法求解过程表
步骤3：求出非齐次线性方程组的一个特解xp。
由于Ax0=0，
故有(A+B)x0=-b，其中B是一个由U矩阵无法得出的矩阵，A为
U矩阵。
将(A+B)x0=-b解出x0，特解xp=A^(-1)(-b-Bx0)即为一个
特解。
步骤4：得到非齐次线性方程组的通解为x=x0+xp，其中x0为
齐次线性方程组Ax=0的通解，xp为步骤3求解得到的一个特解。
实验结果：用本实验的方法，求解线性方程组
2x1+6x2+10x3=12
0x1+7x2+5x3=-3
0x1+0x2+3x3=7
得到的解为
x1=-1
x2=2
x3=7/3
实验结论：本实验所用方法确实能够求解非齐次线性方程组，并得出正确解。
经过本次实验，我掌握了求解非齐次线性方程组的基本原理和方法，以及矩阵变换的基本概念和方法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
高等数学数学实验报告
实验人员：院（系）_土木工程学院___学号____05109225_姓名___唐涛____
实验地点：计算机中心机房
实验一
一、实验题目
作图，观察极限。
二、实验目的和意义
极限是高等数学中最基本的概念之一，初学者往往理解不够准确。
利用图像，数形结合，可以便于初学者直观的认识极限。
加深对极限的了解。
三、计算公式
四、程序设计
五、程序运行结果
六、结果的讨论和分析
由图中可以看到极限无限靠近某个值。
观察比较方便，利于初学者的学习。
实验二
一、实验题目
制作函数y=sincx的图形动画，观察c对函数图形的影响。
二、实验目的和意义
本实验的目的是让同学熟悉数学软件Mathematica所具有的良好的作图功能，并通过函数图形来认识函数，运用函数的图形来观察和分析函数的有关性态，建立
数形结合的思想。
三、计算公式
y=sincx
四、程序设计
五、程序运行结果
六、结果的讨论和分析
由实验结果我们可以清楚地认识到参数c对函数图形的影响。
诸如改变了函数的周期.
实验三
一、实验题目
对f（x）=cosx求不同的x处的泰勒展开的表达形式。
二、实验目的和意义
通过mathematic软件作出的函数图形，观察泰勒公式展开的误差，进一步掌握泰勒展开与函数逼近的思想。
三、计算公式
f(x)=cosx
四、程序设计
(一)
（二）
（三）
（四）
五、程序运行结果
（一）
（二）
（三）
（四）
六、结果的讨论和分析
从本实验我们可以得到一些结论，函数的泰勒多项式对于函数的近似程度随着阶数的提高而提高，但对于任意确定的次数的多项式，它只在展开点附近的一个局部范围内才有较好的近似精确度。
实验四
一、实验题目
计算定积分02sinx2x
的黎曼和
二、实验目的和意义
在现实生活中许多实际问题遇到的定积分，被积函数往往不能用算是给出，而通过图像或表格给出；或虽然给出，但是要计算他的原函数却很困难，甚至原函数非初等函数。
本实验目的，就是为了解决这些问题，进行定积分近似计算。
三、计算公式
四、程序设计
五、程序运行结果
02sinx2x
=0.828123
六、结果的讨论和分析
本实验求的近似值由给出的n的值的不同而不同。
给出的n值越大，得到的结果越接近准确的值，但因而电脑的计算量会变大。
而给出的n值越小，程序运行的结果越不精确。
因而，使用者可根据自己的实际情况确定n的取值。
实验五
一、实验题目
求在区间[2,5]上初值问题{ 的数值解，并求出数值解的图形。
二、实验目的和意义
在实际问题中，需要研究一些变动的量以及它们之间的关系，由于这些量是时刻变化的，因此他们之间的关系不能用简单的代数关系来表达，而要用微分方程来表示。
本实验中，我们求解一些简单常用的微分方程的方法，以及微分方程
的数值解的方法。
三、计算公式。
四、程序设计
五、程序运行结果
{{y[x] -> InterpolatingFunction[{{2., 5.}}, <>][x]}}。