数学实验报告——科赫分形雪花
数学实验报告——科赫分形雪花

实验报告:科赫分形雪花一、算法描述科赫分形雪花clearn=1;p=[0 0;5,sqrt(75)]; A=[cos(pi/3), -sin(pi/3);sin(pi/3) ,co s(pi/3)];for k=1:3j=1;for i=1:nq1=p(i,:);q2=p(i+1,:);d=(q2-q1)/3;r(j,:)=q1;r(j+1,:)=q1+d;r(j+2,:)=q1+d+d*A'; r(j+3,:)=q1+2*d;j=j+4;endn=4*n;p=[];p=[r;q2];endx=p(:,1);y=p(:,2);plot(x,y)hold on clearm=1;p=[5,sqrt(75);10 ,0];A=[cos(pi/3), -sin(pi/3);sin(pi/3) ,cos(pi/3)];for k=1:3e=1;for i=1:mq1=p(i,:);q2=p(i+1,:);d=(q2-q1)/3;r(e,:)=q1;r(e+1,:)=q1+d;r(e+2,:)=q1+d+d*A';r(e+3,:)=q1+2*d;e=e+4;endm=4*m;p=[];p=[r;q2];endx=p(:,1);y=p(:,2);plot(x,y)hold onclearn=1;p=[0,0;10, 0];A=[cos(pi/3), -sin(pi/3);sin(pi/3) ,cos(pi/3)];for k=1:3j=1;for i=1:nq1=p(i,:);q2=p(i+1,:);d=(q2-q1)/3;r(j,:)=q1;r(j+1,:)=q1+d;r(j+2,:)=q1+d+d*A;r(j+3,:)=q1+2*d;j=j+4;endn=4*n;p=[];p=[r;q2];endx=p(:,1);y=p(:,2);plot(x,y)二、证明科赫分形雪花图 Kn 的边数为:用数学归纳法证明:当n=1时,成立;假设当n=k时成立:L(k)=3X4^(k-1)当n=k+1时;因为雪花的边数增加,每一边将变为四边L(k+1)=4*L(K)将L(k)=3Xn^(k-1)代入上式,得:L(k+1)=3X4^k 满足L(n)=3X4^(n-1)综上所述,对于任意的N>0,且N为正整数的等式均成立。
Koch分形雪花图的面积计算

Koch 分形雪花图的面积计算一、问题叙述分形几何图形最基本的特征是自相似性,这种自相似性是指局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似。
在具有自相似性的图形中,图形局部只是整体的缩影,而整体图形则是局部的放大。
而本文我们要分析的是Koch 分形雪花图,包含以下三个问题:1.描述Koch 分形雪花2.证明Koch 分形雪花图K n 的边数为n 1L 34n -=⨯3.求Koch 分形雪花图的面积(数据),求n n lim A rea (K )→∞二、问题分析在分析Koch 分形雪花图之前,我们首先介绍Koch 分形曲线。
Koch 分形曲线的绘制原理是:从一条直线段开始,将线段中间的三分之一部分用一个等边三角形的两边代替,形成四条线段的折线,如图2.1所示:图2.1 对一条线段进行第一次Koch 分形然后,对形成的四条直线段的每一条的中间的三分之一部分用等边三角形的两边代替,形成十六条线段的折线。
这种迭代继续进行下去可以形成Koch 分形曲线。
在迭代过程中,图形中的点数将越来越多,而曲线的最终显示细节的多少将取决于迭代次数和显示系统的分辨率。
设P1和P2分别是原始的两个端点,现在需要在直线段的中间依次插入点Q1,Q2,Q3以产生第一次迭代图形。
显然,Q1位于P1右端直线段的三分之一处,Q3位于P1点右端直线段的三分之二处,而Q2点的位置可以看作由Q3绕Q1逆时针旋转60度而得到的,故可以处理Q Q 13经过正交变换而得到Q Q 12 。
算法如下: (1)Q1P 1+P P Q P 1+P P /3;←←(2-1)/3;32(2-1)(2)TQ 2Q 1+Q 3-Q A ←⨯(1); (3)P 5P 2P 2Q1P 3Q P Q 3←←←←;;2;4。
在算法中,用正交矩阵A 构造正交变换,其功能作用是对向量作旋转,使之成为长度不变的另一向量。
在绘制Koch 曲线的过程中,取旋转的角度为3π,则正交矩阵A 应取为:c o s ()s in ()33A =s in ()c o s ()33ππππ⎛⎫- ⎪⎪⎪⎪⎝⎭1.Koch 分形雪花的描述Koch 分形雪花的原始图形是等边三角形,它是由三条相等的线段围成的三角形。
科赫曲线-雪花曲线

科赫曲线-雪花曲线
科赫曲线
科赫曲线是一种外形像雪花的几何曲线,所以又称为雪花曲线,它是分形曲线中的一种,具体画法如下:
1、任意画一个正三角形,并把每一边三等分;
2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;
3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
和皮亚诺类似:
1、曲线任何处不可导,即任何地点都是不平滑的
2、总长度趋向无穷大
3、曲线上任意两点距离无穷大
4、面积是有限的
5、产生一个匪夷所思的悖论:无穷大的边界,包围着有限的面积。
(保守派数学大师们晕倒撞墙去吧)
Kohn曲线是比较典型的分形图形,它具有严格的自相似特性。
Koch分形雪花图地面积计算

Koch 分形雪花图的面积计算一、问题叙述分形几何图形最基本的特征是自相似性,这种自相似性是指局部与整体在形态、功能、信息、时间、空间等方面具有统计意义上的相似。
在具有自相似性的图形中,图形局部只是整体的缩影,而整体图形则是局部的放大。
而本文我们要分析的是Koch 分形雪花图,包含以下三个问题:1.描述Koch 分形雪花2.证明Koch 分形雪花图K n 的边数为n 1L 34n -=⨯3.求Koch 分形雪花图的面积(数据),求n n lim Area(K )→∞二、问题分析在分析Koch 分形雪花图之前,我们首先介绍Koch 分形曲线。
Koch 分形曲线的绘制原理是:从一条直线段开始,将线段中间的三分之一部分用一个等边三角形的两边代替,形成四条线段的折线,如图2.1所示:图2.1 对一条线段进行第一次Koch 分形然后,对形成的四条直线段的每一条的中间的三分之一部分用等边三角形的两边代替,形成十六条线段的折线。
这种迭代继续进行下去可以形成Koch 分形曲线。
在迭代过程中,图形中的点数将越来越多,而曲线的最终显示细节的多少将取决于迭代次数和显示系统的分辨率。
设P1和P2分别是原始的两个端点,现在需要在直线段的中间依次插入点Q1,Q2,Q3以产生第一次迭代图形。
显然,Q1位于P1右端直线段的三分之一处,Q3位于P1点右端直线段的三分之二处,而Q2点的位置可以看作由Q3绕Q1逆时针旋转60度而得到的,故可以处理Q Q 13经过正交变换而得到Q Q 12 。
算法如下: (1)Q1P1+P P Q P1+P P /3;←←(2-1)/3;32(2-1)(2)T Q2Q1+Q3-Q A ←⨯(1); (3)P5P2P2Q 1P3Q P Q3←←←←;;2;4。
在算法中,用正交矩阵A 构造正交变换,其功能作用是对向量作旋转,使之成为长度不变的另一向量。
在绘制Koch 曲线的过程中,取旋转的角度为3π,则正交矩阵A 应取为: cos()sin()33A=sin()cos()33ππππ⎛⎫- ⎪⎪ ⎪ ⎪⎝⎭ 1.Koch 分形雪花的描述Koch 分形雪花的原始图形是等边三角形,它是由三条相等的线段围成的三角形。
用几何画板画科赫雪花

用几何画板画科赫雪花摘要:科赫曲线是瑞典人科赫于1904年提出了著名分形曲线。
形状形似雪花,也叫雪花曲线。
具有处处连续但却处处不可导的性质。
本文应用几何画板软件在科赫曲线的基础上给出科赫雪花的几种画法。
关键词:几何画板科赫曲线科赫雪花画法一:画科赫曲线1.新建参数n:表示迭代次数2.画初元:画水平线段AB,将线段AB三等分,以中间1/3线段CD为边作等边△CDE(图1)。
3.得到生成元:保留折线段ACEDB,其余线段隐藏(图2)。
4.生成曲线:顺次选中A,B两点和参数n,按住sifit键深度迭代。
将AB按照箭头所指方向,依次迭代到AC,CE,ED,DB上。
得到科赫曲线。
保留含参数n的科赫曲线AB。
其余线段及点隐藏,改变参数n,可以看到不同迭代次数的科赫曲线(图3)。
二:正三角形法画科赫雪花1.含参数n的科赫曲线AB,按ctrl+A全选,再按自定义工具,创建工具(图1)。
2.另外画一个正△FGH。
按自定义工具或点击参数n,依次点击FH,HG,GF。
得到科赫雪花(图2)。
3.生成雪花:保留科赫雪花和参数n,其余点和线段隐藏。
改变参数n,可以看到不同迭代次数的科赫雪花(图3)。
三:正六边形法画科赫雪花1.新建参数n,表示迭代次数。
2.画初元:画水平线段AB,将线段AB三等分,以中间1/3线段CD为边,作正六边形CDEFGH(图1)。
3.画生成元:保留正六边形CDEFGH和A,B两点,其余线段隐藏(图2)。
4.生成雪花:顺次选中A,B两点和参数n,按sifit键进行深度迭代,按照箭头所指方向,将AB依次迭代到DC,ED,FE,GF,HG,CH,CE上,得到科赫雪花。
保留科赫雪花和参数n,其余隐藏。
改变参数n,看到不同迭代次数的科赫雪花(图3)。
四:正六角星法画科赫雪花1.新建参数n,表示迭代次数。
2.画初元:画水平线段AB,以AB为边,画正△ABC,中心为O点。
以O点为旋转中心,将△ABC旋转180°得到对应△DEF,两个三角形的交点依次标记为G,H,I,J,K,L(图1)。
科赫雪花
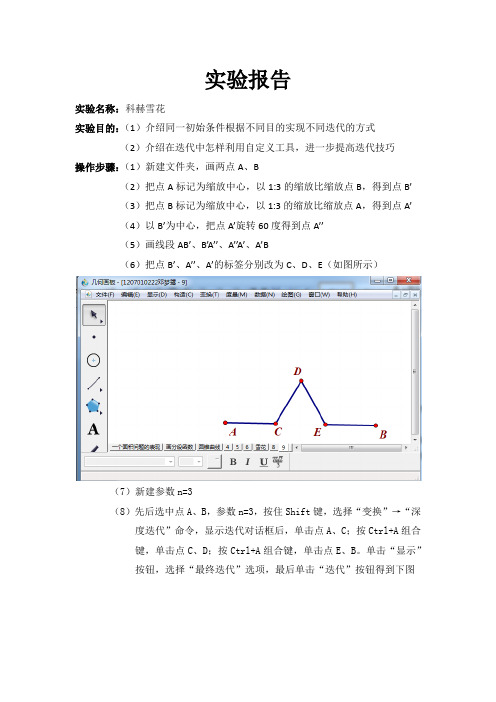
实验报告实验名称:科赫雪花实验目的:(1)介绍同一初始条件根据不同目的实现不同迭代的方式(2)介绍在迭代中怎样利用自定义工具,进一步提高迭代技巧操作步骤:(1)新建文件夹,画两点A、B(2)把点A标记为缩放中心,以1:3的缩放比缩放点B,得到点B’(3)把点B标记为缩放中心,以1:3的缩放比缩放点A,得到点A’(4)以B’为中心,把点A’旋转60度得到点A’’(5)画线段AB’、B’A’’、A’’A’、A’B(6)把点B’、A’’、A’的标签分别改为C、D、E(如图所示)(7)新建参数n=3(8)先后选中点A、B,参数n=3,按住Shift键,选择“变换”→“深度迭代”命令,显示迭代对话框后,单击点A、C;按Ctrl+A组合键,单击点C、D;按Ctrl+A组合键,单击点E、B。
单击“显示”按钮,选择“最终迭代”选项,最后单击“迭代”按钮得到下图(9)使“画线段”工具处于选中状态,按Ctrl+A组合键,选中所有线段。
在按Ctrl+H组合键,隐藏选中的线段(10)选中点C、D、E,按Ctrl+P组合键,填充三角形CDE(11)先后选中A、B以及参数参数n=3,按住Shift键,选择“变换”→“深度迭代”命令,显示“迭代”对话框后单击A、C;按Ctrl+A组合键,单击点C、D;按Ctrl+A组合键,单击点D、E;按Ctrl+A组合键,单击点E、B。
单击“显示”按钮,选择“完整迭代”选项,最后单击“迭代”按钮,得到图示图形(12)选中点C、D、E,按Ctrl+H组合键,隐藏它们(13)选中图形的所有部分,最后选中参数n=3,单击“自定义”工具,单击“创建新工具”,显示“新工具”对话框,输入工具名Koch,单击“确定”按钮,制作工具(14)单击“自定义”工具按钮,单击“显示脚本视图”,如图从“Koch的脚本”对话框中可见,使用这个工具的前提条件是两个点以及一个数值(15)以B为中心,把点A旋转60度得到点A’(16)选中点A、B、A’,按住Ctrl+P组合键填充三角形ABA’(17)选中“自定义”工具Koch,单击点B、A’,最后单击n=3(18)同(17)步,在点A’、A上使用Koch这个“自定义”工具,得到图所示的图形。
科赫曲线

科赫曲线
简介
科赫曲线(Koch curve )是一种像雪花的几何曲线,所以又称为雪花曲线。
1904年瑞典数学家科赫第一次描述了这种不论由直段还是由曲段组成的始终保持连通的线,因此将这种曲线成为科赫曲线。
定义
设想一个边长为1的等边三角形,取每边中间的三分之一,接上去一个形状完全相似的但边长为其三分之一的三角形,结果是一个六角形。
现在取六角形的每个边做同样的变换,即在中间三分之一接上更小的三角形,以此重复,直至无穷。
外界的变得原来越细微曲折,形状接近理想化的雪花。
画法
1、任意画一个正三角形,并把每一边三等分;
2、取三等分后的一边中间一段为边向外作正三角形,并把这“中间一段”擦掉;
3、重复上述两步,画出更小的三角形。
4、一直重复,直到无穷,所画出的曲线叫做科赫曲线。
特性
1、它是一条连续的回线,永远不会自我相交。
2、曲线任何处不可导,即任何地点都是不平滑的。
3、曲线是无限长的,即在有限空间里的无限长度。
4、曲线上任意两点距离无穷大。
5、每次变化面积都会增加,但是总面积是有限的,不会超过初始三角形的外接圆。
思考
科赫曲线中产生一个匪夷所思的悖论:"无穷大"的边界,包围着有限的面积。
这让保守派数学大师们都很难相信。
科赫曲线是比较典型的分形图形,它具有严格的自相似特性。
提问:在有限面积里面,无穷的去选择无穷小的点来组成的"封闭"曲线.会包围着无穷大的面积吗?。
数学实验报告Koch雪花。

数学实验报告试验二迭代与分形练习一实验目的与要求对一个等边三角形,每条边按照Koch曲线的方式进行迭代,产生的分形图称为Koch雪花。
编制程序绘制出它的图形,并计算Koch雪花的面积,以及它的分形维数。
实验过程具体的代码如下:function plotkoch(r,k) %显示等边三角形迭代k次后的曲线图 r代表边长默认(0 0)为起点p=[(r/2) r*sin(pi/3);r 0]; %存放结点坐标,每行一个点,初始值为两结点的坐标代表边1n=1; %存放线段的数量,初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程,计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标,计算迭代后它们之间增加的三个%结点的坐标,并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;b(j,:)=q1; %原起点存入rj=j+1;b(j,:)=q1+d; %新1点存入rj=j+1;b(j,:)=q1+d+d*A'; %新2点存入rj=j+1;b(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点,在迭代下条线段时存入rn=4*n; %全部线段迭代一次后,线段数量乘4clear p %清空p ,注意:最后一个终点q2不在r中p=[b;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例p=[0 0;r 0]; %存放结点坐标,每行一个点,初始值为两结点的坐标代表边2n=1; %存放线段的数量,初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程,计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标,计算迭代后它们之间增加的三个%结点的坐标,并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;z(j,:)=q1; %原起点存入rj=j+1;z(j,:)=q1+d; %新1点存入rj=j+1;z(j,:)=q1+d+d*A; %新2点存入rj=j+1;z(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点,在迭代下条线段时存入rn=4*n; %全部线段迭代一次后,线段数量乘4clear p %清空p ,注意:最后一个终点q2不在r中p=[z;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例p=[0 0;(r/2) r*sin(pi/3)]; %存放结点坐标,每行一个点,初始值为两结点的坐标代表边3n=1; %存放线段的数量,初始值为1A=[cos(pi/3) -sin(pi/3);sin(pi/3) cos(pi/3)]; %用于计算新的结点for s=1:k %实现迭代过程,计算所有的结点的坐标j=0; %%以下根据线段两个结点的坐标,计算迭代后它们之间增加的三个%结点的坐标,并且将这些点的坐标按次序存暂时放到r中for i=1:n %每条边计算一次q1=p(i,:); %目前线段的起点坐标q2=p(i+1,:); %目前线段的终点坐标d=(q2-q1)/3; %j=j+1;a(j,:)=q1; %原起点存入rj=j+1;a(j,:)=q1+d; %新1点存入rj=j+1;a(j,:)=q1+d+d*A'; %新2点存入rj=j+1;a(j,:)=q1+2*d; %新3点存入rend %原终点作为下条线段的起点,在迭代下条线段时存入rn=4*n; %全部线段迭代一次后,线段数量乘4clear p %清空p ,注意:最后一个终点q2不在r中p=[a;q2]; %重新装载本次迭代后的全部结点endplot(p(:,1),p(:,2)) %显示各结点的连线图hold on; %保存图像axis equal %各坐标轴同比例运行得到图像如下:k=1 k=5k=0时23 k=1时 S=234r +2312r k=2时 S=234r +2312r + 2327r k=3时 S=234r +2312r + 2327r + 243243r k=n 时 S=234r +2312r + …2(1)12133*4*()3n n r ---+2(1)233*4*()43n n r r - 每一次迭加,所产生的新三角形的边长变为上一次的13,数量为上一次的4倍. S=234+234*(3*21()3+12*221()3+……+3*(1)4n -*21()3n )2323*(1)211[3*4*()]3n i i i -=∑曲线总面积无穷大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验报告:科赫分形雪花一、算法描述科赫分形雪花
clear
n=1;p=[0 0;5,sqrt(75)]; A=[cos(pi/3), -
sin(pi/3);sin(pi/3) ,co s(pi/3)];
for k=1:3
j=1;
for i=1:n
q1=p(i,:);
q2=p(i+1,:);
d=(q2-q1)/3;
r(j,:)=q1;
r(j+1,:)=q1+d;
r(j+2,:)=q1+d+d*A'; r(j+3,:)=q1+2*d;
j=j+4;
end
n=4*n;p=[];
p=[r;q2];
end
x=p(:,1);y=p(:,2);
plot(x,y)
hold on clear
m=1;p=[5,sqrt(75);
10 ,0];
A=[cos(pi/3), -
sin(pi/3);sin(pi/3
) ,cos(pi/3)];
for k=1:3
e=1;
for i=1:m
q1=p(i,:);
q2=p(i+1,:);
d=(q2-q1)/3;
r(e,:)=q1;
r(e+1,:)=q1+d;
r(e+2,:)=q1+d+d*A';
r(e+3,:)=q1+2*d;
e=e+4;
end
m=4*m;p=[];
p=[r;q2];
end
x=p(:,1);y=p(:,2);
plot(x,y)
hold on
clear
n=1;p=[0,0;10, 0];
A=[cos(pi/3), -
sin(pi/3);sin(pi/3) ,
cos(pi/3)];
for k=1:3
j=1;
for i=1:n
q1=p(i,:);
q2=p(i+1,:);
d=(q2-q1)/3;
r(j,:)=q1;
r(j+1,:)=q1+d;
r(j+2,:)=q1+d+d*A;
r(j+3,:)=q1+2*d;
j=j+4;
end
n=4*n;p=[];
p=[r;q2];
end
x=p(:,1);y=p(:,2);
plot(x,y)
二、证明科赫分形雪花图 Kn 的边数为:
用数学归纳法证明:
当n=1时,成立;假设当n=k时成立:
L(k)=3X4^(k-1)
当n=k+1时;因为雪花的边数增加,
每一边将变为四边
L(k+1)=4*L(K)
将L(k)=3Xn^(k-1)代入上式,得:
L(k+1)=3X4^k 满足L(n)=3X4^(n-1)
综上所述,对于任意的N>0,且N为正整数的等式均成立。
三、求科赫分形雪花图 Kn 的面积 :
设第一个等边三角形的面积为a
第n次图形变换新增面积为an
则第二个图形新增的面积为3*(1/9)*a,
即a2=3*(1/9)
)
(
lim
n
n
K
Area
∞
→
推出an=第n-1个图形的边数*新增小三角形的面积即an=3*4n-2*(1/9)n-1a
则第n个图形的面积Sn为an的前n项和
所以Sn=
34
*[1()] 49
4
1
9
n
a
a
-
+
-
取极限,得
12748 lim lim[1()]
42095
n
n
n n
S a a a →∞→∞
=+-=
所以分形雪花图Kn的面积为(8/5)a。
