大学物理-多媒体课件 -01 静电场的场强
合集下载
静电场中某点的电场强度,其大小和方向
静电场中某点的电场强度,其大小和方向静电场是由电荷产生的一种力场，它与电荷的性质和分布有关。
在静电场中，任何点的电场强度都是以该点为中心的各点电矢量和电荷的性质有关。
下面我们将详细讲解静电场中某点的电场强度的大小和方向的相关参考内容。
大小：根据静电场的基本性质，静电场中某点的电场强度的大小与该点周围电荷的量和分布有关。
静电场的电场强度是标量，一般用大写字母E表示。
电场强度的大小可以通过库仑定律来计算：E = k * (Q / r^2)其中E表示电场强度，k表示库仑常数(8.99×10^9 N·m²/C²)，Q表示电荷的量，r表示离电荷的距离。
根据库仑定律可知，电场强度与电荷的量成正比，与距离的平方成反比。
方向：静电场中某点的电场强度的方向是由电荷产生的力场决定的。
根据库仑定律可以推导出静电场中某点的电场强度的方向与电荷的正负有关：1. 当电荷为正电荷时，电场强度的方向指向远离电荷的方向；2. 当电荷为负电荷时，电场强度的方向指向靠近电荷的方向。
在实际问题中，根据目标点周围电荷分布特点和几何形状，可以采用以下方法求解电场强度的方向：1. 若存在多个电荷，则将各个电场强度矢量叠加，按照平行四边形法则或三角形法则来求解合成的电场强度，最终的合成电场强度矢量方向即为所求的电场强度的方向；2. 若电场强度在一条直线上，可通过选取一点与所求点连线上的点，计算出电场强度大小并与所求点连线的单位矢量方向相乘，即可得到电场强度的方向。
在求解静电场中某点的电场强度的大小和方向时，一般可以应用如下方法：1. 利用电场电势的概念。
电场电势是电场强度的一种描述形式，可通过电场电势的梯度来求解电场强度（即E = -∇V）。
电场电势的梯度方向即为电场强度的方向。
2. 利用静电场的高斯定理。
高斯定理指出，通过任意闭合曲面的电通量与该闭合曲面内所有电荷的代数和成正比。
可以通过高斯定理结合具体问题的几何特点来求解电场强度的大小和方向。
大学物理 电场 电场强度
§5.1 电场 电场强度
一 电荷 电荷是物体状态的一种属性. 1. 电荷有正负之分 表示电荷多少的量叫作电量，单位为库伦，符号为C. 2. 同性电荷相互相斥，异性电荷相互吸引. 静止电荷之间的作用力称为静电力.
3. 电荷量子化
4. 电荷是守恒的
基本电量 e 1.602 10 19 C
q ne
r0 ：施力电荷指向受力电荷的矢径方向的单位矢量
静电力的叠加原理：当空间同时存在几个点电 荷时，它们共同作用于某一点电荷的静电力等于 其他各点电荷单独存在时作用在该点电荷上的静 电力的矢量和.
F F1 F2 F3
三
电场强度（E）
1.电场
电 场 电荷
电场 实物 电荷
电偶极子 指一对等量、异号的点电荷，其间距远小于它们 到考察点的距离的点电荷系统。 电偶极矩:
p ql
+q
(1)电偶极子场强 解：对A点： +q和-q 的场强 分别为
l 2 l 2 4 0 ( r ) 4 0 ( r ) 2 2 1 q q EA E E = [ ]i 4 0 (r l )2 (r l )2 2 2
物 质
电场是一种特殊形态的物质 ——几个电场可以同时占有 同一空间
相对于观察者为静止的带电体周围存在的电场称为 静电场 静电场对外表现主要有： ▲ 处于电场中的任何带电体都受到电场所作用的力.
▲ 当带电体在电场中移动时，电场所作用的力将对 带电体做功.
2.电场强度
电场中某点处的电场强度 E
等于位于该点处的单位试验电荷 所受的力，其方向为正电荷受力 方向.
dE x
1
a
2
x
一 电荷 电荷是物体状态的一种属性. 1. 电荷有正负之分 表示电荷多少的量叫作电量，单位为库伦，符号为C. 2. 同性电荷相互相斥，异性电荷相互吸引. 静止电荷之间的作用力称为静电力.
3. 电荷量子化
4. 电荷是守恒的
基本电量 e 1.602 10 19 C
q ne
r0 ：施力电荷指向受力电荷的矢径方向的单位矢量
静电力的叠加原理：当空间同时存在几个点电 荷时，它们共同作用于某一点电荷的静电力等于 其他各点电荷单独存在时作用在该点电荷上的静 电力的矢量和.
F F1 F2 F3
三
电场强度（E）
1.电场
电 场 电荷
电场 实物 电荷
电偶极子 指一对等量、异号的点电荷，其间距远小于它们 到考察点的距离的点电荷系统。 电偶极矩:
p ql
+q
(1)电偶极子场强 解：对A点： +q和-q 的场强 分别为
l 2 l 2 4 0 ( r ) 4 0 ( r ) 2 2 1 q q EA E E = [ ]i 4 0 (r l )2 (r l )2 2 2
物 质
电场是一种特殊形态的物质 ——几个电场可以同时占有 同一空间
相对于观察者为静止的带电体周围存在的电场称为 静电场 静电场对外表现主要有： ▲ 处于电场中的任何带电体都受到电场所作用的力.
▲ 当带电体在电场中移动时，电场所作用的力将对 带电体做功.
2.电场强度
电场中某点处的电场强度 E
等于位于该点处的单位试验电荷 所受的力，其方向为正电荷受力 方向.
dE x
1
a
2
x
大学物理——电场强度与电势
例题
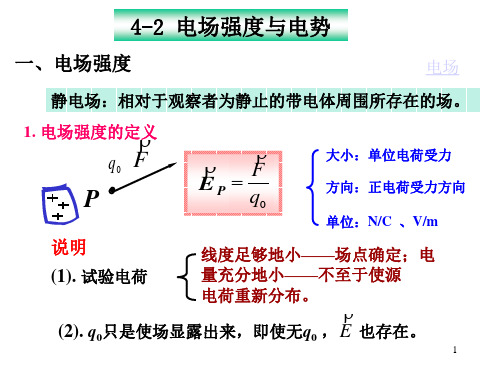
均匀带电细棒，长 L ，电荷线密度 ， 求：中垂面上的场强 。 r dQ
y
dQ dy
解 ： dE 4 r 3 0
r1
L0
dE dE x i dE y j E dE i dE x j 0 dE y
L L L
E r
2
3、场强叠加原理
（1）点电荷系的场强 Q2
点电荷的场强
点 电 Q1 荷
试验电荷 F2 Q
0
E
F F
1
Q 4 0 r
2
r0
由定义
F F3 F1 F2 E E1 E2 E3 Q0 Q0 Q0 Q0
L
E E //
x xQ dQ x dQ cos dE 2 L 3 L r 4 r 40 r 0 （1） x 0 xQ i
dE
E
L
dE 0
E0
4 0 x R
2
2
3
2
Q （2）R <<x E 2 4 0 x
dE
P
x
r
R
O
dr
9
讨论 (1) 当R >> x ，圆板可视为无限大薄板
E 2 0
(2)
E1
E1 E2
E1 E2
EI E1 E2 0 EII E1 E2 0 EIII E1 E2 0
E2
(3) 补偿法
10
例 已知圆环带电量为q ，杆的线密度为 ，长为L
qq 0 1 1 A r 4 0 1 r2
大学物理课件静电场
有限差分法求解边值问题
有限差分法原理
将连续的空间离散化为网格，用差分方程近 似代替微分方程进行数值求解。
有限差分法的离散化方案
常见的离散化方案包括向前差分、向后差分 和中心差分等。
有限差分法的求解步骤
建立差分方程、确定边界条件、采用迭代法 或直接法求解差分方程得到近似解。
06 静电危害防护与 安全措施
连续分布电荷系统势能计算方法
通过积分求解连续分布电荷的势能，需考虑电荷分 布的空间范围和形状。
静电场能量密度和总能量
静电场能量密度定义
单位体积内静电场所具有的能量。
静电场能量密度计算公式
$w = frac{1}{2} varepsilon_0 E^2$，其中$varepsilon_0$为真空 介电常数，$E$为电场强度。
静电场总能量计算
通过对静电场能量密度在空间上的积分，可求得静电场的总能量。
能量守恒定律在静电场中应用
能量守恒定律表述
在一个孤立系统中，无论发生何种变化，系统的总能量保持不变。
静电场中能量转化与守恒
在静电场中，电荷的移动和电场的变化都会伴随着能量的转化，但 总能量保持不变。
应用实例
如电容器充放电过程中，电场能与电源提供的电能或其他形式的能 量相互转化，但总能量不变。
分离变量法的适用范围
适用于具有规则几何形状和简单边界条件的静电场问题。
格林函数法求解边值问题
1 2
格林函数法原理
利用格林函数表示点源产生的场，并通过叠加原 理求解任意源分布产生的场。
格林函数的性质 格林函数具有对称性、奇异性和边界条件等性质。
3
格林函数法的应用步骤 确定格林函数、将源分布表示为点源的叠加、利 用格林函数求解场分布。
大学物理静电场 ppt课件
46
讨论：
a. q0 e0
电量为q的正电荷有q/0条电场线 由它发出伸向无穷远
q0e0
电量为q的负电荷有q/0条 电场线终止于它
对于两个无限接近的球面，通过他们的电通量都相同。 说明电场线在无电荷处连续。
b、若q不位于球面中心， 积分值不变。
+q
c、若封闭面不是球面， 积分值不变。
q
E•dS
第四篇
电磁学
1
2
第九章
静电场----相对于观察者静止的电荷产生的电场 两个物理量：电场场强、电势；
一个实验规律：库仑定律； 两个定理： 高斯定理、环流定理
3
9-1 电荷 库仑定律
一、电荷
1、两种电荷：正电荷“ +”、负电荷“ –” 同号相斥、异号相吸
2、电荷守恒定律 在一个与外界没有电荷交换的系统内, 正负电荷的代数
x
2
dl
dxE dc E od syE dsE in
5. 选择积分变量
r、、l 是 变 量 ， 而 线 积一分个只变能量21
选θ作为积分变量 lac( t g)actg
dlacs2cd r2 a2 l2
y
dE
dEy
a 2 a 2 c tg 2 a 2 csc2
dE x410rd2 lcos
i
讨论（1）当 q0， E 的方向沿x轴正向
当 q0， E 的方向沿x轴负向 （2）当x=0,即在圆环中心处，E0
当
x
E0
dE 0时 dx
x
a 2
aq
E Emax
4
2
0(a2
a2 2
3
)2
28
xq
E
讨论：
a. q0 e0
电量为q的正电荷有q/0条电场线 由它发出伸向无穷远
q0e0
电量为q的负电荷有q/0条 电场线终止于它
对于两个无限接近的球面，通过他们的电通量都相同。 说明电场线在无电荷处连续。
b、若q不位于球面中心， 积分值不变。
+q
c、若封闭面不是球面， 积分值不变。
q
E•dS
第四篇
电磁学
1
2
第九章
静电场----相对于观察者静止的电荷产生的电场 两个物理量：电场场强、电势；
一个实验规律：库仑定律； 两个定理： 高斯定理、环流定理
3
9-1 电荷 库仑定律
一、电荷
1、两种电荷：正电荷“ +”、负电荷“ –” 同号相斥、异号相吸
2、电荷守恒定律 在一个与外界没有电荷交换的系统内, 正负电荷的代数
x
2
dl
dxE dc E od syE dsE in
5. 选择积分变量
r、、l 是 变 量 ， 而 线 积一分个只变能量21
选θ作为积分变量 lac( t g)actg
dlacs2cd r2 a2 l2
y
dE
dEy
a 2 a 2 c tg 2 a 2 csc2
dE x410rd2 lcos
i
讨论（1）当 q0， E 的方向沿x轴正向
当 q0， E 的方向沿x轴负向 （2）当x=0,即在圆环中心处，E0
当
x
E0
dE 0时 dx
x
a 2
aq
E Emax
4
2
0(a2
a2 2
3
)2
28
xq
E
大学物理静电场.ppt
例 求一均匀带电直线在P点的电场。 y
解：建立直角坐标系
dE
取线元 d x 带电 dq dx
P
x
dE 1 dx 4 0 r 2
将 dE 投影到坐标轴上
dEx
1
40
dx
r2
cos
Ex
1
40
r2
cosdx
1
a
r
θ 2
x dx
dEy
1
40
dx
r2
sin
Ey
1
4 0
r2
sin dx
电场强度的计算
负电荷
正电荷
+
电场线
一对等量异号电荷的电场线
§电2场电强度场 电场强度
静电场：相对于观察者静止的电荷在周围空间激
发的电场。
{ •试验电荷q及条件
点电荷(尺寸小)
q足够小，对待测电场影响小
•定义电场强度
E
F
q
电场中某点的电场强度
等于单位正电荷在该点所
受的电场力。方向为正电
荷在该点的受力方向。
FA Aq
B
q
FB
电电场场强强度度叠的计加算原理：
• 宏观带电体的带电量Qe，准连续
库仑定律
3.库仑定律（点电荷的相互作用规律）
点电荷
可以简化为点电荷的条件:
d << r
Q1
r
观察点 P
d
库仑定律：在真空中，两个静止点电荷之间的相
互作用力与这两个点电荷的电荷量q1和q2的乘积成 正比，而与这两个点电荷之间的距离r12（或r21） 的平方成反比，作用力的方向沿着这两个点电荷
积分变量代换
大学物理：电磁学PPT
N F4
O
F2 B
en
M,N F1
O,P B
F2
en
l1 l1 M F1 sin F2 sin Il2 B l1 sin ISB sin 2 2 M IS B m B 线圈有N匝时 m NIS
2 电流元的磁场
dB
P *
I
Idl
0 Idl dB er 2 4 r
——毕奥-萨伐尔定律
r
3
磁场的叠加原理
B Bi
i
B dB
例 1： 判断下列各点磁感强度的方向和大小.
1 8 2Βιβλιοθήκη dB 0 1、 5 点 ：
7
Idl
R
6 5 4
例 5：
一半径为R，均匀带电Q的薄球壳。 求球壳内外任意点的电场强 度。
0 r R 如图，过P点做球面S1 E dS E dS 0 E 0
S1 S1
r
P
+ + +
+
S +1
O
如图，过P点做球面S2 rR E dS E dS Q / 0
rB
(electric potential )
点电荷电场 中的电势:
V
Q 40 r
电势的叠加 原理:
V Vi
i
点电荷电场中常取 无穷远处为电势零点
点电荷的电场线和等势面：
两平行带电平板的电场线和等势面：
+ + + + + + + + + + + +
大学物理电场 电场强度
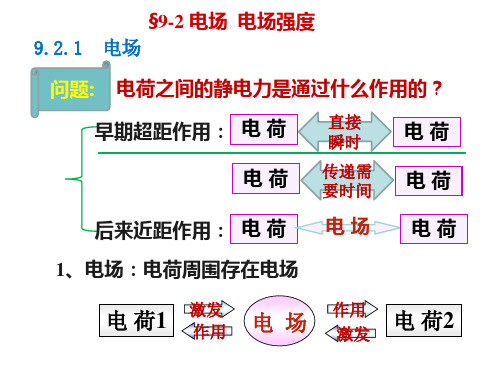
R2 )3
2
E
4π
qx
0(x2
R2 )3
2
讨论
1） x REFra bibliotek4πq
0x2
点电荷电场强度
2） x 0, E0 0
2R E
2
3） dE 0, x 2 R
o 2R x
dx
2
2
例5 均匀带电薄圆盘轴线上的电场强度.
度为有.一求半通径过为盘R心,0电且荷垂均直匀盘分面布的的轴薄线圆上盘任,意其一电点荷处面的密
整理后得： E E1 E2
n
En
i 1
1
4 0
qi ri3
ri
场强叠加原理: 电场中某点的场强等于每个电荷单 独在该点产生的场强的叠加(矢量和)。
9.2.3 连续分布的带电体产生的场强
取电荷元 dq，由点电荷的场强公式：
dE
dq
dE
r
4 0r3
E
dE
V
V
dq
4 0r3 r
★ 注意：是矢量积分
x R0
RdR
2 0 0 ( x2 R 2 )3/ 2
zR0
R
o
dR
P
dE
x
x 1
1
E (
)
20 x2 x2 R02
E x ( 1 1 ) 20 x2 x2 R02
讨论
x R0
E 2 0
无限大均匀带电 平面的电场强度
x R0
E
4π
q
0x2
点电荷电场强度
(1
R2 1 )0 2
P
r dq q
电
体密度
dq
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r
o -q p
+q ··
1 r
3
14
电偶极子场强分布的的特点：E
（3）一般情况 E
E E // E
1 4 o r 1 4 o r
3 3
[ 2 p // e r p e ] [ 2 p cos e r
E
e P
-q
· ·
l
+q
（如有极分子） 。
11
（1）轴线上的场强
× -q o +q
··
l = l ·r e
E-
P
×
E+
r
1 4
o
E
qer qer l 2 l 2 (r ) (r ) 2 2
E E E
r l 时：
电磁学
（Electromagnetism）
▲
电磁学研究的是电磁现象 的基本概念和基本规律： • 电荷、电流产生电场和 磁场的规律；
• 电场和磁场的相互联系； • 电磁场对电荷、电流的作用；
• 电磁场对物质的各种效应。
1
▲
处理电磁学问题的基本观点和方法 电磁作用是“场”的作用 （近距作用） • 观点： 着眼于场的分布 弥散于空间的电磁场， • 对象：
点电荷的概念
电荷守恒定律 电荷的相对论不变性
5
△§1.2
库仑定律（Coulombs law）
r21
q2
F12
q
er
21
1
F21
q1q 2 F 21 k e r F 12 2 21 r21
国际单位制（SI）中：
q — 库仑（C），
F—牛顿（N） ， r —米（m） 实验定出： k = 8.988010 9 N· 2/C2 m 演示 静电跳球（KD004） 静电摆球（KD005）
静电场 相对观测者静止的电荷产生的电场
3
本章目录
△§1.1 △§1.2 △§1.3
电荷、电荷守恒定律 库仑定律 电场和电场强度
§1.4 叠加法求场强 §1.5 电场线和电通量 §1.6 高斯定理
§1.7 高斯定理应用举例
4
△§1.1
电荷、电荷守恒定律
（electric charge， charge conservation law） 自学书 P3 P7 第1.1节，要着重搞清： 电荷的量子性和电荷连续分布的概念
平面电荷的电场线（KD002） 两个平行平面电荷的电场线（KD003） 28
几种电荷的 E 线分布的实验现象：
单个点 电 极
29
正负点电极
30
两个同号的点电极
31
单个带电平板电极
32
分别带正负电的平行平板电极
33
带异号电荷的点电极和平板电极
34
“怒发冲冠”
35
二. 电通量e
定义： Φe E d s
1. E线上某点的切向 即为该点 E 的方向；
2. E 线的密度给出 E
E
线。
E
切线
E
线
的大小。
lim N S d N d S
27
E
N
S 0
S
几种电荷的 E 线分布：
带正电的点电荷
电偶极子
均匀带电的直线段
演示
点电荷的电场线（KD001）
6
▲
库仑定律适用的条件： • 真空中点电荷间的相互作用 • 施力电荷对观测者静止（受力电荷可运动） 有理化：引入常量 0，令
1 4
2
0
▲
k
12
有： o
1 4 k
8 . 85 10
C /N m
2
0 —真空介电常量 （dielectric constant
of vacuum ）
( q i )r 4 0 r
3
1 4 0 r
3
点电荷场强
电偶极子场强
20
三. 连续带电体的场强 将带电体分割成无限多块无限小的带电体
dE P
E d E
q
d q er 4 o r
2
r
q
dq
体电荷 dq = dv ， ：体电荷密度 面电荷 dq = ds， ：面电荷密度 线电荷 dq = dl， ：线电荷密度
1 (r l 2 )
2
1 r
2
(1
l 2r
)
2
1 r
2
(1
l r
)
12
-q
o · ·+q
×
l = l ·r e
P
×
r
o
E
l r ) (1 l r )]
2ql 4
or 3
E
qer 4
1 r
2
[( 1
令 p ql ， l ： q q，
er
E
r
p q
○
+ p sin e ]
3( r p )r p 2 r
1 4 o r
3
-q
p +q
p
E
p 4 o r
3
3 cos
2
1
15
（4）电偶极子在均匀电场中所受的力矩
p FM M
系处 （距离r >>电荷系线度）， 点电荷电场为主， E
1 r
1 r
3
若
电偶极子的电场起主要作用，E 若
qi 0，
电四极子的电场起主要作用， E
2
qi 0 ，
p i 0 ， 则在远离电荷系处，
p i 0 ， 则在远离电荷系处，
1 r
4
18
实际上，点电荷系在远处的场强可以对
θ
F+ E
qE
F qE ， F qE ，
l 2 sin 2
M
qlE sin pE sin
M p E
16
*2. 电四极子（electric quadrupole）的场强
偶极子是 q 有微小位移而得到的；
四极子是 p 有微小位移而得到的：
xm =?，自己计算。
xm
x
R10， R2，此为均匀带电无限大平面：
2 0
E
x
2 o
x x
，
与轴无关 与 x 无关
25
2 0
E E
x
2 o
常量
R10， R2=R ，此为均匀带电圆盘情形：
E
x
x
2 o | x |
[
1
x
[1
则
E
2 p 4 r o
3
p称为电偶极矩（electric dipole moment）
这表明电偶极子的 q 和 l 是作为一个整体
影响它在远处的电场的。
13
（2）中垂线上的场强
E+ E ×P
由书 P1718 例1.3，有：
E p 4 o r
3
E-
（3）积分求
E d E id E
q q
E
：
x
Ex
i
E
x
q
dq 4 o r
2
2
2 R 2
cos
0 R1
r d r d
4
2 o
0
r
2
cos
R2
4
o R1
r d r r
2
x r
一. 点电荷的场强（intensity of point charge）
E P× 场点
由库仑定律和电场
强度定义给出：
E q er 4 o r
2
r
q “源”点电荷 （相对观测者静止）
·
点电荷电场强度分布的特点：E
1 r
2
9
二. 点电荷系的场强
E
×
点电荷qi 的场强：
Ei
P
Ei qier 4
电荷系中的某点（如O点）作台劳展开：
P
E
i
q i ri
ri r
qi q1
4 0 ri
3
i
qi 4
0
r ri 3 r ri
在远场区： r >> ri
r ri
3
ri
q2
( r ri ) ( r ri )
r
3 2
O qn
（ r
3
2
3/2 3 r （1 2 2 r r） i
r ri r
2
r ri
2
）
3/2
r （1 3
）
19
E
i
q i ( r ri ) 3 2 4 0 r ( 1 3 r ri r )
R2