正弦交流电路习题课
《电工技术》课件 正弦交流电路的功率
P
1 T
0T
pdt
1 T
0TUI[cos
cos(2t
)]dt
UI
cos
P UI cos
单位为瓦（W）
u 与 i 的夹角，即阻抗角
= cos 称为功率 因数，用来衡量对电
源的利用程度。
一、一般计算公式
3.无功功率
Q UI sin 单位为乏（Var）
4.视在功率：电路中总电压与总电流有效值的乘积，表示用电设备的容量。
（3）视在功率： S UI
S
Q
φ
功率三角形
P
S UI 单位为伏安（VA）
注： SN＝UN IN 称为发电机、变压器 等供电设备的容量，可用来衡量发电机、变压器可能提供的最大有 功功率。
• 注意 （1）平均功率P、无功功率Q和视在功率S的关系
S2 P2 Q2
（2） P、Q、S 都不是正弦量，不能用相量表示。
S
Q
功率三角形
S PQ P
二、几种特例电路的功率计算
（3） R、 、X L X C
解：
（1）根据电压三角形，求得总电压
U UR2 (UL UC )2 152 (60 80)2 25V
（2）电路中只有电阻是耗能元件，因此电路有功功率就是电阻消耗的功率。
P U R I 151 15W Q QL Q C ULI (UC I ) 20Var S UI 251 25VA
（2）无功功率： Q UI sin
因为电路中只有电感元件和电容元件有无功功率，因此无功功率又可以用公式：
Q QL Q C ULI (UC I )
I2XL I2XC
U
2 L
UC2
XL XC
电工技术第3章课后习题及详细解答
第3章单相正弦电路分析已知正弦电压（V）、（V），则u1与u2的相位差为，是否正确？为什么？分析讨论相位差问题时应当注意，只有同频率正弦量才能对相位进行比较。
这是因为只有同频率正弦量在任意时刻的相位差是恒定的，能够确定超前、滞后的关系，而不同频率正弦量的相位差是随时间变化的，无法确定超前、滞后的关系，因此不能进行相位的比较。
解不正确。
因为u1的角频率为ω，而u2的角频率为2ω，两者的频率不同，相位差随时间变化，无法确定超前、滞后的关系，因此不能进行相位的比较。
已知某正弦电流的有效值为10 A，频率为50 Hz，初相为45°。
（1）写出该电流的正弦函数表达式，并画出波形图；（2）求该正弦电流在s时的相位和瞬时值。
解（1）由题设已知正弦电流的有效值A，频率Hz，初相。
由频率f可得角频率ω为：（rad/s）所以，该电流的正弦函数表达式为：（A）波形图如图所示。
（2）s时的相位为：（rad）瞬时值为：（A）已知正弦电流（A）、（A），试求i1与i2的振幅、频率、初相、有效值和相位差，并画出其波形图。
解i1与i2的振幅分别为：（A）（A）频率分别为：（Hz）初相分别为：有效值分别为：（A）（A）i1与i2的相位差为：说明i1超前i2。
波形图如图所示。
图习题解答用图图习题解答用图设，，试计算、、AB、。
分析复数可用复平面上的有向线段、代数型、三角函数型和指数型（极坐标型）等形式表示。
复数的加减运算就是将实部和虚部分别进行加减，因而采用代数型比较方便。
复数的乘法运算就是将模相乘而辐角相加，复数的除法运算就是将模相除而辐角相减，因而采用指数型（极坐标型）比较方便。
解写出下列各正弦量所对应的相量，并画出其相量图。
（1）（mA）（2）（A）（3）（V）（4）（V）分析用相量来表示正弦量，就是用一个复数来反映正弦量的振幅（或有效值）和初相，即用相量的模来代表正弦量的振幅（或有效值），用相量的辐角来代表正弦量的初相。
电工学课后习题答案-第3章-交流电路习题及答案
I 。求： I 1 、 2 和 U 。 5 30 A
图3.17
返 回 上一页 下一页
图3.15
第 3 章
交 流 电 路
3.5.5
在图3.18（教材图3.09）所
示电路中，已知 R X C , U 220V 总电压 U 与总电流 I 相位相同。
3.8.1 在图3.25（教材图3.14）所示电路中， 80 , R
C 106 F , L 63.7 mH ,U 220 0 V 。
求：（1）f＝ 50Hz时的
I、I C
I 和 IC
I 、L ；
（2）f 为何值时，I 最小，这时的
和 I L 是多少？
图3.25
2.3698.27
B 8 45 A 8 j6 j 190
8 j 6 8 135
2.34 j 0.34
2.368.28
8 j 6 5.66 j 5.66
返 回
上一题
上一页
下一题
第 3 章
交 流 电 路
3.3.1 在图3.6（教材图3.01）所示 电路中，已知 R 100 , L 31.8 mH, C 318 F, 求电源的频率和电压分别为50 Hz、100 V 和1 000 Hz，100 V两种情况下，开关 S 合向 a、b、c 位置时电流表的读数，并 计算各元件中的有功功率和无功功率。
图3.6
【解】 本题目的是为了熟悉 R、C、L 在交流电路中的作用，即熟悉单一参数交流电路。
正弦交流电路习题课
0 由KCL， I1 I 2 I 3 j 2 1 2.263.4 A
U 40 在电压三角形中， arctg arctg 53.130 U2 30
I00 解：设 I
P 1 V1 I cos 1
Z1 Z1 1
240 171 4 cos 1
1 69.460 171 Z1 69.460 42.75 69.460 4 V V2 Z 2 2 60 2 Z1 Z 2 25 I I
提高功率因数的意义方法
• 提高功率因数能使电源设备的容量得到充 分利用； • 提高功率因数能减小线路功耗和电压损耗。 • 提高功率因数的方法通常是在感性负载 两端并联一个电容器，称之为补偿电容 器。补偿电容器的容量为：
正弦稳态电路的分析
• 用相量法分析电路时，线性电阻电路的 各种分析方法和电路定理可推广用于线 性电路的正弦稳态分析，差别仅在于所 得的电路方程是以相量形式表示的代数 方程以及用相量形式描述的电路定理， 而计算则为复数运算。
U I XC
U I XL
I CU
基尔霍夫定律的相量式
• 基尔霍夫定律的相量式与三种基本电路 元件伏安特性的相量形式，是分析正弦 交流电路的基础。 0 U
I 0
• 应用基尔霍夫定律及单一参数电路所得 出的结论，对R、L、C串联、并联电路 进行了分析，分别引出了阻抗Z和导纳Y 的概念。
正弦稳态电路的分析
习题总结课
正弦量及其三要素
1、随时间按正弦规律变化的电流、电压、 电动势等统称为正弦量。 2、正弦量的有效值（振幅）、频率（周期 或角频率）和初相是正弦量的三要素。 三要素是确定一个正弦量的充要条件。 3、直流电的大小和方向恒定不变，在直流 计算时只考虑其大小即可。而在交流电 的分析与计算时，除了考虑大小外，还 要考虑其相位。
正弦稳态电路习题课
⇒ Z1 = Z 2
2 2 2 2
Z2 = R + X
X1 = X 2
性质相反，一个 为感性，另一个 为容性
⇒
U1 = U 2 = 50 2V>U = 50V ⇒
X1 = − X 2
Z = Z1 + Z 2 = R1 + jX 1 + R2 + jX 2 = R1 + R2 = 2 R1
端口电压、电流 同相
B0 = −0.1S < 0
1 1 =− = 1H L0 = − −0.1× 10 B0ω
B0 = −0.1S < 0
⇒
5Ω
1H
正弦稳态电路习题课习题（3/8） ）
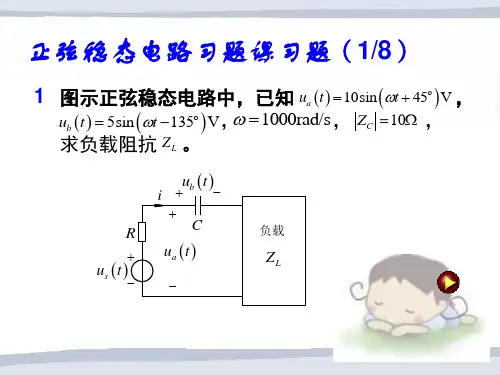
图示正弦交流电路中，已知电流表的示数为2A， 3 图示正弦交流电路中，已知电流表的示数为 ，电 压表1的示数为 的示数为17V，2的示数为 的示数为10V。求电源电压 压表 的示数为 ， 的示数为 。 的有效值。 的有效值。
正弦稳态电路习题课习题（6/8） ）
U 图示电路中，ɺ = 50∠0o V，每一阻抗部分消耗的功 6 图示电路中， 率均为250W，且电压的峰值为 率均为 ，且电压的峰值为100V。求（1）阻抗 。 ） Z1 和 Z 2 ；（ ）若 ω = 800π rad/s ，求电路可能含有 ；（2） 的元件及其数值。 的元件及其数值。
jω L2
R1
ɺ Us −
+
ɺ IC
jω L1
1 jωC
ɺ IC
R2
ZL
7 解（1) 求开路电压
Z L 2 = jω L2 = j100Ω
1 ZC = = − j100Ω + jωC ɺ Us ɺ = − I R = −100 I − ɺ ɺ ⇒U
第3章 正弦交流稳态电路(1.2.3.4节)
φ 'i<0。对于同一电路中的多个相关的正弦量，只能选择一个共同的计时
零点确定各自的初相位。
3.相位差
相位差描述的是两个同频率正弦量之间的相位关系。 假设两个正弦电流
分别为
i1 i2
2 I1 sin(t 1 ) 2 I 2 sin(t 2 )
其中，设φ 1>φ 2，它们的波形如下图所示。 （两电流的相位差）
由于正弦量按周期性变化360°，所以正弦量的相量是旋转相量。 正弦电流i=Imsin(ω t+φ i)在任一时刻的值，等于对应的旋转相量该时 刻在虚轴上的投影，如图3．2-2所示。
将一个正弦量表示为相量或将一个相量表示成正弦量的过程称为相 量变换。由图3．2-2可知，该相量只表示了对应正弦量的两个特征量—
—幅值和初相位。故相量只是用于表示正弦量，并不等于正弦量。
相量在复平面上的图称为相量图。相量图可以形象地表示出各个相 量的大小和相位关系。
例3．2-1： 已知电流
i1 5 2 sin(t 30o ) A, i2 10 2 sin(t 60o ) A 试画出这
两个正弦量的相量和相量图。
2 是220V，而其幅值为
³220=311V。在我国，民用电网的供电电压为
220V，日本和美国的供电电压为110V，欧洲绝大多数国家的供电电压也为 引入有效值后，正弦电流和电压的表达式也可表示为 220V 。
i I m sin(t i ) u U m sin(t u )
弦量的初相位，计时零点在右为正，即φ i>0，如图3．1-2(a)所示初相位
为正。初相位的取值范围为|φ i|≤180°。
在电路中，初相位与计时零点的选择有关。对于同一正弦量，如果其 计时零点不同，其初相位也就不同，对于图3．1-2(a)中所示的正弦量，如 果按图3．1-2(b)所示坐标建立计时零点，则正弦量 的初相为负，即
正弦交流电相位、初相位、相位差教案
教案（31 ）【导入新课】[1]直流电的定义及表示[2]电磁感应现象通过回顾电能的应用引入交流电及本节课题--正弦交流电的产生【教学过程】正弦交流电的相位、初相位、相位差一、相位和相位差[1．]相位定义：任意一个正弦量y = Asin(t 0)的中的(t 0)称为相位。
[2．]初相位：相位中的0，称为初相位，可反映正弦交流电的初始(t=0)的值。
[3．]相位差：两个同频率正弦量的相位之差(与时间t无关)。
可证明：两个同频率正弦量的相位之差等于初相位之差。
设第一个正弦量的初相为01，第二个正弦量的初相为02，则这两个正弦量的相位差为12 = 01 02并规定1212 180或[4．]两个正弦量的相位关系的讨论： (1) 当12 > 0时，称第一个正弦量比第二个正弦量的相位越前(或超前) 12；(2) 当12 < 0时，称第一个正弦量比第二个正弦量的相位滞后(或落后)| 12|；(3) 当12 = 0时，称第一个正弦量与第二个正弦量同相，投影图7-1(a)所示；(4) 当12 = 或180时，称第一个正弦量与第二个正弦量反相，投影图7-1(b)所示；(5) 当 2-12或90时，称第一个正弦量与第二个正弦量正交。
二、应用举例：[1]已知u = 311sin(314t 30) V，I = 5sin(314t 60) A，则u与i的相位差为：ui = (30) ( 60) = 90即u比i滞后90，或i比u超前90。
[2]正弦交流电流 i = 2sin(100t 30) A，如果交流电流i通过R = 10 的电阻时，电流的最大值、有效值、角频率、频率、周期及初相并求电功率P 解：最大值Im = 2 A 有效值I = 2 0.707 = 1.414 A， = 100 rad/s f =/ 2 = 50hz T =1/f=0.02s 0=30在一秒时间内电阻消耗的电能(又叫做平均功率)为P = I2R = 20 W，五、总结：本节介绍了正弦交流电的定义特点及三要素，结合正弦表达式搞清各要素间关系及物理意义，并学会相关计算；正确理解相位差的含义及两正弦交流电间相位关系。
电工学课后习题
相量图可参考教材图 2-10 例 2-3 绘出。 2-5 设有正弦电流 i1 = 14.14sin(ωt − 50°) A, i2 = 28.3cos(ωt − 50°) A, 写出它们的最大值
和有效值相量表示式，并画出相应的相量图。 解： I1m = 14.14e− j50° A = 14.14∠−__5_0_° A, I1 = 10∠−__5_0_° A I2m = 28.3ej(90°−50°) A = 28.3∠_4_0_° A , I2 = 20∠_4_0_° A
解：
（1）可参考教材图 2-5 例 2-2 的电压变化曲线绘出
（2） ϕu1
=
−
π 6
+
⎛ ⎜⎝
1 600
1 50
⎞ ⎟⎠
×
2π
=
0°
ϕu2
=
π 3
+
π 6
=
π 2
=
90°
2-9 写出下列各相量所对应的时间函数： （1） I1 = 10∠_7_2_° A, I2 = 5∠_−_1_5_0_° A; （2）Um = 200∠_1_2_0_° V, U 2m = 300∠_−_6_0_° V。
解： （1） I = I1 + I2 = 1.5(cos17° + jsin17°) A + 0.7[cos(−42°) + jsin(−42°)] A
= (1.954 − j0.02) A = 1.954∠_−_0_._8_5_° A
即
i = 1.954 2 sin(ωt − 0.85°) A
解：
[理学]考试题目：电路基础习题课_课后答案
![[理学]考试题目：电路基础习题课_课后答案](https://img.taocdn.com/s3/m/4ae1abcf524de518964b7d6c.png)
3.7 把L=51mH的线圈（其电阻极小，可忽略不计），接在电压为220V、频率为 50Hz的交流电路中，要求：（1）绘出电路图；（2）求出电流I的有效值；（3） 求出XL。
解：（1）绘出电路图如右图所示； （2）电流有效值为
U 220 103
I
13.75
L 314 51
（3）线圈感抗为
解：根据电路图可画出相量示意图如图所示，由相量图中的电压三角形又可 导出阻抗三角形，由阻抗三角形可得
XC
1
C
10 6 314 0.1
31847
tg 30 X C R
R X C 31847 55165 tg 30 0.5773
4.5 已知RLC串联电路的参数为R=20Ω，L=0.1H，C=30μF，当信号频率分别为 50Hz、1000Hz时，电路的复阻抗各为多少？两个频率下电路的性质如何？
解：（1）电流表A的读数即电路中总电流，即
I 52 (20 25)2 7.07
（2）频率提高一倍时，感抗增大一倍而使得通过电感的电流减半，即A2读 数为10A；容抗则减半而使通过电容的电流加倍，即A3读数为50A。所以总 电流表A的读数为
I 52 (10 50)2 40.3
0 L
1500
计算结果表明，当并谐电路中再并入一个电阻时，电路的品质因数降低，选择性变差
5.10 一个R=13.7Ω，L=0.25mH的电感线圈，与C=100pF的电容器分别接成串 联和并联谐振电路，求谐振频率和两种谐振情况下电路呈现的阻抗。
解：①串联谐振时，电路的谐振频率为
1
10 6
f 0 2
R 2 (0.22 (2.5 52 5) 7.1
第九章正弦稳态电路的分析课本部分习题
第九章正弦稳态电路的分析正弦稳态电路的分析应用相量法。
通过引入相量法，建立了阻抗和导纳的概念，给出了KCL，KVL和欧姆定律的相量形式，由于它们与直流电路的分析中所用的同一公式在形式上完全相同，因此能够把分析直流电路的方法，原理，定律，例如，网孔法（回路法），结点法，叠加定理，戴维宁定理，等效电源原理等等直接应用于分析正弦电路的相量模型，其区别仅在于：（1）不直接引用电压电流的瞬时表达式来表征各种关系，而是用对应的向量形式来表征各种关系；（2）相应的运算不是代数运算，而是复数的运算，因而运算比直流复杂。
但根据复数运算的特点，可画出向量图，利用向量图的几何关系来帮助分析和简化计算，从而扩大了求解问题的思路和方法。
（3）引入了一些新的概念，如平均功率，无功功率，视在功率，复功率，最大功率传输，谐振等。
认识以上区别，对正弦稳态电路的分析是有益的。
9-1试求图示各电路的输入阻抗Z和导纳Y。
解：（a）Z=1+=1+=Y====S(b) Z==Y=（c） Y=SZ=题9-1图设端口电压相量为，根据KVL，得所以输入阻抗为导纳设端口电压，电流相量为，，根据KCL，得且有所以输入阻抗导纳注：本题的求解过程说明，引入阻抗和导纳的概念以后，正弦电路的输入阻抗（或导纳）的定义与计算和直流电路输入电阻（或电导）的定义与计算是相似的。
即输入阻抗若有n个阻抗串联，等效阻抗若有n个导纳并联，等效导纳为只不过Ｚ和Ｙ是复数。
９－２已知图示电路中，。
试求电路中合适的元件值（等效）。
解：把u用余弦函数表示有u和I的相量形式为,根据入端导纳的定义，有既图示的两并联元件为电导和电容，其参数为注：以上计算表明，导纳的模等于电流与电压的模值之比，导纳角等于电流与电压的相位差，若导纳角，表示电流超前电压，导纳为电容性，反之为电感性。
9-3 附图中N为不含独立源的一端口，端口电压u，电流I分别如下列各式所示。
试求没一种情况下的输入阻抗Z和导纳Y，并给出等效电路图（包括元件的参数值）。
第3章习题课 正弦交流电路
3.5 将以下相量转化为正弦量 (1) U 50 j50V (2) Im 30 j40A (3) Um 100 2e j30V (4) I 1 30A
解：(1) u(t) 50 2 2 sin(t 45) 100sin(t 45)V (2) i( t ) 50 sin(t 126.9 )A (3) u(t) 100 2 sin(t 30)V (4) i(t ) 2 sin(t 30)A
3.6 相量图如图所示，已知频率ƒ=50Hz。写出它们对
应的相量式和瞬时值式。
100V
解：
I 100 i( t ) 10 2 sin 314t A
U1 10090 u1( t ) 100 2 sin( 314t 90 )V U2 80 60 u2 ( t ) 80 2 sin( 314t 60 )V Um 3100 u( t ) 310 sin 314tV I1m 10 45 i1( t ) 10 sin( 314t 45 )A I2m 1260 i2 ( t ) 12 sin( 314t 60 )A
(1)求电压uR、uL、 uC和电流i。 (2)求电路的有功功率P、无功功率Q和视在功率S。 (3)画出相量图。
解：
i 10 2 sin(100t)A uR 100 2 sin(100t)V uL 100 2 sin(100t 90)V uC 100 2 sin(100t 90)V P 1000W,Q 0var,S 1000VA
(b) Z2、Z3不能正常工作，Z2上电压仅为126.7V， 低于额定电压，而Z3上电压253.3V，高于额定电压。
解： (1) u1超前于u2 45 。
(2) 60，u 滞后于 i 60 。
(3)由于u 、 i 不同频，故无法比较相位。
电工学第七版第4章 正弦交流电路(南昌大学期末考试必考知识点其他学校只供参考)PPT课件
4.3 单一参数的交流电路
⑶波形关系
ui u
⑷相量关系
UU0 II0 O
i
ωt
U I
U I
R
欧姆定律的相量表示式： U RI
⑸相量图
I U
制作群
21
主 页 总目录 章目录 上一页 下一页 退 出
4.3 单一参数的交流电路
⒉ 功率关系 ⑴瞬时功率p
ui u
电压瞬时值u与电流
i
O
瞬时值i的乘积。
p ui UmImsi2nωt p
R
u
-
R
正半周
负半周
图中虚线箭头代表电流的实际方向；
、 代表电压的实际方向（极性）。
正弦量：正弦电压和电流等物理量统称为正弦量。
制作群
5
主 页 总目录 章目录 上一页 下一页 退 出
4.1 正弦电压与电流
正弦量的特征表现在：
变化的快慢 大小 初始值
频率 幅值
正弦量的三要素
初相位
设正弦交流电流：
i Im
第4章 正弦交流电路
4.1 正弦电压与电流 4.2 正弦量的相量表示法 4.3 单一参数的交流电路 4.4 电阻、电感与电容元件串联的交流电路 4.5 阻抗的串联与并联 *4.6 复杂正弦交流电路的分析与计算 4.7 交流电路的频率特性 4.8 功率因数的提高 4.9 非正弦周期电压和电流
制作群
1
主 页 总目录 章目录 上一页 下一页 退 出
4.2 正弦量的相量表示法
4.2.2 相量
表示正弦量的复数称相量。
相量只是表示正弦量，而不等于正弦量。
⒈ 相量式
设正弦量：uU m si(n ω tψ ) 电压幅值相量表示： U mUm ejψUm ψ 电压有效值相量表示： UUejψUψ
《电工电子学》课程练习题
1.2 利 用 电 源 模 型 的 等 效 变 换 法 化 简 题 图 1.2 所 示 电 路 。 已 知 ： US1=9V, US2=12V,IS1=5A，IS2=2A，R1=3，R2=6。
1.3 用支路电流法求题图 1.3 中所标的各未知电流和电压，并说明电压源和电流源是 发出功率还是吸收功率。
题 5.2 图 题 5.3 图 5.4 求题图 5.4 所示电路输出电压 u0 与输入电压 ui 的关系式。
题 5.4 图 5.5 题图 5.5 所示电路是利用两个运放组成的具有高输入电阻的差动放大器，试求 u0 与 ui1、ui2 的关系式。
题 5.5 图
第六章 数字集成电路及其应用
练习 6-12；6-16；6－22；6-27；6-29；6-30 6.1 设三台电动机 A、B、C，今要求：A 开机则 B 必须开机；B 开机则 C 也必须开 机，如果不满足上述要求，即发出报警信号。试写出报警信号的逻辑表达式，并画出 逻辑图。 6.2 用 8 选 1 数据选择题 MUX 实现 。 6.3 分析题图所示电路的逻辑功能。
cos 0.05 ，试求此线圈在具有铁心时的铜损和铁损。
12.2 有一单相照明变压器，容量为 10V A ，电压为 3300/220V，今欲在副边接上 60W、220V 的白炽灯，如果要变压器在额定情况下运行，这种电灯可接多少个？并 求原、副绕组的额定电流。 12.3 有一台三相异步电动机，其技术数据如下：
练习 2-2；2-8；2-16；2-21；2-28；2-35；2-38 2.1 已知向量 I1=5+j5A，I2=5-j5A，I3=-5+j5A，I4=-5-j5A.试分别用瞬时值表达式及相 量图表示它们（设 1000 rad / s ）。 2.2 在题图 2.2 所示电路中，Z1、Z2 上的电压分别为 U1=6V，U2=8V。 （1）设 Z1=R，Z2=jXL，U=? （2）若 Z2=jXL，Z1 为何种元件时 U 最大，最大值是多少？Z1 为何种元件时 U 最小， 最小值是多少？
第4、5章习题课
U
R
R1
I 1 I 2 - jX C jX L
-
(1) Z1 、Z 2 Z I i (2) I I 、I i , i
1 2 1 2
解：用相量式计算 U 220 0 V Z1 R 1 j X L (100 j200)Ω
I
+
U
A
(1)复数计算
+
U 220 V 22 I1 15.6 A 2 I 2 11 A
A1
A2
u
-
V
R L
i1 C i2
I I1 I 2 15.6 45 11 90A 11 A
所以 I 11 A
(2) 相量图
45
i
I
I2
I1
U
方法2:
I1 I 22A
P 3872 R 2 8Ω 2 I 22
U Z 10 Ω I I
+ +
R1
S
X L Z R 6Ω
2 2
U
XL
所以U R IR 22 8V 176 V U L IX L 22 6V 132 V
(2) 当合K后P不变 I 减小, 说明Z2为纯电容负载 相量图如图示:
5. 直流网络的所有分析方法都可以用于正弦电 流电路,但应将Ｒ改为Ｚ,将Ｇ改为Ｙ,将Ｉ改 为 I ,将Ｕ改为u. [ ]√
6. 对于ＲＬＣ串联电路，当电路中电阻加大时,电 路的谐振频率将减小。 [ ] × 7.对称星形三相电路中,阻抗为5∠30°的中线可 以用0Ω的短路线代替而不影响负载工作。 [ ] √
(Ａ ) 14
最新电工与电子技术第二版陶桓齐课后习题答案
第1章 电路的基本概念与定律 练习题解答（6）1-3 一只额定电压为V 220，功率为100W 的白炽灯，在额定状态下工作时的电阻和电流各为多少？解：根据功率表达式 UI I R P 2L ==则此时流过白炽灯的电流和白炽灯中的电阻分别为A 45.0220100U P I ===Ω===48445.0100I P R 22L1-5 某一直流电源，其输出额定功率P N = 200W ，额定电压U N = 50V ，内阻R 0 = 0.5Ω，负载电阻R可以调节，其电路如图1-15所示。
试求： （1）额定工作状态下的电流及负载电阻； （2）开路状态下的电源端电压；（3）电源短路状态下的电流。
解：（1）电路如解题图3所示，当S 闭合时,根据额定功率表达式N N N I U P = 则A 450200U P I N N N === 又根据额定电压表达式N N N I R U = 那么Ω===5.12450I U R N N N（2）根据全电路欧姆定律和开路状态下电源端电压等于电动势电压，所以V 5245.050I R U E U N 0N 0=⨯+=+== （3）电源电路短路时负载电阻为零，则短路电流为A 1045.052R E I 0S ===1-7 在题图1-7中，五个元件代表电源或负载。
电流和电压的参考方向如图中所示，通过实验测量得知V30U V 80U V 60U V 90U V 140U A10I A 6I A 4I 54321321=-==-====-=（1）试标出各电流的实际方向和电压的实际极性； （2）判断那些元件是电源？那些是负载？（3）计算各元件的功率，电源发出的功率和负载取用的功率是否平衡？E 解题图3题题1-721U U U21U 题题题4解：（1）各元件电流的实际方向和各元件电压的实际极性如解题图4所示。
（2）根据U 和I 的实际方向来判定，当U 和I 的实际方向相反时即为电源（注意，U 的实际方向指的是电位降落的方向，即从正极指向负极），否则为负载。
交流电路习题
R X C 100 Ω ， U
(2) UR = RI = 60 V，UC = X C I = 80 V，显然
U U
2 R
UC
2
(3) arctan(
XC R
) arctan (
80 60
) 53.1
即总电压比电流滞后53.1，电路呈容性。
例
RLC串联电路，已知：u 220 2 sin314t 30 V R=30Ω，L=254mH ，C=80μF。 计算：①感抗、容抗及阻抗 ②电流的I 及i
【例 】在RC串联电路中，已知电阻R=60，电容 C =20F，外加电压为u =141.2sin628tV。试求： (1) 电路中的电流I； (2) 各元件电压UR、UC ； (3) 总电压与电流的相位差 。
解：(1) 由
Z
2 2
XC
1 ωC
80 Ω ， 141 . 2 2 V 100 V
解：R=P/I2=400/25=16Ω |Z|=110/5=22Ω (ωL)2=222-162=228 L=48.1mH
三、习题练习
1．一交流电路，若u＝UmsinωtV，i＝Imsin(ωt十 π/2)A，则可知该电路的负载为_______。 A．纯电感 B．纯电阻 C．纯电容 D．RL串联负载 2．某负载电压和电流分别为u＝100sin(314t十30°)V， i＝2sin(314t一30°)A，该负载的性质和消耗的功率分 别为___。 A．电容性／50W B．电感性／50W C．电容性／200W D. 电感性／200W
解： 有可能出现 UC >U ；而 UR ≤U
17、已知电压相量U =100∠30°V，阻抗Z=6+j8Ω，则电路的 功率因数COSφ为（ ）。 A、0.5 B、0.6 C、0.8 D、0.866
(整理)燕山大学电工技术课后答案第3章
第三章 正弦交流电路三、习题详解3-1 试计算下列正弦量的周期、频率和初相：（1）)30314(sin 5 +t （2）)60(cos 8+πt解 （1）周期 s 02.050131422==π=ωπ=T 频率 Hz 5002.011===T f初相 ︒=300ϕ（2）周期 s 222=ππ=ωπ=T频率 Hz 5.0211===T f初相 ︒=1500ϕ3-2 试计算下列各正弦量间的相位差：（1）A )30(sin 5)(1+ω=t t iA )30(sin 4)(2-ω=t t i（2）V )1520(cos 5)(1+=t t uV )3010(sin 8)(2-=t t u（3）V )45(sin 30)(+ω=t t uA )30(sin 40)(-ω=t t i解 (1)60303021=--=-=）（ϕϕϕ (2) 角频率不同，比较无意义。
(3) ︒=︒--︒=-=75)30(4521ϕϕϕ注意 ①通常只对同频率的两个正弦量才能做相位比较。
②求相位差时要将两个正弦量用相同的sin 函数或cos 函数表示。
③求相位差时，两个正弦量表达式前均带正号。
3-3 已知正弦量 30j 220e U =和A I3j 4--= ，试分别用三角函数式、正弦波形及相量图表示它们。
解 (1)30j 220e U= 三角函数式 )30sin(2220︒+ω=t u2t︒-30330︒图3-1题3-3正弦波形(2) A 3j 4--=I三角函数式 A )43a r c t g s i n (25π-+ω=t i 正弦波形，相量图可参照（1）答案画出。
注意 习惯上常取初相绝对值小于180°。
3-4 写出下列正弦量的相量表示式（1）A cos 25t i ω=（2）V )45314(cos 2125-=t u（3）A )605(sin 10--=t i解 （1）A cos 25t i ω=A t t t t i )90sin(25)90sin(25)90sin(25cos 25︒+=︒--=-︒==ωωωωA 905︒∠=∴I（2）V )45314(cos 2125-=t u)4531490sin(2125)45314(cos 2125︒+-︒=-=t t u)135314sin(2125)314135sin(2125︒--=-︒=t t )45314sin(2125)180135314sin(2125︒+=︒+︒-=t tV 45125︒∠=∴U（3）A )605(sin 10--=t iA )1205sin(10)180605sin(10)605(sin 10︒+=︒+︒-=--=t t t iA 12025︒∠=∴I注意 ①不能认为电流相量I等于正弦量i. 即≠I i. ②以余弦函数表示的正弦电流都要将其化为正弦表达式，再写出相量。
电工技术教学课件常晓玲习题答案第三章
第三章 正弦交流电路习题参考答案1．已知t e 314sin 2220=V ，试问e 的最大值、有效值、角频率、频率和初相位各是多少？解：e 的最大值 V E m 3112220==有效值 E=220V 角频率 ω=314( rad/s)频率和初相位 f = ω/2л = 50Hz 初相位为零2．已知某正弦电流的有效值是10A ，频率为50Hz 。
初相为30°，（1）写出它的瞬时表达式，并画出其波形图；（2）求该正弦电流在t=0.0025s 时的相位和瞬时值。
解：（1）A t i )30314sin(210︒+= （2）当t=0.0025s 时 相位角︒=⨯⨯=452/3600025.0314πφ瞬时值 A i 1022210sin 210=⨯==φ 3．已知)30314sin(2101︒+=t i A ，)30314sin(10︒-=t i A ，画出这个电流的波形图，哪个电流超前？它们的相位差是多少？若用万用表测量这两个电流，试问读数各为多少？解：i 超前60°。
用万用表测量时，i 1=10A,i =7.07A4．已知)30314sin(210︒+=t u V ，t i 314sin 25=A ，求u 、i 的相量并画出相量图。
解: u 的相量为︒∠=3010UV i 的相量为︒∠=05IA 5．指出并改正下列各式的错误1）V 2） A ︒∠=4520u )60sin(10︒+=t Iω 3）V 4）︒∠=120220E )30sin(5︒-=t I ω A解：1） 2）V U︒∠=4520 A t i )60sin(10︒+=ω3） 4）V E︒∠=120220 A t i )30sin(5︒-=ω 6．当频率提高时，R 、X L 、X C 如何变化？解：R 与频率无关。
X L =ωL ，频率提高时，X L 成比例提高。
X C =1/ωC ，频率提高时，X C 成反比例下降。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
• 提高功率因数能减小线路功耗和电压损耗。
• 提高功率因数的方法通常是在感性负载 两端并联一个电容器，称之为补偿电容 器。补偿电容器的容量为：
正弦稳态电路的分析
• 用相量法分析电路时，线性电阻电路的 各种分析方法和电路定理可推广用于线 性电路的正弦稳态分析，差别仅在于所 得的电路方程是以相量形式表示的代数 方程以及用相量形式描述的电路定理， 而计算则为复数运算。
解：I 1000 A 10A 10e j00 A
u 10 2 cos(t 120 0 ) V
U 10 120 0V 10( 1 j 3 ) 5 j5 3V 22
10e j V 1200
练习2：指出下列各式的错误。
(1) u 5cos(t 300 ) 5e j V 300 (2) I 100e j450 100 2 cos(t 450 ) A (3) U 10cost
(4) I 30e300 A
练习2：指出下列各式的错误。
(1) u 5cos(t 300 ) 5e j300V
U 5 e j300 2
(2) I 100e j450 100 2 cos(t 450 ) A
I 100 e j450 A i 100 2 cos(t 450 ) A
练习2：指出下列各式的错误。
正弦稳态电路的分析
习题总结课
正弦量及其三要素
1、随时间按正弦规律变化的电流、电压、 电动势等统称为正弦量。
2、正弦量的有效值（振幅）、频率（周期 或角频率）和初相是正弦量的三要素。 三要素是确定一个正弦量的充要条件。
3、直流电的大小和方向恒定不变，在直流 计算时只考虑其大小即可。而在交流电 的分析与计算时，除了考虑大小外，还 要考虑其相位。
由相量图可知： I1=I2=10A
正弦量的几种表示方法
1、正弦量除了用三角函数式、波形图表示 外，还可以用相量表示。
2、相量表示式包括代数形式、三角式、指 数式和极坐标式，这几种表示方法各有 其特点，在分析和计算时可根据具体情 况选用。
练习1：写出下列正弦量的代数式、指数 式和极坐标式。
1. i 10 2 cost A
2. u 10 2 sin(t 300 ) V
1、R、L、C串联电路如图，已知iS= 6cos100t A , U1 =U2 =U, 负载吸收的平均功率为60Wห้องสมุดไป่ตู้试计算 R、L、C的参数值。
解：据题意，IS 300 A 画P 相6量0W图如IS2R右所R示。630 20
因电压三角形是等边三 角形， 故
XL
Rtg 30 0
11.54
L
XL
115 .4mH
又因为U1
U
，
2
故在串联电路中
XC R jX L R2 X L2 23.09
C 1/ X C 433 F
U2
I 300
300 S
U
U1
2、图示的正弦交流电路中，已知I2=10A，I3=10 2A ，
U=200V，R1=5，R2=L。求I1，1/C，L。
解：令并联部分电压为 参考相量，即 U2 U200 画出相量图如下：
C i C du
dt
I U / XC
I超前U900
P=0，Q=UI
复数关系 U=IR
U=jXLI
相量图
IU U
I 注：XL=ωL=2πfL XC=1/ωC=1/2πfC
U=-jXCI I
U
练习3：判断下列各式是否正确？
(1) i u XL
(2) I u
C
I U XL
I CU
(3) I UC √
• 对正弦交流电路，若其端电压为U，总电 流为I，其U、I相位差为φ ，则：
有功功率 P=UIcosφ
W
无功功率 Q=UIsinφ
var
视在功率 S UI P2 Q2 VA
复功率
S=UI* =P+jQ
VA
功率因数 cos P
S
练习4：按要求求解。
电路中N为线性无源动态网络，已知：
u=200cos(314t+100)，i=50cos(314t+400)A。试求
(3) U 10 cost
u 10costV
(4) I 30e300 A
I 30e j300 A
R、L、C在交流电路中的作用
关系 元件
R
瞬时值关系 u=iR
有效值关系 I U / R
相位关系 U、I同相
功率 P=UI ，Q=0
L u L di
dt
I U / XL
I滞后U900
P=0，Q=UI
i
阻抗角与电路性质的关系
+
u
N
阻抗角φ 大于零 小于零 等于零 等于900 等于-900
电路的性质 感性电路 容性电路
纯电阻电路 纯电感电路 纯电容电路
N是单口无源网络
端口处电压、电流关系 电压超前电流φ角 电压滞后电流φ角 电压与电流同相位 电压超前电流900 电压滞后电流900
正弦交流电路中的功率
的概念。
Z UI R j( X L XC )
[]
Y1
[S]
Z
阻抗的涵义
• 阻抗的大小——阻抗模，反映了电压与电 流之间的大小关系；阻抗的辐角——阻抗 角φ反映了电压与电流之间的相位差，同 时还反映了电路的性质。
Z UI Z
Z U I
u i
• 注意φ的取值范围: -1800≤φ≤1800
(4) i u XC
(5) u L di √ dt
I U XC
基尔霍夫定律的相量式
• 基尔霍夫定律的相量式与三种基本电路 元件伏安特性的相量形式，是分析正弦
交流电路的基础。 I 0 U 0
• 应用基尔霍夫定律及单一参数电路所得
出的结论，对R、L、C串联、并联电路
进行了分析，分别引出了阻抗Z和导纳Y
等效阻抗Z，等效导纳Y及P、Q、S并指出该网 络的性质。
解：
Z
UI
200 100 2
50 400
4 300
2
Y=1/Z=0.25/300 S
P=UIcos =4330 W
Q=UIsin =-2500 var
S=UI=5000 VA 由于阻抗角小于零，所以该网络是容性网络。
提高功率因数的意义方法
常用正弦交流电路的两种分析计算方法的比较
1. 相量图法 据已知条件，选择合适的参考相量，由电路基本
定律画出相量图，然后再根据量量图运用几何知识和 电路基本的计算公式求解电路的待求量。
2. 解析式 各电压和电流用相量表示，各电路元件用阻抗
（或导纳）表示，电阻电路中的所有计算方法都可推 广到正弦交流电路的分析计算中。