控制系统数字仿真实验报告
自动实验一——典型环节的MATLAB仿真 报告
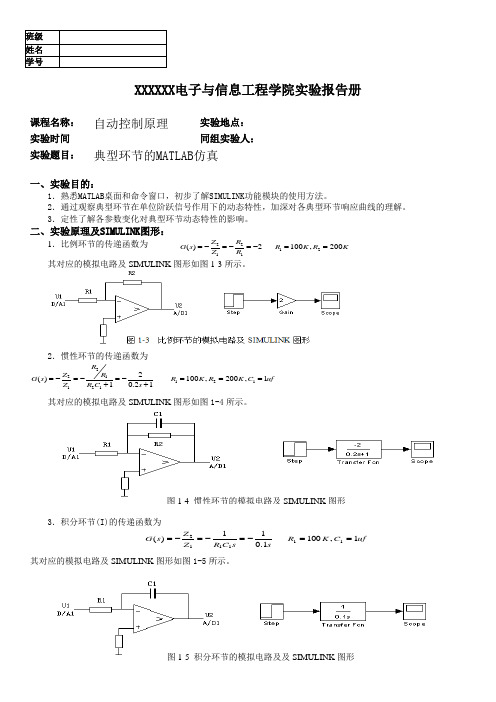
班级 姓名 学号XXXXXX 电子与信息工程学院实验报告册课程名称：自动控制原理 实验地点： 实验时间同组实验人： 实验题目： 典型环节的MATLAB 仿真一、实验目的：1．熟悉MATLAB 桌面和命令窗口，初步了解SIMULINK 功能模块的使用方法。
2．通过观察典型环节在单位阶跃信号作用下的动态特性，加深对各典型环节响应曲线的理解。
3．定性了解各参数变化对典型环节动态特性的影响。
二、实验原理及SIMULINK 图形：1．比例环节的传递函数为 221211()2100,200Z R G s R K R K Z R =-=-=-==其对应的模拟电路及SIMULINK 图形如图1-3所示。
2．惯性环节的传递函数为2211211212()100,200,110.21R Z R G s R K R K C uf Z R C s =-=-=-===++其对应的模拟电路及SIMULINK 图形如图1-4所示。
3．积分环节(I)的传递函数为uf C K R s s C R Z Z s G 1,1001.011)(111112==-=-=-=其对应的模拟电路及SIMULINK 图形如图1-5所示。
图1-5 积分环节的模拟电路及及SIMULINK 图形 图1-4 惯性环节的模拟电路及SIMULINK 图形4．微分环节(D)的传递函数为uf C K R s s C R Z Z s G 10,100)(111112==-=-=-= uf C C 01.012=<<其对应的模拟电路及SIMULINK 图形如图1-6所示。
5．比例+微分环节（PD ）的传递函数为)11.0()1()(111212+-=+-=-=s s C R R R Z Z s G uf C C uf C K R R 01.010,10012121=<<=== 其对应的模拟电路及SIMULINK 图形如图1-7所示。
6．比例+积分环节（PI ）的传递函数为)11(1)(11212s R s C R Z Z s G +-=+-=-= uf C K R R 10,100121===其对应的模拟电路及SIMULINK 图形如图1-8所示。
《计算机控制技术》数字PID控制器设计与仿真实验报告
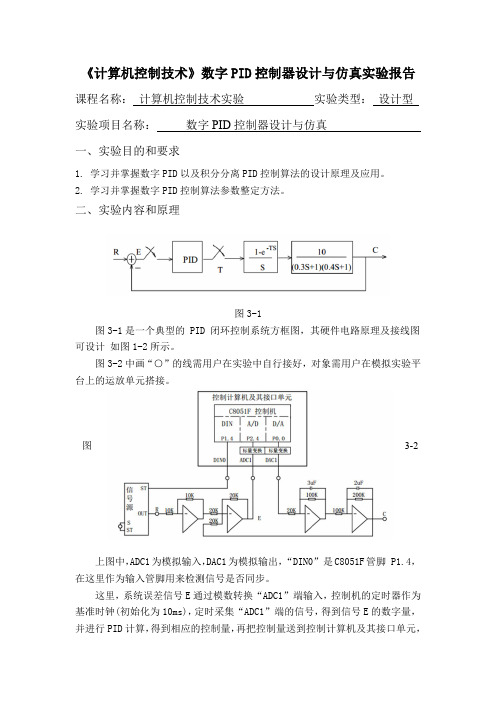
《计算机控制技术》数字PID控制器设计与仿真实验报告课程名称：计算机控制技术实验实验类型：设计型实验项目名称：数字PID控制器设计与仿真一、实验目的和要求1. 学习并掌握数字PID以及积分分离PID控制算法的设计原理及应用。
2. 学习并掌握数字PID控制算法参数整定方法。
二、实验内容和原理图3-1图3-1是一个典型的 PID 闭环控制系统方框图，其硬件电路原理及接线图可设计如图1-2所示。
图3-2中画“○”的线需用户在实验中自行接好，对象需用户在模拟实验平台上的运放单元搭接。
图3-2上图中，ADC1为模拟输入，DAC1为模拟输出，“DIN0”是C8051F管脚 P1.4，在这里作为输入管脚用来检测信号是否同步。
这里，系统误差信号E通过模数转换“ADC1”端输入，控制机的定时器作为基准时钟(初始化为10ms)，定时采集“ADC1”端的信号，得到信号E的数字量，并进行PID计算，得到相应的控制量，再把控制量送到控制计算机及其接口单元，由“DAC1”端输出相应的模拟信号，来控制对象系统。
本实验中，采用位置式PID算式。
在一般的PID控制中，当有较大的扰动或大幅度改变给定值时，会有较大的误差，以及系统有惯性和滞后，因此在积分项的作用下，往往会使系统超调变大、过渡时间变长。
为此，可采用积分分离法PID控制算法，即：当误差e(k)较大时，取消积分作用；当误差e(k)较小时才将积分作用加入。
图3-3是积分分离法PID控制实验的参考程序流程图。
图3-3三、主要仪器设备计算机、模拟电气实验箱四、操作方法与实验步骤1.按照图3-2搭建实验仿真平台。
2.确定系统的采样周期以及积分分离值。
3.参考给出的流程图编写实验程序，将积分分离值设为最大值0x7F，编译、链接。
4.点击，使系统进入调试模式，点击，使系统开始运行，用示波器分别观测输入端R以及输出端C。
5.如果系统性能不满意，用凑试法修改PID参数，再重复步骤3和4，直到响应曲线满意，并记录响应曲线的超调量和过渡时间。
基于MATLAB控制系统仿真实验报告
tf 4
y0
0 1
6、求出 G1(s)
2 (s2 2s 1) 与 G2 (s)
1 (2s3
3s2
1)
的单位阶跃响应，并分别
求出状态空间模型。
解：（1） G1(s) 2 (s2 2s 1) 的状态空间模型求解如下：
function shiyan2 b1=[2];
D(z)
0.62(1 0.136z 1)(1 0.183z (1 0.045z 1)(1 0.53z 1)
1 )
分别用仿真算法得到系统在单位阶跃输入作用下的响应，系统在单位速度输
入是的输出响应。
解：（1）首先将 W1(s)转换为 W1(z)，采样周期 T=0.2s，程序清单如下： function shiyan42 num=[10];den=[0.005 0.15 1 0]; ts=0.2;[nc,dc]=c2dm(num,den,ts)
INTRO（注意：intro 为一个用 MATLAB 语言编写的幻灯片程序，主要演示
常用的 MATLAB 语句运行结果。）
然后，根据现实出来的幻灯片右面按钮进行操作，可按 START——NEXT—
—NEXT 按钮一步步运行，观察。
3、自编程序并完成上机编辑，调试，运行，存盘：
（1）用 MATLAB 命令完成矩阵的各种运算，例如：
5、利用 ode23 或 ode45 求解线性时不变系统微分方程 y(t) Ay(t) ，并绘制出 y(t)
曲线，式中
A
0.5
1
1 0.5
t t0 t 如下： function xdot=fun21(t,x) A=[-0.5 1;-1 -0.5]; xdot=A*x; function fzsy22 t0=0;tf=4;tol=1e-6; x0=[0;1];trace=1; [t,x]=ode23('fun21',t0,tf,x0,tol,trace); plot(t,x) 得到的实验结果如下图所示：
pid控制实验报告[最新版]
![pid控制实验报告[最新版]](https://img.taocdn.com/s3/m/ab6b0408640e52ea551810a6f524ccbff121ca13.png)
pid控制实验报告pid控制实验报告篇一：PID控制实验报告实验二数字PID控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。
因此连续PID控制算法不能直接使用，需要采用离散化方法。
在计算机PID控制中，使用的是数字PID控制器。
一、位置式PID控制算法按模拟PID控制算法，以一系列的采样时刻点kT代表连续时间t，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID位置式表达式：Tu T ?kpeu=para; J=0.0067;B=0.1; dy=zeros= y= -+ = k*ts; %time中存放着各采样时刻rineu_1=uerror_1=error;%误差信号更新图2-1 Simulink仿真程序其程序运行结果如表2所示。
Matlab输出结果errori = error_1 = 表2 例4程序运行结果三、离散系统的数字PID控制仿真1．Ex5 设被控对象为G?num 仿真程序：ex5.m%PID Controller clear all; close all;篇二：自动控制实验报告六-数字PID控制实验六数字PID控制一、实验目的1．研究PID控制器的参数对系统稳定性及过渡过程的影响。
2．研究采样周期T对系统特性的影响。
3．研究I型系统及系统的稳定误差。
二、实验仪器1．EL-AT-III型自动控制系统实验箱一台 2．计算机一台三、实验内容1．系统结构图如6-1图。
图6-1 系统结构图图中 Gc（s）=Kp（1+Ki/s+Kds） Gh（s）=（1－e）/s Gp1（s）=5/（（0.5s+1）（0.1s+1）） Gp2（s）=1/（s（0.1s+1））-TS 2．开环系统（被控制对象）的模拟电路图如图6-2和图6-3，其中图6-2对应GP1（s）,图6-3对应Gp2（s）。
图6-2 开环系统结构图1 图6-3开环系统结构图2 3．被控对象GP1（s）为“0型”系统，采用PI控制或PID控制，可使系统变为“I型”系统，被控对象Gp2（s）为“I型”系统，采用PI控制或PID控制可使系统变成“II型”系统。
PID控制实验报告
实验二 数字PID 控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用，需要采用离散化方法。
在计算机PID 控制中，使用的是数字PID 控制器。
一、位置式PID 控制算法按模拟PID 控制算法，以一系列的采样时刻点kT 代表连续时间t ，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID 位置式表达式：∑∑==--++=⎪⎪⎭⎫ ⎝⎛--++=k j di p k j D I p T k e k e k T j e k k e k k e k e T T j e T T k e k k u 00)1()()()())1()(()()()( 式中，D p d I pi T k k T k k ==,，e 为误差信号（即PID 控制器的输入），u 为控制信号（即控制器的输出）。
在仿真过程中，可根据实际情况，对控制器的输出进行限幅。
二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能，符合数字实时控制的真实情况，计算机及DSP 的实时PID 控制都属于这种情况。
1．Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(，式中J=0.0067,B=0.1。
输入信号为)2sin(5.0t π，采用PD 控制，其中5.0,20==d p k k 。
采用ODE45方法求解连续被控对象方程。
因为Bs Js s U s Y s G +==21)()()(，所以u dt dy B dty d J =+22，另y y y y ==2,1，则⎪⎩⎪⎨⎧+-==/J)*u ((B/J)y y y y 12221 ，因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;close all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列，第一列为tt时刻对应的y，第二列为tt时刻对应的y导数xk = xx(end,:); % A/D，提取xx中最后一行的值，即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');figure(2);plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。
控制系统仿真实验报告
采样控制系统仿真实验报告姓名胡晓健班级13学号08001331课题内容1、应用采样工作原理和离散控制系统设计方法设计采样控制系统。
2、掌握采样控制系统的特点及采样控制系统仿真的特殊问题，运用采样控制系统数字仿真的一般方法（差分方程递推求解法和对离散、连续部分分别计算的双重循环法）及Simulink 对系统进行仿真。
3、给出仿真设计方案和仿真模型。
4、仿真分析。
具体内容：采样控制系统如下图所示：一． 设计要求① 设被控对象sss G o +=21)(，采用零阶保持器，数字控制器为5.015.2)(+-=z z z D ,采样周期T=0.1s 。
应用差分方程递推求解法求系统输出的单位阶跃响应,并求其超调量、上升时间、峰值时间。
设计方案和实现差分方程递推求解法在构成采样控制仿真模型时，若连续部分不要求计算内部状态变量或不含非线性环节，则可以同样的采样周期分别建立离散部分和连续部分的差分方程，然后采用差分方程递推求解。
由题意可知被控对象不含非线性环节且不要求计算其内部状态变量，为了简化仿真过程并提高仿真精度，将连续部分的离散化模型嵌入到整个仿真模型中，即求出系统闭环脉冲传递函数(离散化模型)，得到系统的差分方程后递推求解由题意得数字控制器（离散部分）为5.015.2)(+-=z z z D求解传递函数的程序如下：Ts=0.1 %采样周期num1=[1]den1=[1,1,0]G1c=tf(num1,den1)G1d=c2d(G1c,Ts) %采用零阶保持法进行系统变换G2d=tf([2.5 -1],[1 0.5],0.1)Gd=G1d*G2dGHd=feedback(Gd,1) %建立闭环系统模型Ts =0.1000num1 =1den1 =1 1 0%G1c的传递函数Transfer function:1-------s^2 + s%G1c转换后的Z传递函数Transfer function:0.004837 z + 0.004679----------------------z^2 - 1.905 z + 0.9048Sampling time: 0.1%G2d的传递函数Transfer function:2.5 z - 1---------z + 0.5Sampling time: 0.1%开环系统的Z传递函数Transfer function:0.01209 z^2 + 0.00686 z - 0.004679------------------------------------z^3 - 1.405 z^2 - 0.04758 z + 0.4524Sampling time: 0.1%闭环系统的Z 传递函数 Transfer function:0.01209 z^2 + 0.00686 z - 0.004679 ------------------------------------z^3 - 1.393 z^2 - 0.04072 z + 0.4477Sampling time: 0.1由上式可知当采样周期为T =0.1s 时，连续部分的脉冲传递函数为系统闭环脉冲传递函数系统差分方程为求解差分方程的MATLAB 程序如下clear allm=2;n=3; % 明确脉冲传递函数分子m=2;分母n=3 A=[-1.393 -0.04072 0.4477]; % 脉冲传递函数分母多项式的系数行向量 B=[0.01209 0.00686 -0.004679]; % 脉冲传递函数分子多项式的系数行向量R=zeros(m+1,1); % 建立参与递推运算的输入信号序列存储列向量Y=zeros(n,1); % 建立参与递推运算的输出信号序列存储列向量 T=0.1; % 明确采样周期T =0.1sM=150; % 设定仿真总时间为M*T=15s(进行M=150次递推计算) yt=0;t=0;for k=1:MR(k)=1; % r (t )=1(t )的离散序列R(0)=R(1)=…R(k)=1 R=[R(k);R(1:m)];% 刷新参与递推运算的输入信号序列 yk=-A*Y+B*R; % 递推运算21219048.0905.1104679.0004837.0)(----+-+=zzz z z G 3213214477.004072.0393.11004679.000686.001209.0)()(1)()()()()(------+---+=+==zz z zzzz G z D z G z D z R z Y z G cl )3(004679.0)2(00686.0)1(01209.0)3(4477.0)2(04072.0)1(393.1)(---+-+---+-=k k r k r k y k y k y k yY=[yk;Y(1:n-1)];% 刷新参与递推运算的输出信号序列yt=[yt,yk]; % yt 为记载各采样(kT)时刻输出响应的行向量 t=[t,k*T]; % t 为记载各采样(kT)时刻的行向量(与yt 对应) endplot(t,yt,'*k'); % 绘制各采样(kT)时刻的输出响应图 grid;xlabel('time(s)'); ylabel('y(kT)');超调量 σ% 指响应的最大偏离量h(tp)与终值h （∞）的差与终值h （∞）比的百分数h(tp)-h %*100%h σ∞=∞（）（）峰值时间 tp 指响应超过其终值到达第一个峰值所需的时间上升时间 tr 指响应从终值10%上升到终值90%所需的时间求超调量的程序 maxy=max(yt); yss=yt(length(t));pos=100*(maxy-yss)/yss求峰值时间的程序 for i=1:50if yt(i)==maxy,n=i;end endtp=(n-1)*15/length(t)求上升时间的程序 for i=1:50if (yt(i)<yss*0.1),t1=i;end if (yt(i)<yss*0.9),t2=i;end endts=(t2-t1)*15/length(t)测试和结果．输出的单位阶跃响应为由程序算出的超调量，峰值时间和上升时间超调量pos = 14.0155峰值时间tp =3.5762上升时间ts =1.6887由上面两张截图算出的超调量σ%=（1.163-1.02）/1.02=14.02%峰值时间tp=3.6由上面两张截图可得上升时间tr=2-0.4=1.6性能分析该仿真算法不仅简单易行且仿真精度高。
数字仿真实验报告
一、实验目的本次实验旨在通过数字仿真技术，对线性连续控制系统和非线性环节控制系统进行仿真分析，验证控制系统的性能和稳定性，并加深对控制系统理论的理解。
二、实验环境1. 软件环境：MATLAB R2020a、Simulink2. 硬件环境：计算机三、实验内容1. 线性连续控制系统的数字仿真（1）系统描述本次实验选取两个线性连续控制系统，分别为G(S) = 10/S(S+1)和G(S) = 4/S^2 2.828S。
（2）参数设置输入信号：阶跃信号，阶跃时间：0；初值：0；终值：1迟滞环节：迟滞时间：0开环传递函数：G(S) = 10/S(S+1)，G(S) = 4/S^2 2.828S反馈环节传递函数：H(S) = 1（3）仿真结果与分析通过Simulink对两个系统进行仿真，得到如下结果：系统1：G(S) = 10/S(S+1)阶跃响应曲线如图1所示，系统在t=0s时刻开始输入阶跃信号，经过一段时间后达到稳态值。
相轨迹曲线如图2所示，系统在相平面上的运动轨迹呈现出稳定的闭环运动。
系统2：G(S) = 4/S^2 2.828S阶跃响应曲线如图3所示，系统在t=0s时刻开始输入阶跃信号，经过一段时间后达到稳态值。
相轨迹曲线如图4所示，系统在相平面上的运动轨迹呈现出稳定的闭环运动。
2. 非线性环节控制系统的数字仿真（1）系统描述本次实验选取非线性环节控制系统，为Wk(s) = 10/s(s+1)，并对其进行饱和死区特性的仿真。
（2）参数设置输入信号：阶跃信号，阶跃时间：0；初值：0；终值：1饱和死区：非线性的上下限为（-2，2），幅值为5和10（3）仿真结果与分析通过Simulink对非线性环节控制系统进行仿真，得到如下结果：阶跃响应曲线如图5所示，系统在t=0s时刻开始输入阶跃信号，经过一段时间后达到稳态值。
相轨迹曲线如图6所示，系统在相平面上的运动轨迹呈现出稳定的闭环运动。
3. 典型环节频率响应的数字仿真（1）系统描述本次实验选取典型环节频率响应，为G(S) = 10/S(S+1)，并对其进行频率响应仿真。
《计算机仿真技术》报告
《计算机仿真技术》实验报告实验一 数字仿真方法验证一、实验目的1．掌握基于数值积分法的系统仿真、了解各仿真参数的影响； 2．掌握基于离散相似法的系统仿真、了解各仿真参数的影响； 3．掌握SIMULINK 动态仿真；4．熟悉MATLAB 语言及应用环境。
二、实验环境网络计算机系统，MATLAB 语言环境三、实验内容、要求（一）试将示例1的问题改为调用ode45函数求解，并比较结果。
示例1：设方程如下，取步长 h =0.1。
上机用如下程序可求出数值解。
调用ode45函数求解： 1）建立一阶微分方程组 du=u-2*t/u2）建立描述微分方程组的函数m 文件 function du=sy11vdp(t,u) du=u-2*t/u3）调用解题器指令ode45求解y[t,u]=ode45('sy11vdp',[0 1],1) plot(t,u,'r-'); xlabel('t'); ylabel('u'); 结果对比：euler 法：t=1,u=1.7848; RK 法：t=1,u=1.7321; ode45求解:t=1,u=1.7321;[]1,01)0(2∈⎪⎩⎪⎨⎧=-=t u u t u dt duode45求解t-u 图：00.10.20.30.40.50.60.70.80.9111.11.21.31.41.51.61.71.8tu（二）试用四阶RK 法编程求解下列微分方程初值问题。
仿真时间2s ，取步长h=0.1。
⎪⎩⎪⎨⎧=-=1)0(2y t y dt dy 四阶RK 法程序：clear t=2; h=0.1; n=t/h; t0=0; y0=1;y(1)=y0; t(1)=t0;for i=0:n-1 k1=y0-t0^2;k2=(y0+h*k1/2)-(t0+h/2)^2; k3=(y0+h*k2/2)-(t0+h/2)^2 k4=(y0+h*k3)-(t0+h)^2;y1=y0+h*(k1+2*k2+2*k3+k4)/6; t1=t0+h; y0=y1; t0=t1;y(i+2)=y1; t(i+2)=t1;end y tplot(t,y,'r'); 结果：t=2,y=2.61090.511.522.511.21.41.61.822.22.42.62.83：（三）试求示例3分别在周期为5s 的方波信号和脉冲信号下的响应，仿真时间20s ，采样周期Ts=0.1。
simulink实验报告
simulink实验报告Simulink实验报告引言：Simulink是一种功能强大的图形化建模和仿真环境，广泛应用于控制系统设计、信号处理和通信系统等领域。
本实验报告将介绍Simulink的基本概念和使用方法，并通过一个具体的示例来展示Simulink的应用。
一、Simulink简介Simulink是MathWorks公司开发的一款基于模块化的仿真工具，它可以与MATLAB紧密集成，为系统建模和仿真提供了强大的支持。
相比于传统的编程方法，Simulink使用图形化界面，使得系统建模更加直观和易于理解。
Simulink 提供了丰富的模块库，用户可以通过拖拽和连接不同的模块来构建系统模型，并进行仿真和分析。
二、Simulink的基本概念1. 模块库：Simulink提供了各种各样的模块库，包括数学运算、信号处理、控制系统等。
用户可以从库中选择所需的模块，将其拖拽到工作区，并进行连接和参数配置。
2. 模块：模块是Simulink中的基本单元，它代表了系统中的一个功能模块或组件。
每个模块都有输入和输出端口，用户可以通过连接不同的模块来构建系统模型。
3. 信号：信号是模块之间传递的数据，可以是连续的或离散的。
Simulink支持多种信号类型，如模拟信号、数字信号、布尔信号等。
4. 仿真：Simulink提供了强大的仿真功能，用户可以通过设置仿真参数和模型参数，对系统进行仿真和分析。
仿真结果可以以图表、曲线等形式展示，帮助用户理解系统的行为和性能。
三、Simulink的应用示例：PID控制器设计以PID控制器设计为例，演示Simulink的应用过程。
1. 建立模型首先，我们需要建立一个PID控制器的模型。
在Simulink的模块库中，我们可以找到PID控制器的模块，并将其拖拽到工作区。
然后，我们需要连接输入信号、输出信号和反馈信号，并设置PID控制器的参数。
2. 设置仿真参数在进行仿真之前，我们需要设置仿真参数。
PID控制实验报告
实验二 数字PID 控制计算机控制是一种采样控制，它只能根据采样时刻的偏差值计算控制量。
因此连续PID 控制算法不能直接使用，需要采用离散化方法。
在计算机PID 控制中，使用的是数字PID 控制器。
一、位置式PID 控制算法按模拟PID 控制算法，以一系列的采样时刻点kT 代表连续时间t ，以矩形法数值积分近似代替积分，以一阶后向差分近似代替微分，可得离散PID 位置式表达式： 式中，D p d I pi T k k T k k ==,，e 为误差信号（即PID 控制器的输入），u 为控制信号（即控制器的输出）。
在仿真过程中，可根据实际情况，对控制器的输出进行限幅。
二、连续系统的数字PID 控制仿真连续系统的数字PID 控制可实现D/A 及A/D 的功能，符合数字实时控制的真实情况，计算机及DSP 的实时PID 控制都属于这种情况。
1．Ex3 设被控对象为一个电机模型传递函数BsJs s G +=21)(，式中J=0.0067,B=0.1。
输入信号为)2sin(5.0t π，采用PD 控制，其中5.0,20==d p k k 。
采用ODE45方法求解连续被控对象方程。
因为Bs Js s U s Y s G +==21)()()(，所以u dt dy B dty d J =+22，另y y y y ==2,1，则⎪⎩⎪⎨⎧+-==/J )*u ((B /J )y y y y 12221 ，因此连续对象微分方程函数ex3f.m 如下 function dy = ex3f(t,y,flag,para)u=para;J=0.0067;B=0.1;dy=zeros(2,1);dy(1) = y(2);dy(2) = -(B/J)*y(2) + (1/J)*u;控制主程序ex3.mclear all;ts=0.001; %采样周期xk=zeros(2,1);%被控对象经A/D转换器的输出信号y的初值e_1=0;%误差e(k-1)初值u_1=0;%控制信号u(k-1)初值for k=1:1:2000 %k为采样步数time(k) = k*ts; %time中存放着各采样时刻rin(k)=0.50*sin(1*2*pi*k*ts); %计算输入信号的采样值para=u_1; % D/AtSpan=[0 ts];[tt,xx]=ode45('ex3f',tSpan,xk,[],para); %ode45解系统微分方程%xx有两列，第一列为tt时刻对应的y，第二列为tt时刻对应的y导数xk = xx(end,:); % A/D，提取xx中最后一行的值，即当前y和y导数yout(k)=xk(1); %xk(1)即为当前系统输出采样值y(k)e(k)=rin(k)-yout(k);%计算当前误差de(k)=(e(k)-e_1)/ts; %计算u(k)中微分项输出u(k)=20.0*e(k)+0.50*de(k);%计算当前u(k)的输出%控制信号限幅if u(k)>10.0u(k)=10.0;endif u(k)<-10.0u(k)=-10.0;end%更新u(k-1)和e(k-1)u_1=u(k);e_1=e(k);endfigure(1);plot(time,rin,'r',time,yout,'b');%输入输出信号图xlabel('time(s)'),ylabel('rin,yout');plot(time,rin-yout,'r');xlabel('time(s)'),ylabel('error');%误差图程序运行结果显示表1所示。
数字系统设计及实验实验报告
数字系统设计及实验实验报告一、实验目的数字系统设计及实验课程旨在让我们深入理解数字逻辑的基本概念和原理，掌握数字系统的设计方法和实现技术。
通过实验，我们能够将理论知识应用于实际，提高解决问题的能力和实践动手能力。
本次实验的具体目的包括：1、熟悉数字电路的基本逻辑门、组合逻辑电路和时序逻辑电路的设计方法。
2、掌握使用硬件描述语言（如 Verilog 或 VHDL）进行数字系统建模和设计。
3、学会使用相关的电子设计自动化（EDA）工具进行电路的仿真、综合和实现。
4、培养团队合作精神和工程实践能力，提高解决实际问题的综合素质。
二、实验设备和工具1、计算机：用于编写代码、进行仿真和综合。
2、 EDA 软件：如 Quartus II、ModelSim 等。
3、实验开发板：提供硬件平台进行电路的下载和测试。
4、数字万用表、示波器等测量仪器：用于检测电路的性能和信号。
三、实验内容1、基本逻辑门电路的设计与实现设计并实现与门、或门、非门、与非门、或非门和异或门等基本逻辑门电路。
使用 EDA 工具进行仿真，验证逻辑功能的正确性。
在实验开发板上下载并测试实际电路。
2、组合逻辑电路的设计与实现设计一个 4 位加法器，实现两个 4 位二进制数的相加。
设计一个编码器和译码器，实现数字信号的编码和解码。
设计一个数据选择器，根据控制信号选择不同的输入数据。
3、时序逻辑电路的设计与实现设计一个同步计数器，实现模 10 计数功能。
设计一个移位寄存器，实现数据的移位存储功能。
设计一个有限状态机（FSM），实现简单的状态转换和控制逻辑。
四、实验步骤1、设计方案的确定根据实验要求，分析问题，确定电路的功能和性能指标。
选择合适的逻辑器件和设计方法，制定详细的设计方案。
2、代码编写使用硬件描述语言（如 Verilog 或 VHDL）编写电路的代码。
遵循代码规范，注重代码的可读性和可维护性。
3、仿真验证在 EDA 工具中对编写的代码进行仿真，输入不同的测试向量，观察输出结果是否符合预期。
“双闭环控制直流电动机调速系统”数字仿真实验
“双闭环控制直流电动机调速系统”数字仿真实验24、SIMULINK建模我们借助SIMULINK，根据上节理论计算得到的参数，可得双闭环调速系统的动态结构图如下所示：图7 双闭环调速系统的动态结构图（1）系统动态结构的simulink建模①启动计算机，进入MATLAB系统检查计算机电源是否已经连接，插座开关是否打开，确定计算机已接通，按下计算机电压按钮，打开显示器开关，启动计算机。
打开Windows开始菜单，选择程序，选择MATAB6.5.1，选择并点击MATAB6.5.1，启动MATAB程序，如图8，点击后得到下图9：图8选择MATAB程序图9 MATAB6.5.1界面点击smulink 中的continuous,选择transfor Fc n（传递函数）就可以编辑系统的传递函数模型了，如图10。
图10 smulink界面②系统设置选择smulink界面左上角的白色图标既建立了一个新的simulink模型，系统地仿真与验证将在这个新模型中完成，可以看到在simulink目录下还有很多的子目录，里面有许多我们这个仿真实验中要用的模块，这里不再一一介绍，自介绍最重要的传递函数模块的设置，其他所需模块参数的摄制过程与之类似。
将transfor Fc n（传递函数）模块用鼠标左键拖入新模型后双击transfor Fc n（传递函数）模块得到图11，开始编辑此模块的属性。
图11参数表与模型建立参数对话栏第一和第二项就是我们需要设置的传递函数的分子与分母，如我们需要设置电流环的控制器的传递函数：0.01810.0181()0.2920.0180.062ACR s s W s s s++=⋅=，这在对话栏的第一栏写如：[0.018 1]，第二栏为：[0.062 0]。
点击OK ，参数设置完成。
如图12。
图12传递函数参数设置设置完所有模块的参数后将模块连接起来既得到图7所示的系统仿真模型。
在这里需要注意的是，当我们按照理论设计的仿真模型得到的实验波形与理想的波形有很大的出入。
数字仿真实验实施方案
数字仿真实验实施方案一、实验目的。
数字仿真实验是一种通过计算机模拟和分析系统、信号、电路等电子技术的实验方法。
其目的是通过对电子技术知识的理论学习和实际操作的结合，提高学生对电子技术的理解和应用能力，培养学生的创新意识和实践能力。
本实施方案旨在指导教师和学生进行数字仿真实验，确保实验的顺利进行和实验效果的达到。
二、实施步骤。
1. 确定实验内容和目标。
首先，教师应根据课程要求和学生的实际情况，确定本次数字仿真实验的内容和目标。
实验内容可以包括数字信号处理、数字电路设计、数字系统仿真等方面，目标可以是掌握数字仿真软件的操作技能，理解数字电子技术的原理和应用。
2. 准备实验环境和工具。
在确定实验内容和目标后，教师需要准备好实验所需的计算机、数字仿真软件、实验指导书等工具和资料。
同时，要确保实验环境的安全和稳定，保证实验设备的正常运行。
3. 学生实验操作。
在实验进行时，教师应指导学生按照实验指导书的要求，正确操作数字仿真软件，进行实验内容的模拟和分析。
学生应认真对待实验，按照要求完成实验报告和实验数据的记录。
4. 实验结果分析和总结。
实验结束后，教师应指导学生对实验结果进行分析和总结，讨论实验中遇到的问题和解决方法，总结实验中的经验和教训。
同时，学生应根据实验结果撰写实验报告，展示实验过程和实验成果。
三、实施要求。
1. 教师应具备扎实的电子技术知识和丰富的实践经验，能够熟练操作数字仿真软件，指导学生进行实验操作。
2. 学生应具备一定的电子技术基础知识，能够独立操作计算机和数字仿真软件，完成实验内容和实验报告。
3. 实验环境应具备良好的计算机设备和网络条件，确保实验的顺利进行和实验数据的准确记录。
4. 实验过程中应严格遵守实验室规章制度，保证实验环境的安全和整洁。
四、实施效果评估。
为了确保数字仿真实验的效果和质量，教师应对实验过程和实验结果进行评估和检查。
评估内容可以包括学生的实验操作技能、实验报告的撰写质量、实验成果的达成情况等方面，及时发现问题并进行改进。
先进PID控制器的Simulink仿真设计(计算机控制技术)
电子信息工程学系实验报告
课程名称：计算机工业控制技术
实验项目名称：先进PID 控制器的Simulink 仿真设计 实验时间：
班级： 姓名： 学号：
实 验 目 的:
1.掌握PID 控制规律的特点。
2.研究连续PID 、数字增量PID 、抗积分饱和PID 控制算法的异同。
3.掌握使用Simulink 仿真设计各种PID 控制器。
4.学会使用Matlab 生成子系统封装，并加入控制器模块库；再调用重新构造系统。
实 验 环 境:
计算机、matlab 软件
实 验 内 容 及 步 骤:
1.根据控制算法画出Simulink 框图；
2.设定各模块的参数
3.生成子系统封装，加入控制器模块库；
4.设计应用系统调用控制器模块。
三种PID 控制器实验的图形与数据分别是： 【1】 连续PID 控制器：
【2】数字增量式PID控制器：
【3】抗积分饱和PID控制器：
实验结果及分析：
【1】连续PID控制器：
此时：kp=0.9;ki=0.008;kd=0.002
Mp％＝10.76％；调整时间：0.1161s；稳定输出为1
【2】数字增量式PID控制器：
此时：Kp=0.2;ki=0.001;kd=0.001;T=0.001
Mp％＝11.46％；调整时间：0.16425s；稳定输出为1 【3】抗积分饱和PID控制器：
此时：Kp=1;ki=0.001;kd=0.001。
智能控制实验报告
智能控制仿真实验实验一模糊控制系统的仿真实验实验二 BP神经网络的仿真实验实验三遗传算法仿真实验实验四智能控制实际工程处理（选做）实验一模糊控制系统的仿真实验实验目的：现有被控对象一：G(s)=1/(s2+2s+1)被控对象二：G(s)=K /【(T1s+1)(T2s+1) 】试设计一个模糊控制系统来实现对它的控制，并完成以下任务实验任务一：请根据以上的数据重新仿真一下，看Ke的变化对系统性能的影响是否如此？然后仍以G(s)=1/(s2+2s+1) 为被控对象，按照同样的方法仿真并分析Kc、Ku的变化对系统性能的影响。
1.相同参数不同控制器解模方法下的图形BISECTORMOMSOMLOM2.不同参数相同解模方法下的图形（解模方法均为BISECTOR）（1）Ke的影响（Kc=5，Ku=8）Ke=1（2）Kc的影响（Ke=9，Ku=8）Kc=1（3）Ku的影响（Ke=9，Kc=5）Ku=1小结：由以上图形分析可得，不同的解模方法输出的结果不同，经比较BISECTOR 的解模方法更加合适。
参数Kc、Ku不变时，随着Ke的减小，上升时间将增大；Ke、Ku不变时，随着Kc的减小超调变大；Ke、Kc不变时随着Ku的减小，输出越来越低于1。
可知Ke=9、Kc=5、Ku=8更为合适。
实验任务二：仍使用以上设计的模糊控制器，被控对象为： G(s)=K /【(T 1s+1)(T 2s+1)】 ，被控对象的参数有以下四组： 第一组参数： G(s)=20/【(1.2s+1)(4s+1)】 第二组参数： (s)=20/【(0.4s+1)(4s+1)】 第三组参数： G(s)=20/【(2s+1)(4s+1)】 第四组参数： G(s)=20/【(2s+1)(8s+1)】请根据由任务一得到的Ke 、Kc 、Ku 的变化对系统性能影响的规律，选择第一组参数作为被控对象参数，调试出适合该系统的最佳的Ke 、Kc 、Ku 和反模糊化方法；并在你调出的最佳的Ke 、Kc 、Ku 状态下，将对象参数分别变成第二、三、四组的参数，仿真出结果，并分析fuzzy controller 的适应能力。
最少拍控制系统实验报告
计算机控制技术--基于Matlab的最少拍控制系统设计学院：计算机科学与技术班级：计科0902班学号：姓名：指导老师：日期： 2012年12月15日一、实验目的：1．学习使用Matlab 设计最少拍控系统的方法； 二、实验工具：X86系统兼容型计算机、MATLAB 软件。
三、实验内容： 1．实验原理最少拍设计，是指系统在典型输入信号（如阶跃信号、速度信号、加速度信号等）作用下，经过最少拍（有限拍）使系统输出的系统稳态误差为零。
因此，最少拍控制系统也称最少拍无差系统或最少拍随动系统，它实质上是时间最优控制系统，系统的性能指标就是系统调节时间最短或尽可能短，即对闭环Z 传递函数要求快速性和准确性。
下面以一个具体实例介绍最少拍系统的设计和仿真。
考虑图1所示的采样数字控制系统，被控对象的脉冲传递函数为210G ()(1)s s s =+图0 最少拍采样数字控制系统设采样周期T=1s ，首先求取广义被控对象的脉冲传递函数： 广义被控对象21112111111110()[](1)11(1)10[](1)110.36793.679(10.718)(1)(10.3679)Ts e G z Z s s s z z z z z z z z z -----------=+=-⨯-+---+=--我们知道，最少拍系统是按照指定的输入形式设计的，输入形式不同，数字控制器也不同。
因此，对三种不同的输入信号分别进行考虑： ① 单位阶跃信号：计算可得到最少拍数字控制器为1111()()1()0.2712(10.3679))()()(1())10.718e z z z z z z D z G z z z ----Φ=Φ=-Φ-==-Φ+检验误差序列：()(1())()1E z z R z =-Φ=由误差的变换函数得知，所设计的系统当k>1后，e （k ）=0就是说，一拍以后，系统输出等于输入，设计正确。
② 单位速度信号：原理同上，我们可以得到：1111()0.5434(10.5)(10.3679)()()(1())(1)(10.718)z z z D z G z z z z ----Φ--==-Φ-+检验误差：1()(1())()E z z R z z -=-Φ=从E(z)看出，按单位速度输入设计的系统，当k 大于等于2之后，即二拍之后，误差e （k ）=0，满足题目要求。
计算机仿真Matlab 实验报告二
实验二非线性系统的数字仿真实验一、实验目的学会用数字仿真方法分析线性和非线性系统的动态特性以及各种典型非线性环节对控制系统动态特性的影响。
二、实验内容系统模型如习题2.17所示。
根据控制理论分析，该系统将出现振幅为0.3，频率为0.8的自激振荡。
1. 按实验目的、要求和已知条件，建立系统的Simulink模型。
2. 在不引入非线性环节的情况下运行仿真模型，观察纪录系统动态特性的变化。
3. 在同样的条件下，引入滞环继电特性非线性环节，再运行仿真模型，观察纪录该非线性环节对系统过渡过程的影响。
4. 将滞环继电特性非线性环节换成饱和非线性环节，C1仍为0.3，运行仿真模型，观察纪录饱和非线性环节对系统过渡过程的影响。
实验解答：1.按实验目的、要求和已知条件，建立系统的Simulink模型。
建立Simulink模型如下：2．在不引入非线性环节的情况下运行仿真模型，观察纪录系统动态特性的变化。
去掉上图中的非线性环节—Relay，得到下图仿真结果：从图可以看出，开始会有突变，之后趋于稳定。
3. 在同样的条件下，引入滞环继电特性非线性环节，再运行仿真模型，观察纪录该非线性环节对系统过渡过程的影响。
如下，加入了滞环继电特性非线性环节从图中可以看出，系统产生了自激振荡，可以通过编程找到仿真曲线上的极值点，求出该图线的周期、角频率以及振幅。
通过仿真，由仿真图像可以很明白地看出，产生了自激振荡，且该自激振荡幅度约为0.6，周期约为8，则角频率约为0.8。
仿真结果与题目一致。
4. 将滞环继电特性非线性环节换成饱和非线性环节，C1仍为0.3，运行仿真模型，观察纪录饱和非线性环节对系统过渡过程的影响。
由图可得，仿真曲线的变化趋于缓和，但同时进入稳定的速率变慢。
即加入的饱和环节在系统中起到了限幅的作用。
饱和非线性环节使得系统更加平和的进入了稳定状态。
MATLAB与控制系统仿真实验指导书
《MATLAB与控制系统仿真》实验指导书（2011年第一版）西安邮电学院自动化学院2011年6月目录前言 (1)MATLAB语言实验项目 (3)实验一熟悉MATLAB集成环境与基础运算 (3)实验二 MATLAB的基本计算 (7)实验三 MATLAB图形系统 (9)实验四 MATLAB程序设计 (13)实验五 MATLAB函数文件 (15)实验六MATLAB数据处理与多项式计算 (17)实验七 SIMULINK仿真实验 (21)前言MATLAB 产品家族是美国 MathWorks公司开发的用于概念设计、算法开发、建模仿真、实时实现的理想的集成环境。
是矩阵实验室（Matrix Laboratory）的简称，是美国MathWorks公司出品的商业数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境，主要包括MATLAB和SIMULINK两大部分。
MATLAB由于其完整的专业体系和先进的设计开发思路，使得 MATLAB 在多种领域都有广阔的应用空间，特别是在科学计算、建模仿真以及系统工程的设计开发上已经成为行业内的首选设计工具，它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中，为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案，并在很大程度上摆脱了传统非交互式程序设计语言（如C、Fortran）的编辑模式，代表了当今国际科学计算软件的先进水平。
MATLAB软件工具在自动化专业、测控技术与仪器和电气工程及其自动化等专业的本科生学习中，经常用来计算、仿真和设计，尤其是MATLAB软件的仿真功能，能使学生对所学知识有更加深入的理解和分析。
《MATLAB与控制系统仿真》课程，和《自动控制原理》、《现代控制理论》、《数字信号处理》、《电力电子技术》等重要的专业课程相互支撑、相辅相成，同时也有利于学生完成课程设计和毕业设计等实践教学环节。
自动控制原理实验报告实验一-一、二阶系统的电子模拟及时域响应的动态测试
分组：成绩：__ _______北京航空航天大学自动控制原理实验报告实验一一、二阶系统的电子模拟及时域响应的动态测试学院专业方向班级学号学生姓名指导教师2014年11月目录一、实验目的 (1)二、实验内容 (1)三、实验原理 (1)四、实验设备 (2)五、实验步骤 (2)六、实验数据 (3)1.一阶系统实验数据及图形 (3)2.二阶系统实验数据及图形 (4)七、结论和误差分析 (6)结论： (6)误差分析： (7)八、收获与体会 (7)附录 (7)实验时间2014.11.1 同组同学 无一、实验目的1.了解一、二阶系统阶跃响应及其性能指标与系统参数之间的关系。
2.学习在电子模拟机上建立典型环节系统模型的方法。
3.学习阶跃响应的测试方法。
二、实验内容1.建立一阶系统的电子模型，观测并记录在不同时间常数T 时的阶跃响应曲线，并测定其过渡过程时间Ts 。
2.建立二阶系统的电子模型，观测并记录在不同阻尼比ζ时的阶跃响应曲线，并测定其超调量σ％及过渡过程时间Ts 。
三、实验原理1.一阶系统实验原理系统传递函数为：()()()1C S Ks R S TS φ==+模拟运算电路如图1所示：图1212R R Uo(s)K ==Ui(s)CSR +1Ts+1在实验中始终取R2=R1，则K=1，T=R2*C 取不同的时间常数T ，T=0.25s ，T=0.5s ，T=1s记录不同的时间常数下阶跃响应曲线，测量并记录其过渡时间Ts （Ts=3T ）2.二阶系统实验原理 其传递函数为：222()()()(2)n n n C S S R S S S ωζωωΦ==++令1n ω=弧度/秒，二阶系统模拟线路下图2所示：图2取R2*C1=1,R3*C2=1,则R4/R3=R4*C2=1/(2*ζ)及ζ=1/（2*R4*C2）理论值：3(0.05)s nt ζω≈∆=，%σ100%e =⨯四、实验设备1. HHMN-1 型电子模拟机一台2. PC 机一台3. 数字式万用表一块。
仿真软件实验实验报告
四川大学课程实验报告课程名称：学生姓名：学生学号：专业：系统仿真综合实验一、实验目的系统仿真是运用仿真软件（如simio）创造模型来构建或模拟现实世界的虚拟实验室，它能过帮助你探寻你所关注的系统在给定的条件下的行为或状态，它还能帮助你在几乎没有风险的情况下观察各种改进和备选方案的效果。
尤其是对一些难以建立物理模型和数学模型的复杂的随机问题，可通过仿真模型来顺利地解决预测、分析和评价等系统问题。
通过本次simio系统仿真综合实验，掌握并能熟练使用系统仿真软件simio，利用simio 建立模型，能体验其3d动画效果，并根据需求设定系统参数，如server的processing time、initial capacity，source的interarrival time参数等。
运行并分析系统各个资源的利用率、排队队长及服务等待时间，能发现系统存在的问题，比较各个排队系统的系统资源利用率、排队队长和服务等待时间，评价排队系统的优劣。
二、实验地点及环境四川大学工商管理学院的学院大楼综合实验室，运用pc机及simio系统仿真软件，在老师的指导下完成此次系统仿真实验。
三、实验步骤㈠、建立模型1. modelⅰ首先加入一个source、三个server、一个sink、一个modeentity，并用path连接。
将source更名为arrive，sink更名为depart，modelentity更名为customer。
设置运行时间8小时。
顾客的到达为poisson流,到达间隔时间为均值为15秒钟的指数分布，故arrive设置interarrival time 参数值为random.exponential(15)，并选择units为seconds；服务(售票)时间服从指数分布,平均时间为45秒钟，故3个server都设置为interarrival time 参数值为random.exponential(45)，并选择units为seconds。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
控制系统数字仿真实验报告班级：机械1304姓名：***学号： **********实验一数字仿真方法验证1一、实验目的1.掌握基于数值积分法的系统仿真、了解各仿真参数的影响；2.掌握基于离散相似法的系统仿真、了解各仿真参数的影响；3.熟悉MATLAB语言及应用环境。
二、实验环境网络计算机系统（新校区机电大楼D520），MATLAB语言环境三实验内容（一）试将示例1的问题改为调用ode45函数求解，并比较结果。
实验程序如下；function dy = vdp(t,y)dy=[y-2*t/y];end[t,y]=ode45('vdp',[0 1],1);plot(t,y);xlabel('t');ylabel('y');（二）试用四阶RK 法编程求解下列微分方程初值问题。
仿真时间2s ，取步长h=0.1。
⎪⎩⎪⎨⎧=-=1)0(2y t y dt dy 实验程序如下:cleart0=0;y0=1;h=0.1;n=2/h;y(1)=1;t(1)=0;for i=0:n-1k1=y0-t0^2;k2=(y0+h*k1/2)-(t0+h/2)^2;k3=(y0+h*k2/2)-(t0+h/2)^2;k4=(y0+h*k3)-(t0+h)^2;y1=y0+h*(k1+2*k2+2*k3+k4)/6;t1=t0+h;y0=y1;t0=t1;y(i+2)=y1;t(i+2)=t1;endy1t1figure(1)plot(t,y,'r');xlabel('t');ylabel('y');（三）试求示例3分别在周期为5s的方波信号和脉冲信号下的响应，仿真时间20s，采样周期Ts=0.1。
实验程序如下:clear% Create system modelA=[-0.5572 -0.7814 ;0.7814 0];B=[1;0];C=[1.9691 6.4493];D=0;sys=ss(A,B,C,D);% Pulse response of the system subplot(221)[u,t]=gensig('pulse',5,20,0.1)plot(t,u);hold onlsim(sys,u,t);xlabel('t');ylabel('Y');title('Pulse response of the system'); hold offgrid% Square response of the system subplot(222)[u,t]=gensig('square',5,20,0.1)plot(t,u);hold onlsim(sys,u,t);xlabel('t');ylabel('Y');title('Square response of the system'); hold offgrid四实验体会这是第一次做matlab实验，通过实验，基本熟悉了matlab的基本操作，同时，也可以仿照所给例子来利用数值积分的函数进行解常值系统微分方程，在误差允许范围内，相对于elur法来说，代码更简单点。
实验二SIMULINK动态仿真一、实验目的1. 掌握SIMULINK动态仿真；2. 熟悉MATLAB语言及应用环境二、实验环境网络计算机系统，MATLAB语言环境三、实验内容（一）Simulink的基本操作（1）运行Simulink（2）常用的标准模块（3）模块的操作（二）系统仿真及参数设置（1）算法设置（Solver）（2）工作空间设置（Workspace I/O）某系统框图如图所示，试用SIMULINK进行仿真，并比较在无饱和非线性环节下系统仿真结果。
四、实验体会通过本次实验，我体会到了simlink强大的仿真建模功能，通过仿真实验，我们可以观测到部分模块对系统整体的影响，从而可以更好的调节系统，使其工作在最佳状态。
同时，本次实验也让我对matlab的使用进一步熟悉起来。
实验三PID控制器设计一实验目的1．了解PID控制原理，掌握相应PID控制器设计仿真程序的应用；2．掌握计算机辅助系统瞬态性能指标的计算；3．掌握计算机辅助系统频率性能分析；二实验环境网络计算机系统（新校区机电大楼D520），MATLAB语言环境三实验内容已知如图所示单位反馈系统要求：1．绘制系统的开环Nyquist图和Bode图，并判断该闭环系统是否稳定。
2．应用Ziegler—Nichols方法设计P控制器、PI控制器和PID控制器。
3．计算比较原系统与P控制系统、PI控制系统、PID控制系统的瞬态性能指标。
实验程序：clear clcsys=tf([500 5000],[1 33 337 1775 4950 5000]);figure(1)nyquist(sys)[Re,Im,w1]=nyquist(sys);grid on figure(2)bode(sys)[mag,phase,w2]=bode(sys);grid onsysclose=feedback(sys,1);[z,p,k]=zpkdata(sysclose,'v')实验二function [sysc,Kp,Ti,Td]=pidmargin(sys,type) margin(sys)[Gm,Pm,Wg,Wc]=margin(sys);Kcr=Gm;Wcr=Wg;Tcr=2*pi/Wcr;switch typecase 1disp('P Controler')Kp=0.5*KcrTi='No Design'Td='No Design'sysc=Kp;case 2disp('PI Controler')Kp=0.4*KcrTi=0.8*TcrTd='No Design'sysc=Kp*(1+tf(1,[Ti,0]));case 3disp('PID Controler')Kp=0.6*Kcr;Ti=0.5*TcrTd=0.12*Tcrsysc=Kp*(1+tf(1,[Ti,0])+tf([Td,0],1)); end实验三clfnum=[500 5000];den=[1 33 337 1775 4950 5000]sys=tf(num,den);sysgroup=feedback(sys,1);%Design P-PI -PIDControlerfor i=1:3type=i;[sysc,Kp,Ti,Td]=pidmargin(sys,type);sysopen=sysc*sys;sysclose=feedback(sysopen,1);sysgroup=append(sysgroup,sysclose);endclffor i=1:4subplot(2,2,i)step(sysgroup(i,i))step(sysgroup(i,i))[num,den]=tfdata(sysgroup(i,i),'v')Finalvalue=polyval(num,0)/polyval(den,0)% Compute overshoot[y,t]=step(sysgroup(i,i));[Ymax,k]=max(y);Peaktime=t(k)OvershootPercent=100*(Ymax-Finalvalue)/Finalvaluen=1;while y(n)<0.1*Finalvalue,n=n+1;endm=1;while y(m)<0.9*Finalvalue,m=m+1;endRiseTime=t(m)-t(n)% Compute settling timer=length(t);while (y(r)>0.98*Finalvalue & y(r)<1.02*Finalvalue) r=r-1;endSettlingTime=t(r)end123400.20.40.60.8Step ResponseTime (seconds)A m p l i t u d e024680.51Step ResponseTime (seconds)A m p l i t u d e24680.511.5Step ResponseTime (seconds)A m p l i t u d e0123450.511.5Step ResponseTime (seconds)A m p l i t u d e实验心得体会在第二个实验中主程序通过调用函数m 文件pidmargin.m ，实现了PID 控制器的设计，并在单位阶跃函数作用下的系统输出，列于同一张表，便于分析；第三个实验在第二个实验的基础上，将系统在阶跃函数作用下的状态参数返回，从而实现经PID 控制器修正后的系统与原系统进行量化对比，显示校正效果。
本次实验，我学会了如何运用matlab 画系统的Bode 图和Nyquist 图，很大程度上简化了系统稳定性、动态特性等相关问题的求解。
实验四 模糊逻辑控制器设计一、实验目的4．了解模糊逻辑控制原理；5．掌握MATLAB 辅助模糊逻辑控制器设计流程；二、实验环境网络计算机系统，MATLAB 语言环境三、实验内容、要求设有前后两车（目标车与本车），其速度y 与油门控制输入u 间的传递函数均为427.024)()(2+**+=s s s U s Y 现要求设计一模糊控制器，使得1） 控制汽车（本车）由静止启动，追赶200m 外时速90km 的汽车（目标车）并与其保持30m 距离。
2） 目标车速度改为时速110km 时，仍与其保持30m 距离。
3） 目标车速度改为时速70km 时，仍与其保持30m 距离。
四、实验步骤第一步 利用simulink 构造系统仿真模型。
根据题意，可做出系统结构图如图1所示。
图中，为了控制系统设计方便，将两车的距离相减后再减掉30，用模糊控制使其趋于0。
图1 系统结构图进一步，利用simulink构造了系统仿真模型，如图2所示。
考虑到实际的汽车速度存在极限，系统模型中加入了饱和非线性模块进行模拟。
图中的e和u除以20 是为了使输出量限定在10左右。
然后，将系统模型以文件f-car.mdl保存。
图2 系统simulink仿真模型第二步设计模糊逻辑规则（参考下文，不要自己再设计）。
以误差量（两车距离）及误差对时间的变化量作为输入进行模糊规则设计。