截面与三视图(一)(人教版)word版

合集下载

人教版数学九年级下册(课件)29.2三视图1

主
左
视
视
图
图
俯视图
人生的价值，并不是用时间，而是用深度去衡量的。
——列夫·托尔斯泰
义务教育教科书（人教版）九年级数学下册
1、填空
不同
位置物体平行于投物体倾斜于投物体垂直于
物体
影面
影面
投影面
线段
形状、大小不变（全等）
大小变化
点
面形状、大小不形状、大小线
变（全等）
均变化
2、画出如图摆放的正方体在投影面上的正投影。
（1）正方体的一个面ABCD平行于投影面P；
（2）正方体的一个面ABCD倾斜于投影面，上底面
ADEF垂直于投影面,并且对角线AE垂直于投影面.
A*
D*
F* A* D*
B*
C*
A
D
BБайду номын сангаас
C
P
G*
E
F
D
A
H
G
C
B
C* B*
P
你能指出这些图形分别从哪个角度观察得到的吗?
图是同一本书的三个不同的视图．
你能说出这三个视图分别是从哪个方向观察这本书时得到的吗？
正面
将三个投影面展开在一个平面内，得到这一物体的一张三视图
解：图是支架的三视图．
主
左
视
视
图
图
俯视图
本节课你学习了什么知识？
1、画出如图所示的三棱柱的三视图（这个三柱上下底面是正三角形）．
主
左
视
三图
视图
棱
柱
俯视图
2、画出半球和圆锥的三视图．

《三视图》教用课件人教版1

《三视图》教用课件人教版1
《三视图》教用课件人教版1
正视图
4（高）
3（宽）
5(长)
俯视图
《三视图》教用课件人教版1
长
方
体
的
三
视
侧
图
视
图
《三视图》教用课件人教版1
三视图能反映物体真实的形状和长、宽、高.
三视图之间的投影规律
正
视图
4（高）
俯视图
5(长)
高
长对正
平齐
5(长)
3（宽）
俯视图在正视图的下方、侧视图在正视图的右方
几何体的正视图、左视图、俯视图统称为几何体的三视图.
《三视图》教用课件人教版1
探究、如图所示的长方体的长、宽、高分别为 5cm、3cm、4cm. 5cm
3cm
4cm
讨论：
①这个长方体的三视图分别是什么形状的？ ②正视图、侧视图和俯视图的长方形的长宽高分别为多少厘米？ ③正视图和俯视图中有没有相同的线段？正视图和侧视图呢？侧视图和俯视图呢？
横看成岭侧成峰，远近高低各不同。不识庐山真面目，只缘身在此山中。
思考、正视图、侧视图、俯视图分别是从几何体的哪三个角度观察得到的几何体的正投影图？它们都是平面图形还是空间图形？
1.三视图的概念
(1)光线从几何体的前面向后面正投影所得到的投影图叫做几何体的正视图. (2)光线从几何体的左面向右面正投影所得到的投影图叫做几何体侧视图. (3)光线从几何体的上面向下面正投影所得到的投影图叫做几何体的俯视图.
正视图
侧视图
正视图
侧视图
俯视图
《三视图》教用课件人教版1
俯视图
《三视图》教用课件人教版1

几何体的截面、三视图、平面展开图

1.截面可能是圆的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥2.截面可能是三角形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥3.截面可能是矩形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥4.截面可能是梯形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥5.截面可能是平行四边形的几何体，请打“√”正方体、长方体、圆柱、圆锥、球、六棱柱、三棱锥6.用一个平面截下面的几何体，截面不可能是三角形的是_______A 圆锥B圆柱C长方体 D 六棱柱7. 正方体的截面不可能是________A 三角形B 四边形C 五边形D 六边形E 七边形8. 基本几何体的三视图(主视图反映物体的长和高，俯视图是长和宽，左视图是高和宽）几何体主视图左视图俯视图圆柱圆锥四棱锥空心圆柱9.由一些大小相同的小正方体搭成的几何体的主视图与俯视图如图所示，则搭成这个几何体的小正方体的个数最多为___,最少为____。

___．10. 如图所示是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则小立方体的个数不可能是( )A．6个B．7个C．8个D．9个11. 如图是由若干个大小相同的正方体搭成的几何体的三视图，则该几何体所用的正方形的个数是________12.由一些完全相同的小正方体搭成的几何体的主视图和左视图如图所示，则组成这个几何体的小正方体的个数可能是13. 几个棱长为1的正方体组成的几何体的三视图如图所示，则这个几何体的体积是＿＿＿＿14．几个立方块所搭几何体的俯视图如图所示，小正方形的数字表示在该位置小立方块的个数.请画出这个几何体的主视图和左视图.15.下图，该几何体是_______. 16. 下图，则这个几何体是______17. 下图，该几何体是_______. 18. 下图,三视图表示的几何体是________19.主视图、俯视图和左视图都是．．长方形的几何体是_________(填一个即可) 20. 三视图都相同的几何体可能是_________、____________.(有两种类型)3 2 1 1 2 24 1 3主视图左视图2 2 1 3421.下列四个水平放置的几何体中，三视图如图所示的是( )A．B．C．D22.中央电视台有一个非常受欢迎的娱乐节目：墙来了！选手需按墙上的空洞造型摆出相同姿势，才能穿墙而过，否则会被墙推入水池．类似地，有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞，则该几何体为( )A．B．C．D．23.如图所示，下列水平放置的几何体中，俯视图是矩形的是( )A．B．C．D．24. 下列四个几何体中，主视图是三角形的是( )A．B．C．D．25. 下列几何体中，俯视图相同的是( )A①② B①③C②③ D ②④26.下面四个几何体中，左视图是四边形的几何体共有 ( )A 1 个B 2个C 3个D 4个27.下列四个几何体中，主视图与左视图相同的几何体有( )A.1个B.2个C.3个D.4个28.球和圆柱在水平面上紧靠在一起，组成如图所示的几何体，托尼画出了它的三视图，其中他画的俯视图应该是( )A．两个相交的圆B．两个内切的圆C．两个外切的圆D．两个外离的圆29.我国古代数学家利用“牟合方盖”(如图甲)找到了球体体积的计算方法.“牟合方盖”是由两个圆柱分别从纵横两个方向嵌入一个正方体时两圆柱公共部分形成的几何体，图乙所示的几何体是可以形成“牟合方盖”的一种模型，它的主视图是( )。

29.2 三视图人教版九年级下册课件(共23张)

巩固知识
1.一个直六棱柱和长方体如图所示放置.你能说出下面 (a),(b),(c)三个视图分别是从哪个方向看到的吗?
( 第1题 )
(a)
(b)
2.用4个小立方块搭成的几何体如图.请画出它的三视图.
(c)
( 第2题 )
更上一层楼
3.一个圆柱如图,从正面看到的是什么图形?从上面看到的是什么图形?从左面看到的是什么图形?
主视图
左视图
高平齐
主视方向图3-18
长对正
宽相等
俯视图图3-19
1.说出圆锥、球、正方体的三视图各是什么图形.
圆锥, 球的三视图.
主
视
主视图左视图
图
俯视图
左视图
俯视图
立方体的三视图都是正方形。
主视图左视图俯视图
如图，圆柱的主视图和左视图都是长方形，俯视图是圆。
主视图左视图
俯视图和左视图共同反映了物体前后方向的尺寸, 通常称之为“宽相等”; “长对正,高平齐,宽相等”是画三视图必须遵循的法则.
在画三视图时,一般先画主视图,再把左视图画在主视图的右边,把俯视图画在主视图的下面.
一个长方体的立体图如图3-18所示,请画它的三视图.
重画一次解: 所求三视图如图3-19.
猜猜他们是什么关系？
看必为
事须了从能
物多完方整
不能
面确观切察的
只物表体达
看
。物体
单
的形
方面
状和大
小
பைடு நூலகம்
，
你认识吗？
你认识吗？
你认识吗？
观察物体从哪些方面去考虑呢？

几何体的截面、三视图.doc

1）用一个平面去截一个几何体，截出的面叫做截H 截面的形状既与被截面的几何体有例2：如图, 用一个平面去截一个正方体, 所得的截面形状应是（）1.3截一个几何体学习目标——目标明确、行动有效1）正方体的截面及截面形状2）常见柱体、锥体的截面知识点一正方体的截面及截面形状关,还与截面的角度和方向有关。

2）用平面去截正方体，其截面形状：三角形、四边形、五边形、六边形例1：如图，用一个平面去截一个正方体，截面相同的是（④D.①与②，③与④知识点二常见柱体、锥体的截面1）用平面去截圆柱，截面形状：圆、椭圆、长方形、梯形、类似于拱形2）用平面去截圆锥，截面形状：圆、椭圆、三角形、类似于拱形3）用平面去截球，截面形状:例3：用平面去截下列几何体，能截得长方形、三角形、等腰梯形三种形状的截面，这① ② ③A.①与②B.③与④C.①与③④2个3个4个5个个几何体是（例4：用一个平面去截下列六个几何体，能得到长方形截面的几何体有（例5：用平面去截下列几何体，截面的形状不可能是圆的几何体是（）A.球B.圆锥C.圆柱D.正方体例6： —个几何体的一个截面是三角形，则原几何体一定不是下列图形中的（）A.圆柱和圆锥B.球体和圆锥C.球体和圆柱D.正方体和圆锥巩固练习1. 下列关于截面的说法正确的是（）A.截面是一个平面图形B.截面的形状与所截几何体无关C.同一个几何体，截面只有一个D.同一个几何体，截面的形状都相同 2. 用一个平面截去正方体的一个角，则截面不可能是（）A.锐角三角形B.等腰三角形C.等腰直角三角形D.等边三角形3. 如图①，大正方体上截去一个小正方体后，可得到图②的几何体.设原大正方体的表面积为S,图②中几何体的表面积为S\那么S ，与S 的大小关系是（理色图①图②A. S F>S B. S ，=S C. S ，VS D.不能确定 4.有一个圆锥体，用一个平面从不同的位置去截它，如图①〜④，能得到不同的截面，正确的有（）A. 1种B. 2种C. 3种D. 4种1.4从三个方向看物体的形状学习目标——目标明确、行动有效1）组合体的视图可转化为基本几何体的视图，然后根据位置关系确定组合体的视图.知识点一画出从三个方向看到几何体的图形例1.如图是由6个大小相同的正方体组成的几何体，它的左视图是（）例2.下列几何体中，有一个几何体的俯视图的形状与其他三个不一样，这个几何体是（））平方厘米。

立体几何体的截面及三视图

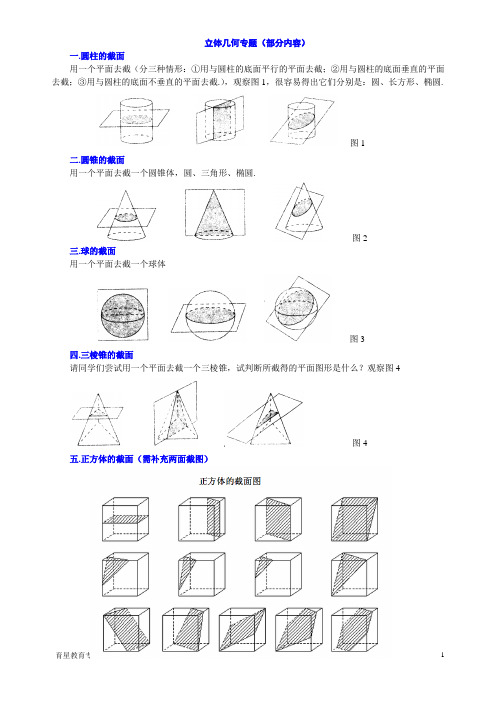
立体几何专题（部分内容）一.圆柱的截面用一个平面去截（分三种情形：①用与圆柱的底面平行的平面去截；②用与圆柱的底面垂直的平面去截；③用与圆柱的底面不垂直的平面去截.），观察图1，很容易得出它们分别是：圆、长方形、椭圆.图1二.圆锥的截面用一个平面去截一个圆锥体，圆、三角形、椭圆.图2三.球的截面用一个平面去截一个球体图3四.三棱锥的截面请同学们尝试用一个平面去截一个三棱锥，试判断所截得的平面图形是什么？观察图4图4五.正方体的截面（需补充两面截图）补充：三视图或投影经典考题公式：空间几何体的表面积棱柱、棱锥的表面积：各个面面积之和圆柱的表面积：222S rl r ππ=+ 圆锥的表面积：2Srl r ππ=+圆台的表面积：22S rl r Rl R ππππ=+++球的表面积：24SR π=扇形的面积公式2211=36022n R S lr r πα==扇形（其中l 表示弧长，r 表示半径，α表示弧度）空间几何体的体积柱体的体积：VS h =⨯底锥体的体积：13V S h =⨯底台体的体积： 1)3V S S S S h =++⨯下下上上（球体的体积：343V R π=空间几何体的三视图和直观图：正俯长相等、正侧高相同、俯侧宽一样正视图：光线从几何体的前面向后面正投影，得到的投影图。

侧视图：光线从几何体的左边向右边正投影，得到的投影图。

俯视图：光线从几何体的上面向右边正投影，得到的投影图。

1、线线平行的判断：（1）、平行于同一直线的两直线平行。

（3）、如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

（6）、如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

（12）、垂直于同一平面的两直线平行。

2、线线垂直的判断：（7）、在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

（8）、在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。

人教版九年级数学下册29.2 三视图(第1课时)课件(1)A

正面
三视图
从左面看
主视图
从上面看
正面
主视图长
左视图高
宽
宽俯视图
从正面看
把主视图、俯视图、左视图摊平在一个平面上，则就是三视图。
物体的三视图实际上是物体在三个不同方向
的正投影.正面上的正投影就是主视图，水平面上的正投影就是俯视图，侧面上的正投影就是左视图
从上面看到的图从左边看到的图
从正面看到的图
§29.2.1 三视图
横看成岭侧成峰，远近高低各不同。
不识庐山真面目，只缘身在此山中。
——苏轼
复习什么是三视图
三视图主视图——从正面看到的图左视图——从左面看到的图俯视图——从上面看到的图
填一填
1.直三棱柱的三视图分别是矩形 , 矩形 , 三角形； 2.圆锥的三视图分别是三角形, 三角形, 圆形 .
例2 画出图所示的支架（一种小零件）的三视图．
分析：支架的现状：由两个大小不等的长方体构成的组合体，画三视图时要注意这两个长方体的上下、前后位置关系．
解：图是支架的三视图．
主
左
视
视
图
图
俯视图
例3 图是一根钢管的直观图，画出它的三视图．
分析：钢管有内外壁，从一定角度看它时，看不见内壁，为全面地反映立体图形的现状，画图时规定：
3.先画出能反映物体真实形状的一个视图(一般为正视图）
正ห้องสมุดไป่ตู้图方向
4.运用长对正、高平齐1、原宽相等则画出其它视图
5.检查
主视图左视图
要求：俯视图安排在主视图的正下方，
左视图安排在主视图的正右方。
俯视图
例1：画出三棱柱的三视图

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

截面与三视图（一）（人教版）
一、单选题(共15道，每道6分)
1.用一个平面去截五棱柱，则截面不可能是( )
A.三角形
B.四边形
C.五边形
D.圆
2.如图，用一个平面去截如图所示的圆锥，得到的图形不可能是( )
A. B.
C. D.
3.如图，用一个平面去截下面的几何体，所得截面是三角形，则这个几何体不可能为( )
A. B.
C. D.
4.从一个多边形的某个顶点出发，分别连接这个点和其余各顶点，可以把这个多边形分割成15个三角形，则这个多边形为( )边形．
A.十五
B.十六
C.十七
D.十八
5.一个多边形的内角和为1260°，则它是( )
A.五边形
B.七边形
C.九边形
D.十边形
6.如图是一个用5个完全相同的小立方块搭成的几何体，那么这个几何体的主视图是( )
A. B.
C. D.
7.如图是一个用6个完全相同的小立方块搭成的几何体，那么这个几何体的俯视图是( )
A. B.
C. D.
8.下图是由8个完全相同的小立方块搭成的几何体，那么这个几何体的左视图是( )
A. B.
C. D.
9.如图是有几个相同的小立方块组成的一个几何体，它的左视图是( )
A. B.
C. D.
10.某几何体的三种视图如图所示，则该几何体是( )
A.三棱柱
B.长方体
C.圆锥
D.圆柱
11.主视图、左视图、俯视图分别是下列三个图形的物体是( )
A. B.
C. D.
12.某几何体的三种视图如图所示，则该几何体是( )
A. B.
C. D.
13.如图是由几个完全相同的小立方块所搭几何体的俯视图，小正方形中的数字表示在该位置的小立方块的个数，这个几何体的左视图是( )
A. B.
C. D.
14.如图是一个由多个相同小立方块堆积而成的几何体的俯视图，图中所示数字为该位置小立方块的个数，则这个几何体的主视图是( )
A. B.
C. D.
15.如图是一个由多个相同小立方块堆积而成的几何体的俯视图，图中所示数字为该位置小立方块的个数，则这个几何体的左视图是( )
A. B.
C. D.
（本资料素材和资料部分来自网络，仅供参考。

请预览后才下载，期待您的好评与关注！）。