第一章 矩阵的运算与初等变换
合集下载
第一章 矩阵

(c)
对称矩阵的和、差、数乘仍是对称矩阵; 反对称矩阵的和、差、数乘仍是反对称矩阵,
但:设 n 方阵 A,B 对称,则 AB 对称 ⇔ AB = BA ; 设 对称 ⇔ AB = BA . 另: A 为任意级方阵,则 A + A′ 为对称矩阵, A − A′ 为反对称矩阵, 且 A 可表为对称矩阵与反对称矩阵之和 A =
⎛ Er ⇔ 对任意 A ∈ P m×n 都可以经过行和列的初等变换化为 ⎜ ⎜ 0 ⎝ ⎛ Er ⇔ 存在可逆矩阵 U ∈ F m× m , Q ∈ F m×n ,使得 UAQ = ⎜ ⎜ 0 ⎝
3.可逆矩阵
(1)定义:设 A ∈ P n×n ,若存在 B ∈ P n×n ,使得 AB = BA = E ,则称 A 是可逆矩阵,并 称 B 是 A 的逆矩阵,记为 B = A −1 。 (2)一些性质:
a12 ⎛ b11 ⎜ ⎜b L ain )⎜ 21 L ⎜ ⎜b ⎝ n1 b12 b22
(ai1
ai 2
L
an2
L b1m ⎞ ⎟ L b2 m ⎟ = (ci1 L L⎟ ⎟ L abm ⎟ ⎠
ci 2 L cin ) ,
及其它分块方法. (ii)可逆分块矩阵的逆: ⎛ A1 ⎜ ⎜ 设A=⎜ ⎜ ⎜ ⎝ A2 ⎞ ⎟ ⎟ ⎟ ,其中 Ai 为方阵,则 O ⎟ As ⎟ ⎠
A 可逆 ⇔ Ai ≠ 0, i = 1,L , s ⇔ Ai可逆, i = 1,L , s ,且
⎡ A1−1 ⎢ −1 A =⎢ ⎢ ⎢ ⎢ ⎣
−1 A2
⎤ ⎥ ⎥ ⎥ O ⎥ As−1 ⎥ ⎦.
2
主讲:陈顺民
数学竞赛:高等代数部分
另:两个相同分法的准对角矩阵的和、积仍然是分块对角矩阵,且主 对角线上的子块是对应子块的和、积。 (iii)一般: AB ≠ BA ; ( AB ) ≠ A k B k (但不排除特殊情况)
矩阵的初等变换与初等矩阵52页PPT

行最简形矩阵再经过初等列变换,可化成标 准形.
第二章 矩阵的运算
14
例如,
1 0 1 0 4
A
0 0
1 0
1 0
0 1
3 3
0 0 0 0 0
c3 c4 c4c1c2
1 0
0 c 5 4 c 1 3 c 2 3 c 3 0
0 1 0 0
0 0 1 0
0 1 0 4 4
0 0 0
1 0 0
x1 1
B4
对应方程组为
x2
0
x 3 0
第二章 矩阵的运算
12
矩阵B3 和B4 都称为行阶梯形 . 矩阵 特点:
(1)、可划出 一条阶梯线,线 的下方全为零;
(2)、每个台 阶 只有一行,
1 0 1 0 4
0 0
1 0
1 0
0 1
3 3
A
0 0 0 0 0
台阶数即是非零行的行数,阶梯线的竖线后面 的第一个元素为非零元,即非零行的第一个非 零元.
A
r42r10
r2 r1
0 0
1 1 0
3 3 0
2 2 0
4 6 2
4 10 6
第二章 矩阵的运算
17
r3 r2
3 0
r4 r3
0 0
2 1 0 0
3 3 0 0
4 2 0 0
5 4 2 0
9
4 6 0
(行阶梯形矩 阵)
2 2×1
x1
2x2 x3 x2 2x3 0
1
3 1 x2 3x3 0
1
2 (B2 )
3
第二章 矩阵的运算
2
3 2
x1
第二章 矩阵的运算
14
例如,
1 0 1 0 4
A
0 0
1 0
1 0
0 1
3 3
0 0 0 0 0
c3 c4 c4c1c2
1 0
0 c 5 4 c 1 3 c 2 3 c 3 0
0 1 0 0
0 0 1 0
0 1 0 4 4
0 0 0
1 0 0
x1 1
B4
对应方程组为
x2
0
x 3 0
第二章 矩阵的运算
12
矩阵B3 和B4 都称为行阶梯形 . 矩阵 特点:
(1)、可划出 一条阶梯线,线 的下方全为零;
(2)、每个台 阶 只有一行,
1 0 1 0 4
0 0
1 0
1 0
0 1
3 3
A
0 0 0 0 0
台阶数即是非零行的行数,阶梯线的竖线后面 的第一个元素为非零元,即非零行的第一个非 零元.
A
r42r10
r2 r1
0 0
1 1 0
3 3 0
2 2 0
4 6 2
4 10 6
第二章 矩阵的运算
17
r3 r2
3 0
r4 r3
0 0
2 1 0 0
3 3 0 0
4 2 0 0
5 4 2 0
9
4 6 0
(行阶梯形矩 阵)
2 2×1
x1
2x2 x3 x2 2x3 0
1
3 1 x2 3x3 0
1
2 (B2 )
3
第二章 矩阵的运算
2
3 2
x1
§1 矩阵的初等变换

2 4 4 9
则对方程组的变换完全可以转换为对矩阵B 方程 则对方程组的变换完全可以转换为对矩阵 (方程
二、矩阵的初等变换
1、定义 下面三种变换称为矩阵的初等行变换 、 下面三种变换称为矩阵的初等行变换 初等行变换: (1) 对调两行 (对调 i , j 两行 记作 ri ↔ rj ). 两行, 对调 (2) 以数 k≠0 乘某一行的所有元素 第 i 行乘 k, 记作 ≠ 乘某一行的所有元素(第 ri × k ). (3) 把某一行所有元素的 k 倍加到另一行对应的元 素上去(第 j 行的 k 倍加到第 i 行, 记作 ri+krj ). 素上去 第 把定义中的“ 即得矩阵的 矩阵的初等 把定义中的“行”换成“列”, 即得矩阵的初等 换成“ 列变换的定义 所用记号是把“r ”换成“c”). 列变换的定义(所用记号是把“ 换成“ . 的定义 所用记号是把 换成
① ② ③ ④
(1)
解
②-① (1) ④-①
2 x1 − 2 x2 − x3 = 1 , 5 x2 − 4 x3 = 6 , x2 − x3 = 1 , 18 x2 − 13 x3 = 23 ,
① ② ③ ④ ① ② ③ ④ ( B2 ) ( B1 )
2 x1 − 2 x2 − x3 = 1 , ②↔③ x2 − x3 = 1 , 5 x2 − 4 x3 = 6 , 18 x2 − 13 x3 = 23 ,
1 (2) ri × k 的逆变换是 ri × ( ) (或记作 ri ÷ k ). 或记作 k
或记作 (3) ri+krj 的逆变换是 ri+(−k)rj (或记作 ri − krj ). −
3、1) 若矩阵 经有限次初等行变换变成矩阵 、 若矩阵A经有限次初等行变换变成矩阵 经有限次初等行变换变成矩阵B, 就称矩阵 与 行等价 行等价, 就称矩阵A与B行等价 记作 A ~ B . 矩阵 2) 若矩阵 经有限次初等列变换变成矩阵 就 若矩阵A经有限次初等列变换变成矩阵 经有限次初等列变换变成矩阵B, 列等价, 称矩阵A与B列等价 记作 A ~ B . 矩阵 与 列等价 3) 若矩阵 经有限次初等变换变成矩阵 就称 若矩阵A经有限次初等变换变成矩阵 经有限次初等变换变成矩阵B, 矩阵A与B等价 记作 A ~ B. 等价, 矩阵 与 等价 等价关系具有性质: 等价关系具有性质: (i) 反身性 A ~ A . (ii) 对称性 若 A ~B, 则 B ~ A. (iii) 传递性 若 A ~B, B ~ C,则A ~C. 则
线性代数1.5 (1)矩阵的初等变换

1 0 1 0 0 0 0 1 0 0 0 0
0
0
0
1
,
0
0 0
0
0
1 0 0
0 1 0
0 0 1
0
0
,
0 0
0
0
1 0 0
0 1 0
0 0 0
0
0
0
,
1 0 0
0 问题,读者将会在学习完第三章第3.3.1 节之后有深入的理解和答案.所有与矩阵 A 等价 的矩阵组成的一个集合,称为一个等价类,标准 形是这个等价类中最简单的矩阵.
Linear Algebra
BUCT
小结
Chapter 1 Matrix
初等变换的定义 化矩阵为行阶梯形的初 等变换法 矩阵的等价及其标准形
4
6 4
r2 3r1
r3 r1
r2 3r1
r3 r1
1 0 0
2 4 0
3 8 0
4
6 0
1 2 3 4
14 r2
0
1
2
3
@B,
4r2
0
0
0
2 0
显然,以上每一步 变换都是可以逆回 去的,具体如下:
0 0 0
1 0 0 0 0
0 c4 c1 c4 2c2 0 c5 3c1 c5 8c2 0 c5 6c3
1 0 0
0
0
0
@N
1 0 0
0 0 0
矩阵的运算与初等变换

基本列向量,则
a11
Ae j
a21
a1 j
a2 j
a1n
a2n
0
1
a1 j a2 j
am1 amj
amn
0
amj
➢ 可见当
§2 矩阵的运算
A=(aij)m×n,则EmA=AEn=A.
§2 矩阵的运算
➢ 运算规律 ➢ (1)设A=(aij)m×s, B=(bij)s×k, C=(Cij)k×n, 则A(BC)=(AB)C ;
A
B
a21
b21
am1 bm1
a12 b12 a22 b22
am2 bm2
a1n b1n a2n b2n
amn bmn
➢ 注:只有同型矩阵才能相加.
§2 矩阵的运算
➢ 定义 m×n矩阵-A=(-aij)称为矩阵A=(aij)的负矩阵. 两个m×n矩阵A=(aij),B=(bij)的差记为A-B,规定 A-B=A+(-B),即
➢ 本章主要介绍矩阵的概念、性质和运算。并把向 量视为特殊的矩阵,自然地引进向量的概念及其 线性运算。还将介绍矩阵的初等变换及分块矩阵 等相关知识,为今后的学习相关知识打下扎实的 理论基础。
§1 矩阵与向量的概念
➢ 本节教学内容 ➢ 1.矩阵的概念 ➢ 2.同型矩阵与矩阵相等的概念 ➢ 3. 几种特殊的矩阵 ➢ 4. 矩阵的应用 ➢ 5. 向量的概念
线性代数 第一章
第一章 矩阵的运算与初等变换
➢ 本章教学内容 ➢ §1 矩阵与向量的概念 ➢ §2 矩阵的运算 ➢ §3 分块矩阵及矩阵的分块运算 ➢ §4 几种特殊的矩阵 ➢ §5 矩阵的初等变换
第一章 矩阵的运算与初等变换
矩阵的初等变换和初等矩阵

23xxx111
x2 3x2 6x2
2x3 x3 9x3
x4 x4 7 x4
4 2 9
增广矩阵的比较
B
2 1 4 3
1 1
6 6
1 2
2 9
1 1 2 7
42 94
B2
1 2 2 3
1 1 3 6
2 1
1 9
1 1 1 7
24 92
显然 把B的第3行乘以(1/2)即得B2
即 方程③两端乘以(1/2) B的第3行乘以(1/2)
E1ij(k)Eij(-k)
Henan Agricultural University
四、初等矩阵与初等变换的关系
设A是一个mn矩阵 对A施行一次初等行变换 相当于在 A的左边乘以相应的m阶初等矩阵 对A施行一次初等列变换 相当于在A的右边乘以相应的n 阶初等矩阵
3 0 1
例如
设
A 10
1 1
4 4 9
①②
①②
x1 x2 2x3 x4 4
423xxx111
x2 6x2 6x2
x3 2x3 9x3
x4 2x4 7 x4
2 4 9
增广矩阵的比较
B
21 43
1 1
6 6
1 2
2 9
1 1 2 7
42 94
1 1 2 1 4
B1
2 4 3
1 6
6
1 2 9
1 2
7
2 94
[i,j]
以数k乘第i行加到第j行上 记作 [i(k)j]
Henan Agricultural University
三、初等矩阵
例如,对于3阶单位矩阵E
第一章线性代数
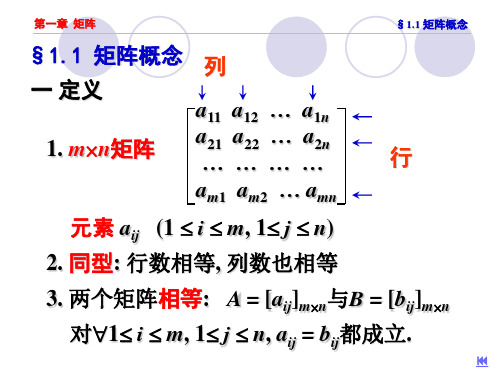
2. 初等矩阵的性质 定理1.1. 定理1.1. 对m×n矩阵A施行一次初等行变换 矩阵A施行一次初等行 相当于在A 相当于在A的左边乘以相应的初等 矩阵; 施行一次初等列 矩阵; 对A施行一次初等列变换相 当于在A 当于在A的右边乘以相应的初等矩 阵.
第一章 矩阵
§1.5 方阵的逆矩阵
§1.5 方阵的逆矩阵 一. 逆矩阵的概念 1. 定义: 设A为方阵, 若存在方阵B, 使得 定义: 为方阵, 若存在方阵B AB = BA = E, 则称A可逆, 并称B 则称A可逆, 并称B为A的逆矩阵. 逆矩阵. 2. 逆矩阵是唯一的, A−1. 逆矩阵是唯一的, 记为A 记为 3. 性质:设A, B为同阶可逆方阵, 数k ≠ 0. 则 性质: 为同阶可逆方阵, (1) (A−1)−1 = A. (2) (AT)−1 = (A−1)T. (A (3) (kA)−1 = k−1A−1. (4) (AB)−1 = B−1A−1.
则λA =
λA11 λA12 … λA1r λA21 λA22 … λA2r
… … … … . λAs1 λAs2 … λAsr
第一章 矩阵
§1.3 分块矩阵
3. 分块乘法
设A为m×l矩阵, B为l ×n矩阵, 将它们分块如下 矩阵, 矩阵, A11 A12 … A1t B11 B12 … B1r A21 A22 … A2t B21 B22 … B2r A= … … … … , B= … … … … , As1 As2 … Ast Bt1 Bt2 … Btr 其中A 的列数分别与B 其中Ai1, Ai2, …, Ait的列数分别与B1j, B2j, …, Btj的 行数相等. 行数相等. C11 C12 … C1r t C21 C22 … C2r 其中C 则AB = … … … … , 其中Cij = Σ AikBkj , k=1 Cs1 Cs2 … Csr (i = 1, 2, …, s; j = 1, 2, …, r.)
第一章 矩阵

1、数乘
阳光普照
定义3 规定数 与矩阵 A [ai j ]mn 的乘积 A 为
A A [ai j ]m n .
显然
0 A O, 1 A A. A (1) A [ai j ]m n 称为矩阵A的负矩阵。
数乘满足运算律:
1 A A; 2 A A A;
二、矩阵的乘法运算
显然可考虑定义矩阵的乘法和除法为:
A B [ai j bi j ]mn
和
A B [ai j bi j ]mn ,
这是个著名的病态矩阵,称为Hilbert矩阵。
例 4 (图的邻接矩阵) 某航空公司在A,B,C,D四城市之间开辟了若干 航线 ,如图所示表示了四城市间的航班图,如果 从A到B有航班,则用箭头从 A指向 B.
到达城市
A
出 发 城 市
B
C
D
A
B
C
A B C D
D
我们先用表格来表示航班图(见前页) 。表格中
太繁琐了,得换个思路!!
注意到二元一次方程组的解完全由未知数系数
a11、a12、a21、a22
及常数项 b1、b2 所确定。
三元一次方程组的解完全由未知数系数
a11、a12、a13、a21、a22、a23、a31、a32、a33
及常数项 b1、b2、b3 所确定。
一般地,归纳可知,n元的线性方程组
将上式回代入
(1)
中,并整理,可得
b1a22 b2a12 x1 a11a22 a12a21
对于三元一次线性方程组
a11 x1 a12 x2 a13 x3 b1 a21 x1 a22 x2 a23 x3 b2 a x a x a x b 32 2 33 3 3 31 1
阳光普照
定义3 规定数 与矩阵 A [ai j ]mn 的乘积 A 为
A A [ai j ]m n .
显然
0 A O, 1 A A. A (1) A [ai j ]m n 称为矩阵A的负矩阵。
数乘满足运算律:
1 A A; 2 A A A;
二、矩阵的乘法运算
显然可考虑定义矩阵的乘法和除法为:
A B [ai j bi j ]mn
和
A B [ai j bi j ]mn ,
这是个著名的病态矩阵,称为Hilbert矩阵。
例 4 (图的邻接矩阵) 某航空公司在A,B,C,D四城市之间开辟了若干 航线 ,如图所示表示了四城市间的航班图,如果 从A到B有航班,则用箭头从 A指向 B.
到达城市
A
出 发 城 市
B
C
D
A
B
C
A B C D
D
我们先用表格来表示航班图(见前页) 。表格中
太繁琐了,得换个思路!!
注意到二元一次方程组的解完全由未知数系数
a11、a12、a21、a22
及常数项 b1、b2 所确定。
三元一次方程组的解完全由未知数系数
a11、a12、a13、a21、a22、a23、a31、a32、a33
及常数项 b1、b2、b3 所确定。
一般地,归纳可知,n元的线性方程组
将上式回代入
(1)
中,并整理,可得
b1a22 b2a12 x1 a11a22 a12a21
对于三元一次线性方程组
a11 x1 a12 x2 a13 x3 b1 a21 x1 a22 x2 a23 x3 b2 a x a x a x b 32 2 33 3 3 31 1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表示。
➢ 注:这里aii=0,即同一个村不考虑相通的道路。
§1 矩阵与向量的概念
➢ 5.向量的概念 ➢ 定义1.2 1×n矩阵称n维行向量, n×1矩阵称n 维列向量, n维行向量与n维列向量统称n维向量,
简称向量。 向量常用黑体字母,,, …或x,y,z,… 表示(或加箭头 )。
➢ 两向量相等当且仅当维数相同且对应的分量相等. ➢ 分量全为零的向量称零向量,记为0.
线性代数 第一章
第一章 矩阵的运算与初等变换
➢ 本章教学内容 ➢ §1 矩阵与向量的概念 ➢ §2 矩阵的运算 ➢ §3 分块矩阵及矩阵的分块运算 ➢ §4 几种特殊的矩阵 ➢ §5 矩阵的初等变换
第一章 矩阵的运算与初等变换
➢ 矩阵是代数学中最重要的基本概念之一,是代数 学研究的主要对象,也是数学许多分支研究及应 用的重要工具,它贯穿于线性代数的各个部分。 在很多领域中的一些数量关系都可以用矩阵来描 述。
➢ 作业:习题1.1(A) 第2题
§2 矩阵的运算
➢ 本节教学内容 ➢ 1.矩阵加、减法 ➢ 2.数乘矩阵 ➢ 3. 矩阵乘法 ➢ 4. 方阵的幂 ➢ 5. 矩阵的转置
§2 矩阵的运算
➢ 1.矩阵加、减法 ➢ 定义2.1 两个m×n矩阵A=(aij),B=(bij)的和记为 A+B,规定
a11 b11
§1 矩阵与向量的概念
➢ 例 主对角线元素均为1,其它元素均为0的
n阶方阵
1 0
0 1
0 0
0 0 1
称n阶单位矩阵,记为En或E.
§1 矩阵与向量的概念
➢ 4.矩阵的应用
➢ 例1 某公司对四名应聘人员进行三项素质考评
的百分制成绩可用矩阵
a11 a12 a13
A
a21 a31 a41
§1 矩阵与向量的概念
➢ 1.矩阵的概念
考察线性方程组
x1 x2 2x3 1, 2x1 3x2 x3 2, x1 2x2 3x3 4,
隐去未知量和等号,分离出各未知量的系数,得
1 1 2 1 2 3 1 2 1 2 3 4
称为矩阵
一般地,我们有如下的定义
§1 矩阵与向量的概念
A
B
a21
b21
am1 bm1
a12 b12 a22 b22
am2 bm2
a1n b1n a2n b2n
amn bmn
➢ 注:只有同型矩阵才能相加.
§2 矩阵的运算
➢ 定义 m×n矩阵-A=(-aij)称为矩阵A=(aij)的负矩阵. 两个m×n矩阵A=(aij),B=(bij)的差记为A-B,规定 A-B=A+(-B),即
➢ 定义1.1由m×n个数排成m个行n个列的数表
a11 a21
a12
a22
a1 j a2 j
是简第称aa i(行i12,nnj)第元j列元素,
ai1 ai2 aiijj ain
am1 am2 amj amn
叫做m行n列的矩阵,或称m×n矩阵.通常用大写
字母A或Am×n表示法. 有时也记为
a1
➢ ⑵ m×1矩阵 a2
am
也称列矩阵,或称m维列向量,ai也称为第i个分量.
§1 矩阵与向量的概念
主对角线
a11
➢ ⑶ n×n矩阵
a21
a12
a22
副对角线
a1n也称n阶方阵(或n级方阵),An×n表可简记为An; 其中aii称为主对角线元素; 而aij (i+j=n+1)称为副对角线元素.
A (aij ) 或 A (aij ) mn
§1 矩阵与向量的概念
➢ 元素是实数的矩阵称为实矩阵 ➢ 元素是复数的矩阵称为复矩阵 ➢ 例如
1 0 3 5 是一个2×4实矩阵, 9 6 4 3
13 6 2i 2 2 2 是一个3×3复矩阵, 2 2 2
§1 矩阵与向量的概念
➢ 2.同型矩阵与矩阵相等的定义
➢ 本章主要介绍矩阵的概念、性质和运算。并把向 量视为特殊的矩阵,自然地引进向量的概念及其 线性运算。还将介绍矩阵的初等变换及分块矩阵 等相关知识,为今后的学习相关知识打下扎实的 理论基础。
§1 矩阵与向量的概念
➢ 本节教学内容 ➢ 1.矩阵的概念 ➢ 2.同型矩阵与矩阵相等的概念 ➢ 3. 几种特殊的矩阵 ➢ 4. 矩阵的应用 ➢ 5. 向量的概念
➢ 3.几种特殊的矩阵
➢ ㈠只与0有关的:
➢ 元素全为零的矩阵称为零矩阵,m×n零矩阵记
作O或Om×n ➢ 注意不同型的零矩阵是不相等的.
➢ 例如
0 0 0
0 0 0
0 0 0
0 0
0 0
00
§1 矩阵与向量的概念
➢ ㈡只与行列相关的:
➢ ⑴ 1×n矩阵 a1, a2 , , an
也称行矩阵,或称n维行向量,ai也称为第i个分量. ➢ 注意分量间用逗号分开。
➢ 注:这里 b11 b21 b31 1,
b12 b22 b32 1.
§1 矩阵与向量的概念
➢ 例3 第i村到第j村有aij条道路相通,四个村的通 路信息可用矩阵
0
a12
a13
a14
A
a a a
21 31 41
0 a 32 a 42
a 23 0 a 43
a24
a 34 0
➢ ⑴两个矩阵的行数相等,列数相等时,称为同型
矩阵.
➢ 例如
1 5
2 14 6与 8
3
4
为同型矩阵.
3 7 3 9
➢ ⑵两个矩阵A=(aij)与B=(bij) 为同型矩阵,并且对
应元素相等,即
aij bij i 1,2,, m; j 1,2,, n,
则称矩阵A与B相等,记作A=B.
§1 矩阵与向量的概念
a22 a32 a42
a23
a33 a43
表示,其中aij为第i名应聘者的第j种素质考评的 成绩。
§1 矩阵与向量的概念
➢ 例2 公司中甲、乙两类岗位对三项素质要求的
权重系数也可用矩阵
b11
b12
B b21 b22
b31 b32
表示,其中bij为第j类岗位对第i种素质要求的权重 系数。
§1 矩阵与向量的概念
➢ n个n维列向量
1
e1
0
,
0
0
e2
1 ,
0
0
, en
0
,
1
称为n维基本列向量。
➢ n个n维行向量
f1 1, 0, , 0, f2 0, 1, , 0, , fn 0, 0, , 1,
称为n维基本行向量。
§1 矩阵与向量的概念
本节学习要求 熟悉矩阵、同型矩阵、矩阵相等、列矩阵、 行矩阵、方阵、单位方阵与向量的概念,懂得矩 阵的应用。
