第七节 分块乘法的初等变换及应用举例v3.
高等代数课程教学大纲.总结

精品文档高等代数( 1)课程教学大纲第一部分前言一、课程基本信息1.课程类别:专业基础课2.开课单位:数学与财经系3.适用专业:数学与应用数学专业4. 备选教材:《高等代数(第三版)》,北京大学数学系几何与代数教研室前代数组编.高等教育出版社,2003.二、课程性质和目标高等代数是数学与应用数学专业的一门重要基础课程。
本课程的主要内容是多项式理论和线性代数理论。
通过本课程的教学,使学生掌握代数基本理论和基本方法,培养学生代数方面的科学的思维、抽象的思维,逻辑推理、提高运算以及解决实际应用的能力,为进一步学习专业后续课程奠定坚实的代数基础。
本课程的教学目的是使学生获得一元多项式,行列式,线性方程组,矩阵等方面的系统知识 , 为进一步学习近世代数,复变函数、等后续课程打下坚实的基础,也为深入理解初等数学、指导中学数学教学提供了高等的专业知识与重要的方法论。
通过本门课程系统的学习与严格的训练,全面掌握高等代数的基本理论知识;培养抽象的逻辑思维能力与推理论证能力;具备熟练的运算能力与技巧;提高建立数学模型,并应用代数学的理论知识解决实际应用问题的能力。
三、课程学时与学分教学时数:96 学时,其中理论教学81 学时,实践教学15 学时学分数: 6 学分教学时数具体分配:教学内容理论教学实践教学合计(学时)(学时)(学时)第一章多项式26632第二章行列式16319第三章线性方程组22325第四章矩阵17320合计811596第二部分教学内容及其要求第一章多项式1.教学目标:要求学生理解数域的概念;掌握一元多项式的概念、运算及基本性质;掌握带余除法与整除性的关系,会进行相关运算;会求多项式的最大公因式;理解不可约多项式的概念,掌握求重因式的方法;理解多项式在不同的数域的因式分解形式;掌握Eisenstein判别法,会求有理系数多项式的根。
2.教学重点:整除概念,带余除法及整除的性质,最大公因式、互素、辗转相除法、不可约多项式概念、性质,k 重因式与 k 重根的关系。
分块矩阵的初等变换及其若干应用

4
Em O
O⎞ .对上述分块 En ⎟ ⎠
矩阵进行分块矩阵的初等行变换,将“ T ”的部分变为单位矩阵:
⎛A O ⎜C D ⎝
第1块行左乘A−1
Em O O
O ⎞ 第1块行左乘-CA−1加到第2块行 ⎛ A O Em ⎯⎯⎯⎯⎯⎯⎯⎯⎯ →⎜ ⎟ −1 En ⎠ ⎝ O D −CA A−1
⎛E (1) 交换分块单位阵 ⎜ m ⎝ 0t × m
用此矩阵左乘 T ,有
3
⎛ 0t × m ⎜ ⎝ Em
Et ⎞ ⎛ A B ⎞ ⎛ C D ⎞ ⎟ ⎟=⎜ ⎟, 0m×t ⎠ ⎜ ⎝C D⎠ ⎝ A B ⎠
这正是交换 T 的两块行得到的矩阵.
⎛E (2) 用 P 乘分块单位阵 ⎜ m ⎝ 0t × m 0m×t ⎞ ⎟ 的第一块行,得分块初等矩阵 Et ⎠ ⎛ P ⎜ ⎝ 0t × m 0m×t ⎞ ⎟. Et ⎠
⎛ En1 ⎜O ⎜ ⎜O ⎜ ⎜O ⎝ O En2 O O O ⎞ O O ⎟ ⎟ % O ⎟ ⎟ O E ns ⎟ ⎠ O
1
的分块矩阵称为分块单位矩阵. 定义 分块单位矩阵经过一次分块矩阵的初等行(列)变换后得到分块矩阵就叫 做分块初等矩阵.因为分块矩阵的初等变换有三种形式,因此分块初等矩阵也相 应的有以下三种类型: (1)交换分块单位矩阵的第 i , j 块行(或块列)得到的分块矩阵.例如,
T 的左边乘上相应的 2×2 分块初等矩阵.同理可证对一个 2×2 分块矩阵
⎛A B⎞ T =⎜ ⎟ 作一分块矩阵的初等列变换就相当于在 T 的右边乘上相应的 2×2 分 ⎝C D⎠ 块初等矩阵. 2.分块矩阵初等变换的应用 ⎛ A O⎞ 例 求T = ⎜ ⎟ 的逆,其中 A 是 m 阶可逆矩阵, B 是 n 阶可逆矩阵. ⎝C D⎠
分块矩阵的初等变换及应用

十.研究创新题解:1.分块矩阵的初等变换分块矩阵的初等变换与初等矩阵吴云在1997年8月的《工科数学》上的《分块矩阵的初等变换》一文中提到 定义1 分块矩阵的行(列)初等变换是指: (1)交换两行(列)的位置;(2)第i行(列)的各个元素分别左乘(右乘)该行(列)的一个)(i h 阶)阶)((i l 左(右)保秩因子H;(3)第i行(列)的各个元素分别左乘(右乘)一个)(i h 阶)阶)((i l 矩阵K后加到第j行. 定义2 对应于分块矩阵t s ij A ⨯)(的初等分块矩阵是指:(1)))((k j i P i +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss ll ii E E K E E11或ijk P =⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ii ll ii jj E O E E O E(2) )(H P il =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss llE H E 或)(H P ik =⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛ii E H E 11其中H为第i行(列)的一个左(右)保秩因子;(1) ))((k j i P i +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ss ll ii E E K E E11(2) 或))((k j i P k +=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛ll ll ii E E K E E11 初等分块矩阵与通常的初等矩阵类似,但由于矩阵乘法不满足交换律,故需要分为左、右两种.直接验算可得: 定理1 (1)交换t s ij A ⨯)(的第i行与第j行,相当于左乘一个m阶初等分块矩阵ijL P,其中ijL P 中的元素ii E 为h(i)阶单位矩阵, jj E 为h(j)阶单位矩阵,当r≠i且r≠j时, rr E 为h(r)阶单位矩阵;交换t s ij A ⨯)(的第i列与第j列相当于右乘一个n阶初等分块矩阵ijk P ,其中ii E 为l(i)阶单位矩阵, jj E 为l(j)阶单位矩阵, 当r≠i且r≠j时, rr E 为l(r)阶单位矩阵;(2) t s ij A ⨯)(的第i行的每一个元素左乘一个矩阵H相当于t s ij A ⨯)(左乘一个m阶分块矩阵)(H P iL 中H为h(i)阶方阵; t s ij A ⨯)(的第i列的每一个元素右乘一个矩阵H,相当于t s ij A ⨯)(右乘一个n阶初等到变换矩阵)(H P ik ,其中H为l(i)阶方阵; (3) t s ij A ⨯)(的第j行的每个元素分别左乘一个h(i)×h(j)矩阵K后加到第i行,相当于t s ij A ⨯)(左乘一个初等分块矩阵))((k j i P L +;第j列的每一个元素分别右乘l(j)×l(i)矩阵K后加到第i列,相当于t s ij A ⨯)(右乘))((k j i P k +. 定理2设A为方阵,则分块矩阵t s ij A ⨯)(施行第一种行初等变换后,对应的行列式为A j i h ),()(1-,其中h(i,j)=h(i)h(j)-l+h(i+l)]+…+h(j)[h(i)+h(i+j)+…+h(j-l)], l(i,j)=l(i)h(j)-l+l(i+l)]+…+l(j)[l(i)+l(i+j)+…+l(j-l)],施行第二种初等变换后,对应的行列式为|H|·|A|;施行第三种初等变换后,对应的行列式的值不变.证明: H H P i =)(,A k j i P =+))((显然成立. 下证),()(j i h irL P 1-=,ii E 所在的第1行逐次与它相邻的行交换,移至jj E 前,共进行h(i)-1+h(i+1)+…+h(j-1)次交换两行,第2行逐次与它相邻的行交换,移至jj E 前,同样进行相同次交换两行,依此类推,把ii E 所在的行移至jj E 所在的行前,共进行h(i)[h(i)-1+h(i+1)+…+h(j-1)]次交换两行,然后把jj E 移至适当的位置,同理共进行h(j)[h(i)+h(i+1)+…+h(j-1)]次交换两行,所以交换两行的总次数为h(i,j),故),()(j i h irL P 1-=;同理),()(j i l irR P 1-=. 所以有A P ilj =ilj P ∙A =(-1)),(l i h A 或ilk AP =A ∙ilkP =(-1)),(j i l AA H P il )(=)(H P il A =H ∙A 或A )(H P ik =H ∙AA k j i p l ))((+=)((k j i P l +A ∙=A ))((k j i AP K +=A ))((k j i P k +=A定理3 分块矩阵进行初等变换后,秩不变.证明: 对于(1),相当于对n m ij a A ⨯=)(进行若干次行(列)的交换,故命题成立;对于(2),根据定义1,显然成立;对于(3),相当于进行若干次把n m ij a A ⨯=)(行(列)乘以一个倍数后加到另一行(列),故命题成立.定理4 (1)设A,B的行数均为m,则矩阵方程AX=B,当rank (A)= rank (A,B)=m时有唯一解,当rank (A)= rank (A,B)<m时有无穷多解, 当rank (A)< rank (A,B)时无解;(2)设A,B的列数均为n,则矩阵方程XA=B,当rank (A)= )(T T B A rank ,=n时有唯一解,当rank (A)= )(T T B A rank ,<n有无穷多解, 当rank (A)< )(T T B A rank ,时无解. 证明: (1)设rank (A)= rank (A,B)<m,则存在可逆矩阵P,Q,使Q O O O I P A r ⎢⎢⎣⎡⎥⎦⎤=,Q O OB B P B ⎢⎢⎣⎡⎥⎦⎤=21 其中r I 为r阶单位矩阵, 1B 为r阶方阵,设Q B B B B Q X o⎢⎣⎡⎥⎦⎤=-43211,则有: Q O O O I P AX r o ⎢⎢⎣⎡⎥⎦⎤= Q B B B B Q ⎢⎣⎡⎥⎦⎤-43211= []⎢⎣⎡⎥⎦⎤⎢⎢⎣⎡⎥⎦⎤4321B B B B O O O I P r = Q O O B B P ⎢⎢⎣⎡⎥⎦⎤21=B所以o X 为AX=B的解,其中3B , 4B 是任意的.当rank (A)= rank (A,B)=m时,A=P(m I O)Q,B=( 1B 2B ),显然,AX=B有唯一解: Q B B Q X o )(211-=;当rank (A)< rank (A,B)时,AX=B无解.同理可证(2)成立(当rank (A)= rank ( tA , TB )<n时,X=P ⎢⎢⎣⎡⎥⎦⎤O OO I r1-P ) 定义3 对于任意的u,v,如果rank ( ij A )= rank ( ij A ,iv A )= rank (T ij A ,Tiv A ),则称ij A 为极大元.定理5 分块矩阵22 ij A ⨯)(可以用分块矩阵的初等变换对角化的充要条件是:它有一个极大元.证明: 充分性.不妨设11A 为极大元(否则可以通过第一种分块矩阵的初等变换把极大元移到第一行,第一列交叉位置).由定理4,存在可逆矩阵P,Q,使Q O O O I P A r⎢⎢⎣⎡⎥⎦⎤=11Q O B O A P A ⎢⎣⎡⎥⎦⎤=2121,Q O O A A P A ⎢⎢⎣⎡⎥⎦⎤=2'1'12,令K=-P⎢⎣⎡⎥⎦⎤4321A A A A 1-P ,其中3A , 4A 为适当阶数的任意矩阵.则 K 11A + 21A =P -⎢⎣⎡⎥⎦⎤4321A A A A 1-P P ⎢⎢⎣⎡⎥⎦⎤O O O I r Q , 所以22 ij A ⨯)( 第一行左乘K加到第二行,得⎢⎢⎣⎡⎥⎦⎤+22121211A KA O A A .同理,令K'=-1-Q ⎢⎢⎣⎡⎥⎥⎦⎤4231,,,,A A A A Q , 则11A K′+12A =0,所以⎢⎢⎣⎡⎥⎦⎤+22121211A KA OA A 的第一列右乘K′后加到第二列,得⎢⎢⎣⎡⎥⎥⎦⎤+221211A KA OO A .(如先进行列变换,再进行行变换,得⎢⎢⎣⎡⎥⎥⎦⎤+222111A K A OO A ,, 因为2221A KA +=⎢⎢⎣⎡⎥⎥⎦⎤-2'21'22'11'1A A A A A A A A +22A =21'A K +22A ,故两种运算顺序结果相同) 必要性.反证法,不妨设rank (11A )≠rank (T A 11,T A 21)或rank (T A 11,TA 221)rank (21A ),则由定理4, X 11A =-21A 或X 21A =-11A 无解,从而不存在K,使22 ij A ⨯)(对角化.同理,当rank (11A )≠rank (11A ,12A )或rank (11A ,12A )≠rank (12A )时,不存在'K 使 -A 11K '=A 12或-'12K A =11A 成立.定理5表明:并不是所有的2×2分块矩阵都可以用分块矩阵初等变换对角化,如果分块矩阵没有极大元,则需分得更细,才能对角化.定理 6 矩阵n m A ⨯的一种分块方法t s ij A ⨯)(可以用分块矩阵的初等变换对角化的充分条件是:存在s-1行且存在t-1列有极大元.证明: 用数学归纳法.当s=t=1时,只有一块,命题成立;设s ≤e,t≤ f时命题成立.当s=e+1,t=f时,存在e行且存在f-1列有极大元,显然可以用第一种分块矩阵的初等变换,通过交换两行或两列的位置,使t s ij A ⨯)(的前e行与前f-1列都有极大元,再把前e行,前f-1列看成一块,得到一个新的2×2分块矩阵,记为22 ij B ⨯)(.显然11B 为极大元,根据定理4, 22 ij B ⨯)(可以化成对角形:⎥⎦⎤⎢⎣⎡+2221B KB O OB ,又)()(111-⨯=f e ij A B ,它的每行、列都有极大,故由假设11B 可以对角化,从而f e ij A ⨯=)()(1可以对角化.同理可证当s=e,t=f+1时, )()(1+⨯f e ij A 可以对角化.由此命题成立.下面讨论对角化后的非零块ii A 进一步化简的方法.设Q O OO I P A i ii ⎥⎦⎤⎢⎣⎡=,121-⎥⎦⎤⎢⎣⎡=P B O B I L i i 与⎥⎦⎤⎢⎣⎡=-211C C O I Q R Ri .根据定理1, i L ,i R 为ii A 的左(右)保秩因子,显然也是ii A 所在行(列)的左(右)保秩因子,故对角化后的分块矩阵第i行、第i列分别左乘i L ,右乘i R 后, ii A 可以化成⎥⎦⎤⎢⎣⎡O O O I i讨论分块方阵行列式的计算,先讨论分块初等阵的行列式. 设I 为S ×S 分块单位阵:I=⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛s r r r r I I I I321 其中I r i 为r i 阶单位阵(1≤i ≤S),对I 施行一次初等变换可得定义2所述的三种分块初等阵,它们的行列式有下列计算公式.引理 分块初等阵的行列式有以下性质:(1)|I(i,j)|= τ)1(-,其中τ=r i (r i +1+…+r j )+ r j (r i +1+…+ r j -1)(i<j). 特别地,若j=i+1,则| I(i,j)|=(-1) r i r j ; (2)|I(i(K))|=|k|,其中K 是r i 阶可逆阵; (3)|I(j(K),i)|=1,其中K 是r i ×r j 矩阵.证(1)不难验证,将I(i,j)的元素行进行τ次相邻的对调可将I(i,j)变成I,由行列式的性质,|I(i,j)|= τ)1(-|I|=τ)1(-.(2),(3)由对角分块方阵及三角形分块方阵的行列式计算方法即知.由于对分块方阵A 施行一次初等行变换,相当于用相应的分块初等阵左乘A,由上述引理,我们有下列分块方阵的行列式计算性质. 定理7 设A 是一个分块方阵.(1)交换|A|的i,j 两行(列),行列式变为(-1)τ|A|,其中τ= r i (r i +1+…+ r j )+ r j (r i +1+…+ r j -1);特别地,交换|A|的相邻两行(列)(i 行和i+1行),行列式变为(-1) r i r i +1|A|; (2)用一个r i 阶可逆阵K 左(右)乘|A|的第i 行(列)的所有矩阵,等于用|K|乘以|A|; (3)用一个矩阵左(右)乘|A|的某一行(列)的所有矩阵再加到另一行(列)的对应元素上,行列式不变. 由定理7的(2)可得推论 分块行列式|A|的某一行(列)的所有矩阵的可逆左(右)因子K,可以行列式|K|的形式提到行列式符号外.2.分块矩阵初等变换的应用一、利用分块矩阵的初等变换求矩阵的逆.廖中行在2002年05期《四川教育学院学报》上的《初等变换在分块矩阵乘法》的一文中提到例1: 已知⎥⎦⎤⎢⎣⎡=C OD BP 其中B是r×r可逆阵,C是s×s可逆阵,求证:P可逆,并求1-P .分析:本题是一个分块阵的求逆问题,一般可用待定子块法,也可利用广义初等变换,还可用左乘分块初等阵的方法.解:因B、C可逆,故|B|≠0,|C|≠0.根据拉普拉斯展开,有C B CO DB P ·==≠0,故P可逆.求C 有三种办法:解法一:利用广义初等行变换法.⎪⎭⎝E C 0012⎪⎭ ⎝-100C E (B 1-D)2r ⨯+r 1 ⎪⎪⎭⎫ ⎝⎛-----1111000C DC B E B E 故P 1-=⎪⎪⎭⎫ ⎝⎛-----11110C DC B B 本题对分块矩阵进行广义初等变换是一般矩阵的初等变换的一种推广,其方法和一般矩阵相同.作初等行(列)变换时,对矩阵P应左(右)乘相应的分块单位阵.上述分块初等变换的过程也可用分块阵左乘相应的分块初等阵,可表示如下: 解法二: 可用左乘分块初等阵的方法求1-P⎪⎪⎭⎫ ⎝⎛--1100C B ⎪⎪⎭⎫ ⎝⎛C D B 0=⎪⎪⎭⎫⎝⎛--110C D B E有 ⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛-E D B E 01=⎪⎪⎭⎫⎝⎛E E 00 即:⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛-C B 001⎪⎪⎭⎫ ⎝⎛C D B 0=⎪⎪⎭⎫⎝⎛E E 00=E 故有P 1-=⎪⎪⎭⎫ ⎝⎛C D B 01-=⎪⎪⎭⎫ ⎝⎛--E D B E 01⎪⎪⎭⎫ ⎝⎛--1100C B =⎪⎪⎭⎫⎝⎛-----11110C DC B B 例2:已知A=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--1001000000643521100010001,求A 1-.分析:本题是一个矩阵的求逆问题,一般可用公式法,矩阵的初等变换法求;可块矩阵初等变换法求1-A .利用分块矩阵初等变换法先A 化分成分块矩阵,即A=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--1001000000643521100010001=⎪⎪⎭⎫ ⎝⎛C D B 0 其中B=⎪⎪⎪⎭⎫ ⎝⎛100010001,C=⎪⎪⎭⎫ ⎝⎛--1001,D=⎪⎪⎪⎭⎫ ⎝⎛654321 从而求得B 1-=⎪⎪⎪⎭⎫ ⎝⎛100010001,C 1-=⎪⎪⎭⎫ ⎝⎛--1001然后对A 进行广义初等变换,即:⎪⎭⎝E C 0012⎪⎭⎝-100C E(B 1-D)⨯r 2+r 1 ⎪⎪⎭⎫⎝⎛-----111100C DC B E B E ∴A 1-=⎪⎪⎭⎫ ⎝⎛-----11110C DC B B =⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛--1000001000651004201031001如果用其它方法来求解将会变得很繁琐,用分块矩阵的初等变换发来求解就显的比较简单.二、利用分块矩阵初等变换求行列式的值宋玉英在2002年04期的《兰州教育学院学报》上的《“用广义初等变换”法求“分块矩阵”的逆矩阵》一文中提到 例3 设P=⎪⎪⎭⎫⎝⎛D C B A 是一个分块方阵,其中A 是r 阶可逆阵,求|P|. 解: 由推论及定理7的(3):P =D C B A =A DCB A Ir 1-=ABCA D B A I r 110---=A B CA D 1-- 若A 与D 可乘,则|P|=|AD-ACAB|;又若A 与C 可交换(即AC=CA),则|P|=|AD-CB|.例例4 设D n 2=d c d c b a b a, 其中a ≠0,求|A|解: D n 2=dcd c b a ba=DC BA由于A,C 可交换,所以D n 2=CB AD -=⎪⎪⎪⎭⎫⎝⎛∙⎪⎪⎪⎭⎫ ⎝⎛bc bc ad ad = =|(ad-bc)I|=(ad-bc)n例5 设A,B,C 和D 是n 阶方阵,试证明DC B A =AB CD证 两次利用定理4的(1),得D C B A =(-1)2n B A D C =(-1)2n (-1)2n A B C D =AB C D三、利用分块矩阵的初等变换求矩阵的秩史永铨在2002年02期《淮南师范学院学报》上的《分块矩阵初等变换及其应用》一文中提到:矩阵的秩有以下初等性质:设A与B分别是r×s与p×q矩阵,则rBC A 0≥r(A)+r(B)并且当A(或B)是方阵且非异时,或者C=0时上式的等号成立.例6. 设A是m×n阵DC BA 的非异顺序主子阵,则r DC B A =r(A)+r(D-CA1-B)证: ⎥⎦⎤⎢⎣⎡---r m rI CA I 10∙⎥⎦⎤⎢⎣⎡D C B A =⎥⎦⎤⎢⎣⎡--B CA D B A10而A是非异阵,由以上性质知r⎥⎦⎤⎢⎣⎡D C B A =⎥⎦⎤⎢⎣⎡--B CA D B A 10≥r(A)+r(D-CA 1-B) 例7. 设n阶方阵A=(Qij )为反对称矩阵,证明:r(A)必为偶数 证: 对n用归纳法n=1,2是命题显然成立设阶数小于n时命题为真则对n阶及对称矩阵A,将A分块成A=DBCA 1,其中A1=01212a a -不妨设12a ≠0.⎥⎦⎤⎢⎣⎡--I BA I 110⎥⎦⎤⎢⎣⎡D B C A 1⎥⎦⎤⎢⎣⎡--I C A I 011=⎥⎦⎤⎢⎣⎡--C BA D A 11100∴r(A)=r⎥⎦⎤⎢⎣⎡D BC A 1=r⎥⎦⎤⎢⎣⎡--C BA D A 11100 =r(A1)+r(D-BA11-C) =2+r(D-BA11-C)但D-BA 11-C为阶数比A低的反对称矩阵,由归纳假设r(D-BA11-C)为偶数,故r(A)为偶数.四、分块矩阵的初等变换在矩阵分解中的应用例8. 设A=(aij )是n阶方阵,它的顺序主子式全不为零,证明: 存在非异下三角形矩阵B与非异上三角形矩阵C,使A=BC 证: 对n用归纳法n=1时显然成立设当n-1时,结论成立,则对n,将A分块成A=⎥⎦⎤⎢⎣⎡-nn n a A βα1由归纳假设对A1-n =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1,11,11,11,1n n n n a a a a 有A1-n =B1C1其中B1C1分别是n-1阶非异下三角形与上三角形矩阵⎥⎦⎤⎢⎣⎡----10111n n A I β∙⎥⎦⎤⎢⎣⎡-b a A n 01,其中b=a nn -11--n A βa 上式两端取行列式有:A =1-n A ∙b, ∴ b ≠0∴ ⎥⎦⎤⎢⎣⎡-b A n 001=⎥⎦⎤⎢⎣⎡I C B 0011∙⎥⎦⎤⎢⎣⎡-b a B C 0111 于是得:A ⎥⎦⎤⎢⎣⎡-m n a A βα1=⎥⎦⎤⎢⎣⎡----10111n n A I β∙⎥⎦⎤⎢⎣⎡1001B ⎥⎦⎤⎢⎣⎡-b B C 0111α=BC 其中B=⎥⎦⎤⎢⎣⎡----10111n n A I β1-∙⎥⎦⎤⎢⎣⎡1001B =⎥⎦⎤⎢⎣⎡---10111n n A I β⎥⎦⎤⎢⎣⎡1001B =⎥⎦⎤⎢⎣⎡-10111C B β, C=⎥⎦⎤⎢⎣⎡-b B C 0111αB =1B ≠0,C =b 1C 0≠∴B 与C 分别是非奇异的下三角与上三角形矩阵.类似的例子还可以举出很多,由于篇幅有限,不再赘述.总之,在矩阵乘法中,只要对矩阵进行恰当的分块,结合矩阵初等变换的方法,就能大大的简化其运算.。
分块矩阵的乘法

分块矩阵的乘法
由于矩阵乘法要求前一个矩阵的列数等于后一个矩阵的行数,所以两个分块矩阵可以相乘的条件就是,前一个分块矩阵列的分法和后一个矩阵行的分法必须相同(也只需相同,也就是有了这个相同,就一定可以相乘了),其含义就是:
前一个矩阵共n列,进行分块以后,记分块矩阵的第一列的每块的列数为n1,第二列的每块的列数为n2,第三列的每块列数为n3,…,…,最后一列的每块的列数为nt,所以前一矩阵分完块以后的列数是t列,
那么后一个矩阵的n行(根据矩阵乘法的定义后,后一个矩阵必须是n行)的分块方法必须满足:后一个矩阵分完块以后,必须是t行,且这个分块后的矩阵的第一行,每块的行数必须是n1行,第二行的每块的行数必须是n2行,第三行的每块的行数必须是n3行,…,…,第t行的每块儿的行数必须是nt 行。
这样我们就介绍了分块矩阵相乘时必须满足的条件,也是只需要满足的条件。
例如abc都是n阶方阵:
又例如:
先说分块矩阵的用法。
它们最重要的用途是(在某些情况下)可以把分块矩阵的块看成数,可以根据普通矩阵(即每一个元素都是数)找到解题的思路,从而帮助我们思考并最终完成解题的过程(其实整个线性代数就是这个思路,就是矩阵有一些数的特性,让我们从更高的角度看问题,看得更清楚。
)
我们举一个例子,就是我们可以把分块矩阵做行变换(当然,必要的时候也可以做列变化),而我们知道做行变换相当于左乘一个初等矩阵(当然,做列变换时相当于右乘一个初等矩阵),因此,我们就可以用矩阵的乘法解决一些分块矩阵的行变换问题,从而完成我们需要做的题目,下面看一个具体的例子:
先举这个例子,后面还有其他合适的例子。
最近有个学生问我一个问题,就以这里为例吧!
只做其中,第一个小题。
分块乘法的初等变换及应用.

§4.7 分块乘法的初等变换及应 用
E分块成,作1次"初等变换"得
引入:
若A可逆,令.上式变为:
(这种形状的矩阵在求行列式、 逆矩阵及解决其他问题时,比较 方便.)
例1.A,D可逆,求.
解:由及,有
例2.,
解:
例3.证明: (A、B为n级方 阵).
证:
其中初等矩阵,为除元素为外, 其余元素皆为0.
例4.设,且,
证明:存在下三角矩阵,使BA为 上三角形.
证:对n作归纳法.
当n=1时,为上三角形.
假设对n-1级矩阵命题成立,即, 对结论成立,于是存在矩阵,满 足:为上三角形.下面考虑n级 矩阵.
对A作分块
则
上三角形.
分块矩阵的初等变换及应用_百度文库.
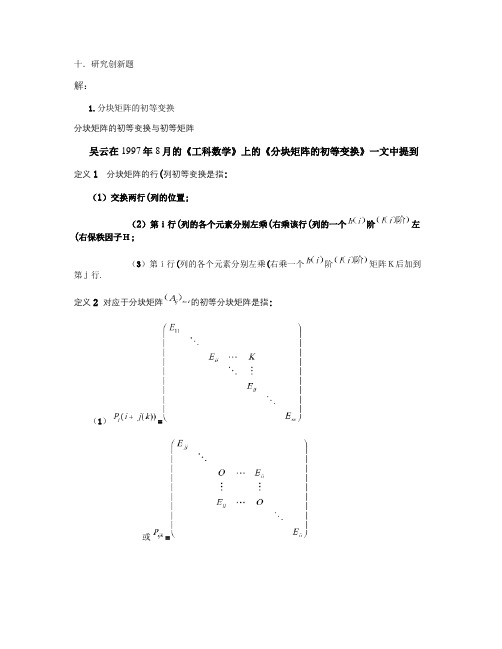
十.研究创新题解:1.分块矩阵的初等变换分块矩阵的初等变换与初等矩阵吴云在1997年8月的《工科数学》上的《分块矩阵的初等变换》一文中提到定义1分块矩阵的行(列初等变换是指:(1)交换两行(列的位置;(2)第i行(列的各个元素分别左乘(右乘该行(列的一个阶左(右保秩因子H;(3)第i行(列的各个元素分别左乘(右乘一个阶矩阵K后加到第j行.定义2 对应于分块矩阵的初等分块矩阵是指:(1)=或=(2)=或=其中H为第i行(列的一个左(右保秩因子;(1 =(2 或=初等分块矩阵与通常的初等矩阵类似,但由于矩阵乘法不满足交换律,故需要分为左、右两种.直接验算可得:定理1(1交换的第i行与第j行,相当于左乘一个m阶初等分块矩阵,其中中的元素为h(i阶单位矩阵,为h(j阶单位矩阵,当r≠i且r≠j时,为h(r阶单位矩阵;交换的第i列与第j列相当于右乘一个n阶初等分块矩阵,其中为l(i阶单位矩阵,为l(j阶单位矩阵,当r≠i且r≠j时,为l(r阶单位矩阵;(2 的第i行的每一个元素左乘一个矩阵H相当于左乘一个m阶分块矩阵中H为h(i阶方阵; 的第i列的每一个元素右乘一个矩阵H,相当于右乘一个n阶初等到变换矩阵,其中H为l(i阶方阵;(3 的第j行的每个元素分别左乘一个h(i×h(j矩阵K后加到第i行,相当于左乘一个初等分块矩阵;第j列的每一个元素分别右乘l(j×l(i矩阵K后加到第i列,相当于右乘.定理2设A为方阵,则分块矩阵施行第一种行初等变换后,对应的行列式为,其中h(i,j=h(ih(j-l+h(i+l]+…+h(j[h(i+h(i+j+…+h(j-l],l(i,j=l(ih(j-l+l(i+l]+…+l(j[l(i+l(i+j+…+l(j-l],施行第二种初等变换后,对应的行列式为|H|·|A|;施行第三种初等变换后,对应的行列式的值不变.证明: ,显然成立.下证,所在的第1行逐次与它相邻的行交换,移至前,共进行h(i-1+h(i+1+…+h(j-1次交换两行,第2行逐次与它相邻的行交换,移至前,同样进行相同次交换两行,依此类推,把所在的行移至所在的行前,共进行h(i[h(i-1+h(i+1+…+h(j-1]次交换两行,然后把移至适当的位置,同理共进行h(j[h(i+h(i+1+…+h(j-1]次交换两行,所以交换两行的总次数为h(i,j,故;同理.所以有==(-1或==(-1)==或=====定理3 分块矩阵进行初等变换后,秩不变.证明: 对于(1,相当于对进行若干次行(列的交换,故命题成立;对于(2,根据定义1,显然成立;对于(3,相当于进行若干次把行(列乘以一个倍数后加到另一行(列,故命题成立.定理4 (1设A,B的行数均为m,则矩阵方程AX=B,当(A= (A,B=m时有唯一解,当(A= (A,B<m时有无穷多解,当(A< (A,B时无解;(2设A,B的列数均为n,则矩阵方程XA=B,当(A= =n时有唯一解,当(A= <n有无穷多解,当(A< 时无解.证明: (1设(A= (A,B<m,则存在可逆矩阵P,Q,使,其中为r阶单位矩阵, 为r阶方阵,设,则有: == =B所以为AX=B的解,其中, 是任意的.当(A= (A,B=m时,A=P(OQ,B=( ,显然,AX=B有唯一解: ;当(A< (A,B时,AX=B无解.同理可证(2成立(当(A= ( , <n时,X=P定义3 对于任意的u,v,如果( = ( ,= (,,则称为极大元.定理5 分块矩阵可以用分块矩阵的初等变换对角化的充要条件是: 它有一个极大元.证明: 充分性.不妨设为极大元(否则可以通过第一种分块矩阵的初等变换把极大元移到第一行,第一列交叉位置.由定理4,存在可逆矩阵P,Q,使,,令K=-P,其中, 为适当阶数的任意矩阵.则K+ =,所以第一行左乘K加到第二行,得.同理,令K'=-, 则K′+ =0,所以的第一列右乘K′后加到第二列,得.(如先进行列变换,再进行行变换,得,因为=+=+,故两种运算顺序结果相同必要性.反证法,不妨设(≠(,或(,(,则由定理4, =-或=-无解,从而不存在K,使对角化.同理,当(≠(,或(,≠(时,不存在使-A K=A或-=成立.定理5表明:并不是所有的2×2分块矩阵都可以用分块矩阵初等变换对角化,如果分块矩阵没有极大元,则需分得更细,才能对角化.定理6 矩阵的一种分块方法可以用分块矩阵的初等变换对角化的充分条件是:存在s-1行且存在t-1列有极大元.证明: 用数学归纳法.当s=t=1时,只有一块,命题成立;设s≤e,t≤ f时命题成立.当s=e+1,t=f时,存在e行且存在f-1列有极大元,显然可以用第一种分块矩阵的初等变换,通过交换两行或两列的位置,使的前e行与前f-1列都有极大元,再把前e行,前f-1列看成一块,得到一个新的2×2分块矩阵,记为.显然为极大元,根据定理4, 可以化成对角形: ,又,它的每行、列都有极大,故由假设可以对角化,从而可以对角化.同理可证当s=e,t=f+1时, 可以对角化.由此命题成立.下面讨论对角化后的非零块进一步化简的方法.设,与.根据定理1, ,为的左(右保秩因子,显然也是所在行(列的左(右保秩因子,故对角化后的分块矩阵第i行、第i列分别左乘,右乘后, 可以化成讨论分块方阵行列式的计算,先讨论分块初等阵的行列式.设I为S×S分块单位阵:I=其中I r为r阶单位阵(1≤i≤S,对I施行一次初等变换可得定义2所述的三种分块初等阵,它们的行列式有下列计算公式.引理分块初等阵的行列式有以下性质:(1|I(i,j|= ,其中τ=r (r+1+…+r+ r (r+1+…+ r-1(i特别地,若j=i+1,则| I(i,j|=(-1 r r;(2|I(i(K|=|k|,其中K是r阶可逆阵;(3|I(j(K,i|=1,其中K是r×r矩阵.证(1不难验证,将I(i,j的元素行进行τ次相邻的对调可将I(i,j变成I,由行列式的性质,|I(i,j|= |I|=.(2,(3由对角分块方阵及三角形分块方阵的行列式计算方法即知.由于对分块方阵A施行一次初等行变换,相当于用相应的分块初等阵左乘A,由上述引理,我们有下列分块方阵的行列式计算性质.定理7 设A是一个分块方阵.(1交换|A|的i,j两行(列,行列式变为(-1τ|A|,其中τ= r (r+1+…+ r+ r (r+1+…+ r-1;特别地,交换|A|的相邻两行(列(i行和i+1行,行列式变为(-1 r r+1|A|;(2用一个r阶可逆阵K左(右乘|A|的第i行(列的所有矩阵,等于用|K|乘以|A|;(3用一个矩阵左(右乘|A|的某一行(列的所有矩阵再加到另一行(列的对应元素上,行列式不变.由定理7的(2可得推论分块行列式|A|的某一行(列的所有矩阵的可逆左(右因子K,可以行列式|K|的形式提到行列式符号外.2.分块矩阵初等变换的应用一、利用分块矩阵的初等变换求矩阵的逆.廖中行在2002年05期《四川教育学院学报》上的《初等变换在分块矩阵乘法》的一文中提到例1: 已知其中B是r×r可逆阵,C是s×s可逆阵,求证:P可逆,并求.分析:本题是一个分块阵的求逆问题,一般可用待定子块法,也可利用广义初等变换span,还可用左乘分块初等阵的方法.解:因B、C可逆,故|B|≠0,|C|≠0.根据拉普拉斯展开,有≠0,故P可逆.求C有三种办法:解法一:利用广义初等行变换法.B r,C r(B D+r故P=本题对分块矩阵进行广义初等变换是一般矩阵的初等变换的一种推广,其方法和一般矩阵相同.作初等行(列变换时,对矩阵P应左(右乘相应的分块单位阵.上述分块初等变换的过程也可用分块阵左乘相应的分块初等阵,可表示如下:解法二: 可用左乘分块初等阵的方法求=有=即:==E故有P===例2:已知A=,求A.分析:本题是一个矩阵的求逆问题,一般可用公式法,矩阵的初等变换法求;可以用分块矩阵初等变换法求.利用分块矩阵初等变换法先A化分成分块矩阵,即A==其中B=,C=,D=从而求得B=,C=然后对A进行广义初等变换,即:B r,C r(B D r+rA==如果用其它方法来求解将会变得很繁琐,用分块矩阵的初等变换发来求解就显的比较简单.二、利用分块矩阵初等变换求行列式的值宋玉英在2002年04期的《兰州教育学院学报》上的《“用广义初等变换”法求“分块矩阵”的逆矩阵》一文中提到例3设P=是一个分块方阵,其中A是r阶可逆阵,求|P|.解: 由推论及定理7的(3:====若A与D可乘,则|P|=|AD-ACAB|;又若A与C可交换(即AC=CA,则|P|=|AD-CB|.例例4 设D=, 其中a≠0,求|A|解: D==由于A,C可交换,所以D=== =|(ad-bcI|=(ad-bc例5 设A,B,C和D是n阶方阵,试证明=证两次利用定理4的(1,得=(-1)=(-1)(-1)=三、利用分块矩阵的初等变换求矩阵的秩史永铨在2002年02期《淮南师范学院学报》上的《分块矩阵初等变换及其应用》一文中提到:矩阵的秩有以下初等性质:设A与B分别是r×s与p×q矩阵,则r≥r(A+r(B并且当A(或B是方阵且非异时,或者C=0时上式的等号成立.例6. 设A是m×n阵的非异顺序主子阵,则r=r(A+r(D-CAB证:=而A是非异阵,由以上性质知r=≥r(A+r(D考情解读B例7. 设n阶方阵A=(Q为反对称矩阵,证明:r2必为偶数(1: 对n用归纳法n=1,2是命题显然成立设阶数小于n时命题为真则对n阶及对称矩阵A,将A分块成A=,其中A=不妨设(30.=∴r(A=r=r=r(A+r作函数图象有两种基本方法:一是描点法,二是图象变换法,其中图象变换有平移变换、伸缩变换、对称变换.C4=2+r(D-BAC但D-BAC为阶数比A低的反对称矩阵,由归纳假设r(D-BAC为偶数,故r(A为偶数.四、分块矩阵的初等变换在矩阵分解中的应用例8. 设A=(a是n阶方阵,它的顺序主子式全不为零,证明: 存在非异下三角形矩阵B与非异上三角形矩阵C,使A=BC证: 对n用归纳法n=1时显然成立设当n-1时,结论成立,则对n,将A分块成A=由归纳假设对A=有A=BC其中BC分别是n-1阶非异下三角形与上三角形矩阵,其中b=-上式两端取行列式有:=b,b0=于是得:A==BC其中B===,C==0,=bB与C分别是非奇异的下三角与上三角形矩阵.类似的例子还可以举出很多,由于篇幅有限,不再赘述.总之,在矩阵乘法中,只要对矩阵进行恰当的分块,结合矩阵初等变换的方法,就能大大的简化其运算.。
分块矩阵的初等变换及其若干应用.

第1块行左乘-D C加到第 2 块行⎯⎯⎯⎯⎯⎯⎯⎯⎯ → −1 ⎛ Em ⎜⎝O 故M −1 O En (A − BD −1C −1 − D −1C(A − BD −1C −1 ⎞ −(A − BD −1C −1 BD −1 . −1 −1 −1 −1 −1 ⎟ D C(A − BD C BD + D ⎠⎛ ( A − BD −1C −1 =⎜ −1 −1 −1 ⎝ − D C ( A − BD C ⎞⎟. D −1C ( A − BD −1C −1 BD −1 + D −1 ⎠−( A − BD −1C −1 BD −1 例设 A, B 是 n 阶方阵.用分块矩阵理论证明 | AB |=| A || B | . ⎛ A O⎞证明考虑分块矩阵⎜⎟ . 对该分块矩阵进行分块矩阵的初等变换:⎝ −E B ⎠⎛ A O ⎞第 2块行左乘A加到第1块行⎛ O →⎜⎜ − E B ⎟⎯⎯⎯⎯⎯⎯⎯⎯⎝⎠⎝ −E ⎛E 于是⎜⎝O A⎞⎛ A O ⎞⎛ O ⎟⎜ −E B ⎟ = ⎜ −E E⎠⎝⎠⎝ AB ⎞⎛E . 记 Pij = ⎜⎟ B ⎠⎝O AB ⎞ . B ⎟⎠ Fij ⎞ , 其中 Fij 是 (i, j 元素为 aij , E⎟⎠⎛ A O⎞而其余元素均为零的 n 阶方阵.则 Pij 是初等矩阵,且用 Pij 左乘矩阵⎜⎟就相⎝ −E B ⎠⎛ A O⎞⎛E 当于将⎜的第 n + j 行乘上 aij 加到第 i 行.容易验证 P 11 P 12 " P nn = ⎜⎟⎝ −E B ⎠⎝O 于是⎛E ⎜O ⎝ A⎞⎛ A O ⎞ A O ⎛ A O⎞ = = P =| A || B | . 11 P 12 " P nn ⎜⎟⎜⎟⎟ E ⎠⎝ −E B ⎠⎝ −E B ⎠ −E B A⎞ . E⎟⎠另一方面, 有O −E 故结论成立. a11 " a1k 例设A = (aij n×n ,且对任意1 ≤ k ≤ n, 有# # ≠ 0. 则存在 n 阶下三角形矩 ak 1 " akk AB O 2 AB 2 2 =( − n = ( −1 n | AB || − E |= ( −1 n + n | AB | = | AB | . B B −E 阵 B 使得 BA 为上三角形矩阵. 证明对 n 用数学归纳法. 当 n = 1 时结论显然成立. 设命题对于n − 1 阶矩阵成立. 考虑 n 阶矩阵 A = (aij n×n 的情形. 记 6⎛a11 " a1,n −1 ⎞⎜⎟ # ⎟. A1 = ⎜ # ⎜a ⎟⎝ n −1,1 " an −1,n −1 ⎠由归纳假设,存在n − 1 阶下三角矩阵 B1 使得 B1 A1 为上三角形矩阵. 对 A 作如下⎛A 分块 A = ⎜ 1 ⎝α ⎟并对其进行初等行变换: ann ⎠⎛ A1 ⎜α ⎝ −1 ⎛A 第1块行左乘-α A1 加到第 2 块行⎯⎯⎯⎯⎯⎯⎯⎯⎯ →⎜ 1 ⎟ ann ⎠⎝O β ⎞ β ⎞ β ⎞ . −α A β + ann ⎟⎠ −1 1 O ⎞⎛ A1 ⎛ E 这表明⎜⎜ −1 1⎟⎝ −α A1 ⎠⎝ α ⎛A =⎜ 1 ⎟ ann ⎠⎝ O β ⎞ β ⎞ . 于是−α A β + ann ⎟⎠ −1 1 O ⎞⎛ A1 ⎛ B1 O ⎞⎛ E ⎜ O 1 ⎟⎜ −α A−1 1 ⎟⎜ α ⎝⎠⎝⎠⎝ 1 ⎛ B O ⎞⎛ A1 =⎜ 1 ⎟⎜⎝ O 1 ⎠⎝ O −1 1 ann ⎟⎠ β ⎞ β B1 β ⎞⎛ B1 A1 ⎞ =⎜⎟ −1 −α A β + ann ⎠⎝ O −α A1 β + ann ⎟⎠是上三角形矩阵.记 O ⎞⎛ B1O⎞⎛B O⎞⎛ E B=⎜ 1 . =⎜⎜⎟⎟ −1 −1 1 ⎠⎝ −α A1 1⎟⎝ O 1 ⎠⎝ −α A1 ⎠则 B 是下三角形矩阵且 BA 为上三角形矩阵. 7。
分块初等变换的应用

n i =1
ai
⎟⎞
2
⎤ ⎥
⎠ ⎥⎦
。
例 2 利用降阶法证明:矩阵 AB 与 BA 的非零特征值相同,其中 A, B 分别
是 m × n, n × m 阶矩阵。 证 设 λ ≠ 0 ,则由降阶公式得到
| Em || λEn − BEm −1 A |=| λEn || Em − A(λEn )−1 B | ,
A = ⎜⎜⎝⎛αBT
α ann
⎟⎟⎠⎞
→
⎜⎜⎝⎛
B 0
ann
α −αT
B பைடு நூலகம்1α
⎟⎟⎠⎞
→
⎜⎜⎝⎛
B 0
ann
0 −αT
B −1α
⎟⎟⎠⎞
,
这表明
A
合同于
⎜⎜⎝⎛
B 0
ann
0 −αT
B −1α
⎟⎟⎠⎞
。又第三类块初等变换不改变矩阵的行列式,
因此
( ) A =| B || ann − α T B −1α |= An−1 ann − α T B −1α ,
乘任一个分块矩阵, 其结果就是对它进行相应的分块行(列)变换.
分块初等变换法解题的技巧往往是通过分块初等变换将分块矩阵化为准三
角阵。比如,
⎛ Em
⎜ ⎝
P
O ⎞⎛ A
En
⎟ ⎠
⎜ ⎝
C
B D
⎞ ⎟ ⎠
=
⎛ ⎜ ⎝
C
A + PA
D
B + PB
⎞ ⎟ ⎠
,
适当选择 P , 可使 C + PA = O ,从而分块矩阵就成为准上三角阵, 这种形状的矩 阵在求行列式、逆矩阵和解决其他问题时是比较方便的.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O A
D
O
O
D
A
O
1
A1
O
且
O
D
O
D1
,
所以
T
1
A1
O
O D1
Em CA1
O
En
A1
O
D
1CA1
D
1
.
本本若若请请本本若若请请本若请节节想想本单单若请节节想想本单单若请节想本单若内内请结结节击 击想本单若内内请结结节击 击想本单若内请结节击想本容 容单若束 束内请返 返结节击想本容容单若束束内请返 返结节击想本容单若束内请返结节已 已击想本 本本容单若回 回束内请返结节已已击想本本本容单若回 回束内请返结节已击想本本容单若回束内结 结请返结堂 堂节已击想按 按本本容单若回束内结结请返结堂堂节已击想按 按本本 本 本容单若 若 若回束内结请 请 请返结本堂若节已击想按本请本 本容束 束单若 若回束课 课内结请 请返结钮 钮堂节已击想按本容束束单回束课课内结返结钮 钮堂节 节 节已击想想 想按本容束单 单单回束节课想内结返结钮堂单节 节已击想想按本,,容束单单回束课..内结!!返结钮堂已击按本,,容束回束课..内 内 内结!!返结结 结钮堂已击 击击按本内,结容束回束课.击内 内结!返结结钮堂已击击按本,容束回束课.结!返钮堂已按本,容 容 容束回束 束束课.结!返返 返钮堂容束已按本,返容 容束回束束课.结!返返钮堂已按本,束回课.结!钮堂已 已 已按本 本本,束回回回课.已本结!钮堂回已 已按本本,束回回课.结!钮堂按,束课.结 结 结!钮堂堂堂按按按,结堂束课.按结结!钮堂堂按按,束课.!钮,束束束课课.课!钮钮钮束课,钮束束课课.!钮钮,.!,,,...,!!!.,,!..!!
例如,设有如下分块矩阵
A B
C
D
,
分别用三种分块初等矩阵左乘它,其结果如下:
O
Em
En A
O
C
B D
C A
D
B
,
P O A B PA PB
O
En
C
D
C
D
,
Em
P
O A
En
C
B D
C
A PA
D
B PB
;
A B
C
D
,
分别用三种分块初等矩阵右乘它,其结果如下:
A
C
B O
D
Em
En O
B D
A
C
,
A B P O AP B
C
D
O
En
CP
D
,
A
C
B Em
D
P
O A BP
En
C
DP
B D
.
在
Em P
O A
En
C
B A
D
C
PA
B
D
PB
中,适当先择 P,可使 C + PA = O . 例如 A 可逆
第七节 分块乘法的初等变换及应用举例
主要内容 分块初等矩阵
应用举例
一、分块初等矩阵
1. 定义
定义15 把单位矩阵 E 如下进行分块:
E
Em O
O
En
对它进行三种初等变换所得到的矩阵称为分块初
等矩阵.
分块初等矩阵有以下三种:
1) 分块对换矩阵 对换两行(列)所得到
O
Em
En O
,
2) 分块倍乘矩阵 某一行(列)左乘(右乘)一个
时,选 P = - CA-1,则 C + PA = O . 于是上式右端
成为
A
B
O
D
CA1B
.
这种形状的矩阵在求行列式、逆矩阵和解决其他问
题时是比较方便的,因此这种运算非常有用.
二、应用举例
例1 设
T
A C
O
D
,
其中 A,D 可逆,求 T -1 .
解 因为
Em
CA1
O A
En
C
矩阵 P 所得到
P
O
O En
,
Em O
O P
,
3) 分块倍加矩阵 一行(列)加上另一行(列)的
P
(矩阵)倍数所得到
Em O
P En
,
Em P
O
En矩阵与初等变换的关系一样,分块初等 矩阵有与初等矩阵类似的性质:
用分块初等矩阵左乘分块矩阵 A, 在保证可乘的 情况下,其作用相当于对分块矩阵 A 进行一次相应 的初等行变换; 用分块初等矩阵右乘分块矩阵 A, 其作用相当于对分块矩阵 A 进行一次相应的初等列 变换.
