在FPGA上优化实现复数浮点计算
vivado ip核之复数浮点数乘法 floating-point

vivado ip核之复数浮点数乘法floating-point
在数字信号处理和科学计算中,复数浮点数乘法是一个非常重要的运算。
Vivado IP核提供了这个功能,使得用户可以在FPGA上实现高效的复数浮点数乘法。
复数浮点数乘法的原理比较简单,主要是将两个复数相乘,得到的结果也是复数。
这个过程需要分别对实部和虚部进行乘法运算,然后将结果合并。
在Vivado IP核中,这个过程被高效地实现了。
使用Vivado IP核进行复数浮点数乘法时,用户需要提供一些参数,例如输入复数的实部和虚部,以及输出结果的精度等。
这些参数对于实现高效的乘法运算非常重要。
此外,Vivado IP核还提供了许多其他有用的特性,例如可配置的流水线深度和多路复用器等。
这些特性可以帮助用户在FPGA上实现更加高效和灵活的复数浮点数乘法运算。
总之,Vivado IP核中的复数浮点数乘法是一个非常有用的功能,可以帮助用户在FPGA上实现高效和灵活的复数浮点数乘法运算。
通过合理地使用这个功能,用户可以大大提高数字信号处理和科学计算的性能。
1。
利用FPGA技术能更方便灵活设计出浮点运算器

利用FPGA技术能更方便灵活设计出浮点运算器FPGA(现场可编程门阵列)技术的理论研究和实际应用正越来越受到人们的重视。
FPGA 技术常常使一些原来比较难解决的技术瓶颈得以轻松实现,从而使产品的开发周期大为缩短,性能价格比大幅提高。
运算器作为计算机的加工处理部件,是CPU(中央处理器)的重要组成部分。
作为典型的PC机一般都至少具有一个定点运算器。
在586 之前的机型中,由于当时硬件条件和工艺的限制,浮点运算器一般以协处理器的形式出现。
进入20 世纪90 年代后,随着工艺水平的提高,一个芯片上集成度不断提高,如今浮点运算所要求的一些硬件已可以集成到CPU 中,因此,作为浮点运算器的代表的协处理器也逐渐被集成度很高的CPU 中的一部分所代替。
浮点运算定点运算器主要是用于实现对定点整数和定点小数的算术运算、对逻辑数据的逻辑运算以及对主存的地址计算等。
浮点数比定点数的表述范围宽,有效精度高,更适合于科学计算与工程计算。
浮点运算可分为两类:非规格化和规格化浮点运算。
非规格化浮点运算,不要求操作数是规格化数,对运算结果也不要求规格化处理。
而规格化浮点运算只能对规格化的浮点数进行操作,并且要求对运算结果加以规格化处理。
由于规格化浮点数具有惟一的表示形式,而且在计算机中尾数能获得最大的有效数字,所以在一般的计算机中一般选用规格化浮点运算。
浮点加、减运算浮点加减法运算规则设有两个浮点数x 和y,分别为其中Ex 和Ey 分别为数x 和y 的阶码,Mx 和My 分别是数x 和y 的尾数。
两浮点数进行加减的运算规则是浮点加减法运算步骤完成两个浮点数加法或减法运算,需要以下几个步骤完成。
(1)对阶:两浮点数进行加减,必须使它们的阶码相等,这个过程称为对阶。
对阶的第1 步是求阶差:对阶的规则是小阶向大阶看齐,即使阶码小的尾数向右移位,每右移一位阶码加1,直至。
浮点运算的FPGA实现

数必须满足
, 还要对运算结果进行规格化, 即判断尾
数的最高位。若为零则将尾数左移一位、阶码加一, 直到阶码最
高为为 1。由于对阶时小阶码数尾数右移, 造成和的尾数位长大
于 23 位。若采用截断处理则相对误差较大, 故采用舍入操作以
减小误差。另外, 当和较大, 超过表示范围; 或当运算结果过小,
超过浮点数的分辨率时会造成运算错误。故须增加电路判断运
技
术
创
新
图 4 乘法运算仿真 图四中数据验证了同号、异号及数据过大强制清零等几种 情况下乘法操作的正确性。其中 5242880(十进制)=101000···0、 4456448 ( 十 进 制 )=1000100 ···0、5570560 ( 十 进 制 ) =101010100···0; 6553600(十进制)=1100100···0、4718592(十进 制 )=1001000···0、7372800(十 进 制 )=1110000100···0。
算结果是否正确。
-208- 360元 / 年 邮局订阅号: 82-946
《现场总线技术应用 200 例》
您的论文得到两院院士关注
PLD CPLD FPGA 应 用
加法运算流程 另外, 对阶时阶码小的数据尾数右移, 而规格化时还有可能 左移, 这可能造成有效数据位的丢失。故为保证计算精度, 须增 加加法器的位宽。由于规格数首位为 1, 同阶数据产生进位无需 左移数据; 而不同阶数据的和亦可保证高位为 1, 故同号加法操 作时不会产生这种情况, 只有异号加法操作存在这种情况。显 然同阶数无需右移操作, 当阶差为二或更大时对阶后尾数差将 大于四分之一, 即次高位为 1, 规格化时只需左移一位数据。而 阶差为 1 时也只可能右溢出一位数据。故在保证浮点数精度不 变的情况只须将加法器增加一位。 对于减法运算, 只需将被减数符号取反然后进行加法运算 即可。 QUARTUS II 下进行仿真其结果如图 3(数据采用十进制) 2.2 浮点乘 / 除法运算 浮点乘法实现 相 对 简 单 , 只 需 将 两 符 号 异 或 、阶 码 做 和 、尾 数做积。即:e3=e1+e2- 127,f3=f1×f2, 。然后进行规格化。由于有条 件 1/ 2 £ f1, f2 < 1成 立 , 使 得 满 足 1/ 4 £ f3 < 1即 可 知 f3 的 最 高 位 和次高位中至少一位为 1。从而使规格化操作流程大大简化。最 后对运算结果进行舍入操作, 同时仍需检查运算结果是否有数 据溢出的问题。
在FPGA里浮点数与定点数表示法原理展示

在FPGA里浮点数与定点数表示法原理展示
浮点数与定点数表示法是我们在计算机中常用的表示方法所以必须要弄懂原理,特别是在FPGA里面,由于FPGA不能像在MCU一样直接用乘除法。
定点数
首先说一下简单的定点数,定点数是克服整数表示法不能表示实数的缺陷,那幺我们就可以通过将实数乘上一个分数来实现,当然要是分数就是2i 倍数,那幺我们的定点数表示法就是精确的表示,但是很不幸我们自然界中的树并不是那幺凑巧。
所以定点数只能是近视表示实数,包括浮点法也是这样的。
具体的实现就是将表示成2进制后,然后在左移k位,那幺对于N为的定点数表示法中,就有N-1-K表示整数部分,低k位表示分数,最高位表示符号。
定点数表达法的缺点在于其形式过于僵硬,固定的小数点位置决定了固定位数的整数部分和小数部分,不利于同时表达特别大的数或者特别小的数。
浮点数。
FPGA中的浮点四则运算
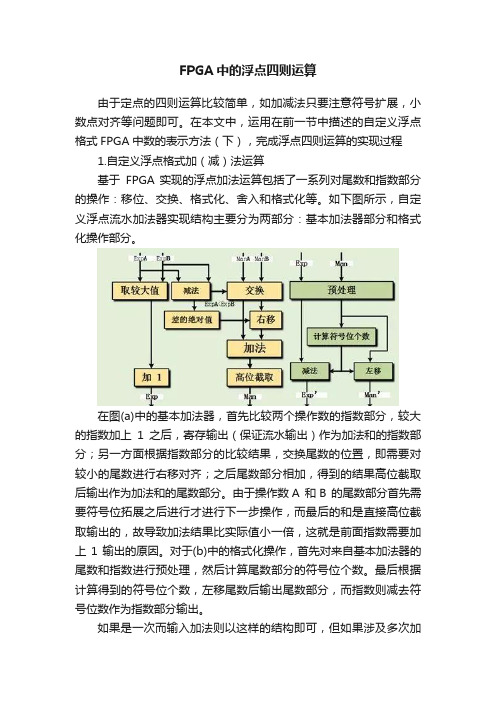
FPGA中的浮点四则运算由于定点的四则运算比较简单,如加减法只要注意符号扩展,小数点对齐等问题即可。
在本文中,运用在前一节中描述的自定义浮点格式FPGA中数的表示方法(下),完成浮点四则运算的实现过程1.自定义浮点格式加(减)法运算基于FPGA 实现的浮点加法运算包括了一系列对尾数和指数部分的操作:移位、交换、格式化、舍入和格式化等。
如下图所示,自定义浮点流水加法器实现结构主要分为两部分:基本加法器部分和格式化操作部分。
在图(a)中的基本加法器,首先比较两个操作数的指数部分,较大的指数加上1之后,寄存输出(保证流水输出)作为加法和的指数部分;另一方面根据指数部分的比较结果,交换尾数的位置,即需要对较小的尾数进行右移对齐;之后尾数部分相加,得到的结果高位截取后输出作为加法和的尾数部分。
由于操作数A 和B 的尾数部分首先需要符号位拓展之后进行才进行下一步操作,而最后的和是直接高位截取输出的,故导致加法结果比实际值小一倍,这就是前面指数需要加上1输出的原因。
对于(b)中的格式化操作,首先对来自基本加法器的尾数和指数进行预处理,然后计算尾数部分的符号位个数。
最后根据计算得到的符号位个数,左移尾数后输出尾数部分,而指数则减去符号位数作为指数部分输出。
如果是一次而输入加法则以这样的结构即可,但如果涉及多次加法,以流水形式完成,则在结构上可以作更好的优化。
如下是四输入和八输入加法器的结构:如上所示的情况,可知,这样的方法可以减少格式化操作,而格式化操作在整个运算过程中消耗相对比较多的资源,因此这样的实现结构可以有效的减少硬件资源的消耗。
3. 乘加运算浮点乘法运算较为简单,对应的尾数部分进行相乘,指数部分进行相加。
尾数相乘部分采用XILINX 乘法器IP即可。
需要注意的是,乘法结果输出的位宽指定,在乘法器IP中,按一般流程下来,乘完之后的结果是保留两位符号位(假设乘数都是一个符号的情况),即多出一个符号位,按小数乘法分析的话,值的情况是比实际结果小一倍,在截位输出的时候需要做一定的取舍(是从最高位开始截位输出,还是次高位开始截位输出;如果从最高位截位输出,则结果比实际值小一倍,如果从次高位截位输出只有一种情况会溢出,即两个乘数都为-1的情况,这种情况如果从次高位截位输出则会错误,其余情况都是正确的)。
基于FPGA的浮点指数函数算法研究与实现

基于FPGA的浮点指数函数算法研究与实现史雄伟;王成;张春雷;陈乃奎【摘要】A large number of floating-point exponential calculations are involved in nuclear power plant instrumentation based on FPGA,and the methods for hardware implementation of exponential function are studied,an improved series approximation algorithm is proposed,aiming at solving the problems such as small calculation scale,low precision existing in CORDIC algorithm and linear approximation algorithm.The lookup table and series approximation algorithm are combined in the proposed algorithm,with input data splitting into two part.It takes advantage of the lookup method and the linear approximation,and can work even using a few expansion series.The validity of the improved algorithm is simulated in Matlab,and algorithm is programmed using Verilog and verified on the IGLOO2 series FPGA of Microsemi Corporation.The Matlab simulation result and the implementation result on FPGA demonstrates that this method can expand the calculation capacity and with high accuracy.%基于FPGA的核电站仪控设备中涉及大量浮点指数运算,而常用的CORDIC算法和线性逼近法等存在计算范围小、计算精度不高等问题,对FPGA硬件实现指数函数的方法进行研究,并提出一种改进的级数近似法;该方法对输入进行预处理,将输入分解后采用查找表和泰勒级数展开结合的方法,在展开很少项数的情况下快速收敛,发挥查找表法和级数近似法的优势,提高算法的运算精度和效率;在Matlab环境下对改进算法的有效性进行仿真验证,且采用Verilog语言进行编程实现,在Microsemi公司的IGLOO2系列FPGA上进行具体算法性能验证;Matlab仿真和FPGA验证结果均表明,改进的级数近似法能够大幅增大指数函数的自变量输入范围,并提高计算精度.【期刊名称】《计算机测量与控制》【年(卷),期】2017(025)010【总页数】4页(P221-223,231)【关键词】指数函数;FPGA;级数近似法【作者】史雄伟;王成;张春雷;陈乃奎【作者单位】北京广利核系统工程有限公司,北京 100094;北京广利核系统工程有限公司,北京 100094;北京广利核系统工程有限公司,北京 100094;北京广利核系统工程有限公司,北京 100094【正文语种】中文【中图分类】TP39在核电站仪控系统中,需要采集堆芯外核检测仪表的数据以实现对核反应堆的实时监控。
基于FPGA的浮点数线性排序器设计
基于FPGA的浮点数线性排序器设计【摘要】本文旨在介绍基于FPGA的浮点数线性排序器设计。
在分别从研究背景、研究目的以及研究意义三个方面进行阐述。
在详细介绍了基于FPGA的浮点数线性排序器设计原理、框架、算法、实现以及实验结果。
结论部分总结了该设计的优点和不足,并展望了未来的发展方向,同时也提出了设计所带来的贡献。
通过本文的介绍,读者将能够全面了解基于FPGA的浮点数线性排序器设计的相关知识和技术,为相关领域的研究和实践提供有益的参考和指导。
【关键词】FPGA、浮点数、线性排序器、设计原理、设计框架、设计算法、设计实现、实验结果、总结、展望、贡献。
1. 引言1.1 研究背景随着科学技术的进步和社会的发展,人们对计算速度和效率的需求越来越高。
而在大数据处理、人工智能、物联网等领域中,浮点数的排序问题一直是一个重要而复杂的任务。
传统的排序算法对于大规模浮点数数据进行排序时会面临效率低下、处理速度慢等问题,无法满足实际需求。
为了解决这一问题,基于FPGA的浮点数线性排序器设计应运而生。
FPGA(Field Programmable Gate Array)是一种灵活可编程的集成电路,具有并行处理能力和高速度的特点,能够有效地实现浮点数的排序任务。
通过充分利用FPGA的优势,设计一种高效的浮点数线性排序器,可以在保证排序准确性的基础上,提高排序速度和效率,满足各种应用场景的需求。
本研究旨在探究基于FPGA的浮点数线性排序器的设计原理、框架、算法、实现以及实验结果,从而为浮点数排序问题的解决提供一种新的思路和方法。
通过本研究的开展,可以为提升计算速度和效率,推动科技发展做出贡献。
1.2 研究目的研究目的是设计基于FPGA的浮点数线性排序器,旨在提高排序算法的效率和速度。
目前,在大数据处理、图像处理、信号处理等领域,对于海量数据的快速排序需求日益增加。
传统的排序算法在处理大规模数据时效率较低,无法满足实时性要求。
vivado floating point 实现复数乘法
vivado floating point 实现复数乘法
在Vivado 中实现复数乘法可以使用FPGA 自带的浮点运算器或者使用LogiCORE 提供的Complex Multiplier IP 核来实现。
下面分别介绍两种方法:
方法一:使用FPGA 自带的浮点运算器
1. 在Vivado 中创建一个新的项目,并将所需的IP 核添加到设计中。
2. 在设计中添加一个浮点运算器IP 核,可以在IP Catalog 中搜索并添加。
3. 在设计中添加一个复数数据类型的输入和输出,并将其连接到浮点运算器IP 核的输入和输出。
4. 在设计中添加一个控制信号,用于控制复数乘法的开始和结束。
5. 编译并实现设计。
方法二:使用LogiCORE 提供的Complex Multiplier IP 核
1. 在Vivado 中创建一个新的项目,并将所需的IP 核添加到设计中。
2. 在设计中添加一个LogiCORE 提供的Complex Multiplier IP 核,可以在IP Catalog 中搜索并添加。
3. 在设计中添加一个复数数据类型的输入和输出,并将其连接到
Complex Multiplier IP 核的输入和输出。
4. 在设计中添加一个控制信号,用于控制复数乘法的开始和结束。
5. 编译并实现设计。
无论采用哪种方法,实现复数乘法的关键是正确处理复数的加法、减法、乘法和除法。
在设计中需要注意输入和输出的数据类型和格式,以及控制信号的正确设置。
基于FPGA的浮点数线性排序器设计
基于FPGA的浮点数线性排序器设计【摘要】本文介绍了基于FPGA的浮点数线性排序器设计。
首先探讨了背景介绍和研究意义,随后详细阐述了基于FPGA的浮点数线性排序器设计原理、设计流程和硬件架构设计。
针对性能优化进行了讨论,并介绍了验证与测试的过程。
最后对基于FPGA的浮点数线性排序器设计进行总结,并展望了未来的研究方向。
通过本文的阐述,读者能够全面了解基于FPGA的浮点数线性排序器的设计和实现过程,为进一步研究和应用提供了重要参考。
【关键词】FPGA、浮点数、线性排序器、设计原理、设计流程、硬件架构、性能优化、验证与测试、总结、未来研究方向1. 引言1.1 背景介绍浮点数排序是计算机领域中一个重要的问题,它通常用于对大量浮点数进行排序操作,以便更好地进行数据分析和处理。
随着科技的发展和计算需求的增加,如何高效地实现浮点数的排序成为一个备受关注的课题。
通过利用FPGA的并行计算能力和硬件加速优势,设计一种高效的浮点数排序器成为了当前研究的热点之一。
本文将介绍基于FPGA的浮点数线性排序器的设计原理、设计流程、硬件架构设计、性能优化以及验证与测试等方面,旨在为研究人员提供一些参考和启发。
希望通过本文的研究,能够进一步推动基于FPGA的浮点数排序器技术的发展,为数据处理和计算加速提供更多可能性。
1.2 研究意义浮点数排序在计算机领域具有重要的应用价值,能够在各种数据处理和计算任务中发挥重要作用。
基于FPGA的浮点数线性排序器设计不仅可以提高排序的效率和性能,同时也具有较低的功耗和成本。
通过对浮点数进行排序,可以帮助用户更快速地找到需要的数据,提高数据处理的效率,降低系统的响应时间。
对于需要处理大规模数据的应用场景,基于FPGA的浮点数线性排序器设计可以发挥更大的优势,通过硬件加速的方式实现高效的数据排序。
基于FPGA的设计具有良好的可扩展性,可以灵活适应不同规模和要求的数据处理任务。
研究基于FPGA的浮点数线性排序器设计在提高数据处理效率、降低成本和节能方面具有重要的意义,对于未来的数据处理和计算任务具有重要的研究价值和应用潜力。
FPGA中高速浮点运算的设计与实现
关键词:FPGA;浮点运算;高速;对称舍入法
中图分类号:TP332.2
文献标识码:A
Design and Implementation of High-speed Floating-point Operations in FPGA
Zhong Xiaoyan,Su Tao,Sun Duo
(Xidian University,Xi’彻:710071)
移位操作是整个加减法操作的瓶颈,由于每次 移位的位数不定,因此设计起来比较复杂,如果像移 位寄存器那样一位一位地移,则延时很大,且延时长 度不固定,不适于流水线操作,所以应在一个时钟周 期内实现整个移位过程。在本处理中,结合slice结 构特点,采用基于数据选择器的方法实现。实现移 位操作,就是将指数较小的浮点数的尾数向右移n 位(n为两浮点数的指数差),移出的高位补上符号 位。对阶处理实现由一系列的数据选择器(2选1, 4选l,8选l,16选l等)组合而成,选择器的输入 是二进制补码表示的较小指数的浮点尾数DAl7~ DAO(DAl7为符号位),选择器的输出就是对阶结 果DBl7~DBO,数据选择器的控制码就是指数差n。 为了便于理解,以DB2为例,当n=0时,DB2= DA2;当n=1时,DB2=DA3;…;当n=15时,DB2 =DAl7;当n>15时,DB2=DAl7(符号位扩展)。 也就是说DB2是一个以DA2一DAl7为输人数据, 以n为控制码的16选l的数据选择器。一个slice 能实现4选l逻辑,两个slice能实现8选l逻辑,4 个slice能实现16选l逻辑。
3I 30
23 22
0
exp。nen‘//\ slgn
…an6ssa
I 开始 l
●
求阶差,XE=IEl—E2l I
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在FPGA上优化实现复数浮点计算
性能浮点处理一直与高性能CPU相关联。
在过去几年中,GPU也成为功能强大的浮点处理平台,超越了图形,称为GP-GPU(通用图形处理单元)。
新创新是在苛刻的应用中实现基于FPGA的浮点处理。
本文的重点是FPGA及其浮点性能和设计流程,以及OpenCL的使用,这是高性能浮点计算前沿的编程语言。
各种处理平台的GFLOP指标在不断提高,现在,TFLOP/s这一术语已经使用的非常广泛了。
但是,在某些平台上,峰值GFLOP/s,即,TFLOP/s表示的器件性能信息有限。
它只表示了每秒能够完成的理论浮点加法或者乘法总数。
分析表明,FPGA单精度浮点处理能够超过1 TFLOP/s。
一种不太复杂的常用算法是FFT。
使用单精度浮点实现了4096点FFT。
它能够在每个时钟周期输入输出四个复数采样。
每一个FFT内核运行速度超过80 GFLOP/s,大容量FPGA 的资源支持实现7个这类的内核。
但是,如图1所示,这一FPGA的FFT算法GFLOP/s接近400 GFLOP/s。
这是按键式OpenCL 编译结果,不需要FPGA专业知识。
使用逻辑锁定和DSE进行优化,7内核设计接近单内核设计的Fmax,将其GFLOP/s提升至500,超过了10 GFLOP/s每瓦。
这一每瓦GFLOP/s要比CPU或者GPU功效高很多。
对比一下GPU,GPU在这些FFT长度上效率并不高,因此,没有进行基准测试。
当FFT长度达到几十万个点时,GPU效率才比较高,能够为CPU提供有效的加速功能。
图1:Altera StraTIx V 5SGSD8 FPGA浮点FFT性能。
总之,实际的GFLOP/s一般只达到峰值或者理论GFLOP/s的一小部分。
出于这一原因,更好的方法是采用算法来对比性能,这种算法能够合理的表示典型应用的特性。
算法越复杂,典型实际应用的基准测试就越具有代表性。
并不是依靠供应商的峰值GFLOP/s指标来确定处理技术,而是使用比较复杂具有代表性的第三方评估。
高性能计算理想的算法是Cholesky分解。
