直线和平面平行与平面与平面平行证明题专题训练
直线与平面平行的判定及其性质 测试题(答案)

直线与平面平行的判定和性质年级__________ 班级_________ 学号_________ 姓名__________ 分数____一、选择题(共26题,题分合计130分)1.直线a //平面M ,直线b ⊂/M ,那么a //b 是b //M 的 条件. A.充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要2.已知l 、m 、n 为两两垂直且异面的三条直线,过l 作平面α与m 垂直,则直线n 与平面α的关系是A.n //αB.n //α或n ⊂αC.n ⊂α或n 不平行于αD.n ⊂α3.能保证直线a 与平面α平行的条件是A.b a b a //,,αα⊂⊄B.b a b //,α⊂C.c a b a c b //////,,,αα⊂D.b D b C a B a A b ∈∈∈∈⊂,,,,α且BD AC =4.如果直线a 平行于平面α,则A.平面α内有且只有一直线与a 平行B.平面α内无数条直线与a 平行C.平面α内不存在与a 平行的直线D.平面α内的任意直线与直线a 都平行5.如果两直线a ∥b ,且a ∥平面α,则b 与α的位置关系A.相交B.α//bC.α⊂bD.α//b 或α⊂b6.下列命题正确的个数是(1)若直线l 上有无数个点不在平面α内,则l ∥α(2)若直线l 与平面α平行,则l 与平面α内的任意一直线平行(3)两条平行线中的一条直线与一个平面平行,那么另一条也与这个平面平行 (4)若一直线a 和平面α内一直线b 平行,则a ∥α A.0个 B.1个 C.2个 D.3个7.若直线a ⊥b ,且a ∥平面α,则直线b 与平面α的位置关系是A.b ⊂αB.b ∥αC.b ⊂α或b ∥αD.b 与α相交或b ∥α或b ⊂α都有可能8.已知α、β是两个不同的平面,在下列条件中,可判断平面α与平面β平行的是A.α、β都垂直于平面γB.a 、b 是α内两条直线,且a ∥β,b ∥βC.α内不共线的三个点到β的距离相等D.a 、b 为异面直线,且a ∥α,b ∥α,a ∥β,b ∥β9.下列命题正确的个数是①若直线l 上有无数个点不在平面α内,则l ∥α②若直线l 与平面α平行,则l 与平面α内的任意一条直线都平行③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行 ④若直线l 与平面α平行,则l 与平面α内的任意一条直线都没有公共点 A.0个 B.1个 C.2个 D.3个10.b 是平面α外的一条直线,下列条件中可得出b ∥α是A.b 与α内的一条直线不相交B.b 与α内的两条直线不相交C.b 与α内的无数条直线不相交D.b 与α内的所有直线不相交11.已知直线l 1、l 2,平面α,l 1∥l 2,l 1∥α,则l 2与α的位置关系是A.l 2∥αB.l 2⊂αC.l 2∥α或l 2⊂αD.l 2与α相交12.已知两条相交直线a 、b ,a ∥平面α,则b 与α的位置关系A.b ∥αB.b 与α相交C.b ⊂αD.b ∥α或b 与α相交13.下列命题中正确的是①过一点,一定存在和两条异面直线都平行的平面②垂直于同一条直线的一条直线和一个平面平行③若两条直线没有公共点,则过其中一条直线一定有一个平面与另一条直线平行 A.① B.③ C.①③ D.①②③14.a、b为平面M外的两条直线,在a∥M的前提下,a∥b是b∥M的A.充要条件B.充分条件C.必要条件D.以上情况都不15.α和β是两个不重合的平面,在下列条件中可判定平面α与β平行的是A.α、β都垂直于平面γB.α内不共线的三点到β的距离相等C.l,m是α平面内的直线,且l∥β,m∥βD.l、m是两条异面直线且l∥α,m∥α,m∥β,l∥β16.在空间中,下述命题正确的A.若直线a∥平面M,直线b⊥直线a,则直线b⊥平面MB.若平面M∥平面N,则平面M内任意一条直线a∥平面NC.若平面M与平面N的交线为a,平面M内的直线b⊥直线a,则直线b⊥平面ND.若平面N内的两条直线都平行于平面M,则平面N∥平面M17.设直线a在平面M内,则直线M平行于平面N是直线a平行于平面N的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分又不必要条件18.设a、b是平面α外的任意两条直线,则"a、b长相等"是"a、b在平面α内的射影长相等"的A.既不充分也不必要条件B.充分必要条件C.必要但不充分条件D.充分但不必要条件19.如果平面α和直线l满足l和α内两条平行直线垂直,则A.l αB.l∥αC.l与α相交D.以上都不对20.如果一条直线和一个平面平行,为了使夹在它们之间的两条线段的长相等,以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行21.直线a∥平面α,平面α内有n条直线交于一点,那么这几条直线中与直线a平行的A.至少有一条B.至多有一条C.有且只有一条D.不可能有22.若直线m平面α,则“平面α∥平面β”是“直线m∥平面β”的A.充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件23.平行于同一个平面的两条直线的位置关系是A.平行B.相交C.异面D.平行或相交或异面24.下列四个命题中假命题的个数是①两条直线都和同一个平面平行,则这两条直线平行②两条直线没有公共点,则这两条直线平行③两条直线都和第三条直线垂直,则这两条直线平行④一条直线和一个平面内无数条直线没有公共点,则这条直线和这个平面平行A.4B.3C.2D.125.如果一条直线和一个平面平行,为了使夹在它们之间的两条线段的长相等,以下结论正确的是A.其充分条件是这两条线段平行B.其必要条件是这两条线段平行C.其充要条件是这两条线段平行D.其必要条件是这两条线段平行26.直线与平面平行的充要条件是这条直线与平面内的A.一条直线不相交B.两条直线不相交C.任意一条直线都不相交D.无数条直线不相交二、填空题(共6题,题分合计25分)1.如图,空间四边形ABCD 中,E 、H 分别是AB 、AD 的中点,F 、G 分别是CB 、CD 上的点.且32==CD CG CB CF ,若BD =6 cm ,梯形EFGH 的面积为28 cm 2,则平行线EH 与FG 间的距离为_______.2.一条直线与平面α相交于点A ,在平面α内不过A 点的直线与这条直线所成角的最大值为_________.3.正方体ABCD -A 1B 1C 1D 1中,E 为DD 1的中点,则BD 1与过点A 、E 、C 的平面的位置关系是__________.4.几何体ABCD -A 1B 1C 1D 1是棱长为A 的正方体,M 、N 分别是下底面的棱A 1B 1、B 1C 1的中点,P 是上底面的棱AD 上的一点,AP =31a ,过P 、M 、N 的平面交上底面于PQ ,Q 在CD 上,则PQ =___________.5.如果两条直线a 与b 互相平行,且a ∥平面α,那么b 与α的位置关系是 .6.直线a ∥平面α,直线b 、c 都在α 内且a ∥b ∥c ,若a 到b , c 的距离分别为d 1、d 2,且d 1>d 2,则直线a 到α 的距离d 的取值范围是___________.三、解答题(共12题,题分合计112分)1.求证:若直线l与平面α有一个公共点,且l平行于α内的一条直线,则l α..2.如图,P是△ABC所在平面外一点,M∈PB,试过AM作一平面平行于BC,并说明画法的理论依据Array3.设AB、CD为夹在两个平行平面α、β之间线段,且直线AB、CD为异面直线,М、P分别为AB、CD的中点,求证:MP ∥α.4.ABCD-A1B1C1D1是棱长为a的正方体,(1)画出过A、C、B1的平面与下底面的交线l;(2)求l与直线AC的距离.5.正方体ABCD-A1B1C1D1中,侧面对角线AB1、BC1分别有E、F,且B1E=C1F,求证:EF∥平面ABCD.6.平面外的两条平行直线中的一条平行于这个平面,那么另一条直线也平行于这个平面.7.设a、b是异面直线,自AB的中点O作平面α与a、b分别平行,M、N分别是a、b上的任意两点,MN与α交于点P,求证:P是MN的中点.8.求证:如果一条直线和两个相交的平面都平行,那么这条直线和它们的交线平行.9.α∩β=c,α∩γ=b,β∩γ=a,若直线a∥直线b,你能得到什么结论?10.如图,正方体ABCD-A1B1C1D1中,E在AB1上,F在BD上,且B1E=BF.求证:EF∥平面BB1C1C.11.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,并且CM=DN.求证:MN∥平面AA1B1B.12.如图,平面EFGH分别平行于CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.(1)求证:EFGH是矩形.(2)点E在什么位置时,EFGH的面积最大.直线与平面平行的判定和性质答案一、选择题(共26题,合计130分)1.答案:A2.答案:A3.答案:A4.答案:B5.答案:D6.答案:A7.答案:D8.答案:B9.答案:B10.答案:D11.答案:C12.答案:D13.答案:B14.答案:B15.答案:D16.答案:B17.答案:A18.答案:A19.答案:D20.答案:A21.答案:B22.答案:A23.答案:D24.答案:A25.答案:A26.答案:C二、填空题(共6题,合计25分)1.答案:8 cm2.答案:90°3.答案:BD1∥平面AEC4.答案:a2 325.答案:b∥α或b α6.答案:) ,0(2 d三、解答题(共12题,合计112分)1.答案:见注释2.答案:见注释3.答案:见注释4.答案:. 26 a5.答案:见注释6.答案:见注释7.答案:见注释8.答案:见注释9.答案:见注释10.答案:见注释11.答案:见注释12.答案:(1)见注释(2)E为BD的中点时。
高中数学直线和平面平行与平面和平面平行专项练习

高中数学直线和平面平行与平面和平面平行专项练习【基础知识必备】一、必记知识精选1.直线和平面的位置关系.直线和平面位置关系有三种:线在面内,直线与平面平行,直线与平面相交.相交与平行又称为线在面外.2.直线与平面平行的判定定理:如果不在一个平面内的直线和平面内的一条直线平行,那么这条直线也和这个平面平行.可简记为:线线平行,线面平行.3.直线与平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.可简记为:线面平行,线线平行.4.平面平行的定义.5.平面平行的判定定理:如果一个平面内有两条相交直线分别平行于另一个平面,那么这两个平面平行.简言之:线面平行,面面平行.6.平面平行的判定定理推论:如果一个平面内有两条相交直线分别平行于另一平面内的两条直线,那么这两个平面平行.简言之:线线平行,面面平行.7.平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行.简言之:面面平行,线线平行.8.平面平行的传递性:如果α∥β,β∥γ,那么α∥γ.二、重点难点突破(一)重点平行线的传递性,直线与平面平行的判定与性质定理,平面与平面平行的判定与性质定理.对于这部分知识的学习要注意记清条件与结论.如直线与平面平行的判定定理要求直线是平面外的直线.(二)难点直线与平面,平面与平面平行的判定定理及性质定理的应用是本节的难点.在解题时要注意与平面几何知识多联系.如在证明线面平行时,一般与公理4以及三角形的中位线、平行四边形的对边多有联系.三、易错点和易忽略点导析1.忽略定理的条件而解题错误.【例1】判断:如果一个平面内两条直线与另一平面平行,则这两个平面平行()错解:√正确答案:×错解分析:利用平面与平面平行的判定定理判断时,忽略了平面内两条直线相交的位置关系.2.对空间中特殊的位置关系考虑不全面.【例2】已知M是两条异面直线a、b外一点,则过M且与a、b都平行的平面有几个?错解:设平面α过点M,且与a、b都平行,则直线a及其外一点M确定的平面与α的交线a′必与a平行.同理存在b′⊂α,且b′∥b,则α为a′与b′确定的平面,由于过M且与a平行的直线a′是惟一的,b′也是惟一的,因而由a′、b′确定的平面α也是惟一的.综上所述,过M且与a、b都平行的平面只有一个.正确解法:过M作直线a′∥a,过M作直线b′∥b,则a′、b′确定平面α,当a、b都不在由a′、b′确定的平面α内时,过M且与a、b都平行的平面只有一个;当a⊂α或b⊂α时,过M且与a、b 都平行的平面不存在.错解分析:错解没有注意到a⊂α或b⊂α的特殊情况,解的结果是不完整的.【综合应用创新思维点拨】一、学科内综合思维点拨【例1】平面外的两条平行线中的一条平行于这个平面.求证:另一条也平行于这个平面.思维入门指导:作出图形如图9-3-1.欲证b∥α,想到直线和平面平行的判定定理只须在平面α内找到一条直线c,使c∥b即可,由已知条件a∥α,想到直线与平面平行的性质定理,只须过直线a作平面β与平面α相交.交线即为所成直线c,因此本题可证.已知:如图9-3-1,直线a∥b,a∥平面α,且b在平面α外.求证:b∥α.证明:过α作平面β,使它与平面α相交,设交线为c.∵a∥α,∴a∥c.∵a∥b,∴b∥c.∴b∥α.点拨:解此题易出现的错误是在找c时,直接在平面M内作直线c∥直线a,这种作法不能保证平行且无理论依据.二、应用思维点拨【例2】如图9-3-2所示的一块木料中,棱BC平行于面A′C′.(1)要经过面A′C′内的一点P和棱BC将木料锯开,应怎样画线?(2)过点P所画的线和面AC是什么位置关系?思维入门指导:要过P和棱BC将木料锯开,就是要画图中BE、EF和CF各线,其中画EF 是关键,显然EF是截面与面A′C′的交线,由已知BC∥面A′C′可知EF∥BC.由于受木料形状及点P的限制,可以通过画出点P与B′C′的平行线来确定EF.解:(1)在面A′C′内,过点P画直线EF,使EF∥B′C′,EF交棱A′B′、C′D′于点E、F,连结BE、CF,则EF、BE、CF就是应画的线.BC∥面A′C′ BC∥B′C′(2) BC⊂面BC′ ⇒⇒EF∥BC面BC′ 面A′C′=B′C′ EF∥B′C′ EF⊄面AC ⇒EF∥面AC.BC⊂面AC点拨:本题的关键在于线面平行与线线平行的关系,将线面平行转化为线线平行,实现由空间向平面的转化.三、创新思维点拨【例3】已知平面α,BC∥α,D∈BC,A∉α,直线AB、AD、AC分别交α于E、F、G,且BC=α,AD=b,DF=c,求EG的长度.思维入门指导:本题涉及的主要是点、直线BC、面α,可根据其位置分情况讨论:若AB、AD 、AC 延长线分别交α于E 、F 、G ;若AB 、AD 、AC 的反向延长线分别交α于E 、F 、G;若A 与直线BC 位于α的两侧.BC ∥α,CGAC DF AD =, 解:(1)如图9-3-3(1),∵BC ⊂面ABC, ⇒BC ∥EF ⇒面ABC∩面α=EF,EG BC AG AC =, ∵c b CG AC =,c b b CG AC AC +=+,即c b b AG AC +=, ∴c b b EG BC +=,则EG=b c b a )(+.(2)如图9-3-3(2),同理EF ∥BC,则AD AF AB AE BC EG ==. ∵AF=DF-DA=c-b,∴EG=bb c a AD BC AF )(-=•. (3)如图9-3-3(3),同理EF ∥BC,则AD AF AB AE BC EG ==. ∴AF=AD-DF=b-c.∴EG=bc b a AD BC AF )(-=•. 点拨:利用点A 与线段BC 之间不同的位置关系,以及点A 、线段BC 与平面α之间的不同位置关系,进行逻辑划分.分类讨论思想是高中数学的一种重要的思想.在分类讨论时要做到理清逻辑关系,分类时做到不重不漏,即不重复讨论,也不遗漏情况.四、高考思维点拨【例4】 正方形ABCD 与正方形ABEF 所在平面相交于AB ,在AE 、BD 上各有一点P 、Q ,且AP=DQ.求证:PQ ∥面BCE.思维入门指导:证明直线与平面平行,可以利用直线与平面平行的判定定理.即由线线平行,得线面平行.在寻找线线平行的条件时,可以有多种方法.证法一:如图9-3-4(1),作PM ∥AB 交BE 于M ,作QN ∥AB 交BC 于N,连接MN,因为面ABCD∩面ABEF=AB,则AE=DB.又∵AP=DQ,∴PE=QB.又∵PM ∥AB ∥QN, ∴AE PE AB PM =,BD BQ DC QN =.∴DCQN AB PM =. ∴PM ∥QN.即四边形PMNQ 为平行四边形.∴PQ ∥MN.又∵MN ⊂面BCE ,PQ ⊄面BCE ,∴PQ ∥面BCE.证法二:如图9-3-4(2),连结AQ 并延长交BC 或BC 的延长线于点K ,连结EK.∵AD ∥BC,∴QKAQ QB DQ =. 又∵正方形ABCD 与正方形ABEF 有公共边AB ,且AP=DQ ,∴PEAP QK AQ =.则PQ ∥EK. ∴EK ⊂面BCE ,PQ ⊄面BCE.∴PQ ∥面BCE.点拨:证明直线和平面平行的方法有:①利用定义采用反证法;②判定定理;③利用面面平行,证线面平行.其中主要方法是②、③两法,在使用判定定理时关键是确定出面内的与面外直线平行的直线.五、经典类型题思维点拨【例5】 经过平面外一点有且只有一个平面和已知平面平行.已知:点A 在平面α外.求证:经过点A 有一个平面且只有一个平面和α平行.思维入门指导:有且只有中“有”是存在性,“只有”是惟一性.对于此类问题的证明要从存在性和惟一性两方面进行.证明:(存在性)如图9-3-5,在平面α内任意作两条相交直线a′、b′,过A在A与a′确定的平面内作直线a∥a′,同理过A作直线b∥b′,则a∥α,b∥α,且a、b为相交直线,那么经过a、b 的平面β∥α,所以经过点A有一个平面β和平面α平行.(惟一性)设平面β′经过A,且β′∥α,则A和a′确定的平面γ必与β′相交.设γ∩β′=l,A∈l且a′∥l,因为经过直线a′外一点A只有一条直线和a′平行,所以l与a重合,即平面β′过a;同理平面β′过直线b,所以平面β′是由a、b确定的平面,故β′与β重合.因此经过点A只有一个平面β∥α,所以经过A有且只有一个平面和α平行.点拨:证明平面与平面平行关键是找到一个面内的两条相交直线与另一个面平行或与另一面内的两条相交直线平行.六、探究性学习点拨【例6】尝试用多种方法证明命题:如果一条直线和两个相交平面都平行,那么这条直线与这两个平面的交线平行.已知:如图9-3-6,面α1∩面α2=b,a∥面α1,a∥面α2.求证:a∥b.思维入门指导:证明几何问题的一般思路是由求证想判定,即由题的“终结”回想证明它有什么样的方法;由已知想性质,即由题设条件,想到由题设能推出什么样的性质.本题中,要证明a∥b,因为直线b是平面α1和平面α2的交线,所以首先应将a平移到平面α1和α2内,使其与直线b 发生联系.证法一:过直线a作两个平面β1和β2,使得平面β1∩平面β1=c,面β2∩面α2=d.∵a∥面α1,a∥面α2,∴a∥c,a∥d.∴c∥d.∵d⊂面α2,c⊄面α2.∴c∥面α2.又∵c⊂面α1,面α1∩面α2=b,∴c∥b.∴a∥b.证法二:经过a作一平面π,使得平面π∩面α1=k,面π∩面α2=l.∵a∥面α1,a∥面α2,∴a∥k,a∥l,则k∥l∥a.∵三个平面α1、α2、π两两相交,交线分别为k、l、b且k∥l,∴k∥l∥b,则a∥b.证法三:在b上任取一点A,过A和直线a作平面和平面α1相交于l1,和平面α2相交于直线l2.∵a∥面α1,a∥面α2,∴a∥l1,a∥l2.∵过一点只能作一条直线与另一直线平行,∴l1与l2重合.又∵l1⊂面α1,l2⊂面α2,∴l1与l2重合于b.∴a∥b.点拨:证明直线与直线平行,有下列方法:(1)若a,b⊂面α,且a∩b=○,则a∥b;(2)若α∩β=a,β∩γ=b,γ∩α=c且a∥b∥c;(3)若a∥b,b∥c,则a∥c;(4)若a∥α;a⊂β,α∩β=b,则a∥b.【同步达纲训练】A卷:教材跟踪练习题(60分45分钟)一、选择题(每小题5分,共30分)1.若直线m不平行于平面α,且m⊄α,则下列结论中正确的是( )A.α内的所有直线与m异面B.α内不存在与m平行的直线C.α内存在惟一的直线与m平行D.α内的直线与m相交2.两条直线都与一个平面平行,则这两条直线的位置关系是()A.平行B.相交C.异面D.以上均有可能3.已知直线a、b、c及平面α,下列哪个条件能确定a∥b()A.a∥α,b∥αB.a⊥c,b⊥cC.a、b与c成等角D.a∥c,b∥c4.具备下列哪个条件时,两个平面一定平行()A.一个平面内有两条直线平行于另一个平面B.一个平面内有无数条直线平行于另一个平面C.一个平面内任何一条直线都平行于另一个平面D.一个平面内有两条直线平行于另一个平面内的两条直线5.如果平面α平行于平面β,那么()A.平面α内任意直线都平行于平面βB.平面α内仅有两条相交直线平行于平面βC.平面α内任意直线都平行于平面β内的任意直线D.平面α内的直线与平面β内的直线不能垂直6.经过平面外两点作该平面的平行平面,可以作()A.0个B.1个C.0个或1个D.1个或2个二、填空题(每小题4分,共16分)7.a、b是异面直线,α、β是平面,a⊂α,b⊂β.甲:α∥β,b∥α,则甲是乙的条件.8.在棱长为a的正方体ABCD-A1B1C1D1中,M、N是下底面的棱A1B1、B1C1的中点,P是a,过P、M、N的平面交上底面于PQ,Q在CD上,则PQ= . 上底面棱AD上的一点,AP=39.过两条平行线中的一条和另一条平行的平面有个.10.给出条件:①α内有两条相交直线分别平行于β;②α内有无数条直线平行于β;③α内有两条直线分别平行于β内的两直线.其中能成为α∥β的必要不充分条件的是.三、解答题(每小题7分,共14分)11.P是平行四边形ABCD所在平面外一点,Q是PA的中点.求证:PC∥面BDQ.12.在棱长为a的正方体ABCD-A1B1C1D1中,设M、N、E、F分别是棱A1B1、A1D1、C1D1、B1C1的中点.求证:(1)E、F、B、D四点共面;(2)面AMN∥面EFBD.B卷:综合应用创新练习题(85分60分钟)一、学科内综合题(每小题5分,共10分)1.三条直线a、b、c两两异面,它们所成的角都相等且存在一个平面与这三条直线都平行、则a与b所成角的度数为.2.空间四边形ABCD中,AC=2cm,BD=4cm,AC与BD成45°角,M、N、P、Q分别是四边中点,则四边形MNPQ的面积是.二、应用题(每小题1O分,共20分)3.教室内,日光灯管所示直线与地面平行,若想在地面上作出一条直线与灯管所示直线平行,该怎样作出?4.桌面β与水平面α平行,在桌面上有一块三角形钢板ABC,AB=24cm,BC=32cm,AC=40cm.在β与α之间有一点P,如图9-3-7所示,直线AP、BP、CP分别交α于点A′、B′、C′,且PA′:PA=2:3,求△A′B′C′所占地面的面积.三、创新题(45分)(一)教材变型题(10分)5.(P16例1变型)如图9-3-8,四边形EFGH为空间四边形ABCD的一个截面,若截面为平行四边形.求证:(1)AB∥平面EFGH;(2)CD∥平面EFGH.(二)一题多解(10分)6.正方体AC1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥面AA1B1B.(三)一题多变(10分)7.已知直线a⊂α,则b∥a是b∥α的条件.(1)一变:已知直线a⊂α,b⊄α,则b∥a是b∥α的条件.(四)新情境题(15分)8.如图9-3-9,在空间六边形(即六个顶点没有任何五点共面)A1B1C1C2D2A2中,每相邻两边互相垂直,边长均为a,并且A2A1∥C2C1.求证:面A2B1C2∥面A1C1D2.四、高考题(10分)9.(2000,上海)设有不同的直线a、b和不同的平面α、β、γ,给出下列三个命题:①若a∥α,b∥α,则a∥b;②若a∥α,a∥β,则α∥β;③若α∥γ,β∥γ,则α∥β.其中正确的个数是()A.OB.1C.2D.3加试题:竞赛趣味题(15分)证明:经过正方体中心的任一截面的面积不小于正方体的一个侧面的面积.【课外阅读】数学证明与解释1.数学证明数学证明是数学中根据某些命题的真实性,来推断另一个命题的真假的一种思维过程,通常推断命题为真,叫做证明为真,也称为证明;而推断命题为假,叫做证明为假,也称为反驳.关于证明应注意两点:(1)命题的“真假”总是相对于某个数学理论来说的,因为“真假”在数学中具有相对性.在整数集中,无倍数关系的两个数的除法就已无意义,即是“假”的;在实数范围内负数不能开偶次方;在初等数学看来,高等数学的一些命题是不真的.实际上,证明也总是在一定的数学理论体系内进行的.(2)证明是一种逻辑推理过程,要求具有一定的逻辑性和严谨性,即数学推理的严格性,重要的是推理要有依据(公理和已证定理)和要严格遵守逻辑规则.注意,这些逻辑规则是假定先于数学而存在的.数学证明所应遵守的一般逻辑规则是:(1)可以在一个证明的任何地方引入一个前提(依据).(2)如果一个证明中有一些先引入的前提,这些前提的合取可以逻辑地推出一个命题P,那么就可以在这一证明中引入这个命题P.(3)如果能从一个命题R和一个前提集合推导出命题S,那么就可以从这个前提集合本身推导出命题R→S.2.解释对于一个理论系统∑,若有一组具体事物M,其性质是已知的,在规定∑中每一基本概念指M中某一具体事物后,可验证∑的每个公理在M中都成立,则称M为理论系统∑的一个解释,或一个模型、一种应用.解释的方法在数学中也是很常用的.例如中学立体几何课程的若干直观教具(正方体等模型),就是中学几何中提供的三维欧氏空间理论的一个解释.在证明一个公理系统自身所必须满足的某些性质如无矛盾性、独立性和完全性等方面时,解释的方法是惟一有效的.现代数学的形式系统中,所处理的只是各种符号和符号序列及其变形,它们的数学意义是靠解释来给定的.参考答案A卷一、1.B 点拨:直线m不平行于α,且m α,则m必与α相交.2.D3.D 点拨:由平行公理可知选项D正确.A、B、C中直线a、b的位置关系可以为平行,异面或相交.4.C 点拨:按照直线与平面平行的定义,注意区分“无数”与“任何”.5.A 点拨:由平面与平面平行的性质定理知A正确;C中直线也可以是异面;D中两直线可以异面垂直.6.C 点拨:若两点在平面两侧测过两点不可能作平面与已知平面平行;若两点在平面同侧且连线平行于平面,则可有一个平面过直线已平行于已知平面;若两点在同侧且连线与平面相交,则不存在符合要求的平面.二、7.充分且必要条件 点拨:过a 作平面 交平面β于直线a′,则a′与b 相交,且a′∥β,又b ∥β故由判定定理知α∥β.反之,α∥β,由性质定理知必有a ∥β,b ∥α. 8.332 a 点拨:如答图9-3-1.∵M 、N 为A 1B 1、B 1C 1的中点,∴MN ∥面AC ,则过点P 、M 、N 的平面与上底面的交线平行于MN.连结AC ,过P 作PQ ∥AC 交DC 于点Q.则PQ 为面MNP 与面AC 的交线.∵AC =2a ,AP =3a ,∴PQ =322 a. 9.无数个 点拨:门扇绕一边门框转动时,门扇所在平面与另一门框所在直线始终是平行的.10.②③ 点拨:若α∥β则α内任何直线与平面β都平行,但α与β相交时α内也有无数条直线与β平行,所以选②;要判断两平面平行依据必须是相交的两直线.三、11.证明:如答图9-3-2,连结AC 交BD 于点O .∵ABCD 是平行四边形,∴A O =O C.连结O Q ,则O Q 在平面BDQ 内,且O Q 是△APC 的中位线,∴PC ∥O Q.∵PC 在平面BDQ 外,∴PC ∥平面BDQ.12.证明:(1)分别连结B 1D 1、ED 、FB ,如答图9-3-3,则由正方体性质得B 1D 1∥BD.∵E 、F 分别是D 1C 1和B 1C 1的中点,∴EF ∥21B 1D 1. ∴EF ∥21BD. ∴E 、F 、B 、D 对共面.(2)连结A 1C 1交MN 于P 点,交EF 于点Q ,连结AC 交BD 于点O ,分别连结PA 、Q O . ∵M 、N 为A 1B 1、A 1D 1的中点,∴MN ∥EF ,EF ⊂面EFBD.∴MN ∥面EFBD.∵PQ ∥A O ,∴四边形PA O Q 为平行四边形.∴PA ∥O Q.而O Q ⊂平面EFBD ,∴PA ∥面EFBD.且PA∩MN=P ,PA 、MN ⊂面AMN ,∴平面AMN ∥平面EFBD.B 卷一、1.60° 点拨:由题中条件知经平移三条异面直线可以平移到同一个面内转化为三条相交直线,且夹角相等,故所成角为60°.2.2cm 2 点拨:如答图9-3-4,M 、N 、P 对分别为四边中点,MN ∥21AC ,MQ ∥21BD.∴四边形MNPQ 为平行四边形,且∠MNP=45°或∠QMN=45°.∴S □MNPQ =2S △QMN =2×21·MQ·MN·sin45°=2(cm 2). 二、3.解:过日光灯管的两端向平面引垂线,连结两垂足的直线与日光灯管所示直线平行.4.解:∵α∥β,且β∩面ABA′B′=AB,面α∩面ABA′B′=A′B′,∴AB ∥A′B′.又∵PA′:PA=2:3,∴A′B′:AB=2:3.同理A′C′:AC=2:3,B′C′:BC=2:3.则A′B′=16,B′C′=364,A′C′=380. ∴A′B′2+B′C′2=A′C′2,∴S △A′B′C′=21·A′B′·B′C′=17032cm 2.故△A′B′C′所占地面的面积为17032cm 2. 三、(一)5.证明:∵HG ∥FF.EF ⊂面ABC ,HG ⊄面ABC ,∴HG ∥面ABC.∵HG ⊂面ABD ,面ABD∩面ABC=AB ,∴HG ∥AB.又HG ⊂面EFGH ,AB ⊄面EFGH ,∴AB ∥平面EFGH.同理可证CD ∥平面EFGH.(二)6.证法一:作ME ∥BC ,NF ∥AD 分别交BB 1和AB 于E 、F ,连结EF.如答图9-3-5.由BC ME =CB M B 11与AD NF =BD BN , 又由已知CM=DN ,可证得ME ∥NF.∴MNFE 是平行四边形.∴MN ∥EF.又MN ⊄平面ABB 1A 1,EF ⊂平面ABB 1A 1,∴MN ∥平面ABB 1A 1.证法二:连接CN 设交AB 于H ,连接HB 1.∵DC ∥BH ,∴CH CN =DBDN . 又CM=DN ,DB=CB 1,∴CH CN =1CB CM , ∴NM ∥HB 1.又MN ⊄平面ABB 1A 1,B 1H ⊂平面ABB 1A 1,∴MN ∥平面ABB 1A 1.(三)7.既不充分也不必要 点拨:b ∥a ,则b 可能在α内;b ∥α,则b 与a 可能异面.(1)充分不必要.(四)8.证明:如答图9-3-6,构造正方体A 1C 2,易证面A 2B 1C 2∥面A 1C 1D 2.四、9.B 点拨:命题①中a 、b 可以平行、相交或异面;命题②中α,β可以相交;命题③依据平面平行的传递性知其正确.加试题:证明:设正方体的棱长为a.易知截面为四边形或六边形.若为四边形,那么它与正方体一相对侧面不相交,且截面在这两个侧面上的射影为整个侧面,从而命题成立.若截面为六边形,考察侧面展开图可知截面周长P≥32a ,从而S >21·P·2a ≥423a 2>1.06a 2>a 2,所以命题得证.。
直线和平面平行与平面与平面平行证明题专题训练
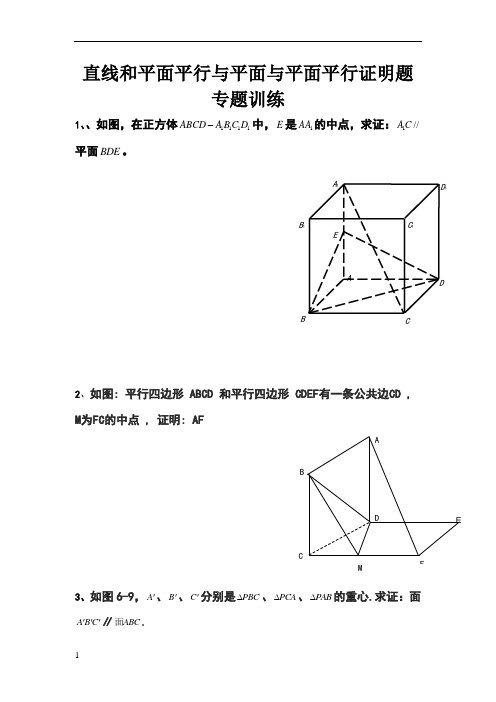
直线和平面平行与平面与平面平行证明题专题训练1、、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证:1//A C 平面BDE 。
2、如图: 平行四边形 ABCD 和平行四边形 CDEF 有一条公共边CD ,M 为FC 的中点 , 证明: AF3、如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:面A B C '''∥ABC 面.A 1ED 1C 1B 1DCBAM ABCDEFv1.0 可编辑可修改4、 在长方体ABCD —A1B1C1D1中. (1)作出过直线AC 且与直线BD1平行的 截面,并说明理由.(2)设E ,F 分别是A1B 和B1C 的中点,求证直线EF5、、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EHABCC 1DA 1B 1D 1∥FG.求证:EH∥BD. (12分)6、P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证://PC平面BDQ.(自己作图)HG FEDBACv1.0 可编辑可修改7、如图,α//a ,A 是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α于E ,F ,G ,若4=BD ,4=CF ,5=AF ,则EG =___________.8、求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.。
点线面关系知识总结和练习题

//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法(1)定义法:直线与平面无公共点。
(2)判定定理:(3)其他方法://a αββ⊂2.性质定理://a a bαβαβ⊂⋂=二、平面与平面平行 1.判定方法(1)定义法:两平面无公共点。
(2)判定定理:////a b a b a b Pββαα⊂⊂⋂= //αβ(3)其他方法:a a αβ⊥⊥ //αβ; ////a γβγ//αβ 2.性质定理://a bαβγαγβ⋂=⋂=三、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b ② 判定定理:a ba cb c A b c αα⊥⊥⋂=⊂⊂ a α⊥③ 推论://a a bα⊥ b α⊥ (3)性质 ①a b αα⊥⊂ a b ⊥ ②a b αα⊥⊥四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理a a αβ⊂⊥ αβ⊥ (3)性质①性质定理la a lαβαβα⊥⋂=⊂⊥ αβ⊥② l P P A A αβαβαβ⊥⋂=∈⊥垂足为 A l ∈④ l P PA αβαβαβ⊥⋂=∈⊥ PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角的平面角例1.如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC于D,交SC于E,又SA=AB,SB=BC,求以BD为棱,以BDE和BDC为面的二面角的度数。
●求线面夹角定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。
直线、平面平行的判定及其性质_测试题有详解

直线、平面平行的判定及其性质 测试题〔有详解〕A一、选择题1.以下条件中,能判断两个平面平行的是( )A .一个平面的一条直线平行于另一个平面;B .一个平面的两条直线平行于另一个平面C .一个平面有无数条直线平行于另一个平面D .一个平面任何一条直线都平行于另一个平面2.E ,F ,G 分别是四面体ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过E ,F ,G 的截面平行的棱的条数是A .0B .1C .2D .33. 直线,a b c ,及平面αβ,,使//a b 成立的条件是〔 〕A .//,a b αα⊂B .//,//a b ααC .//,//a c b cD .//,a b ααβ=4.假设直线m 不平行于平面α,且m ⊄α,则以下结论成立的是〔 〕A .α的所有直线与m 异面B .α不存在与m 平行的直线C .α存在唯一的直线与m 平行D .α的直线与m 都相交5.以下命题中,假命题的个数是〔 〕① 一条直线平行于一个平面,这条直线就和这个平面的任何直线不相交;② 过平面外一点有且只有一条直线和这个平面平行;③ 过直线外一点有且只有一个平面和这条直线平行;④ 平行于同一条直线的两条直线和同一平面平行;⑤a 和b 异面,则经过b 存在唯一一个平面与α平行A .4B .3C .2D .16.空间四边形ABCD 中,,M N 分别是,AB CD 的中点,则以下判断正确的选项是〔 〕A .()12MN AC BC ≥+B .()12MN AC BC ≤+ C .()12MN AC BC =+ D .()12MN AC BC <+ 二、填空题7.在四面体ABCD 中,M ,N 分别是面△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________.8.如以下图所示,四个正方体中,A ,B 为正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,能得到AB//面MNP 的图形的序号的是①②③④9.正方体ABCD -A 1B 1C 1D 1中,E 为DD 1中点,则BD 1和平面ACE 位置关系是.三、解答题10.如图,正三棱柱111C B A ABC -的底面边长是2,侧棱长是3,D 是AC 的中点.求证://1C B 平面BD A 1.11.如图,在平行六面体ABCD -A 1B 1C 1D 1中,E ,M ,N ,G 分别是AA 1,CD ,CB ,CC 1的中点, 求证:〔1〕MN //B 1D 1;〔2〕AC 1//平面EB 1D 1;〔3〕平面EB 1D 1//平面BDG . B一、选择题1.α,β是两个不重合的平面,a ,b 是两条不同直线,在以下条件下,可判定α∥β的是〔 〕A .α,β都平行于直线a ,bB .α有三个不共线点到β的距离相等C .a ,b 是α两条直线,且a ∥β,b ∥βD .a ,b 是两条异面直线且a ∥α,b ∥α,a ∥β,b ∥β2.两条直线a ,b 满足a ∥b ,b α,则a 与平面α的关系是〔 〕A .a ∥αB .a 与α相交C .a 与α不相交D .a α3.设,a b 表示直线,,αβ表示平面,P 是空间一点,下面命题中正确的选项是〔 〕A .a α⊄,则//a αB .//a α,b α⊂,则//a bC .//,,a b αβαβ⊂⊂,则//a bD .,,//,//P a P a βααβ∈∈,则a β⊂4.一条直线假设同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是〔 〕A.异面B.相交C.平行D.不能确定5.以下四个命题中,正确的选项是〔 〕①夹在两条平行线间的平行线段相等;②夹在两条平行线间的相等线段平行;③如果一条直线和一个平面平行,则夹在这条直线和平面间的平行线段相等;④如果一条直线和一个平面平行,则夹在这条直线和平面间的相等线段平行A .①③B .①②C .②③D .③④6.a ,b 是两条异面直线,A 是不在a ,b 上的点,则以下结论成立的是A .过A 有且只有一个平面平行于a ,bB .过A 至少有一个平面平行于a ,bC .过A 有无数个平面平行于a ,bD .过A 且平行a ,b 的平面可能不存在二、填空题7.a ,b ,c为三条不重合的直线,α,β,γ为三个不重合的平面,直线均不在平面,给出六个命题:其中正确的命题是________________.〔将正确的序号都填上〕8.设平面α∥β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于S ,假设AS =18,BS =9,CD =34,则CS =_____________.9.如图,正四棱柱ABCD-A 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,DD 1,DC 中点,N 是BC 中点,点M 在四边形EFGH 及其部运动,则M 满足时,有MN ∥平面B 1BD D 1.三、解答题10.如图,在正四棱锥P ABCD -中,PA AB a ==,点E 在棱PC 上. 问点E 在何处时,//PA EBD 平面,并加以证明.11.如以下图,设P 为长方形ABCD 所在平面外一点,M ,N 分别为AB ,PD 上的点,且MB AM =NPDN ,求证:直线MN ∥平面PBC . C1.平面两正方形ABCD 与ABEF ,点M ,N 分别在对角线AC ,FB 上,且AM:MC=FN:NB ,沿AB 折起,使得∠DAF =900(1)证明:折叠后MN//平面CBE ;〔2〕假设AM:MC =2:3,在线段AB 上是否存在一点G ,使平面MGN //平面CBE "假设存在,试确定点G 的位置.2.设平面α∥平面β,AB 、CD 是两条异面直线,M ,N 分别是AB ,CD 的中点,且A ,C ∈α,B ,D ∈β,求证:MN ∥平面α.参考答案A一、选择题1.D【提示】当l =⋂βα时,α有无数多条直线与交线l 平行,同时这些直线也与平面β平行.故A ,B ,C 均是错误的2.C【提示】棱AC ,BD 与平面EFG 平行,共2条.3.C【提示】//,,a b αα⊂则//a b 或,a b 异面;所以A 错误;//,//,a b αα则//a b 或,a b 异面或,a b 相交,所以B 错误;//,,a b ααβ=则//a b 或,a b 异面,所以D 错误;//,//a c b c ,则//a b ,这是公理4,所以C 正确.4.B【提示】假设直线m 不平行于平面α,且m ⊄α,则直线m 于平面α相交,α不存在与m 平行的直线.5.B【提示】②③④错误.②过平面外一点有且只有一个平面和这个平面平行,有无数多条直线与它平行.③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上.6. D【提示】此题可利用空间中的平行关系,构造三角形的两边之和大于第三边.二、填空题7.平面ABC ,平面ABD【提示】连接AM 并延长,交CD 于E ,连结BN 并延长交CD 于F ,由重心性质可知,E 、F 重合为一点,且该点为CD 的中点E ,由MA EM =NB EN =21得MN ∥AB .因此,MN ∥平面ABC 且MN ∥平面ABD . 8.①③【提示】对于①,面MNP//面AB,故AB//面MNP.对于③,MP//AB,故AB//面MNP,对于②④,过AB 找一个平面与平面MNP 相交,AB 与交线显然不平行,故②④不能推证AB//面MNP.9.平行【提示】连接BD 交AC 于O ,连OE ,∴OE ∥B D 1,OEC 平面ACE ,∴B D 1∥平面ACE.三、解答题10.证明:设1AB 与B A 1相交于点P ,连接PD ,则P 为1AB 中点,D 为AC 中点,∴PD//C B 1.又 PD ⊂平面B A 1D ,∴C B 1//平面B A 1 D11.证明:〔1〕 M 、N 分别是CD 、CB 的中点,∴MN//BD又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形.所以BD//B 1D 1.又MN//BD ,从而MN//B 1D 1〔2〕〔法1〕连A 1C 1,A 1C 1交B 1D 1与O 点四边形A 1B 1C 1D 1为平行四边形,则O 点是A 1C 1的中点E 是AA 1的中点,∴EO 是∆AA 1C 1的中位线,EO//AC 1.AC 1⊄面EB 1D 1 ,EO ⊂面EB 1D 1,所以AC 1//面EB 1D 1〔法2〕作BB 1中点为H 点,连接AH 、C 1H ,E 、H 点为AA 1、BB 1中点,所以EH //C 1D 1,则四边形EHC 1D 1是平行四边形,所以ED 1//HC 1又因为EA //B 1H ,则四边形EAHB 1是平行四边形,所以EB 1//AHAH ⋂HC 1=H ,∴面AHC 1//面EB 1D 1.而AC 1⊂面AHC 1,所以AC 1//面EB 1D 1 〔3〕因为EA //B 1H ,则四边形EAHB 1是平行四边形,所以EB 1//AH因为AD //HG ,则四边形ADGH 是平行四边形,所以DG//AH ,所以EB 1//DG 又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形. 所以BD//B 1D 1.BD ⋂DG=G ,∴面EB 1D 1//面BDGB一、选择题1.D【提示】A 错,假设a ∥b ,则不能断定α∥β;B 错,假设A ,B ,C 三点不在β的同一侧,则不能断定α∥β;C 错,假设a∥b,则不能断定α∥β;D 正确.2.C【提示】假设直线a ,b 满足a ∥b ,b α,则a ∥α或a α3.D【提示】根据面面平行的性质定理可推证之.4.C【提示】设α∩β=l ,a ∥α,a ∥β,过直线a 作与α、β都相交的平面γ,记α∩γ=b ,β∩γ=c ,则a ∥b 且a ∥c ,∴b ∥c .又b ⊂α,α∩β=l ,∴b ∥l .∴a ∥l .5.A【提示】6. D【提示】过点A 可作直线a ′∥a ,b ′∥b ,则a ′∩b ′=A ,∴a ′,b ′可确定一个平面,记为α.如果a ⊄α,b ⊄α,则a ∥α,b ∥α.由于平面α可能过直线a 、b 之一,因此,过A 且平行于a 、b 的平面可能不存在.二、填空题7.①④⑤⑥8.68或368 【提示】如图〔1〕,由α∥β可知BD ∥AC ,∴SA SB =SC SD ,即189=SC SC 34-,∴SC =68. 如图〔2〕,由α∥β知AC ∥BD ,∴SB SA =SD SC =SC CD SC -,即918=SCSC -34. ∴SC =368. 9.M ∈HF【提示】易证平面NHF ∥平面BD D 1B 1,M 为两平面的公共点,应在交线HF 上.三、解答题 10.解:当E 为PC 中点时,//PA EBD 平面.证明:连接AC ,且AC BD O =,由于四边形ABCD 为正方形,∴O 为AC 的中点,又E 为中点,∴OE 为△ACP 的中位线,∴//PA EO ,又PA EBD ⊄平面,∴//PA EBD 平面.11.证法一:过N 作NR ∥DC 交PC 于点R ,连接RB ,依题意得NR NR DC -=NP DN =MBAM =MB MB AB -=MB MB DC -⇒NR =MB .∵NR ∥DC ∥AB ,∴四边形MNRB 是平行四边形.∴MN ∥RB .又∵RB 平面PBC ,∴直线MN ∥平面PBC . 证法二:过N 作NQ ∥AD 交PA 于点Q ,连接QM ,∵MB AM =NP DN =QPAQ ,∴QM ∥PB .又NQ ∥AD ∥BC ,∴平面MQN ∥平面PBC .∴直线MN ∥平面PBC .C1.〔1〕证明:设直线AN 与BE 交与点H ,连接CH ,ANF ∆ ∽HNB ∆,∴NHAN NB FN =. 又NB FN MC AM =,则NH AN =MCAM ,∴MN//CH. 又CBE CBE MN 平面,平面⊂⊄CH ,∴MN//平面CBE.(2)解:存在,过M 作MG ⊥AB,垂足为G ,则MG//BC, ∴MG//平面CBE,又MN//平面CBE ,M MN MG =⋂,平面MGN//平面CBE.即G 在AB 线上,且AG:GB=AM:MC=2:32.证明:连接BC ,AD ,取BC 的中点E ,连接ME 、NE ,则ME 是△BAC 的中位线,故ME ∥AC.ME ⊄α,∴ME ∥α.同理可证,NE ∥BD.又α∥β,设CB 与DC 确定的平面BCD 与平面α交于直线CF ,则CF ∥BD ,∴NE ∥CF. 而NE ⊄平面α,CF ⊂α,∴NE ∥α.O F A B CD P E又ME ∩NE=E ,∴平面MNE ∥α,而MN ⊂平面MNE ,∴MN ∥平面α.一、选择题1.以下条件中,能判断两个平面平行的是( )A .一个平面的一条直线平行于另一个平面;B .一个平面的两条直线平行于另一个平面C .一个平面有无数条直线平行于另一个平面D .一个平面任何一条直线都平行于另一个平面2.E ,F ,G 分别是四面体ABCD 的棱BC ,CD ,DA 的中点,则此四面体中与过E ,F ,G 的截面平行的棱的条数是A .0B .1C .2D .33. 直线,a b c ,及平面αβ,,使//a b 成立的条件是〔 〕A .//,a b αα⊂B .//,//a b ααC .//,//a c b cD .//,a b ααβ=4.假设直线m 不平行于平面α,且m ⊄α,则以下结论成立的是〔 〕A .α的所有直线与m 异面B .α不存在与m 平行的直线C .α存在唯一的直线与m 平行D .α的直线与m 都相交5.以下命题中,假命题的个数是〔 〕① 一条直线平行于一个平面,这条直线就和这个平面的任何直线不相交;② 过平面外一点有且只有一条直线和这个平面平行;③ 过直线外一点有且只有一个平面和这条直线平行;④ 平行于同一条直线的两条直线和同一平面平行;⑤a 和b 异面,则经过b 存在唯一一个平面与α平行A .4B .3C .2D .16.空间四边形ABCD 中,,M N 分别是,AB CD 的中点,则以下判断正确的选项是〔 〕A .()12MN AC BC ≥+B .()12MN AC BC ≤+ C .()12MN AC BC =+ D .()12MN AC BC <+ 二、填空题7.在四面体ABCD 中,M ,N 分别是面△ACD ,△BCD 的重心,则四面体的四个面中与MN 平行的是________.8.如以下图所示,四个正方体中,A ,B 为正方体的两个顶点,M ,N ,P 分别为其所在棱的中点,能得到AB//面MNP 的图形的序号的是①②③④9.正方体ABCD -A 1B 1C 1D 1中,E 为DD 1中点,则BD 1和平面ACE 位置关系是.三、解答题10.如图,正三棱柱111C B A ABC -的底面边长是2,侧棱长是3,D 是AC 的中点.求证://1C B 平面BD A 1.11.如图,在平行六面体ABCD -A 1B 1C 1D 1中,E ,M ,N ,G 分别是AA 1,CD ,CB ,CC 1的中点, 求证:〔1〕MN //B 1D 1;〔2〕AC 1//平面EB 1D 1;〔3〕平面EB 1D 1//平面BDG .B一、选择题1.α,β是两个不重合的平面,a ,b 是两条不同直线,在以下条件下,可判定α∥β的是〔 〕A .α,β都平行于直线a ,bB .α有三个不共线点到β的距离相等C .a ,b 是α两条直线,且a ∥β,b ∥βD .a ,b 是两条异面直线且a ∥α,b ∥α,a ∥β,b ∥β2.两条直线a ,b 满足a ∥b ,b α,则a 与平面α的关系是〔 〕A .a ∥αB .a 与α相交C .a 与α不相交D .a α3.设,a b 表示直线,,αβ表示平面,P 是空间一点,下面命题中正确的选项是〔 〕A .a α⊄,则//a αB .//a α,b α⊂,则//a bC .//,,a b αβαβ⊂⊂,则//a bD .,,//,//P a P a βααβ∈∈,则a β⊂4.一条直线假设同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是〔 〕A.异面B.相交C.平行D.不能确定5.以下四个命题中,正确的选项是〔 〕①夹在两条平行线间的平行线段相等;②夹在两条平行线间的相等线段平行;③如果一条直线和一个平面平行,则夹在这条直线和平面间的平行线段相等;④如果一条直线和一个平面平行,则夹在这条直线和平面间的相等线段平行A .①③B .①②C .②③D .③④6.a ,b 是两条异面直线,A 是不在a ,b 上的点,则以下结论成立的是A .过A 有且只有一个平面平行于a ,bB .过A 至少有一个平面平行于a ,bC .过A 有无数个平面平行于a ,bD .过A 且平行a ,b 的平面可能不存在二、填空题7.a ,b ,c为三条不重合的直线,α,β,γ为三个不重合的平面,直线均不在平面,给出六个命题:其中正确的命题是________________.〔将正确的序号都填上〕8.设平面α∥β,A ,C ∈α,B ,D ∈β,直线AB 与CD 交于S ,假设AS =18,BS =9,CD =34,则CS =_____________.9.如图,正四棱柱ABCD-A 1B 1C 1D 1中,E ,F ,G ,H 分别是棱CC 1,C 1D 1,DD 1,DC 中点,N 是BC 中点,点M 在四边形EFGH 及其部运动,则M 满足时,有MN ∥平面B 1BD D 1.三、解答题10.如图,在正四棱锥P ABCD -中,PA AB a ==,点E 在棱PC上. 问点E 在何处时,//PA EBD 平面,并加以证明.11.如以下图,设P 为长方形ABCD 所在平面外一点,M ,N 分别为AB ,PD 上的点,且MB AM =NP DN,求证:直线MN ∥平面PBC .C1.平面两正方形ABCD 与ABEF ,点M ,N 分别在对角线AC ,FB 上,且AM:MC=FN:NB ,沿AB 折起,使得∠DAF =900(1)证明:折叠后MN//平面CBE ;〔2〕假设AM:MC =2:3,在线段AB 上是否存在一点G ,使平面MGN //平面CBE "假设存在,试确定点G 的位置.2.设平面α∥平面β,AB 、CD 是两条异面直线,M ,N 分别是AB ,CD 的中点,且A ,C ∈α,B ,D ∈β,求证:MN ∥平面α.参考答案A一、选择题1.D【提示】当l =⋂βα时,α有无数多条直线与交线l 平行,同时这些直线也与平面β平行.故A ,B ,C 均是错误的2.C【提示】棱AC ,BD 与平面EFG 平行,共2条.3.C【提示】//,,a b αα⊂则//a b 或,a b 异面;所以A 错误;//,//,a b αα则//a b 或,a b 异面或,a b 相交,所以B 错误;//,,a b ααβ=则//a b 或,a b 异面,所以D 错误;//,//a c b c ,则//a b ,这是公理4,所以C 正确.4.B【提示】假设直线m 不平行于平面α,且m ⊄α,则直线m 于平面α相交,α不存在与m 平行的直线.5.B【提示】②③④错误.②过平面外一点有且只有一个平面和这个平面平行,有无数多条直线与它平行.③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上.6. D【提示】此题可利用空间中的平行关系,构造三角形的两边之和大于第三边.二、填空题7.平面ABC ,平面ABD【提示】连接AM 并延长,交CD 于E ,连结BN 并延长交CD 于F ,由重心性质可知,E 、F 重合为一点,且该点为CD 的中点E ,由MA EM =NB EN =21得MN ∥AB .因此,MN ∥平面ABC 且MN ∥平面ABD . 8.①③【提示】对于①,面MNP//面AB,故AB//面MNP.对于③,MP//AB,故AB//面MNP,对于②④,过AB 找一个平面与平面MNP 相交,AB 与交线显然不平行,故②④不能推证AB//面MNP.9.平行【提示】连接BD 交AC 于O ,连OE ,∴OE ∥B D 1,OEC 平面ACE ,∴B D 1∥平面ACE.三、解答题10.证明:设1AB 与B A 1相交于点P ,连接PD ,则P 为1AB 中点,D 为AC 中点,∴PD//C B 1.又 PD ⊂平面B A 1D ,∴C B 1//平面B A 1 D11.证明:〔1〕 M 、N 分别是CD 、CB 的中点,∴MN//BD又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形.所以BD//B 1D 1.又MN//BD ,从而MN//B 1D 1〔2〕〔法1〕连A 1C 1,A 1C 1交B 1D 1与O 点四边形A 1B 1C 1D 1为平行四边形,则O 点是A 1C 1的中点E 是AA 1的中点,∴EO 是∆AA 1C 1的中位线,EO//AC 1.AC 1⊄面EB 1D 1 ,EO ⊂面EB 1D 1,所以AC 1//面EB 1D 1〔法2〕作BB 1中点为H 点,连接AH 、C 1H ,E 、H 点为AA 1、BB 1中点,所以EH //C 1D 1,则四边形EHC 1D 1是平行四边形,所以ED 1//HC 1又因为EA //B 1H ,则四边形EAHB 1是平行四边形,所以EB 1//AHAH ⋂HC 1=H ,∴面AHC 1//面EB 1D 1.而AC 1⊂面AHC 1,所以AC 1//面EB 1D 1 〔3〕因为EA //B 1H ,则四边形EAHB 1是平行四边形,所以EB 1//AH因为AD //HG ,则四边形ADGH 是平行四边形,所以DG//AH ,所以EB 1//DG 又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形. 所以BD//B 1D 1.BD ⋂DG=G ,∴面EB 1D 1//面BDGB一、选择题1.D【提示】A 错,假设a ∥b ,则不能断定α∥β;B 错,假设A ,B ,C 三点不在β的同一侧,则不能断定α∥β;C 错,假设a∥b,则不能断定α∥β;D 正确.2.C【提示】假设直线a ,b 满足a ∥b ,b α,则a ∥α或a α3.D【提示】根据面面平行的性质定理可推证之.4.C【提示】设α∩β=l ,a ∥α,a ∥β,过直线a 作与α、β都相交的平面γ,记α∩γ=b ,β∩γ=c ,则a ∥b 且a ∥c ,∴b ∥c .又b ⊂α,α∩β=l ,∴b ∥l .∴a ∥l .5.A【提示】6. D【提示】过点A 可作直线a ′∥a ,b ′∥b ,则a ′∩b ′=A ,∴a ′,b ′可确定一个平面,记为α.如果a ⊄α,b ⊄α,则a ∥α,b ∥α.由于平面α可能过直线a 、b 之一,因此,过A 且平行于a 、b 的平面可能不存在.二、填空题7.①④⑤⑥8.68或368 【提示】如图〔1〕,由α∥β可知BD ∥AC ,∴SA SB =SC SD ,即189=SC SC 34-,∴SC =68. 如图〔2〕,由α∥β知AC ∥BD ,∴SB SA =SD SC =SC CD SC -,即918=SCSC -34. ∴SC =368. 9.M ∈HF【提示】易证平面NHF ∥平面BD D 1B 1,M 为两平面的公共点,应在交线HF 上.三、解答题 10.解:当E 为PC 中点时,//PA EBD 平面.证明:连接AC ,且AC BD O =,由于四边形ABCD 为正方形,∴O 为AC 的中点,又E 为中点,∴OE 为△ACP 的中位线,∴//PA EO ,又PA EBD ⊄平面,∴//PA EBD 平面.11.证法一:过N 作NR ∥DC 交PC 于点R ,连接RB ,依题意得NR NR DC -=NP DN =MBAM =MB MB AB -=MB MB DC -⇒NR =MB .∵NR ∥DC ∥AB ,∴四边形MNRB 是平行四边形.∴MN ∥RB .又∵RB 平面PBC ,∴直线MN ∥平面PBC . 证法二:过N 作NQ ∥AD 交PA 于点Q ,连接QM ,∵MB AM =NP DN =QPAQ ,∴QM ∥PB .又NQ ∥AD ∥BC ,∴平面MQN ∥平面PBC .∴直线MN ∥平面PBC .C1.〔1〕证明:设直线AN 与BE 交与点H ,连接CH ,ANF ∆ ∽HNB ∆,∴NHAN NB FN =. 又NB FN MC AM =,则NH AN =MCAM ,∴MN//CH. 又CBE CBE MN 平面,平面⊂⊄CH ,∴MN//平面CBE.(2)解:存在,过M 作MG ⊥AB,垂足为G ,则MG//BC, ∴MG//平面CBE,又MN//平面CBE ,M MN MG =⋂,平面MGN//平面CBE.即G 在AB 线上,且AG:GB=AM:MC=2:32.证明:连接BC ,AD ,取BC 的中点E ,连接ME 、NE ,则ME 是△BAC 的中位线,故ME ∥AC.ME ⊄α,∴ME ∥α.同理可证,NE ∥BD.又α∥β,设CB 与DC 确定的平面BCD 与平面α交于直线CF ,则CF ∥BD ,∴NE ∥CF. 而NE ⊄平面α,CF ⊂α,∴NE ∥α.O F A B CD P E又ME∩NE=E,∴平面MNE∥α,而MN⊂平面MNE,∴MN∥平面α.。
专题08 空间直线与平面的平行问题-高中数学专项训练测试卷(解析版)

专题08空间直线与平面的平行问题知识点1直线与平面平行的判定定理:1、文字语言:如果平面外一条直线与此平面内的一条直线平行,该直线与此平面平行2、符号语言:a⊄α,b⊂α,a∥b⇒a∥α.3、图形语言:知识点2直线与平面平行的性质定理1、文字语言:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行.2、符号语言:a∥α,a⊂β,α∩β=b⇒a∥b.3、图形语言:知识点3平面与平面平行的判定定理1、文字语言:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行(简记为“线面平行⇒面面平行”)2、符号语言:a⊂β,b⊂β,a∩b=P,且a∥α,b∥α⇒β∥α.3、图形:4、判定定理推论:如果一个平面内两条相交直线分别平行于另一个平面内的两条相交直线,则这两个平面平行.知识点4平面与平面平行的性质定理1、文字语言:如果两个平行平面同时和第三个平面相交,那么它们的交线平行2、符号语言:α∥β,α∩γ=a,β∩γ=b⇒a∥b.3、图形:4、平面与平面平行其他常用性质推论(1)平行于同一个平面的两个平面平行.(2)垂直于同一条直线的两个平面平行.(3)如果两个平面平行,那么其中一个平面内的直线平行于另一个平面.(4)如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面.知识点5三种平行关系的转化考点1平行关系的判定【例1】(2023春·全国·高一专题练习)已知a ,b ,c 为三条不同的直线,,αβγ为三个不同的平面,则下列说法正确的是()A .若//a b ,b α⊂,则//a αB .若a α⊂,b β⊂,//a b ,则//αβC .若//αβ,//a α,则//a βD .若a αβ⋂=,b βγ= ,c αγ⋂=,//a b ,则//b c【答案】D【解析】若//a b ,b α⊂,则//a α或a α⊂,故A 选项错误;若a α⊂,b β⊂,//a b ,则//αβ或α与β相交,故B 选项错误.若//αβ,//a α,则//a β或a β⊂,故C 选项错误;若a αβ⋂=,b βγ= ,c αγ⋂=,//a b ,则//b c ,正确,证明如下://a b ,a γ⊄,b γ⊂,//a γ∴,又a α⊂,且c αγ⋂=,//a c ∴,则//b c ,故D 选项正确;故选:D .【变式1-1】(2023·全国·高一专题练习)已知直线a ,b ,c ,平面α.下述命题中,真命题的个数是()(1)若a 与b 是异面直线,b 与c 是异面直线,则a 与c 是异面直线;(2)若a b ,b c P ,则a c P ;(3)若a b ,b α⊂,则a αP ;(4)若a αP ,b αP ,则a b .A .1B .2C .3D .4【答案】A【解析】(1)若a 与b 是异面直线,b 与c 是异面直线,则a 与c 可能是异面直线,也可能不是异面直线,故命题错误;(2)由线线平行关系的传递性可知,命题正确;(3)由线面平行的判断定理可得a αP 或者a α⊂,命题错误;(4)由线面平行的概念可知,a 与b 相交,或者平行或者a 与b 异面,故命题错误.综上所述,真命题的个数是1.故选:A.【变式1-2】(2023·全国·高一专题练习)已知a ,b ,c 为三条不重合的直线,α,β为两个不重合的平面.①a //c ,b //c ⇒a //b ;②a //β,b //β⇒a //b ;③a //c ,c //α⇒a //α;④a //β,a //α⇒α//β;⑤a ⊄α,b ⊂α,a //b ⇒a //α.其中正确的命题是()A .①⑤B .①②C .②④D .③⑤【答案】A【解析】对于①,由平行的传递性公理,则正确;对于②,由//a β,b β//,则,a b 共面或异面,故错误;对于③,由//a c ,//c α,则//a α或a α⊂,故错误;对于④,由//a β,//a α,则,αβ平行或相交,故错误;对于⑤,由a α⊄,b α⊂,//a b ,根据线面平行判定定理,可得//a α,故正确.故选:A.【变式1-3】(2023·全国·高一专题练习)已知,m n 是不同的直线,,αβ是不同的平面,下列命题中真命题为()A .若,m n αα⊂∥,则m n∥B .若,m m αβ∥∥,则αβ∥C .若,m αββ⊂∥,则m αD .若,m αβα∥∥,则m β【答案】C【解析】由题知,不妨将,m n ,,αβ放在长方体中可知,关于选项A,如图所示可知A 错误,关于选项B,如图所示可知B 错误,关于选项D,如图所示可知D 错误,根据面面平行的性质定理可知,选项C 正确.故选:C【变式1-4】(2022春·黑龙江·高一哈九中校考期中)设a ,b 是两条不同的直线,α,β,γ是三个不同的平面,①a α⊂、b β⊂,a β∥,b αP ;②αγ∥,βγ∥;③αγ⊥,βγ⊥;④a α⊥,b β⊥,a b .则αβ∥的充分条件可以是()A .①②B .①④C .②③D .②④【答案】D 【解析】因为a ,b 是两条不同的直线,α,β,γ是三个不同的平面,①a α⊂、b β⊂,a β∥,b αP ,则α与β平行或相交,故①错误;②αγ∥,βγ∥,则αβ∥,故②正确;③αγ⊥,βγ⊥,则α与β平行或相交,故③错误;④a α⊥,b β⊥,a b ,则αβ∥,故④正确;综上②④正确,故选:D【变式1-5】(2023·全国·高一专题练习)如图,点A ,B ,C ,M ,N 为正方体的顶点或所在棱的中点,则下列各图中,不满足直线//MN 平面ABC 的是()A .B .C .D .【答案】D【解析】对于A ,由正方体的性质可得////MN EF AC ,可得直线//MN 平面ABC ,能满足;对于B,作出完整的截面ADBCEF,由正方体的性质可得//MN AD,可得直线//MN平面ABC,能满足;对于C,作出完整的截面ABCD,由正方体的性质可得//BDMN,可得直线//MN平面ABC,能满足;对于D,作出完整的截面,如下图ABNMHC,可得MN在平面ABC内,不能得出平行,不能满足.故选:D.考点2线线平行的证明中,底面ABCD为矩【例2】(2023·全国·高一专题练习)如图,四棱锥P ABCD形,E为棱PB上一点(不与P、B重合),平面ADE交棱PC于点F.求证://AD EF.【答案】证明见解析【解析】因为四边形ABCD 为矩形,所以,//AD BC ,因为AD ⊄平面PBC ,BC ⊂平面PBC ,所以,//AD 平面PBC ,因为AD ⊂平面ADE ,平面ADE 平面PBC EF =,所以,//AD EF .【变式2-1】(2023·全国·高一专题练习)在正四棱锥P ABCD -中,已知2AB =,3PA =,E ,G 分别为PB ,PD 的中点,平面AEG 平面ABCD l =.求证://EG l ;【答案】证明见解析【解析】证明:连接BD ,∵E ,G 分别为PB ,PD 的中点,即EG 是三角形ABD 的中位线,∴//EG BD又∵EG ⊄平面ABCD ,BD ⊂平面ABCD ,∴//EG 平面ABCD ,又∵EG ⊂平面AGE ,平面AGE 平面ABCD l =,∴//EG l【变式2-2】(2023·全国·高一专题练习)如图所示,在四棱锥P ABCD -中,底面ABCD 为正方形,E 为侧棱PC 的中点.设经过A 、B 、E 三点的平面交PD 于F ,证明:F 为PD 的中点.【答案】证明见解析【解析】如下图所示:因为四边形ABCD 为矩形,则//CD AB ,因为CD ⊄平面ABE ,AB ⊂平面ABE ,所以,//CD 平面ABE ,因为CD ⊂平面PCD ,平面PCD 平面ABE EF =,所以,//EF CD ,又因为E 为PC 的中点,所以,点F 为PD 的中点.【变式2-3】(2023·全国·高一专题练习)如图,四棱柱1111ABCD A B C D -的底面ABCD 为菱形,60ABC ∠=︒,其中侧面11B BCC 为平行四边形,,E F 分别为11,BC B C 的中点,P 在线段AE 上,且满足:1:2AP PE =,过11B C 和点P 的平面交AB 于G ,交DC 于H .证明:11//B C GH ;【答案】证明见解析【解析】由题意四棱柱1111ABCD A B C D -中,平面ABCD //平面1111D C B A ,因为过11B C 和点P 的平面交AB 于G ,交DC 于H ,则,G H ∈平面ABCD ,设过11B C 和P 的平面为α,则平面ABCD GH α= ,平面111111A B C D B C α= ,11B C ∴//GH .【变式2-4】(2023·全国·高一专题练习)如图,⊥AE 平面ABCD ,//BF 平面ADE ,//CF AE ,求证://AD BC【答案】证明见解析【解析】由题意//CF AE ,CF ⊄平面ADE ,AE ⊂平面ADE ,∴//CF 平面ADE ,又//BF 平面ADE ,BF CF F ⋂=,∴平面//BCF 平面ADE ,而平面BCF ⋂平面ABCD AD =,平面ADE 平面ABCD BC =,∴//AD BC .考点3线面平行的证明【例3】(2023·全国·高一专题练习)在直三棱柱111ABC A B C -中,3AC =,4BC =,15AA AB ==,D 是AB 的中点.(1)求三棱锥1D BCB -的体积;(2)求证:1//AC 平面1CDB ;【答案】(1)5;(2)证明见解析【解析】(1)因为3AC =,4BC =,15AA AB ==,所以222AC BC AB +=,即AC BC ⊥,又D 是AB 的中点,所以111111134522325D BCB B DBC ABC B V V ---===⨯⨯⨯⨯⨯=;(2)设1B C 与1BC 相交于点E ,连接ED ,在1C AB △中,D 为AB 的中点,E 为1C B 的中点,所以1//AC DE ,因为1AC ⊄平面1CDB ,DE ⊂平面1CDB ,所以1//AC 平面1CDB ;【变式3-1】(2023·全国·高一专题练习)如图所示的四棱锥P ABCD -中,底面ABCD 是梯形,//AB CD ,2AD BD ==,π3BDC ∠=,3BC =PD ⊥平面ABCD ,2FC PF =.证明://AP 平面BDF ;【答案】证明见解析【解析】证明://AB CD Q ,π3DBA BDC ∴∠=∠=,AD BD = ,DAB ∴ 为等边三角形,2AB DB ∴==,在BDC 中,2DB =,π3BDC ∠=,23BC =由余弦定理得2222cos BC BD CD BD CD BDC =+∠-⋅⋅,即2221(23)2222CD CD =+-⨯⨯⨯,4CD ∴=,如图,连接AC 交BD 于点E ,连接EF ,//AB CD Q ,ABE CDE ∴△∽△,::1:2AE EC AB CD ∴==,:1:2PF FC = ,//EF AP ∴,又AP ⊂/平面BDF ,EF ⊂平面BDF ,//AP ∴平面BDF 【变式3-2】(2023·全国·高一专题练习)在三棱柱111ABC A B C -中,AB AC ⊥,1B C ⊥平面ABC ,E 、F 分别是棱AC 、11A B 的中点,求证://EF 平面11BCC B ;【答案】证明见解析【解析】设G 为11B C 的中点,连接FG ,GC ,因为点E ,F ,G 分别为AC ,11A B ,11B C 的中点,所以11FG A C ∥且1112FG A C =,11EC A C ∥,111122EC AC A C ==,所以EC FG ∥,且EC FG =,所以四边形ECGF 是平行四边形,所以EF CG ∥,又因为CG ⊂平面11BCC B ,EF ⊄平面11BCC B ,所以//EF 平面11BCC B .【变式3-3】(2023·全国·高一专题练习)如图,在正方体1111ABCD A B C D -中,S 是11B D 的中点,E ,F ,G 分别是BC ,DC ,SC 的中点,求证:(1)直线EG ∥平面11BDD B ;(2)H 为线段1DD 上一点,且13DD DH =,求证:BH ∥平面EFG【答案】(1)证明见解析;(2)证明见解析【解析】(1)连接SB ,在三角形SBC 中,G 是SC 的中点,E 是BC 的中点,所以EG SB ∥,EG ⊄平面11BDD B ,SB ⊂平面11BDD B ,所以EG ∥平面11BDD B (2)连接SD ,F ,G 分别是DC ,SC 的中点,FG SD∴∥又FG ⊄ 平面11BDD B ,SD ⊂平面11BDD B ,FG ∴∥平面11BDD B 由(1)得EG ∥平面11BDD B ,FG ⊂平面EFG ,EG ⊂平面EFG ,EG FG G= ∴平面EFG ∥平面11BDD B 又BH ⊂ 平面11BDD B ,BH ∴∥平面EFG .【变式3-4】(2023·全国·高一专题练习)如图,四棱台1111ABCD A B C D -中,底面ABCD 为直角梯形,//AB CD ,AB BC ⊥,1112224AB BC CD DD D C ====,P 为棱1CC 的中点,证明://AC 平面1B DP .【答案】证明见解析【解析】在四棱台1111ABCD A B C D -中,在BB 1上取点Q ,使1113B Q BB =,连BD 交AC 于点O ,连接OQ ,如图,延长CC 1,BB 1交于点V ,由111112B C D C BC DC ==,则1113VB B B B Q ==,11122VC C C C P CP ===,则113VB VP PC B Q ==,即1//B P QC ,又QC ⊄平面1B DP ,1B P ⊂平面1B DP ,于是得//QC 平面1B DP ,在直角梯形ABCD 中,//AB CD ,则112B QDO CD OB AB QB ===,于是得1//OQ DB ,又OQ ⊄平面1B DP ,1DB ⊂平面1B DP ,则//OQ 平面1B DP ,又OQ QC Q ⋂=,,OQ QC ⊂平面OQC ,因此得平面1//B DP 平面OQC ,又AC ⊂平面OQC ,所以//AC 平面1B DP .考点4面面平行的证明【例4】(2023·高一课时练习)如图,在长方体1111ABCD A B C D -中,1,2AB AD ==,E ,F ,Q 分别为1,,AD AA BC 的中点,求证:平面//BEF 平面1A DQ .【答案】证明见解析【解析】因为E 是AD 的中点,Q 是BC 的中点,所以,ED BQ ED BQ =∥,所以四边形BEDQ 是平行四边形,所以BE DQ ∥.又因为BE ⊄平面1,A DQ DQ ⊂平面1A DQ ,所以BE ∥平面1A DQ .又因为F 是1A A 的中点,所以1EF A D ∥,因为EF ⊄平面11,A DQ A D ⊂平面1A DQ ,所以EF P 平面1A DQ .因为,BE EF E EF ⋂=⊂平面,BEF BE ⊂平面BEF ,所以平面BEF ∥平面1A DQ .【变式4-1】(2022·高一课时练习)如图所示,在三棱柱111ABC A B C -中,1D 、D 分别为11B C ,BC 的中点,求证:平面11//A BD 平面1AC D .【答案】证明见解析【解析】证明:在三棱柱111ABC A B C -中,四边形11B BCC 、11A ACC 为平行四边形,又1D 、D 分别为11B C ,BC 的中点,所以11//D C BD 且11D C BD =,所以四边形11D C DB 为平行四边形,所以11//D B DC ,因为1D B ⊄平面1AC D ,1DC ⊂平面1AC D ,所以1//D B 平面1AC D ,连接1AC 、1A C ,11A C AC M = ,再连接DM ,由四边形11A ACC 为平行四边形,所以M 为1A C 的中点,所以1//DM A B ,因为1A B ⊄平面1AC D ,DM ⊂平面1AC D ,所以1//A B 平面1AC D ,又11B A D B B = ,11,A B D B ⊂平面11BD A ,所以平面11//A BD 平面1AC D .【变式4-2】(2023春·全国·高一专题练习)如图,在正方体1111ABCD A B C D -中,E ,F ,H ,G 分别是棱''A B ,''A D ,''C D ,B C ''的中点.求证:平面//AEF 平面HGBD .【答案】证明见解析【解析】连接B D '',因为E ,F ,G ,H 分别是棱A B '',A D '',B C '',C D ''的中点,所以//EF B D '',//HG B D '',所以//EF HG ,又EF ⊂平面AEF ,HG ⊂平面AEF ,所以//HG 平面AEF ,连接AC BD O = ,连接A C ''交EF 于M ,交GH 于N ,交B D ''于O ',则12A M C N AO '''==,所以12C MN A ''=,又12AO AC =,AC A C ='',//AC A C '',所以四边形AONM 是平行四边形,所以//AM ON ,又AM ⊂平面AEF ,ON ⊂/平面AEF ,所以//ON 平面AEF ,又ON ⊂平面BGHD ,HG ⊂平面BGHD ,HG ON N ⋂=,所以平面//AEF 平面BGHD .【变式4-3】(2023·全国·高三专题练习)如图,四棱柱1111ABCD A B C D -的底面ABCD为正方形,O 为BD 的中点,124A A AB ==,求证:平面1A BD ∥平面11CD B 【答案】证明见解析【解析】因为四棱柱1111ABCD A B C D -的底面ABCD 为正方形,所以11A B ∥AB ,11A B AB =,AB ∥CD ,AB CD =,所以11A B ∥CD ,11A B CD =,所以四边形11A B CD 为平行四边形,所以1A D ∥1B C .又1A D ⊄平面11CD B ,1B C ⊂平面11CD B ,所以1A D ∥平面11CD B ,同理可证:1A B ∥平面11CD B .又111A D A B A ⋂=,1A D ⊂平面1A BD ,1A B ⊂平面1A BD所以平面1A BD ∥平面11CD B .考点5平行关系的探索性问题【例5】(2023·全国·高一专题练习)如图所示正四棱锥S ABCD -,2,2SA SB SC SD AB =====,P 为侧棱SD 上的点.且3SP PD =,求:侧棱SC 上是否存在一点E ,使得//BE 平面PAC .若存在,求SE EC的值;若不存在,试说明理由.【答案】在侧棱SC 上存在一点E ,使//BE 平面PAC ,满足2SE EC =【解析】在侧棱SC 上存在一点E ,使//BE 平面PAC ,满足2SE EC=.理由如下:取SD 中点为Q ,因为3SP PD =,则PQ PD =,过Q 作PC 的平行线交SC 于E ,连接BQ ,BE .在BDQ △中,有//BQ PO ,PO ⊂ 平面PAC ,⊄BQ 平面PAC ,//BQ ∴平面PAC ,由于2SQ QP =,∴2SE SQ EC QP ==.又由于//QE PC ,PC ⊂平面PAC ,QE ⊄平面PAC ,//QE ∴平面PAC ,BQ QE Q ⋂= ,∴平面//BEQ 平面PAC ,又BE ⊂平面BEQ ,//BE ∴平面PAC ,【变式5-1】(2022春·江苏盐城·高一盐城市伍佑中学校考阶段练习)如图,在正方体1111ABCD A B C D -中,E ,F ,G 分别是AB ,1CC ,AD 的中点.(1)求异面直线1B E 与BG 所成角的余弦值;(2)棱CD 上是否存在点T ,使得//AT 平面1B EF ?若存在,求出DT DC的值;若不存在,请说明理由.【答案】(1)25;(2)存在,14DT DC =.【解析】(1)取11A D 中点M ,连接1MB ,ME ,GE ,MG .因为1111ABCD A B C D -是正方体,M ,G 分别为11A D ,AD 的中点,所以1//BG B M ,所以1MB E ∠(或补角)为异面直线1B E 与BG 所成角.设正方体的棱长为2,则115MB B E ==6ME =所以12cos 5255MB E ∠==⨯⨯,即异面直线1B E 与BG 所成角的余弦值为25.(2)存在,且14DT DC =,证明如下:延长BC ,1B F 交于H ,连接EH 交DC 于K ,因为11//CC BB ,F 是1CC 的中点,所以C 为BH 中点.因为//CD AB ,所以//KC AB ,且1124KC EB CD ==,当14DT DC =时,//TK AE ,且TK AE =,即四边形AKET 为平行四边形,所以//AT EK ,即//AT EH ,又EH ⊂平面1B EF ,AT ⊄平面1B EF ,所以//AT 平面1B EF .【变式5-2】(2022秋·陕西西安·高一统考期末)如图,在四棱锥P ABCD -中,底面ABCD 是平行四边形,M 、N 、Q 分别为BC 、PA 、PB 的中点.(1)证明:平面//MNQ 平面PCD ;(2)在线段PD 上是否存在一点E ,使得//MN 平面ACE ?若存在,求出PE PD的值;若不存在,请说明理由.【答案】(1)证明见解析;(2)存在,12PE PD =.【解析】(1)∵ABCD 是平行四边形,M 、N 、Q 分别为BC 、PA 、PB 的中点,∴////NQ AB CD ,//MQ PC ,又NQ ⊄平面PCD ,CD ⊂平面PCD ,MQ ⊄平面PCD ,PC ⊂平面PCD ,∴//NQ 平面PCD ,//MQ 平面PCD ,∵NQ MQ Q = ,且NQ 、MQ Ì平面MNQ ,∴平面//MNQ 平面PCD .(2)存在点E 是线段PD 的中点,使得//MN 平面ACE ,且12PE PD =.证明如下:取PD 中点E ,连接NE 、CE ,∵N 、E 、M 分别是AP 、PD 、BC 的中点,∴11//,=22NE AD NE AD ,且//,=BC AD BC AD ,即11//,=22MC AD MC AD ,∴//,=NE MC NE MC ,∴四边形MCEN 是平行四边形,∴//MN CE ,∵MN ⊄平面ACE ,CE ⊂平面ACE ,∴//MN 平面ACE ,且12PE PD =.【变式5-3】(2022·全国·高三专题练习)如图所示,四边形ABCD 是平行四边形,PB ⊥平面ABCD ,MA ∥PB ,PB =2MA .在线段PB 上是否存在一点F ,使平面AFC ∥平面PMD ?若存在,请确定点F 的位置;若不存在,请说明理由.【答案】存在,点F 是PB 的中点,证明见解析【解析】当点F 是PB 的中点时,平面AFC ∥平面PMD ,证明如下:如图连接BD 与AC 交于点O ,连接FO ,∵四边形ABCD 是平行四边形,∴O 是BD 的中点,∴OF ∥PD .又OF ⊄平面PMD ,PD ⊂平面PMD ,∴OF ∥平面PMD .又MA ∥PB 且PB =2MA .∴PF ∥MA 且PF =MA ,∴四边形AFPM 是平行四边形,∴AF ∥PM .又AF ⊄平面PMD ,PM ⊂平面PMD ,∴AF ∥平面PMD .又AF ∩OF =F ,AF ⊂平面AFC ,OF ⊂平面AFC ,∴平面AFC ∥平面PMD .【变式5-4】(2022·全国·高三专题练习)在长方体1111ABCD A B C D -中,已知AB AD =,E 为AD 的中点,在线段11B C 上是否存在点F ,使得平面1//A AF 平面1ECC ?若存在,请加以证明,若不存在,请说明理由【答案】存在,证明见解析.【解析】存在,当点F 为线段11B C 的中点时,平面1A AF ∕∕平面1ECC ,证明:连接1,A F AF ,在长方体1111ABCD A B C D -中,11AA CC ∕∕,11AD B C ∕∕.又因为1CC ⊂平面1ECC ,1AA ⊂平面1ECC ,所以1AA ∕∕平面1ECC ,又E 为AD 的中点,F 为11B C 的中点,所以1AE FC ∕∕,且1AE FC =.故四边形1AEC F 为平行四边形,所以1AF EC ∕∕,又因为1EC ⊂平面1ECC ,AF ⊄平面1ECC ,所以AF ∕∕平面1ECC ,又因为1AF AA A = ,1AA ⊂平面1A AF ,AF ⊂平面1A AF ,所以平面1A AF ∕∕平面1ECC .考点6利用平行关系求解截面问题【例6】(2022春·辽宁沈阳·高一校联考期末)如图,在三棱柱111ABC A B C -中,过11A B 的截面与AC 交于点D ,与BC 交于点E ,该截面将三棱柱分成体积相等的两部分,则CD AC =()A .13B .12C .232D .312【答案】D【解析】由题可知平面11A B ED 与棱柱上,下底面分别交于11A B ,ED ,则11A B ∥ED ,ED AB ∥,显然111CDE C A B -是三棱台,设ABC 的面积为1,CDE 的面积为S ,三棱柱的高为h ,111(123h h S S ∴⋅⋅=+312S -=由CDE CAB ∽△△,可得3121CD S AC -==.故选:D.【变式6-1】(2022·高一课时练习)棱长为2的正方体1111ABCD A B C D -中,M 是棱1AA 的中点,过C 、M 、1D 作正方体的截面,则截面的面积是_________.【答案】92【解析】连接1A B ,设截面交棱AB 于点N ,连接MN 、CN ,在正方体1111ABCD A B C D -中,11//A D BC 且11A D BC =,则四边形11A BCD 为平行四边形,所以,11//A B CD ,因为平面11//AA B B 平面11CC D D ,平面1CMD 平面11AA B B MN =,平面1CMD 平面111CC D D CD =,所以,1//MN CD ,则1//MN A B ,M 为1AA 的中点,则N 为AB 的中点,由勾股定理可得222MN AM AN =+=15D M CN ==12CD =所以,四边形1CD MN 为等腰梯形,过点M 、N 分别在平面1CD MN 内作1ME CD ⊥、1NF CD ⊥,垂足分别为点E 、F ,由等腰梯形的性质可得1NCF MD E ∠=∠,1CN D M =,又因为190CFN D EM ∠=∠= ,所以,1CFN D EM △≌△,所以,1CF D E =,因为//MN EF ,ME EF ⊥,NF EF ⊥,则四边形MNFE 为矩形,所以,2EF MN =,所以,11222CD MN CF D E -===,则22322NF CN CF =-=,因此,截面面积为()1922EF CD NF+⋅=.【变式6-2】(2023春·全国·高一专题练习)如图,在正方体1111ABCD A B C D -中,S 是11B D 的中点,E ,F ,G 分别是BC ,DC ,SC 的中点.(1)求证:平面EFG //平面11BDD B ;(2)若正方体棱长为1,过A ,E ,1C 三点作正方体的截面,画出截面与正方体的交线,并求出截面的面积.【答案】(1)证明见解析;(262【解析】(1)证明:如下图所示,连接SB ,由EG 为△CSB 的中位线,可得//EG SB ,由EG ⊄平面11BDD B ,SB ⊂平面11BDD B ,可得EG //平面11BDD B ;由EF 为△CDB 的中位线,可得//EF DB ,由EF ⊄平面11BDD B ,DB ⊂平面11BDD B ,可得//EF 平面11BDD B ,又EF EG E = ,,EF EG ⊂面EFG ,可得平面//EFG 平面11BDD B ;(2)取11B C 的中点N ,连接1A N ,NE ,显然1111////,NE BB AA NE BB AA ==,所以1AENA 为平行四边形,可得1//AE A N ,1AE A N =,取11A D 的中点M ,连接1MC ,AM ,显然1111//,MA C N MA C N =,所以11A NC M 为平行四边形,可得11MC A N =,11//MC A N ,综上,截面1AEC M 为平行四边形,又1151421AE EC AM MC ====+,所以截面1AEC M 为菱形,截面的面积为1111632222AC ME ⨯⨯==.【变式6-3】(2022春·福建福州·高一福建省福州格致中学校考期末)一块三棱锥形木块如图所示,点G 是SAC 的重心,过点G 将木块锯开,使截面平行于侧面SBC .(1)画出截面与木块表面的交线,并说明理由;(2)若ABC为等边三角形,32SA SB SC ====,求夹在截面与平面SBC 之间的几何体的体积.【答案】(1)答案见解析;(2)196【解析】(1)过点G 作//EF SC 交,SA AC 于,E F 点,过点F 作//EH BS 交AB 于H ,则平面//SBC 平面EFH ,EFH △边所在直线即为所画线.理由如下:因为//EF SC ,EF ⊄平面SBC ,SC ⊂平面SBC ,所以//EF 平面SBC ,因为//EH BS ,EH ⊄平面SBC ,SB ⊂平面SBC ,所以//EH 平面SBC ,因为,,EF EH E EF EH =⊂ 平面EFH ,所以平面//SBC 平面EFH.(2)因为ABC为等边三角形,3SA SB SC ====,所以三棱锥S ABC -为正三棱锥,所以点S 在平面ABC 内的射影为ABC 的中心O ,则SO ⊥平面ABC ,如图2连接AO ,由ABC 为等边三角形,ABC 的中心为O,AB =所以223AO ==所以三棱锥S ABC -=所以三棱锥S ABC -的体积为21193342S ABC ABC V S h -==⨯= ,连接AG 并延长,交SC 于点M ,因为点G 是SAC 的重心,所以23AG AM =,所以249EFH SBC S AG S AM ⎛⎫== ⎪⎝⎭所以328()327A EFH A SBCV V --==,所以,8889427272723A EFH A SBC S ABC V V V---⨯====,所以,截面与平面SBC 之间的几何体的体积为9419236S ABC A EFH V V ---=-=【变式6-4】(2022·高一单元测试)如图:正方体ABCD -A 1B 1C 1D 1棱长为2,E ,F 分别为DD 1,BB 1的中点.(1)求证:CF //平面A 1EC 1;(2)过点D 作正方体截面使其与平面A 1EC 1平行,请给以证明并求出该截面的面积.【答案】(1)证明见解析;(2)证明见解析,6【解析】(1)取1CC 中点M ,连接ME由1MC FB //,可得四边形1MCFB 为平行四边形,则1FC MB //由11ME AB //,可得四边形11M EAB 为平行四边形,则11A E MB //则1//A E FC ,又1A E ⊂平面11A EC ,CF ⊄平面11A EC ,则//FC 平面11A EC ;(2)取AA 1,CC 1中点G ,H ,连接DG ,CB 1,B 1H ,HD ,因为四边形ADHF 为平行四边形,所以AF //DH因为四边形AFB 1G 为平行四边形,所以GB 1//AF ,所以GB 1//DH所以GDHB 1即为过点D 长方体截面,∵DG //A 1E ,1A E ⊂平面AEC 1,DG ⊄平面AEC 1,∴DG //平面AEC 1∵DH //C 1E ,1C E ⊂平面AEC 1,DH ⊄平面AEC 1,∴DH //平面AEC 1又∵DH DG D = ,∴平面DHB 1G //平面AEC 1.112223262GDHB S =⨯⨯=1.(2021春·吉林长春·高一长春市第二十九中学校考期末)下列命题中,正确的是()A .若//,,a b b α⊂则//a αB .若//a α,b α⊂则//a bC .若//,//a b αα,则//a bD .若//,//a b b α,a α⊄则//a α【答案】D【解析】A .若//a b ,b α⊂,则//a α或a α⊂,所以该选项错误;B .若//a α,b α⊂,则//a b 或,a b 异面,所以该选项错误;C .若//a α,//b α,则//a b 或,a b 异面或,a b 相交,所以该选项错误;D .若//,//a b b α,a α⊄,由b //α,过b 作平面γ,使α∩γ=m ,则b //m ,又∵a //b ,∴a //m ,∵,a m ⊄⊂αα,∴//a α,所以该选项正确.故选:D2.(2022春·云南昆明·高一昆明市第三中学校考期中)已知直线l ,m 和平面α、β,下列命题正确的是()A .//m l ,////l m αα⇒B .l //β,//m β,l ⊂α,//m ααβ⊂⇒C .//l m ,l ⊂α,//m βαβ⊂⇒D .l //β,//m β,l ⊂α,m α⊂,//l m M αβ⋂=⇒【答案】D【解析】A ://m l ,//l α,则//m α或m α⊂,错误;B :若//m l 时,//αβ或,αβ相交;若,m l 相交时,//αβ,错误;C ://l m ,l ⊂α,m β⊂,则,αβ平行、相交、重合都有可能,错误;D :,l m α⊂,l m M = 且l //β,//m β,根据面面平行的判定知://αβ,正确.故选:D3.(2022春·广东茂名·高一统考期中)已知正方体1111ABCD A B C D -中,E ,F 分别是它们所在线段的中点,则满足1//A F 平面1BD E 的图形个数为()A .0B .1C .2D .3【答案】B 【解析】①中,平移1A F 至1D F ',可知1D F '与面1BD E 只有一个交点1D ,则1A F 与平面1BD E 不平行;②中,由于11//A F D E ,而AF ⊄平面BDE ,DE ⊂平面BDE ,故1//A F 平面1BD E ;③中,平移1A F 至1D F ',可知1D F '与面1BD E 只有一个交点1D ,则1A F 与平面1BD E 不平行;故选:B .4.(2023春·全国·高一专题练习)已知四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是正方形,且PA AB =,点E 是PD 的中点,点F 是棱PC 上的点且2PF FC =,则平面BEF 截四棱锥P ABCD -所得的截面图形是()A .斜三角形B .梯形C .平行四边形D .两组对边均不平行的四边形【答案】D【解析】如图,延长EF 和DC ,设其交点为G ,连接BG ,延长DA 并与直线BG 交于点H ,连接HE 交PA 于点K ,连接KB ,得四边形EFBK ,假设//KE BF ,BF ⊄平面PAD ,KE ⊂平面PAD ,得//BF 平面P AD ,(线面平行的判定定理的应用)因为//BC AD ,BC ⊄平面PAD ,AD ⊂平面PAD ,//BC 平面PAD ,且BC BF B = ,,BC BF ⊂平面PBC ,所以平面//PBC 平面P AD ,(面面平行的判定定理的应用)与平面PBC 与平面P AD 有公共点P 矛盾,故假设不成立,因此KE 与BF 不平行,同理可证KB 与EF 不平行,因此四边形EFBK 的两组对边均不平行.故选:D5.(2023·全国·高一专题练习)如图,在直三棱柱111ABC A B C -中,已知12,,AB BC BB AB BC D ===⊥为AB 的中点.求证:1BC ∥平面1A CD .【答案】证明见解析【解析】连接1AC 与1A C 交于点O ,则O 是1A C 的中点,连接OD ,如图,因为D 是AB 的中点,所以1∥OD BC ,OD ⊂ 平面1A CD ,1BC ⊄平面1A CD ,1BC ∴∥平面1A CD .6.(2023·全国·高一专题练习)如图,四棱锥P ABCD -的底面是边长为2的正方形,PD ⊥平面ABCD ,点E 是AB 的中点,过点E 作平行于平面PAD 的截面,与直线,,CD PC PB 分别交于点,,F G H .证明://GH EF .【答案】证明见解析【解析】证明:因为//,BC AD BC ⊄平面PAD ,AD ⊂平面PAD ,所以//BC 平面PAD ,又平面//PAD 平面 EFGH ,BC ⊄平面 EFGH ,所以//BC 平面 EFGH ,又BC ⊂平面PBC ,平面PBC ⋂平面EFGH GH =,.所以//BC GH ,同理,//BC EF ,所以//GH EF .7.(2023春·全国·高一专题练习)如图,四棱锥P ABCD -中,//AD BC ,12AD BC =,点E 为PC 上一点,F 为PB 的中点,且//AF 平面BDE .(1)若平面PAD 与平面PBC 的交线为l ,求证://l 平面ABCD ;(2)求证://AF DE .【答案】(1)证明见解析;(2)证明见解析【解析】(1)∵//BC AD ,AD ⊂平面,PAD BC ⊄平面PAD ,∴//BC 平面PAD .∵BC ⊂平面PBC ,平面PBC ⋂平面PAD l =,∴//BC l .∵BC ⊂平面,ABCD l ⊄平面ABCD ,∴//l 平面ABCD .(2)连接,AC FC ,设AC BD O = ,FC BE M ⋂=,连接OM ,∵//AF 平面,BDE AF ⊂平面AFC ,平面AFC 平面BDE OM =,∴//AF OM,∵//AD BC,12AD BC=,所以12AO ADOC BC==,∴12 FM AOMC OC==,∴点M是PBC的重心,∴点E是PC的中点,∴12EM DOMB OB==,∴//OM DE,∴//AF DE.8.(2022春·安徽芜湖·高一校考期中)如图,在正四面体S ABC-中,4AB=,E,F,R分别是SB,SC,SA的中点,取SE,SF的中点M,N,点Q为平面SBC内一点(1)求证:平面MNR 平面AEF(2)若RQ 平面AEF,求线段RQ的最小值,【答案】(1)证明见解析;(2112【解析】(1)∵M,N分别为SE,SF的中点,∴MN EF,又∵MN⊄平面AEF,EF⊂平面AEF,∴MN 平面AEF,∵R,M分别为SA,SE的中点,∴RM AE,又∵RM⊄平面AEF,AE⊂平面AEF,∴RM 平面AEF,又∵MN RM M⋂=,MN⊂平面MNR,RM⊂平面MNR,∴平面MNR 平面AEF.(2)由(1)知,平面MNR 平面AEF,∴若平面SBC内存在一点Q,使RQ 平面AEF,则Q在线段MN上,∴线段RQ的最小值为R到直线MN的距离,即MNR在边MN上的高,∵E ,F 分别为SB ,SC 的中点,M ,N 分别为SE ,SF 的中点,∴11124MN EF BC ===,又∵4AS AB ==,2SE BE ==∴AE SB ⊥,2223AE AB BE =-=又∵R ,M 分别为SA ,SE 的中点,∴132RM AE ==3RN =∴当Q 为MN 中点时,RQ MN ⊥,此时MNR 在边MN 上的高,RQ 取最小值,∴线段RQ 的最小值()2222min 111322RQ RM MQ ⎛⎫--= ⎪⎝⎭.9.(2023·全国·高一专题练习)如图,已知正方体1111ABCD A B C D -的棱长为1,,E F 分别是1,A D BD 的中点.(1)求证:平面1A BD //平面11CB D ;(2)求证:EF //平面11DCC D ;【答案】(1)证明见解析;(2)证明见解析【解析】(1)由正方体的性质可得11111111////,A D B C BC A D B C BC ==,∴四边形11A D CB 为平行四边形,∴11//A B CD ,1⊄A B 平面11B D C ,1CD ⊂平面11B D C ,∴1//A B 平面11B D C ,同理可得//BD 平面11B D C ,又11,A B BD B A B BD =⊂ ,平面1A BD ,∴平面1A BD //平面11CB D ;(2)因为,E F 分别是1,A D BD 的中点,所以1//EF A B ,又11//A B CD ,∴1//EF CD ,又EF ⊄平面11DCC D ,1CD ⊂平面11DCC D ,∴//EF 平面11DCC D .10.(2023·全国·高一专题练习)已知正方体1111ABCD A B C D -中,P 、Q 分别为对角线BD 、1CD 上的点,且123CQ BP QD PD ==.作出平面PQC 和平面11AA D D 的交线(保留作图痕迹),并求证://PQ 平面11A D DA;【答案】作图见解析,证明见解析【解析】连接CP 并延长与DA 的延长线交于M 点,则平面PQC 和平面11AA D D 的交线为1D M ,证明:因为四边形ABCD 为正方形,所以//BC AD,故PBC PDM ,所以23CP BP PM PD ==,又因为123CQ BP QD PD ==,所以123CQ CP QD PM ==,所以1//PQ MD .又1MD ⊂平面11A D DA ,PQ ⊄平面11A D DA ,故//PQ 平面11A D DA .11.(2022春·河北唐山·高一统考期中)如图所示,在三棱柱ABC -A 1B 1C 1中,侧面ACC 1A 1为菱形,∠A 1AC =60°,AC =2,侧面CBB 1C 1为正方形,平面ACC 1A 1⊥平面AB C .点M 为A 1C 的中点,点N 为AB 的中点.(1)证明:MN∥平面BCC1B1;(2)求三棱锥A1-ABC1的体积.【答案】(1)证明见解析;(2)233【解析】(1)证明:连接AC1,BC1,因为四边形ACC1A1为菱形,点M为A1C的中点,所以AC1∩A1C=M,点M为A1C的中点,又点N为AB中点,所以MN∥BC1,而BC1⊂平面BCC1B1,MN⊄平面BCC1B1,所以MN∥平面BCC1B1;(2)∵侧面ACC1A1为菱形,∠A1AC=60°,∴△AA1C为等边三角形,AA1=A1C=AC=2.取AC的中点H,连接A1H,则A1H⊥A C.又∵平面ACC1A1⊥平面ABC,平面ACC1A1∩平面ABC=AC,A1H⊂平面ACC1A1,∴A1H⊥平面ABC,BC⊂平面ABC,∴A1H⊥B C.而四边形CBB1C1为正方形,∴BC⊥CC1.又AA1∥CC1,∴BC⊥AA1,又AA1∩A1H=A1,AA1和A1H在平面ACC1A1上,∴BC⊥平面ACC1A1,×2×2×sin120°3又△AA1C1的面积S=12∴11A ABC V -=11B A AC V -=132323312.(2023春·全国·高一专题练习)如图,四边形ABCD 中,,,6,24AB AD AD BC AD BC AB ⊥===∥,E ,F 分别在BC ,AD 上,EF AB ∥,现将四边形ABCD 沿EF 折起,使BE EC ⊥.(1)若3BE =,在折叠后的线段AD 上是否存在一点P ,使得//CP 平面ABEF ?若存在,求出AP PD的值;若不存在,说明理由.(2)求三棱锥A CDF -的体积的最大值,并求出此时点F 到平面ACD 的距离.【答案】(1)存在,12AP PD =;(2)最大值为3,此时点F 到平面ACD 3【解析】(1)AD 上存在一点P ,使得//CP 平面ABEF ,此时12AP PD =,理由如下:当12AP PD =时,13AP AD =,如图,过点P 作PM FD ∥交AF 于点M ,连接ME ,则13MP AP FD AD ==,∵3BE =,∴3FD =,∴1MP =,又1EC =,MP FD EC ∥∥,∴MP EC ∥,故四边形MPCE 为平行四边形,∴CP ME ∥,又CP Ë平面ABEF ,ME ⊂平面ABEF ,∴//CP 平面ABEF .综上,存在点P ,使得//CP 平面ABEF ,12AP PD =.(2)设BE x =,则(04),6AF x x FD x =<≤=-,故21112(6)(3)3323A CDF V x x x -=⨯⨯⨯-⨯=--+,∴当3x =时,A CDF V -有最大值,且最大值为3,∴此时1EC =,3AF =,3FD =,22DC =,∴2232AD AF FD =+=22214AC EF EC AF =++=在ACD 中,由余弦定理得1cos 223222ADC ∠==⨯⨯,3sin 2ADC ∠=,1sin 332ACD S DC AD ADC =⋅⋅⋅∠= 设F 到平面ACD 的距离为h ,A CDF F ACD V V --=,13,33ACD S h h ⋅⋅==△综上,三棱锥A CDF -的最大值为3,此时点F 到平面ACD 的距离313.(2023·全国·高一专题练习)由四棱柱1111ABCD A B C D -截去三棱锥111C B CD -后得到的几何体如图所示,四边形ABCD 为平行四边形,O 为AC 与BD 的交点.(1)求证:1A O ∥平面11B CD ;(2)求证:平面1A BD ∥平面11B CD ;(3)设平面11B CD 与底面ABCD 的交线为l ,求证:BD l ∥.【答案】(1)证明见解析;(2)证明见解析;(3)证明见解析【解析】(1)取11B D 的中点1O ,连接111,CO AO ,∵1111ABCD A B C D -是四棱柱,∴11A O OC ∥,∴四边形11A OCO 为平行四边形,∴11A O O C ∥,又1O C ⊂平面111,B CD AO ⊄平面11B CD ,∴1AO ∥平面11B CD .(2)∵111BB AA DD ∥∥,∴四边形11BB D D 是平行四边形,∴11BD B D ∥,∵BD ⊄平面1111,B CD B D ⊂平面11B CD ,∴BD ∥平面11B CD ,由(1)得1AO ∥平面11B CD 且1BD AO O = ,1BD A O ⊂、平面1A BD ,∴平面1A BD ∥平面11B CD .(3)由(2)得:BD ∥平面11B CD ,又BD ⊂平面ABCD ,平面11B CD ⋂平面ABCD l =,∴BD l ∥.14.(2023·高一课时练习)如图,三棱柱ABC ﹣A 1B 1C 1中,AA 1⊥平面ABC ,D 、E 分别为A 1B 1、AA 1的中点,点F 在棱AB 上,且AF =14AB.(1)求证:EF ∥平面BDC 1;(2)在棱AC 上是否存在一个点G ,使得平面EFG 将三棱柱分割成的两部分体积之比为1:15,若存在,指出点G 的位置;若不存在,说明理由.【答案】(1)证明见解析;(2)点G 不存在,理由见解析【解析】(1)证明:取AB 的中点M ,∵AF =14AB ,∴F 为AM 的中点,又∵E 为AA 1的中点,∴EF ∥A 1M在三棱柱ABC ﹣A 1B 1C 1中,D ,M 分别为A 1B 1,AB 的中点,∴A 1D ∥BM ,A 1D =BM ,∴A 1DBM 为平行四边形,∴AM ∥BD ,∴EF ∥BD .∵BD ⊂平面BC 1D ,EF ⊄平面BC 1D ,∴EF ∥平面BC 1D .(2)设AC 上存在一点G ,使得平面EFG 将三棱柱分割成两部分的体积之比为1:15,则111:1:16E AFG ABC A B C V V --=,∵111111sin 321sin 2E AFG ABC A B C AF AG GAF AE V V AB AC CAB AA --⨯⋅∠⋅=⋅∠⋅111134224AG AG AC AC =⨯⨯⨯=⋅∴112416AG AC ⋅=,∴32AG AC =,∴AG =32AC >AC .所以符合要求的点G 不存在.15.(2023·全国·高一专题练习)如图,在三棱柱111ABC A B C -中,,,D E F 分别为11,,BC AC A C 的中点,AB BC =.求证:(1)11//A B 平面1DEC ;(2)平面//ABF 平面1DEC .【答案】(1)证明见解析;(2)证明见解析【解析】(1) 在三棱柱111ABC A B C -中,,D E 分别为,BC AC 的中点,1111/////,,/DE AB AB A B DE A B ∴∴,DE ⊂ 平面111,DEC A B ⊄平面1DEC ,11//A B ∴平面1DEC .(2)//,AB DE AB ⊄ 平面1DEC ,DE ⊄平面1DEC ,//AB ∴平面1DEC .,F E 分别为11,A C AC 的中点,11//A C AC ,1//FC AE ∴,且1FC AE =.∴四边形1FC EA 是平行四边形.1//AF EC ∴.又1EC ⊂平面1,DEC AF ⊄平面1DEC ,//AF ∴平面1DEC .又,AB AF ⊂平面,ABF AB AF A ⋂=,∴平面//ABF 平面1DEC .16.(2023·全国·高一专题练习)P 为正方形ABCD 所在平面外一点,E ,F ,G 分别为PD ,AB ,DC 的中点,如图.求证:。
直线和平面平行与平面与平面平行证明题专题训练
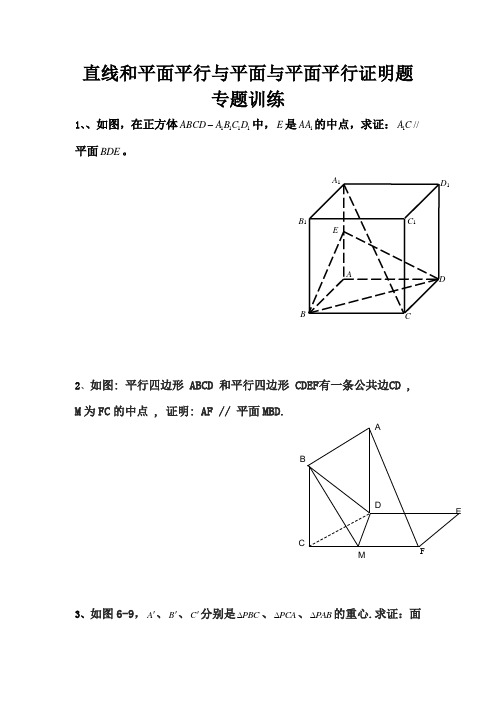
直线和平面平行与平面与平面平行证明题专题训练1、、如图,在正方体1111ABCD A B C D -中,E 是1AA 的中点,求证:1//A C 平面BDE 。
2、如图: 平行四边形 ABCD 和平行四边形 CDEF 有一条公共边CD ,M 为FC 的中点 , 证明: AF // 平面MBD.3、如图6-9,A '、B '、C '分别是PBC ∆、PCA ∆、PAB ∆的重心.求证:面A 1ED 1C 1B 1DCBAMABCDEFA B C '''∥ABC 面.4、 在长方体ABCD —A1B1C1D1中.(1)作出过直线AC 且与直线BD1平行的 截面,并说明理由.(2)设E ,F 分别是A1B 和B1C 的中点, 求证直线EF//平面ABCD.5、、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且EH∥FG.ABCC 1DA 1B 1D 1求证:EH∥BD. (12分)6、P是平行四边形ABCD所在平面外一点,Q是PA的中点,求证://PC平面BDQ.(自己作图)HG FEDBAC7、如图,α//a ,A 是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α于E ,F ,G ,若4=BD ,4=CF ,5=AF ,则EG =___________.8、求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
可复制、编制,期待你的好评与关注)。
直线与平面平行的判定和性质经典练习及详细答案

平面平行的判定及其性质羄直线、1.2.薂下列命题中,正确命题的是④.;肇①若直线I上有无数个点不在平面:.内,则I // :•芆②若直线I与平面「平行,则I与平面「内的任意一条直线都平行;莁③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;④若直线I与平面「平行,则I与平面:.内的任意一条直线都没有公共点3.4. 芀下列条件中,不能判断两个平面平行的是____________ (填序号)肇①一个平面内的一条直线平行于另一个平面蚆②一个平面内的两条直线平行于另一个平面膃③一个平面内有无数条直线平行于另一个平面聿④一个平面内任何一条直线都平行于另一个平面答案①②③5.5. 腿对于平面和共面的直线m n,下列命题中假命题是________________ (填序号)肇①若mL用,m丄n,贝V n / 、丄薁②若mil :- , n // :•,贝V m// n膂③若m二:z , n// :•,贝U m// n芇④若m n与:•所成的角相等,则m// n 答案①②④7.6. 膄已知直线a, b,平面「,则以下三个命题:芃①若a // b, b二:乂,则a //⑶袁②若a // b, a //芒,贝U b //芒;莆③若 a // :•, b // :-,则 a // b.薅其中真命题的个数是答案09.7. 羅直线a//平面M直线b M那么a// b是b〃M的条件.蚀A.充分而不必要 B.必要而不充分 C.充要 D.不充分也不必要11.12.蒆能保证直线a与平面〉平行的条件是, a// b p bu a, a//b肆A. a 広a, b u a, c//a,a//b,a//c蒃C. b u a£a,C^b, D e b 且AC=BD葿D. b u 口,A^a,B13.14. 薆如果直线a平行于平面?,则 _________a平行 B.平面〉内无数条直线与a平行蒇A.平面?内有且只有一直线与a平行的直线 D.平面〉内的任意直线与直线a都平行膅C.平面〉内不存在与15.15. 蒂如果两直线a// b,且a//平面〉,则b与〉的位置关系__________蚆A.相交B. b〃° c.匕匚口D.b〃°或b u°17.16. 薄下列命题正确的个数是______19.17. 蚃(1)若直线I上有无数个点不在平面a内,则I // al与平面a平行,则l与平面a内的任意一直线平行芁(2)若直线,那么另一条也与这个平面平行蚆(3)两条平行线中的一条直线与一个平面平行a和平面a内一直线b平行,则a // a羅(4 )若一直线莄A.0个 B.1个 C.2个 D.3个21.22. 罿b是平面a外的一条直线,下列条件中可得出b/ a是肀A. b与a内的一条直线不相交 B. b与a内的两条直线不相交莅C.b与a内的无数条直线不相交 D.b与a内的所有直线不相交23.23. 螂已知两条相交直线a、b, a//平面a ,则b与a的位置关系肂A. b / a B.b与a相交 C.b」a D.b/ a或b与a相交25.24. 膀如图所示,已知S是正三角形ABC所在平面外的一点,且SA=SB=SC, SGSAB上的高,D E、F分别是AC BC SC的中点,试判断SG与平面DEF的位置关系,并给予证明.螆解SG//平面DEF证明如下:薄方法一:三角形中位线连接CG交螁••• DE是厶ABC的中位线,芀••• DE// AB.腿在△ ACG中, D是AC的中点,羂且DH// AG薀• H为CG的中点.艿• FH是厶SCG的中位线,芄• FH// SG蚄又SG亿平面DEF FHU平面DEF,荿••• SG//平面DEF荿方法二:平面平行的性质蚅••• EF为厶SBC的中位线,• EF/ SB膂••• EF伉平面SAB SBu平面SAB莂• EF//平面SAB葿同理可证,DF//平面SAB EF A DF=F ,肆.••平面SAB/平面DEF,又SG二平面SAB • SG//平面DEF27.25. 袄如图所示,在正方体ABC—ABC1D1中,E、F、G H分别是BC CG、賺CD、A1A的中点.求证:蕿(1)BF/ HD;蒇(2)EG//平面BBDD;莁(3)平面BDF/平面BDH袀证明平行四边形的性质,平行线的传递性虿(1 )如图所示,取BB的中点M易证四边形蚄又••• MC/ BF,「. BF/ HD.肃(2)取BD的中点0,连接E0, D0,贝U OE^蚈又DG& I DC• OE^ DG2蝿.••四边形OEGD是平行四边形,• GE// DO.肄又D 0-平面BB D D, • EG/平面BBD D.蒁(3)由(1)知DH// BF,又BD// BD, BD、HD =平面HBD, BF、BH 平面BDF,且BD A HD=D, DBA BF=B,「.平面BDF// 平面B D H.29.26. 螁如图所示,在三棱柱ABC-A i B C中,M N分别是BC和A i B i的中点. 衿求证:MN//平面AACC.蒅证明方法一:平行四边形的性质膃设AC中点为F,连接NF, FC,蒀••• N为A i B i中点,衿••• NF// BQ,且NF=^B C i,2祎又由棱柱性质知B i C i庄BC蚁又M是BC的中点,艿• NF MC羈.••四边形NFCM^平行四边形.芇• MIN/ CF,又CF 平面AA C i, MN二平面AA C ,• MIN/平面AAC C. 莃方法二:三角形中位线的性质节连接AM交C C于点P,连接A i P, 肇T M是BC的中点,且MC/ B i C i,莄• M是B i P的中点,肅又••• N为A B中点,肁• MN// A P,又 A PU 平面AA C , MW 平面AAC,:MIN/平面AACC.膈方法三:平面平行的性质 螅设BiG 中点为Q 连接NQ MQ ,薃•••M Q 是BG BG 的中点,袀•••MQ CG ,又 CGu 平面 AAGC, MQ 伉平面 AAGC, 芈•••MQ/平面 AA C i C.膆•••N 、Q 是A B i 、B i C 的中点,芅• NQ 二 AQ ,又 A i C 二平面 AAC C, NQ 二平面 AAC C, 蕿• NQ//平面 AA C i C.莈又••• MQ P NQB ,「.平面 MNQ 平面 AAC C, 薇又MN 二平面MNQ. MIN/平面AA C C.3 i .32.螂如图所示,正方体 ABC — A B i C D 中,侧面对角线 AB , BC 上分 别有两点 E , F ,且B E=C F. 蚁求证: EF //平面 ABCD 蒈方法一:平行四边形的性质螃过E 作ES// BB 交AB 于S,过F 作FT // BB 交BC 于 T ,蒄连接ST ,则-AE 更,且AB i B i B BC i C i C莀T B i E=C F , B A=CB,. AE=BF蒈•••旦,••• ES=FTB i B CC i膄又••• ES// B B// FT ,.四边形 EFTS 为平行四边形Bl ______ G袂•••EF// ST ,又 ST=平面 ABCD EFC :平面 ABCD : EF//平面 ABCD腿方法二:相似三角形的性质 薈连接BF 交BC 于点Q 连接AQ薅••• BQ // BC, • B 1L =圧BQ C 1B膂• EF // AQ 又 AQ=平面 ABCD EF 二平面 ABCD •- EF//平面 ABCD 蚇方法三:平面平行的性质 羆过E 作EG/ AB 交BB 于G,肂连接GF,则B 11史£ ,B 1A B 1B羁 TB i E=C i F , BA=CB ,螇••• C i E =B i G , • FG // B l C i // BC C 1B B i B 莇又 EG A FG P G , AB A BC=B ,螄.••平面 EFG/平面 ABCD 而EF 二平面EFG螀• EF//平面ABCD33.34.袇如图所示,在正方体 ABC — A B i C D 中,O 为底面ABCD 的中心,P 是DD 的中点,设薄T B i E=C i F , BiA=GB,B L E B ,FB 1D B i QQ是CC上的点,问:当点Q在什么位置时,平面DBQ// 平面PAO蒄解面面平行的判定节当Q为CC的中点时,A B葿平面 DBQ//平面PAO羇••• Q 为CG 的中点,P 为DD 的中点,••• QB// PA袅:P 、O 为 DD 、DB 的中点,• DB// PO羄又 PO P PA=P , DB A QB=B , 薂DB //平面PAO QB//平面 PAO 肇.••平面 DBQ//平面PAO芆直线与平面平行的性质定理35.EFGH 为空间四边形ABCD 勺一个截面,若截面为平行四边形芀(1)求证:AB//平面 EFGH CD//平面 EFGH肇(2)若AB=4, CD=6,求四边形EFGH 周长的取值范围 蚆(1)证明•••四边形EFGH 为平行四边形,• EF// HG膃•••HX 平面 ABD • EF//平面 ABD 聿•••EF 平面 ABC 平面 ABD A 平面 ABCAB腿• EF// AB. • AB//平面 EFGH 肇同理可证,CD//平面EFGH薁⑵ 解 设EF=x (O v x v 4),由于四边形 EFGH 为平行四边形,膂•••CF=x 则 FG = B F = B C -C F =1- x .从而 F G=6- 1 2 3x . •••四边形 EFGH 的周长 CB 4 6 BC BC 4 21 =2(x+6-5)=12- x.又0v x v 4,则有8v l v 12, •四边形 EFGH 周长的取值范围是(8,212) 37.36.莁如图所示,四边形 AC38.芇如图所示,平面:• //平面[,点A € :. , C €「,点B € 1 , D € [,点E , F 分别在线 段 AB CD 上,且 AE : EB=CF : FD薆••• AC// DH, •••四边形 ACDH 是平行四边形, 蒇在AH 上取一点 G,使AG : GH=CF : FD,膅又••• AE : EB=CF : FD, • GF// HD EG// BH 蒂又EG A GFG, •平面 EFG//平面-蚆•••EF 平面 EFG •- EF / l 综上,EF// I薄(2)解三角形中位线膄(1)求证:EF / -; :. / :,:.门平面 ACDHAC,蚃 如图所示,连接 AD,取AD 的中点 M 连接 ME MF.芁••• E , F 分别为AB, CD 的中点,蚆••• ME// BD, MF// AC,羅且 M ^Z BGB , MF=LAC=2,2 2莄•••/ EMF 为AC 与BD 所成的角(或其补角),罿EMF=60。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与平面平行与平面与平面平行证明题
专题训练
1、、如图,在正方体1111ABCD A B C D -中,E 就是1AA 的中点,求证:1//A C 平面
BDE 。
2、如图: 平行四边形 ABCD 与平行四边形 CDEF 有一条公共边
CD ,
M 为FC 的中点 , 证明: AF // 平面MBD 、
3、如图6-9,A '、B '、C '分别就是PBC ∆、PCA ∆、PAB ∆的重心、求证:
面A B C '''∥ABC 面、
4、 在长方体ABCD —A1B1C1D1中、 (1)作出过直线AC 且与直线BD1平行的 截面,并说明理由、
(2)设E,F 分别就是A1B 与B1C 的中点, 求证直线EF//平面ABCD 、
5、、已知E 、F 、G 、H 为空间四边形ABCD 的边AB 、BC 、CD 、DA 上的点,且
A
B
C
C 1
D
A 1
B 1
D 1
A 1
E
D 1
C 1
B 1
D
C
B
A
M
A
B C
D
E
F
EH∥FG.
求证:EH ∥BD 、 (12分)
6、
P 就是平行四边形ABCD 所在平面外一点,Q 就是PA 的中点,
求证://PC 平面BDQ .(自己作图) 7、
如图,α//a ,A 就是α的另一侧的点,a D C B ∈,,,线段AB ,AC ,AD 交α于
E ,
F ,
G ,若4=BD ,4=CF ,5=AF ,则EG
=___________.
8、求证:如果一条直线与两个相交平面都平行,那么这条直线与它们的交线平行.
H G F
E
D B
A
C。
