直线与平面平行测试题1

合集下载

人教A版必修2第二章2.2.1《直线与平面的判定》精选题高频考点(含答案)-1

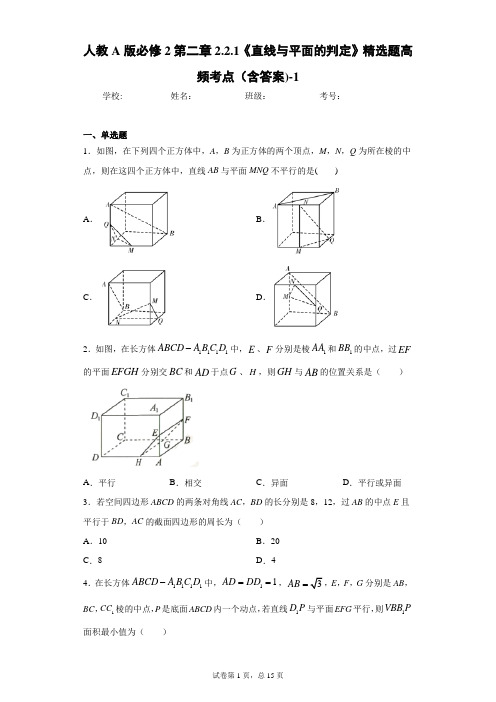
人教A 版必修2第二章2.2.1《直线与平面的判定》精选题高频考点（含答案)-1学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在下列四个正方体中，A ，B 为正方体的两个顶点，M ，N ，Q 为所在棱的中点，则在这四个正方体中，直线AB 与平面MNQ 不平行的是( )A ．B ．C ．D ．2．如图，在长方体1111ABCD A B C D -中，E 、F 分别是棱1AA 和1BB 的中点，过EF 的平面EFGH 分别交BC 和AD 于点G 、H ，则GH 与AB 的位置关系是（）A ．平行B ．相交C ．异面D ．平行或异面 3．若空间四边形ABCD 的两条对角线AC ，BD 的长分别是8，12，过AB 的中点E 且平行于BD ，AC 的截面四边形的周长为（）A ．10B ．20C ．8D ．44．在长方体1111ABCD A B C D -中，11AD DD ==，AB =E ，F ，G 分别是AB ，BC ，1CC 棱的中点，P 是底面ABCD 内一个动点，若直线1D P 与平面EFG 平行，则1BB P V 面积最小值为（）A B ．1 C D ．125．如图，正方体1111ABCD A B C D 中，E ，F ，G ，H 分别为所在棱的中点，则下列各直线中，不与平面1ACD 平行的是（）A ．直线EFB ．直线GHC ．直线EHD ．直线1A B 6．如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为3，线段B 1D 1上有两个动点E ，F 且EF ＝1，则当E ，F 移动时，下列结论中错误的是（）A ．AE ∥平面C 1BDB ．四面体ACEF 的体积不为定值C ．三棱锥A ﹣BEF 的体积为定值D ．四面体ACDF 的体积为定值7．下列四个正方体图形中，A B ，为正方体的两个顶点，M N P ，，分别为其所在棱的中点，能得出AB ∥平面MNP 的图形的序号是（）A ．①③B ．②④C ．②③D ．①④ 8．已知直线m 与平面α，则下列结论成立的是A ．若直线m 垂直于α内的两条直线，则m α⊥B ．若直线m 垂直于α内的无数条直线，则m α⊥C ．若直线m 平行于α内的一条直线，则//m αD ．若直线m 与平面α无公共点，则//m α9．如图,在正方体1111ABCD A B C D -中,M ,N 分别是11,BC CD 的中点,则下列说法错误的是（）A ．MN ∥平面ABCDB ．MN ∥ABC ．MN ⊥ACD ．MN ⊥CC 1 10．如图，在四面体ABCD 中，点P ，Q ，M ，N 分别是棱AB ，BC ，CD ，AD 的中点，截面PQMN 是正方形，则下列结论错误的为( )A ．AC ⊥BDB ．AC ∥截面PQMNC ．AC ＝CDD ．异面直线PM 与BD 所成的角为45°11．设l 为直线，α，β是两个不同的平面，下列命题中正确的是（）A ．若l ∥α，l ∥β，则α∥βB ．若l ⊥α，l ⊥β，则α∥βC ．若l ⊥α，l ∥β，则α∥βD ．若α⊥β，l ∥α，则l ⊥β12．已知m ，n 是两条不同的直线，α，β是两个不同的平面，给出下列命题： ①若αβ∥，m α⊂，n β⊂，则m n P ；②若m αP ，m n P ，则n αP ；③若m ，n 是异面直线，则存在α，β，使m α⊂，n β⊂，且αβ∥；④若α，β不垂直，则不存在m α⊂，使m β⊥．其中正确的命题有（）．A ．1个B ．2个C ．3个D ．4个 13．设平面αβ∥，A α∈，B β∈，C 是AB 的中点，当点,A B 分别在平面,αβ内运动时，则所有的动点C （）A ．不共面B ．当且仅当,A B 分别在两条直线上移动时才共面C ．当且仅当,A B 分别在两条给定的异面直线上移动时才共面D ．不论,A B 如何移动，都共面14．一正方体表面沿着几条棱裁开放平得到如图所示的展开图，则在原正方体中( )A ．AB CD ∥ B ．AB CD 平面∥C ．CD GH ∥ D ．AB GH ∥ 15．如图所示，在三棱台111ABC A B C -中，点D 在11A B 上，且1AA BD ∥，点M 是111A B C △内（含边界）的一个动点，且有平面BDM P 平面1A C ，则动点M 的轨迹是（）A ．平面B ．直线C ．线段，但只含1个端点D ．圆16．以下命题中真命题的个数是（）①若直线l 平行于平面α内的无数条直线，则直线l αP ；②若直线a 在平面α外，则a P α；③若直线,a b b α⊂∥，则a P α；④若直线,a b b α⊂∥，则a 平行于平面α内的无数条直线.A ．1B ．2C ．3D ．4 17．如图，已知正方体1111ABCD A B C D -，E 、F 分别是1BC 、BD 的中点，则至少过正方体3个顶点的截面中与EF 平行的截面个数为（）．A ．2B ．3C ．4D ．5 18．已知直线l ，m ，平面α，β，γ，则下列条件能推出l ∥m 的是（） A ．l ⊂α，m ⊂β，α∥βB ．α∥β，α∩γ＝l ，β∩γ＝mC ．l ∥α，m ⊂αD ．l ⊂α，α∩β＝m19．如图，透明塑料制成的长方体容器ABCD -A 1B 1C 1D 1内灌进一些水，固定容器底面一边BC 于地面上，再将容器倾斜，随着倾斜度的不同，有下面四个命题：①没有水的部分始终呈棱柱形；②水面EFGH 所在四边形的面积为定值；③棱A 1D 1始终与水面所在平面平行；④当容器倾斜如图所示时，BE ·BF 是定值．其中正确的个数是（）A ．1B ．2C ．3D ．420．如图，几何体111A B C ABC -是一个三棱台，在1A 、1B 、1C 、A 、B 、6C 个顶点中取3 个点确定平面α，αI 平面111A B C m =，且//m AB ，则所取的这3个点可以是（）A ．1A 、B 、CB ．1A 、B 、1C C ．A 、B 、1CD ．A 、1B 、1C二、填空题 21．判断下列命题是否正确，正确的在括号内画“√”，错误的画“×”.（1）如果直线//a b ，那么a 平行于经过b 的任何平面.（______）（2）如果直线a 与平面α满足//a α，那么a 与α内的任何直线平行.（______）（3）如果直线a b ，和平面α满足//a α，//b α，那么//a b .（______）（4）如果直线a b ，和平面α满足//a b ，//a α，b α⊄，那么//b α.（______） 22．如图，透明塑料制成的长方体ABCD ﹣A 1B 1C 1D 1内灌进一些水，固定容器底面一边BC 于水平地面上，再将容器倾斜，随着倾斜度不同，有下面五个命题： ①有水的部分始终呈棱柱形；②没有水的部分始终呈棱柱形；③水面EFGH 所在四边形的面积为定值；④棱A 1D 1始终与水面所在平面平行；⑤当容器倾斜如图(3)所示时，BE•BF 是定值．其中所有正确命题的序号是 ____．23．如图，已知在长方体1111ABCD A B C D -中，1 3, 4,5AB AD AA ===，点E 为1CC 上的一个动点，平面1BED 与棱1AA 交于点F ，给出下列命题：①四棱锥11B BED F -的体积为20；②存在唯一的点E ，使截面四边形1BED F 的周长取得最小值；③当E 点不与C ，1C 重合时，在棱AD 上均存在点G ，使得CG P 平面1BED ④存在唯一一点E ，使得1B D ⊥平面1BED ，且165CE = 其中正确的命题是_____________（填写所有正确的序号）24．α，β为两个不同的平面，m ，n 为两条不同的直线，下列命题中正确的是________（填上所有正确命题的序号）．①若α∥β，m ⊂α，则m ∥β； ②若m ∥α，n ⊂α，则m ∥n ； ③若α⊥β，α∩β＝n ，m ⊥n ，则m ⊥β； ④若n ⊥α，n ⊥β，m ⊥α，则m ⊥β． 25．如图，正方体ABCD ﹣A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E 、F ，且EF ＝12，则下列结论中正确的序号是_____．①AC ⊥BE ②EF ∥平面ABCD ③△AEF 的面积与△BEF 的面积相等．④三棱锥A ﹣BEF 的体积为定值26．如图，底面是平行四边形的四棱锥P ABCD -中，E PD ∈，F PC ∈，且:5:2PE ED =，若//BF 平面AEC ，则PF FC=______.27．如图,在矩形ABCD 中,4AB =,2AD =,E 为边AB 的中点.将三角形ADE 沿DE 翻折,得到四棱锥1A DEBC -.设线段1A C 的中点为M ,在翻折过程中,有下列三个命题: ①总有//BM 平面1A DE ;②三棱锥1C A DE -体积的最大值为3; ③存在某个位置,使DE 与1A C 所成的角为90o .其中正确的命题是______.（写出所有．．正确命题的序号）28．如图，P 是平行四边形ABCD 所在平面外一点，E 为PB 的中点，O 为AC ，BD 的交点，则图中与EO 平行的平面有______．29．如图在四面体ABCD 中，若截面PQMN 是正方形，则在下列命题中正确的有______.(填上所有正确命题的序号)①，⊥AC BD②，AC BD=③截面PQMN，//AC④异面直线PM与BD所成的角为45o．30．如图，正方体的底面与正四面体的底面在同一平面α上，且AB//CD,则直线EF与正方体的六个面所在的平面相交的平面个数为.M N Q为所在棱的31．如图，在下列四个正方体中，A、B为正方体的两个顶点，,,中点，则在这四个正方体中，直线AB与平面MNQ平行的是________.①②③④．32．以下四个正方体中，点M为四等分点，其余各点为顶点或者中点，其中四点共面的有____.①②③④33．已知l 、m 是两条直线，α是平面，若要得到“l ∥α”，则需要在条件“m ⊂α，l ∥m ”中另外添加的一个条件是______.34．如图，DC ⊥平面ABC ，EB ∥DC ，EB ＝2DC ，P ，Q 分别为AE ，AB 的中点．则直线DP 与平面ABC 的位置关系是________．35．正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在1CC 上,若//EF 平面1AB C ,则EF =_____.36．如图，1111ABCD-A B C D 为正方体，下面结论中正确的是_______.（把你认为正确的结论都填上）①11A C ⊥平面1BD ；②1BD ⊥平面1ACB ；③1BD 与底面11BCC B ；④过点1A 与异面直线AD 与1CB 成60︒角的直线有2条.37．如图所示，正方体1111ABCD A B C D -的棱长为1，,M N 为线段BC ，1CC 上的动点，过点1,,A M N 的平面截该正方体的截面记为S ，则下列命题正确的是______①当0BM =且0CN 1<<时，S 为等腰梯形；②当,M N 分别为BC ，1CC 的中点时，几何体11A D MN 的体积为112； ③当M 为BC 中点且34CN =时，S 与11C D 的交点为R ，满足116C R =； ④当M 为BC 中点且01CN 剟时，S 为五边形；⑤当13BM =且1CN =时，S 的面积3. 38．如图所示，在几何体ABCDE 中，四边形ABCD 是平行四边形，G F ，分别是BE DC ，的中点，则GF ___________平面ADE .39．如图（1）所示，已知正方形ABCD 中，E F ，分别是AB ，CD 的中点，将ADE V 沿DE 折起，如图（2）所示，则BF 与平面ADE 的位置关系是________.40．下列三个命题在“_______”处都缺少同一个条件，补上这个条件使其构成真命题（其中,l m 为直线，,αβ为平面），则此条件是__________.①____l m m α⎫⎪⎬⎪⎭P P l α⇒P ；②____m l m α⊂⎫⎪⎬⎪⎭P l α⇒P ；③____l m m α⊥⎫⎪⊥⎬⎪⎭l α⇒P三、解答题41．如图，三棱锥P −ABC ，侧棱PA =2，底面三角形ABC 为正三角形，边长为2，顶点P 在平面ABC 上的射影为D ，有AD ⊥DB ，且DB =1.（1）求证：AC//平面PDB ；（2）求二面角P −AB −C 的余弦值；（3）线段PC 上是否存在点E 使得PC ⊥平面ABE ，如果存在，求CE CP 的值；如果不存在，请说明理由.42．如图几何体中，底面ABCD 为正方形，PD ⊥平面ABCD ，//EC PD ，且22PD AD EC ===.（1）求证：//BE 平面PDA ；（2）求PA 与平面PBD 所成角的大小.43．如图所示,PA ⊥平面ABCD ,ABCD 为正方形,PA AB a ==,E ､F ､G 分别为PA ､PD ､CD 的中点.(1)求证:直线//PB 平面FEG ;(2)求直线PB 与直线EG 所成角余弦值的大小.44．在四棱锥P ABCD -中，底面ABCD 为直角梯形，//AD BC ，AB BC ⊥，侧面PAB ⊥底面ABCD ，1PA AD AB ===，2BC =．()1若PB 的中点为E ，求证：//AE 平面PCD ；()2若90PAB ∠=︒，求二面角B PD C --的余弦值．45．如图，在多面体ABCDEF 中，已知ABCD 是边长为2的正方形，BCF ∆为正三角形，4EF =且//EF AB ，EF FB ⊥，G ，H 分别为BC ，EF 的中点.（1）求证：//GH 平面EAD ；（2）求三棱锥F BCH -的体积.46．已知四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，2PA PD AD ===，点E ，F 分别是PD ，AB 的中点.（1）求证：//AE 平面PFC ；（2）若CF 与平面PCD AB 的长. 47．如图所示，AE ⊥平面ABCD ，四边形AEFB 为矩形，//BC AD ，BA AD ⊥，224AE AD AB BC ====．（1）求证：//CF 平面ADE ；（2）求平面CDF 与平面AEFB 所成锐二面角的余弦值．48．如图所示，在四棱锥P ABCD -中，//AD BC ，90ADC PAB ︒∠=∠=，12BC CD AD ==.在平面P AD 内找一点M ，使得直线//CM 平面P AB ，并说明理由.49．如图，在平行六面体1111ABCD A B C D -中，1AA AB =，111AB B C ⊥.求证：//AB 平面11A B C ；50．如图，直三棱柱ABC﹣A′B′C′，∠BAC＝90°，AB＝AC＝λAA′，点M，N分别为A′B 和B′C′的中点．（1）证明：MN∥平面A′ACC′；（2）若二面角A′﹣MN﹣C为直二面角，求λ的值．参考答案1．A2．A3．B4．A5．C6．B7．D8．D9．B10．C11．B12．B13．D14．C15．C16．A17．D18．B19．C20．C21．× × × √22．①②④⑤23．①②④24．①④25．①②④26．3 227．①②28．平面P AD、平面PCD29．①③④30．431．②③④32．②33．l α⊄34．平行3536．①②④37．①②38．平行.39．平行40．l α⊄41．（Ⅰ）见解析;（Ⅱ）−√217;（Ⅲ）见解析. 42．（1）见解析（2）6π43．（1）见证明（2）344．()1证明见解析；()12.345．（1）见解析；（2）346．（1）证明见解析，（2）2a =47．（1）见解析（2）2348．AD 的中点M （M ∈平面P AD ）为所求的一个点，详见解析 49．证明见解析50．（1）见解析（2）λ=。

人教A版必修2第二章2.2.3《直线与平面平行的性质》精选题高频考点(含答案)-1

人教A 版必修2第二章2.2.3《直线与平面平行的性质》精选题高频考点（含答案)-1学校:___________姓名：___________班级：___________考号：___________一、单选题1．如图，在长方体1111ABCD A B C D -中，E 、F 分别是棱1AA 和1BB 的中点，过EF 的平面EFGH 分别交BC 和AD 于点G 、H ，则GH 与AB 的位置关系是（）A ．平行B ．相交C ．异面D ．平行或异面 2．如图所示，在四棱锥P ABCD -中，M N ，分别为AC PC ，上的点，且MN ∥平面PAD ，则（）A ．MN PD PB ．MN PA ∥C ．MN AD P D ．以上均有可能 3．如图，P 为平行四边形ABCD 所在平面外一点，E 为AD 上一点，且13AE ED =，F 为PC 上一点，当//PA 平面EBF 时，PF FC=（）A ．23B ．14C ．13D ．12 4．如图所示，在长方体1111ABCD A B C D -中，121AB BC AA ，===，则1BC 与平面11BB D D 所成角的正弦值为（）A．3 BC．5 D．5 5．在正方体1111ABCD A B C D -中，E 为棱CD 上一点，且2CE DE =，F 为棱1AA 的中点，且平面BEF 与1DD 交于点G ，与1AC 交于点H ，则（）A ．115DG DD =B ．113AH HC = C ．114DG DD = D ．138AH HC = 6．如图，1111ABCD A B C D -是正方体，E 为棱1BB 上的动点（不含端点），平面11AC E 与底面ABCD 的交线为l ，则l 与AC 的位置关系是（）A ．异面B ．平行C ．相交D ．与E 点位置有关 7．已知m ，n 是不同的直线，α，β是不重合的平面，下列命题中正确的有（） ①若m α⊥，m β⊥，则//αβ②若//m α，m β⊂，n αβ=I ，则//m n③若//m α，//m β，则//αβ④若αβ⊥，m α⊂，n β⊂，则m n ⊥A ．①②B ．①③C ．②④D ．③④ 8．已知//,a b αα⊂，则直线a 与直线b 的位置关系是（）A ．平行B ．相交或异面C ．异面D ．平行或异面 9．已知棱长为3的正方体1111ABCD A B C D -,点E 是棱AB 的中点，12CF FC =u u u r u u u u r ，动点P 在正方形11AA DD （包括边界）内运动，且1PB P 面DEF ，则PC 的长度范围为（）A ．B ．5⎡⎢⎣C ．5⎡⎢⎣D ．5⎡⎢⎣10．如图，各棱长均为a 的正三棱柱111ABC A B C -，M 、N 分别为线段1A B 、1B C 上的动点，且MN ∥平面11ACC A ，M ，N 中点S 111ABC A B C -的体积为（）A B C ．3 D ．11．点E ，F 分别是棱长为1的正方体1111ABCD A B C D -中棱BC ，1CC 的中点，动点P 在正方形11BCC B （包括边界）内运动，且1PA ∥面AEF ，则1PA 的长度范围为（）A ．1,2⎡⎢⎣⎦B ．42⎡⎢⎣⎦C ．342⎡⎤⎢⎥⎣⎦D ．31,2⎡⎤⎢⎥⎣⎦12．如图，在正四棱锥S －ABCD 中，E ，M ，N 分别是BC ，CD ，SC 的中点，动点P在线段MN 上运动时，下列四个结论：①EP ⊥AC ；②EP ∥BD ；③EP ∥平面SBD ；④EP ⊥平面SAC ，其中恒成立的为( )A ．①③B ．③④C ．①②D ．②③④13．一条直线若同时平行于两个相交平面，那么这条直线与这两个平面交线的位置关系是（）A ．异面B ．相交C ．不能确定D ．平行 14．如图所示，a P α，A 是α的另一侧的点，B C D a ∈，，，线段AB AC AD ，，分别交α于点EFG ，，，若445BD CF AF ===，，，则EG =（）A ．169B ．209C ．94D ．5415．如图，已知四棱锥P ABCD -的底面是平行四边形，AC 交BD 于点O ，E 为AD 中点，F 在PA 上，AP AF λ=，//PC 平面BEF ，则λ的值为（）A ．1B ．32C ．2D ．3 16．给出下列关于互不相同的直线,,l m n 和平面,,αβγ的三个命题：①若l 与m 为异面直线，,l m αβ⊂⊂，则//αβ；②若//,,l m αβαβ⊂⊂，则//l m ；③若,,,//l m n l αββγγαγ===I I I ，则//m n ．其中正确的个数为（）A ．0B ．1C ．2D ．317．如图，P 为平行四边形ABCD 所在平面外一点，E 为AD 的中点，F 为PC 上一点，当P A ∥平面EBF 时，PF FC＝（）A ．23B ．14C ．13D ．12 18．如果直线m//直线n ，且m//平面α，那么n 与α的位置关系是（） A ．相交 B ．n//α C ．n ⊂α D ．n//α或n ⊂α 19．若直线a 平行于平面α，则下列结论错误的是（）A ．直线a 上的点到平面α的距离相等B ．直线a 平行于平面α内的所有直线C ．平面α内有无数条直线与直线a 平行D ．平面α内存在无数条直线与直线a 所成的角为90o20．已知l ，m 为两条不同直线，α，β为两个不同平面.则下列命题正确的是（） A ．若l αP ，m α⊂，则l m PB ．若l αP ，m αP ，则l m PC ．若l α⊂，m β⊂，αβ∥，则l m PD ．若l αP ，l β∥，m αβ=I ，则l m P二、填空题21．如图,正方体1111ABCD A B C D -中, AB =点E 为11A D 的中点,点F 在11C D 上,若//EF 平面1ACB ,则EF =________．22．在正方体1111ABCD A B C D -中，E 为棱CD 上一点，且2CE DE =，F 为棱1AA 的中点，且平面BEF 与1DD 交于点G ，与1AC 交于点H ，则1DG DD =______，1AH HC =______. 23．如图所示，a ∥α，A 是α的另一侧的点，B 、C 、D ∈a ，线段AB 、AC 、AD 交α于E 、F 、G ，若BD ＝4，CF ＝4，AF ＝5，则EG ＝________．24．如图，E 是棱长为1正方体1111ABCD A B C D -的棱11C D 上的一点，且1//BD 平面1B CE ，则线段CE 的长度为___________．25．如图所示，四面体ABCD 被一平面所截，截面EFGH 是一个矩形．则直线CD 与平面EFGH 的关系是______．26．如图在四面体ABCD 中，若截面PQMN 是正方形，则在下列命题中正确的有______.(填上所有正确命题的序号)AC BD ⊥①，AC BD =②，//AC ③截面PQMN ，④异面直线PM 与BD 所成的角为45o ．27．在三棱锥S ABC -中，ABC ∆是边长为4的正三角形，10SA SB SC ===，平面DEFH 分别与AB ，BC ，SC ，SA 交于D ，E ，F ，H 且D ，E 分别是AB ，BC 的中点，如果直线SB P 平面DEFH ，那么四边形DEFH 的面积为______．28．已知l 、m 是两条直线，α是平面，若要得到“l ∥α”，则需要在条件“m ⊂α，l ∥m ”中另外添加的一个条件是______.29．如图，DC ⊥平面ABC ，EB ∥DC ，EB ＝2DC ，P ，Q 分别为AE ，AB 的中点．则直线DP 与平面ABC 的位置关系是________．30．正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在1CC 上,若//EF 平面1AB C ,则EF =_____.31．如图所示，在三棱柱111ABC A B C -中，过11A B C ，，的平面与平面ABC 的交线为l ，则l 与直线11A C 的位置关系为________.32．如图所示，长方体1111ABCD A B C D -的底面ABCD 是正方形，其侧面展开图是边长为8的正方形，E F ，分别是侧棱11AA CC ，上的动点，且8AE CF +=，P 在棱1AA 上，且2AP =，若EF P 平面PBD ，则CF =________.33．如图所示，在三棱柱111ABC A B C 中，E F G H ，，，分别是1111AB AC A B A C ，，，的中点，则与平面BCHG 平行的平面为________.34．如图（1）所示，已知正方形ABCD 中，E F ，分别是AB ，CD 的中点，将ADE V 沿DE 折起，如图（2）所示，则BF 与平面ADE 的位置关系是________.35．已知A 、B 、C 、D 四点不共面，且AB ∥平面α，CD ∥α，AC ∩α＝E ，AD ∩α＝F ，BD ∩α＝H ，BC ∩α＝G ，则四边形EFHG 是_______四边形.36．如图，棱长为2的正方体1111ABCD A B C D -中，M 是棱AA 1的中点，过C ，M ，D 1作正方体的截面，则截面的面积是________．37．如图所示，在长方体1111ABCD A B C D -中，111BB B D =，点E 是棱1CC 上的一个动点，若平面1BED 交棱1AA 于点F ，给出下列命题：.① 四棱锥11B BED F -的体积恒为定值；②存在点E ，使得1B D ⊥平面1BD E ；③存在唯一的点E ，使得截面四边形1BED F 的周长取得最小值；④存在无数个点E ，在棱AD 上均有相应的点G ，使得CG P 平面1EBD ，也存在无数个点E ，对棱AD 上任意的点G ，直线CG 与平面1EBD 均相交.其中真命题的是____________．（填出所有正确答案的序号）38．已正知方体ABCD-A 1B 1C 1D 1的棱长为2，点P 是平面AA 1D 1D 的中心，点Q 是B 1D 1上一点，且PQ ∥平面AB 1D ，则线段PQ 长为______．39．设,a b 是平面M 外两条直线，且//a M ，那么//a b 是//b M 的________条件.40．已知正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 是平面AA 1D 1D 的中心，点Q 是平面A 1B 1C 1D 1的对角线B 1D 1上一点，且PQ ∥平面AA 1B 1B ，则线段PQ 的长为________．三、解答题41．如图，四棱锥P ABCD -中，底面ABCD 为矩形，侧面PAD 为正三角形，2AD =，3AB =，平面PAD ⊥平面ABCD ，E 为棱PB 上一点（不与P 、B 重合），平面ADE 交棱PC 于点F .（1）求证：AD EF P ；（2）若二面角––B AC E ，求点B 到平面AEC 的距离. 42．如图，在四棱锥P ABCD -中，底面ABCD 是梯形，且//BC AD ，2AD BC =，点Q 是线段AD 的中点，过BQ 的平面BQMN 交平面PCD 于MN ，且PQ AB ⊥，AP PD =，且120APD ∠=︒，24BD AB ==，30ADB ∠=︒.（1）求证：//BQ MN ；（2）求直线PA 与平面PCD 所成角的余弦值.43．如图所示的一块木料中，棱BC 平行于面A C ''.（1）要经过面A C ''内的一点P 和棱BC 将木料锯开，在木料表面应该怎样画线？（2）所画的线与平面AC 是什么位置关系？44．如图，已知E ，F 分别是正方体1111ABCD A B C D -的棱1AA ，1CC 上的点，且1AE C F =.求证：四边形1EBFD 是平行四边形.45．如图所示，P 是平行四边形ABCD 所在平面外一点，E 是PD 的中点、若M 是CD 上异于C ，D 的点，连接PM 交CE 于点G ，连接BM 交AC 于点H ，连接GH ，求证：GH //PB .46．已知如图，斜三棱柱ABC -A 1B 1C 1中，点D 、D 1分别为AC 、A 1C 1上的点．（1）当1111A D D C 等于何值时，BC 1∥平面AB 1D 1？（2）若平面BC 1D ∥平面AB 1D 1，求AD DC的值．47．如图所示，已知三棱柱ABC-A'B'C'中，D 是BC 的中点，D'是B'C'的中点，设平面A'D'B∩平面ABC=a ，平面ADC'∩平面A'B'C'=b ，判断直线a ，b 的位置关系，并证明．48．如图，四棱锥P ABCD -的底面ABCD 为直角梯形，//AD BC ，且112BC AD ==，BC DC ⊥，60BAD ∠=︒，平面PAD ⊥底面ABCD ，E 为AD 的中点，PAD ∆为等边三角形，M 是棱PC 上的一点，设PM k MC=（M 与C 不重合）.（1）当1k =时，求三棱锥M BCE -的体积；（2）若//PA 平面BME ，求k 的值.49．如图，E ，F ，G ，H 分别是空间四边形ABCD 各边上的点，且::AE EB AH HD m ==，::CF FB CG GD n ==.（1）证明：E ，F ，G ，H 四点共面.（2）m ，n 满足什么条件时，四边形EFGH 是平行四边形？50．如图，在四校锥P ABCD -中，底面ABCD 为正方形，平面PAD ⊥平面ABCD ，点M 在线段PB 上，//PD 平面MAC ，PA PD ==4AB =.求证：M 为PB 的中点.参考答案1．A2．B3．B4．D5．D6．B7．A8．D9．B10．D11．B12．A13．D14．B15．D16．B17．D18．D19．B20．D21．222．163823．20 92425．平行26．①③④27．10 28．lα⊄29．平行3031．平行. 32．2. 33．平面1A EF 34．平行35．平行【答案】9 237．①②③④3839．充分不必要40．241．（1）证明见解析；（2.42．（1）证明见解析（243．（1）见解析（2）直线EF与平面AC平行直线,BE CF与平面AC相交. 44．证明见解析45．证明见解析46．（1）1；（2）1.47．直线a，b的位置关系是平行，证明见试题解析．48．（1）14；（2）1.49．（1）见解析（2）当m n时，四边形EFGH是平行四边形. 50．证明见解析。

新高考数学一轮复习考点知识专题讲解与练习 34 空间直线、平面的平行

新高考数学一轮复习考点知识专题讲解与练习考点知识总结34 空间直线、平面的平行高考概览高考中本考点各种题型都有考查，分值为5分或10分，中等难度考纲研读1.以立体几何的定义、基本事实和定理为出发点，认识和理解空间中线面平行的有关性质与判定定理2．能运用基本事实、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题一、基础小题1．两条直线a，b满足a∥b，b⊂α，则a与平面α的位置关系是()A．a∥αB．a⊂αC．a与α相交D．a与α不相交答案D解析由于b⊂α且a∥b，则a∥α或a⊂α.故a与α不相交．故选D.2．如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB的位置关系是()A．异面B．平行C．相交D．以上均有可能答案B解析在三棱柱ABC－A1B1C1中，AB∥A1B1，∵AB⊂平面ABC，A1B1⊄平面ABC，∴A1B1∥平面ABC，∵过A1B1的平面与平面ABC交于DE，∴DE∥A1B1，∴DE∥AB.3．下列命题中错误的是()A．平面内一个三角形各边所在的直线都与另一个平面平行，则这两个平面平行B．平行于同一个平面的两个平面平行C．若两个平面平行，则位于这两个平面内的直线也互相平行D．若两个平面平行，则其中一个平面内的直线平行于另一个平面答案C解析由面面平行的判定定理和性质知A，B，D正确．对于C，位于两个平行平面内的直线也可能异面，故C错误．4．若直线l不平行于平面α，且l⊄α，则()A．α内的所有直线与l异面B．α内不存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交答案B解析因为l⊄α，若在平面α内存在与直线l平行的直线，则l∥α，这与题意矛盾．故选B.5．给出下面结论：①过不在平面内的一点，有且只有一个平面与这个平面平行；②过不在平面内的一条直线，有且只有一个平面与这个平面平行；③过不在直线上的一点，有且只有一条直线与这条直线平行；④过不在直线上的一点，有且只有一个平面与这条直线平行．其中正确结论的序号为()A．①②B．③④ C.①③D．②④答案C解析对于①，过不在平面内的一点，有且只有一个平面与这个平面平行，正确；对于②，当已知直线与平面相交时，不存在平面与已知平面平行，错误；对于③，过不在直线上的一点，有且只有一条直线与这条直线平行，正确；对于④，过不在直线上的一点，有无数个平面与已知直线平行，错误．故选C.6. 在三棱锥A－BCD中，E，F，G，H分别是AB，BC，CD，DA上的点，当BD ∥平面EFGH时，下面结论正确的是()A．E，F，G，H一定是各边的中点B．G，H一定是CD，DA的中点C．BE∶EA＝BF∶FC，且DH∶HA＝DG∶GCD．AE∶EB＝AH∶HD，且BF∶FC＝DG∶GC答案D解析由BD∥平面EFGH，得BD∥EH，BD∥FG，则AE∶EB＝AH∶HD，且BF∶FC＝DG∶GC.故选D.7．设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是()A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α答案D解析若存在一条直线a，a∥α，a∥β，则α∥β或α与β相交；若α∥β，则存在一条直线a，使得a∥α，a∥β，所以A是α∥β的一个必要条件；同理，B，C也是α∥β的一个必要条件而不是充分条件；可以通过平移把两条异面直线平移到一个平面内，成为相交直线，则有α∥β，所以D是α∥β的一个充分条件．故选D.8. (多选)在正方体ABCD－A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，下列四个推断中正确的是()A．FG∥平面AA1D1D B．EF∥平面BC1D1C．FG∥平面BC1D1D．平面EFG∥平面BC1D1答案AC解析∵在正方体ABCD－A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，∴FG∥BC1，∵BC1∥AD1，∴FG∥AD1，∵FG⊄平面AA1D1D，AD1⊂平面AA1D1D，∴FG∥平面AA1D1D，故A正确；∵EF∥A1C1，A1C1与平面BC1D1相交，∴EF与平面BC1D1相交，故B错误；∵FG∥BC1，FG⊄平面BC1D1，BC1⊂平面BC1D1，∴FG∥平面BC1D1，故C正确；∵EF与平面BC1D1相交，∴平面EFG与平面BC1D1相交，故D 错误．二、高考小题9．(2022·浙江高考) 如图，已知正方体ABCD－A1B1C1D1，M，N分别是A1D，D1B 的中点，则()A．直线A1D与直线D1B垂直，直线MN∥平面ABCDB．直线A1D与直线D1B平行，直线MN⊥平面BDD1B1C ．直线A 1D 与直线D 1B 相交，直线MN ∥平面ABCDD ．直线A 1D 与直线D 1B 异面，直线MN ⊥平面BDD 1B 1答案 A解析解法一：连接AD 1，则易得点M 在AD 1上，且AD 1⊥A 1D .因为AB ⊥平面AA 1D 1D ，所以AB ⊥A 1D ，所以A 1D ⊥平面ABD 1，所以A 1D 与D 1B 异面且垂直．在△ABD 1中，由中位线定理可得MN ∥AB ，所以MN ∥平面ABCD .易知直线AB 与平面BDD 1B 1成45°角，所以MN 与平面BDD 1B 1不垂直，所以A 正确，B ，C ，D 错误．故选A.解法二：以点D 为坐标原点，DA ，DC ，DD 1所在直线分别为x ，y ，z 轴建立空间直角坐标系．设AB ＝2，则A 1(2,0,2)，D (0,0,0)，D 1(0,0,2)，B (2，2,0)，所以M (1,0,1)，N (1,1,1)，所以A 1D →＝(－2,0，－2)，D 1B →＝(2,2，－2)，MN →＝(0,1,0)，所以A 1D →·D 1B →＝－4＋0＋4＝0，所以A 1D ⊥D 1B .又由图易知直线A 1D 与直线D 1B 是异面直线，所以直线A 1D与直线D 1B 异面且垂直．因为平面ABCD 的一个法向量为n ＝(0,0,1)，MN →·n ＝0，所以MN ∥平面ABCD .设直线MN 与平面BDD 1B 1所成的角为θ，因为平面BDD 1B 1的一个法向量为a ＝(－1，1,0)，所以sin θ＝|cos 〈MN →，a 〉|＝|MN →·a ||MN→||a |＝12＝22，所以直线MN 与平面BDD 1B 1不垂直．故选A.10．(2022·全国Ⅱ卷)设α，β为两个平面，则α∥β的充要条件是( )A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D．α，β垂直于同一平面答案B解析若α∥β，则α内有无数条直线与β平行，反之则不成立；若α，β平行于同一条直线，则α与β可以平行也可以相交；若α，β垂直于同一个平面，则α与β可以平行也可以相交，故A，C，D中条件均不是α∥β的充要条件．根据平面与平面平行的判定定理知，若一个平面内有两条相交直线与另一个平面平行，则这两个平面平行，反之也成立．因此，B中条件是α∥β的充要条件．故选B.11．(2022·浙江高考)已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m ∥α”的()A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件答案A解析∵m⊄α，n⊂α，m∥n，∴m∥α，故充分性成立．而由m∥α，n⊂α，得m∥n 或m与n异面，故必要性不成立．故选A.12．(2022·全国Ⅰ卷)如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是()答案A解析A项，作如图①所示的辅助线，其中D为BC的中点，则QD∥AB.∵QD与平面MNQ交于点Q，∴直线AB与平面MNQ相交．B项，作如图②所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ.又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ.C项，作如图③所示的辅助线，则AB∥CD，CD∥MQ，∴AB∥MQ.又AB⊄平面MNQ，MQ⊂平面MNQ，∴AB∥平面MNQ.D项，作如图④所示的辅助线，则AB∥CD，CD∥NQ，∴AB∥NQ.又AB⊄平面MNQ，NQ⊂平面MNQ，∴AB∥平面MNQ.故选A.13．(2016·全国Ⅱ卷)α，β是两个平面，m，n是两条直线，有下列四个命题：①如果m⊥n，m⊥α，n∥β，那么α⊥β；②如果m⊥α，n∥α，那么m⊥n；③如果α∥β，m⊂α，那么m∥β；④如果m∥n，α∥β，那么m与α所成的角和n与β所成的角相等．其中正确的命题有________(填写所有正确命题的编号)．答案②③④解析由m⊥n，m⊥α，可得n∥α或n在α内，当n∥β时，α与β可能相交，也可能平行，故①错误．易知②③④都正确．三、模拟小题14．(2022·辽宁铁岭六校高三模拟)已知m，n是两条不同的直线，α，β，γ是三个不同平面，则下列命题中正确的是()A．若m∥α，n∥α，则m∥nB．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n答案D解析若m∥α，n∥α，则m，n平行、相交或异面，故A错误；若α⊥γ，β⊥γ，则α，β平行或相交，故B错误；若m∥α，m∥β，则α，β平行或相交，故C错误；若m⊥α，n⊥α，由线面垂直的性质定理得m∥n，故D正确．故选D.15．(2022·江苏如皋市模拟)四棱锥P－ABCD中，底面ABCD为平行四边形，Q为AD的中点，点M在线段PC上，PM＝tPC，P A∥平面MQB，则实数t的值为()A.15 B ．14 C.13 D ．12答案 C解析四棱锥P －ABCD 中，连接AC 分别交BQ ，BD 于点N ，O .因为底面ABCD 为平行四边形，所以O 是AC 中点，也是BD 中点，而点Q 是AD 中点，于是得点N 是△ABD 的重心，从而得AN ＝23AO ＝13AC .连接MN ，如图．因为P A ∥平面MQB ，P A ⊂平面P AC ，平面P AC ∩平面MQB ＝MN ，所以P A ∥MN ，所以t ＝PM PC ＝AN AC ＝13.所以实数t 的值为13.故选C.16．(2022·河北石家庄期中)已知正方体ABCD －A 1B 1C 1D 1中，E ，F 分别是它们所在线段的中点，则满足A 1F ∥平面BD 1E 的图形的个数为( )A ．0B ．1 C.2 D ．3答案 B解析 ①中，平移A 1F 至D 1F ′，可知D 1F ′与平面BD 1E 只有一个交点D 1，则A 1F 与平面BD 1E 不平行；②中，由于A 1F ∥D 1E ，而A 1F ⊄平面BD 1E ，D 1E ⊂平面BD 1E ，故A1F∥平面BD1E；③中，平移A1F至D1F′，可知D1F′与平面BD1E只有一个交点D1，则A1F与平面BD1E不平行．故选B.17. (2022·福建宁德高三三模)如图，在直四棱柱ABCD－A1B1C1D1中，BC⊥CD，AB ∥CD，BC＝3，AA1＝AB＝AD＝2，点P，Q，R分别在棱BB1，CC1，DD1上，若A，P，Q，R四点共面，则下列结论错误的是()A．任意点P，都有AP∥QRB．任意点P，四边形APQR不可能为平行四边形C．存在点P，使得△APR为等腰直角三角形D．存在点P，使得BC∥平面APQR答案C解析对于A，在直四棱柱ABCD－A1B1C1D1中，因为AB∥CD，BB1∥CC1，所以平面ABB1A1∥平面DCC1D1，又因为平面APQR∩平面ABB1A1＝AP，平面APQR∩平面DCC1D1＝QR，所以AP∥QR，故A正确；对于B，若四边形APQR为平行四边形，则AR∥QP，而AD与BC不平行，即平面ADD1A1与平面BCC1B1不平行，又平面APQR∩平面BCC1B1＝QP，平面APQR∩平面ADD1A1＝AR，所以直线QP与直线AR不平行，与AR∥QP矛盾，所以四边形APQR不可能是平行四边形，故B正确；对于C，假设存在点P，使得△APR为等腰直角三角形，令BP＝x，过点D作DE⊥AB，则DE＝BC＝3，在线段DR上取一点M使得DM＝BP＝x，连接BD，PM，则四边形BDMP为矩形，所以MP＝BD＝2，则PR＝PM2＋MR2＝4＋(DR－x)2，AP＝BP2＋AB2＝x2＋4，AR＝DR2＋AD2＝4＋DR2，显然AR≠PR，若由AP＝PR，得x＝DR2，则AP＝PR＝4＋DR24，由AR＝2AP，即4＋DR2＝2·4＋DR24，得DR＝22＞2，故舍去，若由AP＝AR，则BP＝DR＝x且BP∥DR⇒四边形BPRD为平行四边形，所以RP＝BC2＋CD2＝2＝2AP＝8＋2BP2＝2x2＋8，无解，故C错误；对于D，当BP＝CQ，且DR＝12CQ时，满足BC∥平面APQR，故D 正确．故选C.18. (2022·湖北省襄阳市第四中学高三最后一模)如图，在棱长为2的正方体ABCD －A1B1C1D1中，E，F，G分别是棱AB，BC，CC1的中点，P是底面ABCD内一动点，若直线D1P与平面EFG不存在公共点，则△PBB1的面积的最小值为()A.22B．1 C.2D．2答案C解析延展平面EFG，可得截面EFGHQR，其中H，Q，R分别是所在棱的中点，直线D1P与平面EFG不存在公共点，所以D1P∥平面EFGHQR，由中位线定理可得AC∥EF，EF⊂平面EFGHQR，AC⊄平面EFGHQR，所以AC∥平面EFGHQR，因为Q，R分别是A1D1，AA1的中点，所以QR∥AD1，又AD1⊄平面EFGHQR，QR⊂平面EFGHQR，则AD1∥平面EFGHQR.又AC∩AD1＝A，AC⊂平面AD1C，AD1⊂平面AD1C，所以平面AD1C∥平面EFGHQR，又D1P∥平面EFGHQR，所以点P在AC上，因为BO与AC垂直，所以P与O重合时BP最小，此时△PBB1的面积最小，最小值为12×2×2＝ 2.故选C.19. (多选)(2022·河北衡水中学高三模拟预测)如图，一张矩形白纸ABCD，AB＝10，AD＝102，E，F分别为AD，BC的中点，BE交AC于点G，DF交AC于点H.现分别将△ABE，△CDF沿BE，DF折起，且点A，C在平面BFDE同侧，则下列命题为真命题的是()A．当平面ABE∥平面CDF时，AC∥平面BFDEB．当平面ABE∥平面CDF时，AE∥CDC．当A，C重合于点P时，PG⊥PDD．当A，C重合于点P时，三棱锥P－DEF的外接球的表面积为150π答案AD解析当平面ABE∥平面CDF时，如图，由已知矩形ABCD中，AB＝10，AD＝102，E，F分别为AD，BC的中点，可得AC⊥BE，AC⊥DF，且求得AG＝GH＝CH＝1033.则BE⊥平面AGH，DF⊥平面CHG，由BE∥DF，可得平面AGH与平面CHG重合，即四边形AGHC为平面四边形，∵平面ABE∥平面CDF，∴AG∥CH，又AG＝CH，可得四边形AGHC为平行四边形，则AC∥GH，可得AC∥平面BFDE，故A正确；假设AE∥CD，则四边形AEDC为平面图形，而GH∥AC，可得GH∥平面AEDC，又由GH⊂平面BFDE，平面BFDE∩平面AEDC＝DE，则GH∥DE，即四边形GHDE为平行四边形，可得GH＝DE，与GH≠DE矛盾，∴假设错误，故B 错误；当A ，C 重合于点P 时，如图，连接GD ，PG ＝1033，PD ＝GD ＝10，不满足PG 2＋PD 2＝GD 2，∴PG 与PD 不垂直，故C 错误；在三棱锥P －DEF 中，PE ＝PF ＝52，EF ＝10，∴△EPF 为直角三角形，PE ＝DE ＝52，PD ＝10，∴△PED 为直角三角形，而△FPD 为直角三角形，∴由补形法可知，三棱锥P －DEF 外接球的直径为PF 2＋PE 2＋DE 2＝150，则三棱锥P －DEF 的外接球的表面积为4π×⎝ ⎛⎭⎪⎫15022＝150π，故D 正确．故选AD. 20．(多选)(2022·河北唐山高三开学摸底考试)在直四棱柱ABCD －A 1B 1C 1D 1中，AB ∥CD ，AB ⊥AD ，AB ＝2AD ＝2DC ＝2DD 1＝4.则( )A ．在棱AB 上存在点P ，使得D 1P ∥平面A 1BC 1B ．在棱BC 上存在点P ，使得D 1P ∥平面A 1BC 1C ．若P 在棱AB 上移动，则A 1D ⊥D 1PD ．在棱A 1B 1上存在点P ，使得DP ⊥平面A 1BC 1答案 ABC解析对于A ，当P 是AB 的中点时，依题意可知D 1C 1∥DC ∥PB ，D 1C 1＝DC ＝PB ，所以四边形D 1PBC 1是平行四边形，所以D 1P ∥C 1B ，由于D 1P ⊄平面A 1BC 1，C 1B ⊂平面A 1BC 1，所以D 1P ∥平面A 1BC 1，A 正确；对于B ，设E 是AB 的中点，P 是BC 的中点，由上述分析可知D 1E ∥平面A 1BC 1.由于PE ∥AC ∥A 1C 1，PE ⊄平面A 1BC 1，A 1C 1⊂平面A 1BC 1，所以PE ∥平面A 1BC 1.由于D 1E ∩PE ＝E ，所以平面D 1PE ∥平面A 1BC 1，所以D 1P ∥平面A 1BC 1，B 正确；对于C ，根据已知条件可知四边形ADD 1A 1是正方形，所以A 1D ⊥D 1A ，由于AB ⊥AD ，AB ⊥AA 1，AD ∩AA 1＝A ，所以AB ⊥平面ADD 1A 1，所以AB ⊥A 1D .由于D 1A ∩AB ＝A ，所以A 1D ⊥平面AD 1P ，所以A 1D ⊥D 1P ，C 正确；对于D ，建立如图所示的空间直角坐标系，则A 1(2,0,2)，B (2,4,0)，C 1(0,2,2)，A 1B →＝(0,4，－2)，A 1C 1→＝(－2,2,0)．设P (2，t,2)，t ∈[0,4].⎩⎪⎨⎪⎧ DP →·A 1B →＝4t －4＝0，DP →·A 1C 1→＝－4＋2t ＝0，此方程组无解，所以在棱A 1B 1上不存在点P ，使得DP ⊥平面A 1BC 1，D 错误．故选ABC.一、高考大题1．(2022·天津高考) 如图，在棱长为2的正方体ABCD－A1B1C1D1中，E为棱BC 的中点，F为棱CD的中点．(1)求证：D1F∥平面A1EC1；(2)求直线AC1与平面A1EC1所成角的正弦值；(3)求二面角A－A1C1－E的正弦值．解(1)证法一：以A为原点，AB，AD，AA1所在直线分别为x，y，z轴，建立如图所示的空间直角坐标系，则A(0,0,0)，A1(0,0,2)，B(2,0,0)，C(2,2,0)，D(0,2,0)，C1(2,2,2)，D1(0,2,2)，因为E 为棱BC 的中点，F 为棱CD 的中点，所以E (2,1,0)，F (1,2,0)，所以D 1F →＝(1,0，－2)，A 1C 1→＝(2,2,0)，A 1E →＝(2,1，－2)，设平面A 1EC 1的法向量为m ＝(x 1，y 1，z 1)，则⎩⎪⎨⎪⎧ m ·A 1C 1→＝2x 1＋2y 1＝0，m ·A 1E →＝2x 1＋y 1－2z 1＝0，令x 1＝2，则m ＝(2，－2,1)为平面A 1EC 1的一个法向量，因为D 1F →·m ＝2－2＝0，所以D 1F →⊥m ，因为D 1F ⊄平面A 1EC 1，所以D 1F ∥平面A 1EC 1.证法二：连接B 1D 1与A 1C 1交于点G ，连接EF ，EG ，BD .则GD 1＝12B 1D 1＝12BD ，GD 1∥BD .又E ，F 分别为BC ，CD 的中点，可知EF ∥BD ，且EF ＝12BD ，所以EF ＝GD 1，且EF ∥GD 1.所以四边形GEFD 1为平行四边形．所以D 1F ∥GE .又GE ⊂平面A 1EC 1，D 1F ⊄平面A 1EC 1，所以D 1F ∥平面A 1EC 1.(2)由(1)得，AC 1→＝(2,2,2)，设直线AC 1与平面A 1EC 1所成的角为θ，则sin θ＝|cos 〈m ，AC 1→〉|＝⎪⎪⎪⎪⎪⎪⎪⎪m ·AC 1→|m ||AC 1→|＝23×23＝39. (3)如图，连接DB .由正方体的特征可得，平面AA 1C 1的一个法向量为DB →＝(2，－2,0)，则cos 〈DB →，m 〉＝DB →·m |DB→||m |＝822×3＝223，所以二面角A －A 1C 1－E 的正弦值为1－cos 2〈DB →，m 〉＝13. 2．(2022·北京高考) 如图，在正方体ABCD －A 1B 1C 1D 1中，E 为BB 1的中点．(1)求证：BC 1∥平面AD 1E ；(2)求直线AA 1与平面AD 1E 所成角的正弦值．解 (1)证明：在正方体ABCD －A 1B 1C 1D 1中，AB ∥A 1B 1且AB ＝A 1B 1，A 1B 1∥C 1D 1且A 1B 1＝C 1D 1，∴AB ∥C 1D 1且AB ＝C 1D 1，∴四边形ABC 1D 1为平行四边形，∴BC 1∥AD 1.∵BC 1⊄平面AD 1E ，AD 1⊂平面AD 1E ，∴BC 1∥平面AD 1E .(2)以点A 为坐标原点，AD ，AB ，AA 1所在直线分别为x 轴、y 轴、z 轴，建立如图所示的空间直角坐标系Axyz ，设正方体ABCD －A 1B 1C 1D 1的棱长为2，则A (0，0,0)，A 1(0,0,2)，D 1(2,0,2)，E (0,2,1)，AA 1→＝(0,0,2)，AD 1→＝(2,0,2)，AE →＝(0,2,1)．设平面AD 1E 的法向量为n ＝(x ，y ，z )，由⎩⎪⎨⎪⎧ n ·AD 1→＝0，n ·AE →＝0，得⎩⎨⎧2x ＋2z ＝0，2y ＋z ＝0，令z ＝－2，则x ＝2，y ＝1，则n ＝(2,1，－2)为平面AD 1E 的一个法向量．设直线AA 1与平面AD 1E 所成的角为θ，则sin θ＝|cos 〈n ，AA 1→〉|＝|n ·AA 1→||n ||AA 1→|＝43×2＝23.因此，直线AA 1与平面AD 1E 所成角的正弦值为23.3. (2022·全国Ⅱ卷)如图，已知三棱柱ABC －A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点，过B 1C 1和P 的平面交AB 于E ，交AC 于F .(1)证明：AA1∥MN，且平面A1AMN⊥平面EB1C1F；(2)设O为△A1B1C1的中心，若AO∥平面EB1C1F，且AO＝AB，求直线B1E与平面A1AMN所成角的正弦值．解(1)证明：∵M，N分别为BC，B1C1的中点，∴MN∥BB1.又AA1∥BB1，∴AA1∥MN.∵△A1B1C1为等边三角形，N为B1C1的中点，∴A1N⊥B1C1.又侧面BB1C1C为矩形，∴B1C1⊥BB1.∵MN∥BB1，∴MN⊥B1C1.又MN∩A1N＝N，MN，A1N⊂平面A1AMN，∴B1C1⊥平面A1AMN.又B1C1⊂平面EB1C1F，∴平面A1AMN⊥平面EB1C1F.(2)解法一：连接NP，∵AO∥平面EB1C1F，平面AONP∩平面EB1C1F＝NP，∴AO ∥NP .∵三棱柱上下底面平行，平面A 1AMN ∩平面ABC ＝AM ，平面A 1AMN ∩平面A 1B 1C 1＝A 1N ， ∴ON ∥AP .∴四边形ONP A 是平行四边形． ∴ON ＝AP ，AO ＝NP . 设△ABC 边长是6m (m ＞0)，则NP ＝AO ＝AB ＝6m .∵O 为△A 1B 1C 1的中心，且△A 1B 1C 1的边长为6m ， ∴ON ＝13×6m ×sin60°＝3m . ∴AP ＝ON ＝3m .∵BC ∥B 1C 1，B 1C 1⊂平面EB 1C 1F ，BC ⊄平面EB 1C 1F ， ∴BC ∥平面EB 1C 1F .又BC ⊂平面ABC ，平面ABC ∩平面EB 1C 1F ＝EF ， ∴EF ∥BC ，∴AP AM ＝EP BM ，∴3m 33m ＝EP3m，解得EP＝m.在B1C1截取B1Q＝EP＝m，连接PQ，故QN＝2m.∵B1Q＝EP且B1Q∥EP，∴四边形B1QPE是平行四边形，∴B1E∥PQ.由(1)可知B1C1⊥平面A1AMN，故∠QPN为直线B1E与平面A1AMN所成的角．在Rt△QPN中，根据勾股定理可得PQ＝QN2＋NP2＝(2m)2＋(6m)2＝210m，∴sin∠QPN＝QNPQ ＝2m210m＝1010.∴直线B1E与平面A1AMN所成角的正弦值为1010.解法二：由(1)知B1C1⊥平面A1AMN，又BC∥B1C1，∴BC⊥平面A1AMN，∴平面A1AMN⊥平面ABC，作NQ⊥AM，垂足为Q，则NQ⊥平面ABC.由已知得AM⊥BC，以Q为坐标原点，QA→的方向为x轴正方向，QN→的方向为z轴正方向，|MB →|为单位长，建立如图所示的空间直角坐标系Qxyz ，则AB ＝2，AM ＝ 3.设M (－a,0,0)．连接NP ，则四边形AONP 为平行四边形， ∴NP ＝AO ＝AB ＝2， ∴PQ ＝⎪⎪⎪⎪⎪⎪233－a， NQ ＝NP 2－PQ 2＝4－⎝ ⎛⎭⎪⎫233－a 2， ∴B 1⎝⎛⎭⎪⎫0，1，4－⎝ ⎛⎭⎪⎫233－a 2，E ⎝ ⎛⎭⎪⎫233－a ，13，0，故B 1E →＝⎝ ⎛⎭⎪⎫233－a ，－23，－4－⎝ ⎛⎭⎪⎫233－a 2，|B 1E →|＝2103.又n ＝(0，－1,0)是平面A 1AMN 的一个法向量，设直线B 1E 与平面A 1AMN 所成的角为θ， ∴sin θ＝|cos 〈n ，B 1E →〉|＝|n ·B 1E →||n ||B 1E →|＝1010. ∴直线B 1E 与平面A 1AMN 所成角的正弦值为1010.4. (2022·全国Ⅰ卷)如图，直四棱柱ABCD －A 1B 1C 1D 1的底面是菱形，AA 1＝4，AB ＝2，∠BAD ＝60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．(1)证明：MN∥平面C1DE；(2)求二面角A－MA1－N的正弦值．解(1)证明：如图，连接B1C，ME.因为M，E分别为BB1，BC的中点，所以ME∥B1C，且ME＝12B1C.又因为N为A1D的中点，所以ND＝12A1D.由题设知A1B1綊DC，可得B1C綊A1D，故ME綊ND，因此四边形MNDE为平行四边形，所以MN∥ED.又MN⊄平面C1DE，ED⊂平面C1DE，所以MN∥平面C1DE.(2)由已知可得DE ⊥DA ，以D 为坐标原点，DA→的方向为x 轴正方向，DE →的方向为y 轴正方向，DD 1→的方向为z 轴正方向，建立如图所示的空间直角坐标系Dxyz ，则A (2,0,0)，A 1(2,0,4)，M (1，3，2)，N (1,0,2)，A 1A →＝(0,0，－4)，A 1M →＝(－1，3，－2)，A 1N →＝(－1,0，－2)，MN →＝(0，－3，0)．设m ＝(x ，y ，z )为平面A 1MA 的法向量，则⎩⎪⎨⎪⎧m ·A 1M →＝0，m ·A 1A →＝0，所以⎩⎨⎧－x ＋3y －2z ＝0，－4z ＝0，可取m ＝(3，1,0)．设n ＝(p ，q ，r )为平面A 1MN 的法向量，则⎩⎪⎨⎪⎧n ·MN →＝0，n ·A 1N →＝0，所以⎩⎨⎧－3q ＝0，－p －2r ＝0，可取n ＝(2,0，－1)．于是cos 〈m ，n 〉＝m ·n |m ||n |＝232×5＝155，sin 〈m ，n 〉＝1－⎝⎛⎭⎪⎫1552＝105，所以二面角A －MA 1－N 的正弦值为105.5. (2022·天津高考)如图，AE ⊥平面ABCD ，CF ∥AE ，AD ∥BC ，AD ⊥AB ，AB ＝AD ＝1，AE ＝BC ＝2.(1)求证：BF ∥平面ADE ；(2)求直线CE 与平面BDE 所成角的正弦值；(3)若二面角E －BD －F 的余弦值为13，求线段CF 的长．解 (1)证明：以A 为坐标原点，AB 所在的直线为x 轴，AD 所在的直线为y 轴，AE 所在的直线为z 轴，建立如图所示的空间直角坐标系．则A (0，0,0)，B (1,0,0)，设F (1，2，h )．依题意，AB→＝(1,0,0)是平面ADE 的一个法向量，又BF →＝(0,2，h )，可得BF →·AB→＝0，又因为直线BF ⊄平面ADE ，所以BF ∥平面ADE .(2)依题意，D (0,1,0)，E (0,0,2)，C (1,2,0)，则BD →＝(－1,1,0)，BE →＝(－1,0,2)，CE →＝(－1，－2,2)．设n ＝(x ，y ，z )为平面BDE 的法向量，则⎩⎪⎨⎪⎧n ·BD →＝0，n ·BE →＝0，即⎩⎨⎧－x ＋y ＝0，－x ＋2z ＝0，不妨令z ＝1，可得n ＝(2,2,1)为平面BDE 的一个法向量．设直线CE 与平面BDE 所成的角为θ，则sin θ＝|cos 〈CE →，n 〉|＝|CE →·n ||CE →||n |＝49.所以直线CE 与平面BDE 所成角的正弦值为49. (3)设m ＝(x 1，y 1，z 1)为平面BDF 的法向量，则⎩⎪⎨⎪⎧m ·BD →＝0，m ·BF →＝0，即⎩⎨⎧－x 1＋y 1＝0，2y 1＋hz 1＝0，不妨令y 1＝1，可得m ＝⎝ ⎛⎭⎪⎫1，1，－2h 为平面BDF 的一个法向量．由题意，有|cos 〈m ，n 〉|＝|m ·n ||m ||n |＝⎪⎪⎪⎪⎪⎪4－2h 32＋4h 2＝13，解得h ＝87.经检验，符合题意．所以线段CF 的长为87. 二、模拟大题6. (2022·浙江省名校协作体高三上学期开学考试)如图所示，在三棱柱BCD －B 1C 1D 1与四棱锥A －BB 1D 1D 的组合体中，已知BB 1⊥平面BCD ，四边形ABCD 是菱形，∠BCD ＝60°，AB ＝2，BB 1＝1.(1)设O是线段BD的中点，求证：C1O∥平面AB1D1；(2)求直线B1C与平面AB1D1所成角的正弦值．解(1)证明：取B1D1的中点为E，连接C1E，OA，AE，易知C1E＝OA且C1E∥OA，所以四边形C1EAO为平行四边形，所以C1O∥EA，又C1O⊄平面AB1D1，AE⊂平面AB1D1，所以C1O∥平面AB1D1.(2)解法一：过点C作平面AB1D1的垂线，垂足为G，连接B1G(图略)，则∠CB1G 就是直线B1C与平面AB1D1所成的角．又CG是点O到平面AB1D1的距离的2倍，连接EO，由B1D1⊥EC1，B1D1⊥EO，知B1D1⊥平面AEO，所以平面AEO⊥平面AB1D1，在△AEO中，作OH⊥AE，垂足为H，即OH⊥平面AB1D1.由题可得AO＝3，B1C＝5，AE＝2，所以在Rt△AEO中，OH＝AO·OEAE ＝32，所以点C 到平面AB 1D 1的距离为3，所以sin ∠CB 1G ＝CG B 1C ＝155.解法二：如图所示，以O 为坐标原点，OA ，OB ，OE 所在的直线分别为x ，y ，z 轴，建立空间直角坐标系Oxyz ，得A (3，0,0)，B 1(0,1,1)，D 1(0，－1,1)，C (－3，0,0)，所以AB 1→＝(－3，1,1)，D 1B 1→＝(0,2,0)，B 1C →＝(－3，－1，－1)，设平面AB 1D 1的法向量为n ＝(x ，y ，z )，则⎩⎪⎨⎪⎧n ·AB 1→＝0，n ·D 1B 1→＝0，得⎩⎨⎧－3x ＋y ＋z ＝0，2y ＝0，令x ＝1，有y ＝0，z ＝3，所以n ＝(1,0，3)为平面AB 1D 1的一个法向量．记α为直线B 1C 与平面AB 1D 1所成的角，则sin α＝|n ·B 1C →||n ||B 1C →|＝155.7. (2022·河北张家口第一次模拟)如图，四边形ABCD 是正方形，P A ⊥平面ABCD ，P A ∥EB ，且P A ＝AB ＝3.(1)求证：CE∥平面P AD；(2)若BE＝13P A，求直线PD与平面PCE所成角的正弦值．解(1)证明：因为四边形ABCD是正方形，所以BC∥AD.又AD⊂平面P AD，BC⊄平面P AD，所以BC∥平面P AD.因为P A∥EB，P A⊂平面P AD，EB⊄平面P AD，所以EB∥平面P AD，又BC∩EB＝B，所以平面EBC∥平面P AD，又因为CE⊂平面EBC，所以CE∥平面P AD.(2) 以A为坐标原点，AD，AB，AP所在直线分别为x，y，z轴建立如图所示的空间直角坐标系．因为P A＝AB＝3，所以BE＝13P A＝1，则P(0,0,3)，D(3,0,0)，C(3,3,0)，E(0,3,1)，则PD→＝(3,0，－3)，PC→＝(3,3，－3)，PE→＝(0,3，－2)．设平面PCE的法向量为m＝(x，y，z)，则由⎩⎪⎨⎪⎧ m ·PC →＝(x ，y ，z )·(3，3，－3)＝3x ＋3y －3z ＝0，m ·PE →＝(x ，y ，z )·(0，3，－2)＝3y －2z ＝0，得⎩⎪⎨⎪⎧ x ＝z 3，y ＝2z 3，令z ＝3，得平面PCE 的一个法向量为m ＝(1,2,3)，设直线PD 与平面PCE 所成角为θ，则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪PD →·m |PD →||m |＝⎪⎪⎪⎪⎪⎪(3，0，－3)·(1，2，3)32×14＝77. 所以直线PD 与平面PCE 所成角的正弦值为77.8. (2022·湖南省汨罗市二中高三入学考试)如图，在四棱锥P －ABCD 中，底面ABCD 为边长为2的菱形，∠DAB ＝60°，∠ADP ＝90°，平面ADP ⊥平面ABCD ，点F 为棱PD 的中点．(1)在棱AB 上是否存在一点E ，使得AF ∥平面PCE ？并说明理由；(2)当二面角D －FC －B 的余弦值为24时，求直线PB 与平面ABCD 所成的角．解 (1)在棱AB 上存在点E ，使得AF ∥平面PCE ，点E 为棱AB 的中点．理由如下：取PC 的中点Q ，连接EQ ，FQ ，由题意，FQ ∥CD 且FQ ＝12CD ，AE ∥CD 且AE ＝12CD ，则AE ∥FQ 且AE ＝FQ .所以四边形AEQF 为平行四边形．所以AF ∥EQ ，又EQ ⊂平面PCE ，AF ⊄平面PCE ，所以AF ∥平面PCE .(2)由题意，知△ABD 为正三角形，所以ED ⊥AB ，亦即ED ⊥CD ，又∠ADP ＝90°，所以PD ⊥AD ，且平面ADP ⊥平面ABCD ，平面ADP ∩平面ABCD ＝AD ，所以PD ⊥平面ABCD ，故以D 为坐标原点建立如图所示的空间直角坐标系，设FD ＝a (a >0)，则由题意知D (0,0,0)，F (0,0，a )，C (0，2,0)，B (3，1,0)， FC→＝(0,2，－a )，CB →＝(3，－1,0)，设平面FBC 的法向量为m ＝(x ，y ，z )，则由⎩⎪⎨⎪⎧ m ·FC →＝0，m ·CB →＝0，得⎩⎨⎧2y －az ＝0，3x －y ＝0，令x ＝1，则y ＝3，z ＝23a ，所以取m ＝⎝⎛⎭⎪⎫1，3，23a ，显然可取平面DFC 的一个法向量n ＝(1,0,0)，由题意知24＝|cos〈m，n〉|＝11＋3＋12a2，所以a＝ 3.由于PD⊥平面ABCD，所以PB在平面ABCD内的射影为BD，所以∠PBD即为直线PB与平面ABCD所成的角，易知在Rt△PBD中，tan∠PBD＝PDBD＝a＝3，从而∠PBD＝60°，所以直线PB与平面ABCD所成的角为60°.。

高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理：平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

简记为：线线平行，则线面平行。

符号表示：a αb β => a∥αa∥b●知能训练一．选择题1．已知m，n是两条不同直线，α，β，γ是三个不同平面，下列命题中正确的是（）A．若m∥α，n∥α，则m∥n B．若α⊥γ，β⊥γ，则α∥βC．若m∥α，m∥β，则α∥βD．若m⊥α，n⊥α，则m∥n2．若直线l不平行于平面α，且l⊄α，则（）A．α内存在直线与l异面B．α内存在与l平行的直线C．α内存在唯一的直线与l平行D．α内的直线与l都相交3．如图，M是正方体ABCD-A1B1C1D1的棱DD1的中点，给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交；②过M点有且只有一条直线与直线AB、B1C1都垂直；③过M点有且只有一个平面与直线AB、B1C1都相交；④过M点有且只有一个平面与直线AB、B1C1都平行．其中真命题是（）A．②③④B．①③④C．①②④D．①②③4．正方体ABCD-A1B1C1D1中M，N，Q分别是棱D1C1，A1D1，BC的中点．P在对角线BD1上，且BP＝BD1，给出下面四个命题：（1）MN∥面APC；（2）C1Q∥面APC；（3）A，P，M三点共线；（4）面MNQ∥面APC．正确的序号为（）A．（1）（2）B．（1）（4）C．（2）（3）D．（3）（4）5．在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中，任取两点连成直线，所连的直线中与A1BC1平行的直线共有（）A．12条B．18条C．21条D．24条6．直线a∥平面α，P∈α，那么过P且平行于a的直线（）A．只有一条，不在平面α内B．有无数条，不一定在平面α内C．只有一条，且在平面α内D．有无数条，一定在平面α内7．如果直线a∥平面α，那么直线a与平面α内的（）A．一条直线不相交B．两条直线不相交C．无数条直线不相交D．任意一条直线不相交8．如图在正方体ABCD-A1B1C1D1中，与平面AB1C平行的直线是（）A．DD1B．A1D1C．C1D1D．A1D9．如图，在三棱柱ABC-A1B1C1中，点D为AC的中点，点D1是A1C1上的一点，若BC1∥平面AB1D1，则等于（）A．1/2B．1 C．2 D．310．下面四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形是（）A．①②B．①④C．②③D．③④11．如图，正方体的棱长为1，线段B′D′上有两个动点E，F，EF=，则下列结论中错误的是（）A．AC⊥BEB．EF∥平面ABCDC．三棱锥A-BEF的体积为定值D．异面直线AE，BF所成的角为定值二．填空题12．如图，在正方体ABCD-A1B1C1D1中，E，F，G，H，M分别是棱AD，DD1，D1A1，A1A，AB的中点，点N在四边形EFGH的四边及其内部运动，则当N只需满足条件时，就有MN⊥A1C1；当N只需满足条件时，就有MN∥平面B1D1C．13．如图，正方体ABCD-A1B1C1D1中，AB=2，点E为AD的中点，点F在CD上，若EF∥平面AB1C，则线段EF的长度等于．三．解答题14．如图，在三棱柱ABC-A1B1C1中，侧棱AA1⊥底面ABC，AB⊥BC，D为AC的中点，AA1=AB=2．（1）求证：AB 1∥平面BC1D；（2）若BC=3，求三棱锥D-BC1C的体积．2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理：一个平面内的两条交直线与另一个平面平行，则这两个平面平行。

高中数学练习题线面、面面平行的判定与性质

线面、面面平行的判定与性质基础巩固强化1.已知l是直线，α、β是两个不同平面，下列命题中的真命题是()A．若l∥α，l∥β，则α∥βB．若α⊥β，l∥α，则l⊥βC．若l⊥α，l∥β，则α⊥βD．若l∥α，α∥β，则l∥β2．已知m、n是两条直线，α、β是两个平面，给出下列命题：①若n⊥α，n⊥β，则α∥β；②若平面α上有不共线的三点到平面β的距离相等，则α∥β；③若n、m为异面直线，n⊂α，n∥β，m⊂β，m∥α，则α∥β.其中正确命题的个数是()A．3个B．2个C．1个D．0个一个正方体纸盒展开后如图，在原正方体纸盒中有下列结论：①AB⊥EF②AB与CM成60°③EF与MN是异面直线④MN∥CD其中正确的是()A．①②B．③④C．②③D．①③3．已知平面α∩β＝l，m是α内不同于l的直线，那么下列命题中错误．．的是()A．若m∥β，则m∥l B．若m∥l，则m∥βC．若m⊥β，则m⊥l D．若m⊥l，则m⊥β4．设a、b是两条不同的直线，α、β是两个不同的平面，则下列命题错误的是()A．若a⊥α，b∥α，则a⊥bB．若a⊥α，b∥a，b⊂β，则α⊥βC．若a⊥α，b⊥β，α∥β，则a∥bD．若a∥α，a∥β，则α∥β对于平面α和共面的直线m、n，下列命题是真命题的是()A．若m，n与α所成的角相等，则m∥n B．若m∥α，n∥α，则m∥nC．若m⊥α，m⊥n，则n∥αD．若m⊂α，n∥α，则m∥n5．设α、β是两个不同的平面，a、b是两条不同的直线，给出下列四个命题，其中真命题是() A．若a∥α，b∥α，则a∥b B．若a∥α，b∥β，a∥b，则α∥βC．若a⊥α，b⊥β，a∥b，则α∥βD．若a、b在平面α内的射影互相垂直，则a⊥b 6．设两个平面α、β，直线l，下列三个条件：①l⊥α；②l∥β；③α⊥β.若以其中两个作为前提，另一个作为结论，则可构成三个命题，这三个命题中正确命题的个数为()A ．3B ．2C ．1D ．07．正方体ABCD －A 1B 1C 1D 1的棱长为1cm ，过AC 作平行于对角线BD 1的截面，则截面面积为________．8．在空间中，有如下命题：①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线； ②若平面α∥平面β，则平面α内任意一条直线m ∥平面β；③若平面α与平面β的交线为m ，平面α内的直线n ⊥直线m ，则直线n ⊥平面β； ④若平面α内的三点A 、B 、C 到平面β的距离相等，则α∥β. 其中正确命题的序号为________．9．已知m 、n 是两条不重合的直线，α、β、γ是三个两两不重合的平面，给出下列命题： ①若m ∥α，n ∥α，m ∥β，n ∥β，则α∥β； ②若α⊥γ，β⊥γ，α∩β＝m ，n ⊂γ，则m ⊥n ； ③若m ⊥α，α⊥β，m ∥n ，则n ∥β； ④若n ∥α，n ∥β，α∩β＝m ，那么m ∥n . 其中正确命题的序号是________．10．如图，直三棱柱ABC －A ′B ′C ′，∠BAC ＝90°，AB ＝AC ＝2，AA ′＝1，点M 、N 分别为A ′B 和B ′C ′的中点．(1)证明：MN ∥平面A ′ACC ′；(2)求三棱锥A ′－MNC 的体积(锥体体积公式V ＝13Sh ，其中S 为底面面积，h 为高)．如图，在侧棱垂直底面的四棱柱ABCD －A 1B 1C 1D 1中，AD ∥BC ，AD ⊥AB ，AB ＝2，AD ＝2，BC ＝4，AA 1＝2，E 是DD 1的中点，F是平面B1C1E与直线AA1的交点．(1)证明：①EF∥A1D1；②BA1⊥平面B1C1EF；(2)求BC1与平面B1C1EF所成角的正弦值．能力拓展提升11.如图，正方体ABCD－A1B1C1D1中，E、F分别为棱AB、CC1的中点，在平面ADD1A1内且与平面D1EF平行的直线()A．不存在B．有1条C．有2条D．有无数条12．如图，若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论中不正确．．．的是()A．EH∥FG B．四边形EFGH是矩形C．Ω是棱柱D．Ω是棱台下列命题中，是假命题的是()A．三角形的两条边平行于一个平面，则第三边也平行于这个平面B．平面α∥平面β，a⊂α，过β内的一点B有唯一的一条直线b，使b∥aC．α∥β，γ∥δ，α、β与γ、δ的交线分别为a、b和c、d，则a∥b∥c∥dD．一条直线与两个平面成等角是这两个平面平行的充要条件13．(2012·南昌二模)若P是两条异面直线l、m外的任意一点，则下列命题中假命题的序号是________．①过点P有且仅有一条直线与l、m都平行；②过点P有且仅有一条直线与l、m都垂直；③过点P有且仅有一条直线与l、m都相交；④过点P有且仅有一条直线与l、m都异面．14．下列四个正方体图形中，A、B为正方体的两个顶点，M、N、P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号)．15．(2011·广东揭阳一模)如图，已知平行四边形ABCD中，BC＝6，正方形ADEF所在平面与平面ABCD垂直，G、H分别是DF、BE的中点．(1)求证：GH∥平面CDE；(2)若CD＝2，DB＝42，求四棱锥F－ABCD的体积．[解析](1)证法1：∵EF∥AD，AD∥BC，∴EF∥BC.又EF＝AD＝BC，∴四边形EFBC是平行四边形，∴H为FC的中点．又∵G是FD的中点，∴GH∥CD.∵GH⊄平面CDE，CD⊂平面CDE，∴GH∥平面CDE.证法2：连接EA，∵ADEF是正方形，∴G是AE的中点．∴在△EAB中，GH∥AB.又∵AB∥CD，∴GH∥CD.∵HG⊄平面CDE，CD⊂平面CDE，∴GH∥平面CDE.(2)∵平面ADEF⊥平面ABCD，交线为AD，且F A⊥AD，∴F A⊥平面ABCD.∵AD＝BC＝6，∴F A＝AD＝6.又∵CD＝2，DB＝42，CD2＋DB2＝BC2，∴BD⊥CD. ∵S▱ABCD＝CD·BD＝82，∴V F－ABCD＝13S▱ABCD·F A＝13×82×6＝16 2.(理)如图，在多面体ABCDEF中，四边形ABCD是正方形，AB＝2EF＝2，EF∥AB，EF⊥FB，∠BFC＝90°，BF＝FC，H为BC的中点．(1)求证：FH∥平面EDB；(2)求证：AC⊥平面EDB；(3)求四面体B－DEF的体积．[解析](1)证明：设AC与BD交于点G，联结EG、GH.则G为AC中点，∵H是BC中点，∴GH綊12AB，又∵EF綊12AB，∴四边形EFHG为平行四边形．∴FH∥EG.又EG⊂平面EDB，而FH⊄平面EDB，∴FH∥平面EDB.(2)证明：∵EF∥AB，EF⊥FB.∴AB⊥FB.又四边形ABCD为正方形，∴AB⊥BC，又FB∩BC＝B，∴AB⊥平面BFC.∵FH⊂平面BFC，∴AB⊥FH.又∵FB＝FC，H是BC中点，∴FH⊥BC.又AB∩BC＝B，∴FH⊥平面ABCD，∴FH⊥AC. 又EG∥FH，∴EG⊥AC，又AC⊥BD，BD∩EG＝G，∴AC⊥平面EDB.(3)∵EF⊥BF，BF⊥FC且EF∩FC＝F，∴BF⊥平面CDEF，∴BF 为四面体B —DEF 的高．又∵BC ＝AB ＝2，∴BF ＝FC ＝ 2.四边形CDEF 为直角梯形，且EF ＝1，CD ＝2. ∴S △DEF ＝12(1＋2)×2－12×2×2＝22∴V B —DEF ＝13×22×2＝13. 16.(2012·辽宁大连市、沈阳市联考)如图，在四棱锥P －ABCD 中，P A ⊥底面ABCD ，四边形ABCD 为长方形，AD ＝2AB ，点E 、F 分别是线段PD 、PC 的中点．(1)证明：EF ∥平面P AB ；(2)在线段AD 上是否存在一点O ，使得BO ⊥平面P AC ，若存在，请指出点O 的位置，并证明BO ⊥平面P AC ；若不存在，请说明理由．[解析] (1)证明：∵EF ∥CD ，CD ∥AB ，∴EF ∥AB ，又∵EF ⊄平面P AB ，AB ⊂平面P AB ，(2)在线段AD上存在一点O，使得BO⊥平面P AC，此时点O为线段AD的四等分点，且AO＝14AD，∵P A⊥底面ABCD，∴P A⊥BO，又∵长方形ABCD中，AD＝2AB，∴△ABO△DAC，∴∠ABO＋∠BAC＝∠DAC＋∠BAC＝90°，∴AC⊥BO，又∵P A∩AC＝A，∴BO⊥平面P AC.1．(2012·四川文，6)下列命题正确的是()A．若两条直线和同一个平面所成的角相等，则这两条直线平行B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行D．若两个平面都垂直于第三个平面，则这两个平面平行[答案] C[解析]本题考查了线面角，面面垂直，线面平行，面面平行等位置关系的判定与性质，对于A选项，两条直线也可相交，B选项若三点在同一条直线上，平面可相交．D选项这两个平面可相交(可联系墙角)，而C项可利用线面平行的性质定理，再运用线面平行的判定与性质可得．本题需要我们熟练掌握各种位置关系的判定与性质．2．(2012·石家庄二模)三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等，且长分别为2、m 、n ，其中m 2＋n 2＝6，则该三棱锥体积的最大值为( )A.12B.8327 C.33 D.23[答案] D[解析] 令m ＝n ，由m 2＋n 2＝6得m ＝n ＝3，取AB 的中点E ，则BE ＝22，PB ＝3，∴PE ＝102，CE ＝102，∴EF ＝2，∴V P －ABC ＝13S △PEC ·AB ＝13×(12×2×2)×2＝23，∵23>12，∴23>33，23>8327，故选D.3．如图，正四棱柱ABCD －A 1B 1C 1D 1中，AA 1＝2，AB ＝1，M ，N 分别在AD 1、BC 上移动，且始终保持MN ∥平面DCC 1D 1，设BN ＝x ，MN ＝y ，则函数y ＝f (x )的图象大致是( )[答案] C[解析] 过M 作ME ⊥AD 于E ，连接EN ，则平面MEN ∥平面DCC 1D 1，所以BN ＝AE ＝x (0≤x <1)，ME ＝2x ，MN 2＝ME 2＋EN 2，则y 2＝4x 2＋1，y 2－4x 2＝1(0≤x <1，y >0)，图象应是焦点在y 轴上的双曲线的一部分．故选C.4．(2012·东营市期末)设m 、n 是两条不同的直线，α、β是两个不同的平面，给出下列四个命题：①若m ⊥n ，m ⊥α，n ⊄α，则n ∥α；②若α⊥β，α∩β＝m ，n ⊥m ，则n ⊥α或n ⊥β； ③若m ⊥β，α⊥β，则m ∥α； ④若m ⊥n ，m ⊥α，n ⊥β，则α⊥β. 其中真命题的序号是________． [答案] ①④⎭⎪⎬⎪⎫ ⎭⎪⎬⎪⎫[解析] m ⊥n m ⊥α⇒n ∥α或n ⊂α n ⊄α⇒n ∥α，故①真；正方体ABCD －A 1B 1C 1D 1中，平面ABCD 与ADD 1A 1分别取作平面α，β，其交线AD 为m ，取直线AB 1为n ，则满足n ⊥m ，知②错；m ⊥β，α⊥β时，可能m ∥α，也可能m ⊂α，知③错；⎭⎬⎫ ⎭⎪⎬⎪⎫m ⊥n m ⊥α⇒n ∥α或n ⊂αn ⊥β⇒α⊥β，故④真．。

2022版高考数学一轮复习第8章第3讲直线平面平行的判定与性质训练含解析

第八章第3讲[A级基础达标]1．有下列命题：①若直线l平行于平面α内的无数条直线，则直线l∥α；②若直线a在平面α外，则a ∥α；③若直线a∥b，b∥α，则a∥α；④若直线a∥b，b∥α，则a平行于平面α内的无数条直线．其中真命题的个数是()A．1B．2C．3D．4【答案】A2．下列四个正方体图形中，A，B为正方体的两个顶点，M，N，P分别为其所在棱的中点，能得出AB∥平面MNP的图形的序号是()A．①③B．②③C．①④D．②④【答案】C3．如图所示的三棱柱ABC－A1B1C1中，过A1B1的平面与平面ABC交于DE，则DE与AB的位置关系是()A．异面B．平行C．相交D．以上均有可能【答案】B4．已知m，n表示两条不同直线，α表示平面，下列说法正确的是()A．若m∥α，n∥α，则m∥nB．若m⊥α，n⊂α，则m⊥nC．若m⊥α，m⊥n，则n∥αD．若m∥α，m⊥n，则n⊥α【答案】B5．(2019年枣庄诊断)如图，直三棱柱ABC－A′B′C′中，△ABC是边长为2的等边三角形，AA′＝4，点E，F，G，H，M分别是边AA′，AB，BB′，A′B′，BC的中点，动点P在四边形EFGH内部运动，并且始终有MP∥平面ACC′A′，则动点P的轨迹长度为()A．2B．2πC．23D．4【答案】D【解析】连接MF，FH，MH，因为M，F，H分别为BC，AB，A′B′的中点，所以MF∥平面AA′C′C，FH∥平面AA′C′C，所以平面MFH∥平面AA′C′C，所以M与线段FH上任意一点的连线都平行于平面AA′C′C，所以点P的运动轨迹是线段FH，其长度为4.6．在四面体A－BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________．【答案】平面ABD与平面ABC【解析】如图，取CD的中点E.连接AE，BE，由于M，N分别是△ACD，△BCD的重心，所以AE，BE分别过M，N，且EM∶MA＝1∶2，EN∶BN＝1∶2，所以MN∥AB．因为AB⊂平面ABD，MN⊄平面ABD，AB⊂平面ABC，MN⊄平面ABC，所以MN∥平面ABD，MN∥平面ABC．7．如图所示，正方体ABCD－A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF ∥平面AB 1C ，则线段EF 的长度等于________．【答案】2 【解析】在正方体ABCD －A 1B 1C 1D 1中，AB ＝2，所以AC ＝2 2.又E 为AD 中点，EF ∥平面AB 1C ，EF ⊂平面ADC ，平面ADC ∩平面AB 1C ＝AC ，所以EF ∥AC ，所以F 为DC 中点，所以EF ＝12AC ＝ 2.8．如图所示，在直三棱柱ABC －A 1B 1C 1中，若BC ⊥AC ，∠BAC ＝π3，AC ＝4，M 为AA 1的中点，点P 为BM 的中点，Q 在线段CA 1上，且A 1Q ＝3QC ，则PQ 的长度为________．【答案】13 【解析】由题意知，AB ＝8，过点P 作PD ∥AB 交AA 1于点D ，连接DQ ，则D 为AM 中点，PD ＝12AB ＝4.又因为A 1Q QC ＝A 1D AD＝3，所以DQ ∥AC ，∠PDQ ＝π3，DQ ＝34AC ＝3.在△PDQ 中，PQ ＝42＋32－2×4×3×cos π3＝13.9．(2019年南昌模拟)如图，在四棱锥P －ABCD 中，∠ABC ＝∠ACD ＝90°，∠BAC ＝∠CAD ＝60°，P A ⊥平面ABCD ，P A ＝2，AB ＝1．设M ，N 分别为PD ，AD 的中点．(1)求证：平面CMN∥平面P AB；(2)求三棱锥P－ABM的体积．解：(1)证明：因为M，N分别为PD，AD的中点，所以MN∥P A．因为MN⊄平面P AB，P A⊂平面P AB，所以MN∥平面P AB．在Rt△ACD中，∠CAD＝60°，CN＝AN，所以∠ACN＝60°. 又∠BAC＝60°，所以CN∥AB．因为CN⊄平面P AB，AB⊂平面P AB，所以CN∥平面P AB．又CN∩MN＝N，所以平面CMN∥平面P AB．(2)由(1)知，平面CMN∥平面P AB，所以点M到平面P AB的距离等于点C到平面P AB的距离．由AB＝1，∠ABC＝90°，∠BAC＝60°，所以BC＝ 3.所以三棱锥P－ABM的体积V＝V M－P AB＝V C－P AB＝V P－ABC＝13×12×1×3×2＝33.10．如图所示，在正方体ABCD－A1B1C1D1中，E，F，G，H分别是BC，CC1，C1D1，A1A的中点．求证：(1)BF∥HD1；(2)EG∥平面BB1D1D；(3)平面BDF ∥平面B 1D 1H .证明：(1)如图所示，取BB 1的中点M ，连接MH ，MC 1，易证四边形HMC 1D 1是平行四边形，所以HD 1∥MC 1．又因为MC 1∥BF ，所以BF ∥HD 1．(2)取BD 的中点O ，连接EO ，D 1O ，则OE 綉12DC ．又D 1G 綉12DC ，所以OE 綉D 1G ，所以四边形OEGD 1是平行四边形，所以GE ∥D 1O .又GE ⊄平面BB 1D 1D ，D 1O ⊂平面BB 1D 1D ，所以EG ∥平面BB 1D 1D ．(3)由(1)知BF ∥HD 1，又BF ⊄平面B 1D 1H ，HD 1⊂平面B 1D 1H ，所以BF ∥平面B 1D 1H . 又BD ∥B 1D 1，BD ⊄平面B 1D 1H ，B 1D 1⊂平面B 1D 1H ，所以BD ∥平面B 1D 1H .又DB ∩BF ＝B ，所以平面BDF ∥平面B 1D 1H .[B 级能力提升]11．已知E ，F 分别为正方体ABCD －A 1B 1C 1D 1的棱AB ，AA 1上的点，且AE ＝12AB ，AF ＝13AA 1，M ，N 分别为线段D 1E 和线段C 1F 上的点，则与平面ABCD 平行的直线MN 有( )A ．1条B ．3条C ．6条D ．无数条【答案】D 【解析】在线段A 1F 上任取一点H ，过点H 可以作与平面ABCD 平行的平面α，显然D 1E ，C 1F 都与这个平面α相交，连接两个交点的直线必与平面ABCD 平行，故满足条件的直线MN 有无数条12．(多选)(2020年青岛月考)在正方体ABCD－A1B1C1D1中，下列直线或平面与平面ACD1平行的有()A．直线A1B B．直线BB1C．平面A1DC1D．平面A1BC1【答案】AD【解析】对于A，由于A1B∥D1C，且A1B⊄平面ACD1，可得直线A1B∥平面ACD1；对于B，由于B1B∥D1D，且D1D∩平面ACD1＝D1，可得直线B1B不平行平面ACD1；对于C，由于A1D∩AD1，A1D⊂平面A1DC1，可得平面A1DC1不与平面ACD1平行；对于D，由于A1B∥D1C，C1B∥D1A，A1B，C1B⊂平面A1BC1，可得平面A1BC1∥平面ACD1．13．如图所示，三棱柱ABC－A1B1C1的侧面BCC1B1是菱形，D是A1C1上的点，且A1B ∥平面B1CD，则A1D∶DC1的值为________．【答案】1【解析】设BC1∩B1C＝O，连接OD．因为A1B∥平面B1CD且平面A1BC1∩平面B1CD＝OD，所以A1B∥OD．因为四边形BCC1B1是菱形，所以O为BC1的中点，所以D为A1C1的中点，则A1D∶DC1＝1．14．(2020年北京期末)如图，在直三棱柱ABC －A 1B 1C 1中，∠BAC ＝π2，AA 1＝AB ＝AC＝1，CC 1的中点为H ，点N 在棱A 1B 1上，HN ∥平面A 1BC ，则A 1NA 1B 1的值为______．【答案】12 【解析】取A 1C 1 的中点M ，A 1B 1的中点N ，连接HM ，MN ，由H ，M ，N分别为CC 1，A 1C 1，A 1B 1的中点，得MH ∥A 1C ，MN ∥B 1C 1∥BC ．因为A 1C ⊂平面A 1BC ，MH ⊄平面A 1BC ，所以MH ∥平面 A 1BC ．因为BC ⊂平面A 1BC ，MN ⊄平面A 1BC ，所以MN ∥平面A 1BC ．又MH ∩MN ＝M ，所以平面MNH ∥平面A 1BC ，则NH ∥平面A 1BC ．由N 为A 1B 1的中点，可知A 1N A 1B 1的值为12.15．(2019年河南八市联考)如图，在矩形ABCD 中，AB ＝1，AD ＝2，P A ⊥平面ABCD ，E ，F 分别为AD ，P A 的中点，点Q 是BC 上的一个动点．(1)当Q 是BC 的中点时，求证：平面BEF ∥平面PDQ ； (2)当BD ⊥FQ 时，求BQQC的值．解：(1)证明：因为E ，Q 分别是AD ，BC 的中点，所以ED ＝BQ ，ED ∥BQ ，所以四边形BEDQ 是平行四边形．所以BE ∥DQ . 又BE ⊄平面PDQ ，DQ ⊂平面PDQ .所以BE ∥平面PDQ .又F 是P A 的中点，所以EF ∥PD ．因为EF ⊄平面PDQ ，PD ⊂平面PDQ ，所以EF ∥平面PDQ .因为BE ∩EF ＝E ，BE ⊂平面BEF ，EF ⊂平面BEF ，所以平面BEF ∥平面PDQ .(2)如图，连接AQ ，因为P A ⊥平面ABCD ，BD ⊂平面ABCD ，所以P A ⊥BD ．因为BD ⊥FQ ，P A ∩FQ ＝F ，P A ⊂平面P AQ ，FQ ⊂平面P AQ ，所以BD ⊥平面P AQ . 因为AQ ⊂平面P AQ ，所以AQ ⊥BD ．在矩形ABCD 中，由AQ ⊥BD 得△AQB 与△DBA 相似，所以AB 2＝AD ×BQ . 又AB ＝1，AD ＝2，所以BQ ＝12，QC ＝32.所以BQ QC ＝13.16．(2020年北京期末)如图，在四棱锥P －ABCD 中，已知底面ABCD 为平行四边形，点E 为棱PD 的中点．(1)求证：BC ∥平面P AD ；(2)设平面EBC ∩平面P AD ＝EF ，点F 在P A 上，求证：F 为P A 的中点．证明：(1)因为底面ABCD 为平行四边形，所以BC ∥AD ．因为AD ⊂平面P AD ，BC ⊄平面P AD ，所以BC ∥平面P AD ．(2)因为平面EBC ∩平面P AD ＝EF ，点F 在P A 上，BC ∥平面P AD ，BC ⊂平面EBC ，所以EF ∥BC ．因为点E 为棱PD 的中点，所以点F 为P A 的中点．[C 级创新突破]17．(2020年绍兴期中)如图，在正方体ABCD －A 1B 1C 1D 1中，E 是AB 的中点，点F 在CC 1上，且CF ＝2FC 1，点P 是侧面AA 1D 1D (包括边界)上一动点，且PB 1∥平面DEF ，则tan ∠ABP 的取值范围为________．【答案】⎣⎡⎦⎤13，133 【解析】如图所示，作出平面MNQB 1∥平面DEF ，则A 1Q ＝2AQ ，DN ＝2D 1N .因为PB 1∥平面DEF ，所以P 的轨迹是线段QN .当点P 在Q 处，tan ∠ABP 取最小值，tan ∠ABP ＝13；当P 在N 处，tan ∠ABP 取最大值，tan ∠ABP ＝133.所以tan ∠ABP 的取值范围为⎣⎡⎦⎤13，133.18．(2020年衡水一模)如图，四棱锥P －ABCD 的底面ABCD 为平行四边形，E ，F 分别为CD ，PB 的中点．(1)求证：EF ∥平面P AD ；(2)在线段PC 上是否存在一点Q ，使得A ，E ，Q ，F 四点共面？若存在，求出PQQC的值；若不存在，请说明理由．解：(1)证明：如图，取P A 的中点M ，连接MD ，MF ，因为F ，M 分别为PB ，P A 的中点，所以FM ∥AB ，FM ＝12AB ．又四边形ABCD 是平行四边形，故AB ∥CD ，AB ＝CD ．因为E 为CD 的中点，所以DE ∥AB ，DE ＝12AB ．所以DE ∥FM ，DE ＝FM ，则四边形DEFM 为平行四边形，所以EF ∥DM . 因为EF ⊄平面P AD ，DM ⊂平面P AD ．所以EF ∥平面P AD ．(2)存在点Q 符合题意，且此时PQQC＝2，理由如下：取AB 的中点H ，连接PH 交AF 于点G ，在PC 上取点Q ，使PQ ∶QC ＝2∶1，连接GQ ，HC ．在平行四边形ABCD 中，因为E ，H 分别为CD ，AB 的中点，所以CH ∥AE . 又F 是PB 的中点，所以G 是△P AB 的重心，且PG ∶GH ＝2∶1．又PQ ∶QC ＝2∶1，所以GQ ∥HC ．因为CH ∥AE ，所以GQ ∥AE .所以GQ 与AE 确定一个平面α，而F ∈直线AG ，所以F ∈α，则A ，E ，Q ，F 四点共面．故在线段PC 上存在一点Q ，使得A ，E ，Q ，F 四点共面，此时PQQC＝2.。

人教新课标版数学高一-人教A版必修2 课时提升 -2 直线与平面平行的判定1

关闭Word文档返回原板块。

课时提升作业(十)直线与平面平行的判定平面与平面平行的判定(25分钟60分)一、选择题(每小题5分,共25分)1.(2015·福州高一检测)平面α与△ABC的两边AB,AC分别交于点D,E,且AD︰DB=AE︰EC,如图,则BC与α的位置关系是( )A.平行B.相交C.平行或相交D.异面【解析】选A.因为AD︰DB=AE︰EC,所以DE∥BC,又DE⊂α,BC⊄α,所以BC∥α.2.有以下三种说法,其中正确的是( )①若直线a与平面α相交,则α内不存在与a平行的直线;②若直线b∥平面α,直线a与直线b垂直,则直线a不可能与α平行;③直线a,b满足a∥α,a∥b,且b⊂α,则a平行于经过b的任何平面.A.①②B.①③C.②③D.①【解析】选D.①正确,若在α内存在一条直线b,使a∥b,则a∥α与“a 与平面α相交”矛盾,故①正确,②错误,反例如图(1)所示,③错误,反例如图(2)所示,a,b可能在同一平面内.3.若正n边形的两条对角线分别与平面α平行,则这个正n边形所在的平面一定平行于平面α,那么n的取值可能是( )A.12B.8C.6D.5【解题指南】考虑平面与平面平行的判定定理,只需判断正n边形的两条对角线是否一定相交.【解析】选D.正五边形的两条对角线必相交,而其余正多边形的两条对角线不一定相交.4.点E,F,G,H分别是空间四面体ABCD的棱AB,BC,CD,DA的中点,则空间四面体的六条棱中与平面EFGH平行的条数是( )A.0条B.1条C.2条D.3条【解析】选C.因为E,F分别为AB,BC的中点,所以EF∥AC,又AC⊄平面EFGH,EF⊂平面EFGH,所以AC∥平面EFGH,同理BD∥平面EFGH.5.正方体EFGH-E1F1G1H1中,下列四对截面中,彼此平行的一对截面是( )A.平面E1FG1与平面EGH1B.平面FHG1与平面F1H1GC.平面F1H1H与平面FHE1D.平面E1HG1与平面EH1G【解析】选A.在平面E1FG1与平面EGH1中,因E1G1∥EG,FG1∥EH1,且E1G1∩FG1=G1,EG∩EH1=E,故平面E1FG1∥平面EGH1.二、填空题(每小题5分,共15分)6.过三棱柱ABC-A1B1C1任意两条棱的中点作直线,其中与平面ABB1A1平行的直线有________条.【解析】如图,EF,FG,GH,HE,EG,HF都与平面ABB1A1平行,共6条.答案:67.(2015·广州高一检测)P为矩形ABCD所在平面外一点,矩形对角线交点为O,M为PB的中点,给出下列四种说法:①OM∥平面PCD;②OM∥平面PBC;③OM∥平面PDA;④OM∥平面PBA.其中正确的为________(填序号).【解析】因为OM∥PD,故OM∥平面PCD,OM∥平面PDA,所以①③正确.答案:①③8.(2015·杭州高二检测)如图所示,在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面中与MN平行的是________.【解析】连接AM并延长,交CD于点E,则E为CD的中点,连接BE,则BE过点N.因为M,N分别为△ACD和△BCD的重心,所以==,所以MN∥AB,所以可得MN∥平面ABC,MN∥平面ABD.答案:平面ABC,平面ABD【拓展延伸】三角形的“四心”及主要性质(1)三角形的三条中线的交点叫三角形的重心.重心到顶点的距离等于到对边中点距离的2倍.(2)三角形三边垂直平分线的交点叫三角形的外心.外心到三角形三个顶点的距离相等.(3)三角形三条高线的交点叫三角形的垂心.(4)三角形三个角的角平分线的交点叫三角形的内心.内心到三角形三边的距离相等.三角形的“四心”在数学中应用非常广泛,要熟练掌握.三、解答题(每小题10分,共20分)9.(2014·山东高考改编)如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD 是梯形,AB=2CD=2,M是线段AB的中点.求证:C1M∥平面A1ADD1.【证明】连接AD1,因为ABCD-A1B1C1D1为四棱柱,所以CD∥C1D1,CD=C1D1,又因为M为AB的中点,所以AM=1,所以CD∥AM,CD=AM,所以AM∥C1D1,AM=C1D1,所以四边形AMC1D1为平行四边形,所以AD1∥MC1,又因为C1M⊄平面A1ADD1,AD1⊂平面A1ADD1,所以C1M∥平面A1ADD1.【补偿训练】(2014·天津高考改编)如图,四棱锥P-ABCD的底面ABCD 是平行四边形,E,F分别是棱AD,PC的中点.证明:EF∥平面PAB.【证明】如图,取PB的中点M,连接MF,AM.因为F为PC中点,故MF∥BC且MF=BC.由已知有BC∥AD,BC=AD.又由于E为AD中点,因而MF∥AE且MF=AE,故四边形AMFE为平行四边形,所以EF∥AM.又AM⊂平面PAB,而EF⊄平面PAB,所以EF∥平面PAB.10.(2015·厦门高一检测)在正方体ABCD-A1B1C1D1中,M,N,P分别是AD1,BD和B1C的中点.求证:(1)MN∥平面CC1D1D.(2)平面MNP∥平面CC1D1D.【证明】(1)连接AC,CD 1,因为ABCD为正方形,N为BD的中点,所以N为AC的中点,又因为M为AD1的中点,所以MN∥CD1,因为MN⊄平面CC1D1D,CD1⊂平面CC1D1D,所以MN∥平面CC1D1D.(2)连接BC1,C1D,因为B1BCC1为正方形,P为B1C的中点,所以P为BC1的中点,又因为N为BD的中点,所以PN∥C1D,因为PN⊄平面CC1D1D,C1D⊂平面CC1D1D,所以PN∥平面CC1D1D.由(1)知MN∥平面CC1D1D且MN∩PN=N,所以平面MNP∥平面CC1D1D.(20分钟40分)一、选择题(每小题5分,共10分)1.已知m,n是两条直线,α,β是两个平面,有以下说法:①m,n相交且都在平面α,β外,m∥α,m∥β,n∥α,n∥β,则α∥β;②若m∥α,m∥β,则α∥β;③若m∥α,n∥β,m∥n,则α∥β.其中正确说法的个数是( )A.0B.1C.2D.3【解析】选B.设m∩n=P,则直线m,n确定一个平面,设为γ,由面面平行的判定定理知,α∥γ,β∥γ,因此,α∥β,即①正确;如图,在长方体ABCD-A1B1C1D1中,直线EF平行于平面ADD 1A1和平面A1B1C1D1,即满足②的条件,但平面A1B1C1D1与平面ADD1A1不平行,因此②不正确;图中,EF∥平面ADD1A1,BC∥平面A1B1C1D1,EF∥BC,但平面ADD1A1与平面A1B1C1D1不平行,所以③也不正确.2.(2015·青岛高一检测)在正方体ABCD-A1B1C1D1中,M,N,Q分别是棱D1C1,A1D1,BC的中点,P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥平面APC;(2)C1Q∥平面APC;(3)A,P,M三点共线;(4)平面MNQ ∥平面APC.正确的序号为( )A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4) 【解析】选C.(1)MN∥AC,连接AM,CN,易得AM, CN交于点P,即MN⊂平面PAC,所以MN∥平面APC是错误的;(2)平面APC延展,可知M,N在平面APC上,AN∥C1Q,所以C1Q∥平面APC,是正确的;(3)由BP=BD1,以及相似,可得A,P,M三点共线,是正确的;(4)直线AP延长到M,则M在平面MNQ内,又在平面APC内,所以平面MNQ∥平面APC,是错误的.二、填空题(每小题5分,共10分)3.(2015·太原高二检测)下列四个正方体图形中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是________.(将你认为正确的都填上)【解析】在④中NP平行所在正方体的那个侧面的对角线,从而平行AB,所以AB∥平面MNP;在①中设过点B且垂直于上底面的棱与上底面交点为C,则由NP∥CB,MN∥AC,可知平面MNP∥平行平面ABC,即AB∥平面MNP.答案:①④4.(2015·菏泽高一检测)如图,在正方体ABCD-A 1B1C1D1中,E,F分别是AB和AA1的中点,则下列命题:①E,C,D1,F四点共面;②CE,D1F,DA三线共点;③EF和BD1所成的角为90°;④A1B∥平面CD1E.其中正确的是________(填序号).【解析】由题意EF∥CD 1,故E,C,D1,F四点共面;由EF CD1,故D1F与CE相交,记交点为P,则P∈平面ADD1A1,P∈平面ABCD,所以点P在平面ADD1A1与平面ABCD的交线AD上,故CE,D1F,DA三线共点;∠A1BD1即为EF与BD1所成角,显然∠A1BD1≠90°;因为A1B∥EF,EF⊂平面CD1E,A1B⊄平面CD1E,所以A1B∥平面CD1E.答案:①②④三、解答题(每小题10分,共20分)5.(2014·四川高考)在如图所示的多面体中,四边形ABB1A1和ACC1A1都为矩形.设D,E分别是线段BC,CC1的中点,在线段AB上是否存在一点M,使直线DE∥平面A1MC?请证明你的结论.【解析】存在点M是AB的中点.取线段AB的中点M,连接A1M,MC,A1C,AC1.设O为A 1C,AC1的交点.由已知,O为AC1的中点,连接MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,所以MD AC,OE AC,因此MD OE,连接OM,从而四边形MDEO为平行四边形,则DE∥MO.因为直线DE⊄平面A1MC,MO⊂平面A1MC,所以直线DE∥平面A1MC.即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A1MC. 【延伸探究】本题若加上条件“F是A1C1的中点”其他条件不变,问在AB上是否存在一点M,使平面DEF∥平面A1MC,并证明.打印版【解析】存在点M是AB的中点,证明如下:由本题证明知DE∥平面A1MC,又F为A1C1的中点,E为CC1的中点,所以EF∥A1C,又EF⊄平面A1MC,A1C⊂平面A1MC,所以EF∥平面A1MC,又EF∩DE=E,所以平面DEF∥平面A1MC.故AB上存在一点M(AB中点),使平面DEF∥平面A1MC.6.(2015·福州高一检测)已知直三棱柱ABC-A1B1C1,点N在AC上且CN=3AN,点M,P,Q分别是AA1,A1B1,BC的中点.求证:直线PQ∥平面BMN.【证明】如图,取AB中点G,连接PG,QG分别交BM,BN于点E,F,则E,F分别为BM,BN的中点.而GE∥AM,GE=AM,GF∥AN,GF=AN,且CN=3AN,所以=,==,所以==,所以EF∥PQ,又EF⊂平面BMN,PQ⊄平面BMN,所以PQ∥平面BMN.关闭Word文档返回原板块高中数学。

新高考一轮复习人教版直线、平面平行的判定和性质作业

8.3直线、平面平行的判定和性质基础篇固本夯基考点一直线与平面平行的判定和性质1.(2021江苏扬州大学附中2月检测,5)已知直三棱柱ABC-A1B1C1中,M,N分别是A1B1,AB的中点,P点在线段B1C上,则NP与平面AMC1的位置关系是()A.垂直B.平行C.相交但不垂直D.要依P点的位置而定答案B2.(2021济南二模,7)已知正四面体ABCD的棱长为2,平面α与棱AB、CD均平行,则α截此正四面体所得截面面积的最大值为()A.1B.√2C.√3D.2答案A3.(多选)(2021山东青岛胶州调研,10)在三棱柱ABC-A1B1C1中,E,F,G分别为线段AB,A1B1,AA1的中点,下列说法正确的是()A.平面AC1F∥平面B1CEB.直线FG∥平面B1CEC.直线CG与BF异面D.直线C1F与平面CGE相交答案AC4.(2020福建漳州适应性测试,16)已知正方体ABCD-A1B1C1D1的棱长为3,点N是棱A1B1的中点,点T是棱CC1上靠近点C的三等分点,动点Q在正方形D1DAA1(包含边界)内运动,且QB∥平面D1NT,则动点Q的轨迹的长为.答案√105.(2022届山东潍坊10月过程性测试,18)如图,平面ABCD⊥平面AEBF,四边形ABCD为矩形,△ABE和△ABF 均为等腰直角三角形,且∠BAF=∠AEB=90°.(1)求证:平面BCE⊥平面ADE;(2)若点G为线段FC上任意一点,求证:BG∥平面ADE.证明(1)因为四边形ABCD为矩形,所以BC⊥AB,又因为平面ABCD⊥平面AEBF,BC⊂平面ABCD,平面ABCD∩平面AEBF=AB,所以BC⊥平面AEBF,又因为AE⊂平面AEBF,所以BC⊥AE.因为∠AEB=90°,即AE⊥BE,且BC、BE⊂平面BCE,BC∩BE=B,所以AE⊥平面BCE,又因为AE⊂平面ADE,所以平面ADE⊥平面BCE.(2)因为BC∥AD,AD⊂平面ADE,BC⊄平面ADE,所以BC∥平面ADE.因为△ABF和△ABE均为等腰直角三角形,且∠BAF=∠AEB=90°,所以∠EAB=∠ABF=45°,所以AE∥BF,又AE⊂平面ADE,BF⊄平面ADE,所以BF∥平面ADE,又BC∩BF=B,所以平面BCF∥平面ADE.又BG⊂平面FBC,所以BG∥平面ADE.6.(2022届广东佛山一中10月月考,20)如图所示,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA=PD=√2,四边形ABCD为等腰梯形,BC∥AD,BC=CD=1AD=1,E为PA的中点.2(1)证明:EB∥平面PCD;(2)求平面PAD与平面PCD所成的二面角θ的正弦值.解析(1)证明:取AD的中点O,连接EO,OB,∵E为PA的中点,O为AD的中点,∴OE∥PD,又OE⊄平面PCD,PD⊂平面PCD,∴OE∥平面PCD,又∵BC ∥AD,BC=12AD,∴四边形BCDO 为平行四边形,∴BO ∥CD, 又OB ⊄平面PCD,CD ⊂平面PCD,∴BO ∥平面PCD,又OE ∩BO=O,∴平面EBO ∥平面PCD, 又∵BE ⊂平面EBO,∴BE ∥平面PCD.(2)连接PO,∵PA=PD,O 为AD 的中点,∴PO ⊥AD, 又平面PAD ⊥平面ABCD,平面PAD ∩平面ABCD=AD, 所以PO ⊥平面ABCD,取BC 的中点M,连接OM, ∵四边形ABCD 是等腰梯形,∴OM ⊥AD, 建立如图所示的空间直角坐标系,则P(0,0,1),A(0,-1,0),D(0,1,0),C (√32,12,0),∴PD⃗⃗⃗⃗ =(0,1,-1),CD ⃗⃗⃗⃗ =(−√32,12,0),设平面PCD 的法向量为n=(x,y,z),则{n ·PD ⃗⃗⃗⃗ =y −z =0,n ·CD⃗⃗⃗⃗ =−√32x +12y =0,令x=1,则y=z=√3,则n=(1,√3,√3), 易知平面PAD 的一个法向量为m=(1,0,0), ∴|cos θ|=|cos<m,n>|=|m·n||m||n|=√7,则sin θ=√427. 7.(2019江苏,16,14分)如图,在直三棱柱ABC-A 1B 1C 1中,D,E 分别为BC,AC 的中点,AB=BC.求证: (1)A 1B 1∥平面DEC 1; (2)BE ⊥C 1E.证明(1)因为D,E分别为BC,AC的中点,所以ED∥AB.在直三棱柱ABC-A1B1C1中,AB∥A1B1,所以A1B1∥ED.又因为ED⊂平面DEC1,A1B1⊄平面DEC1,所以A1B1∥平面DEC1.(2)因为AB=BC,E为AC的中点,所以BE⊥AC.因为三棱柱ABC-A1B1C1是直棱柱,所以C1C⊥平面ABC.又因为BE ⊂平面ABC,所以C1C⊥BE.因为C1C⊂平面A1ACC1,AC⊂平面A1ACC1,C1C∩AC=C,所以BE⊥平面A1ACC1.因为C1E ⊂平面A1ACC1,所以BE⊥C1E.8.(2020江苏,15,14分)在三棱柱ABC-A1B1C1中,AB⊥AC,B1C⊥平面ABC,E,F分别是AC,B1C的中点.(1)求证:EF∥平面AB1C1;(2)求证:平面AB1C⊥平面ABB1.证明(1)因为E,F分别是AC,B1C的中点,所以EF∥AB1,又EF⊄平面AB1C1,AB1⊂平面AB1C1,所以EF∥平面AB1C1.(2)因为B1C⊥平面ABC,AB⊂平面ABC,所以B1C⊥AB.又AB⊥AC,B1C⊂平面AB1C,AC⊂平面AB1C,B1C∩AC=C,所以AB⊥平面AB1C,又因为AB⊂平面ABB1,所以平面AB1C⊥平面ABB1.9.(2020北京,16,13分)如图,在正方体ABCD-A1B1C1D1中,E为BB1的中点.(1)求证:BC1∥平面AD1E;(2)求直线AA1与平面AD1E所成角的正弦值.解析 (1)证明:∵ABCD-A 1B 1C 1D 1为正方体,∴D 1C 1∥A 1B 1,D 1C 1=A 1B 1.又AB ∥A 1B 1,AB=A 1B 1,∴D 1C 1∥AB,D 1C 1=AB,∴四边形ABC 1D 1为平行四边形,∴AD 1∥BC 1,又AD 1⊂平面AD 1E,BC 1⊄平面AD 1E,∴BC 1∥平面AD 1E.(2)不妨设正方体的棱长为2,如图,以{AD ⃗⃗⃗⃗ ,AB ⃗⃗⃗⃗ ,AA 1⃗⃗⃗⃗⃗⃗ }为正交基底建立空间直角坐标系A-xyz,则A(0,0,0),A 1(0,0,2),D 1(2,0,2),E(0,2,1),∴AA 1⃗⃗⃗⃗⃗⃗ =(0,0,2),AD 1⃗⃗⃗⃗⃗⃗ =(2,0,2),AE ⃗⃗⃗⃗ =(0,2,1),设平面AD 1E 的法向量为n=(x,y,z),直线AA 1与平面AD 1E 所成的角为θ, 则{n ·AD 1⃗⃗⃗⃗⃗⃗ =0,n ·AE ⃗⃗⃗⃗ =0,即{2x +2z =0,2y +z =0,令z=-2,则{x =2,y =1,此时n=(2,1,-2),∴sin θ=|cos<n,AA 1⃗⃗⃗⃗⃗⃗ >|=|n·AA 1⃗⃗⃗⃗⃗⃗⃗⃗ ||n||AA 1⃗⃗⃗⃗⃗⃗⃗⃗ |=√4+1+4×2=23, ∴直线AA 1与平面AD 1E 所成角的正弦值为23.考点二平面与平面平行的判定和性质1.(2022届重庆巴蜀中学11月月考,8)在棱长为2的正方体ABCD-A 1B 1C 1D 1中,点E,F,G,H 分别为棱AB,BC,C 1D 1,A 1D 1的中点,若平面α∥平面EFGH,且平面α与棱A 1B 1,B 1C 1,B 1B 分别交于点P,Q,S,其中点Q 是棱B 1C 1的中点,则三棱锥B 1-PQS 的体积为( ) A.1 B.12C.13D.16答案 D2.(2019课标Ⅱ文,7,5分)设α,β为两个平面,则α∥β的充要条件是( ) A.α内有无数条直线与β平行 B.α内有两条相交直线与β平行 C.α,β平行于同一条直线D.α,β垂直于同一平面答案 B3.(2021河北邢台月考,19)在直四棱柱ABCD-A 1B 1C 1D 1中,底面ABCD 为正方形,AA 1=2AB=4,M,N,P 分别是AD,DD 1,CC 1的中点.(1)证明:平面MNC ∥平面AD 1P;(2)求直线DP 与平面MNC 所成角的正弦值.解析 (1)证明:因为M,N,P 分别是AD,DD 1,CC 1的中点,所以MN ∥AD 1,CN ∥PD 1.又AD 1⊄平面MNC,MN ⊂平面MNC,所以AD 1∥平面MNC,同理PD 1∥平面MNC, 又AD 1∩PD 1=D 1,所以平面MNC ∥平面AD 1P.(2)以D 为坐标原点,建立如图所示的空间直角坐标系D-xyz,则D(0,0,0),P(0,2,2),M(1,0,0),N(0,0,2),C(0,2,0),则DP ⃗⃗⃗⃗ =(0,2,2),MN ⃗⃗⃗⃗⃗ =(-1,0,2),MC⃗⃗⃗⃗⃗ =(-1,2,0). 设平面MNC 的法向量为n=(x,y,z),则{MN⃗⃗⃗⃗⃗ ·n =−x +2z =0,MC ⃗⃗⃗⃗ ·n =−x +2y =0,令z=1,得n=(2,1,1). 设直线DP 与平面MNC 所成角为θ,则sin θ=|cos<DP⃗⃗⃗⃗ ,n>|=|DP⃗⃗⃗⃗⃗ ·n||DP ⃗⃗⃗⃗⃗ ||n|=√33, 所以直线DP 与平面MNC 所成角的正弦值为√33.综合篇知能转换A 组考法一判断或证明线面平行的方法1.(2022届T8联考,7)如图,已知四棱柱ABCD-A 1B 1C 1D 1的底面为平行四边形,E,F,G 分别为棱AA 1,CC 1,C 1D 1的中点,则( )A.直线BC 1与平面EFG 平行,直线BD 1与平面EFG 相交B.直线BC 1与平面EFG 相交,直线BD 1与平面EFG 平行C.直线BC 1、BD 1都与平面EFG 平行D.直线BC 1、BD 1都与平面EFG 相交答案 A2.(2022届湖南岳阳一中入学考试,18)如图,在三棱柱ABC-A 1B 1C 1中,侧面ABB 1A 1是菱形,∠BAA 1=60°,E 是棱BB 1的中点,CA=CB,F 在线段AC 上,且AF=2FC. (1)证明:CB 1∥平面A 1EF;(2)若CA ⊥CB,平面CAB ⊥平面ABB 1A 1,求二面角F-A 1E-A 的余弦值.解析 (1)证明:连接AB 1交A 1E 于点G,连接FG, 易得△AGA 1∽△B 1GE,所以AG GB 1=AA 1EB 1=2,又因为AF FC =2,所以AF FC =AGGB 1,所以FG ∥CB 1,又CB 1⊄平面A 1EF,FG ⊂平面A 1EF,所以CB 1∥平面A 1EF.(2)过C 作CO ⊥AB 于点O,因为CA=CB,所以O 是线段AB 的中点.因为平面CAB ⊥平面ABB 1A 1,平面CAB ∩平面ABB 1A 1=AB,所以CO ⊥平面ABB 1A 1.连接A 1B,OA 1,由题意易知△ABA 1是等边三角形,又O 是线段AB 的中点,所以OA 1⊥AB.以O 为坐标原点,OA ⃗⃗⃗⃗ ,OA 1⃗⃗⃗⃗⃗⃗ ,OC⃗⃗⃗⃗ 的方向分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系,不妨设AB=2,则A(1,0,0),A 1(0,√3,0),C(0,0,1),B(-1,0,0),F (13,0,23),B 1(-2,√3,0),E (−32,√32,0),则A 1E ⃗⃗⃗⃗⃗⃗ =(−32,−√32,0),A 1F ⃗⃗⃗⃗⃗ =13,-√3,23.设平面A 1FE 的法向量为n 1=(x 1,y 1,z 1), 则{A 1F ⃗⃗⃗⃗⃗ ·n 1=0,A 1E ⃗⃗⃗⃗⃗⃗ ·n 1=0,即{x 13−√3y 1+23z 1=0,−32x 1−√32y 1=0,令x 1=1,则n 1=(1,-√3,-5).易知平面ABB 1A 1的一个法向量为n 2=(0,0,1), 则cos<n 1,n 2>=n 1·n 2|n 1||n 2|=-5√2929,由题图可知,二面角F-A 1E-A 的平面角为锐角,所以二面角F-A 1E-A 的余弦值为5√2929. 3.(2022届南京二十九中10月月考,20)如图,在四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AD ∥BC,AB ⊥AD,AB=2BC=4,E 是棱PD 上的动点(除端点外),F,M 分别为AB,CE 的中点. (1)证明:FM ∥平面PAD;(2)若直线EF 与平面PAD 所成的最大角为30°,求平面CEF 与平面PAD 所成锐二面角的余弦值.解析 (1)证明:取CD 的中点N,连接FN,MN,因为F,N 分别为AB,CD 的中点,所以FN ∥AD,又FN ⊄平面PAD,AD ⊂平面PAD,所以FN ∥平面PAD,因为M,N 分别是CE,CD 的中点,所以MN ∥PD,又MN ⊄平面PAD,PD ⊂平面PAD,所以MN ∥平面PAD,又FN ∩MN=N,所以平面MFN ∥平面PAD,又因为FM ⊂平面MFN,所以FM ∥平面PAD.(2)连接AE,因为平面PAD ⊥平面ABCD,且平面PAD ∩平面ABCD=AD,AB ⊥AD,AB ⊂平面ABCD,所以AB ⊥平面PAD,所以∠AEF 即为直线EF 与平面PAD 所成的角,且tan ∠AEF=AF AE =2AE, 当AE 最小,即AE ⊥PD,亦即E 为PD 中点时,∠AEF 最大,为30°,又因为AF=2,所以AE=2√3,所以AD=4. 取AD 的中点O,连接PO,OC,易知PO ⊥平面ABCD,因为AO ∥BC 且AO=12AD=BC,所以四边形ABCO 为平行四边形,所以AB ∥CO,又AB ⊥AD,所以AO ⊥OC,以O 为坐标原点,建立如图所示的空间直角坐标系O-xyz.则O(0,0,0),C(4,0,0),D(0,2,0),P(0,0,2√3),E(0,1,√3),F(2,-2,0),则CE ⃗⃗⃗⃗ =(-4,1,√3),FC ⃗⃗⃗⃗ =(2,2,0),设平面CEF 的法向量为n 1=(x,y,z),则{n 1·FC⃗⃗⃗ =0,n 1·CE ⃗⃗⃗ =0,即{2x +2y =0,−4x +y +√3z =0,可取n 1=(√3,-√3,5).易知平面PAD 的一个法向量为n 2=(1,0,0), 所以cos<n 1,n 2>=n 1·n 2|n 1|·|n 2|=√3√31=√9331,所以平面CEF 与平面PAD 所成锐二面角的余弦值为√9331.4.(2019课标Ⅰ理,18,12分)如图,直四棱柱ABCD-A 1B 1C 1D 1的底面是菱形,AA 1=4,AB=2,∠BAD=60°,E,M,N 分别是BC,BB 1,A 1D 的中点. (1)证明:MN ∥平面C 1DE; (2)求二面角A-MA 1-N 的正弦值.解析 (1)证明:连接B 1C,ME.因为M,E 分别为BB 1,BC 的中点,所以ME ∥B 1C,且ME=12B 1C.又因为N 为A 1D 的中点,所以ND=12A 1D.由题设知A 1B 1 DC,可得B 1C A 1D,故ME ND,因此四边形MNDE 为平行四边形,则MN ∥ED.又MN ⊄平面EDC 1,所以MN ∥平面C 1DE.(2)由已知可得DE ⊥DA.以D 为坐标原点,DA⃗⃗⃗⃗ 的方向为x 轴正方向,建立如图所示的空间直角坐标系D-xyz, A(2,0,0),A 1(2,0,4),M(1,√3,2),N(1,0,2),A 1A ⃗⃗⃗⃗⃗⃗ =(0,0,-4),A 1M ⃗⃗⃗⃗⃗⃗⃗ =(-1,√3,-2),A 1N ⃗⃗⃗⃗⃗⃗ =(-1,0,-2),MN ⃗⃗⃗⃗⃗ =(0,-√3,0).设m=(x,y,z)为平面A 1MA 的法向量,则{m ·A 1M ⃗⃗⃗⃗⃗⃗⃗ =0,m ·A 1A ⃗⃗⃗⃗⃗⃗ =0.所以{−x +√3y −2z =0,−4z =0.可取m=(√3,1,0).设n=(p,q,r)为平面A 1MN 的法向量,则{n ·MN⃗⃗⃗⃗⃗ =0,n ·A 1N ⃗⃗⃗⃗⃗⃗ =0.所以{−√3q =0,−p −2r =0.可取n=(2,0,-1).于是cos<m,n>=m·n |m||n|=√32×√5=√155, 所以二面角A-MA 1-N 的正弦值为√105.5.(2021广东珠海一模,19)如图,三棱锥P-ABC 中,PA ⊥AB,AB ⊥AC,AB=AC=√2,PB=PC=√6,点M 是PA 的中点,点D 是AC 的中点,点N 在PB 上,且PN=2NB. (1)证明:BD ∥平面CMN;(2)求直线CN 与平面ABC 所成角的正切值.解析 (1)证明:如图,连接PD 交CM 于O,则O 为△PAC 的重心,PO=2OD,连接ON,因为PN=2NB,所以ON ∥BD,因为ON ⊂平面CMN,BD ⊄平面CMN,所以BD ∥平面CMN.(2)因为PB=PC,AB=AC,PA=PA,所以△PAB ≌△PAC,所以∠PAC=∠PAB=90°,所以PA=√PC 2−AC 2=√6−2=2,又因为PA ⊥AB,AB ∩AC=A,所以PA ⊥平面ABC,过N 作NH ⊥AB 于H,连接HC,因为NH ∥PA,所以NH ⊥平面ABC,所以NH ⊥HC,且AH=23AB,直线CN 与平面ABC 所成角为∠NCH,所以直线CN 与平面ABC 所成角的正切值tan ∠NCH=NH HC=13PA √AC 2+(23AB )2=13×2√(√2)2+(23×√2)2=√2613.6.(2017课标Ⅱ理,19,12分)如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,AB=BC=12AD,∠BAD=∠ABC=90°,E 是PD 的中点. (1)证明:直线CE ∥平面PAB;(2)点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M-AB-D 的余弦值.解析 (1)证明:取PA 的中点F,连接EF,BF.因为E 是PD 的中点,所以EF ∥AD,EF=12AD.由∠BAD=∠ABC=90°得BC ∥AD,又BC=12AD,所以EF BC,所以四边形BCEF 是平行四边形,所以CE ∥BF,又BF ⊂平面PAB,CE ⊄平面PAB,故CE ∥平面PAB.(2)由已知得BA ⊥AD,以A 为坐标原点,AB ⃗⃗⃗⃗ 的方向为x 轴正方向,|AB ⃗⃗⃗⃗ |为单位长,建立如图所示的空间直角坐标系A-xyz,则A(0,0,0),B(1,0,0),C(1,1,0),P(0,1,√3),则PC⃗⃗⃗⃗ =(1,0,-√3),AB ⃗⃗⃗⃗ =(1,0,0). 设M(x,y,z)(0<x<1),则BM ⃗⃗⃗⃗⃗ =(x-1,y,z),PM⃗⃗⃗⃗⃗ =(x,y-1,z-√3).因为BM 与底面ABCD 所成的角为45°,而n=(0,0,1)是底面ABCD 的一个法向量,所以|cos<BM⃗⃗⃗⃗⃗ ,n>|=sin45°,即√(x−1)+y 2+z 2=√22,即(x-1)2+y 2-z 2=0.①又M 在棱PC 上,设PM⃗⃗⃗⃗⃗ =λPC ⃗⃗⃗⃗ ,则 x=λ,y=1,z=√3-√3λ.②由①,②解得{ x =1+√22,y =1,z =−√62(舍去),或{ x =1−√22,y =1,z =√62,所以M (1−√22,1,√62),从而AM⃗⃗⃗⃗⃗ =(1−√22,1,√62).设m=(x 0,y 0,z 0)是平面ABM 的法向量,则{m ·AM⃗⃗⃗⃗⃗ =0,m ·AB⃗⃗⃗⃗ =0,即{(2−√2)x 0+2y 0+√6z 0=0,x 0=0,所以可取m=(0,-√6,2). 于是cos<m,n>=m·n |m||n|=√105. 易知所求二面角为锐二面角. 因此二面角M-AB-D 的余弦值为√105.考法二判断或证明面面平行的方法(2021太原一模,19)如图,在三棱锥P-ABC 中,△PAB 是正三角形,G 是△PAB 的重心,D,E,H 分别是PA,BC,PC 的中点,点F 在BC 上,且BF=3FC. (1)求证:平面DFH ∥平面PGE;(2)若PB ⊥AC,AB=AC=2,BC=2√2,求二面角A-PC-B 的余弦值.解析 (1)证明:连接BG,GD,由题意得BG 与GD 共线,且BG=2GD, ∵E 是BC 的中点,BF=3FC,∴F 是CE 的中点, ∴BGGD =BEEF=2,∴GE ∥DF,∵GE ⊂平面PGE,DF ⊄平面PGE,∴DF ∥平面PGE, ∵H 是PC 的中点,∴FH ∥PE,∵HF ⊄平面PGE,PE ⊂平面PGE,∴FH ∥平面PGE, ∵DF ∩FH=F,∴平面DFH ∥平面PGE.(2)∵AB=AC=2,BC=2√2,∴AB 2+AC 2=8=BC 2,∴AB ⊥AC,又∵PB ⊥AC,AB ∩PB=B,∴AC ⊥平面PAB,以A 为坐标原点,向量AB ⃗⃗⃗⃗ ,AC ⃗⃗⃗⃗ 的方向为x 轴,y 轴的正方向建立如图所示的空间直角坐标系A-xyz,由题意得A(0,0,0),B(2,0,0),C(0,2,0),P(1,0,√3),则AC⃗⃗⃗⃗ =(0,2,0),AP ⃗⃗⃗⃗ =(1,0,√3),PC ⃗⃗⃗⃗ =(-1,2,-√3),BC ⃗⃗⃗⃗ =(-2,2,0),设平面PAC 的法向量是m=(x 1,y 1,z 1),则{m ·AC⃗⃗⃗⃗ =0,m ·AP⃗⃗⃗⃗ =0,∴{2y 1=0,x 1+√3z 1=0,则y 1=0,令z 1=-1,则x 1=√3,∴m=(√3,0,-1), 设平面PBC 的法向量是n=(x 2,y 2,z 2),则{n ·PC⃗⃗⃗ =0,n ·BC⃗⃗⃗⃗ =0,∴{−x 2+2y 2−√3z 2=0,−2x 2+2y 2=0,令z 2=1,则{x 2=√3,y 2=√3,∴n=(√3,√3,1), ∴cos<m,n>=m·n |m||n|=√77,又知二面角A-PC-B 是锐二面角,∴二面角A-PC-B 的余弦值为√77. B 组1.(多选)(2021南京航空航天大学附中期中,10)已知棱长为1的正方体ABCD-A 1B 1C 1D 1,过对角线BD 1作平面α交棱AA 1于点E,交棱CC 1于点F,以下结论正确的是( ) A.四边形BFD 1E 不一定是平行四边形 B.平面α分正方体所得两部分的体积相等 C.平面α与平面DBB 1不可能垂直 D.四边形BFD 1E 面积的最大值为√2答案 BD2.(多选)(2021广东肇庆二模,12)在长方体ABCD-A 1B 1C 1D 1中,AB=AD=1,AA 1=2,P 是线段BC 1上的一动点,则下列说法中正确的是( ) A.A 1P ∥平面AD 1CB.A 1P 与平面BCC 1B 1所成角的正切值的最大值是2√55C.A 1P+PC 的最小值为√1705D.以A 为球心,√2为半径的球面与侧面DCC 1D 1的交线长是π2答案 ACD。

点线面关系知识总结和练习题

//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法（1）定义法：直线与平面无公共点。

（2）判定定理：（3）其他方法：//a αββ⊂2.性质定理：//a a bαβαβ⊂⋂=二、平面与平面平行 1.判定方法（1）定义法：两平面无公共点。

（2）判定定理：////a b a b a b Pββαα⊂⊂⋂= //αβ（3）其他方法：a a αβ⊥⊥ //αβ; ////a γβγ//αβ 2.性质定理：//a bαβγαγβ⋂=⋂=三、直线与平面垂直（1）定义：如果一条直线与一个平面内的所有直线都垂直，则这条直线和这个平面垂直。

（2）判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b ② 判定定理:a ba cb c A b c αα⊥⊥⋂=⊂⊂ a α⊥③ 推论://a a bα⊥ b α⊥ （3）性质 ①a b αα⊥⊂ a b ⊥ ②a b αα⊥⊥四、平面与平面垂直（1）定义：两个平面相交，如果它们所成的二面角是直线二面角，就说这两个平面互相垂直。

（2）判定定理a a αβ⊂⊥ αβ⊥ （3）性质①性质定理la a lαβαβα⊥⋂=⊂⊥ αβ⊥② l P P A A αβαβαβ⊥⋂=∈⊥垂足为 A l ∈④ l P PA αβαβαβ⊥⋂=∈⊥ PA α⊂“转化思想”面面平行线面平行线线平行面面垂直线面垂直线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O，在两半平面内分别作射线OA⊥l，OB⊥l，则∠AOB叫做二面角的平面角例1．如图，在三棱锥S-ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC于D，交SC于E，又SA=AB，SB=BC，求以BD为棱，以BDE和BDC为面的二面角的度数。

●求线面夹角定义：斜线和它在平面内的射影的夹角叫做斜线和平面所成的角（或斜线和平面的夹角）方法：作直线上任意一点到面的垂线，与线面交点相连，利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。

高一数学必修二2.2.1直线与平面平行的判定2.2.2平面与平面平行的判定练习题(解析版)

2.2.1 直线与平面平行的判定2.2.2 平面与平面平行的判定一、选择题1.下列说法中正确的是 ( )A.如果一个平面内有一条直线和另一个平面平行,那么这两个平面平行B.如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行C.如果一个平面内任意一条直线和另一个平面平行,那么这两个平面平行D.若果两个平面平行于同一条直线,那么这两个平面平行2.下列命题中,正确的个数为 ( )①若a ∥b ,α⊂b ,则a ∥α②若a ∥α,b ∥α,则a ∥b③若a ∥b ,b ∥α,则a ∥α④若a ∥α,α⊂b ,则a ∥bA.0B.1C.2D.33.已知三条互相平行的直线c b a ,,中，,,βα⊂⊂c b a 、则两个平面βα,的位置关系是（）A.平行B.相交C.平行或相交D.重合4.与两个相交平面的交线平行的直线和这两个平面的位置关系是（）A.都平行B.都相交C.在这两个平面内D.至少和其中一个平面平行5.下列说法正确的是（）①若一个平面内的任何直线都与另一个平面无公共点，则这两个平面平行②过平面外一点有且仅有一个平面和已知平面平行③过平面外两点不能作平面与已知平面平行④若一条直线和一个平面平行，经过这条直线的任何平面都与已知平面平行A. ①③B. ②④C. ①②D. ②③④二、填空题6.若直线b a =A ，a ∥α，则b 与α的位置关系是＿＿＿＿＿＿＿7.若直线a b a 满足，与平面βα,∥b ,a ∥α,b ∥β,则平面α与平面β的位置关系是＿＿＿＿＿＿＿＿8.过平面外一点有＿＿＿条直线与已知平面平行,过平面外一点有且只有＿＿＿个平面与已知平面平行.9.正方体1111D C B A ABCD -中,的平面与过的中点，则为E C A BD DD E ,,11的位置关系是＿＿＿＿＿＿三、解答题10.正方体1111D C B A ABCD -中个，F E N M ,,,分别为棱11111111,,,D C C B D A B A 的中点。

《空间直线、平面的平行》基础练习【高中数学人教版】

《空间直线、平面的平行》基础练习一、选择题1．α，β是两个不重合的平面，在下列条件中，不能判定平面α∥β的条件是（）A ．m ，n 是α内一个三角形的两条边，且m ∥β，n ∥βB ．α内有不共线的三点到β的距离都相等C ．α，β都垂直于同一条直线aD ．m ，n 是两条异面直线，m ⊂α，n ⊂β，且m ∥β，n ∥α 2．下列四个结论：⑴两条直线都和同一个平面平行，则这两条直线平行． ⑵两条直线没有公共点，则这两条直线平行． ⑶两条直线都和第三条直线垂直，则这两条直线平行．⑷一条直线和一个平面内无数条直线没有公共点，则这条直线和这个平面平行．其中正确的个数为（）A ．0B ．1C ．2D ．33．直线,a b c ，及平面αβ，，使//a b 成立的条件是（）A ．//,a b αα⊂B ．//,//a b ααC ．//,//a c b cD ．//,a b ααβ=4．a ，b 是两条异面直线，A 是不在a ，b 上的点，则下列结论成立的是（）A ．过A 有且只有一个平面平行于a ，bB ．过A 至少有一个平面平行于a ，bC ．过A 有无数个平面平行于a ，bD ．过A 且平行a ，b 的平面可能不存在5．已知直线a 与直线b 垂直，a 平行于平面α，则b 与α的位置关系是（）A ．b ∥αB ．b ⊂αC ．b 与α相交D ．以上都有可能 6．下列命题中正确的命题的个数为（）①直线l 平行于平面α内的无数条直线，则l ∥α；②若直线a 在平面α外，则a ∥α； ③若直线a ∥b ，直线b ⊂α，则a ∥α；④若直线a ∥b ，b 平面α，那么直线a 就平行于平面α内的无数条直线．A ．1B ．2C ．3D ．4 二、填空题1．如果空间中若干点在同一平面内的射影在一条直线上，那么这些点在空间的位置是__________．2．若直线a 和b 都与平面α平行，则a 和b 的位置关系是__________．3．已知a 、b 是相交直线，且a 平行于平面α，那么b 与α的位置关系是________． 4．在棱长为a 的正方体ABCD —A 1B 1C 1D 1中，M 、N 分别是棱A 1B 1、B 1C 1的中点，P 是棱AD 上一点，AP =3a ，过P 、M 、N 的平面与棱CD 交于Q ，则PQ =_________．5．正方体ABCD -A 1B 1C 1D 1中，E 为DD 11中点，则BD 1和平面ACE 位置关系是．三、解答题1．已知,,,E F G H 为空间四边形ABCD 的边,,,AB BC CD DA 上的点，且//EH FG ．求证：//EH BD ．2．如图，正三棱柱111ABC A B C -的底面边长是2D 是AC 的中点．求证：1//B C 平面1A BD ．3．如图，在正方体1111ABCD A B C D -中，求证：平面1A BD //平面11CD B ．H G FE D BAC1A4．如图，正方形ABCD的边长为13，平面ABCD外一点P到正方形各顶点的距离都是13，M，N分别是PA，DB上的点，且58==PM M A BN ND∶∶∶．（1）求证：直线MN//平面PBC；（2）求线段MN的长．参考答案一、选择题1．B如图，E 、F 、G 、H 分别是正方体各棱的中点，点B 1，C 1，B 到平面EFGH 距离相等，但平面BCC 1B 1与平面EFGH 相交，故B 错．2．A ⑴两条直线都和同一个平面平行，这两条直线三种位置关系都有可能 ⑵两条直线没有公共点，则这两条直线平行或异面⑶两条直线都和第三条直线垂直，则这两条直线三种位置关系都有可能 ⑷一条直线和一个平面内无数条直线没有公共点，则这条直线也可在这个平面内3．C //,,a b αα⊂则//a b 或,a b 异面；所以A 错误；//,//,a b αα则//a b 或,a b 异面或,a b 相交，所以B 错误；//,,a b ααβ=则//a b 或,a b 异面，所以D 错误；//,//a c b c ，则//a b ，这是公理4，所以C 正确．4． D 如当A 与a 确定的平面与b 平行时，过A 作与a ，b 都平行的平面不存在． 5． D a 与b 垂直，a 与b 的关系可以平行、相交、异面，a 与α平行，所以b 与α的位置可以平行、相交、或在α内，这三种位置关系都有可能．6． A 对于①，∵直线l 虽与平面α内无数条直线平行，但l 有可能在平面α内（若改为l 与α内任何直线都平行，则必有l ∥α），∴①是假命题．对于②，∵直线a 在平面α外，包括两种情况a ∥α和a 与α相交，∴a 与α不一定平行，∴②为假命题．对于③，∵a ∥b ，b ⊂α，只能说明a 与b 无公共点，但a 可能在平面α内，∴a 不一定平行于平面α．∴③也是假命题．对于④，∵a ∥b ，b ⊂α．那么a ⊂α，或a ∥α．∴a 可以与平面α内的无数条直线平行．∴④是真命题．综上，真命题的个数为1．二、填空题1．共线或在与已知平面垂直的平面内． 2．相交或平行或异面．3． b ∥α或b 与α相交 b 与α的位置关系除b 在α内，皆有可能，即平行或相交．4由线面平行的性质定理知MN ∥PQ （∵MN ∥平面AC ，PQ =平面PMN ∩平面AC ，∴MN ∥PQ ）．易知DP =DQ =23a．故PQ =． 5．平行连接BD 交AC 于O ，连OE ，∴OE ∥B D 11，OEC 平面ACE ，∴B D 11∥平面ACE ．三、解答题1．证明：//,////EH BCD FG BCD EH BCD BD BCD EH BD EH FG ⊄⎫⎪⊂⇒⊂⇒⎬⎪⎭2．证明：设AB 1与AB 1相交于点P ，连接PD ，则P 为AB 1中点， D 为AC 中点，∴PD //B 1C ．又PD ⊂平面A 1BD ，∴B 1C //平面A 1BD3．证明：111111B B A A B B D D A A D D ⎧⎪⇒⎨⎪⎩∥ ∥ ∥ ⇒ 四边形11BB D D 是平行四边形⇒ 111111D B DB DB A BD D B A BD⎧⎪⊂⎨⎪⊄⎩平面平面//⇒111111111D B A BDB C A BD D B B C B⎧⎪⎨⎪=⎩平面同理平面////⇒111B CD A BD 平面平面//． 4．解：（1）证明：连接AN 并延长交BC 于E ，连接PE ，则由AD BC //，得BN NEND AN=． BN PM ND MA =∵，NE PMAN MA=∴． MN PE ∴//，又PE ⊂平面PBC ，M N ⊄平面PBC ，∴MN //平面PBC ．（2）由13PB BC PC ===，得60PBC ∠=；由58BE BN AD ND ==，知5651388BE =⨯=，由余弦定理可得918PE =，8713MN PE ==∴．。

高中数学必修二 8 5 2 直线与平面平行(第1课时)直线与平面平行的判断练习(含答案)

8.5.2 直线与平面平行第一课时直线与平面平行的判断一、选择题1．如图，在下列四个正方体中，A，B为正方体的两个顶点，M，N，Q为所在棱的中点，则在这四个正方体中，直线AB与平面MNQ不平行的是( )A．B．C．D．【答案】A【解析】对于B项，如图所示，连接CD，因为AB∥CD，M，Q分别是所在棱的中点，所以MQ∥CD，所以AB∥MQ，又AB⊄平面MNQ，MQ⊂平面MNQ，所以AB∥平面MNQ，同理可证，C，D项中均有AB∥平面MNQ.故选：A.2．已知直线a和平面α，那么能得出a//α的一个条件是（）⊂A．存在一条直线b，a//b且bα⊄B．存在一条直线b，a//b且bα⊂且α//βC．存在一个平面β，aβD．存在一个平面β，a//β且α//β【答案】C【解析】在选项A ，B ，D 中，均有可能a 在平面α内，错误；在C 中，两平面平行，则其中一个平面内的任意一条直线都平行于另一个平面，故C 正确故选：C3．在正方体1111ABCD A B C D -中，下面四条直线中与平面1AB C 平行的直线是（）A ．1DBB ．11A DC ．11CD D ．1A D【答案】D【解析】如图所示，易知11A B DC ∥且11A B DC =，∴四边形11A B CD 是平行四边形， 11A D B C ∴∥，又1A D ⊂/平面1AB C ，1B C ⊂平面1AB C ，1A D ∴∥平面1AB C .故选D.4．如图所示,四面体ABCD 的一个截面为四边形EFGH ,若AE BF BG CE FC GD==,则与平面EFGH 平行的直线有( )A ．0条B ．1条C ．2条D ．3条【答案】C 【解析】解：AE BF CE FC=,//EF AB ∴. 又EF ⊂平面EFGH ,AB ⊂/平面EFGH ,//AB ∴平面EFGH .同理,由BF BG FC GD=,可证//CD 平面EFGH . ∴与平面EFGH 平行的直线有2条.故选：C5.（多选题）如图所示,P 为矩形ABCD 所在平面外一点,矩形对角线的交点为,O M 为PB 的中点,给出以下结论,其中正确的是( )A ．//OM PDB ．//OM 平面PCDC ．//OM 平面PDAD ．//OM 平面PBA【答案】ABC 【解析】由题意知,OM 是BPD △的中位线,//OM PD ∴,故A 正确;PD ⊂平面PCD ,OM ⊄平面PCD ,//OM ∴平面PCD ,故B 正确;同理,可得//OM 平面PDA ,故C 正确;OM 与平面PBA 和平面PBC 都相交,故D 不正确. 故选：ABC .6.（多选题）如图所示，P为矩形ABCD所在平面外一点，矩形对角线的交点为O，M为PB的中点，给出四个结论正确的是（）A.OM∥PD；B.OM∥平面PCD；C .OM∥平面PDA；D.OM∥平面PBA；C.OM∥平面PBC.其中正确的个数是()【答案】ABC【解析】矩形ABCD的对角线AC与BD交于点O，所以O为BD的中点．在△PBD中，M是PB的中点，所以OM是△PBD的中位线，所以OM∥PD，又OM⊄平面PCD，且OM⊄平面PDA，所以OM∥平面PCD，且OM∥平面PDA.因为M∈PB，所以OM与平面PBA、平面PBC均相交．故选ABC。

届数学一轮总复习46直线平面平行的判定及其性质含解析苏教版

课时作业46 直线、平面平行的判定及其性质一、选择题1．如果直线a∥平面α，那么直线a与平面α内的(D) A．一条直线不相交B．两条直线不相交C．无数条直线不相交 D．任意一条直线都不相交解析：因为直线a∥平面α，所以直线a与平面α无公共点，所以直线a和平面α内的任意一条直线都不相交，故选D。

2．(2020·福州质检)下列说法中，错误的是(D)A．一条直线与两个平行平面中的一个相交,则必与另一个平面相交B．平行于同一平面的两个不同平面平行C．若直线l与平面α平行,则过平面α内一点和直线l平行的直线在α内D．若直线l不平行于平面α，则在平面α内不存在与l平行的直线解析：如果已知直线与另一个平面不相交，则有两种情形：直线在平面内或与平面平行，不管哪种情形都得出这条直线与第一个平面不能相交,出现矛盾,即A中说法正确；选项B是两个平面平行的一种判定方法，即B中说法正确；由线面平行的性质定理知C中说法正确;选项D中说法是错误的，事实上，直线l不平行于平面α，可能有l⊂α,则α内有无数条直线与l平行．故选D。

3．（2019·全国卷Ⅱ）设α,β为两个平面，则α∥β的充要条件是(B)A．α内有无数条直线与β平行B．α内有两条相交直线与β平行C．α，β平行于同一条直线D．α，β垂直于同一平面解析:对于A，α内有无数条直线与β平行,当这无数条直线互相平行时，α与β可能相交,所以A不正确；对于B，根据两平面平行的判定定理与性质知,B正确；对于C，平行于同一条直线的两个平面可能相交，也可能平行，所以C不正确；对于D，垂直于同一平面的两个平面可能相交,也可能平行，如长方体的相邻两个侧面都垂直于底面，但它们是相交的，所以D不正确．综上可知选B.4．已知α，β，γ是三个不重合的平面，l是直线．给出下列命题：①若l上两点到α的距离相等，则l∥α；②若l⊥α,l∥β，则α⊥β;③若α∥β，l⊄β，且l∥α，则l∥β.其中正确的命题是（D)A．①②B．①②③C．①③D．②③解析：对于①，若直线l在平面α内，l上有两点到α的距离为0，相等,此时l不与α平行，所以①错误;对于②，因为l ∥β，所以存在直线m⊂β使得l∥m,因为l⊥α,所以m⊥α，又m⊂β,所以β⊥α，所以②正确；对于③，l∥α，故存在m⊂α,使得l∥m，因为α∥β，所以m∥β，因为l∥m，l⊄β，所以l∥β，③正确．故选D.5．在如图所示的三棱柱ABC。

人教A版(2019)必修二第八章立体几何初步单元测试卷(1)(基础版解析版

人教A版（2019）必修二第八章立体几何初步单元测试卷(1)(基础版)1.将一个等边三角形绕它的一条边所在的直线旋转一周，所得的几何体包括A. 一个圆柱、一个圆锥B. 一个圆台、一个圆锥C. 两个圆锥D. 两个圆柱2.祖暅是南北朝时代的伟大数学家，5世纪末提出体积计算原理，即祖暅原理：“幂势既同，则积不容异”．意思是：夹在两个平行平面之间的两个几何体，被平行于这两个平面的任何一个平面所截，如果截面面积都相等，那么这两个几何体的体积一定相等．现有以下四个几何体：图①是从圆柱中挖去一个圆锥所得的几何体，图②、图③、图④分别是圆锥、圆台和半球，则满足祖暅原理的两个几何体为A. ①②B. ①③C. ②④D. ①④3.如图正方形OABC的边长为1，它是水平放置的一个平面图形的直观图，则原图形的面积为A. B. 1 C. D.4.如图，圆柱内有一内切球圆柱侧面和底面都与球面相切，若内切球的体积为，则圆柱的侧面积为A. B. C. D.5.已知空间中不过同一点的三条直线m，n，l，则“m，n，l在同一平面”是“m，n，l两两相交”的A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件6.下面三条直线一定共面的是A. a，b，c两两平行B. a，b，c两两相交C. ，c与a，b均相交D. a，b，c两两垂直7.如图所示，用符号语言可表示为A. B. C. D.8.下列四个命题中错误的是A. 若直线a，b互相平行，则直线a，b确定一个平面B. 若四点不共面，则这四点中任意三点都不共线C. 若两条直线没有公共点，则这两条直线是异面直线D. 两条异面直线不可能垂直于同一个平面9.分别在两个相交平面内的两条直线间的位置关系是A. 平行B. 相交C. 异面D. 以上皆不可能10.设，是两个不同的平面，l是一条直线，若，，，则下列四个结论正确的是A. l与m一定平行B. l与m可能相交C. l与m不会异面D. l与m可以垂直11.设a，b是互不垂直的两条异面直线，则下列命题不成立的是A. 存在唯一直线l，使得，且B. 存在唯一直线l，使得，且C. 存在唯一平面，使得，且D. 存在唯一平面，使得，且12.下列四个命题中正确的是A. 若两条直线互相平行，则这两条直线确定一个平面B. 若四点不共面，则这四点中任意三点都不共线C. 若两条直线没有公共点，则这两条直线是异面直线D. 两条异面直线不可能垂直于同一个平面13.在正方体各个表面的对角线中，与直线异面的有__________ 条．14.如果角的两边与角的两边分别平行，则的大小是__________.15.在正三棱锥中，D，E分别是AB，BC的中点，有下列三个论断：①；②平面PDE；③平面其中正确的个数是__________.16.已知异面直线a，b所成的角为，且直线，，则__________，直线OA，OB所成的角为__________.17.空间四边形ABCD中，的中点分别为，且，，，求证：18.如图，三棱锥中，，，E、F、G分别为PA、AB、PB的中点，求证：平面PBC；求证：平面19.如图，在四棱锥中，侧棱底面ABCD，且底面ABCD是边长为1的正方形，侧棱，AC与BD相交于点证明：；求三棱锥的体积．20.如图，将直角边长为的等腰直角三角形ABC，沿斜边上的高AD翻折，使二面角的大小为，翻折后BC的中点为证明：平面ADM；求点D到平面ABC的距离．21.如图，四棱锥的底面是正方形，底面ABCD，点E在棱PB上．求证：平面平面PDB；当，且E为PB的中点时，求AE与平面PDB所成的角的大小．22.如图所示，在四棱锥中，底面ABCD是正方形，侧面VAD是正三角形，平面底面求证：平面VAD；求平面VAD与平面VDB所成的二面角的正切值．答案和解析【答案】1. C2. D3. A4. C5. B6. C7. B8. C9. ABC10. AC11. ABD12. ABD13. 614. 或15. 216. 或17. 证明：如图，因为分别为的中点，所以，，所以或其补角为异面直线AC和BD所成的角.又，，，所以，所以，即AC和BD所成的角为，所以18. 证明：、F分别为PA、AB的中点，，又平面PBC，平面PBC，平面，，G为PB的中点，，，又，平面ACG，平面ACG，平面ACG，又，平面19. 证明：平面ABCD，平面ABCD，，四边形ABCD是正方形，，又平面SAC，平面SAC，，平面SAC，平面SAC，解：四边形ABCD是边长为1的正方形，20. 证明：折叠前，AD是斜边上的高，是BC的中点，，又因为折叠后M是BC的中点，，折叠后，，又，且AM，平面ADM，平面ADM；解：设点D到平面ABC的距离为d，由题意得，由已知得，则，，，，，21. 证明：四边形ABCD是正方形，，底面ABCD，底面ABCD，，又，PD，平面PDB，平面PDB，且平面AEC，平面平面PDB；解：设，连接OE，由知平面PDB于O，为AE与平面PDB所的角，，E分别为DB、PB的中点，，，又底面ABCD，底面ABCD，底面ABCD，，在中，，，即AE与平面PDB所成的角的大小为22. 证明：底面ABCD是正方形，又平面底面ABCD，平面底面，底面ABCD，平面取VD的中点E，连接AE，BE，是正三角形，，平面VAD，平面VAD，，又，AB，平面ABE，平面底面ABE，，就是平面VAD与平面VDB所成的二面角的平面角．在中，平面VAD与平面VDB所成的二面角的正切值为【解析】1. 【分析】本题考查的知识点是旋转体的结构特征，熟练掌握旋转体的结构特征是解答本题的关键，属于基础题.由等边三角形的结构特点，可得旋转体.【解答】解：将一个等边三角形绕它的一条边所在的直线旋转一周，所得的几何体是共用一个底面的两个圆锥．故选2. 【分析】本题考查满足祖暅原理的两个几何体的判断，是基础题.利用祖暅原理分析题设中的四个图形，能够得到在①和④中的两个几何体满足祖暅原理．【解答】解：设截面与底面的距离为h，则①中截面内圆半径为h，则截面圆环的面积为②中截面圆的半径为，则截面圆的面积为③中截面圆的半径为，则截面圆的面积为④中截面圆的半径为，则截面圆的面积为，所以①④中截面的面积相等，故选3. 【分析】本题考查斜二测画法的应用，属于基础题.将直观图还原成原来的图形，即平行四边形，由题意求出直观图中OB的长度，根据斜二测画法，求出原图形的高，即可求出原图形的面积．【解答】解：由题意正方形OABC的边长为1，它是水平放置的一个平面图形的直观图，所以原图形为平行四边形，且OA为其中一边，OB是其一条对角线直观图中：计算得，所以由斜二测画法知，对应原图形，即平行四边形的高为，所以原图形的面积为：故选4. 【分析】本题考查的知识点是球的体积与圆柱的表面积公式，属于基础题.根据已知得到球的半径．【解答】解：由，可得球的半径，可得圆柱的高为，圆柱的底面周长为，则圆柱的侧面积为故选5. 【分析】本题借助空间的位置关系，考查了充分条件和必要条件，属于基础题．由m，n，l在同一平面，则m，n，l两两相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行，根据充分条件，必要条件的定义即可判断．【解答】解：空间中不过同一点的三条直线m，n，l，若m，n，l在同一平面，则m，n，l两两相交或m，n，l有两个平行，另一直线与之相交，或三条直线两两平行．故充分性不成立；若m，n，l两两相交，则m，n，l在同一平面，故必要性成立.故m，n，l在同一平面”是“m，n，l两两相交”的必要不充分条件，故选：6. 【分析】本题主要考查平面的基本性质，属于基础题.根据空间公理1、公理2即可判断.【解答】解：因为两条平行直线确定一个平面，根据题意得，a与b确定一个平面，又因为c与a，b均相交，所以直线a，b，c一定共面.故选7. 【分析】本题考查直线与平面、平面与平面的位置关系的符号语言的表示，属于基础题. 根据图示的位置关系易得和平行，l在内，再用数学符号语言表达即可.【解答】解：由图可得：，，所以，故选8. 【分析】本题考查平面的基本性质，异面直线，属于基础题.根据相关的知识逐项进行判断即可.【解答】解：A、过两条平行直线，有且只有一个平面，故A正确；B、如果四点中存在三点共线，则四点共面，故B正确；C、若两条直线没有公共点，则这两条直线异面或平行，故C错误；D、垂直于同一个平面的两条直线平行，两直线共面，故D正确．故选9. 【分析】本题考查空间中两直线的位置关系，属于基础题.利用空间中两直线的位置关系，逐一判定即可．【解答】解：当两直线分别平行于交线时，这两条直线平行，A正确；两条直线可以交于交线上一点，故可以相交，B正确；一条直线和交线平行，另一条直线在另一个平面内过交线上一点和交线外一点时，两直线异面，C正确；故选：10. 【分析】本题考查空间中直线和直线、线面平行的性质的应用，属于基础题.根据过l作平面与、相交，交线分别为a，b利用线面平行的性质易得，从而可得答案.【解答】解：过l作平面与、相交，交线分别为a，b，可得，，，，，，，所以。

人教版七年级数学下《5.2.1平行线》课时练习

七年级下册5.2.1平行线同步练习一、选择题：1.在同一平面内，两条不重合直线的位置关系可能是( )A．平行或相交B．垂直或相交C．垂直或平行D．平行、垂直或相交答案：A知识点：平面中直线的位置关系解析：解答：同一平面内两直线的位置关系有两种：平行和相交，题目提示“可能”，因此选A. 分析：考查“位置关系”时，注意“同一平面内”这个关键条件，垂直是相交的特殊情况，不能选C.2．下列说法正确的是( )A．经过一点有一条直线与已知直线平行B．经过一点有无数条直线与已知直线平行C．经过一点有且只有一条直线与已知直线平行D．经过直线外一点有且只有一条直线与已知直线平行答案：D知识点：平行公理及推论解析：解答：平行公理：经过直线外一点有且只有一条直线与已知直线平行。

分析：注意存在性与唯一性。

3．在同一平面内有三条直线，若其中有两条且只有两条直线平行，则它们交点的个数为( )A．0 个B．1个C．2个D．3个答案：C知识点：平面中直线的位置关系解析：解答：同一平面内两直线的位置关系有两种：平行和相交，只有两条直线平行，第三条直线必与这两条直线相交，因此有两个交点。

分析：由已知“若其中有两条且只有两条直线平行”可知不会三条直线两两平行。

4．下列说法正确的有( )①不相交的两条直线是平行线；②在同一平面内，两条直线的位置关系有两种；③若线段AB与CD没有交点，则AB∥CD；④若a∥b，b∥c，则a与c不相交．A．1个B．2个C．3个D．4个答案：B知识点：平面中直线的位置关系解析：解答：正确的有②④分析：两直线的位置关系，注意是否在同一平面内，若没有这个条件，还可能有异面直线，因此①是错误的，线段没有延伸性，因此③错误。

5．过一点画已知直线的平行线，则( )A．有且只有一条B．有两条C．不存在D．不存在或只有一条答案：D知识点：平行公理及推论解析：解答：这一点与直线的位置关系不明确，因此可能在直线上或在直线外，选D分析：平行公理的条件要记牢：过直线外一点。

高考数学一轮经典例题直线与平面的平行判定和性质

典型(diǎnxíng)例题一例1简述以下问题(wèntí)的结论，并画图说明：〔1〕直线(zhíxiàn)平面(píngmiàn)，直线，那么和α的位置关系如何？〔2〕直线，直线，那么直线b和α的位置关系如何？分析：〔1〕由图〔1〕可知：或者；〔2〕由图〔2〕可知：或者αb．⊂说明：此题是考察直线与平面位置关系的例题，要注意各种位置关系的画法与表示方法．典型例题二例2是平行四边形所在平面外一点，是的中点，求证：平面．分析：要证明平面外的一条直线和该平面平行，只要在该平面内找到一条直线和直线平行就可以了．证明：如下图，连结，交于点，∵四边形ABCD是平行四边形∴，连结，那么OQ在平面BDQ内，且OQ是的中位线，∴．∵在平面BDQ外，∴//PC平面(píngmiàn)BDQ．说明(shuōmíng)：应用线面平行的断定(duàndìng)定理证明线面平行时，关键是在平面内找一条直线与直线平行，怎样找这一直线呢？由于两条直线首先要保证一共面，因此常常设法过直线作一平面与平面相交，假如能证明直线和交线平行，那么就可以马上(mǎshàng)得到结论．这一个证明线面平行的步骤可以总结为：过直线作平面，得交线，假设线线平行，那么线面平行．典型例题三例3经过两条异面直线，b之外的一点P，可以作几个平面都与a，b平行？并证明你的结论．分析：可考虑P点的不同位置分两种情况讨论．解：〔1〕当P点所在位置使得a，P〔或者b，P〕本身确定的平面平行于b〔或者a〕时，过P点再作不出与a，b都平行的平面；〔2〕当P点所在位置a，P〔或者b，P〕本身确定的平面与b〔或者a〕不平行时，可过点P作，．由于a，b异面，那么，不重合且相交于P．由于，a'，b'确定的平面α，那么由线面平行断定定理知：，αb．可作一个平面都与a，b平行．//故应作“0个或者1个〞平面．说明：此题解答容易无视对P点的不同位置的讨论，漏掉第〔1〕种情况而得出可作一个平面的错误结论．可见，考虑问题必须全面，应区别不同情形分别进展分类讨论．典型例题四例4平面外的两条平行(píngxíng)直线中的一条平行于这个平面，那么另一条直线也平行于这个平面．：直线(zhíxiàn)，平面(píngmiàn)α，．求证(qiúzhèng)：αb．//证明：如下图，过a及平面α内一点作平面．设，∵αa，//∴．又∵ba//，∴．∵α⊄b，，∴αb．//说明：根据断定定理，只要在α内找一条直线，根据条件αa，为了//利用直线和平面平行的性质定理，可以过a作平面β与α相交，我们常把平面β称为辅助平面，它可以起到桥梁作用，把空间问题向平面问题转化．和平面几何中添置辅助线一样，在构造辅助平面时，首先要确认这个平面是存在的，例如，本例中就是以“直线及直线外一点确定一个平面〞为根据来做出辅助平面的．典型例题五例5四面体的所有棱长均为a．求：〔1〕异面直线的公垂线段及EF的长；〔2〕异面直线EF和所成的角．分析：依异面直线的公垂线的概念求作异面直线ABSC、的公垂线段，进而求出其间隔；对于异面直线所成的角可采取平移构造法求解．解：〔1〕如图，分别(fēnbié)取ABSC、的中点(zhōnɡ diǎn)，连结(liánjié)．由，得≌．∴，是的中点(zhōnɡ diǎn)，∴．同理可证∴EF是ABSC、的公垂线段．在中，，．∴．〔2〕取AC的中点，连结，那么．∴EF和所成的锐角或者直角就是异面直线EF和SA所成的角．连结，在中，，，．由余弦定理，得．∴．故异面直线EF和SA所成的角为．说明：对于立体几何问题要注意转化为平面问题来解决，同时要将转化过程简要地写出来，然后再求值．典型例题六例6 假如一条直线与一个平面(píngmiàn)平行，那么过这个平面内的一点且与这条直线平行的直线必在这个平面内．：直线(zhíxiàn)α//a ，，，a b //．求证(qiúzhèng)：α⊂b ．分析(f ēnx ī)：由于过点与a 平行的直线是惟一存在的，因此，此题就是要证明，在平面α外，不存在过B 与a 平行的直线，这是否认性命题，所以使用反证法．证明：如下图，设α⊄b ，过直线a 和点B 作平面β，且．∵α//a ，∴．这样过B 点就有两条直线b 和同时平行于直线a ，与平行公理矛盾． ∴b 必在α内．说明：(1)本例的结论可以直接作为证明问题的根据． (2)本例还可以用同一法来证明，只要改变一下表达方式．如上图，过直线a 及点B 作平面β，设'b =αβ ．∵α//a ，∴α//'b ．这样，'b 与b 都是过B 点平行于a 的直线，根据平行公理，这样的直线只有一条，∴b 与'b 重合．∵，∴α⊂b ．典型例题七例7 以下命题正确的个数是〔〕．(1)假设直线上有无数个点不在平面α内，那么；(2)假设(jiǎshè)直线l平行(píngxíng)于平面α内的无数条直线(zhíxiàn)，那么α//l；(3)假设(jiǎshè)直线l与平面α平行，那么l与平面α内的任一直线平行；(4)假设直线l在平面α外，那么α//l．A．0个B．1个C．2个D．3个分析：此题考察的是空间直线与平面的位置关系．对三种位置关系定义的准确理解是解此题的关键．要注意直线和平面的位置关系除了按照直线和平面公一共点的个数来分类，还可以按照直线是否在平面内来分类．解：(1)直线l上有无数个点不在平面α内，并没有说明是所在点都不在平面α内，因此直线可能与平面平行亦有可能与直线相交．解题时要注意“无数〞并非“所有〞．(2)直线l虽与α内无数条直线平行，但l有可能在平面α内，所以直线l不一定平行α．(3)这是初学直线与平面平行的性质时常见错误，借助教具我们很容易看到．当αl时，假设且，那么在平面α内，除了与平//行的直线以外的每一条直线与l都是异面直线．(4)直线l在平面α外，应包括两种情况：α//l和l与α相交，所以l与α不一定平行．应选A．说明：假如题中判断两条直线与一平面之间的位置关系，解题时更要注意分类要完好，考虑要全面．如直线l、m都平行于α，那么l与m的位置关系可能平行，可能相交也有可能异面；再如直线、αl，那么m与α的位置关系可//能是平行，可能是m在α内．典型例题八例8如图，求证：两条平行线中的一条和平面相交，那么另一条也与该平面相交．：直线ba//，．求证：直线b与平面α相交．分析(fēnxī)：利用(lìyòng)ba//转化(zhuǎnhuà)为平面问题来解决，由a//可确定一辅助(fǔzhù)平面β，这样可以把题中相关元素集中使用，既创造b了新的线面关系，又将三维降至二维，使得平几知识可以运用．解：∵ba//，∴a和b可确定平面β．∵，∴平面α和平面β相交于过点P的直线l．∵在平面β内l与两条平行直线a、b中一条直线a相交，∴l必定与直线b也相交，不妨设，又因为b不在平面α内〔假设b 在平面α内，那么α和β都过相交直线b和l，因此α与β重合，a在α内，和矛盾〕．所以直线b和平面α相交．说明：证明直线和平面相交的常用方法有：证明直线和平面只有一个公一共点；否认直线在平面内以及直线和平面平行；用此结论：一条直线假如经过平面内一点，又经过平面外一点，那么此直线必与平面相交〔此结论可用反证法证明〕．典型例题九例9如图，求证：经过两条异面直线中的一条，有且仅有一个平面与另一条直线平行．：a与b是异面直线．求证：过b且与a平行的平面有且只有一个．分析：此题考察存在性与唯一性命题的证明方法．解题时要理解“有且只有〞的含义．“有〞就是要证明过直线b存在一个平面α，且αa，“只有〞就//是要证满足这样条件的平面是唯一的．存在性常用构造法找出〔或者作出〕平面，唯一性常借助于反证法或者其它唯一性的结论．证明(zhèngmíng)：(1)在直线(zhíxiàn)b上任(shàng rèn)取一点A，由点A和直线(zhíxiàn)a可确定平面β．在平面β内过点A作直线，使，那么'a和b为两相交直线，所以过'a和b可确定一平面α．∵αb，a与b为异面直线，⊂∴．又∵，，∴αa．//故经过b存在一个平面α与a平行．(2)假如平面也是经过b且与a平行的另一个平面，由上面的推导过程可知γ也是经过相交直线b和'a的．由经过两相交直线有且仅有一个平面的性质可知，平面α与γ重合，即满足条件的平面是唯一的．说明：对于两异面直线a和b，过b存在一平面α且与a平行，同样过a也存在一平面β且与b平行．而且这两个平面也是平行的〔以后可证〕．对于异面直线a和b的间隔，也可转化为直线a到平面α的间隔，这也是求异面直线的间隔的一种方法．典型例题十例10 如图，求证：假如一条直线和两个相交平面都平行，那么这条直线和它们的交线平行．：，α//a ，，求证：．分析(f ēnx ī)：此题考察综合运用线面平行的断定(duàndìng)定理和性质定理的才能．利用线面平行的性质定理，可以先证明直线a 分别和两平面的某些直线(zhíxiàn)平行，即线面平行可得线线平行．然后再用线面平行的断定定理和性质定理来证明a 与l 平行(píngxíng)．证明：在平面α内取点P ，使，过P 和直线a 作平面γ交α于b ．∵α//a ，，，∴b a //．同理过a 作平面交β于． ∵β//a ，，，∴c a //． ∴c b //． ∵，， ∴．又∵α⊂b ，l =βα ， ∴．又∵b a //， ∴l a //．另证：如图，在直线l 上取点，过M 点和直线a 作平面和α相交于直线，和β相交于直线．∵α//a ，∴， ∵β//a ，∴，但过一点只能(zh ī nénɡ)作一条直线与另一直线平行． ∴直线(zhíxiàn)和2l 重合(chónghé)．又∵，，∴直线(zhíxiàn)1l 、2l 都重合于直线l ， ∴l a //．说明：“线线平行〞与“线面平行〞在一定条件下是可以互相转化的，这种转化的思想在立体几何中非常重要．典型例题十一例11 正方形ABCD 与正方形所在平面相交于，在、BD 上各取一点P 、Q ，且．求证：面．分析：要证线面平行，可以根据断定定理，转化为证明线线平行．关键是在平面BCE 中如何找一直线与平行．可考察过PQ 的平面与平面BCE 的交线，这样的平面位置不同，所找的交线也不同．证明一：如图，在平面ABEF 内过P 作交于M ，在平面ABCD 内过Q 作交于，连结．∵ABPM//，∴．又∵，∴，即．∵正方形ABEF与ABCD有公一共(yīgòng)边AB，∴．∵DQAP ，∴．∴．又∵ABPM//，ABQN//，∴．∴四边形为平行四边形．∴．又∵面BCE，∴//PQ面BCE．证明(zhèngmíng)二：如图，连结(lián jié)并延长(yáncháng)交BC于，连结．∵，∴．又∵正方形ABEF 与正方形ABCD 有公一共边AB ， ∴DB AE =， ∵DQ AP =，∴．∴．∴，又∵面， ∴//PQ 面BEC ．说明(shu ōmíng)：从此题中我们可以看出，证线面平行的根本问题是要在平面内找一直线(zhíxiàn)与直线平行，此时常用中位线定理、成比例线段、射影法、平行挪动、补形等方法，详细用何种方法要视条件而定．此题中我们可以把“两个有公一共边的正方形〞这一条件(tiáojiàn)改为“两个(li ǎn ɡ ɡè)全等的矩形〞，那么题中的结论是否仍然成立？典型例题十二例12 三个平面两两相交于三条交线，证明这三条交线或者平行、或者相交于一点．：，，．求证：a 、b 、c 互相平行或者相交于一点．分析：此题考察的是空间三直线的位置关系，我们可以先从熟悉的两条交线的位置关系入手，根据一共面的两条直线平行或者相交来推论三条交线的位置关系．证明：∵a =βα ，b =γβ ， ∴．∴a 与b 平行或者相交． ①假设b a //，如图∵，，∴．又∵c =αγ ，α⊂a ，∴c a //． ∴．②假设(ji ǎshè)a 与b 相交(xi āngji āo)，如图，设，∴，．又∵，．∴，又∵，∴． ∴直线(zhíxiàn)a 、b 、c 交于同一点(y ī di ǎn)O ．说明：这一结论常用于求一个几何体的截面与各面交线问题，如正方体ABCD 中， M 、N 分别是、的中点，画出点、M 、N 的平面与正方体各面的交线，并说明截面多边形是几边形？典型例题十三例13 空间四边形ABCD ，，AE 是的BC 边上的高，是的BC 边上的中线，求证：AE 和DF 是异面直线．证法一：〔定理法〕如图由题设条件可知点E、不重合，设BCD∆所在平面α．∴AE和DF是异面直线(zhíxiàn)．证法(zhènɡ fǎ)二：〔反证法〕假设(jiǎshè)AE和DF不是(bù shi)异面直线，那么AE和DF一共面，设过AE、DF的平面为β．(1)假设E、F重合，那么E是BC的中点，这与题设ACAB≠相矛盾．(2)假设E、F不重合，∵，，，∴．∵，，∴A、B、、D四点一共面，这与题设ABCD是空间四边形相矛盾．综上，假设不成立．故AE和DF是异面直线．说明：反证法不仅应用于有关数学问题的证明，在其他方面也有广泛的应用．首先看一个有趣的实际问题：“三十六口缸，九条船来装，只准装单，不准装双，你说怎么装？〞对于这个问题，同学们可试验做一做．也许你在试验几次后却无法成功时，觉得这种装法的可能性是不存在的．那么你怎样才能清楚地从理论上解释这种装法是不可能呢？用反证法可以轻易地解决这个问题．假设这种装法是可行的，每条船装缸数为单数，那么9个单数之和仍为单数，与36这个双数矛盾．只须两句话就解决了这个问题．典型例题十四例14AB、BC、是不在同一平面内的三条线段，E、F、G分别是AB、BC、CD的中点，求证：平面和AC平行，也和BD平行．分析(fēnxī)：欲证明(zhèngmíng)AC平面(píngmiàn)EFG，根据直线(zhíxiàn)和平面平等的断定定理只须证明AC平行平面EFG内的一条直线，由图可知，只须证明．证明：如图，连结AE、EG、EF、．在ABC∆中，E、F分别是AB、BC的中点．∴EFAC//．于是AC//平面EFG．同理可证，BD//平面EFG．说明：到目前为止，断定直线和平面平行有以下两种方法：(1)根据直线和平面平行定义；(2)根据直线和平面平行的断定定理．典型例题十五例15空间四边形ABCD，P、Q分别是ABC∆的重心，∆和BCD求证：．分析：欲证线面平行，须证线线平行，即要证明PQ与平面中的某条直线平行，根据条件，此直线为，如图．证明：取BC的中点E．∵P 是ABC ∆的重心，连结AE ，那么，连结，∵Q 为BCD ∆的重心， ∴，∴在中，．又，，∴ACD PQ 平面//．说明(shu ōmíng)：(1)本例中构造(gòuzào)直线AD 与PQ 平行，是充分借助于题目(tímù)的条件：P 、Q 分别(f ēnbié)是ABC ∆和BCD ∆的重心，借助于比例的性质证明AD PQ //，该种方法经常使用，望注意把握．(2)“欲证线面平行，只须证线线平行〞．断定定理给我们提供了一种证明线面平等的方法．根据问题详细情况要纯熟运用．典型例题十六例16 正方体中，E 、G 分别是BC 、的中点如以下图．求证：．分析：要证明D D BB EG 11//平面，根据线面平等的断定定理，需要在平面内找到与EG 平行的直线，要充分借助于E 、G 为中点这一条件．证明：取BD 的中点F ，连结EF 、．∵E 为BC 的中点，∴EF 为BCD ∆的中位线，那么，且．∵G 为11D C 的中点， ∴且， ∴且，∴四边形为平行四边形， ∴，而，，∴．典型(di ǎnxíng)例题十七例17 假如(ji ǎrú)直线，那么(nà me)直线a 与平面(píngmiàn)α内的〔〕．A ．一条直线不相交B ．两条相交直线不相交C ．无数条直线不相交D ．任意一条直线都不相交解：根据直线和平面平行定义，易知排除A 、B ．对于C ，无数条直线可能是一组平行线，也可能是一共点线，∴C 也不正确，应排除C ．与平面α内任意一条直线都不相交，才能保证直线a 与平面α平行，∴D 正确．∴应选D ．说明：此题主要考察直线与平面平行的定义．典型例题十八例18 分别和两条异面直线平行的两条直线的位置关系是〔〕． A ．一定平行 B ．一定相交 C ．一定异面 D ．相交或者异面解：如图中的甲图，分别与异面直线a、b平行的两条直线c、是相交关系；如图中的乙图，分别(fēnbié)与异面直线a、b平行(píngxíng)的两条直线c、d 是相交(xiāngjiāo)关系．综上，可知(kě zhī)应选D．说明：此题主要考察有关平面、线面平行等根底知识以及空间想象才能．典型例题十九例19a、b是两条异面直线，以下结论正确的选项是〔〕．A．过不在a、b上的任一点，可作一个平面与a、b平行B．过不在a、b上的任一点，可作一个直线与a、b相交C．过不在a、b上的任一点，可作一个直线与a、b都平行D．过a可以并且只可以作一平面与b平行解：A错，假设点与a所确定的平面与b平行时，就不能使这个平面与平行了．B错，假设点与a所确定的平面与b平等时，就不能作一条直线与a，b相交．C错，假设这样的直线存在，根据公理4就可有ba//，这与a，b异面矛盾．D正确，在a上任取一点A，过A点做直线bc//，那么c与a确定一个平面与b平行，这个平面是惟一的．∴应选Ｄ．说明：此题主要考察异面直线、线线平行、线面平行等根本概念．典型例题二十例20 (1)直线b a //，α平面//a ，那么b 与平面α的位置关系是_____________．(2)A 是两异面直线a 、b 外的一点，过A 最多可作___________个平面同时与a 、b 平行．解：(1)当直线b 在平面α外时，α//b ；当直线b 在平面α内时，α⊂b ． ∴应填：α//b 或者α⊂b ．(2)因为过A 点分别作a ，b 的平行线只能作一条，〔分别称'a ，'b 〕经过'a ，'b 的平面也是惟一的．所以只能作一个平面；还有不能作的可能，当这个平面(píngmiàn)经过a 或者(huòzhě)b 时，这个(zhè ge)平面就不满足条件了．∴应填：1．说明(shu ōmíng)：考虑问题要全面，各种可能性都要想到，是解答此题的关键．典型例题二十一例21 如图，α//a ，A 是α的另一侧的点，，线段AB ，AC ，AD 交α于E ，F ，G ，假设，，，那么EG =___________．解：∵α//a ，．∴，即，∴．那么．∴应填：．说明：此题是一道综合题，考察知识主要有：直线与平面平行性质定理、相似三角形、比例性质等．同时也考察了综合运用知识，分析和解决问题的才能．内容总结（1）典型例题一例1 简述以下问题的结论，并画图说明：〔1〕直线平面，直线，那么和的位置关系如何。

2023年高考数学一轮复习第七章立体几何与空间向量4空间直线平面的平行练习含解析

空间直线、平面的平行考试要求 1.理解空间中直线与直线、直线与平面、平面与平面的平行关系，并加以证明.2.掌握直线与平面、平面与平面平行的判定与性质，并会简单应用．知识梳理1．线面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行错误!⇒a∥α性质定理一条直线与一个平面平行，如果过该直线的平面与此平面相交，那么该直线与交线平行错误!⇒a∥b2.面面平行的判定定理和性质定理文字语言图形语言符号语言判定定理如果一个平面内的两条相交直线与另一个平面平行，那么这两个平面平行错误!⇒β∥α性质定理两个平面平行，如果另一个平面与这两个平面相交，那么两条交线平行错误!⇒a∥b常用结论(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.(2)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.(3)垂直于同一个平面的两条直线平行，即a⊥α，b⊥α，则a∥b.(4)若α∥β，a⊂α，则a∥β.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若一条直线平行于一个平面内的一条直线，则这条直线平行于这个平面．( ×)(2)若直线a∥平面α，P∈α，则过点P且平行于直线a的直线有无数条．( ×)(3)若直线a⊂平面α，直线b⊂平面β，a∥b，则α∥β.( ×)(4)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．( √)教材改编题1．下列说法中，与“直线a∥平面α”等价的是( )A．直线a上有无数个点不在平面α内B．直线a与平面α内的所有直线平行C．直线a与平面α内无数条直线不相交D．直线a与平面α内的任意一条直线都不相交答案 D解析因为a∥平面α，所以直线a与平面α无交点，因此a和平面α内的任意一条直线都不相交．2．已知不重合的直线a，b和平面α，则下列选项正确的是( )A．若a∥α，b⊂α，则a∥bB．若a∥α，b∥α，则a∥bC．若a∥b，b⊂α，则a∥αD．若a∥b，a⊂α，则b∥α或b⊂α答案 D解析若a∥α，b⊂α，则a∥b或异面，A错；若a∥α，b∥α，则a∥b或异面或相交，B错；若a∥b，b⊂α，则a∥α或a⊂α，C错；若a∥b，a⊂α，则b∥α或b⊂α，D对．3.如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为______．答案平行四边形解析∵平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，∴EF∥HG.同理EH∥FG，∴四边形EFGH是平行四边形.题型一直线与平面平行的判定与性质命题点1 直线与平面平行的判定例1 如图，在四棱锥P －ABCD 中，底面ABCD 是平行四边形，E ，F 分别是BC ，PD 的中点，求证：(1)PB ∥平面ACF ；(2)EF ∥平面PAB .证明 (1)如图，连接BD 交AC 于O ，连接OF ，∵四边形ABCD 是平行四边形， ∴O 是BD 的中点，又∵F 是PD 的中点，∴OF ∥PB ，又∵OF ⊂平面ACF ，PB ⊄平面ACF ， ∴PB ∥平面ACF .(2)取PA 的中点G ，连接GF ，BG . ∵F 是PD 的中点， ∴GF 是△PAD 的中位线， ∴GF 綉12AD ，∵底面ABCD 是平行四边形，E 是BC 的中点， ∴BE 綉12AD ，∴GF 綉BE ，∴四边形BEFG 是平行四边形， ∴EF ∥BG ，又∵EF ⊄平面PAB ，BG ⊂平面PAB ， ∴EF ∥平面PAB .命题点2 直线与平面平行的性质例2 如图所示，在四棱锥P－ABCD中，四边形ABCD是平行四边形，M是PC的中点，在DM 上取一点G，过G和PA作平面交BD于点H.求证：PA∥GH.证明如图所示，连接AC交BD于点O，连接OM，∵四边形ABCD是平行四边形，∴O是AC的中点，又M是PC的中点，∴PA∥OM，又OM⊂平面BMD，PA⊄平面BMD，∴PA∥平面BMD，又平面PAHG∩平面BMD＝GH，∴PA∥GH.教师备选如图，四边形ABCD是矩形，P∉平面ABCD，过BC作平面BCFE交AP于点E，交DP于点F，求证：四边形BCFE是梯形．证明∵四边形ABCD为矩形，∴BC∥AD.∵AD⊂平面PAD，BC⊄平面PAD，∴BC∥平面PAD.∵平面BCFE∩平面PAD＝EF，BC⊂平面BCFE，∴BC∥EF.∵AD＝BC，AD≠EF，∴BC≠EF，∴四边形BCFE是梯形．思维升华(1)判断或证明线面平行的常用方法①利用线面平行的定义(无公共点)．②利用线面平行的判定定理(a⊄α，b⊂α，a∥b⇒a∥α)．③利用面面平行的性质(α∥β，a⊂α⇒a∥β)．④利用面面平行的性质(α∥β，a⊄β，a∥α⇒a∥β)．(2)应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面确定交线．跟踪训练1 如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，M是线段EF的中点．(1)求证：AM∥平面BDE；(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．(1)证明如图，记AC与BD的交点为O，连接OE.因为O，M分别为AC，EF的中点，四边形ACEF是矩形，所以四边形AOEM是平行四边形，所以AM∥OE.又因为OE⊂平面BDE，AM⊄平面BDE，所以AM∥平面BDE.(2)解l∥m，证明如下：由(1)知AM∥平面BDE，又AM⊂平面ADM，平面ADM∩平面BDE＝l，所以l∥AM，同理，AM∥平面BDE，又AM⊂平面ABM，平面ABM∩平面BDE＝m，所以m∥AM，所以l∥m.题型二平面与平面平行的判定与性质例3 如图所示，在三棱柱ABC－A1B1C1中，过BC的平面与上底面A1B1C1交于GH(GH与B1C1不重合)．(1)求证：BC∥GH；(2)若E，F，G分别是AB，AC，A1B1的中点，求证：平面EFA1∥平面BCHG.证明(1)∵在三棱柱ABC－A1B1C1中，∴平面ABC∥平面A1B1C1，又∵平面BCHG∩平面ABC＝BC，且平面BCHG∩平面A1B1C1＝HG，∴由面面平行的性质定理得BC∥GH.(2)∵E，F分别为AB，AC的中点，∴EF∥BC，∵EF⊄平面BCHG，BC⊂平面BCHG，∴EF∥平面BCHG.又G，E分别为A1B1，AB的中点，A1B1綉AB，∴A1G綉EB，∴四边形A1EBG是平行四边形，∴A1E∥GB.∵A1E⊄平面BCHG，GB⊂平面BCHG，∴A1E∥平面BCHG.又∵A1E∩EF＝E，A1E，EF⊂平面EFA1，∴平面EFA1∥平面BCHG.延伸探究在本例中，若将条件“E，F，G分别是AB，AC，A1B1的中点”变为“点D，D1分别是AC，A1C1上的点，且平面BC1D∥平面AB1D1”，试求ADDC的值．解如图，连接A1B交AB1于O，连接OD1.由平面BC 1D ∥平面AB 1D 1，且平面A 1BC 1∩平面BC 1D ＝BC 1，平面A 1BC 1∩平面AB 1D 1＝D 1O ，所以BC 1∥D 1O ，则A 1D 1D 1C 1＝A 1OOB＝1. 又由题设A 1D 1D 1C 1＝DC AD，所以DC AD＝1，即AD DC＝1. 教师备选如图，在三棱柱ABC －A 1B 1C 1中，E ，F ，G 分别为B 1C 1，A 1B 1，AB 的中点．(1)求证：平面A 1C 1G ∥平面BEF ；(2)若平面A 1C 1G ∩BC ＝H ，求证：H 为BC 的中点．证明 (1)∵E ，F 分别为B 1C 1，A 1B 1的中点， ∴EF ∥A 1C 1，∵A 1C 1⊂平面A 1C 1G ，EF ⊄平面A 1C 1G ， ∴EF ∥平面A 1C 1G ，又F ，G 分别为A 1B 1，AB 的中点， ∴A 1F ＝BG ，又A 1F ∥BG ，∴四边形A 1GBF 为平行四边形，则BF ∥A 1G ，∵A 1G ⊂平面A 1C 1G ，BF ⊄平面A 1C 1G ， ∴BF ∥平面A 1C 1G ，又EF ∩BF ＝F ，EF ，BF ⊂平面BEF ， ∴平面A 1C 1G ∥平面BEF .(2)∵平面ABC∥平面A1B1C1，平面A1C1G∩平面A1B1C1＝A1C1，平面A1C1G与平面ABC有公共点G，则有经过G的直线，设交BC于点H，如图，则A1C1∥GH，得GH∥AC，∵G为AB的中点，∴H为BC的中点．思维升华证明面面平行的常用方法(1)利用面面平行的判定定理．(2)利用垂直于同一条直线的两个平面平行(l⊥α，l⊥β⇒α∥β)．(3)利用面面平行的传递性，即两个平面同时平行于第三个平面，则这两个平面平行(α∥β，β∥γ⇒α∥γ)．跟踪训练2 如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形．(1)证明：平面A1BD∥平面CD1B1；(2)若平面ABCD∩平面CD1B1＝直线l，证明：B1D1∥l.证明(1)由题设知BB1綉DD1，所以四边形BB1D1D是平行四边形，所以BD∥B1D1.又BD⊄平面CD1B1，B1D1⊂平面CD1B1，所以BD∥平面CD1B1.因为A1D1綉B1C1綉BC，所以四边形A1BCD1是平行四边形，所以A1B∥D1C.又A1B⊄平面CD1B1，D1C⊂平面CD1B1，所以A1B∥平面CD1B1.又因为BD∩A1B＝B，BD，A1B⊂平面A1BD，所以平面A1BD∥平面CD1B1.(2)由(1)知平面A1BD∥平面CD1B1，又平面ABCD∩平面CD1B1＝直线l，平面ABCD∩平面A1BD＝直线BD，所以直线l∥直线BD，在四棱柱ABCD－A1B1C1D1中，四边形BDD1B1为平行四边形，所以B 1D 1∥BD ，所以B 1D 1∥l .题型三平行关系的综合应用例4 如图，在正方体ABCD －A 1B 1C 1D 1中，P ，Q 分别为对角线BD ，CD 1上的点，且CQ QD 1＝BP PD ＝23.(1)求证：PQ ∥平面A 1D 1DA ；(2)若R 是AB 上的点，AR AB的值为多少时，能使平面PQR ∥平面A 1D 1DA ？请给出证明． (1)证明连接CP 并延长，与DA 的延长线交于M 点，如图，连接MD 1，因为四边形ABCD 为正方形，所以BC ∥AD ，故△PBC ∽△PDM ，所以CP PM ＝BP PD ＝23，又因为CQ QD 1＝BP PD ＝23，所以CQ QD 1＝CP PM ＝23，所以PQ ∥MD 1.又MD 1⊂平面A 1D 1DA ，PQ ⊄平面A 1D 1DA ，故PQ ∥平面A 1D 1DA .(2)解当AR AB 的值为35时，能使平面PQR ∥平面A 1D 1DA .如图，证明如下：因为AR AB ＝35，即BR RA ＝23，故BR RA ＝BP PD. 所以PR ∥DA .又DA ⊂平面A 1D 1DA ，PR ⊄平面A 1D 1DA ，所以PR ∥平面A 1D 1DA ，又PQ ∥平面A 1D 1DA ，PQ ∩PR ＝P ，PQ ，PR ⊂平面PQR ，所以平面PQR ∥平面A 1D 1DA . 教师备选如图，四边形ABCD 与ADEF 均为平行四边形，M ，N ，G 分别是AB ，AD ，EF 的中点．求证：(1)BE ∥平面DMF ； (2)平面BDE ∥平面MNG .证明 (1)如图，连接AE ，则AE 必过DF 与GN 的交点O ，连接MO ，则MO 为△ABE 的中位线，所以BE ∥MO . 又BE ⊄平面DMF ，MO ⊂平面DMF ，所以BE ∥平面DMF .(2)因为N ，G 分别为平行四边形ADEF 的边AD ，EF 的中点，所以DE ∥GN ，又DE ⊄平面MNG ，GN ⊂平面MNG ，所以DE ∥平面MNG . 又M 为AB 的中点，所以MN 为△ABD 的中位线，所以BD ∥MN ，又MN ⊂平面MNG ，BD ⊄平面MNG ，所以BD ∥平面MNG ，又DE ，BD ⊂平面BDE ，DE ∩BD ＝D ，所以平面BDE ∥平面MNG .思维升华证明平行关系的常用方法熟练掌握线线、线面、面面平行关系间的相互转化是解决线线、线面、面面平行的综合问题的关键．面面平行判定定理的推论也是证明面面平行的一种常用方法．跟踪训练3 如图所示，四边形EFGH 为空间四边形ABCD 的一个截面，若截面为平行四边形． (1)求证：AB ∥平面EFGH ；(2)若AB ＝4，CD ＝6，求四边形EFGH 周长的取值范围．(1)证明 ∵四边形EFGH 为平行四边形， ∴EF ∥HG .∵HG ⊂平面ABD ，EF ⊄平面ABD ， ∴EF ∥平面ABD . 又∵EF ⊂平面ABC ，平面ABD ∩平面ABC ＝AB ， ∴EF ∥AB ，又∵AB ⊄平面EFGH ，EF ⊂平面EFGH ， ∴AB ∥平面EFGH . (2)解设EF ＝x (0<x <4)，由(1)知EF ∥AB ， ∴CF CB ＝EF AB ＝x4，与(1)同理可得CD ∥FG ， ∴FG CD ＝BF BC，则FG 6＝BF BC＝BC －CF BC ＝1－x4， ∴FG ＝6－32x .∴四边形EFGH 的周长L ＝2⎝⎛⎭⎪⎫x ＋6－32x ＝12－x .又∵0<x <4，∴8<L <12，故四边形EFGH 周长的取值范围是(8,12)．课时精练1．(2022·宁波模拟)下列命题中正确的是( )A．若a，b是两条直线，且a∥b，那么a平行于经过b的任何平面B．若直线a和平面α满足a∥α，那么a与α内的任何直线平行C．平行于同一条直线的两个平面平行D．若直线a，b和平面α满足a∥b，a⊂α，b⊄α，则b∥α答案 D解析A中，a可以在过b的平面内；B中，a与α内的直线也可能异面；C中，两平面可能相交；D中，由直线与平面平行的判定定理知b∥α，正确．2．(2022·呼和浩特模拟)设a，b是两条不同的直线，α，β是两个不同的平面，则α∥β的一个充分条件是( )A．存在一条直线a，a∥α，a∥βB．存在一条直线a，a⊂α，a∥βC．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥αD．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α答案 D解析对于A，一条直线与两个平面都平行，两个平面不一定平行，故A不正确；对于B，一个平面中的一条直线平行于另一个平面，两个平面不一定平行，故B不正确；对于C，两个平面中的两条直线平行，不能保证两个平面平行，故C不正确；对于D，如图，在直线b上取点B，过点B和直线a确定一个平面γ，交平面β于a′，因为a∥β，所以a∥a′，又a′⊄α，a⊂α，所以a′∥α，又因为b∥α，b∩a′＝B，b⊂β，a′⊂β，所以β∥α.3．(2022·广州模拟)如图，在三棱柱ABC－A1B1C1中，AM＝2MA1，BN＝2NB1，过MN作一平面分别交底面△ABC的边BC，AC于点E，F，则( )A．MF∥EBB．A1B1∥NEC．四边形MNEF为平行四边形D．四边形MNEF为梯形答案 D解析由于B，E，F三点共面，F∈平面BEF，M∉平面BEF，故MF，EB为异面直线，故A错误；由于B1，N，E三点共面，B1∈平面B1NE，A1∉平面B1NE，故A1B1，NE为异面直线，故B错误；∵在平行四边形AA1B1B中，AM＝2MA1，BN＝2NB1，∴AM∥BN，AM＝BN，故四边形AMNB为平行四边形，∴MN∥AB.又MN⊄平面ABC，AB⊂平面ABC，∴MN∥平面ABC.又MN⊂平面MNEF，平面MNEF∩平面ABC＝EF，∴MN∥EF，∴EF∥AB，显然在△ABC中，EF≠AB，∴EF≠MN，∴四边形MNEF为梯形，故C错误，D正确．4．(2022·杭州模拟)已知P为△ABC所在平面外一点，平面α∥平面ABC，且α交线段PA，PB，PC于点A′，B′，C′，若PA′∶AA′＝2∶3，则S△A′B′C′∶S△ABC等于( )A．2∶3B．2∶5C．4∶9D．4∶25答案 D解析∵平面α∥平面ABC，∴A′C′∥AC，A′B′∥AB，B′C′∥BC，∴S△A′B′C′∶S△ABC＝(PA′∶PA)2，又PA′∶AA′＝2∶3，∴PA′∶PA＝2∶5，∴S△A′B′C′∶S△ABC＝4∶25.5．(多选)(2022·济宁模拟)如图，在下列四个正方体中，A，B为正方体的两个顶点，D，E，F为所在棱的中点，则在这四个正方体中，直线AB与平面DEF平行的是( )答案AC解析对于A，AB∥DE，AB⊄平面DEF，DE⊂平面DEF，∴直线AB与平面DEF平行，故A正确；对于B，如图，取正方体所在棱的中点G，连接FG并延长，交AB延长线于H，则AB与平面DEF相交于点H，故B错误；对于C，AB∥DF，AB⊄平面DEF，DF⊂平面DEF，∴直线AB与平面DEF平行，故C正确；对于D，AB与DF所在平面的正方形对角线有交点B，DF与该对角线平行，∴直线AB与平面DEF相交，故D错误．6．(多选)如图，透明塑料制成的长方体容器ABCD－A1B1C1D1内灌进一些水，固定容器一边AB 于地面上，再将容器倾斜，随着倾斜程度的不同，有下面几个结论，其中正确的是( )A ．没有水的部分始终呈棱柱形B ．水面EFGH 所在四边形的面积为定值C ．随着容器倾斜程度的不同，A 1C 1始终与水面所在平面平行D ．当容器倾斜如图(3)所示时，AE ·AH 为定值答案 AD解析根据棱柱的特征(有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行)，结合题中图形易知A 正确；由题图可知水面EFGH 的边EF 的长保持不变，但邻边的长却随倾斜程度而改变，可知B 错误；因为A 1C 1∥AC ，AC ⊂平面ABCD ，A 1C 1⊄平面ABCD ，所以A 1C 1∥平面ABCD ，当平面EFGH 不平行于平面ABCD 时，A 1C 1不平行于水面所在平面，故C 错误；当容器倾斜如题图(3)所示时，因为水的体积是不变的，所以棱柱AEH －BFG 的体积V 为定值，又V ＝S △AEH ·AB ，高AB 不变，所以S △AEH 也不变，即AE ·AH 为定值，故D 正确．7．考查①②两个命题，①⎭⎪⎬⎪⎫m ⊂αl ∥m ⇒l ∥α；②⎭⎪⎬⎪⎫l ∥m m ∥α ⇒l ∥α，它们都缺少同一个条件，补上这个条件就可以使其构成真命题(其中l ，m 为直线，α为平面)，则此条件为__________．答案 l ⊄α解析 ①由线面平行的判定定理知l ⊄α；②由线面平行的判定定理知l ⊄α.8.如图所示，在正四棱柱ABCD —A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，D 1D ，DC 的中点，N 是BC 的中点，点M 在四边形EFGH 及其内部运动，则M 只需满足条件______，就有MN ∥平面B 1BDD 1.(注：请填上你认为正确的一个条件即可，不必考虑全部可能情况)答案点M 在线段FH 上(或点M 与点H 重合) 解析连接HN ，FH ，FN (图略)，则FH ∥DD 1，HN ∥BD ，∴平面FHN ∥平面B 1BDD 1，只需M ∈FH ，则MN ⊂平面FHN ，∴MN ∥平面B 1BDD 1.9．如图，在正方体ABCD －A 1B 1C 1D 1中，E ，F ，G ，H 分别是BC ，CC 1，C 1D 1，AA 1的中点，求证：(1)BF ∥HD 1； (2)EG ∥平面BB 1D 1D ； (3)平面BDF ∥平面B 1D 1H . 证明如图．(1)取B 1B 的中点M ，连接HM ，MC 1，易证四边形HMC 1D 1是平行四边形， ∴HD 1∥MC 1. 又MC 1∥BF ， ∴BF ∥HD 1.(2)取BD 的中点O ，连接OE ，OD 1，则OE 綉12DC .又D 1G 綉12DC ，∴OE 綉D 1G .∴四边形OEGD 1是平行四边形， ∴EG ∥D 1O .又D 1O ⊂平面BB 1D 1D ，EG ⊄平面BB 1D 1D ， ∴EG ∥平面BB 1D 1D .(3)由(1)知BF ∥HD 1，由题意易证B 1D 1∥BD .又B 1D 1，HD 1⊂平面B 1D 1H ，BF ，BD ⊂平面BDF ，且B 1D 1∩HD 1＝D 1，DB ∩BF ＝B ， ∴平面BDF ∥平面B 1D 1H .10.如图，在四棱锥P －ABCD 中，AD ∥BC ，AB ＝BC ＝12AD ，E ，F ，H 分别为线段AD ，PC ，CD 的中点，AC 与BE 交于O 点，G 是线段OF 上一点．(1)求证：AP ∥平面BEF ； (2)求证：GH ∥平面PAD . 证明 (1)如图，连接EC ，因为AD ∥BC ，BC ＝12AD ，所以BC ∥AE ，BC ＝AE ，所以四边形ABCE 是平行四边形，所以O 为AC 的中点．又因为F 是PC 的中点，所以FO ∥AP ，因为FO ⊂平面BEF ，AP ⊄平面BEF ，所以AP ∥平面BEF .(2)连接FH ，OH ，因为F ，H 分别是PC ，CD 的中点，所以FH ∥PD ，因为PD ⊂平面PAD ，FH ⊄平面PAD ，所以FH ∥平面PAD .又因为O 是BE 的中点，H 是CD 的中点，所以OH ∥AD ，因为AD ⊂平面PAD ，OH ⊄平面PAD ，所以OH ∥平面PAD .又FH ∩OH ＝H ，FH ，OH ⊂平面OHF ，所以平面OHF ∥平面PAD . 又因为GH ⊂平面OHF ，所以GH ∥平面PAD .11．(多选)已知α，β是两个平面，m，n是两条直线．下列命题正确的是( )A．如果m∥n，n⊂α，那么m∥αB．如果m∥α，m⊂β，α∩β＝n，那么m∥nC．如果α∥β，m⊂α，那么m∥βD．如果α⊥β，α∩β＝n，m⊥n，那么m⊥β答案BC解析如果m∥n，n⊂α，那么m∥α或m⊂α，故A不正确；如果m∥α，m⊂β，α∩β＝n，那么m∥n，这就是线面平行推得线线平行的性质定理，故B正确；如果α∥β，m⊂α，那么m∥β，这就是利用面面平行推线面平行的性质定理，故C正确；缺少m⊂α这个条件，故D不正确．12．(2022·福州检测)如图所示，正方体ABCD－A1B1C1D1中，点E，F，G，P，Q分别为棱AB，C1D1，D1A1，D1D，C1C的中点，则下列叙述中正确的是( )A．直线BQ∥平面EFGB．直线A1B∥平面EFGC．平面APC∥平面EFGD．平面A1BQ∥平面EFG答案 B解析过点E，F，G的截面如图所示(H，I分别为AA1，BC的中点)，连接A1B，BQ，AP，PC，易知BQ与平面EFG相交于点Q，故A错误；∵A1B∥HE，A1B⊄平面EFG，HE⊂平面EFG，∴A1B∥平面EFG，故B正确；AP⊂平面ADD1A1，HG⊂平面ADD1A1，延长HG与PA必相交，故C错误；易知平面A1BQ与平面EFG有交点Q，故D错误．13．(多选)(2022·临沂模拟)如图1，在正方形ABCD 中，点E 为线段BC 上的动点(不含端点)，将△ABE 沿AE 翻折，使得二面角B －AE －D 为直二面角，得到图2所示的四棱锥B －AECD ，点F 为线段BD 上的动点(不含端点)，则在四棱锥B －AECD 中，下列说法正确的有( )图1 图2A ．B ，E ，C ，F 四点不共面 B ．存在点F ，使得CF ∥平面BAE C ．三棱锥B －ADC 的体积为定值D ．存在点E 使得直线BE 与直线CD 垂直答案 AB解析对于A ，假设直线BE 与直线CF 在同一平面上，所以E 在平面BCF 上，又因为E 在折前线段BC 上，BC ∩平面BCF ＝C ，所以E 与C 重合，与E 异于C 矛盾，所以直线BE 与直线CF 必不在同一平面上，即B ，E ，C ，F 四点不共面，故A 正确；对于B ，如图，当点F 为线段BD 的中点，EC ＝12AD 时，直线CF ∥平面BAE ，证明如下：取AB 的中点G ，连接GE ，GF ，则EC ∥FG 且EC ＝FG ，所以四边形ECFG 为平行四边形，所以FC ∥EG ，又因为EG ⊂平面BAE ，则直线CF 与平面BAE 平行，故B 正确；对于C ，在三棱锥B －ADC 中，因为点E 的移动会导致点B 到平面ACD 的距离发生变化，所以三棱锥B －ADC 的体积不是定值，故C 不正确；对于D ，过D 作DH ⊥AE 于H ，因为平面BAE ⊥平面AECD ，平面BAE ∩平面AECD ＝AE ，所以DH ⊥平面BAE ，所以DH ⊥BE ，若存在点E 使得直线BE 与直线CD 垂直，DH ⊂平面AECD ，且DC ⊂平面AECD ，DH ∩DC ＝D ，所以BE ⊥平面AECD ，所以BE ⊥AE ，与△ABE 是以B 为直角的三角形矛盾，所以不存在点E 使得直线BE 与直线CD 垂直，故D 不正确．14．如图，在长方体ABCD －A 1B 1C 1D 1中，AD ＝DD 1＝1，AB ＝3，E ，F ，G 分别是AB ，BC ，C 1D 1的中点，点P 在平面ABCD 内，若直线D 1P ∥平面EFG ，则线段D 1P 长度的最小值是________．答案72解析如图，连接D 1A ，AC ，D 1C .因为E ，F ，G 分别为AB ，BC ，C 1D 1的中点，所以AC ∥EF ，又EF ⊄平面ACD 1，AC ⊂平面ACD 1，则EF ∥平面ACD 1.同理可得EG ∥平面ACD 1，又EF ∩EG ＝E ，EF ，EG ⊂平面EFG ，所以平面ACD 1∥平面EFG . 因为直线D 1P ∥平面EFG ，所以点P 在直线AC 上．在△ACD 1中，易得AD 1＝2，AC ＝2，CD 1＝2，所以1AD C S △＝12×2×22－⎝⎛⎭⎪⎫222＝72，故当D 1P ⊥AC 时，线段D 1P 的长度最小，最小值为7212×2＝72.15．(2022·合肥市第一中学模拟)正方体ABCD －A 1B 1C 1D 1的棱长为1，点M ，N 分别是棱BC ，CC 1的中点，动点P 在正方形BCC 1B 1(包括边界)内运动，且PA 1∥平面AMN ，则PA 1的长度范围为( )A.⎣⎢⎡⎦⎥⎤1，52B.⎣⎢⎡⎦⎥⎤324，52C.⎣⎢⎡⎦⎥⎤324，32 D.⎣⎢⎡⎦⎥⎤1，32答案 B解析取B 1C 1的中点E ，BB 1的中点F ，连接A 1E ，A 1F ，EF ，取EF 的中点O ，连接A 1O ，如图所示，∵点M ，N 分别是棱长为1的正方体ABCD －A 1B 1C 1D 1中棱BC ，CC 1的中点， ∴AM ∥A 1E ，MN ∥EF ，∵AM ∩MN ＝M ，A 1E ∩EF ＝E ，AM ，MN ⊂平面AMN ，A 1E ，EF ⊂平面A 1EF ， ∴平面AMN ∥平面A 1EF ，∵动点P 在正方形BCC 1B 1(包括边界)内运动，且PA 1∥平面AMN ，∴点P 的轨迹是线段EF ，∵A 1E ＝A 1F ＝12＋⎝ ⎛⎭⎪⎫122＝52，EF ＝1212＋12＝22，∴A 1O ⊥EF ，∴当P 与O 重合时，PA 1的长度取最小值A 1O ， A 1O ＝⎝ ⎛⎭⎪⎫522－⎝ ⎛⎭⎪⎫242＝324，当P 与E (或F )重合时，PA 1的长度取最大值A 1E 或A 1F ，A 1E ＝A 1F ＝52.∴PA 1的长度范围为⎣⎢⎡⎦⎥⎤324，52.16．如图，正方体ABCD －A 1B 1C 1D 1中，棱长为a ，M ，N 分别为AB 1，A 1C 1上的点，A 1N ＝AM .(1)求证：MN ∥平面BB 1C 1C ；(2)求MN 的最小值．(1)证明如图，作NE ∥A 1B 1交B 1C 1于点E ，作MF ∥AB 交BB 1于点F ，连接EF ，则NE ∥MF .∵NE ∥A 1B 1，∴NEA 1B 1＝C 1NA 1C 1.又MF ∥AB ，∴MF AB ＝B 1MAB 1，∵A 1C 1＝AB 1，A 1N ＝AM ，∴C 1N ＝B 1M .∴NE A 1B 1＝MF AB，又AB ＝A 1B 1，∴NE ＝MF .∴四边形MNEF 是平行四边形，∴MN ∥EF ，又MN ⊄平面BB 1C 1C ，EF ⊂平面BB 1C 1C ， ∴MN ∥平面BB 1C 1C .(2)解设B 1E ＝x ，∵NE ∥A 1B 1， ∴B 1E B 1C 1＝A 1NA 1C 1.又∵MF ∥AB ，∴B 1F BB 1＝B 1M AB 1，∵A 1N ＝AM ，A 1C 1＝AB 1＝2a ，B 1C 1＝BB 1＝a ，B 1E ＝x ，∴B 1E B 1C 1＋B 1F BB 1＝A 1N A 1C 1＋B 1MAB 1，∴x a ＋B 1F a ＝1，∴B 1F ＝a －x ，从而MN ＝EF ＝B 1E 2＋B 1F 2 ＝x 2＋a －x2 ＝2⎝ ⎛⎭⎪⎫x －a 22＋⎝ ⎛⎭⎪⎫a 22， ∴当x ＝a 2时，MN 的最小值为22a .。

直线与平面平行经典题目1

9.2 直线与平面平行●知识梳理1.直线与平面的位置关系有且只有三种，即直线与平面平行、直线与平面相交、直线在平面内.2.直线与平面平行的判定：如果平面外的一条直线与平面内的一条直线平行，那么这条直线与这个平面平行.3.直线与平面平行的性质：如果一条直线与一个平面平行，经过这条直线的平面与已知平面相交，那么这条直线与交线平行.●点击双基1.设有平面α、β和直线m 、n ，则m ∥α的一个充分条件是A.α⊥β且m ⊥βB.α∩β=n 且m ∥nC.m ∥n 且n ∥αD.α∥β且m β2.设m 、n 是两条不同的直线，α、β、γ是三个不同的平面.给出下列四个命题，其中正确命题的序号是①若m ⊥α，n ∥α，则m ⊥n ②若α∥β，β∥γ，m ⊥α，则m ⊥γ ③若m ∥α，n ∥α，则m ∥n ④若α⊥γ，β⊥γ，则α∥βA.①②B.②③C.③④D.①④3.一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是 A.异面 B.相交 C.平行 D.不能确定4.(06重庆卷)对于任意的直线l 与平同a ,在平面a 内必有直线m ,使m 与l A.平行 B.相交 C.垂直 D.互为异面直线5.已知平面βα,和直线，给出条件：①α//m ；②α⊥m ；③α⊂m ；④βα⊥；⑤βα//. （i ）当满足条件时，有β//m ；（ii ）当满足条件时，有β⊥m .●典例剖析【例1】如下图，两个全等的正方形ABCD 和ABEF 所在平面相交于AB ，M ∈AC ，N ∈FB 且AM =FN ，求证：MN ∥平面BCE .C F【例2】已知正四棱锥P —ABCD 的底面边长及侧棱长均为13，M 、N 分别是PA 、BD 上的点，且PM ∶MA =BN ∶ND =5∶8.C（1）求证：直线MN ∥平面PBC ；（2）求直线MN 与平面ABCD 所成的角.【例3】如图, 在直三棱柱ABC －A 1B 1C 1中，AC ＝3，BC ＝4，AA 1＝4，点D 是AB 的中点，（I ）求证：AC ⊥BC 1；（II ）求证：AC 1//平面CDB 1；（III ）求异面直线 AC 1与 B 1C 所成角的余弦值．●闯关训练夯实基础1. （07福建理）已知m 、n 为两条不同的直线，为两个不同的平面，则下列命题中正确的是A. m n m ,,α⊂α⊂∥β，n ∥β⇒ α∥βB. α∥β，α⊂α⊂n m ,，⇒m ∥nC. m ⊥α，m ⊥n ⇒n ∥α D . n ∥m,n ⊥α⇒m ⊥α 2.（06福建卷）对于平面α和共面的直线m 、n ，下列命题中真命题是 A.若m ⊥α，m ⊥n ，则n ∥α B.若m ∥α，n ∥α，则m ∥nC.若m ⊂α，n ∥α，则m ∥n D.若m 、n 与α所成的角相等，则n ∥m 3.（06湖南卷）过平行六面体ABCD-A 1B 1C 1D 1任意两条棱的中点作直线,其中与平面DBB 1D 1平行的直线共有 ( ) A. 4条 B.6条 C.8条 D.12条1CBD4.(06重庆卷)若P 是平面α外一点，则下列命题正确的是A.过P 只能作一条直线与平面α相交B.过P 可作无数条直线与平面α垂直C.过P 只能作一条直线与平面α平行D.过P 可作无数条直线与平面α平行 5.如图，在三棱柱ABC —A ′B ′C ′中，点E 、F 、H 、 K 分别为AC ′、CB ′、A ′B 、B ′C ′的中点，G 为△ABC 的重心. 从K 、H 、G 、B ′中取一点作为P ，使得该棱柱恰有 2条棱与平面PEF 平行，则P 为（）A ．KB ．HC ．GD ．B ′6.已知a 、b 为不垂直的异面直线，α是一个平面，则a 、b 在α上的射影有可能是①两条平行直线；②两条互相垂直的直线；③同一条直线；④一条直线及其外一点.在上面结论中，正确结论的编号是__________.（写出所有正确结论的编号）AB17.已知Rt △ABC 的直角顶点C在平面α内，斜边AB ∥α，AB =26，AC 、BC 分别和平面α 成45°和30°角，则AB 到平面α的距离为__________.8、（07江西）右图是一个直三棱柱（以A 1B 1C 1为底面）被一平面所截得到的几何体，截面为ABC ．已知A 1B 1＝B 1C 1＝l ，∠A l B l C 1＝90°，AA l ＝4，BB l ＝2，CC l ＝3。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

直线、平面平行的判定及其性质测试题（有详解）A一、选择题1．下列条件中,能判断两个平面平行的是( )A ．一个平面内的一条直线平行于另一个平面;B ．一个平面内的两条直线平行于另一个平面C ．一个平面内有无数条直线平行于另一个平面D ．一个平面内任何一条直线都平行于另一个平面2．E ，F ，G 分别是四面体ABCD 的棱BC ，CD ，DA 的中点，则此四面体中与过E ，F ，G 的截面平行的棱的条数是A ．0B ．1C ．2D ．33．直线,a b c ，及平面αβ，，使//a b 成立的条件是（）A ．//,a b αα⊂B ．//,//a b ααC ．//,//a c b cD ．//,a b ααβ=4．若直线m 不平行于平面α，且m ⊄α，则下列结论成立的是（）A ．α内的所有直线与m 异面B ．α内不存在与m 平行的直线C ．α内存在唯一的直线与m 平行D ．α内的直线与m 都相交5．下列命题中，假命题的个数是（）① 一条直线平行于一个平面，这条直线就和这个平面内的任何直线不相交；② 过平面外一点有且只有一条直线和这个平面平行；③ 过直线外一点有且只有一个平面和这条直线平行；④ 平行于同一条直线的两条直线和同一平面平行；⑤ a 和b 异面，则经过b 存在唯一一个平面与α平行A ．4B ．3C ．2D ．16．已知空间四边形ABCD 中，,M N 分别是,AB CD 的中点，则下列判断正确的是（）A ．()12MN AC BC ≥+B ．()12MN AC BC ≤+ C ．()12MN AC BC =+ D ．()12MN AC BC <+ 二、填空题7．在四面体ABCD 中，M ，N 分别是面△ACD ，△BCD 的重心，则四面体的四个面中与MN 平行的是________.8．如下图所示，四个正方体中，A ，B 为正方体的两个顶点，M ，N ，P分别为其所在棱的中点，能得到AB//面MNP 的图形的序号的是①②③④9．正方体ABCD -A 1B 1C 1D 1中，E 为DD 1中点，则BD 1和平面ACE 位置关系是．三、解答题侧棱长是10.如图，正三棱柱111C B A ABC -的底面边长是2，D C A B B 1A 1C 13，D 是AC 的中点.求证：//1C B 平面BD A 1.11.如图，在平行六面体ABCD -A 1B 1C 1D 1中，E ，M ，N ，G 分别是AA 1，CD ，CB ，CC 1的中点，求证：（1）MN //B 1D 1 ；（2）AC 1//平面EB 1D 1 ；（3）平面EB 1D 1//平面BDG .B一、选择题1．α，β是两个不重合的平面，a ，b 是两条不同直线，在下列条件下，可判定α∥β的是（）A ．α，β都平行于直线a ，bB ．α内有三个不共线点到β的距离相等C ．a ，b 是α内两条直线，且a ∥β，b ∥βD ．a ，b 是两条异面直线且a ∥α，b ∥α，a ∥β，b ∥β2．两条直线a ，b 满足a ∥b ，b α，则a 与平面α的关系是（）A ．a ∥αB ．a 与α相交C ．a 与α不相交D ．a α3．设,a b 表示直线，,αβ表示平面，P 是空间一点，下面命题中正确的是（）A ．a α⊄，则//a αB ．//a α，b α⊂，则//a bC ．//,,a b αβαβ⊂⊂，则//a bD ．,,//,//P a P a βααβ∈∈，则a β⊂4．一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（）A.异面B.相交C.平行D.不能确定5.下列四个命题中，正确的是（）①夹在两条平行线间的平行线段相等；②夹在两条平行线间的相等线段平行；③如果一条直线和一个平面平行，那么夹在这条直线和平面间的平行线段相等；④如果一条直线和一个平面平行，那么夹在这条直线和平面间的相等线段平行A ．①③B ．①②C ．②③D ．③④6．a ，b 是两条异面直线，A 是不在a ，b 上的点，则下列结论成立的是A ．过A 有且只有一个平面平行于a ，bB ．过A 至少有一个平面平行于a ，bC ．过A 有无数个平面平行于a ，bD ．过A 且平行a ，b 的平面可能不存在二、填空题7．a ，b ，ｃ为三条不重合的直线，α，β，γ为三个不重合的平面，直线均不在平面内，给出六个命题：.⇒⎭⎬⎫;⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫⇒⎭⎬⎫αγγαβαγβγαααβαβαγγ∥∥∥⑥∥∥∥⑤∥∥∥④∥∥∥③∥∥∥②∥∥∥①a a a c a c c c b a b a b a c b c a ;;;;其中正确的命题是________________.（将正确的序号都填上）8．设平面α∥β，A ，C ∈α，B ，D ∈β，直线AB 与CD 交于S ，若AS =18，BS =9，CD =34，则CS =_____________.9．如图，正四棱柱ABCD-A 1B 1C 1D 1中，E ，F ，G ，H 分别是棱CC 1，C 1D 1，DD 1，DC 中点，N 是BC 中点，点M 在四边形EFGH及其内部运动，则M 满足时，有MN ∥平面B 1BD D 1．三、解答题10.如图，在正四棱锥P ABCD -中，PA AB a ==,点E 在棱PC上．问点E 在何处时，//PA EBD 平面，并加以证明.11.如下图，设P 为长方形ABCD 所在平面外一点，M ，N 分别为AB ，PD 上的点，且MB AM =NPDN ，求证：直线MN ∥平面PBC .C1.平面内两正方形ABCD 与ABEF ，点M ，N 分别在对角线AC ,FB 上，且AM:MC=FN:NB ，沿AB 折起，使得∠DAF =900(1)证明：折叠后MN//平面CBE ；（2）若AM:MC =2：3，在线段AB 上是否存在一点G ，使平面MGN //平面CBE ?若存在，试确定点G 的位置.2.设平面α∥平面β，AB 、CD 是两条异面直线，M ，N 分别是AB ，CD 的中点，且A ，C ∈α，B ，D ∈β，求证：MN ∥平面α.AB C DE MNαβ参考答案AE PD C B A一、选择题1．D【提示】当l =⋂βα时，α内有无数多条直线与交线l 平行，同时这些直线也与平面β平行.故A ，B ，C 均是错误的2．C【提示】棱AC ，BD 与平面EFG 平行，共2条.3．C【提示】//,,a b αα⊂则//a b 或,a b 异面；所以A 错误；//,//,a b αα则//a b 或,a b 异面或,a b 相交，所以B 错误；//,,a b ααβ=则//a b 或,a b 异面，所以D 错误；//,//a c b c ，则//a b ，这是公理4，所以C 正确.4．B【提示】若直线m 不平行于平面α，且m ⊄α，则直线m 于平面α相交，α内不存在与m 平行的直线.5．B【提示】②③④错误.②过平面外一点有且只有一个平面和这个平面平行，有无数多条直线与它平行.③过直线外一点有无数个平面和这条直线平行④平行于同一条直线的两条直线和同一平面平行或其中一条在平面上.6. D【提示】本题可利用空间中的平行关系，构造三角形的两边之和大于第三边.二、填空题7．平面ABC ，平面ABD【提示】连接AM 并延长，交CD 于E ，连结BN 并延长交CD 于F ，由重心性质可知，E 、F 重合为一点，且该点为CD 的中点E ，由MA EM =NB EN =21得MN ∥AB .因此，MN ∥平面ABC 且MN ∥平面ABD .8. ①③【提示】对于①，面MNP//面AB,故AB//面MNP.对于③，MP//AB,故AB//面MNP,对于②④，过AB 找一个平面与平面MNP 相交，AB 与交线显然不平行，故②④不能推证AB//面MNP.9．平行【提示】连接BD 交AC 于O ，连OE ，∴OE ∥B D 1，OEC 平面ACE ，∴B D 1∥平面ACE.三、解答题10.证明：设1AB 与B A 1相交于点P ，连接PD ，则P 为1AB 中点，D 为AC 中点，∴PD//C B 1.又 PD ⊂平面B A 1D ，∴C B 1//平面B A 1 D11.证明：（1） M 、N 分别是CD 、CB 的中点，∴MN//BD又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形.所以BD//B 1D 1.又MN//BD ，从而MN//B 1D 1（2）（法1）连A 1C 1，A 1C 1交B 1D 1与O 点四边形A 1B 1C 1D 1为平行四边形，则O 点是A 1C 1的中点E 是AA 1的中点，∴EO 是∆AA 1C 1的中位线，EO//AC 1.AC 1⊄面EB 1D 1 ，EO ⊂面EB 1D 1，所以AC 1//面EB 1D 1 （法2）作BB 1中点为H 点，连接AH 、C 1H ，E 、H 点为AA 1、BB 1中点，所以EH //C 1D 1，则四边形EHC 1D 1是平行四边形，所以ED 1//HC 1又因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AHAH ⋂HC 1=H ，∴面AHC 1//面EB 1D 1.而AC 1⊂面AHC 1，所以AC 1//面EB 1D 1（3）因为EA //B 1H ，则四边形EAHB 1是平行四边形，所以EB 1//AH因为AD //HG ，则四边形ADGH 是平行四边形，所以DG//AH ，所以EB 1//DG又 BB 1//DD 1,∴四边形BB 1D 1D 是平行四边形. 所以BD//B 1D 1.BD ⋂DG=G ，∴面EB 1D 1//面BDGB一、选择题1．D【提示】A 错，若a ∥b ，则不能断定α∥β；B 错，若A ，B ，C 三点不在β的同一侧，则不能断定α∥β；C 错，若a ∥b ，则不能断定α∥β；D 正确.2．C【提示】若直线a ，b 满足a ∥b ，b α，则a ∥α 或a α3．D【提示】根据面面平行的性质定理可推证之.4．C【提示】设α∩β=l ，a ∥α，a ∥β，过直线a 作与α、β都相交的平面γ，记α∩γ=b ，β∩γ=c ，则a ∥b 且a ∥c ，∴b ∥c .又b ⊂α，α∩β=l ，∴b ∥l .∴a ∥l .5．A【提示】6． D【提示】过点A 可作直线a ′∥a ，b ′∥b ，则a ′∩b ′=A ，∴a ′，b ′可确定一个平面，记为α.如果a ⊄α，b ⊄α，则a ∥α，b ∥α.由于平面α可能过直线a 、b 之一，因此，过A 且平行于a 、b 的平面可能不存在.二、填空题7.①④⑤⑥8.68或368 【提示】如图（1），由α∥β可知BD ∥AC ，∴SA SB =SC SD ，即189=SC SC 34-，∴SC =68.S S A A B B C C α α ββ(1)(2)D D如图（2），由α∥β知AC ∥BD ，∴SB SA =SD SC =SC CD SC -，即918=SCSC -34. ∴SC =368. 9．M ∈HF【提示】易证平面NHF ∥平面BD D 1 B 1，M 为两平面的公共点，应在交线HF 上.三、解答题 10．解：当E 为PC 中点时，//PA EBD 平面．证明：连接AC ，且AC BD O =，由于四边形ABCD 为正方形，∴O 为AC 的中点，又E 为中点，∴OE 为△ACP 的中位线， ∴//PA EO ，又PA EBD ⊄平面，∴//PA EBD 平面.11．证法一：过N 作NR ∥DC 交PC 于点R ，连接RB ，依题意得NR NR DC -=NP DN =MB AM =MB MB AB -=MBMB DC -⇒NR =MB .∵NR ∥DC ∥AB ，∴四边形MNRB 是平行四边形.∴MN ∥RB .又∵RB 平面PBC ，∴直线MN ∥平面PBC . 证法二：过N 作NQ ∥AD 交P A 于点Q ，连接QM ，∵MB AM =NPDN =QP AQ ，∴QM ∥PB .又NQ ∥AD ∥BC ，∴平面MQN ∥平面PBC .∴直线MN ∥平面PBC .C1.（1）证明：设直线AN 与BE 交与点H ，连接CH ，ANF ∆ ∽HNB ∆,∴NHAN NB FN =. 又NB FN MC AM =,则NH AN =MCAM ，∴MN//CH. 又CBE CBE MN 平面，平面⊂⊄CH ,∴MN//平面CBE.(2)解：存在，过M 作MG ⊥AB,垂足为G ，则MG//BC, ∴MG//平面CBE,又MN//平面CBE ，M MN MG =⋂,平面MGN//平面CBE.即G 在AB 线上，且AG:GB=AM:MC=2：32.证明：连接BC ，AD ，取BC 的中点E ，连接ME 、NE ，则ME 是△BAC 的中位线，故ME ∥AC. ME ⊄α，∴ME ∥α.O F A B CD PE同理可证，NE∥BD.又α∥β，设CB与DC确定的平面BCD与平面α交于直线CF，则CF∥BD，∴NE∥CF. 而NE⊄平面α，CF⊂α，∴NE∥α.又ME∩NE=E，∴平面MNE∥α，而MN⊂平面MNE，∴MN∥平面α.。