密立根油滴实验数据的处理方法
密立根油滴法测电子比荷试验数据处理及思考

f
r
=6 r =mg
(2)
密度 ,质量为 m,则有: m=
其中 是空气粘滞系数,r 是油滴半径,设油滴
3 3 r 4
1
(3)
有(2)和(3)知油滴的半径为:
9 2 r = 2g
将(4)带入(3)可得:
2
(4)
图-1 密立根油滴仪
q=
18 3
q /(10 19 C )
7.99
8.83
8.67
8.99
25.30
6.19
q/e
取整 n 测量值 e
4.99 5 1.599 0.63
5.5 6 1.47 8.0
5.4 5 1.72 7.6
5.6 6 1.50 6.25
15.8 16 1.58 1.25
3.9 4 1.55 3.1 2.3 逐次相减法
油滴匀速下降的距离 修正常数 大气压强
l 2.00 103 m b 8.22 103 m Pa
p 1.013 10 5 Pa
表-2 本实验对实验数据的处理可以有多种处理方法,现 在列举“倒过来验证” 、图像法和“逐次相减法” 三种处理方法。 2.1 倒过来验证
为了证明电荷的不连续性,并得到基本电荷 e 的值,应对实验得到的各油滴的电量 q 求最大公约
1.55 1.599 1.72 1.47 1.50 1.58
其中第三列 q qi 1 qi ,其为逐次相减的结 果,考虑实验误差,可以将基本电荷估计为 1.60 10
19
C(本实验所得数据恰好巧合与基本电
23 .75 - 7.75 10 -19 C =1.60-19 C ei = 15 - 5
密立根油滴实验数据处理

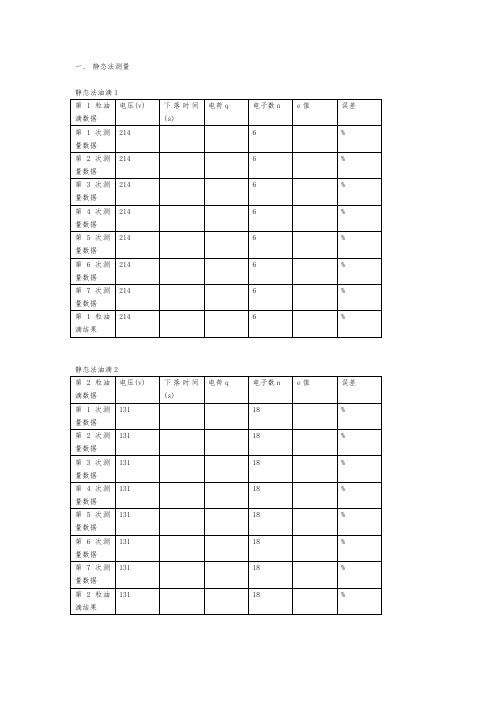
一、静态法测量
静态法油滴1
第1粒油滴数据
电压(v)
下落时间(s)
电荷q
电子数n
e值
误差
第1次测量数据
214
6
%
第2次测量数据
214
6
%
第3次测量数据
214
6
%
第4次测量数据
214
6
%
第5次测量数据
214
6
%
第6次测量数据
214
6
%
第7次测量数据
214
6
%
第1粒油滴结果
214
6
%
静态法油滴2
第2粒油滴数据
电压(v)
下落时间(s)
电荷q
电子数n
e值
误差
第1次测量数据
131
18
%
第2次测量数据
131
18
%
第3次测量数据
131
18
%
第4次测量数据
131
18
%
第5次测量数据
131
18
%
第6次测量数据
131
18
%
第7次测量数据
131
18
%
第2粒油滴结果
131
18
%
静态法油滴3
第3粒油滴数据
电压(v)
201
13
%
第2次测量数据
201
13
%
第3次测量数据
201
12
%
第4次测量数据
201
12
%
第5次测量数据
201
12
%
第6次测量数据
密立根油滴实验的探究性数据处理方案

参考文献
【l】Millikan R丸The Electron柚d n”Light—Q∞Ⅱ组from lhe Experimmt ofⅥew(Noble Lecaut)[R].1924 【2l钱锋。潘人培.大学物理实验(修订版)口哪.北京・高等教育出版社.2005.241~246 pl丁红星。戴丽莉.密立根油滴实验数据处理方法的分析与改进田.大学物理.2005。24(7)t 40~43 【4】刘海力,唐贤健,谢常清.密立根油滴实验数据处理的一种方法田.大学物理实验。20ll。24(6)・93・~95 【5】李登峰,薛书文.密立根油滴实验教学中的几个问题唧.中国现代教育装备.2011.坫:79~∞ 【6】胡永金,刘国营,罗时军等.密立报油滴实验中平衡电压与下落时间关系的研究【J】.湖北汽车工业学院学报,2008。22(3)t 46~48 【7】陆佩.影响密立根油滴实验的因素分析田.实验科学与技术.2007,5(1);34~36
2012年全国高等学校物理基础课程教育学术研讨会论文集
57
密立根油滴实验的探究性数据处理方案
唐定飘1’2陈晓1工陈乾1戴玉蓉1
(1东南大学物理系,江苏南京211189) (2东南大学吴健雄学院高等理工班,江苏南京211189) 摘要本文讨论了一种基于密立根油滴实验的探究性数据处理方法.通过分析平衡电 压和下落时问的隐函数关系,并结合实验数据的具体分布推测出电荷的不连续 性.在此基础上通过拟合出二者的关系曲线计算出基本电荷的电量,从而还原 了该实验富有的研究性内涵.
6narlv=mg (2)
最后,根据球形油滴的半径公式以及修正后的空气粘滞系数,联合方程(1)和(2),・代入相 关数据(油的密度,重力加速度,空气粘滞系数等物理量),化简得平衡电压对下落时间的函数关
密立根油滴实验报告

密立根油滴实验——电子电荷的测量【实验目的】1.通过对带电油滴在重力场和静电场中运动的测量,验证电荷的不连续性,并测定电荷的电荷值e 。
2.通过实验过程中,对仪器的调整、油滴的选择、耐心地跟踪和测量以及数据的处理等,培养学生严肃认真和一丝不苟的科学实验方法和态度。
3. 学习和理解密立根利用宏观量测量微观量的巧妙设想和构思。
【实验原理】1.静态(平衡)测量法用喷雾器将油滴喷入两块相距为d 的平行极板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴的质量为m ,所带的电量为q ,两极板间的电压为V ,如图 1 所示。
如果调节两极板间的电压V ,可使两力达到平衡,这时:dVqqE mg == (1) 为了测出油滴所带的电量q ,除了需测定平衡电压V 和极板间距离d 外,还需要测量油滴的质量m 。
因m 很小,需用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气阻力的作用,下降一段距离达到某一速度g ν后,阻力r f 与重力mg 平衡,如图 2 所示(空气浮力忽略不计),油滴将匀速下降。
此时有:mg v a f g r ==ηπ6 (2)其中η是空气的粘滞系数,是a 油滴的半径。
经过变换及修正,可得斯托克斯定律:pab v a f gr +=16ηπ (3) 其中b 是修正常数, b=6.17×10-6m ·cmHg,p 为大气压强,单位为厘米汞高。
至于油滴匀速下降的速度g v ,可用下法测出:当两极板间的电压V 为零时,设油滴匀速下降的距离为l ,时间为t ,则gg t lv =(4) 最后得到理论公式:V d pa b t lg q g 23)1(218⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=ηρπ (5) 2.动态(非平衡)测量法非平衡测量法则是在平行极板上加以适当的电压V ,但并不调节V 使静电力和重力达到平衡,而是使油滴受静电力作用加速上升。
由于空气阻力的作用,上升一段距离达到某一速度υ 后,空气阻力、重力与静电力达到平衡(空气浮力忽略不计),油滴将匀速上升,如图 3 所示。
密立根油滴实验报告

创作编号:BG7531400019813488897SX 创作者: 别如克*密立根油滴实验——电子电荷的测量【实验目的】1.通过对带电油滴在重力场和静电场中运动的测量,验证电荷的不连续性,并测定电荷的电荷值e 。
2.通过实验过程中,对仪器的调整、油滴的选择、耐心地跟踪和测量以及数据的处理等,培养学生严肃认真和一丝不苟的科学实验方法和态度。
3. 学习和理解密立根利用宏观量测量微观量的巧妙设想和构思。
【实验原理】1.静态(平衡)测量法用喷雾器将油滴喷入两块相距为d 的平行极板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴的质量为m ,所带的电量为q ,两极板间的电压为V ,如图 1 所示。
如果调节两极板间的电压V ,可使两力达到平衡,这时:dVqqE mg == (1) 为了测出油滴所带的电量q ,除了需测定平衡电压V 和极板间距离d 外,还需要测量油滴的质量m 。
因m 很小,需用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气阻力的作用,下降一段距离达到某一速度g ν后,阻力r f 与重力mg 平衡,如图 2 所示(空气浮力忽略不计),油滴将匀速下降。
此时有:mg v a f g r ==ηπ6 (2)其中η是空气的粘滞系数,是a 油滴的半径。
经过变换及修正,可得斯托克斯定律:pab v a f gr +=16ηπ (3) 其中b 是修正常数, b=6.17×10-6m ·cmHg,p 为大气压强,单位为厘米汞高。
至于油滴匀速下降的速度g v ,可用下法测出:当两极板间的电压V 为零时,设油滴匀速下降的距离为l ,时间为t ,则gg t lv =(4) 最后得到理论公式:V d pa b t lg q g 23)1(218⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=ηρπ (5) 2.动态(非平衡)测量法非平衡测量法则是在平行极板上加以适当的电压V ,但并不调节V 使静电力和重力达到平衡,而是使油滴受静电力作用加速上升。
密立根油滴实验数据处理
134
17
%
第2次测量数据
134
18
%
第3次测量数据
134
17
%
第4次测量数据
134
18
%
第5次测量数据
134
17
%
第6次测量数据
134
18
%
第7次测量数据
134
18
%
第4粒油滴结果
134
17
%
静态法油滴5
第5粒油滴数据
电压(v)
下落时间(s)
电荷q
电子数n
e值
误差
第1次测量数据
201
第2粒油滴
平衡电压(v)
上升电压(V)
下落时间tg(s)
上升时间te(s)
电荷q
电子数n
e值
第1次
201
375
13
第2次
201
375
13
第3次
201
375
12
第4次
201
375
12
第5次
201
375
12
第6次
201
375
13
第7次
201
375
13
第2粒油滴结果
201
375
12
测量结果为: 与标准结果误差为:%
13
%
第2次测量数据
201
13
%
第3次测量数据
201
12
%
第4次测量数据
201
12
%
第5次测量数据
201
12
%
第6次测量数据
201
13
密立根油滴实验报告

密立根油滴实验——电子电荷的丈量之巴公井开创作【实验目的】1.通过对带电油滴在重力场和静电场中运动的丈量,验证电荷的不连续性,并测定电荷的电荷值e 。
2.通过实验过程中,对仪器的调整、油滴的选择、耐心地跟踪和丈量以及数据的处理等,培养学生严肃认真和一丝不苟的科学实验方法和态度。
3.学习和理解密立根利用宏观量丈量微观量的巧妙设想和构思。
【实验原理】1.静态(平衡)丈量法用喷雾器将油滴喷入两块相距为d 的平行极板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴的质量为m ,所带的电量为q ,两极板间的电压为V ,如图 1 所示。
如果调节两极板间的电压V ,可使两力达到平衡,这时:dV qqE mg == (1)为了测出油滴所带的电量q ,除了需测定平衡电压V 和极板间距离d 外,还需要丈量油滴的质量m 。
因m 很小,需用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气阻力的作用,下降一段距离达到某一速度g ν后,阻力r f 与重力mg 平衡,如图 2 所示(空气浮力忽略不计),油滴将匀速下降。
此时有:mgv a f g r ==ηπ6 (2)其中η是空气的粘滞系数,是a 油滴的半径。
经过变换及修正,可得斯托克斯定律:pab v a f gr +=16ηπ (3)×10-6m ·cmHg,p 为大气压强,单位为厘米汞高。
至于油滴匀速下降的速度g v ,可用下法测出:当两极板间的电压V 为零时,设油滴匀速下降的距离为l ,时间为t ,则gg t l v =(4)最后得到理论公式:V d pa b t lg q g23)1(218⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=ηρπ (5)2.动态(非平衡)丈量法非平衡丈量法则是在平行极板上加以适当的电压V ,但其实不调节V 使静电力和重力达到平衡,而是使油滴受静电力作用加速上升。
由于空气阻力的作用,上升一段距离达到某一速度υ 后,空气阻力、重力与静电力达到平衡(空气浮力忽略不计),油滴将匀速上升,如图 3 所示。
密立根油滴实验报告

密立根油滴实验——电子电荷的测量【实验目的】1.通过对带电油滴在重力场和静电场中运动的测量,验证电荷的不连续性,并测定电荷的电荷值e 。
2.通过实验过程中,对仪器的调整、油滴的选择、耐心地跟踪和测量以及数据的处理等,培养学生严肃认真和一丝不苟的科学实验方法和态度。
3. 学习和理解密立根利用宏观量测量微观量的巧妙设想和构思。
【实验原理】1.静态(平衡)测量法用喷雾器将油滴喷入两块相距为d 的平行极板之间。
油在喷射撕裂成油滴时,一般都是带电的。
设油滴的质量为m ,所带的电量为q ,两极板间的电压为V ,如图 1 所示。
如果调节两极板间的电压V ,可使两力达到平衡,这时:dVqqE mg == (1) 为了测出油滴所带的电量q ,除了需测定平衡电压V 和极板间距离d 外,还需要测量油滴的质量m 。
因m 很小,需用如下特殊方法测定:平行极板不加电压时,油滴受重力作用而加速下降,由于空气阻力的作用,下降一段距离达到某一速度g ν后,阻力r f 与重力mg 平衡,如图 2 所示(空气浮力忽略不计),油滴将匀速下降。
此时有:mg v a f g r ==ηπ6 (2)其中η是空气的粘滞系数,是a 油滴的半径。
经过变换及修正,可得斯托克斯定律:pab v a f gr +=16ηπ (3) 其中b 是修正常数, b=×10-6m ·cmHg,p 为大气压强,单位为厘米汞高。
至于油滴匀速下降的速度g v ,可用下法测出:当两极板间的电压V 为零时,设油滴匀速下降的距离为l ,时间为t ,则gg t lv =(4) 最后得到理论公式:V d pa b t lg q g 23)1(218⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+=ηρπ (5) 2.动态(非平衡)测量法非平衡测量法则是在平行极板上加以适当的电压V ,但并不调节V 使静电力和重力达到平衡,而是使油滴受静电力作用加速上升。
由于空气阻力的作用,上升一段距离达到某一速度υ 后,空气阻力、重力与静电力达到平衡(空气浮力忽略不计),油滴将匀速上升,如图 3 所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
服这一不足我们在用第 1 个最小值计算完以后 ,
还要用第 2 个最小值去除所有比它大的数; 然后
用第 3 个 ……直到第 n/ 2 个. 这样就可以避免某
一个数值的误差造成系统误差.
3) 程序 (由 Fort ran 编写)
implicit real 3 4 (a2h ,o2z) parameter (n = 13) dimension q (n) ,a (n) ,b (n) external pmm nn = n
第 24 卷 第 12 期
2004 年 12 月
P
H
物 理 实 验
YSICS EXPER IM EN TA
T
ION
Vol. 24 No. 12
Dec. ,2004
密立根油滴实验数据的处理方法
王广涛 ,陈 健 ,魏建宇 ,李喜贵 ,杨聚宝
(河南师范大学 物理与信息工程学院 ,河南 新乡 453002)
(整数) , r 为余数 ] ,则有
d = ( a , b) = ( r , b)
(2)
这样 ,求 a 和 b 的最大公约数则可转化为求 2 个 较小的数 b 和 r 的最大公约数. 可以用同样的办 法去求 b 和 r 的最大公约数 ,即用 r 去除 b 得
b = q1 r + r1 这里的 r1 比 b 和 r 都小. 根据式 (2) 得到
本文只从假设油滴电量已经求出 ( Q1 , Q2 , Q3 , …, Q n) ,再由它们求出电子电量 e.
2 用计算机处理数据
1) 欧几里得算法[3 ] 任意 2 个数 a 和 b , 必有一个最大公约数 d , 可以记为
d = ( a , b)
(1)
若 a > b ,设 a = qb + r ,0 ≤r ≤b - 1[其中 q 为商
收稿日期 :2004205219 ;修改日期 :2004207223 作者简介 :王广涛 (1976 - ) ,男 ,河南洛阳人 ,河南师范大学物理与信息工程学院助教 ,硕士 ,研究方向为凝聚态物理.
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
并且用它去除所有大于 0. 5 余数就得到余数二这
一列. 由于所有的余数都小于 0. 5 ,所以不用再进 行除法运算 ,即找到了最小值 1. 620 3. 但是上述
算法存在严重的不足 :因为第 3 列的值都受到上
一列最小值 (3. 185 4) 的影响 , 如果它误差很大则
以后的所有数据的误差都会很大. 所以 , 为了克
ij = ij + 1 endif 30 continue
if (ij. ne. 0) goto 110 40 r = a1
sum = 0. 0
iij = 0
do ii = kc ,n
iij = iij + 1 enum = b (ii) / r / / 求出每个电荷是最小电荷的多
少倍 ,即带几个基本电荷
[ 4 ] 史志强. 油滴实验方法的研究[J ] . 物理实验 ,2002 , 22 (6) :29~32.
Data processing method in Millikan oil2drop experiment
nn = ij
ij = 0
a1 = a (kc)
do 20 j = kc + 1 ,nn
sang = a (j) / a1
msang = int (sang)
rmod = a (j)2msang 3 a1
if (rmod. ge. delt) t hen
a (ij + 1) = rmod
ij = ij + 1
输入电荷数据语句. 如果想用人机交互方式输
入数 据 则 用 这 段 程 序 , 把 解释符号 c 删除 ,同时把下 面的赋值语句删除.
q(1) = 3. 2378
q(2) = 4. 8800
q(3) = 3. 2207
q(4) = 4. 8057
q(5) = 3. 1854 q(6) = 8. 1209 q(7) = 4. 808 q(8) = 3. 207
参考文献 :
[ 1 ] 赵青生. 大学物理实验 [ M ] . 合肥 : 中国科学技术 大学出版社 ,1993. 255~263.
[ 2 ] 姬婉华. 大学物理实验 [ M ] . 西安 : 西北工业大学 出版社 ,1992. 153~163.
[3 ] 张风雷. 关于密立根油滴实验的数据处理 [J ] . 丹 东纺专学报 ,1998 (3) :45~46.
摘 要 :依据欧几里德算法 ,由计算机处理密立根油滴实验数据 ,得到基本电荷电量 ,并且给出了用 Fortran 编写的 程序.
关键词 :密立根油滴实验 ;欧几里德算法 ;数据处理 ;基本电荷 中图分类号 :O4239 文献标识码 :A 文章编号 :100524642 (2004) 1220022203
定义参量 : n 为电荷个 数 ;q (n) ,a (n) ,b ( n) 一 维数组用电荷数值赋
值 ;pmm 为一个 子 函 数
delt = 0. 5
c do 10 i = 1 ,n c write ( 3 , 3 ) i c read ( 3 , 3 ) q (i) c10 continue 100 format (2F9. 7)
第 12 期 王广涛 ,等 :密立根油滴实验数据的处理方法
23
a = 0. 5) 的数 ,得到一组新数 ; d. 重复以上 b ,c 两步 , 直到某一组数均小于
a ,找出前一组数中的最小值 r1 , 则 r1 即为电子 电量 ;
e. 用 r1 去除被测数据所得的商就是各油滴 所带的电子数 ;
nenum = enum + 0. 5
effn = real (nenum)
effq = b (ii) / effn
sum = sum + effq write ( 3 , 3 ) nenum ,effq / / 输出每个油滴带几个 e
和 e 的值
enddo write ( 3 , 3 ) ’t he average e = ’, sum/ iij / / 输出 e 的
f . 去掉被测数据中的最小值 , 然后重复以上 步骤 ,又得到一个最小值 r2 ;
g. 依次类推 , 可得到一组值 , 求其平均数 r , 即为所求的电子电量 ;
h. 回到第二步 ,不过这时候最小的数是原来 数组中的近邻最小的数.
上述操作过程见表 1.
表 1 欧几里得算法示例
编号
数据 余数一 余数二 商
平均值
enddo
end
subroutine pmm (q ,n) / / 定义一个子函数 ,对油滴 电荷进行排序
implicit real 3 4 (a2h ,o2z)
dimension q (n) do 10 j = 1 ,n21 k=j do 20 i = j + 1 ,n if (q (i) . lt . q (k) ) t hen k=i endif 20 continue pk = q(j) q (j) = q (k) q (k) = pk 10 continue end
d = ( a , b) = rk
(3)
下面我们再讨论求多个数的最大公约数的方
法. 求 q1 , q2 , …, qi 等多个数的最大公约数的通
常方法是先求 q1 和 q2 的最大公约数 p1 , 接着再 求 p1 和 q2 的最大公约数 ,以此类推 ,即可一步步 求出最终结果 , 但是用这个方法计算时所需的运 算量太大 ,本文仿照欧几里得算法对上述方法略 做改进.
24
物理实验 第 24 卷
nn = ij
ij = 0
a1 = a (1)
do 30 j = 2 ,nn
sang = a (j) / a1 msang = int (sang)
求余数
rmod = a (j)2msang 3 a1
if (rmod. ge. delt) t hen a (ij + 1) = rmod
endif 20 continue
if (ij. ne. 0) t hen
goto 110
else
goto 40
endif 110 call pmm (a ,n)
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
d = ( a , b) = ( b , r) = ( r , r1) 再对 r 和 r1 作同样的讨论. 依次下去 , 结果就得 到一串数对 ,对每一对数有相同的最大公因数
d = ( a , b) = ( b , r) = ( r , r1) = …= ( rk - 1 , rk) 直到最后一对数时 , rk - 1可被 rk 整除 , 则 rk 就是 a 与 b 的最大公约数 ,即
在程 序 内 的 赋 值 语 句 , 如 果想在程序内给出电荷的
数值 ,则用这些语句.
q(9) = 9. 613
q(10) = 8. 013
q(11) = 14. 419
q(12) = 11. 213
q(13) = 12. 818 nk = int (n/ 2) / / 定义最大的除数
do k = 1 ,n a (k) = q (k) b (k) = q (k)
把电荷数值赋值给一维数
组 a (k) 和 b (k)
enddo do kc = 1 ,nk / / 依次用第 1 极小值 ,第 2 极小值
