斜齿轮生成的数学模型.doc

合集下载

PROE斜齿轮参数化建模过程

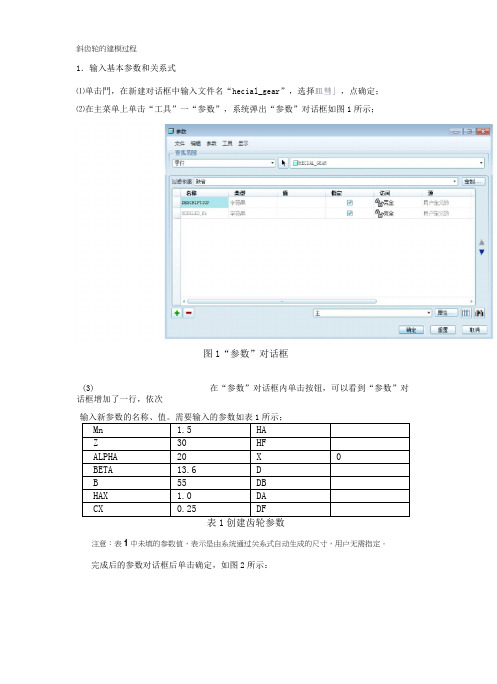
斜齿轮的建模过程1．输入基本参数和关系式⑴单击門，在新建对话框中输入文件名“hecial_gear”，选择皿彗」，点确定；⑵在主菜单上单击“工具”一“参数”，系统弹出“参数”对话框如图1所示；图1“参数”对话框(3)在“参数”对话框内单击按钮，可以看到“参数”对话框增加了一行，依次表1创建齿轮参数注意：表1中未填的参数值，表示是由系统通过关系式自动生成的尺寸，用户无需指定。

完成后的参数对话框后单击确定，如图2所示：图2“参数”对话框(4)在主菜单上依次单击“工具”一“关系”，系统弹出“关系”对话框；(5)在“关系”对话框内输入齿轮的分度圆直径关系、基圆直径关系、齿根圆直径关系和齿顶圆直径关系。

由这些关系式，系统便会自动生成表1所示的未指定参数的值。

输入的关系式如下：ha=(hax+x)*mnhf=(hax+cx-x)*mnd=mn*z/cos(beta)da=d+2*hadb=d*cos(alpha)df=d-2*hf完成后的“关系”对话框如图3所示；图3“关系”对话框(6)单击再生按钮售士，参数对话框里的参数会发生变化2．创建齿轮基本圆(1)在工具栏内单击按钮，系统弹出“草绘”对话框;(2)选择“FRONT”面作为草绘平面，选取“RIGHT”面作为参考平面，参考方向为向右”，如图4所示。

在工具栏内单击按钮，完成草图的绘制;FRONT0I馭玮II亦戸一9图5绘制二维草图注意：在标注尺寸时为了下一步的方便操作，应从最小的圆依次往外标注。

(4)在主菜单上依次单击“工具”一“关系”，系统弹出关系对话框，如图6所示;(5)在“关系”对话框中输入尺寸关系如下：D3=DAD2=DD1=DBD0=DF图6“关系”对话框3．创建渐开线(1)依次在主菜单上单击“插入”一“模型基准”一“曲线”，或者在工具栏上单——按钮，系统弹出“曲线选项”菜单管理器，如图7所示:图7“曲线选项”菜单管理器(2)在“曲线选项”菜单管理器上依次单击“从方程”一“完成”，弹出“得到坐标系”菜单管理器，如图8所示；选取如图9所示的坐标系图8“得到坐标系”菜单管理器IIPRT.CSrS.DEF^=小——■■F4(PRT_CSY5_DEH图9所选坐标系(3)在绘图区单击选取系统坐标系为曲线的坐标系，弹出“设置坐标类型”菜单管理器，如图10所示；图10“设置坐标系类型”菜单管理器4)在“设置坐标类型”菜单管理器中单击“笛卡尔”，系统弹出一个记事本窗口5)在弹出的记事本窗口中输入曲线的方程，如下：ang=90*tr=db/2s=pi*r*t/2xc=r*cos(ang)yc=r*sin(ang)x=xc+s*sin(ang)y=yc-s*cos(ang)z=0(1)在工具栏内单击'"按钮，或者依次在主菜单上单击“插入”一“模型基准”''点”一“点”，系统弹出“基准点”对话框，如图12所示;参照下一相支图12“基准点”对话框(2)单击分度圆曲线作为参照，按住Ctrl键，单击渐开线作为参照，如图13所示。

斜齿轮参数计算

斜齿轮参数计算
斜齿轮是一种常见的传动装置，其参数计算对于机械设计非常重要。

斜齿轮的设计需要考虑到多个因素，如齿轮的模数、压力角、齿数、齿宽等。

这些参数的选择对于传动效率、噪音、寿命等方面都有着直接的影响。

在斜齿轮的参数计算中，首先需要确定齿轮的模数。

模数是齿轮齿数与其分布圆直径的比值，是齿轮设计中的重要参数。

模数的选择需要根据传动的要求和实际应用来确定，一般来说，传动功率越大，模数也越大。

其次是压力角的确定。

压力角是齿轮齿廓与齿轮轴线的夹角，影响着齿轮的传动性能。

较常用的压力角有20度和14.5度两种。

压力角的选择需要根据具体的传动要求和齿轮的材料来确定。

齿数的选择也是斜齿轮参数计算中的重要一环。

齿数的多少直接影响着齿轮的传动比和传动效率。

一般来说，齿数越多，传动比就越大，但齿轮的制造难度也会增加。

因此，在确定齿数时需要综合考虑传动比和制造难度。

最后是齿宽的确定。

齿宽是指齿轮齿廓的宽度，直接影响着齿轮的载荷能力和传动效率。

齿宽的选择需要根据齿轮所承受的载荷和传动功率来确定。

通过对斜齿轮参数的合理选择和计算，可以使得齿轮传动具有较高
的传动效率、较低的噪音和较长的使用寿命。

同时，还可以根据实际需求对齿轮进行优化设计，以满足不同的工程要求。

斜齿轮参数的计算对于机械设计非常重要。

在进行参数计算时，需要综合考虑传动要求、材料特性和制造难度等因素，以确保齿轮传动的性能和可靠性。

只有在合理选择和计算参数的基础上，才能设计出优质的斜齿轮传动装置，满足工程需求。

斜齿轮的参数化建模及接触有限元分析

《装备制造技术》２００７年第１２期设计与计算!!!!"!"!!!!"!"收稿日期：２００７－１０－０７作者简介：王宝昆（１９８２—），男，在读硕士研究生，研究方向：机械设计及理论。

斜齿轮的参数化建模及接触有限元分析王宝昆，张以都（北京航空航天大学，北京１０００８３）摘要：在ＵＧ／ＯｐｅｎＧｒｉｐ中的实现了渐开线以及螺旋线的设计，建立了斜齿轮的三维参数化模型，并利用ＡｎｓｙｓＷｏｒｋｂｅｎｃｈ对斜齿轮进行了接触应力分析。

关键词：斜齿轮；ＵＧ／ＯｐｅｎＧｒｉｐ；ＡＮＳＹＳ；参数化设计；ＦＥＡ中图分类号：ＴＨ１３２．４１３文献标识码：Ａ文章编号：１６７２－５４５Ｘ（２００７）１２－００３７－０２ＵＧ的ＣＡＤ／ＣＡＭ／ＣＡＥ系统提供了一个基于过程的产品设计环境，但ＵＧ并没有提供专用产品所需要的完整计算机辅助设计与制造功能。

利用ＵＧ／ＯｐｅｎＧｒｉｐ语言开发的程序，可以直接完成与ＵＧ的各种交互操作，与ＵＧ系统集成［１］。

ＡＮＳＹＳＷｏｒｋｂｅｎｃｈ整合了ＡＮＳＹＳ各项顶尖产品，可以简单快速地进行各项分析及前后处理操作。

ＡＮＳＹＳＷｏｒｋｂｅｎｃｈ与ＣＡＤ系统的实体及曲面模型具有双向连结，导入ＣＡＤ几何模型成功率高，可大幅降低除错时间且缩短设计与分析流程。

笔者利用ＵＧ／ＮＸ的参数化建模技术和它所提供的二次开发语言模块ＵＧ／ＯｐｅｎＧｒｉｐ实现了成斜齿轮三维实体的参数化设计，并运用ＡＮＳＹＳ最新的ＷｏｒｋＢｅｎｃｈ模块实现了ＣＡＤ／ＣＡＥ的无缝集成，对斜齿轮进行啮合过程中接触状态进行了分析。

１渐开线斜齿圆柱齿轮参数化设计１．１编程思路将ＵＧ的三维参数化造型、自由曲面扫描等功能有机结合起来，采用去除材料法生成三维模型。

由于斜齿轮的齿面为渐开螺旋面，故其端面的齿形和垂直于螺旋线方向的法面齿形是不相同的，法面参数和端面参数也不相同。

在ＵＧ／ＯｐｅｎＧｒｉｐ中建模的方法是，画出端面齿形然后通过投影关系获得其法面轮廓线，再画出能表达端面齿顶圆上某一点沿轴向运动的螺旋线轨迹；然后用特征命令扫描出完成斜齿轮的齿坯，通过布尔运算获得单个齿槽，并通过环形阵列最终获得斜齿轮的完整轮齿。

斜齿轮的精确建模及有限元分析

机电工程技术 !""! 年第 #$ 卷第 % 期
计算机应用
斜齿轮的精确建模及有限元分析
杨汾爱 ! 龙小乐 ! 鲍务均
" 武汉大学动力与机械学院 ! 湖北武汉 &#""’! #
摘要 ! 利用 ()* + , 强大的参数化设计功能 ! 精确地实现了斜齿轮的三维建模 " 通过 ()* + , 与 -./0/ 的连接 ! 运用有限元方法对斜齿轮进行了应力分析 " 关键词 ! ()* + , # 斜齿轮 # 精确建模 # 有限元中图分类号 ! 12$#!3&$ 文献标识码 ! 文章编号 ! $5"464&4! 7!55!8 5%655’$65!
-./0/ 的连接 ! 对其应力进行有限元分析 "
! 斜齿轮的精确建模
&@ ’ 软件介绍
()* + ,.AB.,,C #: 实体设计系统是由 (19 公司开发
出来的! 其界面友好! 功能强大! 已成为业界最普及的
- H!? ! 螺旋角 & H@?K !
法面模数 ./ H#LL ! 法面压力角 %/H!"K ! 法面齿顶高系数 0 2/ H@ ! 法面顶隙系数 3/ H"3!? ! 齿宽 4H#"LL " 可计算出 $ 基圆半径
&’ &
(" $/.0+"
在以上关系式中 # " 为刀顶圆角圆心 )’ 距中线的距离 $ ! 为刀顶圆角圆心 *’ 距刀具齿槽中心线的距离 $ &’ 为刀顶圆角半径 $ +% 为齿顶高系数 $ ( 为径向间隙系数 $ " 为模数 $ " 为分度圆压力角 % 用齿条型刀具加工齿轮 # 是刀具的加工节线与齿轮的加工节圆相切纯滚# 如图 ’ 所示建立坐标系# - 是节点#

斜齿圆柱齿轮的参数及几何尺寸计算(精)

斜齿圆柱齿轮的参数及几何尺寸计算（转载）狂人不狂收录于2007-04-18 阅读数：1093 收藏数：2公众公开原文来源我也要收藏以文找文如何对文章标记，添加批注？9.9.２◆斜齿圆柱齿轮的参数及几何尺寸计算◆斜齿轮的轮齿为螺旋形，在垂直于齿轮轴线的端面（下标以t表示）和垂直于齿廓螺旋面的法面（下标以n表示）上有不同的参数。

斜齿轮的端面是标准的渐开线，但从斜齿轮的加工和受力角度看，斜齿轮的法面参数应为标准值。

1.螺旋角β右图所示为斜齿轮分度圆柱面展开图，螺旋线展开成一直线，该直线与轴线的夹角β称为斜齿轮在分度圆柱上的螺旋角，简称斜齿轮的螺旋角。

tanβ=πd/ps对于基圆柱同理可得其螺旋角βb为:所以有：...（9-9-01）通常用分度圆上的螺旋角β斜进行几何尺寸的计算。

螺旋角β越大，轮齿就越倾斜，传动的平稳性也越好，但轴向力也越大。

通常在设计时取。

对于人子齿轮，其轴向力可以抵消，常取，但加工较为困难，一般用于重型机械的齿轮传动中。

齿轮按其齿廓渐开螺旋面的旋向，可分为右旋和左旋两种。

如何判断左右旋呢？测试一下？2.模数如图所示，pt为端面齿距，而pn为法面齿距，pn = pt·cosβ，因为p=πm, πmn＝πmt·cosβ,故斜齿轮法面模数与端面模数的关系为: mn＝mt·cosβ。

3.压力角因斜齿圆柱齿轮和斜齿条啮合时，它们的法面压力角和端面压力角应分别相等，所以斜齿圆柱齿轮法面压力角αn和端面压力角αt的关系可通过斜齿条得到。

在右图所示的斜齿条中，平面ABD在端面上，平面ACE在法面S 上，∠ACB=90°。

在直角△ABD、△ACEJ及△ABC中，、、、BD=CE，所以有：>>法面压力角和端面压力角的关系<<... （9-9-03）4.齿顶高系数及顶隙系数：无论从法向或从端面来看，轮齿的齿顶高都是相同的，顶隙也是相同的，即5.斜齿轮的几何尺寸计算：只要将直齿圆柱齿轮的几何尺寸计算公式中的各参数看作端面参数，就完全适用于平行轴标准斜齿轮的几何尺寸计算，具体计算公式如下表所示：名称符号公式分度圆直径 d d=m z=(m n/cosβ)z基圆直径d b d b=dcosαt齿顶高h a h a=h*an m n齿根高h f h f=(h*an+c*n)m n全齿高h h=ha+h f(2h*an+c*n)m n齿顶圆直径d a d a=d+2ha中心距 a a=(d1+d2)/2=m n(z1+z2)/2cosβ从表中可以看出，斜齿轮传动的中心距与螺旋角β有关。

Proe5.0斜齿轮建模详细图文教程

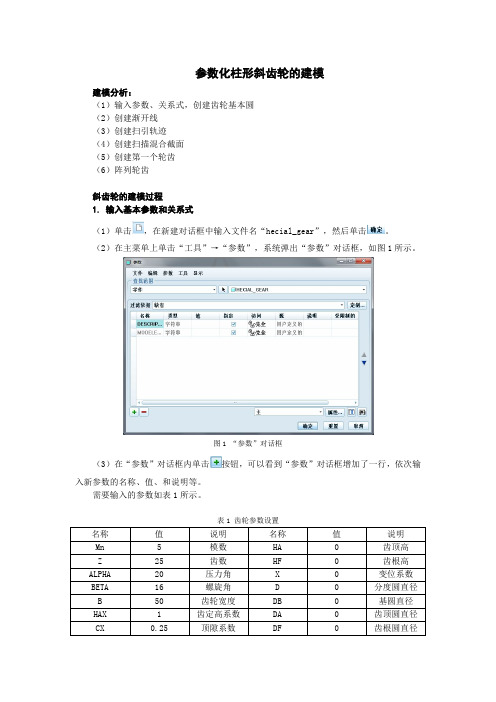
参数化柱形斜齿轮的建模建模分析：（1）输入参数、关系式，创建齿轮基本圆（2）创建渐开线（3）创建扫引轨迹（4）创建扫描混合截面（5）创建第一个轮齿（6）阵列轮齿斜齿轮的建模过程1.输入基本参数和关系式（1）单击，在新建对话框中输入文件名“hecial_gear”，然后单击。

（2）在主菜单上单击“工具”→“参数”，系统弹出“参数”对话框，如图1所示。

图1“参数”对话框（3）在“参数”对话框内单击按钮，可以看到“参数”对话框增加了一行，依次输入新参数的名称、值、和说明等。

需要输入的参数如表1所示。

表1齿轮参数设置名称值说明名称值说明Mn5模数HA0齿顶高Z25齿数HF0齿根高ALPHA20压力角X0变位系数BETA16螺旋角D0分度圆直径B50齿轮宽度DB0基圆直径HAX1齿定高系数DA0齿顶圆直径CX0.25顶隙系数DF0齿根圆直径注意：表1中未填的参数值（暂时写为0），表示是由系统通过关系式将自动生成的尺寸，用户无需指定。

完成后的参数对话框如图2所示。

图2完成后的“参数”对话框（4）在主菜单上依次单击“工具”→“关系”，系统弹出“关系”对话框，如图3所示。

图3“关系”对话框（5）在“关系”对话框内输入齿轮的分度圆直径关系、基圆直径关系、齿根圆直径关系和齿顶圆直径关系。

由这些关系式，系统便会自动生成表1所示的未指定参数的值。

输入的关系式如下：ha=(hax+x)*mnhf=(hax+cx-x)*mnd=mn*z/cos(beta)da=d+2*hadb=d*cos(alpha)df=d-2*hf完成后的“关系”对话框如图4所示。

图4完成后的“关系”对话框点击“再生”按钮，再进入“参数”对话框后，发现数据已经更新，如图5所示。

图5更新后的“参数”对话框（1）在工具栏内单击按钮，系统弹出“草绘”对话框。

（2）选择“FRONT”面作为草绘平面，选取“RIGHT”面作为参考平面，参考方向为向“右”，如图6所示。

斜齿轮轴向力公式

斜齿轮轴向力公式
斜齿轮的轴向力是指在齿轮轴向（平行于齿轮轴线的方向）上的力。

这个轴向力通常是由齿轮啮合时产生的。

轴向力的大小可以通过一些基本的力学公式来估算，具体取决于齿轮的几何形状、齿轮材料、齿轮的模数等因素。

以下是一种常用的估算轴向力的方法，该方法适用于正常啮合的齿轮系统：
F axial=K·P tanα
其中：
F axial是轴向力，
K是齿轮的传动系数，代表了齿轮系统的效率。

通常，K的取值在0.95到0.99之间，具体取决于齿轮的精度、润滑状态等因素。

P是齿轮的模数（Module），表示齿轮齿条的尺寸。

α是齿轮的压力角，表示齿轮齿面的倾斜角度。

这个公式基于简化的假设和实际工程经验，对于一些特殊情况或需要更高精度的应用，可能需要使用更复杂的数学模型和计算方法。

斜齿轮齿轮建模

! EX2.5 腹板式渐开线直齿圆柱齿轮建模finish $ /clear $ /prep7! 1. 定义齿轮参数-------------------------------------------------------------------------m=2.5 $ z=98 $ refa=20 ! 齿轮模数、齿轮齿数、齿形角（即分度圆上的压力角）hax=1 $ cx=0.25 ! 齿顶高系数、顶隙系数rouf=0.38*m $ ks=6 ! 齿根圆角半径、腹板上的圆孔数! 1.1 以下多为计算值，也可调正，但注意相互关系------------------------- ha=hax*m $ hf=(hax+cx)*m ! 齿顶高、齿根高pi=acos(-1) ! 参数πd=m*z ! 分度圆直径db=d*cos(refa*pi/180) ! 基圆直径da=d+2*ha$df=d-2*hf ! 齿顶圆直径、齿根圆直径alfad=acos(db/da) ! 齿顶圆压力角*if,db,gt,df,then ! 如果基圆直径大于齿顶圆直径则 alfag=0.0$*else ! 令齿根圆压力角为 0，否则alfag=acos(db/df) $ *endif ! 齿根求得圆压力角b=0.22*D ! 齿宽，可根据齿的软硬及与轴承相对位置选择系数! 1.2 轴孔参数设定----------------------------dta=6*m ! 轮齿部厚度，一般为 (5～6) m dax=d/5 ! 轴孔直径，可据自行设定，这里为 1/5 分度圆直径d2=1.6*dax ! 轴孔壁外缘直径d1=0.25*(da-2*dta-d2) ! 腹板上圆孔直径d0=0.5*(da-2*dta+d2) ! 腹板上圆孔中心的分布圆直径c=0.3*b ! 腹板厚度，一般为 0.3Bnj=0.5*m$nj1=0.5*m ! 外部倒角和轴孔内部倒角r=5 ! 腹板倒角半径s=1.5*dax ! 轴孔长度，一般采用 (1.2～1.5) dax 且≧ b! 2. 创建齿廓面------------------------------------------------------------------------------- ! 2.1 用极坐标方程计算渐开线上的点，取 20 个点拟合该渐开线!方程为：ρ=a/cosα，θ=tanα-α，其中 a 为基圆半径，α为压力角，θ为极角csys,1 $ n=20 ! 设置柱坐标系，并设 20 个点*do,i,1,n ! 利用 DO 循环创建关键点alfai=alfag+((alfad-alfag)/(n-1))*(i-1) ! 求得 I 点的αroui=0.5*db/cos(alfai) ! 求得 I 点的ρctai=tan(alfai)-alfai ! 求得 I 点的θk,i,roui,ctai*180/pi$*enddo ! 在柱坐标系中创建关键点! 2.2 利用上述关键点创建线，并合并之----------------------------*do,i,1,n-1 $ l,i,i+1 $ *enddo ! 利用 DO 循环创建线ctai=(tan(refa*pi/180)-refa*pi/180)*180/pi ! 求得齿形角的θctai=ctai+360/(4*z) ! 求得上述渐开线的旋转角lgen,,ALL,,,,-ctai,,,,1 ! 旋转该渐开线csys,0 ! 设置直角坐标系创建关键点，并准备对称生成线*if,db,gt,df,then ! 如果基圆直径大于齿顶圆直径则在齿根圆上创建k,n+1,kx(1)-(db-df)/2,ky(1) ! 创建关键点，采用渐开线始点的切线l,1,n+1 $ *endif ! 并与原关键点 1 连线lcomb,all $ numcmp,all ! 合并所有线，并压缩图素编号! 2.3 做对称操作----------------------------lsymm,y,all !设置直角坐标系，并关于Y轴对称操作! 2.4 在齿根圆上创建单齿部分的两个关键点，并倒角----------------------------csys,1 ! 设置柱坐标系k,5,0.5*df,360/(2*z) ! 创建关键点 5k,6,0.5*df,-360/(2*z) ! 创建关键点 6kp1=knear(6) $ l,6,kp1 ! 得到距离关键点 6 最近的点，并创建线kp1=knear(5) $ l,5,kp1 ! 得到距离关键点 5 最近的点，并创建线lfillt,1,3,rouf $ lfillt,2,4,rouf ! 对线实施倒角操作ksel,s,loc,x,da/2 ! 选择齿顶的两个关键点*get,kp1,kp,0,num,min ! 得到选择集中的最小关键点号kp2=kpnext(kp1) $ l,kp1,kp2 ! 得到另外一个关键点号，并创建线allselnumcmp,all! 2.5 复制单齿齿廓线 Z 个，利用线创建面；建议一另外圆面相减，形成齿廓面 lgen,z,all,,,,360/z ! 复制单齿廓线Z次，形成整个齿廓线nummrg,kP $ al,all ! 合并关键点，创建齿廓面cyl4,,,da/2-0.5*(dta+ha+hf) ! 创建圆面，其大小在齿根和腹板齿缘之间asba,1,2 $ numcmp,all ! 齿廓面减上述圆面，形成中空的齿廓面csys,0 $ agen,1,1,,,,,b/2,,,1 ! 设置直角坐标系，移动该面到 B/2 位置! 上述操作目的是由面拖拉形成体后即为齿部，但由于与腹板部分创建方法（旋转）不同，! 因此需要找寻一个结合面，这里取δ-h 的 1/2 处。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

斜齿圆柱齿轮
1，构造斜齿齿条
2，构造圆柱，带有键槽的。

3，齿条与圆柱生成斜齿轮
1构造齿条--- chitiao函数
1》生成单个齿条，齿条的长度L > h/cos(aa),
H 是圆柱齿轮的高度
aa是螺旋角
为了防止生成过程中，由于精度误差引起的齿轮面剥离不完全的现象，取L=1.2h/cos(aa).
在生成过程中，齿条上下各高出齿轮0.1 h/cos(aa).
以，齿轮与齿条上面的交点，也就是构造齿轮的基点为圆点，在xz平面内将齿条旋转aa度
2> 复制生成齿条
利用while循环语句，复制生成z+1个齿，每次移动的距离按照齿轮的端面模数计算。

每复制一次，就将生成的齿条与前面的齿条生成一个并集，存储到一个变量中。

2 构造圆柱齿轮yuanzhu
选取圆心，构造圆，将圆心坐标返回给齿条构造函数—chitiao 生成面域yuan
生成键槽面域
取差集，存入yuan
拉伸圆，0.5*pi*m；生成yuanzhu
3> 生成斜齿轮
While 循环（I ++ < 360）
{ 分度圆周长d*pi=。