CATIA中渐开线斜齿圆柱齿轮的建模方法(上)
使用CATIA绘制斜齿轮(直齿轮)的画法教程
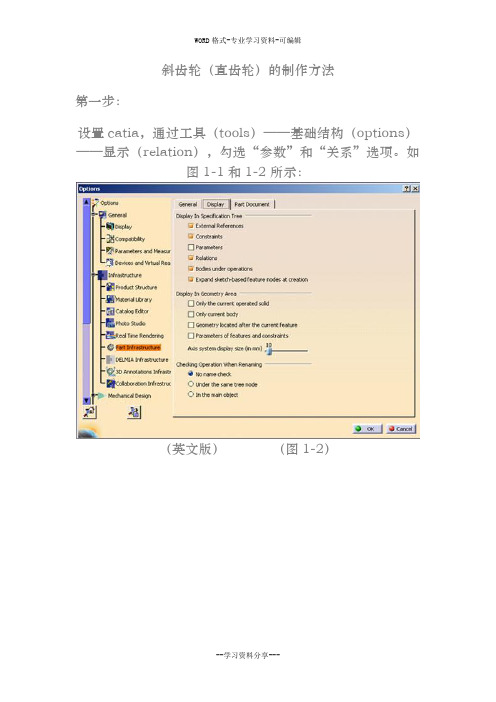
斜齿轮(直齿轮)的制作方法第一步:设置catia,通过工具(tools)——基础结构(options)——显示(relation),勾选“参数”和“关系”选项。
如图1-1和1-2所示:(英文版)(图1-2)(中文版)(图1-2)然后,单击“确定”。
第二步:单击“开始”——形状——创成式外形设计,将会出现“新建零件”窗口,如图2-1,对自己的零件进行命名(注:零件名称只能是英文、下划线和数字,如:xiechilun),单击“确定”,即进入工作界面。
(图2-2)(图2-1)第三步:对齿轮的各项参数进行输入。
参考:斜齿圆柱齿轮中有如下参数及参数关系,不涉及法向参数齿数Z 20 整数模数m 4 实数压力角a 20deg 角度齿顶圆半径 rk = r+m 长度分度圆半径 r = m*z/2 长度基圆半径rb = r*cosa 长度齿根圆半径 rf = r-1.25*m 长度螺旋角 beta 角度齿厚 depth 长度单击界面中的“知识工程”中的“f(x)”,如图3-1所示,进入参数输入界面,如图3-2所示。
(图3-1)输入参数具体步骤:(齿数(整数)、模数(实数)、压力角(角度)、齿厚(长度)螺旋角(角度)五个是需要数值的,其他值由公式计算。
下面以齿数z为例。
)如图3-2(1)选择参数类型,为整数;(2)点击左侧“新类型参数”;(必须先选择参数类型)(3)输入参数名称z;(4)输入参数值20;(5)同样方法输入模数和压力角;(注意更改参数类型)(图3-2)其他四个参数(rk、rf、r和rb)只需执行前三步即可,无需输入数值,可由稍后添加的公式得出;公式的编辑步骤(以rk为例):(5)单击右侧的“添加公式”或是双击参数rk,将会出现“公式编辑器”窗口,如图3-3所示,在黑色框内输入公式:r+m。
单击“确定”,即完成对“rk”的公式的编辑,其值变为“44mm”。
其他三个参数的公式也如此。
最终应为图3-2所示。
渐开线圆柱斜齿轮自动造型方法及画法介绍

渐开线圆柱斜齿轮自动造型方法及画法介绍自动造型方法:1.确定齿轮的基本参数,包括齿轮模数、齿数、齿轮系数等。
这些参数可以根据具体的传动需求来确定,通常需要根据设计要求和传动比例进行计算。
2.建立渐开线函数。
渐开线是齿轮齿廓的基本形状,其方程可以通过数学方法得到。
可以使用CAD或者数学软件编程进行计算,生成齿轮的渐开线方程。
3.将渐开线方程转化为点集,用于绘制齿轮齿廓。
可以通过计算齿轮上多个点的坐标,然后连接这些点来绘制齿轮齿廓。
4.绘制齿轮齿廓。
可以使用CAD软件或者绘图工具,在图纸上绘制齿轮的渐开线齿廓。
需要注意的是,齿轮的齿廓需要保证与相邻齿轮的啮合,以保证传动精度。
5.完成齿轮的其他部分绘制,包括轴孔、轮缘等。
可以参考齿轮的标准图样进行绘制,保证齿轮的几何相关性。
画法介绍:1.选择适当的比例尺和纸张大小,确定绘制齿轮的图纸尺寸。
2.根据齿轮的基本参数,确定齿轮的中心线位置。
在纸上绘制两条相互平行的直线,作为齿轮的中心线和辅助线。
3.根据齿轮的模数和齿数,计算出齿轮的分度圆直径。
在中心线上绘制一个圆,作为齿轮的分度圆。
4.根据齿轮的渐开线方程,计算齿轮齿廓上的多个点的坐标。
在图纸上以分度圆为基准,根据计算得到的点的坐标,绘制齿轮齿廓。
5.根据齿轮的设计要求和标准,绘制齿轮的其他构造,如轮缘、轴孔等。
可以参考齿轮的标准图样进行绘制,保证齿轮的几何相关性。
6.通过绘制不同切面的齿廓来实现3D效果。
可以将齿轮分解成不同的切面,并在每个切面上绘制齿轮齿廓,最后通过将各个切面叠加在一起来得到3D效果。
7.使用合适的线粗和色彩来完成绘图。
在完成齿轮的基本构造绘制后,使用适当的线粗和色彩来增加图纸的可读性和美观性。
总结:渐开线圆柱斜齿轮的自动造型和绘制可以通过计算渐开线方程和绘制齿廓点集来实现。
绘制齿轮的过程可以参考齿轮的标准图样,并结合绘图工具和软件进行绘制。
需要注意的是,绘制齿轮需要考虑齿轮的几何相关性,以及与相邻齿轮的啮合情况。
CATIA齿轮建模(直齿和斜齿)

直齿轮参数化建模预备工作,在设置里面将参数和关系显示出来1、齿轮参数的创建2、渐开线的创建X—xx=db/2*cos(PI/2*t)+db/2*PI/2*t*sin(PI/2*t)Y—yy=db/2*sin(PI/2*t)-db/2*PI/2*t*cos(PI/2*t)t=0,0.1,0.2,0.3,0.4以t=0为例说明3、在创成式模块中点击点,弹出4、在x栏右键单击,点击编辑公式,弹出5、在模型树上双击法则曲线.x,在字典里选择规则,在双击规则成员里的内容,将()里设置为0,再确定即可,完成t=0时x的创建,同理完成t=0时y的创建,z=0,就创建好了(x(0),y(0)z(0))的创建,其他照此6、将上述点用样条曲线连接,如图7、创建对称渐开线,修剪如图8、拉伸,拉伸齿宽时在长度栏右键,其过程同上,选择参数b,如图9、阵略,如图10、完成(键槽简单,省略)斜齿轮参数化建模预备工作,在设置里面将参数和关系显示出来1、齿轮参数的创建2、渐开线的创建X—xx=db/2*cos(PI/2*t)+db/2*PI/2*t*sin(PI/2*t) Y—yy=db/2*sin(PI/2*t)-db/2*PI/2*t*cos(PI/2*t) t=0,0.1,0.2,0.3,0.4,以t=0为例说明3、在创成式模块中点击点,弹出4、在x栏右键单击,点击编辑公式,弹出5、在模型树上双击法则曲线.x,在字典里选择规则,在双击规则成员里的内容,将()里设置为0,再确定即可,完成t=0时x的创建,同理完成t=0时y的创建,z=0,就创建好了(x(0),y(0)z(0))的创建,其他照此将上述点用样条曲线连接,如图6、创建对称渐开线,修剪如图7、将此渐开线投影到另一面上,并且绕z轴旋转一定角度7、将对应齿根圆上的点用直线连接起来,然后在分别投影到齿根圆柱上8、在零部件设计中运用多截面实体,扫略成齿形9、阵略完成(键槽简单,省略)。
catia各种齿轮的制作教程

这种方法同样可以用于画直齿轮一.斜齿圆柱齿轮的几何特征斜齿轮齿廓在啮合过程中,齿廓接触线的长度由零逐渐增长,从某一个位置开始又逐渐缩短,直至脱离接触,这种逐渐进入逐渐脱离的啮合过程减少了传动时的冲击、振动和噪声,从而提高了传动的稳定性,故在高速大功率的传动中,斜齿轮传动获得了较为广泛的应用。
二.斜齿圆柱齿轮与直齿圆柱齿轮的几何关系三.catia画图思路我们已经看到了,斜齿圆柱齿轮与直齿圆柱齿轮相比,就是斜齿圆柱齿轮两端端面旋转了一个角度,如果旋转角度为零,那这个斜齿圆柱齿轮就是一个直齿圆柱齿轮了,因而直齿圆柱齿轮就是螺旋角为零的特殊斜齿圆柱齿轮。
因此,我们可以将直齿圆柱齿轮和斜齿圆柱齿轮用同一个画法画出来,只改变一下参数(为端面的参数)就可以输出不同的直齿或者斜齿的齿轮,大概思路如下:a.首先用formula输入齿轮各参数的关系;b.画出齿轮齿根圆柱坯子;c.通过输入的公式得出一个齿的齿廓;d.在曲面设计模块下将齿廓平移到坯子的另一端面(通过平移复制一个新的齿廓到另一端面);e.将新的齿廓旋转到特定角度;f.多截面拉伸成形一个轮齿;g.环形阵列这个轮齿这样,斜齿圆柱齿轮就画完了。
四.catia绘图步骤1.设置catia,通过tools-->options将relation显示出来,以便待会使用,如图所示:2.输入齿轮的各项参数斜齿圆柱齿轮中有如下参数及参数关系,不涉及法向参数齿数 Z模数 m压力角 a齿顶圆半径 rk = r+m分度圆半径 r = m*z/2基圆半径 rb = r*cosa齿根圆半径 rf = r-1.25*m螺旋角 beta齿厚 depth进入线框和曲面建模模块(或part design零件设计模块)如图:输入各参数及公式,如图所示:3.点击fog按钮,建立一组X,Y,关于参数t的函数,方程为:x=rb*sin(t*PI*1rad)-rb*t*PI*cos(t*PI*1rad)y=(rb*cos(t*PI*1rad))+((rb*t*PI)*sin(t*PI*1rad))如图所示:这时候,可以看到关系树上新建的两个函数了:5.在xy平面画一个点,坐标为(0,0),并以此点为圆心在xy平面上建立齿根圆(就是空间的画圆工具),如图所示:公式内输入rf,即齿根圆半径。
catia两种方法绘制渐开线

首先定义参数及规则:【基本参数】模数:m 齿数:z 压力角:a分度圆直径:D=m*z基圆直径: Db=D*cos(a)=m*z*cos(a)齿顶圆直径:Da=m*(z+2)齿根圆直径:Df=m*(z-2.5)【渐开线公式】压力角范围:0 ~ range(range<=90,常选range=60)横坐标:xt=Db*cos(range*t)/2+Db*PI*t*range*sin(range*t)/360 纵坐标:yt=Db*sin(range*t)/2-Db*PI*t*range*cos(range*t)/360第一种方法构造渐开线(通用)【建立点】点1:x=`关系\xt` ->Evaluate(0)y=`关系\yt` ->Evaluate(0)点2:x=`关系\xt` ->Evaluate(0.1)y=`关系\yt` ->Evaluate(0.1)点3:x=`关系\xt` ->Evaluate(0.3)y=`关系\yt` ->Evaluate(0.3)点4:x=`关系\xt` ->Evaluate(0.5)y=`关系\yt` ->Evaluate(0.5)点5:x=`关系\xt` ->Evaluate(0.7)y=`关系\yt` ->Evaluate(0.7)点6:x=`关系\xt` ->Evaluate(0.8)y=`关系\yt` ->Evaluate(0.8)【建立s曲线】点击“样条曲线”——依次输入上面6个点所得的样条曲线即为所需的渐开线第二种方法构造渐开线(原创)【建立与z轴平行的直线】line1:直线——Point to Point——(0,0,0)-(0,0,10)【在xz面上建立偏移曲线】curve1:平行曲线——曲线:line1——支持面:xz平面——法则曲线:xt 【在yz面上建立偏移曲线】curve2:平行曲线——曲线:line1——支持面:yz平面——法则曲线:yt 【拉伸curve1】surface1:拉伸——轮廓:curve1——方向:xz平面(即y轴)【拉伸curve2】surface2:拉伸——轮廓:curve2——方向:yz平面(即x轴)【求相交曲线】curve3:相交——第一元素:surface1——第二元素:surface2【求投影曲线】curve4:投影——轮廓:curve3——支持面:xy平面所得的投影曲线curve4即为所需的渐开线两种方法比较采用第一种方法时,需要输入离散点,离散点越多,绘制的渐开线越精确。
基于catia的渐开线齿轮参数化精确建模与应用(一)

基于catia的渐开线齿轮参数化精确建模与应用(一)基于Catia的渐开线齿轮参数化精确建模与应用引言Catia是一款强大的计算机辅助设计软件,通过其参数化建模功能,可以实现渐开线齿轮的精确建模与应用。
本文将详细讲解基于Catia的渐开线齿轮参数化精确建模与应用的一些方面。
1. 渐开线的概念及应用渐开线是一种特殊的曲线,广泛应用于齿轮设计中。
它能够使齿轮传递动力更加平稳,减少噪音与磨损,并提高传动效率。
基于Catia 的参数化建模功能,可以方便地生成具有渐开线的齿轮模型,并通过调整参数来实现不同需求的设计。
2. Catia的参数化建模功能Catia具有强大的参数化建模功能,可以通过定义参数和约束条件,灵活地调整模型的尺寸与形状。
在渐开线齿轮设计中,我们可以通过Catia的参数化建模功能,将齿轮的齿数、模数、齿宽等参数定义为变量,以便随时调整齿轮的尺寸与形状。
3. 渐开线齿轮的精确建模基于Catia的参数化建模功能,可以实现渐开线齿轮的精确建模。
首先,我们可以通过定义齿轮的基本参数,如齿数、模数、齿宽等,来生成齿轮的齿廓曲线。
然后,我们可以通过Catia的绘图工具,绘制渐开线曲线,并将其应用到齿轮的齿廓上。
4. 渐开线齿轮的应用场景渐开线齿轮广泛应用于各种机械传动系统中,如汽车发动机、工业机械设备等。
其具有传动效率高、噪音低、磨损小等优点,使其成为理想的传动元件。
通过基于Catia的参数化建模功能,我们可以根据具体的应用场景,灵活地调整渐开线齿轮的参数,并生成精确的齿轮模型。
结论基于Catia的渐开线齿轮参数化精确建模与应用具有很大的优势,不仅能够提高齿轮设计的效率,还能够满足不同场景下的需求。
通过合理利用Catia的参数化建模功能,我们能够快速生成精确的渐开线齿轮模型,并在实际应用中发挥其优越性能。
5. 渐开线齿轮的优势与特点渐开线齿轮相对于其他齿轮类型有一些独特的优势和特点。
首先,渐开线齿轮的传动效率很高,因为其齿形能够使齿轮与齿轮之间的载荷分布更加均匀,减少了啮合损失。
CATIA____斜齿轮教程

CATIA____斜齿轮教程CATIA是一款知名的三维设计软件,广泛应用于机械设计领域。
斜齿轮是一种常见的齿轮类型,其特点是齿轮的齿面与齿轮轴线呈一定的角度。
本文将介绍使用CATIA软件进行斜齿轮设计的基本步骤,以帮助读者更好地了解和使用CATIA进行斜齿轮设计。
首先,启动CATIA软件并创建一个新的零件文件。
选择“零件设计”模板,然后在工作区中选择适当的坐标系。
接下来,选择绘图工具栏上的“齿轮”功能。
在弹出的对话框中,选择所需的齿轮类型为“斜齿轮”。
根据需要设置斜齿轮的系数和参数,如模数、齿数、螺旋角等。
点击确定按钮后,齿轮的几何形状将被创建。
接下来,选择“操作”菜单中的“修剪”功能,用于修剪斜齿轮的边缘。
选择需要修剪的边缘,然后点击确定按钮。
然后,选择“操作”菜单中的“倒角”功能,用于给斜齿轮的边缘添加倒角。
选择需要添加倒角的边缘,然后设置合适的倒角半径和倒角类型,最后点击确定按钮。
接下来,选择“操作”菜单中的“镜像”功能,用于创建斜齿轮的镜像副本。
选择需要镜像的斜齿轮,并选择适当的镜像平面,最后点击确定按钮。
最后,选择“文件”菜单中的“保存”功能,将斜齿轮设计保存为CATIA文件格式。
为了方便之后的参考和修改,建议给文件起一个合适的名称,并选择一个合适的文件夹进行保存。
通过以上步骤,我们完成了使用CATIA软件进行斜齿轮的基本设计。
在实际设计过程中,还可以根据需要对斜齿轮进行进一步的修改和优化,如添加孔洞、修改齿轮参数等。
此外,CATIA还提供了许多其他高级功能,如齿轮的齿面修整、齿轮的装配设计等,可以根据需要深入学习和应用。
总结起来,CATIA是一款功能强大的三维设计软件,在斜齿轮设计中具有广泛的应用。
掌握CATIA的基本操作和斜齿轮的设计原理,能够帮助我们更好地进行斜齿轮的设计和优化。
以上是CATIA斜齿轮设计的基本步骤,希望对读者有所帮助。
如果想要深入学习CATIA的其他设计功能和技巧,还需要进一步的学习和实践。
利用CAXA在CATIA中绘制渐开线齿轮

利用CAXA在CATIA中绘制渐开线齿轮渐开线齿轮作为机械传动中的重要零部件,在机械结构中广泛应用,而渐开线齿轮的绘制却是机械制图中的难点渐开线齿轮作为机械传动中的重要零部件,在机械结构中广泛应用,而渐开线齿轮的绘制却是机械制图中的难点。
二维软件一般可以通过参数模块进行渐开线绘制,而目前的三维软件却很难进行渐开线的精确绘制。
在不要求齿轮渐开线精度的情况下,三维软件中一般采用圆弧代替和圆弧逼近的简化处理,但当所绘制的渐开线齿轮需要进行动力学仿真或者其他精度要求较高时,简化处理很难满足精度要求,此时需要精确的绘制渐开线。
目前,三维软件中的渐开线一般采用的方法,一种是由曲面生成渐开线,即曲面扫描和曲面放样,另一种是差值法生产渐开线,还有一种是程序法生产渐开线,但这些方法在三维软件中的实现都较为繁琐。
本文将介绍一种利用CAXA软件参数功能,在CATIA中快速精确地绘制渐开线齿轮的方法。
一、CAXA中绘制平面齿轮CAXA电子图版应用越来越广泛的一个重要原因是其将一些常用零件或者常用方法进行模块化,而渐开线齿轮就是其中的一个模块,所以在CAXA中绘制渐开线齿轮简单易操作,具体操作步骤如下。
(1)点击绘图工具Ⅱ中的齿轮按钮,弹出渐开线齿轮齿形参数对话框(图1)。
(2)在图1所示的对话框中,选择绘制外齿轮或内齿轮,并填写绘制齿轮的齿数、模数、压力角及变位系数。
同时根据所绘制齿轮的要求选择参数一或者参数二。
(3)单击图1所示对话框中的“下一步”按钮,系统弹出如图2所示对话框。
在对话框的相应位置填写齿轮的齿顶过渡圆角半径和齿根过渡圆角半径。
如果画整个齿轮,要选择有效齿数并在框中填写所画齿轮的齿数。
如果起始角想转过一定角度,可在有效齿起始角处标出。
同时可以根据对渐开线齿轮齿形精度的要求,填写精度要求。
(4)点击图2所示对话框的“预显”按钮,查看生成的齿轮状态,如果满足要求,单击完成,并在CAXA界面中单击,生成所要画的齿轮,如图3所示。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
CATIA中渐开线斜齿圆柱齿轮的建模方法(上) 1.在绘制斜齿圆柱齿轮时,最大的难点就是其渐开线齿廓的
绘制。
(本文所述斜齿轮为平行轴斜齿轮)
(1)提到这个问题很多同学就会问了,斜齿轮中到底端面齿廓曲线是渐开线,还是法面齿廓曲线是渐开线?
斜齿圆柱齿轮的端面齿廓为准确的渐开线,法面齿廓为标准的渐开线。
从理论上端面是标准渐开线,因为渐开线的形成是发生面在基圆柱面上纯滚动,发生面上的斜直线的轨迹是渐开线。
从加工上,法面是标准渐开线,因为加工斜齿轮齿廓是用加工直齿圆柱齿轮的标准刀具,其切削运动方向沿螺旋线切线,刀具面在其法面,因此,法面是标准浙开线。
(2)以下都是小李的个人推断,如有错误,希望大家能够予以指正):
推断一:斜齿圆柱齿轮的法面齿廓曲线是标准渐开线,实际加工后的端面齿廓只是一个准确度很高的渐开线!!!(因为加工斜齿轮齿廓是用加工直齿圆柱齿轮的标准刀具,其切削运动方向沿螺旋线切线,刀具面在其法面)
推断二:斜齿圆柱齿轮啮合过程中最重要的还是端面!!!
因为在平行轴斜齿轮机构中,斜齿轮都是围绕中心轴线转动的,可以想象齿廓上各点也都是围绕中心轴线做转动的,在两个斜齿轮相互啮合时,齿面上的接触线先由长变短,然后由短变长,为一条倾斜的直线,故而产生轴向力,滚动过程系在端面内进行,因而在计算中心距时,起决定性作用的还是端面内的啮合形式,齿廓只在齿高方向滑动和滚动。
由此也应证了推断一,因为啮合时的运动趋势不是围绕法线,
故而法面齿廓曲线是渐开线没有存在的必要!!!
2.斜齿轮渐开线方程的建立。
(d b=dcosαt)αt≠20°
在国标中直齿轮α=20°为一定值,斜齿轮αt≠20°斜齿轮中法面压力角αn=20°,tanαt=tanαn/cosβ
斜齿轮中法面压力角αn=20°,tanαt=tanαn/cosβ
catia中渐开线齿廓的定义方程:
x=rb*sin(t*PI*1rad)-rb*t*PI*cos(t*PI*1rad)
y=(rb*cos(t*PI*1rad))+((rb*t*PI)*sin(t*PI*1rad)) (x,y坐标互换不影响渐开线在xy面形状)(θ=t*PI不影响渐开线在xy面投影形状)。
