2017中考题型四反比例函数与一次函数综合题

合集下载

反比例函数和一次函数结合的题型

反比例函数和一次函数结合的题型
题目：
一条直线贯穿着反比例函数 $y=\dfrac{k}{x}$ 和一次函数
$y=mx+n$ 的图象，交点坐标为 $(2,3)$，求这两个函数的解析式。

解答：
设直线的解析式为 $y=ax+b$，则由于交点坐标为 $(2,3)$，所以有：
$$\begin{cases}3=2a+b \\ \dfrac{k}{2}=3a+b\end{cases}$$
解以上方程组可以得到 $a=-\dfrac{3}{4},b=\dfrac{15}{4}$。

因此，直线的解析式为 $y=-\dfrac{3}{4}x+\dfrac{15}{4}$。

将其与反比例函数 $y=\dfrac{k}{x}$ 和一次函数 $y=mx+n$ 分别相交可以得到：
$$\begin{cases}\dfrac{k}{2}=-\dfrac{3}{4}\cdot
2+\dfrac{15}{4}\\\dfrac{k}{4}=-\dfrac{3}{4}\cdot
4+\dfrac{15}{4}\end{cases}$$
解以上方程组得到 $k=12$，因此反比例函数的解析式为
$y=\dfrac{12}{x}$。

将直线与一次函数相交可以得到：
$$\begin{cases}n=3-\dfrac{3}{4}\cdot
2\\\dfrac{15}{4}=2m+n\end{cases}$$
解以上方程组得到 $m=\dfrac{13}{8},n=\dfrac{9}{4}$，因此一次函数的解析式为 $y=\dfrac{13}{8}x+\dfrac{9}{4}$。

反比例函数与一次函数的综合应用参考答案与试题解析

反比例函数与一次函数的综合应用1．已知一次函数y1＝kx﹣b与反比例函数y2＝，在同一平面直角坐标系中的图象如图所示，则当kx＜+b时，x的取值范围是（）A．x＜﹣1或0＜x＜3B．﹣1＜x＜0或x＞3C．﹣3＜x＜0或x＞1D．x＞32．如图，一次函数y＝k1x+b的图象与x轴，y轴分别交于A，B两点，与反比例函数y＝的图象分别交于C，D两点，若点C坐标是（3，6），且AB＝BC．（1）求一次函数y＝k1x+b与反比例函数y＝的解析式；（2）求△COD的面积；（3）直接写出当x取何值时，k1x+b＜．3．如图，在平面直角坐标系中，一次函数与反比例函数相交于A（2，m）和B（6，2）．（1）求直线AB的表达式；（2）△AOB的面积是；（3）点A到OB的距离AH的长度是．4．如图，一次函数y1＝﹣2x+b的图象分别交x轴，y轴于D，C两点，交反比例函数y2＝图象于A（﹣1，6），B（m，﹣2）两点．（1）求k，b的值；（2）点E是y轴上点C下方一点，若S＝，求E点的坐标；△AEB（3）当y1＞y2时，x的取值范围是．5．如图，一次函数y＝k1x+b的图象与反比例函数y＝的图象相交于A（1，2）、B（﹣2，n）两点．（1）求一次函数和反比例函数的解析式；（2）根据图象，直接写出满足k1x+b＞的x的取值范围；（3）若点P在线段AB上，且S：S△BOP＝1：4，求点P的坐标．△AOP参考答案与试题解析1．已知一次函数y1＝kx﹣b与反比例函数y2＝，在同一平面直角坐标系中的图象如图所示，则当kx＜+b时，x的取值范围是（）A．x＜﹣1或0＜x＜3B．﹣1＜x＜0或x＞3C．﹣3＜x＜0或x＞1D．x＞3【解答】解：根据题意得：当y1＜y2时，x的取值范围是﹣1＜x＜0或x＞3，∴当kx＜+b时，x的取值范围是﹣1＜x＜0或x＞3．故选：B．2．如图，一次函数y＝k1x+b的图象与x轴，y轴分别交于A，B两点，与反比例函数y＝的图象分别交于C，D两点，若点C坐标是（3，6），且AB＝BC．（1）求一次函数y＝k1x+b与反比例函数y＝的解析式；（2）求△COD的面积；（3）直接写出当x取何值时，k1x+b＜．【解答】解：（1）∵点C（3，6）在反比例函数y＝的图象上，∴k2＝3×6＝18，∴反比例函数的解析式为y＝；如图，作CE⊥x轴于E，∵C（3，6），AB＝BC，∴B（0，3），∵B、C在y＝k1x+b的图象上，∴，解得，∴一次函数的解析式为y＝x+3；（2）由，解得或，∴D（﹣6，﹣3），＝S△BOC+S△BOD＝×3×3+×3×6＝；∴S△COD（3）由图象可得，当0＜x＜3或x＜﹣6时，k1x+b＜．3．如图，在平面直角坐标系中，一次函数与反比例函数相交于A（2，m）和B（6，2）．（1）求直线AB的表达式；（2）△AOB的面积是16；（3）点A到OB的距离AH的长度是．【解答】解：（1）设反比例函数的解析式为y＝，由题意可知：k＝6×2＝12，∴y＝，∵A（2，m）在反比例函数y＝的图象上，∴m＝＝6，∴A（2，6），∵A（2，6）、B（6，2）在一次函数y＝ax+b的图象上，∴，解得，∴直线AB的表达式为y＝﹣x+8；（2）设直线AB与x轴的交点为C，令y＝0，则﹣x+8＝0，解得x＝8，∴C（8，0），＝S△AOC﹣S△BOC＝﹣＝16，∴S△AOB故答案为：16；（3）∵B（6，2），∴OB＝＝2，∵S＝OB•AH＝16，△AOB∴AH＝＝，故答案为：．4．如图，一次函数y1＝﹣2x+b的图象分别交x轴，y轴于D，C两点，交反比例函数y2＝图象于A（﹣1，6），B（m，﹣2）两点．（1）求k，b的值；＝，求E点的坐标；（2）点E是y轴上点C下方一点，若S△AEB（3）当y1＞y2时，x的取值范围是x＜﹣1或0＜x＜3．【解答】解：（1）将A（﹣1，6）代入一次函数y＝﹣2x+b，得b＝4；将A（﹣1，6）代入，得k＝﹣6．（2）设E（a，0），将B（m，﹣2）代入，得m＝3，∴B（3，﹣2）∴）＝2CE＝2（4﹣a）＝，∴E（0，）；（3）观察图象，当y1＞y2时，x的取值范围是x＜﹣1或0＜x＜3，故答案为：x＜﹣1或0＜x＜3．5．如图，一次函数y＝k1x+b的图象与反比例函数y＝的图象相交于A（1，2）、B（﹣2，n）两点．（1）求一次函数和反比例函数的解析式；（2）根据图象，直接写出满足k1x+b＞的x的取值范围；：S△BOP＝1：4，求点P的坐标．（3）若点P在线段AB上，且S△AOP【解答】解：（1）∵反比例函数y＝经过A（1，2），∴k2＝1×2＝2，∴反比例函数解析式为y＝，∵B（﹣2，n）在比例函数y＝的图象上，∴n＝＝﹣1，∴B（﹣2，﹣1），∵直线y＝k1x+b经过A（1，2），B（﹣2，﹣1），∴，解得，∴一次函数的解析式为y＝x+1；（2）观察图象，k1x+b＞的x的取值范围是﹣2＜x＜0或x＞1；（3）设P（x，x+1），：S△BOP＝1：4，∵S△AOP∴AP：PB＝1：4，即PB＝4PA，∴（x+2）2+（x+1+1）2＝16[（x﹣1）2+（x+1﹣2）2]，解得x1＝，x2＝2（舍去），∴P点坐标为（，）．。

【人教版】2017年中考数学：题型(4)反比例函数与一次函数综合题(含答案)

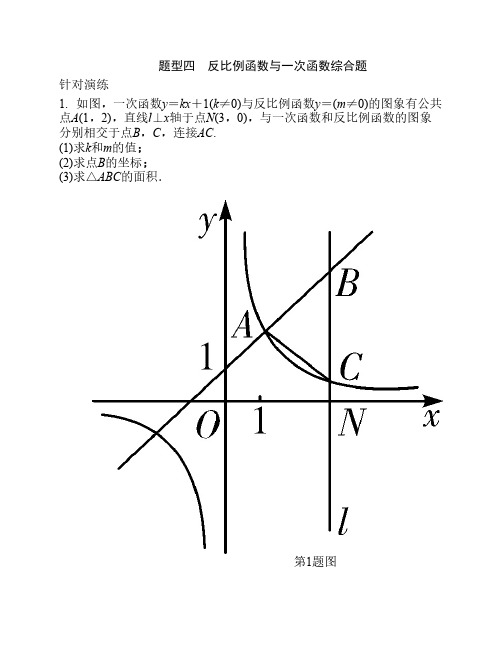
题型四　反比例函数与一次函数综合题针对演练1. 如图，一次函数y＝kx＋1(k≠0)与反比例函数y＝(m≠0)的图象有公共点A(1，2)，直线l⊥x轴于点N(3，0)，与一次函数和反比例函数的图象分别相交于点B，C，连接AC.(1)求k和m的值；(2)求点B的坐标；(3)求△ABC的面积．第1题图2. 已知正比例函数y＝2x的图象与反比例函数y＝(k≠0)在第一象限内的图象交于点A，过点A作x轴的垂线，垂足为点P，已知△OAP的面积为1.(1)求反比例函数的解析式；(2)有一点B的横坐标为2，且在反比例函数图象上，则在x轴上是否存在一点M，使得MA＋MB最小？若存在，请求出点M的坐标；若不存在，请说明理由．第2题图3. 如图，反比例函数的图象与一次函数y＝kx＋b的图象交于点A、B，点A、B的横坐标分别为1、－2，一次函数图象与y轴交于点C，与x轴交于点D.(1)求一次函数的解析式；(2)对于反比例函数，当y＜－1时，写出x的取值范围；(3)在第三象限的反比例函数图象上是否存在一点P，使得S△ODP＝2S△OCA？若存在，请求出点P的坐标；若不存在，请说明理由．第3题图4. (2016巴中10分)已知，如图，一次函数y＝kx＋b(k、b为常数，k≠0)的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴，垂足为D.若OB＝2OA ＝3OD＝6.(1)求一次函数与反比例函数的解析式；(2)求两函数图象的另一个交点坐标；(3)直接写出不等式：kx＋b≤的解集．第4题图5. 如图，点A(－2，n)，B(1，－2)是一次函数y＝kx＋b的图象和反比例函数y＝的图象的两个交点．(1)求反比例函数和一次函数的解析式；(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围；(3)若C是x轴上一动点，设t＝CB－CA，求t的最大值，并求出此时点C的坐标．第5题图6. 如图，直线y1＝x＋1与x轴交于点A，与y轴交于点C，与反比例函数y2＝(x>0)的图象交于点P，过点P作PB⊥x轴于点B，且AC＝BC.(1)求点P的坐标和反比例函数y2的解析式；(2)请直接写出y1>y2时，x的取值范围；(3)反比例函数y2图象上是否存在点D，使四边形BCPD为菱形？如果存在，求出点D的坐标；如果不存在，说明理由．第6题图7. 如图，直线y＝x＋b与x轴交于点C(4，0)，与y轴交于点B，并与双曲线y＝(x＜0)交于点A(－1，n)．(1)求直线与双曲线的解析式；(2)连接OA，求∠OAB的正弦值；(3)若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形△OAB相似？若存在求出D点的坐标，若不存在，请说明理由．第7题图8. (2016金华8分)如图，直线y＝x－与x，y轴分别交于点A，B，与反比例函数y＝(k＞0)图象交于点C，D，过点A作x轴的垂线交该反比例函数图象于点E.(1)求点A的坐标；(2)若AE＝AC.①求k的值；②试判断点E与点D是否关于原点O成中心对称？并说明理由．第8题图9. 如图，已知双曲线y＝经过点D(6，1)，点C是双曲线第三象限上的动点，过点C作CA⊥x轴，过点D作DB⊥y轴，垂足分别为A，B，连接AB，BC.(1)求k的值；(2)若△BCD的面积为12，求直线CD的解析式；(3)判断AB与CD的位置关系，并说明理由．第9题图10. 如图，点B为双曲线y＝(x＞0)上一点，直线AB平行于y轴，交直线y＝x于点A，交x轴于点D，双曲线y＝与直线y＝x交于点C，若OB2－AB2＝4.(1)求k的值；(2)点B的横坐标为4时，求△ABC的面积；(3)双曲线上是否存在点P，使△APC∽△AOD？若存在，求出点P的坐标；若不存在，请说明理由．第10题图【答案】1．解：(1)∵点A(1，2)是一次函数y＝kx＋1与反比例函数y＝的公共点，∴k＋1＝2，＝2，∴k＝1，m＝2；(2)∵直线l⊥x轴于点N(3，0)，且与一次函数的图象交于点B，∴点B的横坐标为3，将x＝3代入y＝x＋1，得y＝3＋1＝4，∴点B的坐标为(3，4)；(3)如解图，过点A作AD⊥直线l，垂足为点D，由题意得，点C的横坐标为3，∵点C在反比例函数图象上，∴y＝＝，∴C点坐标为(3，)，∴BC＝BN－CN＝4－＝，又∵AD＝3－1＝2，∴S△ABC＝BC·AD＝××2＝.第1题解图2．解：(1)设A点的坐标为(x，y)，则OP＝x，PA＝y，∵△OAP的面积为1，∴xy＝1，∴xy＝2，即k＝2，∴反比例函数的解析式为；(2)存在，如解图，作点A关于x轴的对称点A′，连接A′B，交x轴于点M，此时MA＋MB最小，∵点B的横坐标为2，∴点B的纵坐标为y＝＝1，即点B的坐标为（2,1）.又∵两个函数图象在第一象限交于A点，∴，解得x1＝1，x2＝－1(舍去)．∴y＝2，∴点A的坐标为(1，2)，∴点A关于x轴的对称点A′(1，－2)，设直线A′B的解析式为y＝kx＋b，代入A′(1，－2)，B(2，1)得，∴直线A′B的解析式为y＝3x－5，令y＝0，得x＝，∴直线y＝3x－5与x轴的交点为(，0)，即点M的坐标为(，0)．第2题解图3．解：(1)∵反比例函数y＝图象上的点A、B的横坐标分别为1、－2，∴点A的坐标为(1，2)，点B的坐标为(－2，－1)，∵点A(1，2)、B(－2，－1)在一次函数y＝kx＋b的图象上，∴∴一次函数的解析式为y＝x＋1；(2)由图象知，对于反比例函数，当y＜－1时，x的取值范围是－2＜x＜0；(3)存在．对于y＝x＋1，当y＝0时，x＝－1，当x＝0时，y＝1，∴点D的坐标为(－1，0)，点C的坐标为(0，1)，设点P(m，n)，∵S△ODP＝2S△OCA，∴×1×(－n)＝2××1×1，∴n＝－2，∵点P(m，－2)在反比例函数图象上，∴－2＝，∴m＝－1，∴点P的坐标为(－1，－2)．4．解：(1)∵OB＝2OA＝3OD＝6，∴OA＝3，OD＝2.∴A(3，0)，B(0，6)，D(－2，0)．将点A(3，0)和B(0，6)代入y＝kx＋b得，∴一次函数的解析式为y＝－2x＋6. ……………………(3分)将x＝－2代入y＝－2x＋6，得y＝－2×(－2)＋6＝10，∴点C的坐标为(－2，10)．将点C(－2，10)代入y＝，得10＝，解得n＝－20，∴反比例函数的解析式为；………………………(5分)(2)将两个函数解析式组成方程组，得解得x1＝－2，x2＝5. ………………………………………(7分)将x＝5代入∴两函数图象的另一个交点坐标是(5，－4)； …………… (8分)(3)－2≤x＜0或x≥5. …………………………………… (10分)【解法提示】不等式kx＋b≤的解集，即是直线位于双曲线下方的部分所对应的自变量x的取值范围，也就是－2≤x＜0或x≥5.5．解：(1)∵点A(－2，n)，B(1，－2)是一次函数y＝kx＋b的图象和反比例函数y＝的图象的两个交点，∴m＝－2，∴反比例函数解析式为，∴n＝1，∴点A(－2，1)，将点A(－2，1)，B(1，－2)代入y＝kx＋b，得∴一次函数的解析式为y＝－x－1；(2)结合图象知：当－2＜x＜0或x＞1时，一次函数的值小于反比例函数的值；(3)如解图，作点A关于x轴的对称点A′，连接BA′延长交x轴于点C，则点C即为所求，∵A(－2，1)，∴A′(－2，－1)，设直线A′B的解析式为y＝mx＋n，∴y＝－x－，令y＝0，得x＝－5，则C点坐标为(－5，0)，∴t的最大值为A′B＝＝.第5题解图6．解：(1)∵一次函数y1＝x＋1的图象与x轴交于点A，与y轴交于点C，∴A(－4，0)，C(0，1)，又∵AC＝BC，CO⊥AB，∴O为AB的中点，即OA＝OB＝4，且BP＝2OC＝2，∴点P的坐标为(4，2)，将点P(4，2)代入y2＝，得m＝8，∴反比例函数的解析式为y2＝；(2)x>4；【解法提示】由图象可知，当y1＞y2时，即是直线位于双曲线上方的部分，所对应的自变量x的取值范围是x＞4.(3)存在．假设存在这样的D点，使四边形BCPD为菱形，如解图，连接DC与PB交于点E，∵四边形BCPD为菱形，∴CE＝DE＝4，∴CD＝8，∴D点的坐标为(8，1)，将D(8，1)代入反比例函数，D点坐标满足函数关系式，即反比例函数图象上存在点D，使四边形BCPD为菱形，此时D点坐标为(8，1)．第6题解图7．解：(1)∵直线y＝x＋b与x轴交于点C(4，0)，∴把点C(4，0)代入y＝x＋b，得b＝－4，∴直线的解析式为y＝x－4，∵直线也过A点，∴把点A(－1，n)代入y＝x－4，得n＝－5，∴A(－1，－5)，将A(－1，－5)代入y＝(x＜0)，得m＝5，∴双曲线的解析式为；(2)如解图，过点O作OM⊥AC于点M，∵点B是直线y＝x－4与y轴的交点，∴令x＝0，得y＝－4，∴点B(0，－4)，∴OC＝OB＝4，∴△OCB是等腰直角三角形，∴∠OBC＝∠OCB＝45°，∴在△OMB中，sin45°＝＝，∴OM＝2，∵AO＝＝，∴在△AOM中，sin∠OAB＝＝＝；第7题解图(3)存在．如解图，过点A作AN⊥y轴于点N，则AN＝1，BN＝1，∴AB＝＝，∵OB＝OC＝4，∴BC＝＝4，又∵∠OBC＝∠OCB＝45°，∴∠OBA＝∠BCD＝135°，∴△OBA∽△BCD或△OBA∽△DCB，∴＝或＝，即＝或＝，∴CD＝2或CD＝16，∵点C(4，0)，∴点D的坐标是(6，0)或(20，0)．8．解：(1)当y＝0时，得0＝x－，解得x＝3.∴点A的坐标为(3，0)； ……………………………………(2分) (2)①如解图，过点C作CF⊥x轴于点F.设AE＝AC＝t, 点E的坐标是(3，t).在Rt△AOB中， tan∠OAB＝＝，∴∠OAB＝30°.在Rt△ACF中，∠CAF＝30°，∴CF＝t，AF＝AC·cos30°＝t，∴点C的坐标是(3＋t，t)．∵点C、E在y＝的图象上，∴(3＋t)×t＝3t，解得t1＝0(舍去)，t2＝2，∴k＝3t＝6； …………………………………………… (5分)②点E与点D关于原点O成中心对称，理由如下：由①知，点E的坐标为(3，2)，设点D的坐标是(x，x－)，∴x(x－)＝6，解得x1＝6(舍去)，x2＝－3，∴点D的坐标是(－3，－2)，∴点E与点D关于原点O成中心对称．…………………(8分)第8题解图9．解：(1)∵双曲线y＝经过点D(6，1)，∴＝1，解得k＝6；(2)设点C到BD的距离为h，∵点D的坐标为(6，1)，DB⊥y轴，∴BD＝6，∴S△BCD＝×6×h＝12，解得h＝4，∵点C是双曲线第三象限上的动点，点D的纵坐标为1，∴点C的纵坐标为1－4＝－3，∴＝－3，解得x＝－2，∴点C的坐标为(－2，－3)，设直线CD的解析式为y＝kx＋b，则∴直线CD的解析式为y＝x－2；(3)AB∥CD.理由如下：∵CA⊥x轴，DB⊥y轴，点D的坐标为(6，1)，设点C的坐标为(c，)，∴点A、B的坐标分别为A(c，0)，B(0，1)，设直线AB的解析式为y＝mx＋n，则∴直线AB的解析式为y＝－＋1，设直线CD的解析式为y＝ex＋f，则∴直线CD的解析式为y＝－＋，∵AB、CD的解析式中k都等于，∴AB与CD的位置关系是AB∥CD.10．解：(1)设D点坐标为(a，0)，∵AB∥y轴，点A在直线y＝x上，B为双曲线y＝(x＞0)上一点，∴A点坐标为(a，a)，B点坐标为(a，)，∴AB＝a－，BD＝，在Rt△OBD中，OB2＝BD2＋OD2＝()2＋a2，∵OB2－AB2＝4，∴()2＋a2－(a－)2＝4，∴k＝2；(2)如解图，过点C作CM⊥AB于点M，∴C点坐标为(，)，∵点B的横坐标为4，∴A点坐标为(4，4)，B点坐标为(4，)，∴AB＝4－＝，CM＝4－，∴S△ABC＝CM·AB＝×(4－)×＝7－；第10题解图(3)不存在，理由如下：若△APC∽△AOD，∵△AOD为等腰直角三角形，∴△APC为等腰直角三角形，∠ACP＝90°，∴CM＝AP，设P点坐标为(a，)，则A点坐标为(a，a)，∴AP＝|a－|，∵C点坐标为(，)，∴CM＝|a－|，∴|a－|＝|a－|，∴(a－)2＝×，即(a－)2＝×，∴4a2－(a＋)2＝0，解得a＝或a＝－(舍去)，∴P点坐标为(，)，则此时点C与点P重合，所以不能构成三角形，故不存在．。

一次函数,反比例函数与四边形的综合题

一次函数与反比例函数的综合四边形1，如图12，四边形ABCD 是平行四边形，点(10)(31)(33)A B C ，，，，，．反比例函数(0)my x x=>的图象经过点D ，点P 是一次函数33(0)y kx k k =+-≠的图象与该反比例函数图象的一个公共点.（1）求反比例函数的解析式；（2）通过计算，说明一次函数33(0)y kx k k =+-≠的图象一定过点C ；（3）对于一次函数33(0)y kx k k =+-≠，当y x 随的增大而增大时，确定点P 横坐标的取值范围（不必写出过程）. 2，看图说故事。

请你编一个故事，使故事情境中出现的一对变量x 、y 满足图示的函数关系式，要求：①指出x 和y 的含义；②利用图中数据说明这对变量变化过程的实际意义，其中需设计“速度”这个量3，如图，矩形OABC 的顶点A 、C 分别在x 、y 轴的正半轴上，点D 为对角线OB 的中点，点E （4，n ）在边AB 上，反比例函数（k ≠0）在第一象限内的图象经过点D 、E ，且tan ∠BOA=．（1）求边AB 的长；（2）求反比例函数的解析式和n 的值；（3）若反比例函数的图象与矩形的边BC 交于点F ，将矩形折叠，使点O 与点F 重合，折痕分别与x 、y 轴正半轴交于点H 、G ，求线段OG 的长．4．如图5，双曲线)0(>=k xky 与⊙O 在第一象限内交于P 、Q 两点，分别过P 、Q 两点向x 轴和y 轴作垂线，已知点P 坐标为(1，3)，则图中阴影部分的面积为．5，如图9，在平面直角坐标系中，直线l ：y =－2x +b (b ≥0)的位置随b 的不同取值而变化． (1)已知⊙M 的圆心坐标为(4，2)，半径为2．当b = 时，直线l ：y =－2x +b (b ≥0)经过圆心M ：当b = 时，直线l ：y = －2x +b (b ≥0)与OM 相切：(2)若把⊙M 换成矩形ABCD ，其三个顶点坐标分别为：A (2，0)、BC 6，O )、C (6，2). 设直线l 扫过矩形ABCD 的面积为S ，当b 由小到大变化时，请求出S 与b 的函数关系式，6，如图，在平面直角坐标系中有Rt △ABC ，∠A ＝90°，AB ＝AC ，A （－2，0）、B （0，1）、C （d ，2）。

一次函数与反比例函数综合题

一次函数与反比例函数综合题类型一反比例函数与一次函数综合1. (2017湘潭)已知反比例函数y ＝kx 的图象过点A (3，1)． (1)求反比例函数的解析式；(2) 若一次函数y ＝ax ＋6(a ≠0)的图象与反比例函数的图象只有一个交点，求一次函数的解析式．2. (2017武汉)如图，直线y ＝2x ＋4与反比例函数y ＝kx 的图象相交于A (－3，a )和B 两点． (1)求k 的值；(2)直线y ＝m (m >0)与直线AB 相交于点M ，与反比例函数y ＝kx 的图象相交于点N .若MN ＝4，求m 的值．第2题图3. (2017泸州二诊)如图，已知A (－4，n )，B (2，－4)是一次函数y ＝kx ＋b 和反比例函数y ＝mx 的图象的两个交点． (1)求一次函数和反比例函数的解析式； (2)求△AOB 的面积；(3)观察图象，直接写出方程kx ＋b －mx ＝0的解．第3题图4. (2017资阳模拟)如图，已知直线y ＝kx 与双曲线y ＝4x (x >0)相交于点A (2，m )，将直线y ＝kx 向下平移2个单位长度后与y 轴相交于点B ，与双曲线交于点C ，连接AB 、AC .第4题图(1)求直线BC 的函数表达式； (2)求△ABC 的面积．类型二反比例函数与几何图形综合5. 如图，已知，A (0，4)，B (－3，0)，C (2，0)，D 为B 点关于AC 的对称点，反比例函数y ＝kx 的图象经过D 点． (1)证明四边形ABCD 为菱形； (2)求此反比例函数的解析式；(3)已知在y ＝kx 的图象(x >0)上有一点N ，y 轴正半轴上有一点M ，且四边形ABMN 是平行四边形，求M 点的坐标．第5题图6. (2017泰安)如图，在平面直角坐标系中，Rt △AOB 的斜边OA 在x轴的正半轴上，∠OBA ＝90°，且tan ∠AOB ＝12，OB ＝25，反比例函数y ＝kx 的图象经过点B . (1)求反比例函数的表达式；(2)若△AMB 与△AOB 关于直线AB 对称，一次函数y ＝mx ＋n 的图象过点M 、A ，求一次函数的表达式．第6题图类型三反比例函数与一次函数、几何图形综合7. 如图，双曲线y ＝kx (x >0)经过△OAB 的顶点A 和OB 的中点C ，AB ∥x 轴，点A 的坐标为(4，6)，连接AC 交x 轴于D ，连接BD . (1)确定k 的值； (2)求直线AC 的解析式；(3)判断四边形OABD 的形状，并说明理由；(4)求△OAC 的面积．第7题图8. (2017绵阳模拟)如图，直线y ＝－x ＋b 与反比例函数y ＝kx 的图象相交于A (1，4)，B 两点，延长AO 交反比例函数图象于点C ，连接OB .(1)求k 和b 的值；(2)直接写出一次函数值小于反比例函数值的自变量x 的取值范围； (3)在y 轴上是否存在一点P ，使S △PAC ＝25S △AOB ？若存在，请求出点P 坐标；若不存在，请说明理由．第8题图答案1. 解：(1)将点A (3，1)代入反比例函数解析式中，得1＝k 3， ∴k ＝3，∴反比例函数的解析式为y ＝3x ； (2)对于一次函数y ＝ax ＋6(a ≠0)，联立两解析式得⎩⎨⎧y ＝3x y ＝ax ＋6，消去y 得3x ＝ax ＋6，去分母得ax 2＋6x －3＝0 ①，∵一次函数与反比例函数图象只有一个交点， ∴①式中Δ＝62－4a ×(－3)＝0，解得a ＝－3≠0，∴一次函数解析式为y ＝－3x ＋6.2. 解：(1) ∵直线y ＝2x ＋4与反比例函数y ＝kx 的图象相交于A (－3，a )，∴a ＝2×(－3)＋4＝－2， ∴点A 坐标为(－3，－2)， k ＝xy ＝(－3)×(－2)＝6； (2) ∵M 在直线y ＝2x ＋4上， ∴设M (m －42，m )，∵N 在反比例函数y ＝6x 上， ∴设N (6m ，m )，∴MN ＝x M －x N ＝m －42－6m ＝4或MN ＝x N －x M ＝6m －m －42＝4， ∵m ＞0，∴解得m ＝6＋43或m ＝2.3. 解：(1)∵点B (2，－4)在函数y ＝mx 的图象上， ∴m ＝－8，∴反比例函数的解析式为y ＝－8x ；又∵点A (－4，n )在函数y ＝－8x 的图象上， ∴n ＝2， ∴A (－4，2)，∵y ＝kx ＋b 经过A (－4，2)，B (2，－4)两点，∴⎩⎪⎨⎪⎧－4k ＋b ＝22k ＋b ＝－4，解得⎩⎪⎨⎪⎧k ＝－1b ＝－2，∴一次函数的解析式为y ＝－x －2； (2)如解图，设直线AB 与x 轴交于点C ，第3题解图当y ＝0时，x ＝－2， ∴点C (－2，0)，即OC ＝2，∴S △AOB ＝S △ACO ＋S △BCO ＝12×2×2＋12×2×4＝6； (3)方程kx ＋b －mx ＝0的解为x 1＝－4，x 2＝2. 4. 解：(1)∵点A (2，m )在y ＝4x 的图象上， ∴m ＝2，A 点坐标为(2，2)， ∵点A 在y ＝kx 上， ∴k ＝1，∴直线BC 的解析式为y ＝x －2；(2)如解图，过点A 作AD ∥y 轴交BC 于点D ，第4题解图把x ＝2代入y ＝x －2中得，y ＝0， ∴D (2，0)， ∴AD ＝2，∵点C 为直线BC 与反比例函数的交点，∴⎩⎨⎧y ＝4x y ＝x －2，解得x ＝1±5， ∴C (1＋5，5－1)，∴S △ABC ＝S △ABD ＋S △ACD ＝12×2×2＋12×2×(1＋5－2)＝1＋ 5. 5. (1)证明：∵A (0，4)，B (－3，0)，C (2，0)， ∴OA ＝4，OB ＝3，OC ＝2， ∴AB ＝OA 2＋OB 2＝5，BC ＝5， ∴AB ＝BC ，∵D 为B 点关于AC 的对称点， ∴AB ＝AD ，CB ＝CD ， ∴AB ＝AD ＝CD ＝CB ， ∴四边形ABCD 为菱形； (2)解：∵四边形ABCD 为菱形， ∴D 点的坐标为(5，4)，∵反比例函数y ＝kx 的图象经过D 点， ∴4＝k 5， ∴k ＝20，∴反比例函数的解析式为y ＝20x ； (3)解：∵四边形ABMN 是平行四边形， ∴AN ∥BM ，AN ＝BM ，∴AN 是BM 经过平移得到的， ∴首先BM 向右平移了3个单位长度， ∴N 点的横坐标为3，代入y ＝20x ，得y ＝203， ∴M 点的纵坐标为203－4＝83， ∴M 点的坐标为(0，83)．6. 解：(1)如解图，过点B 作BD ⊥OA ，垂足为点D ，设BD ＝a ， ∵tan ∠AOB ＝BD OD ＝12， ∴OD ＝2BD ＝2a ，∵∠ODB ＝90°，OB ＝25， ∴a 2＋(2a )2＝(25)2，解得a ＝±2(－2舍去)， ∴a ＝2，∴BD ＝2，OD ＝4， ∴B (4，2)，∵反比例函数y ＝kx 的图象经过点B ， ∴k ＝4×2＝8，∴反比例函数表达式为y ＝8x ；第6题解图(2)∵tan ∠AOB ＝12，∴AB ＝12OB ＝5，∴OA ＝OB 2＋AB 2＝（25）2＋（5）2＝5，∴点A 的坐标为(5，0)，又∵OM ＝2OB ，B (4，2)，∴M(8，4)，把点M 、A 的坐标代入y ＝mx ＋n 中得：⎩⎪⎨⎪⎧0＝5m ＋n 4＝8m ＋n，解得m ＝43，n ＝－203， ∴一次函数的表达式为y ＝43x －203.7. 解：(1)将A (4，6)代入解析式y ＝k x 得：k ＝24；(2)∵AB ∥x 轴，B 的纵坐标是6，C 为OB 中点，∴把y ＝3代入反比例函数解析式y ＝24x 得x ＝8，即C 点坐标为(8，3)，设直线AC 的解析式为y ＝kx ＋b (k ≠0)，将A (4，6)，C (8，3)代入得⎩⎪⎨⎪⎧4k ＋b ＝68k ＋b ＝3，解得⎩⎨⎧k ＝－34b ＝9，∴直线AC 的解析式为y ＝－34x ＋9；(3)四边形OABD 为平行四边形．理由如下：∵点C 的坐标为(8，3)，点A 的坐标为(4，6)，∴点B 的坐标为(16，6)，∴AB ＝16－4＝12，把y ＝0代入y ＝－34x ＋9中得：x ＝12，即D (12，0)，∴OD ＝12，∴AB ＝OD ，又∵AB ∥OD ，∴四边形OABD 为平行四边形；(4)S ▱OABD ＝12×6＝72，根据平行四边形的性质可知，S △OAC ＝14S ▱OABD ＝18.8. 解：(1)将A (1，4)分别代入y ＝－x ＋b 和y ＝k x 得：4＝－1＋b ，4＝k 1，解得：b ＝5，k ＝4；(2)x >4或x <0<1；【解法提示】联立两解析式⎩⎨⎧y ＝－x ＋5y ＝4x，解得⎩⎪⎨⎪⎧x 1＝1y 1＝4，⎩⎪⎨⎪⎧x 2＝4y 2＝1， ∴B 点坐标为(4，1)，∴一次函数值小于反比例函数值的自变量x 的取值范围为x ＞4或0＜x ＜1；第8题解图(3)存在．理由如下：如解图，过点A 作AN ⊥x 轴于点N ，过点B 作BM ⊥x 轴于点M ，由(2)知，B 点坐标为(4，1)，∴S △AOB ＝S 四边形ANMB ＝12(AN ＋BM )×MN ＝12×(4＋1)×3＝152，∵S △P AC ＝25S △AOB ，∴S △P AC ＝25×152＝3，如解图，过点A 作AE ⊥y 轴于点E ，过点C 作CD ⊥y 轴于点D ，设P (0，t )，∴S△PAC＝12OP·CD＋12OP·AE＝12OP·(CD＋AE)＝12|t|×2＝|t|＝3，解得：t＝3或－3，∴P(0，3)或(0，－3)．。

中考一次函数与反比例函数[含答案]

反比例函数与一次函数综合题针对演练1. 已知正比例函数y ＝2x 的图象与反比例函数y ＝k x(k ≠0)在第一象限内的图象交于点A ，过点A 作x 轴的垂线，垂足为点P ，已知△OAP 的面积为1. (1)求反比例函数的解析式；(2)有一点B 的横坐标为2，且在反比例函数图象上，则在x 轴上是否存在一点M ，使得MA ＋MB 最小若存在，请求出点M 的坐标；若不存在，请说明理由．第1题图2. 如图，反比例函数2y x=的图象与一次函数y ＝kx ＋b 的图象交于点A 、B ，点A 、B 的横坐标分别为1、－2，一次函数图象与y 轴交于点C ，与x 轴交于点D . (1)求一次函数的解析式；(2)对于反比例函数2y x=，当y ＜－1时，写出x 的取值范围；(3)在第三象限的反比例函数图象上是否存在一点P，使得S△ODP＝2S△OCA若存在，请求出点P的坐标；若不存在，请说明理由．第2题图3. 已知，如图，一次函数y＝kx＋b(k、b为常数，k≠0)的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝nx(n为常数且n≠0)的图象在第二象限交于点⊥x轴，垂足为D.若OB＝2OA＝3OD＝6.(1)求一次函数与反比例函数的解析式；(2)求两函数图象的另一个交点坐标；(3)直接写出不等式：kx＋b≤nx的解集．4. 如图，点A (－2，n )，B(1，－2)是一次函数y ＝kx ＋b 的图象和反比例函数y＝mx的图象的两个交点． (1)求反比例函数和一次函数的解析式；(2)根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围；(3)若C 是x 轴上一动点，设t ＝CB －CA ，求t 的最大值，并求出此时点C 的坐标．第4题图5. 如图，直线y 1＝14x ＋1与x 轴交于点A ，与y 轴交于点C ，与反比例函数y 2＝m x (x >0)的图象交于点P ，过点P 作PB ⊥x 轴于点B ，且AC ＝BC . (1)求点P 的坐标和反比例函数y 2的解析式； (2)请直接写出y 1>y 2时，x 的取值范围；(3)反比例函数y 2图象上是否存在点D ，使四边形BCPD 为菱形如果存在，求出点D 的坐标；如果不存在，说明理由．第5题图6. 如图，直线y＝x＋b与x轴交于点C(4，0)，与y轴交于点B，并与双曲线y＝mx(x＜0)交于点A(－1，n)．(1)求直线与双曲线的解析式；(2)连接OA，求∠OAB的正弦值；(3)若点D在x轴的正半轴上，是否存在以点D、C、B构成的三角形△OAB相似若存在求出D点的坐标，若不存在，请说明理由．第6题图7. 如图，直线y＝33x－3与x，y轴分别交于点A，B，与反比例函数y＝kx(k＞0)图象交于点C，D，过点A作x轴的垂线交该反比例函数图象于点E.(1)求点A的坐标；(2)若AE＝AC.①求k的值；②试判断点E与点D是否关于原点O成中心对称并说明理由．第7题图8. 如图，已知双曲线y＝kx经过点D(6，1)，点C是双曲线第三象限上的动点，过点C作CA⊥x轴，过点D作DB⊥y轴，垂足分别为A，B，连接AB，BC.(1)求k的值；(2)若△BCD的面积为12，求直线CD的解析式；(3)判断AB与CD的位置关系，并说明理由．第8题图9. 如图，点B 为双曲线y ＝kx(x ＞0)上一点，直线AB 平行于y 轴，交直线y ＝x于点A ，交x 轴于点D ，双曲线y ＝k x与直线y ＝x 交于点C ，若OB 2－AB 2＝4.(1)求k 的值；(2)点B 的横坐标为4时，求△ABC 的面积；(3)双曲线上是否存在点P ，使△APC ∽△AOD 若存在，求出点P 的坐标；若不存在，请说明理由．第9题图答案1．解：(1)设A点的坐标为(x，y)，则OP＝x，PA＝y，∵△OAP的面积为1，∴12xy＝1，∴xy＝2，即k＝2，∴反比例函数的解析式为2yx；(2)存在，如解图，作点A关于x轴的对称点A′，连接A′B，交x轴于点M，此时MA＋MB最小，∵点B的横坐标为2，∴点B的纵坐标为y＝22＝1，即点B的坐标为（2,1）.又∵两个函数图象在第一象限交于A点，∴2 2xx=，解得x1＝1，x2＝－1(舍去)．∴y＝2，∴点A的坐标为(1，2)，∴点A关于x轴的对称点A′(1，－2)，设直线A′B的解析式为y＝kx＋b，代入A′(1，－2)，B(2，1)得，23,215k b kk b b+=-=⎧⎧⎨⎨+==-⎩⎩解得，∴直线A′B的解析式为y＝3x－5，令y＝0，得x＝53，∴直线y＝3x－5与x轴的交点为(53，0)，即点M的坐标为(53，0)．第1题解图2．解：(1)∵反比例函数y＝2x图象上的点A、B的横坐标分别为1、－2，∴点A的坐标为(1，2)，点B的坐标为(－2，－1)，∵点A (1，2)、B (－2，－1)在一次函数y ＝kx ＋b 的图象上，∴21,211k b k k b b +==⎧⎧⎨⎨-+=-=⎩⎩解得，∴一次函数的解析式为y ＝x ＋1；(2)由图象知，对于反比例函数2y x=，当y ＜－1时，x 的取值范围是－2＜x＜0；(3)存在．对于y ＝x ＋1，当y ＝0时，x ＝－1，当x ＝0时，y ＝1， ∴点D 的坐标为(－1，0)，点C 的坐标为(0，1)，设点P (m ，n )，∵S △ODP ＝2S △OCA ，∴12×1×(－n )＝2×12×1×1，∴n ＝－2，∵点P (m ，－2)在反比例函数图象上，∴－2＝ 2m， ∴m ＝－1，∴点P 的坐标为(－1，－2)． 3．解：(1)∵OB ＝2OA ＝3OD ＝6， ∴OA ＝3，OD ＝2.∴A (3，0)，B (0，6)，D (－2，0)．将点A (3，0)和B (0，6)代入y ＝kx ＋b 得，302,66k b k b b +==-⎧⎧⎨⎨==⎩⎩解得， ∴一次函数的解析式为y ＝－2x ＋6. ……………………(3分) 将x ＝－2代入y ＝－2x ＋6，得y ＝－2×(－2)＋6＝10， ∴点C 的坐标为(－2，10)．将点C (－2，10)代入y ＝nx ，得10＝2n -，解得n ＝－20，∴反比例函数的解析式为20y x=-；………………………(5分) (2)将两个函数解析式组成方程组，得26,20y x y x =-+⎧⎪⎨=-⎪⎩解得x 1＝－2，x 2＝5. ………………………………………(7分)将x ＝5代入204,y x=-=- ∴两函数图象的另一个交点坐标是(5，－4)； …………… (8分) (3)－2≤x＜0或x≥5. …………………………………… (10分)【解法提示】不等式kx ＋b ≤nx的解集，即是直线位于双曲线下方的部分所对应的自变量x 的取值范围，也就是－2≤x ＜0或x ≥5.4．解：(1)∵点A (－2，n )，B (1，－2)是一次函数y ＝kx ＋b 的图象和反比例函数y ＝mx的图象的两个交点，∴m ＝－2，∴反比例函数解析式为2y x=-，∴n ＝1，∴点A (－2，1)，将点A (－2，1)，B (1，－2)代入y ＝kx ＋b ，得211,21k b k k b b -+==-⎧⎧⎨⎨+=-=-⎩⎩解得， ∴一次函数的解析式为y ＝－x －1；(2)结合图象知：当－2＜x ＜0或x ＞1时，一次函数的值小于反比例函数的值；(3)如解图，作点A 关于x 轴的对称点A ′，连接BA ′延长交x 轴于点C ，则点C 即为所求，∵A (－2，1)， ∴A ′(－2，－1)，设直线A ′B 的解析式为y ＝mx ＋n ，1123,253m m n m n n ⎧=-⎪-=-+⎧⎪⎨⎨-=+⎩⎪=-⎪⎩解得， ∴y ＝－13x －53，令y＝0，得x＝－5，则C点坐标为(－5，0)，∴t的最大值为A′B＝（－2－1）2＋（－1＋2）2＝10.第4题解图5．解：(1)∵一次函数y1＝14x＋1的图象与x轴交于点A，与y轴交于点C，∴A(－4，0)，C(0，1)，又∵AC＝BC，CO⊥AB，∴O为AB的中点，即OA＝OB＝4，且BP＝2OC＝2，∴点P的坐标为(4，2)，将点P(4，2)代入y2＝mx，得m＝8，∴反比例函数的解析式为y2＝8 x；(2)x>4；【解法提示】由图象可知，当y1＞y2时，即是直线位于双曲线上方的部分，所对应的自变量x的取值范围是x＞4.(3)存在．假设存在这样的D点，使四边形BCPD为菱形，如解图，连接DC 与PB交于点E，∵四边形BCPD为菱形，∴CE＝DE＝4，∴CD＝8，∴D点的坐标为(8，1)，将D(8，1)代入反比例函数8yx=，D点坐标满足函数关系式，即反比例函数图象上存在点D，使四边形BCPD为菱形，此时D点坐标为(8，1)．第5题解图6．解：(1)∵直线y＝x＋b与x轴交于点C(4，0)，∴把点C(4，0)代入y＝x＋b，得b＝－4，∴直线的解析式为y＝x－4，∵直线也过A点，∴把点A(－1，n)代入y＝x－4，得n＝－5，∴A(－1，－5)，将A(－1，－5)代入y＝mx(x＜0)，得m＝5，∴双曲线的解析式为5yx=；(2)如解图，过点O作OM⊥AC于点M，∵点B是直线y＝x－4与y轴的交点，∴令x＝0，得y＝－4，∴点B(0，－4)，∴OC＝OB＝4，∴△OCB是等腰直角三角形，∴∠OBC＝∠OCB＝45°，∴在△OMB中，sin45°＝OMOB＝4OM，∴OM＝22，∵AO＝12＋52＝26，∴在△AOM中，sin∠OAB＝OMOA＝2226＝21313；第6题解图(3)存在．如解图，过点A作AN⊥y轴于点N，则AN＝1，BN＝1，∴AB＝12＋12＝2，∵OB＝OC＝4，∴BC＝42＋42＝42，又∵∠OBC＝∠OCB＝45°，∴∠OBA＝∠BCD＝135°，∴△OBA∽△BCD或△OBA∽△DCB，∴OBBC＝BACD或OBDC＝BABC，即442＝2CD或4DC＝242，∴CD＝2或CD＝16，∵点C(4，0)，∴点D的坐标是(6，0)或(20，0)．7．解：(1)当y ＝0时，得0＝33x －3，解得x ＝3.∴点A 的坐标为(3，0)； ……………………………………(2分) (2)①如解图，过点C 作CF ⊥x 轴于点F . 设AE ＝AC ＝t , 点E 的坐标是(3，t ).在Rt △AOB 中， tan ∠OAB ＝OB OA ＝33，∴∠OAB ＝30°.在Rt △ACF 中，∠CAF ＝30°，∴CF ＝12t ，AF ＝AC ·cos30°＝32t ，∴点C 的坐标是(3＋32t ，12t )．∵点C 、E 在y ＝kx 的图象上，∴(3＋32t )×12t ＝3t ，解得t 1＝0(舍去)，t 2＝23，∴k ＝3t ＝63； …………………………………………… (5分) ②点E 与点D 关于原点O 成中心对称，理由如下：由①知，点E 的坐标为(3，23)，设点D 的坐标是(x ，33x －3)，∴x (33x －3)＝63，解得x 1＝6(舍去)，x 2＝－3， ∴点D 的坐标是(－3，－23)，∴点E 与点D 关于原点O 成中心对称．…………………(8分)第7题解图8．解：(1)∵双曲线y ＝kx 经过点D (6，1)，∴6k ＝1，解得k ＝6；(2)设点C 到BD 的距离为h ，∵点D 的坐标为(6，1)，DB ⊥y 轴， ∴BD ＝6，∴S △BCD ＝12×6×h ＝12，解得h ＝4，∵点C 是双曲线第三象限上的动点，点D 的纵坐标为1，∴点C 的纵坐标为1－4＝－3，∴6x＝－3，解得x ＝－2，∴点C 的坐标为(－2，－3)，设直线CD 的解析式为y ＝kx ＋b ，则123,2612k b k k b b ⎧-+=-=⎧⎪⎨⎨+=⎩⎪=-⎩解得，∴直线CD 的解析式为y ＝12x －2； (3)AB ∥CD .理由如下：∵CA ⊥x 轴，DB ⊥y 轴，点D 的坐标为(6，1)，设点C 的坐标为(c ，6c)，∴点A 、B 的坐标分别为A (c ，0)，B (0，1)，设直线AB 的解析式为y ＝mx ＋n ，则10,11mc n m c n n ⎧+==-⎧⎪⎨⎨=⎩⎪=⎩解得，∴直线AB 的解析式为y ＝－1x c＋1，设直线CD 的解析式为y ＝ex ＋f ，则16,661e ec f cc c e f f c ⎧=-⎧⎪+=⎪⎪⎨⎨+⎪⎪+==⎩⎪⎩解得， ∴直线CD 的解析式为y ＝－1x c ＋6c c +，∵AB 、CD 的解析式中k 都等于1c-，∴AB 与CD 的位置关系是AB ∥CD . 9．解：(1)设D 点坐标为(a ，0)，∵AB ∥y 轴，点A 在直线y ＝x 上，B 为双曲线y ＝kx(x ＞0)上一点，∴A 点坐标为(a ，a )，B 点坐标为(a ，k a)，∴AB ＝a －k a ，BD ＝k a ，在Rt △OBD 中，OB 2＝BD 2＋OD 2＝(k a)2＋a 2，∵OB 2－AB 2＝4，∴(k a )2＋a 2－(a －k a)2＝4，∴k ＝2；(2)如解图，过点C 作CM ⊥AB 于点M ，,2y xy x =⎧⎪⎨=⎪⎩联立2222x x y y ⎧⎧==⎪⎪⎨⎨==⎪⎪⎩⎩解得（舍去），∴C 点坐标为(2，2)，第9题解图∵点B 的横坐标为4，∴A 点坐标为(4，4)，B 点坐标为(4，12)，∴AB ＝4－12＝72，CM ＝4－2，∴S △ABC ＝12CM ·AB ＝12×(4－2)×72 ＝7－724；(3)不存在，理由如下：若△APC ∽△AOD ，∵△AOD 为等腰直角三角形，∴△APC 为等腰直角三角形，∠ACP ＝90°，∴CM ＝12AP ，设P 点坐标为(a ，2a )，则A 点坐标为(a ，a )，∴AP ＝|a －2a|，∵C 点坐标为(2，2)，∴CM ＝|a －2|，∴|a －2|＝12|a －2a|，∴(a －2)2＝14×222(2)a a -，即(a －2)2＝14×222((a a a +⨯-，∴4a 2－(a ＋2)2＝0，解得a ＝2或a ＝－23(舍去)，∴P 点坐标为(2，2)，则此时点C 与点P 重合，所以不能构成三角形，故不存在．。

【人教版】2017年中考数学：题型4反比例函数与一次函数综合题含答案

题型四反比率函数与一次函数综合题
针对操练
m
1. 如图，一次函数 y＝kx＋1(k≠0)与反比率函数 y＝x(m≠0)的图象有公共点A(1，
2)，直线 l ⊥x 轴于点 N(3，0)，与一次函数和反比率函数的图象分别订交于点B，C，连结 AC.
(1)求 k 和 m 的值；
(2)求点 B 的坐标；
(3)求△ ABC 的面积．
第1题图
k
2.已知正比率函数 y＝2x 的图象与反比率函数 y＝x(k≠0)在第一象限内的图象交
于点 A，过点 A 作 x 轴的垂线，垂足为点P，已知△ OAP 的面积为 1.
(1)求反比率函数的分析式；
(2)有一点 B 的横坐标为 2，且在反比率函数图象上，则在x 轴上能否存在一点M，使得 MA ＋MB 最小？若存在，恳求出点M 的坐标；若不存在，请说明原因．
第2题图
3. 如图，反比率函数y 2
的图象与一次函数 y＝kx＋b 的图象交于点 A、B，点 A、x
B 的横坐标分别为1、－ 2，一次函数图象与 y 轴交于点 C，与 x 轴交于点 D.
(1) 求一次函数的分析式；
(2) 关于反比率函数y 2
，当 y＜－ 1 时，写出 x 的取值范围；
x
(3)在第三象限的反比率函数图象上能否存在一点P，使得 S△ODP＝2S△OCA？若存在，恳求出点P 的坐标；若不存在，请说明原因．
第 3题图。

综合题：一次函数二次函数反比例函数中考综合题复习

第一部分：一次函数考点归纳：一次函数：若y=kx+b(k,b 是常数，k ≠0)，那么y 叫做x 的一次函数，特别的，当b=0时，一次函数就成为y=kx(k 是常数，k ≠0)，这时，y 叫做x 的正比例函数，当k=0时，一次函数就成为若y=b ，这时，y 叫做常函数。

☆A 与B 成正比例 A=kB(k ≠0)直线位置与k ，b 的关系：（1）k ＞0直线向上的方向与x 轴的正方向所形成的夹角为锐角；（2）k ＜0直线向上的方向与x 轴的正方向所形成的夹角为钝角；（3）b ＞0直线与y 轴交点在x 轴的上方；（4）b ＝0直线过原点；（5）b ＜0直线与y 轴交点在x 轴的下方；平移1，直线x y 31=向上平移1个单位，再向右平移1个单位得到直线。

2，直线143+-=x y 向下平移2个单位，再向左平移1个单位得到直线________方法：直线y=kx+b ，平移不改变斜率k ，则将平移后的点代入解析式求出b 即可。

直线y=kx+b 向左平移2向上平移3 <=> y=k(x+2)+b+3;（“左加右减，上加下减”）。

练习：直线m:y=2x+2是直线n 向右平移2个单位再向下平移5个单位得到的，而（2a,7）在直线n 上，则a=____________；函数图形的性质例题：1．下列函数中，y 是x 的正比例函数的是（）A．y=2x-1 B．y=3xC．y=2x2 D．y=-2x+12，一次函数y=-5x+3的图象经过的象限是（）A．一、二、三 B．二、三、四C．一、二、四 D．一、三、四3，若函数y=（2m+1）x2+（1-2m）x（m为常数）是正比例函数，则m的值为（）A．m>12B．m=12C．m<12D．m=-124、直线y kx b=+经过一、二、四象限，则直线y bx k=-的图象只能是图4中的（）5，若一次函数y=（3-k）x-k的图象经过第二、三、四象限，则k的取值范围是（）A．k>3 B．0<k≤3 C．0≤k<3 D．0<k<36，已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（）A．y=-x-2 B．y=-x-6 C．y=-x+10 D．y=-x-17，已知关于x的一次函数27y mx m=+-在15x-≤≤上的函数值总是正数，则m的取值范围是（）A．7m>B．1m>C．17m≤≤D．都不对8、如图，两直线1y kx b=+和2y bx k=+在同一坐标系内图象的位置可能是（）9，一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（）xyo xyoxyoxyoA B C D10，,已知一次函数（1）当m 取何值时，y 随x 的增大而减小？（2）当m 取何值时，函数的图象过原点？函数解析式的求法：正比例函数设解析式为： ,一个点的坐标带入求k. 一次函数设解析式为：；两点带入求k,b1，已知一个正比例函数与一个一次函数的图象交于点A （3,4），且OA=OB（1）求两个函数的解析式；（2）求△AOB 的面积；第二部分：二次函数（待讲）课前小测：1，抛物线3)2x (y 2-+=的对称轴是（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第 10 题图
文案大全
标准实用
【答案】
1．解： (1) ∵点 A(1 ，2) 是一次函数 y＝kx＋1 与反比例函数 y
m ＝ x的公共点，
m ∴ k＋1＝ 2， 1 ＝2，∴ k＝1，m＝2； (2) ∵直线 l ⊥x 轴于点 N(3 ，0) ，且与一次函数的图象交于点 B，
∴点 B的横坐标为 3，
将 x＝3 代入 y＝x＋1，得；
(3) 如解图，过点 A 作 AD⊥直线 l ，垂足为点 D，
由题意得，点 C的横坐标为 3，
∵点 C在反比例函数图象上，
22
2
∴ y＝ x ＝3， ∴ C点坐标为 (3 ，3) ，
2 10 ∴ BC＝BN－CN＝4－3＝ 3 ，
第 7 题图
文案大全
标准实用
3 8. (2016 金华 8 分) 如图，直线 y＝ 3 x－ 3与 x，y 轴分别交于点 A，
k B，与反比例函数 y＝x( k＞0) 图象交于点 C，D，过点 A 作 x 轴的垂线交该反比例函数图象于点 E. (1) 求点 A 的坐标； (2) 若 AE＝AC.
第 1 题图
文案大全
标准实用
k 2. 已知正比例函数 y＝2x 的图象与反比例函数 y＝x( k≠0) 在第一象限内的图象交于点 A，过点 A 作 x 轴的垂线，垂足为点 P，已知△ OAP 的面积为 1. (1) 求反比例函数的解析式； (2) 有一点 B 的横坐标为 2，且在反比例函数图象上，则在 x 轴上是否存在一点 M，使得 MA＋MB最小？若存在，请求出点 M的坐标；若不存在，请说明理由．
(3) 在第三象限的反比例函数图象上是否存在一点 P，使得 S ＝ △ODP
2S△OCA？若存在，请求出点 P 的坐标；若不存在，请说明理由．
第 3 题图
文案大全
标准实用
4. (2016 巴中 10 分 ) 已知，如图，一次函数 y＝kx＋b( k、b 为常数， n
k≠0) 的图象与 x 轴、y 轴分别交于 A、B 两点，且与反比例函数 y＝x ( n 为常数且 n≠0) 的图象在第二象限交于点 C. CD⊥x 轴，垂足为 D. 若 OB＝2OA＝3OD＝6. (1) 求一次函数与反比例函数的解析式； (2) 求两函数图象的另一个交点坐标；
第 5 题图
文案大全
标准实用
1 6. 如图，直线 y1＝4x＋1 与 x 轴交于点 A，与 y 轴交于点 C，与反比
m 例函数 y2＝x( x>0) 的图象交于点 P，过点 P作 PB⊥x 轴于点 B，且 AC ＝ BC. (1) 求点 P 的坐标和反比例函数 y2 的解析式； (2) 请直接写出 y1>y2 时， x 的取值范围； (3) 反比例函数 y2 图象上是否存在点 D，使四边形 BCPD为菱形？如果存在，求出点 D的坐标；如果不存在，说明理由．
第 2 题图
文案大全
标准实用
2
3. 如图，反比例函数 y 的图象与一次函数 y＝kx＋b 的图象交于
x
点 A、B，点 A、B 的横坐标分别为 1、－2，一次函数图象与 y 轴交于
点 C，与 x 轴交于点 D.
(1) 求一次函数的解析式；
(2) 对于反比例函数 y
2
x ，当 y＜－ 1 时，写出 x 的取值范围；
第 6 题图
文案大全
标准实用
7. 如图，直线 y＝x＋b 与 x 轴交于点 C(4，0) ，与 y 轴交于点 B，并 m
与双曲线 y＝x( x＜0) 交于点 A( －1，n) ． (1) 求直线与双曲线的解析式； (2) 连接 OA，求∠ OAB的正弦值； (3) 若点 D在 x 轴的正半轴上，是否存在以点 D、C、B 构成的三角形 △OAB相似？若存在求出 D点的坐标，若不存在，请说明理由．
n (3) 直接写出不等式： kx＋b≤x的解集．
第 4 题图
文案大全
标准实用
5. 如图，点 A( －2，n) ，B(1，－ 2) 是一次函数 y＝kx＋b 的图象和 m
反比例函数 y＝x的图象的两个交点． (1) 求反比例函数和一次函数的解析式； (2) 根据图象写出使一次函数的值小于反比例函数的值的 x 的取值范围； (3) 若 C是 x 轴上一动点，设 t ＝CB－CA，求 t 的最大值，并求出此时点 C的坐标．
又∵ AD＝ 3－1＝2，
1
1 10
10
∴ S△ ＝ ABC 2BC· AD＝ 2× 3 ×2＝ 3 .
文案大全
第 1 题解图
标准实用
2．解： (1) 设 A 点的坐标为 ( x，y) ，则 OP＝x，PA＝y，
∵△ OAP的面积为 1，
1 ∴ 2xy＝1，
∴ xy＝2，即 k＝2，
标准实用
题型四反比例函数与一次函数综合题针对演练
m 1. 如图，一次函数 y＝kx＋1( k≠0) 与反比例函数 y＝x( m≠ 0) 的图象有公共点 A(1 ，2) ，直线 l ⊥x 轴于点 N(3 ，0) ，与一次函数和反比例函数的图象分别相交于点 B，C，连接 AC. (1) 求 k 和 m的值； (2) 求点 B 的坐标； (3) 求△ ABC的面积．
第 9 题图
文案大全
标准实用
k 10. 如图，点 B 为双曲线 y＝x( x＞0) 上一点，直线 AB平行于 y 轴，
k 交直线 y＝x 于点 A，交 x 轴于点 D，双曲线 y＝x与直线 y＝x 交于点 C，若 OB2－ AB2＝4. (1) 求 k 的值； (2) 点 B 的横坐标为 4 时，求△ ABC的面积； (3) 双曲线上是否存在点 P，使△ APC∽△ AOD？若存在，求出点 P 的坐标；若不存在，请说明理由．
①求 k 的值； ②试判断点 E 与点 D 是否关于原点 O成中心对称？并说明理由．
第 8 题图
文案大全
标准实用
k 9. 如图，已知双曲线 y＝x经过点 D(6 ，1) ，点 C 是双曲线第三象限上的动点，过点 C作 CA⊥x 轴，过点 D作 DB⊥y 轴，垂足分别为 A， B，连接 AB，BC. (1) 求 k 的值； (2) 若△ BCD的面积为 12，求直线 CD的解析式； (3) 判断 AB与 CD的位置关系，并说明理由．