波动光学-2薄膜干涉
光的干涉(第1讲)详解

S
d S2 r
r2
O
d
暗纹中心坐标: d x = (2 k +1) 2d (k=0,1,2,) 0级,1级暗纹 (11-3)
明纹 暗纹
d x = k d P ( k =0,1,2, ) d x = (2 k +1) 2d B r1 S
复色光: 具有多个波长(频率)的光。: 1~2
激光的单色性最好! 如何获得单色光?
E S
2.光的干涉条件
频率相同;E 的振动方向相同; 相差恒定。
普通光源发出的光一般不能满足干涉条件。
3. 获得相干光的方法 对实验仪器的要求: ① 两束相干光取自同一波列:“一分为二”
② 光波的波程差小于波列长度。
理论:(1) 牛顿的微粒说: 光是按照惯性定律沿直线飞行的微粒流。
u水 u空气
(2)惠更斯的波动说: u水 光是在特殊媒质“以太”中传播的机械波。 此间微粒说占据统治地位。
u空气
三.波动光学时期 (19世纪)
实验: 光的干涉(杨-英) 光的衍射(费涅耳-法)。 此间波动 理论: 麦克斯韦建立电磁场理论,指出光也是电磁波。说占主导 地位。 赫兹证实电磁波的存在;并测出光速。 确定光不是机械波 四.量子光学时期(19世纪后期——20世纪初) 普朗克提出能量量子化假说 爱因斯坦提出光量子假说 认为: 光是以光速运动的粒子流。 光到底是什麽? , 光也是物质的一种 它既具有波的性质、也具有粒子的性质。 它既非波、也非粒子、更不是两者的混合物。它就是它自己!
电磁波动说在解释“热幅射”及“光电效应”等实验时遇到困难。
在某些条件下,波动性表现突出,在另一些条件下,粒子性
波动光学-2薄膜干涉资料
单 色
S1 *
光 S2 *
源 S3 *
e
屏 透镜
n1
薄膜 n2 n2 > n1
n1
单 色
S1 *
光 S2 *
源 S3 *
e
屏 透镜
n1
薄膜 n2 n2 > n1
n1
单 色
S1 *
光 S2 *
源 S3 *
e
屏 透镜
n1
薄膜 n2 n2 > n1
n1
单 色
S1 *
光 S2 *
源 S3 *
e
屏 透镜
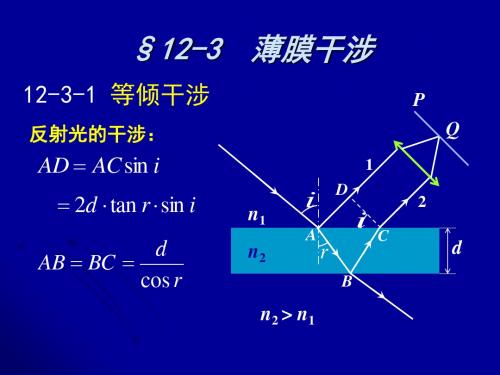
§12-3
12-3-1 等倾干涉
反射光的干涉:
AD AC sin i 2d tan r sin i
AB BC d cos r
薄膜干涉
P Q
1
iD
2
n1
i
A
C
n2
r
d
B
n2 > n1
光程差:
P
n2(AB BC) n1AD
Q
1
2d n2 cos r
2d
tan
d o
4n
增透膜
12-3-2 等厚干涉
一. 劈尖(劈形膜)
夹角很小的两个平面所构成的薄膜
:104 ~ 105 rad
S· 反射光2
单色平行光
n
2 1
·
反射光1 1、2两束反射光来自同一束入
n A e 射光,它们可以产生干涉 。
n(设n > n )
实际应用中,大都是平行光垂直入射到劈尖上。 考虑到劈尖夹角极小, 反射光1、 2在膜面的 光程差可简化为图示情况计算。
大学物理薄膜干涉

大学物理薄膜干涉薄膜干涉是光学干涉的一种常见形式,它涉及到两个或多个薄膜层的反射和透射光的相互叠加。
薄膜干涉现象的复杂性使得其在实际应用中具有广泛的应用,例如在光学仪器、光学通信和生物医学领域。
本文将介绍大学物理中薄膜干涉的基本原理及其应用。
一、薄膜干涉的基本原理1、光的干涉现象光的干涉是指两个或多个波源发出的光波在空间中叠加时,产生明暗相间的条纹的现象。
干涉现象的产生需要满足以下条件:(1)光波的波长和传播方向必须相同;(2)光波的相位差必须恒定;(3)光波的振幅必须相等。
2、薄膜干涉的形成薄膜干涉是指光在两个或多个薄膜层之间反射和透射时产生的干涉现象。
当光线照射到薄膜上时,一部分光线会被反射回来,一部分光线会穿透薄膜继续传播。
由于薄膜的厚度通常很薄,所以光的反射和透射都会受到薄膜的影响。
当多个反射和透射的光线相互叠加时,就会形成薄膜干涉现象。
3、薄膜干涉的公式薄膜干涉的公式可以表示为:Δφ = 2πnΔndλ,其中Δφ为光程差,n为薄膜的折射率,Δn为薄膜的厚度变化量,λ为光波的波长。
当光程差满足公式时,就会形成明暗相间的条纹。
二、薄膜干涉的应用1、光学仪器中的应用在光学仪器中,薄膜干涉被广泛应用于表面形貌测量、光学厚度控制和光学表面质量检测等方面。
例如,在表面形貌测量中,可以利用薄膜干涉原理测量表面的粗糙度和高度变化;在光学厚度控制方面,可以利用薄膜干涉原理控制材料的折射率和厚度;在光学表面质量检测方面,可以利用薄膜干涉原理检测表面的缺陷和划痕等。
2、光学通信中的应用在光学通信中,薄膜干涉被广泛应用于光信号的调制和解调等方面。
例如,在光信号的调制方面,可以利用薄膜干涉原理将电信号转换为光信号;在光信号的解调方面,可以利用薄膜干涉原理将光信号转换为电信号。
薄膜干涉还被广泛应用于光学通信中的信号传输和处理等方面。
3、生物医学中的应用在生物医学中,薄膜干涉被广泛应用于生物组织的光学成像和生物分子的检测等方面。
薄膜干涉公式推导 原理

薄膜干涉公式推导原理薄膜干涉是一种光学现象,它是由于光线通过一个非常薄的膜时,由于光线的干涉而产生的颜色变异。
薄膜干涉公式是计算出这种干涉的方法之一,也是理解薄膜干涉的基础。
薄膜由于其极薄的厚度和透明性,可以把光线进行反射、透射和折射,从而引起干涉现象。
当光线经过两个介质的分界面时,会发生反射和折射。
光线与薄膜相交时,会发生多次反射和透射,甚至还会形成多次反射和透射的干涉。
根据薄膜原理,光线从薄膜表面反射后,与透射光线相遇,因而形成干涉,产生波动干涉的现象。
那么薄膜干涉公式如何推导呢?假设一个平行光束入射一块平行的亚克力薄膜,并且从薄膜的两面均反射一次,这个过程中,光束在薄膜内产生波动干涉。
我们可以用傅利叶光学的方法将反射和透射波分解为振幅和相位的函数。
光波在经过全反射时会受到反射系数r的损失,而透射波不受反射系数损失,但是它在传播的过程中会受到相位延迟,因为它必须穿过薄膜两次。
在干涉光学中,我们假设光的相位是连续递增的。
在实际计算过程中,我们往往使用两条光线之间的相位差来计算薄膜干涉的影响。
在理想情况下,这个相位差可以表示为:Δφ = 2π(2d/nλ)(cosθ−cosθi)其中,d是膜的厚度,n是膜的折射率,λ是入射光波长,θ是出射角,θi是入射角。
这个公式展示了光波在薄膜中反射和透射的过程,从而导致干涉的发生。
这个公式可以帮助我们计算薄膜的干涉效果,并进一步使我们理解波动光学的原理和应用。
综上所述,薄膜干涉公式的推导涉及多种基本的光学原理,它解释了光线在薄膜内部反射和透射的过程,由此产生的干涉效果。
这个公式展示了理论和实际操作上的重要性和实用性,对我们理解和应用光学技术有重要指导意义。
薄膜干涉的原理与应用论文

薄膜干涉的原理与应用论文1. 引言薄膜干涉是一种基于光的干涉现象,通过利用光在不同介质中传播时发生的相位差,实现光的干涉与衍射效应。
薄膜干涉在科学研究和工程应用中具有广泛的应用。
本文将介绍薄膜干涉的基本原理及其在光学领域的应用。
2. 薄膜干涉的原理薄膜干涉的原理基于波动光学的理论,下面是薄膜干涉的基本原理:2.1 波长和相位差薄膜干涉的基本原理是光在两个介质界面间传播时产生的相位差。
根据光的波动性质,相位差与波长有关。
2.2 光的反射与透射当光从一种介质进入另一种介质时,一部分光会反射回来,另一部分光会透射到第二种介质中。
薄膜干涉的原理即是基于光的反射与透射。
2.3 干涉条纹的形成当两束光线相遇时,由于相位差的存在,会发生干涉现象。
这种干涉现象在薄膜上形成干涉条纹,可以通过光的波长、入射角度、薄膜的厚度等因素来控制。
3. 薄膜干涉的应用薄膜干涉在科学研究和工程应用中有多种应用,下面是几个典型的应用例子:3.1 反射镀膜薄膜干涉在光学反射镀膜中有重要应用。
通过设计合适的薄膜结构,可以使得特定波长的光得到增强或者完全反射,实现光学器件的性能优化。
3.2 光学滤波器薄膜干涉可以用来制作光学滤波器。
通过设计合适的薄膜结构,可以选择性地透过或者反射特定波长的光,实现光的分离和滤波。
3.3 透明导电膜在电子学领域中,透明导电膜是一种重要的材料。
通过利用薄膜干涉的原理,可以制备具有高透过率和低电阻率的透明导电膜,用于触摸屏、太阳能电池等器件中。
3.4 光学涂层薄膜干涉可以用于制备光学涂层,用于反射、抗反射、增透等应用中。
通过调节薄膜的结构和厚度,可以实现对特定波长光的优化处理。
4. 结论薄膜干涉是一种基于光的干涉现象,通过光在不同介质中传播时产生的相位差,实现光的干涉与衍射效应。
薄膜干涉在光学领域具有广泛的应用,包括反射镀膜、光学滤波器、透明导电膜和光学涂层等。
通过合理设计薄膜结构和厚度,可以实现对光的控制和优化。
大学物理11-4 薄膜干涉(2)汇总

例 11-8 干涉膨胀仪如图所示,
干涉膨胀仪
一个石英圆柱环B放在平台上,
其热膨胀系数极小,可忽略不计。l
环上放一块平破璃板P,并在环
内放置一上表面磨成稍微倾斜的 柱形待测样品R,石英环和样品
l0
B
的上端面已事先精确磨平,于是
R的上表面与P的下表面之间形
成楔形空气膜,用波长为 的
单色光垂直照明,即可在垂直方 向上看到彼此平行等距的等厚条
dk
2n
n
2
b
n1 n
sin n 2
b
3)条纹间距(明纹或暗纹)
b 2n
tan D L
D n L L
2b 2nb
L
n n / 2 D
n1
b
劈尖干涉
11 - 4 薄膜干涉(2)
4 )干涉条纹的移动
每一条 纹对应劈尖 内的一个厚 度,当此厚 度位置改变 时,对应的 条纹随之移 动.
2
所以对于厚度均匀的平面薄膜来说,光程差是随光线的倾
角(入射角)的改变而改变,倾角相同,光程差相同,干
涉条纹的级数也相同。
11 - 4 薄膜干涉(2)
第十一章 波动光学
1 劈 尖干涉
n
T
L
n1
n1
d
S
劈尖角
M
2nd
D
2
n n1
k, k 1,2, 明纹
b
(2k 1) , k 0,1, 暗纹
B
膨胀值为 l N
2
根据热膨胀系数的定义
l
l0T
得样品的热膨胀系数
l N
l0T 2l0T
11 - 4 薄膜干涉(2) 劈尖干涉的应用
波动光学第2讲等倾干涉等厚干涉牛顿环

i i
A
① D
P
②
n1
C
n2
r
B
d
4
n3
' n ( AB BC ) n AD
2 1
AB BC d / cos r
AD AC sin i
2 d tg r sin i
i i ' n 2 AB n AD
2 1
① D
P
②
2 n d cos r 2
A
2
i r
B
n1
2
①
2 n dcos r 2 2
i
② n1 n2
d
由干涉的加强减弱条件
n3
加强 ( k 1 , 2 )
2 n dcos r 2 2 (2k 1) 2
k
减弱 ( k 0 , 1 , 2 )
7
等倾干涉条纹图样
8
屏幕
P
O'
透镜 L
S
光源
半透半反镜
M
O
薄膜
( a ) 观察等倾干涉的装置
波动光学第2讲
——等倾干涉、等厚干涉、 牛顿环
主要内容
17-3 17-4 薄膜干涉 劈尖 牛顿环
1
薄膜干涉
1、半波损失
产生条件: 光从光疏媒质进入光密媒质; 反射光中产生半波损失。
n n 1 2 反射光存在半波损失
n 1 n 2 反射光无半波损失
而折射光都无半波损失
i
n1
r
n2
2
2、薄膜干涉公式
使两束反射光满足干涉加强条件
k 1 , 2 ) 2 n d cos r k ( 加强 2
薄膜干涉概述
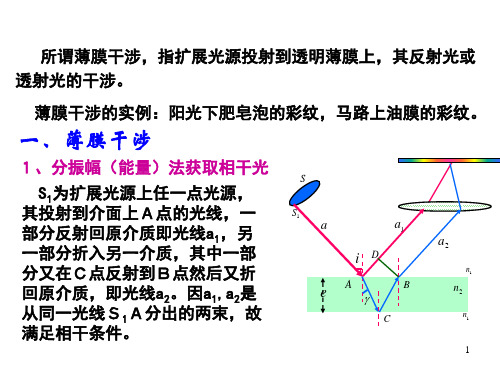
由图中几何关系可知
2
2
AC CB e / cos
AD ABsin i 2etg sin i
由折射定律有 n1 sin i n2 sin
7
三、增透膜与增反膜
1、增透膜 在比较复杂的光学系统中,普通光学镜头都有反射:①带来
光能损失;②影响成象质量。为消除这些影响,用增透膜使反射 光干涉相消。
2
通常习惯上用入射角i表示光程差:
由于 cos 1 sin2 1 ( n1 )2 sin2 i
n2
2n2e
n22
n12 sin2 i n22
2
2e
n22
n12
sin2
i
2
2
❖透射光的光程差
同理,可得 2e n22 n12 sin2 i
与反射光不同的是,没有半波损失。
3、干涉加强、减弱条件
回原介质,即光线a2。因a1,a2是 从同一光线S1A分出的两束,故 满足相干条件。
S
S1
a
a1
iD
e
A
B
C
a2
n1
n2
n1
1
ቤተ መጻሕፍቲ ባይዱ
n2 ( AC
CB) 2n2e / cos
2n2
e
cos
2n2e
sin2 cos
n1
BD
2
2n1etg
n2 n1
sin
即
2n2
e
cos
(1 sin2
)
2
2n2e cos
2e
n22
n12
sin2
i
2
其具体运用之一就是增透膜或增反膜。
5
2、等厚干涉:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
l=
讨论: 讨论:
λ 2 n 2sinθ θ
,微小厚度及 微小厚度及
1. 利用劈尖可以测量微小角度 照射光的波长。 照射光的波长。 2.
δ =δ (e )
光程差是介质厚度的函数, 光程差是介质厚度的函数,
3.对于同一级干涉条纹,具有相同的介质厚度。 对于同一级干涉条纹,具有相同的介质厚度。 对于同一级干涉条纹 等厚干涉
等 倾 干 涉 条 纹 等 厚 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
M2 M1
M2 M1
M2 M1
M1 M2
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹 等 厚 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
M2 M1
M2 M1
M2 M1
n1
薄膜
n2 n2 > n1 n1
屏
透镜 单 S1 * 色 S2 * 光 S3 源 * e
n1
薄膜
n2 n2 > n1 n1
屏
透镜 单 S1 * 色 S2 * 光 S3 源 * e
n1
薄膜
n2 n2 > n1 n1
屏
透镜 单 S1 * 色 S2 * 光 S3 源 * e
n1
薄膜
n2 n2 > n1 n1
等 倾 干 涉 条 纹 等 厚 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
M2 M1
M2 M1
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹 等 厚 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
M2 M1
M2 M1
M2 M1
迈克耳逊干涉仪的干涉条纹
屏
等倾干涉 条纹
透镜 单 S1 * 色 S2 * 光 S3 源 * e
n1
薄膜
n2 n2 > n1 n1
透镜镀膜 —— 薄膜干涉的应用
n1=1.0 n = 1.38 n2 = 1.5
反射光干涉相消条件: 反射光干涉相消条件:
δ = 2nd = (2k +1)
λo
2
增透膜
最薄的膜层厚度( 最薄的膜层厚度(k = 0)为: )
2 2 2 1 2
2 2 δ = 2d n2 − n1 sin 2 i λ
1 n1 n2 n1
i D
A
i
C
2 G
r
B
d
4
F 3
= (2k +1)
2
干涉减弱
干涉条纹 等倾干涉条纹观察装置
屏
透镜 单 S1 * 色 S2 * 光 S3 源 * e
n1
薄膜
n2 n2 > n1 n1
屏
透镜 单 S1 * 色 S2 * 光 S3 源 * e
§12-3 薄膜干涉 1212-3-1 等倾干涉
反射光的干涉: 反射光的干涉: P Q
1 D
AD = ACsin i
= 2d ⋅ tan r ⋅ sin i
d AB = BC = cos r
n1 n2 n2 > n1
i
A
2
i
r
B
C
d
光程差: 光程差:
P Q 1 n1 n2 n1
δ = n2 ( AB + BC) − n1AD
取 k =1
λ 1 = 2 n 2e = 8250 A
取 k =2
0
2 n 2e 4125 0 λ 2= 2 = A
反射光呈现紫蓝色。 反射光呈现紫蓝色。
12-3-2 等厚干涉
一. 劈尖(劈形膜) 劈尖(劈形膜) 夹角很小的两个平面所构成的薄膜
θ: 10 · S
−4
~ 10
−5
rad
反射光2 反射光
2 2 2 1 2
λ
λ
2
2
k = 0,1,2,⋯
等倾干涉:条纹级次取决于入射角的干涉。 等倾干涉:条纹级次取决于入射角的干涉。 条纹特点: 形状——一系列同心圆环 条纹特点 形状 一系列同心圆环 条纹间隔分布—— 条纹间隔分布 内疏外密 透射光的干涉: 透射光的干涉:
P Q
δ = 2d n − n sin i = kλ 干涉加强
d=
λo
4n
[例] 增透膜 例 增透膜——两膜表面平行 两膜表面平行 薄膜, 在玻璃表面镀上一层 MgF 2 薄膜,使波长为 0 的绿光全部通过。 n λ = 5500 A 的绿光全部通过。 求:膜的厚度。 膜的厚度。 解:使反射绿光干涉相消 使反射绿光干涉相消 绿光
0
=1
MgF 2 n 2 = 1.38
M1 M2
M1 M2
例题. 当把折射率n 例题 当把折射率 = 1.40的薄膜放入迈克耳孙 的薄膜放入迈克耳孙 干涉仪的一臂时,如果产生了7.0条条纹的移动 条条纹的移动, 干涉仪的一臂时,如果产生了 条条纹的移动, 求薄膜的厚度。(已知钠光的波长为λ 。(已知钠光的波长为 求薄膜的厚度。(已知钠光的波长为λ = 5893A) ) 解:
(e ) = (2k ′ + 1)
λ
2
, k ′ = 0,1,2, …
说明: 说明:
1. 条纹级次 k 随着劈尖的厚度而变化,因此这种干涉 随着劈尖的厚度而变化, 称为等厚干涉。条纹为一组平行于棱边的平行线。 称为等厚干涉。条纹为一组平行于棱边的平行线。 等厚干涉 2 . 由于存在半波损失,棱边上为零级暗纹。 由于存在半波损失,棱边上为零级暗纹。
∵ R >> d →2Rd >> d 2
r d= 2R
2
牛顿环半径公式: 牛顿环半径公式:
(2k −1)Rλ r= 2n
(k =1,2,⋯ 明环 )
kRλ r= n
(k = 0,1,2,⋯ )
暗环
r
透 镜 曲 率 半 径 变 小 时
干 涉 条 纹 变 密
例题: 求如图干涉实验中第K级牛顿 例题 : 求如图干涉实验中第 级牛顿 环暗环半径。 环暗环半径。 R 解
2d ⋅ n2 = − 2d ⋅ tan r sin i ⋅ n1 cos r 2d = (n2 − n1 sin r sin i) cos r
i D
A
i
2 C
r
B
d
n2 ∵ sin i = sin r n1 2dn2 δ= (1− sin 2 r ) = 2n2d cos r cos r
δ = 2dn2 cos r = 2d n − n sin r
夹角变小,条纹变宽, 夹角变小,条纹变宽, 条纹向右移动
夹角变大,条纹变密 夹角变大,条纹变密 条纹向左移动
λ = 550nm,θ = 2 ×10−4 rad, [例题 已知 例题] 例题 如果劈尖内充满折射率为n=1.40的液体 , 求从劈 的液体, 如果劈尖内充满折射率为 的液体 棱数起第5个明纹在充入液体前后的 移动距离。 棱数起第 个明纹在充入液体前后的 移动距离。
单色平行光 反射光1 反射光 2 λ 1 1、2两束反射光来自同一束入 · n′ ′ 射光, 射光,它们可以产生干涉 。 e n θ A n′(设n > n′ ) ′设 ′
实际应用中,大都是平行光垂直入射到劈尖上。 实际应用中 大都是平行光垂直入射到劈尖上。 大都是平行光垂直入射到劈尖上 考虑到劈尖夹角极小 反射光1、 在膜面的 夹角极小, 考虑到劈尖夹角极小 反射光 、 2在膜面的 光程差可简化为图示情况计算。 光程差可简化为图示情况计算。 简化为图示情况计算 入射光(单色平行 光垂直入射) λ 光垂直入射 反射光2 反射光1 反射光 反射光 A: 1、2的光程差 n′ · A ′ λ e θ n δ ≈ 2 ne + = δ (e ) n′ (设n > n′ ) ′ 设 ′ 2 明 纹 :δ ( e ) = k λ , k = 1,2,3, … 暗纹: 暗纹 : δ
λ
)
牛顿环的应用:
2 2 rk+m − rk = mRλ
• 测透镜球面的曲率半径R: 已知λ, 测 m、rk+m、rk,可得R 。 • 测波长λ: 已知R,测出m 、 rk+m、rk, 可得λ。
λ
• 检验透镜球表面质量 光纤端面的平整度
标准验规 待测透镜
暗纹
12-3-3 迈克耳逊干涉仪 M2
反射镜 2
M2 M1
M 1与M 2 重合
M1 M2
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹 等 厚 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
M1 M2
M1 M2
M2 M1
迈克耳逊干涉仪的干涉条纹
2 ( n − 1 )d = N λ
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹
M2 M1
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹
M2 M1
M2 M1
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹
M2 M1
M2 M1
M 1与M 2 重合
迈克耳逊干涉仪的干涉条纹
等 倾 干 涉 条 纹
M2 M1
条纹的级数变为K+N, , 条纹的级数变为 则 2( L2 + d − L1 ) = ( K + N )λ 由式( ) ( ) 由式(2)-(1)得
