浙江省杭州市2019年5月联考数学考试试题
2019学年第二学期浙江省五校联考 高三数学试卷(定稿)

且此展开式中含 x 项的系数是
12.已知复数 z x yi(x, y R) ,若| z 2i | 1,则| z |max
; x 2 y 的取值
范围是
13.两个实习生每人加工一个零件.加工为一等品的概率分别为 2 和 1 ,两个零件是否加工 32
为一等品相互独立,设两人加工的零件中为一等品的个数为 ,则 E
选择题部分(共 40 分)
一、选择题:本大题共 10 小题,每小题 4 分,共 40 分。在每小题给出的四个选项中,只有 一项是符合题目要求的。
1.已知全集 U R ,集合 A {x | | x | 1, x R} ,集合 B {x | 2x 1, x R} ,
则集合 A B 是( )
A. (,1]
18.(本小题满分 14 分)
已知函数 f (x) 23Leabharlann sinxcos
x
3
2 cos2
x
5 2
(
0) ,且
f
(x)
图像上
相邻两个最低点的距离为 .
(Ⅰ)求 的值以及 f (x) 的单调递减区间;
(Ⅱ)若
f
( )
5 13
,且
0,2
,求
cos 2
的值.
19. (本小题满分 15 分)
在三棱锥 P ABC 中, PC BC 2, AC 3, AP 7, ACB 90 , 点 D 在线段 AB 上,且满足 DB DP . (Ⅰ)求证: PB CD ; (Ⅱ)当 面PDC 面ABC 时,求直线CD 与平面 PAC 所成角的
最大值为 0;③设二面角 A BE C 的平面角为 B
B C
,则 ABA 。其中正确命题的个数是( )
2019年5月2019届高三第三次全国大联考(新课标Ⅰ卷)-文科数学(考试版)

文科数学试题 第1页(共6页) 文科数学试题 第2页(共6页)绝密★启用前|2019年第三次全国大联考【新课标Ⅰ卷】文科数学(考试时间:120分钟 试卷满分:150分)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3.回答第Ⅱ卷时,将答案写在答题卡上。
写在本试卷上无效。
4.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集R U =,集合{|3}A x x =>,{|ln 1}B x x =>,则()U A B =ðA .[e,)+∞B .[3,)+∞C .(1,3]D .(e,3]2.设实数,m n 满足35ii 1im n ++=-,则2m n += A .3 B .2C .5D .63.已知等差数列{}n a 满足:310a =,722a =,则数列1{(1)}n n a +-⋅的前40项和为A .60-B .60C .120-D .1204.运行如图所示的程序框图,m 为常数,若输出的k 的值为2,则m=A .503B .507C .103D .10075.设函数2||4()3x x f x =,则函数()f x 的图象大致为6.如图,边长为2的正方形ABCD 中,点E 是线段BD 上靠近D 的三等分点,F 是线段BD 的中点,则AF CE ⋅=A .4-B .3-C .6-D .2-7.设定义域为R 的奇函数()f x 满足(2)(1)f x f x +=-,若(1)1f =,则62()i f i ==∑A .0B .1C .41D .428.已知双曲线2222:1(0,0)x y C a b a b -=>>的左、右焦点分别为12,F F ,点M 与M '关于x 轴对称,12M F MF '⊥.若122,,MF MF bk k a成等比数列(其中1MF k 2,MF k 分别是直线12,MF MF 的斜率),则双曲线C 的离心率为A .2B C D .3文科数学试题 第3页(共6页) 文科数学试题 第4页(共6页)9.欧拉三角形定义如下:ABC △的三个欧拉点(顶点与垂心连线的中点)构成的三角形称为ABC △的欧拉三角形.已知ABC △中,3,2AB AC BC ===,ABC △的垂心为P ,,,AP BP CP 的中点分别为111,,A B C ,111A B C △即为ABC △的欧拉三角形,往ABC △中随机投掷一点,该点落在11PA B △或11PB C △内的概率为A .19B .18C .532D .96410.正三棱柱111ABC A B C -中,12AA AC =,点D 是线段1AA 的中点,O 是ABC △的中心,则直线OD与直线1BC所成角的余弦值为A .5 B .5 C .5 D .511.已知函数()2cos()f x x ωϕ=+π(0,0)2ωϕ><<的图象的一条对称轴为π3x =,ϕ满足条件π3tan 2sin()2ϕϕ=+,则ω取得最小值时函数)(x f 的最小正周期为A.π2 B .π5C .πD.4π512.已知圆锥OO '如图所示,,,,A B C D 在圆O '上,其中2OA =,则四棱锥O ABCD -体积的最大值为A .9B .27 C .27 D .3第Ⅱ卷二、填空题(本题共4小题,每小题5分,共20分)13.为了调研甲、乙、丙三个地区公务员的平均工资,研究人员拟采用分层抽样的方法在这三个地区中抽取m 名公务员进行调研.已知甲、乙、丙三个地区的公务员人数情况如下表所示,且甲地区的公务员被抽取了15人,则丙地区的公务员被抽取了____________人.14.设实数,x y 满足3302930x y x y x -+≤⎧⎪+≤⎨⎪+≥⎩,则z x y =-的最大值为____________.15.已知圆C 过点(6,0),(6,8)-,且与x 轴交于点,M N .若||6MN =,则圆C 的圆心坐标为____________.16.记等差数列{}n a 的前n 项和为n S ,且59a =,10100S =.若数列{}n b 满足1(21)12nii n ni b a =+-=∑,则满足8k k b S ≥的k 的最小值为____________.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)已知ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,π02B <<,63=b ,22a c +- sin sin tan A C B 112=. (1)求内角B 的大小;(2)求)2)(2(b c a b c a -+++的最大值. 18.(本小题满分12分)如图所示,三棱柱111ABC A B C -中,1AA ⊥平面ABC ,,,M N P 分别是棱111,,BC CC B C 上的点,且1190AMN A PC ∠=∠=︒. (1)求证:1AM B C ⊥;(2)若ABC △为等边三角形,124AA AB ==,求三棱锥1M A PN -的体积.文科数学试题 第5页(共6页) 文科数学试题 第6页(共6页)19.(本小题满分12分)为了了解某校高三年级800名学生的体能状况,研究人员在该校高三学生中抽取了10名学生的体能测试成绩进行统计,统计结果如图所示(满分100分),已知这10名学生体能测试的平均成绩为85分.(1)求m 的值以及这10名学生体能测试成绩的方差;(2)若从上述成绩在90分以下的学生中随机抽取3名,求恰有1人成绩为82分的概率;(3)为了研究高三男、女生的体能情况,现对该校高三所有学生的体能测试成绩进行分类统计,得到的数据如下表所示:试判断是否有99.9%的把握认为体能测试成绩是否超过80分与性别具有相关性.参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.临界值表:20.(本小题满分12分)已知椭圆22:12x C y +=的左、右焦点分别为12,F F ,过点(2,0)-且不与坐标轴垂直的直线l 与椭圆C 交于,M N 两点.(1)求直线l 的斜率的取值范围;(2)若点P 在椭圆C 上,且1,,N F P 三点共线,求证:点M 与点P 的横坐标相同.21.(本小题满分12分)已知函数1()ln f x m x x x=--. (1)若4m =,求证:函数()f x 有且仅有2个零点; (2)若关于x 的不等式2()0ef x +≤在(0,)+∞上恒成立,其中e 是自然对数的底数,求实数m 的取值范围.参考数据:ln 20.693,ln 3 1.099,ln 5 1.609===.请考生在第22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目计分.22.(本小题满分10分)选修4-4:坐标系与参数方程在以极点O 为原点,极轴为x 轴正半轴的直角坐标系中,曲线1C 的参数方程为2x y t⎧=⎪⎨=⎪⎩(t 为参数),曲线1C 在点),(00y x P 处的切线l 的极坐标方程为θθρsin 2cos 323-=.(1)求切线l 的直角坐标方程及切点P 的直角坐标;(2)若切线l 和曲线:2C 016sin 6cos 342=+--θρθρρ相交于不同的两点B A ,,求1||PA +1||PB 的值. 23.(本小题满分10分)选修4-5:不等式选讲已知函数()|3||1|f x x mx =-++.(1)若3m =,求不等式()7f x ≤的解集;(2)若不等式()4f x x ≤-的解集包含[1,3],求实数m 的取值范围.。
浙江省2019年5月高二年级阶段性测试联考 数学学科试题 含答案

−
x2 x1
=2+4k 2
∈ (2,10] 3,
令 − x1 =t ,∴t + 1 ∈ (2,10] ,解得 1 ≤ t ≤ 3且t ≠ 1
x2
t
3
3
∴ tmin
=
1 3
∴ S∆OPN S∆OQN
的最小值为 1 3
………………………15 分
22.解析:
(1)当 a = 2 时, f (x) = ln(x + 1) + 2e−x , f (0) = 2
(m, n) mn
2
4
4
1
3
9
4
f (x) x2 ax b(a,b R)
b1 4
x
f ( f (x)) 0
ABCD
EF M
AB CD
M
EF
BE DF
a,b R
z ai i
a 2 b log2 3
ab
f (x) x 2)2 x 4 x 0) x
ABC
ABC
15 c
ABC
x2 2x, x 0 f (x)
n N*
a1, a2 n 2 Tn
an n N*
bn
n
Tn
S2 3
C x2 4y
F AC
A
C
y
B FA FB
FANB
N
NF C P Q
NF
k (0, 3 ]
S OPN
3
S OQN
f (x) ln(x 1) ae x a 2 a
a2
f (x) x 0
a f (x)
x
浙江省 2019 年 5 月高二年级阶段性测试联考
浙江省杭州市2019年5月联考数学试题

2019中考杭州市5月联考数学注意事项:1.本试题卷共8页,满分120分,考试时间100分钟.2.答题前,考生务必将自己的姓名、准考证号填写在答题卡的相应位置.3.全部答案在答题卡上完成,答在本试题卷上无效.4.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.5.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题共30分)一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.12-的倒数是() A.2B.2-C.12-D.122.下列计算中,正确的是() A.()222a b a b +=+B.()222a b a b -=-C.()()122a b ab ++=+D.()()22a b a b a b +-+=-+3.据统计局公布,2018年浙江居民人均可支配收入45840元,数据45840用科学记数法表示为() A.34.58410⨯B.44.58410⨯C.50.458410⨯D.345.8410⨯4.如图,一个木块沿着倾斜角为47︒的斜坡,从A 滑行至B 巳知5AB =米,则这个木块的高度约下降了(参考数据:470.73sin ︒≈,cos470.68︒≈,tan 47 1.07︒≈)()A.3.65米B.3.40米C.3.35米D.3.55米5.下面由四个相同正方形拼成的图形中,是中心对称图形但不是轴对称图形的是()A. B. C. D.6.在圆内接四边形ABCD 中,若::2:3:4A B C ∠∠∠=,则D ∠=() A.90︒B.120︒C.150︒D.240︒7.实数a ,b ,c 在数轴上对应点的位置如图所示,若11a b>,则下列结论中一定成立的是()A.0a c +>B.1bc>C.1b a +>D.0ab >8.某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高() A.60元B.50元C.40元D.40元或60元9.如图,在直角三角形ABC ∆中,90B ∠=︒,4AB =,3BC =,动点E 从点B 开始沿B C →以2cm/s 的速度运动至C 点停止;动点F 从点B 同时出发沿B A →以1cm/s 的速度运动至A 点停止,连接EF .设运动时间为x (单位:s ),ABC ∆去掉BEF ∆后剩余部分的面积为y (单位:2cm ),则能大致反映y 与x 的函数关系的图象是()A. B. C. D.10.如图,已知O e 的内接ABC ∆中,12AB AC +=,AD BC ⊥于D ,3AD =,直径AE 交BC 边于点G ,有下列四个结论:①AG EG BG CG ⋅=⋅;②2BE EG AE =⋅;③当6AB =时,O e 的面积取得最大值36π;④三角形外接圆直径等于它的任两边的积与第三边上的高的比.其中正确结论有()A.1个B.2个C.3个D.4个第Ⅱ卷(非选择题共90分)二、填空题:本题共6小题,每小题4分,共24分.11.写出一个比2大且比4小的无理数:_______.12.袋子中有30个除颜色外完全相同的小球.在看不到球的条件下,随机地从袋子中摸出1个球,记录颜色后放回,将球摇匀.大量重复上述过程后发现,每1800次,摸到红球420次,由此可以估计口袋中的红球个数是_______.13.已知某银行的贷款年基准利率是5%,老王和小张在这家银行贷款100万元,分别购买了一套新房,由于购入的时间不同,老王在年基准利率打七折时购入,小张在年基准利率上浮25%时购入.在各自贷款满一年后,这一年老王比小张少付______万元利息.14.如图,在ABC ∆中,点D ,E 分别是上一点,:1:3CE EB =,//DE AC .若ADE ∆的面积为S ,则ABC ∆的面积为________.15.已知二次函数2y ax bx c =++(0a ≠)图象上部分点的坐标(),x y 对应值列表如下:则关于x 的方程250ax bx ++=的解是_______.16.在平面直角坐标系xOy 中,点(),3A m -绕坐标原点O 顺时针旋转90︒后,恰好落在图中阴影区域(包括边界)内,则m 的取值范围是______.三、解答题:共66分.解答应写出文字说明、证明过程或演算步骤.17.已知方程()22110kx k x k +++-=.(1)当1k =时,求该方程的解; (2)若方程有实数解,求k 的取值范围.18.日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为70%,并把实验数据绘成两幅统计图(部分信息未给出):(1)求实验中“红袍”品种的种子数量;(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图; (3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.19.如图,已知在O e 中,弦AB 垂直平分半径ON ,NO 的延长线交O e 于P ,连接AP ,过点A ,B 的切线相交于点M .(1)求证:ABM ∆是等边三角形; (2)若O e 的半径为2,求AP 的长.20.如图,正方形ABCD 两条对角线AC 、BD 交于O ,过O 任作一直线L 与边AB ,CD 交于M ,N ,MN 的垂直平分线与边BC ,AD 交于P ,Q .设正方形ABCD 的面积为1S ,四边形MPNQ 的面积为2S .(1)求证:四边形MPNQ 是正方形; (2)若11S =,求2S 的取值范围.21.如图,在平面直角坐标系xOy 中,一次函数1y k x b =+的图象与反比例函数2k y x=(0x >)的图象交于(),1A m m +,()3,1B m m +-两点.(1)求m 的值;(2)求出一次函数与反比例函数的表达式;(3)过点(),0P a 作x 轴的垂线,与直线1y k x b =+和函数2k y x=(0x >)的图象的交点分别为点M ,N ,当点M 在点N 下方时,写出a 的取值范围.22.已知二次函数243y ax ax b =-++(0a ≠). (1)求出二次函数图象的对称轴;(2)若该二次函数的图象经过点()1,3,且整数a ,b 满足49a b <+<,求二次函数的表达式; (3)对于该二次函数图象上的两点()11,A x y ,()22,B x y ,设11t x t ≤≤+,当25x ≥时,均有12y y ≤,请结合图象,直接写出t 的取值范围.23.定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.(1)如图1,ABC ∆中,90ACB ∠=︒,2BC AC =,点P 在AB 上,PD AC ⊥于点D ,PE BC ⊥于点E ,连接BD ,DE 求证:BDE ∆是“半高”三角形;(2)如图2,ABC ∆是“半高”三角形,且BC 边上的高是“半高”,点P 在AB 上,//PQ BC 交AC 于点Q ,PM BC ⊥于点M ,QN BC ⊥于点N .①请探究BM ,PM ,CN 之间的等量关系,并说明理由; ②若ABC ∆的面积等于16,求MQ 的最小值.2019中考杭州市5月联考数学答案详解【解析】本题考查无理数的定义.,π小.12.7【解析】本题考查概率.根据实验频率估计概率,则估计口袋中的红球个数为4203071800⨯=,故答案为7.13.2.75【解析】本题考查列方程解决实际问题.老王应付利息1005%0.7 3.5⨯⨯=(万元);小张应付利息()1005%125% 6.25⨯⨯+=(万元),两者相减得2.75万元,故答案为2.75万元. 14.163S 【解析】本题考查相似三角形的性质.∵//DE AC ,∴ABC DBE ∆∆:,∴2239416DBE ABC S BE S BC ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,而13ADE DBE S S ∆∆=,两式相乘得163ABC S S ∆=,故答案为163S . 15.110x =,220x =【解析】本题考查二次函数图象的性质.当0x =,30x =时,2y =,故二次函数图象的对称轴是直线15x =,且2c =,所以二次函数解析式为22y ax bx =++,由此可知方程250ax bx ++=的解即是223ax bx ++=-的解,即是求当3y =-时对应的x 值,由图象知x 为10或20,故答案为:110x =,220x =.16. 3.5 2.5m -≤≤-【解析】本题考查图象的旋转.将等腰三角形(阴影区域)逆时针旋转90︒,再求出该图形与直线3y =-相交的部分,故答案为 3.5 2.5m -≤≤-. 17.【名师指导】本题考查一元二次方程的解法.(1)把1k =代入,利用因式分解法解方程;(2)分0k =及0k ≠两种情况讨论.解:(1)把1k =代入原方程得230x x +=,解得10x =,23x =-.(2)当0k =时,方程10x -=有解;当0k ≠时,()()221410k k k +--≥,解得18k ≥-. 综上可得18k ≥-.18.【名师指导】本题考查扇形统计图和条形统计图.(1)根据扇形统计图得出“红袍”种子所占比例,即可求解;(2)根据条件及扇形统计图,得出结果;(3)根据条形统计图判断每个品种的种子发芽率,进而判断.解:(1)“红袍”品种的种子数量:()500130%25%25%100⨯---=(粒)(2)“白砂”品种的种子发芽的株数:50030%70%105⨯⨯=(株);补全条形统计图略.(3)“红袍”品种的种子发芽率:85100%85%100⨯=; “宝珠”品种的种子发芽率:100100%=80%50025%⨯⨯;“夹脚”品种的种子发芽率:100100%=80%50025%⨯⨯;因此,应该选择“红袍”品种进行推广. 19.【名师指导】本题考查三角形以及圆的性质.(1)连接OA ,利用圆的切线性质及等边三角形的判定即可证明;(2)由(1)中求得的结论,利用勾股定理,可算出AP 的长.解:(1)证明:连接OA ,设AB 与ON 的交点为D . ∵MA ,MB 分别切O e 于A ,B , ∴OA MA ⊥,MA MB =, ∵弦AB 垂直平分半径ON , ∴1122OD ON OA ==, ∴30OAD ∠=︒,故60BAM ∠=︒, ∴ABM ∆是等边三角形.(2)∵2OA OP ==,由(1)可知1OD =,∴在Rt AOD ∆中,AD =∴在Rt APD ∆中,AP ===20.【名师指导】本题考查正方形的性质、二次函数的性质.(1)利用全等三角形的判定定理及正方形的性质证明;(2)利用二次函数的性质进行求解. 解:(1)证明:∵QP 垂直平分线段MN , ∴MQ NQ =,PM PN =, 由条件可证()AOQ DON ASA ∆≅∆, ∴OQ ON =,∴45OQN ONQ ∠=∠=︒,同理可得45OQM OMQ OMP OPM ∠=∠=∠=∠=︒, ∴90NQM QMP MPN PNQ ∠=∠=∠=∠=︒, ∴四边形MPNQ 是矩形,而MQ NQ =, ∴四边形MPNQ 是正方形.(2)设AQ DN x ==,则1QD x =-,∴()22222211112212222S QN x x x x x ⎛⎫==+-=-+=-+≥ ⎪⎝⎭而211S S ≤=, ∴2112S ≤≤. 21.【名师指导】本题考查一次函数和反比例函数.(1)由反比例函数的性质可以求出m 的值;(2)列出关于1k 与b 的二元一次方程组,解方程组,进而可得到一次函数解析式,由反比例函数的概念可得反比例函数的解析式;(3)观察图象,再利用一次函数和反比例函数的性质即可得出a 的取值范围.解:(1)由反比例函数概念可得()()()131m m m m +=+-,解得3m =.(2)将点()3,4A ,()6,2B 代入1y k x b =+得1134,62,k b k b +=⎧⎨+=⎩解得12,36,k b ⎧=-⎪⎨⎪=⎩所以一次函数的解析式为263y x =-+. 由23412k =⨯=,可得反比例函数的解析式为2y x=(0x >).(3)观察图象可得出03a <<或6a >. 22.【名师指导】本题考查二次函数的性质.(1)由对称轴公式即可求解;(2)观察函数图象,在给定的范围内,找出对应关系,即可求得二次函数的表达式;(3)分类讨论,利用函数图象,结合函数的对称性即可得出t 的取值范围. 解:(1)二次函数图象的对称轴是422ax a-=-=. (2)该二次函数的图象经过点()1,3, ∴433a a b -++=,∴3b a =, 把3b a =代入49a b <+<, 得439a a <+<.当0a >时,449a <<,则914a <<. 而a 为整数,∴2a =,则6b =, ∴二次函数的表达式为2289y x x =-+; 当0a <时,429a <-<,则922a -<<-. 而a 为整数,∴3a =-或4-, 则对应的9b =-或12-,∴二次函数的表达式为23126y x x =-+-或24169y x x =-+-. (3)14t -≤≤.23.【名师指导】本题考查新定义、相似三角形、二次函数的性质.(1)根据新定义进行证明;(2)①利用新定义的概念进行转化;②将MQ 的长度用二次函数表示出来,利用二次函数的性质进行求解.解:(1)证明:由题意可证得PBE ABC ∆∆:, ∴12PE AC BE BC ==, ∴2BE PE =,由题意可证得四边形CEPD 为矩形,∴DC PE =, ∴2BE DC =,∴BDE ∆是“半高”三角形.(2)①2BM CN PM +=.理由如下:如图,过A 作AE BC ⊥于E ,交PQ 于D ,∵ABC ∆是“半高”三角形,且BC 边上的高是“半高”,∴2BC AE =∵//PQ BC ,∴APQ ABC ∆∆:,∴2PQ AD =,∴()2BC PQ AE AD -=-,由题意可证得四边形MNQP 是矩形,有PQ MN =,PM DE QN ==, ∴2BC MN PM -=,即2BM CN PM +=. ②∵2111624ABC S BC AE BC ∆=⨯==,故8BC =, 设PM x =,由①得82PQ x =-,∴MQ ==∴当165x =时,MQ .。
2019年5月2019届高三第三次全国大联考(新课标Ⅰ卷)-文科数学(试卷及答案)
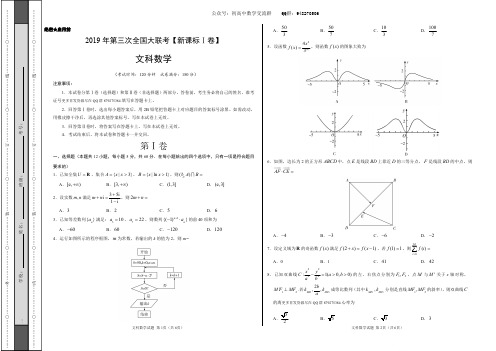
,则函数
f
(x)
的图象大致为
C. 10 3
D. 100 7
(考试时间:120 分钟 试卷满分:150 分) 注意事项:
1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。答卷前,考生务必将自己的姓名、准考 证号更多首发资源尽在 QQ 群 879275384 填写在答题卡上。
2.回答第Ⅰ卷时,选出每小题答案后,用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改动, 用橡皮擦干净后,再选涂其他答案标号。写在本试卷上无效。
e
值范围.
参考数据: ln 2 0.693, ln 3 1.099, ln 5 1.609 .
请考生在第 22、23 两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一个题目
计更多首发资源尽在 QQ 群 879275384 分.
22.(本小题满分 10 分)选修 4-4:坐标系与参数方程
2
3
3 tan 2 sin( π ) ,则 取得最小值时函数 f (x) 的最小正周期为 2
π
A.
2
π
B.
5
C. π
4π
D.
5
12.已知圆锥 OO 如图所示, A, B, C, D 在圆 O 上,其中 OA 2 ,则四棱锥 O ABCD 体积的最大值为
地区
甲
乙
丙
公务员人数
600
900
400
x 3y 3 0
14.设实数
x,
y
满足
x
2
y
9
,则 z x y 的最大值为____________.
x 3 0
15.已知圆 C 过点 (6, 0), (6, 8) ,且与 x 轴交于点 M , N .若 | MN | 6 ,则圆 C 的圆心坐标为____________.
浙江省杭州市学军中学2019 学年第二学期高三年级数学月考试卷(word版含答案)

浙江省杭州市学军中学2019 学年第二学期高三年级月考数学试卷考生须知:1.本卷满分150分,考试时间120分钟;2.答题前,在答题卷指定区域填写学校、班级、姓名、试场号、座位号及准考证号。
3.所有答案必须写在答题卷上,写在试卷上无效;.4.考试结束后,只需上交答题卷。
选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合A={-1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=A.{2}B.{2,3}C.{-1,2,3}D.{1,2,3,4}2.双曲线22221(0,0x ya ba b-=>>)的离心率为3,则其渐近线方程为2.2A y x=±3.B y x=±.2C y x=±.3D y x=±3.设x,y满足约束条件23302330,30x yx yy+-≤⎧⎪-+≥⎨⎪+≥⎩则z=2x+y的最小值是A-9 B.-15 C.1 D.94.如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为A.20πB.24πC.28πD.32π5.已知直线a,b分别在两个不同的平面a,β内,则“直线a和直线b相交”是“平面α和平面β相交”的A.充分不必要条件B.必要不充分条件。
C.充要条件D.既不充分也不必要条件6.函数2sin()cosx xf xx x+=+在[-π,π]的图像大致为7.已知a,b 为实数,随机变量X,Y 的分布列如下:若E(Y)=P(Y=-1),随机变量ξ满足ξ=XY ,其中随机变量XY 相互独立,则E(ξ)取值范围的是3.[,1]4A - 1.[,0]18B - 1.[,1]18C 3.[,1]4D 8.抛物线22(0)y px p =>的焦点为F,直线l 过点F 且与抛物线交于点M,N(点N 在轴上方),点E 为轴上F 右侧的一点,若||||3||,123,MNE NF EF MF S ∆===则p=A.1B.2C.3D.99.已知函数2(4),53(),(2),3x x f x f x x ⎧+-≤<-=⎨-≥-⎩若函数g(x)=f(x)-|k(x+1)|有9个零点,则实数k 的取值范围是 1111.(,)(,)4664A --⋃1111.(,)(,)3553B --⋃ 11.(,)64C11.(,)53D 10.已知函数()1,x f x e x =--数列{}n a 的前n 项和为,n S ,且满足111,(),2n n a a f a +==则下列有关数列{}n a 的叙述正确的是A.521|43|a a a <-B.78a a ≤C.101a >D.10026S >非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.11.若复数31i z i+=- (i 为虚数单位),则z|=___,复数z 对应的点在坐标平面的第____象限. 12.在二项式262()x x -的展开式中,常数项是____,所有二项式系数之和是______.13.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c.若△ABC 的面积是b 13,cos ,3C ==则c=___;sin 2sin B C=___. 14.某公司有9个连在一起的停车位,现有5辆不同型号的轿车需停放,若停放后恰有3个空车位连在一起,则不同的停放方法有____种.15.已知e r 为单位向量,平面向量,a b r r 满足||||1,a e b e +=-=r r r r a b ⋅r r 的取值范围是____.16.已知a,b ∈R,且满足2ab-4a+3b-8=0,则22238a b a b ++-的最小值是_____.17.在长方体1111ABCD A B C D -中,14,1,AB BC AA E ===是底面ABCD 的中心,又1(0),2AF AB λλ=≤≤u u u r u u u r 则当λ=____时,长方体过点1,,A E F 的截面面积的最小值为____. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.(本小题满分14分)设函数2()sin cos (2f x x x x ωωωω=-->0),且y=f(x) 的图象的一个对称中心到最近的对称轴的距离为.4π (I)求ω的值;(II)求f(x)在区间3[,]2ππ上的最大值和最小值.19.(本小题满分15分) 如图,四棱锥P-ABCD 中,侧面PAD 为等边三角形且垂直于底面ABCD,底面四边形ABCD 中,1,2AB BC AD ==∠BAD=∠ABC=90°,又E 是PD 的中点. (I )证明:直线CE//平面PAB ;(II )点M 在棱PC 上,且直线BM 与底面ABCD 所成角为45°,求二面角M-AB-D 的余弦值。
2019学年浙江省杭州市5月中考模拟数学试卷【含答案及解析】

2019学年浙江省杭州市5月中考模拟数学试卷【含答案及解析】姓名____________ 班级________________ 分数 ___________、选择题1. 下列各对数是互为倒数的是()A. 4 和-4 B . -3 和—C . -2 和一D . 0 和0 3 12. 下列运算中,结果正确的是()A. 3x2+2x2=5x4 B . (x+y)2=x2+y2 C . (x2)3=x5 D . x3?x3=x63. 据统计,2011年经义乌海关出口小商品总价达98.7亿美元据统计,98.7亿美元用科学记数法表示为()A. 9.87 X 107 美元 B . 9.87 X 108 美元C. 9.87 X 109 美元 D . 9.87 X 1010 美元4. 下列图形中,中心对称图形有()® O *A. 1个B . 2个C . 3个D . 4个5. 若两圆的半径分别为5和2,圆心距是4 .则这两圆的位置关系是()A.外离B .外切C .相交D .内切6. 某校A、B两队10名参加篮球比赛的队员的身高(单位:cm)如下表所示:7. 队员队 1 号 2 号 3 号 4 号 5 号 A 队176175174171174B 队170173171174182tdD=35。
,则/ O的度数是()9. 用直尺和圆规作一个菱形,如图,能得到四边形ABCD是菱形的依据是()A. —组邻边相等的四边形是菱形B. 四边相等的四边形是菱形C. 对角线互相垂直的平行四边形是菱形D. 每条对角线平分一组对角的平行四边形是菱形10. 已知:二次函数y=ax2+bx+c (a工0 )的图象如图所示,下列结论中:①0;c >②2a+b v 0;③a+b v m(am+b (m^1 的实数);a+c)2v b2;⑤a> 1 .其中正确的C .②⑤D .①③④11. 如图,点A、B分别在射线OM ON上,C、D分别是线段OA和OB上的点,以OC OD3 1为邻边作平行四边形OCE D下面给出三种作法的条件:①取OC〒OAODgOB ②取1 3 3 3OC^OA OD齐OB③取OC〒OA ODg OB能使点E落在阴影区域内的作法有()、填空题12. 使“一^有意义的x 的取值范围是13. 分解因式:2x2-8=15. 已知圆锥的底面半径为 3,侧面积为15 n ,则这个圆锥的高为16. 如图,破残的轮子上弓形的弦 AB 为4cm,高CD 为1cm,则这个轮子的直径大小为仁60 °,则/ 2=EF 交CD 于17. 已知,如图直线I的解析式为y=x+4,交x、y轴分别于A、B两点,点M( -1 , 3)在直线I上,0为原点.(1)点N在x轴的负半轴上,且/ MNO=60,贝V AN= ;(2)点P在y轴上,线段PM绕点P旋转60°得到线段PQ且点Q恰好在直线I上,贝V点P的坐标为或三、解答题18. (1)计算:工...- 一, .'.1 r(2)解分式方程:----- -----19. 如图,梯形ABCD中,AD// BC, 点M是BC的中点,且MA=MD求证:四边形ABCD是等20. 随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点•据某市交通部门统计,2008年底全市汽车拥有量为15万辆,而截止到2010年底,全市的汽车拥有量已达21.6万辆.(1)求2008年底至2010年底该市汽车拥有量的年平均增长率;(2)为保护城市环境,缓解汽车拥堵状况,从2011年初起,该市交通部门拟控制汽车总量,要求到2012年底全市汽车拥有量不超过23.196万辆;另据估计,该市从2011年起每年报废的汽车数量是上年底汽车拥有量的10%假定在这种情况下每年新增汽车数量相同,请你计算出该市每年新增汽车数多不能超过多少万辆.21. 如图,在△ AB中, AB=AC D是BC中点,AE平分/ BA交BC于点E,点O是AB上一点,00过A、E两点,交AD于点G,交AB于点F.(1) 求证:BC与OO相切;(2) 当/ BAC=120时,求/ EFG的度数.22. 为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.23. 如图,一次函数y=kx+2的图象与反比例函数y=—的图象交于点P,点P在第一象A限.PAL x轴于点A, PB丄y轴于点B. —次函数的图象分别交x轴、y轴于点C、D,且全校留守儿童人数扇形貌计團(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;(1)求点D的坐标;(2) 求一次函数与反比例函数的解析式; (3)根据图象写出当x >0时,一次函数的值大于反比例函数的值的x 的取值范围.(3)若BC=6点D 在边AC 的三等分点处,将线段 AD 绕点A 旋转,点F 始终为BD 中点, 求线段CF 长度的最大值.25.如图1,已知:抛物线 y=f x2+bx+c 与x 轴交于A, B 两点,与y 轴交于点C,经过B , C 两点的直线是尸一x-2,连结ACkb乙 乎* -圏1產2(1) 求出抛物线的函数关系式; (2) 若厶ABC 内部能否截出面积最大的矩形 DEFC(顶点D E 、F 、G 在厶ABC 各边上)? 若能,求出在AB 边上的矩形顶点的坐标;若不能,请说明理由.(3) 点P (t , 0)是x 轴上一动点,P 、Q 两点关于直线 BC 成轴对称,PQ 交BC 于点M 作QH Lx 轴于点H.连结OQ 是否存在t 的值,使△ 004与厶APM 相似?若存在,求出t 的值;若不存在,说连接CFA 旋转,使得 D EB 三点共线,点F 仍为BD 中点,如图若过点 若将图24.在 Rt △ ABC 中/ ACB=90 ° , tan (1) (2) D 作 DEL AB 于E , 1中的△ ADE 绕点 CE 如图 1 .设 CF=kEF 贝V k= EF A , C 重合),连接明理由.参考答案及解析第1题【答案】C.【解析】试題解析:扒4X (T)护1,选项错误j-3X —丰选项错误;C、-旷(-* )=l f选项正确jX 0XO=tl,选项错误.故选C・考点,倒数.第2题【答案】D.【解析】试题解析:A% 3出+2屮=5屮,故本选项错误〕E, <x+Y> *=ic2+2xy+y\ 故本选项错误;C,&)已許上朮故本选项错误jD*込汽严0爲故本选项正确*故选D.第5题【答案】第3题【答案】^3.吃美元用科学记数法表示为:5.87X 诃美元.故选;C.考点2科学记数法一表示较大的数. 第4题【答案】|c.【解析】试题解析:第一个團形是中心对称图形」 第二个图形是中心協图形* 第三个團形是中谕慨®形‘頁四个團形不是中心对称團形・故共目个中心对恋團形■ 雌C.考点,中心对称團形.槃雪 3 F;□!勢【解析】试題解析:由lamai圆心距“<衣©乜故两融目交,故选C・考点:圆与圆的位羞关系.第6题【答案】D.【解析】(176+175+174U71+174 > =174cm,(17O+LT3+171+174+182) 丁4s.[(176-174)討( 173-174) ;+ (171-174) :+ (174-174)科(132-174) i] =3.Genii:[{170-174) * < 175-174}讥(174-174)肝(171-174) £4- <174-174)习=5■氏m右故选D・考点:方差,算术平均数・EJ.第7题【答案】【解析】试题解析:7ZM54』;.ZAOC=2ZD=7O^ ;/,ZOAC^ <160°-仙Cl H-2=110° H-2=55°故选B・第8题【答案】E).【解析】:匸乔解析:由剧形作法可知;AD=AE^C=BC?二四边形AECD是菱形』故逖5考点£菱形的羽垸j作團一复杂作團.第9题【答案】【解析】试题解析^①丁抛柳线的开口冋上,.->0; •••与yf由的交点为在审由的负半轴上,二虫。
浙江2019第二次五校联考-数学(理)

浙江2019第二次五校联考-数学(理)本试卷分选择题和非选择题两部分、总分值150分,考试时间120分钟、请考生按规定用笔将所有试题的答案涂、写在答题纸上、选择题部分〔共50分〕本卷须知1、答题前,考生务必将自己的姓名、准考证号用黑色字亦的签字笔或钢笔镇写在答题纸规定的位置上、2、每题选出后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号、不能答在试题卷上、参考公式:假如事件A ,B 互斥,那么棱柱的体积公式P (A +B )=P (A )+P (B )V =Sh假如事件A ,B 相互独立,那么其中S 表示棱柱的底面积,h 表示棱柱的高 P (A ·B )=P (A )·P (B )棱锥的体积公式假如事件A 在一次试验中发生的概率是p ,那么nV =13Sh次独立重复试验中事件A 恰好发生k 次的概率 其中S 表示棱锥的底面积,h 表示棱锥的高 P n (k )=C k np k (1-p )n -k (k =0,1,2,…,n )球的表面积公式棱台的体积公式S =4πR 213V =12()h s s球的体积公式其中S 1,S 2分别表示棱台的上、下底面积,h 表示棱台V =43πR 3的高其中R 表示球的半径第I 卷〔共50分〕【一】选择题:本大题共10小题,每题5分,共50分、在每题给出的四个选项中,只有一项为哪一项符合题目要求的、1、设全集R U =,集合15{|||}22M x x =-≤,{|14}P x x =-≤≤,那么()UC M P 等于〔A 〕{|42}x x -≤≤-〔B 〕{|13}x x -≤≤〔C 〕{|34}x x ≤≤〔D 〕{|34}x x <≤ 2、将长方体截去一个四棱锥,得到的几何体如下图,那么该几何体的侧视图为3、假设“01x <<”是“()[(2)]0x a x a --+≤”的充分不必要条件,那么实数a 的取值范围是〔A 〕(,0][1,)-∞+∞〔B 〕(1,0)- 〔C 〕[1,0]-〔D 〕(,1)(0,)-∞-+∞ 4、直线l ,m 与平面αβγ,,满足//l l m βγαα=⊂,,,m γ⊥,那么有(第12题)〔A 〕αγ⊥且//m β〔B 〕αγ⊥且l m ⊥ 〔C 〕//m β且l m ⊥〔D 〕//αβ且αγ⊥5、设实数,x y 满足1230x x y y x ≥⎧⎪-+≥⎨⎪≥⎩,那么2x y +的最大值和最小值之和等于〔A 〕12〔B 〕16〔C 〕8〔D 〕14 6、假设(,)2παπ∈,且3cos2sin()4παα=-,那么sin2α的值为 〔A 〕118〔B 〕118-〔C 〕1718〔D 〕1718-7、过双曲线22221(0,0)x y a b a b-=>>的右焦点2F 作斜率为1-的直线,该直线与双曲线的两条渐近线的交点分别为,A B 、假设2F A AB =,那么双曲线的渐近线方程为〔A 〕30x y ±=〔B 〕30x y ±=/〔C 〕230x y ±=〔D 〕320x y ±=/ 8、设1AB =,假设2CA CB=,那么CA CB ⋅的最大值为〔A 〕13〔B 〕2/〔C D 〕/39、数列{}na 共有12项,其中10a =,52a =,125a =,且11,1,2,3,11k ka a k +-==⋅⋅⋅,那么满足这种条件的不同数列的个数为〔A 〕84〔B 〕168/〔C 〕76〔D 〕152/ 10、将函数sin (02)y x x π=≤≤的图象绕坐标原点逆时针方向旋转(02)θθπ≤<角,得到曲线C .假设关于每一个旋转角θ,曲线C 基本上一个函数的图象,那么满足条件的角θ的范围是〔A 〕[0,]4π〔B 〕35[0,][,]444πππ⋃/ 〔C 〕357[0,][,][,2)4444πππππ⋃⋃〔D 〕7[0,][,2)44πππ⋃/第II 卷〔共100分〕【二】填空题:本大题共7小题,每题4分,共28分、11、复数1i 2ia +-〔,i a R ∈为虚数单位〕为纯虚数,那么复数i z a =+的CBDAE(第20题)模为、12、某程序框图如下图,那么程序运行后输出的S 值为、13、在25(1)(1)x x x ++-的展开式中,含3x 的项的系数是.14、平面内与直线平行的非零向量称为直线的方向向量,与直线的方向向量垂直的非零向量称为直线的法向量、在平面直角坐标系中,利用求动点轨迹方程的方法,能够求出过点(2,1)A 且法向量为(1,2)n =-的直线〔点法式〕方程为(2)2(1)0x y --+-=,化简后得20x y -=、那么在空间直角坐标系中,平面通过点(2,1,3)A ,且法向量为(1,2,1)n =-的平面〔点法式〕方程化简后的结果为、15、过抛物线22(0)y px p =>焦点的直线与抛物线交于,A B 两点,3AB =,且AB 终点的纵坐标为12,那么p的值为、16、甲、乙两个篮球队进行竞赛,竞赛采纳5局3胜制〔即先胜3局者获胜〕、假设甲、乙两队在每场竞赛 中获胜的概率分别为23和13,记需要竞赛的场次为ξ,那么E ξ=、17、三棱锥O ABC -中,,OA OB OC ,两两垂直且相等,点P ,Q 分别是BC 和OA 上的动点,且满足1233BC BP BC ≤≤,1233OA OQ OA ≤≤,那么PQ 和OB 所成角余弦值的取值范围是、 【三】解答题:本大题共5小题,共72分、解承诺写出文字说明,证明过程或演算步骤、 18、〔此题总分值14分〕在ABC ∆中,角,,A B C 所对的边分别为,,a b c /,,,a b c 成等比数列,且3sin sin 4A C =、〔Ⅰ〕求角B 的大小;〔Ⅱ〕假设[0,)x π∈,求函数()sin()sin f x x B x =-+的值域、19、〔此题总分值14分〕设公比为正数的等比数列{}n a 的前n 项和为n S ,328,48a S ==,数列{}n b 满足24log n nb a =、〔Ⅰ〕求数列{}n a 和{}nb 的通项公式;〔Ⅱ〕是否存在m N *∈,使得12m m m b b b ++⋅是数列{}n b 中的项?假设存在,求出m 的值;假设不存在,请说明理由、20、〔此题总分值14分〕如图,DC 垂直平面ABC ,90BAC ∠=,(第21题)12AC BC kCD ==,点E 在BD 上,且3BE ED =、 〔Ⅰ〕求证:AE BC ⊥;〔Ⅱ〕假设二面角B AE C --的大小为120,求k 的值、21、〔此题总分值15分〕设点P 为圆2212C xy +=:上的动点,过点P 作x 轴的垂线,垂足为Q 、动点M PQ =〔其中P ,Q 不重合〕、〔Ⅰ〕求点M 的轨迹2C 的方程;〔Ⅱ〕过直线2x =-上的动点T 作圆1C 的两条切线,设切点分别为,A B 、假设直线AB 与〔Ⅰ〕中的曲线2C 交于,C D 两点,求AB CD的取值范围、 22、〔此题总分值15分〕设函数()(,)bf x ax a b R x=+∈,假设()f x 在点(1,(1))f 处的切线斜率为1、〔Ⅰ〕用a 表示b ;〔Ⅱ〕设()ln ()g x x f x =-,假设()1g x ≤-对定义域内的x 恒成立, 〔ⅰ〕求实数a 的取值范围; 〔ⅱ〕对任意的[0,)2πθ∈,证明:(1sin )(1sin )g g θθ-≤+、数学〔理科〕答案【一】选择题: 题号1 2 3 4 5 6 7 8 9 10 答案 D D C B AD ABAC【二】填空题:11;12、10;13、-5;14、230x y z --+=;1516、10727;17、1[317、方法一:考虑几种极端情况; 方法二:过点O 作PQ 的平行线OP ',那么点P ,Q 的运动相当于点P '在如下图的四边形MNGH 上运动.显然,HOB ∠最大,NOB ∠最小.以OB ,OA 和OC 为x 轴、y 轴和z 轴建立空间直角坐标系,O 〔0,0,0〕,设点B 〔3,0,0〕那么点H 为〔1,-2,2〕,点N 〔2,-1,1〕,可得.【三】解答题:18、解:〔Ⅰ〕因为a 、b 、c 成等比数列,那么2b ac =.由正弦定理得2sin sin sin B A C =. 又3sin sin 4A C =,因此23sin 4B =.因为sinB >0,那么sin B =.……………………4′ 因为B ∈(0,π),因此B =3π或23π.又2b ac =,那么b a ≤或b c ≤,即b 不是△ABC 的最大边,故3B =π.……………………3′ 〔Ⅱ〕因为3B =π,那么()s i n()s i nsi n c o s c o ss i n s i n333f x x x x x x πππ=-+=-+3sin )26x x x π==-.……………………4′[0,)x π∈,那么5666x πππ-≤-<,因此1sin()[,1]62x π-∈-. 故函数()f x 的值域是[.……………………3′ 19、解:〔Ⅰ〕设{}na 的公比为q ,那么有211181228a q q a a q ⎧⋅=⇒=⎨+=⎩或12q =-〔舍〕.那么12832a q==,16132()22n nna --=⋅=, 6224log 4log 2424n n nb a n -===-+.即数列{}n a 和{}n b 的通项公式为16132()22n n n a --=⋅=,424n b n =-+.……………………6′ 〔Ⅱ〕12(244)(204)4(6)(5)(164)(4)m m m b b m m m m b m m ++⋅----==--,令4(3,)t m t t Z =-≤∈,因此 124(6)(5)4(2)(1)24(3)(4)m m m b b m m t t t b m t t++⋅--++===++-, 假如12m m m b b b ++⋅是数列{}n b 中的项,设为第0m 项,那么有024(3)4(6)t m t ++=-,那么23t t ++为小于等于5的整数,因此{2,1,1,2}t ∈--.……………………4′ 当1t =或2t =时,236t t++=,不合题意; 当1t =-或2t =-时,230t t++=,符合题意. 因此,当1t =-或2t =-时,即5m =或6m =时,12m m m b b b ++⋅是数列{}n b 中的项.…………………8′20、解:〔Ⅰ〕过E 点作EF BC ⊥与点F ,连AF ,因此//EF DC 因此EF ABC ⊥平面,又BC ABC ⊂平面,因此EF BC ⊥; 又90BAC ∠=,12AC BC =,因此30ABF ∠=,因此AB , 34BE BF BD BC ==,34BF BC =,因此BF AB AB BC =,因此BAF ∆与BCA ∆相似,因此90BFA ∠=,即A F B C ⊥;又A F E F F ⋂=,因此BC AEF ⊥平面,又AE AEF ⊂平面, 因此BC AE ⊥.…………………6′〔2〕解法一〔空间向量法〕如右图,以F 为原点,FA 为x 轴,FC 为y 轴,FE 为z 轴,建立空间直角坐标系,那么A ,3(0,,0)2B -,1(0,,0)2C ,3(0,0,)4E k,因此3()4AEk=-,1(,0)2AC=-, 3(,0)2AB =--,设平面ABE 的法向量为1111(,,)n x y z =,1200AB n AE n ⎧⋅=⎪⎨⋅=⎪⎩,因此1111302304x y x z k⎧-=⎪⎪⎨⎪+=⎪⎩,令11z =,得1112x y k ==-,得131(,1)2n k=-. 设平面ACE 的法向量为2222(,,)n x y z =,1200AC n AE n ⎧⋅=⎪⎨⋅=⎪⎩,因此2222102304y z k⎧+=⎪⎪⎨⎪+=⎪⎩,令21z =,得2232x y k =,得133(,1)2n k=. 1212|||cos120|||||3n n n n ⋅==⋅,解得:k =……………………8′解法二:〔综合几何法〕过F 作FG AE ⊥于G 点,连GC,GB ,由AE BC ⊥,可得AE BCG ⊥平面,因此,AE CG AEBG ⊥⊥,因此BGC ∠为B-AE-C 的平面角,设AC=1,那么34AF EF k =,因此GF =,因此 GB =GC ,因此由222cos1202BG CG BC BG CG +-=⋅,得到k =…………………8′ 21、解:〔Ⅰ〕设点(,)M x y ,MQ PQ =,得()P x ,由于点P 在2212C x y +=:上,那么2222x y +=, 即M 的轨迹方程为2212x y +=.…………………4′〔Ⅱ〕设点(2,)T t -,1122(,),(,)A x y B x y '''',那么AT ,BT 的方程为:112x x y y ''+=,222x x y y ''+=,又点(2,)T t -在AT 、BT 上,那么有:1122x ty ''-+=①,2222x ty ''-+=②,由①、②知AB 的方程为:22x ty -+=.…………3′设点1122(,),(,)C x y D x y ,那么圆心O 到AB的距离d ,||AB =;又由222212x ty x y -+=⎧⎪⎨+=⎪⎩,得22(8)440t y ty +--=,因此12248t y y t +=+,12248y y t -=+,因此12|||CD y y -=因此||||AB CD =,…………………3′设24t s +=,那么4s ≥,因此||||AB CD 11,(0]4m m s =∈,,因此||||AB CD 3()1632f m m m =+-,2'()696f m m =-,令'()0f m =,得41=m . 得)(m f 在]41,0(上单调递增,故]2,1()(∈m f .即||||AB CD的范围为…………………5′ 22、解:〔Ⅰ〕2()b f x a x '=-,依题意有:2(1)11bf a a b b a x '=-=-=⇒=-;…………2′ 〔Ⅱ〕1()ln ()ln ()1a g x x f x x ax x-=-=-+≤-恒成立. 〔ⅰ〕()1g x ≤-恒成马上max()1g x ≤-.方法一:()1g x ≤-恒成立,那么(1)11101g a a a +=--++≤⇒≥.当1a ≥时,221[(1)](1)(1)(1)1()01,1a x x ax a x a g x x x x x a---+--+--'===⇒==-+ 110,x a=-+≤2(0)0x g '≥,那么(0,1)x ∈,()0g x '>,()g x 单调递增,当(1,)x ∈+∞,()0g x '<,()g x 单调递减,那么max ()(1)121g x g a ==-≤-,符合题意;即()1g x ≤-恒成立,实数a 的取值范围为1a ≥;……………6′方法二:2222111(1)(1)()a ax x a ax a x g x a x x x x --++--+--'=-+==, ①当0a =时,21()x g x x-'=,(0,1)x ∈,()0g x '<,()g x 单调递减,当(1,)x ∈+∞,()0g x '>,()g x 单调递增,那么max()(1)1g x g ==,不符题意;②当0a ≠时,221[(1)](1)(1)(1)1()01,1a x x ax a x a g x x x x x a---+--+--'===⇒==-+, 〔1〕假设0a <,110a-+<,(0,1)x ∈,()0g x '<,()g x 单调递减;当(1,)x ∈+∞,()0g x '>,()g x 单调递增,那么max ()(1)1211g x g a a ==-<-⇒>,矛盾,不符题意;〔2〕假设0a >, 假设102a <≤,111a-+>,(0,1)x ∈,()0g x '<,()g x 单调递减,不符题意;假设112a <<,1011a <-+<,1(0,1)x a∈-+,()0g x '<,()g x 单调递减,不符题意;〔11(1)ln(1)10g a a -+=-+->矛盾;〕 假设1a ≥,110a-+≤,(0,1)x ∈,()0g x '>,()g x 单调递增;当(1,)x ∈+∞,()0g x '<,()g x 单调递减,那么max ()(1)121g x g a ==-≤-,符合题意;综上,得()1g x ≤-恒成立,实数a 的取值范围为1a ≥;……………6′ 〔ⅱ〕由〔ⅰ〕知,()1g x ≤-恒成立,实数a 的取值范围为1a ≥. 方法一:令sin [0,1)t θ=∈,考虑函数11()(1)(1)ln(1)(1)[ln(1)(1)]11a a P t g t g t t a t t a t t t--=+--=+-+------+-222221111211()22(1)[]11(1)(1)1(1)(1)a a P t a a a t t t t t t t --'=--++=-+-++-+--+-, 下证明()0P t '≥,即证:2222112(1)[]01(1)(1)a a t t t -+-+≥-+-,即证明 222211(1)[]01(1)(1)t a a t t t +-+-≥-+-,由2111t ≥-,即证22211(1)[]0(1)(1)t a a t t +-+-≥+-, 又10a -≥,只需证222110(1)(1)t t t +-+≥+-,即证22242221(1)(1)30(3)0t t t t t t t +≥+-⇐-≤⇐-≤,显然成立.即()p t 在[0,1)t ∈单调递增,min()(0)0p t p ==,那么()0p t ≥,得(1)(1)g t g t +≥-成立,那么对任意的[0,)2πθ∈,(1sin )(1sin )g g θθ-≤+成立、……………7′方法二:考虑函数11()(1sin )(1sin )ln(1sin )(1sin )[ln(1sin )(1sin )]1sin 1sin a a h g g a a θθθθθθθθθ--=+--=+-+------+-1sin 11ln2sin 1sin 1sin 1sin a a a θθθθθ+--=--+-+-1sin 11ln 2sin (1)()1sin 1sin 1sin a a θθθθθ+=-+-+--+ 21sin 2ln 2sin (1)()1sin 1sin a a θθθθ+=-+---。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019中考杭州市5月联考数学注意事项:1.本试题卷共8页,满分120分,考试时间100分钟.2.答题前,考生务必将自己的姓名、准考证号填写在答题卡的相应位置.3.全部答案在答题卡上完成,答在本试题卷上无效.4.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.5.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题共30分)一、选择题:本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.12-的倒数是( ) A.2B.2-C.12-D.122.下列计算中,正确的是( ) A.()222a b a b +=+B.()222a b a b -=-C. ()()122a b ab ++=+D.()()22a b a b a b +-+=-+3.据统计局公布,2018年浙江居民人均可支配收入45840元,数据45840用科学记数法表示为( ) A.34.58410⨯B.44.58410⨯C.50.458410⨯D.345.8410⨯4.如图,一个木块沿着倾斜角为47︒的斜坡,从A 滑行至B 巳知5AB =米,则这个木块的高度约下降了(参考数据:470.73sin ︒≈,cos470.68︒≈,tan 47 1.07︒≈)( )A.3.65米B.3.40米C.3.35米D.3.55米5.下面由四个相同正方形拼成的图形中,是中心对称图形但不是轴对称图形的是( )A. B. C. D.6.在圆内接四边形ABCD 中,若::2:3:4A B C ∠∠∠=,则D ∠=( ) A.90︒B.120︒C.150︒D.240︒7.实数a ,b ,c 在数轴上对应点的位置如图所示,若11a b>,则下列结论中一定成立的是( )A.0a c +>B.1bc>C.1b a +>D.0ab >8.某旅社有100张床位,若每张床位每晚收费100元,床位可全部租出,若每张床位每晚收费提高20元,则减少10张床位租出;若每张床位每晚收费再提高20元,则再减少10张床位租出.以每次提高20元的这种方法变化下去,为了投资少而收入最多,每张床位每晚应提高( ) A.60元B.50元C.40元D.40元或60元9.如图,在直角三角形ABC ∆中,90B ∠=︒,4AB =,3BC =,动点E 从点B 开始沿B C →以2cm/s 的速度运动至C 点停止;动点F 从点B 同时出发沿B A →以1cm/s 的速度运动至A 点停止,连接EF .设运动时间为x (单位:s ),ABC ∆去掉BEF ∆后剩余部分的面积为y (单位:2cm ),则能大致反映y 与x 的函数关系的图象是( )A. B. C. D.10.如图,已知O e 的内接ABC ∆中,12AB AC +=,AD BC ⊥于D ,3AD =,直径AE 交BC 边于点G ,有下列四个结论:①AG EG BG CG ⋅=⋅;②2BE EG AE =⋅;③当6AB =时,O e 的面积取得最大值36π;④三角形外接圆直径等于它的任两边的积与第三边上的高的比.其中正确结论有( )A.1个B.2个C.3个D.4个第Ⅱ卷(非选择题共90分)二、填空题:本题共6小题,每小题4分,共24分.11.写出一个比2大且比4小的无理数:_______.12.袋子中有30个除颜色外完全相同的小球.在看不到球的条件下,随机地从袋子中摸出1个球,记录颜色后放回,将球摇匀.大量重复上述过程后发现,每1800次,摸到红球420次,由此可以估计口袋中的红球个数是_______.13.已知某银行的贷款年基准利率是5%,老王和小张在这家银行贷款100万元,分别购买了一套新房,由于购入的时间不同,老王在年基准利率打七折时购入,小张在年基准利率上浮25%时购入.在各自贷款满一年后,这一年老王比小张少付______万元利息.14.如图,在ABC ∆中,点D ,E 分别是上一点,:1:3CE EB =,//DE AC .若ADE ∆的面积为S ,则ABC ∆的面积为________.15.已知二次函数2y ax bx c =++(0a ≠)图象上部分点的坐标(),x y 对应值列表如下:则关于x 的方程250ax bx ++=的解是_______.16.在平面直角坐标系xOy 中,点(),3A m -绕坐标原点O 顺时针旋转90︒后,恰好落在图中阴影区域(包括边界)内,则m 的取值范围是______.三、解答题:共66分.解答应写出文字说明、证明过程或演算步骤.17.已知方程()22110kx k x k +++-=. (1)当1k =时,求该方程的解; (2)若方程有实数解,求k 的取值范围.18.日前,某公司决定对塘栖枇杷品种进行培育,育苗基地对其中的四个品种“白砂”“红袍”“夹脚”“宝珠”共500粒种子进行发芽试验,从中选择发芽率最高的品种进行推广,通过实验得知“白砂”品种的发芽率为70%,并把实验数据绘成两幅统计图(部分信息未给出):(1)求实验中“红袍”品种的种子数量;(2)求实验中“白砂”品种的种子发芽的株数,并补全条形统计图; (3)从以上信息,你认为应选哪一个品种进行推广,请说明理由.19.如图,已知在O e 中,弦AB 垂直平分半径ON ,NO 的延长线交O e 于P ,连接AP ,过点A ,B 的切线相交于点M .(1)求证:ABM ∆是等边三角形; (2)若O e 的半径为2,求AP 的长.20.如图,正方形ABCD 两条对角线AC 、BD 交于O ,过O 任作一直线L 与边AB ,CD 交于M ,N ,MN 的垂直平分线与边BC ,AD 交于P ,Q .设正方形ABCD 的面积为1S ,四边形MPNQ 的面积为2S .(1)求证:四边形MPNQ 是正方形;(2)若11S =,求2S 的取值范围.21.如图,在平面直角坐标系xOy 中,一次函数1y k x b =+的图象与反比例函数2k y x=(0x >)的图象交于(),1A m m +,()3,1B m m +-两点.(1)求m 的值;(2)求出一次函数与反比例函数的表达式;(3)过点(),0P a 作x 轴的垂线,与直线1y k x b =+和函数2k y x=(0x >)的图象的交点分别为点M ,N ,当点M 在点N 下方时,写出a 的取值范围.22.已知二次函数243y ax ax b =-++(0a ≠). (1)求出二次函数图象的对称轴;(2)若该二次函数的图象经过点()1,3,且整数a ,b 满足49a b <+<,求二次函数的表达式; (3)对于该二次函数图象上的两点()11,A x y ,()22,B x y ,设11t x t ≤≤+,当25x ≥时,均有12y y ≤,请结合图象,直接写出t 的取值范围.23.定义:若一个三角形一条边上的高等于这条边长的一半,则称该三角形为“半高”三角形,这条高称为“半高”.(1)如图1,ABC ∆中,90ACB ∠=︒,2BC AC =,点P 在AB 上,PD AC ⊥于点D ,PE BC ⊥于点E ,连接BD ,DE 求证: BDE ∆是“半高”三角形;(2)如图2,ABC ∆是“半高”三角形,且BC 边上的高是“半高”,点P 在AB 上,//PQ BC 交AC 于点Q ,PM BC ⊥于点M ,QN BC ⊥于点N .①请探究BM ,PM ,CN 之间的等量关系,并说明理由;②若ABC ∆的面积等于16,求MQ 的最小值.2019中考杭州市5月联考数学 答案详解1.B 【解析】本题考查倒数的定义.2-的倒数是2-,故选B. 2.D 【解析】本题考查平方差公式.()2222a b a b ab +=++,()2222a b a b ab -=+-,()()1222a b ab a b ++=+++,()()221a a b a b +-+=-+,故选D.两个数的和与这两个数的差的积等于这两个数的平方差,这个公式就叫做乘法的平方差公式. 3.B 【解析】本题考查科学记数法.445840 4.58410=⨯,故选B.科学记数法是把一个数表示成10na ⨯的形式(其中110a ≤<,n 为整数).4.A 【解析】本题考查三角函数的定义.过A 点作水平面的垂线AC ,垂足为C ,则sin 47ACAB︒=,故50.73 3.65AC ≈⨯=(米),故选A. 5.D 【解析】本题考查轴对称和中心对称.根据中心对称图形的概念与轴对称图形的概念可知A ,C 既是中心对称图形又是轴对称图形;B 是轴对称图形但不是中心对称图形;D 是中心对称图形但不是轴对称图形,故选D.6.A 【解析】本题考查圆内接四边形的性质.因为圆内接四边形的对角互补,所以::2:3:4:3A B C D ∠∠∠∠=:,即33609012D ∠=︒⨯=︒,故选A. 7.D 【解析】本题考查不等式的性质.借助于数轴可知a c b <<,因此不能判断0a c +>,1b c>,1b a +>,故A ,B ,C 错误;而由11a b >得1100b a a bab -->⇒>,由于0b a ->,故0ab >,因此D 正确,故选D.8.A 【解析】本题考查一元二次方程的应用.设每张床位每晚收费应提高x 个20元,收入为y 元,根据题意得:()()21002010010200100010000y x x x x =+-=-++,∵()10002.52200x =-=⨯-时,y 取得最大值,又∵x 取整数,∴当2x =或3时,y 取得最大值,当3x =时,每张床位每晚收费提高60元,床位最少,即投资少,∴为了投资少而收入多,每张床位每晚收费应提高60元,故选A.9.B 【解析】本题考查根据分段函数来判断函数图象. 当302x ≤≤时,26y x =-;当342x <≤时,362y x =-,故选B. 10.C 【解析】本题考查内接三角形与外接圆的概念、相交弦定理、相似三角形的性质、圆周角定理、二次函数的性质.由相交弦定理得①是正确的;由条件并不能得出BEG ∆与AEB ∆相似,故②是错误的;由条件可证ABE ∆与ADC ∆相似,从而可得AE AD AB AC ⋅=⋅,进而可得O e 的半径,设AB x =,O e 的半径为y ,则有2126y x x =-+,故当6AB =时,O e 的最大面积为36π,故③是正确的;由AE AD AB AC ⋅=⋅这一结论一般化,得④是正确的,故选C.【解析】本题考查无理数的定义.,π小.12.7【解析】本题考查概率.根据实验频率估计概率,则估计口袋中的红球个数为4203071800⨯=,故答案为7.13.2.75【解析】本题考查列方程解决实际问题.老王应付利息1005%0.7 3.5⨯⨯=(万元);小张应付利息()1005%125% 6.25⨯⨯+=(万元),两者相减得2.75万元,故答案为2.75万元. 14.163S 【解析】本题考查相似三角形的性质.∵//DE AC ,∴ABC DBE ∆∆:,∴2239416DBE ABC S BE S BC ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭,而13ADE DBE S S ∆∆=,两式相乘得163ABC S S ∆=,故答案为163S . 15.110x =,220x =【解析】本题考查二次函数图象的性质.当0x =,30x =时,2y =,故二次函数图象的对称轴是直线15x =,且2c =,所以二次函数解析式为22y ax bx =++,由此可知方程250ax bx ++=的解即是223ax bx ++=-的解,即是求当3y =-时对应的x 值,由图象知x 为10或20,故答案为:110x =,220x =.16. 3.5 2.5m -≤≤-【解析】本题考查图象的旋转.将等腰三角形(阴影区域)逆时针旋转90︒,再求出该图形与直线3y =-相交的部分,故答案为 3.5 2.5m -≤≤-. 17.【名师指导】本题考查一元二次方程的解法.(1)把1k =代入,利用因式分解法解方程;(2)分0k =及0k ≠两种情况讨论.解:(1)把1k =代入原方程得230x x +=,解得10x =,23x =-.(2)当0k =时,方程10x -=有解;当0k ≠时,()()221410k k k +--≥,解得18k ≥-. 综上可得18k ≥-.18.【名师指导】本题考查扇形统计图和条形统计图.(1)根据扇形统计图得出“红袍”种子所占比例,即可求解;(2)根据条件及扇形统计图,得出结果;(3)根据条形统计图判断每个品种的种子发芽率,进而判断.解:(1)“红袍”品种的种子数量:()500130%25%25%100⨯---=(粒)(2)“白砂”品种的种子发芽的株数:50030%70%105⨯⨯=(株);补全条形统计图略.(3)“红袍”品种的种子发芽率:85100%85%100⨯=; “宝珠”品种的种子发芽率:100100%=80%50025%⨯⨯;“夹脚”品种的种子发芽率:100100%=80%50025%⨯⨯;因此,应该选择“红袍”品种进行推广. 19.【名师指导】本题考查三角形以及圆的性质.(1)连接OA ,利用圆的切线性质及等边三角形的判定即可证明;(2)由(1)中求得的结论,利用勾股定理,可算出AP 的长.解:(1)证明:连接OA ,设AB 与ON 的交点为D . ∵MA ,MB 分别切O e 于A ,B , ∴OA MA ⊥,MA MB =, ∵弦AB 垂直平分半径ON , ∴1122OD ON OA ==, ∴30OAD ∠=︒,故60BAM ∠=︒, ∴ABM ∆是等边三角形.(2)∵2OA OP ==,由(1)可知1OD =,∴在Rt AOD ∆中,AD =∴在Rt APD ∆中,AP ===20.【名师指导】本题考查正方形的性质、二次函数的性质.(1)利用全等三角形的判定定理及正方形的性质证明;(2)利用二次函数的性质进行求解. 解:(1)证明:∵QP 垂直平分线段MN , ∴MQ NQ =,PM PN =, 由条件可证()AOQ DON ASA ∆≅∆, ∴OQ ON =,∴45OQN ONQ ∠=∠=︒,同理可得45OQM OMQ OMP OPM ∠=∠=∠=∠=︒, ∴90NQM QMP MPN PNQ ∠=∠=∠=∠=︒, ∴四边形MPNQ 是矩形,而MQ NQ =, ∴四边形MPNQ 是正方形.(2)设AQ DN x ==,则1QD x =-, ∴()22222211112212222S QN x x x x x ⎛⎫==+-=-+=-+≥ ⎪⎝⎭而211S S ≤=, ∴2112S ≤≤. 21.【名师指导】本题考查一次函数和反比例函数.(1)由反比例函数的性质可以求出m 的值;(2)列出关于1k 与b 的二元一次方程组,解方程组,进而可得到一次函数解析式,由反比例函数的概念可得反比例函数的解析式;(3)观察图象,再利用一次函数和反比例函数的性质即可得出a 的取值范围.解:(1)由反比例函数概念可得()()()131m m m m +=+-,解得3m =.(2)将点()3,4A ,()6,2B 代入1y k x b =+得1134,62,k b k b +=⎧⎨+=⎩解得12,36,k b ⎧=-⎪⎨⎪=⎩所以一次函数的解析式为263y x =-+.由23412k =⨯=,可得反比例函数的解析式为2y x=(0x >). (3)观察图象可得出03a <<或6a >. 22.【名师指导】本题考查二次函数的性质.(1)由对称轴公式即可求解;(2)观察函数图象,在给定的范围内,找出对应关系,即可求得二次函数的表达式;(3)分类讨论,利用函数图象,结合函数的对称性即可得出t 的取值范围. 解:(1)二次函数图象的对称轴是422ax a-=-=. (2)该二次函数的图象经过点()1,3, ∴433a a b -++=,∴3b a =, 把3b a =代入49a b <+<, 得439a a <+<.当0a >时,449a <<,则914a <<. 而a 为整数,∴2a =,则6b =, ∴二次函数的表达式为2289y x x =-+; 当0a <时,429a <-<,则922a -<<-. 而a 为整数,∴3a =-或4-, 则对应的9b =-或12-,∴二次函数的表达式为23126y x x =-+-或24169y x x =-+-. (3)14t -≤≤.23.【名师指导】本题考查新定义、相似三角形、二次函数的性质.(1)根据新定义进行证明;(2)①利用新定义的概念进行转化;②将MQ 的长度用二次函数表示出来,利用二次函数的性质进行求解.解:(1)证明:由题意可证得PBE ABC ∆∆:, ∴12PE AC BE BC ==, ∴2BE PE =,由题意可证得四边形CEPD 为矩形,∴DC PE =, ∴2BE DC =,∴BDE ∆是“半高”三角形.(2)①2BM CN PM +=.理由如下:如图,过A 作AE BC ⊥于E ,交PQ 于D ,∵ABC ∆是“半高”三角形,且BC 边上的高是“半高”,∴2BC AE =∵//PQ BC ,∴APQ ABC ∆∆:,∴2PQ AD =,∴()2BC PQ AE AD -=-,由题意可证得四边形MNQP 是矩形,有PQ MN =,PM DE QN ==, ∴2BC MN PM -=,即2BM CN PM +=. ②∵2111624ABC S BC AE BC ∆=⨯==,故8BC =, 设PM x =,由①得82PQ x =-,∴MQ ==∴当165x =时,MQ .。
