运筹学实验1答案
运筹学

目录试验一(习题1.1)试验二(例题1.1)试验三(习题1.2)试验四(习题3.1)试验五(习题3.2)试验六(习题3.6)试验七(习题4.1)试验八(习题4.2)试验九(习题4.5)试验十(习题5.1)试验一(习题1.1)一、问题的提出某工厂利用甲、乙、丙三种原料,生产A、B、C、D四种产品。
每月可供应应该厂原料甲600吨、乙500吨、丙300吨。
生产1吨不同产品所消耗的原料数量及可获得的利润如表1-4所示。
问:工厂每月应如何安排生产计划,才能使总利润最大?表1-4 三种原来生产四种产品的有关数据二、线性规划模型解(1)决策变量。
本问题的决策变量是两种产品A、产品B、产品C、产品D、的每月产量,可设:x1表示产品A的产量;x2表示产品B的产量;x3表示产品C的产量;x4表示产品D的产量。
(2)目标函数。
本问题的目标是四种产品的总利润。
由于产品A、产品B、产品C和产品D单位利润分别为200元、250元、300元和400元,所以,每月总利润z可表示为:z=200x1+250x2+300x3+400x4。
(元)(3)约束条件。
本问题的约束条件共有四个。
第一个约束条件是原料甲的供应量限制,生产产品A需要原料甲1吨;生产产品B需要原料甲1吨;生产产品C需要原料甲2吨:生产产品D需要原料甲2吨,所以生产x1吨产品A、x2吨产品B、x3吨产品C和x4吨产品D所需的原料为x1+x2+2x3+2x4。
由题意,原料甲每月原料供应量为600吨。
由此可得第一个约束条件:x1+x2+2x3+2x4<=600第二个约束条件是原料甲的供应量限制,生产产品A需要原料乙0吨;生产产品B需要原料乙1吨;生产产品C需要原料乙1吨:生产产品D需要原料乙3吨,所以生产x1吨产品A、x2吨产品B、x3吨产品C和x4吨产品D所需的原料为 x2+x3+3x4。
由题意,原料甲每月原料供应量为500吨。
由此可得第一个约束条件:x2+x3+3x4<=500第三个约束条件是原料甲的供应量限制,生产产品A需要原料丙0吨;生产产品B需要原料丙2吨;生产产品C需要原料丙1吨:生产产品D需要原料丙0吨,所以生产x1吨产品A、x2吨产品B、x3吨产品C和x4吨产品D所需的原料为x1+2x2+x3。
运筹学部分课后习题集解答1

,.运筹学部分课后习题解答用图解法求解线性规划问题min z=2x 1 3x 24x 1 6 x 26a )2 x 2 4s..t 4x 1 x 1, x 2 0解:由图 1 可知,该问题的可行域为凸集 MABCN ,且可知线段 BA 上的点都为最优解,即该问题有无量多最优解,这时的最优值为z min =233 0 32用图解法和纯真形法求解线性规划问题max z=10x 15x 2a )3x 1 4x 295x 1 2 x 2 8st..x 1, x 2 0解:由图 1 可知,该问题的可行域为凸集 OABCO ,且可知 B 点为最优值点,3x 1 4x 2x 1 1T93 ,即最优解为 x *3即2 x 2 8x 21,5x 1 22这时的最优值为 z max =10 1 53 352 2,.纯真形法:原问题化成标准型为max z=10x15x23x1 4 x2x39st.. 5x12x2x48x1 , x2 , x3 , x40c j10500C B X B b x1x2x3x40x3934100x48[5]201C j Z j105000x321/50[14/5]1-3/510x18/512/501/5C j Z j010-25x23/2015/14-3/1410x1110-1/72/7C j Z j00-5/14-25/14,.1,3T1015335因此有 x*, zmax222已知线性规划问题:max z 2 x14x2x3 x4x13x2x482x1x26x2x3x46x1x2x39x1 , x2 , x3, x40求: (1)写出其对偶问题;(2)已知原问题最优解为X*(2,2,4,0) ,试依据对偶理论,直接求出对偶问题的最优解。
解:( 1)该线性规划问题的对偶问题为:min w8 y1 6 y26 y3 9 y4y1 2 y2y423y1y2y3y44y3y41y1y31y1, y2 , y3 , y40(2 )由原问题最优解为X*(2,2,4,0) ,依据互补废弛性得:y1 2 y2y423 y1y2y3y44y3y41把 X *(2,2,4,0)代入原线性规划问题的拘束中得第四个拘束取严格不等号,即22489y40y1 2 y22进而有3y1y2y34y31,.得 y143, y2, y3 1, y45543因此对偶问题的最优解为 y*(,,1,0)T,最优值为w min1655考虑以下线性规划问题:min z 60x140x280x33x12x2x324x1x23x342x12x22x33x1, x2 , x30( 1)写出其对偶问题;(2 )用对偶纯真形法求解原问题;解:( 1)该线性规划问题的对偶问题为:max w 2y1 4 y23y33y1 4 y2 2 y3602 y1 y22y340y13y22y380y1, y2 , y30(2 )在原问题加入三个废弛变量x4 , x5 , x6把该线性规划问题化为标准型:max z60x140 x280x33x12x2x3x424x1x23x3x542 x12x22x3x63x j0, jL,6 1,c j-60-40-80000 C B X B b x1x2x3x4x5x6 0x4-2-3-2-1100 0x5-4[-4]-1-30100x6-3-2-2-2001C j Z j-60-40-800000x410-5/45/41-1/12080x1111/43/40-1/400x6-10[-3/2]-1/20-1/21C j Z j0-25-350-1500x411/6005/311/3-5/6 80x15/6102/30-1/31/6 40x22/3011/301/3-2/3 C j Z j00-80/30-20/3-50/3x*( 5,2,0) T , z max60540280 023063633某厂生产A、B、C三种产品,其所需劳动力、资料等相关数据见下表。
运筹学习题答案(1)

第一章 线性规划及单纯形法(作业)1.4 分别用图解法和单纯型法求解下列线性规划问题,并对照指出单纯形表中的各基可行解对应图解法中可行域的哪一顶点。
(1)Max z=2x 1+x 2St.⎪⎩⎪⎨⎧≥≤+≤+0,24261553212121x x x x x x 解:①图解法:由作图知,目标函数等值线越往右上移动,目标函数越大,故c 点为对应的最优解,最优解为直线⎩⎨⎧=+=+242615532121x x x x 的交点,解之得X=(15/4,3/4)T 。
Max z =33/4. ② 单纯形法:将上述问题化成标准形式有: Max z=2x 1+x 2+0x 3+0x 4St. ⎪⎩⎪⎨⎧≥≤++≤++0,,,242615535421421321x x x x x x x x x x其约束条件系数矩阵增广矩阵为:P 1 P 2 P 3 P 4⎥⎦⎤⎢⎣⎡241026150153 P 3,P 4为单位矩阵,构成一个基,对应变量向,x 3,x 4为基变量,令非基变量x 1,x 2为零,找到T 优解,代入目标函数得Max z=33/4.1.7 分别用单纯形法中的大M 法和两阶段法求解下列线性规划问题,并指出属哪一类。
(3)Min z=4x 1+x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 解:这种情况化为标准形式: Max z '=-4x 1-x 2⎪⎪⎩⎪⎪⎨⎧=≥=++=-+=+)4,3,2,1(0426343342132121j xj x x x x x x x x 添加人工变量y1,y2Max z '=-4x 1-x 2+0x 3+0x 4-My 1-My 2⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x(2) 两阶段法: Min ω=y 1+y 2St.⎪⎪⎩⎪⎪⎨⎧≥=≥=++=+-+=++0,).4,3,2,1(04263433214112321121y y j xj x x x y x x x y x x第二阶段,将表中y 1,y 2去掉,目标函数回归到Max z '=-4x 1-x 2+0x 3+0x 4第二章 线性规划的对偶理论与灵敏度分析(作业)2.7给出线性规划问题:Max z=2x 1+4x 2+x 3+x 4⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥≤++≤++≤+≤++)4,3,2,1(096628332143221421j x x x x x x x x x x x x j要求:(1)写出其对偶问题;(2)已知原问题最优解为X *=(2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
运筹学部分课后习题集解答1

运筹学部分课后习题解答P47 1.1用图解法求解线性规划问题min z=2x 3x 2 4为 6x 2 6 a )s.t 4x i 2x 24X i ,X 2 0解:由图1可知,该问题的可行域为凸集 MABCN ,且可知线段BA 上的点3都为最优解,即该问题有无穷多最优解,这时的最优值为Z m i n =2 3 * 3 0 3P47 1.3用图解法和单纯形法求解线性规划问题max z=10x.| 5x 23x 1 4x 2 9 s.t 5x 1 2x>8x 1, x> 0解:由图1可OABCO ,且可知B 点为最优值点,小 3x-| 4x 29 即125x 1 2x 28x 1X 213,即最优解为x * 21,3v1图1单纯形法:原问题化成标准型为max z=10x15x23\ 4x2 x39 s.t 5\ 2x2 x48X i,X2,X3,X40P78 2.4已知线性规划问题:max z 2X | 4x 2 x 3 x-i 3X 2 X 4 82为 x 26 x 2 x 3 x 4 6 x | x 2 x 39XiXX, x 4求:(1)写出其对偶问题;(2)已知原问题最优解为X * (2,2,4,0),试根据对偶理论,直接求出对偶问题的最优解。
解:(1)该线性规划问题的对偶问题为:min w 8y 1 6y 2 6y 3 9y 4y 1 2y 2 y 4 2 3y 1 y 2 y 3 y 4 4 y 3 y 4 1y 1y 31%,丫2”3,丫4(2)由原问题最优解为X * (224,0),根据互补松弛性得:y 1 2y 2 y 4 2 3y 1 y 2 y w 4y a y 4 1把X *(2,2,4,0)代入原线性规划问题的约束中得第四个约束取严格不等号, 即 2 2 48 9 y 4 0 y 1 2y 22从而有3y 1 y 2 y 34所以有x *13,zmax 10 1 5I35 "2X 4y a 1/曰 4 3 “门得y i 、目2 ,y3 i,y4 05 5所以对偶问题的最优解为y* (-,3,1,0)T,最优值为W min 165 5P79 2.7考虑如下线性规划问题:(1)写出其对偶问题;min z 60为40x2 80x33为2x2x3 24x1 X2 3x3 42x1 2x2 2x3 3捲必,怡0(2 )用对偶单纯形法求解原问解:(1)该线性规划问题的对偶问题为:max w 2y1 4y2 3y33y i 4y2 2y3 602y1 y2 2y3 40 >y1 3y2 2y3 80 ,y1,y2,y3 0(2)在原问题加入三个松弛变量X4,X5,X6把该线性规划问题化为标准型max z 6 0x140X280x3x12x2X3 X4 24为x3x3 x 42x-| 2x22X3 X6 3X j 0,j 1L ,6* 52max 56 3 6 3 3P81 2.12某厂生产A、B、C三种产品,其所需劳动力、材料等有关数据见下表。
运筹学答案(1,2章)

1.1解(1)用图1-1中的阴影部分分为此线性规划问题的可行域,目标函数123z x x =+,即21133z x x =-+是斜率为13-的一族平行线,易知123,0x x ==为可行解,由线性规划的性质知,其最值在可行域的顶点取得,将直线1233x x +=沿其法线方向逐渐向上平移,直至A 点,A 点坐标为(2,4)。
所以 max 23414z =+⨯= 此线性规划问题有唯一最优解。
(2)用图1-2中的阴影部分分为此线性规划问题的可行域,目标函数121.5z x x =+,即212233x x z =-+是斜率为23-的一族平行线,易知123,0x x ==为可行解,由线性规划的性质知,其最值在可行域的顶点取得。
将直线121.53x x +=沿其法线方向逐渐向下平移,直至B 点,B 点坐标为31(,)22。
所以 319max 1.5224z =+⨯= 此线性规划问题有唯一最优解。
(3)用图1-3中的阴影部分分为此线性规划问题的可行域,目标函数1222z x x =+,即212zx x =-+是斜率为1-的一族平行线,易知120,0x x ==为可行解。
在将直线12220x x +=沿其法线方向逐渐向上平移的过程中发现:目标函数的值可以增加到无穷大,故此线性规划问题为无界解。
(4)如图1-4所示,此问题的可行域为空集,故此线性规划问题无可行解。
1.4 (2)解法一:图解法图中的阴影部分为此线性规划问题的可行域,目标函数1225z x x =+,即21255z x x =-+是斜率为25-的一族平行线,易知120,0x x ==为可行解,将直线12250x x +=沿其法线方向逐渐向上平移,直至B 点,B 点坐标为(2,6)。
所以 m a x22563z =⨯+⨯=解法2:单纯形法将上述问题化为标准型如下:12345max 25000z x x x x x =++++132412512345 + =4 212..3x 2 =18,,,,0x x x x s t x x x x x x x ⎧⎪+=⎪⎨++⎪⎪≥⎩下面用单纯形法进行计算,见下表:表的最终结果表明:最优解(2,6,2,0,0)TX=目标函数最优值m a x34z=迭代第一步得(1)(0,0,4,12,18)TX=表示图中原点。
运筹学1至6章习题参考答案

-0.25
1
1.5
2
C(j)-Z(j)
-1.75
0
0
1.25
0
-12.5
X1
-3
1
0
2
-1
0
2
M
X2
-5
0
1
-0.5
0.5
0
2
4
X5
0
0
0
-1.5
[0.5]
1
0
0
C(j)-Z(j)
0
0
3.5
-0.5
0
-16
X1
-3
1
0
-1
0
2
2
X2
-5
0
1
1
0
-1
2
X4
0
0
0
-3
1
2
0
C(j)-Z(j)
0
0
2
0
1
【解】设xj、yj(j=1,2,…,6)分别为1~6月份的生产量和销售量,则数学模型为
(1)
(2)目标函数不变,前6个约束右端常数800改为1000,第7~11个约束右端常数200改为0,第12个约束“≤200”改为“=-200”。
1.4某投资人现有下列四种投资机会,三年内每年年初都有3万元(不计利息)可供投资:
0
0
0
R. H. S.
Ratio
Basis
C(i)
X1
X2
X3
X4
X5
X6
X4
0
-1
2
3
1
0
0
4
M
X5
0
[4]
运筹学实验一
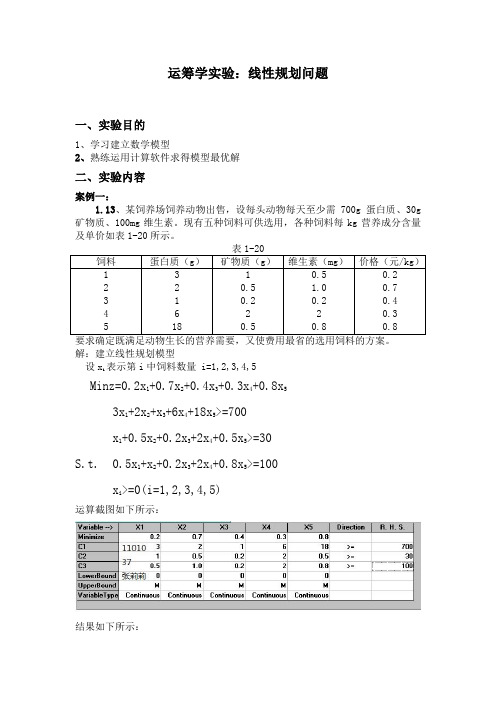
运筹学实验:线性规划问题一、实验目的1、学习建立数学模型2、熟练运用计算软件求得模型最优解二、实验内容案例一:1.13、某饲养场饲养动物出售,设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。
现有五种饲料可供选用,各种饲料每kg 营养成分含量及单价如表1-20所示。
表1-20饲料 蛋白质(g ) 矿物质(g ) 维生素(mg ) 价格(元/kg ) 1 2 3 4 5 3 2 1 6 18 1 0.5 0.2 2 0.5 0.5 1.0 0.2 2 0.8 0.2 0.7 0.4 0.30.8 要求确定既满足动物生长的营养需要,又使费用最省的选用饲料的方案。
解:建立线性规划模型设x i 表示第i 中饲料数量 i=1,2,3,4,5Minz=0.2x 1+0.7x 2+0.4x 3+0.3x 4+0.8x 53x 1+2x 2+x 3+6x 4+18x 5>=700x 1+0.5x 2+0.2x 3+2x 4+0.5x 5>=30S.t. 0.5x 1+x 2+0.2x 3+2x 4+0.8x 5>=100x i >=0(i=1,2,3,4,5)运算截图如下所示:结果如下所示:案例二:1.18、宏银公司承诺为某建设项目从2003年起的4年中每年初分别提供以下数额贷款:2003年——100万元,2004年——150万元,2005年——120万元,2006年——110万元。
以上贷款资金均需于2002年底前筹集齐。
但为了充分发挥这笔资金的作用,在满足每年贷款额情况下,可将多余资金分别用于下列投资项目:(1)、于2003年初购买A种债券,期限3年,到期后本息合计为投资额的140%,但限购60万元;(2)、于2003年初购买B种债券,期限2年,到期后本息合计为投资额的125%,且限购90万元;(3)、于2004年初购买C种债券,期限2年,到期后本息合计为投资额的130%,但限购50万元;(4)、于每年年初将任意数额的资金存放于银行,年息4%,于每年年底取出。
运筹学(第五版) 习题答案

1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
(1)min z=-3 +4 -2 +5
4 - +2 - =-2
+ +3 - 14
-2 +3 - +2 2
, , 0, 无约束
(2)max
0 (i=1…n; k=1,…,m)
(1)解:设z=- , = - , , 0
标准型:
从行差额或者列差额中找出最大的选择它所在的行或者列中的最小元素丙列中的最小元素为3由此可以确定产地的产品应先供应丙的需要而产地的产量等于丙地的销量故在2丙处填入0同时将运价表中的丙列和第二行的数字划去得到
运筹学习题答案
第一章(39页)
1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
初始单纯形表:
-M
-M
…
-M
…
…
…
b
…
…
…
…
-M
1
1
0
…
0
1
1
…
…
0
0
…
0
-M
1
0
1
…
0
0
…
…
0
0
…
0
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
…
-M
1
0
0
…
1
0
0
…
0
…
1
1
…
1
-s
nM
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学
一、素材:北方化工厂月生产计划安排
根据经营现状和目标,合理制定生产计划并有效组织生产,使一个企业提高效益的核心。
特别是对于一个化工厂而言,由于其原料品种多,生产工艺复杂,原材料和产成品存储费用较高,并有一定的危险性,对其生产计划作出合理安排就显得尤为重要。
现要求对北方化工厂的生产计划作出合理安排。
有关数据
1、生产概况
北方化工厂现有职工120人,其中生产工人105人,该厂主要设备是2套提取生产线,每套生产线容量为800kg,至少需要10人看管,该厂每天24小时连续生产,节假日不停机,从原料投入到成品出线平均需要10小时,成品率约为60%,该厂只有4t卡车1辆,可供原材料运输。
2、产品结构及有关资料
该厂目前的产品可分为5类,所用原料15种,根据厂方提供的资料,经整理得表1-1。
3、供销情况
(1)根据现有运输条件,原料3从外地购入,每月只能购入1车。
(2)根据前几个月的购销情况,产品1和产品3应占总产量的70%,产品2的产量最好不要超过总产量的5%,产品1的产量不要低于产品3与产品4产量之和。
二、建模思路
分析:
设:Xi为产品i=(1、2、3……5)的月生产量,Pi为产品的产品价格,Cj为原料j(j=1……
15)的原料价格,aji为原料j在产品i中的含量。
总利润=总收入-总成本
目标函数:
整理得:maxZ=4.44X1+6.09X2+5.30X3+26.95X4+6.95X5
约束条件:
①2套提取生产线,每套容量为800kg,每天24小时连续连续生产,原料投入到成品出线
平均需要10小时,成品率约为60%。
X1+X2+X3+X4+X5=(30×24×800×2×60%)/10
②原料3从外地购入,每月只能购入1车,4吨卡车1辆。
9.4%X1+5.4%X2+4.5%X3+1.7%X4+8.6%X5≤4000
③产品1和产品3应占总产量的70%
X1+X3=70%(X1+X2+X3+X4+X5)
④产品2的产量最好不要超过总产量的5%
X2≤5%(X1+X2+X3+X4+X5)
⑤产品1的产量不要低于产品3与产品4的产量之和。
X1≥X3+X4
三、约束条件
目标函数:maxZ= 4.44X1+6.09X2+5.30X3+26.95X4+6.95X5
约束条件:
X1+X2+X3+X4+X5=(30×24×800×2×60%)/10
9.4%X1+5.4%X2+4.5%X3+1.7%X4+8.6%X5≤4000
X1+X3=70%(X1+X2+X3+X4+X5)
X2≤5%(X1+X2+X3+X4+X5)
X1≥X3+X4
X1,X2,X3,X4,X5≥0
四、求解方法
打开管理运筹学软件,打开软件……选择线性规划……新建……输入数据……解决……输出结果
五、输出结果
六、数据分析。
