数据结构第三章栈教学ppt
合集下载
数据结构 课件 第3章 栈

实用数据结构基础
第3章 栈
第 3 章 栈
知
识点
栈的定义和特点 栈的基本运算和算法 栈的典型应用
难
点
后缀表达式的算法 数制的换算 利用本章的基本知识设计相关的应用问题
要
求
掌握栈的特点 掌握栈的基本运算 熟悉栈的各种实际应用 能设计栈应用的典型算法 了解栈的运算时间复杂度分析
第3章 目录
2.顺序栈运算的基本算法 (1)置空栈 首先建立栈空间,然后初始化栈顶指针。 SeqStack *Snull( ) { SeqStack *s; s=new (SeqStack);
// 在C语言中用s=malloc(sizeof(SeqStack)) ;
s->top= –1; return s; }
3-1 栈的定义与运算 3-2 栈的存储和实现 3-3 栈的应用举例 小 结 验证性实验3: 栈子系统 自主设计实验3:后缀表达式求值 单元练习3
3-1 栈的定义和运算
3-1-1 栈(Stack)的定义
1. 栈的定义 栈是限制在表尾进行插入和删除的线性表。 进栈 出栈
an …… a3 a2 a1
图3-1栈的 示意图
3-3.
3-3-1 数制转换
栈的应用举例
数值进位制的换算是计算机实现计算和处理的 基本问题。比如将十进制数N转换为j进制的数,其 解决的方法很多,其中一个常用的算法是除j取余法。 将十进制数每次除以j,所得的余数依次入栈,然后 按“后进先出”的次序出栈便得到转换的结果。 其算法原理是: N =(N / j)* j + N % j
由于栈的操作只能在栈顶进行的,所以用链表的头部做
栈顶是最合适的。链栈结构如图3-4所示。
第3章 栈
第 3 章 栈
知
识点
栈的定义和特点 栈的基本运算和算法 栈的典型应用
难
点
后缀表达式的算法 数制的换算 利用本章的基本知识设计相关的应用问题
要
求
掌握栈的特点 掌握栈的基本运算 熟悉栈的各种实际应用 能设计栈应用的典型算法 了解栈的运算时间复杂度分析
第3章 目录
2.顺序栈运算的基本算法 (1)置空栈 首先建立栈空间,然后初始化栈顶指针。 SeqStack *Snull( ) { SeqStack *s; s=new (SeqStack);
// 在C语言中用s=malloc(sizeof(SeqStack)) ;
s->top= –1; return s; }
3-1 栈的定义与运算 3-2 栈的存储和实现 3-3 栈的应用举例 小 结 验证性实验3: 栈子系统 自主设计实验3:后缀表达式求值 单元练习3
3-1 栈的定义和运算
3-1-1 栈(Stack)的定义
1. 栈的定义 栈是限制在表尾进行插入和删除的线性表。 进栈 出栈
an …… a3 a2 a1
图3-1栈的 示意图
3-3.
3-3-1 数制转换
栈的应用举例
数值进位制的换算是计算机实现计算和处理的 基本问题。比如将十进制数N转换为j进制的数,其 解决的方法很多,其中一个常用的算法是除j取余法。 将十进制数每次除以j,所得的余数依次入栈,然后 按“后进先出”的次序出栈便得到转换的结果。 其算法原理是: N =(N / j)* j + N % j
由于栈的操作只能在栈顶进行的,所以用链表的头部做
栈顶是最合适的。链栈结构如图3-4所示。
数据结构 第3章 栈和队列PPT课件
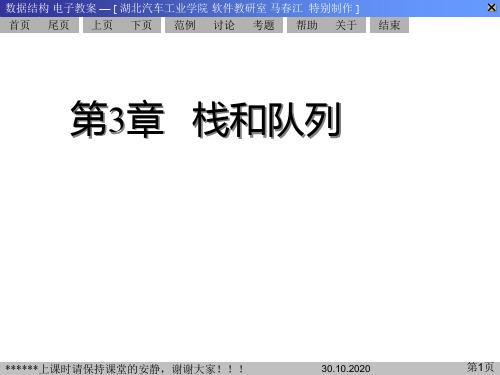
else
{
s.top++;
s.stack[s.top]=x;
}
}
******上课时请保持课堂的安静,谢谢大家!!!
30.10.2020
× 第11页
数据结构 电子教案 — [ 湖北汽车工业学院 软件教研室 马春江 特别制作 ] 首页 尾页 上页 下页 范例 讨论 考题 帮助 关于 结束
(3)退栈
void pop(seqstack &s)
30.10.2020
× 第9页
数据结构 电子教案 — [ 湖北汽车工业学院 软件教研室 马春江 特别制作 ] 首页 尾页 上页 下页 范例 讨论 考题 帮助 关于 结束
2、栈的五种运算
(1)初始化栈
void inistack(seqstack &s)
{
s.top=0;}源自******上课时请保持课堂的安静,谢谢大家!!!
×
首页 尾页 上页 下页 范例 讨论 考题 帮助 关于 结束
主要内容 栈
队列
这两种结构都是特殊的线性表
******上课时请保持课堂的安静,谢谢大家!!!
30.10.2020
第2页
数据结构 电子教案 — [ 湖北汽车工业学院 软件教研室 马春江 特别制作 ]
×
首页 尾页 上页 下页 范例 讨论 考题 帮助 关于 结束
Operation:
Void inistack(&s) //将栈S置为一个空栈(不含任何元素)
Void Push(&s,x) //将元素X插入到栈S中,也称为 “入栈”、 “插 入”、 “压入”
Void Pop(&s) //删除栈S中的栈顶元素,也称为”退栈”、 “删 除”、 “弹出”
第3章栈和队列素材PPT课件

{
if (top == NULL) return 1;
else return 0;
}
3) Lpush(slink *ptop, datatype x ) //进栈
{
slink p = (slink)malloc(sizeof(snode)) ; //生成进栈p节点
p->data = x;
p->next = *ptop; *ptop = p; //p节点作为新的栈顶链入
X出栈
栈顶top 栈底bottom
X
an-1
…
a1 a0
.
C语言函数调用和返回 是如何正确实现的?
2
栈的定义及其基本操作
栈的特点: ✓ 后进先出(Last In First Out,LIFO)
若元素进栈顺序为a0,a1,…,an-1,则出栈顺序是an-1,an-2,…, a0,即后进栈的元素先出栈,故栈可称作“后进先出” 的线性表。 ✓ 栈顶是唯一的出入口
Push(&S, e) 初始条件:栈S存在且未满。 操作结果:插入数据元素e,使之成为新栈顶元素。
Pop(&S) 初始条件:栈S存在且非空。 操作结果:删除S的栈顶元素并返回其值。
GetTop(S) 初始条件:栈S存在且非空。 操作结果:返回栈顶元素的值。
...... } ADT Stack;
.
5
3.1 栈
S->top
S = (sqlink)malloc(sizeof(sqstack));
则S指向一个顺序栈,如右图所示。
1
栈顶元素an-1写作:S->data [S->top] 栈空时S->top == -1
0
ch03_1栈和队列1-栈PPT教学课件

while(ch!=EOF) {
while(ch!=EOF && ch!=‘\n’) {
switch(ch) {
case ‘#’: Pop(S, ch);
break;
case ‘@’: ClearStack(S); break;
default: Push(S, ch); break;
}
ch=getchar();
只须证明,若借助栈由输入序列(1,2,…,n)得到输出序列
(p1,p2,…,pn),那么在输出序列中,不可能出现这种情况:存 在i<j<k,使pj<pk<pi. 这里(p1,p2,…,pn)是(1,2,…,n)的一个全排 列,每个元素只能按1,2,…,n的次序进一次栈。
提示
2020/12/12
i<j<k说明进栈顺序为(…i…j…k…),它们的出 栈排列只有6种可能:
}
ClearStack(S);
if(ch!=EOF) ch=getchar();
}
DestroyStack(S);
} 2020/12/12
12
栈的应用:迷宫求解
东南西北 (顺时针)
演示
2020/12/12
13
迷宫求解策略
求迷宫中一条路径的算法的基本思想是:
若当前位置"可通",则纳入"当前路径",并继续朝"下一位置“
a2
栈底
a1
2020/12/12
2
栈的基本操作
1.初始化栈:IniStack(&S) 将栈S置为一个空栈(不含任何元素)。
注意这两个 操作的区别
2.进栈:Push(&S,X)
数据结构栈和队列ppt课件

栈的运用 例3.1 将一个十进制正整数N转换成r进制的数
N 〕
1835
229
28
3
N / 8 〔整除〕 N % 8〔求余
229
3
低
28
5
3
4
0
3
高
❖例3.2 算术表达式中括号匹配的检查
❖用栈来实现括号匹配检查的原那么是,对表达式从左 到右扫描。
❖〔1〕当遇到左括号时,左括号入栈;
❖〔2〕当遇到右括号时,首先检查栈能否空,假设栈 空,那么阐明该“右括弧〞多余;否那么比较栈顶左 括号能否与当前右括号匹配,假设匹配,将栈顶左括 号出栈,继续操作;否那么,阐明不匹配,停顿操作 。
❖在顺序栈上实现五种根本运算的C函数 ❖〔3〕入栈 ❖int push (SeqStack *s, DataType x) ❖{ if (s->top==MAXSIZE-1) /*栈满不能入栈*/ ❖{ printf("overflow"); ❖return 0; ❖} ❖ s->top++; ❖ s->data[s->top]=x; ❖ return 1; ❖}
链队列及运算的实现
采用链接方法存储的队列称为链队列〔Linked Queue〕
采用带头结点的单链表来实现链队列,链队列中 的t结ype点de类f st型ruc与t N单od链e 表一样。将头指针front和尾指针 re{arD封at装aTy在pe一da个ta;构造体中,链队列用C言语描画如 下:struct Node *next;
❖只设了一个尾指针r ❖头结点的指针,即r->next ❖队头元素的指针为r->next->next ❖队空的断定条件是r->next==r
数据结构3栈和队列PPT教学课件

~AStack() { delete [] elements; } // Destructor
void clear() { top = 0; }
注意:这里top在第I个位置
2020/12/12
8
一些重要的条件
栈满:top==maxSize-1; 栈空:top==-1
2020/12/12
9
链式栈
{
private:
int MaxSize;
// 栈中最大元素个数
int top;
// 栈中实际元素个数
T *elements; // 存储栈元素的数组
public:
AStack(int sz =DefaultListSize) // Constructor
{ size = sz; top = 0; elements = new T[sz]; }
virtual void MakeEmpty() = 0; virtual int isEmpty() virtual int isFull()=0
};
2020/12/12
5
顺序栈
由于栈是运算受限的线性表,因此 线性表的存储结构对栈也适应。
栈的顺序存储结构简称为顺序栈, 它是运算受限的线性表。因此,可用 数组来实现顺序栈。因为栈底位置是 固定不变的,所以可以将栈底位置设 置在数组的两端的任何一个端点;栈 顶位置是随着进栈和退栈操作而变化 的,故需用一个整型变量top
时间上:顺序栈为O(1),链式栈为O(1) 空间上:顺序栈要一个固定的长度,当栈不够
满时,空间浪费;链式栈长度可变,但对于每 个元素需要一个链接域,产生结构性开销。 何时使用顺序栈? 当要实现多个栈时,可用一个数组存储两个栈, 且最好是一个栈增长时另一个栈缩短。
第3章1 栈和队列 (数据结构教程PPT课件)

*x)
{ StackNode *p; if (top= =NULL) return NULL;
else { *x = top->data;
p = top; top = top->next; free (p); return top; } }
3.2 栈的应用举例
例 3.1 简单应用:数制转换问题
将十进制数N转换为r进制的数,其转换方法利用辗转相除法: 以N=3467,r=8为例转换方法如下:
N 3467 433 N / 8 (整除) N % 8(求余) 433 54 3 1 低
54
6
6
0
6
6 高
所以:(3467)10 =(6613)8
我们看到所转换的8进制数按低位到高位的顺序产生 的,而通常的输出是从高位到低位的,恰好与计算过程 相反,因此转换过程中每得到一位8进制数则进栈保存, 转换完毕后依次出栈则正好是转换结果。
基本操作算法: ⑴ 置空栈:首先建立栈空间,然后初始化栈顶指针。 SeqStack *Init_SeqStack()
{ SeqStack *s;
s=malloc(sizeof(SeqStack)); s->top= -1; return s; } ⑵ 判空栈
int Empty_SeqStack(SeqStack *s)
第3章 栈和队列
本章主要介绍以下内容:
栈的概念、存储结构及其基本操作
队列的概念、存储结构及其基本操作 栈与队列的应用举例
退出
3.1 栈
3.2 栈的应用举例 3.3 队列
3.4 队列的应用举例
3.1 栈
3.1.1 栈的定义
栈是一种特殊的线性表。其特殊性在于限定插入 和删除数据元素的操作只能在线性表的一端进行。如 下所示: a1, a2, a3, ..., an 插入和删除端
数据结构第03章栈和队列.ppt

a1 称为 栈底元素 an 称为 栈顶元素
插入元素到栈顶(即表尾)的操作,称为入栈。 从栈顶(即表尾)删除最后一个元素的操作,称为出栈。
强调:插入和删除都只能在表的一端(栈顶)进行!
6
栈的抽象数据类型
ADT Stack{ 数 据 对 象 : D={ai | ai ElemSet , i=1 , 2,... ,n,n>=0} 数据关系: R={<ai-1 , ai >| ai-1 , ai D , i=2,...,n} 基本操作: 栈初始化:StackInit() 判栈空:StackEmpty(S) 入栈:Push(S,x) 出栈:Pop(S)
较好的做法是,设立一个输入缓冲区,用以 接受用户输入的一行字符,然后逐行存入用户数 据区。允许用户输入出错,并在发现有误时可以 及时更正。
29
可以把输入缓冲区设为一个栈结构,每当 从终端接受了一个字符后先作如下判别:如果 它既不是退格符也不是退行符,则将该字符压 入栈顶;如果是一个退格符,则从栈顶删去一 个字符;如果是一个退行符,则将字符栈清空 为空栈。
19
顺序栈基本操作--初始化
SqStack InitStack(SqStack &S) {//构造一个空栈S S.base=(SElemtype *)malloc (STACK_INIT_SIZE)*sizeof(SElemtype); if(!S.base) exit(OVERFLOW); S.top=s.base; S.stackzise=STACK_INIT_SIZE; return OK; }
] 6
) 7
] 8
可能出现的不匹配的情况: 1.到来的右括弧不是所“期待”的; 2.到来的是“不速之客”(左括号); 3.直到结束,也没有到来所“期待”的;
插入元素到栈顶(即表尾)的操作,称为入栈。 从栈顶(即表尾)删除最后一个元素的操作,称为出栈。
强调:插入和删除都只能在表的一端(栈顶)进行!
6
栈的抽象数据类型
ADT Stack{ 数 据 对 象 : D={ai | ai ElemSet , i=1 , 2,... ,n,n>=0} 数据关系: R={<ai-1 , ai >| ai-1 , ai D , i=2,...,n} 基本操作: 栈初始化:StackInit() 判栈空:StackEmpty(S) 入栈:Push(S,x) 出栈:Pop(S)
较好的做法是,设立一个输入缓冲区,用以 接受用户输入的一行字符,然后逐行存入用户数 据区。允许用户输入出错,并在发现有误时可以 及时更正。
29
可以把输入缓冲区设为一个栈结构,每当 从终端接受了一个字符后先作如下判别:如果 它既不是退格符也不是退行符,则将该字符压 入栈顶;如果是一个退格符,则从栈顶删去一 个字符;如果是一个退行符,则将字符栈清空 为空栈。
19
顺序栈基本操作--初始化
SqStack InitStack(SqStack &S) {//构造一个空栈S S.base=(SElemtype *)malloc (STACK_INIT_SIZE)*sizeof(SElemtype); if(!S.base) exit(OVERFLOW); S.top=s.base; S.stackzise=STACK_INIT_SIZE; return OK; }
] 6
) 7
] 8
可能出现的不匹配的情况: 1.到来的右括弧不是所“期待”的; 2.到来的是“不速之客”(左括号); 3.直到结束,也没有到来所“期待”的;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
连续出现的两个操作数和在它 例如:Exp= a ×b + (c –d /e) ×f 们之前且仅靠它们的运算符构 前缀式(波兰式):+ ×ab ×-c/def 成一个最小表达式 中缀式:a ×b + c –d /e ×f 后缀式(逆波兰式):ab × cde/-f ×+
结论:1)操作数之间的相对次序不变 2)运算符的相对次序不同 3)中缀式丢失了括号信息,致使运算的次序变得不确定 4)前缀式的运算规则为: 5)后缀式的运算规则为: 运算符在式中出现的顺序恰为表达式的运算顺序
a1称为栈底元素 强调:插入和删除都只能在表 的一端(栈顶)进行!
an称为栈顶元素
插入元素到栈顶的 操作,称为入栈。 从栈顶删除最后一 个元素的操作,称 为出栈。
想一想:要从栈中取出a1, 应当如何操作?
栈的存储结构
• 顺序栈 – 实现:一维数组s[M] top top F 5 top E 4 top D 3 top 2 C
栈底
Struct SNode * next; } Node; Node *st, *p; int m=sizeof(Node);
(2) 操作
链栈 入栈 函数
Push (SElemType e) { p=(Node*)malloc(m); if(!p){上溢} else{ p->data=e; p->next=st; st=p;} }
“进”=插入=压入=PUSH(an+1) “出”=删除=弹出=POP(an)
Q2:顺序表和顺序栈的操作有何区别?
以线性表 S= (a1 , a2 , …. , an-1 , an )为例 顺序表S 顺序栈S 表尾 高地址 an+1 高地址 an an …… …… S[i] ai ai ……
低地址
栈顶top 栈顶top
Q1:堆栈是什么?它与一般线性表有什么不同?
堆栈是一种特殊的线性表,它只能在表的一端(即 栈顶)进行插入和删除运算。 与一般线性表的区别:仅在于运算规则不同。
一般线性表 逻辑结构:1:1 存储结构:顺序表、链表 运算规则:随机存取 堆栈 逻辑结构: 1:1 存储结构:顺序栈、链栈 运算规则:后进先出(LIFO)
4. 运算规则
5. 实现方式
基本操作有:建栈、判断栈满或栈空、入栈、出栈、 读栈顶元素值,等等。
栈 是仅在表尾进行插入、删除操作的线性表。 表尾(即 an 端)称为栈顶 /top ; 表头(即 a1 端)称为栈底/base 例如: 栈 S= (a1 , a2 , a3 , ……….,an-1 , an )
栈也可以用链式结构来表示,用链式结构来表示的栈就是链栈
data next
(1) 链栈的构造方式——以头指针为栈顶,在头指针处插入或删除. st
an an-1
栈顶
链栈中每个结点由两个域构成: data域和next域,其定义为: typedef Struct SNode{
SElemType
data;
a2 a1
每个运算符和它之前出现且仅靠它的两 个操作数构成一个最小表达式
后缀表达式求值步骤: 如何求后缀表 1、读入表达式一个字符 达式呢? 2、若是操作数,压入栈,转4 3、若是运算符,从栈中弹出2个数,将运算结果再压入栈 4、若表达式输入完毕,栈顶即表达式值; 若表达式未输入完,转1
例 计算 4+3*5=
等价于 --s.top e=*s.to p
top
低地址L
核心语句: Pop ( ); Pop ( ); Printf( Pop () );
顺序栈出栈函数POP() status Pop( ) { if(top=L) { 下溢 } else { e=* --s.top; return(e);} }
链栈的入栈操作和出栈操作
初始条件:栈s已经存在 操作结果:若栈为空栈,则返回TRUE,否则FALSE
Push(&s,e)
初始条件:栈s已经存在且非空 操作结果:插入元素e为新的栈顶元素
StackLength(s)
初始条件:栈s已经存在 操作结果:返回栈的元素个数,即栈的长度
Pop(&s,&e)
初始条件:栈s已经存在且非空 操作结果:删除s的栈顶元素, 并用e返回其值
插入表头
链栈 出栈 函数
Status Pop( ) { if(st==NULL){下溢} else{e=st->data;p=st; st=st->next; free(p); return(e);} }
从表头删除
由此可以看出:一个链栈由其栈顶指针唯一指定 设st指向栈顶元素,当st=NULL时表示栈空
数 据 结 构
李
鑫
辽宁工程技术大学
辽宁工程技术大学电信学院
数据结构课程的内容
第三章 栈和队列
3.1 栈(Stack) 3.2 队列(Queue)
1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式
1. 定义 2. 逻辑结构 3. 存储结构 4. 运算规则 5. 实现方式
3.1 栈
基本操作
InitStack(&s)
操作结果:构造一个空栈
DestroyStack(&s)
初始条件:栈s已经存在 操作结果:栈s被销毁
ClearStack(&s)
初始条件:栈s已经存在 操作结果:将s清为空
GetTop(s,&e)
初始条件:栈s已经存在且非空 操作结果:用e返回s的栈顶元素
StackEmpty(s)
Q3:什么叫“向上生成”的栈? “向下生成”又是何意?
若入栈动作使地址向高端增长,称为“向上生成”的栈; 若入栈动作使地址向低端增长,称为“向下生成”的栈;
对于向上生成的堆栈:
入栈口诀:堆栈指针top ―先压后加” : S[ top++ ]=an+1 出栈口诀:堆栈指针top ―先减后弹” : e=S[ --top ]
本节重点:顺序栈和链栈的基本操作
栈的抽象数据类型定义: (教材P44-45) ADT Stack{ 数据对象:D={D={ai | ai∈ElemSet, i=1,2,…,n,n≥0} 数据关系:R=={< ai –1, ai > | ai ห้องสมุดไป่ตู้1, ai ∈D, i=2,…,n}} 约定an端为栈顶,a1端为栈底。 入栈、出栈、 基本操作: 建栈初始化、 …… 判断栈满或栈空、 读栈顶元素值等。 } ADT Stack
几点说明:
1) 链栈不必设头结点,因为栈顶(表头)操作频繁;
2) 链栈一般不会出现栈满情况,除非没有空间导致 malloc分配失败。
3) 链栈的入栈、出栈操作就是栈顶的插入与删除操作, 修改指针即可完成。 4) 采用链栈存储方式的优点是,可使多个栈共享空间; 当栈中元素个数变化较大,且存在多个栈的情况下, 链栈是栈的首选存储方式。
动态数组 顺序栈的存储表示(教材P46): #define #define STACK-INIT-SIZE STACKINCREMENT 100 //存储空间初始分配量 10 //存储空间分配增量
//栈的基址即栈底指针
//栈顶指针
typedef struct{
SElemType
SElemType int
*base;
*top;
stacksize; //当前分配的空间
}SqStack;
顺序栈的入栈操作——例如用堆栈存放(A,B,C,D)
高地址M
top B top A top C B A top D C B A
低地址L
top A
核心语句: top=L; Push (A); Push (B); Push (C); Push (D);
A)a,b,c,d C)b,c,d,a
B)c,d,a,b D)a,c,d,b
答: A)、D)可以, B)、C)不行。 讨论:有无通用的判别原则? 有!若输入序列是 …,Pj…Pk…Pi …(Pj<Pk<Pi) , 一定不存在这样的输出序列 …,Pi…Pj…Pk …
即对于输入序列1,2,3,不存在输出序列3,1,2
1 0 栈空 top B A 进栈 栈满 5 4 3 2 1 0 top top F E D C
栈空
5
top
top top
4 3
2 1 0
top
top
B
A 出栈
top=0
栈顶指针top,指向实际栈顶 后的空位置,初值为0
设数组维数为M top=0,栈空,此时出栈,则下溢(underflow) top=M,栈满,此时入栈,则上溢(overflow)
a2 a1
表头
低地址
…… a2 a1
栈底base
写入:S[i]= ai 读出: e= S[i]
压入(PUSH): S[top++]=an+1 弹出( POP) : e=S[--top]
前提:一定要预设栈顶指针top
顺序栈S
高地址
栈顶top
an+1 an …… ai …… a2 a1
低地址
栈底base 栈不存在的条件: base=NULL; 栈为空 的条件 : base=top; 栈满的条件 : top-base=stacksize;
例 把十进制数159转换成八进制数
8 159 余7 余3 top top 7 2 3 7 top 3 7
top
8 19 8 2 0
余2
2 3 7
(159)10=(237)8
Void conversion(){ //对于输入的任意一个非负十进制整数,打印输出与其等值的八进制数。 InitStack(s)//构造空栈 scanf(“%d”,N); while(N){ Push(s,N%8); N=N/8;} While(!StackEmpty(s)){ pop(s,e); printf(“%d”,e); } } //conversion
