2.3 平行线的特征(含答案)-
平行线的特征

动手做一做 实验:在准备好的横格本上任选两条平行线 、 实验 在准备好的横格本上任选两条平行线a、 在准备好的横格本上任选两条平行线 b 与平行线a、 相交 相交. (1)任意画一条直线 与平行线 、b相交. )任意画一条直线c与平行线 (2)任选一对同位角,用量角器度量,看 )任选一对同位角,用量角器度量, 看这一对同位角有什么关系? 看这一对同位角有什么关系?
问题讨论
请大家想一想:两条平行线被第三条直线所截,内错角、 请大家想一想:两条平行线被第三条直线所截,内错角、 同旁内角有什么关系呢 ? 如图,已知直线a//b,思考 如图,已知直线 , c ∠1与∠2、 ∠2与∠3之间有什么关 与 、 与 之间有什么关 为什么? 系?为什么? 4 a 1 已知) (1) ∵ a//b (已知 ) 已知 3 2 ∴∠2=∠ ( 两直线平行, ∴∠ ∠4( 两直线平行,同位角相等 ) b 又∵∠1=∠4 ( 对顶角相等 ) ∵∠ ∠ ∴∠1=∠ ∴∠ ∠2
同旁内角互补 )
平行线的三个特征: 平行线的三个特征 :
同位角相等 内错角相等 同旁内角互补
两直线平行
两直线平行的三个条件: 两直线平行的三个条件: 同位角相等 内错角相等 同旁内角互补 两直线平行
例1:小青不小心把家里的梯形玻璃块打碎了,还剩下梯 :小青不小心把家里的梯形玻璃块打碎了, 形上底的一部分(如图).要订造一块新的玻璃, ).要订造一块新的玻璃 形上底的一部分(如图).要订造一块新的玻璃,已经 你想一想, 量得 ∠A=1150,∠D=1000. 你想一想,梯形另外两个 角 各是多少度? 已知梯形的两底AD//BC) 各是多少度?(已知梯形的两底 ) 已知) 解:∵ AD//BC (已知). ∵ A+ B= C+ D= ∴ ∠A+∠B=1800;∠C+∠D=1800 两直线平行,同旁内角互补) (两直线平行,同旁内角互补). 已知) 又∵ ∠A=1150;∠D=1000. (已知 已知 ∴ ∠C=1800-∠D=1800-1000=800. = = ? B ? C ∠B=1800-∠A=1800-1150=650. = = A
七年级数学2.3平行线的特征(1)

课题:2.3平行线的特征(1)课型:新授课授课人:授课时间:2013年4月2日,星期二,第二节教学目标:1.经历观察、操作、推理、交流等活动,了解平行线的性质,能运用这些性质进行简单的推理或计算.2.经历观察、操作、推理、交流等活动,进一步发展空间观念、推理能力和有条理地表达的能力;经历探索平行线的特征的过程.3.通过学生学习动手操作、观察、合作、交流,进一步感受学习数学的意义,培养主动探索、合作以及解决问题的能力.教学重点:经历观察、操作、推理、交流等活动,经历探索平行线的特征的过程.教学难点:进一步发展空间观念、推理能力和有条理地表达的能力.设计理念:为学生提供充足的探索与交流的时间和空间,重视学生在实际操作以及在操作过程中的思考,使学生的空间观念、推理能力得到培养.教法与学法:我设计的思路是先让学生去猜测结论,然后再动手操作验证自己的猜想,遇到困难时可以在组内相互交流、探讨,然后以组为单位汇报成果或困惑,最终达成共识.对于本节课的难点,我设计了三个层次,先运用自己的语言叙述,再根据“框图”进行推理,第三个层次是通过填空来感受逻辑推理过程.这样设计,是为了给学生们足够的思维空间,当学生“够不到”时,我就设计一个“台阶”,如果还“够不到”,就再设计一个台阶.我设计了第一个层次,为他们提供了这样一个平台,体现了教师是数学学习的组织者.而第二、第三个层次,则体现了教师是数学学习的引导者.在这三个层次中,学生始终是数学学习的主人.教学准备:直尺、量角器、圆头剪刀.一、创设情景,导入新课师:演示课件:(过马路的片段)你是怎样穿过马路的呢?生:(非常感兴趣)生1:走斑马线.生2:有时着急没等到绿灯就斜穿过去了.师:把笔直马路的两边近似看成两条平行线,人走过的路径近 似看成一条直线演示课件,大家注意,这些角它们之间有 什么关系,这就是今天我们要研究的内容. 师:板书课题:2.3平行线的特征(1)【设计意图】从实物中抽象出数学模型,体现出数学来源于实践,展现了学生由“感性”到“理性”的认识过程.[教学效果]:学生积极性都很高,为本课的学习开了个好头. 二、实验探究,合作交流师:让每个学生利用三角尺在练习本上画出两条平行线(你还记得点画平行线的方法吗) 生:(齐声回答)记得找出其中的同位角、内错角,同旁内角. 学生:(小组活动交流动手操作)生1:同位角 4对 ∠2与∠6 ∠4与∠8 ∠1与∠5 ∠3与∠7 生2:内错角 2对 ∠3与∠6 ∠4与∠5 生3:同旁内角:2对 ∠3与∠5 ∠4与∠6 师:每对同位角大小有什么关系?例如:∠1与∠5小组合作:测量、剪拼,组内交流,相互释疑,再以组为单位,汇总成果或困惑,全班展示 【实验结论】文字叙述,两条平行线被第三条直线所载,同位角相等,简记为,两直线平行,同位角相等. 符号:∵a ∥b∴∠1=∠2(两直线平行,同位角相等)【设计意图】设计这一环节,是为了让学生经历探索平行线性质的过程,通过猜想,操作、验证、交流等一系列活动进一步发展学生的空间观念,同时有利于学生对平行线性质的理解. [教学效果]:引导学生用符号表示性质,为今后书写推理过种奠定基础.加深了对性质的理解.1 2 3 45 6 7 8·1 2 3 45 67 8a bc师:我们已经知道,两直线平行,同位角相等,那么大家猜想一下,在两直线平行的条件下内错角、同旁内角会有什么样的数量关系呢?能否用符号语言表示它们的关系呢? 生:探讨(留给学生充分探索时间)师:可利用“两直线平行,同位角相等”来说明内错角、同旁内角的大小关系. 生:(小组交谈后)有的说用量角器,有的说可以剪下来拼一拼,课堂气氛可热烈了. 师:那么大家就按照你们说的做一做吧! 生1:小组实验结果:两直线平行内错角相等.生2:两直线平行,同旁内角互补. 两直线平行,同位角相等 师:随之教师结合图理解板书平行线的特征: 两直线平行,内错角相等 两直线平行,同旁内角互补 师:符号:(1)∵ a ∥b ∴∠3=∠6 生1:(两直线平行,内错角相等) 师:符号:(2)∵ a ∥b∴∠3+∠5=180°生2:(两直线平行,同旁内角互补)【设计意图】:通过鼓励学生实际操作,以及在操作过程中进行思考,发展学生的空间观念,使学生对平行线的性质更深入理解.[教学效果]:学生不仅能用语言说出性质,而且能用符号表示. 牛刀小试(走近生活)师:生活中有许多现象与平行线的特征有关系,比如:太阳光射在镜子上,在墙上形成的亮点.生:光的反射师:(演示课件P50页 做一做)你是怎么思考的,你的想法与它的想法一样吗? 生:(小组形式展开讨论,充分交流后回答) 生1:(1) ∵ AB ∥DEB E 1234CFDABE∴∠1=∠3(两直线平行,同位角相等)又∵∠1=∠2(已知)∠3=∠4∴∠2=∠4(等量代换)生2:(2)∵∠2=∠4∴BC ∥EF (同位角相等,两直线平行)师:学生回答非常好,教师要给予表扬鼓励.【设计意图】实际问题出发,激发学生的学习兴趣培养学生的自信以,为后面的学习打下基础.三、判定性质,对比记忆师:提问、叙述平行线的判定和性质的区别和联系. 生1:平行线的判定 生2:平行线的性质 生3:区别(各叙己见)师:平行线的判定和性质的条件,结论刚好相反.直线平行的条件是由角的“数量关系”确定直线的“位置关系”;而平行线的特征是由两直线“位置关系”确定角的“数量关系” 归纳:判定:角的数量关系线的位置关系 性质:线的位置关系角的数量关系接着课件显示如图: 师:已知:AD ∥BCAB ∥CD (1)∠1=∠B 吗? (2)∠2=∠D 吗? (3)∠C +∠D =180°吗? 生1:(1)∵ AD ∥BC (已知)∴∠B =∠1 (两直线平行,同位角相等)生2:(2)∵ AB ∥CD (已知)∴∠D =∠1 (两直线平行,内错角相等)生3:(3)∵ AD ∥BC (已知)∴∠C +∠D =180°(两直线平行,同旁内角互补)【设计意图】学生勇跃的回答,在思维碰撞的过程中,学生思维敏捷性得到了训练,学的知A BCD 1识得到巩固.[教学效果]:通过类比思考学生能够总结步骤.为下一步运用做准备. 四、巩固练习,掌握新知 1.建筑趣问用投影展示著名的比萨斜塔,求它与地面所成的较大的角是多少度?对比发现,加深理解填写下表,并思考二者有何区别和联系分层练习,小组比赛在下图中a ∥b ,你知道∠1的度数吗?(1) (2) (3)2.写出能够推得直线AB ∥CD 的条件.【设计意图】通过具体问题,使学生进一步认识和理解平行线的性质和判定直线平行的条件平行线的特征直线平行的条件85°?a b c1ab c1 36°abc1120°ACBD4 1 32 5 6 78的区别和联系。
平行线的判定及性质 例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (2)平行公理的推论:平行于同一条直线的两条直线. (3)在同一平面内,垂直于同一条直线的两条直线. (4)同位角相等,两直线平行. (5)内错角相等,两直线平行.(6)同旁内角互补,两直线平行.3、平行线的性质(1)两直线平行,同位角相等. (2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.二、【例题精讲】专题一:余角、补角、对顶角与三线八角例题1:∠A的余角与∠A的补角互为补角,那么2∠A是()A.直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中,下列判断正确的是()A.4对同位角,2对内错角,4对同旁内角B.4对同位角,2对内错角,2对同旁内角C.6对同位角,4对内错角,4对同旁内角D.6对同位角,4对内错角,2对同旁内角【活学活用2】如图2-82,下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是()A.对顶角B.互余C.互补D相等例题2:如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角分别是_______.【活学活用4】如图,∠AOC +∠DOE +∠BOF = .专题二:平行线的判定例题3:如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行,那么这样的平行棱共有 ( )A .9对B .16对 C.18对 D .以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图2-97,已知:∠1=∠2=,∠3=∠4,∠5=∠6.求证:AD ∥BC.4、如图2—101,若要能使AB ∥ED ,∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ,若a ∥b ,a ⊥c ,b ⊥d ,则c 、d 的位置关系为( ) A.互相垂直 B .互相平行 C.相交 D .没有确定关系专题三:平行线的性质1、如图,110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行,则BOC ∠= . 2、如图,AB //CD ,BC //DE ,则∠B+∠D = .3、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE .若60DOE ∠=,则∠AOC 的度数是 .4、 如图,175,2120,375∠=∠=∠=,则4∠= .13 425、如图,//AB CD ,直线EF 分别交AB 、CD 于E 、F ,ED 平分BEF ∠,若172∠=,则2∠= .【例题讲解】例1:如图,已知:AD ∥BC, ∠AEF=∠B,求证:AD ∥EF 。
2.3 平行线的特征(原卷版)

第二单元第3课时平行的特征一、选择题1.下列说法:①两直线平行,同旁内角互补;②内错角相等,两直线平行;③同位角相等,两直线平行;④垂直于同一条直线的两条直线平行,其中是平行线的性质的是 ( ) . A.① B.②和③ C.④ D.①和④2. 若∠1和∠2是同旁内角,若∠1=45°,则∠2的度数是 ( )A.45° B.135° C.45°或135° D.不能确定3.如图AB∥CD,∠E=40°,∠A=110°,则∠C的度数为()A.60° B.80°C.75° D.70°4.如图所示,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为( )A.150° B.130° C.120° D.100°5.如图,OP∥QR∥ST,则下列等式中正确的是( )A.∠1+∠2-∠3=90°B.∠2+∠3-∠1=180°C.∠1-∠2+∠3=180°D.∠1+∠2+∠3=180°6. 如图,AB∥CD∥EF,BC∥AD,AC平分∠BAD,且交EF于点O,则与∠AOE相等的角有( )A.5个 B.4个 C.3个 D.2个7.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于()A.23°B.16°C.20°D.26°8.如图所示,AB∥CD,若∠2是∠1的2倍,则∠2等于 ( ) .A.60° B.90° C.120° D.150°9.下列图形中,由AB∥CD,能得到∠1=∠2的是( ) .10.如图所示,已知AD与BC相交于点O,CD∥OE∥AB.如果∠B=40°,∠D=30°,则∠AOC的大小为( ) .A.60° B.70° C.80° D.120°二、填空题11. 画线段AB,延长线段AB到点C,使BC=2AB;反向延长AB到点D,使AD=•AC,则线段CD=______AB.12.如图,已知AB∥CD,∠α= .13.如图,BC∥DE,AD⊥DF,∠l=30°,∠2=50°,则∠A= .14.一个人从点A出发向北偏东60°方向走了4m到点B,再向南偏西80°方向走了3m到点C,那么∠ABC的度数是________.三、解答题15.已知如图,AB∥CD,试解决下列问题:(1)∠1+∠2= ;(2)∠1+∠2+∠3= ;(3)∠1+∠2+∠3+∠4= ;(4)试探究∠1+∠2+∠3+∠4+…+∠n= .16.如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?。
2.3平行线的特征-主观

2.3 平行线的特征填空题一、性质1. 两条直线被第三条直线所截,如果同位角相等,那么同旁内角。
难易程度:易答案:互补2.(1)若一个角的两边与另一个角的两边分别垂直,那么这两个角的关系是;(2)若一个角的两边与另一个角的两边分别平行,那么这两个角的关系是。
难易程度:易答案:(1)相等或互补(2)相等或互补3.两条直线被第三条直线所截,如果有一组同位角相等,那么其他三组同位角也一定。
难易程度:易答案:分别相等4.若两个角的一边在同一条直线上,另一边互相平行,则这两个角。
难易程度:易答案:相等或互补5.若两条平行线被第三条直线所截,则同旁内角的平分线相交所成的角的度数是。
难易程度:易答案:90°6.两条直线平行,相等,相等,互补。
难易程度:易答案:同位角,内错角,同旁内角二、根据图形求角的度数1.如图,a∥b,c是截线,∠1=49°53’,则∠2= ,∠2的补角= 。
难易程度:易答案:49°53’130°7’2.如果AB∥CD,∠ABE=120°,∠DCE=35°,则∠BEC= 。
难易程度:易答案:95°3.已知l1∥l2∥l3,AB⊥l1,垂足为点A,∠ABC=120°,则α= 。
难易程度:易答案:30°4.一个人从点A出发向北偏东方向走了4 m,到点B再从点B向南偏西15°方向走了3 m 到点C,那么∠ABC= 。
难易程度:易答案:30°5.如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD= 。
难易程度:易答案:25°6.如图,已知∠1与∠2互余,∠3是∠2余角的补角,若∠3=132°,则∠4= 。
难易程度:易答案:138°7.如图所示,直线AB∥ED,∠B=70°,∠BCM=∠ECM,则∠DCM 。
难易程度:易答案:125°8.如图所示,AB∥CD,∠ABE=66°,∠CDE=54°,则∠E的度数为。
2022-2023学年北师大版七年级数学下册《2-3平行线的性质》知识点分类练习题(附答案)

2022-2023学年北师大版七年级数学下册《2.3平行线的性质》知识点分类练习题(附答案)一.平行线的性质1.如图,已知AB∥CD,BE,DE分别平分∠ABF和∠CDF,且交于点E,则()A.∠E=∠F B.∠E+∠F=180°C.2∠E+∠F=360°D.2∠E﹣∠F=180°2.如图,AB∥CD,连接AC、BC、BD,且BD⊥BC,下列结论:①若∠A=2∠BDC,则∠ABC=∠ACB;②若∠BDC与∠A互补,则2∠ABC+∠ACB=90°,则()A.仅①正确B.仅②正确C.①②都正确D.①②都不正确3.如图,已知AB∥CD,点E,F分别在AB,CD上,点G,H在两条平行线AB,CD之间,∠AEG和∠GHF的平分线交于点M.若∠EGH=82°,∠HFD=20°,则∠M的度数为()A.31°B.36°C.41°D.51°4.如图,AB∥CD,BF平分∠ABE,且BF⊥DE,垂足为F,则∠ABE与∠EDC的数量关系是()A.∠EDC﹣∠ABE=90°B.∠ABE+∠EDC=180°C.∠ABE=∠EDC D.∠ABE+∠EDC=90°5.如图,AB∥CD,点E为AB上方一点,FB、CG分别为∠EFG、∠ECD的角平分线,若∠E+2∠G=210°,则∠EFG的度数为()A.140°B.150°C.130°D.160°6.如图,AB∥DE,BC⊥CD,则以下说法中正确的是()A.α,β的角度数之和为定值B.α随β增大而增大C.α,β的角度数之积为定值D.α随β增大而减小7.如图,AB∥EF,∠C=90°,则α、β和γ的关系是()A.β=α+γB.α+β+γ=180°C.α+β﹣γ=90°D.β+γ﹣α=180°8.如图,l1∥l2∥l3,∠1,∠2,∠3如图所示,则下列各式正确的是()A.∠3=∠1+∠2B.∠2+∠3﹣∠1=90°C.∠1﹣∠2+∠3=180°D.∠2+∠3﹣∠1=180°9.如图,已知直线AB,CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB,CD,AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③180°﹣α﹣β,④360°﹣α﹣β,∠AEC的度数可能是()A.①②③B.①②④C.①③④D.①②③④10.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,则两次拐弯的角度可以是()A.第一次向右拐40°,第二次向左拐140°B.第一次向左拐40°,第二次向右拐40°C.第一次向左拐40°,第二次向右拐140°D.第一次向右拐40°,第二次向右拐40°11.如图,已知长方形纸片ABCD,点E和点F分别在边AD和BC上,且∠EFC=37°,点H和点G分别是边AD和BC上的动点,现将点A,B,C,D分别沿EF,GH折叠至点N,M,P,K,若MN∥PK,则∠KHD的度数为()A.37°或143°B.74°或96°C.37°或105°D.74°或106°12.如图,在墙面上安装某一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行.若第一个弯道处∠B=140°,则第二个弯道处∠C也为140°,能解释这一现象的数学知识是()A.两直线平行,内错角相等B.内错角相等,两直线平行C.两直线平行,同位角相等D.同位角相等,两直线平行13.如图,将一条两边互相平行的纸带折叠,折痕为DE,∠ABE平分线所在直线与∠EDH 平分线所在直线相交于点F,若∠F=∠BED,则∠1的度数为.14.如图,点F是长方形ABCD的边BC上一点,将长方形的一角沿AF折叠,点B落在点E处,若AE∥BD,∠ADB=28°,则∠AFC=°.15.如图,在四边形纸片ABCD中,AB∥CD,将纸片沿EF折叠,点A、D分别落在A′、D′处,且A′D′经过点B,FD′交BC于点G,连结EG,EG平分∠BEF.(1)若∠CFG=76°,则∠BEG的度数是;(2)若EG∥A′D′,∠A+∠DFE=125°,则∠CFE的度数是.16.如图1,在矩形纸片ABCD中,点P在AD上,点Q在BC上,将纸片沿PQ折叠,点C,D的对应点分别为点E,F.PF交BQ于点G.设∠QPG=α.继续折叠纸片,使GF 落在BC边上(如图2),折痕为GM.(1)若α=60°,则∠MGF=°.(2)沿GF继续折叠,若GM恰好是∠PGF的三等分线,则α=°.17.如图,已知AM∥CN,D为AM,CN之间一点,∠EAD=32°,∠DCN=88°,∠EAD 与∠DCN的角平分线交于点B,连结BD交AM、CN与点E、F,若∠ABD:∠CBD=4:1,则∠ADF:∠CDF的比值为.18.如图1,将一条两边互相平行的纸袋折叠.(1)若图中α=70°,则β=°(2)在图1的基础上继续折叠,使得图1中的CD边与CB边重合(如图2),若继续沿CB边折叠,CE边恰好平分∠ACB,则此时β的度数为度.19.如图1,将长方形纸片ABCD沿MN折叠得到图2,点A,B的对应点分别为点A′,B',折叠后A′M与CN相交于点E.(1)若∠B′NC=48°,求∠A′MD的度数.(2)设∠B′NC=α,∠A′MN=β.①请用含α的代数式表示β.②当MA′恰好平分∠DMN时,求∠A′MD的度数.20.如图,已知C为两条相互平行的直线AB,ED之间一点,∠ABC和∠CDE的角平分线相交于F.(1)当∠FDC+∠ABC=180°时:①判断直线AD与BC的关系,并说明理由.②若∠ABC=130°,求∠DFB的度数.(2)当∠C=α时,直接写出∠DFB的度数(用含α的代数式表示).二.平行线的判定与性质21.小明和小亮在研究一道数学题,如图EF⊥AB,CD⊥AB,垂足分别为E,D,G在AC 上.小明说:“如果∠CDG=∠BFE,则能得到∠AGD=∠ACB”;小亮说:“连接FG,如果FG∥AB,则能得到∠GFC=∠ADG”.则下列判断正确的是()A.小明说法正确,小亮说法错误B.小明说法正确,小亮说法正确C.小明说法错误,小亮说法正确D.小明说法错误,小亮说法错误22.如图,AD,BC相交于点O,∠MCD=∠BCM=α,∠B=4α.(1)求证:AB∥CD;(2)若∠A=∠B,求∠BOD的度数;(用含α的式子表示)(3)若点E在AB上,连接OE,EP平分∠OEB交CM于点P,如备用图所示,求证:∠COE=2∠EPC+∠B.23.如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.(1)求证:EF∥BC;(2)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.24.已知:直线EF分别与直线AB,CD相交于点G,H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∥CD;(2)如图2,点M在直线AB,CD之间,连接GM,HM,求证:∠M=∠AGM+∠CHM;(3)如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N,连接GN,若∠N=∠AGM,∠M=∠N+∠FGN,求∠MHG的度数.25.如图,已知∠1+∠BDE=180°,∠2+∠4=180°.(1)证明:AD∥EF;(2)若∠3=90°,∠4=140°,求∠BAC的度数.参考答案一.平行线的性质1.解:过点E作EM∥AB,如图:∵AB∥CD,EM∥AB∴CD∥EM,∴∠ABE=∠BEM,∠CDE=∠DEM,∵∠ABF的平分线与∠CDF的平分线相交于点E,∴∠ABE=∠ABF,∠CDE=∠CDF,∴∠BED=∠BEM+∠DEM=(∠ABF+∠CDF),∵∠ABF+∠BFD+∠CDF=360°,∴∠ABF+∠CDF=360°﹣∠BFD,∴∠BED=(360°﹣∠BFD),整理得:2∠BED+∠BFD=360°.故选:C.2.解:∵AB∥CD,∴∠ABC=∠BCD,∠A+∠ACD=180°,∵BD⊥BC,∴∠CBD=90°,∴∠ABC=∠BCD=90°﹣∠BDC,①∵∠A=2∠BDC,∴∠ACD=180°﹣∠A=180°﹣2∠BDC,∴∠ACB=∠ACD﹣∠BCD=180°﹣2∠BDC﹣(90°﹣∠BDC)=90°﹣∠BDC,∴∠ACB=∠ABC,故①正确;②∵∠BDC与∠A互补,∴∠BDC=180°﹣∠A,∴∠ACD=180°﹣∠A=∠BDC,∴∠ACB=∠ACD﹣∠BCD=∠BDC﹣(90°﹣∠BDC)=2∠BDC﹣90°,∴2∠ABC+∠ACB=2(90°﹣∠BDC)+(2∠BDC﹣90°)=90°,故②正确;故选:C.3.解:如图:过点G,M,H作GN∥AB,MP∥AB,HK∥AB,∵AB∥CD,∴AB∥GN∥MP∥KH∥CD,∵GN∥AB,∴∠AEG=∠EGN,∵GN∥KH,∴∠NGH=GHK,∵HK∥CD,∴∠HFD=∠KHF,∵∠EGH=82°,∠HFD=20°,∴∠AEG+∠GHF=102°,∵EM和MH是角平分线,∴∠AEM+∠NHF=51°,∵∠HFD=∠KHF=20°,∴∠AEM+∠MHK=31°,∵MP∥AB∥HK,∴∠EMP=∠AEM,∠PMH=∠NHK,∴∠EMP+∠PMH=31°,即∠EMH=31°.故选:A.4.解:过F点作FG∥AB,∵AB∥CD,∴FG∥CD,∴∠BFG=∠ABF,∠DFG+∠CDF=180°,∵BF⊥DE,∴∠BFD=90°,∵BF平分∠ABE,∴∠ABE=2∠ABF,∴∠BFG+∠DFG+∠CDF=∠ABF+180°,∴90°+∠CDE=∠ABE+180°,即∠EDC﹣∠ABE=90°.故选:A.5.解:过G作GM∥AB,∴∠2=∠5,∵AB∥CD,∴MG∥CD,∴∠6=∠4,∴∠G=∠5+∠6=∠2+∠4,∵FB、CG分别为∠EFG,∠ECD的角平分线,∴∠1=∠2=∠EFG,∠3=∠4=∠ECD,∴∠E+∠EFG+∠ECD=210°,∵AB∥CD,∴∠ENB=∠ECD,∴∠E+∠EFG+∠ENB=210°,∵∠1=∠E+∠ENB,∴∠1+∠EFG=∠1+∠1+∠2=210°,∴3∠1=210°,∴∠1=70°,∴∠EFG=2×70°=140°.故选:A.6.解:过C点作MF∥AB,∵AB∥DE,∴MF∥DE,∴∠α=∠BCM,∠β+∠DCM=180°,∵BC⊥CD,∴∠BCD=90°,∴∠BCM+∠DCM=360°﹣∠BCD=270°,∴∠α+(180°﹣∠β)=270°,∴∠α﹣∠β=90°,∴α随β增大而增大,故选:B.7.解:延长DC交AB与G,延长CD交EF于H.在直角△BGC中,∠1=90°﹣α;△EHD中,∠2=β﹣γ,∵AB∥EF,∴∠1=∠2,∴90°﹣α=β﹣γ,即α+β﹣γ=90°.故选:C.8.解:∵l1∥l2∥l3,∴∠1=∠2+∠4,∠4+∠3=180°,∴∠1﹣∠2+∠3=180°,故选:C.9.解:(1)如图1,由AB∥CD,可得∠AOC=∠DCE1=β,∵∠AOC=∠BAE1+∠AE1C,∴∠AE1C=β﹣α.(2)如图2,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,∴∠AE2C=α+β.当AE2平分∠BAC,CE2平分∠ACD时,∠BAE2+∠DCE2=(∠BAC+∠ACD)=180°=90°,即α+β=90°,又∵∠AE2C=∠BAE2+∠DCE2,∴∠AE2C=180°﹣(α+β)=180°﹣α﹣β;(3)如图3,由AB∥CD,可得∠BOE3=∠DCE3=β,∵∠BAE3=∠BOE3+∠AE3C,∴∠AE3C=α﹣β.(4)如图4,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,∴∠AE4C=360°﹣α﹣β.(5)(6)当点E在CD的下方时,同理可得,∠AEC=α﹣β或β﹣α.综上所述,∠AEC的度数可能为β﹣α,α+β,α﹣β,180°﹣α﹣β,360°﹣α﹣β.故选:D.10.解:A、如图1:∵∠1=40°,∠2=140°,∴AB与CD不平行;故本选项错误;B、如图2:∵∠1=40°,∠2=40°,∴∠1=∠2,∴AB与CD平行;故本选项正确;C、如图3:∵∠1=40°,∠2=140°,∴∠1≠∠2,∴AB不平行CD;故本选项错误;D、如图4:∠1=40°,∠2=40°,∴∠3=140°,∴∠1≠∠3,∴AB与CD不平行;故本选项错误.故选:B.11.解:当PK在AD上方时,延长MN、KH交于点Q,由折叠可知,∠K=∠P=90°,∠ENM=90°,∵PK∥MN,∴∠K=∠Q=90°,∴∠ENM=∠Q,∴EN∥KH,∵∠EFC=37°,∴∠AEF=37°,∴∠AEN=74°,∴∠AHQ=74°,∵∠KHD=∠AHQ,∴∠KHD=74°;当PK在AD下方时,延长HK,MN交于点T,由折叠可知,∠HKP=90°,∠MNE=90°,∵MN∥KP,∴∠T=∠HKP=90°,∴∠ENM=∠T=90°,∴EN∥HK,∵∠EFC=37°,∴∠AEF=37°,∴∠AEN=74°,∴∠AHK=74°,∵∠KHD=180°﹣∠AHK=106°;综上所述:∠KHD=74°或106°,故选:D.12.解:因为拐弯后的管道与拐弯前的管道平行,所以根据两直线平行,内错角相等可得∠B=∠C=140°,故选A.13.解:如图.令∠BED=x,则∠F=.由题意得:∠BED=∠DEM=x,AH∥EM.∴∠BDE=∠DEH=x,∠EDH=180°﹣x.∴∠EBD=180°﹣∠BED﹣∠BDE=180°﹣2x.∴∠ABE=180°﹣∠EBD=2x.又∵直线BN是∠ABE的角平分线.∴∠ABN=.∴∠FBD=∠ABN=x.又∵直线DF是∠EDH的角平分线所在直线.∴∠FDE=.∴∠BDF=∠FDE﹣∠BDE=(90°+)﹣x=90°﹣.又∵∠BFD+∠FBD+∠FDB=180°.∴.∴x=72°.∴∠1=∠EBD=180°﹣2x=36°.14.解:∵四边形ABCD为矩形,∴∠BAD=∠ABC=90°,∵AE∥BD,∴∠DAE=∠ADB=28°,∴∠BAE=∠BAD+∠DAE=90°+28°=118°,∵矩形ABCD沿AF折叠,点B落在点E处,∴∠BAF=∠EAF=∠BAE=×118°=59°,∴∠AFC=∠BAF+∠ABF=59°+90°=149°.故答案为149.15.解:(1)由折叠可知∠DFE=∠EFG,∵∠CFG=76°,∴∠DFE=52°,∵AB∥CD,∴∠FEB=∠DFE=52°,∵EG平分∠BEF,∴∠BEG=26°,故答案为:26°;(2)设∠BEG=α,则∠FEB=2α,∴∠DFE=∠FEB=2α,由折叠可知,∠A=∠A',∵∠A+∠DFE=125°,∴∠A'+2α=125°,∵EG∥A′D′,∴∠A'+∠A'EB+α=180°,∴∠A'EB=55°+α,∵∠AEF+2α=180°,∴∠A'EB+2α+2α=180°,∴α=25°,∴∠DFE=50°,∴∠CFE=130°,故答案为:130°.16.解:(1)如图:∵四边形ABCD是矩形,∴BC∥AD,∴∠F′GF=∠GPD,由折叠得:∠GPQ=∠GPD,∠MGF=∠F′GF,∴∠MGF=∠GPQ=α=60°,故答案为:60;(2)如图:由折叠得:∠MGF=∠M′GF=α,∵BC∥AD,∴∠PGF=180°﹣∠GPD=180°﹣2α,∵GM是∠PGF的三等分线,∴分两种情况:当∠MGF=∠PGF时,∴α=(180°﹣2α),∴α=,当∠MGF=∠PGF时,∴α=(180°﹣2α),∴α=36°,综上所述,α=或36°,故答案为:或36.17.解:设直线AD与CN交于点Q.∵AM∥CN,∠EAD=32°,∴∠EAD=∠DQC=32°,∵AB为∠EAD的角平分线,CB为∠DCN的角平分线,∠DCN=88°,∴∠DCB=∠BCN=44°,∠DAB=∠EAB=16°,∵∠BCN+∠DQC=∠BAD+∠ABC,即44°+32°=16°+∠ABC,∴∠ABC=∠ABD+∠CBD=60°,∵∠ABD:∠CBD=4:1,∴∠ABD=48°,∠CBD=12°,∴∠ADF=∠ABD+∠BAD=64°,∠CDF=∠CBD+∠BCD=56°,∴∠ADF:∠CDF=8:7.故答案为:8:7.18.解:(1)根据上下边互相平行可知,α=∠OAD,∵α=70°,∴∠OAD=70°.又∠OAD+2β=180°,∴β=55°.故答案为:55.(2)根据折叠的性质可知,折叠两次后形成的三个角都相等,根据题意可知,折叠两次后形成的三个角与折叠后的∠ACE都相等,而这四个角的和为180°,故每个角为45°,∴∠ACB=90°,即α=90°,由(1)中可得,β=(180°﹣90°)=45°.故答案为:45.19.解:(1)∵NB′∥A′M,∴∠A′EC=∠B′NC=48°,∵CN∥MD,∴∠A′MD=∠A′EC=48°.(2)①由(1)得:∠A′MD=∠B′NC=α,又∵2∠A′MN+∠A′MD=180°,∴β=90°﹣.②∵MA′恰好平分∠DMN,∴∠A′MD=180°÷3=60°.20.解:(1)①AD∥BC,理由如下:∵ED∥AB,∴∠EDF=∠DAB,∵DA是∠CDE的角平分线,∴∠EDF=∠ADC,∴∠DAB=∠ADC,∵∠FDC+∠ABC=180°,∴∠DAB+∠ABC=180°,∴AD∥BC;②∵BE是∠ABC的角平分线,∠ABC=130°,∴∠FBC=65°,∵AD∥BC,∴∠DFB=180°﹣∠FBC=115°;(2)作CG∥AB,∵AB∥DE,∴CG∥AB∥DE,∴∠1=180°﹣∠EDC,∠2=180°﹣∠ABC,∴∠BCD=∠1+∠2=180°﹣∠EDC+180°﹣∠ABC=180°﹣2∠EDA+180°﹣2∠ABF=180°﹣2∠DAB+180°﹣2∠ABF=360°﹣2(∠DAB+∠ABF)=360°﹣2∠DFB=α,∴∠DFB=180°﹣α.二.平行线的判定与性质21.解:∵EF⊥AB,CD⊥AB,∴CD∥EF,若∠CDG=∠BFE,∵∠BCD=∠BFE,∴∠BCD=∠CDG,∴DG∥BC,∴∠AGD=∠ACB,故小明说法正确;∵FG∥AB,∴∠B=∠GFC,故得不到∠GFC=∠ADG,故小亮说法错误,故选:A.22.证明:(1)∵∠MCD=∠BCM=α,∴∠BCD=∠BCM+∠MCD=4α=∠B,∴AB∥CD.解:(2)过O做OF,使OF∥AB∥CD∵AB∥CD,∴∠D=∠A=∠B=3α,∵AB∥OF,∴∠B=∠BOF,CD∥OF,∴∠FOD=∠D,∠BOD=∠BOF+∠FOD=∠B+∠D=4α+3α=7α.证明:(3)过点P作AB、CD的平行线PQ,∵AB∥PQ∥CD,∴∠QPC=∠PCD=α,∴∠BEP=∠EPQ=∠OEB,∵∠COE=∠OEP+∠ENO,且∠ENO=∠B+∠BEN=∠BNP,∴∠COE=∠B+∠BEN+∠OEP=∠B+∠OEB,又∵EP平分∠OEB,∴∠COE=2∠EPC+∠B.23.(1)证明:∵∠E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,∴EF∥BC;(2)解:∵∠3+∠4=180°,∠4=∠MNF,∴∠3+∠MNF=180°,∴AB∥FP,∴∠F+∠BAF=180°,∵∠BAF=3∠F﹣20°,∴∠F+3∠F﹣20°=180°,解得∠F=50°,∵AB∥FP,EF∥BC,∴∠B=∠1,∠1=∠F,∴∠B=∠F=50°.24.(1)证明:如图1,∵∠AGE+∠DHE=180°,∠AGE=∠BGF.∴∠BGF+∠DHE=180°,∴AB∥CD;(2)证明:如图2,过点M作MR∥AB,又∵AB∥CD,∴AB∥CD∥MR.∴∠GMR=∠AGM,∠HMR=∠CHM.∴∠GMH=∠GMR+∠RMH=∠AGM+∠CHM.(3)解:如图3,令∠AGM=2α,∠CHM=β,则∠N=2α,∠M=2α+β,∵射线GH是∠BGM的平分线,∴,∴∠AGH=∠AGM+∠FGM=2α+90°﹣α=90°+α,∵,∴,∴∠FGN=2β,过点H作HT∥GN,则∠MHT=∠N=2α,∠GHT=∠FGN=2β,∴∠GHM=∠MHT+∠GHT=2α+2β,∠CHG=∠CHM+∠MHT+∠GHT=β+2α+2β=2α+3β,∵AB∥CD,∴∠AGH+∠CHG=180°,∴90°+α+2α+3β=180°,∴α+β=30°,∴∠GHM=2(α+β)=60°.25.(1)证明:∵∠1+∠BDE=180°,∴AC∥DE,∴∠2=∠ADE,∵∠2+∠4=180°.∴∠ADE+∠4=180°,∴AD∥EF;(2)解:∵AD∥EF,∴∠BAD=∠3=90°,∵∠2+∠4=180°,∠4=140°,∴∠2=40°,∴∠BAC=90°﹣40°=50°.。
【精心整理】平行线的性质知识点总结、例题解析
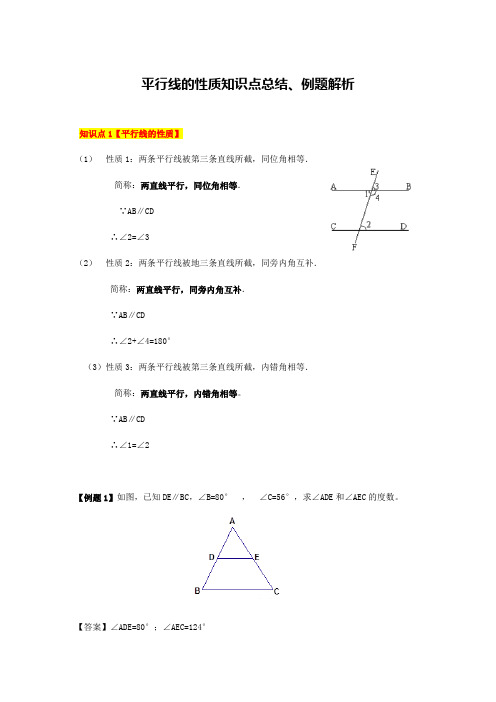
平行线的性质知识点总结、例题解析知识点1【平行线的性质】(1)性质1:两条平行线被第三条直线所截,同位角相等.简称:两直线平行,同位角相等.∵AB∥CD∴∠2=∠3(2)性质2:两条平行线被地三条直线所截,同旁内角互补.简称:两直线平行,同旁内角互补.∵AB∥CD∴∠2+∠4=180°(3)性质3:两条平行线被第三条直线所截,内错角相等.简称:两直线平行,内错角相等。
∵AB∥CD∴∠1=∠2【例题1】如图,已知DE∥BC,∠B=80°,∠C=56°,求∠ADE和∠AEC的度数。
【答案】∠ADE=80°;∠AEC=124°【例题2】如图,平行线AB。
CD被直线AE所截,若∠1=110°,则∠2等于()A、70B、80C、90D、110【答案】A【例题3】如图,已知AB∥CD,∠1=150°,∠2=______【答案】30°【例题4】在平面内,将一个直角三角板按如图所示摆放在一组平行线上:若∠1=55°,则∠2的度数是_______【答案】35°【例题5】如图所示,已知∠AOB=50 °,PC ∥OB ,PD 平分∠OPC ,则∠APC=______ °,∠PDO=______°【答案】50 ,50 ;【例题6】如图所示,OP∥QB∥ST,若∠2=110°,∠3=120°,则∠1的度数为________【答案】10°【例题7】如图,已知AB∥CD,AE∥CF,求证:∠BAE=∠DCF【答案】证明:∵AB∥CD,∴∠BAC=∠DCA.(两直线平行,内错角相等)∵AE∥CF,∴∠EAC=∠FCA.(两直线平行,内错角相等)∵∠BAC=∠BAE+∠EAC,∠DCA=∠DCF+∠FCA,∴∠BAE=∠DCF.【例题8】如图,已知AB∥CD,∠B=40°CN是∠BCE的平分线,CM⊥CN,求∠BCM的度数。
数学:2.3《平行线的特征》同步测试(北师大七年级下)

2.3 平行线的特征一、填空题:(每题4分,共28分)1.如图1,AB ∥CD ,AF 分别交AB 、CD 于A 、C ,CE 平分∠D CF ,∠1=100 °,则∠2=_____.毛21FE DCB AG 1F EDCBAG21FEDCB A(1) (2) (3)2.如图2,AB ⊥EF ,CD ⊥EF ,∠1=∠F =45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。
3.如图3,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF ,若∠1=72°,则∠2=_________。
4.如图4,DH ∥EG ∥BC ,DC ∥EF ,图中与∠1相等的角有________________________。
K H G 1FED CBA DCBA ED C B A(4) (5) (6)5.如图5,AD ∥BC ,∠A 是∠ABC 的2倍。
(1)∠A =_______度。
(2)若BD 平分∠ABC ,则∠ADB =___________。
6.如图6,BA ∥DE ,∠B =150°,∠D =130°,则∠C 的度数是__________。
7.如图7,∠ACD =∠BCD ,DE ∥BC 交AC 于E ,若∠ACB =6 0°,∠B =74°,则∠EDC =___°,∠CDB =____°。
E D CBA FEDCB A30︒北西南东B AγβαDCBA(7) (8) (9) (10) 二、选择题:(每题4分,共28分)8.如图8,由AC ∥ED ,可知相等的角有( ) A.6对 B.5对 C.4对 D.3对9.如图9,由A 到B 的方向是( )A.南偏东30°B.南偏东60°C.北偏西30°D.北偏西60°10.如图10,如果AB ∥CD ,则角α、β、γ之间的关系为( ) A. α+β+γ=360° B. α-β+γ=180° C. α+β-γ=180° D. α+β+γ=180°11.如图11,AB ∥CD ∥EF ,若∠ABC =50°,∠CEF =150°,则∠BCE =( ) A.60° B.50° C.30° D.20°F EDCB AFEDCBA(11) (12) 12.下列说法中,为平行线特征的是( )①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行. A.① B.②③ C.④ D.②和④13.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( ) A.相等 B.互补 C.相等或互补 D.相等且互补14.如图12,AB ⊥BC ,BC ⊥CD ,∠EBC =∠BCF ,那么,∠ABE 与∠DCF 的位置与大小关系是 ( ) A.是同位角且相等; B.不是同位角但相等; C.是同位角但不等; D.不是同位角也不等 三、解答题:(共44分)15.已知,如图,MN ⊥AB ,垂足为G ,MN ⊥CD ,垂足为H ,直线EF 分别交AB 、CD 于G 、Q ,∠GQC =120°,求∠EGB 和∠HGQ 的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 平行线的特征
一、填空题:(每题4分,共28分) 1.如图1,AB ∥CD ,AF 分别交AB 、CD 于A 、C ,CE 平分∠D CF ,∠1=100 °,则∠2=_____.
2
1
F
E D
C
B A
G 1
F E
C
B
A
G
2
1
E
D
C
B A
(1) (2) (3)
2.如图2,AB ⊥EF ,CD ⊥EF ,∠1=∠F =45°,那么与∠F CD 相等的角有_________个,它们分别是___________________________。
3.如图3,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF ,若∠1=72°,则∠2=_________。
4.如图4,DH ∥EG ∥BC ,DC ∥EF ,图中与∠1相等的角有________________________。
K H G 1
F
E
D C
B
A D
C
B
A E
D C B A
(4) (5) (6) 5.如图5,AD ∥BC ,∠A 是∠ABC 的2倍。
(1)∠A =_______度。
(2)若BD 平分∠ABC ,则∠ADB =___________。
6.如图6,BA ∥DE ,∠B =150°,∠D =130°,则∠C 的度数是__________。
7.如图7,∠ACD =∠BCD ,DE ∥BC 交AC 于E ,若∠ACB =6 0°,∠B =74°,则∠EDC =___°,∠CDB =____°。
E D C
B
A F
E
D
C
B A
30︒
北
西
南
东
B A
γ
β
αD
C
B
A
(7) (8) (9) (10)
二、选择题:(每题4分,共28分)
8.如图8,由AC ∥ED ,可知相等的角有( ) A.6对 B.5对 C.4对 D.3对 9.如图9,由A 到B 的方向是( )
A.南偏东30°
B.南偏东60°
C.北偏西30°
D.北偏西60°
10.如图10,如果AB ∥CD ,则角α、β、γ之间的关系为( ) A. α+β+γ=360° B. α-β+γ=180° C. α+β-γ=180° D. α+β+γ=180°
11.如图11,AB ∥CD ∥EF ,若∠ABC =50°,∠CEF =150°,则∠BCE =( ) A.60° B.50° C.30° D.20°
F E
D
C
B A F
E
D
C
B
A
(11) (12) 12.下列说法中,为平行线特征的是( )
①两条直线平行, 同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行. A.① B.②③ C.④ D.②和④
13.如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( ) A.相等 B.互补 C.相等或互补 D.相等且互补
14.如图12,AB ⊥BC ,BC ⊥CD ,∠EBC =∠BCF ,那么,∠ABE 与∠DCF 的位置与大小关系是 ( )
A.是同位角且相等;
B.不是同位角但相等;
C.是同位角但不等;
D.不是同位角也不等 三、解答题:(共44分)
15.已知,如图,MN ⊥AB ,垂足为G ,MN ⊥CD ,垂足为H ,直线EF 分别交AB 、CD 于G 、Q ,∠GQC =120°,求∠EGB 和∠HGQ 的度数。
(7分)
Q
H G
M N
F
E
D
C B
A
16.如图,∠CAB =100°,∠ABF =130°,AC ∥MD ,BF ∥ME ,求∠DME 的度数,(7分)
M F
E D C
B
A
17.如图,DE ∥CB ,试证明∠AED =∠A +∠B 。
(7分)
E
D C
B
A
18.如图,∠1=∠2,∠C =∠D ,那么∠A =∠F ,为什么?(7)
1
4
32F
E
D C
B
A
19.如图,AB ∥CD ,∠1=∠2,∠BDF 与 ∠EFC 相等吗?为什么?(8分)
1
2
F E D
C
B A
20.如图,已知∠1+∠2=180°,∠3=∠B ,试判断∠ AED 与∠C 的关系。
(8分)
1
54
32
F E
D
C
A
答案:
1. 50°
2. 4,∠F,∠1,∠FAB,∠ABG
3. 54°
4. ∠FEK,∠DCF,∠CKG,∠EKD,∠KDH
5.(1)120°(2)30°
6.80°
7.30°,76°
8.B 9.B 10.C 11.D 12.A 13.C 14.B
15. ∵MN⊥AB,MN⊥CD
∴∠MGB=∠MHD=90°
∴AB∥CD
∴∠EGB=∠EQH
∵∠EQH=180°-∠GQC=180°-120°
=60°
∴∠EGB=60°
∴∠EGM=90°-∠EGB=30°
∴∠EGB=60°,∠HGQ=30°
16. ∵AC∥MD,∠CAB=100°
∴∠CAB+∠AMD=180°,∠AMD=80°
理可得∠EMF=50°
∴∠DME=∠AMB-∠AMD-∠EMB
=180°-80°-50°=50°
17.作EF∥AB交OB于F
∵EF∥AB
∴∠2=∠A,∠3=∠B
∵DE∥CB
∴∠1=∠3
∴∠1=∠B
∴∠1+∠2=∠B+∠A
∴∠AED=∠A+∠B
18. ∵∠2=∠3,∠1=∠2
∴∠1=∠3
∴DB∥EC
∴∠4=∠C
∵∠C=∠D
∴∠D=∠4
∴DF∥AC
∴∠A=∠F
19. ∠BEF=∠EFC,理由如下:
连结BC
∵AB∥CD
∴∠ABC=∠DCB
∵∠1=∠2
∴∠ABC-∠1=∠DCB-∠2
即∠EBC=∠BCF
∴BE∥CF
∴∠BEF=∠EFC
20.∠AED=∠C
∵∠1+∠2=180°
∵∠1+∠4=180°
∴∠2=∠4
∴EF∥AB
∴∠3=∠5
∵∠3=∠B
∴∠5=∠B
∴DE∥BC
∴∠C=∠AED.
更多资料请访问。
