三角形全等之倍长中线
三角形全等之倍长中线(讲义及答案)
9
∴∠1=∠M ∴∠1=∠F ∵AD∥EF ∴∠3=∠F,∠1=∠2 ∴∠2=∠3 即 AD 为△ABC 的角平分线 6. 解:如图,延长 AF 交 BC 的延长线于点 G
6
2. 证明:如图,延长 AD 到 E,使 DE=AD,连接 BE
在△ADC 和△EDB 中 CD BD ADC EDB AD ED ∴△ADC≌△EDB(SAS) ∴AC=EB,∠2=∠E ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB=BE ∴AB=AC 3. 证明:如图,延长 CD 到 F,使 DF=CD,连接 BF
4. 如图,在△ABC 中,D 是 BC 边的中点,E 是 AD 上一点, BE=AC,BE 的延长线交 AC 于点 F. 求证:∠AEF=∠EAF.
3
5. 如图,在△ABC 中,AD 交 BC 于点 D,点 E 是 BC 的中点, EF∥AD 交 CA 的延长线于点 F,交 AB 于点 G,BG=CF. 求证:AD 为△ABC 的角平分线.
=52.7 =2.3
10
7. 证明:如图,延长 EG 交 CD 的延长线于点 M
由题意,∠FEB=90°,∠DCB=90° ∴∠DCB+∠FEB=180° ∴EF∥CD ∴∠FEG=∠M ∵点 G 为 FD 的中点 ∴FG=DG 在△FGE 和△DGM 中 1 M FGE DGM FG DG ∴△FGE≌△DGM(AAS) ∴EF=MD,EG=MG ∵△FEB 是等腰直角三角形 ∴EF=EB ∴BE=MD 在正方形 ABCD 中,BC=CD ∴BE+BC=MD+CD 即 EC=MC ∴△ECM 是等腰直角三角形 ∵EG=MG ∴EG⊥CG,∠3=∠4=45° ∴∠2=∠3=45° ∴EG=CG
三角形全等之倍长中线(类倍长一)(人教版)(含答案)

学生做题前请先回答以下问题问题1:“三角形全等”的辅助线:见中线,要________,________之后___________,全等之后_________,_________.问题2:倍长中线的作法,图中的虚线为辅助线,请叙述图1、图2的辅助线.三角形全等之倍长中线(类倍长一)(人教版)一、单选题(共4道,每道25分)1.已知:如图,点E是BC的中点,∠BAE=∠D.求证:AB=CD.如图,先在图上走通思路后再填写空格内容:①因为点E是BC的中点,考虑延长AE到点F,使EF=AE,连接CF;②进而利用全等三角形的判定_________,证明_______≌_______;③由全等可得________________;④结合已知条件∠BAE=∠D,得∠F=∠D,在△DCF中,利用________________,可得CF=CD,等量代换得AB=CD.以上空缺处依次所填最恰当的是( )A.②SAS,△ABE,△ECF;③AB=CF;④等角对等边B.②SAS,△ABE,△DEC;③AB=CF,∠BAE=∠F;④等边对等角C.②SA S,△ABE,△FCE;③∠ABE=∠FCE,∠BAE=∠F;④等边对等角D.②SAS,△ABE,△FCE;③AB=FC,∠BAE=∠F;④等角对等边答案:D解题思路:试题难度:三颗星知识点:三角形全等之倍长中线2.已知:如图,点E是BC的中点,∠BAE=∠D.求证:AB=CD.证明:如图,延长DE到点F,使EF=DE,连接BF.∵E是BC的中点∴BE=CE在△BEF和△CED中∴△BEF≌△CED(SAS)∴____________________________∵∠BAE=∠D____________________________∴AB=CD请你仔细观察下列序号所代表的内容:①BF=CD,∠EBF=∠C;②BF=CD,∠F=∠D;③;④.以上空缺处依次所填最恰当的是( )A.①③B.②③C.①④D.②④答案:B解题思路:试题难度:三颗星知识点:三角形全等之倍长中线3.已知:如图,在△ABC中,AB>AC,E为BC的中点,AD平分∠BAC,过E作EF∥AD,交AB于点G,交CA的延长线于点F,求证BG=CF.如图,先在图上走通思路后再填写横线上的内容:①因为点E是BC的中点,考虑延长GE到点H,使EH=GE,连接CH;②进而利用全等三角形的判定_________,证明_______≌_______;③由全等可得________________;④再与已知条件重新组合,经过推理,可得BG=CF.以上空缺处依次所填最恰当的是( )A.②SAS,△ABD,△FEC;③BG=CF;B.②SAS,△BEG,△CEH;③BG=CH,∠BGE=∠H;C.②SAS,△BEG,△CEH;③GE=HE,∠BGE=∠H;D.②SAS,△BEG,△EHC;③BG=CH;答案:B解题思路:试题难度:三颗星知识点:三角形全等之倍长中线4.已知:如图,在△ABC中,AB>AC,E为BC的中点,AD平分∠BAC,过E作EF∥AD,交AB于点G,交CA的延长线于点F,求证BG=CF.证明:延长FE到点H,使得EH=FE,连接BH.∵E为BC的中点∴BE=CE在△BEH和△CEF中∴△BEH≌△CEF(SAS)∴____________________________∵AD平分∠BAC∴∠1=∠2∵AD∥EF∴____________________________∴∠3=∠H∴BG=BH∴BG=CF请你仔细观察下列序号所代表的内容:①∠H=∠F,BH=CF;②BH=CF,∠EBH=∠C;③∴∠1=∠3;④∴∠1=∠3,∠2=∠F.以上空缺处依次所填最恰当的是( )A.①③B.②③C.①④D.②④答案:C解题思路:试题难度:三颗星知识点:三角形全等之倍长中线。
三角形全等之倍长中线(习题及答案)知识讲解

三角形全等之倍长中线(习题)➢ 例题示范例1:已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC . 求证:AE 平分∠BAC .A B D CE F【思路分析】 读题标注:??FE CD B A见中线,要倍长,倍长之后证全等.结合此题,DE =EC ,点E 是DC 的中点,考虑倍长,有两种考虑方法: ①考虑倍长FE ,如图所示: ②考虑倍长AE ,如图所示:A B DCE F??GG??FECDBA (这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF ≌△CEG ,由全等转移边和角,重新组织条件证明即可. 【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG .A B DCE F??在△DEF 和△CEG 中,ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS ) ∴DF =CG ,∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAE ∴∠BAE =∠CAE ∴AE 平分∠BAC➢ 巩固练习1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.D CBA2.已知:如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF∥BC交BD于F.求证:AB=EF.3.已知:如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形,AB=AE,AC=AF,∠BAE=∠CAF=90°.求证:EF=2AD.F EDC BAF ED CBA如图,在△ABC中,AB >AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB 于F,交CA的延长线于G.求证:BF=CG.4.如图,在四边形ABCD中,AD∥BC,点E在BC上,点F是CD的中点,连接AF,EF,AE,若∠DAF=∠EAF,求证:AF⊥EF.GFE D CAFEDB CA➢ 思考小结1. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .CDBA比较下列两种不同的证明方法,并回答问题. 方法1:如图,延长AD 到E ,使DE =AD ,连接BE 在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴AC =BE ,∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E 21ECDB A∴AB =BE ∴AB =AC 方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E ∵BE ∥AC ∴∠E =∠2在△BDE 和△CDA 中2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS ) ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等. 不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等.2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt △ABC 中,∠BCA =90°,CD 是斜边AB 的中线.求证:CD 12=AB . 21ECDBADCBA【参考答案】 ➢ 巩固练习1. 22. 证明略(提示:延长FD 到点G ,使得DG =DF ,连接AG ,证明△ADG ≌△EDF ,转角证明AB =EF )3. 证明略(提示:延长AD 到点G ,使得GD =AD ,连接CG ,证明△ABD ≌△GCD ,△EAF ≌△GCA )4. 证明略(提示:延长FE 到点H ,使得EH =FE ,连接CH ,证明△BFE ≌△CHE ,转角证明BF =CG )5. 证明略(提示:延长AF 交BC 的延长线于点G ,证明△ADF ≌△GCF ,转角证明AF ⊥EF )➢ 思考小结1. 倍长中线 SAS AAS 角2. 证明略。
8三角形全等之倍长中线尖子班讲义

A BCDEF三角形全等之倍长中线(讲义)一、知识点睛1.辅助线的定义:为了解决几何问题,在原图基础之上另外添加的直线或线段称为辅助线.辅助线通常画成虚线.2.辅助线的原则:添加辅助线,构造新图形,形成新关系,建立已知和未知之间的桥梁,把问题转化成自己已经会解的情况. 3.辅助线的作用:①把分散的条件转为集中;②把复杂的图形转为基本图形. 4.添加辅助线的注意事项:明确目的,多次尝试. 5.“三角形全等”辅助线:见中线要___________,_________之后________________. 6.倍长中线的作法:ABCDDCB AM延长AD 到E ,使DE=AD , 延长MD 到E ,使DE=MD ,连接BE 连接CE二、精讲精练1. 如图,AD 为△ABC 的中线.求证:AB +AC >2AD .2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .BADCABDC延长FE 交BC 的延长线于点G3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AC =AB .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 边的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F . 求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线.6. 如图,在正方形ABCD 中,E 为AB 边的中点,G ,F 分别为AD ,BC 边上的点,GE ⊥EF . 求证:GF =AG +BF .A F EB D CAEB DCB GE D CAF DG AEBFCA F EB DC BGEDC AF7. 如图,在正方形ABCD 的边CB 的延长线上取一点E ,△FEB 为等腰直角三角形,∠FEB =90°,连接FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .三、回顾与思考________________________________________________________________________________________________________________________________________________________________________________________________【参考答案】【知识点睛】见中线要倍长,倍长之后证全等. 【精讲精练】1.证明略(提示:延长AD 到点E ,使DE =AD ,连接BE ,证明△BED ≌△CAD ) 2.证明略(提示:延长AD 到点E ,使DE =AD ,连接BE ,证明△BED ≌△CAD ) 3.证明略(提示:延长CD 到点F ,使DF =CD ,连接BF ,证明△BDF ≌△ADC ,△CBE ≌△CBF )4.证明略(提示:延长AD 到点M ,使DM =AD ,连接BM ,证明△ADC ≌△MDB )5.证明略(提示:延长EF 到点M ,使EM =EF ,连接BM ,证明△CFE ≌△BME ) 6.证明略(提示:延长GE 交CB 延长线于点M ,证明 △AEG ≌△BEM )7.证明略(提示:延长EG 交CD 延长线于点M ,证明 △FGE ≌△DGM ,再证明三角形EGC 是等腰直角三角形)AF EBGCD三角形全等之倍长中线每日一题(4.15 4.19)1. 已知:如图,在梯形ABCD 中,AD ∥BC ,AB =AD +BC ,E 是CD 的中点. 求证:AE ⊥BE .EDCB A2. 已知:如图,在△ABC 中,D 为BC 边中点,∠BDA =∠BAD ,E 为BD 中点,连接AE .求证:∠C =∠BAE .E D CA3. 已知:如图,△ABC 与△BDE 均为等腰直角三角形,BA ⊥AC ,ED ⊥BD ,垂足分别为点A ,点D ,连接EC ,F 为EC 中点,连接AF ,DF ,猜测AF ,DF 的数量关系和位置关系,并说明理由.FED CA4. 已知:如图,D 为线段AB 的中点,在AB 上任取一点C (不与点A ,B ,D 重合),分别以AC ,BC 为斜边在AB 同侧作等腰Rt △ACE 与等腰Rt △BCF ,∠AEC =∠CFB =90°,连接DE ,DF ,EF . 求证:△DEF 为等腰直角三角形.ABCDE F5. 已知:如图,在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE =∠EAF ,AF 与DC 的延长线相交于点F .试探究线段AB 与AF ,CF 之间的数量关系,并说明理由.EDCBA【参考答案】1. 证明:延长AE 交BC 的延长线于点F .FADEC B∵AD ∥BC∴∠D =∠DCF ,∠DAE =∠F ∵E 是CD 的中点∴DE =CE在△ADE 和△FCE 中=⎧⎪∠=∠⎨⎪=⎩∠∠D FCE DAE F DE CE ∴△ADE ≌△FCE (AAS ) ∴AD =FC ,AE =FE ∵AB =AD +BC ∴AB =CF +BC =BF 在△ABE 和△FBE 中=⎧⎪=⎨⎪=⎩AB FB BE BE AE FE ∴△ABE ≌△FBE (SSS ) ∴∠ABE =∠FBE =90° 即AE ⊥BE2. 证明:延长AE 到F ,使得EF =AE ,连接DF .AB CDE∵E 为BD 中点 ∴BE =ED在△ABE 和△FDE 中=⎧⎪=⎨⎪=⎩∠∠BE DE BEA DEF AE FE ∴△ABE ≌△FDE (SAS )∴AB =FD ,∠BAF =∠F ,∠B =∠FDE ∵∠BDA =∠BAD ∴BD =AB∵D 为BC 边中点 ∴CD =BD =AB =FD ∵∠BDA =∠BAD∴∠ADF =∠BDA +∠FDE ,∠ADC =∠B +∠BAD 即∠ADF =∠ADC 在△FAD 和△CAD 中=⎧⎪=⎨⎪=⎩∠∠FD CD FDA CDA AD AD ∴△FAD ≌△CAD (SAS ) ∴∠F =∠C ∴∠C =∠BAE3. 解:AF ⊥DF ,AF =DF ,理由如下: 延长DF 交AC 于点P .P AD EFC∵BA ⊥AC ,ED ⊥BD ∴∠BAC =∠EDA=90° ∴DE ∥AC ∴∠DEC =∠ECA ∵F 为EC 中点 ∴EF =FC在△EDF 和△CPF 中DEF PCF EFD CFP EF CF ∠=∠⎧⎪=⎨⎪=⎩∠∠ ∴△EDF ≌△CPF (AAS ) ∴DE =CP ,DF=PF∵△ABC 与△BDE 均为等腰直角三角形 ∴AB =AC ,DE=BD ∴AB -BD=AB -DE=AC -CP 即AD =AP在△DAF 和△PAF 中DF PF AF AF AD AP =⎧⎪=⎨⎪=⎩∴△DAF ≌△PAF (SSS )∴∠DFA =∠PFA =90°,∠DAF =∠PAF =45° ∴AF ⊥DF ,AF =DF4. 证明:延长ED 到点G ,使得DG =DE ,连接BG ,FGDCAE FB∵D 为线段AB 的中点 ∴AD =BD在△EDA 和△GDB 中=⎧⎪=⎨⎪=⎩∠∠ED GD EDA GDB DA DB ∴△EDA ≌△GDB (SAS ) ∴EA =GB ,∠A =∠GBD∵△ACE 与△BCF 是等腰直角三角形∴AE =CE =BG ,CF =FB ,∠A =∠ECA =∠FCB =∠FBC =45° ∴∠ECF =90°,∠FBG =∠FBD +∠GBD =90° 在△ECF 和△GBF 中=⎧⎪=⎨⎪=⎩∠∠EC BG ECF GBF CF BF ∴△ECF ≌△GBF (SAS ) ∴EF =GF ,∠EFC =∠GFB ∵∠CFB =∠CFG +∠GFB =90° ∴∠EFG =∠EFC +∠CFG =90° 在△EFD 和△GFD 中,=⎧⎪=⎨⎪=⎩EF GF FD FD ED GD ∴△EFD ≌△GFD (SSS )∴∠EDF =∠GDF =90°,∠EFD =∠GFD =45° ∴ED =DF∴△DEF 为等腰直角三角形 5. 解:AB =AF +CF ,理由如下: 延长AE 交DF 的延长线于点G .CFEBAD∵E 为BC 边的中点 ∴BE =CE ∵AB ∥DC∴∠B =∠BCG ,∠BAG =∠G 在△ABE 和△GCE 中=⎧⎪=⎨⎪=⎩∠∠∠∠B GCE BAE G BE CE ∴△ABE ≌△GCE (AAS ) ∴AB =GC ∵∠BAE =∠EAF ∴∠G =∠EAF ∴AF =GF ∵GC = GF +FC ∴AB =AF +CF三角形全等之倍长中线(随堂测试)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是____________________.2. 已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC . 求证:AE 平分∠BAC .FEC A【参考答案】1.3<AB<132.证明略(提示:延长AE 到点M ,使EM =AE ,连接DM , 证明△DME ≌△CAE )三角形全等之倍长中线(作业)3. 已知:如图,在△ABC 中,AB =5,AC =3,则中线AD 的取值范围是________________.B C D A4. 如图,在梯形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,若AD =2.7,BE =AE =5,求CE 的长.ABC D EF5. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形.求证:EF =2AD .EAFCB6. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G .求证:BF =CG .AC DEFG7. 如图,在正方形ABCD 的边AB 上任取一点E ,作EF ⊥AB 交BD 于点F ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .BE AFGC D8. 已知:如图,∠ACB =90°,AC =BC ,D 为AB 上一点,连接CD ,AE ⊥CD 于E ,BF ⊥CD 交CD 的延长线于F . 求证:△BCF ≌△CAE .ABC D EF9. 多项式9x 2+1加上一个单项式后,能使它成为一个整式的完全平方式,则可以加上的单项式共有________个,分别是______________________________.【参考答案】1.1<AD <42.2.3(提示:延长AF 交BC 于点G ,导角证明AE =EG )3.证明略(提示:延长AD 到点P ,使得AD =PD ,连接CP ,证明△ABD ≌△PCD ,△EAF ≌△PCA )4.证明略(提示:延长FE 到点H ,使得FE =EH ,连接CH ,证明△BFE ≌△CHE ,导角)5.证明略(提示:延长EG 交AD 于点P ,连接CE ,CP ) 6.证明略7.5;-1,-9x 2,-6x ,6x ,814x 4。
三角形全等之倍长中线

三角形全等之倍长中线“倍长中线”是指加倍延长中线,使所延长部分与中线相等,然后往往需要连接相应的顶点,则对应角对应边都对应相等。
常用于构造全等三角形。
中线倍长法多用于构造全等三角形和证明边之间的关系(通常用“SAS”证明)(注:一般都是原题已经有中线时用,不太会有自己画中线的时候),如果让我翻译我会翻译成:Double thelength of the center line。
例1:如图,在△ABC中,AD⊥AC,AB=2AC,AD平分BC,求∠BAC的度数。
解题思路:延长AD到A’,使AD=DA’。
连接B、A’。
利用BD=DC,∠BDA’=∠ADC,AD=DA’等三个条件证明△ADC≌△A’DB(S.A.S),从而得出BA’=AC,∠A’=∠A’AC=90°,以此证明构造出来的新三角形△AA’B为直角三角形,其中AB为斜边。
由题意得知AB=2AC,则AB=2BA’,那么∠BAA’=30°,那么∠BAC=30°+90°=120°解:延长AD到A’,使AD=DA’。
连接B、A’。
∵AD⊥AC(已知),∴∠A’AC=90°∵AD平分BC,∴DB=DC在△ADC和△A’DB中,DA=DA’,∠ADC=∠BDA’,DB=DC,∴△ADC≌△A’DB(SAS)。
∴AC=BA’∴∠A’=∠A’AC=90°∵AB=2AC,∴AB=2BA’即AB/2=BA’。
∴∠BAA’=30°∴∠BAC=∠BAA’+∠A’AC=30°+90°=120°例2:如图,在△ABC中,AB=5a,AC=3a(a>0),求中线AD的取值范围。
解题思路:延长AD到A’,使AD=DA’。
连接C、A’。
然后利用三角形全等,把三条边放到同一个三角形中间,利用三角形三边长度的关系,来确定中心的长度范围。
解:延长AD至AA’,交BC于D,使D A’=AD。
三角形全等之倍长中线(习题及答案)
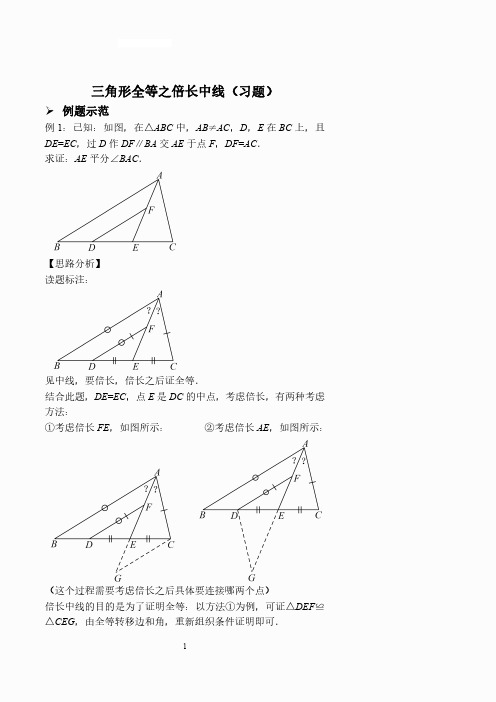
三角形全等之倍长中线(习题)例题示范例1:已知:如图,在△ABC中,AB≠AC,D,E在BC上,且DE=EC,过D作DF∥BA交AE于点F,DF=AC.求证:AE平分∠BAC.【思路分析】读题标注:见中线,要倍长,倍长之后证全等.结合此题,DE=EC,点E是DC的中点,考虑倍长,有两种考虑方法:①考虑倍长FE,如图所示:②考虑倍长AE,如图所示:(这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF≌△CEG,由全等转移边和角,重新组织条件证明即可.【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG.在△DEF 和△CEG 中,ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS )∴DF =CG ,∠DFE =∠G∵DF =AC∴CG =AC∴∠G =∠CAE∴∠DFE =∠CAE∵DF ∥AB∴∠DFE =∠BAE∴∠BAE =∠CAE∴AE 平分∠BAC巩固练习1.已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.2.已知:如图,BD平分∠ABC交AC于D,点E为CD上一点,且AD=DE,EF∥BC交BD于F.求证:AB=EF.3.已知:如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形,AB=AE,AC=AF,∠BAE=∠CAF=90°.求证:EF=2AD.4.如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA 的延长线于G.求证:BF=CG.5.如图,在四边形ABCD中,AD∥BC,点E在BC上,点F是CD的中点,连接AF,EF,AE,若∠DAF=∠EAF,求证:AF⊥EF.思考小结1.如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC.比较下列两种不同的证明方法,并回答问题.方法1:如图,延长AD 到E ,使DE =AD ,连接BE在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS )∴AC =BE ,∠E =∠2∵AD 平分∠BAC∴∠1=∠2∴∠1=∠E∴AB =BE∴AB =AC方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E∵BE ∥AC∴∠E =∠2在△BDE 和△CDA 中2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS )∴BE =AC∵AD 平分∠BAC∴∠1=∠2∴∠1=∠E∴AB=BE∴AB=AC相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等.不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等.2.利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt△ABC中,∠BCA=90°,CD是斜边AB的中线.求证:CD12AB.【参考答案】巩固练习1.22.证明略(提示:延长FD到点G,使得DG=DF,连接AG,证明△ADG≌△EDF,转角证明AB=EF)3.证明略(提示:延长AD到点G,使得GD=AD,连接CG,证明△ABD≌△GCD,△EAF≌△GCA)4.证明略(提示:延长FE到点H,使得EH=FE,连接CH,证明△BFE≌△CHE,转角证明BF=CG)5.证明略(提示:延长AF交BC的延长线于点G,证明△ADF≌△GCF,转角证明AF⊥EF)思考小结1.倍长中线SAS AAS角2.证明略。
三角形全等之倍长中线(含问题详解和练习)

三角形全等之倍长中线1. 如图,AD 为△ABC 的中线. (1)求证:AB +AC >2AD .(2)若AB =5,AC =3,求AD 的取值范围.2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .求证:①CE =2CD ;②CB 平分∠DCE .4. 如图,在△ABC 中,D 是BC 边的中点,E 是AD 上一点,BE =AC ,BE 的延长线交AC 于点F .求证:∠AEF =∠EAF .5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA 的延长线于点F ,交AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线.GFE DBAD CB AE D CBF EDC AGFE DB ADB A6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,且AF ⊥AB ,已知AD =2.7,AE =BE =5,求CE 的长.7. 如图,在正方形ABCD 的边CB 的延长线上取一点E ,△FEB 为等腰直角三角形,∠FEB =90°,连接FD ,取FD 的中点G ,连接EG ,CG . 求证:EG =CG 且EG ⊥CG .FE DCB A GF EDCBA【参考答案】1. (1)证明:如图,21BCDA延长AD 至E ,使DE =AD ,连接BE ,∴AE =2AD .∵AD 是△ABC 的中线 ∴BD =CD在△BDE 和△CDA 中12BD CD ED AD =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴BE =AC在△ABE 中,AB +BE >AE ∴AB +AC >2AD (2)解:由①可知 AE =2AD ,BE =AC 在△ABE 中, AB -BE <AE <AB +BE ∵AC =3,AB =5 ∴5-3<AE <5+3 ∴2<2AD <8 ∴1<AD <42. 证明:如图,延长AD 到E ,使DE =AD ,连接BE .4321ECDBA在△ADC 和△EDB 中34CD BD AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS ) ∴AC =EB ,∠2=∠E ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 3. 证明:如图,54EC AFB31D2延长CD 到F ,使DF =CD ,连接BF . ∴CF =2CD∵CD 是△ABC 的中线 ∴BD =AD在△BDF 和△ADC 中21BD AD DF DC =⎧⎪∠=∠⎨⎪=⎩∴△BDF ≌△ADC (SAS ) ∴BF =AC ,∠3=∠A ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =AC ∴BE =BF∵∠CBE 是△ABC 的一个外角 ∴∠CBE =∠BCA +∠A=∠BCA +∠3∵AC =AB ∴∠BCA =∠CBA ∴∠CBE =∠CBA +∠3 =∠CBF 在△CBE 和△CBF 中CB CB CBE CBF BE BF =⎧⎪∠=∠⎨⎪=⎩∴△CBE ≌△CBF (SAS ) ∴CE =CF ,∠4=∠5 ∴CE =2CD CB 平分∠DCE4. 证明:如图,延长AD 到M ,使DM =AD ,连接BM .MCDBEFA∵D 是BC 边的中点∴BD =CD在△ADC 和△MDB 中CD BD ADC MDB AD MD =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△MDB (SAS ) ∴∠CAD =∠M ,AC =MB∵BE =AC ∴BE =MB ∴∠M =∠BEM ∴∠CAD =∠BEM ∵∠AEF =∠BEM ∴∠CAD =∠AEF 即∠AEF =∠EAF5. 证明:如图,延长FE 到M ,使EM =EF ,连接BM .321MBG EDCA F∵点E 是BC 的中点∴BE =CE在△CFE 和△BME 中FE ME CEF BEM CE BE =⎧⎪∠=∠⎨⎪=⎩∴△CFE ≌△BME (SAS ) ∴CF =BM ,∠F =∠M ∵BG =CF ∴BG =BM ∴∠3=∠M ∴∠3=∠F ∵AD ∥EF∴∠2=∠F ,∠1=∠3 ∴∠1=∠2即AD 为△ABC 的角平分线.6. 解:如图,延长AF 交BC 的延长线于点G .54321GA B CD EF∵AD ∥BC ∴∠3=∠G∵点F 是CD 的中点 ∴DF =CF在△ADF 和△GCF 中312G DF CF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△GCF (AAS )∴AD =CG ∵AD =2.7 ∴CG =2.7 ∵AE =BE ∴∠5=∠B ∵AB ⊥AF ∴∠4+∠5=90° ∠B +∠G =90° ∴∠4=∠G ∴EG =AE =5 ∴CE =EG -CG=5-2.7=2.37. 证明:如图,延长EG ,交CD 的延长线于M .MAFEBGC D由题意,∠FEB =90°,∠DCB =90°∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 中点 ∴FG =DG在△FGE 和△DGM 中FEG M FGE DGM FG DG ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△FGE ≌△DGM (AAS ) ∴EF =MD ,EG =MG ∵△FEB 是等腰直角三角形 ∴EF =EB ∴BE =MD在正方形ABCD 中,BC =CD ∴BE +BC =MD +CD 即EC =MC∴△ECM 是等腰直角三角形 ∵EG =MG∴EG ⊥CG ,∠ECG =∠MCG =45° ∴EG =CG全等三角形之倍长中线每日一题1. (4月21日)已知:如图,在梯形ABCD 中,AD ∥BC ,AB =AD +BC ,E 是CD 的中点. 求证:AE ⊥BE .EDCB A A2.(4月22日)已知:如图,△ABC与△BDE均为等腰直角三角形,BA⊥AC,ED⊥BD,垂足分别为A,D,连接EC,F为EC中点,连接AF,DF,猜测AF,DF的数量关系和位置关系,并说明理由.3.(4月23日)已知:如图,D为线段AB的中点,在AB上任取一点C(不与点A,B,D重合),分别以AC,BC为斜边在AB同侧作等腰Rt△ACE与等腰Rt△BCF,∠AEC=∠CFB=90°,连接DE,DF,EF.求证:△DEF为等腰直角三角形.4.(4月24日)已知:如图,在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.试探究线段AB与AF,CF之间的数量关系,并说明理由.FEDCFEDCBA【参考答案】1. 证明:延长AE 交BC 的延长线于点F .FEDC B A∵AD ∥BC∴∠D =∠DCF ,∠DAE =∠F ∵E 是CD 的中点 ∴DE =CE在△ADE 和△FCE 中=⎧⎪∠=∠⎨⎪=⎩∠∠D FCE DAE F DE CE ∴△ADE ≌△FCE (AAS ) ∴AD =FC ,AE =FE ∵AB =AD +BC ∴AB =CF +BC =BF 在△ABE 和△FBE 中=⎧⎪=⎨⎪=⎩AB FB BE BE AE FE ∴△ABE ≌△FBE (SSS ) ∴∠AEB =∠FEB =90°即AE ⊥BE2. 解:AF ⊥DF ,AF =DF ,理由如下:延长DF 交AC 于点P .P FE D CBA∵BA ⊥AC ,ED ⊥BD ∴∠BAC =∠EDA=90° ∴DE ∥AC ∴∠DEC =∠ECA ∵F 为EC 中点 ∴EF =CF在△EDF 和△CPF 中DEF PCF EF CFEFD CFP ∠=∠⎧⎪=⎨⎪=⎩∠∠ ∴△EDF ≌△CPF (ASA ) ∴DE =CP ,DF=PF∵△ABC 与△BDE 均为等腰直角三角形 ∴AB =AC ,DE=BD ∴AB -BD=AC -DE=AC -CP 即AD =AP在△DAF 和△P AF 中DF PF AF AF AD AP =⎧⎪=⎨⎪=⎩∴△DAF ≌△P AF (SSS )∴∠DF A =∠PF A =90°,∠DAF =∠P AF =45° ∴AF ⊥DF ,AF =DF3. 证明:延长ED 到点G ,使DG =DE ,连接BG ,FG .GFE DCB A∵D 为线段AB 的中点 ∴AD =BD在△EDA 和△GDB 中=⎧⎪=⎨⎪=⎩∠∠ED GD EDA GDB DA DB ∴△EDA ≌△GDB (SAS ) ∴EA =GB ,∠A =∠GBD∵△ACE 与△BCF 是等腰直角三角形∴AE =CE =BG ,CF =FB ,∠A =∠ECA =∠FCB =∠FBC =45° ∴∠ECF =90°,∠GBF =∠GBD +∠FBD =90° 在△ECF 和△GBF 中EC GB ECF GBF CF BF =⎧⎪=⎨⎪=⎩∠∠ ∴△ECF ≌△GBF (SAS ) ∴EF =GF ,∠EFC =∠GFB ∵∠CFB =∠CFG +∠GFB =90° ∴∠EFG =∠EFC +∠CFG =90° 在△EFD 和△GFD 中=⎧⎪=⎨⎪=⎩EF GF FD FD ED GD ∴△EFD ≌△GFD (SSS )∴∠EDF =∠GDF =90°,∠EFD =∠GFD =45° ∴DE =DF∴△DEF 为等腰直角三角形 4. 解:AB =AF +CF ,理由如下:延长AE 交DF 的延长线于点G .FECBA∵E 为BC 边的中点 ∴BE =CE ∵AB ∥DC∴∠B =∠BCG ,∠BAG =∠G 在△ABE 和△GCE 中=⎧⎪=⎨⎪=⎩∠∠∠∠B GCE BAE G BE CE ∴△ABE ≌△GCE (AAS ) ∴AB =GC ∵∠BAE =∠EAF ∴∠G =∠EAF ∴AF =GF ∵GC =GF +FC ∴AB =AF +CF三角形全等之倍长中线(随堂测试)1. 在△ABC 中,AC =5,中线AD =4,则边AB 的取值范围是_______________.2. 已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥AB 交AE 于点F ,DF =AC .求证:AE 平分∠BAC .FE CBA【参考答案】1. 3<AB <132. 证明略(提示:延长AE 到点G ,使EG =EF ,连接CG ,证明△DEF ≌△CEG ).三角形全等之倍长中线(作业)1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.D CB A2. 已知:如图,BD 平分∠ABC 交AC 于D ,点E 为CD 上一点,且AD =DE ,EF ∥BC 交BD 于F .求证:AB =EF .F E DA3. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形.求证:EF =2AD .FED CA4. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G .求证:BF =CG .G FE CBA5. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,连接AF ,若∠DAF =∠EAF ,求证:AF ⊥EF .FE DB CA【参考答案】1. 22. 证明略(提示:延长FD 到点G ,使得DG =DF ,连接AG ,证明△ADG ≌△EDF ,转角证明AB =EF )3. 证明略(提示:延长AD 到点G ,使得AD =GD ,连接CG ,证明△ABD ≌△GCD ,△EAF ≌△GCA )4. 证明略(提示:延长FE 到点H ,使得FE =EH ,连接CH ,证明△BFE ≌△CHE ,转角证明BF =CG )5. 证明略(提示:延长AF 交BC 的延长线于点G ,证明△ADF ≌△GCF ,转角证明AF ⊥EF )。
人教版八年级数学上册:三角形全等之倍长中线(习题及答案)

三角形全等之倍长中线(习题)➢ 例题示范例1:已知:如图,在△ABC 中,AB ≠AC ,D ,E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC . 求证:AE 平分∠BAC .A D CE F【思路分析】 读题标注:??FE C D BA见中线,要倍长,倍长之后证全等.结合此题,DE =EC ,点E 是DC 的中点,考虑倍长,有两种考虑方法: ①考虑倍长FE ,如图所示: ②考虑倍长AE ,如图所示:A B DCE F??GG??FECDBA (这个过程需要考虑倍长之后具体要连接哪两个点)倍长中线的目的是为了证明全等:以方法①为例,可证△DEF ≌△CEG ,由全等转移边和角,重新组织条件证明即可. 【过程书写】证明:如图,延长FE 到G ,使EG =EF ,连接CG .A B D CE F??G在△DEF 和△CEG 中, ED EC DEF CEG EF EG =⎧⎪∠=∠⎨⎪=⎩∴△DEF ≌△CEG (SAS ) ∴DF =CG ,∠DFE =∠G ∵DF =AC ∴CG =AC ∴∠G =∠CAE ∴∠DFE =∠CAE ∵DF ∥AB ∴∠DFE =∠BAE ∴∠BAE =∠CAE ∴AE 平分∠BAC➢ 巩固练习1. 已知:如图,在△ABC 中,AB =4,AC =2,点D 为BC 边的中点,且AD 是整数,则AD =________.D CBA2. 已知:如图,BD 平分∠ABC 交AC 于D ,点E 为CD 上一点,且AD =DE ,EF ∥BC 交BD 于F . 求证:AB =EF .F E DCBA3. 已知:如图,在△ABC 中,AD 是BC 边上的中线,分别以AB ,AC 为直角边向外作等腰直角三角形,AB =AE ,AC =AF ,∠BAE =∠CAF =90°. 求证:EF =2AD .4. 如图,在△ABC 中,AB >AC ,E 为BC 边的中点,AD 为∠BAC 的平分线,过E 作AD 的平行线,交AB 于F ,交CA 的延长线于G . 求证:BF =CG .FED C B A G FED CBA5. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,连接AF ,EF ,AE ,若∠DAF =∠EAF ,求证:AF ⊥EF .➢ 思考小结1. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .求证:AB =AC .CDB A比较下列两种不同的证明方法,并回答问题.方法1:如图,延长AD 到E ,使DE =AD ,连接BEFE DB CA在△BDE 和△CDA 中BD CD BDE CDA DE DA =⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (SAS ) ∴AC =BE ,∠E =∠2 ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 方法2:如图,过点B 作BE ∥AC ,交AD 的延长线于点E ∵BE ∥AC∴∠E =∠2在△BDE 和△CDA 中2E BDE CDA BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDE ≌△CDA (AAS ) ∴BE =AC ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE ∴AB =AC 相同点:两种方法都是通过辅助线构造全等,利用全等转移条件进而解决问题.方法1是看到中点考虑通过___________构造全等,方法2是通过平行夹中点构造全等. 不同点:倍长中线的方法在证明全等时,利用的判定是________,实质是构造了一组对应边相等;利用平行夹中点证明全等时,利用的判定是_____,实质是利用平行构造了一组_____相等.2. 利用“倍长中线”我们就可以证明直角三角形中非常重要的一个定理:直角三角形斜边中线等于斜边的一半.请你尝试进行证明.已知:如图,在Rt △ABC 中,∠BCA =90°,CD 是斜边AB 的中线.求证:21ECDB A 21ECDB ACD12AB.DCB A【参考答案】➢巩固练习1. 22.证明略(提示:延长FD到点G,使得DG=DF,连接AG,证明△ADG≌△EDF,转角证明AB=EF)3.证明略(提示:延长AD到点G,使得GD=AD,连接CG,证明△ABD≌△GCD,△EAF≌△GCA)4.证明略(提示:延长FE到点H,使得EH=FE,连接CH,证明△BFE≌△CHE,转角证明BF=CG)5.证明略(提示:延长AF交BC的延长线于点G,证明△ADF≌△GCF,转角证明AF⊥EF)➢思考小结1.倍长中线SAS AAS 角2.证明略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形全等之倍长中线
课前预习
1. 填空
(1)三角形全等的判定有:
三边分别___________的两个三角形全等,即(____); 两边和它们的_____分别相等的两个三角形全等,即(____); 两角和它们的_____分别相等的两个三角形全等,即(____); 两角和其中一个角的______分别相等的两个三角形全等,即(____); 斜边和_______边分别相等的两个直角三角形全等,即(____).
(2)要证明两条边相等或者两个角相等,可以考虑放在两个三角形中证________;要证明两个三角形全等需要准备______组条件,这三组条件里面必须有______;然后依据判定进行证明,其中AAA ,SSA 不能证明两个三角形全.
2. 想一想,证一证
已知:如图,AB 与CD 相交于点O ,且O 是AB 的中点. (1)当OC =OD 时,求证:△AOC ≌△BOD ; (2)当AC ∥BD 时,求证:△AOC ≌△BOD .
O
B
C D
A
➢ 知识点睛
1. “三角形全等”辅助线:
见中线,要__________,构造______________. 2. 中点的思考方向:
① (类)倍长中线
延长AD 到E ,使DE =AD , 延长MD 到E ,使DE =MD , 连接BE 连接CE
D C
B A
M A
B
C
D
②平行夹中点
F E
D
C
B
A
延长FE 交BC 的延长线于点G
➢ 精讲精练
1. 如图,在△ABC 中,AD 为BC 边上的中线.
(1)按要求作图:延长AD 到点E ,使DE =AD ;连接BE . (2)求证:△ACD ≌△EBD . (3)求证:AB +AC >2AD .
(4)若AB =5,AC =3,求AD 的取值范围.
2. 如图,在△ABC 中,AD 平分∠BAC ,且BD =CD .
求证:AB =AC .
3. 如图,CB 是△AEC 的中线,CD 是△ABC 的中线,且AB =AC .
求证:①CE =2CD ;②CB 平分∠DCE .
D C
B A
D
B A
D C
B A
4. 如图,在△ABC 中,D 是BC 的中点,E 是AD 上一点,BE =AC ,BE 的延长
线交AC 于点F . 求证:∠AEF =∠EAF .
5. 如图,在△ABC 中,AD 交BC 于点D ,点E 是BC 的中点,EF ∥AD 交CA
的延长线于点F ,交AB 于点G ,BG =CF . 求证:AD 为△ABC 的角平分线.
6. 如图,在四边形ABCD 中,AD ∥BC ,点E 在BC 上,点F 是CD 的中点,
且AF ⊥AB ,已知AD =2.7,AE =BE =5,求CE 的长.
7. 如图,在正方形ABCD 中,CD =BC ,∠DCB =90°,点E 在CB 的延长线上,
过点E 作EF ⊥BE ,且EF=BE .连接BF ,FD ,取FD 的中点G ,连接EG ,CG .
求证:EG =CG 且EG ⊥CG .
F E
D
B
A
G
F
E
D
B
A
G
D
A
F
E D
C
B A
【参考答案】
➢ 课前预习
1. (1)相等,SSS ;夹角,SAS ;夹边,ASA ;对边,AAS ;
直角,HL
(2)全等,三,边 2. (1)证明:如图
∵O 是AB 的中点 ∴AO =BO
在△AOC 和△BOD 中
AO BO AOC BOD OC OD =⎧⎪
∠=∠⎨⎪=⎩
∴△AOC ≌△BOD (SAS ) (2)证明:如图 ∵O 是AB 的中点 ∴AO =BO ∵AC ∥BD ∴∠A =∠B
在△AOC 和△BOD 中
A B AO BO
AOC BOD ∠=∠⎧⎪
=⎨⎪∠=∠⎩
∴△AOC ≌△BOD (ASA ) ➢ 精讲精练 1. 解:(1)如图,
2
1B
C
D
A
(2)证明:如图, ∵AD 为BC 边上的中线
∴BD =CD
在△BDE 和△CDA 中
12BD CD ED AD =⎧⎪
∠=∠⎨⎪=⎩
∴△BDE ≌△CDA (SAS ) (3)证明:如图, ∵△BDE ≌△CDA ∴BE =AC ∵DE =AD ∴AE =2 AD
在△ABE 中,AB +BE >AE ∴AB +AC >2AD (4)在△ABE 中,
AB -BE <AE <AB +BE
由(3)得 AE =2AD ,BE =AC ∵AC =3,AB =5 ∴5-3<AE <5+3 ∴2<2AD <8 ∴1<AD <4
2. 证明:如图,延长AD 到E ,使DE =AD ,连接BE
在△ADC 和△EDB 中
CD BD ADC EDB AD ED =⎧⎪
∠=∠⎨⎪=⎩
∴△ADC ≌△EDB (SAS ) ∴AC =EB ,∠2=∠E ∵AD 平分∠BAC ∴∠1=∠2 ∴∠1=∠E ∴AB =BE
∴AB =AC
3. 证明:如图,延长CD 到F ,使DF =CD ,连接BF
∴CF =2CD
∵CD 是△ABC 的中线 ∴BD =AD
2
1E
D
C
B A
在△BDF 和△ADC 中
BD AD ADC BDF DF DC =⎧⎪
∠=∠⎨⎪=⎩
∴△BDF ≌△ADC (SAS ) ∴BF =AC ,∠1=∠F ∵CB 是△AEC 的中线 ∴BE =AB ∵AC =AB ∴BE =BF ∵∠1=∠F ∴BF ∥AC
∴∠1+∠2+∠5+∠6=180° 又∵AC =AB ∴∠1+∠2=∠5 又∵∠4+∠5=180° ∴∠4=∠5+∠6 即∠CBE =∠CBF 在△CBE 和△CBF 中
CB CB CBE CBF BE BF =⎧⎪
∠=∠⎨⎪=⎩
∴△CBE ≌△CBF (SAS ) ∴CE =CF ,∠2=∠3 ∴CE =2CD
CB 平分∠DCE
4. 证明:如图,延长AD 到M ,使DM =AD ,连接BM
∵D 是BC 边的中点
∴BD =CD
在△ADC 和△MDB 中
321A B
C
D
E F
ADC MDB AD MD ⎪
∠=∠⎨⎪=⎩
∴△ADC ≌△MDB (SAS ) ∴∠1=∠M ,AC =MB ∵BE =AC ∴BE =MB ∴∠M =∠3 ∴∠1=∠3 ∵∠3=∠2 ∴∠1=∠2 即∠AEF =∠EAF
5. 证明:如图,延长FE 到M ,使EM =EF ,连接BM
∵点E 是BC 的中点
∴BE =CE
在△CFE 和△BME 中
FE ME
CEF BEM CE BE =⎧⎪
∠=∠⎨⎪=⎩
∴△CFE ≌△BME (SAS ) ∴CF =BM ,∠F =∠M ∵BG =CF ∴BG =BM ∴∠1=∠M ∴∠1=∠F ∵AD ∥EF
∴∠3=∠F ,∠1=∠2 ∴∠2=∠3
即AD 为△ABC 的角平分线
6. 解:如图,延长AF 交BC 的延长线于点G
∵AD ∥BC
∴∠3=∠G ∵点F 是CD 的中点 ∴DF =CF
在△ADF 和△GCF 中
3
21
M
A
B
C
D E
F G
AFD GFC DF CF ⎪
∠=∠⎨⎪=⎩
∴△ADF ≌△GCF (AAS )
∴AD =CG ∵AD =2.7 ∴CG =2.7 ∵AE =BE ∴∠1=∠B ∵AB ⊥AF ∴∠1+∠2=90° ∠B +∠G =90° ∴∠2=∠G ∴EG =AE =5 ∴CE =EG -CG
=5-2.7
=2.3
7. 证明:如图,延长EG 交CD 的延长线于点M
由题意,∠FEB =90°,∠DCB =90° ∴∠DCB +∠FEB =180° ∴EF ∥CD ∴∠FEG =∠M ∵点G 为FD 的中点 ∴FG =DG
在△FGE 和△DGM 中
1M FGE DGM FG DG ∠=∠⎧⎪
∠=∠⎨⎪=⎩
∴△FGE ≌△DGM (AAS )
∴EF=MD,EG=MG
∵△FEB是等腰直角三角形
∴EF=EB
∴BE=MD
在正方形ABCD中,BC=CD
∴BE+BC=MD+CD
即EC=MC
∴△ECM是等腰直角三角形
∵EG=MG
∴EG⊥CG,∠3=∠4=45°
∴∠2=∠3=45°
∴EG=CG
6.(本小题17分)已知:如图,△ABC和△CDE均为等腰直角三角形,∠ABC=∠CDE=90°,AB=BC,DC=DE,,点C,B,D在同一直线上,M是AE的中点.
求证:MD⊥MB,MD=MB.
证明:如图,延长BM交DE于点N.
3.(本小题17分)如图,在四边形ABCD中,AD∥BC,M是CD的中点,若AB=AD+BC,∠ABC=50°,
则∠BAM=( )
• A. 75°
• B. 65°
• C. 50°
• D. 40°。
