第二章 传热习题答案
第二章传热答案
第二章传热答案【篇一：传热学第二章答案第四版-杨世铭-陶文铨】p> 1 试写出导热傅里叶定律的一般形式，并说明其中各个符号的意义。
?t??q＝－?gradt???n?x，其中：gradt为空间某点的温答：傅立叶定律的一般形式为： ??qn度梯度；是通过该点的等温线上的法向单位矢量，指向温度升高的方向；为该处的热流密度矢量。
2 已知导热物体中某点在x,y,z三个方向上的热流密度分别为qx,qy及qz，如何获得该点的热密度矢量？???????q?q?i?q?j?q?kxyz答：，其中i,j,k分别为三个方向的单位矢量量。
3 试说明得出导热微分方程所依据的基本定律。
答：导热微分方程式所依据的基本定律有：傅立叶定律和能量守恒定律。
4 试分别用数学语言将传热学术语说明导热问题三种类型的边界条件。
答：①第一类边界条件：??0时，tw?f1(?)②第二类边界条件：??0时??(??(?t)w?f2(?)?x③第三类边界条件：5 试说明串联热阻叠加原则的内容及其使用条件。
答：在一个串联的热量传递过程中，如果通过每个环节的热流量都相同，则各串联环节的总热阻等于各串联环节热阻的和。
使用条件是对于各个传热环节的传热面积必须相等。
7.通过圆筒壁的导热量仅与内、外半径之比有关而与半径的绝对值无关，而通过球壳的导热量计算式却与半径的绝对值有关，怎样理解？答：因为通过圆筒壁的导热热阻仅和圆筒壁的内外半径比值有关，而通过球壳的导热热阻却和球壳的绝对直径有关，所以绝对半径不同时，导热量不一样。
6 发生在一个短圆柱中的导热问题，在下列哪些情形下可以按一维问题来处理？答：当采用圆柱坐标系，沿半径方向的导热就可以按一维问题来处理。
8 扩展表面中的导热问题可以按一维问题来处理的条件是什么？有人认为，只要扩展表面细长，就可按一维问题来处理，你同意这种观点吗？答：只要满足等截面的直肋，就可按一维问题来处理。
不同意，因为当扩展表面的截面不均时，不同截面上的热流密度不均匀，不可看作一维问题。
传热计算习题附详细答案
传热计算题1.在一内径为0.25cm的管轴心位置上，穿一直径为 0.005cm的细导线，用以测定气体的导热系数。
当导线以0.5A 的电流时，产生的电压降为0.12V/cm，测得导线温度为167℃，空心管内壁温度为150℃。
试求充入管内的气体的导热系数试分析仪器精度以外造成结果误差的客观原因。
2．有两个铜质薄球壳，内球壳外径为0。
015m，外球壳内径为 0.1m，两球壳间装入一种其导热系数待测的粉粒料。
内球用电加热，输入功率为 50w，热量稳定地传向外球，然后散发到周围大气中。
两球壁上都装有热电偶，侧得内球壳的平均温度为120℃，外求壳的平均温度为50℃，周围大气环境温度为20℃；设粉粒料与球壁贴合，试求：（1）待测材料的导热系数（2）外球壁对周围大气的传热系数3．有一面积为10cm2带有保护套的热电偶插入一输送空气的长管内，用来测量空气的温度。
已知热电偶的温度读数为300℃，输气管的壁温为 200℃，空气对保护套的对流传热系数为60w/m2.k，该保护套的黑度为 0.8，试估算由于辐射造成的气体温度测量误差。
并叙述减小测量误差的途径。
已知 Stefan-Bohzman常数σ=5.67×10-9w/m2k 。
4．用两个结构尺寸相同的列管换热器按并联方式加热某中料液。
换热器的管束由32根长 3m 的Ф25×3mm 的钢管组成。
壳程为120℃的饱和蒸汽。
料液总流量为20m3/h，按相等流量分配到两个换热器中作湍流流动，由 25℃加热到 80℃。
蒸汽冷凝对流传热系数为8Kw/m2.℃，管壁及污垢热阻可不记，热损失为零，料液比热为 4.1KJ/kg.℃，密度为 1000kg/m3。
试求：（1）管壁对料液的对流传热系数（2）料液总流量不变，将两个换热器串联，料液加热程度有何变化？（3）此时蒸汽用量有无变化？若有变化为原来的多少倍？（两者情况下蒸汽侧对流传热系数和料液物性不变）5．某厂现有两台单壳程单管程的列管式空气加热器，每台传热面积为A0=20m2（管外面积），均由128根Ф25×2.5mm的钢管组成。
第二章 传热习题答案
【2-1】一食品冷藏室由内层为19 mm 厚的松木，中层为软木层，外层为51 mm 厚的混凝土所组成。
内壁面温度为-17.8 ℃,混凝土外壁面温度为29.4 ℃。
松木、软木和混凝土的平均热导率分别为0.151,0.043 3,0.762 W/(m ·K )，要求该冷藏室的热损失为15W/m 2。
求所需软木的厚度及松木和软木接触面处的温度。
解：三层平壁的导热。
1）所需软木的厚度2b由 ∑=-=3141i ii b T T q λ 得 151.0019.00433.0762.0051.08.174.29152+++=b 解得： m b 128.02=2）松木和软木接触面处的温度3T由 151.0019.08.17153+==T q 解得：9.153-=T ℃解题要点：多层平壁热传导的应用。
【2-2】为减少热损失，在外径为150 mm 的饱和蒸汽管道外加有保温层。
已知保温材料的热导率λ=0.103+0.000 198 T(式中T 为℃),蒸汽管外壁温度为180 ℃,要求保温层外壁温度不超过50 ℃,每米管道由于热损失而造成蒸汽冷凝的量控制在1×10-4 kg/(m ·s)以下,问保温层厚度应为多少?(计算时可假定蒸汽在180 ℃下冷凝)。
解：保温层平均热导率为： )./(126.02501801098.1103.04K m W =+⨯⨯+=-λ 由于本题已知的是蒸汽管道外壁面温度，即保温层内壁面温度，故为一层导热。
由 )()(21221r r Ln T T L Q -=λπ 得： )()(21221r r Ln T T L Q -=πλ （1）式中：m W L Wr L Q /9.2011103.201910134=⨯⨯⨯==- 将其及其它已知数据代入式（1）得：)075.0()50180(126.029.2012r Ln -⨯⨯=π 解得：m r 125.02=mm m 5005.0075.0125.0==-=∴δ壁厚解题要点：单层圆筒壁热传导的应用。
化工原理课后习题答案传热习题解答
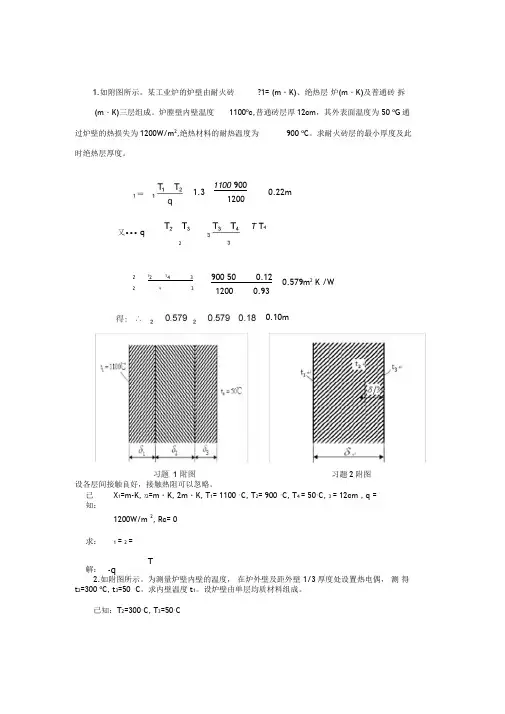
1.如附图所示。
某工业炉的炉壁由耐火砖 ?1= (m ・K)、绝热层 炉(m ・K)及普通砖 拆(m ・K)三层组成。
炉膛壁内壁温度1100o c,普通砖层厚12cm ，其外表面温度为 50 o G 通过炉壁的热损失为1200W/m 2,绝热材料的耐热温度为 900 o C 。
求耐火砖层的最小厚度及此时绝热层厚度。
设各层间接触良好，接触热阻可以忽略。
已知：X 1=m-K, ?2=m ・K, 2m ・K, T 1= 1100 °C, T 2= 900 °C, T 4 = 50°C, 3 = 12cm , q = 1200W/m 2, Rc= 0求：1 =2 =解： T-q2.如附图所示。
为测量炉壁内壁的温度， 在炉外壁及距外壁 1/3厚度处设置热电偶， 测 得t 2=300 o C, t 3=50 °C 。
求内壁温度t 1。
设炉壁由单层均质材料组成。
已知：T 2=300°C, T 3=50°C1100 90012000.22m又••• q900 50 0.12 12000.930.579m 2 K /W1.32T T 42 T 2T 4 3 2q30.10m习题2附图其中 r i =30mm , r 2=60mm , r 3=160mm 所以2 100 10丄ln60丄in 型0.043 300.076025W/m负号表示由外界向系统内传热，即为冷量损失量。
4.蒸汽管道外包扎有两层导热系数不同而厚度相同的绝热层，设外层的平均直径为内 层的两倍。
其导热系数也为内层的两倍。
若将二层材料互换位置，假定其它条件不变， 试问每米管长的热损失将改变多少说明在本题情况下，哪一种材料包扎在内层较为合适解：设外层平均直径为d m,2，内层平均直径为d m,1，则d m,2= 2d m,1 且 ?2=2 入由导热速率方程知bbbb5 b 1 S m12S m21 d m1L2 1 2d m1 L4 1两层互换位置后Qttd m 丄所以q_1.25求： T i =T i = 2(T 2— T 3)+T 3=3 X (300-50)+56= 800 °C3.直径为60 X 3mml 的钢管用30mm 厚的软木包扎，其外又用 100mm 厚的保温灰包扎， 以作为绝热层。
传热学第二章答案
第二章3.导热系数为常数的无内热源的平壁稳态导热过程，试问，若平壁两侧给定边界条件Tw1和Tw2，为什么这一导热过程的温度分布与平壁的材料无关？相同的平壁厚度，不同的平壁材料，仍给定第一类边界条件，热流密度是否相同？ （1）温度分布为 121w w w t t t t x δ-=-(设12w w t t >)其与平壁的材料无关的根本原因在coust λ=（即常物性假设），否则t 与平壁的材料有关 （2）由 dtq dxλ=- 知，q 与平壁的材料即物性有关 6.同上题，若已知边界条件为第三类，即已知Tf1，h1，Tf2，h2.试倒通过空心球壁热量的计算公式和球壁的传热热阻。
9.某教室有一层厚度为240mm 的砖层和一厚度为20mm 的灰泥构层。
现安装空调设备，并在内表面加贴一层硬泡某塑料，是导入室内的热量比原来少了80%。
已知砖的导热系数λ=0.7W/(m*k)，灰泥为λ=0.58W/(m*k)，硬泡某塑料的导热系数为λ=0.06W/(m*k)，试求出硬泡某塑料厚度。
已知：12240,20mm mmδδ==，120.7/(),0.58/()W m k W m k λλ=⋅=⋅3210.06/(),0.2W m k q q λ=⋅= 求：3δ解： 设两种情况下的内外面墙壁温度12w w t t 和保持不变，且12w w t t >由题意知：1211212w w t t q δδλλ-=+122312123ww t t q δδδλλλ-=++再由： 210.2q q =，有121231212121230.2w w w w t t t t δδδδδλλλλλ--=+++221313212tw 1tw 2q 11λ12λ23λ3得： 123312240204()40.06()90.60.70.58mm δδδλλλ=+=⨯⨯+= 12.已测得三层平壁的壁面温度为Tw1，Tw2，Tw3和Tw4依次为600℃，480℃，200℃和60℃，再稳态情况下，试问各层导热热阻在总热阻中所占的比例为多少？1600w t =℃，2480w t =℃，3200w t =℃，460w t =℃求：123,,R R R R R R λλλλλλ解：由题意知其为多层平壁的稳态导热 故有： 14122334123w w w w w w w w t t t t t t t t q R R R R λλλλ----==== ∴112146004800.2260060w w w w R t t R t t λλ--===-- 223144802000.5260060w w w w R t t R t t λλ--===--33414200600.2660060w w w w R t t R t t λλ--===-- 15.如图，一刚进混泥土空斗强，刚进混泥土的导热系数为λ=1.52W/(m*k)，空气层的当量导热系数为λ=0.742W/(m*k)。
高等传热第二章习题答案
2-1首先对铝导线进行分析求出铝导线的温度场，这是一个一维稳态有内热源的问题 在圆柱坐标系中建立其导热微分方程得10v d dt r q λ⎛⎫⎪⎝⎭+= (2.1)其中λ按常物性处理解导热微分方程得212ln 4v q t r c r c λ=-++ (2.2)把边界条件带入上式求解两个常数0r =，0tr∂=∂求得10c =，所以（2.2）式变为224v qt r c λ=-+(2.3)r R =，w t t =求得224v w q c t R λ=+(2.4)铝导线内温度场为()224v w q t t R r λ=+- (2.5)铝导线单位长度发热量： 222l v I Q q R R ρππ==，所以224v I q Rρπ=横截面积2A R π=，所以0.977R mm ===， 1.954D mm =1R R =为裸线直径；2R 为塑胶线的外径对于裸线：()12l w f Q h t t R π=-(2.6)12lw f Q t t h R π=+(2.7)把（2.7）式带入（2.5）式得()2211124l v f Q qt t R r h R πλ=++-(2.8)把lQ 、vq 带入得（2.8）式得()22221232411124f I I t t R r h R R ρρπλπ=++- (2.9)对于塑胶线：21221122ln w fl D D h R t t Q πλπ-=+ (2.10)222111ln 22w f l D t t Q h R D ππλ⎛⎫=++ ⎪⎝⎭(2.11)把lQ 代入得222122111ln 22w f D I t t R h R D ρπππλ⎛⎫=++ ⎪⎝⎭(2.12)把（2.12）式带入（2.5）式得 ()2222121221111ln 224v f q D I t t R r R h R D ρπππλλ⎛⎫=+++- ⎪⎝⎭即()2222212412211111ln 224f D I I t t R r R h R D R ρρπππλλπ⎛⎫=+++- ⎪⎝⎭ (2.13)设导线内部0r =时温度为0t ，根据题目要求导线内部最高温度与环境温度的温差不得超过 80℃，即080f t t -=℃时通过导线的电流取到最大值。
(完整版)建筑物理(第四版)刘加平课后习题答案第2章
第二章 建筑围护结构的传热原理及计算习 题2-1、建筑围护结构的传热过程包括哪几个基本过程，几种传热方式？分别简述其要点。
答：建筑围护结构传热过程主要包括三个过程：表面吸热、结构本身传热、表面放热。
表面吸热——内表面从室内吸热（冬季），或外表面从事外空间吸热（夏季）结构本身传热——热量由高温表面传向低温表面表面放热——外表面向室外空间散发热量（冬季）,或内表面向室内散热（夏季）2-2、为什么空气间层的热阻与其厚度不是成正比关系？怎样提高空气间层的热阻？答：在空气间层中，其热阻主要取决于间层两个界面上的空气边界层厚度和界面之间的辐射换热强度。
所以，空气间层的热阻于厚度之间不存在成比例地增长关系。
要提高空气间层的热阻可以增加间层界面上的空气边界层厚度以增加对流换热热阻；或是在间层壁面上涂贴辐射系数小的反射材料以增加辐射换热热阻。
2-3、根据图2-17所示条件，定性地作为稳定传热条件下墙体内部的温度分布线，应区别出各层温度线的倾斜度，并说明理由。
已知λ3〉λ1〉λ2。
答：由可知，由于是稳定传热，各壁面内的热流都相同，当值越大时，dxd q θλ-=λ各壁层的温度梯度就越小，即各层温度线的倾斜度就越小。
dx d θ2-4、如图2-18所示的屋顶结构，在保证内表面不结露的情况下，室外外气温不得低于多少？并作为结构内部的温度分布线。
已知：ti=22℃，ψi=60%，Ri=0.115m2•k/W ，Re=0.043 m2•k/W 。
解：由t i =22℃，ψi =60% 可查出Ps=2642.4Pa 则 pap p i s 44.15856.04.2642=⨯=⨯=ϕ可查出露点温度 ℃88.13=d t 要保证内表面不结露，内表面最低温度不得低于露点温度1）将圆孔板折算成等面积的方孔板ma a d 097.0422==π2）计算计算多孔板的传热阻有空气间层的部分（其中空气间层的热阻是0.17）W K m R /)(35.004.011.074.10265.017.074.10265.0201⋅=++++=无空气间层的部分W K m R /)(24.004.011.074.115.0202⋅=++=3）求修正系数)/(74.11K m W ⋅=λ)/(57.017.0097.02K m W ⋅==λ33.074.157.012==λλ所以修正系数取0.934）计算平均热阻W K m R /)(143.093.015.024.0053.035.0097.0053.0097.02⋅=⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-++=5）计算屋顶总的传热系数W K m R /)(63.015.0143.019.005.093.002.017.001.02⋅=++++=6）计算室外温度11.088.132263.022-=--=-e i i i e i t R t R t t θ得 te=-24.79℃由此可得各层温度是θ1=3.45℃ θ2=-15.92℃θ3=-17.5℃ θe=-21.84℃可画出结构内部的温度分布线。
传热学杨世铭第四版第二章答案
传热学杨世铭第四版第二章答案篇一：传热学第四版课后习题答案(杨世铭)第一章思考题1．试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答：导热和对流的区别在于：物体内部依靠微观粒子的热运动而产生的热量传递现象，称为导热；对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是：在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式，只有在物质存在的条件下才能实现，而辐射可以在真空中传播，辐射换热时不仅有能量的转移还伴有能量形式的转换。
2．以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩－玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答：①傅立叶定律：“－”表示热量传递的方向是沿着温度降低的方向。
qdtdtdx，其中，q－热流密度；?－导热系数；dx－沿x方向的温度变化率，②牛顿冷却公式：q?h(tw?tf)，其中，q－热流密度；h－表面传热系数；tw－固体表面温度；tf－流体的温度。
4q??T③斯忒藩－玻耳兹曼定律：，其中，q－热流密度；?－斯忒藩－玻耳兹曼常数；T－辐射物体的热力学温度。
3．导热系数、表面传热系数及传热系数的单位各是什么？哪些是物性参数，哪些与过程有关？答：①导热系数的单位是：W/()；②表面传热系数的单位是：W/()；③传热系数的单位是：W/()。
这三个参数中，只有导热系数是物性参数，其它均与过程有关。
4．当热量从壁面一侧的流体穿过壁面传给另一侧的流体时，冷、热流体之间的换热量可以通过其中任何一个环节来计算（过程是稳态的），但本章中又引入了传热方程式，并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答：因为在许多工业换热设备中，进行热量交换的冷、热流体也常处于固体壁面的两侧，是工程技术中经常遇到的一种典型热量传递过程。
5．用铝制的水壶烧开水时，尽管炉火很旺，但水壶仍然安然无恙。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
【2-1】一食品冷藏室由内层为19 mm 厚的松木，中层为软木层，外层为51 mm 厚的混凝土所组成。
内壁面温度为-17.8 ℃,混凝土外壁面温度为29.4 ℃。
松木、软木和混凝土的平均热导率分别为, 3, W/(m ·K)，要求该冷藏室的热损失为15W/m 2。
求所需软木的厚度及松木和软木接触面处的温度。
解：三层平壁的导热。
1）所需软木的厚度2b由 ∑=-=3141i ii b T T q λ 得 151.0019.00433.0762.0051.08.174.29152+++=b 解得： m b 128.02=2）松木和软木接触面处的温度3T由 151.0019.08.17153+==T q 解得：9.153-=T ℃解题要点：多层平壁热传导的应用。
【2-2】为减少热损失，在外径为150 mm 的饱和蒸汽管道外加有保温层。
已知保温材料的热导率λ=+ 198 T(式中T 为℃),蒸汽管外壁温度为180 ℃,要求保温层外壁温度不超过50 ℃,每米管道由于热损失而造成蒸汽冷凝的量控制在1×10-4 kg/(m ·s)以下,问保温层厚度应为多少(计算时可假定蒸汽在180 ℃下冷凝)。
解：保温层平均热导率为： )./(126.02501801098.1103.04K m W =+⨯⨯+=-λ 由于本题已知的是蒸汽管道外壁面温度，即保温层内壁面温度，故为一层导热。
由 )()(21221r r Ln T T L Q -=λπ 得： )()(21221r r Ln T T L Q -=πλ （1） 式中：m W L Wr L Q /9.2011103.201910134=⨯⨯⨯==- 将其及其它已知数据代入式（1）得：)075.0()50180(126.029.2012r Ln -⨯⨯=π 解得：m r 125.02=mm m 5005.0075.0125.0==-=∴δ壁厚解题要点：单层圆筒壁热传导的应用。
【2-8】烤炉内在烤一块面包。
已知炉壁温度为175 ℃，面包表面的黑度为,表面温度为100 ℃,表面积为 5 m 2，炉壁表面积远远大于面包表面积。
求烤炉向这块面包辐射 传递的热量。
解：两物体构成封闭空间，且21S S <<，由下式计算辐射传热量：W T T S Q 0.65)448373(0645.085.01067.5)(448424111012-=-⨯⨯⨯⨯=-=-εσ负号表示炉壁向面包传递热量。
解题要点：辐射传热的应用，两个灰体构成的封闭空间。
【2-10】在逆流换热器中，用初温为20 ℃的水将1.25 kg/s 的液体［比热容为 kJ/(kg ·K)、密度为850 kg/m 3］由80 ℃冷却到30 ℃。
换热器的列管直径为Φ25 mm ×2.5 mm,水走管内。
水侧和液体侧的对流传热系数分别为850 W/（m 2·K ）和1 700W/（m 2·K ）,污垢热阻可忽略。
若水的出口温度不能高于50 ℃，求水的流量和换热器的传热面积。
解：传热量为W T T c W Q h h ph h 33211075.118)3080(109.125.1)(⨯=-⨯⨯⨯=-=又 )(12c c pc c T T c W Q -=s kg T T c QW c c pc c /9454.0)2050(10187.41075.118)(3312=-⨯⨯⨯=-=∴ 即冷水流量为s kg /9454.0。
取管壁的热导率 )./(45K m W =λ，则有)./(5.47185012025)2025(45210251700111)(21123K m W Ln d d d d Ln d K ii Oi O O O O =⨯+⨯⨯+=++=-αλα 传热面积由下式计算：mO O T K Q S ∆= （1） 热流体：3080→℃冷流体：2050←℃301=∆T ℃ 102=∆T ℃ 2.1810301030)(2121=-=∆∆∆-∆=∆∴Ln T T Ln T T T m ℃ 将已知值代入式（1），得：238.132.185.4711075.118m S O =⨯⨯= 解题要点：能量平衡方程与传热速率方程的综合应用。
【2-11】在一单程列管换热器中用饱和水蒸气加热食用油。
温度为160 ℃的饱和蒸汽在壳程冷凝，冷凝液在饱和温度下排出。
食用油在管程流动，并由20 ℃加热到106 ℃。
列管换热器尺寸为：列管直径为Φ19 mm ×2 mm 、管长为4 m ，共有25根管子。
若换热器的传热量为125 kW ，蒸汽冷凝传热系数为7 000 W/（m 2·K ）,油侧污垢热阻为 5 m 2·K/W,管壁热阻和蒸汽侧污垢热阻可忽略,求管内油侧对流传热系数。
又若油的流速增加一倍，此时若换热器的总传热系数为原来的倍,求油的出口温度。
假设油的物性不变。
解：（1）管内油侧的对流传热系数对数平均温差：水蒸汽： 160160→℃食用油： 20106→℃541=∆T ℃ 1402=∆T ℃ 3.90)14054(14054)(2121=-=∆∆∆-∆=∆Ln T T Ln T T T m ℃ 传热面积：2966.54019.025m L d n S O O =⨯⨯⨯==ππ总传热系数：)./(0.2323.90966.51012523K m W T S Q K m O O =⨯⨯=∆= 而)./(0.23215190005.015197000111112K m W R d d d d K i si io i i o O O =⨯++=++=ααα 解得： )./(4.3582K m W i =α（2）油的流速加倍后的出口温度由 )()()()(212112c s c s c s c s O O c c pc c T T T T Ln T T T T S K T T c W -----=- 得： pcc O O c s c s c W S K T T T T Ln =--)(21 ))(()()(''''21'21c c O O pc c O O pc c OO c s c s c s c s W W K K c W S K c W S K T T T T Ln T T T T Ln ==----∴ 即 875.02175.1)10616020160()16020160('2=⨯=----Ln T Ln c 解得：2.99'2=c T ℃ 解题要点：能量平衡方程与传热速率方程的综合应用。
【2-12】在列管换热器中用冷水冷却油。
水在直径为Φ19 mm ×2 mm 的列管内流动。
已知管 内水侧对流传热系数为3 490 W/（m 2·K ）,管外油侧对流传热系数为258 W/(m 2·K)。
换热器在使用一段时间后，管壁两侧均有污垢形成，水侧污垢热阻为 26 m 2·K/W, 油侧污垢热阻为 176 m 2·K/W 。
管壁的热导率为45 W/（m ·K ）。
求：（1）基于管 外表面积的总传热系数；（2）产生污垢后热阻增加的百分数。
解：以外表面为基准。
（1）基于管外表面的总传热系数O K产生污垢前的总热阻： W K m Ln r r r r Ln r R i i O i O O O O /.1029.434901519)1519(45210192581)(1233--⨯=⨯+⨯⨯+=++=αλα)./(2331029.41123K m W R K O O =⨯==- （2）产生污垢后热阻增加的百分数R %产生污垢后的总热阻：W K m r r R R R R iO si sO O O /.1079.4151900026.0000176.01029.4233'--⨯=⨯++⨯=++= %7.11%10029.429.479.4%'=⨯-=-=O O O R R R R 解题要点：传热系数的计算。
【2-13】在套管换热器中采用并流的方式用水冷却油。
水的进、出口温度分别为15 ℃和40 ℃，油的进、出口温度分别为150 ℃和100 ℃。
现因生产任务要求油的出口温度降至80 ℃，假设油和水的流量、进口温度及物性均不变，且仍为并流，换热器除管长外，其他尺寸不变，若原换热器的管长为1 m ，求现在需要的管长。
设换热器的热损失可忽略。
解：热量衡算（忽略热损失）：情况改变前：)1540()100150(-=-=pc c ph h c W c W Q （1）情况改变后：)15()80150('2'-=-=c pc c ph h T c W c W Q （2）（2）/（1），得： 10015080150154015'2--=--c T 解得：50'2=c T ℃情况改变前：热油： 100150→℃冷水： 4015→℃1351=∆T ℃ 602=∆T ℃5.92)60135(60135)(2121=-=∆∆∆-∆=∆Ln T T Ln T T T m ℃ 情况改变后：热油： 80150→℃冷水： 5015→℃1351=∆T ℃ 302=∆T ℃8.69)30135(30135)(2121'=-=∆∆∆-∆=∆Ln T T Ln T T T m ℃ 情况改变前：m ph h T dL K c W Q ∆=-=)()100150(π （3） 情况改变后： ''')()80150(m ph h T dL K c W Q ∆=-=π （4）（4）/（3），得： 5.9218.6910015080150'''⨯⨯=∆∆=--L T L T L m m 解得：m L 86.1'= 解题要点：能量平衡方程与传热速率方程的综合应用。