第三章 连续梁的矩阵位移法
矩阵位移法的计算步骤及示例
单元①②和③：
35
⎡ 500 0 0 − 500 0 0 ⎤
⎢ ⎢
0
12 24
0
− 12
24
⎥ ⎥
(1)
k
=
(2)
k
=
(3)
k
=
10
3
⎢ ⎢⎢−
0 500
24 0
64 0
0 − 24 32 ⎥
500 0
0
⎥ ⎥
⎢ 0 −12 − 24 0 12 − 24⎥
⎢ ⎢⎣ 0
24 32
0
− 24
⎥ 64 ⎥⎦
8-8 矩阵位移法的计算步骤及示例 1
矩阵位移法的计算步骤：（以后处理为例）
（1）对结点和单元进行编号，建立结构（整
体）坐标系和单元（局部）坐标系，并对结
点位移进行编号。
（2）计算各杆的单元刚度矩 k (e)、k (e) 。
（3）形成结构原始刚度矩阵K。
（4）计算固端力
F
(e) F
、等效结点荷载FE及综合
⎢⎣0.0 0.0 6.0 12.0⎥⎦
由于连续梁的单元刚度矩阵为非奇异矩阵， 由此组集而成的结构刚度矩阵K 也是非奇异 的，故无需再进行支座约束条件处理。
（4）计算固端力列阵及等效结点 15 荷载列阵。
②单元的固端力列阵
F (2) F
=
⎧ 300 ⎫ ⎩⎨− 300⎭⎬kN
⋅
m
等效结点荷载列阵：
k(3)
=
⎢ ⎢ ⎢
l(3) 2EI
⎢⎣ l ( 3 )
4
2EI l(3) 4EI l(3)
⎤ ⎥ ⎥ ⎥ ⎥⎦
3 4
（3）集成结构刚度矩阵K
结构力学——矩阵位移法
整理版ppt
4
第一节 矩阵位移法概述
矩阵位移法以传统的结构力学作为理论基础; 以矩阵作为数学表达形式; 以电子计算机作为计算手段
三位一体的解决各种杆系结构受力、变形等计算的方法。
采用矩阵进行运算，不仅公式紧凑，而且形式统一，便 于使计算过程规格化和程序化。这些正是适应了电子计 算机进行自动化计算的要求。
结构力学
整理版ppt
学习内容
有限单元法的基本概念，结构离散化。 平面杆系结构的单元分析：局部坐标系下的单元刚度矩
阵和整体坐标系下的单元刚度矩阵。 平面杆系结构的整体分析：结构整体刚度矩阵和结构整
体刚度方程。 边界条件的处理，单元内力计算。 利用对称性简化位移法计算。 矩阵位移法的计算步骤和应用举例。
整理版ppt
16
第二节 单元分析（局部坐标系下的单元分析 ）
3、局部坐标系中的单元刚度矩阵性质
与单元刚度方程相应的正、反两类问题
力学 模型
解的 性质
正问题 e
F e
将单元视为两端有人为 约束控制的杆件。
控e 制附加约束加以指
定。
e 为任何值时，F e都
有对应的唯一解，且总 是平衡力系。
整理版ppt
1、整体刚度矩阵的集成 将单元刚度矩阵按单元定位向量扩展为单元贡献矩阵
（换码扩阵）
1
1
3
K
1
k11
0
1
k21
1
0 0
0
k12
1
0
k22
1
2
2
3
0
K 2
结构力学十三讲矩阵位移法
-6EI l2
4EI l
4
§13-3 单元刚度矩阵(整体座标系)
一、单元座标转换矩阵 Y1
X1
X1
Y1
MM21
e
x
M2 X2
正交矩阵 [T]-1 =[T]T
e e
e T T e
v1
y e
X 2
Y2
Fⓔ T T F ⓔ
ee
F T F ee
座标转换矩阵
5
二、整体座标系中旳单元刚度矩阵
[k] e = [T]T k e [T]
(4)
(6)
00
(5)
y
单元 局部码总码
单元 局部码总码
（1） 1 （2） 2 （3） 3 （4） 0 （5） 0 （6） 4
1
2
3 0
0
4
（1） 1
1
（2） 2
2
（3） 3 （4） 0
3 0
（5） 0
0
（6） 0
0
18
1 2
[k] 1 = 3
0 0 4
1 2
[k] 2= 3
0 0 0
123004 101 102 103 104 105 106 201 202 203 204 205 206 301 302 303 304 305 306 401 402 403 404 405 406 501 502 503 504 505 506 601 602 603 604 605 606 123000 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66
结构力学基础矩阵位移法基本概念、计算程序和例题讲解
例形成图示刚架可动结点劲度矩阵，E,I ,A为常数。
解： 1.编号，如图（b) 2.确定单元杆端自由度序号。
3.计算 kmi 4.计算单元转换矩阵
5.形成单元在整体坐标系中的劲度矩阵
6.根据单元杆端自由度序号叠加
二、可动结点劲度矩阵性质
1.对称方阵
反力互等定理
2.非奇异矩阵 考虑了约束条件，排除了刚体位移
7.求杆端力Fmi
8.求支座反力 支座反力由下式
计算，得
9.内力图
例2 求图2-21(a)所示平面刚架的内力,已知各杆 I 0.005m4
A0.05m2，E2106kNmA2B杆、CD杆杆
返回
§9—3 可动结点劲度矩阵
一、形成可动结点劲度矩阵的步骤
步骤： 1.对结构进行结点编号、单元标号、自由度编号： 2.确定单元杆端自由度序号（考虑约束条件）； 3.计算单元在局部坐标系中的劲度矩阵kmi 4.计算单元转换矩阵Ti 5.形成单元在整体坐标系中的劲度矩阵ki TiTkmiTi
6.按”对号入座”原则，将ki叠加到 k 中。
结构力学基础 矩阵位移法基本概念、计算程
序和例题讲解
§9-1 矩阵位移法基本概念 §9-2 单元劲度矩阵 §9-3 可动结点劲度矩阵 §9-4 可动结点等效荷载列阵 §9-5 单元杆端力和支座反力 §9-6 例题 §9-7 平面刚架计算程序
§9—1 矩阵位移法的基本概念
一、坐标系和符号规定 图示连续梁：
4.求 K
（1）计算机各单元的方向余弦和杆长：
（2）求 kmi
(3)求ki
单元（1）:Cx=0 Cy=1
杆长：l 同理：
（4）求 按照“对号入座“原则，由ki形成k哪
例如： 同理：
矩阵位移法
第9章矩阵位移法9.1 概述前面介绍的力法、位移法和渐近法都是传统的解算超静定结构的方法，它们是建立在手算基础上的。
随着基本未知量数目的增加，其计算工作极为冗繁和困难。
而计算机的问世及其广泛应用，为结构计算提供了有效工具。
矩阵位移法就是以计算机为运算工具的一种新的结构分析方法，它完全可以代替人来完成大型复杂结构的计算问题。
矩阵位移法是以位移法为理论基础，结构分析的全部过程中运用了线性代数中的矩阵理论。
引入矩阵运算的目的就是使计算过程程序化，便于把结构分析的过程用算法语言编成计算程序，实现计算机自动化处理。
目前，应用矩阵位移法编制的结构分析软件，已在结构设计中得到了广泛的应用。
矩阵位移法又称为杆件有限元法。
它的主要解题思路是：首先将结构离散成为有限个独立的单元，进行单元分析，建立单元杆端力与单元杆端位移之间的关系式——单元刚度方程；然后利用结构的变形连续条件和平衡条件将各单元组合成整体，建立结点力与结点位移之间的关系式——结构刚度方程，这一过程称为整体分析；最后求得结构的位移和内力。
矩阵位移法就是在一分一合，先拆后搭的过程中，把复杂结构计算问题转化为简单的单元分析和集合问题。
本章主要讨论杆系结构的单元刚度矩阵及其在单元局部坐标系与结构整体坐标系间的变换、结构刚度矩阵的形成、荷载及边界条件处理等内容。
9.2 单元分析9.2.1 结构离散化结构离散化是指把结构分离成有限个独立杆件(单元)，由单元的组合体代替原结构(图9.1)。
一般单元为等截面直杆，杆系结构中每根杆件可以作为一个或几个单元。
单元的联接点称为结点。
对于等截面直杆所组成的杆系结构，只要确定了一个结构的所有结点，则它的各个单元也就随之确定了。
根据杆件联接的方式，可以将构造结点，如转折点、汇交点、支承点和截面的突变点取为结点。
在有些情况下，非构造点，如集中力作用点，也可作为结点处理。
离散化的结构用数字进行描述，即对各结点和单元进行编号。
通常用①,②,…表示单元编号，用1,2,…表示结点编号。
矩阵位移法
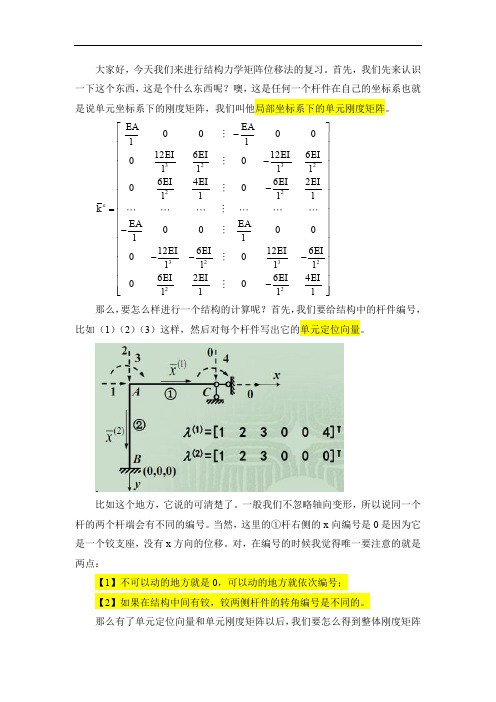
那么就是说，这个杆端力它首先呢，是在局部坐标系下的（我只想知道我的 杆的轴力，剪力啊，什么的，并不想知道某个大方向上的力） ，那么就要用到局 部坐标系的各种参数。 其次，力是刚度乘位移的。 所以就是说，应该有这样
e e e F e k e e F e P k T F P
不过这个位移的话， 其实之前求出来了的话反正就这样吧。注意如果原来有 节点荷载的话这里是不用加它的， 我们只要加杆内荷载计算得到的固端力就好了， 这个力之前是查表得到的，非常方便加上去哦。 然后这里就告一段落啦。
呢？ 在这之前， 必须要把局部坐标系下的单元刚度矩阵转化为整体坐标系下的单 元刚度矩阵。 那么必须要有这个杆件的方位角。假设这个杆件的正方形和水平向 右的夹角 （顺时针） 是 ， 那么， 就有一个坐标变换矩阵的问题， 这个玩意叫 T 。 还有一个玩意叫坐标变化子矩阵，这玩意叫 t 。 这两个家伙有这么个关系。
e
e
t T kii et
其实还是挺麻烦的。如果说刚好是 90°的话，倒是就把对角线上第一第二 排换一下，然后右上角左下角的和旁边的换一下位子就 OK 了。 然后就可以用整体坐标系下的单元刚度矩阵集成整体刚度矩阵了。 这个其实 非常简单， 只要在整体坐标系下的单元刚度矩阵的周围写好它的定位向量，然后 在空白的地方把 0 以外的数字从小到大写好， 在相应的空位里把上面的抄下来加 起来就好啦。 因为这个整体刚度矩阵具有对称性和带状稀疏性， 所以只要把左下角三角形 的都写出来就好了，右上角是一模一样的。至于带状稀疏性的话，就是说它中间 的是有的，周围的基本都是 0，这是编码造成的，很小的码和很大的码应该是没 有交集的。 那么现在我们得到了一个整体刚度矩阵。
12 EI l3 6 EI l2 ke k e 12 EI 3 l 6 EI l2 6 EI l2 4 EI l 6 EI l2 2 EI l 12 EI l3 6 EI 2 l 12 EI l3 6 EI 2 l 6 EI 2 l 4 EI l 6 EI l2 2 EI l
矩阵位移法3综述
STDU
Program Design for Static Analysis of Planar Frame
(4) 实型数组 X(NN),Y(NN): 存放结点的 x , y 坐标数组； EA(NE),EI(NE),AL(NE): 存放各单元的 EA, EI, L 值； e [ k ] C(6,6): 存放单元在结构的整体坐标系下的单元刚度矩阵 ; e 以后各章在叙述中常用 [C] 代替 [k] ; T(6,6): 存放坐标转换矩阵 [T] ； R(N,N): 存放结构的整体刚度矩阵 [K] ; 以后各章常以[R]表示 总刚； QJ(NPJ,3): 存放直接结点荷载的 XD, YD, MD 三个分量值, 其 中分量 1, 2, 3 分别对应 X, Y, M； AQ(NPE),BQ(NPE),Ql(NPE),Q2(NPE): 分别存放表 2-3中的 a,b,q1 和 q2 值； P(N): 先存放综合结点荷载向量，解方程后存放未知结点位移 向量；
(2) 实型变量 CX: 单元的方向余弦 cosα 值; CY: 单元的方向正弦 sinα 值; U,V,FAI: 结点在 x, y 和转动方向上的位移分量; (3) 整型数组 JL(NE),JR(NE): 单元的始, 末端结点号数组； II(6): 单元的杆端位移分量的定位数组；
MJ(NPJ): 具有直接结点荷载作用的结点所对应的结点整 体编号数组； ME(NPE): 具有非结点荷载作用的单元所对应的单元整体 编号数组； IND(NPE): 非结点荷载的类型数组； IBD(NDF): 非固定支座中各约束所对应的位移分量整体 编号数组。
STDU
Program Design for Static Analysis of Planar Frame
矩阵位移法
k22坐k11标局k01成部1k029坐200标时kk20与32，3 整局k0体12部45 单k0k20514
0 k26 k26
To 47
k e ke
刚和有何整k关体3k3系单33 ？刚k0k间454535
k35 00
k3k6 36
0 k56
对称对称
kk5544
kk65k66 66
F e FEe k e e
单元杆端位移矩阵
e 1
2
3
4
T e
单元刚度矩阵(应熟记)
12 6l 12 6l
k
e
EI l3
6l
12
4l 2 6l
6l 12
2l
2
6l
6l 2l 2 6l 4l 2
是转角位移方程的矩阵表示
单元等效结点荷载矩阵
根据单跨梁的载常数，可得
向上满跨均布荷载 q 作用
(F FE )e k e e F e FEe k e e
连续梁单元需要 进行坐标转换吗？
连续梁的局部坐标与整 体坐标一致，所以不需 要转换。
第一种做法
桁架单元如何
进行坐标转换？ T
力的转换
T
F1
F2
F3
F4
T
cos
0
位移的转换
sin
0
0
cos
0 T F1
sin F2
1 2
3. 坐标转换问题
在搞清单元特性后，像位移法一样，需将单 元拼装回去。在结点处位移自动满足协调条件 的基础上，令全部结点平衡，即可建立求解位 移的方程，这是下一节将讨论的内容。
除连续梁外，一般结构单元不全同方位， 为保证协调和平衡，应将杆端位移和杆端力 都转换成统一的，对整体坐标的量，因此要 先解决坐标转换问题。下面先讨论自由式梁 单元的转换问题。
矩阵位移法程序化解题方法
矩阵位移法解法步骤解：1）、单元及结点位移分量统一编码单元及结点位移分量编码、整体坐标系如图所示，局部坐标系横轴正向在各单元上标出。
注：编结点位移分量总码时，后处理法和先处理法有区别：采用后处理法编码时暂不考虑边界条件对支座处位移分量的限制，皆视为一般情形处理；采用先处理法时，对已知为零的位移分量总是以零编码。
对于连接于铰结点的杆端编码时，线位移采用同码，而角位移异码。
2）、形成局部坐标中单元刚度矩阵 k e：首先，计算各单元杆件的几何特征：⋯ ⋯各单元的单元刚度矩阵如下：单元①： ⋯ ⋯3）、形成整体坐标中单元刚度矩阵：（计算公式： k e = T T ke T ） 整体坐标系中的各单元刚度矩阵转换如下：单元①： ⋯ ⋯4）、集成整体刚度矩阵 K （单元集成法或直接刚度法）：首先，由各单元的局部码与总码的对应关系写出各单元的定位向量如下：λ e = ⋯ ⋯ T其次，将各单元刚度矩阵 k e 按其定位向量 λ e 在整体刚度矩阵 K 中定位并累加 得整体刚度矩阵如下：K =(⋯ ⋯)5）、计算综合等效结点荷载向量 F P ：①、计算局部坐标系中各杆件单元的固端力向量：F P e =(F N1F ，F Q1F ，M 1F ，F N2F ，F Q2F ，M 2F )T ②、转换整体坐标系中各杆件单元的固端力向量：{F P }e =(F x1F ，F y1F ，M 1F ，F x2F ，F y2F ，M 2F )T ③、将各杆件单元的固端力反其指向，并按其定位向量 λ e 在综合等效结点荷载向量 F P 定位并累加，得综合等效结点荷载向量如下：F P = ⋯ ⋯ T6）、计入边界条件条件，写出刚度方程并解之：刚度方程： K Δ = F P采用后处理法时，对已知为零的结点位移，在整体刚度矩阵 K 中将其所对应行列的主元素记为1，其余都变为零，然后写出刚度方程，解之。
采用先处理法时，由于在进行位移分量编码时已考虑边界条件，因而无须再计入，只写出刚度方程求解即可。
矩阵位移法——连续梁的结构刚度矩阵
矩阵位移法——连续梁的结构刚度矩阵import numpy as npfrom math import sqrt, sin, cos, acosnp.set_printoptions(precision=3)np.set_printoptions(suppress=True) # 将科学数组转化为浮点数EI = 1 # 为了⽅便计算，设EI=1# n = input("请输⼊位移数量：")n = 3ElemNode = np.array([[0, 1], [1, 2], [2, 3]]) # 组成单元的两结点编号NodeForce = np.array([[-60], [50], [30]]) # 作⽤在结点上的⼒，单位N·mEi = [0.75, 1.5, 1]ki = np.array([[4 * EI, 2 * EI],[2 * EI, 4 * EI]]) # 单元刚度矩阵*LNodeCoord = np.array([[0, 0], [6, 0], [14, 0], [20, 0]]) # 结点整体坐标NodeX = NodeCoord[:, 0] # 结点x坐标NodeY = NodeCoord[:, 1] # 结点y坐标def k_i(i):"""整体坐标系下单元刚度矩阵,i为单元编号:param i:结点编号:return: 整体坐标系下单元刚度矩阵，由于连续梁不⽤坐标变换，所以k = ke"""NodeIndex = ElemNode[i, :]#print(NodeIndex)Node1_locx = NodeX[NodeIndex[0]]Node1_locy = NodeY[NodeIndex[0]]Node2_locx = NodeX[NodeIndex[1]]Node2_locy = NodeY[NodeIndex[1]]Len = sqrt((Node1_locx - Node2_locx) ** 2 + (Node1_locy - Node2_locy) ** 2)# print("len = %d " % (Len))return ki * Ei[i] / Len # 假设为⽔平def TransMatrix(angle):#坐标转换矩阵Treturn np.array([[ cos(angle), sin(angle) , 0, 0 , 0 ],[-sin(angle), cos(angle), 0, 0 , 0 ],[ 0 , 0 , 1, 0 , 0 ],[ 0 , 0 , 0, cos(angle), sin(angle)],[ 0 , 0 , 0, -sin(angle), cos(angle)],[ 0 , 0 , 0, 0 , 1 ],])# 对上述单元刚度矩阵的各元素，按照其⾏码和列码直接送⼊结构刚度矩阵，进⾏”对号⼊座“NumberOfNodeFreeDof = 3K = np.zeros((NumberOfNodeFreeDof, NumberOfNodeFreeDof))for i in range(0, n):kii = k_i(i)# print(kii)for j in range(0, 2):for k in range(0, 2):if i + j - 1 < 0 or i + k - 1 < 0:continueK[i + j - 1, i + k - 1] += kii[j, k]# print(K)print("结构刚度矩阵K = ")print(K)print('-' * 20)K_1 = np.linalg.inv(K) # 求K矩阵的逆print('K的逆 = ')print(K_1)print('-' * 20)NodeDis = np.matmul(K_1, NodeForce) # = K-1*FNodeDisplacement = np.zeros((1,n+1))for i in range(0, n):NodeIndex = NodeDis[i,:]NodeDisplacement[0,i+1] = NodeIndex[0]print(NodeDisplacement)for i in range(0,n):kii = k_i(i)M1 = kii[0,0]*NodeDisplacement[0,i]+kii[0,1]*NodeDisplacement[0,i+1]M2 = kii[1, 0] * NodeDisplacement[0, i] + kii[1, 1] * NodeDisplacement[0, i + 1]print("在%d号杆件上，左端弯矩为M = %.3f, 右端弯矩为M = %.3f" % (i,M1,M2))。
矩阵位移法
TT T T T T I
Fx1 F y1 M1 单元坐标 转换矩阵 F x2 Fy 2 M 2
e
Hale Waihona Puke eF e TF e
T 1 T T
单元坐标转换矩阵T是一正交矩阵。
EI 25 104 kN m l
0 300 0
5m
0 为了简洁，下面将矩阵 中各元素的单位略去。 12 30 0 12 30 30 100 0 30 50 4 EA 10 0 0 l 0 0 300 0 0 12 30 0 12 30 12 EI 6 EI [k11 ] 0 3 2 30 50 0 30 100 l l 6 EI 4 EI 第一列元素变符号即第四列，第二列元素变符号即第五列 0 ①： 2 ②求整体坐标系中的单刚， k l l 第一行元素变符号即第四行，第二行元素变符号即第五行
3、有限单元法的三个基本环节： ①单元划分：一根等截面直杆作为一个单元，单元间由结点相联。 ②单元分析：建立单元刚度方程，形成单元刚度矩阵(物理关系)。 ③整体分析：由单元刚度矩阵形成整体刚度矩阵，建立结构的 位移法基本方程(几何关系、平衡条件)。
§9-2 单元刚度矩阵(element stiffnessmatrix)（局部坐标系）
T11 T12 T T T 21 22
因此，(a)式的逆转换式为： 同理
F e T TF e
e T e
(b)
e T T e
整体坐标系中的单元刚度矩阵
F e TF e
(a)
e T e
(b)
单元刚度矩阵的性质 设局部坐标系中、整体坐标系中的单元刚度方程分别为： ①单元刚度矩阵是杆端力用杆端位移来表达的联系矩阵。 e e e F k Δ (c) ②其中每个元素称为单元刚度系数，表示由于单位杆端位移引起的杆端力。 ③单元刚度矩阵是对称矩阵。 F e k eΔe (d ) ④第k列元素分别表示当第k个杆端位移=1时引起的六个杆端力分量。 e e e e ⑤一般单元刚度矩阵是奇异矩阵。不存在逆矩阵。因此， 将式(a)、(b)代入式(c) k eT IF T T TTF ke T T 可由单元刚度方程，由杆端位移唯一确定杆端力；但由杆端力反推杆端位移时， 可能无解、可能解不唯一。 k e T T k eT
矩阵位移法-先处理法
0 0 0 1 2 3
单元② 单元②
k6×6
②
坐标变换
α2
0
k 6×6
0]
T
②
1
2
3
0
0
0
λ = [1 2
②
3
0
k
② 6×6
=
1 2 3 0 0 0
1
2
3
3）组合→K
K =
0 ② k 23 ② k 33
1 2 3
1，2，3 对应总码数
1. K中的各元素由单元刚度阵中对应的元素组成
K的性质
2. 单元刚度阵中, Kij 在结构刚度阵K中的位置: i→行 j→列 3. 单元刚度阵中, Kij 按其下标 对“号”入
座
e
e
生成K
“号”为总 码
先处理法： 先处理法：先考虑结构的支承条件 计算步骤： 计算步骤： 将K 的行和列
λ = [0
③
α = 90o
坐标变换
x
y
0 0
y
③
0
0
2
−1
3]
T
x
0 2 -1 3 2 1 3
③ k = 变号
变号
1 2 3
0 0 0 2 -1 3 6× 6
k
③
EA L = 0 0
0 12 EI L3 6 EI L2
2 0 6 EI 1 2 L 4 EI L 3
0 1 2i2 2 4i2 3
∆1 M 1 ∆ = M 2 2 ∆3 M 3
连续梁弯矩图的计算
结力大作业报告连续梁的矩阵位移计算水工812008010226彭慧民2010-10-30结力大作业报告1、问题描述通过矩阵位移法计算连续梁的杆端弯矩，画出弯矩图。
报告通过用matlab编程序，实现了连续梁杆端弯矩的计算机计算，并且输出弯矩图。
2、知识介绍矩阵位移法的要点是先将结构整体拆开，分解成若干个单元，然后再将这些单元通过定位向量集合成整体，包括单元分析和集合成整体两部分。
单元分析中，要建立单元刚度方程，形成单元刚度矩阵；整体分析中，要将单元集合成整体，由单元刚度矩阵按照刚度集成规则形成整体刚度矩阵，建立整体结构的位移法方程，从而求出解答。
计算连续梁的杆端弯矩的步骤如下：➢将连续梁的结点和位移进行编号，写出定位向量；➢对应于连续梁的单元刚度矩阵是4224EI EIl lEI EIl l⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭，根据连续梁上的实际情况，分别写出每一段的单元刚度矩阵；➢根据定位向量，写出整体刚度矩阵；➢根据外加荷载，求等效结点荷载；➢解方程组，求位移；➢根据单元刚度矩阵和定位向量，求出杆端弯矩；➢画出弯矩图。
3、程序代码>> L=[4,6,8];%定义梁长度的数组，L(1)=4M,L(2)=6M,L(3)=8M>> EI=[1,1.5,2];%定义梁刚度，EI（1）=EI，EI（2）=1.5EI，EI（3）=2EI>> P=[40,50,80];%定义跨中荷载的大小，P（1）=40，P（2）=50，P（3）=80 >> q=[15,30,20];%定义跨上的连续荷载大小，q(1)=15,q(2)=30,q(3)=20>> n=5;>> rEI=[EI(1),EI(3),EI(1),EI(1),EI(2)];>> rL=[L(1),L(2),L(3),L(2),L(1)];>> ri=[rEI(1)/rL(1),rEI(2)/rL(2),rEI(3)/rL(3),rEI(4)/rL(4),rEI(5)/rL(5)];>> %下面是固端荷载>> outerP=[0,P(3),0,P(2),0];>> outerQ=[q(2),0,q(2),0,0];>> direct=zeros(n,2);>> for i=1:ndirect(i,1)=i-1;direct(i,2)=i;end %输入定位向量和连续梁的数据>> element=zeros(2*n,2);for i=1:nelement(2*i-1,1)=4*ri(i);element(2*i-1,2)=2*ri(i);element(2*i,1)=2*ri(i);element(2*i,2)=4*ri(i);end %单元刚度矩阵>> structure=zeros(n,n);for i=1:(n-1)structure(i,i)= structure(i,i)+element(2*i,2)+element(2*i+1,1);structure(i,i+1)= structure(i,i+1)+element(2*i+1,2);end>> structure(n,n)= structure(n,n)+element(2*n,2);>> %这是整体刚度矩阵>> for i=2:nstructure(i,i-1)=structure(i-1,i);end>> %得到对称的整体刚度矩阵>> %下面是结点固端荷载P=zeros(1,n);for i=1:(n-1)P(i)=P(i)+(1/8)*outerP(i)*rL(i)+(1/12)*outerQ(i)*rL(i)*rL(i)-(1/8)*outerP(i+1)*rL(i+1)-(1/12)*outerQ( i+1)*rL(i+1)*rL(i+1);end>> P(n)=P(n)+(1/8)*outerP(n)*rL(n)+(1/12)*outerQ(n)*rL(n)*rL(n);>> P=-P;>> P=P';>> %下面解方程组，求位移向量>> X=structure\P;>> %下面求杆端弯矩>> F=zeros(2*n,1);>>F(1:2)=element(1:2,:)*[0,X(1,1)]'+[-(1/8)*outerP(1)*rL(1),(1/8)*outerP(1)*rL(1)]'+[-(1/12)*outerQ( 1)*rL(1)*rL(1),(1/12)*outerQ(1)*rL(1)*rL(1)]';>> for i=2:nF((2*i-1):(2*i))=element((2*i-1):(2*i),:)*X((i-1):i)+[-(1/8)*outerP(i)*rL(i),(1/8)*outerP(i)*rL(i)]'+[-(1/ 12)*outerQ(i)*rL(i)*rL(i),(1/12)*outerQ(i)*rL(i)*rL(i)]';end>> %下面开始画弯矩图>> line=zeros(1,2*n+1);>> for i=2:(2*n+1)line(i)=line(i-1)+(1/2)*rL(floor(i/2));end>> torque=zeros(1,2*n+1);>> torque(1)=-F(1);>> torque(2*n+1)=-F(2*n);>> for i=1:(n-1)torque(2*i+1)=F(2*i);end>> for i=1:ntorque(2*i)=(1/2)*(torque(2*i-1)+torque(2*i+1))-(1/8)*outerQ(i)*rL(i)*rL(i)-(1/4)*outerP(i)*rL(i); end>> plot(line,torque,'r*');>> hold on, z=0*line;plot(line,z),hold off;程序说明：➢可以改变输入的n值，相应地改变输入的连续梁各跨的长度、EI、i，可以改变相应向量的维数，但是维数必须等于每次输入的n；➢输入好数据之后，将以上代码粘贴到matlab里面，就可以输出弯矩图了，输出的弯矩图是散点图，可以自己根据实际作用的外加荷载，将散点连接起来。
矩阵位移法过程
矩阵位移法过程嘿，朋友们！今天咱就来好好唠唠矩阵位移法这个神奇的玩意儿。
你想想啊，矩阵位移法就像是搭积木，一块一块地把整个结构给拼凑起来。
只不过这积木有点特别，是用数字和公式搭成的。
咱先说说这第一步，得确定结构的节点和单元吧。
这就好比是给要盖的房子先确定好柱子和梁的位置。
每个节点就像是一个关键点，单元呢就是连接这些关键点的部件。
然后呢，咱要给这些节点和单元编上号，就跟给小朋友分学号似的，可不能乱了套。
接下来，就得建立这些节点和单元的关系啦。
这就像是给每个积木块找到它该放的位置，它们之间的连接呀、力的传递呀，都得搞清楚。
这可不是个简单事儿，但咱得耐着性子慢慢来。
然后呢，咱要根据这些关系列出矩阵。
哎呀呀，这矩阵可就像个大表格，里面装满了各种数字和符号。
别被它吓着，其实它就是把那些复杂的关系用一种整齐的方式表现出来。
再说说这计算过程，就跟解谜题似的。
你得一步步地去推导、去计算，找到那个正确的答案。
有时候可能会遇到一些难题，就像走在路上碰到了一块大石头，但咱可不能退缩，得想法子把它挪开或者绕过去。
还有啊，这矩阵位移法还得考虑各种边界条件呢。
就好像盖房子得考虑地基稳不稳呀，周围环境怎么样呀。
这些边界条件可不能马虎，要不然整个结构可就不牢固啦。
咱在实际运用的时候，可得细心再细心。
一个小数字算错了，可能整个结果就全错啦。
这就跟下棋一样，一步错步步错。
总之呢，矩阵位移法虽然有点复杂，但它可是结构分析的得力助手呢！只要咱认真学，多练习，就一定能掌握它。
别害怕困难，别嫌麻烦，等你真正搞懂了它，你就会发现它的神奇之处啦！就像打开了一扇通往新世界的大门，让你看到结构背后的奥秘。
所以呀，加油吧朋友们，和矩阵位移法这个小伙伴好好相处，让它为我们的工程建设出一份力！原创不易，请尊重原创，谢谢!。
矩阵位移法
原理同源---
(1)以结点位移为基本未知量,
(2)以单元分析为基础(力法计算的 结果单元刚度方程);
(3) 建立平衡方程求出结点位移,
(4) 将结点位移代入单元刚度方 程求得内力
矩 阵 位 移 法
作法有别-(1)矩阵组织数据，矩阵运算;
(2)设计计算机程序（正确）;
(3) 原始数据的准备、输入、计算 结果的输出及正确性判别等 特点： 省力；计算速度快；计算结果精度高 ；使用者要力学概念清楚。
1 0 0 1 0 0 8 2 4 i i 2 42 i i 0 2 4 3
修改后的位移 法方程
(6) 解方程
矩 阵 位 移 法
0 1 3.571 2 i 3 12.286 i
(5)引入支承条件修改原始刚度方程
矩 阵 位 移 法
K FP
4 i 2i 0 1 4 2 i 8 i 2i 4 2 i 0 2 4 42 i 3
主1副0法修改后 原始刚度方程
整 体 刚 度 方 程
单元刚度集成法
矩 阵 位 移 法
单元(1)对号 入座
单元刚度集成法 单元(2)对号入 座并累加
矩 阵 位 移 法 单元(3)对号入座
并累加 整体刚度矩阵
连续梁刚度方程
矩 阵 位 移 法
9.5 等效结点荷载向量
矩 阵 位 移 法 加刚臂
去刚臂
(1)加约束求杆端固端弯矩、刚臂约束力矩
矩 阵 位 移 法
（5）集成等效结点荷载向量 形成过程如下：
矩 阵 位 移 法
连续梁的矩阵位移法
§ 3.1 概述 § 3.2 连续梁的单元刚度矩阵 § 3.3 整体刚度矩阵 § 3.4 非结点荷载的处理 § 3.5 连续梁的矩阵位移法举例
§ 3.1 概述
一、结构矩阵分析方法
结构矩阵分析方法的广泛应用是近年来结构力学最重要的
发展之一，这与计算机技术的迅速发展有直接的关系。它是以 传统的结构力学作为理论基础，以矩阵作为数学表述形式，以 电子计算机作为计算手段的三位一体的方法。
MM3223
(2)
------称为单元杆端力列阵。
(1)
1 2
(1)
(2)
2 3
(
2
)
------称为单元杆端位移列阵。
§ 3.3 整体刚度矩阵
将方程组也用矩阵表示：
4i1
2i1
0
1
M1
2i1 0
4i1 4i2 2i2
2i2 4i2
32
M2 M3
简写为： K F ------称为整体刚度方程
有非结点荷载作用时的单元杆端力，可以由两部分叠加而 得：一部分是结点受有约束、各杆件为固端梁情况下的杆端力 (固端力)，另部分是综合结点荷载作用下的杆端力，即
F(e) Ff(e)k(e) (e)
§ 3.5 直接刚度法的解题步骤和算例
直接刚度法中后处理作法的解题步骤： 1．对各单元和结点进行编号 2．计算整体坐标系的单元刚度矩阵。 3．将各单元刚度矩阵的子块“对号入座”形成整体刚度矩阵。 4．计算总的荷载列阵，建立整体刚度方程。 5．引入支承条件，修改整体刚度矩阵和整体刚度方程。 6．解整体刚度方程求各结点位移。 7．计算各单元的杆端力，并进一步求各单元的其它内力。 。 8．校核。
矩阵位移法-先处理法
1）编号： 编号：结点
单元
总码
ϕ1
X
(0,0,1)
ϕ2
X
②
(0,0,2)
结点位移列向量
1 ①
2
3 (0,0,3)
ϕ3
∆ = [ϕ1 ϕ 2 ϕ3 ]
T
L y M
③
④
θ
L x
0 0
X
4
(0,0,0)
X
5
2）单元分析—单元刚度阵（ 单元刚度阵（对应总码） 对应总码） 单元① 单元① 单元② 单元②
2
6
0
0
0]
T
0
2
6
0
0
0
k
③
=
EA 0 l 12 EI 0 l3 6 EI 0 l2 EA 0 − l 12 EI 0 − 3 l 6 EI 0 l2
0 6 EI l2 4 EI l 0 − 6 EI l2 2 EI l
−
EA l 0 0
0 − 12 EI l3 6 EI − 2 l 0 12 EI l3 6 EI − 2 l
0 12 EI l3 6 EI l2 0 − 12 EI l3 6 EI l2 −
0 6 EI l2 4 EI l 0 6 EI l2 2 EI l
−
EA l 0 0
0 − 12 EI l3 6 EI − 2 l 0 12 EI l3 6 EI − 2 l
EA l 0 0
6 EI 2 l 2 EI l 0 6 EI − 2 l 4 EI l 0
0 1 2i2 2 4i2 3
∆1 M 1 ∆ = M 2 2 ∆3 M 3
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§ 3.3 整体刚度矩阵
将方程组也用矩阵表示： 将方程组也用矩阵表示：
4 i1 2i 1 0 2 i1 4 i1 + 4 i 2 2 i2 0 δ1 M 1 2 i2 δ 2 = M 2 4 i2 δ 3 M 3
a)
2
c)
Fqe2
Fqe1
Fqe2
2
δ1
=
δ2
=
2
+
1
1、在施加荷载之前先在结点处各加上一个刚臂用以限制结 、 点角位移，这样，单元即成为固端梁，而后施加荷载。 点角位移，这样，单元即成为固端梁，而后施加荷载。由于荷 载作用，在各杆端将产生固端剪力和固端弯矩。 载作用，在各杆端将产生固端剪力和固端弯矩。 2、在原结构的结点处分别施加与约束反力数值相等、方 、在原结构的结点处分别施加与约束反力数值相等、
e e 将两种情况进行叠加， 向相反的外力 Fq1 、 Fq 2 ，将两种情况进行叠加，就可得到
原来的荷载作用情况。 原来的荷载作用情况。
Fqe1 、Fqe2 称为单元的等效结点荷载 这里所识“等效”，是 称为单元的等效结点荷载(这里所识 等效” 这里所识“ 指图c与图 两种情况的结点位移是相等的，因为图b情况的结点位 与图a两种情况的结点位移是相等的 指图 与图 两种情况的结点位移是相等的，因为图 情况的结点位 移为零)。 移为零 。
------为结点力 为结点力 荷载） （荷载）列阵
------称为整体刚度矩阵 称为整体刚度矩阵
结构刚度矩阵 的性质： 的性质：
1、对称性：结构刚度矩阵是一个对称矩阵，即位于主对角线 、对称性：结构刚度矩阵是一个对称矩阵， 两边对称位置的两个元素是相等的。 两边对称位置的两个元素是相等的。 2、由于连续梁结构为几何不变体系，因此其整体刚度矩阵为 、由于连续梁结构为几何不变体系， 非奇异矩阵。 非奇异矩阵。 3、结构刚度矩阵是一带状矩阵。 、结构刚度矩阵是一带状矩阵。
§ 3.4
非结点荷载的处理
以上关于矩阵位移法的讨论， 以上关于矩阵位移法的讨论，是说结构的结点位移作为基 本未知量。在讨论中，我们只考虑了作用结点荷载的情况。 本未知量。在讨论中，我们只考虑了作用结点荷载的情况。由 此所得到的矩阵位移法基本方程，即整体刚度方程，表述了结 此所得到的矩阵位移法基本方程，即整体刚度方程， 点位移和给点荷裁的关系。而实际上， 点位移和给点荷裁的关系。而实际上，不论是恒载还是活载常 常是作用在杆件单元上的均布荷载、分布荷载或集中荷载。 常是作用在杆件单元上的均布荷载、分布荷载或集中荷载。对 于这种非结点荷载的处理，一种方法是， 于这种非结点荷载的处理，一种方法是，不论均布或分布荷载 都适当地改用若干集中荷载加以代替， 都适当地改用若干集中荷载加以代替，并把集中荷载的作用点 也看作结点。这样处理的结果是，加多了单元和结点位移，从 也看作结点。这样处理的结果是，加多了单元和结点位移， 而增加了计算工作量。另一种则是目前通用的处理方法， 而增加了计算工作量。另一种则是目前通用的处理方法，即采 用所谓的等效结点荷载。 举例说明如下： 举例说明如下：
1．对结构的结点和单元进行编号； ．对结构的结点和单元进行编号； 2．进行结构的离散化：将结构拆成两个杆件单元①和②； ． 将结构拆成两个杆件单元① 3．进行单元分析：建立单元刚度矩阵； ． 建立单元刚度矩阵； 4．进行整体分析：将离散化的各单元重新集合，满足原结 ． 将离散化的各单元重新集合， 构的平衡条件和位移连续条件，而得到整体刚度方程。 构的平衡条件和位移连续条件，而得到整体刚度方程。我们利 用已求得的各单元刚度矩阵形成整体刚度矩阵。 用已求得的各单元刚度矩阵形成整体刚度矩阵。形成整体刚度 矩阵的方法，以直接刚度法最为常用。 矩阵的方法，以直接刚度法最为常用。
(1)
(1)
(h)
F
( 2)
=k δ
(2)
( 2)
(i )
------称为单元刚度方程 称为
4i1 2i1 4i 2 2i2 ( 2) k = 其中： 其中： k = ( j) (k ) 2i1 4i1 2i 2 4i2 ------称为单元刚度矩阵。 称为 矩阵中的各元素称为单元刚度影响系数。 矩阵中的各元素称为单元刚度影响系数。
(2) M23 ,δ2(2)
1 (1) M12
M
(1) 21
2
(2) M23
3
(1 单元 M 12 ) = 4i1δ (1) + 2i1δ 2(1) (a ) ①： (1) (1) (1) M 21 = 2 i1δ + 4 i1δ 2
1
(2 M 23 ) = 4i2δ 2( 2 ) + 2i2δ 3( 2 ) 单元 (b ) (2) (2) (2) ②: M 32 = 2i2δ 2 + 4i2δ 3
由位移连续条件得： 由位移连续条件得： δ 1(1) = δ 1 (1) (2) δ 2 = δ 2 = δ 2 ( c ) (2) δ3 = δ3
(1 M 12 ) = 4i1δ 1 + 2i1δ 2 (1) M 21 = 2i1δ 1 + 4i1δ 2 ( d ) (2) M 23 = 4i2δ 2 + 2i2δ 3 (2 M 32 ) = 2i2δ 2 + 4i2δ 3
(1)
4i1 = 2i1
2i1 δ 1 4i1 δ 2
(1)
(g )
M 23 M 32
(2)
4i 2 = 2i 2
2i2 δ 2 δ 4i 2 3
(2)
(g ′)
简写为： 简写为：
F
(1)
=k δ
总结为： 化整为零，积零为整” 总结为：“化整为零，积零为整”
§ 3.2 连续梁的单元刚度矩阵
y x
(1) M12 ,δ1(1)
(1) ( M21 ,δ21)
M 1 , δ1
1
M2
① i1
M 2 ,δ2
② i2
(2) M32 ,δ3(2)
M 3 ,δ3
2 ② i2
3
M3
(2) M32
M1
① i1
1
由结点平衡条件： 由结点平衡条件：
(1 Σ M 1 = M 12 ) − M 1 = 0
再将(d)式代入， 再将 式代入，得： 式代入
(1) (2) Σ M 2 = M 21 + M 23 − M 2 = 0 (e ) (2) Σ M 3 = M 32 − M 3 = 0
即为位移法 方程
* * * \ * \ * \ * \ * 0 \ * \ * \ * \ * \ \ * \ * \ * \ 0 * *
综上所述，可将直接刚度法的解算步骤归纳如下： 综上所述，可将直接刚度法的解算步骤归纳如下： (1)将结点和单元进行编号；选择结构坐标系和局部坐标系。 将结点和单元进行编号；选择结构坐标系和局部坐标系。 将结点和单元进行编号 (2)把所有结点力沿结构坐标系分解；建立结点位移列向量和 把所有结点力沿结构坐标系分解； 把所有结点力沿结构坐标系分解 结点力列向量(两者的分量要一一对应 两者的分量要一一对应)。 结点力列向量 两者的分量要一一对应 。 (3) 计算结构坐标系中各单元刚度矩阵的四个子块。 计算结构坐标系中各单元刚度矩阵的四个子块。 (4)将各单元刚度矩阵的四个子块，按其两个下标在结构原始 将各单元刚度矩阵的四个子块， 将各单元刚度矩阵的四个子块 刚度矩阵中“对号入座” 刚度矩阵中“对号入座”。 (5)根据边界条件修改结构原始刚度矩阵计算自由结点位移。 根据边界条件修改结构原始刚度矩阵计算自由结点位移。 根据边界条件修改结构原始刚度矩阵计算自由结点位移 (6)计算在结构坐标系中由杆端位移产生的杆端力；再计算单 计算在结构坐标系中由杆端位移产生的杆端力； 计算在结构坐标系中由杆端位移产生的杆端力 元在局部坐标系中的杆端力。 元在局部坐标系中的杆端力。 (7)计算支座反力。 计算支座反力。 计算支座反力 (8)校核。 校核。 校核
二、结构矩阵分析方法的分类
与传统的力法、位移法和混合法对应， 与传统的力法、位移法和混合法对应，也有矩阵力法、矩 阵位移法和矩阵混合法。矩阵位移法具有易于实现计算过程程 序化的优点而被广泛应用， 序化的优点而被广泛应用，我们主要介绍矩阵位移法。
矩阵位移法又分为刚度法和直接刚度法。两者的基本原理 并无本质的区别， 并无本质的区别，只是在形成所谓整体刚度矩阵时使用的方法
简写为： K ∆ = F 简写为：
------称为整体刚度方程 称为
0 2 i2 4 i2
4i1 2i K= 1 0
2i1 4i1 + 4i2 2i 2
δ 1 ∆ = δ 2 δ 3
------为结点 为结点 位移列阵
M1 F = M 2 M 3
第三章 连续梁的矩阵位移法
§ 3.1 概述 § 3.2 连续梁的单元刚度矩阵 § 3.3 整体刚度矩阵 § 3.4 非结点荷载的处理 § 3.5 连续梁的矩阵位移法举例
§ 3.1 概述
一、结构矩阵分析方法 结构矩阵分析方法
结构矩阵分析方法的广泛应用是近年来结构力学最重要的
发展之一，这与计算机技术的迅速发展有直接的关系。 发展之一，这与计算机技术的迅速发展有直接的关系。它是以 传统的结构力学作为理论基础，以矩阵作为数学表述形式，以 传统的结构力学作为理论基础，以矩阵作为数学表述形式， 电子计算机作为计算手段的三位一体的方法。 电子计算机作为计算手段的三位一体的方法。
结构矩阵分析方法的基本思想是：把整个结构看作是由若 基本思想是