第三章数据分析(梅长林)习题答案
第三章数据分析(梅长林)习题答案
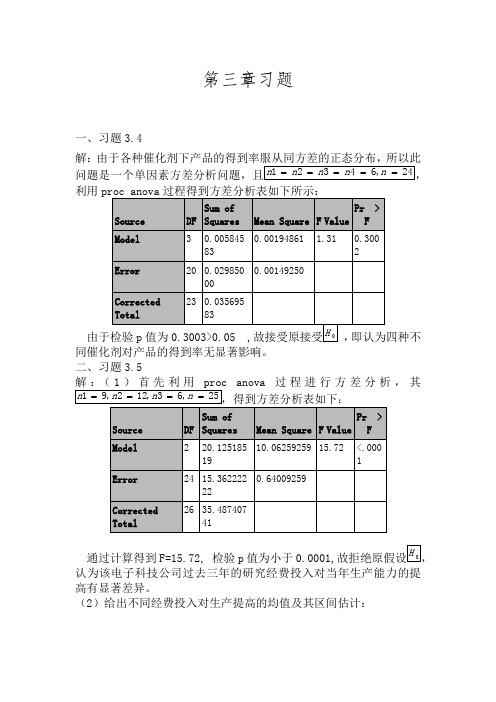
第三章习题一、习题3.4解:由于各种催化剂下产品的得到率服从同方差的正态分布,所以此利用proc anova过程得到方差分析表如下所示:同催化剂对产品的得到率无显著影响。
二、习题3.5anova过程进行方差分析,其通过计算得到F=15.72, 检验p值为小于0.0001,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。
(2)给出不同经费投入对生产提高的均值及其区间估计:为95%的置信区间为:95%的Bonferroni 同时置信区间为:Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高,当年生产能力的改善越显著。
三、习题3.6解:(1)首先利用SAS 的proc anova 过程的means 语句,求出各水平的均值和标准差:如下所示:由上表可知,(a1,b1)组合和(a1,b3)组合的标准差分别为2.030875、2.8067751与其他组合的标准差相差较大,所以我认为假定误差的等方差性不太合理。
故不能直接进行方差分析。
(2)由(1)可知直接进行方差分析是不合理的,所以对观测数据做对数变换,首先来分析个水平组合是否是方差齐性的。
由以上结果可以看出各组合水平上的标准差趋于一致,各组之间的标准差差异比较小。
说明各组合的离散程度比较接近。
故可以利用变换之后的数据在进行方差分析。
(3)由SAS系统的proc anova过程对进行自然对数变换后的数据进行方差分析,得到如下的误差分析表:x1*x2的影响是不显著的,检验P=0.3143>0.05,即两种铁离子残留量的百分比差异在不同剂量水平下可认为是相同的。
而由因素A和因素B对残留量的百分比的影响均显著,检验P值分别为0.0161和<.0001,所以两种铁离子残留量的百分比是有显著差异的,不同剂量水平下残留量的百分比也是有显著差异的。
(4)求出各因素在不同水平下的均值以及估计区间:SAS系统的proc anova过程对数据进行方差分析,得到各因素两两的Bonferroni同时置信区间为:均值之差的置信度为95%(注:可编辑下载,若有不当之处,请指正,谢谢!)。
数据分析方法实验(范金城梅长林)习题报告

习题4.5实验报告一、实验目的问题描述:在习题1.5表1.9中,列出了历年人口出生率、死亡率和自然增长率(单位:%)。
设对应于人口出生率、人口死亡率、自然增长率的数据变量分别为x1,x2,x3。
(1)分别从样本协方差矩阵S及样本相关矩阵R出发,求x1,x2,x3的样本主成分y1,y2,计算各样本主成分的贡献率。
(2)分别从样本协方差矩阵S及样本相关矩阵R出发,将第一样本主成分y1从小到大排序,并给与分析。
二、所用方法及工具(1)主成分分析法与贡献率:主成分分析法即构造原变量的一系列线性组合,使各线性组合在彼此不相关的前提下尽可能多地反映原变量的信息,即使其方差最大。
求的各主成分,等价于求它的协方差矩阵的各特征值及相应的正交单位化特征向量.按特征值由大到小所对应的正交单位化特征向量为组合系数的X,Xz ,…,X,的线性组合分别为X的第一,第二、直至第p个主成分,而各主成分的方差等于相应的特征值。
(2)SAS编程:SAS语言是一种专用的数据管理与分析语言,它提供了一种完善的编程语言。
类似于计算机的高级语言,SAS用户只需要熟悉其命令、语句及简单的语法规则就可以做数据管理和分析处理工作。
因此,掌握SAS编程技术是学习SAS的关键环节。
在SAS中,把大部分常用的复杂数据计算的算法作为标准过程调用,用户仅需要指出过程名及其必要的参数。
这一特点使得SAS编程十分简单。
三、实验内容本次实验采用SAS编程实现,代码如下:data a;set sjfx.rk1;run;proc princomp n=2 cov out=out1;var x1 x2 x3;run;proc sort data=out1 out=a1;by prin1;run;proc print data=a1;run;proc princomp n=2 out=out2;var x1 x2 x3;run;proc sort data=out2 out=a2;by prin1;run;proc print data=a2;run;实验结果:PRINCOMP 过程。
数据分析答案完整版(整理)

x n n x j ( x j x) n 1 n 1 n 1
n2
x j x( j ) x j
服 从 正 态 分 布 。 故 有 E xi x E i
1 n j 0 , n j 1
1 n 1 n n 1 2 D xi x D i j E i j ,故 xi x 服从分 n n n j 1 j 1
N (0, 2 I n ) , (1 , 2 ,
, n ) ,则
,1 .
N (0, 2 ( I n H n )) 。其中:
1
1 1 n 1 , H n n 1, n 1 1
n n 1
n 1 n 2 n n 1 2
——证毕—— 3.条件同第 2 题,证明: (1) x N 0, n
2
(2) N 1 S 2 / 2 x2 n 1 , (4 ) t n
x t n 1
由与此变换为正交变换知, yi 2 xi 2 ,同时 x1 , x2 , , xn 为相互独
i 1 i 1
n
n
立的正态分布。
密度函数 f x1 , x2 ,
xi 1 2 2 i 1 由于正交的雅可比行列 , xn e 2 n
2
1 , n 1 , 1 ,由正交性有 n 1
2 , 3n,
a
第2章 数据分析(梅长林)习题题答案
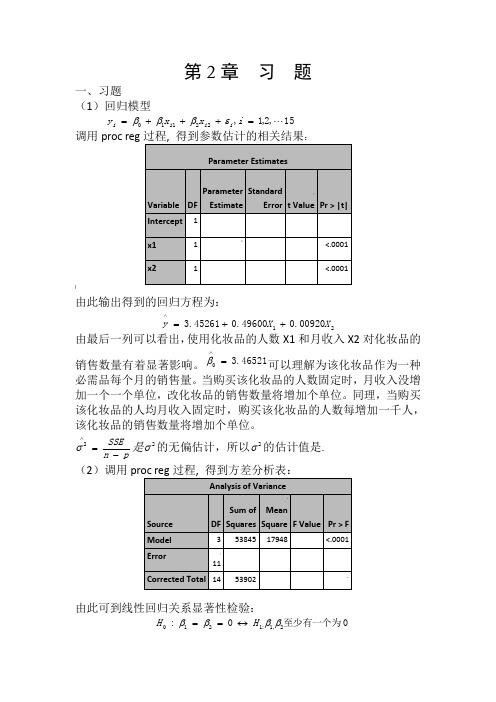
第2章 习 题一、习题(1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用proc reg:]由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔==的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( )2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
管理会计学第3章教材习题解析.doc

第三章教材习题解析一、思考题1.木一量一利分析的基木假设有哪些?说明它们的具体含义。
答:木一量一利分析的基木假设主要包括:(1)相关范I韦I假设,即木_量_利分析屮对成木性态的划分都是在一定的相关范围Z内的。
相关范围假设同时乂包含了“期间”假设和“业务量"假设两层含义。
(2)模型线性假设。
具体包括:固定成本不变假设;变动成本与业务最呈完全线性关系假设;销伟收入与销伟数量呈完全线性关系假设。
(3)产销平衡假设。
由于木—量—利分析屮的“量”指的是销售数量而非生产数量,在销售价格不变的情况下,这个量也就是销伟收入。
木利分析的核心是分析收入与成本Z间的对比关系。
但产量这一业务量的变动无论是对固定成木还是变动成木都可能产生影响,这种影响当然也会影响到收入与成本之间的对比关系。
所以从销售数量的角度进行木—量—利分析时,就必须假定产销关系平衡。
(4 )品种结构不变假设。
木假设是指在一个多品种生产和销售的企业屮,各种产品的销售收入在总成木屮所占的比重不会发生变化。
上述假设的背后都暗藏肴一个共同的假设,就是:假设企业的全部成木可以合理地或者说比较准确地分解为固定成木与变动成本。
2.盈亏临界点分析在企业经营决策中有什么作用?试结合具体实例进行分析。
答:盈亏临界点又叫盈亏分歧点、保本点等,是指企业的经营规模(销售量)刚好使企业达到不盈不亏的状态。
盈亏临界点分析就是根据成木、销售收入、利润等因素之间的函数关系,预测企业在怎样的情况下达到不盈不亏的状态。
盈亏临界点分析所提供的信息,对于企业合理计划和有效控制经营过稈极为有用,如预测成木、收入、利润和预计伟价、销量、成木水平的变动对利润的影响,等等。
应该指出的是,盈亏临界点分析是在研究成本、销伟收入与利润三者Z间相互关系的基础上进行的,所以除了销售量因素外,销竹价格、固定成木与变动成木诸因素的变动,同时可以使企业达到不盈不亏的状态,只不过在进行盈亏临界点分析时,某一因素与其他因素Z间表现为互为因果关系。
数据分析参考答案

数据分析参考答案数据分析参考答案数据分析是一项重要的技能,它帮助我们从大量的数据中提取有用的信息和洞察力。
在当今信息爆炸的时代,数据分析已经成为了各行各业的必备技能。
无论是企业决策、市场营销还是科学研究,数据分析都扮演着重要的角色。
在本文中,我将提供一些数据分析的参考答案,帮助读者更好地理解和应用数据分析。
首先,数据分析的第一步是数据清洗和整理。
在进行数据分析之前,我们需要确保数据的质量和准确性。
这包括删除重复数据、处理缺失值、解决异常值等。
只有经过清洗和整理的数据才能真正反映出问题的本质和规律。
其次,数据分析需要选择合适的方法和工具。
根据问题的性质和数据的类型,我们可以选择不同的数据分析方法。
常见的数据分析方法包括描述性统计、推断统计、机器学习等。
同时,我们还需要选择适合的数据分析工具,如Excel、Python、R等。
选择合适的方法和工具可以提高数据分析的效率和准确性。
第三,数据可视化是数据分析的重要环节。
通过数据可视化,我们可以将抽象的数据转化为直观的图表和图形,更好地理解数据的分布和趋势。
数据可视化不仅可以提高数据分析的效果,还可以帮助我们向他人传达分析结果。
在进行数据可视化时,我们需要选择适当的图表类型,如柱状图、折线图、散点图等,以及合适的颜色和字体。
第四,数据分析需要进行合理的假设和推断。
在进行数据分析时,我们需要建立合理的假设,并通过数据进行验证。
通过统计方法和推断统计学,我们可以对数据进行推断和预测。
然而,我们需要注意的是,数据分析只能提供相关性而非因果性的结论。
因此,在进行数据分析时,我们需要谨慎解读结果,并避免错误的推断。
最后,数据分析需要不断的学习和实践。
数据分析是一个不断发展和演进的领域,新的方法和工具不断涌现。
为了保持竞争力,我们需要不断学习新的数据分析技术,并将其应用到实际问题中。
同时,我们还需要通过实践不断提高自己的数据分析能力,不断优化分析结果和方法。
综上所述,数据分析是一项重要的技能,它帮助我们从大量的数据中提取有用的信息和洞察力。
最新第2章 数据分析(梅长林)习题题答案
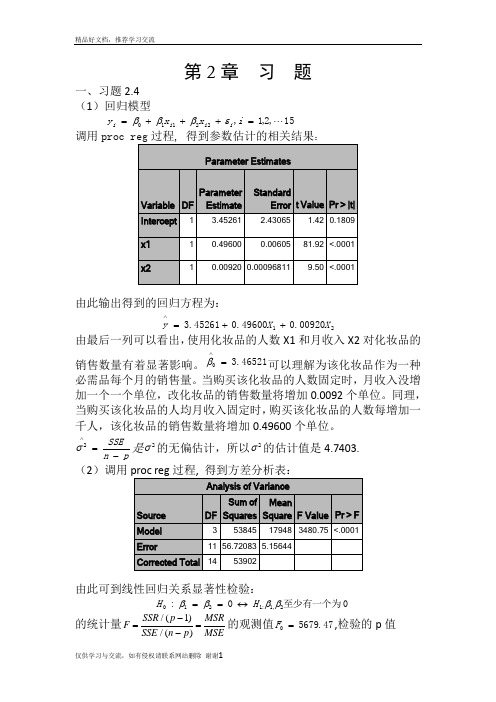
第2章 习 题一、习题2.4 (1)回归模型15,2,1,22110 =+++=i x x y i i i i εβββ调用:由此输出得到的回归方程为:2100920.049600.045261.3X X y ++=∧由最后一列可以看出,使用化妆品的人数X1和月收入X2对化妆品的销售数量有着显著影响。
46521.30=∧β可以理解为该化妆品作为一种必需品每个月的销售量。
当购买该化妆品的人数固定时,月收入没增加一个一个单位,改化妆品的销售数量将增加0.0092个单位。
同理,当购买该化妆品的人均月收入固定时,购买该化妆品的人数每增加一千人,该化妆品的销售数量将增加0.49600个单位。
pn SSE-=∧2σ是2σ的无偏估计,所以2σ的估计值是4.7403. (2)调用由此可到线性回归关系显著性检验:0至少有一个为0:2,1:1210ββββH H ↔== 的统计量/(1)/()SSR p MSRF SSE n p MSE-==-的观测值47.56790=F ,检验的p 值0001.0)(000<>==F F p p H另外9989.053902538452===SST SSR R ,2R 描述了由自由变量的线性关系函数值所能反映的Y 的总变化量的比例。
2R 越大,表明线性关系越明显。
这些结果均表明Y 与X1,X2之间的回归关系高度显著。
(3)若置信水平05.0=α,由17881.2)12(975.0=t ,利用参数估计值得到21,0,βββ的置信区间分别为:对,0β2942.54516.343065.21781.245216.3±=⨯±,即)7458.8,8426.1(-) 对1β:01318.049600.000605.01781.249600.0±=⨯±,即)50198.0,48282.0( 2β:0021.000920.00009681.01781.200920.0±=⨯±,即)00113.0,0071.0(-(4)首先检验X1对Y 是否有显著性影:假设其约简模型为:15,2,1,220 =++=i x y i i i εββ 由观测数据并利用proc reg 过程拟合此模型求得:88137.484)(=R SSE 13215=-=R f 88357.56)(=F SSE 12315=-=R f由[()()]()()/R F FSSE R SSE F f f F SSE F f --=求得检验统计量的值为:3.9012/88357.5688357.5688137.4840=-=F05.0))13,1(()(0000<>==>==F F P F F p p H由此拒绝原假设,所以x2对Y 有显著影响。
数据分析答案梅长林

数据分析答案梅长林数据分析答案梅长林【篇一:1.1一维数据数字特征】013学年第一学期主讲教师李晓燕课程名称数据分析课程类别专业限选课学时及学分 68;4授课班级信息101 102使用教材《数据分析方法》系(院.部) 数理系教研室(实验室) 信息和计算科学教研室数据分析总学时:68 理论38.上机28 适用专业:信息和计算科学内容:sas软件介绍 3学时 ? 数据的描述性分析10学时 ? 线性回归分析13学时 ? 方差分析 10学时 ? 主成分分析和典型相关分析8学时判别分析 8学时 ? 聚类分析 8学时 ? 学生报告 8学时教材:《数据分析方法》,梅长林、范金城编,高等教育出版社.2006. 参考资料:《实用统计方法》,梅长林编,科学出版社;《使用多元统计分析》,高惠璇编,北京大学出版社,2005;《使用统计方法和sas系统》,高惠璇编,北京大学出版社,2001;《多元统计分析》(二版),何晓群编,中国人民大学出版社,2008;《使用回归分析》(二版),何晓群编,中国人民大学出版社,2007;《统计建模和r软件》,薛毅编著,清华大学出版社,2007. 考核:期末成绩(闭卷测试+上机测试):70%。
平时成绩(平时作业+考勤+大报告):30%。
课程作业(1)作业题目在网络教学平台公布,按格式要求,以电子版方式通过平台提交。
(2)大报告:2-3人一组,每组一个选题,成员按相同的成绩计分。
收集数据,撰写小论文,做ppt讲解。
每组讲10-20分钟,提问环节。
同学打分。
课时授课计划课次序号: 01一、课题:1.1 一维数据的数字特征及相关系数二、课型:新授课三、目的要求:1.掌握数据的数字特征(均值、方差等);2.掌握几种描述性分析的sas过程和作图过程计算这些数字特征及进行描述性分析.四、教学重点:均值、方差等数字特征.教学难点:基本概念的理解.五、教学方法及手段:传统教学和上机实验相结合.六、参考资料:1.《实用统计方法》,梅长林,周家良编,科学出版社;2.《sas统计分析使用》,董大钧主编,电子工业出版社.七、作业:1.1八、授课记录:九、授课效果分析:0 绪论0.1 课程内涵数据分析(即多元统计学statistics):是以数据为依据,以统计方法为理论、计算机及软为工具,研究多变量问题、挖掘数据的统计规律的学科. 通过收集数据、整理数据、分析数据和由数据得出结论的一组概念、原则和方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章习题
一、习题3.4
解:由于各种催化剂下产品的得到率服从同方差的正态分布,所以此问题是一个单因素方差分析问题,且24,64321=====n n n n n ,利用proc anova 过程得到方差分析表如下所示:
由于检验p 值为0.3003>0.05 ,故接受原接受0 ,即认为四种不同催化剂对产品的得到率无显著影响。
二、习题3.5
解:(1)首先利用proc anova 过程进行方差分析,其25,63,122,91====n n n n ,得到方差分析表如下:
通过计算得到F=15.72, 检验p 值为小于0.0001,故拒绝原假设0H ,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。
(2)给出不同经费投入对生产提高的均值及其区间估计:
由以上结果得到三年经费投入为低、中、高情况下当年生产能力提高量的均值为2000.9,1333.8,8778.6===H M L u u u ,H M L u u u 、、的置信度为95%的置信区间为:
]4282.7.3174.6[∈L u 、]6100.8.,6567.7[∈M u 、]8741.9.,5259.8[∈H u 通过计算得到两两均值之差的计算表:
得到H M H L M L u u u u u u ---和,的置信都不小于95%的Bonferroni 同时置信区间为:
]3476.0.1635.2[--∈-M L u u , ]2370.1.4074.3[--∈-H L u u , ]0371.0.0962.2[--∈-H M u u
从H M H L M L u u u u u u ---和,的Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高,当年生产能力的改善越显著。
三、习题3.6
解:(1)首先利用SAS 的proc anova 过程的means 语句,求出各水平
的均值和标准差:如下所示:
由上表可知,(a1,b1)组合和(a1,b3)组合的标准差分别为2.030875、2.8067751与其他组合的标准差相差较大,所以我认为假定误差的等方差性不太合理。
故不能直接进行方差分析。
(2)由(1)可知直接进行方差分析是不合理的,所以对观测数据做对数变换,首先来分析个水平组合是否是方差齐性的。
由以上结果可以看出各组合水平上的标准差趋于一致,各组之间的标准差差异比较小。
说明各组合的离散程度比较接近。
故可以利用变换之后的数据在进行方差分析。
(3)由SAS系统的proc anova过程对进行自然对数变换后的数据进
行方差分析,得到如下的误差分析表:
从结果中可以看出在显著性水平0.05α=下交叉因子x1*x2的影响是不显著的,检验P=0.3143>0.05,即两种铁离子残留量的百分比差异在不同剂量水平下可认为是相同的。
而由因素A 和因素B 对残留量的百分比的影响均显著,检验P 值分别为0.0161和<.0001,所以两种铁离子残留量的百分比是有显著差异的,不同剂量水平下残留量的百分比也是有显著差异的。
(4)求出各因素在不同水平下的均值以及估计区间:
SAS系统的proc anova过程对数据进行方差分析,得到各因素两两均值之差的置信度为95%的Bonferroni同时置信区间为:。
