数据分析练习题(解答)
《好题》初中八年级数学下册第二十章《数据的分析》经典练习(含答案)

一、选择题1.某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )A .21,21B .21,21.5C .21,22D .22,22C解析:C 【解析】这组数据中,21出现了10次,出现次数最多,所以众数为21, 第15个数和第16个数都是22,所以中位数是22. 故选C.2.在我县“我的中国梦”演讲比赛中,有7名同学参加了比赛,他们最终决赛的成绩各不相同.其中一名学生想要知道自己是否进入前3名,不仅要知道自己的分数,还得知道这7名学生成绩的( ) A .众数 B .方差C .平均数D .中位数D解析:D 【分析】由于其中一名学生想要知道自己能否进入前3名,共有7名选手参加,故应根据中位数的意义分析. 【详解】由于总共有7个人,且他们的成绩各不相同,第3的成绩是中位数,要判断是否进入前3名,故应知道中位数的多少. 故选:D . 【点睛】此题主要考查统计的有关知识,主要包括平均数、中位数、众数、方差的意义.反映数据集中程度的统计量有平均数、中位数、众数、方差等,各有局限性,因此要对统计量进行合理的选择和恰当的运用. 3.已知数据12,,,n x x x 的平均数是2,方差是0.1,则1242,42,,42n x x x ---的平均数和标准差分别为( ) A .2,1.6 B .210C .6,0.4D .210D 解析:D【分析】根据平均数和方差公式直接计算即可求得. 【详解】 解:()12312n x x x x x n=+++⋯+=, ∴()1231424242424226n x x x x n -+-+-+⋯+-=⨯-=, ()()()()22222123122220.1n S x x x x n ⎡⎤=-+-+-+⋯+-=⎣⎦,()()()()22222421231426426426426x n S x x x x n -⎡⎤=--+--+--+⋯+--⎣⎦ 0.116=⨯1.6=,∴42x S -=故选:D . 【点睛】本题考查了方差和平均数,灵活利用两个公式,进行准确计算是解答的关键. 4.下列说法正确的是( )A .为了解我国中学生课外阅读的情况,应采取全面调查的方式B .一组数据1、2、5、5、5、3、3的中位数和众数都是5C .若甲组数据的方差是003,乙组数据的方差是0.1,则甲组数据比乙组数据稳定D .抛掷一枚硬币100次,一定有50次“正面朝上”C 解析:C 【分析】可根据调查的选择、中位数和众数的求法、方差及随机事件的意义,逐个判断得结论. 【详解】解:因为我国中学生人数众多,其课外阅读的情况也不需要特别精确, 所以对我国中学生课外阅读情况的调查,宜采用抽样调查,故选项A 不正确; 因为B 中数据按从小到大排列为1、2、3、3、5、5、5,位于中间的数是3,故该组数据的中位数为3, 所以选项B 说法不正确;因为0.003<0.1,方差越小,波动越小,数据越稳定, 所以甲组数据比乙组数据稳定,故选项C 说法正确;因为抛掷硬币属于随机事件,抛掷一枚硬币100次,不一定有50次“正面朝上” 故选项D 说法不正确. 故选:C . 【点睛】本题的关键在于掌握调查的选择、中位数和众数的求法、方差及随机事件的意义.5.通过统计甲、乙、丙、丁四名同学某学期的四次数学测试成绩,得到甲、乙、丙、丁三明同学四次数学测试成绩的方差分别为S甲2=17,S乙2=36,S丙2=14,丁同学四次数学测试成绩(单位:分).如下表:第一次第二次第三次第四次丁同学 80 80 90 90则这四名同学四次数学测试成绩最稳定的是()A.甲B.乙C.丙D.丁C解析:C【分析】求得丁同学的方差后与前三个同学的方差比较,方差最小的成绩最稳定.【详解】丁同学的平均成绩为:14⨯(80+80+90+90)=85;方差为S丁214=[2×(80﹣85)2+2×(90﹣85)2]=25,所以四个人中丙的方差最小,成绩最稳定.故选C.【点睛】本题考查了方差的意义及方差的计算公式,解题的关键是牢记方差的公式,难度不大.6.如图是根据我市某天七个整点时的气温绘制成的统计图,则下列说法正确的是()A.这组数据的众数是14B.这组数据的中位数是31C.这组数据的标准差是4D.这组是数据的极差是9D解析:D【解析】【分析】根据中位数,众数、极差、标准差的定义即可判断.【详解】解:七个整点时数据为:22,22,23,26,28,30,31所以中位数为26,众数为22,平均数为:22+22+23+26+28+3032167+=;极差是31-22=9,标准差是:故D正确,故选:D【点睛】此题考查中位数,众数、极差、标准差的定义,解题关键在于看懂图中数据7.有甲乙两个箱子,其中甲箱内有98颗球,分别标记号码1~98,且号码不重复的整数,乙箱内没有球。
数据分析技巧及练习题含答案

【解析】
【分析】
根据中位数、众数的概念分别求得这组数据的中位数、众数.
【详解】
解:众数是一组数据中出现次数最多的数,即8;
由统计表可知,处于20,21两个数的平均数就是中位数,
∴这组数据的中位数为 ;
故选:D.
【点睛】
考查了中位数、众数的概念.本题为统计题,考查众数与中位数的意义,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
3.某校四个绿化小组一天植树的棵数如下:10,x,10,8,已知这组数据的众数与平均数相等,则这组数据的中位数是( )
A.8B.9C.10D.12
【答案】C
【解析】
【分析】
根据这组数据的众数与平均数相等,可知这组数据的众数(因10出现了2次)与平均数都是10;再根据平均数是10,可求出这四个数的和是40,进而求出x的数值;然后把这四个数据按照从大到小的顺序排列,由于是偶数个数据,则中间两个数的平均数就是中位数.
6.回忆位中数和众数的概念;
7.在去年的体育中考中,某校6名学生的体育成绩统计如下表:
成绩
17
18
20
人数
2
3
1
则下列关于这组数据的说法错误的是( )
A.众数是18B.中位数是18C.平均数是18D.方差是2
【答案】D
【解析】
【分析】
根据众数、中位数的定义和平均数、方差的计算公式分别进行解答即可.
【详解】
∵乙的成绩方差<甲成绩的方差,
∴乙的成绩比甲的成绩稳定,
故选B.
【点睛】
本题主要考查方差,方差是反映一组数据的波动大小的一个量.方差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
六年级数学数据分析专项练习题及答案

六年级数学数据分析专项练习题及答案一、选择题1. 下列哪个不是连续统计资料A. 今天上午10点钟每10分钟的体温B. 近一周每天的降水量C. 放在实验室里的草虫的重量D. 不同年级学生的体重2. 下列资料中哪个是离散统计资料A. 月份和季节的关系B. 过去一周每天的最高气温C. 一年级学生的身高D. 一天中不同时间段的读书时间3. 小明一周的学习时间如下:4, 5, 6, 7, 4, 5, 8(单位:小时)。
平均学习时间是多少?A. 5小时B. 6小时C. 7小时D. 8小时4. 某班学生参加了一次考试,得到的分数如下:85, 90, 92, 88, 83, 86, 95。
以下哪个图形可以正确表示这些分数?A. 折线图B. 饼图C. 柱状图D. 散点图5. 某班学生的年龄分布如下:10, 11, 11, 10, 12, 10, 11, 10, 12, 13。
以下哪个图形可以正确表示这些数据?A. 折线图B. 饼图C. 柱状图D. 散点图二、填空题1. 下列是连续数据的是________ (体温, 体重, 学生姓名)2. 某班同学的身高如下 (120cm, 130cm, 125cm, 135cm),其中众数为________3. 折线图适合表示________的变化4. 某地区一周的降水量如下 (10mm, 5mm, 15mm, 20mm, 8mm),其中极差为________三、解答题1. 小明的家人去年9月份的电费如下:120元、130元、110元、140元、130元。
求这些电费的平均值和中位数。
解析:平均值 = (120 + 130 + 110 + 140 + 130) / 5 = 130元中位数 = 130元2. 某小组同学去年参加了一次数学竞赛,得到的分数如下:80分、90分、85分、95分、88分。
请画出这些分数的柱状图,并标明横轴和纵轴的单位。
解析:横轴:分数纵轴:人数|100 ||90 || x80 | x x x|_____________80 85 90 953. 某年级的同学身高如下:120cm、125cm、115cm、130cm、135cm。
八年级数据的分析练习题及答案

一、单选题1、某射击运动员在一次射击练习中,5次射击成绩(单位:环)记录如下:8,9,x,7,1 0,因记录员不小心,有一个数字被污染了,但记录员记得这组数据的众数为8,则这组数据的中位数是()A. 7B. 8C. 9D. 10参考答案: B【思路分析】本题为统计题,考查众数与中位数的意义.众数是一组数据中出现次数最多的数.中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.先根据众数求出被污染了的数字,再根据中位数的定义即可求解。
【解题过程】解:∵记录员记得数据8,9,x,7,10的众数为8,∴x=8,从小到大排列为7,8,8,9,10,∴这组数据的中位数是8。
故选B。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -2、数据5、7、5、8、6、13、5 的中位数是()。
A. 5B. 6C. 7D. 8参考答案: B【思路分析】本题主要考查中位数。
仔细读题,获取题中已知条件,结合中位数的相关知识,即可解答此题。
【解题过程】解:当变量值的项数N为奇数时,处于中间位置的变量值即为中位数;当N为偶数时,中位数则为处于中间位置的2个变量值的平均数。
这组数据按从小到大排列为:5、5、5、6、7、8、13,则中位数是6,故B项正确。
故本题正确答案为B。
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -3、某中学足球队的18名队员的年龄情况如表,这些队员年龄的众数和中位数分别是()。
第三章数据分析习题答案
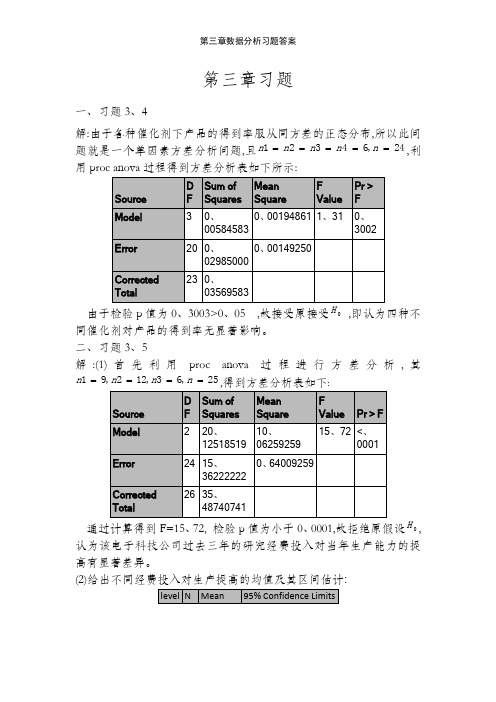
第三章习题一、习题3、4解:由于各种催化剂下产品的得到率服从同方差的正态分布,所以此问题就是一个单因素方差分析问题,且24,64321=====n n n n n ,利用proc anova 过程得到方差分析表如下所示:由于检验p 值为0、3003>0、05 ,故接受原接受0 ,即认为四种不同催化剂对产品的得到率无显著影响。
二、习题3、5解:(1)首先利用proc anova 过程进行方差分析,其25,63,122,91====n n n n ,得到方差分析表如下:通过计算得到F=15、72, 检验p 值为小于0、0001,故拒绝原假设0H ,认为该电子科技公司过去三年的研究经费投入对当年生产能力的提高有显著差异。
(2)给出不同经费投入对生产提高的均值及其区间估计:高量的均值为2000.9,1333.8,8778.6===H M L u u u ,H M L u u u 、、的置信度为95%的置信区间为:]4282.7.3174.6[∈L u 、]6100.8.,6567.7[∈M u 、]8741.9.,5259.8[∈H u 通过计算得到两两均值之差的计算表:得到H M H L M L u u u u u u ---和,的置信都不小于95%的Bonferroni 同时置信区间为:]3476.0.1635.2[--∈-M L u u , ]2370.1.4074.3[--∈-H L u u ,]0371.0.0962.2[--∈-H M u u从H M H L M L u u u u u u ---和,的Bonferroni 同时置信区间都位于负值区间可知随着三年科研经费的投入越高,当年生产能力的改善越显著。
三、习题3、6解:(1)首先利用SAS 的proc anova 过程的means 语句,求出各水平的均值与标准差:如下所示:由上表可知,(a1,b1)组合与(a1,b3)组合的标准差分别为2、030875、2、8067751与其她组合的标准差相差较大,所以我认为假定误差的等方差性不太合理。
初中数学:数据的分析专项练习含答案

一.选择题1.九年级一班和二班每班选8名同学进行投篮比赛,每名同学投篮10次,对每名同学投中的次数进行统计,甲说:“一班同学投中次数为6个的最多”乙说:“二班同学投中次数最多与最少的相差6个.”上面两名同学的议论能反映出的统计量是(D)A.平均数和众数 B.众数和极差C.众数和方差 D.中位数和极差2.在“我的阅读生活”校园演讲比赛中,有11名学生参加比赛,他们决赛的最终成绩各不相同,其中一名学生想知道自己能否进入前6名,除了要了解自己的成绩外,还要了解这11名学生成绩的(D)A.众数 B.方差 C.平均数 D.中位数3.下列特征量不能反映一组数据集中趋势的是(C)A.众数 B.中位数 C.方差 D.平均数4.表为甲班55人某次数学小考成绩的统计结果,关于甲班男、女生此次小考成绩的统计量,下列叙述何者正确?(A)A.男生成绩的四分位距大于女生成绩的四分位距B.男生成绩的四分位距小于女生成绩的四分位距C.男生成绩的平均数大于女生成绩的平均数D.男生成绩的平均数小于女生成绩的平均数5.刻画一组数据波动大小的统计量是(B)A.平均数 B.方差 C.众数 D.中位数6.某班要从9名百米跑成绩各不相同的同学中选4名参加4×100米接力赛,而这9名同学只知道自己的成绩,要想让他们知道自己是否入选,老师只需公布他们成绩的(B)A.平均数 B.中位数 C.众数 D.方差7.小颖随机抽样调查本班20名女同学所穿运动鞋尺码,并统计如表:学校附近的商店经理根据表中决定本月多进尺码为23.0cm的女式运动鞋,商店经理的这一决定应用了哪个统计知识(A)A.众数 B.中位数 C.平均数 D.方差8.小洪根据演讲比赛中九位评委所给的分数制作了如下表格:如果去掉一个最高分和一个最低分,那么表格中数据一定不发生变化的是(B)A.平均数 B.中位数 C.众数 D.方差9.以下是期中考试后,班里两位同学的对话:小晖:我们小组成绩是85分的人最多;小聪:我们小组7位同学成绩排在最中间的恰好也是85分以上两位同学的对话反映出的统计量是(D)A.众数和方差 B.平均数和中位数C.众数和平均数 D.众数和中位数10.下列说法不正确的是(A)A.数据0、1、2、3、4、5的平均数是3B.选举中,人们通常最关心的数据是众数C.数据3、5、4、1、2的中位数是3D.甲、乙两组数据的平均数相同,方差分别是S=0.1,S乙²=0.11,则甲组数据比乙组数据更稳定甲²二.填空题11.用于衡量一组数据的波动程度的三个量为极差、方差、标准差.12.有13位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设7个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在这13名同学成绩的统计量中只需知道一个量,它是中位数(填众数或方差或中位数或平均数)13.某服装店销售一款新式女式T恤,试销期间对该款不同型号女式T恤的销售量统计如下表:该店经理如果想要了解哪种型号女式T恤销售量最大,那么他应关注的统计量是众数.14.从甲、乙、丙三个厂家生产的同一种产品中各抽取8件,对它们的使用寿命进行跟踪调查,结果如下:(单位:年)甲:4,6,6,6,8,9,12,13.乙:3,3,4,7,9,10,11,12.丙:3,4,5,6,8,8,8,10.三个厂家在广告中都称该产品的使用寿命是8年.请根据结果判断,厂家在广告中分别运用了平均数、众数、中位数中的哪一种集中趋势的特征数:甲:平均数,乙:中位数,丙:众数.三.解答题15.某校要从八年级甲、乙两个班中各选取10名女同学组成礼仪队,选取的两个班女生的身高如下(单位:cm):甲班:168 167 170 165 168 166 171 168 167 170乙班:165 167 169 170 165 168 170 171 168 167(1)补充完成下面的统计分析表:(2)根据如表,请选择一个合适的统计量作为选择标准,说明哪一个班能被选取.解:(1)甲班的方差=1/10×[(168﹣168)2+(167﹣168)2+(170﹣168)2+…+(170﹣168)2]=3.2;乙班的中位数为168;补全表格如下:(2)选择方差做标准,∵甲班方差<乙班方差,∴甲班可能被选取.16.某酒店共有6名员工,所有员工的工资如下表所示:(1)酒店所有员工的平均月工资是多少元?(2)平均月工资能准确反映该酒店员工工资的一般水平吗?若能,请说明理由;若不能,如何才能较准确地反映该酒店员工工资的一般水平?谈谈你的看法.解:(1)平均月工资=(4000+600+900+500+500+400)÷6=1150(元),(2)∵能达到这个工资水平的只有1人,∴平均月工资不能准确反映该酒店员工工资的一般水平,这组数据的众数是500元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平.17.在洋浦一新开业的以经营男式皮鞋为主的鞋店当服务员的阿丽是个做事善于观察的小姑娘,上班一段时间后,她发现各种尺码的男式皮鞋销量并不均衡,于是她把这个发现记录下来交给了她的老板:你认为这个销售记录对老板管理鞋店生意有用吗?如果你认为有用,请说明你的理由,并请你帮这个老板策划一下如何利用这些信息?解:这个销售记录对老板有用,∵众数体现数据的最集中的一点,这样可以确定进货的数量,∴鞋店老板最喜欢的是众数.∴建议老板进货时多进41号的男鞋.18.在八次数学测试中,甲、乙两人的成绩如下:甲:89,93,88,91,94,90,88,87乙:92,90,85,93,95,86,87,92请你从下列角度比较两人成绩的情况,并说明理由:(1)分别计算两人的极差;并说明谁的成绩变化范围大;(2)根据平均数来判断两人的成绩谁优谁次;(3)根据众数来判断两人的成绩谁优谁次;解:(1)甲的极差为:94﹣87=7分乙的极差为:95﹣85=10∴乙的变化范围大;∴乙的变化范围大.89,93,88,91,94,90,88,87 乙:92,90,85,93,95,86,87,92(2)甲的平均数为:(89+93+88+91+94+90+88+87)÷8=90,乙的平均数为:(92+90+85+93+95+86+87+92)÷8=90,∴两人的成绩相当;(3)甲的众数为88,乙的众数为92,∴从众数的角度看乙的成绩稍好;。
数据分析技巧及练习题附解析

6
5
4
2
每天加工零件数的中位数和众数为( )
A.6,5B.6,6C.5,5D.5,6
【答案】A
【解析】
【分析】
根据众数、中位数的定义分别进行解答即可.
【详解】
由表知数据5出现了6次,次数最多,所以众数为5;
因为共有20个数据,
所以中位数为第10、11个数据的平均数,即中位数为 =6,
故选A.
【点睛】
[(110﹣109)2+(106﹣109)2+(109﹣109)2+(111﹣109)2+(108﹣109)2+(110﹣109)2]= ,B错误;
中位数是109.5,D错误;
故选A.
【点睛】
本题考查的是众数、平均数、方差、中位数,掌握它们的概念和计算公式是解题的关键.
14.某兴趣小组为了解我市气温变化情况,记录了今年月份连续6天的最低气温(单位:℃): ,关于这组数据,下列结论不正确的是()
B.任意掷一枚质地均匀的硬币10次,一定有5次正面向上
C.如果有一组数据为5,3,6,4,2,那么它的中位数是6
D.“用长分别为 、12cm、 的三条线段可以围成三角形”这一事件是不可能事件
【答案】D
【解析】
【分析】
根据矩形的判定定理,数据出现的可能性的大小,中位数的计算方法,不可能事件的定义依次判断即可.
数据分析技巧及练习题附解析
一、选择题
1.一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是( )
A.6B.5C.4.5D.3.5
【答案】C
【解析】
若众数为1,则数据为1、1、5、7,此时中位数为3,不符合题意;
若众数为5,则数据为1、5、5、7,中位数为5,符合题意,
数据的分析单元练习题(附答案)

数据的分析单元练习题(附答案)数据的分析单元练习题⼀、选择题(每⼩题3分,共36分)1.为了解我校⼋年级800名学⽣期中数学考试情况,从中抽取了200名学⽣的数学成绩进⾏统计.下列判断:①这种调查⽅式是抽样调查;②800名学⽣是总体;③每名学⽣的期中考试数学成绩是个体;④200名学⽣是总体的⼀个样本;⑤200名学⽣是样本容量.其中正确的判断有()A.1个B.2个C.3个D.4个2.天⽓预报报道宜春市今天最⾼⽓温34℃,最低⽓温20℃,则今天宜春市⽓温的极差是() A.54℃ B.14℃ C.-14℃ D.-62℃3.⼀次数学测试后,随机抽取了⼋(⼀)班6名学⽣的成绩:80,85,86,88,88,95。
关于这组数据的说法中错误的是() A.极差是15 B.众数是88 C.中位数是86 D.平均数是874.⼈数相同的⼋年级甲、⼄两班学⽣在同⼀次数学单元测试,班级平均分和⽅差如下:80x x ==⼄甲,2240s =甲,2180s =⼄,则成绩较为稳定的班级是()A.甲班B.⼄班C.两班成绩⼀样稳定D.⽆法确定 5.某地连续9天的最⾼⽓温统计如下:这组数据的中位数和众数别是()A.24,25B.24.5,25C.25,24D.23.5,246.在学校对学⽣进⾏的晨检体温测量中,学⽣甲连续10天的体温与36℃的上下波动数据为0.2,0.3,0.1,0.1,0,0.2,0.1,0.1,0, 0.1,则在这10天中该学⽣的体温波动数据中不正确的是() A.平均数为0.12 B.众数为0.1 C.中位数为0.1 D. ⽅差为0.027.体育课上,⼋(1)班两个组各10⼈参加⽴定跳远,要判断哪⼀组成绩⽐较整齐,通常需要知道这两个组⽴定跳远成绩的()A .平均数 B.众数 C .⽅差 D .频率分布8.甲、⼄、丙、丁四⼈的数学测验成绩分别为90分、90分、x 分、80分,若这组数据的众数与平均数恰好相等,则这组数据的中位数是()A.100分B.95分C.90分D.85分 9.已知⼀组数据1、2、y 的平均数为4,那么()A.y=7B.y=8C.y=9D.y=1010.已知⼋年级四班全班35⼈⾝⾼的平均数与中位数都是160厘⽶,但后来发现其中有⼀位同学的⾝⾼登记错误,误将160厘⽶写成166厘⽶,正确的平均数为a 厘⽶,中位数为b 厘⽶。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E X 1-0
设来自样本观测值如下表:
T EX1-1 某小学10名11岁学生的身高(单位:cm)数据如下: (1) 计算均值、方差、标准差、变异系数、偏度、峰度; (2) 计算中位数、上、下四分位数、四分位极差、三均数; (3) 作出直方图(范围130~145,a i-1≤x<a i ,间距3个单位); (4) 作出茎叶图;
(5) 写出次序统计量)()2()1(,...,,n x x x ;
(6) 进行正态性W 检验(适合与小样本3<=n<=50)。
需要计算)()1(i i n i x x d -=-+,试写出i d (其中,当n 为偶
数时,21n k i =≤≤;当n 为奇数时,2
11-=≤≤n k i ) 解:(1)
均值:∑==
n
i i
x
n
x 1
1;
方差:21
2
)(1
1
∑=--=
n
i i
x x
n s ;标准差2s s =;
变异系数:(%)100x
s
CV ⨯=;
偏度:∑=---=
n
i i
x x
s n n n g 1
33
1)(1
)2)(1(;
峰度:)
3)(2()1(3)(1
)3)(2)(1()1(3
1
4
4
2--------+=
∑
=n n n x x s n n n n n g n
i i 。
(2)
中位数:⎪⎩⎪
⎨⎧+=++是整数
不是整数
np x x np x M np np np )(2
1
,)1()()1]([;
上、下四分位数:75.03M Q =,25.01M Q =; 四分位极差:131Q Q R -=;
三均数:314
1
2141ˆQ M Q M
++=。
EX1-4 2002年11月以及1至11月全国部分省、市、区财政预算收入数据如表1.4所示(单位:亿元)。
设X 1为11月预算收入,X 2为1至11月预算收入,分别对X 1,X 2的观测值计算:
(7) X 1,X 2的观测值的Pearson 相关系数Spearman 相关系数。
Pearson 相关系数:yy
xx
xy xy s s s r =
其中∑=--=
n
i i
xx
x x
n s 1
2
)(1
1,∑=--=
n
i i
yy
y y
n s 1
2
)(1
1,21
2)()(1
1y y x x
n s i n
i i
xy
---=
∑=。
Spearman 相关系数:∑
∑
∑===----=
n
i i n i i n
i i i xy S S R R S S R R q 1
2
1
2
1
)()()
)((,
其中n R R R ,...,,21为n x x x ,...,,21的秩统计量,n S S S ,...,,21为n y y y ,...,,21的秩统计量。
例2-1,2-2 对于只有一个自变量的线性回归模型εββ++=110X Y ,利用观测值),...,2,1(),(n i x y i i =
(1)求β0,β1的最小二乘估计及)(2εσVar =的估计,其中x i 不完全相同。
(2)当回归模型为εβ+=X Y 时,它的最小二乘估计β
ˆ是否为β的无偏估计? (3)求X 的一个新观测值x 0处因变量Y 预测值y 0的置信度区间。
(4)求置信区间长度最小的x 0取值? 解:
(1)参考书中例2-1
由Y X X X T T T p 11
10)()ˆ,...,ˆ,ˆ(ˆ--==ββββ可得 ∑
∑
∑
===--=n i i n
i n
i i
i i x x y x x
x y
1
2
1
120
)
(ˆβ,∑
∑==--=n
i i n
i i i x x y x n y x 1
2
11
)
(ˆβ
(2)
由回归模型)1(ε
β+=X Y
其中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n εεεε...21⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=n x x x X (2)
1,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n y y y Y (21)
0)(2)
(1
=--=∑
=n
i i i i x x y d dS ββ
β,即
∑
∑
===n
i i n
i i i x x y 1
21
β
设x i 不全为0,则最小二乘估计β
ˆ是∑
∑
=-==n
i i i n
i i x y x 1
1
1
2)(ˆβ
因为
02
)(1
22
2>=∑
=n
i i x d S d β
β故β
ˆ确实是)(βS 的最小值点。
由(1)X Y E β=)(
所以,它的最小二乘估计β
ˆ是β的无偏估计。
(3)参考书中的例2-2 对于给定置信水平α,由
)(]
)(1[ˆ01
00p n t x X X x MSE y y
T
T
-+-- 式,可得Y 在),...,,(1,00201-p x x x 处取值y 0的置信度为1-α的置信区间为
所以新观测值处取值y 0的置信度为1-α的置信区间为: 其中,∑
=---=
-=n
i i i x y n n SSE MSE 12
10)ˆˆ(2
1
)2/(ββ。
∑==n
i i
x
n
x 1
1。
(4)由上式可知,置信区间的长度在x 0=x 时达到最小,为
]1
1[)2(ˆ2/10n
MSE n t y
+-±-α。
