湖北省鄂州市吴都中学2015年春季九年级数学第二次月考试题 新人教版
湖北省鄂州市城区学校九年级下学期第二次月考数学考试卷(解析版)(初三)月考考试卷.doc

湖北省鄂州市城区学校九年级下学期第二次月考数学考试卷(解析版)(初三)月考考试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题评卷人得分(每空xx 分,共xx分)【题文】的倒数是()A. B. 8 C. ﹣8 D. ﹣1【答案】C【解析】试题解析:根据倒数的定义知:∴的倒数是-8.故选C.【题文】下列运算正确的是( )A. =-1B. (﹣a3b)2=a6b2C. a+a=a2D. a2•4a4=4a8【答案】B【解析】A. =-1,运算不正确,不符合题意;B. ,运算正确,符合题意;C. ,运算不正确,不符合题意;D. ,运算不正确,不符合题意;故选B.【题文】过度包装既浪费资源又污染环境,据测算,如果全国每年减少十分之一的包装纸用量,那么能减少3120000吨二氧化碳的排放量,把数据3120000用科学记数法表示为()A. 312×104B. 0.312×107C. 3.12×106D. 3.12×107【答案】C【解析】试题解析:3120000=3.12×106故选C.【题文】如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是()A. 从前面看到的形状图的面积为5B. 从左面看到的形状图的面积为3C.从上面看到的形状图的面积为3D. 三种视图的面积都是4【答案】B【解析】试题分析:主视图为4个正方形,左视图为3个正方形,俯视图为4个正方形.考点:三视图【题文】对于一组统计数据:2,3,6,9,3,7,下列说法错误的是( )A. 众数是3B. 中位数是4.5C. 方差是7.5D. 极差是7【答案】C【解析】A. ∵3出现了2次,最多,∴众数为3,故此选项正确;B. ∵排序后为:2,3,3,6,7,9,∴中位数为:(3+6)÷2=4.5;故此选项正确;C. ,;故此选项不正确;D. 极差是9−2=7,故此选项正确;故选C.【题文】如图,在△ABC中,∠B=44°,∠C=54°,AD平分∠BAC,l【题文】如图,已知菱形ABCD的边长为2cm,∠A=60°,点M从点A出发,以1cm/s的速度向点B运动,到B点停止,点N从点A同时出发,以2cm/s的速度经过点D向点C运动,到C点停止。
湖北省鄂州市吴都中学2015届九年级上学期期中考试数学试卷(无答案)

1.若(x+y)(1-x-y)+6=0,则x+y 的值是( ) A.2B.3C.-2或3D.2或-32.如果关于x 的一元二次方程k 2x 2-(2k+1)x+1=0有两个不相等的实数根,那么k 的取值范围是( ) A.k>- B.k>-且k ≠0 C.k<-D.k ≥-且k ≠03.如图,☉O 中,∠CBO=45°,∠CAO=15°,则∠AOB 的度数是( ) A.75° B.60° C.45°D.30°4.已知m,n,k 为非负实数,且m-k+1=2k+n=1,则代数式2k 2-8k+6的最小值为( ) A.-2B.0C.2D.2.55.如图,DC 是⊙O 直径,弦AB ⊥CD 于F ,连接BC ,DB ,则下列结论错误的是( ) .90ACB DEC ∠=∠=,45A ∠=,30D ∠=,斜边6AB =,7DC =,把三角板DCE 绕着点C 顺时针旋转15得到△11D CE (如图乙),此时AB 与1CD 交于点O ,则线段1AD 的长度为 A.5 B.7.如图,⊙O 的半径为2,点O 到直线l 的距离为3,点P 是直线DC AE B AD 1OE 1BC图甲甲图乙OCA Bl 上的一个动点,PQ 切⊙O 于点Q ,则PQ 的最小值为A BC .3D .58.当-2≤x ≤l 时。
二次函数()221y x m m =--++有最大值4,则实数m 的值为( ) (A) 74-(B)或或(D)2或74-9.如图,正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上, 点D (5, 3)在边AB 上,以C 为中心,把△CDB 旋转90°,则旋 转后点D 的对应点D '的坐标是A .(2,10)B .(-2,0)C .(2,10)或(-2,0)D .(10,2)或(-2,0)12.已知二次函数y=(x-2a)2+(a-1)(a 为常数),当a 取不同的值时,其图象构成一个“抛物线系”.如图分别是当a=-1,a=0,a=1,a=2时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是y= .13.如图,⊙O 是△ABC 的外接圆,∠BAC=60°,若⊙O 的半径OC 为2,则弦BC 的长为 .14.如图,在等边△ABC 中,AB =6,D 是BC 的中点,将△ABD 绕点A 旋转后得到△ACE ,那么线段DE 的长度为.15.如右图,一圆与平面直角坐标系中的x 轴切于点A(8,0),与y 轴交于点B(0,4),C(0,16),则该圆的直径为 .16. 如图,抛物线y =ax 2+bx +c (a >0)的对称轴是过点(1,0)且平行于y轴的直线,若点P (4,0)在该抛物线上,则2a ﹣b +21c 的值为 .二.解答题(17~20每题8分,21~22每题9分,23题10分,24题12分,共计72分)17.(8分)关于x 的一元二次方程(a-6)x 2-8x+9=0有实根. (1)求a 的最大整数值.(2)当a 取最大整数值时,①求出该方程的根;②求2x 2-的值.18.如图,在平面直角坐标系中,Rt △ABC 的三个顶点分别是A(-3,2),B(0,4),C(0,2).(1)将△ABC 以点C 为旋转中心旋转180°,画出旋转后对应的△A 1B 1C;平移△ABC,若点A 的对应点A 2的坐标为(0,-4),画出平移后对应的△A 2B 2C 2.(3分) (2)若将△A 1B 1C 绕某一点旋转可以得到△A 2B 2C 2;请直接写出旋转中心的坐标.(3分) (3)在x 轴上有一点P,使得PA+PB 的值最小,请直接写出点P 的坐标.(2分)19.(8分)已知:关于x 的一元二次方程错误!未找到引用源。
湖北省鄂州市吴都中学2015届九年级春季第二次月考数学试卷

2015年春九年级第二次月考数学试题考生注意:1.考试时间为120分钟,试卷满分120分.2.所有答案都要做在答题卡上指定的区域内,书写在区域外不给分.3.不准使用手机.不准使用计算器.一.选择题(每小题3分,共30分)1.四个实数﹣2,0,﹣,1中,最小的实数是()A.﹣2 B.0 C.﹣ D.12.下列计算正确的是()A. 6a3•6a4=6a7 B.(2+a)2=4+2a+ a2 C.(3a3)2=6a6 D.(π﹣3.14)0=13.如图,是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是下面四个立体图形中的()A.①② B.②③ C.②③④ D.①②④4.如图,已知直线AB∥CD,∠GEB的平分线EF交C D于点F,∠1=60°,则∠2等于()A.130° B.140° C.150° D.160°5.下面这几个车标中,是中心对称图形而不是轴对称图形的共有()A.1个 B.2个 C.3个 D.4个6. 下列说法①的算术平方根是9 ,②将8450亿元用科学记数法表示为8.45×1011元,③,④正八边形中心角是45°,⑤若一次函数的图象不经过第三象限,则,其中正确的有()A.0个 B.1个 C.2个 D.3个7.如图,在2×2的正方形网格中有9个格点,已经取定点A和点B,在余下的7个点中任取一点C,使△ABC为等腰直角三角形的概率是()A. B. C. D.8.如图,⊙O的弦AB垂直于直径CD,垂足为E,∠BDC=22.5°,OB=,AB的长为()A.8 B.8 C.4 D.49.已知函数的图象在第一象限的一支曲线上有一点A(a,c+1),在该函数图象的另外一支上有点B(b,c),则关于一元二次方程ax2+bx+c=0的两根x1,x2判断正确的是()A.0<x1+x2<1,x1•x2>0 B.x1+x2<0,x1•x2>0C.x1+x2>1,x1•x2>0 D.x1+x2与x1•x2的符号都不确定10.如图,在菱形ABCD中,AB=BD.点E、F分别在BC、CD上,且BE=CF.连接BF与DE相交于点G,连接AG与BD相交于点H.下列结论:①△B ED≌△CFB;②若DF=2CF,则DG=4GE;③S四边形ABGD=AG2.其中正确的结论()A.只有②③ B.只有①③ C.只有①② D.①②③二.填空题(每小题3分,共18分)11.计算.12.函数的自变量的取值范围是.13.已知为方程的两个实数根,且,则的值为.14.如图,已知点A是双曲线在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第二象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线上运动,则的值是.15.等腰△ABC中AB=AC,AC的垂直平分线DE与直线AB相交于点D,垂足为E,连接CD,已知AD=10cm,tan∠ADE=,则AC的长度是.16.在直角坐标系中直线与以O为圆心17为半径的圆相交于A、B两点,则弦AB的长度的最小值与最大值的和为.三.解答题(8分+8分+8分+8分+9分+10分+9分+12分=72分)17.(8分)先化简代数式,然后从-2、-1、0、1、2五个数中选取一个你喜欢的数作为的值,求代数式的值.18.(8分)为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:(1)求表中a的值;(2)请把频数分布直方图补充完整;(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?(4)第5组8名同学中,有4名男同学,现将这8名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小亮与小华两名男同学分在同一组的概率.19.如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB 上,连接EF、CF,求证(1)EF=CF;(2)∠DFE=3∠AEF.(8分)20.(8分)对x,y定义一种新运算F,规定:(其中、均为非零常数),这里等式右边是通常的四则运算,例如:.(1)已知F(1,﹣1)=﹣2,F(4,2)=1.①求,的值;②若关于的不等式组有解,求实数的取值范围;(2)若F(x,y)=F(y,x)对任意实数x,y都成立(这里F(x,y)和F(y,x)均有意义),则,应满足怎样的关系式?直接写出关系式,不用写推理过程。
人教版九年级上册第二次月考数学试卷含答案解析-精选
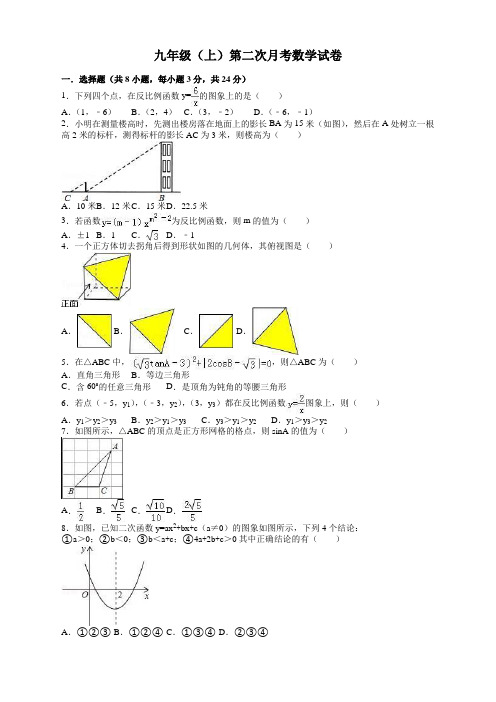
九年级(上)第二次月考数学试卷一.选择题(共8小题,每小题3分,共24分)1.下列四个点,在反比例函数y=的图象上的是()A.(1,﹣6)B.(2,4)C.(3,﹣2)D.(﹣6,﹣1)2.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为()A.10米B.12米C.15米D.22.5米3.若函数为反比例函数,则m的值为()A.±1 B.1 C.D.﹣14.一个正方体切去拐角后得到形状如图的几何体,其俯视图是()A. B.C.D.5.在△ABC中,,则△ABC为()A.直角三角形B.等边三角形C.含60°的任意三角形D.是顶角为钝角的等腰三角形6.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数图象上,则()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y1>y3>y27.如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.B.C.D.8.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有()A.①②③ B.①②④ C.①③④ D.②③④二、填空题(共7小题,每小题3分,共21分)9.若α为锐角,tanα•tan30°=1,则α=度.10.如图,一次函数y=mx与反比例函数y=的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM =3,则k的值是.11.在我们刚刚学过的九年级数学下册课本第11页,用“描点法”画某个二次函数图象时,列了如下表格:x … 3 4 5 6 7 8 …y …7.5 5 3.5 3 3.5 5 …根据表格上的信息回答问题:该二次函数在x=9时,y=.12.用配方法将二次函数y=﹣x2+x﹣1化成y=a(x﹣h)2+k的形式,则y=.13.如图,直线y=kx与双曲线y=(x>0)交于点A(1,a),则k=.14.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为.15.如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为米.三、解答题:(共75分16.计算(1)﹣2cos45°+(7﹣)0﹣()﹣1+tan30°(2)×sin45°﹣()﹣2+|﹣3|﹣.17.如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.(1)指定路灯的位置(用点P表示);(2)在图中画出表示大树高的线段;(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.18.已知y=y1﹣y2,y1与x成反比例,y2与(x﹣2)成正比例,并且当x=3时,y=5,当x=1时,y=﹣1;求y与x之间的函数关系式.19.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.(1)求反比例函数y=和一次函数y=kx+b的表达式;(2)连接OA,OC.求△AOC的面积.(3)当kx+b>时,请写出自变量x的取值范围.20.小刚学想测量灯杆AB的高度,结果他在D处时用测角仪测灯杆顶端A的仰角∠AEG=30°,然后向前走了8米来到C处,又测得A的仰角∠AFG=45°,又知测角仪高1.6米,求灯杆AB的高度.(结果保留一位小数;参考数据:≈1.73)21.已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,3).(1)求二次函数的解析式;(2)画出它的图象;(3)写出它的对称轴和顶点坐标.22.如图,已知二次函数y=x2+bx+c的图象经过点A(0,3)且对称轴是直线x=2.(1)求该函数的表达式;(2)在抛物线上找点,使△PBC的面积是△ABC的面积的2倍,求点P的坐标.23.如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)参考答案与试题解析一.选择题(共8小题,每小题3分,共24分)1.下列四个点,在反比例函数y=的图象上的是()A.(1,﹣6)B.(2,4)C.(3,﹣2)D.(﹣6,﹣1)【考点】反比例函数图象上点的坐标特征.【分析】根据反比例函数图象上点的坐标特征进行判断.【解答】解:∵1×(﹣6)=﹣6,2×4=8,3×(﹣2)=6,(﹣6)×(﹣1)=6,∴点(3,﹣2)在反比例函数y=的图象上.故选D.2.小明在测量楼高时,先测出楼房落在地面上的影长BA为15米(如图),然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为()A.10米B.12米C.15米D.22.5米【考点】相似三角形的应用.【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.【解答】解:∵=即=,∴楼高=10米.故选A.3.若函数为反比例函数,则m的值为()A.±1 B.1 C.D.﹣1【考点】反比例函数的定义.【分析】根据反比例函数的定义即可求出m的值.【解答】解:根据题意得:m2﹣2=﹣1,且m﹣1≠0解得:m=﹣1.故选D.4.一个正方体切去拐角后得到形状如图的几何体,其俯视图是()A. B.C.D.【考点】简单几何体的三视图.【分析】根据俯视图是从上面看到的图形判定则可.【解答】解:从上面看,是正方形右下角有阴影,故选C.5.在△ABC中,,则△ABC为()A.直角三角形B.等边三角形C.含60°的任意三角形D.是顶角为钝角的等腰三角形【考点】特殊角的三角函数值;非负数的性质:绝对值;非负数的性质:偶次方.【分析】首先结合绝对值以及偶次方的性质得出tanA﹣3=0,2cosB﹣=0,进而利用特殊角的三角函数值得出答案.【解答】解:∵(tanA﹣3)2+|2cosB﹣|=0,∴tanA﹣3=0,2cosB﹣=0,∴tanA=,cosB=,∠A=60°,∠B=30°,∴△ABC为直角三角形.故选:A.6.若点(﹣5,y1),(﹣3,y2),(3,y3)都在反比例函数图象上,则()A.y1>y2>y3B.y2>y1>y3C.y3>y1>y2D.y1>y3>y2【考点】反比例函数图象上点的坐标特征.【分析】根据反比例函数图象上点的坐标特征,分别计算出y2、y1、y3的值,然后比较大小即可.【解答】解:当x=﹣5时,y1=﹣;当x=﹣3时,y2=﹣;当x=3时,y3=,所以y2<y1<y3.故选C.7.如图所示,△ABC的顶点是正方形网格的格点,则sinA的值为()A.B.C.D.【考点】锐角三角函数的定义;勾股定理.【分析】利用网格构造直角三角形,根据锐角三角函数的定义解答.【解答】解:如图:在B点正上方找一点D,使BD=BC,连接CD交AB于O,根据网格的特点,CD⊥AB,在Rt△AOC中,CO==;AC==;则sinA===.故选:B.8.如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列4个结论:①a>0;②b<0;③b<a+c;④4a+2b+c>0其中正确结论的有()A.①②③ B.①②④ C.①③④ D.②③④【考点】二次函数图象与系数的关系.【分析】①首先根据抛物线开口向上,可得a>0,故①正确;②然后根据抛物线的对称轴为直线x=﹣>0,可得b<0,故②正确;③根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=﹣1时,y>0,所以a﹣b+c>0,故③正确.④根据二次函数y=ax2+bx+c(a≠0)的图象,可得当x=2时,y<0,所以4a+2b+c<0,故③不正确;故选A.【解答】解:∵抛物线开口向上,∴a>0,故①正确;∵抛物线的对称轴为直线x=﹣>0,∴b<0,故②正确;∵当x=﹣1时,y>0,∴a﹣b+c>0,∴故③正确;∵x=2时,y<0,∴4a+2b+c<0,∴结论④错误;综上,可得正确的结论有:①②③.故选A.二、填空题(共7小题,每小题3分,共21分)9.若α为锐角,tanα•tan30°=1,则α=60度.【考点】特殊角的三角函数值.【分析】本题可根据tan30°=,得出tanα的值,再运用三角函数的特殊值解出α的值.【解答】解:∵tan30°=,tanα•tan30°=1,∴tanα=,又∵α为锐角,∴α=60°.故答案为:60.10.如图,一次函数y=mx与反比例函数y=的图象交于A、B两点,过点A作AM⊥x轴,垂足为M,连接BM,若S△ABM =3,则k的值是3.【考点】反比例函数系数k 的几何意义;反比例函数图象的对称性.【分析】由反比例函数图象的对称性和反比例函数系数k 的几何意义可得:△ABM 的面积为△AOM 面积的2倍,S △ABM =2S △AOM =|k |.【解答】解:由题意得:S △ABM =2S △AOM =3,S △AOM =|k |=,则k=3.故答案为:3.11.在我们刚刚学过的九年级数学下册课本第11页,用“描点法”画某个二次函数图象时,列了如下表格:x … 3 4 5 6 7 8 …y … 7.5 5 3.5 3 3.5 5 …根据表格上的信息回答问题:该二次函数在x=9时,y= 7.5 . 【考点】二次函数的图象. 【分析】根据二次函数的图象关于对称轴对称并观察表格知当x=3和当x=9时的函数值相等,据此可以求得当x=9时的函数值.【解答】解:∵二次函数的图象关于对称轴对称,且观察表格知低昂x=4和当x=8时的函数值相等,∴当x=3和当x=9时的函数值相等,∵当x=3时y=7.5,∴当x=9时y=7.5.故答案为7.5.12.用配方法将二次函数y=﹣x 2+x ﹣1化成y=a (x ﹣h )2+k 的形式,则y= ﹣(x ﹣1)2﹣ .【考点】二次函数的三种形式.【分析】利用配方法先提出二次项系数,再加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式.【解答】解:y=﹣x 2+x ﹣1,=﹣(x 2﹣2x +1)﹣1﹣,=﹣(x ﹣1)2﹣,即y=﹣(x ﹣1)2﹣,故答案是:﹣(x ﹣1)2﹣.13.如图,直线y=kx 与双曲线y=(x >0)交于点A (1,a ),则k= 2 .【考点】反比例函数与一次函数的交点问题.【分析】直接利用图象上点的坐标性质进而代入求出即可.【解答】解:∵直线y=kx 与双曲线y=(x >0)交于点A (1,a ),∴a=2,k=2,故答案为:2.14.如图,在矩形ABCD中,点E在AB边上,沿CE折叠矩形ABCD,使点B落在AD边上的点F处.若AB=4,BC=5,则tan∠AFE的值为.【考点】翻折变换(折叠问题).【分析】由四边形ABCD是矩形,可得:∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由折叠的性质可得:∠EFC=∠B=90°,CF=BC=5,由同角的余角相等,即可得∠DCF=∠AFE,然后在Rt△DCF中,即可求得答案.【解答】解:∵四边形ABCD是矩形,∴∠A=∠B=∠D=90°,CD=AB=4,AD=BC=5,由题意得:∠EFC=∠B=90°,CF=BC=5,∴∠AFE+∠DFC=90°,∠DFC+∠FCD=90°,∴∠DCF=∠AFE,∵在Rt△DCF中,CF=5,CD=4,∴DF=3,∴tan∠AFE=tan∠DCF==.故答案为:.15.如图,已知AB、CD分别表示两幢相距30米的大楼,小明在大楼底部点B处观察,当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,那么大楼AB的高度为20米.【考点】解直角三角形的应用-仰角俯角问题.【分析】根据仰角为30°,BD=30米,在Rt△BDE中,可求得ED的长度,根据题意恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,可得AB=2ED.【解答】解:在Rt△BDE中,∵∠EBD=30°,BD=30米,∴=tan30°,解得:ED=10(米),∵当仰角增大到30度时,恰好能通过大楼CD的玻璃幕墙看到大楼AB的顶部点A的像,∴AB=2DE=20(米).故答案是:20.三、解答题:(共75分16.计算(1)﹣2cos45°+(7﹣)0﹣()﹣1+tan30°(2)×sin45°﹣()﹣2+|﹣3|﹣.【考点】二次根式的混合运算;零指数幂;负整数指数幂;特殊角的三角函数值.【分析】(1)原式第一项化为最简二次根式,第二项利用特殊角的三角函数值计算,第三项利用零指数幂法则计算,第四项利用负指数幂法则计算,最后一项利用特殊角的三角函数值计算即可得到结果;(2)根据二次根式、特殊角的三角函数值、负整数指数幂、绝对值的意义运算,再根据实数的运算顺序即可得出答案.【解答】解:(1)﹣2cos45°+(7﹣)0﹣()﹣1+tan30°=2﹣2×+1﹣2+×=2﹣+1﹣2+1=;(2)×sin45°﹣()﹣2+|﹣3|﹣=2×﹣4+3﹣(﹣1)=2﹣4+3﹣+1=2﹣.17.如图,路灯下一墙墩(用线段AB表示)的影子是BC,小明(用线段DE表示)的影子是EF,在M处有一颗大树,它的影子是MN.(1)指定路灯的位置(用点P表示);(2)在图中画出表示大树高的线段;(3)若小明的眼睛近似地看成是点D,试画图分析小明能否看见大树.【考点】中心投影.【分析】根据中心投影的特点可知,连接物体和它影子的顶端所形成的直线必定经过点光源.所以分别把AB和DE的顶端和影子的顶端连接并延长可交于一点,即点光源的位置,再由点光源出发连接MN顶部N的直线与地面相交即可找到MN影子的顶端.线段GM是大树的高.若小明的眼睛近似地看成是点D,则看不到大树,GM处于视点的盲区.【解答】解:(1)点P是灯泡的位置;(2)线段MG是大树的高.(3)视点D看不到大树,GM处于视点的盲区.18.已知y=y1﹣y2,y1与x成反比例,y2与(x﹣2)成正比例,并且当x=3时,y=5,当x=1时,y=﹣1;求y与x之间的函数关系式.【考点】待定系数法求反比例函数解析式.【分析】根据题意设出反比例函数与正比例函数的解析式,代入y=y1﹣y2,再把当x=3时,y=5,当x=1时,y=﹣1代入关于y的关系式,求出未知数的值,即可求出y与x之间的函数关系式.【解答】解:因为y1与x成反比例,y2与(x﹣2)成正比例,故可设y1=,y2=k2(x﹣2),因为y=y1﹣y2,所以y=﹣k2(x﹣2),把当x=3时,y=5;x=1时,y=﹣1,代入得,解得,再代入y=﹣k2(x﹣2)得,y=+4x﹣8.19.如图,一次函数y=kx+b的图象与反比例函数y=的图象交于点A﹙﹣2,﹣5﹚,C﹙5,n﹚,交y轴于点B,交x轴于点D.(1)求反比例函数y=和一次函数y=kx+b的表达式;(2)连接OA,OC.求△AOC的面积.(3)当kx+b>时,请写出自变量x的取值范围.【考点】反比例函数与一次函数的交点问题.【分析】(1)把A的坐标代入y=求出m,即可得出反比例函数的表达式,把C的坐标代入y=求出C的坐标,把A、C的坐标代入y=kx+b得出方程组,求出k、b,即可求出一次函数的表达式;(2)把x=0代入y=x﹣3求出OB,分别求出△AOB和△BOC的面积,相加即可;(3)根据A、C的坐标和图象得出即可.【解答】解:(1)把A﹙﹣2,﹣5﹚代入y=得:m=10,即反比例函数的表达式为y=,把C﹙5,n﹚代入y=得:n=2,即C(5,2),把A、C的坐标代入y=kx+b得:,解得:k=1,b=﹣3,所以一次函数的表达式为y=x﹣3;(2)把x=0代入y=x﹣3得:y=﹣3,即OB=3,∵C(5,2),A﹙﹣2,﹣5﹚,∴△AOC的面积为×3×|﹣2|+×3×5=10.5;(3)由图象可知:当kx+b>时,自变量x的取值范围是﹣2<x<0或x>5.20.小刚学想测量灯杆AB的高度,结果他在D处时用测角仪测灯杆顶端A的仰角∠AEG=30°,然后向前走了8米来到C处,又测得A的仰角∠AFG=45°,又知测角仪高1.6米,求灯杆AB的高度.(结果保留一位小数;参考数据:≈1.73)【考点】解直角三角形的应用-仰角俯角问题.【分析】设AG的长为x米,根据正切的概念分别表示出GF、GE的长,计算即可得到AG,求出AB即可.【解答】解:设AG的长为x米,在Rt△AGE中,EG==x,在Rt△AGF中,GF=AG=x,由题意得,x﹣x=8,解得,x≈10.9,则AB=AG+GB≈12.5米,答:灯杆AB的高度约为12.5米.21.已知二次函数y=ax2+bx的图象经过点(2,0)、(﹣1,3).(1)求二次函数的解析式;(2)画出它的图象;(3)写出它的对称轴和顶点坐标.【考点】待定系数法求二次函数解析式;二次函数的图象.【分析】(1)利用待定系数法求二次函数解析式解答;(2)根据二次函数图象的画法,列表、描点、连线,画出图象即可;(3)把二次函数解析式化为顶点式解析式,然后写出对称轴与顶点坐标即可.【解答】解:(1)依题意,得:,解得:,所以,二次函数的解析式为:y=x2﹣2x;(2)y=x2﹣2x=x2﹣2x+1﹣1=(x﹣1)2﹣1,由对称性列表如下:x …﹣2 ﹣1 0 1 2 3 4 …y …8 3 0 ﹣1 0 3 8 …;(3)由y=(x﹣1)2﹣1可知对称轴为直线x=1,顶点坐标为(1,﹣1).22.如图,已知二次函数y=x2+bx+c的图象经过点A(0,3)且对称轴是直线x=2.(1)求该函数的表达式;(2)在抛物线上找点,使△PBC的面积是△ABC的面积的2倍,求点P的坐标.【考点】待定系数法求二次函数解析式.【分析】(1)将点A坐标代入可得c的值,根据对称轴可得b的值;(2)先根据解析式求得点B、C的坐标,继而可得△ABC的面积,设点P(a,a2﹣4a+3),从而表示出△PBC的面积,根据二次函数的最小值及面积间关系得出关于a的方程,即可求得a的值,可得答案.【解答】解:(1)将点A(0,3)代入y=x2+bx+c,得:c=3,∵抛物线对称轴为x=2,∴﹣=2,得:b=﹣4,∴该二次函数解析式为y=x2﹣4x+3;(2)令y=0,得:x2﹣4x+3=0,解得:x=1或x=3,∴点B(1,0)、C(3,0),=×2×3=3,则S△ABC设点P(a,a2﹣4a+3),=×2×|a2﹣4a+3|=|a2﹣4a+3|,则S△PBC∵y=x2﹣4x+3=(x﹣2)2﹣1,∴二次函数的最小值为﹣1,根据题意可得a2﹣4a+3=6,解得:a=2,∴点P的坐标为(2+,6)或(2﹣,6).23.如图所示,某数学活动小组选定测量小河对岸大树BC的高度,他们在斜坡上D处测得大树顶端B的仰角是30°,朝大树方向下坡走6米到达坡底A处,在A处测得大树顶端B的仰角是48°,若坡角∠FAE=30°,求大树的高度(结果保留整数,参考数据:sin48°≈0.74,cos48°≈0.67,tan48°≈1.11,≈1.73)【考点】解直角三角形的应用-仰角俯角问题;解直角三角形的应用-坡度坡角问题.【分析】根据矩形性质得出DG=CH,CG=DH,再利用锐角三角函数的性质求出问题即可.【解答】解:如图,过点D作DG⊥BC于G,DH⊥CE于H,则四边形DHCG为矩形.故DG=CH,CG=DH,在直角三角形AHD中,∵∠DAH=30°,AD=6,∴DH=3,AH=3,∴CG=3,设BC为x,在直角三角形ABC中,AC==,∴DG=3+,BG=x﹣3,在直角三角形BDG中,∵BG=DG•tan30°,∴x﹣3=(3+)解得:x≈13,∴大树的高度为:13米.。
湖北省鄂州市九年级数学第二次月考试卷(无答案) 新人教版

选择题1.下列等式一定成立的是( )A. B. C. × = D. 2.下列平面图案中,既是轴对称又是中心对称的是( )A .B .C .D .3.已知a <b,化简二次根式 的结果正确的是( )A. –aB. –aC. aD. a4.两实根之积为3的方程是( )A. x2+2x+3=0B. 2x2—2x+3=0C. —2x2+5x+6=0D. x2+5x+3=05.①等弧所对的弦相等 ②在同圆或等圆中,相等的两条弦所对的圆周角相等 ③平分弦的直径垂直于弦 ④ =x —1不是一元二次方程 ⑤正三角形至少绕中心旋转60º与自身重合,上面正确的个数为( )A. 1B. 2C. 3D. 4 6.已知点P(x, y)满足等式x2+y2—4x+6y+13=0, 则点P 关于原点对称的点的坐标为( ) A. (—2, 3) B. (—2. —3) C. (2, —3) D. (2, 3)7.已知x 是实数且满足(x2+3x )2+2(x2+3x )—3=0, 那么x2+3x 的值为( ) A. 3 B. —3或1 C. 1 D. —1或3 8.如图,把△ABC 绕点C 顺时针旋转某个角度θ后得到△A′B′C,若∠A=30°,∠1=70°,则旋转角θ可能等于下列哪一个角度( ) A .4A. 40B .50°C .70°D .100º9.已知⊙O 过正方形的顶点A, B 且与CD 相切,若正方形的边长为2,则该圆的半径为( )A. B. C. D. 1 10.十年后,某班同学聚会,见面时相互间均握了一次手,好事者统计,一共握了780次,则这次聚会的同学共有( )人. A. 38 B. 39 C. 40 D. 41(第8题图) (第9题图)填空题ba 3-ab -ab ab ab-x 2344525F E D C B A 169169+=+ba b a --22=4994⨯)(b a b a +=+211.y= 中x 的取值范围是____________________12.若x, y 为实数,且y= +3, 则 =______________.13.已知方程x2+bx+a=0有一根是—a ,(a ≠0), 则a —b=________. 14. 若关于x 一元二次方程(m —1)x2+ x+1=0有两个实数根,则m 的取值范围是___________.15.Rt △ABC 中,已知∠C=90º, ∠B=50º,点D 在边BC 上,且BD=2CD,把△ABC 绕点D 逆时针旋转m(0<m <180º﹚度后,如果点B 刚好落在初始Rt △ABC 的边上,那么m=______________. 16. 如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O ,另一边所在直线与半圆相交于点D 、E ,量出半径OC=5cm ,弦DE=8cm ,则直尺的宽度___________________17. 以正方形ABCD 的AB 边为直径作半圆O ,过点C 作直线切半圆于点F ,交AB 边于点E ,若△CDE 的周长为12,则直角梯形ABCE 周长为_______________.(第15题图) (第16题图) (第17题图)18. 观察下列各式: , , , …请你将猜想的规律用含自然数n(n ≥1)的代数式表示出来_________________.19. 设m, n 是方程x2—x —2001=0的两个实数根,则m2+2mn+n 的值为______________ 20.已知AB 是半径为20cm 的⊙O 中的一条弦,∠AOB=120º, 点C 在⊙O 上,且到 弦AB 所在直线的距离为10cm,则∠CAB 的度数是______________________.解答题 21. 化简与计算① —﹙ ﹚-1+3﹙3-1﹚-2008º-︱3-2︱②先化简再求值 ﹙21+x -1﹚÷-41222x x x ++, 其中x=3—2(第23题图)22 . 已知关于x 的方程x2+2(a —1)x+a2—7a —4=0的两根为x1, x2, 且满足x1x2—3x1—3x2—2=0, 求 2-1x x +xx -26-3+y x1+m 2143-1=32951=-542591=-431671=-2510-2+a a 1233OGEDC BA D C BA∣1—a∣+ 的值。
湖北省鄂州市吴都中学2015届九年级数学下学期期中试卷

2015年春季期中考试九年级数学试题(时间:120分钟 满分:120分)一、选择题(每题3分,共30分) 1.下列实数中,无理数是 ( )A .52- B .7 C .|-2| D .92.下列计算正确的是( ) A .ab b a 532=+ B .22212a a =- C .623a a a =• D .842)(a a = 3.如图所示的工件的主视图是( )A .B .C .D .4.如图,把一块等腰直角三角板的直角顶点放在直尺的一边上,如果∠1=40°,那么∠2=( )A .40°B .45° C.50°D.60°5.计算8216-313+的结果是( ) A .3-2B .3-52C .33-2D .2-36.一个边长为2cm 的等边三角形ABC 与⊙O 等高,如图放置,⊙O 与BC 相切于点C ,⊙O 与AC 相交于点E ,则CE 的长为( )cm .A .3B .32C .23D .37.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y (米)与乙出发的时间t (秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )A .①②③B .仅有①②C .仅有①③D .仅有②③4题图6题图 7题图8.已知下列命题:①若a b ≠,则22a b ≠;②若代数式有意义,则x 的取值X 围为x ≤1且x ≠0;③我市生态旅游初步形成规模,201426×108元;④已知d c b a ,,,都是正实数,且d c b a <,则dc db a b +<+;⑤在反比例函数x y 2=中,如果函数值y < 1时,那么自变量x > 2;⑥解分式方程3323-+=-x x x 的结果是原方程无解。
是真命题的个数是( ) A.5个 B.4个 C.3个 D.2个9.已知二次函数y =a(x ﹣h)2+k 在坐标平面上的图形通过(0,5)、(10,8)两点.若a <0, 0<h <10,则h 可能的取值是( )A .1B .3C .5D .710.如图,已知正方形ABCD ,顶点A (1,3)、B (1,1)、C (3,1).规定“把正方形ABCD 先沿x 轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2015次变换后,正方形ABCD 的对角线交点M 的坐标变为( ) A .(—2013,2) B .(一2013,一2) C . (—2014,—2) D . (—2014,2)二、填空题(每题3分,共18分)11.不等式组⎩⎨⎧->->+23,732x x 的解集是.12.分解因式:=-822m .13.已知4个数据:2-,22,a ,b ,其中b a ,是方程0122=--x x 的两个根,则这4个数据的中位数是.14.如图,在一次函数5y x =-+的图象上取点P ,作PA⊥x 轴,PB⊥y 轴;垂足为B ,且矩形OAPB 的面积为6,则这样的点P 个数共有个.10题图16题图14题图15题图15.如图,在边长为2的菱形ABCD 中,∠A =60°,M 是AD 边的中点,N 是AB 边上的一动点,将△AMN 沿MN 所在直线翻折得到△A ′MN ,连接A ′C ,则A ′C 长度的最小值是. 16.如图,在△ABC 中,AB=AC=10,点D 是边BC 上一动点(不与B ,C 重合),∠ADE=∠B=α,DE 交AC 于点E ,且cos α=54.下列结论: ①△ADE ∽△ACD ;②当BD=6时,△ABD 与△DCE 全等;③△DCE 为直角三角形时,BD 为8;④0<CE ≤6.4.其中正确的结论是.(把你认为正确结论的序号都填上)三、解答题:(17-20题各8分,21-22题各9分, 23题10分,24题12分,共计72分) 17.先化简,再求代数式2112()x x x x x x +++÷+的值,其中x =cos30︒+12. 18. 学校举办一项小制作评比活动.作品上交时限为3月1日至30日,组委会把同学们交来的作品按时间顺序每5天组成一组,对每一组的作品件数进行统计,绘制成如图所示的统计图.已知从左到右各矩形的高度比为2:3:4:6:4:1.第三组的件数是12.请你回答:(1)本次活动共有件作品参赛;各组作品件数的众数是件;(2)经评比,第四组和第六组分别有10件和2件作品获奖,那么你认为这两组中哪个组获奖率较高?为什么?(3)小制作评比结束后,组委会决定从4件最优秀的作品A 、B 、C 、D 中选出两件进行全校展示,请用树状图或列表法求出刚好展示作品B 、D 的概率. 19.如图所示是反比例函数)0(>=x xky 与正比例函数)0(≥=x x y 的图象,点)4,1(A 与点'B 均在反比例函数的图象上,点B 在直线x y =上,点'A 是点A 关于直线x y =的对称点,四边形B B AA ''是平行四边形.(1)试说明点'A 在反比例函数图象上;(2)设点B 的横坐标为m ,试用m 表示出点'B 的坐标并求出m 的值.20.为丰富居民业余生活,某居民区组建筹委会,该筹委会动员居民自愿集资建立一个书刊阅览室.经预算,一共需要筹资50000元,其中一部分用于购买书桌、书架等设施,另一部分用于购买书刊.19题图18题图(1)筹委会计划,购买书刊的资金不少于购买书桌、书架等设施资金的3倍,问最多用多少资金购买书桌、书架等设施?(2)经初步统计,有200户居民自愿参与集资,那么平均每户需集资150元.镇政府了解情况后,赠送了一批阅览室设施和书籍,这样,只需参与户共集资20000元.经筹委会进一步宣传,自愿参与的户数在200户的基础上增加了a %(其中a >0).则每户平均集资的资金在150元的基础上减少了a %,求a 的值.21.如图1,直角△ABC 中,∠ABC =90°,AB 是⊙O 的直径,⊙O 交AC 于点D ,过点D 的直线交BC 于点E ,交AB 的延长线于点P ,∠A =∠PDB .(1)求证:PD 是⊙O 的切线;(2)若BD =BP=23,求图中曲边三角形(阴影部分)的周长;(3)如图2,点M是AB 的中点,连接DM ,交AB 于点N ,若tan ∠A =21,求MNDN 的值. 22.市政府对城市建设进行了整改,如图,已知斜坡AB 长90米,坡角(即∠BAC )为45°,BC ⊥AC ,现计划在斜坡中点D 处挖去部分斜坡,修建一个平行于水平线CA 的休闲平台DE 和一条新的斜坡BE (后两个小题结果都保留根号).(1)若修建的斜坡BE 的坡比为:1,求休闲平台DE 的长是多少米?(2)一座建筑物GH 距离A 点33米远(即AG =33米),小亮在D 点测得建筑物顶部H 的仰角(即∠HDM )为30°.点B 、C 、A 、G ,H 在同一个平面内,点C 、A 、G 在同一条直线上,且HG ⊥CG ,问建筑物GH 高为多少米?23.猜想与证明:如图1摆放矩形纸片ABCD 与矩形纸片ECGF ,使B 、C 、G 三点在一条直线上,CE 在边CD 上,连接AF ,若M 为AF 的中点,连接DM 、ME ,试猜想DM 与ME 的数量关系,并证明你的结论.拓展与延伸:(1)若将”猜想与证明“中的纸片换成正方形纸片ABCD 与正方形纸片ECGF ,其他条件不变,则DM 和ME 的关系为.(2)如图2摆放正方形纸片ABCD 与正方形纸片ECGF ,使点F 在边CD 上,点M 仍为AF 的中点,试证明(1)中的结论仍然成立.24.如图,已知抛物线y =(x +2)(x ﹣4)(k 为常数,且k >0)与x 轴从左至右依次交于A ,B 两点,与x 轴交于点C ,经过点B 的直线y =﹣x +b 与抛物线的另一交点为D .(1)若点D 的横坐标为﹣5,求抛物线的函数表达式;(2)若在第一象限内的抛物线上有点P ,23题图 图1图2使得以A ,B ,P 为顶点的三角形与△ABC 相似,求k 的值;(3)在(1)的条件下,设F 为线段BD 上一点(不含端点),连接AF ,一动点M 从点A 出发,沿线段AF 以每秒1个单位的速度运动到F ,再沿线段FD 以每秒2个单位的速度运动到D 后停止,当点F 的坐标是多少时,点M 在整个运动过程中用时最少?九年级数学参考答案一、选择题1.B2.D 3.B 4.C 5.A 6.C 7.A 8.D 9.D 10.B 二、填空题11.2<x <5 12.2(m+2)(m-2) 13. 1 14.2 15.﹣1 16.①②④三、解答题17.解:原式=2(1)12x x x x x x ++⋅=++∵x=131cos30222︒+=+∴原式=31331222+++= 18.解:(1)由题意可得出,本次活动参赛共有:12÷=12÷=60(件),各组作品件数的众数是12;故答案为:60,12;(2)∵第四组有作品:60×=18(件),第六组有作品:60×=3(件),∴第四组的获奖率为:=,第六组的获奖率为:;∵<,∴第六组的获奖率较高; (3)画树状图如下:,由树状图可知,所有等可能的结果为12种,其中刚好是(B ,D )的有2种, 所以刚好展示作品B 、D 的概率为:P ==. 19.解:(1) )4,1(A 在xky =上,441=⨯=∴k ,点'A 是点A 关于直线x y =的对称点,∴点'A 为)1,4(,当4=x 时,代入xy 4=中,1=y ,∴点)1,4('A 在反比例函数图象上; (2) 点B 在直线x y =上,又点B 的横坐标为m ,∴ 点B 的坐标为 ),(m m , 四边形B B AA ''是平行四边形, ∴'AA 与'BB 平行且相等,∴'B 可由),(m m B 沿'AA 方向平移而得,由点的坐标的平移规律,可知点'B 的坐标为)3,3(-+m m ,点'B 在反比例函数的图象上,∴4)3()3(=-⨯+m m ,解得13±=m ,0>m ,13=∴m .20.解:(1)设用于购买书桌、书架等设施的费用为x 元,则购买书籍费用(50000﹣x )元, 根据题意得:50000﹣x ≥3x , 解得:x ≤12500.答:最多用12500元购买书桌、书架等设施; (2)根据题意得:200(1+a %)×150(1﹣a %)=20000整理得:a 2+10a ﹣3000=0, 解得:a =50或a =﹣60(舍去), 所以a 的值是50. 21解:(1)连结OD∵AB 是⊙O 的直径 ∴∠ADB =90° OA =OB ∠A +∠ABD =90°又∵OA =OB =OD ∴∠ADO =∠A ∴∠BDO =∠ABD 又∵∠A =∠PDB ∴∠PDB +∠BD0=90°即∠PDO =90°且D 在圆上∴PD 是⊙O 的切线;(2)由已知和(1)可得,△ABD ≌△POD ,易得△BOD 为等边三角形,∴∠ADB =∠ACB =60° OA =OB =OD =BD第24题图1F 第24题图2N EDCPO BA∴6023180BD l π⋅⋅==233π又在Rt △BDC 中,∠ACB =60°,BD =23 ∴DC =2 BC =4∴曲边三角形(阴影部分)的周长为:2363π+ (3)连结OM ,过D 作DF ⊥AB 于F∵点M 是AB 的中点, ∴OM ⊥AB 设BD =x ,则AD =2x ,AB =5x =2OM ,DF =255x 由△OMN ∽△FDN 得2545552xDN DF MN OM x === 22.解:(1)∵FM ∥CG , ∴∠BDF =∠BAC =45°, ∵斜坡AB 长90米,D 是AB 的中点,∴BD =45米,∴DF =BD •cos ∠BDF =45×=45(米),BF =DF =45米,∵斜坡BE 的坡比为:1,∴=,解得:EF =15(米),∴DE =DF ﹣EF =45﹣15(米);答:休闲平台DE 的长是(45﹣15)米;(2)设GH =x 米,则MH =GH ﹣GM =x ﹣45(米),DM =AG +AP =33+45=78(米), 在Rt △DMH 中,tan 30°=,即7845-x =,解得:x =45+26,答:建筑物GH的高为(45+26)米.23.证明:如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=EM,∴DM=HM=ME,∴DM=ME.(1)如图1,延长EM交AD于点H,∵四边形ABCD和CEFG是矩形,∴AD∥EF,∴∠EFM=∠HAM,又∵∠FME=∠AMH,FM=AM,在△FME和△AMH中,∴△FME≌△AMH(ASA)∴HM=EM,在RT△HDE中,HM=EM,∴DM=HM=ME,∴DM=ME,故答案为:DM=ME.(2)如图2,连接AE,∵四边形ABCD和ECGF是正方形,∴∠FCE=45°,∠FCA=45°,∴AE和EC在同一条直线上,在RT△ADF中,AM=MF,∴DM=AM=MF,在RT△AEF中,AM=MF ,∴AM=MF=ME,∴DM=ME .24.解:(1)抛物线y=(x +2)(x ﹣4),令y=0,解得x=﹣2或x=4,∴A(﹣2,0),B(4,0).∵直线y=﹣x+b经过点B(4,0),∴﹣×4+b=0,解得b=,∴直线BD解析式为:y=﹣x+.当x=﹣5时,y=3,∴D(﹣5,3).∵点D(﹣5,3)在抛物线y=(x+2)(x﹣4)上,∴(﹣5+2)(﹣5﹣4)=3,∴k=.(2)由抛物线解析式,令x=0,得y=k,∴C(0,﹣k),OC=k.因为点P在第一象限内的抛物线上,所以∠ABP为钝角.因此若两个三角形相似,只可能是△ABC∽△APB或△ABC∽△ABP.①若△ABC∽△APB,则有∠BAC=∠PAB,如答图2﹣1所示.设P(x,y),过点P作PN⊥x轴于点N,则ON=x,PN=y.tan∠BAC=tan∠PAB,即:,∴y=x+k.∴D(x,x+k),代入抛物线解析式y=(x+2)(x﹣4),得(x+2)(x﹣4)=x+k,整理得:x2﹣6x﹣16=0,解得:x=8或x=2(与点A重合,舍去),∴P(8,5k).∵△ABC∽△APB,∴,即,解得:k=.②若△ABC∽△ABP,则有∠ABC=∠PAB,如答图2﹣2所示.与①同理,可求得:k=.综上所述,k=或k=.(3)由(1)知:D(﹣5,3),如答图2﹣2,过点D作DN⊥x轴于点N,则DN=3,ON=5,BN=4+5=9,∴tan∠DBA===,∴∠DBA=30°.过点D作DK∥x轴,则∠KDF=∠DBA=30°.过点F作FG⊥DK于点G,则FG=DF.word由题意,动点M运动的路径为折线AF+DF,运动时间:t=AF+DF,∴t=AF+FG,即运动时间等于折线AF+FG的长度.由垂线段最短可知,折线AF+FG的长度的最小值为DK与x轴之间的垂线段.过点A作AH⊥DK于点H,则t最小=AH,AH与直线BD的交点,即为所求之F 点.∵A点横坐标为﹣2,直线BD解析式为:y=﹣x +,∴y=﹣×(﹣2)+=2,∴F(﹣2,2).综上所述,当点F坐标为(﹣2,2)时,点M在整个运动过程中用时最少.11 / 11。
2014-2015年鄂州一中九年级下第二次月考数学试卷及答案解析

2014-2015学年湖北省鄂州一中九年级(下)第二次月考数学试卷一、选择题(每题3分,共30分)2.(3分)(2014春•鄂城区校级月考)如果a 3xb y与﹣a 2y b x+1是同类项,则x+y 的值为( )3.(3分)(2013•吉林)用6个完全相同的小正方体组合成如图所示的立方体图形,它的主视图为( ).4.(3分)(2013•临沂)如图,已知AB ∥CD ,∠2=135°,则∠1的度数是( )5.(3分)(2010•眉山)如图,已知双曲线y=(k <0)经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(﹣6,4),则△AOC 的面积为( )6.(3分)(2014春•鄂城区校级月考)如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为()7.(3分)(2013•自贡)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=,则△EFC的周长为()8.(3分)(2014春•鄂城区校级月考)设x1、x2是一元二次方程x2+4x﹣3=0的两个根,2x1 29.(3分)(2013•十堰)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是()10.(3分)(2014春•鄂城区校级月考)如图,圆柱形容器中,高为1.2米,底面周长为1米,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为()米.二、填空题(3’×6=18’)11.(3分)(2014春•鄂城区校级月考)计算+(﹣1)+()0=.12.(3分)(2014春•鄂城区校级月考)小李和小王准备到古隆中、水镜庄、黄家湾三个景点去游玩,如果他们各自在这三个景点中任选一个作为游玩的第一站(每个景点被选为第一站的可能性相同),那么他们都选古隆中为第一站的概率是.13.(3分)(2015•江都市模拟)若关于x的一元一次不等式组无解,则a 的取值范围是.14.(3分)(2009•武汉)如图,直线y=kx+b经过A(2,1),B(﹣1,﹣2)两点,则不等式x>kx+b>﹣2的解集为.15.(3分)(2015•黄冈中学自主招生)在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是.16.(3分)(2012•东营)在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(),那么点A n的纵坐标是.三、解答题(17-20每题8分,21-22每题9分,23题10分,24题12分)17.(8分)(2014春•鄂城区校级月考)先化简,再求值(1)÷(﹣a),其中a=1+,b=1﹣(2)÷+1.在1,0,2三个数中选一个合适的代入求值.18.(8分)(2013•泰安)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB•AD;(2)求证:CE∥AD;(3)若AD=4,AB=6,求的值.19.(8分)(2012•宜宾)为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.请你根据统计图解答下列问题:(1)在这次调查中一共抽查了名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为,喜欢“戏曲”活动项目的人数是人;(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.20.(8分)(2011•南充)关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2.(1)求k的取值范围;(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.21.(9分)(2013•自贡)在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.22.(9分)(2013•扬州)如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.(1)求证:AB=AC;(2)若AD=4,cos∠ABF=,求DE的长.23.(10分)(2009•武汉)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?24.(12分)(2013•襄阳)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.(1)求抛物线与x轴的另一个交点B的坐标;(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E 向上运动.设点P运动的时间为t秒.①当t为秒时,△PAD的周长最小?当t为秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.2014-2015学年湖北省鄂州一中九年级(下)第二次月考数学试卷参考答案与试题解析一、选择题(每题3分,共30分)2.(3分)(2014春•鄂城区校级月考)如果a3x b y与﹣a2y b x+1是同类项,则x+y的值为()解:根据题意得:3.(3分)(2013•吉林)用6个完全相同的小正方体组合成如图所示的立方体图形,它的主视图为().4.(3分)(2013•临沂)如图,已知AB ∥CD ,∠2=135°,则∠1的度数是( )解:5.(3分)(2010•眉山)如图,已知双曲线y=(k <0)经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB 相交于点C .若点A 的坐标为(﹣6,4),则△AOC 的面积为( )|k|经过点×6.(3分)(2014春•鄂城区校级月考)如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画AC,连AF、CF,则图中阴影部分面积为()=+)﹣7.(3分)(2013•自贡)如图,在平行四边形ABCD中,AB=6,AD=9,∠BAD的平分线交BC于E,交DC的延长线于F,BG⊥AE于G,BG=,则△EFC的周长为(),=BG=4AG=8.(3分)(2014春•鄂城区校级月考)设x1、x2是一元二次方程x2+4x﹣3=0的两个根,2x1(x22+5x2﹣3)+a=2,则a的值为()﹣9.(3分)(2013•十堰)如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是()﹣10.(3分)(2014春•鄂城区校级月考)如图,圆柱形容器中,高为1.2米,底面周长为1米,在容器内壁离容器底部0.3m处的点B处有一蚊子.此时,一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为()米.=二、填空题(3’×6=18’)11.(3分)(2014春•鄂城区校级月考)计算+(﹣1)+()0=3.=2=312.(3分)(2014春•鄂城区校级月考)小李和小王准备到古隆中、水镜庄、黄家湾三个景点去游玩,如果他们各自在这三个景点中任选一个作为游玩的第一站(每个景点被选为第一站的可能性相同),那么他们都选古隆中为第一站的概率是.∴他们都选古隆中为第一站的概率是:故答案为:13.(3分)(2015•江都市模拟)若关于x的一元一次不等式组无解,则a 的取值范围是≥1.解:14.(3分)(2009•武汉)如图,直线y=kx+b经过A(2,1),B(﹣1,﹣2)两点,则不等式x>kx+b>﹣2的解集为﹣1<x<2.的值,即可得到不等式解:由题意可得方程组解得不等式x x可化为15.(3分)(2015•黄冈中学自主招生)在平面直角坐标系中,⊙P的圆心是(2,a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为,则a的值是.AE=PD=a=PD+DC=2+16.(3分)(2012•东营)在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上.△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2(),那么点A n的纵坐标是()n﹣1.(,∴解得x+y=时,x+,==(,×MNO==)(的纵坐标是((三、解答题(17-20每题8分,21-22每题9分,23题10分,24题12分)17.(8分)(2014春•鄂城区校级月考)先化简,再求值(1)÷(﹣a),其中a=1+,b=1﹣(2)÷+1.在1,0,2三个数中选一个合适的代入求值.(﹣=÷﹣•﹣a=1+﹣﹣===﹣18.(8分)(2013•泰安)如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,(1)求证:AC2=AB•AD;(2)求证:CE∥AD;(3)若AD=4,AB=6,求的值.CE=,然后由相似三角形的对应边成比例,求得CE=CE=CE=∴∴19.(8分)(2012•宜宾)为了解学生的艺术特长发展情况,某校音乐组决定围绕“在舞蹈、乐器、声乐、戏曲、其它活动项目中,你最喜欢哪一项活动(每人只限一项)”的问题,在全校范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如下两幅不完整的统计图.请你根据统计图解答下列问题:(1)在这次调查中一共抽查了50名学生,其中,喜欢“舞蹈”活动项目的人数占抽查总人数的百分比为24%,喜欢“戏曲”活动项目的人数是4人;(2)若在“舞蹈、乐器、声乐、戏曲”活动项目任选两项设立课外兴趣小组,请用列表或画树状图的方法求恰好选中“舞蹈、声乐”这两项活动的概率.活动项目的人数占抽查总人数的百分比为:两项活动的概率是两项活动的概率是.总体数目20.(8分)(2011•南充)关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2.(1)求k的取值范围;(2)如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.21.(9分)(2013•自贡)在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距km的C处.(1)求该轮船航行的速度(保留精确结果);(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.AC=BC===16∴60=12AC=8=8=20×所以=22.(9分)(2013•扬州)如图,△ABC内接于⊙O,弦AD⊥AB交BC于点E,过点B作⊙O的切线交DA的延长线于点F,且∠ABF=∠ABC.(1)求证:AB=AC;(2)若AD=4,cos∠ABF=,求DE的长.ADB=,∴BD===ABE=BE==AE=﹣=23.(10分)(2009•武汉)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.(1)求y与x的函数关系式并直接写出自变量x的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?24.(12分)(2013•襄阳)如图,已知抛物线y=ax2+bx+c与x轴的一个交点A的坐标为(﹣1,0),对称轴为直线x=﹣2.(1)求抛物线与x轴的另一个交点B的坐标;(2)点D是抛物线与y轴的交点,点C是抛物线上的另一点.已知以AB为一底边的梯形ABCD的面积为9.求此抛物线的解析式,并指出顶点E的坐标;(3)点P是(2)中抛物线对称轴上一动点,且以1个单位/秒的速度从此抛物线的顶点E 向上运动.设点P运动的时间为t秒.①当t为2秒时,△PAD的周长最小?当t为4或4﹣或4+秒时,△PAD是以AD为腰的等腰三角形?(结果保留根号)②点P在运动过程中,是否存在一点P,使△PAD是以AD为斜边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.=得解得﹣4+﹣∴=∴=。
湖北省鄂州市吴都中学2015届九年级数学上学期10月月考试卷新人教版

湖北省鄂州市吴都中学2015届九年级数学上学期10月月考试卷1.下列是一元二次方程有( ) 个.①4x 2=0;②ax 2+bx +c =0;③3(x-1)2=3x 2+2x10=.A 、1B 、2C 、3D 、42.方程(a-b )x 2+(b-c )x+c-a=0的一个解必是( )A .x=-1B .x=1C .x=a-bD .x=c-a3.如果关于x 的一元二次方程kx 2-x +1=0有两个不相等的实数根,那么k 的取值范围是( ) A .-≤k <1且k ≠0 B .k <1且k ≠0 C .-≤k <1 D .k <14.二次函数2()y a x k k =++,当k 取不同的实数值时,图像顶点所在的直线是( )A 、 y x =B 、 x 轴C 、 y x =-D 、 y 轴 5.已知实数a ,b 分别满足,且a ≠b ,则的值是【 】A .7B .-7C .11D .-116.把抛物线y =x 2+bx +c 的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式为y =x 2-3x +5,则 ( ).A .b =3,c =7B .b =6,c =3C .b =-9,c =-5D .b =-9,c =21 7. 如图,在宽为20m ,长为32m 的矩形地面上修筑同样宽的道路(图中阴影部分),余下的部分种上草坪.要使草坪的面积为2540m ,求道路的宽. 如果设小路宽为xm ,根据题意,所列方程正确的是( )A .(20-x )(32-x )= 540B .(20-x )(32-x )=100C .(20+x )(32-x )=540D .(20+x )(32-x )= 5408.某厂大门是抛物线形水泥建筑,大门地面路宽为6m ,顶部距离地面的高度为4m ,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4米,要想通过此门,则设备及车辆总高度应小于( )A .2.66米B .2.60米C .3.36米D .2.58米9.若、(<),是关于x 的方程(x-a )(x-b)=1(a<b )的两个根,则实数、,a 、b 的大小关系为( ). A 、<< a <b B 、<a <<b C 、<a <b < D 、a <<b 32m 20m<10.已知二次函数2(0)y ax bx c a =++≠的图象如图所示,则下列结论:0abc >①;②方程20ax bx c ++=的两根之和大于0;③2a+b>0;④0a b c -+<,其中正确的个数( )A .1个B .2个C .3个D .4个 二、填空题(每小题3分,共18分)11. 等腰三角形的两边长分别是方程23740x x -+=的两个根,则此三角形的周长为 .12. 已知3a <-,点A (a,y 1 ), B( a+1,y 2)都在 二次函数223y x x =+图像上,那么y 1 、y 2的大小关系是 .13.若关于x 的一元二次方程220x x m --=的两根为a ,b ,且满足2213(1)(241)22a ab b -+--=,则m=________.三、解答题 (第17至20题每题8分,第21、22题每题9分,第23题10分,第24题12分,共72分):17.用适当的方法解下列方程:(1)2(5x -1)2=3(5x -1) (2) 50+50(1+x )+50(1+x )2=18218.春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如图对话中收费标准.某位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元.请问该单位这次共有多少员工去天水湾风景区旅游?19.关于x 的方程2(2)04k kx k x +++=有实数根. (1)求k 的取值范围.(2)若12,x x 是方程2(2)04k kx k x +++=的两个实数根,且满足2121122x k kx x x =-+,求k.20.已知抛物线y =x 2+(k -2)x +1的顶点为M ,与x 轴交于A (a ,0)、B (b ,0)两点,且k 2-(a 2+ka +1)·(b 2+kb +1)=0,⑴求k 的值;⑵问抛物线上是否存在点N ,使△ABN 的面积为?若存在,求点N 的坐标,若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年春九年级第二次月考数学试题考生注意:1.考试时间为120分钟 ,试卷满分120分.2.所有答案都要做在答题卡上指定的区域内,书写在区域外不给分.3.不准使用手机.不准使用计算器.一.选择题(每小题3分,共30分)1.四个实数﹣2,0,﹣,1中,最小的实数是( ) A .﹣2 B .0 C .﹣ D .1 2.下列计算正确的是( )A . 6a 3•6a 4=6a 7B .(2+a )2=4+2a+ a 2C .(3a 3)2=6a 6D .(π﹣3.14)0=1 3.如图,是由四个相同的小立方体组成的立体图形的主视图和左视图,那么原立体图形可能是下面四个立体图形中的( )A .①②B .②③C .②③④D .①②④4.如图,已知直线AB ∥CD ,∠GEB 的平分线EF 交C D 于点F ,∠1=60°,则∠2等于( ) A .130° B .140° C .150° D .160°5.下面这几个车标中,是中心对称图形而不是轴对称图形的共有( )A .1个B .2个C .3个D .4个6. 819 ,②将8450亿元用科学记数法表示为8.45×1011元 ,③tan303︒=④正八边形中心角是45°,⑤若一次函数y kx b =+的图象不经过第三象限,则0,0k b <> ,其中正确的有( )A .0个B .1个C .2个D .3个7.如图,在2×2的正方形网格中有9个格点,已经取定点A 和点B ,在余下的7个点中任取一点C ,使△ABC 为等腰直角三角形的概率是( ) A .25 B .37 C .12 D .478.如图,⊙O 的弦AB 垂直于直径CD ,垂足为E ,∠BDC =22.5°,OB=42AB 的长为( ) A .8 B .8 C .4 D .4 9.已知函数2y x=的图象在第一象限的一支曲线上有一点A (a ,c+1),在该函数图象的另外一支上有点B (b ,c ),则关于一元二次方程ax 2+bx+c=0的两根x 1,x 2判断正确的是( )第4题图第5题图第7题图第8题图A .0<x 1+x 2<1,x 1•x 2>0B .x 1+x 2<0,x 1•x 2>0C .x 1+x 2>1,x 1•x 2>0D .x 1+x 2与x 1•x 2的符号都不确定 10.如图,在菱形ABCD 中,AB=BD .点E 、F 分别在BC 、CD 上,且BE=CF .连接BF 与DE 相交于点G ,连接AG 与BD 相交于点H .下列结论:①△B ED≌△CFB ;②若DF=2CF ,则DG=4GE ;③S 四边形ABGD=AG 2.其中正确的结论( )A .只有②③B .只有①③C .只有①②D .①②③二.填空题(每小题3分,共18分) 112= .12.函数y 1x =-的自变量x 的取值范围是 . 13.已知21x x 和为方程220x x m -+=的两个实数根,且12329x x -=,则m 的值为 .14.如图,已知点A 是双曲线6y x=在第一象限的分支上的一个动点,连结AO 并延长交另一分支于点B ,以AB 为边作等边△ABC,点C 在第二象限.随着点A 的运动,点C 的位置也不断变化,但点C 始终在双曲线ky x=上运动,则k 的值是 . 15.等腰△ABC 中AB=AC ,AC 的垂直平分线DE 与直线AB 相交于点D,垂足为E ,连接CD ,已知AD=10cm ,tan ∠ADE=43,则AC 的长度是 . 16.在直角坐标系xoy 中直线129y kx k =--与以O 为圆心17为半径的圆相交于A 、B 两点,则弦AB 的长度的最小值与最大值的和为 .三.解答题(8分+8分+8分+8分+9分+10分+9分+12分=72分)17.(8分)先化简代数式222211111x x x x x x --⎛⎫÷--+ ⎪-+⎝⎭,然后从-2、-1、0、1、2五个数中选取一个你喜欢的数作为x 的值,求代数式的值.18.(8分)为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出请结合图表完成下列各题: (1)求表中a 的值; (2)请把频数分布直方图补充完整; (3)若测试成绩不低于40分为优秀,则 本次测试的优秀率是多少? (4)第5组8名同学中,有4名男同学, 第10题图第14题图现将这8名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小亮与小华两名男同学分在同一组的概率.19.如图,在平行四边形ABCD 中,AD=2AB ,F 是AD 的中点,作CE⊥AB,垂足E 在线段AB 上,连接EF 、CF ,求证 (1)EF=CF ;(2)∠DFE=3∠AEF.(8分)20.(8分)对x ,y 定义一种新运算F ,规定:(),4mx nyF x y x y +=+(其中m 、n 均为非零常数),这里等式右边是通常的四则运算,例如:()010,1401m n F n ⨯+⨯==⨯+. (1)已知F (1,﹣1)=﹣2,F (4,2)=1. ①求m ,n 的值;②若关于x 的不等式组()()2,585,34F x x F x x a -≤⎧⎪⎨->⎪⎩有解,求实数a 的取值范围;(2)若F (x ,y )=F (y ,x )对任意实数x ,y 都成立(这里F (x ,y )和F (y ,x )均有意义),则m ,n 应满足怎样的关系式?直接写出关系式,不用写推理过程。
21.(9分)如图,在东西方向的海岸线AB 上,有C 、D 两艘巡逻船,现均收到故障船F 的求救信号.已知C 、D 两船相距50海里,船F 在船C 的北偏东30°方向上,船F 在船D 的西北方向上,海岸线AB 上有一观测点E ,测得船F 正好在观测点E 的北偏西15°方向上.(1)分别求出F 与C ,F 与D 之间的距离FC 和FD (如果运算结果有根号,请保留根号).(2)已知距观测点E 处1003海里范围内有暗礁.若巡逻船C 沿直线CF 去营救船F ,在去营救的途中有无触暗礁危险?(参考数据:2 1.41≈,3 1.73≈,6 2.45≈) 22.(10分)某宾馆有40个房间供游客住宿,当每个房间的房价为每天160元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出40元的各种费用.根据规定,要提高房价,但每个房间每天的房价不得高于280元.设每个房间的房价调整为每天x 元(x 为10的正整数倍).(1)设一天订住的房间数为y ,直接写出y 与x 的函数关系式及自变量x 的取值范围; (2)设宾馆一天的利润为w 元,求w 与x 的函数关系式;(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元? 23.(9分)如图,PA 为⊙O 的切线,点A 为切点,直线PO 交⊙O 于点E ,F ,过点A 作PO 的垂线AB ,垂足为点C ,交⊙O 于点B ,延长BO 与⊙O 交于点D ,连接AD ,连接BE , (1)求证:直线PB 为⊙O 的切线,(2)试探究线段EF ,OP ,OC 之间的数量关系,并加以证明, (3)若BC=9,tan∠E=,求cos∠A DB 的值和线段PE 的长.24.(12分)如图,在平面直角坐标系xOy 中,四边形OACB 是平行四边形,A 、B 两点的坐标分别为(2,﹣4),(﹣4,0),抛物线Q 经过O 、A 、B 三点,D 是抛物线Q 的顶点. (1)求抛物线Q 的解析式及顶点D 的坐标;(2)将抛物线Q 和平行四边形OACB 一起先向左平移4个单位后,再向上平移m (0<m <3)个单位,得到抛物线Q ′和平行四边形O′A′C′B′,在向下平移的过程中,设平行四边形O′A′C′B′与平行四边形OACB 的重叠部分的面积为S ,试探究:当m 为何值时S 有最大值,并求出S 的最大值;(3)在(2)的条件下,当S 取最大值时,设此时抛物线Q ′的顶点为G ,若点M 是x 轴上的动点,点N 是抛物线Q ′上的动点,试判断是否存在这样的点M 和点N ,使得以D 、G 、M 、N 为顶点的四边形是平行四边形?若存在,请求出点所有的M 的坐标;若不存在,请说明理由.2015年春九年级第二次月考数学参考答案一、选择题1—5 ADDCB 6—10 CDBCB 二、填空题11、272- 12、x ≥0且x ≠1 13、-6 14、-18 15、16或36 16、50 三、解答题17、1-x x ,x 只能取-2,得3218、(1)a =12 (2)16、12画图 (3) 40% (4) 3119、略20、(1)①m =1,n =-7②化为⎪⎪⎩⎪⎪⎨⎧+>≤292132930a x x ∴a <3(2)m =4n21、(1)CF =1002 DF =1003(2)E 到CF 的距离506<1003,有触礁危险。
22、(1)略(2)EF 2=4·PO ·CO(3)设半径为r ,Rt △BCO 中,92+(18-r)2=r 2,53cos ,427,445===D OC r Rt △BPO 中,OB 2=CO ·PO ,得PO =475∴PE =475+445=3023、(1)y =56-101x (160≤x ≤280)(2)6760)300(101)10156)(40(2+--=--=x x x w (3)6720w 280=时=x ,即订住28个房间时最大利润为6720元。
24、(1)x 34-x 31-y 2= D (-2,34)(2)22)-m 21m)-(4m 21S 2+⋅(=-=(3)抛物线Q ’的解析式为()2110y 633x =-++,G 点(-6,310)当N 点在x 轴上方时,N 点(-8,2)或(-4,2) M 点(-4,0)或(0,0)当N 点在x 轴下方时,N 点(-10,-2)或(-2,-2) M 点(-14,0)或(-6,0) 故M 点坐标为(-4,0),(0,0), (-14,0)或(-6,0)。
