经典奥数时钟问题
六年级奥数第23讲:时钟问题

时钟问题时钟问题就是研究钟面上时针和分针关系的问题。
(1)我们知道钟面的一周分为60格,分针每走60格,时针正好走5格,所以时针的速度是分针速度的5÷60=121。
(2)分针每分钟转3600÷60=60,时针每分钟转3600÷12÷60=0.50。
时钟问题经常围绕着两针(指时针与分针,下同)重合、两针垂直、两针垂直、两针成多少度角提出问题。
因为时针与分针的速度不同,并且都沿顺时针方向转动,所以经常将时钟问题转化为追及问题来解。
例1、现在时间是2点,问:什么时间时针与分针第一次重合?做一做:时针与分针在5点几分重合?例2、在5点10分时,时针和分针的夹角是多少度?做一做:计算2点24分时,时针与分针所成的角度。
例3、问:在7点与8点之间,时针与分针在什么时刻相互垂直?做一做:问:在6点与7点之间,钟面上的时针和分针在何时成直角?例4、某人离开学校,看了看钟;外出了两个多小时以后,回到学校又看了一下钟,发现时针和分针恰好互换了位置。
问:这个人离开学校有多长时间?做一做:一部动画片放映时间不到1小时,结束时小明发现手表上时针、分针的位置正好与开始时的时针、分针交换了位置。
那么,这部动画片放映了多少分钟?例5、问:在3点与4点间,时针和分针在什么时刻位于一条直线上?做一做:问:4点几分,时针与分针成一直线?例6、问:在1点与2点之间的什么时刻,分针与时针的夹角被钟面上“12”这个刻度平分?做一做:问:3点过多少分,时针和分针离“3”距离相等,并且在“3”的两边?例7、王叔叔家有一块手表,他发现手表比家里的闹钟每小时快30秒,而闹钟比标准时间每小时慢30秒。
那么,王叔叔的手表一昼夜比标准时间差多少秒?做一做:某人有一块手表和一个闹钟,手表比闹钟每小时慢30秒,而闹钟比标准时间每小时快30秒。
问:这块手表一昼夜比标准时间差多少秒?1.小明上午8点要到学校上课,可是家里的闹钟早晨5点50分钟就停了。
五年级时钟问题奥数题及答案【三篇】

五年级时钟问题奥数题及答案【三篇】
【第二篇】
时钟的表盘上按标准的方式标着1,2,3,…,11,12这12个数,在其上任意做n个120°的扇形,每一个都恰好覆盖4个数,每两个覆盖的数不全相同.如果从这任做的n个扇形中总能恰好取出3个覆盖整个钟面的全部12个数,求n的最小值.
解答:(1)当时,有可能不能覆盖12个数,比如每块扇形错开1个数摆放,盖住的数分别是:(12,1,2,3);(1,2,3,4);(2,3,4,5);(3,4,5,6);(4,5,6,7);(5,6,7,8);(6,7,8,9);(7,8,9,10),都没盖住11,其中的3个扇形当然也不可能盖住全部12个数.
(2)每个扇形覆盖4个数的情况可能是:
(1,2,3,4)(5,6,7,8)(9,10,11,12)覆盖全部12个数
(2,3,4,5)(6,7,8,9)(10,11,12,1)覆盖全部12个数
(3,4,5,6)(7,8,9,10)(11,12,1,2)覆盖全部12个数
(4,5,6,7)(8,9,10,11)(12,1,2,3)覆盖全部12个数
当时,至少有3个扇形在上面4个组中的一组里,恰好覆盖整个钟面的全部12个数.
所以n的最小值是9.
【第三篇】。
五年级时钟问题奥数题及答案【三篇】

【导语】成功根本没有秘诀可⾔,如果有的话,就有两个:第⼀个就是坚持到底,永不⾔弃;第⼆个就是当你想放弃的时候,回过头来看看第⼀个秘诀,坚持到底,永不⾔弃,学习也是⼀样需要多做练习。
以下是⽆忧考为⼤家整理的《五年级时钟问题奥数题及答案【三篇】》供您查阅。
【第⼀篇】
现在是3点,什么时候时针与分针第⼀次重合?
【第⼆篇】
时钟的表盘上按标准的⽅式标着1,2,3,…,11,12这12个数,在其上任意做n个120°的扇形,每⼀个都恰好覆盖4个数,每两个覆盖的数不全相同.如果从这任做的n个扇形中总能恰好取出3个覆盖整个钟⾯的全部12个数,求n的最⼩值.
解答:(1)当时,有可能不能覆盖12个数,⽐如每块扇形错开1个数摆放,盖住的数分别是:(12,1,2,3);(1,2,3,4);(2,3,4,5);(3,4,5,6);(4,5,6,7);(5,6,7,8);(6,7,8,9);
(7,8,9,10),都没盖住11,其中的3个扇形当然也不可能盖住全部12个数.
(2)每个扇形覆盖4个数的情况可能是:
(1,2,3,4)(5,6,7,8)(9,10,11,12)覆盖全部12个数
(2,3,4,5)(6,7,8,9)(10,11,12,1)覆盖全部12个数
(3,4,5,6)(7,8,9,10)(11,12,1,2)覆盖全部12个数
(4,5,6,7)(8,9,10,11)(12,1,2,3)覆盖全部12个数
当时,⾄少有3个扇形在上⾯4个组中的⼀组⾥,恰好覆盖整个钟⾯的全部12个数.
所以n的最⼩值是9.
【第三篇】。
二年级奥数——时钟问题

时钟问题
1、小光去食堂吃饭,出发前他看见钟面上显示大约是12:15分,到了食堂以后却发现食堂关门了,小光很不解,同学都笑小光看错了时间,把时针和分针看反了,因为现在根本不是饭点,你认为现在的时间应该是大约()。
2、有一个钟,每逢整点和半点敲,1点敲一下,2点敲两下,以此类推,每逢半点敲1下,那么这个钟一天(24小时)一共敲了()下。
3、有一个闹钟,一昼夜(一天)快3分钟,小华要赶火车,明天早上8点必须准时报时,现在是下午4点,这个闹钟应该拨慢()分钟。
4、下图是几个时钟在镜子里反射的图像,实际的时间是多少
5、观察下列时钟所表示的时间,按规律在第五个钟面上画出正确的
时针和分针。
5、一辆汽车早上5:20出发,到7点整到达终点站,经过了()时()分。
6、一节课40分钟,然后下课10分钟休息,接着上第二节课,如果早上8点开始第一节课,那么第三节课下课是()时()分。
7、一只电子表,每分钟要慢1秒,现在是早上8点整,表面时间完全正确,那么当表上显示到12点时,标准的时间应该是()时()分。
8、小明参加学校一年一度的“野外绝地求生大逃杀”活动,活动结束后到家发现时间在中午12点整,他算了一下这次出门一共用了200个小时,那么他是()点出门的。
9、小东家的钟坏了,奶奶在下午2点时对钟,由于老花眼,把时针
和分针很颠倒了,小东放学回家一看才3点整,吓坏了,那么现在应该是()时()分。
(完整)小学六年级奥数时钟问题(含例题讲解分析和答案)

时钟问题知识点拨:时钟问题知识点说明时钟问题可以看做是一个特殊的圆形轨道上2人追及或相遇问题,不过这里的两个“人”分别是时钟的分针和时针。
我们通常把研究时钟上时针和分针的问题称为时钟问题,其中包括时钟的快慢,时钟的周期,时钟上时针与分针所成的角度等等。
时钟问题有别于其他行程问题是因为它的速度和总路程的度量方式不再是常规的米每秒或者千米每小时,而是2个指针“每分钟走多少角度”或者“每分钟走多少小格”。
对于正常的时钟,具体为:整个钟面为360度,上面有12个大格,每个大格为30度;60个小格,每个小格为6度。
分针速度:每分钟走1小格,每分钟走6度小格,每分钟走0.5度时针速度:每分钟走112注意:但是在许多时钟问题中,往往我们会遇到各种“怪钟”,或者是“坏了的钟”,它们的时针和分针每分钟走的度数会与常规的时钟不同,这就需要我们要学会对不同的问题进行独立的分析。
要把时钟问题当做行程问题来看,分针快,时针慢,所以分针与时针的问题,就是他们之间的追及问题。
另外,在解时钟的快慢问题中,要学会十字交叉法。
分。
例如:时钟问题需要记住标准的钟,时针与分针从一次重合到下一次重合,所需时间为56511例题精讲:模块一、时针与分针的追及与相遇问题【例 1】王叔叔有一只手表,他发现手表比家里的闹钟每小时快30 秒.而闹钟却比标准时间每小时慢30 秒,那么王叔叔的手表一昼夜比标准时间差多少秒?【解析】闹钟比标准的慢那么它一小时只走(3600-30)/3600个小时,手表又比闹钟快那么它一小时走(3600+30)/3600个小时,则标准时间走1小时手表则走(3600-30)/3600*(3600+30)/3600个小时,则手表每小时比标准时间慢1—【(3600-30)/3600*(3600+30)/3600】=1—14399/14400=1/14400个小时,也就是1/14400*3600=四分之一秒,所以一昼夜24小时比标准时间慢四分之一乘以24等于6秒【巩固】小强家有一个闹钟,每时比标准时间快3分。
小学奥数趣味学习《时钟问题》典型例题及解答

小学奥数趣味学习《时钟问题》典型例题及解答时钟问题就是研究钟面上时针与分针关系的问题,如两针重合、两针垂直、两针成一线、两针夹角为60度等,这类问题可转化为行程问题中的追及问题。
时钟的数量关系:分针的速度是时针的12倍,二者的速度差为5.5度/分。
通常按追及问题来对待,也可以按差倍问题来计算。
解题思路和方法:将两针重合,两针垂直,两针成一线,两针夹角60°等为“追及问题”后可以直接利用公式。
例题1:钟面上从时针指向8开始,再经过多少分钟,时针正好与分针第一次重合?(精确到1分)解:1、此类题型可以把钟面看成一个环形跑道,那么本题就相当于行程问题中的追及问题,即分针与时针之间的路程差是240°。
2、分针每分钟比时针多转6°-0.5°=5.5°,所以需要240÷5.5≈44(分钟)。
也就是从8时开始,再经过44分钟,时针正好与分针第一次重合。
例题2:从早晨6点到傍晚6点,钟面上时针和分针一共重合了多少次?解:我们可以把钟面看成一个环形跑道,这样分针和时针的转动就可以转化成追及问题。
从早晨6点到傍晚6点,一共经过了12小时,12个小时分针要跑12圈,时针只能跑1圈,分针比时针多跑12-1=11(圈)。
而分针每比时针多跑1圈,就会追上时针一次,也就是和时针重合1次,所以12小时内两针一共重合了11次。
例题3:一部记录中国军队时代变迁的纪录片时长有两个多小时,小明发现,纪录片播放结束时,手表上时针、分针的位置正好与开始时时针、分针的位置交换了一下,这部纪录片时长多少分钟?(精确到1分)解:1、解决本题的关键是认识到时针与分针合走的路程是1080°,进而转化成相遇问题来解决。
2、两个多小时,分针与时针位置正好交换,所以分针与时针所走的路程和正好是三圈,也就是分针和时针合走了360°×3=1080°,而分针和时针每分钟的合走6°+0.5°=6.5°,所以合走1080°需要1080÷6.5≈166(分钟),即这部纪录片时长166分钟。
小学奥数专题之时钟问题

小学奥数专题之时钟问题
小学奥数专题之时钟问题
1、某人有一块手表和一个闹钟,手表比闹钟每时慢30秒,而闹钟比标准时间每时快30秒.问:这块手表一昼夜比标准时间差多少秒?
2、一节课40分,从8点30分上课应当到几点几分下课?
3、王老师上午7:30到校上班,11:30下班,上午在校的时间是多少?
4、贝贝做家庭作业用了50分,正好在晚上8:00做完,贝贝是晚上几时几分开始做作业的?
5、做一个零件从上午7:40分开始做,上午9:20分完成,做这个零件用了多长时间?
6、小玲家的钟停了,之声广播2点时,奶奶跟之声对时,由于年老眼花,把时针与分针颠倒了,小玲放学回家时见钟才2点整,大吃一惊,,请你帮助想一想,现在应该是几点钟?
7、小王骑自行车去A地,上午8时出发,在途中因有事停留了15分钟,到中午12时才到达A地,小王骑自行车行了多少时间?
8、钟面上有12个数,你能画两条线将钟面分成三部分,使每部分的数相加的.和相等吗?
9、小奇从家到学校跑步去和回要8分钟,如果去时步行,回来时跑步一共需要10分,那么小奇来回都是步行要几分钟?
10、冬冬做作业,写语文作业用去规定时间的一半,写数学作业用去剩下时间的一半,最后5分钟读书,冬冬完成全部作业作去了多长时间?
11、一只蜗牛从20厘米深的沟底往上爬,每爬4厘米要2分钟,然后停1分,问蜗牛从沟底爬到沟沿上要用多长时间?
12.明明家的台钟,一点钟响铃一下,两点钟响铃两下,三点钟响铃三下,八点钟响铃八下,有一次明明听见台钟响铃一下,没多久又响响了一下,后来又响了一下,你知道最后一响是几点钟吗?。
奥数时钟问题
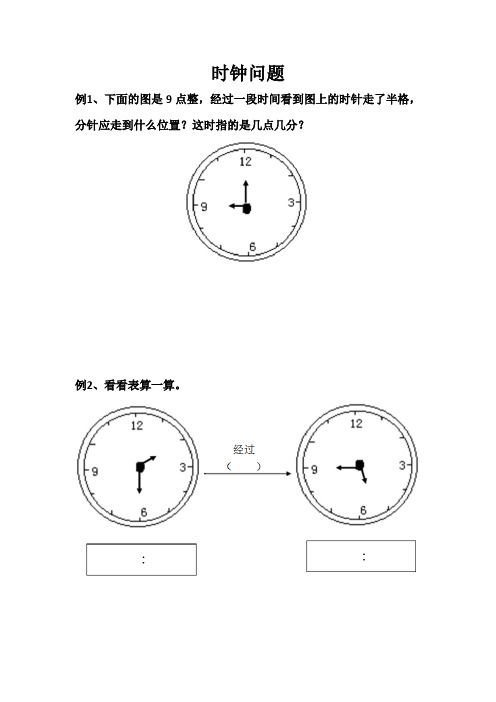
时钟问题
例1、下面的图是9点整,经过一段时间看到图上的时针走了半格,分针应走到什么位置?这时指的是几点几分?
例2、看看表算一算。
例3、王老师上午7:30到校上班,11:30下班,下午1:00上班,5:00下班,王老师上午在校是多少时间?下午在校是多少时间?一共在校小时?
例4、找出钟面上时刻的规律,填空。
举一反三
1、下图是3点整,经过一段时间看到图上的时针走了半格,分针应走到什么位置?这时指的是几点几分?
2、下图是1点整,经过一段时间看到图上的分针走了半圈(从12走到6),时针走过了多少?这时指的是几点几分?
3、下面是反射在镜子中的钟面时针和分针的位置,原来钟面的时刻是几点几分?
4、在括号里写出从上一个钟面到下一个钟面所经过的时间。
5、在下面括号里写出从上一个钟面到下一个钟面所经过的时间。
6、小明每天练毛笔字,今天他是6点40分开始的,7点结束的,他练写毛笔字用了多长时间?
7、做一个零件,从上午7点40分开始做,上午9点20分完成,做这个零件用了多少时间?
8、同学们看电影《一个也不能少》,看完这部电影需要1小时50分,如果9点10分开映,放映结束时应该是什么时间?
9、按规律填出下面空白钟面所应表示的时间。
10、按规律填出空白钟面所应表示的时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四、时钟问题解法与算法公式解题关键:时钟问题属于行程问题中的追及问题。
钟面上按“时”分为12大格,按“分”分为60小格。
每小时,时针走1大格合5小格,分针走12大格合60小格,时针的转速是分针的,两针速度差是分针的速度的,分针每小时可追及。
1、二点到三点钟之间,分针与时针什么时候重合?分析:两点钟的时候,分针指向12,时针指向2,分针在时针后5×2=10(小格)。
而分针每分钟可追及1-=(小格),要两针重合,分针必须追上10小格,这样所需要时间应为(10÷)分钟。
解:(5×2)÷(1-)=10÷=10(分)答:2点10分时,两针重合。
2、在4点钟至5点钟之间,分针和时针在什么时候在同一条直线上?分析:分针与时针成一条直线时,两针之间相差30小格。
在4点钟的时候,分针指向12,时针指向4,分针在时针后5×4=20(小格)。
因分针比时针速度快,要成直线,分针必须追上时针(20小格)并超过时针(30小格)后,才能成一条直线。
因此,需追及(20+30)小格。
解:(5×4+30)÷(1-)=50÷=54(分)答:在4点54分时,分针和时针在同一条直线上。
3、在一点到二点之间,分针什么时候与时针构成直角?分析:分针与时针成直角,相差15小格(或在前或在后),一点时分针在时针后5×1=5小格,在成直角,分针必须追及并超过时针,才能构成直角。
所以分针需追及(5×1+15)小格或追及(5×1+45)小格。
解:(5×1+15)÷(1-)=20÷=21(分)或(5×1+45)÷(1-)=50÷=54(分)答:在1点21分和1点54分时,两针都成直角。
4、星期天,小明在室内阳光下看书,看书之前,小明看了一眼挂钟,发现时针与分针正好处在一条直线上。
看完书之后,巧得很,时针与分针又恰好在同一条直线上。
看书期间,小明听到挂钟一共敲过三下。
(每整点,是几点敲几下;半点敲一下)请你算一算小明从几点开始看书?看到几点结束的?分析:连半点敲声在内,一共敲了三下,说明小明看书的时间是在中午12点以后。
12点以后时针与分针:第一次成一条直线时刻是:(0+30)÷(1-)=30÷=32(分)即12点32分。
第二次成一条直线时刻是:(5×1+30)÷(1-)=35÷=38(分)即1点38分。
第三次成一条直线的时刻是:(5×2+30)÷(1-)=40÷=43(分)即2点43分。
如果从12点32分开始,到1点38分,只敲2下,到2点43分,就共敲5下(不合题意)如果从1点38分开始到2点43分,共敲3下。
因此,小明应从1点38 分开始看书,到 2 点43 分时结束的。
5、一只挂钟,每小时慢 5 分钟,标准时间中午12 点时,把钟与标准时间对准。
现在是标准时间下午 5 点30 分,问,再经过多长时间,该挂钟才能走到 5 点30 分?分析:1、这钟每小时慢 5 分钟,也就是当标准钟走60 分时,这挂钟只能走60-5=55(分),即速度是标准钟速度的=。
2、因每小时慢 5 分,标准钟从中午12 点走到下午 5 点30 分时,此挂钟共慢了5×(17-12)=27(分),也就是此挂钟要差27 分才到5 点30 分。
3、此挂钟走到 5 点30 分,按标准时间还要走27 分,因它的速度是标准时钟速度的,实际走完这27 分所要时间应是27÷。
解:5×(17-12)=27 (分)27÷=30(分)答:再经过30 分钟,该挂钟才能走到 5 点30 分。
时钟是我们日常生活中不可缺少的计时工具。
生活中也时常会遇到与时钟相关的问题。
关于时钟的问题有:求某一时刻时针与分针的夹角,两针重合,两针垂直,两针成直线等类型。
要解答时钟问题就要了解、熟悉时针和分针的运动规律和特点。
一个钟表一圈有60 个小格,这里计算就以小格为单位。
1 分钟时间,分针走 1 个小格,时针指走了1/60*5=1/12 个小格,所以每分钟分针比时针多走11/12个小格,以此作为后续计算的基础,对于解决类似经过多长时间时针、分针垂直或成直线的问题非常方便、快捷。
例1:从5 时整开始,经过多长时间后,时针与分针第一次成了直线?5 时整时,分针指向正上方,时针指向右下方,此时两者之间间隔为25 个小格(表面上每个数字之间为 5 个小格),如果要成直线,则分针要超过时针30 个小格,所以在此时间段内,分针一共比时针多走了55 个小格。
由每分钟分针比时针都走11/12 个小格可知,此段时间为55/(11/12)=60 分钟,也就是经过60 分钟时针与分针第一次成了直线。
例2:从6 时整开始,经过多少分钟后,时针与分针第一次重合?6 时整时,分针指向正上方,时针指向正下方,两者之间间隔为30 个小格。
如果要第一次重合,也就是两者之间间隔变为0,那么分针要比时针多走30 个小格,此段时间为30/(11/12)=360/11分钟。
例3:在8 时多少分,时针与分针垂直?8 时整时,分针指向正上方,时针指向左下方,两者之间间隔为40 个小格。
如果要两者垂直,有两种情况,一个是第一次垂直,此时两者间隔为15 个小格(分针落后时针),也就是分针比时针多走了25 个小格,此段时间为25/(11/12)=300/11分钟;另一次是第二次垂直,此时两者间隔仍为15 个小格(但分针超过时针),也就是分针比时针多走了55 个小格,此段时间为55/(11/12)=60 分钟,时间变为9 时,超过了题意的8 时多少分要求,所以在8 时300/11 分时,分针与时针垂直。
由上面三个例题可以看出,求解此类问题(经过多少时间,分针与时间成多少夹角)时,采用上述方法是非常方便、简单、快捷的,解题过程形象易懂,结果正确率高,是一种非常好的方法。
解决此类问题的一个关键点就是抓住分针比时针多走了多少个小格,而不论两者分别走了多少个小格。
下面再通过几个例题来介绍这种方法的用法和要点。
例4:从9 点整开始,经过多少分,在几点钟,时针与分针第一次成直线?9 时整时,分针指向正上方,时针指向正右方,两者之间间隔为45 个小格。
如果要第一次成直线,也就是两者之间间隔变为30 个小格,那么分针要比时针多走15 个小格,此段时间为15/(11/12)=180/11分钟。
例5:一个指在九点钟的时钟,分针追上时针需要多少分钟?9 时整时,分针指向正上方,时针指向正右方,两者之间间隔为45 个小格。
如果要分针追上时针,也就是两者之间间隔变为0 个小格,那么分针要比时针多走45 个小格,此段时间为45/(11/12)=540/11分钟。
例6:时钟的分针和时针现在恰好重合,那么经过多少分钟可以成一条直线?时针和分针重合,也就是两者间隔为0 个小格,如果要成一条直线,也就是两者间隔变为30 个小格,那么分针要比时针多走30 个小格,此段时间为30/(11/12)=360/11分钟。
【针对性练习】1. 十点与11点之间,两针在什么时刻成直线(不包括重合情况)?( )A. 10 时21 分B. 10 时22 分C.10 时21D.10 时21 分2 现在是下午3 点,从现在起时针和分针什么时候第一次重合?3。
分针和时针每隔多少时间重合一次?一个钟面上分针和时针一昼夜重合几次?4。
钟面上 5 点零8 分时,时针与分针的夹角是多少度?5。
在4 点与5 点之间,时针与分针什么时候成直角?6.9 点过多少分时,时针和分针离“9”的距离相等,并且在“9”的两边?【参考答案详解】1. 答案A 满足. 分针:6 度/分时针0.5 度/分,十点时,两针夹角为60 度,设需要时间为x 分,则如图有60-0.5x=180-6x,x= 分,即10 时分两针成直线。
答案 A 满足。
2. 现在是下午 3 点,从现在起时针和分针什么时候第一次重合?解析:分针: 6 度/分时针0.5 度/分3 点整,时针在分针前面15 格,所以第一次重合时,分针应该比时针多走15 格,即90 度,用追及问题的处理方法解:90/(6-0.5)度/分=16 分钟,所以下午 3 点16 分钟,时针和分针第一次重合。
3. 分针和时针每隔多少时间重合一次?一个钟面上分针和时针一昼夜重合几次?解析:分针: 6 度/分时针0.5 度/分当两针第一次重合到第二次重合,分针比时针多转360 度。
所以两针再次重合需要的时间为:360/(6-0.5)=720/11 分,一昼夜有:24×60=1440 分,所以两针在一昼夜重合的次数:1440 分/(720/11)分/次=22 次4. 钟面上5 点零8 分时,时针与分针的夹角是多少度?解析:分针: 6 度/分时针0.5 度/分5 点零8 分,时针成角:5×30+8×0.5=154 度,分针成角:8×6=48 度,所以夹角是154-48=106度。
5 在4 点与5 点之间,时针与分针什么时候成直角?解析:整 4 点时,分针指向12,时针指向4。
此时,时针领先分针20 格。
时,分两针成直角,必须使时针领先分针15 格,或分针领先时针15 格。
因此,在相同时间内,分针将比时针多走(20-15)格或(20+15)格。
(20-15)/(1-1/12)=60/11,即4 点5 分,(20+15)/(1-1/12)=38分,即 4 点38 分。
6. 9 点过多少分时,时针和分针离“9”的距离相等,并且在“9”的两边?解析:设经过X 分,0.5×X=270-6×X ,解得X=540/13 分,所以答案是9 点过41 分。
行测数学运算:时钟问题作者:公务员考试网时间:2010-01-08 | 公务员考试论坛| 来源:中国公务员考试信息网行测数学运算:时钟问题基本知识点:1.设时钟一圈分成了12 格,则时针每小时转 1 格,分针每小时转12 格。
2.时针一昼夜(24 小时)转 2 圈,分针一昼夜转24 圈。
3.钟面上每两格之间为30°,时针与分针成某个角度一般都有对称的两种情况。
4.时针与分针一昼夜重合22 次,垂直44 次,成180°也是22 次。
【例1】清晨 5 点时,时钟的时针和分针的夹角是多少度?()A. 30 度B. 60 度C. 90 度D. 150 度[答案]D[解析]清晨 5 点时,时针和分针相差 5 格,则5×30°=150°。
【例2】中午12 点整时,钟面上时针与分针完全重合。
