第九讲(序贯博弈)
电网连锁故障预防的多阶段序贯博弈模型

图2 中的 模 型 中 ,在 某 一 阶段 的 博 弈过 程 中 ,博弈 方 B 选 择 行 动 时 ,应 考 虑 下一 阶 段 博弈 方 A的可 能 行 动 ,进 而 防止 博 弈 方 A 下 一 阶 段 的行 动 导致 系统 出现 博 弈 方 B 来 不 及 调 整 的 情 况 。 进 入 下 一 阶 段 博 弈 ,博 弈 方 A采 取 行 动后 ,博 弈方 B 继 续 调 整 ,如 此 反复 ,形 成 多 阶 段序 贯博 弈。 3 . 2目标 函数 连 锁 故障 预防 的 目标 是 以最 少的 负荷 损 失作 为控 制 代
1 引 言
近 年 来 ,国内 外 电力 系统 发生 过 多次 大 规 模连 锁 故障 导 致 的大 停 电 事 故“ 】 ,如 何 有效 地 防 止 电 力 系统 连锁 故障 是 避 免 大 停 电事 故 的 关 键 ,这 一 问 题 成 为 当 前 的 研 究 热 点 。现 有 的研 究方 法 尚未 很 好解 决连 锁 故 障预 防 问题 ,这 问题 也是 当前 的研 究难 点 。 博弈 理 论应 用 于 电 力系统 的研 究主要 集 中于 电力 市场 方 向 ,其 在社 会 学 、经 济学 、管理 学 、政 治学 、军 事 学等 领 域 】 ,将 博弈 理论 用于 电网连锁 故障 及大 停 电的预 防 尚
常 辉’ 刘树 伟’ 朱旭 凯 张 艳 徐得 超 徐树 文
1 中 国民航机 场建 设集 团公 司规 划设计总院 ,北京 朝 阳 1 O 0 1 0 1 2 中 国 电 力科 学研 究院 ,北 京 海 淀 1 0 0 0 5 : 5
常 辉
常辉 ( 1 9 8 2 -) , 女 .工 程 师 ,主 要
摘要 将博弈理 论应 用于 电网连锁 故障 的预 防 ,赋 予 电网扰 动 以理性 ,把 电网的扰 动 与运 行单位 的调整看成博弈 的双 方 ,建立 了电网扰 动具有 有限理 性 的连锁 故障序贯博弈模型 。 关键词 电力系统 ;连锁 故障 ;博弈论
序贯博弈纳什均衡

序贯博弈纳什均衡序贯博弈是博弈论中一种重要的博弈形式,也是实际生活中的普遍存在。
在序贯博弈中,参与者的行动是有先后顺序的,并且每个参与者的行动都会对自己和其他参与者的收益产生影响。
其中,纳什均衡是对于序贯博弈的一种重要的分析方法和结果。
序贯博弈可以分成两种情形:完全和不完全信息序贯博弈。
在完全信息的序贯博弈中,参与者可以获得游戏的所有信息,并且可以推导出所有参与者的策略和结果。
而在不完全信息的序贯博弈中,参与者只能知道一部分信息,并且需要进行一定的推断和猜测。
每个参与者的策略和结果都是不确定的。
不过,无论是完全信息还是不完全信息的序贯博弈,都可以利用纳什均衡来求解。
纳什均衡是序贯博弈中确定最优策略的一种方法。
纳什均衡指的是在博弈中所有参与者都遵循自己的最优策略时,达到的均衡状态。
也就是说,任何一方都不能通过单独改变自己的策略来获得更好的结果。
纳什均衡的概念是由约翰·纳什提出的,并且被广泛应用于博弈论中,是对于博弈问题的一种比较普遍的解决方法。
在序贯博弈中,纳什均衡可以通过反复应用最优化原理来求解。
最优化原理指的是,每个参与者都会选择一种最优策略,以尽可能地获得最好的结果。
也就是说,每个参与者都会根据自己的利益来做出决策。
通过比较不同的策略组合的结果,可以对于最终结果进行分析和预测。
如果某个策略组合成为纳什均衡,就意味着这个组合对于所有参与者都是最好的决策。
举一个例子,假设有两个商人X和Y,他们都出售同样的产品,并且都有两种售价可供选择。
如果两个人的售价不同,则会影响另一个商人的收益。
他们在某个时候进行交易,Y先决定自己的售价,然后X再根据Y的售价来决定自己的售价。
如果X的售价高于Y,则X会获得更高的利润,但Y就会失去他的订单,反之亦然。
这是一个典型的不完全信息的序贯博弈。
为了找到最好的策略组合,可以使用最优化原理和纳什均衡。
首先,假设Y选择售价为a,那么X的最优策略是选择一个更低的售价b,这样他就能获得更高的利润。
序贯均衡定义

序贯均衡定义
序贯均衡是指参与人在选择策略时,根据给定的信念,在每个决策点上选择的策略都是最优的。
具体来说,在博弈中,每个参与人都有自己的信念,即对其他参与人可能采取的策略的预期。
基于这些信念,参与人在每个决策点上都会选择他认为最优的策略。
这种选择过程是序贯的,即每个参与人都是在其他参与人选择策略之后,再根据这些策略选择自己的最优策略。
因此,在序贯均衡中,每个参与人在每个决策点上选择的策略都是最优的,从而形成了一种均衡。
序贯均衡是一种博弈论中的概念,用于描述动态博弈中的均衡状态。
与静态博弈不同,动态博弈中参与人的行动是有先后顺序的,每个参与人在做出决策时都需要考虑其他参与人的行动。
序贯均衡强调的是在动态博弈中,参与人的策略选择应该是一致的,即每个参与人在选择策略时都应该考虑其他参与人的行动,并选择最优的策略。
在实际应用中,序贯均衡可以用于分析各种动态博弈问题,如国际关系、市场竞争、团队合作等。
通过序贯均衡的分析,可以了解参与人在动态博弈中的行为特征和策略选择,从而为实际问题的解决提供理论支持和实践指导。
博弈论的分类

博弈论的分类博弈的分类博弈可以按照不同的分类方式进行分类,比如按照博弈者出招的顺序,博弈者对其他参与博弈者特征、策略空间和收益是否了解进行分类。
1、从按照博弈者出招的顺序、博弈持续时间和重复次数的角度,博弈可以分为静态博弈(Static Game)和动态博弈(Dynamic Game)。
静态博弈指的是参与博弈的各方同时采取策略,这些博弈者的收益取决于博弈者们不同的策略组合。
因此静态博弈又称为“同时行动的博弈”(Simultaneous-Move Games)。
有时候博弈方采取策略有先后,但是他们并不知道之前其他人做出的策略。
比如“囚徒困境”中罪犯1采取策略后,轮到罪犯2采取策略时他并不知道罪犯1所做出的策略。
动态博弈(序贯博弈)指的是在博弈中,参与博弈的博弈方所采取策略是有先后顺序的(Sequential-Move),且博弈者能够知道先采取策略者所选择的策略。
2、从博弈者对其他参与博弈者所了解的信息的完全程度,博弈可以分为完全信息博弈(Complete Information Game)与不完全信息博弈(Incomplete Information Game),以及完美信息博弈(Perfect Information Game)与不完美信息博弈(Imperfect Information Game),确定的博弈(Certainty Game)与不确定的博弈(Uncertain Game),对称信息博弈(Symmetric Game)与非对称信息博弈(Asymmetric Game)等等。
其中,完全信息是指博弈中每一个博弈者对其他博弈者的特征、策略空间和收益函数都了解,也就是博弈者的收益集(Pay offs)是所有博弈者都知道的。
完美信息是指博弈者完全知道在他采取策略时其他博弈者的所有策略信息。
完美信息是针对记忆而言,也就是他知道博弈已经发生过程的所有信息。
又或者说,如果博弈者在采取策略时观察到他所处的信息节点是唯一的,即他知道以前发生的所有事情,如果所处的信息节点不唯一,说明他对之前的信息没有完美的记忆(不知道博弈过程是怎么过来的)。
第九讲(序贯博弈)
反击
• 然而,美军可以通过调整在西德的部署来改变这 个结果。 • 假设美军增加西德的军队,会出现怎样的结果?
增加部署不是为了能打败苏军。 事实上,其数量无法战胜苏军。 同时还会增加美国的开销。 然而,苏军进攻后,如果美军 选择反击,还是能够救援一部 分的部队。这比全军覆没要好。 从左图可以看出,最终结果对 美军来说是变好了。
纳什均衡与子博弈完美均衡
• 再看金雀与蓝鸟的案例:
– 纳什均衡为蓝鸟进入,金雀接受;和蓝鸟不进入,而 金雀威胁展开价格战。 – 通过对扩展式的简化,两个纳什均衡中只有一个是子 博弈完美均衡。即蓝鸟进入,金雀容纳。 – 价格战的威胁是不可信的。
金雀与蓝鸟的收益矩阵:
金雀 如果蓝鸟进 如果蓝鸟进入, 入,就接受 就展开价格战 3,5 -5,2 0,10 0,10
一个商业案例 – 解答
3 PDF 文件使用 "pdfFactory Pro" 试用版本创建
一个商业案例 – 解答
Exercise – 离婚诉讼费
• 琼斯夫人因为先生外遇要与琼斯先生离婚。 根据婚前协定,如果琼斯夫人能够证明她 先生有外遇就能得到10万美元,否则只能 得到5万美元。她的律师只有雇佣私家侦探 才能证明琼斯先生有外遇,所需费用为1万 美元,包含在律师费中。琼斯夫人有两个 选择:无论诉讼结果是什么,都支付2万美 元的律师费用,或者支付诉讼收入的1/3。 • 琼斯夫人该如何选择呢?
序贯博弈有一定的承诺结构commitmentstructure囚徒困境中由于一方在不知道另即谁先做出战略承诺这使序贯博弈拥有一个或多个一方具体会做出怎样的决策下进行的适当子博弈
序贯博弈
• 序贯博弈 (sequential game):
第九讲 序贯博弈
序贯决策博弈概述

序贯决策博弈:局中人做出策略选 择时知道对手的策略选择。
实验 : 枪手博弈1
三个快枪手相互之间的仇恨到了不可 调和的地步。这天他们三在街上不期而遇, 每个人的手都握住了枪把,一场生死决斗 马上就要开始……
已知这三个人中甲枪法精准,十发八 中;乙的枪法也不错,十发六中,丙的枪 法拙劣,十发四中。假如三个人同时开枪, 决一死战,一枪后谁最后活下来的机会大 一些?
八种策略组合,纳什均衡在哪
该博弈有八种可能的策略组合: ( {足球},{(上)足球,(下)足球} ) ( {足球},{(上)足球,(下)芭蕾} ) ( {足球},{(上)芭蕾,(下)足球} ) ( {足球},{(上)芭蕾,(下)芭蕾} ) ( {芭蕾},{(上)足球,(下)足球} ) ( {芭蕾},{(上)足球,(下)芭蕾} ) ( {芭蕾},{(上)芭蕾,(下)足球} ) ( {芭蕾},{(上)芭蕾,(下)芭蕾} )
实 验 : 枪手博弈2
假设现在三个枪手决定轮流开枪,谁活下 来的机会大一些?
实验:海盗分宝
五个海盗抢到100颗宝石,他们决定按如下方 法来分配:先抽签决定顺序(1,2,3,4,5); 然后先由1号提出分配方案,其余的人进行 表决,当且仅当半数和超过半数的人同意 时,则按1号所提方案分配,否则将1号扔进 大海喂鲨鱼,当1号方案被否决,则由2号提 出分配方案,其余的人进行表决,以此类 推,假定这些海盗都是理性人,问第一个 海盗应提出怎样的分配方案才能获得通过 并使自己的收益最大?
用箭头排除确定法寻找纳什均衡
将以上策略在博弈书中用粗线表示。
将存在单独改变激励的策略用箭头标示。方法如下:
(1)找到第二阶段两根粗线所对应的支付。
(2)比较这两个支付前面的数字,如果大的数字所 对应的那条“树枝”是细的,则男方存在单独偏离 的动机,则男方的策略选择用箭头标示。
序贯博弈名词解释

序贯博弈名词解释
嘿,你知道啥是序贯博弈不?序贯博弈啊,就好比是一场精彩的棋局!想象一下,两个人在下棋,一个人先走一步,然后另一个人再根
据对方的走法来决定自己的下一步。
这就是序贯博弈啦!比如说,你
和朋友玩猜拳游戏,你先出拳,这就是序贯博弈中的第一步呀。
序贯博弈可不简单哦!它涉及到很多策略和决策呢。
就好像你在走
一条充满选择的路,每一步都得深思熟虑。
比如说在商业竞争中,一
家公司先推出一款产品,另一家公司就得根据这个来决定自己要不要
跟进,推出类似的产品或者采取其他策略,这多有意思啊!
它也像是一场心理战呢!你得去猜对方会怎么做,然后根据这个来
调整自己的行动。
比如你和小伙伴玩捉迷藏,你找的时候,就得想想
他可能会藏在哪里,这就是在进行序贯博弈呀!
而且哦,序贯博弈中先后顺序很重要呢!先行动的一方可能会有一
些优势,但也不一定哦,后行动的一方也可能通过观察和分析来找到
更好的策略。
这就好像跑步比赛,先跑的人不一定就能赢,后面的人
也可能奋起直追呢!
在生活中,序贯博弈无处不在呀!找工作面试的时候,你先展示自己,然后面试官根据你的表现来决定要不要录用你,这也是序贯博弈呀!还有谈恋爱的时候,你先表达自己的感情,对方再决定怎么回应,这同样是序贯博弈。
序贯博弈就是这样,充满了策略、智慧和不确定性。
它让我们的生活变得更加丰富多彩,也让我们不断地去思考和决策。
所以啊,可别小瞧了序贯博弈哦,它真的很重要呢!我的观点就是,序贯博弈就像生活中的一场大冒险,每一步都充满挑战和惊喜,我们要好好去感受和应对它呀!。
序贯博弈的例子

序贯博弈的例子《序贯博弈的例子:生活中的“盘算”与“心机”》嘿,大家好呀!今天咱们来聊聊序贯博弈这个听上去有点高大上的玩意儿。
其实呢,序贯博弈在咱们生活中那可是无处不在,充满了各种有趣的例子和让人哭笑不得的场景。
比如说,你和你的朋友一起去吃火锅。
点单的时候,这就是一场序贯博弈啊。
你先点,那你就得考虑到朋友的口味,你要是一下子把朋友爱吃的都点了,朋友后面没得点,说不定心里就嘀咕着:“这家伙,也不给我留点发挥的余地。
”反过来,你要是太客气,啥都不点,等着朋友来点,朋友可能又会埋怨你:“咋这么不积极呢,一点主见都没有。
”所以啊,这第一个点单的人就处于一种微妙的境地,得好好盘算盘算怎么既能照顾到大家的口味,又不会显得自己太霸道或者太窝囊。
还有啊,逛街买东西的时候也经常有这种情况。
你和闺蜜一起看到一件漂亮衣服,都挺喜欢。
这时候就看谁先下手了。
要是你先去试穿,然后表示很喜欢,闺蜜也许就会想:“她都这么喜欢了,我再抢好像不太好。
”可要是闺蜜先表态,你又可能在心里琢磨:“哎呀,她都这么说了,我再争是不是不太合适啊。
”这就是一场心理上的博弈,谁先出招,谁后出招,都有着不一样的影响。
再说说工作中的情况。
有个项目来了,大家都想争取负责。
第一个站出来说自己要干的人,可能会被其他人视为有野心,但也可能赢得领导的赞赏。
而后面那些人呢,就得考虑怎么表现才能既不显得太退缩,又能有机会突出自己的能力。
这就像是在走钢丝,稍不注意就会掉下去。
序贯博弈其实就是我们生活中的那些小心思、小盘算的体现。
它有时候让我们纠结,有时候让我们偷笑,有时候又让我们懊悔。
但这也正是生活的趣味所在呀。
就像一场游戏,我们都在其中不断地摸着石头过河,试探着别人的反应,也调整着自己的策略。
所以啊,下次当你遇到这种情况的时候,不妨笑着想想,哈哈,这不就是一场序贯博弈嘛。
别太紧张,放轻松,好好发挥自己的“心机”,说不定就能赢得这场小小的博弈呢。
生活就是这样,充满了各式各样的挑战和乐趣,让我们尽情地享受这些有趣的序贯博弈吧!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 序贯博弈 (sequential game):
第九讲 序贯博弈
– 人们只能按一定的顺序选择战略,只有在特定的限制 条件下或一段时间过后,才能实施他们承诺的战略。
• 案例:遏制进入的战略性投资:
– S公司是生产工作站专用计算机处理芯片的公司。其 年产量为300万个,总成本为10亿美元。 – 下表列出了该芯片市场的需求关系。
– 序贯博弈有一定的承诺结构(commitment structure), 即谁先做出战略承诺,这使序贯博弈拥有一个或多个 的适当子博弈。 – 子博弈完美均衡(sub-game perfect equilibrium):
• 所有参与者总是按照这种均衡状态预测对手的决策。
1 PDF 文件使用 "pdfFactory Pro" 试用版本创建
纳什均衡与子博弈完美均衡
• 再看金雀与蓝鸟的案例:
– 纳什均衡为蓝鸟进入,金雀接受;和蓝鸟不进入,而 金雀威胁展开价格战。 – 通过对扩展式的简化,两个纳什均衡中只有一个是子 博弈完美均衡。即蓝鸟进入,金雀容纳。 – 价格战的威胁是不可信的。
金雀与蓝鸟的收益矩阵:
金雀 如果蓝鸟进 如果蓝鸟进入, 入,就接受 就展开价格战 3,5 -5,2 0,10 0,10
蓝 进入 鸟 不进入
椰子博弈
• R和J乘着划艇漂流到了一个小岛,他们需要补充食物然后 继续划艇。小岛上有4棵椰树,椰子可以提供食物。每棵 椰树有5个椰子。他们必须有一人爬上树去摘,而另一人 在树下捡,否则椰子会滚到海里。R和J可以轮流摘椰子和 捡椰子,最后两人平分这些椰子。然而,每个阶段,树下 的人都有机会带着摘到的椰子乘坐划艇离开。 • 下图表现了这个博弈。 • 该博弈的子博弈完美均衡是怎样的?
反击
• 然而,美军可以通过调整在西德的部署来改变这 个结果。 • 假设美军增加西德的军队,会出现怎样的结果?
增加部署不是为了能打败苏军。 事实上,其数量无法战胜苏军。 同时还会增加美国的开销。 然而,苏军进攻后,如果美军 选择反击,还是能够救援一部 分的部队。这比全军覆没要好。 从左图可以看出,最终结果对 美军来说是变好了。
鲍勃 埃 如果B挑 尔 衅,就报 复;否则什 么也不做 如果B挑 衅,不管 它;否则什 么也不做 挑衅 -50, -100 不挑衅 5,4
道路冲突 – 解答
4,个子博弈。 其中蓝色的为基本子博弈。 子博弈完美均衡为:B挑衅,A不管它。 政府可以通过惩罚挑衅者减少道路冲突。如右上图,假设 惩罚为-10,则此时的子博弈完美均衡为:B不挑衅,A什 么也不做。 • 如果针对报复者惩罚,这样并不能改变原来的均衡状态。
蜈蚣博弈
• 如果安娜(A)和鲍勃(B)要分一坛子钱。规则是A先从坛子 里抓钱然后传给B,也可以选择不抓然后传给B。B选择抓 钱,也可以选择不抓继续传给A。如果B选择传,坛子中 的钱会增加,最后他们平分坛子里的钱。 • 这个简单的蜈蚣博弈只有两个阶段,它可以延伸至上百个 阶段。 • 无论有多少段,其子博弈完美均衡都为:“A抓了钱就跑”。
2 PDF 文件使用 "pdfFactory Pro" 试用版本创建
反击
• 冷战时期,美国在西德境内驻扎军队,以阻止苏 联向西德攻击。驻扎的军队数量不足以抗衡苏 军,但是如果苏联攻击,美国可以选择反击或不 反击。 • 下图表现了两国之间的博弈。 • 该博弈的子博弈完美均衡是怎样的? • 苏军进攻,而美军不反击。
子博弈完美均衡是: 苏军不进攻。
Exercise – 道路冲突
• 有两个参与者埃尔(A)和鲍勃(B)。当遇到道路冲突 的时候B有两个选择:向A挑衅或不挑衅。在A挑 衅的情况下B可选择不去管它或者进行报复。 • 下表为该博弈的收益矩阵。
请写出这个博弈的扩展式(决 策树)。 这个博弈的子博弈是什么? 哪些为基本子博弈? 子博弈完美均衡是什么?它与 现实是否相符? 如果你是政府官员,想要通过 惩罚减少道路上的才冲突,你 应该对谁进行惩罚?为什么?
– 蓝色的两个椭圆也为基本子博弈。 – 而始于S的博弈被称为复合子博弈,即紫色的椭圆。
• PA和PB的节点为完全信息节点。
– 所有子博弈起始于完全信息节点。 – 子博弈不能起始于一个信息集。
囚徒困境中,由于一方在不知道另 一方具体会做出怎样的决策下进行 选择,因此只有节点1是完全信息 节点,而节点2是个信息集。 该博弈中只有一个子博弈,即为博 弈本身,且不含承诺结构
椰子博弈
• 子博弈完美均衡:
– J获得了5个椰子,而R一无所获。 – 这是个不效率的非合作博弈均衡。 – R会拒绝这个计划。
• 该博弈解释了工业化国家在生产方面的一些问题。
– 劳动分工:亚当·斯密认为分工是提高劳动生产率和人们生 活标准的主要途径。 – 迂回生产:首先生产中间产品(e.g.机器),然后利用它们生 产最终产品。 – 劳动分工与迂回生产是相互配合的。而这种配合需要有国家 法律保障下的合同制度。人们违反合约就会受到处罚。 – 因此,一些不发达国家政府腐败问题,法制缺失问题会导致 缺乏有效措施保证合同的执行,使得经济发展进一步落后。
遏制进入的战略性投资
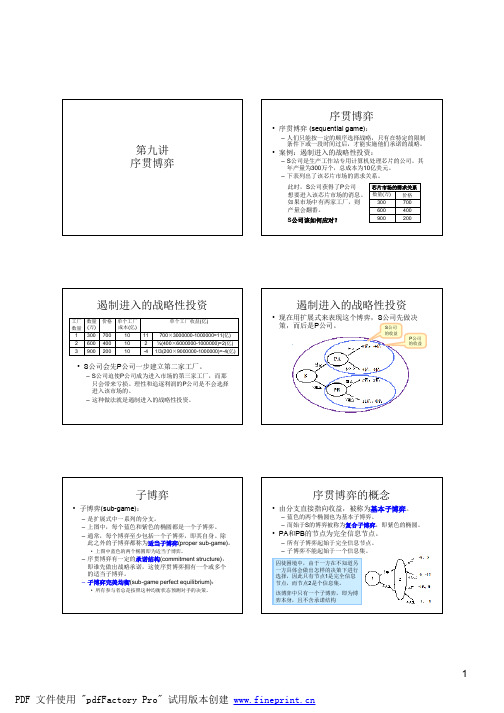
• 现在用扩展式来表现这个博弈,S公司先做决 策,而后是P公司。 S公司
的收益 P公司 的收益
• S公司会先P公司一步建立第二家工厂。
– S公司迫使P公司成为进入市场的第三家工厂,而那 只会带来亏损。理性和追逐利润的P公司是不会选择 进入该市场的。 – 这种做法就是遏制进入的战略性投资。
一个商业案例 – 解答
3 PDF 文件使用 "pdfFactory Pro" 试用版本创建
一个商业案例 – 解答
Exercise – 离婚诉讼费
• 琼斯夫人因为先生外遇要与琼斯先生离婚。 根据婚前协定,如果琼斯夫人能够证明她 先生有外遇就能得到10万美元,否则只能 得到5万美元。她的律师只有雇佣私家侦探 才能证明琼斯先生有外遇,所需费用为1万 美元,包含在律师费中。琼斯夫人有两个 选择:无论诉讼结果是什么,都支付2万美 元的律师费用,或者支付诉讼收入的1/3。 • 琼斯夫人该如何选择呢?
子博弈
• 子博弈(sub-game):
– 是扩展式中一系列的分支。 – 上图中,每个蓝色和紫色的椭圆都是一个子博弈。 – 通常,每个博弈至少包括一个子博弈,即其自身。除 此之外的子博弈都称为适当子博弈(proper sub-game)。
• 上图中蓝色的两个椭圆即为适当子博弈。
序贯博弈的概念
• 由分支直接指向收益,被称为基本子博弈。
• 该博弈的子博弈完美均衡为:
– X进入市场,而O与X共享市场。 – O价格战的威胁是不可信的。
离婚诉讼费 – 解答
• 该博弈的子博弈完美均衡为:
– 琼斯夫人支付1/3的诉讼收入,律师雇佣侦探。 – 此时两人的收益为(20/3,7/3)。
4 PDF 文件使用 "pdfFactory Pro" 试用版本创建
后向归纳法
• 后向归纳法是用以求解子博弈完美均衡的方法。
– 从每个序列中最后一个决策开始,确定这个决策的均 衡,然后向前移动,找到每一阶段的均衡,直到到达 第一个决策点。 – 遏制进入博弈可以简化为一个小博弈: 子博弈完美均衡为:
S公司自己建立第二家工 厂,而P公司不建立。
尼姆游戏
在这个游戏中,由于A是先做出决策 的一方,因此他会获得最终的胜利。 子博弈完美均衡为:A选择第二排取 走一个硬币。
芯片市场的需求关系 此时,S公司获得了P公司 价格 想要进入该芯片市场的消息。 数量(万) 300 700 如果市场中有两家工厂,则 产量会翻番。 600 400
S公司该如何应对?
900
200
遏制进入的战略性投资
工厂 数量 数量 (万) 1 300 2 3 600 900 价格 单个工厂 成本(亿) 700 400 200 10 10 10 11 2 -4 单个工厂收益(亿) 700×3000000-1000000=11(亿) ½(400×6000000-1000000)=2(亿) 1/3(200×9000000-1000000)=-4(亿)
• • • •
Exercise – 一个商业案例
• 欧姆(O)公司是扫描仪的垄断销售商。新公司(X) 获得了能以更低成本生产扫描仪的技术,并考虑 是否进入该市场。O扬言如果X进入就会压低价格 打价格战。已知两家公司的价格战略都为p1或p2。 老工艺的生产成本为c1,新工艺的生产成本为 c2,且p1>c1>p2>c2。如果价格相同,两家会平 分市场Q,否则低价的公司会获得整个市场。 • 请画出该博弈的扩展式。 • 请问O公司打价格战的威胁是否可信?
