动圆过定点问题
动圆过定点问题公式

动圆过定点问题公式在数学的奇妙世界里,动圆过定点问题可是个挺有趣的家伙。
咱先来说说啥是动圆过定点问题。
想象一下啊,有一个圆,它不像咱平时画的那些老老实实呆在一个地方的圆,而是会动来动去的,就像个调皮的小孩子。
但神奇的是,不管它怎么动,总会经过一个固定的点,这个固定的点就像是它的“家”,无论在外怎么撒欢,最后都得回到这儿。
为了解决动圆过定点问题,咱们有一些实用的公式和方法。
比如说,假设动圆的方程是$(x - a)^2 + (y - b)^2 = r^2$,其中$(a, b)$是圆心的坐标,$r$是半径。
如果这个动圆经过一个定点$(x_0, y_0)$,那就把这个点的坐标代进去,就能得到一个关于$a$、$b$或者$r$的关系式。
我记得有一次给学生们讲这个知识点的时候,有个小同学眼睛瞪得大大的,一脸迷茫地问我:“老师,这圆为啥要动来动去啊,它不累吗?”我笑着跟他说:“这圆啊,就像你在操场上跑步,虽然跑的路线不一样,但总有个终点等着你。
”这小家伙似懂非懂地点点头,继续埋头琢磨去了。
咱们再深入一点,动圆过定点问题还常常和其他的数学知识结合在一起。
比如说和直线方程啦,圆锥曲线啦等等。
这就像是一场数学知识的大派对,大家都凑到一块儿,热闹非凡。
比如说,如果动圆与一条直线相切,并且经过一个定点,那咱们就得先求出直线的方程,再结合圆的方程,找出其中的关联。
这就好像是解开一道复杂的谜题,每一个条件都是一块拼图,咱们得把它们拼到一起,才能看到完整的画面。
还有的时候,动圆过定点问题会出现在实际生活中呢。
就像建筑工人在建造圆形的花坛时,要确保某个位置总是能被花坛覆盖,这其实就是在解决一个动圆过定点的问题。
总之啊,动圆过定点问题虽然有点小复杂,但只要咱们掌握了方法,多做几道题练练手,就一定能把它拿下。
就像那个一开始迷茫的小同学,后来经过自己的努力,也能熟练地解决这类问题啦。
所以同学们,别害怕,大胆地去探索这个奇妙的数学世界吧!。
与圆有关的定点定值最值与范围问题
抓住2个考点
突破3个考向
揭秘3年高考
【助学·微博】 一个考情分析
与圆有关的综合性问题,其中最重要的类型有定点问题、定值 问题、最值与范围问题. 解这类问题可以通过建立目标函数、利用几何意义、直接求解 或计算求得.
抓住2个考点
突破3个考向
揭秘3年高考
考点自测
1.已知两圆C1:x2+y2-2x+10y-24=0,C2:x2+y2+2x+ 2y-8=0,则经过两圆交点且面积最小的圆的方程为 ________________.
抓住2个考点
突破3个考向
揭秘3年高考
2.若直线 y=x+b 与曲线 y= 1-x2有两个公共点,则 b 的取值
范围是________.
解析 如图,当直线介于 l1 与 l2 之间时满
足题意,即圆心到直线
y=x+b
的距离
2 2
≤ |b|<1,解得 1≤b< 2. 2
答案 [1, 2)
抓住2个考点
突破3个考向
由yx=-02,2-3=0,
得x=2+ y=0
3,
或x=2- y=0.
3,
故以 MN 为直径的圆恒过定点(2+ 3,0)和(2- 3,0).
抓住2个考点
突破3个考向
揭秘3年高考
考向二 与圆有关的定值问题
【例2】 (2013·扬州调研)已知圆C:x2 +y2=9,点A(-5,0),直线l:x-2y =0. (1)求与圆C相切,且与直线l垂直的 直线方程; (2)在直线 OA 上(O 为坐标原点),存在定点 B(不同于点 A), 满足:对于圆 C 上任一点 P,都有PPAB为一常数,试求所有满 足条件的点 B 的坐标.
抓住2个考点
圆锥曲线中的四种经典模型

圆锥曲线中的定点定值问题的四种经典模型定点问题是常见的出题形式,化解这类问题的关键就是引进变的参数表示直线方程、数量积、比例关系等,根据等式的恒成立、数式变换等寻找不受参数影响的量。
直线过定点问题通法,是设出直线方程,通过韦达定理和已知条件找出k 和m 的一次函数关系式,代入直线方程即可。
技巧在于:设哪一条直线?如何转化题目条件?圆锥曲线是一种很有趣的载体,自身存在很多性质,这些性质往往成为出题老师的参考。
如果大家能够熟识这些常见的结论,那么解题必然会事半功倍。
下面总结圆锥曲线中几种常见的几种定点模型:模型一:“手电筒”模型例题、已知椭圆C :13422=+y x 若直线m kx y l +=:与椭圆C 相交于A ,B 两点(A ,B 不是左右顶点),且以AB 为直径的圆过椭圆C 的右顶点。
求证:直线l 过定点,并求出该定点的坐标。
解:设1122(,),(,)A x y B x y ,由223412y kx m x y =+⎧⎨+=⎩得222(34)84(3)0k x mkx m +++-=, 22226416(34)(3)0m k k m ∆=-+->,22340k m +->212122284(3),3434mk m x x x x k k -+=-⋅=++22221212121223(4)()()()34m k y y kx m kx m k x x mk x x m k-⋅=+⋅+=+++=+ 以AB 为直径的圆过椭圆的右顶点(2,0),D 且1AD BD k k ⋅=-, 1212122y yx x ∴⋅=---,1212122()40y y x x x x +-++=, 2222223(4)4(3)1640343434m k m mkk k k --+++=+++,整理得:2271640m mk k ++=,解得:1222,7k m k m =-=-,且满足22340k m +-> 当2m k =-时,:(2)l y k x =-,直线过定点(2,0),与已知矛盾;当27k m =-时,2:()7l y k x =-,直线过定点2(,0)7综上可知,直线l 过定点,定点坐标为2(,0).7◆方法总结:本题为“弦对定点张直角”的一个例子:圆锥曲线如椭圆上任意一点P 做相互垂直的直线交圆锥曲线于AB ,则AB 必过定点))(,)((2222022220ba b a y b a b a x +-+-。
恒过定点问题的解题策略

宜兴市丁蜀高级中学高三理科二轮复习微专题恒过定点问题的解题策略一课前热身:1.动直线(2)(34)210()a x a y a a R ++-+-=∈过定点 .2.动圆22(2)(4)440()x y a x a y a a R ++++---=∈过定点 .3.在平面直角坐标系xOy 中,设抛物线x y 42=的焦点为F ,准线为P l ,为抛物线上一点,以P 为圆心的圆与直线l 相切,则圆过定点4.如图,已知圆224x y +=,直线:4l x =,圆O 与x 轴交A ,B 两点, M 是圆O 上异于A ,B 的任意一点,直线AM 交直线l 于点P ,直线BM 交直线l 于点Q .求证:以PQ 为直径的圆C 过定点,并求出定点坐标.二 例题讲评例1. 1.已知椭圆22221(0)xy a b a b +=>>过点3(1,)2,离心率为32.过椭圆右顶点A 的两条斜率乘积为14-的直线分别交椭圆C 于,M N 两点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)直线MN 是否过定点D ?若过定点D ,求出点D 的坐标;若不过,请说明理由.例2.已知圆M 的方程;4)4(22=+-y x ,点C )0,1(,设P 是圆M 上一动点,在x 轴上是否存在异于C 的定点B ,使得PBPC 恒为定值λ?若存在,求出定点B 的坐标,并求λ的值;若不存在,说明理由.x y O M A B P Q三巩固训练1.已知椭圆22:142x y C +=的上顶点为A ,过A 点引两条直线分别交椭圆于,P Q 两点,设直线,AP AQ 的斜率分别为12,k k .若121k k =-时,问直线PQ 是否过定点2.已知点P 是椭圆C 上任意一点,点P 到直线的距离为,到点的距离为,且.直线与椭圆C 交于不同的两点A,B (A,B 都在轴的上方),且.(1)求椭圆C 的方程;(2)当A 为椭圆与轴正半轴的交点时,求直线的方程;(3)对于动直线,是否存在一个定点,无论如何变化,直线总经过此定点?若存在,求出该定点的坐标;若不存在,说明理由.1:2l x =-1d ()1,0F -2d 212d d l x 180OFA OFB ∠+∠=y l l OFA ∠l。
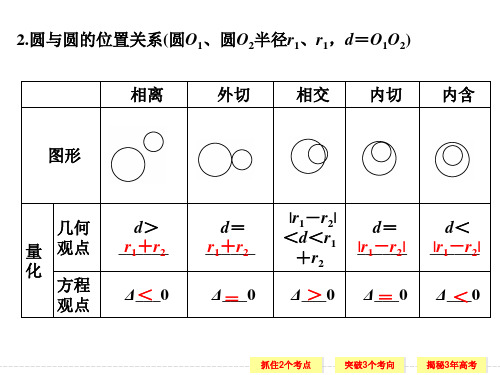
微专题12 与圆有关的定点、定值、最值、范围问题

微专题12与圆有关的定点、定值、最值、范围问题真题感悟(2019·全国Ⅰ卷)已知点A,B关于坐标原点O对称,AB=4,⊙M过点A,B且与直线x+2=0相切.(1)若A在直线x+y=0上,求⊙M的半径;(2)是否存在定点P,使得当A运动时,MA-MP为定值?并说明理由.解(1)因为⊙M过点A,B,所以圆心M在AB的垂直平分线上.由已知A在直线x+y=0上,且A,B关于坐标原点O对称,所以M在直线y=x上,故可设M(a,a).因为⊙M与直线x+2=0相切,所以⊙M的半径为r=|a+2|.连接MA,由已知得AO=2.又MO⊥AO,故可得2a2+4=(a+2)2,解得a=0或a=4.故⊙M的半径r=2或r=6.(2)存在定点P(1,0),使得MA-MP为定值.理由如下:设M(x,y),由已知得⊙M的半径为r=|x+2|,AO=2.由于MO⊥AO,故可得x2+y2+4=(x+2)2, 化简得M的轨迹方程为y2=4x.因为曲线C:y2=4x是以点P(1,0)为焦点,以直线x=-1为准线的抛物线,所以MP=x+1.因为MA-MP=r-MP=x+2-(x+1)=1,所以存在满足条件的定点P.考点整合1.最值与范围问题(1)研究与圆有关的最值问题时,可借助圆的性质,利用数形结合求解.(2)常见的最值问题有以下几种类型:①形如μ=y-bx-a的最值问题,可转化为动直线斜率的最值问题;②形如t=ax+by的最值问题,可转化为动直线截距的最值问题;③形如μ=(x -a )2+(y -b )2的最值问题,可转化为动点到定点的距离的平方的最值问题.(3)对于圆的方程也可以利用三角代换,转化为三角函数问题:对于圆(x -a )2+(y -b )2=r 2,可设x =a +r cos θ,y =b +r sin θ.2.定点问题的求解步骤(1)选参变量:需要证明过定点的动直线(曲线)往往随着某一个量的变化而变化,可以选择这个量为参变量.(2)求动直线(曲线)方程:求出含上述参变量的动直线(曲线)方程,通过消元或整体思想,使得方程只含有一个参量(当根据几何条件建立的等式中含有多个参量时,要注意区别对待,与动点、动直线、动圆有关的参量是主要参量,其他参量可看作系数).(3)定点:求出定点坐标.利用方程ax +b =0恒成立来处理定点问题.在处理时也可以用从特殊到一般的思想,先求出一个特殊点,再代入进行验证.3.定值问题的处理(1)可以直接求出相关等式,再论证该等式与参数无关,类似于三角化简求值.(2)也可以用从特殊到一般的思想,先让参数取特殊值来论证性质,再将性质推广至一般情形.热点一 最值与范围问题【例1】 已知圆M 的圆心M 在x 轴上,半径为1,直线l :y =43x -12被圆M 所截的弦长为3,且圆心M 在直线l 的下方.(1)求圆M 的方程;(2)设A (0,t ),B (0,t +6)(-5≤t ≤-2),若圆M 是△ABC 的内切圆,求△ABC 的面积S 的最大值和最小值.解 (1)设圆心M (a ,0),由已知得圆心M 到l :8x -6y -3=0的距离为12-⎝ ⎛⎭⎪⎫322=12,∴|8a -3|82+(-6)2=12,又∵M (a ,0)在l 的下方,∴8a -3>0,∴8a -3=5,a =1.故圆M 的方程为(x -1)2+y 2=1.(2)由已知可设AC 的斜率为k 1,BC 的斜率为k 2(k 1>k 2),则直线AC 的方程为y =k 1x +t ,直线BC 的方程为y =k 2x +t +6.由方程组⎩⎨⎧y =k 1x +t ,y =k 2x +t +6, 得C 点的横坐标为x 0=6k 1-k 2. ∵AB =t +6-t =6,∴S =12⎪⎪⎪⎪⎪⎪6k 1-k 2×6=18k 1-k 2. ∵圆M 与AC 相切,∴1=|k 1+t |1+k 21,∴k 1=1-t 22t , 同理,k 2=1-(t +6)22(t +6),∴k 1-k 2=3(t 2+6t +1)t 2+6t, ∴S =6(t 2+6t )t 2+6t +1=6⎝ ⎛⎭⎪⎫1-1t 2+6t +1. ∵-5≤t ≤-2,∴-2≤t +3≤1,∴-8≤t 2+6t +1≤-4,∴S max =6×⎝ ⎛⎭⎪⎫1+14=152,S min =6×⎝ ⎛⎭⎪⎫1+18=274, ∴△ABC 的面积S 的最大值为152,最小值为274.探究提高 直线与圆中的最值问题主要包含两个方面(1)参量的取值范围:由直线和圆的位置关系或几何特征,引起的参量如k ,b ,r 的值变化.此类问题主要是根据几何特征建立关于参量的不等式或函数.(2)长度和面积的最值:由于直线或圆的运动,引起的长度或面积的值变化.此类问题主要是建立关于与参数如k 或(x ,y )的函数,运用函数或基本不等式求最值.【训练1】 已知实数x ,y 满足方程x 2+y 2-4x +1=0.(1)求y -x 的最大值和最小值;(2)求x 2+y 2的最大值和最小值.解 由x 2+y 2-4x +1=0得(x -2)2+y 2=3,它表示以(2,0)为圆心,3为半径长的圆.(1)y -x 可看作是直线y =x +b 在y 轴上的截距,当直线y =x +b 与圆相切时,纵截距b 取得最大值或最小值,此时|2-0+b |2=3,解得b =-2±6. 所以y -x 的最大值为-2+6,最小值为-2- 6.(2)x 2+y 2表示圆上的点与原点距离的平方,由平面几何知识知,过原点和圆心的直线与圆有两个交点,在这两个交点处x 2+y 2取得最值.因为圆心到原点的距离为(2-0)2+(0-0)2=2, 所以x 2+y 2的最大值是(2+3)2=7+43,x 2+y 2的最小值是(2-3)2=7-4 3.热点二 与圆有关的定点问题【例2】 (2019·北京卷)已知抛物线C :x 2=-2py (p >0)经过点(2,-1).(1)求抛物线C 的方程及其准线方程;(2)设O 为原点,过抛物线C 的焦点作斜率不为0的直线l 交抛物线C 于两点M ,N ,直线y =-1分别交直线OM ,ON 于点A 和点B .求证:以AB 为直径的圆经过y 轴上的两个定点.(1)解 由抛物线C :x 2=-2py 经过点(2,-1)得p =2.所以抛物线C 的方程为x 2=-4y ,其准线方程为y =1.(2)证明 抛物线C 的焦点为F (0,-1).设直线l 的方程为y =kx -1(k ≠0).由⎩⎨⎧y =kx -1,x 2=-4y ,得x 2+4kx -4=0. 设M (x 1,y 1),N (x 2,y 2),则解方程得 x 1,2=-2k ±2k 2+1,从而x 1x 2=-4.直线OM 的方程为y =y 1x 1x . 令y =-1,得点A 的横坐标x A =-x 1y 1, 同理得B 的横坐标x B =-x 2y 2.所以A ⎝ ⎛⎭⎪⎫-x 1y 1,-1,B ⎝ ⎛⎭⎪⎫-x 2y 2,-1. 设点D (0,n ),则DA →=⎝ ⎛⎭⎪⎫-x 1y 1,-1-n , DB →=⎝ ⎛⎭⎪⎫-x 2y 2,-1-n , DA →·DB →=x 1x 2y 1y 2+(n +1)2=x 1x 2⎝ ⎛⎭⎪⎫-x 214⎝ ⎛⎭⎪⎫-x 224+(n +1)2 =16x 1x 2+(n +1)2=-4+(n +1)2. 令DA →·DB→=0,即-4+(n +1)2=0,得n =1或n =-3. 故以AB 为直径的圆经过y 轴上的定点(0,1)和(0,-3).探究提高 圆锥曲线中的定值与定点问题是高考的常考题型,运算量较大,题目逻辑性较强.解决这类问题一般有两种方法:一是根据题意求出相关的表达式,再根据已知条件列出方程组,消去参数,求出定值或定点坐标;二是先利用特殊情况确定定值或定点坐标,再从一般情况进行验证.【训练2】 已知圆x 2+y 2=9的圆心为P ,点Q (a ,b )在圆P 外,以PQ 为直径作圆M 与圆P 相交于A ,B 两点.(1)试判断直线QA 与圆P 的位置关系;(2)若QA =QB =4,试问点Q 在什么曲线上运动?(3)若点Q 在直线x +y -9=0上运动,问:直线AB 是否过定点?若过定点,求出定点的坐标;若不过定点,请说明理由.解 (1)因为以PQ 为直径的圆M 与圆P 相交于A ,B ,所以P A ⊥QA ,又AP 为圆P 的半径,所以AQ 为圆P 的切线,从而直线QA 与圆P 相切.(2)因为P A ⊥QA ,AP =3,AQ =4,所以PQ =32+42=5,故点Q 在以P 为圆心,5为半径的圆上运动.(3)因为点Q (a ,b )在直线x +y -9=0上,所以点Q (a ,9-a ),所以,以PQ 为直径的圆M 的方程为x 2+y 2-ax -(9-a )y =0,又AB 为圆P 与圆M 的公共弦,所以直线AB 的方程为ax +(9-a )y -9=0,即a(x-y)-9y-9=0,从而此直线过x-y=0与9y-9=0的交点,即过定点(1,1).热点三与圆有关的定值问题【例3】(2018·高邮调研)如图,已知圆O的方程为x2+y2=1,直线l的方程为x-y+22=0,点P是直线l上的动点,过点P作圆O的切线P A,PB,切点为A,B.(1)若∠APB=60°,试求点P的坐标;(2)在(1)的条件下,对于圆O上任意一点M,平面内是否存在一定点R,使MR MP为定值?如果存在,求出点R的坐标;如果不存在,请说明理由.解(1)连接OP,OA,OB,因为P A,PB为过点P的圆O的切线,切点为A,B,所以OA⊥P A,OB⊥PB.因为∠APB=60°,∠APO=30°,在Rt△APO中,OA=1,所以OP=2.设点P的坐标为(t,t+22),则t2+(t+22)2=4,t2+22t+2=0,即(t+2)2=0,解得t=-2,所以点P的坐标为(-2,2).(2)假设存在符合条件的定点R.设点M(x,y),R(x0,y0),MR2MP2=λ,则x2+y2=1,即(x-x0)2+(y-y0)2=λ[(x+2)2+(y-2)2],整理得-2x0x-2y0y+x20+y20+1=λ(22x-22y+5),上式对任意x,y∈R,且x2+y2=1恒成立,则⎩⎨⎧-2x 0=22λ,-2y 0=-22λ,x 20+y 20+1=5λ,解得⎩⎪⎨⎪⎧λ=14,x 0=-24,y 0=24或⎩⎨⎧λ=1,x 0=-2,(舍去)y 0=2.所以R 的坐标为⎝ ⎛⎭⎪⎫-24,24, 经检验,符合条件MR MP =12,所以对于圆O 上任意一点M ,平面内存在一定点R ,使MR MP 为定值,且R 的坐标为⎝ ⎛⎭⎪⎫-24,24. 探究提高 本题考查直线与圆相切问题以及定值问题.相切问题的基本处理方法是将切点与圆心连接,从而它与切线相互垂直,利用这一直角来进行转化研究问题;第(2)问是探索性问题,在研究探索性问题时,先假设存在是一般性的处理方法,其次将所要研究的问题转化为关于点M 的坐标为元的方程问题,利用该方程的解与点M 的坐标无关来研究问题.【训练3】 (2019·泰州中学检测)已知圆O :x 2+y 2=4与坐标轴交于点A 1,A 2,B 1,B 2(如图).(1)点Q 是圆O 上除A 1,A 2外的任意点(如图1),A 2Q ,A 1Q 与直线y +3=0交于不同的两点M ,N ,求MN 的最小值;(2)点P 是圆O 上除A 1,A 2,B 1,B 2外的任意点(如图2),直线B 2P 交x 轴于点F ,直线A 1B 2交A 2P 于点E .设A 2P 的斜率为k ,EF 的斜率为m ,求证:2m -k 为定值.(1)解 由题意可设直线A 2Q 的方程为y =k ′(x -2),直线A 1Q 的方程为y =-1k ′(x+2),k ′≠0.由⎩⎨⎧y =k ′(x -2),y +3=0,解得⎩⎪⎨⎪⎧x =2-3k ′,y =-3,由⎩⎪⎨⎪⎧y =-1k ′(x +2),y +3=0,解得⎩⎨⎧x =3k ′-2,y =-3. 所以直线A 2Q 与直线y +3=0的交点为M ⎝ ⎛⎭⎪⎫2-3k ′,-3, 直线A 1Q 与直线y +3=0的交点为N (3k ′-2,-3),所以MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4. 当k ′>0时,MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4≥6-4=2,当且仅当k ′=1时等号成立; 当k ′<0时,MN =⎪⎪⎪⎪⎪⎪3k ′+3k ′-4≥|4-(-6)|=10,当且仅当k ′=-1时等号成立. 故线段MN 长度的最小值是2.(2)证明 由题意可知点A 1(-2,0),A 2(2,0),B 1(0,-2),B 2(0,2),A 2P 的斜率为k ,所以直线A 2P 的方程为y =k (x -2),由⎩⎨⎧y =k (x -2),x 2+y 2=4,得P ⎝ ⎛⎭⎪⎫2k 2-2k 2+1,-4k k 2+1, 则直线B 2P 的方程为y =-k +1k -1x +2, 令y =0,则x =2(k -1)k +1,即F ⎝ ⎛⎭⎪⎫2(k -1)k +1,0. 因为直线A 1B 2的方程为x -y +2=0,由⎩⎨⎧x -y +2=0,y =k (x -2),解得⎩⎪⎨⎪⎧x =2k +2k -1,y =4k k -1,所以E ⎝ ⎛⎭⎪⎫2k +2k -1,4k k -1, 所以EF 的斜率m =4kk -12k +2k -1-2(k -1)k +1=k +12, 所以2m -k =2·k +12-k =1(定值).【新题感悟】 (2019·苏北七市高三一模)在平面直角坐标系xOy 中,圆O :x 2+y 2=1,圆C :(x -4)2+y 2=4.若存在过点P (m ,0)的直线l ,l 被两圆截得的弦长相等,则实数m 的取值范围是________.解析 直线l 的斜率k 不存在或为0时均不成立,设直线l 的方程为kx -y -km =0,则圆心O (0,0)到直线l 的距离d 1=|km |k 2+1,圆心C (4,0)到直线l 的距离d 2=|4k -km |k 2+1.因为l 被两圆截得的弦长相等,所以21-d 21=24-d 22,即d 22-d 21=3,所以16k 2+k 2m 2-8k 2m -k 2m 2k 2+1=3,化为:16k 2-8k 2m =3k 2+3,k 2=313-8m>0,得:m <138.又d 21=k 2m 2k 2+1=m 21+1k 2=m 21+13-8m 3=3m 216-8m <1,即3m 2+8m -16<0,解得:-4<m <43.综上,-4<m <43.答案 ⎝ ⎛⎭⎪⎫-4,43一、填空题1.(2015·江苏卷)在平面直角坐标系xOy 中,以点(1,0)为圆心且与直线mx -y -2m -1=0(m ∈R )相切的所有圆中,半径最大的圆的标准方程为________.解析直线mx-y-2m-1=0恒过定点(2,-1),由题意,得半径最大的圆的半径r=(1-2)2+(0+1)2= 2.故所求圆的标准方程为(x-1)2+y2=2.答案(x-1)2+y2=22.(2019·靖江调研)已知圆C:x2+y2-2x-2y+1=0,直线l:3x+4y-17=0.若在直线l上任取一点M作圆C的切线MA,MB,切点分别为A,B,则AB的长度取最小值时直线AB的方程为________.解析圆C的标准方程为(x-1)2+(y-1)2=1,当AB的长度最小时,圆心角∠ACB最小,设为2θ,则由cos θ=ACCM=1CM,知当θ最小时,cos θ最大,即CM最小,那么CM⊥l,所以k AB=k l=-34.设直线AB的方程为3x+4y=m.又由CM=|3+4-17|5=2,此时cos θ=12,则点C到直线AB的距离为AC cos θ=12,即1 2=|3+4-m|5,解得m=192或m=92,经检验m=192,则直线AB的方程为6x+8y-19=0.答案6x+8y-19=03.在平面直角坐标系中,A,B分别是x轴和y轴上的动点,若以AB为直径的圆C与直线2x+y-4=0相切,则圆C面积的最小值为________.解析由题意可知以线段AB为直径的圆C过原点O,要使圆C的面积最小(D 为切点),只需圆C的半径或直径最小,又圆C与直线2x+y-4=0相切,所以由平面几何知识,当OC所在直线与直线2x+y-4=0垂直时,OD最小(D为切点),即圆C的直径最小,此时OD=|2×0+0-4|5=45,所以圆的半径为25,圆C的面积的最小值为S=πr2=4 5π.答案4 5π4.(2018·全国Ⅲ卷改编)直线x+y+2=0分别与x轴、y轴交于A,B两点,点P 在圆(x-2)2+y2=2上,则△ABP面积的取值范围是________.解析由题意知圆心的坐标为(2,0),半径r=2,圆心到直线x+y+2=0的距离d=|2+2|1+1=22,所以圆上的点到直线的最大距离是d+r=32,最小距离是d-r= 2.易知A(-2,0),B(0,-2),所以AB=22,所以2≤S△ABP≤6. 答案[2,6]5.(2019·常州调研)在平面直角坐标系xOy中,若圆(x-2)2+(y-2)2=1上存在点M,使得点M关于x轴的对称点N在直线kx+y+3=0上,则实数k的最小值为________.解析圆(x-2)2+(y-2)2=1关于x轴的对称圆的方程为(x-2)2+(y+2)2=1,由题意得圆心(2,-2)到直线kx+y+3=0的距离d=|2k-2+3|k2+1≤1,解得-43≤k≤0,所以实数k的最小值为-4 3.答案-4 36.(2019·南京、盐城模拟)在平面直角坐标系xOy中,已知点P为函数y=2ln x的图象与圆M:(x-3)2+y2=r2的公共点,且它们在点P处有公切线,若二次函数y=f(x)的图象经过点O,P,M,则y=f(x)的最大值为________.解析设P(x0,2ln x0),x0>0,则函数y=2ln x在点P处的切线斜率为2x0,则2x0·2ln x0x0-3=-1,即4ln x0=-x0·(x0-3)①.由二次函数y=f(x)的图象经过点O和M可设f (x )=ax (x -3),代入点P (x 0,2ln x 0),x 0>0,得2ln x 0=ax 0(x 0-3) ②.由①②比较可得a =-12,则f (x )=-12x (x -3),则f (x )max =f ⎝ ⎛⎭⎪⎫32=-12×32×⎝ ⎛⎭⎪⎫-32=98.答案 987.直线2ax +by =1与圆x 2+y 2=1相交于A ,B 两点(其中a ,b 是实数),且△AOB 是直角三角形(O 是坐标原点),则点P (a ,b )与点(0,1)之间距离的最小值为________.解析 根据题意画出图形,如图所示,过点O 作OC ⊥AB 于C ,因为△AOB 为等腰直角三角形,所以C 为弦AB 的中点,又OA =OB =1,根据勾股定理得AB =2, ∴OC =12AB =22.∴圆心(0,0)到直线2ax +by =1的距离为12a 2+b 2=22,即2a 2+b 2=2,即a 2=-12b 2+1≥0.∴-2≤b ≤ 2.则点P (a ,b )与点(0,1)之间的距离d =(a -0)2+(b -1)2=a 2+b 2-2b +1=12b 2-2b +2.设f (b )=12b 2-2b +2=12(b -2)2,此函数图象为对称轴为b =2的开口向上的抛物线,∴当-2≤b ≤2<2时,函数为减函数.∴f (b )min =f (2)=12(2-2)2, ∴d 的最小值为12(2-2)2=(2-1)2=2-1.答案2-18.(2019·南京师大附中模拟)已知直线x -y +b =0与圆x 2+y 2=9交于不同的两点A ,B .若O 是坐标原点,且|OA →+OB →|≥22|AB →|,则实数b 的取值范围是________. 解析 设AB 的中点为D ,则OA→+OB →=2OD →,故|OD →|≥24|AB →|,即|OD →|2≥18|AB →|2.再由直线与圆的弦长公式可得,AB =2r 2-d 2(d 为圆心到直线的距离),又直线与圆相交,故d <r ,得|b |2<3,所以-32<b <32,根据|OD→|2≥18|AB →|2,|AB →|2=4(9-OD →2),得|OD →|2≥3.由点到直线的距离公式可得|OD →|2=b 22,即b 22≥3,所以b ≥6或b ≤- 6.综上可得,b 的取值范围是(-32,-6]∪[6,32). 答案 (-32,-6]∪[6,32) 二、解答题9.如果实数x ,y 满足(x +2)2+y 2=3. (1)求yx 的最大值; (2)求2x -y 的最小值.解 (1)问题可转化为求圆(x +2)2+y 2=3上任意一点到原点连线的斜率k =yx 的最大值,由图形性质可知,由原点向圆(x +2)2+y 2=3作切线,其中切线斜率的最大值即为yx 的最大值.设切线方程为y =kx ,即kx -y =0,由|-2k -0|k 2+1=3,解得k =3或k =-3,所以yx 的最大值为 3.(2)将2x -y 看作直线y =2x +b 在y 轴上的纵截距的相反数,当直线y =2x +b 与圆(x +2)2+y 2=3相切时,纵截距b 取得最大值或最小值.此时|-4+b |22+1=3,所以b =4±15,所以2x -y 的最小值为-4-15. 10.(2019·扬州模拟)已知圆O :x 2+y 2=4.(1)直线l 1:3x +y -23=0与圆O 相交于A ,B 两点,求弦AB 的长度; (2)如图,设M (x 1,y 1),P (x 2,y 2)是圆O 上的两个动点,点M关于原点的对称点为M 1,点M 关于x 轴的对称点为M 2,如果直线PM 1,PM 2与y 轴分别交于(0,m )和(0,n ),问mn 是否为定值?若是,求出该定值;若不是,请说明理由.解 (1)由于圆心(0,0)到直线l 1:3x +y -23=0的距离d =|-23|2= 3.圆的半径r =2,所以AB =2r 2-d 2=2.(2)由于M (x 1,y 1),点M 关于原点的对称点为M 1,点M 关于x 轴的对称点为M 2,可得M 1(-x 1,-y 1),M 2(x 1,-y 1), 由M (x 1,y 1),P (x 2,y 2)是圆O 上的两个动点,可得x 21+y 21=4,x 22+y 22=4.直线PM 1的方程为y +y 1y 2+y 1=x +x 1x 2+x 1,令x =0,求得y =m =x 1y 2-x 2y 1x 2+x 1.直线PM 2的方程为y +y 1y 2+y 1=x -x 1x 2-x 1,令x =0,求得y =n =-x 1y 2-x 2y 1x 2-x 1.所以mn =x 22y 21-x 21y 22x 22-x 21=x 22(4-x 21)-x 21(4-x 22)x 22-x 21=4. 故mn 为定值.11.如图所示,已知圆A 的圆心在直线y =-2x 上,且该圆上存在两点关于直线x +y -1=0对称,又圆A 与直线l 1:x +2y +7=0相切,过点B (-2,0)的动直线l 与圆A 相交于M ,N 两点,Q 是MN 的中点,直线l 与l 1相交于点P .(1)求圆A 的方程;(2)当MN =219时,求直线l 的方程;(3)(BM →+BN →)·BP→是否为定值?如果是,求出此定值;如果不是,请说明理由.解 (1)由圆上存在两点关于直线x +y -1=0对称知圆心A 在直线x +y -1=0上.由⎩⎨⎧y =-2x ,x +y -1=0,得A (-1,2). 设圆A 的半径为R ,∵圆A 与直线l 1:x +2y +7=0相切,∴R =|-1+4+7|5=25, ∴圆A 的方程为(x +1)2+(y -2)2=20.(2)当直线l 与x 轴垂直时,易知x =-2符合题意; 当直线l 与x 轴不垂直时, 设直线l 的方程为y =k (x +2),即kx -y +2k =0,连接AQ ,则AQ ⊥MN , ∵MN =219,∴AQ =20-19=1. 由AQ =|k -2|k 2+1=1,得k =34, ∴直线l 的方程为y =34(x +2),即3x -4y +6=0, ∴所求直线l 的方程为x =-2或3x -4y +6=0. (3)∵AQ ⊥BP ,∴AQ →·BP→=0,∴(BM →+BN →)·BP →=2BQ →·BP →=2(BA →+AQ →)·BP →=2BA →·BP →; 当直线l 与x 轴垂直时,得P ⎝ ⎛⎭⎪⎫-2,-52,则BP →=⎝ ⎛⎭⎪⎫0,-52,又BA →=(1,2), ∴(BM →+BN →)·BP →=2BA →·BP→=-10;当直线l 的斜率存在时,设直线l 的方程为y =k (x +2), 由⎩⎨⎧y =k (x +2),x +2y +7=0,解得P ⎝ ⎛⎭⎪⎫-4k -71+2k ,-5k 1+2k , ∴BP →=⎝⎛⎭⎪⎫-51+2k ,-5k 1+2k , ∴(BM →+BN →)·BP →=2BA →·BP→=2⎝ ⎛⎭⎪⎫-51+2k -10k 1+2k =-10. 综上所述,(BM →+BN →)·BP→为定值-10.。
圆过定点问题(非常好)

实用文档圆过定点问题班级_________________姓名_______________1.已知定点G(﹣3,0),S是圆C:(X﹣3)2+y2=72(C为圆心)上的动点,SG的垂直平分线与SC交于点E.设点E的轨迹为M.(1)求M的方程;(2)是否存在斜率为1的直线,使得直线与曲线M相交于A,B两点,且以AB为直径的圆恰好经过原点?若存在,求出直线的方程;若不存在,请说明理由.2.在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x﹣3)2+(y﹣4)2=1.(Ⅰ)判断圆C1与圆C2的位置关系;(Ⅱ)若动圆C同时平分圆C1的周长、圆C2的周长,则动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.3.已知定点A(﹣2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F 的距离是它到定直线l的距离的倍,设点M的轨迹为E,点C是轨迹E上的任一点,直线AC与BC分别交直线l与点P,Q.(1)求点M的轨迹E的方程;(2)试判断以线段PQ为直径的圆是否经过定点F,并说明理由.4.如图,已知椭圆C:+y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=﹣2分别交于点M、N,(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.5.如图所示,已知圆C:x2+y2=r2(r>0)上点处切线的斜率为,圆C与y轴的交点分别为A,B,与x轴正半轴的交点为D,P为圆C在第一象限内的任意一点,直线BD与AP相交于点M,直线DP与y轴相交于点N.(1)求圆C的方程;(2)试问:直线MN是否经过定点?若经过定点,求出此定点坐标;若不经过,请说明理由.6.二次函数f(x)=3x2﹣4x+c(x∈R)的图象与两坐标轴有三个交点,经过这三个交点的圆记为⊙C.(1)求实数c的取值范围;(2)求⊙C的方程;(3)问⊙C是否经过某定点(其坐标与c的取值无关)?请证明你的结论.7.如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.(I)求证:当b变化时,圆C的圆心在一条定直线上;(II)求证:圆C经过除原点外的一个定点;(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?8.在平面直角坐标系xoy中,点M到两定点F1(﹣1,0)和F2(1,0)的距离之和为4,设点M的轨迹是曲线C.(1)求曲线C的方程;(2)若直线l:y=kx+m与曲线C相交于不同两点A、B(A、B不是曲线C和坐标轴的交点),以AB为直径的圆过点D(2,0),试判断直线l是否经过一定点,若是,求出定点坐标;若不是,说明理由.9.如图.直线l:y=kx+1与椭圆C1:交于A,C两点,A.C在x轴两侧,B,D是圆C2:x2+y2=16上的两点.且A与B.C与D的横坐标相同,纵坐标同号.(I)求证:点B纵坐标是点A纵坐标的2倍,并计算||AB|﹣|CD||的取值范围;(II)试问直线BD是否经过一个定点?若是,求出定点的坐标:若不是,说明理由.10.已知A(﹣1,0),B(2,0),动点M(x,y)满足=,设动点M的轨迹为C.(1)求动点M的轨迹方程,并说明轨迹C是什么图形;(2)求动点M与定点B连线的斜率的最小值;(3)设直线l:y=x+m交轨迹C于P,Q两点,是否存在以线段PQ为直径的圆经过A?若存在,求出实数m的值;若不存在,说明理由.11.已知定直线l:x=﹣1,定点F(1,0),⊙P经过F且与l相切.(1)求P点的轨迹C的方程.(2)是否存在定点M,使经过该点的直线与曲线C交于A、B两点,并且以AB为直径的圆都经过原点;若有,请求出M点的坐标;若没有,请说明理由.12.已知动圆P与圆M:(x+1)2+y2=16相切,且经过M内的定点N(1,0).(1)试求动圆的圆心P的轨迹C的方程;(2)设O是轨迹C上的任意一点(轨迹C与x轴的交点除外),试问在x轴上是否存在两定点A,B,使得直线OA与OB的斜率之积为定值(常数)?若存在,请求出定值,并求出所有满足条件的定点A、B 的坐标;若不存在,请说明理由.13.已知在△ABC中,点A、B的坐标分别为(﹣2,0)和(2,0),点C在x轴上方.(Ⅰ)若点C的坐标为(2,3),求以A、B为焦点且经过点C的椭圆的方程;(Ⅱ)若∠ACB=45°,求△ABC的外接圆的方程;(Ⅲ)若在给定直线y=x+t上任取一点P,从点P向(Ⅱ)中圆引一条切线,切点为Q.问是否存在一个定点M,恒有PM=PQ?请说明理由.2015年03月12日yinyongxia100的高中数学组卷参考答案与试题解析一.填空题(共1小题)1.已知定点G(﹣3,0),S是圆C:(X﹣3)2+y2=72(C为圆心)上的动点,SG的垂直平分线与SC交于点E.设点E的轨迹为M.(1)求M的方程;(2)是否存在斜率为1的直线,使得直线与曲线M相交于A,B两点,且以AB为直径的圆恰好经过原点?若存在,求出直线的方程;若不存在,请说明理由.考点:直线与圆锥曲线的综合问题.专题:圆锥曲线中的最值与范围问题.分析:(1)由已知条件推导出点E的轨迹是以G,C为焦点,长轴长为6的椭圆,由此能求出动点E的轨迹方程.(2)假设存在符合题意的直线l与椭圆C相交于A(x1,y1),B(x2,y2)两点,其方程为y=x+m,由,得3x2+4mx+2m2﹣18=0.由此能求出符合题意的直线l存在,所求的直线l的方程为y=x或y=x﹣2.解答:解:(1)由题知|EG|=|ES|,∴|EG|+|EC|=|ES|+|EC|=6.又∵|GC|=6,∴点E的轨迹是以G,C为焦点,长轴长为6的椭圆,∴动点E的轨迹方程为=1.…(4分)(2)假设存在符合题意的直线l与椭圆C相交于A(x1,y1),B(x2,y2)两点,其方程为y=x+m,由消去y,化简得3x2+4mx+2m2﹣18=0.∵直线l与椭圆C相交于A,B两点,∴△=16m2﹣12(2m2﹣18)>0,化简得m2<27,解得﹣3.…(6分)∴x1+x2=﹣,x1•x2=.∵以线段AB为直径的圆恰好经过原点,∴=0,所以x1x2+y1y2=0.…(8分)又y1y2=(x1+m)(x2+m)=x1x2+m(x1+x2)+m2,x1x2+y1y2=2x1x2+m(x1+x2)+m2=﹣+m2=0,解得m=.…(11分)由于(﹣3,3),∴符合题意的直线l存在,所求的直线l的方程为y=x或y=x﹣2.…(13分)点评:本题考查点的方程的求法,考查满足条件的直线是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.二.解答题(共12小题)2.在平面直角坐标系xOy中,已知圆C1:(x+1)2+y2=1,圆C2:(x﹣3)2+(y﹣4)2=1.(Ⅰ)判断圆C1与圆C2的位置关系;(Ⅱ)若动圆C同时平分圆C1的周长、圆C2的周长,则动圆C是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.考点:直线和圆的方程的应用.专题:直线与圆.分析:(Ⅰ)求出两圆的圆心距离,即可判断圆C1与圆C2的位置关系;(Ⅱ)根据圆C同时平方圆周,建立条件方程即可得到结论.解答:解:(Ⅰ)C1:(x+1)2+y2=1的圆心为(﹣1,0),半径r=1,圆C2:(x﹣3)2+(y﹣4)2=1的圆心为(3,4),半径R=1,则|C1C2|=,∴圆C1与圆C2的位置关系是相离.(Ⅱ)设圆心C(x,y),由题意得CC1=CC2,即,整理得x+y﹣3=0,即圆心C在定直线x+y﹣3=0上运动.设C(m,3﹣m),则动圆的半径,于是动圆C的方程为(x﹣m)2+(y﹣3+m)2=1+(m+1)2+(3﹣m)2,整理得:x2+y2﹣6y﹣2﹣2m(x﹣y+1)=0.由,解得或,即所求的定点坐标为(1﹣,2﹣),(1+,2+).点评:本题主要考查圆与圆的位置关系的判断,以及与圆有关的综合应用,考查学生的计算能力.3.已知定点A(﹣2,0),B(2,0),及定点F(1,0),定直线l:x=4,不在x轴上的动点M到定点F的距离是它到定直线l的距离的倍,设点M的轨迹为E,点C是轨迹E上的任一点,直线AC与BC分别交直线l与点P,Q.(1)求点M的轨迹E的方程;(2)试判断以线段PQ为直径的圆是否经过定点F,并说明理由.考点:轨迹方程;圆的标准方程.专题:直线与圆.分析:(1)由椭圆的第二定义即可知道点M的轨迹E为椭圆;(2)设出椭圆上的点C的坐标,进而写出直线AC、BC的方程,分别求出点P、Q的坐标,只要判断k PF•k QF=是否成立即可.﹣1解答:解:(1)由椭圆的第二定义可知:点M的轨迹E是以定点F(1,0)为焦点,离心率e=,直线l:x=4为准线的椭圆(除去与x轴相交的两点).∴c=1,,∴a=2,b2=22﹣12=3,∴点M的轨迹为椭圆E,其方程为(除去(±2,0)).(2)以线段PQ为直径的圆经过定点F.下面给出证明:如图所示:设C(x0,y0),(x0≠±2),则直线AC的方程为:,令x=4,则y P=,∴,∴=;直线BC的方程为:,令x=4,则y Q=,∴,∴k QF==.∴k PF•k QF==,∵点C(x0,y0)在椭圆上,∴,∴=﹣1,∴k PF•k QF=﹣1.因此以线段PQ为直径的圆经过定点F.点评:熟练掌握椭圆的定义、直线垂直与斜率的关系是解题的关键.4.如图,已知椭圆C:+y2=1的上、下顶点分别为A、B,点P在椭圆上,且异于点A、B,直线AP、BP与直线l:y=﹣2分别交于点M、N,(ⅰ)设直线AP、BP的斜率分别为k1、k2,求证:k1•k2为定值;(ⅱ)当点P运动时,以MN为直径的圆是否经过定点?请证明你的结论.考点:椭圆的应用.专题:综合题;圆锥曲线的定义、性质与方程.分析:(ⅰ)由椭圆方程求出两个顶点A,B的坐标,设出P点坐标,写出直线AP、BP的斜率k1,k2,结合P 的坐标适合椭圆方程可证结论;(ⅱ)设出以MN为直径的圆上的动点Q的坐标,由=0列式得到圆的方程,化为圆系方程后联立方程组可求解圆所过定点的坐标.解答:(ⅰ)证明:由题设椭圆C::+y2=1可知,点A(0,1),B(0,﹣1).令P(x0,y0),则由题设可知x0≠0.∴直线AP的斜率k1=,PB的斜率为k2=.又点P在椭圆上,∴+y02=1(x0≠1)从而有k1•k2=•=﹣;(ⅱ)解:以MN为直径的圆恒过定点(0,﹣2+2)或(0,﹣2﹣2).事实上,设点Q(x,y)是以MN为直径圆上的任意一点,则=0,故有+(y+2)(y+2)=0.又k1•k2=﹣∴以MN为直径圆的方程为x2+(y+2)2﹣12+=0.令x=0,则(y+2)2=12,解得y=﹣2±2.∴以MN为直径的圆恒过定点(0,﹣2+2)或(0,﹣2﹣2).点评:本题考查了直线的斜率,考查了直线与圆锥曲线的关系,考查了圆系方程,考查了学生的计算能力,是有一定难度题目.5.如图所示,已知圆C:x2+y2=r2(r>0)上点处切线的斜率为,圆C与y轴的交点分别为A,B,与x轴正半轴的交点为D,P为圆C在第一象限内的任意一点,直线BD与AP相交于点M,直线DP与y轴相交于点N.(1)求圆C的方程;(2)试问:直线MN是否经过定点?若经过定点,求出此定点坐标;若不经过,请说明理由.考点:直线与圆的位置关系.专题:直线与圆.分析:(1)根据条件结合点在圆上,求出圆的半径即可求圆C的方程;(2)根据条件求出直线MN的斜率,即可得到结论.解答:解:(1)∵,∴.∵点在圆C:x2+y2=r2上,∴.故圆C的方程为x2+y2=4.(2)设P(x0,y0),则x02+y02=4,直线BD的方程为x﹣y﹣2=0,直线AP的方程为y=+2联立方程组,得M(,),易得N(0,),∴k MN=2X===,∴直线MN的方程为y=x+,化简得(y﹣x)x0+(2﹣x)y0=2y﹣2x…(*)令,得,且(*)式恒成立,故直线MN经过定点(2,2).点评:本题主要考查圆的方程的求解,以及直线和圆的位置关系的应用,考查学生的计算能力.6.二次函数f(x)=3x2﹣4x+c(x∈R)的图象与两坐标轴有三个交点,经过这三个交点的圆记为⊙C.(1)求实数c的取值范围;(2)求⊙C的方程;(3)问⊙C是否经过某定点(其坐标与c的取值无关)?请证明你的结论.考点:圆的标准方程;二次函数的性质;圆系方程.专题:直线与圆.分析:(1)令x=0求出y的值,确定出抛物线与y轴的交点坐标,令f(x)=0,根据与x轴交点有两个得到c不为0且根的判别式的值大于0,即可求出c的范围;(2)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,令y=0得,x2+Dx+F=0,这与x2﹣x+=0是同一个方程,求出D,F.令x=0得,y2+Ey+F=0,此方程有一个根为c,代入得出E,由此求得圆C的一般方程;(3)圆C过定点(0,)和(,),证明:直接将点的坐标代入验证.解答:解:(1)令x=0,得抛物线与y轴的交点(0,c),令f(x)=3x2﹣4x+c=0,由题意知:c≠0且△>0,解得:c<且c≠0;(2)设圆C:x2+y2+Dx+Ey+F=0,令y=0,得到x2+Dx+F=0,这与x2﹣x+=0是一个方程,故D=﹣,F=;令x=0,得到y2+Ey+F=0,有一个根为c,代入得:c2+cE+=0,解得:E=﹣c﹣,则圆C方程为:x2+y2﹣x﹣(c+)y+=0;(3)圆C必过定点(0,)和(,),理由为:由x2+y2﹣x﹣(c+)y+=0,令y=,解得:x=0或,∴圆C必过定点(0,)和(,).点评:本题主要考查圆的标准方程,一元二次方程根的分布与系数的关系,体现了转化的数学思想,属于中档题.7.如图,抛物线M:y=x2+bx(b≠0)与x轴交于O,A两点,交直线l:y=x于O,B两点,经过三点O,A,B作圆C.(I)求证:当b变化时,圆C的圆心在一条定直线上;(II)求证:圆C经过除原点外的一个定点;(III)是否存在这样的抛物线M,使它的顶点与C的距离不大于圆C的半径?考点:圆与圆锥曲线的综合;圆的一般方程;抛物线的简单性质.专题:计算题.分析:(I)在方程y=x2+bx中.令y=0,y=x,易得A,B的坐标表示,设圆C的方程为x2+y2+Dx+Ey=0,利用条件得出,写出圆C的圆心坐标的关系式,从而说明当b变化时,圆C的圆心在定直线y=x+1上.(II)设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,它对任意b≠0恒成立,从而求出m,n的值,从而得出当b变化时,(I)中的圆C经过除原点外的一个定点坐标;(III)对于存在性问题,可先假设存在,即假设存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,再利用不等关系,求出b,若出现矛盾,则说明假设不成立,即不存在;否则存在.解答:解:(I)在方程y=x2+bx中.令y=0,y=x,易得A(﹣b,0),B(1﹣b,1﹣b)设圆C的方程为x2+y2+Dx+Ey=0,则⇒,故经过三点O,A,B的圆C的方程为x2+y2+bx+(b﹣2)y=0,设圆C的圆心坐标为(x0,y0),则x0=﹣,y0=﹣,∴y0=x0+1,这说明当b变化时,(I)中的圆C的圆心在定直线y=x+1上.(II)设圆C过定点(m,n),则m2+n2+bm+(b﹣2)n=0,整理得(m+n)b+m2+n2﹣2n=0,它对任意b≠0恒成立,∴⇒或故当b变化时,(I)中的圆C经过除原点外的一个定点坐标为(﹣1,1).(III)抛物线M的顶点坐标为(﹣,﹣),若存在这样的抛物线M,使它的顶点与它对应的圆C的圆心之间的距离不大于圆C的半径,则|﹣|≤,整理得(b2﹣2b)2≤0,因b≠0,∴b=2,以上过程均可逆,故存在抛物线M:y=x2+2x,使它的顶点与C的距离不大于圆C的半径.点评:本题考查了二次函数解析式的确定,圆的一般方程,抛物线的简单性质等知识点.综合性较强,考查学生数形结合的数学思想方法.8.在平面直角坐标系xoy中,点M到两定点F1(﹣1,0)和F2(1,0)的距离之和为4,设点M的轨迹是曲线C.(1)求曲线C的方程;(2)若直线l:y=kx+m与曲线C相交于不同两点A、B(A、B不是曲线C和坐标轴的交点),以AB为直径的圆过点D(2,0),试判断直线l是否经过一定点,若是,求出定点坐标;若不是,说明理由.考点:轨迹方程;直线与圆锥曲线的关系.专题:综合题;圆锥曲线的定义、性质与方程.分析:(1)由椭圆的定义可知,点M的轨迹C是以两定点F1(﹣1,0)和F2(1,0)为焦点,长半轴长为2的椭圆,由此可得曲线C的方程;(2)直线y=kx+m代入椭圆方程,利用韦达定理,结合以AB为直径的圆过点D(2,0),即可求得结论.解答:解:(1)设M(x,y),由椭圆的定义可知,点M的轨迹C是以两定点F1(﹣1,0)和F2(1,0)为焦点,长半轴长为2的椭圆∴短半轴长为=∴曲线C的方程为;(2)设A(x1,y1),B(x2,y2),则直线y=kx+m代入椭圆方程,消去y可得(3+4k2)x2+8mkx+4(m2﹣3)=0∴x1+x2=﹣,x1x2=∴y1y2=(kx1+m)(kx2+m)=∵以AB为直径的圆过点D(2,0),∴k AD k BD=﹣1∴y1y2+x1x2﹣2(x1+x2)+4=0∴∴7m2+16mk+4k2=0∴m=﹣2k或m=﹣,均满足△=3+4k2﹣m2>0当m=﹣2k时,l的方程为y=k(x﹣2),直线过点(2,0),与已知矛盾;当m=﹣时,l的方程为y=k(x﹣),直线过点(,0),∴直线l过定点,定点坐标为(,0).点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.9.(2013•温州二模)如图.直线l:y=kx+1与椭圆C1:交于A,C两点,A.C在x轴两侧,B,D是圆C2:x2+y2=16上的两点.且A与B.C与D的横坐标相同.纵坐标同号.(I)求证:点B纵坐标是点A纵坐标的2倍,并计算||AB|﹣|CD||的取值范围;(II)试问直线BD是否经过一个定点?若是,求出定点的坐标:若不是,说明理由.考点:直线与圆锥曲线的关系;两点间的距离公式.专题:综合题;圆锥曲线的定义、性质与方程.分析:(I)设A(x1,y1),B(x1,y2),分别代入椭圆、圆的方程可得,消掉x1得,由y1,y2同号得y2=2y1,设C(x3,y3),D(x3,y4),同理可得y4=2y3,联立直线与椭圆方程消掉y得x 的二次方程,由A、C在x轴的两侧,得y1y3<0,代入韦达定理可求得k2范围,而||AB|﹣|CD||=||y1|﹣|y3||=|y1+y3|=|k(x1+x3)+2|,再由韦达定理及k2范围即可求得答案;(II)由斜率公式求出直线BD的斜率,由点斜式写出直线BD方程,再由点A在直线l上可得直线BD方程,从而求得其所过定点.解答:(I)证明:设A(x1,y1),B(x1,y2),根据题意得:⇒,∵y1,y2同号,∴y2=2y1,设C(x3,y3),D(x3,y4),同理可得y4=2y3,∴|AB|=|y1|,|CD|=|y3|,由⇒(4k2+1)x2+8kx﹣12=0,△>0恒成立,则,,∵A、C在x轴的两侧,∴y1y3<0,∴(kx1+1)(kx3+1)=k2x1x3+k(x1+x3)+1=<0,∴,∴||AB|﹣|CD||=||y1|﹣|y3||=|y1+y3|=|k(x1+x3)+2|=∈(0,);(II)解:∵直线BD的斜率=2k,∴直线BD的方程为y=2k(x﹣x1)+2y1=2kx﹣2(kx1﹣y1),∵y1=kx1+1,∴直线BD的方程为y=2kx+2,∴直线BD过定点(0,2).点评:本题考查直线与圆锥曲线的位置关系、两点间的距离公式,考查学生分析解决问题的能力,本题中多次用到韦达定理,应熟练掌握.10.已知A(﹣1,0),B(2,0),动点M(x,y)满足=,设动点M的轨迹为C.(1)求动点M的轨迹方程,并说明轨迹C是什么图形;(2)求动点M与定点B连线的斜率的最小值;(3)设直线l:y=x+m交轨迹C于P,Q两点,是否存在以线段PQ为直径的圆经过A?若存在,求出实数m的值;若不存在,说明理由.考点:轨迹方程;圆方程的综合应用.专题:综合题;探究型.分析:解:(1)先将条件化简即得动点M的轨迹方程,并说明轨迹C是图形:轨迹C是以(﹣2,0)为圆心,2为半径的圆.(2)先设过点B的直线为y=k(x﹣2).利用圆心到直线的距离不大于半径即可解得k的取值范围,从而得出动点M与定点B连线的斜率的最小值即可;(3)对于存在性问题,可先假设存在,即存在以线段PQ为直径的圆经过A,再利用PA⊥QA,求出m的长,若出现矛盾,则说明假设不成立,即不存在;否则存在.解答:解:(1)化简可得(x+2)2+y2=4.轨迹C是以(﹣2,0)为圆心,2为半径的圆(3分)(2)设过点B的直线为y=k(x﹣2).圆心到直线的距离≤2∴,k min=(7分)(3)假设存在,联立方程得2x2+2(m+2)x+m2=0设P(x1,y1),Q(x2,y2)则x1+x2=﹣m﹣2,x1x2=PA⊥QA,∴(x1+1)(x2+1)+y1y2=(x1+1)(x2+1)+(x1+m)(x2+m)=0,2x1x2+(m+1)(x1+x2)+m2+1=0得m2﹣3m﹣1=0,且满足△>0.∴(12分)点评:求曲线的轨迹方程是解析几何的两个基本问题之一求符合某种条件的动点的轨迹方程,其实质就是利用题设中的几何条件,用“坐标化”将其转化为寻求变量间的关系,求曲线的轨迹方程常采用的方法有直接法、定义法、代入法、参数法.本题是利用的直接法.直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.11.已知定直线l:x=﹣1,定点F(1,0),⊙P经过F且与l相切.(1)求P点的轨迹C的方程.(2)是否存在定点M,使经过该点的直线与曲线C交于A、B两点,并且以AB为直径的圆都经过原点;若有,请求出M点的坐标;若没有,请说明理由.考点:直线与圆锥曲线的综合问题.专题:直线与圆.分析:(1)由已知得点P的轨迹C是以F为焦点,l为准线的抛物线,由此能求出点P的轨迹C的方程.(2)设AB的方程为x=my+n,代入抛物线方程整理,得:y2﹣4my﹣4n=0,由此利用韦达定理、直径性质能求出直线AB:x=my+4恒过M(4,0)点.解答:解:(1)由题设知点P到点F的距离与点P到直线l的距离相等,∴点P的轨迹C是以F为焦点,l为准线的抛物线,∴点P的轨迹C的方程为y2=4x.(2)设AB的方程为x=my+n,代入抛物线方程整理,得:y2﹣4my﹣4n=0,设A(x1,y1),B(x2,y2),则,∵以AB为直径的圆过原点,∴OA⊥OB,∴y1y2+x1x2=0,∴,∴y1y2=﹣16,∴﹣4n=﹣16,解得n=4,∴直线AB:x=my+4恒过M(4,0)点.点评:本题考查点的轨迹方程的求法,考查满足条件的点的坐标是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.12.已知动圆P与圆M:(x+1)2+y2=16相切,且经过M内的定点N(1,0).(1)试求动圆的圆心P的轨迹C的方程;(2)设O是轨迹C上的任意一点(轨迹C与x轴的交点除外),试问在x轴上是否存在两定点A,B,使得直线OA与OB的斜率之积为定值(常数)?若存在,请求出定值,并求出所有满足条件的定点A、B的坐标;若不存在,请说明理由.考点:圆方程的综合应用;圆与圆的位置关系及其判定.分析:(1)利用动圆P与定圆(x﹣1)2+y2=16相内切,以及椭圆的定义,可得动圆圆心P的轨迹M的方程;(2)先设任意一点以及A、B的坐标,k QA•k QB=k(常数),根据轨迹方程列出关于k、s、t的方程,并求出k、s、t的值,即可求出结果.解答:解:(1)由题意,两圆相内切,故,|PM|=4﹣|PN|,即|PM|+|PN|=4.又∵MN=2<4∴动圆的圆心P的轨迹为以M、N为焦点,长轴长为4的椭圆.动点P的轨迹方程为.(2)设点Q(x0,y0),则,x0≠±2设A(s,0),B(t,0),k QA•k QB=k(常数)∴k QA•k QB=整理得(4k+3)x02﹣4k(s+t)x0+4(kst﹣3)=0由题意,上面的方程对(﹣2,2)内的一切x0均成立∴4k+3=0,﹣4k(s+t)=0且4(kst﹣3)=0解得k=﹣,s=2,t=﹣2,或s=﹣2,t=2∴在x轴上只存在两定点A(2,0)、B(﹣2,0)使得直线QA与QB的斜率之积为定值﹣.点评:题考查圆的基本知识和轨迹方程的求法以及斜率的求法,解题时要注意公式的灵活运用,此题有一定难度.13.(2010•盐城二模)已知在△ABC中,点A、B的坐标分别为(﹣2,0)和(2,0),点C在x轴上方.(Ⅰ)若点C的坐标为(2,3),求以A、B为焦点且经过点C的椭圆的方程;(Ⅱ)若∠ACB=45°,求△ABC的外接圆的方程;(Ⅲ)若在给定直线y=x+t上任取一点P,从点P向(Ⅱ)中圆引一条切线,切点为Q.问是否存在一个定点M,恒有PM=PQ?请说明理由.考点:椭圆的标准方程;圆的标准方程;直线和圆的方程的应用.专题:计算题;存在型.分析:(Ⅰ)根据椭圆的定义和AC,BC求得椭圆的长轴,进而根据c求得b,则椭圆的方程可得.(Ⅱ)先用正弦定理可知=2R,进而求得R,设出圆心坐标,根据勾股定理求的s,则外接圆的方程可得.(Ⅲ)假设存在这样的点M(m,n),设点P的坐标,进而根据PM=PQ,求得关于x的方程,进而列出方程组,消去m,得到关于n的一元二次方程,分别讨论当判别式大于0或小于等于0时的情况.解答:解:(Ⅰ)因为AC=5,BC=3,所以椭圆的长轴长2a=AC+BC=8,又c=2,所以b=2,故所求椭圆的方程为(Ⅱ)因为=2R,所以2R=4,即R=2又圆心在AB的垂直平分线上,故可设圆心为(0,s)(s>0),则由4+S2=8,所以△ABC的外接圆的方程为x2+(y﹣2)2=8(Ⅲ)假设存在这样的点M(m,n),设点P的坐标为(x,x+t),因为恒有PM=PQ,所以(x﹣m)2+(x+t ﹣n)2=x2+(x+t﹣2)2﹣8,即(2m+2n﹣4)x﹣(m2+n2﹣2nt+4t+4)=0,对x∈R,恒成立,从而,消去m,得n2﹣(t+2)n+(2t+4)=0因为方程判别式△=t2﹣4t﹣12,所以①当﹣2<t<6,时,因为方程无实数解,所以不存在这样的点M②当t≥6或t≤﹣2时,因为方程有实数解,且此时直线y=x+t与圆相离或相切,故此时这样的点M存在.点评:本题主要考查了椭圆的标准方程和椭圆与直线的关系.考查了学生综合分析问题的能力.。
圆锥曲线中动圆恒过一类定点问题的研究

圆锥曲线中动圆恒过一类定点问题的研究林㊀蔓(福建省石狮市石光中学ꎬ福建石狮362700)摘㊀要:笔者通过探究圆锥曲线中满足某些条件的动圆恒过定点的问题ꎬ得到的结论是这些问题中的动圆都恒过定点O1(-b-aꎬ0)ꎬO2(b-aꎬ0).关键词:圆锥曲线ꎻ圆ꎻ定点ꎻ切线ꎻ研究中图分类号:G632㊀㊀㊀文献标识码:A㊀㊀㊀文章编号:1008-0333(2023)36-0029-03收稿日期:2023-09-25作者简介:林蔓(1980.5-)ꎬ女ꎬ福建省石狮人ꎬ本科ꎬ中学一级教师ꎬ从事高中数学教学研究.㊀㊀圆锥曲线中动圆恒过定点问题ꎬ十年前的高考题考过几次ꎬ最近几年的模拟题也经常出现.笔者经过研究ꎬ发现不少的圆锥曲线问题中的动圆都恒过相同的定点ꎬ即都经过点O1(-b-aꎬ0)ꎬO2(b-aꎬ0).1预备知识引理1㊀设A(x1ꎬy1)ꎬB(x2ꎬy2)ꎬ则以线段AB为直径的圆的方程为(x-x1)(x-x2)+(y-y1)(y-y2)=0.证明㊀设M(xꎬy)是所求圆上的任一点ꎬ则AMʅBMꎬ即AMң BMң=0ꎬ即(x-x1ꎬy-y1) (x-x2ꎬy-y2)=0ꎬ化简得(x-x1)(x-x2)+(y-y1)(y-y2)=0.引理2㊀设P(x0ꎬy0)是椭圆x2a2+y2b2=1上的一点ꎬ则椭圆在点P(x0ꎬy0)处的切线方程为x0xa2+y0yb2=1[1].证明㊀当y0=0时ꎬ点P(x0ꎬy0)处的切线的斜率不存在ꎬ其方程为x=ʃa.当y0ʂ0时ꎬ设椭圆在点P(x0ꎬy0)处的切线方程为y-y0=k(x-x0)ꎬ代入椭圆方程化简得ꎬ(b2+a2k2)x2+2a2k(y0-kx0)x+a2[(y0-kx0)2-b2]=0[2].由题意ꎬә=4a4k2(y0-kx0)2-4(b2+a2k2)a2[(y0-kx0)2-b2]=0ꎬ化简得k2(x20-a2)-2kx0y0+(y20-b2)=0.因为点P(x0ꎬy0)在椭圆上ꎬ所以x20-a2=-a2y20b2ꎬy20-b2=-b2x20a2ꎬ代入上式化简得(a2y0k+b2x0)2=0ꎬ从而k=-b2x0a2y0.因此切线方程为y-y0=-b2x0a2y0(x-x0)ꎬ即b2x0x+a2y0y=b2x20+a2y20ꎬ等式两边同时除以a2b2ꎬ得x0xa2+y0yb2=x20a2+y20b2.又点P(x0ꎬy0)在椭圆上ꎬ所以x20a2+y20b2=1ꎬ故切线方程为x0xa2+y0yb2=1.引理3㊀设A(x0ꎬy0)为双曲线x2a2-y2b2=192(a>0ꎬb>0)外一点ꎬ则由点A作此双曲线的两切线的方程为(x20a2-y20b2-1)(x2a2-y2b2-1)=(x0xa2-y0yb2-1)2.2主要结果及证明命题1㊀如图1ꎬ双曲线Γ:x2a2-y2b2=1(a>0ꎬb>0)ꎬ设直线l平行于y轴且与Γ相切ꎬA是y轴上任一点ꎬ过A且与Γ相切的两条直线分别交l于PꎬQꎬ以PQ为直径作圆ꎬ此圆交x轴于两点.求证:这两点是定点(记为O1ꎬO2).图1㊀命题1图证明㊀设A(0ꎬm)ꎬP(0ꎬyP)ꎬQ(0ꎬyQ)ꎬ由引理3知过A的两切线方程为(-m2b2-1)(x2a2-y2b2-1)=(-myb2-1)2.令x=-aꎬ得m2+b2b2 y2b2=(my+b2b2)2⇒y2-2my-b2=0ꎬ故yPyQ=-b2.由引理1知以PQ为直径的圆为(x-a)2+(y-yP)(y-yQ)=0ꎬ令y=0ꎬ得(x+a)2+yPyQ=0⇒(x+a)2=b2⇒x=-aʃbꎬ所以圆与x轴交于两个定点ꎬ其坐标为O1(-b-aꎬ0)ꎬO2(b-aꎬ0).命题2㊀如图2ꎬ设椭圆的方程为x2a2+y2b2=1a>b>0()ꎬAꎬB为椭圆的左㊁右顶点ꎬ过AꎬB且与椭圆相切的直线分别为lꎬlᶄꎬ再作椭圆的任一切线分别交lꎬlᶄ于CꎬDꎬDO交l于Eꎬ设以线段CE为直径的圆交x轴于O1ꎬO2ꎬ求证:O1ꎬO2为定点[3].图2㊀命题2图证明㊀设切点Fx0ꎬy0()ꎬ则由引理2知切线CD:x0xa2+y0yb2=1ꎬ又l:x=-aꎬlᶄ:x=aꎬ得C-aꎬb2x0+a()ay0æèçöø÷ꎬDaꎬb2a-x0()ay0æèçöø÷ꎬ则E-aꎬb2x0-a()ay0æèçöø÷ꎬ由引理1知以线段CE为直径的圆为x+a()2+y-b2x0+a()ay0æèçöø÷y-b2x0-a()ay0æèçöø÷=0ꎬ令y=0ꎬ得x+a()2=b4a2-x20()a2y20=b4a2-x20()b2a2-x20()=b2ꎬ⇒x=-aʃbꎬ故以线段CE为直径的圆过两定点O1-b-aꎬ0()ꎬO2b-aꎬ0().命题3㊀如图3ꎬ设椭圆的方程为x2a2+y2b2=1a>b>0()ꎬA为椭圆的下顶点ꎬB为椭圆上任一点ꎬ过A的切线为lꎬ过B的切线交l于Cꎬ过O且与BA平行的直线交l于Eꎬ设以线段CE为直径的圆交y轴于O1ꎬO2ꎬ求证:O1ꎬO2为定点.图3㊀命题3图证明㊀设切点Bx0ꎬy0()ꎬ则由引理2知切线BC:x0xa2+y0yb2=1ꎬ又切线l:y=-bꎬ则03Ca2y0+b()bx0ꎬ-bæèçöø÷ꎬ因直线OE平行于BAꎬ故直线OE的方程为y=y0+bx0x.令y=-bꎬ则x=-bx0y0+bꎬE-bx0y0+bꎬ-bæèçöø÷ꎬ由引理1知以线段CE为直径的圆的方程为x-a2y0+b()bx0[]x+bx0y0+bæèçöø÷+y+b()2=0.令x=0ꎬ得y+b()2=a2ꎬy=-bʃaꎬ故以线段CE为直径的圆过两定点O10ꎬ-a-b()ꎬO20ꎬa-b().命题4㊀如图4ꎬ设椭圆的方程为x2a2+y2b2=1a>b>0()ꎬAꎬB为椭圆的上㊁下顶点ꎬ过AꎬB且与椭圆相切的直线分别为lꎬlᶄꎬ再作椭圆的任一切线分别交lꎬlᶄ于CꎬPꎬCO交l于Qꎬ设以线段PQ为直径的圆交x轴于O1ꎬO2ꎬ求证:O1ꎬO2为定点.图4㊀命题4图证明㊀设切点Dx0ꎬy0()ꎬ则由引理2知切线CP:x0xa2+y0yb2=1ꎬ又l:y=aꎬlᶄy:=-aꎬ得Ca2b-y0()bx0ꎬbæèçöø÷ꎬPa2y0+b()bx0ꎬ-bæèçöø÷ꎬQ与C关于O对称ꎬ得Qa2y0-b()bx0ꎬ-bæèçöø÷.由引理1知以线段PQ为直径的圆的方程为x-a2y0-b()bx0[]x-a2y0+b()bx0[]+y+b()2=0.令x=0ꎬ得y+b()2=a4b2-y20()b2x20=a4b2-y20()a2b2-y20()=a2ꎬ即y=-bʃa.故以线段PQ为直径的圆过两定点O10ꎬ-a-b()ꎬO20ꎬa-b().圆锥曲线内容是高中数学的难点ꎬ高中生要想突破这一块内容ꎬ需要有探索和研究的精神.掌握一些重要的结论是非常必要的ꎬ比如上文提到的3个引理.当然了ꎬ学生对于圆锥曲线的困难主要还是在运算上ꎬ那就需要我们平时多练ꎬ熟悉解题过程中设点或者设线的一些方法ꎬ这可以帮我们简化运算.有时结合同构思想㊁点差法或者对称思想ꎬ也可简化运算.追溯圆锥曲线的研究ꎬ最有影响力的还得属于阿波罗尼奥斯ꎬ他的著作«圆锥曲线论»揽尽了圆锥曲线几乎所有的性质ꎬ而且他是用几何方法给出的证明.后来笛卡尔创立了直角坐标系后ꎬ人们就可以利用坐标法来研究圆锥曲线问题了.再到后来ꎬ产生了射影几何ꎬ圆锥曲线的研究得到了新的突破.而最近十年的高考真题中ꎬ有不少题就是以射影几何中的极点㊁极线或者调和点列㊁调和线束为背景来命制的ꎬ这需要一线教师掌握一定的射影几何知识ꎬ这样才能居高临下ꎬ教学才能做到深入浅出.研究圆锥曲线是有意义的ꎬ有价值的.一线教师可以根据圆的性质ꎬ进行类比推广得到圆锥曲线的性质ꎬ也可以对高考中的圆锥曲线题进行一般化探究ꎬ还可以把射影几何中的经典结合初等化后ꎬ利用初等方法进行研究.圆锥曲线的性质是优美的ꎬ也是丰富的ꎬ很多高考圆锥曲线题就是命题人的最新研究成果.总而言之ꎬ不论是高中教师还是高中生ꎬ都很有必要去探索㊁去研究圆锥曲线的各种优美性质.参考文献:[1]刘海涛.极点极线视角下对一道模考题的探析㊁变式㊁推广[J].中学数学研究(华南师范大学版)ꎬ2023(11):7-10.[2]李鸿昌.高考题的高数探源与初等解法[M].合肥:中国科学技术大学出版社ꎬ2022(4).[3]陈传麟.圆锥曲线习题集[M].哈尔滨:哈尔滨工业大学出版社ꎬ2013(6).[责任编辑:李㊀璟]13。
高考数学一轮复习考点知识专题讲解67---圆锥曲线中定点与定值问题

高考数学一轮复习考点知识专题讲解圆锥曲线中定点与定值问题题型一 定点问题例1已知定圆A :(x +3)2+y 2=16,动圆M 过点B (3,0),且和圆A 相切. (1)求动圆圆心M 的轨迹E 的方程;(2)设不垂直于x 轴的直线l 与轨迹E 交于不同的两点P ,Q ,点N (4,0).若P ,Q ,N 三点不共线,且∠ONP =∠ONQ .证明:动直线PQ 经过定点. (1)解圆A 的圆心为A (-3,0),半径r 1=4. 设动圆M 的半径为r 2, 依题意有r 2=|MB |.由|AB |=23,可知点B 在圆A 内,从而圆M 内切于圆A , 故|MA |=r 1-r 2,即|MA |+|MB |=4>2 3.所以动点M 的轨迹E 是以A ,B 为焦点,长轴长为4的椭圆, 其方程为x 24+y 2=1.(2)证明设直线l 的方程为y =kx +b (k ≠0), 联立⎩⎨⎧y =kx +b ,x 2+4y 2=4,消去y 得,(1+4k 2)x 2+8kbx +4b 2-4=0,Δ=16(4k 2-b 2+1)>0,设P (x 1,kx 1+b ),Q (x 2,kx 2+b ),则x1+x2=-8kb1+4k2,x1x2=4b2-41+4k2,于是k PN+k QN=kx1+bx1-4+kx2+bx2-4=2kx1x2-(4k-b)(x1+x2)-8b(x1-4)(x2-4),由∠ONP=∠ONQ知k PN+k QN=0.即2kx1x2-(4k-b)(x1+x2)-8b=2k·4b2-41+4k2-(4k-b)-8kb1+4k2-8b=8kb2-8k1+4k2+32k2b-8kb21+4k2-8b=0,得b=-k,Δ=16(3k2+1)>0.故动直线l的方程为y=kx-k,过定点(1,0).教师备选在平面直角坐标系中,已知动点M(x,y)(y≥0)到定点F(0,1)的距离比到x轴的距离大1.(1)求动点M的轨迹C的方程;(2)过点N(4,4)作斜率为k1,k2的直线分别交曲线C于不同于N的A,B两点,且1k1+1k2=1.证明:直线AB恒过定点.(1)解由题意可知x2+(y-1)2=y+1,化简可得曲线C:x2=4y.(2)证明由题意可知,N(4,4)是曲线C:x2=4y上的点,设A(x1,y1),B(x2,y2),则l NA:y=k1(x-4)+4,l NB:y=k2(x-4)+4,联立直线NA 的方程与抛物线C 的方程, ⎩⎨⎧y =k 1(x -4)+4,x 2=4y⇒x 2-4k 1x +16(k 1-1)=0, 解得x 1=4(k 1-1),① 同理可得x 2=4(k 2-1),② 而l AB :y -x 214=x 1+x 24(x -x 1),③又1k 1+1k 2=1,④由①②③④整理可得l AB :y =(k 1+k 2-2)x -4, 故直线AB 恒过定点(0,-4).思维升华 求解直线或曲线过定点问题的基本思路(1)把直线或曲线方程中的变量x ,y 当作常数看待,把方程一端化为零,既然是过定点,那么这个方程就要对任意参数都成立,这时参数的系数就要全部等于零,这样就得到一个关于x ,y 的方程组,这个方程组的解所确定的点就是直线或曲线所过的定点. (2)由直线方程确定其过定点时,若得到了直线方程的点斜式y -y 0=k (x -x 0),则直线必过定点(x 0,y 0);若得到了直线方程的斜截式y =kx +m ,则直线必过定点(0,m ).跟踪训练1(2022·邯郸质检)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的焦距为23,且过点⎝⎛⎭⎪⎫3,12.(1)求椭圆方程;(2)设直线l :y =kx +m (k ≠0)交椭圆C 于A ,B 两点,且线段AB 的中点M 在直线x =12上,求证:线段AB 的中垂线恒过定点N . (1)解椭圆过点⎝ ⎛⎭⎪⎫3,12,即3a 2+14b 2=1,又2c =23,得a 2=b 2+3,所以a 2=4,b 2=1,即椭圆方程为x 24+y 2=1.(2)证明由⎩⎨⎧x 24+y 2=1,y =kx +m ,得(1+4k 2)x 2+8kmx +4m 2-4=0,Δ=16(4k 2-m 2+1)>0, 设A (x 1,y 1),B (x 2,y 2), 则x 1+x 2=-8km1+4k 2, 设AB 的中点M 为(x 0,y 0), 得x 0=-4km 1+4k 2=12,即1+4k 2=-8km ,所以y 0=kx 0+m =12k -1+4k 28k =-18k .所以AB 的中垂线方程为y +18k =-1k ⎝ ⎛⎭⎪⎫x -12,即y =-1k ⎝ ⎛⎭⎪⎫x -38,故AB 的中垂线恒过点N ⎝ ⎛⎭⎪⎫38,0.题型二 定值问题例2(2022·江西赣抚吉名校联考)已知抛物线E :y 2=2px (p >0)上的动点M 到直线x =-1的距离比到抛物线E 的焦点F 的距离大12.(1)求抛物线E 的标准方程;(2)设点Q 是直线x =-1(y ≠0)上的任意一点,过点P (1,0)的直线l 与抛物线E 交于A ,B 两点,记直线AQ ,BQ ,PQ 的斜率分别为k AQ ,k BQ ,k PQ ,证明:k AQ +k BQk PQ为定值. (1)解由题意可知抛物线E 的准线方程为x =-12,所以-p 2=-12,即p =1,故抛物线E 的标准方程为y 2=2x .(2)证明设Q (-1,y 0),A (x 1,y 1),B (x 2,y 2),因为直线l 的斜率显然不为0,故可设直线l 的方程为x =ty +1. 联立⎩⎨⎧x =ty +1,y 2=2x ,消去x ,得y 2-2ty -2=0.Δ=4t 2+8>0,所以y 1+y 2=2t ,y 1y 2=-2,k PQ =-y 02.又k AQ +k BQ =y 1-y 0x 1+1+y 2-y 0x 2+1=(y 1-y 0)(x 2+1)+(y 2-y 0)(x 1+1)(x 1+1)(x 2+1)=(y 1-y 0)(ty 2+2)+(y 2-y 0)(ty 1+2)(ty 1+2)(ty 2+2)=2ty 1y 2+(2-ty 0)(y 1+y 2)-4y 0t 2y 1y 2+2t (y 1+y 2)+4=2t ·(-2)+(2-ty 0)·2t -4y 0t 2·(-2)+2t ·2t +4=-y 0(t 2+2)t 2+2=-y 0.所以k AQ +k BQ k PQ =-y 0-y 02=2(定值).教师备选(2022·邯郸模拟)已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1,F 2,过点F 1的直线l 交椭圆于A ,B 两点,交y 轴于点M ,若|F 1F 2|=2,△ABF 2的周长为8. (1)求椭圆C 的标准方程;(2)MA →=λF 1A —→,MB →=μF 1B —→,试分析λ+μ是否为定值,若是,求出这个定值,否则,说明理由.解(1)因为△ABF 2的周长为8, 所以4a =8,解得a =2,由|F 1F 2|=2,得2a 2-b 2=24-b 2=2, 所以b 2=3,因此椭圆C 的标准方程为x 24+y 23=1.(2)由题意可得直线l 的斜率存在, 设直线l 的方程为y =k (x +1),由⎩⎨⎧y =k (x +1),x 24+y23=1,整理得(3+4k 2)x 2+8k 2x +4k 2-12=0, 显然Δ>0,设A (x 1,y 1),B (x 2,y 2), 则⎩⎪⎨⎪⎧x 1+x 2=-8k 23+4k 2,x 1x 2=4k 2-123+4k 2.设M (0,k ),又F 1(-1,0),所以MA →=(x 1,y 1-k ),F 1A —→=(x 1+1,y 1), 则λ=x 1x 1+1.同理可得MB →=(x 2,y 2-k ), F 1B —→=(x 2+1,y 2),则μ=x 2x 2+1.所以λ+μ=x 1x 1+1+x 2x 2+1=x 1(x 2+1)+x 2(x 1+1)(x 1+1)(x 2+1)=2x 1x 2+x 1+x 2x 1x 2+x 1+x 2+1=2×4k 2-123+4k 2-8k 23+4k 24k 2-123+4k 2-8k 23+4k 2+1 =8k 2-24-8k 24k 2-12-8k 2+3+4k 2 =-24-9=83, 所以λ+μ为定值83.思维升华 圆锥曲线中的定值问题的常见类型及解题策略(1)求代数式为定值.依题设条件,得出与代数式参数有关的等式,代入代数式、化简即可得出定值.(2)求点到直线的距离为定值.利用点到直线的距离公式得出距离的解析式,再利用题设条件化简、变形求得.(3)求某线段长度为定值.利用长度公式求得解析式,再依据条件对解析式进行化简、变形即可求得.跟踪训练2在平面直角坐标系xOy 中,已知椭圆C :x 2a 2+y 2b 2=1(a >b >0)的离心率为12,AB为椭圆的一条弦,直线y =kx (k >0)经过弦AB 的中点M ,与椭圆C 交于P ,Q 两点,设直线AB 的斜率为k 1,点P 的坐标为⎝ ⎛⎭⎪⎫1,32.(1)求椭圆C 的方程; (2)求证:k 1k 为定值.(1)解由题意知⎩⎪⎨⎪⎧1a2+94b 2=1,c a =12,a 2=b 2+c 2,解得⎩⎨⎧a =2,b =3,c =1,故椭圆C 的方程为x 24+y 23=1.(2)证明设M (x 0,y 0),A (x 1,y 1),B (x 2,y 2), 由于A ,B 为椭圆C 上的点, 所以x 214+y 213=1,x 224+y 223=1,两式相减得(x 1+x 2)(x 1-x 2)4=-(y 1+y 2)(y 1-y 2)3,所以k 1=y 1-y 2x 1-x 2=-3(x 1+x 2)4(y 1+y 2)=-3x 04y 0. 又k =y 0x 0,故k 1k =-34,为定值.课时精练1.(2022·运城模拟)已知P (1,2)在抛物线C :y 2=2px 上.(1)求抛物线C 的方程;(2)A ,B 是抛物线C 上的两个动点,如果直线PA 的斜率与直线PB 的斜率之和为2,证明:直线AB 过定点.(1)解将P 点坐标代入抛物线方程y 2=2px ,得4=2p ,即p =2, 所以抛物线C 的方程为y 2=4x .(2)证明设AB :x =my +t ,将AB 的方程与y 2=4x 联立得y 2-4my -4t =0,Δ>0⇒16m 2+16t >0⇒m 2+t >0, 设A (x 1,y 1),B (x 2,y 2), 则y 1+y 2=4m ,y 1y 2=-4t ,k PA =y 1-2x 1-1=y 1-2y 214-1=4y 1+2, 同理k PB =4y 2+2, 由题意知4y 1+2+4y 2+2=2, 即4(y 1+y 2+4)=2(y 1y 2+2y 1+2y 2+4), 解得y 1y 2=4,故-4t =4,即t =-1, 故直线AB :x =my -1恒过定点(-1,0).2.已知椭圆x 2a 2+y 2b 2=1(a >b >0)的离心率为23,且其左顶点到右焦点的距离为5.(1)求椭圆的方程;(2)设点M ,N 在椭圆上,以线段MN 为直径的圆过原点O ,试问是否存在定点P ,使得P 到直线MN 的距离为定值?若存在,求出点P 的坐标;若不存在,请说明理由.解(1)由题设可知⎩⎨⎧ c a =23,a +c =5,解得a =3,c =2,b 2=a 2-c 2=5,所以椭圆的方程为x 29+y 25=1. (2)设M (x 1,y 1),N (x 2,y 2),①若直线MN 与x 轴垂直,由对称性可知|x 1|=|y 1|,将点M (x 1,y 1)代入椭圆方程,解得|x 1|=37014, 原点到该直线的距离d =37014; ②若直线MN 不与x 轴垂直,设直线MN 的方程为y =kx +m ,由⎩⎨⎧ y =kx +m ,x 29+y 25=1,消去y 得(9k 2+5)x 2+18kmx +9m 2-45=0,由根与系数的关系得⎩⎪⎨⎪⎧ x 1x 2=9m 2-459k 2+5,x 1+x 2=-18km 9k 2+5,由题意知,OM →·ON →=0,即x 1x 2+(kx 1+m )(kx 2+m )=0,得(k2+1)9m2-459k2+5+km⎝⎛⎭⎪⎫-18km9k2+5+m2=0,整理得45k2+45=14m2,则原点到该直线的距离d=|m|k2+1=4514=37014,故存在定点P(0,0),使得P到直线MN的距离为定值.3.已知双曲线C的渐近线方程为y=±3x,右焦点F(c,0)到渐近线的距离为 3.(1)求双曲线C的方程;(2)过F作斜率为k的直线l交双曲线于A,B两点,线段AB的中垂线交x轴于D,求证:|AB||FD|为定值.(1)解设双曲线方程为3x2-y2=λ(λ>0),由题意知c=2,所以λ3+λ=4⇒λ=3,所以双曲线C的方程为x2-y23=1.(2)证明设直线l的方程为y=k(x-2)(k≠0)代入x2-y23=1,整理得(3-k2)x2+4k2x-4k2-3=0,Δ=36(k2+1)>0,设A(x1,y1),B(x2,y2),所以x 1+x 2=-4k 23-k 2,x 1x 2=-4k 2-33-k 2, 由弦长公式得 |AB |=1+k 2·(x 1+x 2)2-4x 1x 2=6(k 2+1)|3-k 2|, 设AB 的中点P (x 0,y 0),则x 0=x 1+x 22=-2k 23-k 2, 代入l 得y 0=-6k 3-k 2, AB 的垂直平分线方程为y =-1k ⎝ ⎛⎭⎪⎫x +2k 23-k 2-6k 3-k 2, 令y =0得x D =-8k 23-k 2, 即|FD |=⎪⎪⎪⎪⎪⎪-8k 23-k 2-2=6(1+k 2)|3-k 2|, 所以|AB ||FD |=1为定值. 当k =0时,|AB |=2,|FD |=2,|AB ||FD |=1, 综上所述,|AB ||FD |为定值.4.(2022·河南九师联盟模拟)已知椭圆C :x 2a 2+y 2b2=1(a >b >0)的左、右焦点分别为F 1,F 2,焦距为2,长轴长为4.(1)求椭圆C 的方程;(2)设过点F 1不与x 轴重合的直线l 与椭圆C 相交于E ,D 两点,试问在x 轴上是否存在一个点M ,使得直线ME ,MD 的斜率之积恒为定值?若存在,求出该定值及点M 的坐标;若不存在,请说明理由.解(1)因为焦距为2,长轴长为4,即2c =2,2a =4,解得c =1,a =2,所以b 2=a 2-c 2=3,所以椭圆C 的方程为x 24+y 23=1.(2)由(1)知F 1(-1,0),设点E (x 1,y 1),D (x 2,y 2),M (m ,0),因为直线l 不与x 轴重合,所以设直线l 的方程为x =ny -1,联立⎩⎨⎧ x =ny -1,x 24+y23=1,得(3n 2+4)y 2-6ny -9=0,所以Δ=(-6n )2+36(3n 2+4)>0,所以y 1+y 2=6n 3n 2+4,y 1y 2=-93n 2+4,又x 1x 2=(ny 1-1)(ny 2-1)=n 2y 1y 2-n (y 1+y 2)+1=-9n23n2+4-6n23n2+4+1=-12n2-4 3n2+4,x 1+x2=n(y1+y2)-2=6n23n2+4-2=-83n2+4.直线ME,MD的斜率分别为k ME=y1x1-m,k MD =y2x2-m,所以k ME·k MD=y1x1-m·y2x2-m=y1y2(x1-m)(x2-m)=y1y2x1x2-m(x1+x2)+m2=-93n2+4-12n2-43n2+4-m⎝⎛⎭⎪⎫-83n2+4+m2=-9-12n2+4+8m+3m2n2+4m2=-9(3m2-12)n2+4(m+1)2,要使直线ME,MD的斜率之积恒为定值,3m2-12=0,解得m=±2,当m=2时,存在点M(2,0),使得k ME ·k MD=-9(3m2-12)n2+4(m+1)2=-936=-14,当m=-2时,存在点M(-2,0),使得k ME ·k MD=-9(3m2-12)n2+4(m+1)2=-94,综上,在x轴上存在点M,使得ME,MD的斜率之积恒为定值,当点M的坐标为(2,0)时,直线ME,MD的斜率之积为定值-1 4,当点M的坐标为(-2,0)时,直线ME,MD的斜率之积为定值-9 4 .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个圆过定点问题的探究和推广
已知圆O 的方程为221x y +=,直线1l 过定点(3,0)A 且与圆O 相切.
(1)求直线1l 的方程;
(2)设圆O 与x 轴交与,P Q 两点,M 是圆O 上异于,P Q 的任意一点,过点A 且与x 轴垂直的直线为 2l ,直线PM 交直线2l 于点'P ,直线QM 交直线2l 于点'Q .求证:以''Q P 为直径的圆C 总经过定点,并求出定点坐标.
解:(1)省略;
(2)对于圆方程122=+y x ,令0y =,得1x =±,即(1,0),(1,0)P Q -.
又直线2l 过点A 且与x 轴垂直,∴直线2l 方程为3x =.
设(,)M s t ,则直线PM 方程为).1(1
++=x s t y 解方程组3,(1)1x t y x s =⎧⎪⎨=+⎪+⎩
,得).14,3('+s t P 同理可得,).1
2,3('-s t Q ∴以P Q ''为直径的圆C '的方程为0)12)(14()3)(3(=--+-
+--s t y s t y x x , 又122=+t s ,∴整理得2262(61)0s x y x y t
-+-++=, 若圆C '经过定点,只需令0y =,从而有2610x x -+=,
解得3x =±
∴圆C '
总经过定点坐标为(3±.
备注:本题是09年江苏省苏北四市(徐州、宿迁、淮安、连云港)第三次调研考试第17题)
笔者对命题者提出的参考解法不是很认同,参考解法中引进的参数不太合理,导致后期定点的出现不自然,同时完全掩盖了该问题的几何背景.对此,笔者给出了如下的改进解法:
解:设直线,PM QM 的斜率分别为12,k k ,则121k k =-
直线1:(1)PM y k x =+,令3x =,则1'(3,4)P k ,
直线2:(1)QM y k x =-,令3x =,则2'(3,2)Q k ,
以P Q ''为直径的圆C '的方程为12(3)(3)(4)(2)0x x y k y k --+--=,
即2211
1(3)82(2)0x y k y k -+---= 令0y =,
则3x =即以P Q ''为直径的圆C '
总经过定点坐标为(3±.
从上述的改进解法中,我们注意到,由点M 在圆上运动而生成的两个动点,P Q ''始终满足一个不变的条件,即它们纵坐标的乘积始终为定值.记以P Q ''为直径的圆与x 轴的交点为12,H H ,则由圆的相交弦定理可
得到结论:2212AH AH AP AQ ''==⋅,易知,点12,H H 即为以P Q ''为直径的圆C '经过的定点.
由此,我们不难发现,此类圆过定点的问题是根据圆的相交弦定理来命制的.将问题一般化后,即可得到如下的命题:
命题1:已知圆222:O x y a +=与x 轴交与,A B 两点,垂直于x 轴的直线l 过定点(,0)()Q m m a >,P 是圆O 上异于,A B 的任意一点,若直线PA 交直线l 于点M ,直线PB 交直线l 于点N ,则以MN 为直径的圆C
总经过定点(m .
证明:设直线,PA PB 的斜率分别为12,k k ,则121k k =-
直线1:()PA y k x a =+,令x m =,则1()M y k m a =+,
直线2:()PB y k x a =-,令x m =,则2()N y k m a =-,
2212()()()M N y y k m a k m a m a ⋅=+-=--
即22QM QN m a ⋅=-
设以MN 为直径的圆C 与x 轴的交点为12,H H ,则由圆的相交弦定理可得2212QH QH QM QN ==⋅,所
以12((H m H m +即为以MN 为直径的圆C 经过的定点.
在得到圆的优美结论后,我们自然会产生联想,圆锥曲线也有这样的优美性质吗?笔者经过探究,得到如下的一组命题:
命题2:已知椭圆22
22:1(0)x y O a b a b
+=>>与x 轴交与,A B 两点,垂直于x 轴的直线l 过定点(,0)()Q m m a >,P 是椭圆O 上异于,A B 的任意一点,若直线PA 交直线l 于点M ,直线PB 交直线l 于点N ,则以MN 为直径的圆C
总经过定点(m ±. 证明:设直线,PA PB 的斜率分别为12,k k ,则2
122b k k a
=-
直线1:()PA y k x a =+,令x m =,则1()M y k m a =+,
直线2:()PB y k x a =-,令x m =,则2()N y k m a =-,
2
22122()()()M N b y y k m a k m a m a a
⋅=+-=-- 即22QM QN m a ⋅=-
设以MN 为直径的圆C 与x 轴的交点为12,H H ,则由圆的相交弦定理可得2212QH QH QM QN ==⋅,所
以12((H m H m +即为以MN 为直径的圆C 经过的定点. 特别地,当2
a m c
=时,以MN 为直径的圆C 经过椭圆的右焦点. 命题3:已知双曲线22
22:1(,0)x y O a b a b
-=>与x 轴交与,A B 两点,垂直于x 轴的直线l 过定点(,0)(0)Q m m a <<,P 是双曲线O 上异于,A B 的任意一点,若直线PA 交直线l 于点M ,直线PB 交直线
l 于点N ,则以MN 为直径的圆C 总经过定点(m . 证明:设直线,PA PB 的斜率分别为12,k k ,则2
122b k k a
=- 直线1:()PA y k x a =+,令x m =,则1()M y k m a =+,
直线2:()PB y k x a =-,令x m =,则2()N y k m a =-,
2
22122()()()M N b y y k m a k m a m a a
⋅=+-=-- 即22QM QN m a ⋅=-
设以MN 为直径的圆C 与x 轴的交点为12,H H ,则由圆的相交弦定理可得2212QH QH QM QN ==⋅,所
以12((H m H m +即为以MN 为直径的圆C 经过的定点. 特别地,当2
a m c
=时,以MN 为直径的圆C 经过椭圆的右焦点. 命题4:已知抛物线2
:2(0)O y px p =>,垂直于x 轴的直线l 过定点(,0)(0)Q m m <,P 是抛物线O 上异于O 的任意一点,点P 在直线l 上的射影为点M ,直线PO 交直线l 于点N ,则以MN 为直径的圆C
总经过定点(m . 证明:设00(,)P x y ,则直线00:y PN y x x =,令x m =,则00N y y m x = 000
2M N y y y y m pm x ⋅=⋅=,所以2QM QN pm ⋅=- 设以MN 为直径的圆C 与x 轴的交点为12,H H ,则由圆的
相交弦定理可得2212QH QH QM QN ==⋅,
所以12((H m H m 即为以MN 为直径的圆C 经过的定点.
特别地,当2p m =-
时,以MN 为直径的圆C 经过抛物线的焦点(,0)2
p .。
