湖北省“荆荆襄宜四地七校考试联盟”2020届高三历史10月联考试题(含答案)
湖北省“荆、荆、襄、宜四地七校考试联盟”(襄阳五中襄阳四中)2020届高三10月联考数学(文)试题含答案
2019年秋“荆、荆、襄、宜四地七校考试联盟”高三10月联考文科数学试题一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1. 已知集合{{}|1,|20A y y B x x ===-≤，则A B =A. []1,2B. []0,2C. (],1-∞D. [)2,+∞2. 在平面直角坐标系中，点22(cos ,sin )55P ππ是角α终边上的一点，若[0,)απ∈，则α= A.5π B. 25π C. 35π D. 310π3. 函数|2|y x a =-在[1,)-+∞上单调递增，则实数a 的取值范围是 A. (,1]-∞-B. (,2]-∞-C.(,1]-∞D.(,2]-∞4. 设0.1323,log log a b c ===,,a b c 的大小关系为 A. a b c <<B. a c b <<C. b c a <<D. c b a <<5. 已知函数()f x 满足2(1)f x x x -=-，则()y f x =在点(1,(1))f 处的切线方程是 A. 20x y +-=B. 30x y -=C. 310x y --=D. 20x y -=6. 函数()()ln xxf x e e x -=+的图象大致为7.给出下列三个命题①命题:P x R ∀∈，都有sin 1x ≤，则非0:P x R ∃∈，使得0sin 1x > ②在ABC ∆中，若sin 2sin 2A B =，则角A 与角B 相等③命题：“若tan x =3x π=”的逆否命题是假命题以上正确的命题序号是 A.①②③B.①②C.①③D.②③8. 若奇函数()f x 满足当[0,)x ∈+∞时，2()log (2)f x x x b =+++，则不等式()3f x ≥成立的一个充分不必要条件是 A. 2x ≥B. 3x ≥C. 1x ≥D. 3x <9. 《九章算术》是我国古代的数学巨著，其中《方田》章给出了计算弧田面积所用的经验公式为：弧田面积12=⨯（弦×矢+矢2），弧田（如图阴影部分所示）是由圆弧和弦围成，公式中的“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为23π，矢为2的弧田，按照上述方法计算出其面积是A. B.12C.D. 10. 在ABC ∆中，,BD DC E =是AD 的中点，则EB =A. 2133AB AC - B. 2133AB AC -+C. 3144AB AC -+D. 3144AB AC -11. 已知函数23()123x x f x x =+-+，若()(2020)h x f x =-的零点都在(,)a b 内，其中,a b 均为整数，当b a -取最小值时，则b a +的值为 A. 4039B. 4037C. 1D. 1-12. 已知函数()sin()6f x x πω=+(0)ω>的最小正周期为π，若()f x 在[0,)x t ∈时所求函数值中没有最小值，则实数t 的范围是 A ．0,6π⎛⎤⎥⎝⎦B ．20,3π⎛⎤ ⎥⎝⎦C ．5,36ππ⎛⎤⎥⎝⎦ D ．2,33ππ⎛⎤⎥⎝⎦ 二、填空题（本题共4小题，每小题5分，共20分）13．已知向量(1,1),(2,)a b y ==，若()a a b ⊥-，则实数y = ．14．已知函数2,(0,2]()1(1),(2)22x xf x x f x ⎧∈⎪⎪=⎨⎪-∈+∞⎪⎩则(8)f = ．15. 公元前6世纪，古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图，发现了黄金分割值约为0.618，这一数值也可以表示为2sin18m =︒.若24m n +=，则2＝ ．（用数字作答） 16．定义min{,}a b =,,a a bb a b≤⎧⎨>⎩，若{}()min 1,3f x x x =+-，则使不等式(2)(2)f x f x ≤-成立的x 的取值范围是 ．三、解答题：共70分。
“荆、荆、襄、宜四地七校联盟”2020届高三数学上学期10月月考试题文(含解析)
“荆、荆、襄、宜四地七校联盟”2020届高三数学上学期10月月考试题文（含解析）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.已知集合，则( )A. B. C. D.【答案】A【解析】【分析】先求出集合，根据交集的定义即可求得结果.【详解】，，所以，故选A.【点睛】该题考查的是有关集合的问题，涉及到的知识点有集合的运算，属于简单题目.2.在平面直角坐标系中，点是角终边上的一点，若，则( )A. B. C. D.【答案】B【解析】【分析】首先根据的余弦值和正弦值的符号，判断出点所属的象限，再根据三角函数的定义确定出角的大小，得出结果.【详解】因为，所以角的终边落在第一象限，并且根据角的三角函数值的定义，，结合，得出，故选B.【点睛】该题考查的是有关根据角的终边上一点的坐标确定角的大小的问题，涉及到的知识点有三角函数的定义，属于简单题目.3.函数在上单调递增，则实数的取值范围是( )A. B. C. D.【答案】B【解析】【分析】根据函数的单调增区间是，根据题意可得，从而确定出的范围.【详解】因为函数的单调增区间是，又函数在上单调递增，所以，所以，解得，所以的取值范围是，故选B.【点睛】该题考查的是有关根据函数在给定区间上单调增确定参数的取值范围的问题，属于简单题目.4.设，则的大小关系为( )A. B. C. D.【答案】C【解析】【分析】根据指数函数与对数函数的图象与性质，即可得出的大小关系.【详解】因为，，，所以，故选C.【点睛】该题考查的是有关指数幂与对数值的比较大小的问题，涉及到的知识点有指数函数和对数函数的性质，应用中介值比较，属于简单题目.5.已知函数满足，则在点处的切线方程是( )A. B. C. D.【答案】C【解析】【分析】先求出函数的解析式，求出切点坐标，应用导数求出切线的斜率，然后由直线方程的点斜式得在点处的切线方程.【详解】由得，，，即曲线在点处的切线的斜率为：，所以在点处的切线方程为：，即，故选C.【点睛】该题考查的是有关曲线在某个点处的切线方程的求解问题，涉及到的知识点有导数的几何意义，直线方程的点斜式，属于简单题目.6.函数的图象大致为( )A. B.C. D.【答案】D【解析】分析】根据题意，求出函数的定义域，分析可得为偶函数，进而分析可得当时，，当时，，当时，，分析选项，从而选出正确的结果.【详解】根据题意，函数的定义域，因为，所以为偶函数，图象关于轴对称，排除B项，当时，，当时，，排除选项，当时，，所以D项是正确的，故选D.【点睛】该题考查的是有关函数图象的选择问题，在选择的过程中，注意从函数的定义域，图象的对称性，函数值的符号，函数图象的变化趋势，属于简单题目.7.给出下列三个命题①命题，都有，则非，使得②在中，若，则角与角相等③命题：“若，则”的逆否命题是假命题以上正确的命题序号是( )A. ①②③B. ①②C. ①③D. ②③【答案】C【解析】【分析】①根据命题的否定的形式可知其正确；②根据三角形内角的关系以及两角正弦值相等的时候除了相等还可以互补从而得到两种结果，所以错误；③根据原命题和逆否命题等价可知其正确；从而得到答案.【详解】①根据命题的否定的形式可知，命题，都有，则非，使得，所以是正确的；②在中，若，则有2A=2B或2A+2B=,所以角与角相等或互余，所以错误；③因为命题：“若，则”是假命题，所以其逆否命题是假命题，所以正确；所以正确命题的序号是①③，故选C.【点睛】该题考查的是有关命题真假的判断问题，涉及到的知识点有含有一个量词的命题的否定，三角函数公式，原命题和逆否命题等价，属于简单题目.8.若奇函数满足当时，，则不等式成立的一个充分不必要条件是( )A. B. C. D.【答案】B【解析】【分析】利用，求出，确定，函数在上单调递增，利用函数的单调性，即可求出的解集.【详解】由题意，，所以，所以，所以，函数在上单调递增，，所以不等式的解集为，不等式成立的一个充分不必要条件是的真子集，分析选项可得满足条件，故选B.【点睛】该题考查的是有关充分不必要条件的问题，涉及到的知识点有根据奇函数求参数值，根据函数的单调性解不等式，充分不必要条件的定义，属于简单题目.9.《九章算术》是我国古代的数学巨著，其中《方田》章给出了计算弧田面积所用的经验公式为：弧田面积（弦×矢+矢），弧田（如图阴影部分所示）是由圆弧和弦围成，公式中的“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差，现有圆心角为，矢为的弧田，按照上述方法计算出其面积是( )A. B. C. D.【答案】A【解析】【分析】根据在直角三角形的边角关系求出，以及弦长“矢”的大小，结合弧田面积公式进行计算即可.【详解】如图，由题意可得，在中，，所以，结合题意可知矢，半径，弦，所以弧田面积（弦矢矢），故选A.【点睛】该题考查的是有关与数学文化相关的问题，涉及到的知识点有应用题中所给的条件与公式解决相关的问题，在解题的过程中，注意对条件的正确转化，属于简单题目.10.在中，是的中点，则( )A. B.C. D.【答案】D【解析】【分析】利用向量的加减运算和中线向量的表示，计算可得所求向量.【详解】在中，为边上的中线，为的中点，所以，故选D.【点睛】该题考查的是有关向量的问题，涉及到的知识点有向量的加减运算法则，以及向量共线时的表示方法，再有就是中线向量的表示，属于简单题目.11.已知函数，若的零点都在内，其中均为整数，当取最小值时，则的值为( ) A. B. C. D.【答案】A【解析】【分析】首先对函数求导，可以发现恒成立，从而判断出函数在上单调递增，从而函数只有一个零点，结合函数图象的平移求得的零点落在区间上，从而得到结果.【详解】由可得恒成立，所以函数在上单调递增，所以函数只有一个零点，又，所以函数仅有的一个零点落在区间上，而由的图象向右平移个单位，所以函数的零点落在区间上，根据题意可知，所以，故选A.【点睛】该题考查的是有关函数的零点所在区间的问题，涉及到的知识点有利用导数研究函数的单调性，零点存在性定理得到函数零点所在的区间，属于简单题目.12.已知函数的最小正周期为，若在时所求函数值中没有最小值，则实数的范围是( )A. B. C. D.【答案】D【解析】【分析】首先根据函数的最小正周期为，求得，根据函数在给定区间上没有最小值，结合函数的图象，得出，从而求得结果.【详解】因为函数的最小正周期为，所以，当时，，因为时所求函数值中没有最小值，所以，解得，所以的取值范围是，故选D.【点睛】该题考查的是有关三角函数的问题，涉及到的知识点有正弦函数的图象和性质，函数的最小正周期以及函数的最值，属于简单题目.二、填空题（本题共4小题，每小题5分，共20分）13.已知向量,,若,则实数__________.【答案】【解析】【分析】由得，化简求解即可.【详解】，由得，得【点睛】本题考查向量的四则运算，属于简单题.14.已知函数则____．【答案】【解析】【分析】首先根据题中所给的分段函数的解析式，将自变量代入，依次代换，确定出自变量对应的函数值，代入求解即可.【详解】因为,所以,故答案是:1.【点睛】该题考查的是有关分段函数的求值问题，在解题的过程中，注意对自变量进行转化，注意对分段函数的解析式的正确理解，属于简单题目.15.公元前6世纪，古希腊的毕达哥拉斯学派通过研究正五边形和正十边形的作图，发现了黄金分割值约为，这一数值也可以表示为.若，则＝____．（用数字作答）【答案】【解析】【分析】首先利用余弦的倍角公式以及同角三角函数关系中的平方关系和正弦的倍角公式，对式子进行化简，求得结果.【详解】根据题中的条件可得：，故答案是：.【点睛】该题考查的是有关三角函数的求值问题，涉及到的知识点有新定义，利用条件对式子进行正确的变形是解题的关键.16.定义，若，则使不等式成立的的取值范围是____【答案】【解析】【分析】首先利用题中所给函数条件，确定出函数的解析式，画出函数的图象，从图象中判断出自变量离1越近，函数值越大，得到等价的不等式，求解即可得结果.【详解】因为，，所以，画出函数图象如图所示：不等式等价于如下不等式：，即，解得或，所以不等式的解集为，即答案是：.【点睛】该题考查的是有关利用函数值的大小确定自变量大小的问题，涉及到的知识点有新函数的定义，在解题的过程中，注意应用函数的图象，解决利用函数值的大小得自变量大小的问题，属于简单题目.三、解答题：共70分。
2020届湖北省“荆、荆、襄、宜四地七校考试联盟高三上学期10月联考数学(理)试题(解析版)
2020届湖北省“荆、荆、襄、宜四地七校考试联盟高三上学期10月联考数学（理）试题一、单选题1．设集合{}|3,xA y y x R ==∈，{}|B x y x R ==∈，则AB =（）A.12⎧⎫⎨⎬⎩⎭B.()0,1C.10,2⎛⎫ ⎪⎝⎭D.10,2⎛⎤ ⎥⎝⎦【答案】D【解析】集合A 表示函数3,xy x R =∈的值域，集合B表示函数y =由函数的定义域、值域的求法，求出集合A 、B ，再求A B 即可.【详解】解：因为3,xy x R =∈，则0y >，即()0,A =+∞，又y =x ∈R ,由120x -≥，解得12x ≤，即1,2B ⎛⎤=-∞ ⎥⎝⎦，即AB =10,2⎛⎤⎥⎝⎦，故选D. 【点睛】本题考查了函数的定义域、值域的求法，重点考查了集合交集的运算，属基础题.2．函数()332,0log 6,0x x f x x x ⎧->=⎨+≤⎩的零点之和为（）A.-1B.1C.-2D.2【答案】A【解析】由函数零点与方程的根的关系可得函数()332,0log 6,0x x f x x x ⎧->=⎨+≤⎩的零点即方程320x -=，3log 60x +=的根，解方程后再将两根相加即可得解. 【详解】解：令320x -=，解得3log 2x =， 令3log 60x +=，解得3log 6x =-，则函数()f x 的零点之和为3331log 2log 6log 13-==-， 故选A. 【点睛】本题考查了分段函数零点的求解，重点考查了对数的运算，属基础题.3．若ln 2a =，125b -=，201cos 2c xdx π=⎰，则a ，b ，c 的大小关系（） A.a b c << B.b a c << C.c b a << D.b c a <<【答案】D【解析】由定积分的运算可得c =1sin 2x |20π=11(sin sin 0)222π-=，再由以e 为底的对数函数的单调性可得1ln 22a =>=，再由以12y x -=的单调性可得 11221542b --=<=，比较即可得解. 【详解】解：201cos 2c xdx π=⎰=1sin 2x |20π=11(sin sin 0)222π-=，又 11221542b --=<=，1ln 22a =>=，即b c a <<， 故选D. 【点睛】本题考查了定积分的运算、对数值比较大小，指数幂比较大小，重点考查了不等关系，属中档题.4．下列四个结论：①若点()(),20P a a a ≠为角α终边上一点，则sin α=②命题“存在0x R ∈，2000x x ->”的否定是“对于任意的x ∈R ，20x x -≤”； ③若函数()f x 在()2019,2020上有零点，则()()201920200f f ⋅<； ④“log 0a b >（0a >且1a ≠）”是“1a >，1b >”的必要不充分条件. 其中正确结论的个数是（） A.0个 B.1个C.2个D.3个【答案】C【解析】对于①，由三角函数的定义，讨论0a >，0a <即可； 对于②，由全称命题与特称命题的关系判断即可得解； 对于③，由零点定理，需讨论函数在()2019,2020是否单调； 对于④，由充分必要性及对数的运算即可得解. 【详解】解：对于①，当0a >时，有sin α===当0a <时，有sin α===①错误；对于②，命题“存在0x R ∈，2000x x ->”的否定是“对于任意的x ∈R ，20x x -≤”；由特称命题的否定为全称命题，则②显然正确；对于③，若函数()f x 在()2019,2020上有零点，则()()201920200f f ⋅<； 若函数在()2019,2020为单调函数，则必有()()201920200f f ⋅<，若函数在()2019,2020不单调，则必有()()201920200f f ⋅<，不一定成立，即③错误；对于④，当“1a >，1b >”时，可得到“log 0a b >（0a >且1a ≠）”，当“log 0a b >（0a >且1a ≠）”时，则“1a >，1b >”或“01a <<，01b <<”， 即④正确， 故选C. 【点睛】本题考查了三角函数的定义、全称命题与特称命题、零点定理及充分必要条件，重点考查了逻辑推理能力，属综合性较强的题型. 5．已知()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，且()1tan 3αβ+=，则tan β的值为（）A.-7B.7C.1D.-1【答案】B【解析】由了诱导公式得sin 2cos αα=-，由同角三角函数的关系可得tan 2α=-， 再由两角和的正切公式()tan αβ+=tan tan 1tan tan αβαβ+-，将tan 2α=-代入运算即可.【详解】解：因为()cos 2cos 2παπα⎛⎫-=+ ⎪⎝⎭，所以sin 2cos αα=-，即tan 2α=-， 又()1tan 3αβ+=， 则tan tan 11tan tan 3αβαβ+=-，解得tan β= 7， 故选B. 【点睛】本题考查了诱导公式及两角和的正切公式，重点考查了运算能力，属中档题.6．已知()121sin 221xx f x x x -⎛⎫=-⋅ ⎪+⎝⎭，则函数()y f x =的图象大致为（）A. B.C. D.【答案】D【解析】由函数解析式可得()()f x f x =-，则函数()y f x =为偶函数，其图像关于y轴对称，再取特殊变量4π得04f π⎛⎫< ⎪⎝⎭，即可得在()0,∞+存在变量使得()0f x <，再观察图像即可. 【详解】解：因为()121sin 221xx f x x x -⎛⎫=-⋅ ⎪+⎝⎭，则()121sin 221x x f x x x ---⎛⎫-=-+⋅ ⎪+⎝⎭=121sin 221xx x x -⎛⎫-⋅ ⎪+⎝⎭，即()()f x f x =-，则函数()y f x =为偶函数，其图像关于y 轴对称，不妨取4x π=，则 ()4421(08221f x πππ-=-<+，即在()0,∞+存在变量使得()0f x <， 故选D. 【点睛】本题考查了函数奇偶性的判断及函数的图像，重点考查了函数的思想，属中档题. 7．若函数()()()3,af x m xm a R =+∈是幂函数，且其图像过点(，则函数()()2log 3a g x x mx =+-的单调递增区间为（）A.(),1-∞-B.(),1-∞C.()1,+∞D.()3,+∞【答案】A【解析】由幂函数的定义可得31m +=，由其图像过点(，则2α=，即12α=， 由复合函数的单调性有：()y g x =的单调递增区间等价于223,(0)t x x t =-->的减区间，一定要注意对数的真数要大于0，再求单调区间即可. 【详解】解：因为()()()3,af x m xm a R =+∈，则31m +=，即2m =-，又其图像过点(，则2α=12α=， 则()()212log 23g x x x =--， 由复合函数的单调性有：()()212log 23g x x x =--的单调递增区间等价于223,(0)t x x t =-->的减区间，又223,(0)t x x t =-->的减区间为(),1-∞-，故选A.本题考查了幂函数的定义及复合函数的单调性，重点考查了对数的真数要大于0，属中档题.8．将函数()sin 26f x x π⎛⎫+⎝=⎪⎭的图象向右平移6π，再把所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数()g x 的图象，则下列说法正确的是（） A.函数()g x 的图象关于点,03π⎛-⎫⎪⎝⎭对称 B.函数()g x 的最小正周期为2πC.函数()g x 的图象关于直线6x π=对称D.函数()g x 在区间2,63ππ⎡⎤⎢⎥⎣⎦上单调递增 【答案】D【解析】由三角函数图像的平移变换及伸缩变换可得()sin()6g x x π=-，再结合三角函数的周期、单调区间、对称轴、对称点的求法求解即可. 【详解】解：将函数()sin 26f x x π⎛⎫+⎝=⎪⎭的图象向右平移6π，所得图像的解析式为 sin[2()]sin(2)666y x x πππ=-+=-，再把所有点的横坐标伸长到原来的2倍（纵坐标不变）得到函数()g x 的图象，则()sin()6g x x π=-，令6x k ππ-=，则6x k ππ=+，即函数()g x 的图象关于点,06k ππ⎛+⎫⎪⎝⎭，k Z ∈对称,即A 错误； 令62x k πππ-=+，则23x k ππ=+，即函数()g x 的图象关于直线23x k ππ=+，k Z ∈对称,及C 错误；由221T ππ==，即C 错误； 令 22262k x k πππππ-≤-≤+，得22233k x k ππππ-≤≤+，即函数()g x 的单调递增区间为22,233k k ππππ⎡⎤-+⎢⎥⎣⎦，k Z ∈，故D 正确，【点睛】本题考查了三角函数图像的平移变换及伸缩变换，重点考查了三角函数图像的性质，属中档题.9．已知定义在R 上的函数()f x 满足对任意x ∈R 都有()()110f x f x ++-=成立，且函数()1f x +的图像关于直线1x =-对称，则()2019f =（）A.0B.2C.-2D.-1【答案】A【解析】由()()110f x f x ++-=，可得()()20f x f x ++-=， 又由函数()1f x +的图像关于直线1x =-对称，可得函数()f x 的图像关于y 轴对称，即 ()()f x f x =-，再结合函数对称性及奇偶性可得函数的周期为4，再运算即可. 【详解】由()()110f x f x ++-=，则()()20f x f x ++-=，① 又函数()1f x +的图像关于直线1x =-对称，则函数()f x 的图像关于y 轴对称，即()()f x f x =-，②联立①②可得()()4f x f x =+，即函数()f x 的周期为4， 即()2019f =(50541)(1)f f ⨯-=-， 又因为()()110f x f x ++-=，令0x =得(1)0f =，又函数()f x 的图像关于y 轴对称，则(1)0f -=， 即()2019f =0， 故选A. 【点睛】本题考查了函数的对称性、奇偶性、周期性及利用函数的性质求值，属中档题. 10．已知函数()()sin xf x e x a =-有极值，则实数a 的取值范围为（）A.()1,1-B.[]1,1-C.⎡⎣D.(【答案】D【解析】由函数()()sin x f x ex a =-有极值，等价于sin cos x x a +-=0有变号根，即()0>g x ，()0<g x均有解，又()g x a a ⎡⎤∈⎣⎦，即00a a ⎧<⎪>，运算即可得解. 【详解】 解：因为()()sin xf x e x a =-，所以()()'sin cos x fx e x x a =+-，令()sin cos g x x x a =+-， 由函数()()sin xf x ex a =-有极值，则sin cos x x a +-=0有变号根， 即()0>g x ，()0<g x 均有解，又()sin cos )4g x x x a x a π=+-=+-，即()g x a a ⎡⎤∈⎣⎦，即0a a ⎧<⎪>，即a << 故选D. 【点睛】本题考查了导数的运算、函数的极值及三角函数的值域，重点考查了方程有解问题，属中档题.11．设函数()22cos f x x x =+，[]1,1x ∈-，则不等式()()12f x f x ->的解集为（）A.1,13⎛⎫- ⎪⎝⎭B.10,3⎡⎫⎪⎢⎣⎭C.11,32⎛⎤ ⎥⎝⎦D.10,2⎡⎤⎢⎥⎣⎦【答案】B【解析】由()2()2cos()f x x x -=-+-=22cos ()x x f x +=，即函数()f x 为偶函数，由()'2(sin )0fx x x =-≥在[]0,1x ∈恒成立，即函数()f x 在[]0,1为增函数，再结合函数的性质解不等式11112112x x x x ⎧-≤-≤⎪-≤≤⎨⎪->⎩即可得解.【详解】解：因为函数()22cos f x x x =+，[]1,1x ∈-，所以()2()2cos()f x x x -=-+-=22cos ()x x f x +=，即函数()f x 为偶函数， 又()'2(sin )0fx x x =-≥在[]0,1x ∈恒成立，即函数()f x 在[]0,1为增函数， 又()()12f x f x ->，则11112112x x x x⎧-≤-≤⎪-≤≤⎨⎪->⎩，解得103x ≤<，即不等式()()12f x f x ->的解集为10,3⎡⎫⎪⎢⎣⎭故选B. 【点睛】本题考查了函数的奇偶性及利用导数研究函数的单调性，重点考查了函数性质的应用，属中档题.12．已知函数()f x 在R 上可导，其导函数为()'f x ，若函数()f x 满足：()()()1'0x f x f x --<⎡⎤⎣⎦，()()222xf x f x e --=，则下列判断一定正确的是（）A.()()10f ef <B.()()12ef f <C.()()303e f f >D.()()514e f f -<【答案】C【解析】先设函数()()x f x g x e=，求导可得函数()g x 在(,1)-∞为增函数，()g x 在(1,)+∞为减函数，再由2(2)()xx f x f x e e--=，得()(2)g x g x =-，即函数()g x 的图像关于直线1x =对称，再结合函数()g x 的性质逐一判断即可. 【详解】解：令()()x f x g x e = ，则''()()()xf x f xg x e-= 因为()()()1'0x f x f x --<⎡⎤⎣⎦， 所以当1x >时，'()0g x <，当1x <时，'()0g x >，即函数()g x 在(,1)-∞为增函数，()g x 在(1,)+∞为减函数， 又()()222xf x f x e--=，所以2(2)()xx f x f x e e--=， 则 ()(2)g x g x =-，即函数()g x 的图像关于直线1x =对称，则(0)(1)g g <，即()()10f ef >即A 错误；(1)(2)g g >，即()()12ef f >即B 错误；(0)(3)g g >，即03(0)(3)f f e e>，即()()303e f f >，即C 正确；(1)(4)g g ->，即()()514e f f ->，即D 错误.故选C. 【点睛】本题考查了分式函数求导、利用导数的符号研究函数的单调性，再结合函数的单调性、对称性判断值的大小关系，重点考查了函数的性质，属中档题.二、填空题13．设函数()3ln 2f x x x x =+，则曲线()y f x =在点()1,2处的切线方程是___________． 【答案】750x y --=【解析】先求函数()f x 的导函数()'fx ，再由导数的几何意义，求()'17f =，则曲线()y f x =在点()1,2处的切线的斜率为7，再由直线的点斜式方程求解即可. 【详解】解：因为()3ln 2f x x x x =+，所以()'2ln 16fx x x =++，则()'21ln11617f =++⨯=，即曲线()y f x =在点()1,2处的切线方程是27(1)y x -=-，即750x y --=， 故答案为750x y --=. 【点睛】本题考查了导数的几何意义、直线的点斜式方程，重点考查了导数的应用及运算能力，属基础题.14．已知函数()(()32log 1f x ax x a R =++∈且()13f =-，则()1f -=__________．【答案】5【解析】先观察函数()f x 的结构，再证明()()2f x f x +-=，再利用函数的性质求解即可. 【详解】解：因为()(32log 1f x ax x =++，所以()(332()log ()log(22f x f x ax x a x x +-=++-+-++=，又()13f =-，则()1f -=2(1)235f -=+=， 故答案为5. 【点睛】本题考查了对数的运算及函数()f x 性质的判断，重点考查了观察能力及逻辑推理能力，属中档题.15．在ABC ∆中，角A ，B ，C 所对的边分别是a ，b ，c 且满足sin b C a =，22285a cb ac +-=，则tan C =___________．【答案】-3【解析】由余弦定理可得cos 45B =，3sin 5B =， 再由正弦定理可得sin sin sin cos cos sin BC B C B C =+， 再结合运算即可得解. 【详解】解：因为22285a cb ac +-=， 则2224cos 25a cb B ac +-==，则3sin 5B =， 又因为sin b C a =，则sin sin sin B C A =，则sin sin sin sin()sin cos cos sin B C A B C B C B C ==+=+，将cos 45B =，3sin 5B =代入得，sin 3cosC C =-, 即sin tan 3cos CC C==-， 故答案为-3. 【点睛】本题考查了利用正弦定理、余弦定理进行边角互化，重点考查了两角和的正弦公式及运算能力，属中档题. 16．若函数()22xk f x e x kx =-+在[]0,2上单调递增，则实数k 的取值范围是________．【答案】21,e ⎡⎤-⎣⎦【解析】由()'x fx e kx k =-+，利用导数再分情况讨论当0k ≤，当2k e ≥，当01k <≤时，当21k e <<时函数()xg x e kx k =-+的最小值，即可求得实数k 的取值范围. 【详解】解：由()22xk f x e x kx =-+， 则()'x fx e kx k =-+，由函数()f x 在[]0,2上单调递增， 则()'0x fx e kx k =-+≥在[]0,2恒成立，设()xg x e kx k =-+，[]0,2x ∈①当0k ≤时，()xg x e kx k =-+，[]0,2x ∈为增函数，要使()0g x ≥，则只需()00g ≥，求得10k -≤≤， ②由()'xg x e k =-，1 当2k e ≥时，()'0g x ≤，即函数()g x 为减函数，即()2min (2)g x g e k ==-，要使()0g x ≥，则只需()2min 0g x e k =-≥，即2k e =，2当01k <≤时，有()'0xg x e k =-≥，即函数()g x 为增函数，要使()0g x ≥，则只需()min (0)10g x g k ==-≥，即01k <≤，3当21k e <<时，有当0ln x k <<时，()'0g x <，当2ln k x e <<时，()'0g x >，即函数()g x 在(0,ln )k 为减函数，在2(ln ,)k e 为增函数，即()min (ln )2ln g x g k k k k ==-，要使()0g x ≥，则只需()min 2ln 0g x k k k =-≥，即2k e <，综上可得实数k 的取值范围是21,e ⎡⎤-⎣⎦， 故答案为21,e ⎡⎤-⎣⎦.【点睛】本题考查了利用导数求函数的单调区间，函数的最值，重点考查了分类讨论的数学思想方法，属综合性较强的题型.三、解答题17．在ABC ∆中，设内角A ，B ，C 所对的边分别为a ，b ，c ，且2cos cos a c Cb B-=. （1）求角B 的大小；（22sin cos 222C A A-的取值范围.【答案】（1）3B π=（2）,44⎛⎫⎪ ⎪⎝⎭【解析】（1）由正弦定理化边为角可得2sin sin cos sin cos A C CB B -=，再由两角和的正弦可得2sin cos sin A B A =，即得1cos 2B =，得解； （2）由三角恒等变换结合倍角公式可得2sin cos 222C A A -=1cos 26C π⎛⎫+ ⎪⎝⎭，再结合203C π<<求解即可. 【详解】 解：（1）由2cos cos a c C b B -=得到2sin sin cos sin cos A C CB B-=， 即()2sin cos sin A B B C =+，即2sin cos sin A B A =， 又∵A 为三角形内角，∴sin 0A ≠，所以1cos 2B =，从而3B π=.（2)21sin cos cos 1sin 22222C A A C A -=+-12sin 2232C C ⎛⎫=--+⎪⎝⎭π11sin cos 426C C C π⎛⎫=-=+ ⎪⎝⎭， ∵203C π<<，∴5666C <+<πππ，∴cos 6C ⎛⎫<+< ⎪⎝⎭π1cos 26C π⎛⎫<+<⎪⎝⎭.2sin cos 222C A A-的取值范围为⎝⎭. 【点睛】本题考查了正弦定理、正弦与余弦的二倍角公式及三角函数求值域问题，重点考查了运算能力，属中档题.18．湖北省第二届（荆州）园林博览会于2019年9月28日至11月28日在荆州园博园举办，本届园林博览会以“辉煌荆楚，生态园博”为主题，展示荆州生态之美，文化之韵，吸引更多优秀企业来荆投资，从而促进荆州经济快速发展.在此次博览会期间，某公司带来了一种智能设备供采购商洽谈采购，并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元，每生产一台．．．．．需另投入80元，设该公司一年内生产该设备x 万台且全部售完，每万台．．．的销售收入()G x （万元）与年产量x （万台）满足如下关系式：()()1802,0202000900070,201x x G x x x x x -<≤⎧⎪=⎨+->⎪+⎩.（1）写出年利润()W x （万元）关于年产量x （万台）的函数解析式；（利润=销售收入-成本）（2）当年产量为多少万台时，该公司获得的年利润最大？并求最大利润.【答案】（1）()W x 2210050,0209000101950,201x x x x x x ⎧-+-<≤⎪=⎨--+>⎪+⎩（2）当年产量为29万台时，该公司获得的利润最大为1360万元【解析】（1）先阅读题意，再建立起年利润()W x 关于年产量x 的函数解析式即可；（2）利用配方法求二次函数的最值可得当020x <≤时()()22251200W x x =--+，即()()max 201150W x W ==，再利用重要不等式可得当90011x x +=+即29x =时()max 1360W x =，再比较两段上的最大值即可得解.【详解】解：（1）()()8050W x xG x x =--2210050,0209000101950,201x x x x x x ⎧-+-<≤⎪=⎨--+>⎪+⎩. （2）当020x <≤时()()222100502251200W x x x x =-+-=--+， ∴()()max 201150W x W ==. 当20x >时()90010119601W x x x ⎛⎫=-+++ ⎪+⎝⎭1019601360≤-⨯=， 当且仅当90011x x +=+即29x =时等号成立，∴()()max 291360W x W ==. ∵13601150>，∴当年产量为29万台时，该公司获得的利润最大为1360万元. 【点睛】本题考查了分段函数及分段函数的最值，主要考查了重要不等式，重点考查了阅读能力及解决实际问题的能力，属中档题.19．已知在多面体ABCDE 中，DE AB ∥，AC BC ⊥，24BC AC ==，2AB DE =，DA DC =且平面DAC ⊥平面ABC .（1）设点F 为线段BC 的中点，试证明EF ⊥平面ABC ；（2）若直线BE 与平面ABC 所成的角为60，求二面角B AD C --的余弦值.【答案】（1）详见解析（2【解析】（1）由四边形DEFO 为平行四边形.∴EF DO P ，再结合DO ⊥平面ABC ，即可证明EF ⊥平面ABC ；（2）由空间向量的应用，建立以O 为原点，OA 所在直线为x 轴，过点O 与CB 平行的直线为y 轴，OD 所在直线为z 轴的空间直角坐标系，再求出平面ADC 的法向量()0,1,0m =u r，平面ADB的法向量()n =r ，再利用向量夹角公式求解即可.【详解】（1）证明：取AC 的中点O ，连接EF ，OF ， ∵在DAC ∆中DA DC =，∴DO AC ⊥.∴由平面DAC ⊥平面ABC ，且交线为AC 得DO ⊥平面ABC . ∵O ，F 分别为AC ，BC 的中点，∴OF AB P ，且2AB OF =. 又DE AB ∥，2AB DE =，∴OF DE P ，且OF DE =. ∴四边形DEFO 为平行四边形.∴EF DO P ， ∴EF ⊥平面ABC .（2）∵DO ⊥平面ABC ，AC BC ⊥，∴以O 为原点，OA 所在直线为x 轴，过点O 与CB 平行的直线为y 轴，OD 所在直线为z 轴，建立空间直角坐标系.则()1,0,0A ，()1,0,0C -，()1,4,0B -. ∵EF ⊥平面ABC ，∴直线BE 与平面ABC 所成的角为60EBF ∠=.∴tan 60DO EF BF ===o∴(D .可取平面ADC 的法向量()0,1,0m =u r，设平面ADB 的法向量(),,n x y z =，()2,4,0AB =-uu u r，(AD =-uuu r ，则240x y x -+=⎧⎪⎨-+=⎪⎩，取1z =，则x =y =∴()n =r ，∴cos ,4m n m n m n⋅<>==u r ru r r u r r ，∴二面角B AD C --的余弦值为4.【点睛】本题考查了线面垂直的判定及利用空间向量求解二面角的大小，重点考查了空间想象能力，属中档题.20．如图，过点()2,0P 作两条直线2x =和l ：()20x my m =+>分别交抛物线22y x =于A ，B 和C ，D （其中A ，C 位于x 轴上方），直线AC ，BD 交于点Q .（1）试求C ，D 两点的纵坐标之积，并证明：点Q 在定直线2x =-上； （2）若PQC PBDS S λ∆∆=，求λ的最小值.【答案】（1）详见解析（2）3【解析】（1）联立直线方程与抛物线方程求得2240y my --=，从而可得124y y =-，再由点斜式方程求得直线AC 的方程为()12222y x y -=-+，直线BD 的方程为()22222y x y +=--，消去y 求出2x =，得解； （2）由题意有()()111222PQC PBDS x x S x λ∆∆+==-，再令()120t x t =->，则432t tλ=++，再由重要不等式求最小值即可得解. 【详解】解：（1）将直线l 的方程2x my =+代入抛物线22y x =得：2240y my --=， 设点()11,C x y ，()22,D x y ，则124y y =-.由题得()2,2A ，()2,2B -，直线AC 的方程为()12222y x y -=-+， 直线BD 的方程为()22222y x y +=--，消去y 得()12121224y y y yx y y -+=-+， 将124y y =-代入上式得2x =-，故点Q 在直线2x =-上. （2）∵()111222PQC S AP x x ∆=+=+，()221222PBD S BP x x ∆=-=-， 又221212164224y y x x =⋅==，∴()()111121122242222PQCPBD S x x x x S x x x λ∆∆+++====---.令()120t x t =->，则()()2443322t t t ttλ++==++≥，当且仅当t =即12x =+λ取到最小值3. 【点睛】本题考查了直线过定点问题及三角形面积公式，重点考查了圆锥曲线的运算问题，属中档题.21．已知函数()()()1sin cos 2f x a x x x x a R =--∈，()()'g x f x =（()'f x 是()f x 的导函数），()g x 在0,2π⎡⎤⎢⎥⎣⎦上的最大值为12π-. （1）求实数a 的值；（2）判断函数()f x 在()0,π内的极值点个数，并加以证明. 【答案】（1）1a =（2）()f x 在()0,π上共有两个极值点，详见解析 【解析】（1）先求得()()1'sin 2g x f x ax x ==-，再求得()()'sin cos g x a x x x =+，再讨论a 的符号，判断函数()g x 的单调性，再求最值即可得解； （2）利用（1）的结论，结合()1002g =-<，10222g ππ⎛⎫=-> ⎪⎝⎭，由零点定理可()g x 在0,2π⎛⎤⎥⎝⎦上有且仅有一个变号零点；再当,2x ππ⎛⎫∈⎪⎝⎭时，由导数的应用可0,2x ππ⎛⎫∃∈ ⎪⎝⎭使()0'0g x =，即()g x 在0,2x π⎛⎫⎪⎝⎭上单调递增，在()0,x π上单调递减，再结合特殊变量所对应的函数值的符号可得()g x 在,2ππ⎛⎫⎪⎝⎭上有且仅有一个变号零点，综合即可得解. 【详解】解：（1）由()()()1sin cos 2f x a x x x x a R =--∈ 则()()1'sin 2g x f x ax x ==-， 则()()'sin cos g x a x x x =+， ①当0a =时()12g x =-，不合题意，舍去. ②当0a <时()'0g x <，∴()g x 在0,2π⎡⎤⎢⎥⎣⎦上单调递减，∴()()max 11022g x g π-==-≠，不合题意，舍去. ③当0a >时()'0g x >，∴()g x 在0,2π⎡⎤⎢⎥⎣⎦上单调递增，∴()max 112222a g x g πππ-⎛⎫==-= ⎪⎝⎭，解得1a =， ∴综上：1a =.（2）由（Ⅰ）知()1sin 2g x x x =-，()'sin cos g x x x x =+， 当0,2x π⎛⎤∈ ⎥⎝⎦时，()g x 在0,2π⎛⎤⎥⎝⎦上单调递增，()1002g =-<，10222g ππ⎛⎫=-> ⎪⎝⎭，∴()g x 在0,2π⎛⎤⎥⎝⎦上有且仅有一个变号零点；当,2x ππ⎛⎫∈⎪⎝⎭时，()''2cos sin 0g x x x x =-<，∴()'g x 在,2ππ⎛⎫⎪⎝⎭上单调递减.又'102g π⎛⎫=>⎪⎝⎭，()'0g ππ=-<，∴0,2x ππ⎛⎫∃∈⎪⎝⎭使()0'0g x =且当0,2x x π⎛⎫∈ ⎪⎝⎭时()'0g x >，当()0,x x π∈时()'0g x <，∴()g x 在0,2x π⎛⎫⎪⎝⎭上单调递增，在()0,x π上单调递减. 又10222g ππ⎛⎫=->⎪⎝⎭，()002g x g π⎛⎫>> ⎪⎝⎭，()102g π=-<，∴()g x 在,2ππ⎛⎫ ⎪⎝⎭上有且仅有一个变号零点.∴()g x 在0,2π⎛⎤ ⎥⎝⎦和,2ππ⎛⎫ ⎪⎝⎭上各有一个变号零点，∴()f x 在()0,π上共有两个极值点. 【点睛】本题考查了利用导数研究函数的单调性及最值，主要考查了零点定理，重点考查了函数的思想及运算能力，属综合性较强的题型.22．在直角坐标系xOy 中，以原点O 为极点，x 轴正半轴为极轴建立极坐标系.若曲线C 的极坐标方程为2cos 4sin 0ρθθ-=，P 点的极坐标为3,2π⎛⎫⎪⎝⎭，在平面直角坐标系中，直线l 经过点P ，且倾斜角为60.（1）写出曲线C 的直角坐标方程以及点P 的直角坐标；（2）设直线l 与曲线C 相交于A ，B 两点，求11PA PB+的值.【答案】（1）曲线C 的直角坐标方程为24x y =；P 点的直角坐标为()0,3（2）6【解析】（1）由极坐标与直角坐标的互化可得C 的直角坐标方程为24x y =，P 点的直角坐标为()0,3P ；（2）将直线l 的参数方程代入曲线C 的直角坐标方程，利用直线的参数方程中t 的几何意义1212PA PB t t t t +=+=-，再求解即可. 【详解】解：（1）曲线C 的极坐标方程化为直角坐标方程为24x y =，P 点的极坐标为：3,2P π⎛⎫ ⎪⎝⎭，化为直角坐标为()0,3P . （2）直线l 的参数方程为cos 33sin 3x t y t ππ⎧=⎪⎪⎨⎪=+⎪⎩，即123x t y ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数）， 将l 的参数方程代入曲线C的直角坐标方程，得21124t =+，整理得：2480t --=，显然有>0∆，则1248t t ⋅=-，12t t +=121248PA PB t t t t ⋅=⋅=⋅=，1212PA PB t t t t +=+=-==所以116PA PB PA PB PA PB ++==⋅【点睛】本题考查了极坐标与直角坐标的互化，直线的参数方程及，直线的参数方程中t 的几何意义，属中档题.23．已知函数()5f x x =-，()523g x x =--.（1）解不等式()()f x g x <；（2）若存在x ∈R 使不等式()()2f x g x a -≤成立，求实数a 的取值范围.【答案】（1）()1,3（2）2a ≥【解析】（1）由绝对值的意义，分别讨论5x ≥，352x ≤<，32x <即可； （2）原命题等价于()()2f x g x -的最小值小于或等于a ，再利用绝对值不等式的性质可得()()2f x g x -=()2102352102352x x x x =-+--≥----=.即()()2f x g x -的最小值为2，即可得解. 【详解】 解：（1）原不等式即5235x x -+-<，∴55235x x x ≥⎧⎨-+-<⎩或3525235x x x ⎧≤<⎪⎨⎪-+-<⎩或325325x x x ⎧<⎪⎨⎪-+-<⎩， 所以x 无解或332x ≤<或312x <<，即13x <<, ∴原不等式的解集为()1,3.（2）若存在x ∈R 使不等式()()2f x g x a -≤成立，则()()2f x g x -的最小值小于或等于a .()()225523f xg x x x -=--+-()2102352102352x x x x =-+--≥----=. 当且仅当3,52x ⎡⎤∈⎢⎥⎣⎦时取等号，∴()()2f x g x -的最小值为2. ∴2a ≥.【点睛】本题考查了绝对值不等式的解法及绝对值不等式的性质，重点考查了分类讨论的数学思想方法，属中档题.。
2020届湖北省荆州中学、宜昌一中等“荆、荆、襄、宜四地七校高三上学期期末考试文科综合试题
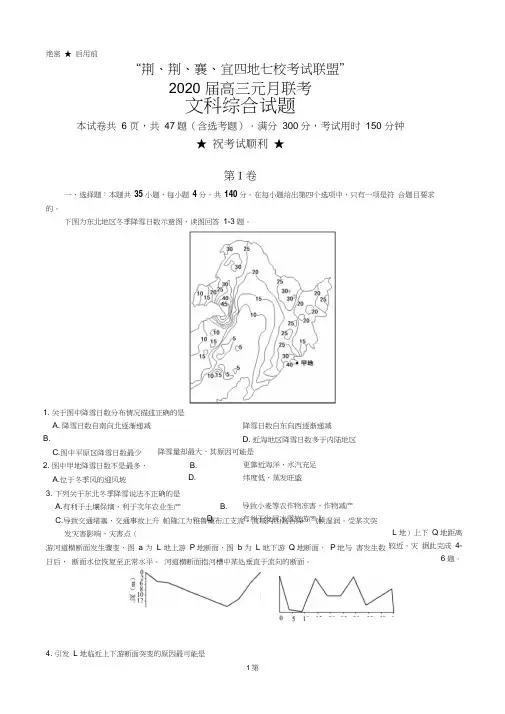
绝密 ★ 启用前“荆、荆、襄、宜四地七校考试联盟”2020 届高三元月联考 文科综合试题本试卷共 6 页，共 47题（含选考题）．满分 300分，考试用时 150 分钟★ 祝考试顺利 ★第Ⅰ卷 一、选择题：本题共 35小题，每小题 4 分，共 140分。
在每小题给出第四个选项中，只有一项是符 合题目要求的。
下图为东北地区冬季降雪日数示意图，读图回答 1-3 题。
1. 关于图中降雪日数分布情况描述正确的是A. 降雪日数自南向北逐渐递减B.C.图中平原区降雪日数最少2. 图中甲地降雪日数不是最多，A.位于冬季风的迎风坡降雪日数自东向西逐渐递减 D. 近海地区降雪日数多于内陆地区 降雪量却最大，其原因可能是 更靠近海洋，水汽充足 纬度低，蒸发旺盛 B. D. 3. 下列关于东北冬季降雪说法不正确的是A.有利于土壤保墒，利于次年农业生产C.导致交通堵塞，交通事故上升 帕隆江为雅鲁藏布江支流，流域内山高谷深，气候湿润。
受某次突发灾害影响，灾害点（D. B. 导致小麦等农作物冻害，作物减产 有利于发展冰雪旅游产业 游河道横断面发生骤变，图 a 为 L 地上游 P 地断面，图 b 为 L 地下游 Q 地断面， P 地与 害发生数日后， 断面水位恢复至正常水平。
河道横断面指河槽中某处垂直于流向的断面。
4. 引发 L 地临近上下游断面突变的原因最可能是1第L 地）上下 Q 地距离较近。
灾 据此完成 4-6 题。
C.位于夏季风的迎风坡A.强降雨致山洪爆发B.滑坡土石阻塞河道C.地震迫使河流改道D.上游大坝开闸泄流5. 此次灾害的生消过程中L 地下游水量A. 不断增加B.不断减少C. 先增加后减少D.先减少后增加6. 河道断面骤变至水位恢复正常水平期间，L 地下游应A. 迁离沿岸居民B.清理河道淤泥C. 大坝蓄水防旱D.积极恢复生产截至2019 年7月底，全国依法登记的农民合作社达220.7 万家，辐射带动了全国近一半的农户。
湖北省高三上学期历史10月联考试卷
湖北省高三上学期历史10月联考试卷姓名:________ 班级:________ 成绩:________一、选择题（本大题共24小题，每小题2分，共48分。
） (共24题；共48分)1. （2分） (2020高二下·安徽月考) 公卿的族属是商周政治建构的重要因素。
下列商周异、同姓公卿的比例差异说明西周政治制度的特点是（）A . 家国同构B . 等级森严C . 君主专制D . 官僚政治2. （2分） (2019高二上·西安期中) 某校高二（3）班在历史研究性学习的中期报告中，提到了如下关键词：克己复礼、仁政、罢黜百家、朱熹、黄宗羲。
据此判断他们研究的主题最有可能是（）A . 儒学的形成及发展B . 中央集权体制的演变C . 法家思想的形成与发展D . 科举制度的发展与完善3. （2分）《墨子》记载：“农夫早出暮入，耕稼树艺……妇人夙兴夜寐，纺绩积纴……”，农民如此兢兢业业主要是①缴纳租税的需要②商品交换的需要③自家基本生活的需要（）A . ①②B . ②③C . ①③D . ①②③4. （2分） (2017高一上·枣庄月考) 按唐制，中男（男丁16岁以上至21岁为中男）不服兵役，成男（男丁22岁以上为成男）才服兵役。
封德彝提出中男服役的建议，得到太宗许可。
但是魏征不肯签署文件，并指出这是竭泽而渔的做法。
最终此提议没有通过。
据此，你认为魏征供职于（）A . 尚书省B . 中书省C . 门下省D . 兵部5. （2分） (2019高二上·齐齐哈尔期末) 下列观点属于智者学派的是（）①万物由水生成，又复归于水②每个人都有自己的感觉，因此一切都是相对的③正义、善德、真理等价值标准都是由人制定的④“知识就是美德”。
A . ①②B . ③④C . ①④D . ②③6. （2分） (2018高二上·长春期中) 宋朝是一个文化昌盛、科技发展的朝代，这主要得益于宋朝的文化和知识分子政策。
湖北剩荆襄宜四地七校2020届高三化学10月联考试题含解析
A.若甲为Cl2，则丁可能是铁B.若甲为NH3，则丁可能是氧气
C.若甲为AlCl3溶液，则丁可能是氨水D.若甲为NaOH，则丁可能是SO2
【答案】C
【解析】
【详解】A、若甲为Cl2，丁是Fe，则乙是FeCl3，丙是FeCl2，符合转化关系，A正确；
A.糯米、粳米、大麦等谷物中均含有淀粉
B.古法酿酒工艺中有多种酶参与催化反应
C.酒化酶将葡萄糖转化为乙醇时，温度越高反应速率一定越快
D.该过程中涉及蒸馏操作
【答案】C
【解析】
【详解】A.糯米、粳米、大麦等谷物中均含有淀粉,故A正确；
B.古法酿酒是利用淀粉在酶的作用下转化为乙醇，所以古法酿酒工艺中有多种酶参与催化反应，故B正确；
D.a点是Ba(OH)2溶液和H2SO4恰好反应产生BaSO4沉淀，此时溶液中只有水，溶液显中性，b点恰好发生反应：NaHSO4+Ba(OH)2=BaSO4↓+NaOH+H2O，所对应的溶液为NaOH溶于，显碱性，D错误；
故合理选项是A。
【点睛】本题考查酸、碱混合溶液反应的定性判断，注意：溶液导电能力与离子浓度成正比，弄清物质的量与反应的关系及各点溶液中溶质成分是解本题关键，侧重考查学生分析判断及识图能力。
湖北省荆、荆、襄、宜四地七校2020届高三化学10月联考试题（含解析）
相对原子质量：H:1 C:12 N:14 O:16 Na:23 S:32 Cl:35.5 Fe:56 Zn:65
第Ⅰ卷选择题（共48分）
一、选择题（本题包括16小题，每小题3分，共48分。每题只有一个选项符合题意）
湖北省部分学校高三上学期10月联考试题历史
2023—2024学年度上学期高三年级十月联考历史试卷★祝考试顺利★注意事项：1.答题前，先将自己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答：用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后，请将本试卷和答题卡一并上交。
一、选择题：本题共15小题，每小题3分，共45分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.公元前536年，郑国子产颁布“铸刑书”,此举遭到晋国保守贵族叔向的指责，批评他此举会导致“民知争端矣，将弃礼而征于书”。
公元前513年，晋国也颁布“铸刑鼎”。
上述现象表明春秋晚期2.西汉思想家陆贾在《新语》中指出：“夫欲富国强威，辟地服远者，必得之于民；欲建功兴誉，垂名烈，流荣华者，必取之于身……天地之性，万物之类，怀德者众归之，恃刑者民畏之，归之则充其侧，畏之则去其域。
”陆贾的上述思想3.表1不同历史人物对历史上某一赋税制度(措施)的评价表1评价的是4.(宋代)岳州知州指出：“(农民)自来兼作商旅……欲出榜招召，务令疾速归业。
如贪恋作商，不肯回归，其田权许人请射(承佃耕种)。
”宋高宗采纳户部意见：“商人田产，身虽在外，家有承管，见今输送二税者，难(不应)许人请射。
”这些现象出现的根源是5.朱元璋对能力、品性都很出众的“老人”进行授官，改变他们半民半公的尴尬身份，成为大明朝的正式“公务员”,光宗耀祖。
如：洪武十五年(公元1382年),“老人”陈原九被任命为松江知府。
洪武二十四年(公元1391年),徽州歙县“老人”胡伯顺被任命为监察御史。
材料表明朱元璋重视6.鸦片战争后的一段时间内，清政府对中外条约的认识是“照会该夷，申以盟誓”,且认为只有在两国连年构兵导致相互失信，为停战议和、避免猜疑，须“立条约以坚其信”。
湖北省宜荆荆随2023-2024学年高二上学期10月联考历史试卷(含部分解析)
2023 年宜荆荆随高二10 月联考高二历史试卷考试时间：2023 年10 月10 日上午08：00-09：15 试卷满分：100 分注意事项:1.答题前，先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。
写在试卷、草稿纸和答题卡上的非答题区域均无效。
一、选择题：本题共15 小题，每小题3 分，共45 分。
每小题给出的四个选项中，只有一个选项是最符合题目要求。
1.相传，五帝之一的尧出于“方（违）命圮（同）族”的忧虑，本不同意让鲧去治水，但面对四岳（相传为重臣羲和的四个儿子，分别在四方任职）、百姓的“强请”，尧也只能顺从。
这说明，传说时代末期的中国（）A ．君主权力尚未集中B ．原始民主发挥功用C ．尚贤观念深入人心D ．神权干预部落决策2.湖北省云梦县出土的官箴竹简《为吏之道》对吏的道德模范作用和为基层地方提供教化的作用要求颇高，为吏职赋予了三大职能：法律执行者、知识传授者和道德表率者。
由此可见，《为吏之道》（）A ．明确了秦对吏的教化要求B ．代表了秦朝官员管理水平C ．打破了长期官位世袭制度D ．强化了地方监察体制建设3.对历代帝王陵墓的保护是中国古代固有的文化传统。
北魏孝文帝在恢复祭陵制度的同时，对汉、魏、晋诸陵的维护沿袭了魏明帝的做法，并以古代帝王祭祀的礼仪“太牢之礼”祭汉光武及明、章三帝陵。
孝文帝这一做法旨在（）A ．尊重历代的贤明君主B ．传承和弘扬鲜卑族文化传统C ．彰显其人道主义情怀D ．表明北魏入主中原的正统性4.唐代传奇《枕中记》中的主角卢生“明年，举进士，登第释褐，秘校，应制，转渭南尉，俄迁监察御史，转起居舍人知制诰，三载，出典同州，迁陕牧，生性好土功，自陕西凿河八十里，以济不通，邦人利之，刻石纪德，移节汴州，领河南道采访使，征为京兆尹”。
湖北省“荆、荆、襄、宜四地七校考试联盟”2020届高三地理10月联考试题
湖北省“荆、荆、襄、宜四地七校考试联盟”2020届高三地理10月联考试题一、选择题（每个小题只有一个正确的选项。
22小题，每小题2分，共44分。
）二十四节气是我国独有的农业物候历，是我国优秀传统文化之一。
2016年11月30日已被联合国教科文组织列入人类非物质文化遗产名录。
读图，回答1-2题。
1．地球绕太阳运行一周为360°，以春分日地球在黄道上的位置为0°，则立春日地球在黄道上的位置为A．45° B．105° C．195° D．315°2．我国劳动人民根据二十四节气总结出了很多谚语，以下说法错误的是A. 吃了冬至面，一天长一线B. 清明竹笋出，谷雨笋出齐C. 寒露早，白露迟，秋分种麦正当时D. 白露秋风夜，一夜凉一夜地球表面的陨石易风化和发生化学成分变化，南极大陆却因环境特殊保存了大量陨石，被称为“陨石宝库”。
下图为南极冰流域和陨石富集区分布示意图。
读图回答3-5题。
3．陨石富集于图示地区的原因是A. 小天体闯入地球，受地磁引力大量落入该地B. 因洋流、海浪搬运作用富集该区域山脉附近C. 落到南极的陨石随冰川移动，在低处富集D. 因板块运动，落入海洋的陨石不断汇入该地4．相对于其它地区，南极陨石科考价值较高的原因是A. 气候湿润，陨石不易风化B. 冰雪覆盖，保存年代久远C. 环境洁净，对陨石污染小D. 臭氧层薄，坠落的陨石多5．全球变暖对南极陨石富集区的影响可能是A. 陨石类型减少B. 陨石风化减弱C. 出露数量增加D. 陨石埋藏加深大约在800万年前，冰川融水带着泥土通过贝拉库勒河注入太平洋，在出海口遇到太平洋地热温泉，冰川泥被温泉扰动像沸水那样翻滚在百丈冰层之下。
百万年后，在海底形成了约40英亩（1英亩约等于4046平方米）细如雾、柔似棉的冰川泥，这是加拿大独有的美容护肤品原料。
但是加拿大至今只允许2家企业开采冰川泥，并限制采挖的数量。
2020年秋“荆、荆、襄、宜四地七校考试联盟高三期中联考地理试卷
2020年秋“荆、荆、襄、宜四地七校考试联盟”高三期中联考地理试题本试卷共3页，共19题。
满分100分，考试用时90分钟★祝考试顺利★注意事项:1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上，写在本试卷上无效。
3.考试结束后，将本试卷和答题卡一并交回。
一、选择题：本题共15小题，每小题3分，共45分。
在每小题给出的四个选项中，只有一项符合题目要求。
①②③④表示某区域地形类型中的山脊和山谷，点a、b、c对应的海拔分别为800米、600米、400米，读下图，完成1～2题。
1．①②③④可能发育河流且流速较快的是A．① B．② C．③ D．④2．降落到P点的雨水会向哪个方向流动A．东南 B．东北 C．西南 D．西北2020年6月1日至7月12日，长江流域的平均降水量为403毫米，较常年同期偏多49%，据此完成3～4题。
3．长江中下游流域降水量大、历时长的主要原因是A．雨带向北推进快 B．暖锋控制时间长C．副高势力偏弱 D．受台风影响大4．长江中下游流域易发生洪涝灾害，为防治洪灾应采取的生态措施是A．疏浚河道，加固河堤 B．加强洪灾的监测和预警C．完善城市排水系统 D．退垸还湖、退田还湖下图示意海口某栋住宅楼（约20ºN，110ºE）二至日8时和16时的日影（注：本题所涉及的时间均为北京时间）。
读图文材料，回答5～6题。
5．图中①②③④表示冬至日16时日影的是A．① B．② C．③ D．④6．下列时段中，住宅楼日影长度变化最大的时段最可能是A．夏至日8:00～12:00 B．夏至日12:00～16:00C．冬至日8:00～12:00 D．冬至日12:00～16:00下图中的桃花河位于我国鄱阳湖平原地区，村民为了灌溉之便，开挖了两条水渠，并在河中修筑两条低矮的水坝（低于河水水面）。
湖北省“荆荆襄宜四地七校考试联盟”2020届高三生物10月联考试题202004180352
湖北省“荆、荆、襄、宜四地七校考试联盟”2020届高三生物10月联考试题一、选择题（1-10每题1分，11-30每题2分，共50分）1.2002年7月12日美国《科学快报》报道了纽约州立大学几位病毒学家人工合成的脊髓灰质炎病毒的消息和简略过程。
用人工合成的脊髓灰质炎病毒感染小鼠后，小鼠患脊髓灰质炎，只是其毒性比天然病毒小得多。
下列相关说法正确的是A．人工合成了脊髓灰质炎病毒就是人工制造了生命B．人工合成的脊髓灰质炎病毒可通过无丝分裂的方式进行增殖C．人工合成的脊髓灰质炎病毒主要是由以碳链为骨架的生物大分子构成的D．人工合成病毒的研究对人类健康存在威胁，应该禁止2.有关生命系统的结构层次的表述，下列正确的是A. 病毒是能进行生命活动的最小系统B. 一棵小叶榕树与一只老虎，在生命系统中具有相同的层次C. 一片农田中的所有动、植物个体是一个群落D. 某个培养基上长出的一个大肠杆菌菌落是一个种群3.科学家在美国黄石公园发现一种嗜热好氧杆菌，长有许多触角（又叫集光绿色体），内含大量叶绿素，能在菌苔上同其他细菌争夺阳光。
下列相关叙述正确的是A．该菌细胞内无细胞器，但能进行有氧呼吸B．除去该菌的细胞壁需要利用纤维素酶和果胶酶C．培养该细菌的培养基可以不含碳源，但必须给予光照D．该菌细胞质高度区室化、功能专一化4.下列有关细胞中的元素和化合物的说法，正确的是A．干旱环境生长的仙人掌细胞中结合水的含量多于自由水B．盐析会改变蛋白质的空间结构，使其成为白色絮状物C．叶肉细胞吸收的氮元素可用于合成核苷酸、蛋白质、磷脂和淀粉D．油料作物种子成熟过程中，糖类不断转化成脂肪导致脂肪含量增加5.利用紫色洋葱鳞片叶外表皮细胞和不同浓度的蔗糖溶液，可以探究细胞发生质壁分离和复原的情况。
下列有关该实验的叙述正确的是A．在逐渐发生质壁分离的过程中，细胞的吸水能力逐渐增强B．该实验利用同一块植物组织探究了质壁分离和复原的情况，没有对照C．将装片在酒精灯上加热后再观察，质壁分离及复原现象会更明显D．不同浓度蔗糖溶液下发生质壁分离的细胞，滴加清水后都能复原6.下列有关蛋白质和核酸的叙述正确的是A. a-鹅膏蕈碱是一种环状八肽，分子中含有7个肽键B. DNA是双链结构有氢键，RNA是单链结构没有氢键C. 细胞内蛋白质水解时，通常需要另一种蛋白质的参与D. 蛋白质变性是由肽键的断裂造成的7.下列关于细胞膜成分和功能的叙述，正确的是A．细胞膜的成分可以使用双缩脲试剂和苏丹Ⅲ进行鉴定B．科研上常用染色法鉴定细胞死活，是因为细胞膜可以将细胞与外界环境分隔开C．改变细胞膜上某种蛋白质的结构可能会影响细胞间的信息交流D．细胞膜外侧的糖类只可与细胞膜上的蛋白质结合形成糖蛋白，具有保护和润滑作用8.下列有关细胞的叙述，正确的是A. 老年人和白化病患者的白头发都是由于细胞中酪氨酸酶活性降低引起的B. 真核细胞的细胞膜能维持细胞的形态并保持细胞内部结构的有序性C. 生物膜是生物体内所有膜结构的统称D. 洋葱根尖分生区细胞具有分裂和分化能力，也具有发育成完整个体的潜能9.细胞核控制着细胞的代谢和遗传。
2022-2023学年湖北省荆荆宜三校高三上学期10月联考历史试题及答案
2022年湖北省荆荆宜三校高三上学期10月联考高三历史试卷考试时间：2022年10月26日上午10：30-11：45试卷满分：100分注意事项:1.答卷前，考生务必将自己的姓名、考号等填写在答题卡和试卷指定的位置上。
2.回答选择题时，选出每题答案后，用铅笔把答案卡对应题目的答案标号涂黑。
如需要改动，先用橡皮擦干净后，再选涂其他答案标号。
回答非选择题时，将答案写在答题卡上，写在试卷上无效。
一、选择题：本题共16小题，每小题3分，共48分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1.西周时期，各诸侯国之间存在大量无主的土地和田野，并无明确的边界，直到春秋战国时期，边界的概念才逐渐形成。
这一变化反映了春秋战国时期（）A．土地兼并加剧B．诸侯争霸频繁C．分封制度强化D．郡县制度普及2.妖言容易引发损害国家统治稳定的叛乱，因而备受统治者重视。
秦代存在“行沃（同妖）律”甚至不惜兴起大狱，汉文帝废除诽谤妖盲之法，东汉统治者曾多次针对妖言案颁布赦令。
这一变化反映了汉代（）A.统治者反省和慎重的态度B.全面废除关于妖言的法律C.国家统治坚持以妖言入罪D.政治制度受到鬼神论影响3.隋初的军事制度沿用西魏、北周时期创建的府兵制，兵农分离，军人世代为兵，户口由军队管理，不入州县户籍，国家不分配土地。
开皇十年（590），增加了士兵受田。
这一变化说明（）A.均田制遭到破坏B.政治局势影响政策C.军人身份的转化D.运河修建消耗民力4.据下表可以推知（）中英关税、土地税及其在财政收入中所占比率（单位：白银万两）英国中国年份土地税土地税关税关税土地税土地税关税关税总额占比总额占比总额占比总额占比149030.421.77% 6.75%161493%30.17%155228.340.81%7.511%130973%80.45%16026525.52% 3.614%184480%200.87%A.中国被卷入资本主义世界市场B.圈地运动导致英国农业衰落C.明朝社会对转型的反应较迟滞D.经济结构决定社会发展方向5.中国关税自主运动，主要可分为两大阶段：1902-1917年为第一阶段，主要表现为要求修订税则，提高税率；第二阶段为1918-1927年，其主要表现变化为要求制定国定税则。
2020高三历史上学期10月联考试题
2020届高三历史上学期10月联考试题考生注意：1.本试卷分选择题和非选择题两部分。
满分100分，考试时间90分钟。
2.答题前，考生务必用直径0.5毫米黑色，墨水签字笔将密封线内项目填写清楚。
3.考生作答时，请将答案答在答题卡上。
选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．．．．．．．．．．．．．．．．．．．．．．．．．．．。
4.本卷命题范围：高考范围。
一、选择题(本大题共24小题，每小题2分，共计48分。
在每小题列出的四个选项中，只有一项是最符合题目要求的。
)1.夏商时期，王位世袭有“兄终弟及”和“父子相传”两种方式。
夏朝主要以“父子相传”为主，商朝两者并有。
这些方式A.利于奴隶制国家的长治久安B.奠定后世王位继承的原则C.促成了“家天下”观念的出现D.容易导致统治集团的分裂2.据史载，环钱(方孔圆钱)早在西周时期就已出现，春秋时期渗入刀布钱区。
战国后期，除楚国外，其余诸国大都铸行环钱。
这表明春秋战国时期A.商业货币的属性发生了变化B.环钱最能迎合商业发展需要C.环钱利于加强各地经济联系D.货币出现了统一的发展趋向3.瞿兑之在《秦汉史纂》中云：“中国成为一统国，自秦启之，而汉承之，虽遇乱世，终犹心焉一统，人人皆拭目翘足以为庶几复见太平。
二千年来如一日，此秦汉之所赐也。
”据此，该学者强调秦汉时期A.奠定了中国封建时代统一的基础B.大一统王朝出现具有一定合理性C.形成专制制度和思想文化的统一D.思想嬗替是王朝取得成功的经验4.《续文献通考》记载宋代江苏书院，“至理宗时尤夥。
其得讫于朝，或赐田，或赐额，或赐御书，间有设官者。
应天有明道书院，苏州有鹤山书院，丹阳有丹阳书院……丹徒有淮海书院，唯不及徐、淮地区。
”这反映了当时江苏A.书院的制度化趋势在不断加强B.传统儒学在宋代受到质疑C.政治中心与文化中心日趋一致D.文化发展相对比较的繁荣5.明朝建立之初，在妇女服饰上面，各有定制，禁止僭越。
湖北省荆、荆、襄、宜四地七校考试联盟2024年高三冲刺模拟历史试卷含解析
湖北省荆、荆、襄、宜四地七校考试联盟2024年高三冲刺模拟历史试卷注意事项1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。
第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。
一、选择题：共30小题，每小题2.5分，共75分。
在每小题列出的四个选项中，只有一项是符合题目要求的。
1．1952年欧洲煤钢共同体成立时，英国决定不加入。
1957年《罗马条约》签署时，英国也缺席。
1963年1月，英国的入欧申请遭到法国的否决。
1973年英国加入欧共体。
1975年6月，英国进行第一次脱欧公投，结果67％的民众赞成留在欧共体。
2020年1月，英国正式脱离欧盟。
英国在欧洲联合上的态度反映了A．经济区域集团化违背历史发展潮流B．世界格局左右英国在一体化上的选择C．主权国家利益与一体化之间的纠葛D．经济区域集团化对发达国家更为不利2．钱乘旦认为：1415年起历次重大探险活动,绝大部分是在国王或在政府有关部门委派、支持下进行的。
15世纪开始的探险队领导人大多数是贵族,到达印度的达伽马,发现太平洋的巴尔沃亚，首次环球航行的麦哲伦都是贵族，形成了商人出钱，国王牵线组织，贵族冲锋陷阵的扩张格局。
据此，新航路开辟A．扩大了商品销售市场B．是新旧力量共同推动的结果C．壮大了资产阶级力量D．促进了统一的世界市场形成3．中国古代的治世或盛世通常以皇帝年号命名，下列概念不符合这一规则的是A．文景之治B．贞观之治C．开元盛世D．康乾盛世4．宋代江西赣州的“福寿沟”，出口之处安装有“十二水宿”闸门。
该闸门设计十分巧妙，江水低于闸门时，凭借高度差，用城中排出的积污水冲开闸门，排入江中。
若闸门低于江水，则江水的压力迫使闸门封闭，江水不会倒灌。
由此可知A．工艺设计贯穿理学思想B．技术水平彰显工匠精神C．古代科技重视理论总结D．设计思想体现天人感应5．若以“市舶司”“十三行”“鸦片战争”“北伐战争”等概念来介绍某城，此城是A．南京B．武汉C．上海D．广州6．史学家傅斯年说：“我们存而不补，这是我们对于材料的态度；我们证而不疏，这是我们处理材料的手段。
湖北省＂荆、荆、襄、宜四地七校考试联盟＂2020届高三数学上学期10月联考试题 理
荆、荆、襄、宜四地七校考试联盟2020届高三10月联考理科数学试题本试卷共4页，23题（含选考题）。
全卷满分150分。
考试用时120分钟。
注意事项：1．答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。
2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。
如需改动，用橡皮擦干净后，再选涂其它答案标号。
回答非选择题时，将答案写在答题卡上。
写在本试卷上无效。
3．考试结束后，将答题卡交回。
一、选择题：（本大题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
请将正确的答案填涂在答题卡上。
）1．已知全集U =R ，函数ln(1)y x =-的定义域为M ，集合{}20N x x x =-<，则下列结论正确的是A ．M N N =IB ．()U M N =∅I ðC ．M N U =UD ．()U M N ⊆ð 2．下列函数中，既是偶函数，又在(),0-∞上单调递增的是A ．()22x x f x -=-B ．2()1f x x =-C ．()cos f x x x =D ．()ln f x x =- 3．下列命题中错误的是A ．命题“若x y =，则sin sin x y =”的逆否命题是真命题B ．命题“()0000,,ln 1x x x ∃∈+∞=-”的否定是“()0,,ln 1x x x ∀∈+∞≠-”C ．若p q ∨为真命题，则p q ∧为真命题D ．00,x ∃>使“00x x ab >”是“0a b >>”的必要不充分条件4．若tan 2α=，则sin 4cos 5sin 2cos αααα-+的值为A ．16B ．16-C ．12D ．12-5．已知11617a =，16log b =，17log c =，则a ，b ，c 的大小关系为 A ．a b c >> B ．a c b >> C ．b a c >> D ．c b a >> 6．若将函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭的图象向左平移ϕ()0ϕ>个单位，所得图象关于原点对称，则ϕ最小时，tan ϕ=A．3- B．3C． D7．已知函数21()7,0(x)2log (1),0xx f x x ⎧-<⎪=⎨⎪+≥⎩，若()1f a <，则实数a 的取值范围是A.()[),30,1-∞-UB.()()3,01,1--UC.()3,1-D.()(),31,-∞-+∞U 8．某辆汽车每次加油都把油箱加满，下表记录了该车相邻两次加油时的情况．注：为A ．6升 B．8升 C ．10升 D ．12升 9．平面直角坐标系xOy 中，点00(,)P x y 在单位圆O上，设xOP α∠=，若5 36ππα⎛⎫∈⎪⎝⎭，，且3sin()65πα+=，则0x 的值为A．310- B ．310+ C ．310 D ．310-10．已知函数2()(1)x f x e x =-+（e 为自然对数的底），则()f x 的大致图象是A B C D 11．已知函数()xf x e =，,,a b c 分别为ABC ∆的内角,,A B C 所对的边，且222334a b c ab +-=，则下列不等式一定成立的是A ．()()sin cos f A fB ≤ B ．()()sin sin f A f B ≤C ．()()cos sin f A f B ≤D ．()()cos cos f A f B ≤12．设实数0λ>，若对任意的()2,x e ∈+∞，不等式ln 0x e x λλ-≥恒成立，则λ的最小值为A ．22eB ．22eC ．212eD ．22e二、填空题（本大题共4小题，每小题5分，共20分）13．函数log (1)4a y x =-+的图象恒过定点P , 点P 在幂函数()f x 的图象上，则(3)f = ． 14．若函数()()3212f x a x ax x =++-为奇函数，则曲线()y f x =在点()()1,1f 处的切线方程为 ．15．已知命题2:,10p x R mx ∃∈+≤，命题2:,10q x R x mx ∀∈++>，若p q ∨为真命题，则实数m的取值范围为． 16．已知1()2sin (,)64f x x x R πωω⎛⎫=+>∈ ⎪⎝⎭，若()f x 的任何一条对称轴与x 轴交点的横坐标都不属于区间(,2)ππ，则ω的取值范围是 ．三、解答题：（本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤） 17．（本小题满分12分）如图,D 是直角ABC ∆斜边BC 上一点,AC =． （Ⅰ）若30DAC ∠=o ，求角B 的大小；（Ⅱ）若2BD DC =，且AD =DC 的长．18．（本小题满分12分）如图，已知多面体PABCDE 的底面ABCD 是边长为2的菱形，PA ⊥底面ABCD ，ED PA ∥，且22PA ED ==．（Ⅰ）证明：平面PAC ⊥平面PCE ；（Ⅱ）若直线PC 与平面ABCD 所成的角为45︒，求二面角P CE D --的余弦值．19．（本小题满分12分）国家质量监督检验检疫局于2020年5月31日发布了新的《车辆驾驶人员血液、呼气酒精含量阀值与检验》国家标准．新标准规定，车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升，小于80毫克/百毫升为饮酒驾车，血液中的酒精含量大于或等于80毫克/百毫升为醉酒驾车．经过反复试验，喝一瓶啤酒后酒精在人体血液中的变化规律的“散点图”如下：该函数模型如下：0.540sin()13,02()39014,2x x x f x e x π-⎧+≤<⎪=⎨⎪⋅+≥⎩根据上述条件，回答以下问题：（Ⅰ）试计算喝1瓶啤酒多少小时血液中的酒精含量达到最大值？最大值是多少？ （Ⅱ）试计算喝一瓶啤酒多少小时后才可以驾车？（时间以整小时计算）（参考数据：ln15 2.71,ln30 3.40,ln90 4.50≈≈≈）20．（本小题满分12分）已知椭圆()2222:10x y E a b a b+=>>过点(2,0)，且其中一个焦点的坐标为()1,0.（Ⅰ）求椭圆E 的方程；（Ⅱ）过椭圆E 右焦点F 的直线l 与椭圆交于两点,A B ，在x 轴上是否存在点M ，使得MA MB ⋅u u u r u u u r为定值？若存在，求出点M 的坐标；若不存在，请说明理由．21．（本小题满分12分）已知函数()ln(1)1()xf x e ax x x R =+++-∈.（Ⅰ）若0x ≥时,()0f x ≥恒成立，求实数a 的取值范围；（Ⅱ）求证：23e2<.请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．（本小题满分10分）选修4-4：极坐标和参数方程选讲已知极坐标系的极点在直角坐标系的原点处，极轴与x 轴非负半轴重合，直线l 的参数方程为：1(x tt y t =-⎧⎨=⎩为参数)，曲线C 的极坐标方程为:4cos ρθ=． （Ⅰ）写出曲线C 的直角坐标方程和直线l 的普通方程； （Ⅱ）设直线l 与曲线C 相交于,P Q 两点, 求PQ 的值．23．（本小题满分10分）选修4-5：不等式选讲已知函数()1f x x =-． （Ⅰ）解关于x 的不等式()0f x x ->；（Ⅱ）若2(43)((4)1)f a f a -+>-+，求实数a 的取值范围．荆、荆、襄、宜四地七校考试联盟E DB C AP2020届高三10月联考理科数学参考答案13．9 14．20x y--= 15．2m< 16．12,33⎡⎤⎢⎥⎣⎦三、解答题：17．解：（Ⅰ）在△ABC中,根据正弦定理,有sin sinAC DCADCDAC=∠∠.因为AC=,所以sin ADC DAC∠=∠=.………………………………3分又οο6060>+∠=∠+∠=∠BBADBADC所以120ADC∠=°.于是οοοο3030120180=--=∠C,所以60B∠=°. ……………………………………6分（Ⅱ）设DC x=,则2BD x=,3BC x=,AC=.于是sinACBBC==,cos B=,.6xAB=………………………………………9分在ABD∆中,由余弦定理,得2222cosAD AB BD AB BD B=+-⋅,即222264222x x x x=+-⨯=,得x=DC=．………12分18．证明：（Ⅰ）连接BD，交AC于点O，设PC中点为F，连接,OF EF．因为O，F分别为AC，PC的中点，所以OF PAP，且12OF PA=，因为DE PAP，且12DE PA=，所以OF DEP，且OF DE=．所以四边形OFED为平行四边形，所以OD EFP，即BD EFP．······2分因为PA⊥平面ABCD，BD⊂平面ABCD，所以PA BD⊥．因为ABCD是菱形，所以BD AC⊥．因为PA AC A=I，所以BD⊥平面PAC．···············4分因为BD EFP，所以EF⊥平面PAC．因为FE⊂平面PCE，所以平面PAC⊥平面PCE．··········5分（Ⅱ）因为直线PC与平面ABCD所成角为45o，所以45PCA∠=o，所以2AC PA==．所以AC AB=，故△ABC为等边三角形．设BC的中点为M，连接AM，则AM BC⊥．以A为原点，AM，AD，AP分别为x yz，，轴，建立空间直角坐标系A xyz-．···························7分则()0,02P，，)0C，，()0,21E，，()0,20D，，)2,PC=-u u u r(),CE=u u u r()0,0,1DE=u u u r．设平面PCE的法向量为()111,,x y z=n，则0,0,PCCE⎧=⎪⎨=⎪⎩nnuu u rguu u rg即11111120,0.y zy z+-=++=⎪⎩令11y=，则112.xz⎧=⎪⎨=⎪⎩所以)=n．…………………………………………9分设平面CDE的法向量为()222,,x y z=m，则0,0,DECE⎧⋅=⎪⎨⋅=⎪⎩mmuu u ruu u r即22220,0.zy z=⎧⎪⎨++=⎪⎩令21,x=则220.yz⎧=⎪⎨=⎪⎩所以()=m．cos,4⋅===⋅n mn mn m，设二面角P CE D--的大小为θ，由于θ为钝角，所以cosθ=，···11分即二面角P CE D--的余弦值为．················12分19．解：（Ⅰ）由图可知，当函数()f x取得最大值时，02x<<，…………………1分此时()40sin()133f x xπ=+，……………………………………………………………2分当32xππ=，即32x=时，函数()f x取得最大值为max401353y=+=．………………4分故喝一瓶啤酒1.5小时血液中的酒精含量达到最大值53毫克/百毫升．………………5分（Ⅱ）由题意知，当车辆驾驶人员血液中的酒精小于20毫克/百毫升时可以驾车，此时2x>．由0.5901420xe-⋅+<，得0.5115xe-<，…………………………………………………7分两边取自然对数，得0.51ln ln15xe-<………………………………………………………8分即0.5ln15x-<-，所以ln15 2.715.420.50.5x->==-，…………………………………11分故喝啤酒后需6个小时后才可以合法驾车．………………………………………………12分注：如果根据图象猜6个小时，可给结果分2分．20．解：（Ⅰ）由已知得2,1a c==，∴b=E的方程为22143x y+=；...........4分（Ⅱ）假设存在点0(,0)M x,使得MA MB⋅u u u r u u u r为定值，当直线l的斜率不为0时，可设直线l的方程为1x my=+，联立221431x yx my⎧+=⎪⎨⎪=+⎩, 得22(34)690m y my++-= (6)分设1122(,),(,)A x y B x y ，则12122269,3434m y y y y m m +=-⋅=-++，............................7分101202(,),(,)MA x x y MB x x y =-=-u u u r u u u r22102012120120()()(1)(1)()(1)MA MB x x x x y y m y y x m y y x ∴⋅=-⋅-+⋅=+⋅+-++-u u u r u u u r=22002296(1)()(1)()(1)3434mm x m x m m +-+--+-++22002(615)9(1)34x m x m --=+-+.............................................................................9分要使上式为定值, 即与m 无关，应有0615934x -=- 解得0118x =，此时13564MA MB ⋅=-u u u r u u u r ．.................................................................................11分当直线l 的斜率为0时，不妨设(2,0),(2,0)A B -，当M 的坐标为11(,0)8时13564MA MB ⋅=-u u u r u u u r综上，存在点11(,0)8M 使得13564MA MB ⋅=-u u u r u u u r 为定值．.……………………………………12分21．解:（Ⅰ）法一：若0x ≥时, 则()11x f x e a x '=+++..................................................1分()()211x f x e x ''=-+，()()211xf x e x ''=-+在[)0+∞，上单调递增， 则()()0=0f x f ''''≥................................................................................................................. .....3分 则()f x '在[)0+∞，上单调递增，()()0=2f x f a ''≥+..............................................................4分① 当20a +≥，即-2a ≥时，()0f x '≥，则()f x 在[)0+∞，上单调递增， 此时()()0=0f x f ≥，满足题意................................................................................................5分②若2a <-,由()f x '在[)0+∞，上单调递增， 由于()020f a '=+<，,()0x f x '→+∞>.故()00,x ∃∈+∞,使得()00f x '=. 则当00x x <<时,()()00f x f x ''<=,∴函数()f x 在()00,x 上单调递减. ∴()()000f x f <=,不恒成立.舍去．综上所述,实数a 的取值范围是[)2,-+∞. ............................................ .....................................7分 法二：若0x ≥时, 则()11x f x e a x '=+++...................................................................................1分① 2a ≥-，令()1xg x e x =--，则()10xg x e '=-≥，()g x 在[)0,+∞上单调递增，则()(0)0g x g ≥=，故1x e x ≥+．………………………………………………….... .... .... ...3分∴()()1112011xf x e a x a a a x x '=++≥+++≥=+≥++. ∴函数()f x 在区间[)0,+∞上单调递增. ∴()()00f x f ≥=，成立.......….............5分 ②若2a <-,由()()()()222111011x xx e f x e x x +-''=-=≥++. ∴函数()f x '在[)0,+∞上单调递增.由于()020f a '=+<，,()0x f x '→+∞>.故()00,x ∃∈+∞,使得()00f x '=. 则当00x x <<时,()()00f x f x ''<=, ∴函数()f x 在()00,x 上单调递减. ∴()()000f x f <=,不恒成立.舍去．综上所述,实数a 的取值范围是[)2,-+∞. .........................................................................7分 （Ⅱ）证明:由(Ⅰ)知,当2a =-时,()f x =()2ln 11xe x x -++-在[)0,+∞上单调递增....................... ........ ..................... ........................ ...................................... .....................9分则()102f f ⎛⎫> ⎪⎝⎭,即1211ln 1102e ⎛⎫-++-> ⎪⎝⎭. ∴3ln 22>∴232e>,即232e <.............................................................................................. .....12分22.解：（Ⅰ）.24cos ,4cos ρθρθ=∴=Q , 由222,cos x y x ρρθ=+=,得224x y x +=, 所以曲线C 的直角坐标方程为()2224x y -+=,由1x t y t =-⎧⎨=⎩,消去t 解得：10x y +-=.所以直线l 的普通方程为10x y +-=．………5分（Ⅱ）把1x y ⎧=⎪⎪⎨⎪⎪⎩ 代入224x y x +=,整理得230t +-=,设其两根分别为 12,t t，则12123t t t t +=⋅=-12PQ t t ∴=-== .……………………………………………10分亦可求圆心()2,0到直线10x y +-=的距离为d =，从而PQ =23．解：（Ⅰ）()0f x x ->可化为1x x ->， 所以22(1)x x ->，所以12x <， 所以所求不等式的解集为12x x ⎧⎫<⎨⎬⎩⎭．………………………………………………………5分（Ⅱ）因为函数()1f x x =-在[1)+∞，上单调递增，431a -+>，2(4)11a -+≥，2(43)((4)1)f a f a -+>-+.所以243(4)1a a -+>-+所以(41)(42)0a a -+--<，所以42a -<，所以26a <<.即实数a 的取值范围是(2,6)．……………………………………………………………10分荆、荆、襄、宜四地七校考试联盟 2020届高三10月联考理科数学参考答案13．9 14．20x y --= 15．2m < 16．12,33⎡⎤⎢⎥⎣⎦三、解答题：17．解：（Ⅰ）在△ABC 中,根据正弦定理,有sin sin AC DCADC DAC=∠∠. 因为AC =,所以sin ADC DAC ∠=∠=.………………………………3分 又οο6060>+∠=∠+∠=∠B BAD BADC 所以120ADC ∠=°.于是οοοο3030120180=--=∠C ,所以60B ∠=°. (6)分 （Ⅱ）设DC x =,则2BD x =,3BC x =,AC =.于是sin 3AC B BC ==,cos 3B =,.6x AB = ………………………………………9分 在ABD ∆中,由余弦定理,得 2222cos AD AB BD AB BD B =+-⋅,即222264222x x x x =+-⨯=,得x =DC =．………12分 18．证明：（Ⅰ）连接BD ，交AC 于点O ，设PC 中点为F ，连接,OF EF ．因为O ，F 分别为AC ，PC 的中点，所以OF PA P ，且12OF PA =， 因为DE PA P ，且12DE PA =，所以OF DE P ，且OF DE =． 所以四边形OFED 为平行四边形，所以OD EF P ，即BD EF P ． ······· 2分因为PA ⊥平面ABCD ，BD ⊂平面ABCD ，所以PA BD ⊥． 因为ABCD 是菱形，所以BD AC ⊥．因为PA AC A =I ，所以BD ⊥平面PAC． ··············· 4分 因为BD EF P ，所以EF ⊥平面PAC ．因为FE ⊂平面PCE ，所以平面PAC ⊥平面PCE ． ·········· 5分（Ⅱ）因为直线PC 与平面ABCD 所成角为45o ，所以45PCA ∠=o ，所以2AC PA ==．所以AC AB =，故△ABC 为等边三角形．设BC 的中点为M ，连接AM ， 则AM BC ⊥．以A 为原点，AM ，AD ，AP 分别为x y z ，，轴，建立空间直角坐标系A xyz -． ··························· 7分则()0,02P ，，)0C ，，()0,21E ，，()0,20D ，，)2,PC =-u u u r (),CE =u u u r()0,0,1DE =u u u r ．设平面PCE的法向量为()111,,x y z =n ，则0,0,PC CE ⎧=⎪⎨=⎪⎩n n uu u rg uu u r g 即11111120,0.y z y z +-=++=⎪⎩ 令11y =，则112.x z ⎧=⎪⎨=⎪⎩所以)=n ．…………………………………………9分设平面CDE 的法向量为()222,,x y z =m ，则0,0,DE CE ⎧⋅=⎪⎨⋅=⎪⎩m m uu u ruu u r 即22220,0.z y z =⎧⎪⎨++=⎪⎩令21,x =则220.y z ⎧=⎪⎨=⎪⎩所以()=m ． cos ,⋅==⋅n m n m n m ， 设二面角P CE D --的大小为θ，由于θ为钝角，所以cos θ=， ··· 11分 即二面角P CE D --的余弦值为．················ 12分 19．解：（Ⅰ）由图可知，当函数()f x 取得最大值时，02x <<，…………………1分 此时()40sin()133f x x π=+，……………………………………………………………2分当32x ππ=，即32x =时，函数()f x 取得最大值为max 401353y =+=．………………4分 故喝一瓶啤酒1.5小时血液中的酒精含量达到最大值53毫克/百毫升．………………5分（Ⅱ）由题意知，当车辆驾驶人员血液中的酒精小于20毫克/百毫升时可以驾车，此时2x >．由0.5901420x e -⋅+<，得0.5115x e -<， …………………………………………………7分两边取自然对数，得0.51ln ln 15x e -< ………………………………………………………8分即0.5ln15x -<-，所以ln15 2.715.420.50.5x ->==-， …………………………………11分故喝啤酒后需6个小时后才可以合法驾车．………………………………………………12分注：如果根据图象猜6个小时，可给结果分2分．20．解：（Ⅰ）由已知得2,1a c ==，∴b =E 的方程为22143x y +=；...........4分（Ⅱ）假设存在点0(,0)M x ,使得MA MB ⋅u u u r u u u r为定值，当直线l 的斜率不为0时，可设直线l 的方程为1x my =+，联立221431x y x my ⎧+=⎪⎨⎪=+⎩,得22(34)690m y my ++-= (6)分设1122(,),(,)A x y B x y ，则12122269,3434m y y y y m m +=-⋅=-++，............................7分101202(,),(,)MA x x y MB x x y =-=-u u u r u u u r22102012120120()()(1)(1)()(1)MA MB x x x x y y m y y x m y y x ∴⋅=-⋅-+⋅=+⋅+-++-u u u r u u u r=22002296(1)()(1)()(1)3434mm x m x m m +-+--+-++22002(615)9(1)34x m x m --=+-+.............................................................................9分要使上式为定值, 即与m 无关，应有0615934x -=- 解得0118x =，此时13564MA MB ⋅=-u u u r u u u r ．.................................................................................11分当直线l 的斜率为0时，不妨设(2,0),(2,0)A B -，当M 的坐标为11(,0)8时13564MA MB ⋅=-u u u r u u u r综上，存在点11(,0)8M 使得13564MA MB ⋅=-u u u r u u u r 为定值．.……………………………………12分21．解:（Ⅰ）法一：若0x ≥时, 则()11x f x e a x '=+++..................................................1分()()211x f x e x ''=-+，()()211xf x e x ''=-+在[)0+∞，上单调递增， 则()()0=0f x f ''''≥................................................................................................................. .....3分 则()f x '在[)0+∞，上单调递增，()()0=2f x f a ''≥+..............................................................4分① 当20a +≥，即-2a ≥时，()0f x '≥，则()f x 在[)0+∞，上单调递增， 此时()()0=0f x f ≥，满足题意................................................................................................5分②若2a <-,由()f x '在[)0+∞，上单调递增， 由于()020f a '=+<，,()0x f x '→+∞>.故()00,x ∃∈+∞,使得()00f x '=. 则当00x x <<时,()()00f x f x ''<=,∴函数()f x 在()00,x 上单调递减. ∴()()000f x f <=,不恒成立.舍去．综上所述,实数a 的取值范围是[)2,-+∞. ............................................ .....................................7分 法二：若0x ≥时, 则()11x f x e a x '=+++...................................................................................1分② 2a ≥-，令()1xg x e x =--，则()10xg x e '=-≥，()g x 在[)0,+∞上单调递增，则()(0)0g x g ≥=，故1x e x ≥+．………………………………………………….... .... .... ...3分∴()()1112011xf x e a x a a a x x '=++≥+++≥=+≥++. ∴函数()f x 在区间[)0,+∞上单调递增. ∴()()00f x f ≥=，成立.......….............5分②若2a <-,由()()()()222111011x xx e f x e x x +-''=-=≥++. ∴函数()f x '在[)0,+∞上单调递增.由于()020f a '=+<，,()0x f x '→+∞>.故()00,x ∃∈+∞,使得()00f x '=. 则当00x x <<时,()()00f x f x ''<=, ∴函数()f x 在()00,x 上单调递减. ∴()()000f x f <=,不恒成立.舍去．综上所述,实数a 的取值范围是[)2,-+∞. .........................................................................7分 （Ⅱ）证明:由(Ⅰ)知,当2a =-时,()f x =()2ln 11xe x x -++-在[)0,+∞上单调递增....................... ........ ..................... ........................ ...................................... .....................9分则()102f f ⎛⎫> ⎪⎝⎭,即1211ln 1102e ⎛⎫-++-> ⎪⎝⎭.∴3ln 22>∴232e >,即232e <.............................................................................................. .....12分22.解：（Ⅰ）.24cos ,4cos ρθρθ=∴=Q , 由222,cos x y x ρρθ=+=,得224x y x +=, 所以曲线C 的直角坐标方程为()2224x y -+=,由1x ty t =-⎧⎨=⎩,消去t 解得：10x y +-=.所以直线l 的普通方程为10x y +-=．………5分（Ⅱ）把12x y ⎧=⎪⎪⎨⎪=⎪⎩ 代入224x y x +=,整理得230t +-=, 设其两根分别为 12,t t，则12123t t t t +=⋅=-12PQ t t ∴=-== .……………………………………………10分亦可求圆心()2,0到直线10x y +-=的距离为2d =，从而PQ =23．解：（Ⅰ）()0f x x ->可化为1x x ->， 所以22(1)x x ->，所以12x <， 所以所求不等式的解集为12x x ⎧⎫<⎨⎬⎩⎭．………………………………………………………5分（Ⅱ）因为函数()1f x x =-在[1)+∞，上单调递增，431a -+>，2(4)11a -+≥，2(43)((4)1)f a f a -+>-+.所以243(4)1a a -+>-+所以(41)(42)0a a -+--<，所以42a -<，所以26a <<.即实数a 的取值范围是(2,6)．……………………………………………………………10分。
2019-2020年高三历史10月联考试题试题(含解析)
2019-2020年高三历史10月联考试题试题（含解析）一、选择题（共30小题，每小题2分，共60分。
在每小题给出的四个选项中，选择正确的一项）忽必烈说：“中书省是我的左手，枢密院是我的右手，御史台是我用来医治左右手的”。
以下理解正确的是A．三权相互牵制达到政治平衡 B．建立独立监察体制加强君权C．中书省独大威胁皇权专制D．行政权和军权受制于司法权【答案】B【解析】考点：汉到元政治制度的演变。
本题主要考查的是对材料的理解分析能力。
材料“御史台是我用来医治左右手的”强调御史台的“医治”功能可知当时建立独立监察体制加强君权。
所以答案选B。
2、有学者认为，1688年“光荣革命”开辟了一条英国式的发展道路，其基本含义是A．资本主义发展导致政治制度变革 B．保留国王但是实现了民主C．各阶层沟通妥协最终实现制度变更 D．议会成为国家政治权力的中心【答案】C【解析】考点：“光荣革命”。
本题主要考查学生关于英国君主立宪制的建立和完善。
光荣革命是资产阶级和新贵族妥协的结果，既保护资产阶级的革命成果，又没有发生大的流血事件，有利于英国资本主义的稳定发展。
不同集团的利益斗争，都在议会中以和平的方式实现。
因此选择C。
选项A、B、C不符合题意，排除。
3、《儒林外史》记载：两个读书人在茶馆喝茶，看到一个商人，大概挺有钱，也儒冠儒服，一副知识分子的打扮，坐在那里喝茶，于是把那个商人一阵好打：你也敢来冒充儒生！出现这种情形的主要原因是A．抑商政策大行其道 B．商人败坏社会风气C．社会秩序需要维护 D．社会等级观念盛行【答案】D【解析】考点:材料中描述了在明清之际,社会生活中经商意识较为深厚,出现了大商人群体。
但是从读书人对商人的态度可以看出,社会等级观念还是存在轻视商人群体的思想。
4、“我但愿你们天天注视着宏伟的雅典，这会使你们心中逐渐充满对她的热爱。
当你们为她那壮丽的景象倾倒时……你们要明白自己的职责并有履行职责的勇敢精神，直至为她慷慨地献出生命。
湖北省宜荆荆随2023-2024学年高三上学期10月联考 历史答案
2023年宜荆荆随高三10月联考高三历史试卷参考答案1.【答案】A【考点】文物与考古【解析】根据铭文“楚王滕随仲芈加”,可知在曾国的墓葬中发现了随国的信息，说明曾与随是同一个诸侯国的不同称呼，“曾随之谜”的争论得以平息，所以A项正确，B项错误。
中国的传世文献中从来没有曾国的记载，但1978年曾侯乙墓的发现却证明历史上湖北随州确实存在一个姬姓曾国，而史籍中明确记载这一地区的只有一个随国，却从未见随国青铜器出土，文献记载与考古发现存在不一致，而2019年的考古发现则解决了文物考古和文献记载不一致的矛盾，弥补了文献史料中对曾国记载的空白，故C项说法错误。
曾侯宝夫人墓出土的铜缶是青铜器，但材料体现不出中国古代的青铜铸造技术领先世界，故D项错误。
2.【答案】D【考点】人物评价【解析】此题为人物评价题，桓伊既是猛将、又是名士、也是忠臣，集豪情、才情、悲情于一身，不只有笛艺的风流，不只有淝水之战的战功，不能因为出身累世为官的门阀士族而否定他，故排除A、B、C三项，选D。
3.【答案】C【考点】中国古代医学【解析】孙思邈认为生命的价值贵于千金，医生首先要确立“普救含灵之苦”的志向，体现《千金方》这部医书医德伦理观念的特色突出，故选C。
材料没有体现佛教轮回及经世致用思想，排除A项、B项。
中医学理论体系形成的标志是先秦秦汉时期所出现的《黄帝内经》,《千金方》是一部综合性临床医著，排除D项。
故此题答案为C。
4.【答案】D【考点】宋代商人【解析】材料强调的是宋代商人社会地位提高的途径多元化，并不能直接判断商人的社会地位是否得到了明显提高，阶级属性是否发生了变化，但却可以体现宋代商人改变自身地位的途径多元化，社会环境具有开放性特征，故A、B不准确，D符合材料主旨；文化水平只符合“其次”的内容，不是材料主旨，故C不准确。
5.【答案】B【考点】清朝的军机处【解析】叫魂案源于浙江德清乡下的沈姓农夫，他要求石匠将写有人名的符粘在桥桩上，然后用锤子砸此符以泄私愤。
湖北省“荆、荆、襄、宜“四地七校联盟2021届高三上学期期中联考 历史
2020年秋“荆、荆、襄、宜四地七校考试联盟”高三期中联考历史试题一、选择题：本题共15小题，每小题3分，共45分。
每小题只有一个选项符合题目要求。
1.表1为原始社会晚期部分墓葬出土情况，表中现象出现的根本原因是表1遗址墓编号出土情况大何庄墓14随葬三十六块猪的下颚骨半坡墓152三岁女孩墓，随葬七十九件手工业产品，陶器六件，石球三个，青白色带孔玉石耳坠一件华县元君庙墓458男性老人墓，随葬六件陶器，砾石围成石棺姜寨墓7随葬尖底瓶、陶错和精美玉石耳坠共二十多件A.社会等级观念逐渐产生B.氏族成员经济待遇的差异C.劳动生产水平日益提高D.私人占有财物和商品交换2.从现有文献看，东晋十一位帝王中，明确与僧尼有交往的就有元帝、明帝等八位之多；东晋权力实际掌握者王导与高僧帛尸梨密多罗交往甚厚，琅琊王氏家族中有两名成员出家为僧，其一即为王导之弟释道宝。
东晋僧人与统治阶层的交往A.打破了儒学封建社会的正统地位B.标志着佛教中国化进程基本完成C.形成了外佛内儒的士族意识形态D.扩大了佛教对世俗政治的影响力3.唐蕃会盟碑（图1）立于大昭寺门前，是唐穆宗时唐朝与吐蕃会盟的遗物。
这次会盟史称“长庆会盟”，盟约里道：“患难相恤，暴掠不作”。
这次会盟A.加强了中央政府对西藏地区的管辖B.初步建立唐蕃政权之间的政治联系C.促进了汉藏的友好关系和文化交流D.改变了吐蕃落后和割据纷争的状态4.宋初政事堂下发的政令文书称为“中书札子”，每一份札子发出时都要有宰执押字，结尾处必须要有“奉圣旨，依奏”的字样。
这一史实表明宋初A.宰相失去政务裁决能力B.君主权力对行政事务渗透加强图1C.中央集权程度日趋强化D.君主实现对政治权力全面控制5.明朝万历年间常熟县令根据吴中风俗总结经验：“农事之获利倍而劳最，愚懦之民为之；工之获利二而劳多，雕巧之民为之；商贾之获利三而劳轻，心计之民为之；贩盐之获利五而无劳，豪猾之民为之。
”这一材料表明当地A.农产品商品化趋势明显B.生产资料和劳动力面临重新分配C.社会经济结构发生质变D.独具特色的地域分工已初步形成6.清末新政期间，不仅先进的知识分子，其他社会阶层如工人、商人、新军以及部分开明官僚都在不同阶段、不同程度上参与或者卷入其中,并形成两大社会集团，革命派和立宪派。
湖北省荆、荆、襄、宜四地七校联盟2020届高三上学期期末联考历史试题
湖北省荆、荆、襄、宜四地七校联盟2020届高三上学期期末联考文综历史试题24．考古学家通过比较广汉三星堆遗址和河南偃师二里头遗址的出土文物发现，两者都有玉质礼器牙璋，在陶器方面都有封口盉、敞口觚、高柄豆，尤其是镶嵌绿松石的铜牌饰只见于三星堆和二里头，据此可知，该时期A．两地手工业制作工艺精湛B．中华文化呈现大一统倾向C．跨区域之间文化交流显现D．两地农业文明较为发达25．宋元之际著名的历史学家马端临在论述三省制度形成时，认为“魏晋以来，中书、尚书之官始真为宰相，而三公遂为具员”，究其原因：“汉之典尚书、中书者，号为天子之私人。
”这说明A．内朝制逐步孕育出三省制度B．三省制是削弱宰相权力的具体举措C．三省的建立打破了旧有体制D．三省制是加强皇帝权力的必然结果26．据《宋史·向敏中传》、《续资治通鉴长编》记载，宋初大臣薛居正子薛惟吉之嫠妇（寡妇）柴氏，将携资再嫁，士大夫向敏中、张齐贤争相求娶，最终张齐贤如愿所偿，后来双方因此事闹得不可开交。
这表明宋代A．妇女不受儒家伦理观念束缚B．理学对士大夫群体影响小C．士大夫婚姻观念日趋世俗化D．士大夫阶层流动日益封闭27．酥油茶原是藏族特色饮品，到了元代，蒙古人也广泛接受它，研制出许多不同类型的酥油茶，明代汉族地区人民也颇为接受，记录百姓居家必用的类书《居家必用事类全集》专门记载了酥油茶的制作方法。
这表明当时A．西藏开始纳入国家政治版图B．北方茶文化影响力日益超过南方C．跨区域间长途贸易日益普遍D．少数民族习俗丰富汉族饮食生活28．19世纪六七十年代，王韬在谈到“中体西用”时说：“形而上者中国也，以道胜；形而下者西人也，以器胜，如徒颂美西人，而贬己所守，未窥为治之本原者也”。
该言论A．对士大夫具有诱导作用B．是早期维新派的典型主张C．认识到洋务运动的弊端D．表明中体和西用互不关联29．1912年2月12日，清政府颁布《清帝逊位诏书》，“……即由袁世凯以全权组织临时共和政府，与民军协商统一办法，总期人民安堵，海宇乂安，仍合满、汉、蒙、回、藏五族完全领土，为一大中华民国，……”，由材料可知A．清帝退位袁世凯窃取了辛亥革命的成果B．清帝退位避免民族分裂，维护国家统一C．清帝退位宣告清王朝的结束D．清帝退位新的共和政体产生30．陈云在编制“一五”计划草案时指出：“我国因为经济落后，要在短时期内赶上去，因此，计划中的平衡是一种紧张的平衡。