人教版七年级下数学8.3课题:二元一次方程组的同解、错解、参数等问题 (无答案)
课题:二元一次方程组的同解、错解、参数等问题

课题:二元一次方程组的同解、错解、参数等问题一. 解下列方程组:二.含参数的二元一次方程组的解法1.同解 两个二元一次方程组有相同的解,求参数值。
例:已知方程 与 有相同的解,则a 、b 的值为 。
2、错解 由方程组的错解问题,求参数的值。
例:解方程组⎩⎨⎧=-=+872y cx by ax 时,本应解出⎩⎨⎧-==23y x 由于看错了系数c,从而得到解⎩⎨⎧=-=22y x 试求a+b+c 的值。
方法:是正确的解代入任何一个方程当中都对,再把看错的解代入没有看错的方程中去从而求出参数的值。
(1) (2) ⎩⎨⎧=+=+4535y ax y x (3) (4) ⎩⎨⎧=+=-1552by x y x3、参数问题 根据方程组解的性质,求参数的值。
例:1、m 取什么整数时,方程组的解是正整数?方法:是把参数当作已知数求出方程的解,再根据已知条件求出参数的值。
4、根据所给的不定方程组,求比值。
2、求适合方程组⎩⎨⎧=++=-+05430432z y x z y x 的 z y x z y x +-++ 的值。
练习:①②⎩⎨⎧=-=-0362y x my x2.已知关于x y 、的方程组210320mx y x y +=⎧⎨-=⎩有整数解,即x y 、都是整数,m 是正整数,求m 的值3、已知关于x y 、的方程组2647x ay x y -=⎧⎨+=⎩有整数解,即x y 、都是整数,a 是正整数, 求a 的值.4. 已知方程组 由于甲看错了方程①中的a 得到方程组的解为31x y =-⎧⎨=-⎩;乙看错了方程②中的b 得到方程组的解为54x y =⎧⎨=⎩,若按正确的a b 、计算,求原方程组的解.5..关于x y 、的二元一次方程组59x y k x y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解,则k 的值?6. 若()4360,2700,x y z x y z xyz --=+-=≠求代数式222222522310x y z x y z +---的值.a 515 42x y x by +=⎧⎨-=-⎩① ②7、先阅读,再做题:1.一元一次方程ax b =的解由a b 、的值决定:⑴若0a ≠,则方程ax b =有唯一解b x a=; ⑵若0a b ==,方程变形为00x ⋅=,则方程ax b =有无数多个解; ⑶若0,0a b =≠,方程变为0x b ⋅=,则方程无解.2.关于x y 、的方程组111222a xb yc a x b y c +=⎧⎨+=⎩的解的讨论可以按以下规律进行:⑴若1122a b a b ≠,则方程组有唯一解; ⑵若111222a b c a b c ==,则方程组有无数多个解; ⑶若111222a b c a b c ≠=,则方程组无解. 请解答:已知关于x y 、的方程组()312y kx b y k x =+⎧⎪⎨=-+⎪⎩分别求出k,b 为何值时, 方程组的解为: ⑴有唯一解; ⑵有无数多个解; ⑶无解?① 例2. 选择一组a,c 值使方程组⎩⎨⎧=+=+c y ax y x 275 1.有无数多解, 2.无解, 3.有唯一的解。
专题 二元一次方程组的同解、错解、参数等问题(原卷版)
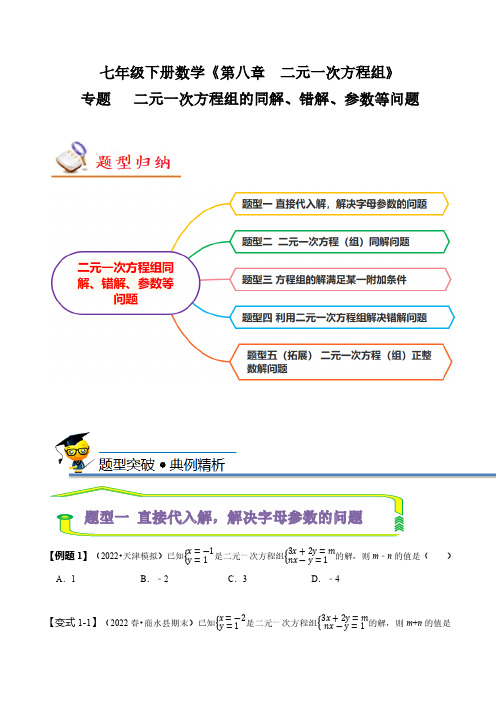
七年级下册数学《第八章二元一次方程组》专题二元一次方程组的同解、错解、参数等问题【例题1】(2022•天津模拟)已知x=―1y=1是二元一次方程组3x+2y=mnx―y=1的解,则m﹣n的值是( )A.1B.﹣2C.3D.﹣4【变式1-1】(2022春•商水县期末)已知x=―2y=1是二元一次方程组3x+2y=mnx―y=1的解,则m+n的值是( )A .﹣2B .﹣5C .1D .﹣4【变式1-2】(2022秋•青岛期末)已知关于x ,y 的二元一次方程组ax ―y =43x +b =4的解是x =2y =―2,则a +b 的值是( )A .﹣1B .1C .﹣3D .3【变式1-3】(2022春•永川区期末)已知x =2y =1是二元一次方程组mx +ny =8nx ―my =1的解,则m +3n 等于( )A .9B .6C .5D .12【变式1-4】(2022春•凤庆县期末)已知x =2y =1是二元一次方程组mx +ny =8nx ―my =1平方根( )A .±2B .2C .4D 【变式1-5】(2022春•平舆县期中)关于x ,y 的方程组2x ―ay =1bx +y =5的解是x =2y =1,则6a ﹣b 的平方根是( )A .4B .±4CD .【变式1-6】(2022秋•迎泽区校级月考)小亮求得方程组2x +y =●2x ―y =12的解为x =5y =★,由于不小心,滴上了两滴墨水,刚好遮住了两个数●和★,请你帮他找回这两个数,“●”“★”表示的数分别为( )A .5,2B .5,﹣2C .8,2D .8,﹣2【变式1-7】(2022春•武山县校级月考)关于x 、y 的方程组3x ―y =m x +my =n 的解是x =1y =―1,则|m ﹣n |的值是 .【变式1-8】(2022秋•海淀区校级期中)已知关于x ,y 的二元一次方程x +y =m ,x =1y =a +8和x =2ay =1都是该方程的解.(1)求a的值;(2)x=by=b也是该方程的一个解,求b的值.【变式1-9】(2022春•东莞市校级期中)已知方程组ax―by=―4bx+ay=―8的解为x=2y=―2.(1)求a、b的值;(2)求a﹣b的值及其算术平方根.【例题2】(2021秋•昌图县期末)已知方程组5x+y=3x―2y=5和ax+2y=12x+by=8有相同的解,则a,b的值为( )A.a=﹣5,b=3B.a=3,b=﹣5C.a=5,b=﹣3D.a=﹣3,b=5【变式2-1】(2022春•禹州市期末)已知关于x,y的方程组4x+y=―5ax―by=1和3x―y=―93ax+2by=18有相同的解,则a2﹣b2的值是( )A.﹣3B.3C.0D.﹣4【变式2-2】(2022秋•北碚区校级期末)关于x,y的方程组2x+3y=19ax+by=―1与3x―2y=9bx+ay=―7有相同的解,则a+4b−3的值为( )A.−1B.−6C.−10D.−12【变式2-3】(2022春•营口期末)已知方程组5x+y=3ax+5y=4和x―2y=55x+by=1有相同的解,求a﹣5b的平方根.【变式2-4】(2022春•沙坪坝区校级期中)已知关于x,y的方程组2x―3y=―10ax+by=14和方程组3x+2y=11 ay―bx=5的解相同.(1)这两个方程组的解;(2)求2a+b的值.【变式2-5】(2021春•岳麓区校级期中)若关于x,y的二元一次方程组3x―5y=36bx+ay=―8与方程组2x+5y=―26ax―by=―4有相同的解,求:(1)这两个方程组的相同解;(2)求(2a+b)2021的值.【变式2-6】(2021春•荔浦市期中)已知方程组2x+y=―2ax+by=―4和方程组3x―y=12bx+ay=―8的解相同,求(5a+b)2的值.【变式2-7】(2022春•德州期中)已知方程组2x+y=1ax―by=7和方程组bx―ay=8x+2y=―4的解相同.(1)求a,b的值.(2)求a|b―的值.【例题3】(2022秋•峄城区校级期末)已知关于x,y的二元一次方程组2x―5y=3n+7x―3y=4的解相等,则n的值是( )A.3B.―13C.1D.13【变式3-1】(2022•东平县校级开学)若方程组4x+3y=1ax+(1―a)y=3的解x和y互为相反数,则a = .【变式3-2】(2022秋•大渡口区校级期末)关于x,y的二元一次方程组3x+5y=a+22x+3y=a的解适合x+y=10,则a的值为( )A.14B.12C.6D.﹣10【变式3-3】(2022春•镇江期末)若方程组x+y=5kx+y=8的解中,x的值比y的值大1,则k为( )A.5B.2C.3D.﹣2【变式3-4】(2022秋•邢台期末)若关于x,y的二元一次方程组x+y=―a+1x―y=3a+5的解,也是二元一次方程x+2y=﹣1的解,则a的值为( )A.2B.1C.12D.0【变式3-5】(2022春•荣县校级期中)已知方程组3x+2y=k2x+3y=k+3的解满足x+y=5,求k的值.【变式3-6】(2022春•昌平区校级期中)已知关于x,y的方程组5x+3y=2m―1x―y=―m+2的解中x与y的和为3,求m的值及此方程组的解.【变式3-7】(2022春•广州期中)已知关于x,y的方程组3x+5y=2mx+y=m―1的解满足x+2y=2.(1)求m的值;(2)化简:1|―2|.【变式3-8】(2022春•广州期中)已知实数a,b+|a+b|=0,且以关于x,y的方程组ax+by=m2ax―by=m+1的解为横、纵坐标的点P(x,y)在第二、四象限的角平分线上,求m的值.【例题4】(2022春•石河子期末)已知方程组ax+by=35x―cy=1,甲正确地解得x=2y=3,而乙粗心地把c看错了,得x=3y=6,试求出a,b,c的值.【变式4-1】(2021春•柳南区校级期中)在解方程组ax+by=2cx―7y=8时,小明正确地解得方程组的解为x=3y=―2,小刚因把c看错而解得方程组的解为x=―2y=2,求a+b+c的值.【变式4-2】(2022春•陆河县期末)已知方程组2x+ay=10①bx―3y=―3②,由于甲看错了方程①中a得到方程组的解为x=3y=―1,乙看错了方程②中的b得到方程组的解为x=―1y=2.若按正确的a、b计算,求原方程组的解.4x―by=―4而得解为x=―3y=―1,乙看错了方程组中的b,而得解为x=5y=4.求出原方程组的正确解.【变式4-4】(2022秋•霍邱县月考)已知关于x、y的二元一次方程组2ax+y=5①x―by=2②.(1)若a=1,请写出方程①的所有正整数解;(2)由于甲看错了方程①中的a得到方程组的解为x=―2y=1,乙看错了方程②中的b得到方程组的解为x=1y=3,求a、b的值及原方程组的解.【变式4-5】(2022春•上蔡县期中)甲、乙两人共同解方程组ax+5y=15,①4x―by=―2②,由于甲看错了方程①中的a,得到方程组的解为x=―3y=―1乙看错了方程②中的b,得到方程组的解为x=5y=4.,试计算a2015+(―110b)2016.x+by=7得到方程组的解为x=1y=6,乙看错了方程组中的b,而得到方程组的解为x=―1y=12(1)甲把a看成了什么?乙把b看成了什么?(2)求出原方程组的正确解.【变式4-7】(2021春•九龙坡区校级期中)已知:甲、乙两人同解方程组ax+5y=15(1)4x=by―2(2)时,甲看错了方程(1)中的a,解得x=―2y=1,乙看错了(2)中的b,解得x=5y=―4,试求a+b的平方根.【例题5】若关于x,y的二元一次方程组2x+ay=122x―y=0有整数解,则满足要求的所有整数a的个数为( )A.0B.4C.8D.12【变式5-1】(2022秋•东宝区期末)已知关于x,y的方程组x+2y―6=0x―2y+mx+5=0,若方程组的解中x恰为整数,m也为整数,则m的值为( )A.﹣1B.1C.﹣1或3D.﹣1或﹣3【变式5-2】(2021秋•南岸区校级期中)m为正整数,已知二元一次方程组mx―2y=103x―2y=0有整数解,则m2=( )A.4B.1或4或16或25C.64D.4或16或64【变式5-3】(2021春•沙坪坝区校级月考)已知m为整数,二元一次方程组4x―3y=66x+my=26有整数解,则m的值为( )A.4或﹣4或﹣5B.4或﹣4或﹣13C.4或﹣5或﹣13D.4或﹣4或﹣5或﹣13【变式5-4】(2020春•雨花区校级月考)m为正整数,已知二元一次方程组mx+2y=103x―2y=0有整数解,则m2﹣1的值为( )A.3或48B.3C.4或49D.48【变式5-5】(2022春•商水县期末)m为负整数,已知二元一次方程组mx+2y=103x+2y=0有整数解,则m的值为 .【变式5-6】(2022春•西区期中)若关于x、y的方程组x+y=2ax+2y=8的解为整数,则满足条件的所有整数a的值的和为( )A.6B.9C.12D.16【变式5-7】已知k为正整数,且关于x,y的二元一次方程组kx+2y=103x―2y=0有整数解,则2k+x+y的平方根为 .【变式5-8】(2022春•合浦县期中)方程组x+y=―13x―2y=7的解满足2x﹣ky=10(k是常数),(1)求k的值.(2)直接写出关于x,y的方程(k﹣1)x+2y=13的正整数解【变式5-9】(2022春•吴江区期末)已知关于x,y的方程组x+2y―6=0x―2y+mx+5=0(1)请直接写出方程x+2y﹣6=0的所有正整数解;(2)若方程组的解满足x+y=0,求m的值;(3)无论实数m取何值,方程x﹣2y+mx+5=0总有一个固定的解,请直接写出这个解?(4)若方程组的解中x恰为整数,m也为整数,求m的值.。
(完整版)二元一次方程组的同解错解参数等问题(最新整理)

请解答:已知关于
x、y
的方程组
y y
kx b
3k 1
x
2
分别求出 k,b 为何值时, 方程组的解为:
⑴有唯一解; ⑵有无数多个解; ⑶无解?
5x y 7 ① 例 2. 选择一组 a,c 值使方程组 ax 2 y c
1.有无数多解, 2.无解, 3.有唯一的解
与
x 2y 5 5x by 1
(3) (4)
。
有相同的解,
2、错解 由方程组的错解问题,求参数的值。
ax by 2
x 3
x 2
例:解方程组 cx 7 y 8
时,本应解出
y
2
由于看错了系数
c,从而得到解
y
2
试求 a+b+c 的值。
方法:是正确的解代入任何一个方程当中都对,再把看错的解代入没有看错的方程中去从而求出参数的 值。
4. 已知方程组
4
x
by
2
① ②
x 3
由于甲看错了方程①中的
a
得到方程组的解为
y
1
;
x 5
乙看错了方程②中的
b
得到方程组的解为
y
4
,若按正确的
a、b
计算,求原方程组的解.
5..关于
x、y
的二元一次方程组
x x
y y
5k 9k
的解也是二元一次方程
2x
3y
6
的解,则
k
的值?
6.
若
4x
3y
6z
0,
x
2y
7z0 xyz来自0,求代数式5x2 2y2 z2 2x2 3y2 10z2
课题:二元一次方程组的同解、错解、参数等问题之欧阳数创编

课题:二元一次方程组的同解、错解、参数等问题一. 解下列方程组:二.含参数的二元一次方程组的解法二元一次方程组是方程组的基础,是学习一次函数的基础,是中考和竞赛的常见的题目,所以这一部分知识非常重要。
1.、同解 两个二元一次方程组有相同的解,求参数值。
例:已知方程 与有相同的解,则a 、b 的值为 。
2、错解 由方程组的错解问题,求参数的值。
例:解方程组⎩⎨⎧=-=+872y cx by ax 时,本应解出⎩⎨⎧-==23y x 由于看错了系数c,从而得到解⎩⎨⎧=-=22y x 试求a+b+c 的值。
方法:是正确的解代入任何一个方程当中都对,再把看错的解代入没有看错的方程中去从而求出参数的值。
(1) (2) ⎩⎨⎧=+=+4535y ax y x (3)(4) ⎩⎨⎧=+=-1552by x y x3、参数问题 根据方程组解的性质,求参数的值。
例:1、m 取什么整数时,方程组的解是正整数? 方法:是把参数当作已知数求出方程的解,再根据已知条件求出参数的值。
4、根据所给的不定方程组,求比值。
2、求适合方程组⎩⎨⎧=++=-+05430432z y x z y x 的z y x z y x +-++ 的值。
练习:2.已知关于x y 、的方程组210320mx y x y +=⎧⎨-=⎩有整数解,即x y 、都是整数,m 是正整数,求m 的值3、已知关于x y 、的方程组2647x ay x y -=⎧⎨+=⎩有整数解,即x y 、都是整数,a 是正整数,求a 的值.4. 已知方程组 由于甲看错了方程①中的a 得到方程组的解为31x y =-⎧⎨=-⎩;乙看错了方程②中的b 得到方程组的解为54x y =⎧⎨=⎩,若按正确的a b 、计算,求原方程组的解. 5..关于x y 、的二元一次方程组59x y k x y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解,则k 的值?a 515 42x y x by +=⎧⎨-=-⎩① ②① ② ⎩⎨⎧=-=-0362y x my x6. 若()4360,2700,x y z x y z xyz --=+-=≠求代数式222222522310x y z x y z +---的值.7、先阅读,再做题:1.一元一次方程ax b =的解由a b 、的值决定: ⑴若0a ≠,则方程ax b =有唯一解b x a=; ⑵若0a b ==,方程变形为00x ⋅=,则方程ax b =有无数多个解; ⑶若0,0a b =≠,方程变为0x b ⋅=,则方程无解.2.关于x y 、的方程组111222a xb yc a x b y c +=⎧⎨+=⎩的解的讨论可以按以下规律进行: ⑴若1122a b a b ≠,则方程组有唯一解; ⑵若111222a b c a b c ==,则方程组有无数多个解; ⑶若111222a b c a b c ≠=,则方程组无解. 请解答:已知关于x y 、的方程组()312y kx b y k x =+⎧⎪⎨=-+⎪⎩分别求出k,b 为何值时, 方程组的解为:⑴有唯一解; ⑵有无数多个解; ⑶无解? ① 例2. 选择一组a,c 值使方程组⎩⎨⎧=+=+c y ax y x 275 1.有无数多解, 2.无解, 3.有唯一的解。
人教版七年级下数学8.3课题:二元一次方程组的同解、错解、参数等问题(无答案)

课题:二元一次方程组的同解、错解、参数等问题一.解以下方程组 :二.含参数的二元一次方程组的解法二元一次方程组是方程组的基础,是学习一次函数的基础,是中考和比赛的常有的题目,因此这一部分知识特别重要。
1.、同解两个二元一次方程组有同样的解,求参数值。
例:已知方程则 a、 b 的值为5x y 3 (1)x 2 y5与ax5y 4 (2)5x by1。
(3)有同样的解,(4)2、错解由方程组的错解问题,求参数的值。
例:解方程组ax by2x3c, 进而获得解x2cx7 y8时,本应解出因为看错了系数y试求 a+b+c 的值。
y22方法:是正确的解代入任何一个方程中间都对,再把看错的解代入没有看错的方程中去进而求出参数的值。
3、参数问题依据方程组解的性质,求参数的值。
例: 1、 m 取什么整数时,方程组的解是正整数?2x my 6 ①x 3y 0②方法:是把参数看作已知数求出方程的解,再依据已知条件求出参数的值。
4、依据所给的不定方程组, 求比值。
2、求合适方程组2x3y4z0的x y z的值。
3x 4 y5z0x y z 练习:2.已知对于 x、y 的方程组mx 2 y 10有整数解 ,即 x、y 都是整数 , m是正整数 ,求m的值3x 2 y02x ay63、已知对于 x、y 的方程组有整数解,即x、y都是整数,a是正整数,求 a 的值.4. 已知方程组ax5y15①因为甲看错了方程①中的 a 获得方程组的解为x3 4x by2②;y1乙看错了方程②中的 b 获得方程组的解为x5若按正确的、b 计算求原方程组的解.y,a, 4x y5k2x 3y6的解 ,则 k 的值?、的二元一次方程组的解也是二元一次方程5..对于 x y x y9k6. 若 4x 3y6z 0, x 2 y 7 z 0 xyz 0 , 求代数式5x2 2 y2z2的值 .2x23y210z27、先阅读 ,再做题 :1.一元一次方程 ax b 的解由 a、 b 的值决定 :⑴若 a 0 , 则方程 ax b 有独一解x b ; a⑵若 a b 0 , 方程变形为 0 x 0 , 则方程 ax b 有无数多个解 ;⑶若 a0, b0, 方程变成 0 x b , 则方程无解 .2.对于的方程组a1x b1 yc1的解的议论能够按以下规律进行 :x、y a2 x b2 y c2⑴若a1b1 , 则方程组有独一解 ;a2b2⑵若a1b1c1, 则方程组有无数多个解 ;a2b2c2⑶若a1b1c1, 则方程组无解 .a2b2c2y kx b请解答 :已知对于 x、 y 的方程组3k 分别求出 k,b 为什么值时 , 方程组的解为 :y 1 x 2⑴有独一解 ;⑵有无数多个解;⑶无解 ?①例 2.选择一组 a,c 值使方程组5xy7有无数多解,无解,有独一的解ax2y c 1. 2. 3.。
人教版初一数学下册含参二元一次方程组的同解问题

若方程组 的解也是方程 的解,求 的值.
解题技巧:.
学生:小组讨论→展示成果→归纳总结
教师:提示可利用课前预习所得到的结论。对于仍不得其法的学生,教师可进一步提示,联立新的方程组。
尝试解决方程与方程,方程组与方程同解问题,提炼技巧,为后面的学习打下基础。
深入探究拓展提升
探究三:方程组与方程组同解
4、通过学生课下作业的完成情况了解学生对知识的掌握程度。
教学设计特色
本节从学生感兴趣的问题入手,意在让学生经历一个实际背景,激发了学生自觉探究数学问题、体验发现问题的乐趣。在本节课的学习中让学生通过运用自主学习、观察猜想、合作交流、抽象概括、总结归纳等方法。学生的角色从学会转变为会学,本节课,学生不是停留在学会课本知识的层面上,而是与老师一起站在探究者的角度深入其境,体验探究的氛围与真谛。
已知关于 、 的方程组 和 有公共解,求 、 的值.
变式训练1
预备知识:
解下列方程组(用含 的式子表示 、 )
若关于 、 的方程组 的解也是二元一次方程 的解,求 的值.
解题技巧:.
学生:小组讨论→展示成果
教师:引导学生解决两个方程均含参的同解问题,在小组展示的基础上,启发学探究三能够很好地检验学习成果。变式训练的出现,提升了难度,具有一定的代表性,能够较好的锻炼学生的数学思维。
2、二元一次方程组解的定义:
一般地,二元一次方程组的两个方程的,叫做二元一次方程组的解.
3、解下列方程组
(1)
(2)
(3)分别从方程组(1)(2)中任选两个方程,组成新方程组,并求解.
结论:.
探究同解方程组规律,为后面的学习进行铺垫。
合作交流
解决问题
课题:二元一次方程组的同解、错解、参数等问题之欧阳文创编

课题:二元一次方程组的同解、错解、参数等问题一. 解下列方程组:二.含参数的二元一次方程组的解法二元一次方程组是方程组的基础,是学习一次函数的基础,是中考和竞赛的常见的题目,所以这一部分知识非常重要。
1.、同解 两个二元一次方程组有相同的解,求参数值。
例:已知方程 与 有相同的解,则a 、b 的值为 。
2、错解 由方程组的错解问题,求参数的值。
例:解方程组⎩⎨⎧=-=+872y cx by ax 时,本应解出⎩⎨⎧-==23y x 由于看错了系数c,从而得到解⎩⎨⎧=-=22y x 试求a+b+c 的值。
方法:是正确的解代入任何一个方程当中都对,再把看错的解代入没有看错的方程中去从而求出参数的值。
3、参数问题 根据方程组解的性质,求参数的值。
例:1、m 取什么整数时,方程组的解是正整数? (1) (2) ⎩⎨⎧=+=+4535y ax y x (3) (4) ⎩⎨⎧=+=-1552by x y x ① ⎧=-62my x方法:是把参数当作已知数求出方程的解,再根据已知条件求出参数的值。
4、根据所给的不定方程组,求比值。
2、求适合方程组⎩⎨⎧=++=-+05430432z y x z y x 的z y x z y x +-++ 的值。
练习:2.已知关于x y 、的方程组210320mx y x y +=⎧⎨-=⎩有整数解,即x y 、都是整数,m 是正整数,求m 的值3、已知关于x y 、的方程组2647x ay x y -=⎧⎨+=⎩有整数解,即x y 、都是整数,a 是正整数,求a 的值.4. 已知方程组 由于甲看错了方程①中的a 得到方程组的解为31x y =-⎧⎨=-⎩;乙看错了方程②中的b 得到方程组的解为54x y =⎧⎨=⎩,若按正确的a b 、计算,求原方程组的解. 5..关于x y 、的二元一次方程组59x y k x y k +=⎧⎨-=⎩的解也是二元一次方程236x y +=的解,则k 的值?6. 若()4360,2700,x y z x y z xyz --=+-=≠求代数式222222522310x y z x y z +---的值.7、先阅读,再做题:1.一元一次方程ax b =的解由a b 、的值决定:a 515 42x y x by +=⎧⎨-=-⎩① ②⑴若0a ≠,则方程ax b =有唯一解b x a=; ⑵若0a b ==,方程变形为00x ⋅=,则方程ax b =有无数多个解; ⑶若0,0a b =≠,方程变为0x b ⋅=,则方程无解.2.关于x y 、的方程组111222a x b y c a x b y c +=⎧⎨+=⎩的解的讨论可以按以下规律进行: ⑴若1122a b a b ≠,则方程组有唯一解; ⑵若111222a b c a b c ==,则方程组有无数多个解; ⑶若111222a b c a b c ≠=,则方程组无解. 请解答:已知关于x y 、的方程组()312y kx b y k x =+⎧⎪⎨=-+⎪⎩ 分别求出k,b为何值时, 方程组的解为:⑴有唯一解; ⑵有无数多个解; ⑶无解? ① 例2. 选择一组a,c 值使方程组⎩⎨⎧=+=+c y ax y x 275 1.有无数多解, 2.无解, 3.有唯一的解。
2021年人教版七年级数学下册第八章《8.3 实际问题与二元一次方程组》公开课课件(共20张PPT)

鼓励学 生积极 探究
遇到困难时, 教师应启发诱 导
教学过程
环节一:创设情境,提出问题
昨天,我们一家8 个人去韶山公园玩, 买门票花了65元。
哦,那你们家去 了几个大人?几
个小孩呢?
真笨,自己不会算吗?成 人票每人10元,小孩票每 人5元啊。
聪明的同学们,你能帮 他算算吗?
怎样判断李 大叔的估计 是否正确
已知量、 未知量、 等量关 系有哪 些
如何解 决这个 问题
探
环索
节新
二
知 解
决
问
题
环节二:探究新知,解决问题
例题:养牛场原有30只大牛和15只小牛,1天约需用饲料675kg; 一周后又购进12只大牛和5只小牛,这时1天约需用饲料940kg。饲养 员李大叔估计平均每只大牛1天约需用饲料18~20kg,每只小牛1天约 需饲料7~8kg。你能够通过计算检验他的估计?
教 材 分 析
另一方面使学
生能在解决实 际问题的情境 中运用所学数 学知识,进一 步提高分析问 题和解决问题 的综合能力 本节内容是具有一定综
合性的问题,提供给学 生利用方程组为工具进 行具有一定深度的思考, 增加运用方程组解决实 际问题的实践,将全章 所强调的以方程组为工 具把实际问题模型化的 思想提高到新的高度
螺栓15个或螺帽24个,要使一个螺栓配套两
个螺帽,应如何分配工人才能使螺栓和螺帽
刚好配套?设生产螺栓x人,生产螺帽y人,
列方程组为(
)
A
x y 90 15x 24y
B、
x 90 48 y 15
y x
C、x y 90 D、 y 90x
30x 24y
2(15x) 24y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:二元一次方程组的同解、错解、参数等问题
一. 解下列方程组
:
二.含参数的二元一次方程组的解法
二元一次方程组是方程组的基础,是学习一次函数的基础,是中考和竞赛的常见的题目,所以这一部分知识非常重要。
1.、同解 两个二元一次方程组有相同的解,求参数值。
例:已知方程 与 有相同的解,
则a 、b 的值为 。
2、错解 由方程组的错解问题,求参数的值。
例:解方程组⎩⎨⎧=-=+872y cx by ax 时,本应解出⎩⎨⎧-==23y x 由于看错了系数c,从而得到解⎩⎨⎧=-=2
2y x 试求a+b+c 的值。
方法:是正确的解代入任何一个方程当中都对,再把看错的解代入没有看错的方程中去从而求出参数的值。
3、参数问题 根据方程组解的性质,求参数的值。
例:1、m 取什么整数时,方程组的解是正整数?
(1) (2) ⎩⎨⎧=+=+4535y ax y x (3) (4) ⎩⎨⎧=+=-1552by x y x ①
② ⎩
⎨⎧=-=-0362y x my x
方法:是把参数当作已知数求出方程的解,再根据已知条件求出参数的值。
4、根据所给的不定方程组,求比值。
2、求适合方程组⎩⎨
⎧=++=-+05430432z y x z y x 的 z y x z y x +-++ 的值。
练习:
2.已知关于x y 、的方程组210320
mx y x y +=⎧⎨-=⎩有整数解,即x y 、都是整数,m 是正整数,求m 的值
3、已知关于x y 、的方程组2647x ay x y -=⎧⎨+=⎩
有整数解,即x y 、都是整数,a 是正整数, 求a 的值.
4. 已知方程组 由于甲看错了方程①中的a 得到方程组的解为31x y =-⎧⎨=-⎩
;乙看错了方程②中的b 得到方程组的解为54
x y =⎧⎨=⎩,若按正确的a b 、计算,求原方程组的解.
5..关于x y 、的二元一次方程组59x y k x y k +=⎧⎨-=⎩
的解也是二元一次方程236x y +=的解,则k 的值?
6. 若()4360,2700,x y z x y z xyz --=+-=≠求代数式222
222522310x y z x y z +---的值.
7、先阅读,再做题:
1.一元一次方程ax b =的解由a b 、的值决定:
⑴若0a ≠,则方程ax b =有唯一解b x a
=; ⑵若0a b ==,方程变形为00x ⋅=,则方程ax b =有无数多个解;
a 515 42x y x by +=⎧⎨-=-⎩① ②
⑶若0,0a b =≠,方程变为0x b ⋅=,则方程无解.
2.关于x y 、的方程组111222
a x
b y
c a x b y c +=⎧⎨+=⎩的解的讨论可以按以下规律进行: ⑴若1122
a b
a b ≠,则方程组有唯一解;
⑵若111
222
a b c a b c ==,则方程组有无数多个解;
⑶若11
1222
a b c a b c ≠=,则方程组无解.
请解答:已知关于x y 、的方程组()312
y kx b
y k x =+⎧⎪⎨=-+⎪⎩
分别求出k,b 为何值时, 方程组的解为: ⑴有唯一解; ⑵有无数多个解; ⑶无解?
① 例2. 选择一组a,c 值使方程组⎩⎨⎧=+=+c y ax y x 27
5
1.有无数多解,
2.无解,
3.有唯一的解。
