树(算法设计)习题练习答案
算法设计与分析知到章节答案智慧树2023年天津大学

算法设计与分析知到章节测试答案智慧树2023年最新天津大学第一章测试1.下列关于效率的说法正确的是()。
参考答案:提高程序效率的根本途径在于选择良好的设计方法,数据结构与算法;效率主要指处理机时间和存储器容量两个方面;效率是一个性能要求,其目标应该在需求分析时给出2.算法的时间复杂度取决于()。
参考答案:问题的规模;待处理数据的初态3.计算机算法指的是()。
参考答案:解决问题的有限运算序列4.归并排序法的时间复杂度和空间复杂度分别是()。
参考答案:O(nlog2n);O(n)5.将长度分别为m,n的两个单链表合并为一个单链表的时间复杂度为O(m+n)。
()参考答案:错6.用渐进表示法分析算法复杂度的增长趋势。
()参考答案:对7.算法分析的两个主要方面是时间复杂度和空间复杂度的分析。
()参考答案:对8.某算法所需时间由以下方程表示,求出该算法时间复杂度()。
参考答案:O(nlog2n)9.下列代码的时间复杂度是()。
参考答案:O(log2N)10.下列算法为在数组A[0,...,n-1]中找出最大值和最小值的元素,其平均比较次数为()。
参考答案:3n/2-3/2第二章测试1.可用Master方法求解的递归方程的形式为()。
参考答案:T(n)=aT(n/b)+f(n) , a≥1, b>1, 为整数, f(n)>0.2.参考答案:对3.假定,, 递归方程的解是. ( )参考答案:对4.假设数组A包含n个不同的元素,需要从数组A中找出n/2个元素,要求所找的n/2个元素的中点元素也是数组A的中点元素。
针对该问题的任何算法需要的时间复杂度的下限必为。
( )参考答案:错5.使用Master方法求解递归方程的解为().参考答案:6.考虑包含n个二维坐标点的集合S,其中n为偶数,且所有坐标点中的均不相同。
一条竖直的直线若能把S集合分成左右两部分坐标点个数相同的子集合,则称直线L为集合S的一条分界线。
若给定集合S,则可在时间内找到这条分界线L。
第五章-树-练习-答案
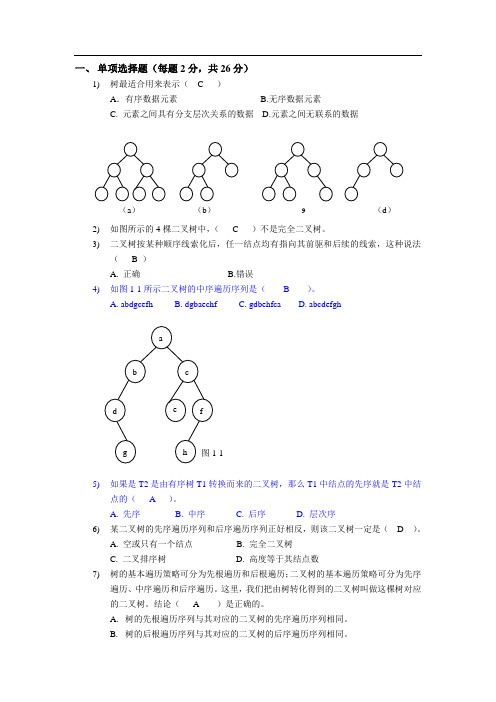
一、 单项选择题(每题2分,共26分)1) 树最适合用来表示( C )A .有序数据元素 B.无序数据元素C. 元素之间具有分支层次关系的数据D.元素之间无联系的数据2) 如图所示的4棵二叉树中,( C )不是完全二叉树。
3) 二叉树按某种顺序线索化后,任一结点均有指向其前驱和后续的线索,这种说法( B )A. 正确B.错误4) 如图1-1所示二叉树的中序遍历序列是( B )。
A. abdgcefhB. dgbaechfC. gdbehfcaD. abcdefgh5) 如果是T2是由有序树T1转换而来的二叉树,那么T1中结点的先序就是T2中结点的( A )。
A. 先序B. 中序C. 后序D. 层次序6) 某二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树一定是( D )。
A. 空或只有一个结点B. 完全二叉树C. 二叉排序树D. 高度等于其结点数7) 树的基本遍历策略可分为先根遍历和后根遍历;二叉树的基本遍历策略可分为先序遍历、中序遍历和后序遍历。
这里,我们把由树转化得到的二叉树叫做这棵树对应的二叉树。
结论( A )是正确的。
A. 树的先根遍历序列与其对应的二叉树的先序遍历序列相同。
B. 树的后根遍历序列与其对应的二叉树的后序遍历序列相同。
(a ) (b ) 9 (d )C. 树的先根遍历序列与其对应的二叉树的中序遍历序列相同。
D. 以上都不对8) 如图所示的T2是由森林T1转换而来的二叉树,那么森里T1有( C )个叶子结点。
A. 4B. 5C. 6D. 79) 深度为5的二叉树至多有( C )个结点。
A. 16B. 32C. 31D. 1010) 在一非空二叉树的中序遍历序列中,根结点的右边( A )。
A. 只有右子树上的所有结点B. 只有右子树的部分结点C. 只有左子树上的部分结点D. 只有左子树上的所有结点11) 设n ,m 为一棵二叉树上的两个结点,在中序遍历时,n 在m 前的条件是( C )。
树练习题(答案)

一、单项选择题
1、在一棵度为3的树中,度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数为( )个。
A. 4B.5C. 6D. 7
2、假设在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为( )个。
A. 15B.16C. 17D. 47
10、下面叙述正确的是( )。
A. 二叉树不是树
B. 二叉树等价于度为2的树
C. 完全二叉树必为满二叉树
D. 二叉树的左右子树有次序之分
11、任何一棵二叉树的叶子结点在先序、中序和后序遍历序列中的相对次序( )。
A. 不发生改变 B. 发生改变
C. 不能确定D. 以上都不对
12、已知一棵完全二叉树的结点总数为9个,则最后一层的结点数为( )。
6、由三个结点构成的二叉树,共有5种不同的形态。
7、设高度为h的二叉树中只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为2h+1。(根的高度为1)
8、对于一棵具有n个结点的二叉树,若一个结点的编号为i(0≤i≤n-1),则它的左孩子结点的编号为2i+1,右孩子结点的编号为2i+2,双亲结点的编号为(i-1)/2。
7. 满二叉树也是完全二叉树。(1)
8. 哈夫曼树一定是完全二叉树。(0)
9. 树的子树是无序的。(0)
10.度小于等于2的有序树即为二叉树。(0)
三、填空题
1、由带权为3,9,6,2,5的5个叶子结点构成一棵哈夫曼树,则带权路径长度为_55__。
2、在一棵二叉排序树上按中序遍历得到的结点序列是一个有序序列。
A. 1B.2C. 3D. 4
13、下列图示的顺序存储结构表示的二叉树是( )。
树、图习题及答案

树、图习题一、选择题1 已知一算术表达式的中缀形式为 A+B*C-D/E,后缀形式为ABC*+DE/-,其前缀形式为( D )A.-A+B*C/DE B. -A+B*CD/E C.-+*ABC/DE D. -+A*BC/DE2 一个具有1025个结点的二叉树的高h为( C )A.11 B.10 C.11至1025之间 D.10至1024之间3 二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历: HFIEJKG 。
该二叉树根的右子树的根是:( C )A、 EB、 FC、 GD、 H4 引入二叉线索树的目的是( A )A.加快查找结点的前驱或后继的速度 B.为了能在二叉树中方便的进行插入与删除C.为了能方便的找到双亲 D.使二叉树的遍历结果唯一5 设森林F中有三棵树,第一,第二,第三棵树的结点个数分别为M1,M2和M3。
与森林F对应的二叉树根结点的右子树上的结点个数是( D )。
A.M1 B.M1+M2 C.M3 D.M2+M36 有n个叶子的哈夫曼树的结点总数为( D )。
A.不确定 B.2n C.2n+1 D.2n-17 一个有n个结点的图,最少有( B )个连通分量,最多有( D )个连通分量。
A.0 B.1 C.n-1 D.n8 无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是( D )。
A.a,b,e,c,d,f B.a,c,f,e,b,d C.a,e,b,c,f,d D.a,e,d,f,c,b 9 已知有向图G=(V,E),其中V={V1,V2,V3,V4,V5,V6,V7},E={<V1,V2>,<V1,V3>,<V1,V4>,<V2,V5>,<V3,V5>,<V3,V6>,<V4,V6>,<V5,V7>,<V6,V7>},G的拓扑序列是( A )。
数据结构-树习题

数据结构-树习题第六章树⼀、选择题1、⼆叉树的深度为k,则⼆叉树最多有( C )个结点。
A. 2kB. 2k-1C. 2k-1D. 2k-12、⽤顺序存储的⽅法,将完全⼆叉树中所有结点按层逐个从左到右的顺序存放在⼀维数组R[1..N]中,若结点R[i]有右孩⼦,则其右孩⼦是(B )。
A. R[2i-1]B. R[2i+1]C. R[2i]D. R[2/i]3、设a,b为⼀棵⼆叉树上的两个结点,在中序遍历时,a在b前⾯的条件是( B )。
A. a在b的右⽅B. a在b的左⽅C. a是b的祖先D. a是b的⼦孙4、设⼀棵⼆叉树的中序遍历序列:badce,后序遍历序列:bdeca,则⼆叉树先序遍历序列为()。
A. adbceB. decabC. debacD. abcde5、在⼀棵具有5层的满⼆叉树中结点总数为(A)。
A. 31B. 32C. 33D. 166、由⼆叉树的前序和后序遍历序列( B )惟⼀确定这棵⼆叉树。
A. 能B. 不能7、某⼆叉树的中序序列为ABCDEFG,后序序列为BDCAFGE,则其左⼦树中结点数⽬为( C )。
A. 3B. 2C. 4D. 58、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为( C )。
A. 67B. 68C. 69D. 709、将⼀棵有100个结点的完全⼆叉树从根这⼀层开始,每⼀层上从左到右依次对结点进⾏编号,根结点的编号为1,则编号为49的结点的左孩⼦编号为( A )。
A. 98B. 99C. 50D. 4810、表达式a*(b+c)-d的后缀表达式是( B )。
A. abcd+-B. abc+*d-C. abc*+d-D. -+*abcd11、对某⼆叉树进⾏先序遍历的结果为ABDEFC,中序遍历的结果为DBFEAC,则后序遍历的结果是( B )。
A. DBFEACB. DFEBCAC. BDFECAD. BDEFAC12、树最适合⽤来表⽰( C )。
算法设计与分析智慧树知到答案章节测试2023年山东交通学院

第一章测试1.解决一个问题通常有多种方法。
若说一个算法“有效”是指( )A:这个算法能在人的反应时间内将问题解决B:(这个算法能在一定的时间和空间资源限制内将问题解决)和(这个算法比其他已知算法都更快地将问题解决)C:这个算法能在一定的时间和空间资源限制内将问题解决D:这个算法比其他已知算法都更快地将问题解决答案:B2.农夫带着狼、羊、白菜从河的左岸到河的右岸,农夫每次只能带一样东西过河,而且,没有农夫看管,狼会吃羊,羊会吃白菜。
请问农夫能不能过去?()A:不一定B:不能过去C:能过去答案:C3.下述()不是是算法的描述方式。
A:自然语言B:程序设计语言C:E-R图D:伪代码答案:C4.有一个国家只有6元和7元两种纸币,如果你是央行行长,你会设置()为自动取款机的取款最低限额。
A:40B:42C:29D:30答案:D5.算法是一系列解决问题的明确指令。
()A:对B:错答案:A6.程序=数据结构+算法()A:错B:对答案:B7.同一个问题可以用不同的算法解决,同一个算法也可以解决不同的问题。
()A:错答案:B8.算法中的每一条指令不需有确切的含义,对于相同的输入不一定得到相同的输出。
( )A:错B:对答案:A9.可以用同样的方法证明算法的正确性与错误性 ( )A:对B:错答案:B10.求解2个数的最大公约数至少有3种方法。
( )A:错B:对答案:A11.没有好的算法,就编不出好的程序。
()A:对B:错答案:A12.算法与程序没有关系。
( )A:错B:对答案:A13.我将来不进行软件开发,所以学习算法没什么用。
( )A:对B:错答案:B14.gcd(m,n)=gcd(n,m m od n)并不是对每一对正整数(m,n)都成立。
( )A:错B:对答案:A15.既然程序设计语言可以描述算法,所以算法就是程序。
( )A:错B:对答案:A第二章测试1.并不是所有的算法,规模更大的输入需要更长的运行时间。
( )A:对答案:B2.算法效率分析框架主要关心一个算法的基本操作次数的增长次数,并把它作为算法效率的主要指标。
树习题解答

数据结构——树习题解答1、单词查找树(word.pas)【问题描述】在进行文法分析的时候,通常需要检测一个单词是否在我们的单词列表中。
为了提高查找和定位的速度,通常都画出与单词列表所对应的单词查找树,其特点如下:(1)根节点不包含字母,除根街店为每一个节点都包含一个大写英文字母;(2)从根节点到某一节点,路径上经过的字母依次连起来所构成的字母序列,称为该结点对应的单词。
单词列表中的每个单词,都是该单词查找树某个节点所对应的单词;(3)在满足上述条件下,该单词查找树的节点数最少。
要求:对一个确定的单词列表,请统计对应的单词查找树的结点数(包括根节点).输入:输入文件名为word.in,该文件为一个单词列表,每行仅包含一个单词和一个换行/回车符。
每个单词仅由大写字母组成,长度不超过63个字符。
文件总长度不超过32K,至少有一行数据。
输出:输出文件名为word.out,该文件仅包含一个整数,该整数为单词列表对应的单词查找树的结点数。
【样例输入】AANASPASASCASCIIBASBASIC【样例输出】13【题解】首先要对建树的过程有一个了解。
对于当前被处理的单词和当前树:在根节点的子节点中找单词的为第一位字母,若存在则进而在该节点的子节点中寻找第二位……,如此直到单词结束,既不需要在该书中添加节点;若单词的第n个字母不能找到,即将单词的第n个字母及其后的字母依次加入单词查找树中。
但本题只是问你结点总数,而非建树方案,且有32K大小的单词文件,所以应该考虑能不能通过不建树就直接算出结点数。
为了说明问题本质,我们定义单词相对于另一个单词的差:设单词1的长度为L,且与单词2从第N位开始不一致,则定义单词1相对于单词2的差为L-N+1,这是描述单词相似程度的量。
可见,将一个单词加入单词树的时候,须加入的节点数等于该单词树中已有的单词的差得最小值。
单词的字典顺序排列后的序列则具有类似的特性,即在一个字典顺序序列中,第m个单词相对于第m-1个单词的差必定是它对于前m-1个单词的差中最小的。
《数据结构与算法设计》树-习题

• 已知二叉树 – 先序序列为:ABCDEF – 中序序列为:CBAEDF • 请画出该二叉树。
A
B
C E
D
F
9
A
D
10
• 已知二叉树 – 中序序列为:ABCEFGHD – 后序序列为:ABFHGEDC • 请画出该二叉树。 – 中序:LDR A – 后序:LRD A B C E F G H D A B F H G E D C
swap(b->rchild );
}
交换左右子树
15
• 请指出下列函数的功能
void preserve(BiTNode *b, ElemType a[], int n){
static int i = 0; if(b != NULL) { preserve(b->lChild, a,n); a[i++] = b->data;
preserve(b->rChild, a,n);
} }
得到二叉树b的中序遍历序列,结果放在数组a中
16
2005考研试题
根据______可以唯一地确定一棵二叉树。 A. 先序遍历和后序遍历 B. 先序遍历和层次遍历 C. 中序遍历和层次遍历 D. 中序遍历和后序遍历
D. 中序遍历和后序遍历
所有分支结点的度为2的二叉树称为正则二叉树,试 用二叉链表做存储结构,编写一递归函数int FormalTree(Bitree t),判断二叉树是否为正则二叉树。 int FormalTree(Bitree t) { if (t == NULL) return 1; if ((t->lchild == NULL) && (t->rchild == NULL)) return 1; if ((t->lchild == NULL) || (t->rchild == NULL)) return 0; return (FormalTree(t->lchild)) && (FormalTree(t->rchild)); }
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第6xx(算法设计)习题练习答案*6.22二叉树的遍历算法可写为通用形式。
例如通用的中序遍历为:void Inorder(BinTree,T,void(* visit)(DataType x)){if (T){Inorder(T->lchild,Visit);//遍历左子树Visit(T->data);//通过函数指针调用它所指的函数来访问结点Inorder(T->rchild,Visit);//遍历右子树}}其中Visit是一个函数指针,它指向形如void f(DataType x)的函数。
因此我们可以将访问结点的操作写在函数f中通过调用语句Inorder(root,f)将f的地址传递给Visit,来执行遍历操作。
请写一个打印结点数据的函数,通过调用上述算法来完成书中6.3节的中序遍历。
解:函数如下:void PrintNode(BinTree T){printf("%c",T->data);}//定义二叉树链式存储结构typedef char DataType;//定义DataType类型typedef struct node{DataType data;struct node *lchild, *rchild;//左右孩子子树}BinTNode; //结点类型typedef BinTNode *BinTree ;//二叉树类型void Inorder(BinTree T,void(* Visit)(DataType x)){if(T){Inorder(T->lchild,Visit);//遍历左子树Visit(T->data); //通过函数指针调用它所指的函数访问结点Inorder(T->rchild,Visit);//遍历右子树}}6.23以二叉链表为存储结构,分别写出求二叉树结点总数及叶子总数的算法。
解:(1)求结点数的递归定义为:若为空树,结点数为0若只有根结点,则结点数为1;否则,结点数为根结点的左子树结点数+右子树结点数+1(2)求xx数的递归定义为:若为空树,xx数为0若只有根结点,则xx数为1;否则,叶子数为根结点的左子树叶子数+右子树叶子数typedef char DataType;//定义DataType类型typedef struct node{DataType data;struct node *lchild, *rchild;//左右孩子子树}BinTNode; //结点类型typedef BinTNode *BinTree ;//二叉树类型int Node(BinTree T){//算结点数if (T->lchild==NULL)&&(T->rchild==NULL)return 1;else return Node(T->lchild)+Node(T->rchild)+1;else return 0;}int Leaf(BinTree T){ //算xx数if(T)if (T->lchild==NULL)&&(T->rchild==NULL)return 1;else return Leaf(T->lchild)+Node(T->rchild);else return 0;}6.24以二叉链表为存储结构,分别写出求二叉树高度及宽度的算法,所谓宽度是指二叉树的各层上,具有结点数最多的那一层上的结点总数。
解:(1)根据递归定义:二叉树的高度为:当为空树时,高度为0;当只有一个结点时,高度为1;其他情况:高度为max(根的左子树高度,根的右子树高度)+1int Height(BinTree T){int hl,hr;{//非空树if(t->lchild==NUll)&&(t->rchild==NULL)//只含一个根结点return 1;else {hl=height(t->lchild);//根的左子树高度hr=height(t->rchild);//根的右子树高度if (hl>=hr)return hl+1;else return h2+1;}}else return 0;}(2)要求二叉树的宽度的话,则可根据树的高度设置一个数组temp。
temp[i]用于存放第i层上的结点数(即宽度)。
在访问结点时,把相应计算该结点下一层的孩子数并存入相应数组元素中,遍历左子树后向上返回一层计算右子树的宽度,并取出最大的一个数组元素作为树的宽度。
#define M 10 //假设二叉树最多的层数int Width(BinTree T){int static n[M];//向量存放各层结点数int static i=1;int static max=0;//最大宽度if(T){if(i==1) //若是访问根结点{n[i]++; //第1层加1i++; //到第2层if(T->lchild)//若有左孩子则该层加1n[i]++;if(T->rchild)//若有右孩子则该层加1n[i]++;}else{ //访问xx结点i++; //下一层结点数if(T->lchild)n[i]++;if(T->rchild)n[i]++;}if(max<n[i])max=n[i];//取出最大值Width(T->lchild);//遍历左子树i--; //往上退一层Width(T->rchild);//遍历右子树}return max;}//算法结束6.25以二叉链表为存储结构,写一算法交换各结点的左右子树。
答:要交换各结点的左右子树,最方便的办法是用后序遍历算法,每访问一个结点时把两棵子树的指针进行交换,最后一次访问是交换根结点的子树。
void ChangeBinTree(BinTree *T){ //交换子树if(*T){ //这里以指针为参数使得交换在实参的结点上进行后序遍历BinTree temp;ChangeBinTree(&(*T)->lchild);ChangeBinTree(&(*T)->rchild);temp=(*T)->lchild;(*T)->lchild=(*T)->rchild;(*T)->rchild=temp;}}6.26以二叉链表为存储结构,写一个拷贝二叉树的算法voidCopyTree(BinTree root,BinTree *newroot),其中新树的结点是动态申请的,为什么newroot要说明为BinTree型指针的指针?解:因为调用函数只能进行值传递,当返回类型为void时,就必须把实参的地址传给函数,否则函数不会对实际参数进行任何操作,也就得不到所需结果了。
所以,newroot要说明为BinTree型指针void CopyTree(BinTree root,BinTree *newroot){ //拷贝二叉树if(root)//如果结点非空{ //按前序序列拷贝*newroot=(BinTNode *)malloc(sizeof(BinTNode));//生成新结点(*newroot)->data=root->data;//拷贝结点数据CopyTree(root->lchild,&(*newroot)->lchild);//拷贝左子树CopyTree(root->rchild,&(*newroot)->rchild);//拷贝右子树}else //如果结点为空*newroot=NULL;//将结点置空}6.27以二叉链表为存储结构,分别写出在二叉树中查找值为x的结点及求x所在结点在树中层数的算法。
解:根据上几题的算法可以得出本题的算法如下:#define M 10 //假设二叉树最多的层数BinTree SearchBTree(BinTree *T,DataType x){//以前序遍历算法查找值为x的结点if(*T){if((*T)->data==x )return *T;SearchBTree(&(*T)->lchild,x);SearchBTree(&(*T)->rchild,x);}}int InLevel(BinTree T,DataType x){int static l=0;//设一静态变量保存层数if(T){if(l==0)//若是访问根结点{l++;//第1层if(T->data==x)return l;if(T->lchild||T->rchild)l++;//若根有子树,则层数加1}else{ //访问xx结点if(T->data==x)return l;if(T->lchild||T->rchild)l++;//若该结点有子树,则层数加1else return 0;}InLevel(T->lchild,x);//遍历左子树InLevel(T->rchild,x);//遍历右子树}}6.28一棵n个结点的完全二叉树以向量作为存储结构,试写一非递归算法实现对该树的前序遍历。
解:以向量为存储结构的完全二叉树,其存储在向量中的结点其实是按层次遍历的次序存放的,可以根据课本第74页的内容设计出算法:typedef char DataType;//设结点数据类型为char#define M 100//设结点数不超过100typedef DataType BinTree[M];void Preorder(BinTree T){ //前序遍历算法int n=T[0];int p[M];//设置一队列存放结点值int i,j;for(i=1;i<=n;i++){if (i==1)//根结点j=1;else if(2*j<=n)//左子树j=2*j;else if(j%2==0&&j<n)//右兄弟j=j+1;else if(j>1)//双亲之右兄弟j=j/2+1;p[i]=T[j];//入队printf("%c",p[i]);//打印结点值}}6.29以二叉链表为存储结构,一算法对二叉树进行层次遍历(层次遍历的定义见6.13).提示:应使用队列来保存各层的结点。
答:#define M 100 //假设结点数最多为100typedef char DataType;//队列结点值类型typedef struct//定义一个队列{int front;int rear;int count;DataType data[M];}QBTree;static QBTree Q;//设一全局静态变量保存遍历结果void Levelorder(BinTree T){//层次遍历if(T){if(QueEmpty(&Q)){ //根结点及子树结点入队EnQue(&Q,T->data);if(T->lchild)EnQue(&Q,T->lchild->data);if(T->rchild)EnQue(&Q,T->rchild->data);}else{ //xx结点入队if(T->lchild)EnQue(&Q,T->lchild->data);if(T->rchild)EnQue(&Q,T->rchild->data);}Levelorder(T->lchild);//遍历左子树Levelorder(T->rchild);//遍历右子树}}6.30以二叉链表为存储结构,写一算法用括号形式(key LT,RT)打印二叉树,其中key是根结点数据,LT和RT是括号形式的左子树和右子树。
