2010级研究生弹性力学及有限元试题
弹性力学历届考试试题
卷一、简答题1. 何谓平面应变问题?举例说明。
2. 在什么情况下,平面应力问题和平面应变问题的应力分布与材料的弹性常数无关?又在什么情况下,两类平面问题具有相同的应力解? 3. 何谓逆解法?4. 简述小挠度薄板弯曲问题的基本假定。
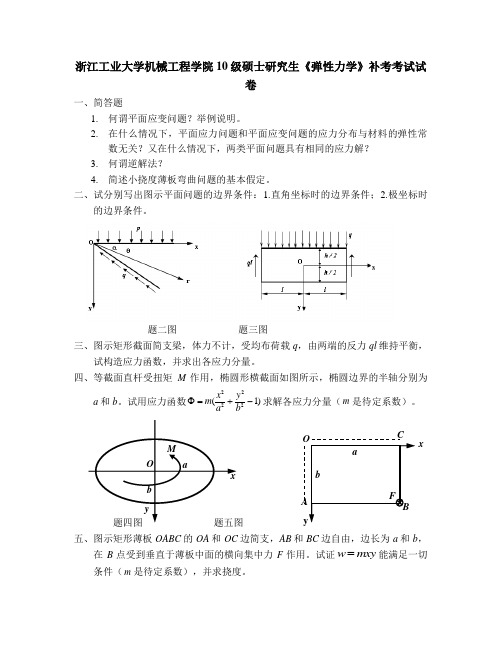
二、试分别写出图示平面问题的边界条件:1.直角坐标时的边界条件;2.极坐标时的边界条件。
题二图 题三图三、图示矩形截面简支梁,体力不计,受均布荷载q ,由两端的反力ql 维持平衡,试构造应力函数,并求出各应力分量。
四、等截面直杆受扭矩M 作用,椭圆形横截面如图所示,椭圆边界的半轴分别为a 和b 。
试用应力函数2222(1)x y m a bΦ=+-求解各应力分量(m 是待定系数)。
五、图示矩形薄板OABC 的OA 和OC 边简支,AB 和BC 边自由,边长为a 和b ,在B 点受到垂直于薄板中面的横向集中力F 作用。
试证w mxy =能满足一切条件(m 是待定系数),并求挠度。
OA CxOA Cx卷六、简答题5. 何谓平面应力问题?举例说明。
6. 何谓轴对称问题?举例说明。
7. 何谓半逆解法?8. 何谓圣维南原理?圣维南解的价值何在?七、设Airy 应力函数为3cx =Φ,其中c 为常数。
试在图中绘出边界上的面力。
题二图 题三图八、设有矩形截面的长梁,其长度为l ,深度为h ,宽度为b ,三者之间的关系为b h l >>>>。
在两端的集中力偶M 作用下(不计体力),梁发生纯弯曲变形。
试用Airy 应力函数求解应力分量。
九、等截面直杆的椭圆形横截面如图所示,椭圆边界的半轴分别为a 和b 。
试用应力函数2222(1)x y m a bΦ=+-求解各应力分量(m 是待定系数)。
十、图示矩形薄板OABC 的OA 和OC 边简支,AB 和BC 边自由,边长为a 和b ,在B 点受到垂直于薄板中面的横向集中力F 作用。
试证w m xy =能满足一切xx 条件(m 是待定系数),并求挠度。
试题及其答案--弹性力学与有限元分析

8、表示位移分量与应力分量之间关系的方程为物理方程。(×)
9、当物体的形变分量完全确定时,位移分量却不能完全确定。(√)
10、当物体的位移分量完全确定时,形变分量即完全确定。(√)
11、按应力求解平面问题时常采用位移法和应力法。(×)
12、按应力求解平面问题,最后可以归纳为求解一个应力函数。(×)
10、在有限单元法中,为什么要求位移模式必须能反映单元的常量应变
答:每个单元的应变一般总是包含着两部分:一部分是与该单元中各点的位置坐标有关的,是各点不相同的,即所谓变量应变;另一部分是与位置坐标无关的,是各点相同的,即所谓常量应变。而且,当单元的尺寸较小时,单元中各点的应变趋于相等,也就是单元的应变趋于均匀,因而常量应变就成为应变的主要部分。因此,为了正确反映单元的形变状态,位移模式必须能反映该单元的常量应变。
4、简述平面应力问题与平面应变问题的区别。
答:平面应力问题是指很薄的等厚度薄板,只在板边上受有平行于板面并且不沿厚度变化的面力,同时,体力也平行于板面并且不沿厚度变化。对应的应力分量只有 , , 。而平面应变问题是指很长的柱形体,在柱面上受有平行于横截面并且不沿长度变化的面力,同时体力也平行于横截面并且不沿长度变化,对应的位移分量只有u和v
13、在有限单元法中,结点力是指单元对结点的作用力。(×)
14、在有限单元法中,结点力是指结点对单元的作用力。(√)
15、在平面三结点三角形单元的公共边界上应变和应力均有突变。(√ )
三、简答题
1、简述材料力学和弹性力学在研究对象、研究方法方面的异同点。
在研究对象方面,材料力学基本上只研究杆状构件,也就是长度远大于高度和宽度的构件;而弹性力学除了对杆状构件作进一步的、较精确的分析外,还对非杆状结构,例如板和壳,以及挡土墙、堤坝、地基等实体结构加以研究。
南昌大学弹性力学2010级——2012级考试试卷(含答案)

(e)
联立式(d)和式(e),解得: P 3P P P (4 分) A cos , B cos , C sin , D sin ; 3 8a 8a 32a 32a 2 4)、应力分量为: 3P P 3 3P 1 x xy cos sin (1 y ), y 0, xy cos ( 2 y 2 1) (3 分) 3 4a 4a 8a 16a 4a
(4 分)
q 1 g 0.75 0.5 v1 3 2 3 K =E FL F 1 g 11 0.5 0.75 v2 6 2 9q 12 F 8 g v1 1 15 1 124 求解得: 5E 156 v2 E 4 q 3F 7 g 5 6
x yx 0 y 2 2 x y 0 ;(2 分)(3)在边 ;(2 分)(2)在区域内的相容方程 2 2 x x y y xy 0 x y
x
l x m yx s f 界上的应力边界条件 m y l xy s f
2 Xx 6 Axy 2C 6 Dy y 2
(a)
(2 分)
x y xy
2 Yy 0 x 2 2 B 3 Ay 2 xy
(b)
(3 分)
3)、用应力边界条件求待定常数 A、B、C、D: 应力边界条件,在上、下表面 y 2a 处,必须精确满足:
1、 材料各向同性的含义是什么?“各向同性”在弹性力学物理方程中的表现是什么? 答:材料的各向同性假定物体的物理性质在各个方向上均相同。因此,物体的弹性常 数不随方向而变化。(2 分) 在弹性力学物理方程中,由于材料的各向同性,三个弹性常数,包括弹性模量 E,切 变模量 G 和泊松系数(泊松比)μ都不随方向而改变(在各个方向上相同)。(3 分) 2、 写出弹性力学中正应力和剪应力的符号表示,并说明正负如何规定? 答:弹性力学中正应力用 表示,并加上一个下标字母,表明这个正应力的作用面与 作用方向;切应力用 表示,并加上两个下标字母,前一个字母表明作用面垂直于哪一个 坐标轴,后一个字母表明作用方向沿着哪一个坐标轴。(3 分) 并规定作用在正面上的应力以沿坐标轴正方向为正,沿坐标轴负方向为负。相反,作 用在负面上的应力以沿坐标轴负方向为正,沿坐标轴正方向为负。(2 分) 3、 在有限单元法中,为什么要求位移模式必须能反映单元的刚体位移? 答:每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的;(2 分) 另一部分是本单元的形变无关的,即刚体位移, 它是由于其他单元发生了形变而连带 引起的。甚至在弹性体的某些部位,例如在靠近悬臂梁的自由端处,单元的形变很小,单 元的位移主要是由于其他单元发生形变而引起的刚体位移。因此, 为了正确反映单元的位 移形态,位移模式必须能反映该单元的刚体位移。(3 分)
弹性力学与有限元分析试题及其答案

弹性力学与有限元分析复习题及其答案(绝密试题)一、填空题1、弹性力学研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
2、在弹性力学中规定,线应变以伸长时为正,缩短时为负,与正应力的正负号规定相适应。
3、在弹性力学中规定,切应变以直角变小时为正,变大时为负,与切应力的正负号规定相适应。
4、物体受外力以后,其内部将发生内力,它的集度称为应力。
与物体的形变和材料强度直接有关的,是应力在其作用截面的法线方向和切线方向的分量,也就是正应力和切应力。
应力及其分量的量纲是L -1MT -2。
5、弹性力学的基本假定为连续性、完全弹性、均匀性、各向同性。
6、平面问题分为平面应力问题和平面应变问题。
7、已知一点处的应力分量100=x σMPa ,50=y σMPa ,5010=xy τ MPa ,则主应力=1σ150MPa ,=2σ0MPa ,=1α6135' 。
8、已知一点处的应力分量, 200=x σMPa ,0=y σMPa ,400-=xy τ MPa ,则主应力=1σ512MPa ,=2σ-312 MPa ,=1α-37°57′。
9、已知一点处的应力分量,2000-=x σMPa ,1000=y σMPa ,400-=xy τ MPa ,则主应力=1σ1052 MPa ,=2σ-2052 MPa ,=1α-82°32′。
10、在弹性力学里分析问题,要考虑静力学、几何学和物理学三方面条件,分别建立三套方程。
11、表示应力分量与体力分量之间关系的方程为平衡微分方程。
12、边界条件表示边界上位移与约束,或应力与面力之间的关系式。
分为位移边界条件、应力边界条件和混合边界条件。
13、按应力求解平面问题时常采用逆解法和半逆解法。
14、有限单元法首先将连续体变换成为离散化结构,然后再用结构力学位移法进行求解。
其具体步骤分为单元分析和整体分析两部分。
15、每个单元的位移一般总是包含着两部分:一部分是由本单元的形变引起的,另一部分是由于其他单元发生了形变而连带引起的。
有限元试题2010及答案

(1)对图中网格进行结点编号,并使其系统总刚度矩阵的带 宽最小;
(2)计算在你的结点编号下的系统刚度矩阵的半带宽; (3)给出约束节点自由度的已知位移信息。
3
p
10
y
8 99
7
x
5 66 8 7
12 3 4 5
12 3 4
4 0 0)T p
(2).长度因子:a 略写
单元1: 0.5, bi y j ym 0, bj 1, bm 1
ci x j xm 1, c j 1, cm 0
kii
E0h 0.5 2 0
0 1
kij
E0h 2
0.5 0
0.5 1
kim
E0h 2
0 0
0.5 0
13
k jj
6
2 1
1 2
m2
l
6
2 1
1 2
k 1
2E
l
1 1
1 1
整体一致质量矩阵和刚阵
k 2
E
l
1 1
1 1
4 2 0
M
l
6
2
6
1
0 1 2
2 2 0
K
E
l
2
3
1
0 1 1
9
2) 因为节点3固结, u3 0 ;
在 K M 0 中划去第3行和第3列,系统振动的特
征方程为:
K
M
AE l
2 2
Ni 0 ; Ni 1 。
2)位移模式必须能反映单元的刚体位移; 位移模式移的连续性。
2
3)在有限单元法中最普遍采用的是等参变换,即单元几何形 状的变换和单元内的场函数采用相同数目的节点参数及相 同的插值函数进行变换。采用等参变换的单元称之为等参 元。所谓“等参元”是指几何形状插值形函数和单元上的 位移插值形函数相同,参数个数相等。 相邻等参元之间,位移场是连续的,应力场不连续。
弹性力学与有限元分析试题及参考答案

按应力求解平面应变问题的相容方程:
将已知应力分量 , , 代入上式,可知满足相容方程。
4、试写出平面问题的应变分量存在的必要条件,并考虑下列平面问题的应变分量是否可能存在。
(1) , , ;
(2) , , ;
(3) , , ;
其中,A,B,C,D为常数。
弹性力学与有限元分析试题及参考答案
四、分析计算题
1、试写出无体力情况下平面问题的应力分量存在的必要条件,并考虑下列平面问题的应力分量是否可能在弹性体中存在。
(1) , , ;
(2) , , ;
其中,A,B,C,D,E,F为常数。
解:应力分量存在的必要条件是必须满足下列条件:(1)在区域内的平衡微分方程 ;(2)在区域内的相容方程 ;(3)在边界上的应力边界条件 ;(4)对于多连体的位移单值条件。
6、证明应力函数 能满足相容方程,并考察在如图所示的矩形板和坐标系中能解决什么问题(体力不计, )。
解:将应力函数 代入相容方程
可知,所给应力函数 能满足相容方程。
由于不计体力,对应的应力分量为
, ,
对于图示的矩形板和坐标系,当板内发生上述应力时,根据边界条件,上下左右四个边上的面力分别为:
上边, , , , , ;
解:应变分量存在的必要条件是满足形变协调条件,即
将以上应变分量代入上面的形变协调方程,可知:
(1)相容。
(2) (1分);这组应力分量若存在,则须满足:B=0,2A=C。
(3)0=C;这组应力分量若存在,则须满足:C=0,则 , , (1分)。
5、证明应力函数 能满足相容方程,并考察在如图所示的矩形板和坐标系中能解决什么问题(体力不计, )。
2009-2010弹性力学及有限元试卷

四川大学期考试试题A
(2009 ——2010 学年第 1 学期)
课程号:30620030 课序号:0 课程名称:弹性力学及有限元任课教师:张建海成绩:适用专业年级:水工03 学生人数:印题份数:学号:姓名:
注:1试题字迹务必清晰,书写工整。
本题 2 页,本页为第 1 页
2 题间不留空,一般应题卷分开教务处试题编号:
3务必用A4纸打印
学号:姓名:
2 题间不留空,一般应题卷分开教务处试题编号:
3务必用A4纸打印
四川大学期考试试题B
(2009 ——2010 学年第 1 学期)
课程号:30620030 课序号:0 课程名称:弹性力学及有限元任课教师:张建海成绩:适用专业年级:水工03 学生人数:印题份数:学号:姓名:
注:1试题字迹务必清晰,书写工整。
本题2 页,本页为第 2 页
2 题间不留空,一般应题卷分开教务处试题编号:
3务必用A4纸打印。
弹性力学及有限元10级研究生课程试题

弹性力学及有限元10级研究生课程试题湖南工业大学研究生课程考试试题课程名称:《弹性力学及有限元》(开卷)适用专业年级:机械设计及理论、机械制造及其自动化 10级注意事项:1.答卷可采取打印或手写方式在A4打印纸上完成。
如果手写,必须字迹工整,以便老师批阅;2.下载《标准答卷模版》;3.凡有相同答案的试卷均按零分计;4.答卷于11月30日之前交机械工程学院研究生办公室,过期不交按缺考处理。
试题:本试卷共2大题,共100分。
一、撰写读书报告(60分)读书报告应包含以下内容:1、论述弹性力学研究的对象和分析问题的方法。
2、本门课程讲授了弹性力学的哪些内容?3、任何一个有限元分析问题都是空间问题,什么情况下可以简化为平面问题、轴对称问题?并举例说明平面应变问题、平面应力问题和轴对称问题。
4、你学习弹性力学和有限单元法以后最大的收获是什么?学习过程中遇到的最大困难是什么?你认为自己学懂了这门课程的知识没有?二、结合你的研究课题,撰写一篇运用有限元进行仿真分析计算的报告(40分)。
分析报告要求如下:1、问题的提出;2、建立有限元模型;3、施加载荷和边界条件;4、求解,分析计算结果;5、结论。
湖南工业大学研究生课程考试《弹性力学及有限元》答卷本人承诺:本试卷确为本人独立完成,若有违反愿意接受处理。
签名:______________学号:____________________专业:__________________所在院(部):_________________优良中差评阅人签字成绩注:90~100分为优,70~89分为良,60~69分为中,0~59分为差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
弹性力学及有限元试题(2010级硕士研究生)
(一) 问答题 (20分)
1、试叙述弹性力学的基本假定及其意义。
2、什么是形函数? 在有限元方法中它起什么作用?
3、何谓逆解法和半逆解法?它们的理论依据是什么?
4、试分别叙述李滋法和伽辽金法的近似性。
(二)设有一刚体,具有半径为R 的圆柱型孔道,孔道内放置外半径为R 而内半径为r 的圆筒,圆筒内受压力q ,试求圆筒的压力。
(20分)
(三)如图所示的薄板为正方形,边长a=b ,厚度为一个单位,μ=0。
在x=a 的边界上受有均布压力q 的作用,试用瑞利-里茨变分法求解位移。
(20分)
(四)分别给出位移微分方程、最小势能原理和虚功方程的表达式,并说明公式的含义和三者之间的关系。
(20分)
(五)对于如图所示的四节点平面四边形单元,若取位移模式为
xy a y a x a a v xy
a y a x a a u 87654321+++≡+++≡
试考察此位移模式的收敛性条件,并列出求解其系数a 1~a 8的方程(20分)。
