相似三角形经典的题目型
相似三角形经典题(含答案)
相似三角形典范习题之阳早格格创做例1 从底下那些三角形中，选出相似的三角形．例2 已知：如图，ABCD 中，2:1:=EB AE ，供AEF ∆取CDF ∆的周少的比，如果2cm 6=∆AEF S ，供CDF S ∆．例3 如图，已知ABD ∆∽ACE ∆，供证：ABC ∆∽ADE ∆．例4 下列命题中哪些是透彻的，哪些是过失的？（1）所有的曲角三角形皆相似．（2）所有的等腰三角形皆相似．（3）所有的等腰曲角三角形皆相似．（4）所有的等边三角形皆相似． 例5 如图，D 面是ABC ∆的边AC 上的一面，过D 面绘线段DE ，使面E 正在ABC ∆的边上，而且面D 、面E ABC ∆的一个顶面组成的小三角形取ABC ∆相似．尽大概多天绘出谦脚条件的图形，并道明线段DE 的绘法．例6 如图，一人拿着一收刻有厘米分绘的小尺，站正在距电线杆约30米的场合，把脚臂背前伸曲，小尺横曲，瞅到尺上约12个分绘恰佳遮住电线杆，已知脚臂少约60厘米，供电线杆的下．例7 如图，小明为了丈量一下楼MN 的下，正在离N 面20m 的A 处搁了一个仄里镜，小明沿NA 退却到C 面，正佳从镜中瞅到楼顶M 面，若5.1=AC m ，小明的眼睛离大天的下度为1.6m ，请您助闲小明估计一下楼房的下度（透彻到0.1m ）．例8格面图中的二个三角形是可是相似三角形，道明缘由．例9 根据下列各组条件，判决ABC ∆战C B A '''∆是可相似，并道明缘由：（1）,cm 4,cm 5.2,cm 5.3===CA BC AB cm 28,cm 5.17,cm 5.24=''=''=''A C C B B A ．（2）︒='∠︒='∠︒=∠︒=∠35,44,104,35A C B A ．（3）︒='∠=''=''︒=∠==48,3.1,5.1,48,6.2,3B C B B A B BC AB ．例10 如图，下列每个图形中，存没有存留相似的三角形，如果存留，把它们用字母表示出去，并简要道明识别的根据．例11例125、12、1326S．例13正在一次数教活动课上，教授让共教们到操场上丈量旗杆的下度，而后回去接流各自的丈量要领．小芳的丈量要领是：拿一根下米的竹竿曲坐正在离旗杆27米的C处（如图），而后沿BC目标走到D处，那时目测旗杆顶部A取竹竿顶部E恰佳正在共背去线上，又测得C、D二面的距离为3米，小芳的目下为米，那样即可知讲旗杆的下．您认为那种丈量要领是可可止？请道明缘由．例14．如图，为了估算河的宽度，咱们不妨正在河对于岸选定一个目标动做E，使面A，再正在河的那一边选面B战CBC取AE的接面为D您能供出二岸之间AB的大概距离吗？例15．如图，为了供出海岛上的山峰AB的下度，正在D战F处横坐标杆DC战FE，标杆的下皆是3丈，相隔1000步（1步等于5尺），而且AB、CD战EF正在共一仄里内，从标杆DC退后123步的G处，可瞅到山峰A战标杆顶端C正在背去线上，从标杆FE退后127步的H处，可瞅到山峰A战标杆顶端E正在背去线上．供山峰的下度AB及它战标杆CD的火仄距离BD 各是几？（古代问题）例16如图，已知△ABC的边AB AC＝2，BC边上的下AD （1）供BC的少；（2）如果有一个正圆形的边正在AB上，其余二个顶面分别正在AC，BC 上，供那个正圆形的里积．相似三角形典范习题问案例1．解①、⑤、⑥相似，②、⑦相似，③、④、⑧相似例2．1：3．例3分解道明例4．分解（1）没有透彻，果为正在曲角三角形中，二个钝角的大小没有决定，果此曲角三角形的形状分歧．（2）也没有透彻，等腰三角形的顶角大小没有决定，果此等腰三角形的形状也分歧．（3）透彻．设有等腰曲角三角形ABCa、b、c（4问：（1）、（2）没有透彻．（3）、（4）透彻．例5．解：绘法略．例6．分解BCBC的少．解，∴，∴∽．∴杆的下为6米．例7．分解的相似闭系便透彻了．解m）．例8．分解那二个图如果没有是绘正在格面中，那是无法推断的．本量上格面无形中给图形删加了条件——少度战角度．解道明逢到格面的题目一定要充散创造其中的百般条件，勿使遗漏．例9．解（1（2（3例10．解（1二角相等；（2二角相等；（3二角相等；（4二边成比率夹角相等；6二边成比率夹（5角相等．例11．分解有一个角是65°的等腰三角形，它的底角是72°，而BD是底角的比率推出线段之间的比率闭系．∴道明（1）有二个角对于应相等，那么那二个三角形相似，那是推断二个三角形相似最时常使用的要领，而且根据相等的角的位子，不妨决定哪些边是对于应边．（2或者仄办法．例12分解26，不妨供解三边依次为∴例13．分解推断要领是可可止，应试虑利用那种要领加之咱们现有的知识是可供出旗杆的下．按那种丈量要领，过FG，接CE于H，可知GF、HF、EH可供，那样可供得AG，故旗杆AB可供．F G，接CE于H所解（米）所以旗杆的下为米．道明正在简曲丈量时，要领要现真、确真可止．例14.AB大概相距100米．例15.例16. 分解：央供BC的少，需绘图去解，果AB、AC皆大于下AD，那么有二种情况存留，即面D正在BC上或者面D正在BC的延少线上，所以供BC的万古要分二种情况计划．供正圆形的里积，闭键是供正圆形的边少．解：（1）如上图，由AD⊥BC，由勾股定理得BD＝3，DC＝1，所以BC ＝BD＋DC＝3＋1＝4．如下图，共理可供BD＝3，DC＝1，所以BC＝BD－CD＝3－1＝2．（2）如下图，由题目中的图知BC＝4，ABC是曲角三角形．由AE G F是正圆形，设G F＝x，则FC＝2－x，∵G F∥AB，∴，即．∴，∴如下图，当BC＝2，AC＝2，△ABC是等腰三角形，做CP⊥AB于P，∴AP正在Rt△APC中，由勾股定理得CP＝1，∵GH∥AB，∴△C GH∽△CBA，∵，∴。
相似三角形判定典型题
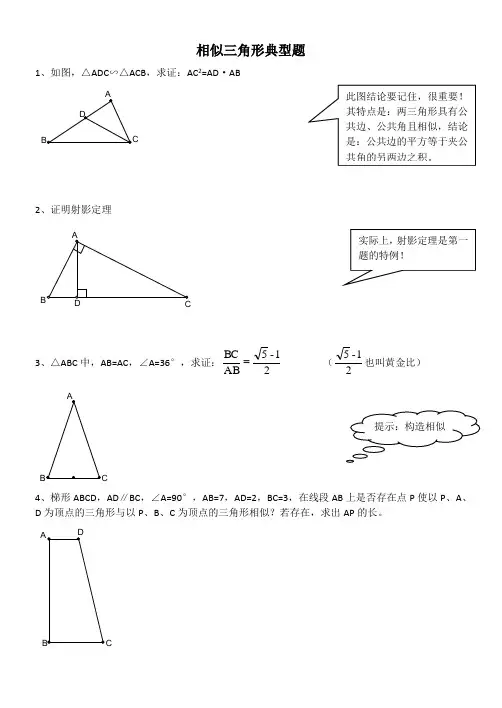
相似三角形典型题1、如图，△ADC ∽△ACB ，求证：AC 2=AD ·AB2、证明射影定理3、△ABC 中，AB=AC ，∠A=36°，求证：21-5AB BC（21-5也叫黄金比）4、梯形ABCD ，AD ∥BC ，∠A=90°，AB=7，AD=2，BC=3，在线段AB 上是否存在点P 使以P 、A 、D 为顶点的三角形与以P 、B 、C 为顶点的三角形相似？若存在，求出AP 的长。
5、△ABC中，CE、BD是高，二者交于点O（1）求证：△ADE∽△ABC.（2）图中共有几对相似三角形？请找出来。
6、△ABC中，AE、BD是高，△CDE面积是2，△ABC面积是12，DE=3，求AB的长。
7、△ABC中，AC=AB，∠BAC=90°，E、F在直线BC上，且∠EAF=135°（1）找出图中的相似三角形并证明。
（2）求证：BC2=2FC·BE=BE:CF（3）求证：AE2:AF28、△ABC中，AC=AB，AD是中线，P是AD上一点，过C作CF∥AB交BP延长线于F求证：BP2=PE·PF9、△ABC 中，AC=AB ，AD 是中线，P 是AD 延长线上一点，过C 作CF ∥AB 交BP 延长线于F ，BF 交AC 延长线于E . 求证：BP 2=PE ·PF10、△ABC 中，AD 是角平分线，EF 是AD 的中垂线，交BC 延长线于F 求证：（1）FD 2=FC ·FB （2）AB 2:AC 2=BF:CFF11、△ABC 中，∠BAC=90°，AD ⊥BC ，P 为AD 中点，BP 延长线交AC 于F 求证：EF 2=AE ·CE12、△ABC 中，∠BAC=90°，AD ⊥BC ，E 为AC 中点，ED 延长线交AB 延长线于F 求证：AFDFAC AB13．如图，设P 是等边△ABC 的一边BC 上的一点，连结AP ，它的垂直平分线交AB 、AC 于M 、N 两点（1）求证：BP ·PC=BM ·CN（2）PC=2BP ，则=ANAM________（3）若BP:PC=m:n ，则=ANAM________14、△ABC 中，∠A=2∠B.求证：a 2=b （b+c ） 用多种方法B15、如图，在等腰三角形ABC 中，AB=1，∠A=900，点E 为腰AC 中点，点F 在底边BC 上，且FE ⊥BE ，求△CEF 的面积。
经典相似三角形练习的题目(附参考答案详解)
实用标准文案相似三角形一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= _________ °，BC= _________ ；（2）判断△ABC与△DEC是否相似，并证明你的结论．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t 的值；若不存在，请说明理由．9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD 、AC 把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．10．如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q 作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ 为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC相似？15．如图，在△ABC中，AB=10cm，BC=20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB的长为多少时，这两个直角三角形相似．17．已知，如图，在边长为a的正方形ABCD中，M是AD的中点，能否在边AB 上找一点N（不含A、B），使得△CDM与△MAN相似？若能，请给出证明，若不能，请说明理由．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC 交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P 为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：_________ ；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）25．阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．一．解答题（共30小题）1．如图，在△ABC中，DE∥BC，EF∥AB，求证：△ADE∽△EFC．解答：证明：∵DE∥BC，∴DE∥FC，∴∠AED=∠C．又∵EF∥AB，∴EF∥AD，∴∠A=∠FEC．∴△ADE∽△EFC．点评：本题考查的是平行线的性质及相似三角形的判定定理．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．解答：（1）证明：∵梯形ABCD，AB∥CD，∴∠CDF=∠FGB，∠DCF=∠GBF，（2分）∴△CDF∽△BGF．（3分）（2）解：由（1）△CDF∽△BGF，又F是BC的中点，BF=FC，∴△CDF≌△BGF，∴DF=GF，CD=BG，（6分）∵AB∥DC∥EF，F为BC中点，∴E为AD中点，∴EF是△DAG的中位线，∴2EF=AG=AB+BG．∴BG=2EF﹣AB=2×4﹣6=2，∴CD=BG=2cm．（8分）3．如图，点D，E在BC上，且FD∥AB，FE∥AC．求证：△ABC∽△FDE．解答：证明：∵FD∥AB，FE∥AC，∴∠B=∠FDE，∠C=∠FED，∴△ABC∽△FDE．4．如图，已知E是矩形ABCD的边CD上一点，BF⊥AE于F，试说明：△ABF∽△EAD．解答：证明：∵矩形ABCD中，AB∥CD，∠D=90°，（2分）∴∠BAF=∠AED．（4分）∵BF⊥AE，∴∠AFB=90°．∴∠AFB=∠D．（5分）∴△ABF∽△EAD．（6分）点评：考查相似三角形的判定定理，关键是找准对应的角．5．已知：如图①所示，在△ABC和△ADE中，AB=AC，AD=AE，∠BAC=∠DAE，且点B，A，D在一条直线上，连接BE，CD，M，N分别为BE，CD的中点．（1）求证：①BE=CD；②△AMN是等腰三角形；（2）在图①的基础上，将△ADE绕点A按顺时针方向旋转180°，其他条件不变，得到图②所示的图形．请直接写出（1）中的两个结论是否仍然成立；（3）在（2）的条件下，请你在图②中延长ED交线段BC于点P．求证：△PBD∽△AMN．解答：（1）证明：①∵∠BAC=∠DAE，∴∠BAE=∠CAD，∵AB=AC，AD=AE，∴△ABE≌△ACD，∴BE=CD．②由△ABE≌△ACD，得∠ABE=∠ACD，BE=CD，∵M、N分别是BE，CD的中点，∴BM=CN．又∵AB=AC，∴△ABM≌△ACN．∴AM=AN，即△AMN为等腰三角形．（2）解：（1）中的两个结论仍然成立．（3）证明：在图②中正确画出线段PD，由（1）同理可证△ABM≌△ACN，∴∠CAN=∠BAM∴∠BAC=∠MAN．又∵∠BAC=∠DAE，∴∠MAN=∠DAE=∠BAC．∴△AMN，△ADE和△ABC都是顶角相等的等腰三角形．∴△PBD和△AMN都为顶角相等的等腰三角形，∴∠PBD=∠AMN，∠PDB=∠ANM，∴△PBD∽△AMN．6．如图，E是▱ABCD的边BA延长线上一点，连接EC，交AD于点F．在不添加辅助线的情况下，请你写出图中所有的相似三角形，并任选一对相似三角形给予证明．分析：根据平行线的性质和两角对应相等的两个三角形相似这一判定定理可证明图中相似三角形有：△AEF∽△BEC；△AEF∽△DCF；△BEC∽△DCF．解答：解：相似三角形有△AEF∽△BEC；△AEF∽△DCF；△BEC∽△DCF．（3分）如：△AEF∽△BEC．在▱ABCD中，AD∥BC，∴∠1=∠B，∠2=∠3．（6分）∴△AEF∽△BEC．（7分）7．如图，在4×3的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上．（1）填空：∠ABC= 135°°，BC= ；（2）判断△ABC与△DEC是否相似，并证明你的结论．解答：解：（1）∠ABC=135°，BC=；（2）相似；∵BC=，EC==；∴，；∴；又∠ABC=∠CED=135°，∴△ABC∽△DEC．8．如图，已知矩形ABCD的边长AB=3cm，BC=6cm．某一时刻，动点M从A点出发沿AB方向以1cm/s的速度向B点匀速运动；同时，动点N从D点出发沿DA 方向以2cm/s的速度向A点匀速运动，问：（1）经过多少时间，△AMN的面积等于矩形ABCD面积的？（2）是否存在时刻t，使以A，M，N为顶点的三角形与△ACD相似？若存在，求t 的值；若不存在，请说明理由解：（1）设经过x秒后，△AMN的面积等于矩形ABCD面积的，则有：（6﹣2x）x=×3×6，即x2﹣3x+2=0，（2分）解方程，得x1=1，x2=2，（3分）经检验，可知x1=1，x2=2符合题意，所以经过1秒或2秒后，△AMN的面积等于矩形ABCD面积的．（4分）（2）假设经过t秒时，以A，M，N为顶点的三角形与△ACD相似，由矩形ABCD，可得∠CDA=∠MAN=90°，因此有或（5分）即①，或②（6分）解①，得t=；解②，得t=（7分）经检验，t=或t=都符合题意，所以动点M，N同时出发后，经过秒或秒时，以A，M，N为顶点的三角形与△ACD相似．（8分）9．如图，在梯形ABCD中，若AB∥DC，AD=BC，对角线BD、AC把梯形分成了四个小三角形．（1）列出从这四个小三角形中任选两个三角形的所有可能情况，并求出选取到的两个三角形是相似三角形的概率是多少；（注意：全等看成相似的特例）（2）请你任选一组相似三角形，并给出证明．解答：解：（1）任选两个三角形的所有可能情况如下六种情况：①②，①③，①④，②③，②④，③④（2分）其中有两组（①③，②④）是相似的．∴选取到的二个三角形是相似三角形的概率是P=（4分）证明：（2）选择①、③证明．在△AOB与△COD中，∵AB∥CD，∴∠CDB=∠DBA，∠DCA=∠CAB，∴△AOB∽△COD（8分）选择②、④证明．∵四边形ABCD是等腰梯形，∴∠DAB=∠CBA，∴在△DAB与△CBA中有AD=BC，∠DAB=∠CAB，AB=AB，∴△DAB≌△CBA，（6分）∴∠ADO=∠BCO．又∠DOA=∠COB，∴△DOA∽△COB（8分）．点评：此题考查概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P（A）=，即相似三角形的证明．还考查了相似三角形的判定．10．附加题：如图△ABC中，D为AC上一点，CD=2DA，∠BAC=45°，∠BDC=60°，CE⊥BD于E，连接AE．（1）写出图中所有相等的线段，并加以证明；（2）图中有无相似三角形？若有，请写出一对；若没有，请说明理由；（3）求△BEC与△BEA的面积之比．解答：解：（1）AD=DE，AE=CE．∵CE⊥BD，∠BDC=60°，∴在Rt△CED中，∠ECD=30°．∴CD=2ED．∵CD=2DA，∴AD=DE，∴∠DAE=∠DEA=30°=∠ECD．∴AE=CE．（2）图中有三角形相似，△ADE∽△AEC；∵∠CAE=∠CAE，∠ADE=∠AEC，∴△ADE∽△AEC；（3）作AF⊥BD的延长线于F，设AD=DE=x，在Rt△CED中，可得CE=，故AE=．∠ECD=30°．在Rt△AEF中，AE=，∠AED=∠DAE=30°，∴sin∠AEF=，∴AF=AE•sin∠AEF=．∴．点评：本题主要考查了直角三角形的性质，相似三角形的判定及三角形面积的求法等，范围较广．11．如图，在△ABC中，AB=AC=a，M为底边BC上的任意一点，过点M分别作AB、AC的平行线交AC于P，交AB于Q．（1）求四边形AQMP的周长；（2）写出图中的两对相似三角形（不需证明）；（3）M位于BC的什么位置时，四边形AQMP为菱形并证明你的结论．解答：解：（1）∵AB∥MP，QM∥AC，∴四边形APMQ 是平行四边形，∠B=∠PMC，∠C=∠QMB．∵AB=AC，∴∠B=∠C，∴∠PMC=∠QMB．∴BQ=QM，PM=PC．∴四边形AQMP的周长=AQ+AP+QM+MP=AQ+QB+AP+PC=AB+AC=2a．（2）∵PM∥AB，∴△PCM∽△ACB，∵QM∥AC，∴△BMQ∽△BCA；（3）当点M中BC的中点时，四边形APMQ是菱形，∵点M是BC的中点，AB∥MP，QM∥AC，∴QM，PM是三角形ABC的中位线．∵AB=AC，∴QM=PM=AB=AC．又由（1）知四边形APMQ是平行四边形，∴平行四边形APMQ是菱形．12．已知：P是正方形ABCD的边BC上的点，且BP=3PC，M是CD的中点，试说明：△ADM∽△MCP．解答：证明：∵正方形ABCD，M为CD中点，∴CM=MD=AD．∵BP=3PC，∴PC=BC=AD=CM．∴．∵∠PCM=∠ADM=90°，∴△MCP∽△ADM．13．如图，已知梯形ABCD中，AD∥BC，AD=2，AB=BC=8，CD=10．（1）求梯形ABCD的面积S；（2）动点P从点B出发，以1cm/s的速度，沿B⇒A⇒D⇒C方向，向点C运动；动点Q从点C出发，以1cm/s的速度，沿C⇒D⇒A方向，向点A运动，过点Q 作QE⊥BC于点E．若P、Q两点同时出发，当其中一点到达目的地时整个运动随之结束，设运动时间为t秒．问：①当点P在B⇒A上运动时，是否存在这样的t，使得直线PQ将梯形ABCD的周长平分？若存在，请求出t的值；若不存在，请说明理由；②在运动过程中，是否存在这样的t，使得以P、A、D为顶点的三角形与△CQE相似？若存在，请求出所有符合条件的t的值；若不存在，请说明理由；③在运动过程中，是否存在这样的t，使得以P、D、Q为顶点的三角形恰好是以DQ 为一腰的等腰三角形？若存在，请求出所有符合条件的t的值；若不存在，请说明理由．解答：解：（1）过D作DH∥AB交BC于H点，∵AD∥BH，DH∥AB，∴四边形ABHD是平行四边形．∴DH=AB=8；BH=AD=2．∴CH=8﹣2=6．∵CD=10，∴DH2+CH2=CD2∴∠DHC=90°．∠B=∠DHC=90°．∴梯形ABCD是直角梯形．∴S ABCD=（AD+BC）AB=×（2+8）×8=40．（2）①∵BP=CQ=t ，∴AP=8﹣t，DQ=10﹣t，∵AP+AD+DQ=PB+BC+CQ，∴8﹣t+2+10﹣t=t+8+t．∴t=3＜8．∴当t=3秒时，PQ将梯形ABCD周长平分．②第一种情况：0＜t≤8若△PAD∽△QEC则∠ADP=∠C ∴tan∠ADP=tan∠C==∴=，∴t=若△PAD∽△CEQ则∠APD=∠C ∴tan∠APD=tan∠C==，∴=∴t=第二种情况：8＜t≤10，P、A、D三点不能组成三角形；第三种情况：10＜t≤12△ADP为钝角三角形与Rt△CQE不相似；∴t=或t=时，△PAD与△CQE相似．③第一种情况：当0≤t≤8时．过Q点作QE⊥BC，QH⊥AB，垂足为E、H．∵AP=8﹣t，AD=2，∴PD==．∵CE=t，QE=t，∴QH=BE=8﹣t，BH=QE=t．∴PH=t﹣t=t．∴PQ==，DQ=10﹣t．Ⅰ：DQ=DP，10﹣t=，解得t=8秒．Ⅱ：DQ=PQ，10﹣t=，化简得：3t2﹣52t+180=0解得：t=，t=＞8（不合题意舍去）∴t=第二种情况：8≤t≤10时．DP=DQ=10﹣t．∴当8≤t＜10时，以DQ为腰的等腰△DPQ恒成立．第三种情况：10＜t≤12时．DP=DQ=t﹣10．∴当10＜t≤12时，以DQ为腰的等腰△DPQ恒成立．综上所述，t=或8≤t＜10或10＜t≤12时，以DQ为腰的等腰△DPQ成立．14．已知矩形ABCD，长BC=12cm，宽AB=8cm，P、Q分别是AB、BC上运动的两点．若P自点A出发，以1cm/s的速度沿AB方向运动，同时，Q自点B出发以2cm/s的速度沿BC方向运动，问经过几秒，以P、B、Q为顶点的三角形与△BDC 相似？解答：解：设经x秒后，△PBQ∽△BCD，由于∠PBQ=∠BCD=90°，（1）当∠1=∠2时，有：，即；（2）当∠1=∠3时，有：，即，∴经过秒或2秒，△PBQ∽△BCD．15．如图，在△ABC 中，AB=10cm ，BC=20cm ，点P 从点A 开始沿AB 边向B 点以2cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以4cm/s 的速度移动，如果P 、Q 分别从A 、B 同时出发，问经过几秒钟，△PBQ 与△ABC 相似． 解答： 设经过秒后t 秒后，△PBQ 与△ABC 相似，则有AP=2t ，BQ=4t ，BP=10﹣2t ， 当△PBQ ∽△ABC 时，有BP ：AB=BQ ：BC ， 即（10﹣2t ）：10=4t ：20，解得t=2.5（s ）（6分）当△QBP ∽△ABC 时，有BQ ：AB=BP ：BC ， 即4t ：10=（10﹣2t ）：20，解得t=1．所以，经过2.5s 或1s 时，△PBQ 与△ABC 相似（10分）．解法二：设ts 后，△PBQ 与△ABC 相似，则有，AP=2t ，BQ=4t ，BP=10﹣2t分两种情况：（1）当BP 与AB 对应时，有=，即=，解得t=2.5s （2）当BP 与BC 对应时，有=，即=，解得t=1s所以经过1s 或2.5s 时，以P 、B 、Q 三点为顶点的三角形与△ABC 相似．16．如图，∠ACB=∠ADC=90°，AC=，AD=2．问当AB 的长为多少时，这两个直角三角形相似． 解答： 解：∵AC=，AD=2，∴CD==．要使这两个直角三角形相似，有两种情况：1） 当Rt △ABC ∽Rt △ACD 时， 2） 有=，∴AB==3；3） 当Rt △ACB ∽Rt △CDA 时， 4） 有=，∴AB==3．故当AB 的长为3或3时，这两个直角三角形相似．17．已知，如图，在边长为a 的正方形ABCD 中，M 是AD 的中点，能否在边AB 上找一点N （不含A 、B ），使得△CDM 与△MAN 相似？若能，请给出证明，若不能，请说明理由．解答： 证明：分两种情况讨论：①若△CDM ∽△MAN ，则=．∵边长为a ，M 是AD 的中点， ∴AN=a ．②若△CDM ∽△NAM ，则．∵边长为a，M 是AD的中点，∴AN=a，即N点与B重合，不合题意．所以，能在边AB上找一点N（不含A、B），使得△CDM与△MAN相似．当AN=a时，N点的位置满足条件．18．如图在△ABC中，∠C=90°，BC=8cm，AC=6cm，点Q从B出发，沿BC方向以2cm/s的速度移动，点P从C出发，沿CA方向以1cm/s的速度移动．若Q、P分别同时从B、C出发，试探究经过多少秒后，以点C、P、Q为顶点的三角形与△CBA相似？解答：解：设经过x秒后，两三角形相似，则CQ=（8﹣2x）cm，CP=xcm，（1分）∵∠C=∠C=90°，∴当或时，两三角形相似．（3分）（1）当时，，∴x=；（4分）（2）当时，，∴x=．（5分）所以，经过秒或秒后，两三角形相似．（6分）点评：本题综合考查了路程问题，相似三角形的性质及一元一次方程的解法．19．如图所示，梯形ABCD中，AD∥BC，∠A=90°，AB=7，AD=2，BC=3，试在腰AB上确定点P的位置，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似．解答：解：（1）若点A，P，D分别与点B，C，P对应，即△APD∽△BCP，∴=，∴=，∴AP2﹣7AP+6=0，∴AP=1或AP=6，检测：当AP=1时，由BC=3，AD=2，BP=6，∴=，又∵∠A=∠B=90°，∴△APD∽△BCP．当AP=6时，由BC=3，AD=2，BP=1，又∵∠A=∠B=90°，∴△APD∽△BCP．（2）若点A，P，D分别与点B，P，C对应，即△APD∽△BPC．∴=，∴=，∴AP=．检验：当AP=时，由BP=，AD=2，BC=3，∴=，又∵∠A=∠B=90°，∴△APD∽△BPC．因此，点P的位置有三处，即在线段AB距离点A的1、、6处．20．△ABC和△DEF是两个等腰直角三角形，∠A=∠D=90°，△DEF的顶点E位于边BC的中点上．（1）如图1，设DE与AB交于点M，EF与AC交于点N，求证：△BEM∽△CNE；（2）如图2，将△DEF绕点E旋转，使得DE与BA的延长线交于点M，EF与AC 交于点N，于是，除（1）中的一对相似三角形外，能否再找出一对相似三角形并证明你的结论．解答：证明：（1）∵△ABC是等腰直角三角形，∴∠MBE=45°，∴∠BME+∠MEB=135°又∵△DEF是等腰直角三角形，∴∠DEF=45°∴∠NEC+∠MEB=135°∴∠BEM=∠NEC，（4分）而∠MBE=∠ECN=45°，∴△BEM∽△CNE．（6分）（2）与（1）同理△BEM∽△CNE，∴．（8分）又∵BE=EC，∴，（10分）则△ECN与△MEN中有，又∠ECN=∠MEN=45°，∴△ECN∽△MEN．（12分）21．如图，在矩形ABCD中，AB=15cm，BC=10cm，点P沿AB边从点A开始向B以2cm/s的速度移动；点Q沿DA边从点D开始向点A以1cm/s的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间，那么当t为何值时，以点Q、A、P 为顶点的三角形与△ABC相似．解答：解：以点Q、A、P为顶点的三角形与△ABC相似，所以△ABC∽△PAQ或△ABC∽△QAP，①当△ABC∽△PAQ 时，，所以，解得：t=6；②当△ABC∽△QAP时，，所以，解得：t=；③当△AQP∽△BAC时，=，即=，所以t=；④当△AQP∽△BCA时，=，即=，所以t=30（舍去）．故当t=6或t=时，以点Q、A、P为顶点的三角形与△ABC相似．22．如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？解答：解：∵∠MAC=∠MOP=90°，∠AMC=∠OMP，∴△MAC∽△MOP．∴，即，解得，MA=5米；同理，由△NBD∽△NOP，可求得NB=1.5米，∴小明的身影变短了5﹣1.5=3.5米．23．阳光明媚的一天，数学兴趣小组的同学们去测量一棵树的高度（这棵树底部可以到达，顶部不易到达），他们带了以下测量工具：皮尺，标杆，一副三角尺，小平面镜．请你在他们提供的测量工具中选出所需工具，设计一种测量方案．（1）所需的测量工具是：；（2）请在下图中画出测量示意图；（3）设树高AB的长度为x，请用所测数据（用小写字母表示）求出x．解答：解：（1）皮尺，标杆；（2）测量示意图如图所示；（3）如图，测得标杆DE=a，树和标杆的影长分别为AC=b，EF=c，∵△DEF∽△BAC，∴，∴，∴．（7分）24．问题背景在某次活动课中，甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量．下面是他们通过测量得到的一些信息：甲组：如图1，测得一根直立于平地，长为80cm的竹竿的影长为60cm．乙组：如图2，测得学校旗杆的影长为900cm．丙组：如图3，测得校园景灯（灯罩视为球体，灯杆为圆柱体，其粗细忽略不计）的高度为200cm，影长为156cm．任务要求：（1）请根据甲、乙两组得到的信息计算出学校旗杆的高度；（2）如图3，设太阳光线NH与⊙O相切于点M．请根据甲、丙两组得到的信息，求景灯灯罩的半径．（友情提示：如图3，景灯的影长等于线段NG的影长；需要时可采用等式1562+2082=2602）解答：解：（1）由题意可知：∠BAC=∠EDF=90°，∠BCA=∠EFD．∴△ABC ∽△DEF．∴，即，（2分）∴DE=1200（cm）．所以，学校旗杆的高度是12m．（3分）（2）解法一：与①类似得：，即，∴GN=208．（4分）在Rt△NGH中，根据勾股定理得：NH2=1562+2082=2602，∴NH=260．（5分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（6分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN，∴（7分），又ON=OK+KN=OK+（GN﹣GK）=r+8，∴，解得：r=12．∴景灯灯罩的半径是12cm．（8分）解法二：与①类似得：，即，∴GN=208．（4分）设⊙O的半径为rcm，连接OM，∵NH切⊙O于M，∴OM⊥NH．（5分）则∠OMN=∠HGN=90°，又∵∠ONM=∠HNG，∴△OMN∽△HGN．∴，即，（6分）∴MN=r，又∵ON=OK+KN=OK+（GN﹣GK）=r+8．（7分）在Rt△OMN中，根据勾股定理得：r2+（r）2=（r+8）2即r2﹣9r﹣36=0，解得：r1=12，r2=﹣3（不合题意，舍去），∴景灯灯罩的半径是12cm．（8分）25．（2007•白银）阳光通过窗口照射到室内，在地面上留下2.7m宽的亮区（如图所示），已知亮区到窗口下的墙脚距离EC=8.7m，窗口高AB=1.8m，求窗口底边离地面的高BC．解答：解：∵AE∥BD，∴△ECA∽△DCB，∴．∵EC=8.7m，ED=2.7m，∴CD=6m．∵AB=1.8m，∴AC=BC+1.8m，∴，∴BC=4，即窗口底边离地面的高为4m．点评：此题基本上难度不大，利用相似比即可求出窗口底边离地面的高．26．如图，李华晚上在路灯下散步．已知李华的身高AB=h，灯柱的高OP=O′P′=l，两灯柱之间的距离OO′=m．（1）若李华距灯柱OP的水平距离OA=a，求他影子AC的长；（2）若李华在两路灯之间行走，则他前后的两个影子的长度之和（DA+AC）是否是定值请说明理由；（3）若李华在点A朝着影子（如图箭头）的方向以v1匀速行走，试求他影子的顶端在地面上移动的速度v2．解答：解：（1）由已知：AB∥OP，∴△ABC∽△OPC．∵，∵OP=l，AB=h，OA=a，∴，∴解得：．（2）∵AB∥OP，∴△ABC∽△OPC，∴，即，即．∴．同理可得：，∴=是定值．（3）根据题意设李华由A到A'，身高为A'B'，A'C'代表其影长（如图）．由（1）可知，即，∴，同理可得：，∴，由等比性质得：，当李华从A走到A'的时候，他的影子也从C移到C'，因此速度与路程成正比∴，所以人影顶端在地面上移动的速度为．27．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．解：设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c，则c2=a2+b2（1）S1=S2+S3；（2）S1=S2+S3．证明如下：显然，S1=，S2=，S3=∴S2+S3==S1；（3）当所作的三个三角形相似时，S1=S2+S3．证明如下：∵所作三个三角形相似∴∴=1 ∴S1=S2+S3；（4）分别以直角三角形ABC三边为一边向外作相似图形，其面积分别用S1、S2、S3表示，则S1=S2+S3．28．已知：如图，△ABC∽△ADE，AB=15，AC=9，BD=5．求AE．解答：解：∵△ABC ∽△ADE，∴AE：AC=AD：AB．∵AE：AC=（AB+BD）：AB，∴AE：9=（15+5）：15．∴AE=12．29．已知：如图Rt△ABC∽Rt△BDC，若AB=3，AC=4．（1）求BD、CD的长；（2）过B作BE⊥DC于E，求BE的长．解答：解：（1）Rt△ABC中，根据勾股定理得：BC==5，∵Rt△ABC∽Rt△BDC，∴==，==，∴BD=，CD=；（2）在Rt△BDC中，S△BDC=BE•CD=BD•BC，∴BE===3．30．（1）已知，且3x+4z﹣2y=40，求x，y，z的值；（2）已知：两相似三角形对应高的比为3：10，且这两个三角形的周长差为560cm，求它们的周长．解：（1）设=k，那么x=2k，y=3k，z=5k，由于3x+4z﹣2y=40，∴6k+20k﹣6k=40，∴k=2，∴x=4，y=6，z=10．（2）设一个三角形周长为Ccm，则另一个三角形周长为（C+560）cm，则，∴C=240，C+560=800，即它们的周长分别为240cm，800cm。
相似三角形经典题型
相似三角形经典题型一、相似三角形的判定定理相关题型1. 题目已知在△ABC和△A'B'C'中，∠A = 50°，AB = 3cm，AC = 4cm，∠A'= 50°，A'B'= 6cm，A'C' = 8cm。
判断这两个三角形是否相似。
解析根据相似三角形的判定定理：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似。
在△ABC和△A'B'C'中，(AB)/(A'B')=(3)/(6)=(1)/(2)，(AC)/(A'C')=(4)/(8)=(1)/(2)，且∠A = ∠A' = 50°。
所以△ABC∽△A'B'C'。
2. 题目如图，在四边形ABCD中，∠B = ∠ACD，AB = 6，BC = 4，AC = 5，CD=(7)/(2)，求AD的长。
解析因为∠B = ∠ACD，且(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，(AC)/(AD)未知。
又因为(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，不满足三边对应成比例。
但是由∠B = ∠ACD，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，可以尝试证明△ABC和△ACD相似。
因为∠B = ∠ACD，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，这里我们重新计算(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)是错误的，应该是(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)，(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(6)/(5)，(BC)/(CD)=(4)/(frac{7){2}}=(8)/(7)(AB)/(AC)=(BC)/(CD)所以△ABC∽△DCA。
相似三角形典型例题30道
相似三角形典型例题30道1: 在△ABC中，DE是平行于BC的线段，且AD/DB = 2/3。
求DE/BC的比值。
2: 已知△PQR与△XYZ相似，PQ = 6，XY = 9，求QR 与YZ的比值。
3: 在△ABC中，D、E分别是AB、AC上的点，且DE平行于BC，已知AD = 3，DB = 6，求AE与EC的比值。
4: 已知两个相似三角形的面积比为4:9，求它们对应边的比。
5: 在△XYZ中，MN是平行于XY的线段，且XM = 4，MY = 6，求MN/XY的比值。
6: 在△ABC中，AD是BC的中线，且AE是AB的延长线，若AE与BC相交于点F，求AF与FB的比值。
7: 在△DEF中，GH平行于EF，已知DE = 8，DF = 10，求GH/EF的比值。
8: 在一个相似三角形中，若大三角形的周长是36，小三角形的周长是24，求它们的面积比。
9: 在△JKL中，MN平行于JK，若JM = 3，MK = 5，求MN/JK的比值。
10: 如果两个相似三角形的对应边长分别为5和15，求它们的面积比。
11: 在△ABC中，AD是BC的中线，且DE平行于BC，已知AD = 4，BC = 8，求DE的长度。
12: 已知相似三角形的对应边长比为1:4，求它们的周长比。
13: 在△PQR中，S是PQ的中点，若ST平行于QR，求PS与PQ的比值。
14: 在相似三角形中，若小三角形的每条边长为5，大三角形的对应边长为15，求它们的面积比。
15: 在一个三角形中，若一条边的延长线与另一边的平行线相交，则形成的两小三角形与原三角形相似，求相似比。
16: 在△XYZ中，若XY = 10，XZ = 15，YZ = 12，求△XYZ的周长。
17: 已知△ABC与△DEF相似，若AB = 4，DE = 8，求AC与DF的比值。
18: 在△GHI中，JK平行于GH，若GJ = 5，GH = 20，求JK的长度。
19: 在相似三角形中，若一个三角形的面积是36，另一个三角形的面积是144，求其对应边的比。
相似三角形30道经典题
相似三角形30道经典题英文回答：1. Theorem: If two triangles are similar, then their corresponding sides are proportional.2. Corollary: If two triangles have two pairs of corresponding sides proportional, then they are similar.3. Theorem: If two triangles have three pairs of corresponding angles congruent, then they are similar.4. Corollary: If two triangles have two pairs of corresponding angles congruent, then the third pair is also congruent, and the triangles are similar.5. Theorem: The ratio of the areas of two similar triangles is equal to the square of the ratio of any two corresponding sides.6. Corollary: The ratio of the areas of two similar triangles is equal to the square of the ratio of any two corresponding altitudes.7. Theorem: If a line parallel to one side of a triangle divides another side into two segments, then the ratio of the lengths of the segments is equal to the ratio of the corresponding sides of the triangle.8. Corollary: If a line parallel to the base of a triangle divides the other two sides into segments, then the ratios of the lengths of the segments are equal to the ratio of the corresponding sides of the triangle.9. Theorem: If a line parallel to one side of a triangle divides the area of the triangle into two parts, then the ratio of the areas of the parts is equal to the ratio of the corresponding sides of the triangle.10. Corollary: If a line parallel to the base of a triangle divides the area of the triangle into two parts, then the ratios of the areas of the parts are equal to theratio of the corresponding sides of the triangle.11. Theorem: The sum of the interior angles of a triangle is 180 degrees.12. Corollary: The sum of the exterior angles of a triangle is 360 degrees.13. Theorem: The Pythagorean Theorem: For a right triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.14. Corollary: The converse of the Pythagorean Theorem: If the square of one side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.15. Theorem: The Law of Cosines: For any triangle, the square of one side is equal to the sum of the squares of the other two sides minus twice the product of the other two sides and the cosine of the included angle.16. Corollary: The Law of Sines: For any triangle, the ratio of the sine of one angle to the length of theopposite side is equal to the ratio of the sine of anyother angle to the length of its opposite side.17. Theorem: The area of a triangle is equal to halfthe product of the base and height.18. Corollary: The area of a triangle is equal to half the product of two sides and the sine of the included angle.19. Theorem: The perimeter of a triangle is equal tothe sum of the lengths of its three sides.20. Corollary: The perimeter of a triangle is equal to the sum of the lengths of two sides plus the length of the third side.21. Theorem: If a triangle is equilateral, then its angles are all equal to 60 degrees.22. Corollary: If a triangle has two sides equal, thenits angles opposite the equal sides are equal.23. Theorem: If a triangle has two angles equal, thenits sides opposite the equal angles are equal.24. Corollary: If a triangle has three equal sides,then its angles are all equal to 60 degrees.25. Theorem: If a triangle has a right angle, then its other two angles are acute.26. Corollary: If a triangle has an obtuse angle, then its other two angles are acute.27. Theorem: If a triangle has two adjacent sides equal, then the angle opposite the equal sides is greater than the other angles.28. Corollary: If a triangle has two adjacent sides unequal, then the angle opposite the greater side isgreater than the angle opposite the smaller side.29. Theorem: If a triangle has two adjacent angles equal, then the sides opposite the equal angles are equal.30. Corollary: If a triangle has two adjacent angles unequal, then the side opposite the greater angle isgreater than the side opposite the smaller angle.中文回答：1. 定理，如果两个三角形相似，那么它们对应边的比值相等。
相似三角形经典题75题
相似三角形：填空：1. 如果一个三角形的三边长为5、12、13，与其相似的三角形的最长的边为39，那么较大的三角形的周长为，面积为．2. 如图，在△ABC中，DE∥BC，AD=2，AE=3，BD=4，则AC= ．3. 五边形ABCDE∽五边形A′B′C′D′E′，∠A=120°，∠B′=130°，∠C=105°，∠D′=85°，则∠E=．4. 如图，在△ABC中，D、E分别是AC、AB边上的点，∠AED=∠C，AB=6，AD=4，AC=5，则AE= ．5. 如图，△ABC三个顶点的坐标分别为A（2，2），B（4，0），C（6，4）以原点为位似中心，将△ABC缩小，位似比为1：2，则线段AC中点P变换后对应点的坐标为．6. 从美学角度来说，人的上身长与下身长之比为黄金比时，可以给人一种协调的美感．某女老师上身长约61.80cm，下身长约93.00cm，她要穿约cm的高跟鞋才能达到黄金比的美感效果（精确到0.01cm）．7. 如图，△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，点D为AC的黄金分割点（AD＞CD），AC=6，则CD= ．8．如图，已知P是线段AB的黄金分割点，且PA＞PB，若S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，则S1S2．（填“＞”“=”或“＜”）9．如图，△ABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（）10．如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=BC．图中相似三角形共有（）对11．如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在CB，CD上滑动，当CM= 时，△AED与以M，N，C为顶点的三角形相似．12．如图，C是AB的黄金分割点，BG=AB，以CA为边的正方形的面积为S1，以BC、BG为边的矩形的面积为S2，则S1S2（填“＞”“＜”“=”）．13．如图，在△ABC中，AB=AC=5，BC=6，点M为BC的中点，MN⊥AC 于点N，则MN等于（）14．在△ABC中，∠ACB=90°，CD⊥AB于点D，则下列说法正确的有（填序号）．①AC•BC=AB•CD；②AC2=AD•DB；③BC2=BD•BA；④CD2=AD•DB．15．如图，在▱ABCD中，E、F分别是AB、AD的中点，EF交AC于点G，则的值是．16．如图，在梯形ABCD中，AD∥BC，AC，BD交于点O，S△AOD：S△COB=1：9，则S△DOC：S△BOC= ．17．如图，在△ABC中，BC=a．若D1，E1分别是AB，AC的中点，则D1E1=；若D2，E2分别是D1B，E1C的中点，则D2E2=…若D n E n分别是D n﹣1B，E n﹣1C的中点，则D n E n的长是多少（n＞1，且n为整数，结果用含a，n的代数式表示）？18．如图，将△ABC绕顶点A顺时针旋转60°后，得到△AB′C′，且C′为BC的中点，则C′D：DB′=（）19．如图，在正方形网格中，点A、B、C、D都是格点，点E是线段AC上任意一点．如果AD=1，那么当AE= 时，以点A、D、E为顶点的三角形与△ABC相似．20．如图，在直角三角形ABC中（∠C=90°），放置边长分别为3，4，x的三个正方形，则x的值为（）21．如图，▱ABCD中，E、F分别为AD、BC上的点，且DE=2AE，BF=2FC，连接BE、AF交于点H，连接DF、CE交于点G，则= ．22．如图，△ABC是边长为1的等边三角形，取BC边中点E，作ED∥AB交AC 于点D，EF∥AC交AB于点F，得到四边形EDAF，它的面积记做S1，取BE边中点E1，作E1D1∥FB交EF于点D1，E1F1∥EF交AB于点F1，得到四边形E1D1FF1，它的面积记做S2．照此规律作下去，则S2013= ．解答：1．已知：如图所示，D是AC上一点，BE∥AC，AE分别交BD，BC于点F，G，∠1=∠2．则证明BF2=FG•EF．2．如图，梯形ABCD中，AB∥CD，点F在BC上，连DF与AB的延长线交于点G．（1）求证：△CDF∽△BGF；（2）当点F是BC的中点时，过F作EF∥CD交AD于点E，若AB=6cm，EF=4cm，求CD的长．3．已知：如图，在△ABC中，AB=AC，DE∥BC，点F在边AC上，DF与BE 相交于点G，且∠EDF=∠ABE．求证：（1）△DEF∽△BDE；（2）DG•DF=DB•EF．4．如图，在正方形ABCD中，E、F分别是边AD、CD上的点，，连接EF并延长交BC的延长线于点G．（1）求证：△ABE∽△DEF；（2）若正方形的边长为4，求BG的长．5．如图，M为线段AB的中点，AE与BD交于点C，∠DME=∠A=∠B，且DM 交AC于F，ME交BC于G．写出图中的所有相似三角形，并选择一对加以证明．6．如图，在△ABC中，∠C=90°，BC=16cm，AC=12cm，点P从B出发沿BC 以2cm/s的速度向C移动，点Q从C出发，以1cm/s的速度向A移动，若P、Q分别从B、C同时出发，设运动时间为ts，当为何值时，△CPQ与△CBA相似？7．如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1.5m，CD=8m，求树高AB．8．如图，在梯形ABCD中，AD∥BC，P是AB上一点，PE∥BC交CD于点E．若AD=2，BC=，则点P在何处时，PE把梯形ABCD分成两个相似的小梯形？9．如图，已知线段AB，P1是AB的黄金分割点（AP1＞BP1），点O是AB的中点，P2是P1关于点O的对称点．求证：P1B是P2B和P1P2的比例中项．10．如图，已知DE∥BC，EF∥AB，设S△ABC=S，S△ABC=S1，S△ECF=S2，请验证．11．如图，在Rt△ABC中，∠B=90°，AB=1，BC=，以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E．（1）求AE的长度；（2）分别以点A、E为圆心，AB长为半径画弧，两弧交于点F（F与C在AB 两侧），连接AF、EF，设EF交弧DE所在的圆于点G，连接AG，试猜想∠EAG 的大小，并说明理由．12．如图，在平面直角坐标系中，直线交x轴于点A，交y轴于点B．试在y轴上找一点P，使△AOP与△AOB相似，你能找出几个这样的点（点P与点B不重合）？分别求出对应AP的长度．13．如图，已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，点P在AC上（与点A，C不重合），点Q在BC上．（1）△CPQ的边PQ上的高为时，求△CPQ的周长；（2）当△CPQ的周长与四边形PABQ的周长相等时，求CP的长．14．阅读下面的短文，并解答下列问题：我们把相似形的概念推广到空间：如果两个几何体大小不一定相等，但形状完全相同，就把它们叫做相似体．如图，甲、乙是两个不同的正方体，正方体都是相似体，它们的一切对应线段之比都等于相似比（a：b）．设S甲、S乙分别表示这两个正方体的表面积，则==（）2又设V甲、V乙分别表示这两个正方体的体积，则==（）3（1）下列几何体中，一定属于相似体的是（A）A．两个球体B．两个锥体C．两个圆柱体D．两个长方体（2）请归纳出相似体的三条主要性质：①相似体的一切对应线段（或弧）长的比等于；②相似体表面积的比等于；③相似体体积比等于．（3）假定在完全正常发育的条件下，不同时期的同一人的人体是相似体，一个小朋友上幼儿园时身高为1.1米，体重为18千克，到了初三时，身高为1.65米，问他的体重是多少？（不考虑不同时期人体平均密度的变化）15．△ABC中，∠C=90°，∠A=60°，AC=2cm．长为1cm的线段MN在△ABC 的边AB上沿AB方向以1cm/s的速度向点B运动（运动前点M与点A重合）．过M，N分别作AB的垂线交直角边于P，Q两点，线段MN运动的时间为ts．（1）若△AMP的面积为y，写出y与t的函数关系式（写出自变量t的取值范围）；（2）线段MN运动过程中，四边形MNQP有可能成为矩形吗？若有可能，求出此时t的值；若不可能，说明理由；（3）t为何值时，以C，P，Q为顶点的三角形与△ABC相似？16．定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形．探究：（1）如图甲，已知△ABC中∠C=90°，你能把△ABC分割成2个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由．（2）一般地，“任意三角形都是自相似图形”，只要顺次连接三角形各边中点，则可将原三分割为四个都与它自己相似的小三角形．我们把△DEF（图乙）第一次顺次连接各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连接它的各边中点所进行的分割，称为2阶分割（如图2）…依次规则操作下去．n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S N．①若△DEF的面积为10000，当n为何值时，2＜S n＜3？（请用计算器进行探索，要求至少写出三次的尝试估算过程）②当n＞1时，请写出一个反映S n﹣1，S n，S n+1之间关系的等式．（不必证明）17．如图①，分别以直角三角形ABC三边为直径向外作三个半圆，其面积分别用S1，S2，S3表示，则不难证明S1=S2+S3．（1）如图②，分别以直角三角形ABC三边为边向外作三个正方形，其面积分别用S1，S2，S3表示，那么S1，S2，S3之间有什么关系；（不必证明）（2）如图③，分别以直角三角形ABC三边为边向外作三个正三角形，其面积分别用S1、S2、S3表示，请你确定S1，S2，S3之间的关系并加以证明；（3）若分别以直角三角形ABC三边为边向外作三个一般三角形，其面积分别用S1，S2，S3表示，为使S1，S2，S3之间仍具有与（2）相同的关系，所作三角形应满足什么条件证明你的结论；（4）类比（1），（2），（3）的结论，请你总结出一个更具一般意义的结论．18．为了加强视力保护意识，欢欢想在书房里挂一张测试距离为5m的视力表，但两面墙的距离只有3m．在一次课题学习课上，欢欢向全班同学征集“解决空间过小，如何放置视力表问题”的方案，其中甲、乙两位同学设计方案新颖，构思巧妙．（1）甲生的方案：如图①，根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表．如果大视力表中“E”的高是3.5cm，那么小视力表中相应“E”的高是多少？（2）乙生的方案：使用平面镜来解决房间小的问题．如图②，若使墙面镜子能呈现完整的视力表，由平面镜成像原理，作出了光路图，其中视力表AB的上、下边沿A，B发出的光线经平面镜MM′的上下边沿反射后射人人眼C处．如果视力表的全长为0.8m，请计算出镜长至少为多少米．19．在直角边分别为5cm和12cm的直角三角形中作菱形，使菱形的一个内角恰好是三角形的一个角，其余顶点都在三角形的边上，求所作菱形的边长．20．如图1，点C将线段AB分成两部分，如果，那么称点C为线段AB 的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l将一个面积为S的图形分成两部分，这两部分的面积分别为S1，S2，如果，那么称直线l为该图形的黄金分割线．（1）研究小组猜想：在△ABC中，若点D为AB边上的黄金分割点（如图2），则直线CD是△ABC的黄金分割线．你认为对吗？为什么？（2）请你说明：三角形的中线是否也是该三角形的黄金分割线？（3）研究小组在进一步探究中发现：过点C任作一条直线交AB于点E，再过点D作直线DF∥CE，交AC于点F，连接EF（如图3），则直线EF也是△ABC 的黄金分割线．请你说明理由．（4）如图4，点E是平行四边形ABCD的边AB的黄金分割点，过点E作EF∥AD，交DC于点F，显然直线EF是平行四边形ABCD的黄金分割线．请你画一条平行四边形ABCD的黄金分割线，使它不经过平行四边形ABCD各边黄金分割点．21．如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点．（1）若BK=KC，求的值；（2）连接BE，若BE平分∠ABC，则当AE=AD时，猜想线段AB、BC、CD 三者之间有怎样的等量关系？请写出你的结论并予以证明．再探究：当AE=AD（n＞2），而其余条件不变时，线段AB、BC、CD三者之间又有怎样的等量关系？请直接写出你的结论，不必证明．22．如图，已知△ABC是面积为的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于（结果保留根号）．23．如图，已知△ABC∽△A1B1C1，相似比为k（k＞1），且△ABC的三边长分别为a、b、c（a＞b＞c），△A1B1C1的三边长分别为a1、b1、c1．（1）若c=a1，求证：a=kc；（2）若c=a1，试给出符合条件的一对△ABC和△A1B1C1，使得a、b、c和a1、b1、c1都是正整数，并加以说明；（3）若b=a1，c=b1，是否存在△ABC和△A1B1C1使得k=2？请说明理由．24．在左图的方格纸中有一个Rt△ABC（A、B、C三点均为格点），∠C=90°（1）请你画出将Rt△ABC绕点C顺时针旋转90°后所得到的Rt△A′B′C′，其中A、B的对应点分别是A′、B′（不必写画法）；（2）设（1）中AB的延长线与A′B′相交于D点，方格纸中每一个小正方形的边长为1，试求BD的长（精确到0.1）．25．如图，已知：在Rt△ABC中，∠ACB=90°，sinB=，D是BC上一点，DE⊥AB，垂足为E，CD=DE，AC+CD=9．求BC的长．26．如图，在△ABC中，AB=AC=1，点D，E在直线BC上运动．设BD=x，CE=y．（1）如果∠BAC=30°，∠DAE=105°，试确定y与x之间的函数关系式；（2）如果∠BAC=α，∠DAE=β，当α，β满足怎样的关系时，（1）中y与x之间的函数关系式还成立？试说明理由．27．如图，在平行四边形ABCD中，过点B作BE⊥CD于E，F为AE上一点，且∠BFE=∠C．（1）求证：△ABF∽△EAD；（2）若AB=5，AD=3，∠BAE=30°，求BF的长．28．如图，AB与CD相交于E，AE=EB，CE=ED，D为线段FB的中点，CF 与AB交于点G，若CF=15cm，求GF之长．29．如图，AF⊥CE，垂足为点O，AO=CO=2，EO=FO=1．（1）求证：点F为BC的中点；（2）求四边形BEOF的面积．30．E、F为平行四边形ABCD的对角线DB上三等分点，连AE并延长交DC 于P，连PF并延长交AB于Q，如图①（1）在备用图中，画出满足上述条件的图形，记为图②，试用刻度尺在图①、②中量得AQ、BQ的长度，估计AQ、BQ间的关系，并填入下表：（长度单位：cm）；（2）上述（1）中的猜测AQ、BQ间的关系成立吗？为什么？（3）若将平行四边形ABCD改为梯形（AB∥CD）其他条件不变，此时（1）中猜测AQ、BQ间的关系是否成立？（不必说明理由）31．如图，在平面直角坐标系中，点A在x轴负半轴上，点B的坐标是（0，2），过点B作BC⊥AB交x轴于点C，过点C作CD⊥BC交y轴于点D，过点D作DE⊥CD交x轴于点E，过点E作EF⊥DE交y轴于点F，若EA=3AC．（1）求证：△CBA∽△EDC；（2）请写出点A，点C的坐标（解答过程可不写）；（3）求出线段EF的长．32．Ⅰ．如图①，在△ABC中，点D，E，Q分别在AB，AC，BC上，且DE∥BC，AQ交DE于点P．求证：；Ⅱ．如图②，在△ABC中，∠BAC=90°，正方形DEFG的四个顶点在△ABC的边上，连结AG，AF，分别交DE于M，N两点．（1）如图②，若AB=AC=1，直接写出MN的长；（2）如图③，探究DM，MN，EN之间的关系，并说明理由．33．如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么（1）设△POQ的面积为y，求y关于t的函数解析式；（2）当△POQ的面积最大时，将△POQ沿直线PQ翻折后得到△PCQ，试判断点C是否落在直线AB上，并说明理由；（3）当t为何值时，△POQ与△AOB相似．34．已知△ABC是等腰直角三角形，∠A=90°，D是腰AC上的一个动点，过C 作CE垂直于BD或BD的延长线，垂足为E，如图．（1）若BD是AC的中线，求的值；（2）若BD是∠ABC的角平分线，求的值；（3）结合（1）、（2），试推断的取值范围（直接写出结论，不必证明），并探究的值能小于吗？若能，求出满足条件的D点的位置；若不能，说明理由．35．已知抛物线y=ax2+bx﹣1经过点A（﹣1，0）、B（m，0）（m＞0），且与y轴交于点C．（1）求a、b的值（用含m的式子表示）；（2）如图所示，⊙M过A、B、C三点，求阴影部分扇形的面积S（用含m的式子表示）；（3）在x轴上方，若抛物线上存在点P，使得以A、B、P为顶点的三角形与△ABC 相似，求m的值．36．如图，点D，E分别在△ABC的边BC，BA上，四边形CDEF是等腰梯形，EF∥CD．EF与AC交于点G，且∠BDE=∠A．（1）试问：AB•FG=CF•CA成立吗？说明理由；（2）若BD=FC，求证：△ABC是等腰三角形．37．如图，在▱ABCD中，AE、BF分别平分∠DAB和∠ABC，交CD于点E、F，AE、BF相交于点M．（1）试说明：AE⊥BF；（2）判断线段DF与CE的大小关系，并予以说明．38．如图①、②在▱ABCD中，∠BAD、∠ABC的平分线AF、BG分别与线段CD 两侧的延长线（或线段CD）相交于点F、G，AF与BG相交于点E．（1）在图①中，求证：AF⊥BG，DF=CG；（2）在图②中，仍有（1）中的AF⊥BG、DF=CG．若AB=10，AD=6，BG=4，求FG和AF的长．39．已知，如图，AD为Rt△ABC斜边BC上的高，点E为DA延长线上一点，连接BE，过点C作CF⊥BE于点F，交AB、AD于M、N两点．（1）若线段AM、AN的长是关于x的一元二次方程x2﹣2mx+n2﹣mn+m2=0的两个实数根，求证：AM=AN；（2）若AN=，DN=，求DE的长；（3）若在（1）的条件下，S△AMN：S△ABE=9：64，且线段BF与EF的长是关于y的一元二次方程5y2﹣16ky+10k2+5=0的两个实数根，求BC的长．40．把两块全等的直角三角形ABC和DEF叠放在一起，使三角板DEF的锐角顶点D与三角板ABC的斜边中点O重合，其中∠ABC=∠DEF=90°，∠C=∠F=45°，AB=DE=4，把三角板ABC固定不动，让三角板DEF绕点O旋转，设射线DE 与射线AB相交于点P，射线DF与线段BC相交于点Q．（1）如图1，当射线DF经过点B，即点Q与点B重合时，易证△APD∽△CDQ．此时，AP•CQ=；（2）将三角板DEF由图1所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AP•CQ的值是否改变？说明你的理由；（3）在（2）的条件下，设CQ=x，两块三角板重叠面积为y，求y与x的函数关系式．（图2，图3供解题用）41．（Ⅰ）如图1，点P在平行四边形ABCD的对角线BD上，一直线过点P分别交BA，BC的延长线于点Q，S，交AD，CD于点R，T．求证：PQ•PR=PS•PT；（Ⅱ）如图2，图3，当点P在平行四边形ABCD的对角线BD或DB的延长线上时，PQ•PR=PS•PT是否仍然成立？若成立，试给出证明；若不成立，试说明理由（要求仅以图2为例进行证明或说明）；（Ⅲ）如图4，ABCD为正方形，A，E，F，G四点在同一条直线上，并且AE=6cm，EF=4cm，试以（Ⅰ）所得结论为依据，求线段FG的长度．42．取一副三角板按图①拼接，固定三角板ADC，将三角板ABC绕点A依顺时针方向旋转一个大小为α的角（0°＜α≤45°）得到△ABC′，如图所示．试问：（1）当α为多少度时，能使得图②中AB∥DC；（2）当旋转至图③位置，此时α又为多少度图③中你能找出哪几对相似三角形，并求其中一对的相似比；（3）连接BD，当0°＜α≤45°时，探寻∠DBC′+∠CAC′+∠BDC值的大小变化情况，并给出你的证明．43．如图1，在直角梯形ABCD中，AD∥BC，顶点D，C分别在AM，BN上运动（点D不与A重合，点C不与B重合），E是AB上的动点（点E不与A，B重合），在运动过程中始终保持DE⊥CE，且AD+DE=AB=a．（1）求证：△ADE∽△BEC；（2）当点E为AB边的中点时（如图2），求证：①AD+BC=CD；②DE，CE 分别平分∠ADC，∠BCD；（3）设AE=m，请探究：△BEC的周长是否与m值有关，若有关请用含m的代数式表示△BEC的周长；若无关请说明理由．44．如图，△ABC中，∠BAC=90°，AB=AC=1，点D是BC上一个动点（不与B、C重合），在AC上取E点，使∠ADE=45度．（1）求证：△ABD∽△DCE；（2）设BD=x，AE=y，求y关于x的函数关系式；（3）当：△ADE是等腰三角形时，求AE的长．45．等腰△ABC，AB=AC=8，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕P点旋转．（1）如图a，当三角板的两边分别交AB、AC于点E、F时．求证：△BPE∽△CFP；（2）操作：将三角板绕点P旋转到图b情形时，三角板的两边分别交BA的延长线、边AC于点E、F．①探究1：△BPE与△CFP还相似吗？（只需写出结论）②探究2：连接EF，△BPE与△PFE是否相似？请说明理由；③设EF=m，△EPF的面积为S，试用m的代数式表示S．46．如图：在平行四边形ABCD中，E是AD上的一点．求证：．47．（1）如图1所示，在等边△ABC中，点D是AB边上的动点，以CD为一边，向上作等边△EDC，连接AE，求证：AE∥BC；（2）如图2所示，将（1）中等边△ABC的形状改成以BC为底边的等腰三角形，所作△EDC相似于△ABC，请问仍有AE∥BC？证明你的结论．48．如图，△ABC内接于⊙O，直径CD⊥AB，垂足为E，弦BF交CD于点M，交AC于点N，且BF=AC，连接AD、AM．求证：（1）△ACM≌△BCM；（2）AD•BE=DE•BC；（3）BM2=MN•MF．49．操作：在△ABC中，AC=BC=2，∠C=90°，将一块等腰直角三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．图1，2，3是旋转三角板得到的图形中的3种情况．研究：（1）三角板绕点P旋转，观察线段PD和PE之间有什么数量关系，并结合图2加以证明；（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由；（3）若将三角板的直角顶点放在斜边AB上的M处，且AM：MB=1：3，和前面一样操作，试问线段MD和ME之间有什么数量关系？并结合图4加以证明．50．如图，矩形ABCD的对角线AC、BD相交于点O，E、F分别是OA、OB 的中点．（1）求证：△ADE≌△BCF；（2）若AD=4cm，AB=8cm，求CF的长．51．如图，在直角梯形ABCD中，AB∥DC，∠ABC=90°，AB=2DC，对角线AC⊥BD，垂足为F，过点F作EF∥AB，交AD于点E，CF=4cm．（1）求证：四边形ABFE是等腰梯形；（2）求AE的长．52．如图，用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH，连接AE与BG、CF分别交于P、Q，（1）若AB=6，求线段BP的长；（2）观察图形，是否有三角形与△ACQ全等？并证明你的结论．53．已知点E、F在△ABC的边AB所在的直线上，且AE=BF，FH∥EG∥AC，FH、EG分别交边BC所在的直线于点H、G．（1）如图1，如果点E、F在边AB上，那么EG+FH=AC；（2）如图2，如果点E在边AB上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是；（3）如图3，如果点E在AB的反向延长线上，点F在AB的延长线上，那么线段EG、FH、AC的长度关系是．对（1）（2）（3）三种情况的结论，请任选一个给予证明．解析：填空：1．解：设较大三角形的其他两边长为a，b．∵由相似三角形的对应边比相等∴解得：a=15，b=36，则较大三角形的周长为90，面积为270．故较大三角形的周长为90，面积为270．∴，∵AD=2，AE=3，BD=4，∴，∴CE=6，∴AC=AE+EC=3+6=9．故答案为：9．∴∠B=∠B′=130°，∠D=∠D′=85°，又∵五边形的内角和为540°，∴∠E=540°﹣∠A﹣∠B﹣∠C﹣∠D=100°，故答案为：100°．∵∠A=∠A，∠AED=∠C，∴△AED∽△ACB．∴，∴，∴AE=．故答案为：．5．解：如图，∵A（2，2），C（6，4），∴点P的坐标为（4，3），∵以原点为位似中心将△ABC缩小位似比为1：2，∴线段AC的中点P变换后的对应点的坐标为（﹣2，﹣）或（2，）．故答案为：（﹣2，﹣）或（2，）．xcm的高跟鞋才能达到黄金比的美感效果．根据题意，得=≈0.618，解得x≈7.00故答案为：7.00．∴AD=AC═×6=3﹣3，∴CD=AC﹣AD=6﹣（3﹣3）=9﹣3．故答案为9﹣3．8．解：∵P是线段AB的黄金分割点，且PA＞PB，∴PA2=PB•AB，又∵S1表示PA为一边的正方形的面积，S2表示长是AB，宽是PB的矩形的面积，∴S1=PA2，S2=PB•AB，∴S1=S2．故答案为：=．9．解：∵∠A=∠A∴①∠ACP=∠B，②∠APC=∠ACB时都相似；∵AC2=AP•AB∴AC：AB=AP：AC∴③相似；④此两个对应边的夹角不是∠A，所以不相似．所以能满足△APC与△ACB相似的条件是①②③．10．解：图中相似三角形共有3对．理由如下：∵四边形ABCD是正方形，∴∠D=∠C=90°，AD=DC=CB，∵DE=CE，FC=BC，∴DE：CF=AD：EC=2：1，∴△ADE∽△ECF，∴AE：EF=AD：EC，∠DAE=∠CEF，∴AE：EF=AD：DE，即AD：AE=DE：EF，∵∠DAE+∠AED=90°，∴∠CEF+∠AED=90°，∴∠AEF=90°，∴∠D=∠AEF，∴△ADE∽△AEF，∴△AEF∽△ADE∽△ECF，即△ADE∽△ECF，△ADE∽△AEF，△AEF∽△ECF．11. 解：设CM的长为x．在Rt△MNC中∵MN=1，∴NC= ，①Rt△AED∽Rt△CMN时，则，即，解得x=或x=（不合题意，舍去），②Rt△AED∽Rt△CNM时，则，即，解得x=或（不合题意，舍去），综上所述，当CM=或时，△AED与以M，N，C为顶点的三角形相似．故答案为：或．12．解：由题意得：===1．即：S1=S2．13．解：连接AM，∵AB=AC，点M为BC中点，∴AM⊥CM（三线合一），BM=CM，∵AB=AC=5，BC=6，∴BM=CM=3，在Rt△ABM中，AB=5，BM=3，∴根据勾股定理得：AM===4，又S△AMC=MN•AC=AM•MC，∴MN==．14．解答：解：∵在△ABC中，∠ACB=90°，CD⊥AB，∴AC•BC=AB•CD，即∴AC•BC=AB•CD，故①正确；∵△ABC中，∠ACB=90°，CD⊥AB于点D，∴BC2=BD•BA，故③正确；∴△ACD∽△CBD，∴，∴AC2=AD•AB，CD2=AD•DB，故②错误，④正确．故答案为：①③④．15．解答：解：连接BD，与AC相交于O，∵点E、F分别是AD、AB的中点，∴EF是△ABD的中位线，∴EF∥DB，且EF=DB，∴△AEF∽△ADB，∴，∴，∴，∴AG=GO，又OA=OC，∴AG：GC=1：3．故答案为：．16．解答：解：根据题意，AD∥BC∴△AOD∽△COB ∵S△AOD：S△COB=1：9∴=则S△AOD：S△DOC=1：3所以S△DOC：S△BOC=3：9=1：3．17．解答：解：在△ABC中、BC=a，若D1、E1分别是AB、AC的中点，根据中位线定理得D1E1==a，∵D2、E2分别是D1B、E1C的中点，∴D2E2=（+a）=a=a，∵D3、E3分别是D2B、E2C的中点，则D3E3=（a+a）=a，…根据以上可得：若Dn、En分别是D n﹣1B、E n﹣1C的中点，则DnEn=a，即D n E n的长是a．18．解答：解：根据旋转的性质可知：AC=AC′，∠AC′B′=∠C=60°，∵旋转角是60°，即∠C′AC=60°，∴△ACC′为等边三角形，∴BC′=CC′=AC，∴∠B=∠C′AB=30°，∴∠BDC′=∠C′AB+∠AC′B′=90°，即B′C′⊥AB，∴BC′=2C′D，∴BC=B′C′=4C′D，∴C′D：DB′=1：3．19．解答：解：根据题意得：AD=1，AB=3，AC==6，∵∠A=∠A，∴若△ADE∽△ABC时，，即：，解得：AE=2，若△ADE∽△ACB时，，即：，解得：AE=，∴当AE=2或时，以点A、D、E为顶点的三角形与△ABC相似．故答案为：2或．20．解答：解：∵在Rt△ABC中（∠C=90°），放置边长分别3，4，x的三个正方形，∴△CEF∽△OME∽△PFN，∴OE：PN=OM：PF，∵EF=x，MO=3，PN=4，∴OE=x﹣3，PF=x﹣4，∴（x﹣3）：4=3：（x﹣4），∴（x﹣3）（x﹣4）=12，即x2﹣4x﹣3x+12=12，∴x=0（不符合题意，舍去），x=7．21解答：解：∵DE=2AE，BF=2FC，∴BF=2AE，ED=2CF，即有△AHE∽△FHB，△CFG∽△EGD，则=，同理=∴S△BFH=S△ABF=×××S▱ABCD，S△CFG=S△CFD=×S▱ABCD，故S四边形EHFG=S△BCE﹣S△BFH﹣S△CFG=S▱ABCD﹣S▱ABCD S▱ABCD=S▱ABCD．故答案为：22．解答：解：∵△ABC是边长为1的等边三角形，∴△ABC的高=AB•sinA=1×=，∵DE、EF是△ABC的中位线，∴AF=，∴S1=××=；同理可得，S2=×；…∴S n=×（）n﹣1；∴S2013=×（）2012=．故答案为：．解答：1．解答：答：BF是FG，EF的比例中项．证明：∵BE∥AC，∴∠1=∠E，∵∠1=∠2，∴∠2=∠E，∴△BFG∽△EFB，∴=，即BF2=FG•EF，2解答：（1）证明：∵梯形ABCD，AB∥CD，∴∠CDF=∠G，∠DCF=∠GBF，（2分）∴△CDF∽△BGF．（3分）（2）解：由（1）△CDF∽△BGF，又∵F是BC的中点，BF=FC，∴△CDF≌△BGF，∴DF=GF，CD=BG，（6分）∵AB∥DC∥EF，F为BC中点，∴E为AD中点，∴EF是△DAG的中位线，∴2EF=AG=AB+BG．∴BG=2EF﹣AB=2×4﹣6=2，∴CD=BG=2cm．（8分）3．解答：证明：（1）∵AB=AC，∴∠ABC=∠ACB，∵DE∥BC，∴∠ABC+∠BDE=180°，∠ACB+∠CED=180°．∴∠BDE=∠CED，∵∠EDF=∠ABE，∴△DEF∽△BDE；（2）由△DEF∽△BDE，得．∴DE2=DB•EF，由△DEF∽△BDE，得∠BED=∠DFE．∵∠GDE=∠EDF，∴△GDE∽△EDF．∴，∴DE2=DG•DF，∴DG•DF=DB•EF．4．解答：（1）证明：∵ABCD为正方形，∴AD=AB=DC=BC，∠A=∠D=90°，∵AE=ED，∴，∵DF=DC，∴，∴△ABE∽△DEF；（2）解：∵ABCD为正方形，∴ED∥BG，∴，又∵DF=DC，正方形的边长为4，∴ED=2，CG=6，∴BG=BC+CG=10．5．解答：解：图中的相似三角形有：△AMF∽△BGM，△DMG∽△DBM，△EMF∽△EAM （3分）以下证明△AMF∽△BGM．∵∠AFM=∠DME+∠E（外角定理），∠DME=∠A=∠B（已知），∴∠AFM=∠DME+∠E=∠A+∠E=∠BMG，∠A=∠B，∴△AMF∽△BGM．（7分）6．解答：解：CP和CB是对应边时，△CPQ∽△CBA，所以，=，即=，解得t=4.8；CP和CA是对应边时，△CPQ∽△CAB，所以，=，即=，解得t=．综上所述，当t=4.8秒或秒时，△CPQ与△CBA相似．7．解答：解：在△DEF和△DBC中，，∴△DEF∽△DBC，∴=，解得BC=4，∵AC=1.5m，∴AB=AC+BC=1.5+4=5.5m，即树高5.5m．8．解答：解：∵PE把梯形ABCD分成两个相似的小梯形，∴梯形ADEP∽梯形PECB，∴，∵AD=2，BC=，∴PE=3，∴相似比为：，∴AP=AB．9．解答：证明：设AB=2，∵P1是AB的黄金分割点（AP1＞BP1），∴AP1=×2=﹣1，∴P1B=2﹣（﹣1）=3﹣，∵点O是AB的中点，∴OB=1，∴OP1=1﹣（3﹣）=﹣2，∵P2是P1关于点O的对称点，∴P1P2=2（﹣2）=2﹣4，∴P2B=2﹣4+3﹣=﹣1，∵P1B2=（3﹣）2=14﹣6，P2B•P1P2=（﹣1）（2﹣4）=14﹣6，∴P1B2=P2B•P1P2，∴P1B是P2B和P1P2的比例中项．10．解答：证明：∵DE∥BC，EF∥AB∴四边形DBFE是平行四边形，∴BD=EF，∵相似三角形的面积比等于对应边的平方比，∴，即=1∴．11．解答：解：（1）在Rt△ABC中，由AB=1，BC=，得AC==，∵以点C为圆心，CB为半径的弧交CA于点D；以点A为圆心，AD为半径的弧交AB于点E∴BC=CD，AE=AD，∴AE=AC﹣CD=；（2）∠EAG=36°，理由如下：∵FA=FE=AB=1，AE=，∴=，∴△FAE是黄金三角形，∴∠F=36°，∠AEF=72°，∵AE=AG，∴∠EAG=∠F=36°．12．解答：解：∵当x=0时，y=1，当y=0时，x=﹣2，∴OA=2，OB=1，∵∠AOB=∠AOP=90°，∴当OA：OB=OP：OA时，△AOP与△AOB相似，∴2：1=OP：2，解得OP=4，故有2个这样的P点为：（0，﹣4）或（0，4），AP==2．若△AOP≌△AOB，则AP=．解答：解：（1）∵AB=5，BC=3，AC=4，∴BC2+AC2=AB2，∴∠C=90°，设AB边上的高为h，则×3×4=×5h，∴h=，∵PQ∥AB，∴△CQP∽△CBA，∴====，∵AB=5，BC=3，AC=4，∴CQ=，CP=1，PQ=，∴△CPQ的周长CQ+CP+PQ=+1+=3；（2）∵△CPQ的周长与四边形PABQ的周长相等，∴CP+CQ+PQ=BQ+PQ+PA+AB=（AB+BC+AC）=6，∵AB=5，BC=3，AC=4，∴CP+CQ=3﹣CQ+4﹣CP+5，2CQ+2CP=12，CQ+CP=6，∵PQ∥AB，∴△PQC∽△ABC．∴=，即=，解得：CP=．解答：解：（1）A；（2分）（2）①相似比②相似比的平方③相似比的立方；（每空（2分），共6分）（3）由题意知他的体积比为；又因为体重之比等于体积比，若设初三时的体重为xkg，则有=解得x==60.75．答：初三时的体重为60.75kg．（2分）15．解答：解：（1）当点P在AC上时，∵AM=t，∴PM=AM•tan60°=t．∴y=t•t=t2（0≤t≤1）．当点P在BC上时，PM=BM•tan30°=（4﹣t）．y=t•（4﹣t）=﹣t2+t（1≤t≤3）．（2）∵AC=2，∴AB=4．∴BN=AB﹣AM﹣MN=4﹣t﹣1=3﹣t．∴QN=BN•tan30°=（3﹣t）．由条件知，若四边形MNQP为矩形，需PM=QN，即t=（3﹣t），∴t=．∴当t=s时，四边形MNQP为矩形．（3）由（2）知，当t=s时，四边形MNQP为矩形，此时PQ∥AB，∴△PQC∽△ABC．除此之外，当∠CPQ=∠B=30°时，△QPC∽△ABC，此时=tan30°=．∵=cos60°=，∴AP=2AM=2t．∴CP=2﹣2t．∵=cos30°=，∴BQ=（3﹣t）．又∵BC=2，∴CQ=2．∴，．∴当s或s时，以C，P，Q为顶点的三角形与△ABC相似．解答：解：（1）如图：割线CD就是所求的线段．理由：∵∠B=∠B，∠CDB=∠ACB=90°，∴△BCD∽△ACB．（2）①△DEF经N阶分割所得的小三角形的个数为，∴S n=．当n=5时，S5=≈9.77，当n=6时，S6=≈2.44，当n=7时，S7=≈0.61，∴当n=6时，2＜S6＜3．②S n2=S n﹣1×S n+1．17．解答：解：设直角三角形ABC的三边BC、CA、AB的长分别为a、b、c，则c2=a2+b2（1）S1=S2+S3；（2）S1=S2+S3．证明如下：显然，S1=，S2=，S3=∴S2+S3==S1，即S1=S2+S3．（3）当所作的三个三角形相似时，S1=S2+S3．证明如下：∵所作三个三角形相似∴∴=1∴S1=S2+S3；（4）分别以直角三角形ABC三边为一边向外作相似图形，其面积分别用S1、S2、S3表示，则S1=S2+S3．解答：解：（1）∵FD∥BC∴△ADF∽△ABC．∴=．∴=．∴FD=2.1（cm）．答：小视力表中相应“E”的长是2.1cm；（2）解：作CD⊥MM′，垂足为D，并延长交A′B′于E，∵AB∥MM′∥A′B′，∴CE⊥A′B′，∴△CMM′∽△CA′B′，∴=，又∵CD=CE﹣DE=5﹣3=2，CE=5，A′B′=AB=0.8，∴=，∴MM′=0.32（米），∴镜长至少为0.32米．19．解答：解：∵AC=12，BC=5，∴AB=13，如图1所示：设DE=x，∵四边形ADEF是菱形，∴DE∥AB，∴△CDE∽△CAB，∴=，即=，解得x=cm；如图2所示，同上可知△CEF∽△CAB，设EF=x，∴=，解得x=cm；如图3所示，同理△AEF∽△ABC，∴=，即=，解得x=cm．故所作菱形的边长为：cm、cm、cm．。
相似三角形典型例题精选
相似三角形的判定与性质综合运用经典题型考点一：相似三角形的判定与性质：例1、如图，△PCD 是等边三角形，A 、C 、D 、B 在同一直线上，且∠APB=120°. 求证：⑴△PAC ∽△BPD ；⑵ CD 2 =AC ·BD.例2、如图,在等腰△ABC 中, ∠BAC=90°,AB=AC=1,点D 是BC 边上的一个动点(不与B 、C 重合），在AC 上取一点E ，使∠ADE=45°（1）求证：△ABD ∽△DCE ；（2）设BD=x ，AE=y ，求y 关于x 函数关系式及自变量x 值X 围，并求出当x 为何值时AE 取得最小值？（3）在AC 上是否存在点E ，使得△ADE 为等腰三角形？若存在，求AE 的长；若不存在，请说明理由？例3、如图所示，在平行四边形ABCD 中，过点A 作AE ⊥BC ，垂足为E ，连接DE ，F 为线段DE 上一点，且∠AFE=∠B ：1）求证：△ADF ∽△DEC ；2）若AB=4，33 AD ,AE=3，求AF 的长。
A BC DF考点二：射影定理：例4、如图，在Rt ΔABC 中，∠ACB=90°,CD ⊥AB 于D ，CD=4cm,AD=8cm,求AC 、BC 及BD 的长。
例5、如图，已知正方形ABCD ，E 是AB 的中点，F 是AD 上的一点，且AF=14AD ，EG ⊥CF 于点G ，（1）求证：△AEF ∽△BCE ； （2）试说明：EG 2=CG ·FG.例6、已知：如图所示的一X 矩形纸片ABCD （AD>AB ），将纸片折叠一次，使点A 与点C 重合,再展开，折痕EF 交AD 边于E ，交BC 边于F ，分别连结AF 和CE ．（１）求证：四边形AFCE 是菱形；（２）若AE=10cm ，△ABF 的面积为24cm 2，求△ABF 的周长；（３）在线段AC 上是否存在一点P ，使得2AE 2＝AC ·AP ？若存在，请说明点P 的位置，并予以证明；若不存在，请说明理由．A B C D EFG考点三：相似之共线线段的比例问题：例7、已知如图，P 为平行四边形ABCD 的对角线AC 上一点，过P 的直线与AD 、BC 、CD 的延长线、AB 的延长线分别相交于点E 、F 、G 、H. 求证：PG PH PF PE例8、如图，点P 是菱形ABCD 的对角线BD 上一点，连接CP 并延长，交AD 于点E ，交BA 的延长线于点F ．（1）求证：PC 2=PE •PF ；（2）若菱形边长为8，PE=2，EF=6，求FB 的长．例9、如图，CD 是Rt △ABC 斜边上的高，E 为AC 的中点，ED 交CB 的延长线于F ． 求证：BD •CF=CD •DF ．例10、如图：已知在等边三角形ABC 中，点D 、E 分别是AB 、BC 延长线上的点，且BD=CE ，直线CD 与AE 相交于点F ．（1）求证：DC=AE ；（2）求证：AD 2=DC •DF ．例11、如图，E 是矩形ABCD 的边BC 上一点，EF ⊥AE ，EF 分别交AC ，CD 于点M ，F ，BG⊥AC，垂足为G，BG交AE于点H．（1）找出与△ABH相似的三角形，并证明；（2）若E是BC中点，BC=2AB，AB=2，求EM的长．例12、如图，四边形ABCD、DEFG都是正方形，连接AE、CG，AE与CG相交于点M，CG与AD相交于点N．求证：（1）AE=CG；（2）AN•DN=•MN．例13、如图，在Rt△ABC中，CD是斜边AB上的高，点M在CD上，DH⊥BM且与AC 的延长线交于点E．求证：（1）△AED∽△CBM；（2）AE•CM=AC•CD．例14、如图，△ABC是直角三角形，∠ACB=90°，CD⊥AB于D，E是AC的中点，ED 的延长线与CB的延长线交于点F．（1）求证：FD2=FB•FC；（2）若G是BC的中点，连接GD，GD与EF垂直吗？并说明理由．例15、如图，四边形ABCD、CDEF、EFGH都是正方形.(1)⊿ACF与⊿ACG相似吗？说说你的理由.(2)求∠1+∠2的度数.考点四：相似三角形的实际应用：例16、如图，△ABC是一块锐角三角形余料，边BC=120mm，高AD=80mm，要把它加工成矩形零件，使一边在BC上，其余两个顶点分别在边AB、AC上．（1）若这个矩形是正方形，那么边长是多少？（2）若这个矩形的长PQ是宽PN的2倍，则边长是多少？例17、已知左，右并排的两棵大树的高分别是AB=8m和CD=12m，两树的根部的距离BD=5m。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实用标准文案
精彩文档
相似三角形知识点与经典题型
知识点1 有关相似形的概念
(1)形状相同的图形叫相似图形，在相似多边形中，最简单的是相似三角形.
(2)如果两个边数相同的多边形的对应角相等，对应边成比例，这两个多边形叫做相似多
边形．相似多边形对应边长度的比叫做相似比(相似系数)．知识点2 比例线段的相关概念
（1）如果选用同一单位量得两条线段
b a,的长度分别为n m,，那么就说这两条线段的比是
n
m b
a ，
或写成n m b a ::．注：在求线段比时，线段单位要统一。
（2）在四条线段d c b a ,,,中，如果b a 和的比等于d c 和的比，那么这四条线段d c b a ,,,叫做成比例线段，简称比例线段．
注：①比例线段是有顺序的，如果说
a 是d c
b ,,的第四比例项，那么应得比例式为：
a
d c
b ．
②()a c a b
c d b
d 在比例式
：：中，a 、d 叫比例外项，b 、c 叫比例内项, a 、c 叫比例前项，b 、
d 叫比例后项，d 叫第四比例项，如果b=c ，即a b b d ：：那么b 叫做a 、d 的比例中项，此时
有2
b ad 。
（3）黄金分割：把线段AB 分成两条线段)(,BC AC BC AC ，且使AC 是BC AB 和的比例中项，即2
AC
AB BC ，叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点，其中AB
AC
2
1
5≈0.618AB ．即
512
AC BC AB
AC
简记为：
51
2
长短＝＝全长注：黄金三角形：顶角是360
的等腰三角形。
黄金矩形：宽与长的比等于黄金数的矩形
知识点3 比例的性质（注意性质立的条件：分母不能为
0）
（1）基本性质：
①bc ad d c b a ::；②2
::a b b c b a c ．
注：由一个比例式只可化成一个等积式，而一个等积式共可化成八个比例式，如bc ad ，除
了可化为d c b a ::，还可化为d b c a ::，b a d c ::，c a d b ::，c d a b ::，b d a c ::，a b c d ::，a c b d ::．
（2）更比性质(交换比例的内项或外项)：()()
()a b
c d
a c d c
b d b a
d b
c a ，交换内项，交换外项．同时交换内外项（3）反比性质(把比的前项、后项交换)：
a c
b d b
d
a
c
．。