小学奥数(学而思讲义)
三年级学而思奥数讲义

三年级学而思奥数讲义学而思奥数作为一门培养孩子数学思维和解题能力的课程,为三年级的学生提供了更广阔的数学发展空间。
下面将对三年级学而思奥数课程的内容进行介绍,帮助孩子们更好地理解和应用数学。
一、思维培养学而思奥数注重培养孩子的数学思维能力,通过课程设计和题目训练,培养学生的逻辑思维、创造思维和问题解决能力。
在三年级的课程中,学生将接触到一些有趣的数学题目,例如数独、迷宫等,以此激发他们对数学问题的兴趣,同时提高他们的逻辑思维和推理能力。
二、数学知识点在三年级学而思奥数讲义中,包含了一系列的数学知识点。
例如,学生将学习整数的概念和运算规律,了解到整数的正负和绝对值。
同时,他们还会学习到分数的相关知识,包括分数的大小比较、分数的加减乘除等。
此外,几何图形的认识和计算也是三年级奥数的重点内容,学生将学习到平面几何和立体几何的基本概念,如长方形、正方形、圆等。
三、应用能力展示学而思奥数注重培养学生的应用能力,即将所学的数学知识应用到实际问题中。
三年级学而思奥数讲义会通过一些实际生活中的问题,如选购食材、算账等,让学生应用所学的数学知识和技巧解决问题。
这样的训练能够培养学生的数学思维和解决实际问题的能力,提高他们的数学应用水平。
四、趣味性培养学而思奥数注重培养学生对数学的兴趣和热爱。
在三年级学而思奥数讲义中,通过一些趣味的数学游戏和趣味题目,激发学生的求知欲和好奇心。
例如,谜题、魔方等,这些富有趣味性的内容能够让学生更加主动地投入到数学学习中,提高学习的积极性和主动性。
五、知识拓展除了三年级学而思奥数讲义中的基础知识之外,还有一些拓展内容供学生学习。
这些拓展内容包括数学奥赛题、高年级数学的预习等,帮助学生扩展数学知识面,提高数学素养和综合应用能力。
对于有特长或对数学感兴趣的学生而言,这些拓展内容能够提供更多的挑战和学习机会。
总结起来,在三年级学而思奥数课程中,学生将通过对数学思维的培养、数学知识点的学习、应用能力的展示、趣味性的培养以及知识的拓展等方面来提高自己的数学素养和解题能力。
学而思小学奥数知识点梳理大纲视图

学而思小学奥数知识点梳理学而思教材编写组侍春雷前言小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③连除的性质④同级运算移项的性质⑤增减括号的性质⑥变式提取公因数形如:3.估算求某式的整数部分:扩缩法4.比较大小①通分a. 通分母b. 通分子②跟“中介”比③利用倒数性质若,则c>b>a.。
形如:,则。
5.定义新运算6.特殊数列求和运用相关公式:①②③④⑤⑥⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n 二、数论1.奇偶性问题奇奇=偶奇×奇=奇奇偶=奇奇×偶=偶偶偶=偶偶×偶=偶2.位值原则形如:=100a+10b+c3.数的整除特征:整除数特征2 末尾是0、2、4、6、83 各数位上数字的和是3的倍数5 末尾是0或59 各数位上数字的和是9的倍数11 奇数位上数字的和与偶数位上数字的和,两者之差是11的倍数4和25 末两位数是4(或25)的倍数8和125 末三位数是8(或125)的倍数7、11、13 末三位数与前几位数的差是7(或11或13)的倍数4.整除性质①如果c|a、c|b,那么c|(a b)。
学而思小学奥数知识点梳理解读

学而思小学奥数知识点梳理概述一、计算1.四则混合运算繁分数⑴运算顺序⑵分数、小数混合运算技巧一般而言:①加减运算中,能化成有限小数的统一以小数形式;②乘除运算中,统一以分数形式。
⑶带分数与假分数的互化⑷繁分数的化简 2.简便计算⑴凑整思想⑵基准数思想⑶裂项与拆分⑷提取公因数⑸商不变性质⑹改变运算顺序①运算定律的综合运用②连减的性质③连除的性质④同级运算移项的性质⑤增减括号的性质⑥变式提取公因数形如:1212...... (...... n n a b a b a b a a a b ÷±÷±±÷=±±±÷3.估算求某式的整数部分:扩缩法 4.比较大小①通分a. 通分母b. 通分子②跟“中介”比③利用倒数性质若111a b c >>,则c>b>a.。
形如:312123m m m n n n >>,则312123n n nm m m <<。
5.定义新运算6.特殊数列求和运用相关公式:①(21321+=++n n n ②((612121222++=+++n n n n③(21n a n n n n =+=+ ④((412121222333+=++=+++n n n n ⑤131171001⨯⨯⨯=⨯=abc abc abcabc ⑥((b a b a b a -+=-22 ⑦1+2+3+4…(n-1)+n+(n-1)+…4+3+2+1=n2二、数论1.奇偶性问题奇±奇=偶奇×奇=奇奇±偶=奇奇×偶=偶偶±偶=偶偶×偶=偶2.位值原则形如:abc =100a+10b+c4.整除性质①如果c|a、c|b,那么c|(a±b 。
②如果bc|a,那么b|a,c|a。
③如果b|a,c|a,且(b,c )=1,那么bc|a。
学而思网校小学奥数(一年级)

我会比一比推理比较图形的折叠我会算一算——加法数学活动我会算一算——减法你能把下面的加法算式改成道加法算式和两道减法算式吗?你能把下面的加法算式改成一道加法算式和两道减法算式吗小动物教你学减法,一起来练一练。
小猫钓鱼算出小鱼身上算式的结果小鱼就被钓上来啦!比一比小猫钓鱼,算出小鱼身上算式的结果小鱼就被钓上来啦!比比,看谁钓的又快又多!每只小动物的车应该停在几号停车场呢?连一连。
聪明的小朋友们,你能在一分钟内口算出下面各题吗?我们来比赛吧!吗?请画出找球的线路。
生活中的数学小老虎在和小牛捉迷藏,小老虎只有从1开始按每次多2的数字往前走才能找到小牛小朋友们试试小牛。
小朋友们试一试。
小朋友们,学习了20以内加减法的计算大家都成了计算小能手的计算,大家都成了计算小能手了。
你知道加减法有什么用途呢?利用加减法可以解决生活中的许利用减可解决中的许多数学问题,这节课我们就一起看图来解决问题。
⑴根据下面的图写算式⑴根据下面的图写算式。
⑵根据下面的图写算式⑵根据下面的图写算式。
说一说每个图表示什么意思然后写出算式说说每个图表示什么意思,然后写出算式。
看图填空,并列出算式。
⑴⑵聪明的小朋友,你知道下面每幅图的意思吗?请你根据图意写出算式。
⑴原来有11只兔子。
我已经卖出去了5只。
还剩下几只没有卖出去?棵花还有棵没有栽已经栽了多少棵了?⑵一共要栽14棵花。
还有4棵没有栽。
已经栽了多少棵了?你能根据下面的图列出算式吗?⑴⑵原来车上有15人。
草地上原来有15只白兔子和7只灰兔子,后来又跑来了4只灰兔子,跑走了5只白兔子。
你能跟据下面不同的问题列出不同的算式吗?⑴草地上原来共有几只兔子?⑵草地上现在有几只白兔子?⑶草地上现在有几只灰兔子?比一比,算一算。
⑴小明折了多少架纸飞机?12个同学排成一队去游玩,小明的后面有3个同学,他的前面有几个同学?钟面上的数学钟面上有时针、分针和12个数字。
短而粗的是时针,长而细的是分针。
钟面上把一圈平均分成12个大格,每个大格又分成相等的5个小格,分针走一圈是分钟;时针走一圈是分针走圈是60分钟;时针走圈是12小时。
学而思小学六年级奥数教师讲义版工程问题精编版.doc

例4一批零件,张师傅独做20时完成,王师傅独做30时完成。如果两人同时做,那么完成任务时张师傅比王师傅多做60个零件。这批零件共有多少个?
分析与解: 这道题可以分三步。首先求出两人合作完成需要的时间,
例5一水池装有一个放水管和一个排水管, 单开放水管5时可将空池灌满, 单开排水管7时可将满池水排完。如果一开始是空池, 打开放水管1时后又打开排水管, 那么再过多长时间池内将积有半池水?
例6甲、乙二人同时从两地出发, 相向而行。走完全程甲需60分钟,乙需40分钟。出发后5分钟,甲因忘带东西而返回出发点,取东西又耽误了5分钟。甲再出发后多长时间两人相遇?
分析:这道题看起来像行程问题,但是既没有路程又没有速度,所以不能用时间、路程、速度三者
的关系来解答。甲出发5分钟后返回,路上耽误10分钟,再加上取东西的5分钟,等于比乙晚出发15
2
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
分钟。我们将题目改述一下:完成一件工作,甲需60分钟,乙需40分钟,乙先干15分钟后,甲、乙合干还需多少时间?由此看出,这道题应该用工程问题的解法来解答。
1.某工程甲单独干10天完成,乙单独干15天完成,他们合干多少天才可完成工程的一半?
2.某工程甲队单独做需48天,乙队单独做需36天。甲队先干了6天后转交给乙队干,后来甲队重新回来与乙队一起干了10天,将工程做完。求乙队在中间单独工作的天数。
3.一条水渠,甲、乙两队合挖需30天完工。现在合挖12天后,剩下的乙队单独又挖了24天挖完。这条水渠由甲队单独挖需多少天?
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新 料推荐⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
学而思-第四讲-长方体和正方体
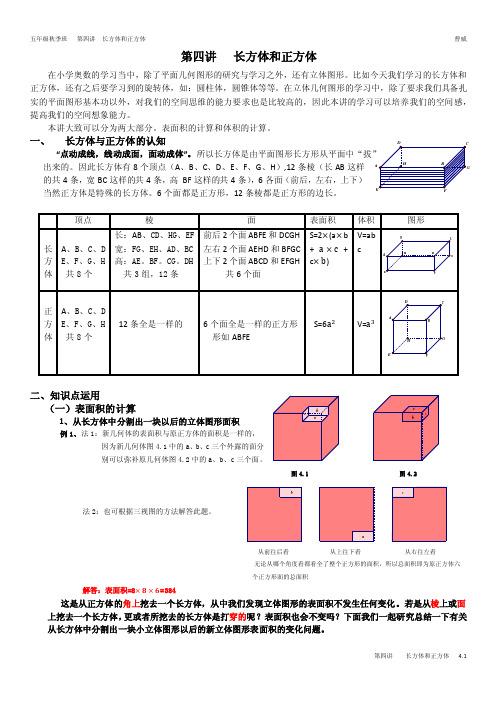
小的长方体 60块 ,那么这 60块长方体表面积的总和是 多少平方米?答案: 96平方米
(2)三个小正方体拼成如图右所示,表面积比原来少了 100平方厘米,求这个图形的体积?
答案:375立 方厘米
3、堆积体的 表面积问题 对于 由若干个小正方体堆积而成的不规则 立体图形的表面积,只要掌握“三视 图”的这个法宝即可 。
比原来正方体的总面积多两个 AEFB 的面积。
解答:表面积=8
+(2 ) =396
(2)如图 4.4 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的几何体, 求该几何体的表面积?
分析:由图 4.4 可知,挖去后新几何体中的 BFHC 面可弥补原正方体的 AEGD 面。此时已经构成了原正方体的 6 个
2 个 AEFB 面,上下面则没有发生变化,( EHGF 面可弥补 ABCD 面)。因此,新几何体的表面积总体来说比
原来正方体的总面积少了 2 个 AEHD 面而多了 2 个 AEFB 面。
解答:表面积=8
-(2 ) +(2 ) =400
(5)如图 4.7 从棱长为 8 的正方体的面上挖去一个 2
的长方体形成一个新的 几何体,求该几何体的表面积?
分析:由图 4.7 可知,新几何体的前后两个面比原来的正方体前后面也是共少了 2 个 AEHD 面,而左右面共多了
2 个 AEFB 面,上下面也多了 2 个 EHGF 面。因此,新几何体的表面积总体来说比原来正方体的总面积少了
2 个 AEHD 面而多了 4 个内壁面积(2 个 AEFB+2 个 EHGF)。
体有几个。答案:8块 (此题为1层的长方体)
第四讲 长方体和正方体 4.4
五年级秋季班 第四讲 长方体和正方体
学而思四年级奥数暑期班讲义 (7)

2
【例5】(★★★★)
【超常大挑战】(★★★★)
四张卡片上分别写着奥、林、匹、克四个字(一张上写一个字),取出三 张朝下放在桌上,A、B、C三人分别猜每张卡片上是什么字,猜的情 况见下表:
在一所学校里,有穿绿、黑、青、白、紫五种不同运动服的五支运动 队参加长跑比赛,其中,有A、B、C、D、 E五位小学生猜比赛者的 名次,条件是每个小学生只准猜两支运动队的名次.
板块二:假设法 【例4】(★★★)
传说有个说谎国,这个国家的男人在星期四、五、六、日说真话,在 星期一、二、三说假话;女人在星期一、二、三、日说真话,在星期 四、五、六说假话。有一天,一个人到说谎国去旅游,他在那里认识 了一男一女。男人说:“昨天我说的是假话”,女人说:“昨天也是 我说假话的日子”。这下,那个外来的游人可发愁了,到底今天星期 几呢?请同学们根据他们说的话,判断今天是星期几?
第一张 第二张 第三张
学生 A猜:紫队第二,黑队第三.
A林
奥
克
学生 B猜:青队第二,绿队第四.
B林
匹
克
学生 C猜:绿队第一,白队第五.
C匹
奥பைடு நூலகம்
林
学生 D猜:青队第三,白队第四.
结果,有一人一张也没有猜对,一人猜对两张,另一人猜对三张.问:
学生 E猜:黑队第二,紫队第五.
这三张卡片上个写着什么字?
在这五名同学猜完后发现每人都只猜对了一个队的名次,请判断一下,
【例3】(★★★) 甲、乙、丙在2012年高考中考取了北大,清华和理工大学的数学系, 物理系和化学系,现知道下列情况 ⑴ 甲不在北大 ⑵ 乙不在清华 ⑶ 在北大的不学数学 ⑷ 在清华的学物理 ⑸ 乙不学化学 根据以上情况判断甲、乙、丙三人各在哪个学校?哪个系?
小学奥数(学而思讲义)

【分析】 设11112005200620072008a +++=,则 114420082004a ´<<´,所求数1111110111219+++ 的整数部分是几? [分析] 11111111111110101112191010101010>==++++++ 111 1.91111111110101112191919191919<==++++++ 即1<原式<1.9,所以原式的整数部分是1. (第四届2试试题)若11111a =,1111111b =,111111111c =,则a ,b ,c 中最大的是________,最小的是________.【分析】 此题比较方法很多,方法之一倒数法:111011a =,1110111b =,11101111c =,111a b c>>,即a b c <<(第六届2试试题)(10.120.23)(0.120.230.34)(10.120.230.34)(0.120.23)++´++-+++´+=______.【分析】 换元的思想即“打包”,令0.120.23a =+,0.120.230.34b =++,原式(1)(1)a b b a =+´-+´b a =-=0.34(第六届五年级2试试题)计算下面的算式(7.88 6.77 5.66++)´(9.3110.9810++)-(7.88 6.77 5.6610+++)´(9.3110.98+) [分析] 换元的思想即“打包”,令7.88 6.77 5.66a =++,9.3110.98b =+,则原式a =´(10b +)-(10a +)b ´=(10ab a +)-(10ab b +)101010ab a ab b =+--=´(a b -) 10=´(7.88 6.77 5.669.3110.98++--)100.020.2=´=(第五届2试试题)111112005200620072008+++的整数部分是 以20081200450250144a =>>= 所以整数部分是501(第三届华杯赛复赛试题)(祖冲之杯数学邀请赛)如果222221333331,222223333334A B ==,那么A 和B 中较大的数是 .[分析] 222221666663666662333331222223666669666668333334A B ==>==, 即A 大(希望杯培训题)计算:11111111112345678910612203042567290110+++++++++= 【分析】 原式11112310612110=++++++++1115523341011=++++´´´ 1155211=+-已知三位数abc 如上,三位数abc 与它的反序数cba 的和能否等于999?如果和等于989,这样的三位数有 个.【分析】 否,十位29b ¹;和等于989,4b =,a 、c 的情况有1+8、2+7、3+6、4+5、5+4、6+3、7+2、8+1这7种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(第六届2试试题)
(10.120.23)(0.120.230.34)(10.120.230.34)(0.120.23)++⨯++-+++⨯+=______. 【分析】 换元的思想即“打包”,令0.120.23a =+,0.120.230.34b =++,
原式(1)(1)a b b a =+⨯-+⨯
b a =-
=0.34
(第六届五年级2试试题)计算下面的算式
(7.88 6.77 5.66++)⨯(9.3110.9810++)-(7.88 6.77 5.6610+++)⨯(9.3110.98+) [分析] 换元的思想即“打包”,令7.88 6.77 5.66a =++,9.3110.98b =+,
则
原
式
a =⨯(10
b +)-(10a +)b ⨯=(10ab a +)-(10ab b +)101010ab a ab b =+--=⨯(a b -)
10=⨯(7.88 6.77 5.669.3110.98++--)100.020.2=⨯=
(第五届2试试题)
1
1111
2005200620072008
+++
的整数部分是
【分析】 设
1111
2005200620072008a +++=,则 11
4420082004
a ⨯<<⨯,所以200812004
50250144
a =
>>= 所以整数部分是501
(第三届华杯赛复赛试题)求数
1
1111101112
19
+++的整数部分是几?
[分析]
1
1
1
11111111110101112
19101010
1010>=
=++++++ 1
1
1
1.91111111110101112
19
191919
1919
<=
=++++++
即1<原式<1.9,所以原式的整数部分是1.
(第四届2试试题)
若11111
a =
,1111111b =,111111111c =,则a ,b ,c 中最大的是________,最小的是
________.
【分析】 此题比较方法很多,方法之一倒数法:
111011a =,1110
111b =,11
101111
c =,111
a b c
>>,即a b c <<
(祖冲之杯数学邀请赛)如果222221333331
,222223333334
A B ==
,那么A 和B 中较大的数是 .
[分析] 222221666663666662333331
222223666669666668333334
A B =
=>==,
即A 大
(希望杯培训题)计算:111111111
12345678910612203042567290110
+++++++++=
【分析】 原式111
12310612110
=++++++++
111
5523341011=++++
⨯⨯⨯ 1155211=+-
95522
=
(第二届2试试题)某年4月所有星期六的日期数之和是54,这年4月的第一个星期六的日期数是_______.
【分析】 因为一个月可以有4个或5个星期六,当某年4月有5个星期六时,设第一个星期
六日期为a ,列方程得(7)(14)(21)(28)54a a a a a ++++++++=,即57054a +=,符合题意的a 不存在
当某年4月有4个星期六时,设第一个星期六日期为a ,列方程得
(7)(14)(21)54a a a a ++++++=,即44254a +=,解得3a =
某年4月所有星期六的日期数之和是80,这年4月的第一个星期六的日期数是_______. [分析] 因为一个月可以有4个或5个星期六,当某年4月有5个星期六时,设第一个星期
六日期为a ,列方程得(7)(14)(21)(28)80a a a a a ++++++++=,即57080a +=,解得2a =
当某年4月有4个星期六时,设第一个星期六日期为a ,列方程得
(7)(14)(21)80a a a a ++++++=,即44280a +=,符合题意的a 不存在
有没有所有星期六日期数之和为90的呢(答案是不存在)
(第六届2试试题)已知三位数abc 与它的反序数cba 的和等于888,这样的三位数有______个.
【分析】 显然a c +、b b +都没有发生进位,所以8a c +=、8b b +=,则4b =,a 、c 的
情况有1+7、2+6、3+5、4+4、5+3、6+2、7+1这7种.所以这样的三位数有7种.
如上,三位数abc 与它的反序数cba 的和能否等于999?如果和等于989,这样的三位数有
个.
【分析】 否,十位29b ≠;和等于989,4b =,a 、c 的情况有1+8、2+7、3+6、4+5、
5+4、6+3、7+2、8+1这7种。
(第三届2试试题)右图中的“我爱希望杯”有______种不同的读法
.
杯杯杯杯杯
望望望望希
希希爱爱
我16
1511353211111111
杯杯杯杯杯望望
望望
希希希爱爱我
【分析】 “我爱希望杯”的读法也就是从“我”走到“杯”的方法.如上右图所示,共16种方法. (教师可以根据本班情况适当铺垫标数法计数最短路线问题)。
