哈工大威海实际力学试题及答案
高考物理威海力学知识点之理想气体难题汇编含答案
高考物理威海力学知识点之理想气体难题汇编含答案一、选择题1．如图所示，长L＝34 cm的粗细均匀的长直玻璃管竖直放置，上端开口，用长h=15 cm 的水银将一定质量的气体封闭在管的下端，稳定后气体长度l=10 cm。
已知外界大气压p0=75cmHg，现保持温度不变的情况下从管的上端开口处缓慢加入水银，则加入水银的最大长度为A．9 cmB．10 cmC．14 cmD．15 cm2．在射向高空的火箭仪器舱内，起飞前用水银气压计测舱内气体的压强P0=76cmHg，气体温度T0=300K，仪器舱是密封的。
取竖直向上为正方向，当火箭以加速度a竖直方向运动时，仪器舱内水银气压计指示的压强为P=0.6P0，则( )A．a=g，舱内气体温度比起飞前温度增加20%B．a=g，舱内气体温度是起飞前温度的0.6倍C．a=12g，舱内气体温度比起飞前温度增加10%D．a=-12g，舱内气体温度比起飞前温度降低10%3．如图所示为一定质量的某种理想气体压强P与热力学温度T的变化关系图象，下列说法正确的是( )A．A→B压强不变，体积减小B．B→C温度不变，体积增大C．C→A温度降低，体积不变D．C→A压强减小，体积减小4．（3-3）一定质量的理想气体经历如图所示的一系列过程，ab、bc、cd和da这四段过程在p T图上都是直线段，ab和dc的延长线通过坐标原点O，bc垂直于ab，ad平行于纵轴，由图可以判断( )A．ab过程中气体体积不断减小,外界对气体做正功，气体内能减小B．bc过程中气体体积不断减小，外界对气体做正功，气体内能不变C．cd过程中气体体积不断增大，气体对外界做正功，气体内能增加D．da过程中气体体积不断增大，气体对外界做正功，气体内能不变5．一定质量的气体，在体积不变的情况下，温度由0 ℃升高到10 ℃时，其压强的增加量为Δp1，当它由100 ℃升高到110 ℃时，其压强的增加量为Δp2，则Δp1与Δp2之比是() A．1:1B．1:110C．10:110D．110:106．下列说法正确的是A．外界对气体做功，气体的内能一定增大B．气体从外界吸收热量，气体的内能一定增大C．气体的温度越低，气体分子无规则运动的平均动能越大D．温度一定，分子密集程度越大，气体的压强越大7．一定质量的理想气体，在温度不变的条件下，使其压强增大，则在这一过程中气体 ( ) A．从外界吸收了热量B．对外界做了功C．密度增大D．分子的平均动能增大8．氧气分子在不同温度下的速率分布规律如图所示，横坐标表示速率，纵坐标表示某一速率内的分子数占总分子数的百分比，由图可知()A．随着温度的升高，氧气分子中速率小的分子所占的比例增大B．随着温度的升高，每一个氧气分子的速率都增大C．①状态的温度比②状态的温度高D．同一温度下，氧气分子呈现“中间多，两头少”的分布规律9．下列说法正确的是（）A．一定质量的气体，当温度升高时，压强一定增大B．一定质量的气体，当体积减小压强一定增大C．一定质量的气体，当温度不变时,体积减小，压强一定增大D．一定质量的气体，当体积不变时,温度升高，压强一定减小10．一定质量的理想气体经历了如图所示的一系列过程，ab、bc、cd和da这四个过程在p ﹣T图上都是直线段，其中ab的延长线通过坐标原点O，bc垂直于ab而cd平行于ab，由图可以判断下列说法错误的是（）A．ab过程中气体体积不断减小B．bc过程中气体体积不断减小C．cd过程中气体体积不断增大D．da过程中气体体积不断增大11．如图所示，两端开口的均匀玻璃管竖直插入水银槽中，管中有一段水银柱（高为h1）封闭一定质量的气体，这时管下端开口处内、外水银面高度差为h2，若保持环境温度不变，当外界压强增大时，下列分析正确的是（）A．h2变长B．h2变短C．h1上升D．h1下降12．如图所示，一端开口，一端封闭的玻璃管，封闭端有一定质量的气体，开口端置于水银槽中，用弹簧测力计拉着玻璃试管而平衡，此时管内外水银面高度差为h1，弹簧测力计示数为F1．若在水银槽中缓慢地倒入部分水银，使槽内水银面升高一些，稳定后管内外水银面高度差为h2，弹簧测力计示数为F２，则（填选项前的字母）A．h1= h2，F1= F２B．h1 > h2，F1 > F２C．h1> h2，F1<F２D．h1< h2，F1> F２13．以下说法中正确的是A．分子力做正功，分子势能一定增大B．气体的压强是由气体分子间的吸引和排斥产生的C．分子间距离增大时，分子间的引力和斥力都减小D．绝对零度就是当一定质量的气体体积为零时，用实验方法测出的温度14．气体压强从微观角度看是大量气体分子频繁碰撞容器壁而产生的一个持续的压力效果。
2011-2012哈工大威海理论力学试题及答案
哈尔滨工业大学（威海）2011 / 2012 学年秋季学期理论力学试题卷（A）考试形式（开、闭卷）：闭卷答题时间：120（分钟）本卷面成绩占课程成绩 80 %一、填空题（每题6分，共30分）1、图示滚轮的半径为R ，轮心速度为v，加速度为a，沿水平直线作纯滚动，M点加速度的大小为。
2、图示匀质细杆各以匀角速度ω绕轴Ｏ转动。
已知：杆长为l，重为P。
惯性力系向转轴Ｏ简化，主矢的大小为，主矩的大小为。
3、如图所示，物块重P =150N，靠在粗糙的水平天花板上，物体间静滑动摩擦因数f s=0.3，动滑动摩擦因数f =0.2, 在物块上加一力F，且F =200N,θ=30°，摩擦力大小为。
教研室主任签字：姓名:班级：学号：遵守考试纪律注意行为4、如图所示结构受集中力P 作用，各杆自重不计。
则杆1的内力为 。
（须注明拉、压）5、如图所示，沿长方体的三个不相交且不平行的棱作用着3个大小相等的力F ，若力系简化为一合力，求棱a ,b ,c 的关系 。
二、计算题（10分）如图所示简支梁，不计梁的重量，在C 处作用一铅垂力P 。
试求支座B 处的约束力（要求用虚位移原理求解，用其它方法做不给分）。
遵守 考 试 纪 律注 意 行 为 规 范三、计算题（20分）如图所示，已知F ,a ,M=Fa ，各杆不计自重。
求：支座A 、D 处的约束力。
遵 守考 试 纪 律注 意 行 为 规 范四、计算题（20分）如图所示机构中，曲柄ＯA 长r ，以匀角速度ω0绕Ｏ轴转动，带动连杆AC 在套筒B 内滑动，套筒及与其固连的杆BD 可绕B 铰转动，BD 长l ，且垂直于AC 。
求在∠A ＯB = 90°,∠AB Ｏ = 30° 时，杆BD 上D 点的速度和加速度。
遵守 考 试 纪 律注 意 行 为 规 范五、计算题（20分）如图所示，在倾角为α的斜面上，有重为P 的小车与绳索相连，绳索绕定滑轮A 、动滑轮B 后与固定点C 相连。
理论力学复习试题和答案(哈工大版)
C ：作用于质点系的约束反力主矢恒等于零； D：作用于质点系的主动力主矢恒等于零；
..
..
6、 若作用在 A 点的两个大小不等的力 F 1 和 F 2，沿同一直
反。则其合力可以表示为
③
。
① F 1－ F 2； ② F 2－ F 1； ③ F 1＋ F 2；
7、 作用在一个刚体上的两个力 F A、 F B，满足 F A=－ F B 的条件，则该二力可能是②
（ √） （× ）
14、 已知质点的质量和作用于质点的力，质点的运动规律就完全确定。
（× ）
15、 质点系中各质点都处于静止时，质点系的动量为零。于是可知如果质点
系的动量为零，则质点系中各质点必都静止。
（×）
16、 作 用 在 一 个 物 体 上 有 三 个 力 ， 当 这 三 个 力 的 作 用 线 汇 交 于 一 点 时 ， 则 此 力 系 必 然 平 衡 。
..
..
..
..
2、图示平面结构，自重不计。 求支座 A 的约束反力。
B 处为铰链联接。已知： P = 100 kN ， M = 200 kN · m， L1 = 2m ， L2 = 3m 。试
3、 一 水平 简支梁 结 构， 约 束和载 荷如 图 所示 ， 求支座
q A
D
M B
E
P C
A和
B 的约束反力。
一、 是非题
1、 力 有 两 种 作 用 效 果 ， 即 力 可 以 使 物 体 的 运 动 状 态 发 生 变 化 ， 也 可 以 使 物 体 发 生 变 形 。
（ √）
2、 在理论力学中只研究力的外效应。
（ √）
3、 两端用光滑铰链连接的构件是二力构件。
17秋理论力学试题A
姓名: 班级: 学号:遵 守 考 试 纪 律 注意 行 为 规 范哈尔滨工业大学（威海）2017 / 2018 学年 秋 季学期理论力学 试题卷（A ）考试形式（开、闭卷）： 闭卷 答题时间：120 （分钟） 本卷面成绩占课程成绩 80 %一、填空题 （每题 6 分，共 30 分）1. 如图所示，沿长方体的三个棱作用着3个大小相等的力F ，在水平面作用有一力偶M=3Fb 。
若力系简化为一合力，则棱a ,b ,c 的关系应为。
2.如图所示，两物块A 和B 叠放在水平面上，A 物块通过不可伸长柔绳连接于铅垂墙面上。
物块A 重5 kN ，物块B 重2kN ，物块A 、B 之间的动摩擦因数为0.25，物块B 与固定水平面之间的静摩擦系数为0.1，则拉动物块B 所需力F 的最小值为 。
F3．如图所示桁架，在点G 作用有大小为F 的水平力，方向向右。
ABC 为等边三角形，D 、E 、G 分别为三边的中点，则杆ED 的内力ED F = ，杆BG 的内力BG F = 。
F4. 如图所示, 均质L 形刚杆的总质量为m ，在铅垂面内以角速度ω绕O 轴转动，OA=AB=l ，则它的动量为 ，对O 轴的动量矩为 。
wA5、图示均质圆盘，半径为R ，质量为m ，可在铅垂面内绕轴O 转动。
若突然将绳HE 剪断，此时角加速度为α。
则剪断瞬间惯性力向其质心简化的主矢大小F IC = ，主矩大小M IC = 。
a二、 计算题 （15分）结构由AB 、BC 和CD 三部分组成，所受载荷及尺寸如图所示，各部分自重不计，求A ，D 和E 处的约束反力。
（15分）A三、计算题（15分）图示平面机构中，轮A在固定平面上纯滚动，半径R=3cm，杆AB长15 cm。
杆AB通过套筒与轴O相连，AB与轮A通过铰链相连。
角度θ=60o时，轮A的角速度ωA=5 rad/s，角加速度αA=103rad/ s2。
求该瞬时B点的速度和加速度。
（15分）ω四、计算题（20分）如图所示铅直平面内，轮A和轮B为均质圆盘，轮A半径为R，质量为m，轮B半径均为2R，质量均为2m，一均质板C水平放置在两个轮上，质量为m。
哈工大理论力学期末考试及答案
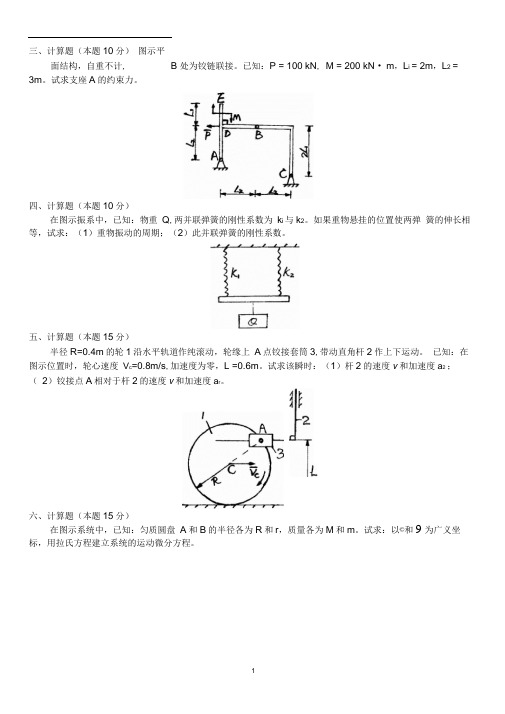
三、计算题（本题10分）图示平面结构，自重不计,3m。
试求支座A的约束力。
四、计算题（本题10分）在图示振系中，已知：物重Q,两并联弹簧的刚性系数为k i与k2。
如果重物悬挂的位置使两弹簧的伸长相等，试求：（1）重物振动的周期；（2）此并联弹簧的刚性系数。
五、计算题（本题15分）半径R=0.4m的轮1沿水平轨道作纯滚动，轮缘上A点铰接套筒3,带动直角杆2作上下运动。
已知：在图示位置时，轮心速度V c=0.8m/s,加速度为零，L =0.6m。
试求该瞬时：（1）杆2的速度v 和加速度a2 ；（2）铰接点A相对于杆2的速度v和加速度a r。
六、计算题（本题15分）在图示系统中，已知：匀质圆盘A和B的半径各为R和r，质量各为M和m。
试求：以©和9 为广义坐标，用拉氏方程建立系统的运动微分方程。
B 处为铰链联接。
已知：P = 100 kN, M = 200 kN • m，L i = 2m，L2=七、计算题（本题20分） 在图示机构中，已知：纯滚动的匀质轮与物 A 的质量均为m ,轮半径为r , 与斜面的动摩擦因数为f'，不计杆0A 的质量。
试求：（1）0点的加速度；（2答案、解，以整体为研究对象，受力如图所示再以EADB 为研究对象受力如图所示斜面倾角为B ，物A 杆OA 的内力。
由' Mc(F) =0P 2L^ - F x (2L - D -AFy 2L - M 0(1)由' MB (F) =0F AX J - F Ay L Q -M =0(2)联立(1) (2)两式得四、解：(1)选取重物平衡位置为基本原点，并为零势能零点，其运动规律为x = A sin( wt0)在瞬时t 物块的动能和势能分别为 T =*mv 2=2 w n2A 2cos 2(3n t 0)1v = ?(k i ■ k2)| ： x ■i 2 = -(k i k 2)x当物块处于平衡位置时S n 2A 2当物块处于偏离振动中心位置极端位置时,=1(k 1 k 2)A 22由机械能守恒定律，有(k i k 2)g重物振动周期为(k 「k 2)g(2)两个弹簧并联，则弹性系数为 k 1 k 2。
哈工大力学基础考研真题
哈工大力学基础考研真题哈尔滨工业大学力学基础考研真题一、引言力学基础是力学学科的基础和核心，对于力学学科的理论研究和工程应用都具有重要意义。
哈尔滨工业大学作为国内一流的工科院校，力学基础考研真题也一直备受关注。
本文将分享一道哈尔滨工业大学力学基础考研真题，并根据题目的要求来详细讨论解答方法。
二、力学基础考研真题**题目：**已知一质点在二维坐标系中运动，其位置由位矢r(t) = x(t) i + y(t) j 表示，其中i、j为单位基矢量。
(a) 求质点的速度v(t)；(b) 求质点的加速度a(t)；(c) 若质点的运动满足v(t) = t^2 i + 2t j，求质点的位矢r(t)。
三、解答方法(a) 求质点的速度v(t)根据速度的定义，速度v(t)是位矢r(t)对时间t的导数。
根据题目给出的位矢r(t)，可以得到质点的速度v(t)如下：v(t) = dr(t)/dt = (dx(t)/dt) i + (dy(t)/dt) j(b) 求质点的加速度a(t)加速度a(t)是速度v(t)对时间t的导数，即速度的导数。
根据题目给出的速度v(t)，可以得到质点的加速度a(t)如下：a(t) = dv(t)/dt = d^2x(t)/dt^2 i + d^2y(t)/dt^2 j(c) 求质点的位矢r(t)根据速度v(t)等于t^2 i + 2t j，可以进行速度的积分，得到位矢r(t)如下：r(t) = ∫v(t)dt = ∫(t^2 i + 2t j)dt = (t^3/3) i + (t^2) j + C四、解答过程(a) 求质点的速度v(t)根据速度的定义，速度v(t)是位矢r(t)对时间t的导数。
由题意得到位矢r(t) = x(t) i + y(t) j ，所以质点的速度v(t)可以表示为：v(t) = dr(t)/dt = (dx(t)/dt) i + (dy(t)/dt) j(b) 求质点的加速度a(t)加速度a(t)是速度v(t)对时间t的导数，即速度的导数。
最新哈工大计算力学考试题及答案
（1）For a plane stress state, if the y-coordinate is regarded as a symmetric axis, try to make a sketch and write down the displacement boundary conditions at the symmetric axis in finite element modeling. (6 points) Solution:As shown in the figure, for a symmetric problem, we may define 0==A A v u at point A ; and at point B , 0=B u（2）Try to use the Castigliano’s first theorem to obtain the matrix equilibrium equations for the system of springs shown in the following Figure.(10 points)Solution ：For the spring element, the strain energy is given by ()221u k U e ∆=In which, k – stiffness of the spring, u ∆ - deflection of the spring.The total strain energy of the system of four springs is expressed by means of the nodal displacements and spring constants as2454234322322121)(21)(21)(21)(21U U k U U k U U k U U k U e -+-+-+-=By application of the Castigliano’s first theorem for each element12111211)()1)((F U U k U U k U U e=-=--=∂∂23221212)()(F U U k U U k U U e=-+-=∂∂ 34332323)()(F U U k U U k U U e=-+-=∂∂ 45443434)()(F U U k U U k U U e=-+-=∂∂ 54545)(F U U k U U e=-=∂∂ The system stiffness matrix can be written as⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--+--+--+--54321432444433332222111100000000000000F F F F F U U U k k k k k k k k k k k k k k k k（3）The interpolation functions for a beam element of length L arewrite down a polynomial representation of the displacement field )(x v in terms of the above interpolation functions and show that 22/dx v d = constant for the beam element subject to pure bending. (12 points) Solution ：The displacement field for a beam element is332220)(x a x a x a a x v +++=It can also be expressed in terms of interpolation functions and nodal variables as24231211)(θθN v N N v N x v +++=Substitute the interpolation functions into the above equation and after a few manipulations, we have24231211θθdxdN v dx dN dx dN v dx dN dx dv +++=22223221221322326634166θθ⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+-+⎪⎪⎭⎫ ⎝⎛+-=L x L x v L x L x L x L x v L x L x 2223212132226212664126θθ⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛+-=L x L v L x L L x L v L x L dx v d for the beam element subject to pure bending, we have21v v =, 21θθ-=So, constant 22411122=-=+-=θθθLL L dx v d （4）For a 2D problem, if the mid-points of each side of a triangular element are alsodefined as nodal points, try to write down an appropriate polynomial representationof the displacement field variable, and discuss its convergence conditions. (14 points ）Solution ：The polynomial representation of the displacement field variable can be written as26524321y a xy a x a y a x a a u +++++=21211210987y a xy a x a y a x a a v +++++=The convergence conditions include: (1) the compatibility conditions.Since the above equations are continuous within the element, so the displacement field iscontinuous in the element.On the common boundary, the side line is a quadratic function that has three independent constants. And since there are three nodes, the boundary curve can be uniquely determined by the quadratic function, so on the common boundary, there is no void, no material overlap either.(2) the completeness condition.The rigid body motion can be determined by the constants 1a and 7a The rigid body rotation can be realized by3a y u =∂∂, and 8a xv =∂∂ The constant strain condition can be satisfied by2a xux =∂∂=ε, 9a y v y =∂∂=ε, and 83a a x v y u xy +=∂∂+∂∂=γIn summary, convergence conditions are satisfied for the element.（5）Considering a beam element, Denoting the element length by L and the moment ofinertia of the cross-sectional area by z I , write down an appropriate function to express the displacement field, and finally, derive the finite element equation and nodal forces of the element by using the Galerkin ’s method. (18 points)Solution ：The governing equation for the problem of beam flexure is)(d d d d 2222x q x v EI x z =⎪⎪⎭⎫ ⎝⎛ The displacement solution can be written as∑==+++=4124231211)()()()()()(i i i x N x N v x N x N v x N x v δθθTherefore, the element residual equations are4,10d )(d d d d )(212222==⎥⎦⎤⎢⎣⎡-⎪⎪⎭⎫⎝⎛⎰i x x q x v EI x x N x x z iIntegrating the derivative term by parts and assuming a constant z EI , we obtain4,10d )(d d d d d d d )(2121213333==--⎰⎰i x x q N x x vx N EI xvEI x N xx i x x i z x x z iand since3322d d d d d d d d x vEI x v EI x x M V z z -=⎪⎪⎭⎫ ⎝⎛-=-= Integrating again by parts and rearranging gives4,1d d d d d d d )(d d d d d 2121212122332222=+-=⎰⎰i xvEI x N x v EI N x x q N x x v x N EI x x z i x x z i xx i x x i zThe shear forces and bending moments at element nodes now explicitly appear in the element equations.The above equation can be written in the matrix form }{}]{[F k =δ where the terms of thestiffness matrix are defined by4,1,d d d d d 222221==⎰j i x x N xN EI k jx x i z ijThe terms of the element force vector are defined by4,1d d d d d d d )(2121212233=+-=⎰i xvEI x N x vEI N x x q N F x x z i x x x x z i i ior,4,1)(d d )(d )(212121=++=⎰i x M xN x V N x x q N F xx i x x xx i i iwhere the integral term represents the equivalent nodal forces and moments produced by the distributed load.（6）Consider the three-node line element with interpolation functionsUse the element as the parent element in the isoparametric mapping332211)()()(x r N x r N x r N x ++=with 321x x x << but otherwise arbitrary nodal coordinates. a.b. How does the x coordinate vary between nodes of the isoparametric element?c. Has the basic element geometry changed from that of the parent element?d.e.Determine the Jacobian matrix for the transformation ，and calculate the Jacobianmatrix for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=.f. Find the inverse of the Jacobian matrix, and calculate its value for the above basic element too.g. Calculate the value of determinate J at a point with 25.0=r .(20 points)Solution ：a. 332211)()()(x r N x r N x r N x ++=32212)2()44()132(x r r x r r x r r -+-++-=It can be seen that the x coordinate vary as a quadratic function between nodes of the isoparametric elementb. the basic element geometry may change from that of the parent element. The basic element is still a straight line element, however, its length may change. The length of the parent element is 1, and the length of the basic element is 13x x -.c. the Jocabian matrix can be written as[]⎥⎦⎤⎢⎣⎡∂∂=⎥⎦⎤⎢⎣⎡∂∂=∑=31i i i x r N r x JThat is 321)14()21(4)34(][x r x r x r J -+-+-=for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=we have 3431268][+=-++-=r r r Jd. the inverse of the Jocabian matrix is 3211)14()21(4)34(1][x r x r x r J -+-+-=-for the basic element with nodal coordinates 03and ,0,0.2321.x x x ==-=we have 341][1+=-r Je. T he value of determinate J at a point with 25.0=r is calculated by434=+=r J。
高考物理威海力学知识点之分子动理论难题汇编含答案
高考物理威海力学知识点之分子动理论难题汇编含答案一、选择题1．下列有关热学的叙述中，正确的是（）A．同一温度下，无论是氢气还是氮气，它们分子速率都呈现出“中间多，两头少”的分布规律，且分子平均速率相同B．在绝热条件下压缩理想气体，则其内能不一定增加C．布朗运动是指悬浮在液体中的花粉分子的无规则热运动D．液体表面层分子间距离大于液体内部分子间距离，故液体表面存在张力2．已知某气体的摩尔体积为22.4L/mol，摩尔质量为18g/mol，阿伏加德罗常数为23110mol-，由以上数据不能估算出这种气体（）⨯2316.0210mol-A．每个分子的质量B．每个分子的体积C．每个分子占据的空间D．1g气体中所含的分子个数3．物质由大量分子组成，下列说法正确的是（）A．1摩尔的液体和1摩尔的气体所含的分子数不相同B．分子间引力和斥力都随着分子间距离减小而增大C．当分子间距离减小时，分子间斥力增大，引力减小D．当分子间距离减小时，一定是克服分子力做功4．下列说法正确的是A．布朗运动就是水分子的热运动B．水结成冰后水分子的热运动停止C．水流速度越大水分子的热运动越剧烈D．布朗运动反映了水分子的运动5．下列说法正确的是A．各向异性的一定是晶体，各向同性的一定是非晶体B．晶体有固定的熔点，非晶体没有固定的熔点C．只要知道气体的摩尔体积和阿伏加德罗常数，就可算出气体分子的体积D．温度不变时，饱和汽压随体积增加而减小6．以下说法正确的是()A．机械能为零、内能不为零是可能的B．温度相同，质量相同的物体具有相同的内能C．温度越高，物体运动速度越大，物体的内能越大D．0 ℃的冰的内能比等质量的0 ℃的水的内能大7．如图所示，甲分子固定在坐标原点O上，乙分子位于r轴上距原点r3的位置。
虚线分别表示分子间斥力F斥和引力F引的变化情况，实线表示分子间的斥力和引力的合力变化情况。
若把乙分子由静止释放，则乙分子( )A ．从r 3到r 1，分子势能先减小后增加B ．从r 3到r 2做加速运动，从r 2向r 1做减速运动C ．从r 3到r 1做加速运动，从r 1向O 做减速运动D ．从r 3到r 1，分子势能先增加后减小8．把墨汁用水稀释后取出一滴放在显微镜下观察，如图所示，下列说法中正确的是A ．在显微镜下能看到水分子不停地撞击炭粒B ．小炭粒在不停地做无规则运动，这就是所说的布朗运动C ．当水结成冰后，炭粒不再运动，因为此时水分子已停止运动D ．在显微镜下看起来连成一片的液体，实际上是由许许多多的静止不动的水分子组成的9．下列关于热学问题的说法正确的是( )A ．一个孤立系统总是从熵小的状态向熵大的状态发展，熵值较大代表着较为有序B ．当人们感到潮湿时，空气的绝对湿度一定较大C ．.某气体的摩尔质量为M 、密度为ρ，用N A 表示阿伏加德罗常数，每个气体分子的质量m 0，每个气体分子的体积V 0，则m 0＝A M N ，V 0＝0mD ．密封在容积不变的容器内的气体，若温度升高，则气体分子对器壁单位面积上的平均作用力增大10．关于热现象，下列说法正确的是（ ）A ．物体温度不变， 其内能一定不变B ．物体温度升高，其分子热运动的平均动能一定增大C ．外界对物体做功，物体的内能一定增加D ．物体放出热量，物体的内能一定减小11．下列说法正确的是( )A ．布朗运动是固体分子的无规则运动B ．液体温度越高，悬浮颗粒越小，布朗运动越剧烈C ．布朗运动是由于液体各部分的温度不同而引起的D．物体的温度可以比绝对零度还低12．下列说法中正确的是（）A．物体温度不变，其内能一定不变B．物体的内能是指物体内所有分子热运动动能的总和C．系统从外界吸收热量，内能一定增加D．温度升高，分子热运动的平均动能增大13．以下说法中正确的是A．分子力做正功，分子势能一定增大B．气体的压强是由气体分子间的吸引和排斥产生的C．分子间距离增大时，分子间的引力和斥力都减小D．绝对零度就是当一定质量的气体体积为零时，用实验方法测出的温度14．下列关于热现象和热力学规律的说法正确的是（）A．布朗运动就是液体分子的无规则运动B．物体的温度越高，其分子平均动能一定越大C．热量不可能从低温物体传到高温物体D．压缩气体需要用力，这是气体分子间斥力的宏观表现15．关于分子动理论，下列说法正确的是（）A．布朗运动是液体或气体分子的无规则运动B．若两分子间的距离增大，则两分子间的作用力也一定增大C．在扩散现象中，温度越高，扩散得越快D．若两分子间的作用力表现为斥力，则分子间距离增大时，分子势能增大16．下列说法正确的是( )A．布朗运动是液体分子的无规则运动B．布朗运动是指液体中悬浮颗粒的无规则运动C．温度降低，物体内每个分子的动能一定减小D．温度低的物体内能一定小17．某气体的摩尔体积和摩尔质量分别为Vm和Mm,密度为ρ，每个分子的质量和体积分别为m和V0阿伏加德罗常数为N A,则以下关系正确的是（）A．摩尔质量为M m =B．摩尔体积为V m=C．分子体积为V0=D．阿伏伽德罗常数为N A==18．已知铜的摩尔质量为M，密度为ρ，阿伏加德罗常数为N，下列说法中正确的是（）A．1个铜原子的质量为M NB．1个铜原子的质量为N MC．1个铜原子所占的体积为MN ND．1个铜原子所占的体积为ρM N19．图描绘了一颗悬浮在液体中的固体微粒受到周围液体分子撞击的情景，下列关于布朗运动的说法中正确的是A．悬浮微粒做布朗运动，是液体分子的无规则运动撞击造成的B．布朗运动是固体分子的无规则运动C．液体温度越低，布朗运动越剧烈D．悬浮微粒越大，液体分子撞击作用的不平衡性表现得越明显20．如图，F-r 图象中两条曲线表示两分子间引力、斥力的大小随分子间距离的变化关系，其中纵坐标 F表示两分子间引力、斥力的大小，横坐标 r 表示两个分子间的距离，e 为两曲线的交点，则：（）A．ab 为斥力曲线，cd 为引力曲线B．当 r＞r e时，分子间作用力的合力表现为斥力C．当 r=r e时，分子势能为零D．当 r＜re时，若减小分子间的距离，分子势能将增大21．一定质量的理想气体，其状态变化的P-T图像如图所示。
哈工大(威海)大物往年试题 (5)
7. 在单缝夫琅禾费衍射实验中， 波长为的单色光垂直入射到单缝上． 对应于衍射角为 30°
的方向上，若单缝处波面可分成 5 个半波带，则该方向屏幕上观察到的条纹明暗及缝宽度 正确的是［ ］. 出题教师签字: 教研室主任签字: 第 1 页(共 4 页)
(A) 暗条纹， 5．
(B) 明条纹， 2.5． (C) 明条纹， 5． (D) 暗条纹，2.．
3 kT ，则相应的 2
图 6
第 4 页(共 4 页)
3. (14 分) 两个偏振片 P1、P2 叠在一起，由强度相同的自然光和线偏振光混合而成的光束
垂直入射在偏振片上．已知穿过 P1 后的透射光强为入射光强的 1 / 2；连续穿过 P1、P2 后 的透射光强为入射光强的 1 / 4．求 (1) 若不考虑 P1、P2 对透射光的反射和吸收，入射光中线偏振光的光矢 量振动方向与 P1 的偏振化方向夹角为多大？ (2) P1、P2 的偏振化方向间的夹角为多大？ (3) 若考虑每个偏振光对透射光的吸收率为 5％，且透射光强与入射光强 第 3 页(共 4 页)
根细丝之间的距离为 2.0mm， 则人眼的最小分辨角和恰能分辨两细丝的距离分别是 ［ (A) × rad, 8.2mm. (B) × rad, 8.9mm (C) × rad, 8.2mm (D) × rad, 8.9mm ］
11. 用频率为1 的单色光照射某种金属时，测得饱和电流为 I1，以频率为2 的单色光照射
该金属时，测得饱和电流为 I2，若 I1> I2，则下列说法正确的是［ ］ (A) 1 >2 且两种情况下光电子的最大初动能相等． (B) 1 <2 且两种情况下光电子的最大初动能相等． (C) 1 与2 的关系不能确定但是两种情况下光电子的最大初动能相等． (D) 1 与2 的关系不能确定而且两种情况下光电子的最大初动能也不能确定.Biblioteka i0玻璃1
高考物理威海力学知识点之牛顿运动定律难题汇编含答案
高考物理威海力学知识点之牛顿运动定律难题汇编含答案一、选择题1．如图所示，两个质量均为m 的物块A 和B 通过一轻弹簧连接在一起，并放置于水平传送带上，水平轻绳一端连接A ，另一端固定在墙上，A 、B 与传送带间的动摩擦因数均为μ。
传送带沿顺时针方向匀速转动，系统达到稳定后，突然剪断轻绳的瞬间，设A 、B 的加速度大小分别为A a 和B a （弹簧在弹性限度内），重力加速度为g ，则（ ）A ．A 2a g μ=，B 0a =B ．A 2a g μ=，B a g μ=C ．A a g μ=，B 0a =D ．A a g μ=，B a g μ=2．下列关于超重和失重的说法中，正确的是（ ）A ．物体处于超重状态时，其重力增加了B ．物体处于完全失重状态时，其重力为零C ．物体处于超重或失重状态时，其惯性比物体处于静止状态时增加或减小了D ．物体处于超重或失重状态时，其质量及受到的重力都没有变化3．如图是塔式吊车在把建筑部件从地面竖直吊起的a t -图，则在上升过程中（ ）A ．3s t =时，部件属于失重状态B ．4s t =至 4.5s t =时，部件的速度在减小C ．5s t =至11s t =时，部件的机械能守恒D ．13s t =时，部件所受拉力小于重力4．如图所示，倾角为θ的光滑斜面体始终静止在水平地面上,其上有一斜劈A,A 的上表面水平且放有一斜劈B ，B 的上表面上有一物块C ，A 、B 、C 一起沿斜面匀加速下滑。
已知A 、B 、C 的质量均为m ，重力加速度为g ，下列说法正确的是A ．A 、B 间摩擦力为零gB．A加速度大小为cosC．C可能只受两个力作用D．斜面体受到地面的摩擦力为零5．2018 年 11 月 6 日,第十二届珠海航展开幕．如图为某一特技飞机的飞行轨迹，可见该飞机先俯冲再抬升，在空中画出了一个圆形轨迹，飞机飞行轨迹半径约为 200 米，速度约为300km/h．A．若飞机在空中定速巡航，则飞机的机械能保持不变．B．图中飞机飞行时，受到重力，空气作用力和向心力的作用C．图中飞机经过最低点时，驾驶员处于失重状态．D．图中飞机经过最低点时，座椅对驾驶员的支持力约为其重力的 4.5 倍．6．如图所示，小球从高处落到竖直放置的轻弹簧上，则小球从开始接触弹簧到将弹簧压缩至最短的整个过程中（）A．小球的动能不断减少B．小球的机械能在不断减少C．弹簧的弹性势能先增大后减小D．小球到达最低点时所受弹簧的弹力等于重力7．质量分别为m1、m2的甲、乙两球，在离地相同高度处，同时由静止开始下落，由于空气阻力的作用，两球到达地面前经时间t0同时到达稳定速度v1、v2，已知空气阻力大小f与小球的下落速率v成正比，即f=kv（k>0），且两球的比例常数k完全相同，两球下落的v-t关系如图所示，下列说法正确的是（）A．甲球质量m1较小B．稳定速度与质量成正比C．释放瞬间甲球的加速度较大D．t0时间内两球下落的高度相等8．如图所示，A、B两物块质量均为m，用一轻弹簧相连，将A用长度适当的轻绳悬挂于天花板上，系统处于静止状态，B物块恰好与水平桌面接触而没有挤压，此时轻弹簧的伸长量为x．现将悬绳剪断，则（）A．悬绳剪断瞬间A物块的加速度大小为2gB．悬绳剪断瞬间A物块的加速度大小为gC．悬绳剪断瞬间B物块的加速度大小为2gD．悬绳剪断瞬间B物块的加速度大小为g9．如图所示，一个箱子中放有一个物体，已知静止时物体对箱子的下底面压力大小等于物体的重力大小，且物体与箱子上底面刚好接触现将箱子以初速度v0竖直向上抛出，已知运动时箱子所受空气阻力大小不变，且箱子运动过程中始终保持图示姿态，重力加速度为g。
高考物理威海力学知识点之相互作用难题汇编含答案
高考物理威海力学知识点之相互作用难题汇编含答案一、选择题1．以下几组共点力分别作用在物体上，有可能使物体所受合力为零的是( ) A ．10Ｎ，50Ｎ，100Ｎ. B ．5Ｎ，10Ｎ，20Ｎ.C ．10Ｎ，40Ｎ，5Ｎ.D ．30Ｎ，40Ｎ，50Ｎ.2．两个物体相互接触，关于接触处的弹力和摩擦力，以下说法正确的是 （ ） A ．一定有弹力，但不一定有摩擦力B ．如果有弹力，则一定有摩擦力C ．如果有摩擦力，则一定有弹力D ．如果有摩擦力，则其大小一定与弹力成正比3．一人站在体重计上称体重，保持立正姿势称得体重为G ，当其缓慢地把一条腿平直伸出台面，体重计指针稳定后读数为'G ，则 （ ）A ．G G >'B ．G G <'C ．G G ='D ．无法判定4．如图所示，小球用细绳系住，绳的另一端固定于O 点，现用水平F 缓慢推动斜面体，小球在斜面上无摩擦地滑动，细绳始终处于直线状态，当小球升到接近斜面顶端时细绳接近水平，此过程中斜面对小球的支持力F N ，以及绳对小球的拉力F T 的变化情况是（ ）A ．F N 保持不变，F T 不断增大B ．F N 不断增大，F T 不断减小C ．F N 保持不变，F T 先增大后减小D ．F N 不断增大，F T 先减小后增大5．如图所示，一个重为5N 的大砝码，用细线悬 挂在O 点，现在用力F 拉砝码，使悬线偏离竖直方向30°时处于静止状态，此时所用拉力F 的最小值为 （ ）A ．8.65NB ．5.0NC ．4.3ND ．2.5N6．如图所示，轻绳一端系在小球A 上，另一端系在圆环B 上，B 套在固定粗糙水平杆PQ 上．现用水平力F 作用在A 上，使A 从图中实线位置（轻绳竖直）级慢上升到虚线位置，但B 仍保持在原来位置不动．则在这一过程中，杆对B 的摩擦力F1、杆对B 的支持力F2、绳对B 的拉力F3的变化情况分别是（ ）A．F1逐渐增大，F2逐渐增大，F3逐渐增大B．F1保持不变，F2逐渐增大，F逐渐减小C．F1逐渐增大，F2保持不变，F3逐渐增大D．F1逐渐减小，F2逐渐减小，F3保持不变7．磁力棒是可拆卸类拼搭玩具。
哈工大理力习题及习题答案
理论力学（I）第六版哈尔滨工业大学理论力学教研室第二章 平面汇交力系与平面力偶系2-1铆接薄板在孔心A 、B 和C 处受三力作用，如题2-1图（a ）所示。
F 1=100N ，沿铅直方向；F 3=50N ，沿水平方向，并通过点A ；F 2=50N ，力的作用线也通过点A ，尺寸如题2-1图(a)所示。
求此力系的合力。
解法一 几何法。
应用力的多边形法，将力F 1、F 2和F 3首尾相接后，再从F 1的起点至F 3的终点连一直线，此封闭边便是三力的合力F R ，如题2-1图（b ）所示。
根据预先选好的比例尺，利用直尺和量角器便可确定合力F R 的大小和方向。
解法二 解析法。
合力的矢量表达式为∑∑+=+=j F i F j F i F F y x Ry Rx R即合力R F 在x 轴和y 轴上的投影，分别等于力系各力在同一坐标轴上投影的代数和，所以有：N N F F F F xx x Rx 805080606050022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= N N F F F F yy y Rx 14008060805010022321=⎪⎪⎭⎫ ⎝⎛++⨯+=++= 所以，合力的大小为：N N F F F Ry Rx R2.161140802222=+=+=合力F R 与x 轴的夹角为：︒===24.602.16180arccos cosR Rx F F acr α 2-3物体重P=20kN ，用绳子挂在支架的滑轮B 上，绳子的另一端接在铰车D 上，如题2-3图（a ）所示。
转动铰车，物体便能升起。
设滑轮的大小、AB 与CB 杆自重及磨擦略去不计，A 、B 、C 三处均为铰链连接。
当物体处于平衡状态时，试求拉杆AB 和支杆CB 处受的力。
解：这是一个平面汇交力系的平衡问题。
选取滑轮B 为研究对象，并作B 点的受力图，如题2-3图（b ）所示。
由平衡方程∑∑==0,0y xF F，有：030sin 30cos =︒-︒+-T F F BC BA （1） 030cos 30sin =-︒-︒P T F BC （2）因忽略了滑轮B 的磨擦，所以P=T ，将P 、T 的数值代入（2）式，得KN F BC 64.74=将T 和F BC 的数值代入（1）式，得：kN F BA64.54=所以拉杆AB 和CB 分别受拉力54.64kN 和压力74.64kN 。
(推荐下载)哈工大理论力学期末考试及答案
(完整word版)哈工大理论力学期末考试及答案编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整word版)哈工大理论力学期末考试及答案）的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。
本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整word版)哈工大理论力学期末考试及答案的全部内容。
三、计算题（本题10分）图示平面结构，自重不计,B 处为铰链联接。
已知：P = 100 kN ，M = 200 kN·m，L 1 = 2m ，L 2 = 3m.试求支座A 的约束力。
四、计算题（本题10分）在图示振系中，已知：物重Q ，两并联弹簧的刚性系数为k 1与k 2。
如果重物悬挂的位置使两弹簧的伸长相等，试求：（1)重物振动的周期；（2）此并联弹簧的刚性系数。
五、计算题(本题15分）半径R =0.4m 的轮1沿水平轨道作纯滚动，轮缘上A 点铰接套筒3，带动直角杆2作上下运动。
已知：在图示位置时，轮心速度=0。
8m/s ，加速度为零，L =0。
6m.试求该瞬时：（1）杆2的速度和加速度;(2）铰接点A 相对于杆2的速度和加速度。
六、计算题（本题15分）在图示系统中，已知：匀质圆盘A 和B 的半径各为R 和r ，质量各为M 和m 。
试求：以φ和θ为广义坐标，用拉氏方程建立系统的运动微分方程.C v 2v 2a r v ra七、计算题（本题20分)在图示机构中,已知：纯滚动的匀质轮与物A 的质量均为m ，轮半径为r ，斜面倾角为β，物A 与斜面的动摩擦因数为，不计杆OA 的质量。
试求:（1）O 点的加速度；（2）杆OA 的内力.答案三、解，以整体为研究对象，受力如图所示.由 (1)再以EADB 为研究对象受力如图所示,'f ()0C M F =∑11222(2)20Ax Ay P L F L L F L M ⋅-⋅--⋅-=由 (2)联立（1）（2）两式得四、解：（1)选取重物平衡位置为基本原点，并为零势能零点，其运动规律为在瞬时t 物块的动能和势能分别为当物块处于平衡位置时当物块处于偏离振动中心位置极端位置时，由机械能守恒定律，有重物振动周期为（2）两个弹簧并联，则弹性系数为。
高考物理威海力学知识点之功和能难题汇编附答案
高考物理威海力学知识点之功和能难题汇编附答案一、选择题1．起重机以加速度a竖直向上加速吊起质量为m的重物，若物体上升的高度为h，重力加速度为g，则起重机对货物所做的功是A．B．C．D．2．我国的传统文化和科技是中华民族的宝贵精神财富，四大发明促进了科学的发展和技术的进步，对现代仍具有重大影响，下列说法正确的是（）A．春节有放鞭炮的习俗，鞭炮炸响的瞬间，动量守恒但能量不守恒B．火箭是我国的重大发明，现代火箭发射时，火箭对喷出气体的作用力大于气体对火箭的作用力C．装在炮弹中的火药燃烧爆炸时，化学能全部转化为弹片的动能D．指南针的发明促进了航海和航空，静止时指南针的N极指向北方3．把小球放在竖立的弹簧上，并把球往下按至A位置，如图甲所示．迅速松手后，球升高至最高位置C（图丙），途中经过位置B时弹簧正处于原长（图乙）．忽略弹簧的质量和空气阻力．则小球从A运动到C的过程中，下列说法正确的是A．经过位置B时小球的加速度为0B．经过位置B时小球的速度最大C．小球、地球、弹簧所组成系统的机械能守恒D．小球、地球、弹簧所组成系统的机械能先增大后减小4．物体仅在拉力、重力作用下竖直向上做匀变速直线运动，重力做功-2J，拉力做功3J，则下列说法正确的是A．物体的重力势能减少2JB．物体的动能增加3JC．物体的动能增加1JD．物体的机械能增加1J5．如图所示,固定的竖直光滑长杆上套有质量为m的小圆环,圆环与水平状态的轻质弹簧一端连接,弹簧的另一端连接在墙上,且处于原长状态．现让圆环由静止开始下滑,已知弹簧原长为L,圆环下滑到最大距离时弹簧的长度变为2L(未超过弹性限度),则在圆环下滑到最大距离的过程中( )A ．圆环的机械能守恒B ．弹簧弹性势能变化了3mgLC ．圆环下滑到最大距离时,所受合力为零D ．圆环重力势能与弹簧弹性势能之和保持不变6．如图所示，一轻弹簧的左端固定在竖直墙壁上，右端自由伸长，一滑块以初速度v 0在粗糙的水平面上向左滑行，先是压缩弹簧，后又被弹回。
高考物理威海力学知识点之曲线运动难题汇编附答案
高考物理威海力学知识点之曲线运动难题汇编附答案一、选择题1．如图所示，沿竖直杆以速度v匀速下滑的物体A通过轻质细绳拉光滑水平面上的物体B，细绳与竖直杆间的夹角为θ，则以下说法正确的是（）A．物体B向右做匀速运动B．物体B向右做加速运动C．物体B向右做减速运动D．物体B向右做匀加速运动2．小船横渡一条两岸平行的河流，水流速度与河岸平行，船相对于水的速度大小不变，船头始终垂直指向河岸，小船的运动轨迹如图中虚线所示。
则小船在此过程中（）A．无论水流速度是否变化，这种渡河耗时最短B．越接近河中心，水流速度越小C．各处的水流速度大小相同D．渡河的时间随水流速度的变化而改变3．如图所示，有两条位于同一竖直平面内的水平轨道，轨道上有两个物体A和B，它们通过一根绕过定滑轮O的不可伸长的轻绳相连接，物体A以速率v A＝10m/s匀速运动，在绳与轨道成30°角时，物体B的速度大小v B为（）A 53B．20 m/s C203D．5 m/s4．某质点同时受到在同一平面内的几个恒力作用而平衡，某时刻突然撤去其中一个力，以后这物体将（）①可能做匀加速直线运动；②可能做匀速直线运动；③其轨迹可能为抛物线；④可能做匀速圆周运动．A．①③B．①②③C．①③④D．①②③④5．一个人在岸上以恒定的速度v，通过定滑轮收拢牵引船上的绳子，如图所示，当船运动到某点，绳子与水平方向的夹角为α时，船的运动速度为（）A ．υB ．cos vC ．v cosαD ．v tanα6．下列与曲线运动有关的叙述，正确的是A ．物体做曲线运动时，速度方向一定时刻改变B ．物体运动速度改变，它一定做曲线运动C ．物体做曲线运动时，加速度一定变化D ．物体做曲线运动时，有可能处于平衡状态7．如图，abc 是竖直面内的光滑固定轨道，ab 水平，长度为2R ：bc 是半径为R 的四分之一的圆弧，与ab 相切于b 点．一质量为m 的小球．始终受到与重力大小相等的水平外力的作用，自a 点处从静止开始向右运动，重力加速度大小为g ．小球从a 点开始运动到其他轨迹最高点，机械能的增量为A ．2mgRB ．4mgRC ．5mgRD ．6mgR8．一条小河宽100m ，水流速度为8m/s ，一艘快艇在静水中的速度为6m/s ，用该快艇将人员送往对岸．关于该快艇的说法中正确的是（ ）A ．渡河的最短时间为10sB ．渡河时间随河水流速加大而增长C ．以最短位移渡河，位移大小为100mD ．以最短时间渡河，沿水流方向位移大小为400m 39．如图所示，质量为05kg ．的小球在距离小车底部20m 高处以一定的初速度向左平抛，落在以75/m s ．的速度沿光滑水平面向右匀速行驶的敞篷小车中，车底涂有一层油泥，车与油泥的总质量为4kg ．设小球在落到车底前瞬间速度是25/m s ，重力加速度取210/m s ．则当小球与小车相对静止时，小车的速度是（ ）m sA．4/m sB．5/m sC．8.5/D．9.5/m s10．乘坐如图所示游乐园的过山车时，质量为m的人随车在竖直平面内沿圆周轨道运动.下列说法正确的是（）A．车在最高点时人处于倒坐状态，全靠保险带拉住，若没有保险带，人一定会掉下去B．人在最高点时对座位仍可能产生压力，但压力一定小于mgC．人在最高点和最低点时的向心加速度大小相等D．人在最低点时对座位的压力大于mg11．演示向心力的仪器如图所示。
高考物理威海力学知识点之动量难题汇编含答案
高考物理威海力学知识点之动量难题汇编含答案一、选择题1．中国空间站的建设过程是，首先发射核心舱，核心舱入轨并完成相关技术验证后，再发射实验舱与核心舱对接，组合形成空间站。
假设实验舱先在近地圆形过渡轨道上运行，某时刻实验舱短暂喷气，离开过渡轨道与运行在较高轨道上的核心舱安全对接。
忽略空气阻力，以下说法正确的是A．实验舱应当向前喷出气体B．喷气前后，实验舱与喷出气体的总动量不变C．喷气前后，实验舱与喷出气体的机械能不变D．实验舱在飞向核心舱过程中，机械能逐渐减小2．如下图所示，将质量为M，半径为R且内壁光滑的半圆槽置于光滑水平面上，左侧靠墙。
今让一质量为m的小球自左侧槽口A的正上方h高处从静止开始落下，与圆弧槽相切自A点进入槽内，则以下结论中正确的是（）A．槽离开墙后，将不会再次与墙接触B．小球离开C点以后，将做竖直上抛运动C．小球在槽内运动的全过程中，小球与半圆槽在水平方向动量守恒D．小球在槽内运动的全过程中，小球与半圆槽组成的系统动量守恒3．质量为1.0kg的小球从高20m处自由下落到软垫上，反弹后上升的最大高度为5.0m．小球与软垫接触的时间为1.0s，在接触时间内小球受到合力的冲量大小为（空气阻力不计，g取10m/s2）A．10N·s B．20N·s C．30N·s D．40N·s4．“天津之眼”是一座跨河建设、桥轮合一的摩天轮，是天津市的地标之一．摩天轮悬挂透明座舱，乘客随座舱在竖直面内做匀速圆周运动．下列叙述正确的是（）A．摩天轮转动过程中，乘客的机械能保持不变B．在最高点，乘客重力大于座椅对他的支持力C．摩天轮转动一周的过程中，乘客重力的冲量为零D．摩天轮转动过程中，乘客重力的瞬时功率保持不变5．如图，一个倾角为α的直角斜面体静置于光滑水平面上，斜面体质量为M，顶端高度为h，今有一质量为m的小物体，沿光滑斜面下滑，当小物体从斜面顶端自由下滑到底端时，斜面体在水平面上移动的距离是()A．mhM m+B．MhM m+C．cotmhM mα+D．cotMhM mα+6．如图所示，一个质量为M的滑块放置在光滑水平面上，滑块的一侧是一个四分之一圆弧EF，圆弧半径为R=1m．E点切线水平．另有一个质量为m的小球以初速度v0从E点冲上滑块，若小球刚好没跃出圆弧的上端，已知M=4m，g取10m/s2，不计摩擦．则小球的初速度v0的大小为（）A．v0=4m/s B．v0=6m/s C．v0=5m/s D．v0=7m/s7．如图所示，足够长的传送带以恒定的速率v1逆时针运动，一质量为m的物块以大小为v2的初速度冲上传送带，最后又滑回，已知v1＜v2。
高考物理威海力学知识点之机械振动与机械波难题汇编含答案
高考物理威海力学知识点之机械振动与机械波难题汇编含答案一、选择题1．某质点做简谐运动的振幅为A,周期为T ,则质点在6T时间内的最大路程是 A ．1.5AB ．AC ．0.5AD ．0.2A2．如图所示，S 是x 轴上的上下振动的波源，振动频率为10Hz.激起的横波沿x 轴向左右传播，波速为20m/s.质点a 、b 与S 的距离分别为36.8m 和17.2m ，已知a 和b 已经振动.若某时刻波源S 正通过平衡位置向上振动，则该时刻下列判断中正确的是A ．b 位于x 轴上方，运动方向向下B ．b 位于x 轴下方，运动方向向上C ．a 位于x 轴上方,运动方向向上D ．a 位于x 轴下方，运动方向向上3．如图所示，A 、B 两物体组成弹簧振子，在振动过程中，A 、B 始终保持相对静止，下列给定的四幅图中能正确反映振动过程中物体A 所受摩擦力F f 与振子对平衡位置位移x 关系的图线为A ．B ．C ．D ．4．如图所示，弹簧振子以O 点为平衡位置，在M 、N 两点之间做简谐运动．下列判断正确的是（ ）A ．振子从O 向N 运动的过程中位移不断减小B．振子从O向N运动的过程中回复力不断减小C．振子经过O时动能最大D．振子经过O时加速度最大5．下列说法正确的是（）A．物体做受迫振动时，驱动力频率越高，受迫振动的物体振幅越大B．医生利用超声波探测病人血管中血液的流速应用了多普勒效应C．两列波发生干涉，振动加强区质点的位移总比振动减弱区质点的位移大D．遥控器发出的红外线波长比医院“CT”中的X射线波长短6．一质点做简谐运动的图象如图所示，该质点在t=3.5s时刻( )A．速度为正、加速度为正B．速度为负、加速度为负C．速度为负、加速度为正D．速度为正、加速度为负7．若单摆的摆长不变，摆球的质量由20g增加为40g，摆球离开平衡位置的最大角度由4°减为2°，则单摆振动的( )A．频率不变，振幅不变B．频率不变，振幅改变C．频率改变，振幅不变D．频率改变，振幅改变8．如图所示，为一列沿x轴正方向传播的机械波在某一时刻的图像，由图可知，这列波的振幅A、波长λ和x=l米处质点的速度方向分别为：（）A．A=0.4 m λ=1m 向上B．A=1m λ=0.4m 向下C．A=0.4m λ=2m 向下D．A=2 m λ=3m 向上t=时刻的波形图，虚线为9．如图所示为一列沿x轴负方向传播的简谐横波，实线为0T>，则：（）t=时的波形图，波的周期0.6s0.6sA ．波的周期为2.4sB ．波的速度为10 m/s 3C ．在0.5 s =t 时，Q 点到达平衡位置D ．在0.5 s =t 时，Q 点到达波峰位置10．如图所示两个频率、相位、振幅均相同的波的干涉图样，实线表示波峰，虚线表示波谷，对叠加的结果正确的描述是（ ）A ．在A 点出现波峰后，经过半个周期该点还是波峰B ．B 点在干涉过程中振幅始终为零C ．两波在B 点路程差是波长的整数倍D ．当C 点为波谷时，经过一个周期此点出现波峰11．如图所示，MN 为半径较大的光滑圆弧轨道的一部分，把小球A 放在MN 的圆心处，再把另一小球B 放在MN 上离最低点C 很近的B 处，今使两球同时自由释放，则在不计空气阻力时有（ ）A ．A 球先到达C 点B ．B 球先到达C 点 C ．两球同时到达C 点D ．无法确定哪一个球先到达C 点12．下列关于简谐振动和简谐机械波的说法正确的是（ ） A ．简谐振动的平衡位置一定是物体所受合外力为零的位置。
高考物理威海力学知识点之动量难题汇编附答案
高考物理威海力学知识点之动量难题汇编附答案一、选择题1．如图所示，甲木块的质量为1m ，以速度v 沿光滑水平地面向前运动，正前方有一静止的、质量为2m 的乙木块，乙上连有一轻质弹簧．甲木块与弹簧接触后A ．甲木块的动量守恒B ．乙木块的动量守恒C ．甲、乙两木块所组成的系统的动量守恒D ．甲、乙两木块所组成的系统的动能守恒2．质量为1.0kg 的小球从高20m 处自由下落到软垫上，反弹后上升的最大高度为5.0m ．小球与软垫接触的时间为1.0s ，在接触时间内小球受到合力的冲量大小为（空气阻力不计，g 取10m/s 2）A ．10N·s B ．20N·s C ．30N·s D ．40N·s 3．自然界中某个量D 的变化量D ∆，与发生这个变化所用时间t ∆的比值Dt∆∆，叫做这个量D 的变化率．下列说法正确的是 A ．若D 表示某质点做平抛运动的速度，则Dt∆∆是恒定不变的 B ．若D 表示某质点做匀速圆周运动的动量，则Dt∆∆是恒定不变的 C ．若D 表示某质点做竖直上抛运动离抛出点的高度，则Dt∆∆一定变大． D ．若D 表示某质点的动能，则Dt∆∆越大，质点所受外力做的总功就越多 4．如图所示，A 、B 是位于水平桌面上两个质量相等的小滑块，离墙壁的距离分别为L 和2L，与桌面之间的动摩擦因数分别为A μ和B μ，现给滑块A 某一初速度，使之从桌面右端开始向左滑动，设AB 之间、B 与墙壁之间的碰撞时间都很短，且碰撞中没有能量损失，若要使滑块A 最终不从桌面上掉下来，滑块A 的初速度的最大值为（ ）A ()AB gL μμ+B ()2A B gL μμ+C ．()2A B gL μμ+D ．()12A B gL μμ+ 5．质量为m 的子弹以某一初速度0v 击中静止在粗糙水平地面上质量为M 的木块，并陷入木块一定深度后与木块相对静止，甲、乙两图表示这一过程开始和结束时子弹和木块可能的相对位置，设地面粗糙程度均匀，木块对子弹的阻力大小恒定，下列说法正确的是（ ）A ．若M 较大，可能是甲图所示情形：若M 较小，可能是乙图所示情形B ．若0v 较小，可能是甲图所示情形：若0v 较大，可能是乙图所示情形C ．地面较光滑，可能是甲图所示情形：地面较粗糙，可能是乙图所示情形D ．无论m 、M 、0v 的大小和地面粗糙程度如何，都只可能是甲图所示的情形6．如图所示，一个质量为M 的滑块放置在光滑水平面上，滑块的一侧是一个四分之一圆弧EF ，圆弧半径为R =1m ．E 点切线水平．另有一个质量为m 的小球以初速度v 0从E 点冲上滑块，若小球刚好没跃出圆弧的上端，已知M =4m ，g 取10m/s 2，不计摩擦．则小球的初速度v 0的大小为（ ）A ．v 0=4m/sB ．v 0=6m/sC ．v 0=5m/sD ．v 0=7m/s7．将充足气后质量为0.5kg 的篮球从1.6m 高处自由落下，篮球接触地面的时间为0.5s ，竖直弹起的最大高度为0.9m 。
高考物理威海力学知识点之相互作用难题汇编附答案
高考物理威海力学知识点之相互作用难题汇编附答案一、选择题1．如图所示，物块A 放在直角三角形斜面体B 上面，B 放在弹簧上面并紧挨着竖直墙壁，初始时A 、B 静止，现用力F 沿斜面向上推A ，但A 、B 仍未动．则施加力F 后，下列说法正确的是( )A ．A 、B 之间的摩擦力一定变大B ．B 与墙面间的弹力可能不变C ．B 与墙之间可能没有摩擦力D ．弹簧弹力一定不变2．如图所示，5月28日央视新闻报道：格鲁吉亚物理学家安德里亚仅靠摩擦力将25个网球垒成9层高的直立“小塔”。
网球A 位于“小塔”顶层，下面各层均有3个网球，网球B 位于“小塔”的第6层，已知每个网球质量均为m 。
下列说法正确的是（ ）A ．其他网球对B 球的作用力大于B 球的重力B ．将A 球拿走后，“小塔”仍能保持直立平衡C ．第8层的三个网球与A 球间的弹力大小各为mg/3D ．最底层的3个网球受到地板的支持力均为25mg/33．如图所示，在一粗糙水平面上有两个质量分别为m 1和m 2的木块1和2，中间用一原长为L ，劲度系数为k 的轻弹簧连接起来，木块与地面间的滑动摩擦因数均为μ.现用一水平力向右拉木块2，当两木块一起匀速运动时两木块之间的距离为（ ）A ．1+L m g k μ B ．()12+L m m g k μ+ C ．2+L m g k μD ．1212+m m L g k m m μ⎛⎫ ⎪+⎝⎭4．如图所示，质量为m的小球用水平轻质弹簧系住，并用倾角θ＝37°的木板托住，小球处于静止状态，弹簧处于压缩状态，则( )A．小球受木板的摩擦力一定沿斜面向上B．弹簧弹力不可能为34 mgC．小球可能受三个力作用D．木板对小球的作用力有可能小于小球的重力mg5．磁力棒是可拆卸类拼搭玩具。
如图所示为一磁力棒吸着一颗钢球，下列说法正确的是（）A．磁力棒对刚球弹力是由于钢球发生形变产生的B．钢球受到磁力棒的磁力等于钢球的重力C．钢球受到磁力棒的作用力方向竖直向上D．钢球和磁力棒整体一起白由下落，则磁力棒对钢球弹力等于零6．木块沿粗糙斜面(斜面相对地面静止)运动，下列对木块的受力分析正确的是（G是重力，N是支持力，f是摩擦力）A． B． C． D．7．叠放在水平地面上的四个完全相同的排球如图所示，质量均为m，相互接触，球与地面间的动摩擦因数均为μ，则：A ．上方球与下方3个球间均没有弹力B ．下方三个球与水平地面间均没有摩擦力C ．水平地面对下方三个球的支持力均为43mgD ．水平地面对下方三个球的摩擦力均为43mg μ 8．如图所示，某球用一根轻绳悬在空中，球的重量为G ，轻绳对球的拉力大小为F 1，墙壁对球的支持力大小为F 2，则（ ）A ．若增加悬绳的长度，则F 1、F 2都增大B ．若增加悬绳的长度，则F 1、F 2都减小C ．若增大球的半径，则F 1增大、F 2减小D ．若增大球的半径，则F 1减小、F 2增大9．如图所示，质量为1kg 的物体与地面间的动摩擦因数0.2μ=，从0t =开始以初速度0v 沿水平地面向右滑行，同时受到一个水平向左的恒力1N F =的作用，取向右为正方向，该物体受到的摩擦力f F 随时间变化的图像是下列图中的（ ）A ．B ．C．D．10．小华同学利用如图所示的实验装置来测定物体与滑板间的滑动摩擦力．下列关于用这种装置做实验的说法中，你认为正确的是A．必须调节托盘中重物的重量，确保滑板做匀速运动B．不一定要使滑板做匀速运动，但必须要用恒力拉滑板C．托盘中放的重物越重，滑板运动得越快，弹簧秤读数越大D．只要滑板与木块有相对运动，无论滑板做什么运动，弹簧秤的读数都相同11．如图所示，一物块置于水平地面上．当用与水平方向成060角的力1F拉物块时，物块做匀速直线运动；当改用与水平方向成030角的力2F推物块时，物块仍做匀速直线运动．若1F和2F的大小相等，则物块与地面之间的动摩擦因数为A．31-B．23-C．3122-D．1-3212．如图所示，一质量为m的木块靠在竖直粗糙墙壁上，受到水平力F的作用，保持静止，下列说法正确的是（重力加速度为g）（）A．木块受到的摩擦力大于mg，方向竖直向上B．若F减小，木块一定向下滑动C．若F增大，木块受到的摩擦力增大D．若F增大，木块受到的摩擦力保持不变13．如图所示，物体A 置于水平地面上，力F 竖直向下作用于物体B 上，A 、B 保持静止，则物体A 的受力个数为( )A ．3B ．4C ．5D ．614．如图所示，质量为M 的斜面体A 放在粗糙水平面上，用轻绳拴住质量为m 的小球B 置于斜面上，轻绳与斜面平行且另一端固定在竖直墙面上，不计小球与斜面间的摩擦，斜面体与墙不接触，整个系统处于静止状态。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
F =200N,θ=30°，摩擦力大小为
F
教研室主任签字：
。
30
P
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
作纯滚动，M 点加速度的大小为
M
va
2、图示匀质细杆各以匀角速度 ω 绕轴Ｏ转动。已知：杆长为 l ，重为
P。惯性力系向转轴Ｏ简化，主矢的大小为
矩的大小为
。
3、如图所示，物块重 P =150N，靠在粗糙的水平天花板上，物体间静滑
动摩擦因数 fs=0.3， 动滑动摩擦因数 f =0.2, 在物块上加一力 F，且
P
a
F
b
F
C
P
b
a
。
B
第 2 页（共 5 页）
遵守考试纪律
注意行为规范
三、计算题（20 分） 得分
卷面 总分
试题卷（A）
平时 成绩
。
A 1l
3
O
2l
3
。
B
课程 总成绩
，主
第 1 页（共 5 页）
遵守考试纪律
注意行为规范
4、如图所示结构受集中力 P 作用，各杆自重不计。则杆 1 的内力为
。（须注明拉、压）
F
c
a
a
a
a
1
5、如图所示，沿长方体的三个不相交且不平行的棱作用着 3 个大小相等
的力 F，若力系简化为一合力，求棱 a,b,c 的关系
二、计算题（10 分） 得分
如图所示简支梁，不计梁的重量，在 C 处作用一铅垂力 P。试求支座
B 处的约束力（要求用虚位移原理求解，用其它方法做不给分）。
A
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。
姓名:
班级：
学号：
遵守考试纪律 注意行为规范
哈尔滨工业大学（威海） 2011 / 2012 学年 秋 季学期
理论力学
考试形式（开、闭卷）：闭卷 答题时间：120（分钟）本卷面成绩占课程成绩 80 %
题一 二 三 四 五 号
分 数
一、填空题（每题 6 分，共 30 分） 得分
1、图示滚轮的半径为 R ，轮心速度为 v ，加速度为 a ，沿水平直线