特殊四边形中的动点问题 打印1
特殊四边形动点问题专题训练及答案解析汇编

特殊四边形动点问题专题训练及答案解析(一)已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,(1)求证:四边形ADCE是平行四边形;(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?证明:(1)因为四边形BCED是平行四边形,所以BD=CE且BD∥CE,又因为D是△ABC的边AB的中点,所以AD=BD,即DA=CE,又因为CE∥BD,所以四边形ADCE是平行四边形.(2)当△ABC为等腰三角形且AC=BC时,四边形ADCE是矩形理由:∵AC=BC,D是△ABC的边AB的中点∴CD⊥AD,即∠ADC=90°,由(1)可知,四边形ADCE是平行四边形∴四边形ADCE是矩形.(二)如图,已知E是▱ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE.(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.(三)如图,O为△ABC的边AC上一动点,过点O的直线MN∥BC,设MN分别交∠ACB的内、外角平分线于点E、F。
(1)求证:OE=OF(2)若CE=12,CF=5,求OC的长(3)当点O在AC边上运动到何处时,四边形AECF是矩形?证明你的结论(4)在(3)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并说明你的理由。
(1)证明:∵CE平分∠ACB∴∠ACE=∠BCE∵MN∥BC∴∠OEC=∠BCE,∴∠ACE=∠OEC,∴OE=OC,同理:OF=OC∴OE=OF(2)∵CE平分∠ACB∴∠ACE=∠ACB/2∵CF平分∠ACD∴∠ACF=∠ACD/2∴∠ECF=∠ACE+∠ACF=∠ACB/2+∠ACD/2=(∠ACB+∠ACD)/2=180/2=900在Rt△ECF中,EF2= CE2+ CF2= 122+ 52=169∴EF=13由(1)可知OE=OF∴OC=EF/2=13/2(3)、当O运动到AC的中点时,AECF是矩形证明:∵O是AC的中点∴AO=CO∵OE=OF∴四边形AECF是平行四边形由(2)可知∠ECF=900∴四边形AECF是矩形3、△ABC为直角三角形,且∠ACB=90时,四边形AECF是正方形证明:∵∠ACB=900,MN∥BC∴∠AOM=∠ACB=900,由(3)知四边形AECF 是矩形∴四边形AECF 是矩形(四)如图,已知平行四边形ABCD 的对角线AC 、BD 相交于点O ,AC=20cm 、BD=12cm ,两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动.(1)求证:当E 、F 运动过程中不与点O 重合时,四边形BEDF 一定为平行四边形; (2)当E 、F 运动时间t 为何值时,四边形BEDF 为矩形?(1)解:连接DE ,EB ,BF ,FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动. ∴AE=CF在平行四边形ABCD 中,OD=OB ,OA=OC ∴OA-AE=OC-CF 或AE-OA=CF-OC 即OE=OF∴四边形BEDF 为平行四边形.(2)当点E 在OA 上,点F 在OC 上时EF=BD=12cm , 四边形BEDF 为矩形 ∵运动时间为t∴AE=CF=2t ∴EF=20-4t=12 ∴t=2(s )当点E 在OC 上,点F 在OA 上时,EF=BD=12cm EF=4t-20=12 ∴t=8(s )因此当E 、F 运动时间2s 或8s 时,四边形BEDF 为矩形.(五)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,BD=12cm ,AC=6cm ,点E 在线段BO 上从点B 以1cm/s 的速度运动,点F 在线段OD 上从点O 以2cm/s 的速度运动.(1)若点E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形AECF 是平行四边形. (2)在(1)的条件下,①当AB 为何值时,四边形AECF 是菱形;②四边形AECF 可以是矩形吗?为什么?OCDBAEF解:(1)连接DE,EB,BF,FD∵两动点E、F同时分别以2cm/s的速度从点A、C出发在线段AC相对上运动.∴AE=CF∵平行四边形ABCD的对角线AC、BD相交于点O,∴OD=OB,OA=OC(平行四边形的对角线互相平分)∴OA-AE=OC-CF或AE-OA=CF-OC即OE=OF∴四边形AECF为平行四边形.(对角线互相平分的四边形是平行四边形)(2)当点E在OA上,点F在OC上时EF=BD=12cm,四边形BEDF为矩形∵运动时间为t∴AE=CF=2t∴EF=20-4t=12∴t=2(s)当点E在OC上,点F在OA上时,EF=BD=12cmEF=4t-20=12∴t=8(s)因此当E、F运动时间2s或8s时,四边形AECF为矩形.(六)如图,已知在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形ABQP为矩形?(七)(1)设经过xs的时间,四边形PQCD是平行四边形因为四边形PQCD是平行四边形所以DP=CQ由已知得:DP=AD-AP=24-xCQ=3x所以24-x=3xx=6答:经过6s的时间,四边形PQCD是平行四边形(2)设经过xs的时间,四边形PQBA是矩形因为四边形PQBA是矩形所以AP=BQ由已知得:AP=XBQ=BC-CQ=26-3x所以x=26-3xx=13/2答:经过13/2s的时间,四边形PQBA是矩形。
四边形中的动点问题

四边形中的动点问题动点问题是初中数学中常见的问题之一。
这种问题涉及到一些物体或点在平面或空间中的运动轨迹,从而引发一系列有趣的问题。
本文将重点讨论四边形中的动点问题。
一、定义四边形是一个拥有四个端点并且每个端点有两条相邻的边相连的图形。
在四边形中,如果一些点在边界或内部移动,我们称这些点是动点。
二、基本问题四边形中的动点问题主要有三个基本问题:1. 四边形内任取一个动点,这个点的移动轨迹是什么?2. 四边形内任取两个动点,它们的运动是否有任何联系?3. 四边形内任取三个动点,它们是否存在特殊的位置关系?三、解决方法1. 关于第一个问题,我们可以采用向量法、坐标法、三角函数法等不同的方式来解决。
其中最常用的方法是向量法,即用向量表示动点在平面内的位置,并利用向量的加减法来求得动点的移动轨迹。
比如,对于任意一边AB,在边AB上取一点C,设动点P的向量表示为向量a,向量AC表示为向量b,则P点在AC向量上的投影可以表示为向量b’。
而向量a’可以表示为由向量b’平移而来的向量,其中平移的大小和方向取决于向量b和a之间的夹角。
2. 第二个问题比较复杂,需要利用向量叉乘、双曲线函数等高深的数学知识来解决。
一般来说,我们需要找到两个动点之间的代数关系式,再根据这个关系式来判断它们是否有联系。
比如,如果我们发现两个动点在一条直线上运动,则它们存在一定的约束条件,这个约束条件可以用向量叉乘来表达。
3. 第三个问题则是考验计算几何能力的问题。
一般来说,我们需要找到一种不变量来描述三个动点之间的特殊位置关系。
比如,如果我们发现这三个动点共线,则我们可以通过向量叉乘或线性方程组来计算它们的位置关系。
如果我们发现这三个点可以构成一个三角形,则我们可以通过三角形的几何性质来判断它们的位置关系。
如果我们发现这三个动点可以构成一个正方形或者矩形,则我们可以通过它们的对角线、边长、面积等几何参数来计算它们的位置关系。
四、典型例题1. 在正方形ABCD中,点E、F分别在边AB、CD上,且AE=CF。
特殊四边形的动点问题

10
4、当堂检测
11
小结
通过本节课的学习,同学们有哪些收获?
(动点型问题的解题策略)
1:以静制动,把动态问题化为静态 问题解决 2:构建方程模型 3:运用数学思想:
(1)AP=___t__;PD=___1_2__-t____.
A
P
CQ=_1_._5_t_;BQ=__2_1__-_1_._5_t_.
(用含t的代数式表示)
(2)若四边形PQCD是平行四边形,
只需条件:__P__D_=__C_Q____
B
因此可列方程:___1_2_-_t=__1_.5__t __
6
AB=12cm,CD=15cm.在P在BC边上、Q在AD上时,问是否存在以点P、
D、C、Q为顶点的四边形是平行四边形?若存在,求出t的值;若
不存在,请说明理由.
A
P
D
A
QD
B
Q
C
B
PC
图①
图②
探究动点关键:化动为静,8 分类讨论,关注全过程
合作交流,探索新知
解: (3)存在.
∵tp=(12+15+21) ÷1=48(秒), tQ=(21+12+12) ÷1.5=30(秒)
2
学习目标
1、学会动点问题中的化动为静,以 静制动的解题策略。 2、经历列方程解决实际问题的过程, 体会数学建模、数形结合、分类讨论 等数学思想。
3
复习提问
1.平行四边形的判定有哪些? 2.菱形的判定有哪些? 3.矩形的判定呢?
特殊的平行四边形动点专题
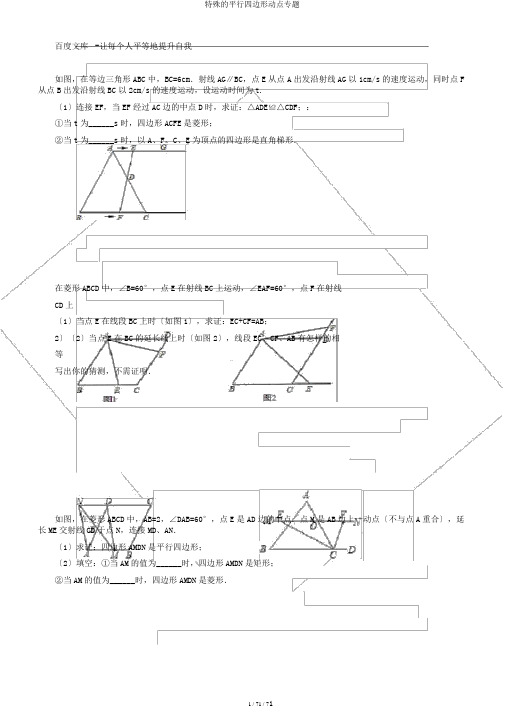
百度文库-让每个人平等地提升自我如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F 从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t.〔1〕连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;:①当t为______s时,四边形ACFE是菱形;②当t为______s时,以A、F、C、E为顶点的四边形是直角梯形.在菱形ABCD中,∠B=60°,点E在射线BC上运动,∠EAF=60°,点F在射线CD上〔1〕当点E在线段BC上时〔如图1〕,求证:EC+CF=AB;2〕〔2〕当点E在BC的延长线上时〔如图2〕,线段EC、CF、AB有怎样的相等写出你的猜测,不需证明.如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点.点M是AB边上一动点〔不与点A重合〕,延长ME交射线CD于点N,连接MD、AN.〔1〕求证:四边形AMDN是平行四边形;〔2〕填空:①当AM的值为______时,四边形AMDN是矩形;②当AM的值为______时,四边形AMDN是菱形.〔第4题〕如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.〔1〕探究:线段OE与OF的数量关系并加以证明;〔2〕当点O运动到何处,且△ABC满足什么条件时,四边形AECF是正方形?〔3〕当点O在边AC上运动时,四边形BCFE会是菱形吗?假设是,请证明,假设不是,那么说明理由.1如以下图,在?ABCD中,AC⊥BC,AC=BC=2,动点P从点A出发沿AC向终点C移动,过点P分别作PM∥AB,PN∥AD,连结AM,设AP=x,△AMP的面积为y.〔1〕四边形PMCN是不是菱形,请说明理由.〔2〕写出y与x之间的函数关系式.如图,菱形ABCD中,∠ABC=60°,AB=8,过线段BD上的一个动点P〔不与B、D重合〕分别向直线AB、AD作垂线,垂足分别为E、F.〔1〕BD的长是______;〔2〕连接PC,当PE+PF+PC取得最小值时,此时PB的长是______.如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q。
特殊四边形动点问题专题训练及解析精编版

2015特殊四边形动点问题专题训练及答案解析(一)已知,如图,点D是△ABC的边AB的中点,四边形BCED是平行四边形,(1)求证:四边形ADCE是平行四边形;(2)当△ABC满足什么条件时,平行四边形ADCE是矩形?证明:(1)因为四边形BCED是平行四边形,所以BD=CE且BD∥CE,又因为D是△ABC的边AB的中点,所以AD=BD,即DA=CE,又因为CE∥BD,所以四边形ADCE是平行四边形.(2)当△ABC为等腰三角形且AC=BC时,四边形ADCE是矩形理由:∵AC=BC,D是△ABC的边AB的中点∴CD⊥AD,即∠ADC=90°,由(1)可知,四边形ADCE是平行四边形∴四边形ADCE是矩形.(二)如图,已知E是▱ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F.(1)求证:△ABE≌△FCE.(2)连接AC、BF,若∠AEC=2∠ABC,求证:四边形ABFC为矩形.(三)如图,O为△ABC的边AC上一动点,过点O的直线MN∥BC,设MN分别交∠ACB的内、外角平分线于点E、F。
(1)求证:OE=OF(2)若CE=12,CF=5,求OC的长(3)当点O在AC边上运动到何处时,四边形AECF是矩形?证明你的结论(4)在(3)的条件下,当△ABC满足什么条件时,四边形AECF为正方形,并说明你的理由。
(1)证明:∵CE平分∠ACB∴∠ACE=∠BCE∵MN∥BC∴∠OEC=∠BCE,∴∠ACE=∠OEC,∴OE=OC,同理:OF=OC∴OE=OF(2)∵CE平分∠ACB∴∠ACE=∠ACB/2∵CF平分∠ACD∴∠ACF=∠ACD/2∴∠ECF=∠ACE+∠ACF=∠ACB/2+∠ACD/2=(∠ACB+∠ACD)/2=180/2=900在Rt△ECF中,EF2= CE2+ CF2= 122+ 52=169∴EF=13由(1)可知OE=OF∴OC=EF/2=13/2(3)、当O运动到AC的中点时,AECF是矩形证明:∵O是AC的中点∴AO=CO∵OE=OF∴四边形AECF是平行四边形由(2)可知∠ECF=900∴四边形AECF是矩形3、△ABC为直角三角形,且∠ACB=90时,四边形AECF是正方形证明:∵∠ACB=900,MN∥BC∴∠AOM=∠ACB=900,由(3)知四边形AECF是矩形∴四边形AECF 是矩形(四)如图,已知平行四边形ABCD 的对角线AC 、BD 相交于点O ,AC=20cm 、BD=12cm ,两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动.(1)求证:当E 、F 运动过程中不与点O 重合时,四边形BEDF 一定为平行四边形; (2)当E 、F 运动时间t 为何值时,四边形BEDF 为矩形?(1)解:连接DE ,EB ,BF ,FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动. ∴AE=CF在平行四边形ABCD 中,OD=OB ,OA=OC ∴OA-AE=OC-CF 或AE-OA=CF-OC 即OE=OF∴四边形BEDF 为平行四边形.(2)当点E 在OA 上,点F 在OC 上时EF=BD=12cm , 四边形BEDF 为矩形 ∵运动时间为t∴AE=CF=2t ∴EF=20-4t=12 ∴t=2(s )当点E 在OC 上,点F 在OA 上时,EF=BD=12cm EF=4t-20=12 ∴t=8(s )因此当E 、F 运动时间2s 或8s 时,四边形BEDF 为矩形.(五)如图,平行四边形ABCD 的对角线AC 、BD 相交于点O ,BD=12cm ,AC=6cm ,点E 在线段BO 上从点B 以1cm/s 的速度运动,点F 在线段OD 上从点O 以2cm/s 的速度运动.(1)若点E 、F 同时运动,设运动时间为t 秒,当t 为何值时,四边形AECF 是平行四边形. (2)在(1)的条件下,①当AB 为何值时,四边形AECF 是菱形;②四边形AECF 可以是矩形吗?为什么?解:(1)连接DE ,EB ,BF ,FD∵两动点E 、F 同时分别以2cm/s 的速度从点A 、C 出发在线段AC 相对上运动. ∴AE=CFOCDBAEF∵平行四边形ABCD的对角线AC、BD相交于点O,∴OD=OB,OA=OC(平行四边形的对角线互相平分)∴OA-AE=OC-CF或AE-OA=CF-OC即OE=OF∴四边形AECF为平行四边形.(对角线互相平分的四边形是平行四边形)(2)当点E在OA上,点F在OC上时EF=BD=12cm,四边形BEDF为矩形∵运动时间为t∴AE=CF=2t∴EF=20-4t=12∴t=2(s)当点E在OC上,点F在OA上时,EF=BD=12cmEF=4t-20=12∴t=8(s)因此当E、F运动时间2s或8s时,四边形AECF为矩形.(六)如图,已知在四边形ABCD中,AD∥BC,∠B=90°,AD=24cm ,AB=8cm,BC=26cm,动点P从A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB边向点B以3cm/s的速度运动,P、Q别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动的时间为t 秒.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形ABQP为矩形?(七)(1)设经过xs的时间,四边形PQCD是平行四边形因为四边形PQCD是平行四边形所以DP=CQ由已知得:DP=AD-AP=24-xCQ=3x所以24-x=3xx=6答:经过6s的时间,四边形PQCD是平行四边形(2)设经过xs的时间,四边形PQBA是矩形因为四边形PQBA是矩形所以AP=BQ由已知得:AP=XBQ=BC-CQ=26-3x所以x=26-3xx=13/2答:经过13/2s的时间,四边形PQBA是矩形。
特殊四边形动点问题专题训练及解析精编版

最新资料推荐2015特殊四边形动点问题专题训练及答案解析(一)已知,如图,点D是^ ABC的边AB的中点,四边形BCED是平行四边形,(1)求证:四边形ADCE!平行四边形;(2)当^ ABC满足什么条件时,平行四边形ADCE是矩形?证明:(1)因为四边形BCED是平行四边形,所以BD=CE且BD// CE又因为D是^ABC的边AB的中点,所以AD=BD 即卩DA=CE又因为CE//BD, E所以四边形ADCE是平行四边形.(2)当^ ABC为等腰三角形且AC=BC寸,四边形ADCE是矩形理由:••• AC=BC D是^ ABC的边AB的中点••• CDIAD 即/ ADC=90 ,由(1)可知,四边形ADCE是平行四边形•••四边形ADCE是矩形.(二)如图,已知E是? ABCD中BC边的中点,连接(1)求证:△ ABE^A FCE(2)连接AC BF,若/ AEC=N ABC求证:四边形AE并延长AE交DC的延长线于点F. ABFC为矩形.证明:C 1 J =四边形ABCD为平荷四I边瑋亠-■-AB//DC > -'-^ABE=^ECF *又YE为BC的中点*-■-BE =CE >在ZiABE和GCE中上'上ABE=/ECFBE=CE >^AEB=^FEC OS寸顶角相等)-A ABE^A FCE C :C 2 } AABE^ZXFCE >AB=匚F r 又丸BZZ 匚F r 四边形ABF匚为平行四边形“---BE=EC ■ AE=EF >又,KE匚三2/ABU , 且NAEC为△ ABE的夕卜角* ^AEG=^ABG+^EAB >-"-^ABC=^EAB A-■-AE=BE >---AE+EF=BE+EC > 艮卩AF=BC > 则四边形为矩形・............................................ 最新资料推荐 .................................(三)如图,O 为^ABC 的边AC 上一动点,过点O 的直线MN/ BC ,设MN 分别交 / ACB 的内、外角平分线于点E 、F 。
特殊四边形中的动点问题专项训练题
特殊四边形中的动点问题专项训练题一选择题1.如图,在平行四边形ABCD中,∠BCD=30°,BC=4,CD=.点M是AD边的中点,点N是AB边上的一个动点.将△AMN沿MN所在的直线翻折到△A′MN,连接A′C.则线段A′C长度的最小值为()A.5 B.7 C.4D.52.如图,边长为1的正方形ABCD绕点A逆时针旋转30°到正方形AB′C′D′,图中阴影部分的面积为()A.B. C.1﹣D.1﹣3.我们给出如下定义,顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.如图,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,则中点四边形EFGH的形状是()A.平行四边形 B.矩形 C.菱形 D.正方形4.如图①,点P为矩形ABCD边上一个动点,运动路线是A→B→C→D→A,设点P运动的路径长为x,S△ABP=y,图②是y随x变化的函数图象,则矩形对角线AC的长是()A.2 B.6 C.12 D.245.如图,在菱形ABCD中,∠ABC=120°,AB=2.动点P从点A出发,以每秒2个单位的速度沿折线AD→DC运动到点C,同时动点Q也从点A出发,以每秒个单位的速度沿AC运动到点C,当一个点停止运动时,另一个点也随之停止.设△APQ的面积为y,运动时间为x秒,则下列图象能大致反映y与x之间函数关系的是()A.B.C.D.6.如图,在矩形ABCD中,AB=3,BC=4,点P在BC边上运动,连接DP,过点A作AE⊥DP,垂足为E,设DP=x,AE=y,则能反映y与x之间函数关系的大致图象是()A.B.C.D.7.如图,点P是正方形ABCD的对角线BD上一个动点,PE⊥BC于点E,PF⊥CD于点F,连接EF,有下列5个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤EF的最小值等于.其中正确结论的个数是()A.2个B.3个C.4个D.5个8.如图,正方形ABCD的边长为4,点E,F分别在边DC,BC上,且BF=CE,AE平分∠CAD,连接DF,分别交AE,AC于点G,M.P是线段AG上的一个动点,过点P作PN⊥AC,垂足为N,连接PM.有下列四个结论:①AE垂直平分DM;②PM+PN的最小值为3√2;③CF2=GE•AE;④S△ADM=6√2.其中正确的是()A.①②B.②③④C.①③④D.①③9.如图,在正方形ABCD中,点E为边CD的中点,连接AE,过点B作BF⊥AE于点F,连接BD交AE于点G,FH平分∠BFG交BD于点H.则下列结论中,正确的个数为()①AB2=BF•AE②S△BGF:S△BAF=2:3③当AB=a时,BD2﹣BD•HD=a2A.0个B.1个C.2个D.3个10.如图,在正方形ABCD中,点E,F分别是AB,BC上的动点,且AF⊥DE,垂足为G,将△ABF沿AF翻折,得到△AMF,AM交DE于点P,对角线BD交AF于点H,连接HM,CM,DM,BM,下列结论正确的是()①AF=DE;②BM∥DE;③若CM⊥FM,则四边形BHMF是菱形;④当点E运动到AB的中点,tan∠BHF=2√2;⑤EP•DH=2AG•BH.A.①②③④⑤ B.①②③⑤ C.①②③ D.①②⑤二填空题11.在四边形ABCD中,AD∥BC,BC=6 cm,AD=9cm.点P以1cm/s的速度由A点向D点运动,同时点Q以2 cm/s的速度由C点向B点运动,当点P,Q运动s时,直线QP将四边形ABCD截出一个平行四边形.12.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为.13.如图,已知菱形ABCD的边长为8,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是.14.如图,在边长为6的菱形ABCD中,∠ABC=30°,P为BC上方一点,且S△PBC=S菱形,则PB+PC的最小值为.ABCDB C A M NP F E15.如图,在矩形OAHC 中,OC =8,OA =16,B 为CH 中点,连接AB .动点M 从点O 出发沿OA 边向点A 运动,动点N 从点A 出发沿AB 边向点B 运动,两个动点同时出发,速度都是每秒1个单位长度,连接CM ,CN ,MN ,设运动时间为t (0<t <16)秒,则t=时,△CMN 为直角三角形.三 解答题16.如图,△ABC 中,点P 是边AC 上的一个动点,过P 作直线MN ∥BC ,设MN 交∠BCA 的平分线于点E ,交∠BCA 的外角平分线于点F .(1)求证:PE =PF ;(2)当点P 在边AC 上运动时,四边形BCFE 可能是矩形吗?说明理由;(3)若在AC 边上存在点P ,使四边形AECF 是正方形,且 AP BC =32.求此时∠A 的大小.17.▱ABCD 的对角线AC ,BD 交于点O ,∠AOD=60°,∠ADO=90°,BD=12,点P 是AO 上一动点,点Q 是OC 上一动点(P ,Q 不与端点重合),且AP=OQ ,连接BQ ,DP .(1)线段PQ 的长为 ;(2)设△PDO 的面积为S 1,△QBO 的面积为S 2,S 1+S 2的值是否发生变化?若不变,求出这个不变的值;若变化,请说明随着AP 的增大,S 1+S 2的值是如何变化的;(3)DP+BQ 的最小值是 .18.如图,在矩形ABCD 中,AB =4,AD =10,直角尺的直角顶点P 在AD 上滑动时(点P 与A ,D 不重合),一直角边经过点C ,另一直角边AB 交于点E ,我们知道,结论“Rt △AEP ∽Rt △DPC ”成立.(1)当∠CPD =30°时,求AE 的长;(2)是否存在这样的点P,使△DPC的周长等于△AEP周长的2倍?若存在,求出DP的长;若不存在,请说明理由.19.如图,在平面直角坐标系中,已知▱OABC的顶点A(10,0)、C(2,4),点D是OA的中点,点P在BC上由点B向点C运动.(1)求点B的坐标;(2)若点P运动速度为每秒2个单位长度,点P运动的时间为t秒,当四边形PCDA是平行四边形时,求t的值;(3)当△ODP是等腰三角形时,直接写出点P的坐标.20.如图,在口ABCD中,AB⊥AC,AB=1,,对角线BD、AC交于点O.将直线AC 绕点O顺时针旋转分别交BC、AD于点E、F.(1)试说明在旋转过程中,AF与CE总保持相等;(2)证明:当旋转角为90⁰时,四边形ABEF是平行四边形;(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,求出此时AC绕点O顺时针旋转的角度.21.如图①,将矩形纸片ABCD(AD>AB)折叠,使点C刚落在线段AD上,且折痕分别与边BC,AD相交,设折叠后点C,D的对应点分别为点G,H,折痕分别与边BC,AD相交于点E,F.(1)求证:四边形CEGF是菱形;(2)如图②,若AB=3,BC=9,当点G与点A重合时,求折痕EF的长.22.已知正方形ABCD,点F是射线DC上一动点(不与C、D重合),连接AF并延长交直线BC于点E,交BD于H,连接CH,过点C作CG⊥HC交AE于点G.(1)若点F在边CD上,如图1.①证明:∠DAH=∠DCH;②猜想△GFC的形状并说明理由.(2)取DF中点M,连结MG.若MG=5,正方形边长为8,求BE的长.23.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD 的中点.(1)求证:四边形PMEN是平行四边形;(2)请直接写出当AP为何值时,四边形PMEN是菱形;(3)四边形PMEN有可能是矩形吗?若有可能,求出AP的长;若不可能,请说明理由.24.如图,四边形OABC为矩形,OA=4,OC=5,正比例函数y=2x的图象交AB于点D,连接DC,动点Q从D点出发沿DC向终点C运动,动点P从C点出发沿CO向终点O运动.两点同时出发,速度均为每秒1个单位,设从出发起运动了ts.(1)求△PCQ的面积S△PCQ=?(用t的代数式表示);(2)问:是否存在时刻t使S△DOP=S△PCQ?为什么?(3)当t为何值时,△DPQ是一个以DP为腰的等腰三角形?25.如图1,平行四边形ABCD中,AB=7,BC=10,点P是BC边上的点,连结AP,以AP 为对称轴作△ABP的轴对称图形△AQP.(1)如图1,连接CQ,若CQ∥AP,求BP的长;(2)如图2,当点P,Q,D三点共线时,恰有∠DCQ=∠DPC,求BP的长;(3)如图3,若点P在边BC运动的过程中,点Q到CD的最短距离为1,求BP的长.26.矩形ABCD的边长AB=18cm,点E在BC上,把△ABE沿AE折叠,使点B落在CD边的点F处,∠BAE=30°.(1)如图1,求DF的长度;(2)如图2,点N从点F出发沿FD以每秒1cm的速度向点D运动,同时点P从点A出发沿AF以每秒2cm的速度向点F运动,运动时间为t秒(0<t<9),过点P作PM⊥AD,于点M.①请证明在N、P运动的过程中,四边形FNMP是平行四边形;②连接NP,当t为何值时,△MNP为直角三角形?27.在矩形ABCD中,点E为射线BC上一动点,连接AE.(1)当点E在BC边上时,将△ABE沿AE翻折,使点B恰好落在对角线BD上点F处,AE 交BD于点G.①如图1,若BC=AB,求∠AFD的度数;②如图2,当AB=4,且EF=EC时,求BC的长.(2)在②所得矩形ABCD中,将矩形ABCD沿AE进行翻折,点C的对应点为C',当点E,C',D三点共线时,求BE的长.28.如图1,在正方形ABCD中,边长为2a,点E是AB边上的一个动点(点E与点A,B不重合),连接CE,过点B作BF⊥CE于点G,交AD于点F.(1)求证:AF=BE;(2)如图2,当点E运动到AB中点时,连接DG,求证:DG=2a;(3)如图3,在(2)的条件下,过点C作CM⊥DG于点H,分别交AD,BF于点M,N,求的值.29.如图,点F在四边形ABCD的边AB上.(1)如图1,当四边形ABCD是正方形时,过点B作BE⊥CF,垂足为O,交AD于点E.求证:BE=CF;(2)当四边形ABCD是矩形,AD=6,AB=8时,①如图2,点P是BC上的一点,过点P作PE⊥CF,垂足为O,点O恰好落在对角线BD上,求的值;②如图3,点P是BC上的一点,过点P作PE⊥CF,垂足为O,点O恰好落在对角线BD上,延长EP、AB交于点G,当BG=2时,请直接写出DE的值.30.如图,矩形ABCD中,AD=3厘米,AB=a厘米(a>3).动点M,N同时从B点出发,分别沿B⇒A,B⇒C运动,速度是1厘米/秒.过M作直线垂直于AB,分别交AN,CD于P,Q.当点N到达终点C时,点M也随之停止运动.设运动时间为t秒.(1)若a=4厘米,t=1秒,则PM=厘米;(2)若a=5厘米,求时间t,使△PNB∽△PAD,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形PMBN与梯形PQDA的面积相等,求a的取值范围;(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN,梯形PQDA,梯形PQCN的面积都相等?若存在,求a的值;若不存在,请说明理由.。
专题5 特殊平行四边形的动点问题
专题5特殊平行四边形的动点问题类型一、一般动点问题【例1】如图,在Rt ABC ∆中,90,60B AC ∠=︒=cm,60A ∠=︒,点D 从点C 出发沿CA 方向以4cm/s 的速度向点A 匀速运动,同时点E 从点A 出发沿AB 方向以2cm/s 的速度向点B 匀速运动.当其中一个点到达终点时,另一个点也随之停止运动.设点,D E 运动的时间是t s (015)t <≤.过点D 作DF BC ⊥于点F ,连接,DE EF .(1)求证:AE=DF ;(2)四边形AEFD 能够成为菱形吗?如果能,求出相应的t 值,如果不能,说明理由;(3)当t 为何值时,△DEF 为直角三角形?请说明理由.【解答】(1)证明:根据题意可知CD=4t ,AE=2t ,∵∠B=90°,∠A=60°,∴∠C=30°,∴DF=21DC=2t.∵AE=2t ,DF=2t ,∴AE=DF.(2)能.理由如下:∵AB ⊥BC ,DF ⊥BC ,∴AE ∥DF.∵AE=DF ,AE ∥DF ,∴四边形AEFD 为平行四边形,∴要使平行四边形AEFD 为菱形,则需AE=AD ,即2t=60-4t ,解得t=10,∴当t=10时,四边形AEFD 为菱形.(3)根据题意可知需分∠EDF=90°或∠DEF=90°两种情况讨论.①当∠EDF=90°时,∵∠EDF=∠B=∠DFE=90°,∴四边形DEBF 是矩形,∴∠DEB=90°,∴∠AED=90°.∵∠AED=90°,∠A=60°,∴∠ADE=30°.∵∠AED=90°,∠ADE=30°,∴AD=2AE ,即60-4t=4t ,解得t=215.②当∠DEF=90°时,∵四边形AEFD 为平行四边形,∴EF ∥AD ,∴∠ADE=∠DEF=90°.∵∠ADE=90°,∠A=60°,∴AD=21AE ,即60-4t=21×2t ,解得t=12.综上所述,当t=215或12时,△DEF 为直角三角形.【例2】如图在平面直角坐标系中,A (16,0)、C (0,8),四边形OABC 是矩形,D 、E 分别是OA 、BC 边上的点,沿DE 折叠矩形,点A 恰好落往y 轴上的点C 处,点B 落B '处。
特殊平行四边形动点及存在性问题(压轴题)
特殊平行四边形动点及存在性问题(压轴题)例1】在正方形ABCD中,DM=2,N是AC上的动点,求使得DN+MN最小的N点坐标。
解:由于正方形对称性,不妨设N在AC上且AN=x,则NC=8-x,由勾股定理得DN=sqrt(x^2+4),MN=sqrt((8-x)^2+4),因此DN+MN=sqrt(x^2+4)+sqrt((8-x)^2+4),对XXX求导得到x=2,即N点坐标为(2,6)。
练1】在平面直角坐标系中,矩形OACB的顶点O在坐标原点,顶点A、B分别在x轴、y轴的正半轴上,OA=3,OB=4,D为边OB的中点。
1)若E为边OA上的一个动点,求使得△CDE周长最小的E点坐标。
解:由于矩形OACB的对称性,不妨设E在OA上且AE=x,则OE=3-x,CE=4-x,DE=sqrt((3-x)^2+x^2),CD=sqrt((4-x)^2+9),因此△CDE周长为sqrt((3-x)^2+x^2)+sqrt((4-x)^2+9),对其求导得到x=1/2,即E点坐标为(1/2,3/2)。
2)若E、F为边OA上的两个动点,且EF=2,求使得四边形CDEF周长最小的E、F点坐标。
解:同样设AE=x,则EF=2,AF=3-x,OE=3-x/2,OF=2-x/2,CE=4-x,CF=5/2-x/2,DE=sqrt((3-x/2)^2+x^2),DF=sqrt((2-x/2)^2+(5/2-x/2)^2),因此四边形CDEF的周长为sqrt((3-x/2)^2+x^2)+sqrt((2-x/2)^2+(5/2-x/2)^2)+2,对其求导得到x=1/2,即E、F点坐标分别为(1/2,3/2)和(2,1/2)。
例2】在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P 在BC上运动,当三角形△ODP是腰长为5的等腰三角形时,求P点坐标。
解:由于OD=DA=5,因此△ODP是等腰直角三角形,即OP=DP=5/sqrt(2),又因为P在BC上,设BP=x,则PC=4-x,由勾股定理得到x^2+PC^2=OP^2,代入PC=4-x,解得x=2,因此P点坐标为(2,2)。
四边形中的动点问题
例5、如图,直角梯形OABC中,AB∥OC,O为坐标原点, 点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2, 2√3 ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发, 沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A 运动,两点同时出发,速度都为每秒1个单位长度.设点P运 动的时间为t秒.
APQD是平行四边形.
(1)求a的值; (2)线段PQ是否可能平分对角线BD?若能,求t的值, 若不能,请说明理由;
(3)若在某一时刻点P恰好在DQ的垂直平分线上,求此 时t的值.
例3.在梯形ABCD中, AD∥BC,AB=AD=CD=5cm,BC=11cm,点P从 点D开始沿DA边以每秒1cm的速度移动,点Q从点B开始沿BC边以每 秒2cm的速度移动(当点P到达点A时,点P与点Q同时停止移动), 假设点P移动的时间为x(秒),四边形ABQP的面积为y(cm2). (1)求y关于x的函数解析式,并写出x的取值范围; (2)在移动的过程中,求四边形ABQP的面积与四边形QCDP的面 积相等时x的值; (3)在移动的过程中,是否存在x使得PQ=AB,若存在求出所有x的 值,若不存在请说明理由.
(1)求OH的长; (2)若△OPQ的面积为S,求S与t之间的函数关系式. (3)设PQ与OB交于点M.当t为何值时,△OPM为等腰三 角形?y
A
B
QM
H
P
O
Cx
例7、如图,在平面直角坐标系中,直线y=- x+b(b>0)分别交x轴、 y轴于A、B两点,以OA、OB为边作矩形OACB,D为BC的中点.以M(4, 0)、N(8,0)为斜边端点作等腰直角三角形PMN,点P在第一象限, 设矩形OACB与△PMN重叠部分的面积为S. (1)求点P的坐标; (2)求S与b的函数关系式; (3)若在直线y=- x+b(b>0)上存在点Q,使∠OQM=90°,求b的 取值范围;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊四边形中的动态问题所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题。
关键:动中求静.数学思想:分类思想 数形结合思想 转化思想1、如图,在四边形ABCD 中,E F G H 、、、分别是AB BC CD DA 、、、边上的中点,阅读下列材料,回答问题: ⑴连结AC BD 、,由三角形中位线的性质定理可证四边形EFGH 是 .⑵对角线AC BD 、满足条件 时,四边形EFGH 是矩形. ⑶对角线AC BD 、满足条件 时,四边形EFGH 是菱形. ⑷对角线AC BD 、满足条件 时,四边形EFGH 是正方形。
N OHGFEABD2、如图1,梯形ABCD 中,AD ∥BC ,90B ︒∠=,14,18,21AB cm AD cm BC cm ===,点P 从A 开始沿AD 边以1cm /秒的速度移动,点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,如果,P Q 分别从,A C 同时出发,设移动时间为t 秒.当t = 时,四边形是平行四边形;当t = 时,四边形是等腰梯形.3、如图2,正方形ABCD 的边长为4,点M 在边DC 上,且1DM =,N 为对角线AC 上任意一点,则DN MN +的最小值为4、在△ABC 中,90ACB ︒∠=,AC BC =,直线MN 经过点C ,且AD MN ⊥于D ,BE MN ⊥于E 。
(1)当直线MN 绕点C 旋转到图1的位置时,求证:DE AD BE =+; (2)当直线MN 绕点C 旋转到图2的位置时,求证:DE AD BE =-; (3)当直线MN 绕点C 旋转到图3的位置时,试问DE AD BE 、、具有怎样的等量关系?请写出这个等量关系,并加以证明.CBAE D图1NMABCDE MN图2ACBEDN M 图35、如图,在梯形ABCD 中,3545AD BC AD DC AB B ====︒∥,,,.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △6、在矩形ABCD 中,204AB cm BC cm ==,,点P 从A 开始沿折线A B C D →→→以4/cm s 的速度运动,点Q 从C 开始沿CD 边以1/cm s 的速度移动,如果点P Q 、分别从A C 、同时出发,当其中一点到达点D 时,另一点也随之停止运动,设运动时间为()t s ,t 为何值时,四边形APQD 也为矩形?7、如图,梯形OABC 中, O 为直角坐标系的原点, A B C 、、的坐标分别为(14,0)、(14,3)、(4,3)点P Q 、同时从原点出发,分别作匀速运动,点P 沿OA 以每秒1个单位向终点A 运动,点Q 沿OC CB 、以每秒2个单位向终点B 运动.当这两点中有一点到达自己的终点时,另一点也停止运动 ⑴设从出发起运动了x 秒,且 2.5x >时,Q 点的坐标; ⑵当x 等于多少时,四边形OPQC 为平行四边形? ⑶四边形OPQC 能否成为等腰梯形?说明理由.⑷设四边形OPQC 的面积为y ,求出当 2.5x >时y 与x 的函数关系式;并求出y 的最大值;8、如图(1),小明在研究正方形ABCD 的有关问题时,得出:“在正方形ABCD 中,如果点E 是CD 的中点,点F是BC 边上一点,且EAD FAE ∠=∠,那么AE EF ⊥。
”他又将“正方形”改为“矩形”、“菱形”、和“任意平行四边形”(如图(2),图(3),图(4),其他条件不变,发现仍然有“AE EF ⊥”的结论. 你同意小明的观点吗?若同意,请结合图(4)加以说明;若不同意,请说明理由。
COA(14,0) xDADAD E③②P Q D C B A D C B QP A B C D ①F O M NE A B C ﻩ(1) (2)ﻩ(3)(4)8、操作:将一把三角尺放中正方形ABCD 中,并使它的直角顶点F 在对角线AC 上滑动,直角的一边始终经过点B ,另一边与射线DC 相交于点Q ,探究:①当点Q 在DC 上时,线段PQ 与线段PB 之间有怎样的大小关系?试说明你观察到的结论;②当点Q 在DC 的延长线上时,①中你观察到的结论还成立吗?说明理由.10、如图所示,在ΔABC 中,点O 是AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交BCA ∠的平分线于点E ,交BCA ∠的外角平分线于点F 。
①试说明OE OF =;②当点O 运动到何处时,四边形AECF 是矩形?请简要说明理由; ③当点O 运动时,四边形AECF 有可能是正方形吗?请简要说明理由.11。
(2014•黑龙江绥化,第27题10分)如图,在平面直角坐标系中,已知矩形A OBC 的顶点C 的坐标是(2,4),动点P 从点A出发,沿线段AO 向终点O 运动,同时动点Q 从点B 出发,沿线段BC向终点C运动.点P 、Q 的运动速度均为1个单位,运动时间为t 秒.过点P 作P E⊥AO 交AB 于点E. (1)求直线AB 的解析式;(2)设△PEQ 的面积为S ,求S 与t 时间的函数关系,并指出自变量t 的取值范围;(3)在动点P 、Q 运动的过程中,点H 是矩形AO BC 内(包括边界)一点,且以B 、Q 、E 、H 为顶点的四边形是菱形,直接写出t 值和与其对应的点H 的坐标.12.(2014•四川成都,第20题10分)如图,矩形ABCD中,AD=2AB,E是AD边上一点,DE=AD(n 为大于2的整数),连接BE,作BE的垂直平分线分别交AD,BC于点F,G,FG与BE的交点为O,连接BF和EG。
(1)试判断四边形BFEG的形状,并说明理由;(2)当AB=a(a为常数),n=3时,求FG的长;(3)记四边形BFEG的面积为S1,矩形ABCD的面积为S2,当=时,求n的值.(直接写出结果,不必写出解答过程)13.(2014•四川绵阳,第24题12分)如图1,矩形ABCD中,AB=4,AD=3,把矩形沿直线AC 折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△DEC≌△EDA;(2)求DF的值;(3)如图2,若P为线段EC上一动点,过点P作△AEC的内接矩形,使其定点Q落在线段AE上,定点M、N落在线段AC上,当线段PE的长为何值时,矩形PQMN的面积最大?并求出其最大值。
14. (2014•山西,第23题11分)课程学习:正方形折纸中的数学.动手操作:如图1,四边形ABCD是一张正方形纸片,先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后沿直线CG折叠,使B点落在EF上,对应点为B′.数学思考:(1)求∠CB′F的度数;(2)如图2,在图1的基础上,连接AB′,试判断∠B′AE与∠GCB′的大小关系,并说明理由;解决问题:(3)如图3,按以下步骤进行操作:第一步:先将正方形ABCD对折,使BC与AD重合,折痕为EF,把这个正方形展平,然后继续对折,使AB与DC重合,折痕为MN,再把这个正方形展平,设EF和MN相交于点O;第二步:沿直线CG折叠,使B点落在EF上,对应点为B′,再沿直线AH折叠,使D点落在EF上,对应点为D′;第三步:设CG、AH分别与MN相交于点P、Q,连接B′P、PD′、D′Q、QB′,试判断四边形B′PD′Q 的形状,并证明你的结论.15。
(2014•丽水,第23题10分)提出问题:(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;类比探究:(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;综合运用:(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.中考数学与特殊四边形有关的压轴题(选择一)1.(2014•浙江湖州,第10题3分)在连接A地与B地的线段上有四个不同的点D、G、K、Q,下列四幅图中的实线分别表示某人从A地到B地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是()ﻩ A.ﻩB.ﻩC.ﻩD。
分析:分别构造出平行四边形和三角形,根据平行四边形的性质和全等三角形的性质进行比较,即可判断.解:A选项延长AC、BE交于S,∵∠CAE=∠EDB=45°,∴AS∥ED,则SC∥DE。
同理SE∥CD,∴四边形SCDE是平行四边形,∴SE=CD,DE=CS,即乙走的路线长是:AC+CD+DE+EB=AC+CS+SE+EB=AS+BS;B选项延长AF、BH交于S,作FK∥GH,1∵∠SAB=∠S1AB=45°,∠SBA=∠S1BA=70°,AB=AB,∴△SAB≌△S1AB,∴AS=AS1,BS=BS1,∵∠FGH=67°=∠GHB,∴FG∥KH,∵FK∥GH,∴四边形FGHK是平行四边形,∴FK=GH,FG=KH,∴AF+FG+GH+HB=AF+FK+KH+HB,∵FS1+S1K>FK,∴AS+BS>AF+FK+KH+HB,即AC+CD+DE+EB>AF+FG+GH+HB,同理可证得AI+IK+KM+MB<AS2+BS2<AN+NQ+QP+PB,又∵AS+BS<AS2+BS2,故选D.点评:本题考查了平行线的判定,平行四边形的性质和判定的应用,注意:两组对边分别平行的四边形是平行四边形,平行四边形的对边相等。
2.(2014年广西南宁,第11题3分)如图,在▱ABCD中,点E是AD的中点,延长BC到点F,使CF:BC=1:2,连接DF,E C。
若AB=5,AD=8,sinB=,则DF的长等于()A.B.C。
ﻩ D.ﻩ2考点:ﻩ平行四边形的判定与性质;勾股定理;解直角三角形.。
分析:ﻩ由“平行四边形的对边平行且相等”的性质推知AD∥BC,且AD=BC;然后根据中点的定义、结合已知条件推知四边形CFDE的对边平行且相等(DE=CF,且DE∥CF),即四边形CFDE是平行四边形.如图,过点C作CH⊥AD于点H。
利用平行四边形的性质、锐角三角函数定义和勾股定理求得CH=4,DH=1,则在直角△EHC中利用勾股定理求得CE的长度,即DF的长度.解答:证明:如图,在▱ABCD中,∠B=∠D,AB=CD=5,AD∥BC,且AD=BC=8.∵E是AD的中点,∴DE=A D。
