梯形的面积4
梯形的4个面积公式

我们要找出梯形的4个面积公式。
首先,我们需要了解梯形面积的基本公式,然后在此基础上推导出其他公式。
梯形面积的基本公式是:
面积= (上底+ 下底) ×高÷ 2
这个公式是梯形面积的基础,我们将在此基础上推导其他公式。
根据梯形面积的基本公式,我们可以推导出以下3个公式:1. 已知上底a、下底b和高h,求面积:
面积= (a + b) × h ÷ 2
2. 已知下底b、高h和面积S,求上底a:
a = (2 × S × b) ÷ h - b
3. 已知上底a、高h和面积S,求下底b:
b = (2 × S × a) ÷ h - a
根据梯形面积的基本公式,我们可以得到以下3个公式:
1. 已知上底a、下底b和高h,求面积:
面积= (a + b) × h ÷ 2
2. 已知下底b、高h和面积S,求上底a:
a = 2*S/h - b
3. 已知上底a、高h和面积S,求下底b:
b = 2*S/h - a。
人教版数学五年级上册 第六单元《 梯形的面积》(同步练习)(含答案)

《梯形的面积》(同步练习)-五年级上册数学人教版一.选择题(共6小题)1.空地上有一堆圆木,顶层有2根,底层有6根,一共5层,且每相邻的两层相差1根,这堆圆木有()根。
A.20B.40C.602.一个梯形的上底增加2厘米,下底减少2厘米,高不变,它的面积与原面积相比()A.变大了B.变小了C.不变D.高不知道,所以无法比较3.有一堆钢管,最上层是6根,最下层是10根,一共5层.这堆钢管有()根.A.40B.50C.804.如图,这个梯形的面积是m2。
()A.100B.80C.60D.405.如图,两条平行线间的三个图形,()的面积最大。
A.①B.②C.③D.无法确定6.一个梯形若上底增加2厘米,则成为一个正方形;若上底缩小4厘米,则成为一个三角形。
这个梯形的面积是()平方厘米。
A.120B.60C.30D.24二.填空题(共8小题)7.一个零件的截面是梯形,梯形上、下底的和与高相等,都是40毫米,这个零件截面的面积是平方毫米.8.一个梯形的上底增加2厘米后就变成了一个边长为6厘米的正方形,这个梯形的面积是平方厘米。
9.一堆圆木堆成横截面为梯形的形状,底层有12根,顶层有5根,共8层,这堆圆木一共有根。
10.用12根1米长的篱笆靠一面墙围成一个高为6米的直角梯形(如图),围成的梯形面积是。
11.用两个完全一样的梯形拼成一个平行四边形。
已知平行四边形的面积是30平方厘米,梯形的上下底之和是10厘米,每个梯形的高是厘米。
12.一个梯形的上底是5厘米,比下底短2厘米,高是上底的1.5倍,这个梯形的面积是cm2。
一个三角形与这个梯形的面积和高都相等,这个三角形的底是cm。
13.一块梯形木板的上底是4分米,下底是8分米。
高是2分米,如果从这块木板上锯下一块最大的三角形,剩下的面积是平方分米。
14.一堆水管,上层3根,底层12根,每相邻层都是相差1根,共堆放了10层,这堆水管共有根。
三.判断题(共5小题)15.在梯形内画一个最大的三角形,三角形面积等于这个梯形面积的一半。
梯形的面积_《梯形的面积》典型例题
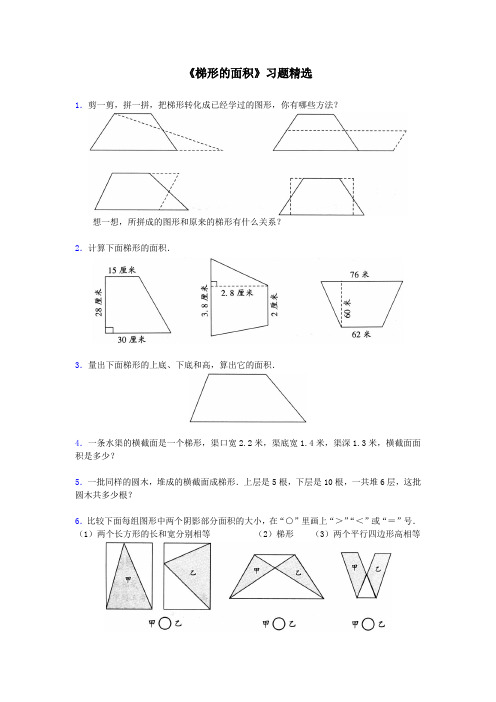
《梯形的面积》习题精选1.剪一剪,拼一拼,把梯形转化成已经学过的图形,你有哪些方法?想一想,所拼成的图形和原来的梯形有什么关系?2.计算下面梯形的面积.3.量出下面梯形的上底、下底和高,算出它的面积.4.一条水渠的横截面是一个梯形,渠口宽2.2米,渠底宽1.4米,渠深1.3米,横截面面积是多少?5.一批同样的圆木,堆成的横截面成梯形.上层是5根,下层是10根,一共堆6层,这批圆木共多少根?6.比较下面每组图形中两个阴影部分面积的大小,在“○”里画上“>”“<”或“=”号.(1)两个长方形的长和宽分别相等(2)梯形(3)两个平行四边形高相等参考答案1.略2.630平方厘米 8.12平方厘米 4140平方米3.略4.2.34平方米5.45根6.(1)=(2)=(3)=《梯形的面积》习题精选一、填空1.0.45公顷=()平方米2.两个完全一样的梯形可以拼成一个()形.3.一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是()平方厘米.4.平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是()平方厘米.5.梯形的上底增加3厘米,下底减少3厘米,高不变,面积().6.有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有()根.二、判断题1.平行四边形的面积大于梯形面积.()2.梯形的上底下底越长,面积越大.()3.任何一个梯形都可以分成两个等高的三角形.()4.两个形状相同的三角形可以拼成一个平行四边形.()三、选择1.两个()梯形可以拼成一个长方形.①等底等高②完全一样③完全一样的直角2.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则两腰长是().①24厘米②12厘米③18厘米④36厘米四、应用题1.一条水渠横截面是梯形,渠深0.8米,渠底宽1.2米,渠口宽2米,横截面积是多少平方米?2.两个同样的梯形,上底长23厘米,下底长27厘米,高20厘米.如果把这两个梯形拼成一个平行四边形,这个平行四边形的面积是多少?3.梯形的上底是3.8厘米,高是4厘米,已知它的面积是20平方厘米,下底是多少厘米?参考答案一、填空1.0.45公顷=( 4500 )平方米2.两个完全一样的梯形可以拼成一个(平行四边)形.3.一个梯形上底与下底的和是15厘米,高是8.8厘米,面积是( 66 )平方厘米.4.平行四边形的底是2分米5厘米,高是底的1.2倍,它的面积是( 750 )平方厘米.5.梯形的上底增加3厘米,下底减少3厘米,高不变,面积(不变).6.有一堆圆木堆成梯形,最上面一层有3根,最下面一层有7根,一共堆了5层,这堆圆木共有( 25 )根.二、判断题1.平行四边形的面积大于梯形面积.(×)2.梯形的上底下底越长,面积越大.(×)3.任何一个梯形都可以分成两个等高的三角形.(√)4.两个形状相同的三角形可以拼成一个平行四边形.(√)三、选择1.两个(③)梯形可以拼成一个长方形.①等底等高②完全一样③完全一样的直角2.等腰梯形周长是48厘米,面积是96平方厘米,高是8厘米,则两腰长是(①).①24厘米②12厘米③18厘米④36厘米四、应用题1.(1.2+2)×0.8÷2=1.28(平方米)答:横截面积是1.28平方米.2.(23+27)×20÷2×2=1000(平方厘米)答:这个平行四边形的面积是1000平方厘米.3.20×2÷4-3.8=6.2(厘米)答:下底是6.2厘米.例.学校航空模型小组制作的飞机平面图,是由两个完全相同的梯形组成的,如图所示.这个平面图的面积是多大?(图中单位:毫米)分析:机翼是由两个梯形组成的,所以解法可以是:根据梯形面积公式,求出一个梯形的面积,再乘2,就得出了这个机翼平面图的面积.解:(100+48)×250÷2×2=148×125÷2×2=37000(平方毫米)答:平面图的面积是37000平方毫米.例.下图中直角梯形的面积是多少平方厘米?分析:要求梯形的面积,先要求出梯形的高,我们可以根据45°这个角再连出一个梯形的高,如下图连出的三角形为等腰直角三角形,这就得出梯形的高就是2厘米,解决了关键问题.解:(4+6)×2÷2=10(平方厘米)答:直角梯形的面积是10平方厘米.例.一个梯形,它的高与上底的乘积是15平方厘米,高与下底的乘积是21平方厘米,这个梯形的面积是多少平方厘米?分析:根据题意可知:高×上底=15,高×下底=21,所以:高×上底+高×下底=(上底+下底)×高……乘法分配率又因为(上底+下底)×高=梯形面积×2,即15+21=36是梯形面积的2倍.解:(15+21)÷2=18(平方厘米)答:梯形面积是18平方厘米.例.如图所示,为一直角梯形土地,已知阴影部分的面积为2145平方米,若在另一不知面积的部分上种上水稻,每平方米收得稻谷1.2千克.可收水稻多少千克?分析1:不知面积部分是三角形,已知其底是60米,关键是求出它的高.在直角梯形中,它的高就是阴影三角形的高,也是不知道.而已知面积的三角形的底为78米,高可求出来,问题得解.解法1:60×(2145×2÷78)÷2×1.2=60×55÷2×1.2=3300÷2×1.2=1650×1.2=1980(千克)答:可收水稻1980千克.分析2:可以先求出直角梯形的面积,再减去已知阴影部分的面积,同样可得解.解法2:[(60+78)×(2145×2÷78)÷2-2145]×1.2=[138×55÷2-2145]×1.2=(3795-2145)×12=1650×1.2=1980(千克)答:可收水稻1980千克.例.一个直角梯形,若下底增加1.5米,则面积就增加3.15平方米,上底增加1.2米,就得到一个正方形.这个直角梯形的面积是多少平方米?分析:若下底增加1.5米,则面积增加一个底为1.5米的三角形,已知三角形的面积是3.15 平方米,底是1.5米,就可以求出该三角形的高,也就是梯形的高,3.15×2÷1.5=4.2(米).又知上底延长1.2米能得到一个正方形,说明梯形的下底和高相等,并且下底比上底多1.2米,这样可以求出梯形的上底,4.2-1.2=3(米),已知梯形上底3米,下底和高都是4.2米,可以求出直角梯形的面积.解:(3+4.2)×4.2÷2=15.12(平方米)答:这个直角梯形的面积是15.12平方米.例.一个梯形,如果它的上底增加3米,下底和高都不变,那么它的面积就增加9.6平方米;如果上底和下底都不变,高增加3米,那么它的面积就增加18.6米,求原梯形的面积.分析:根据题意,图中有阴影部分的三角形的面积就是9.6平方米,此三角形的底为3米,从而可以求出高h ,h 也是梯形的高. 梯形的面积=h b a ⨯+2.如果上、下底都不变,高增加3米,梯形的面积变为 322)3(2⨯++⨯+=+⨯+b a h b a h b a . 由6.1832=⨯+b a ,可得2.636.182=÷=+b a (米).问题得解.解:h =9.6×2÷3=6.4(米)2.636.182=÷=+b a (米) 原梯形的面积=h b a ⨯+2=6.2×6.4=39.68(平方米)答:原梯形的面积是39.68平方米.例1.下图中梯形的面积是360平方厘米.图形甲比乙少多少平方厘米?分析1:已知梯形的面积是360平方厘米,又知梯形的上底和下底,可以求出梯形的高,也是三角形的高,再通过三角形的底和高分别计算甲、乙的面积,进而求出甲比乙的面积少多少平方厘米.解:360×2÷(10+30)=18(厘米)10×18÷2=90(平方厘米)30×18÷2=270(平方厘米)270-90=180(平方厘米)分析2:根据梯形的性质,上底和下底平行,所以甲和乙这两个三角形的高相等.由已知条件乙三角形的底是甲三角形底的3倍(30÷10),所以乙的面积是甲的3倍,即乙的面积比甲多2倍.梯形面积一共是360平方米,一共分成4份,一份是90平方米,所以甲比乙少90×2=180平方米.解:30÷10=3360÷(3+1)×(3-1)=90×2=180(平方米)答:甲的面积比乙少180平方厘米.例.有一个零件的横截面如下图.求这个零件横截面的面积.(图中单位:毫米)分析:由对图形的观察可知,这个零件的横截面面积,是一个长方形面积减去一个梯形面积所得的差.解:60×28-(36+24)×10÷2=1680-300=1380(平方毫米)答:这个零件横截面的面积是1380平方毫米.例.已知ABC ∆和EFG ∆是两个完全一样的直角三角形,4=BD ,3=DF ,12=FG ,求梯形ABDE 的面积.分析:因为ABC ∆和EFG ∆面积相等,从中同时减去EDC ∆,剩下的面积也一定相等,即:梯形ABDE 与梯形DFGC 的面积相等,也就是说,要求梯形ABDE 的面积,只要求出梯形DFGC 的面积就可以了.解:在梯形DFGC 中,8412=-=DC ,3=DF ,12=FG(8+12)×3÷2=30答:梯形ABDE 的面积是30.。
四年级下册数学教案 2.3梯形的面积 青岛版(五四学制) (1)

梯形的面积计算教学内容:课本34--39页.教学目标:1、知道梯形面积计算公式的推导过程;2、会用梯形面积计算公式计算梯形面积;3、培养同学们分析问题,解决问题的能力。
教学重点:探索推导梯形面积计算公式。
教学难点:探索推导梯形面积计算公式及对计算公式的理解运用。
教具准备:自制教具、课件、白板软件。
学具准备:两个完全一样的卡纸梯形(一红一蓝)。
教学过程:一、导入。
1、生活中有许多图形。
回忆一下,我们曾经学过哪些图形的面积?(长方形、正方形、平行四边形、三角形),它们的面积计算公式是什么?2、(出示梯形)认识这个图形吗?梯形的面积怎么求?要想求出梯形的面积,先让我们来回忆一下梯形吧!梯形是由几条边组成的?而且有一组边是互相()的;(分别出示梯形的上底、下底、腰和高);说说梯形的面积是指哪个部分?1、认识了梯形的面积,我们就要想办法求出它的面积。
请同学们先来看看咱们今天的学习目标有哪些(一生读学习目标)。
希望通过这节课的学习,同学们都能达到学习目标。
二、探索梯形面积计算公式1、学生拿出准备好的两个梯形,教师在白板软件上也出示两个梯形。
师:这是两个什么样的梯形?怎么证明它们是完全一样的?(学生动手操作完全重合)师:请一位同学到白板软件上来操作(学生在白板软件上动手旋转、平移直到完全重合)。
师:要想求出梯形的面积,就要想办法把它转化成我们已经学过的图形的面积。
你能用这两个完全一样的梯形拼成一个我们学过的图形吗?(学生尝试动手操作,并请一生上白板来动手操作演示。
)师:同学们拼成一个什么图形?(板书平行四边形)教师用教具在黑板上再次演示。
师:现在我们来思考两个问题。
①平行四边形的底与梯形的底有什么关系?②平行四边形的高与梯形的高有什么关系?(四人一小组讨论)学生汇报发现,教师出示课件演示过程。
师:因为平行四边形的底等于梯形的上底与下底的和,平行四边形的高等于梯形的高,所以我们可以用平行四边形的面积公式推导出梯形的面积公式。
四年级下册数学教案-6.2 运用多种方法推导梯形的面积公式 ︳西师大版

四年级下册数学教案-6.2 运用多种方法推导梯形的面积公式︳西师大版一、教学目标1. 让学生掌握梯形的面积公式,并能运用公式计算梯形的面积。
2. 通过多种方法推导梯形的面积公式,培养学生的逻辑思维能力和空间想象力。
3. 使学生能够运用梯形的面积公式解决实际问题,提高学生的应用能力。
二、教学内容1. 梯形的面积公式:梯形的面积 = (上底下底) × 高÷ 22. 推导梯形面积公式的方法:拼凑法、分割法、三角形面积法。
3. 运用梯形面积公式解决实际问题。
三、教学过程1. 导入:通过复习三角形的面积公式,引导学生思考如何计算梯形的面积。
2. 探究:引导学生运用拼凑法、分割法、三角形面积法推导梯形的面积公式。
a. 拼凑法:将两个完全相同的梯形拼成一个平行四边形,推导出梯形的面积公式。
b. 分割法:将梯形分割成两个三角形和一个矩形,推导出梯形的面积公式。
c. 三角形面积法:将梯形分割成两个三角形,计算两个三角形的面积之和,推导出梯形的面积公式。
3. 讲解:讲解梯形面积公式的推导过程,强调公式中的各个要素。
4. 练习:布置一些梯形面积的计算题目,让学生独立完成,巩固所学知识。
5. 应用:给出一些实际问题,如计算梯形花坛的面积、梯形水渠的体积等,让学生运用梯形面积公式解决。
6. 总结:总结本节课所学的梯形面积公式及其推导方法,强调在实际问题中的应用。
四、教学评价1. 课堂问答:通过提问检查学生对梯形面积公式的理解和掌握程度。
2. 练习完成情况:检查学生完成练习题目的正确率和速度,评价学生对梯形面积公式的运用能力。
3. 课后作业:布置一些梯形面积相关的作业,让学生在课后独立完成,进一步巩固所学知识。
4. 学生反馈:听取学生对本节课教学的意见和建议,不断改进教学方法,提高教学质量。
五、教学反思本节课通过多种方法推导梯形的面积公式,培养了学生的逻辑思维能力和空间想象力。
在教学过程中,要注意引导学生积极参与,鼓励学生提出自己的想法和疑问,及时解答学生的疑惑。
专题05:多边形的面积-2023-2024学年五年级数学期末核心考点集训(人教版)

4 组合图形的面积(阴影部分面积)
【例8】求下列图形的面积。
【分析】正方形面积=边长×边长 梯形的面积=(上底+下底)×高÷2 阴影部分面积=正方形面积+梯形面积
9×9=81(平方厘米) (5+9)×(21-9)÷2 =14×12÷2 =84(平方厘米) 81+84=165(平方厘米)
1、求平面的组合图形面积时可以合理地进行割或补,使组合图形的面积转化成 我们学过的基础图形的面积进行求解。 2、求组合图形的方法: (1)分割法: 把一个组合图形分割成几个基础图形(平行四边形、正方形、长方形、三角形 和梯形、圆等),分别求出面积,再进行求和。 (2)添补法: 把一个组合图形补成一个基础图形,再从这个基础图形的面积减去几个基础图 形的面积,从而求出它们的面积差。
【分析】平行四边形的底=平行四边形的面积÷高
30.15÷4.5=6.7(厘米)
2、观察下图,图中长方形和平行四边形的面积相比,( C )。 A、长方形的面积大 B、平行四边形的面积大 C、面积一样大
3、一个边长为12厘米的正方形,和一个底为18厘米的平行四边形的 面积相等,那么这个平行四边形的高是多少厘米? 【分析】正方形的面积=边长×边长 平行四边形的高=平行四边形的面积÷底 12×12=144(平方厘米) 144÷18=8(厘米) 答:这个平行四边形的高是8厘米。
【例3】有一块平行四边形的空地,要在空地中间留出一条小路请 你求出空地的实际面积是多少平方米?
【分析】空地的实际面积=大平行四边形面积-小平行四边形面积 平行四边形面积=底×高 9×4-9×1.5 =9×(4-1.5) =9×2.5 =22.5(平方米) 答:空地的实际面积是22.5平方米。
1、一个平行四边形的面积是30.15平方厘米,高是4.5厘米,则底是 ( 6.7 )厘米。
面积公式大全(精品收藏)
面积公式大全1、长方形的周长=(长+宽)×2 C=(a+b)×22、正方形的周长=边长×4C=4a3、长方形的面积=长×宽S=ab4、正方形的面积=边长×边长 S=a。
a=a5、三角形的面积=底×高÷2 S=ah÷26、平行四边形的面积=底×高 S=ah7、梯形的面积=(上底+下底)×高÷2 S=(a+b)h÷28、直径=半径×2 d=2r半径=直径÷2 r=d÷29、圆的周长=圆周率×直径=圆周率×半径×2c=πd =2πr10、圆的面积=圆周率×半径×半径?=πr11、长方体的表面积=(长×宽+长×高+宽×高)×212、长方体的体积 =长×宽×高V =abh13、正方体的表面积=棱长×棱长×6 S=6a14、正方体的体积=棱长×棱长×棱长 V=a。
a.a= a15、圆柱的侧面积=底面圆的周长×高 S=ch16、圆柱的表面积=上下底面面积+侧面积S=2πr +2πrh=2π(d÷2)+2π(d÷2)h=2π(C÷2÷π) +Ch17、圆柱的体积=底面积×高V=ShV=πr h=π(d÷2) h=π(C÷2÷π) h18、圆锥的体积=底面积×高÷3V=Sh÷3=πrh÷3=π(d÷2) h÷3=π(C÷2÷π) h÷319、长方体(正方体、圆柱体)的体积=底面积×高 V=Sh表面积S=π*r^2+πrl (l为母线长)把圆锥体的侧面积打开是扇形,扇形的半径就是母线坐标几何一对垂直相交于平面的轴线,可以让平面上的任意一点用一组实数来表示。
北师大版数学五年级上册4.5《梯形的面积》说课稿2(3)
北师大版数学五年级上册4.5《梯形的面积》说课稿2 (3)一. 教材分析《梯形的面积》是北师大版数学五年级上册第4.5节的内容。
本节课是在学生已经掌握了三角形、平行四边形和梯形的基本概念以及三角形、平行四边形的面积计算方法的基础上进行学习的。
梯形的面积计算方法是数学中的重要内容,它在日常生活和解决实际问题中有着广泛的应用。
梯形的面积计算方法不仅涉及到数学知识,还培养学生的逻辑思维能力和解决问题的能力。
二. 学情分析五年级的学生已经具备了一定的几何图形认知能力和逻辑思维能力。
他们在学习三角形、平行四边形的面积计算时,已经掌握了转化、归纳、推理等基本的数学学习方法。
但是,对于梯形的面积计算,学生可能还存在着一定的困难,需要通过实例和操作来进一步理解和掌握。
三. 说教学目标1.知识与技能目标:学生能够理解梯形的面积计算方法,并能够运用梯形的面积公式计算实际问题。
2.过程与方法目标:学生通过自主探究、合作交流的方式,培养解决问题的能力和团队协作的能力。
3.情感态度与价值观目标:学生能够体验到数学与生活的联系,增强对数学的兴趣和信心。
四. 说教学重难点1.教学重点:学生能够理解梯形的面积计算方法,并能够运用梯形的面积公式计算实际问题。
2.教学难点:学生能够理解和推导梯形的面积公式,并能够灵活运用解决实际问题。
五. 说教学方法与手段1.教学方法:本节课采用问题驱动法、自主探究法、合作交流法等教学方法,引导学生主动参与学习,培养学生的解决问题的能力和团队协作的能力。
2.教学手段:利用多媒体课件、实物模型、学习单等教学手段,帮助学生直观地理解梯形的面积计算方法。
六. 说教学过程1.导入:通过复习三角形、平行四边形的面积计算方法,引出梯形的面积计算,激发学生的学习兴趣。
2.探究:学生自主探究梯形的面积计算方法,通过实物操作、小组讨论等方式,归纳出梯形的面积公式。
3.讲解:教师讲解梯形的面积公式,并通过实例来解释和应用梯形的面积公式。
梯形的面积计算
梯形面积一、知识点剖析梯形面积h=s×2÷(a+b)S=(a+b)h÷2 → a=s×2÷h—bb=s×2÷h—a二、典型例题类型①——已知上底、下底和高,求梯形面积例:求下图的面积(单位:dm)。
1524 2625同类型题计算下列各图的面积类型②——已知上底和下底与高的关系,求梯形面积例:下图是一个饲养场的平面图,一面靠墙,三面用铁丝围起来。
已知铁丝的长度是450米。
求为个包头场上面积。
120米同类型题如右图所示,一个花园一面靠墙,其它三面用篱笆围起,篱笆全长84米。
这个花园面积有多大?墙类型③——已知梯形的面积,求上底或下底或高例:一个梯形的面积是48平方分米,上底6分米,下底100厘米,高是多少分米?同类型题填一填。
图形上底/cm 下底/cm 高/cm 面积/cm2梯形7 4 204 8 125 5 50类型④——求阴影部分的面积例:如图:已知三角形的面积是64平方厘米,求梯形面积。
(单位:厘米)同类型题求出下列各图阴影部分的面积。
三、综合练习(一)填空1、一个梯形花坛,高10米,上下底之和是16米,面积是()。
2、一个梯形果园,上底27m,下底108m,高18m,每9㎡栽果树一棵,这个果园栽果树()棵3、一块直角梯形的地,它的下底是40米,如果上底增加38米,这块地就变成了正方形,原梯形的面积是( )平方米。
4、当梯形的上底逐渐缩小到一点时,梯形就转化成();当梯形的上底增大到与下底相等时,梯形就转化成()或()。
(二)判断1、面积相等的两个梯形,一定能拼成一个平行四边形。
()2、梯形的上底和下底越大,梯形的面积就越大。
()3、梯形的面积是平行四边形面积的一半。
()4、面积相等的两个梯形,形状不一定相等。
()5、一个平行四边形一定是由两个面积一样的梯形组成的。
()(三)选择1、右边梯形中,左右两个阴影部分的面积()A、左边大B、右边大C、一样大D、无法确定2、两个完全一样的梯形可以拼成一个平行四边形,这个平行四边形的底等于())。
四年级奥数.几何.风筝模型和梯形蝴蝶定理
板块一 风筝模型:(又叫任意四边形模型)S 4S 3S 2S 1O DC BA①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++风筝模型为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.板块二 梯形模型的应用梯形中比例关系(“梯形蝴蝶定理”):A BCDO baS 3S 2S 1S 4①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.梯形蝴蝶定理给我们提供了解决梯形面积与上、下底之间关系互相转换的渠道,通过构造模型,直接应用结论,往往在题目中有事半功倍的效果.(具体的推理过程我们可以用将在第九讲所要讲的相似模型进行说明)知识框架风筝模型和梯形蝴蝶定理【例 1】 图中的四边形土地的总面积是52公顷,两条对角线把它分成了4个小三角形,其中2个小三角形的面积分别是6公顷和7公顷.那么最大的一个三角形的面积是多少公顷?76EDCBA76【巩固】 如图,某公园的外轮廓是四边形ABCD ,被对角线AC 、BD 分成四个部分,△AOB 面积为1平方千米,△BOC 面积为2平方千米,△COD 的面积为3平方千米,公园由陆地面积是6.92平方千米和人工湖组成,求人工湖的面积是多少平方千米?OCDBA【例 2】 如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC的面积;⑵:AG GC ?321GDCBA【巩固】 在△ABC 中DC BD =2:1, EC AE =1:3,求OEOB=? 例题精讲【例 3】 如图相邻两个格点间的距离是1,则图中阴影三角形的面积为 .BA【巩固】 如图,每个小方格的边长都是1,求三角形ABC 的面积.A B【例 4】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGF EDC BA【巩固】 如右上图,已知BO=2DO ,CO=5AO ,阴影部分的面积和是11平方厘米,求四边形ABCD 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
返回
2、合作探索
把两个完全相同的梯形拼成一个平行四边形。
上底 下底
梯形的面积= 平行四边形的面积 梯形的面积 = 底 × 高
÷
2
高 下底 上底
÷ 2 ÷ 2
梯形的面积 =(上底+下底) × 高
返回
2、合作探索
把两个完全相同的梯形拼成一个长方形。
上底 下底
高
说说怎样计算下列图形的面积:
长方形的面积= 长×宽 正方形面积= 边长×边长 平行四边形的面积= 底×高
三角形的面积= 底×高÷2
1、思考方法:怎样求梯形的面积
?
∟
2、合作探究:
1、用两个完全相同的梯形拼拼看,能够 拼成已经学过的什么图形? 2、拼成的图形与梯形有什么关系?
拼
联
拓
继续
2、合作探索
(3) (13+10) ×12.5÷2
(4) (8.5+12.5) ×10÷2
√
10
三、巩固练习、拓展应用:
3. 某水渠的横截面是梯形(如图)渠口宽8米。渠底5米,
渠深1.8米。求它的横截面面积。
(8+5)×1.8÷2 = 13×1.8÷2 = 11.7(平方米) 答:它的横截面是11.7平方米。
三、巩固练习、拓展应用:
5 、 6. 计算下面每个梯形的面积,你发现了什么?(单位:cm)
3
3
3
7
6
6
6
(3+6)×7 ÷2 = 9×7 ÷2 = 31.5(c㎡) 如果几个梯形等底等高,那 么它们的面积一定相等。
这节课你有什么收获?
下底
上底
梯形的面积 =(上底+下底)×高÷2
返回
2、合作探索
把两个完全相同的梯形拼成一个正方形。
上底
下底 梯形的面积 =(上底+下底)×高÷2
高
下底
返回
上底
3、解决问题
制作这个椅子面需要多少平方厘米的木材? (32+36)×32÷2
=68×32÷2
=2176÷2 =1088(平方厘米) 答:制作这个椅子面需要1088平方厘米的木材。
三、巩固练习、拓展应用:
1、计算下面图形的面积。
(17+23)×15÷2 =40×15÷2 =300(m2)
(18+9)×10÷2 :
2、选择正确的列式 13 (1) (13+10)×8.5÷2 (2) (8.5+12.5) ×13÷2 8.5 12.5
